Removal rate constants are not necessarily constant: the case of organic micropollutant removal in wastewater treatment plants

Abstract

The removal of organic micropollutants (OMPs) in wastewater treatment plants (WWTPs) is critical to avoid pollution of the aquatic environment. While it is commonly assumed that removal rates are constant at low concentrations, this assumption remains untested across multiple WWTPs. The aim of this study was to test if removal rate constants of OMPs in activated sludge are indeed constant at low OMP concentrations. To that end, we related removal rate constants of 58 OMPs obtained from 14 WWTPs to influent OMP concentrations by applying linear mixed effect modelling in an all subsets modelling approach, also accounting for WWTP characteristics as well as physicochemical OMP properties. Influent OMP concentration and hydraulic retention time (HRT) were retained as predictors of removal rate constants in all best-supported models (within 2 AIC-units from the best model). The relationship between removal rate constant and concentration varied between OMPs. For most OMPs, the relationship was positive, except for valsartan and 2-hydroxyibuprofen, which may reflect toxic effects at higher concentrations. Our results indicate that the assumption of a constant removal rate at low concentrations is too simplistic and highlight the relevance of considering influent concentration in OMP fate predictions. This in turn may help in optimising OMP removal strategies, for example by concentrating wastewater in WWTPs.

---

Water impact

Our work shows that removal rate constants of organic micropollutants (OMPs) in wastewater treatment plants are not necessarily constant and that influent OMP concentration positively affects the removal of OMPs in most cases. The relationship between concentration and removal rate constants may help improving fate predictions and OMP removal strategies by microorganisms.

1. Introduction

Organic micropollutants (OMPs) comprise a wide array of structurally diverse chemical compounds with different types of use, such as pharmaceuticals, personal care products and pesticides. Although OMPs mostly occur in low concentrations in the environment (nmol L⁻¹ to μmol L⁻¹), they pose ecological and human health risks.^1,2 For example, prevailing environmental concentrations of antidepressants can already affect fish behaviour.¹ The removal of OMPs during wastewater treatment reduces such ecological and human health risks. Optimising the removal of OMPs in wastewater treatment plants (WWTPs) requires a good understanding of removal processes. In general, the fate of OMPs in WWTPs is determined by two main processes: sorption onto activated sludge and biotransformation.³ However, the underlying processes are still poorly understood.

Unravelling removal processes is challenging as they are influenced by a multitude of factors related to both WWTP conditions and physicochemical properties of OMPs.^4–7 A longer sludge retention time (SRT) has, for instance, been shown to enhance removal.^8,9 Other WWTP conditions that might affect OMP removal (both biotransformation and sorption) are pH and temperature. The pH of wastewater is known to influence the speciation state of OMPs (depending on the OMP's acid dissociation constant, pK_a), which might influence both biotransformation and sorption onto sludge flocs.^10,11 For some OMPs, removal increases with increasing temperature.¹² OMP removal in WWTPs has also been linked to more complex physicochemical OMP descriptors.^7,13–16 These descriptors are related to partitioning and geometric and electronic properties, reflecting nucleophilic and electrophilic reactivity of a compound. Only a few studies analysed the influence of both WWTP conditions and physicochemical OMP properties on OMP removal. Examples include the studies of Wang et al. (2020)⁶ and Douziech et al. (2018),⁵ which included 209 and 106 OMPs, respectively. These studies identified partition coefficients (that may affect sorption) and SRT as important variables influencing OMP removal.

Both Wang et al., 2020 and Douziech et al. 2018 focused on removal efficiency (RE). RE, however, does not take the rate of the process into account. When optimising OMP removal at WWTPs, the removal rate is highly important, as higher rates imply a shorter turnaround time hence a larger capacity of the WWTP. In addition, the comparison of REs at WWTPs with different hydraulic retention times (HRT) is problematic, as the duration of exposure of the OMP to activated sludges can affect the total amount removed.^12,17 A standardised approach to account for differences in exposure duration of OMPs to the activated sludge community, as well as differences in influent concentration, is the pseudo first-order reaction rate constant (k, see ESI† S1 for extra information).^7,18,19 Pseudo first-order rate constants rely on assumptions from Michaelis–Menten theory.²⁰ According to Michaelis–Menten theory, the enzyme-catalysed removal rate of OMPs in WWTPs depends on the OMP concentrations. At low concentrations however (< k_m, the substrate concentration at half of the maximum reaction rate), the velocity of the reaction is not limited by enzyme availability, because the enzymes are not saturated. In this case, the reaction rate depends linearly on the substrate concentration and the slope of the curve (which is k) is constant. Hence, according to this theory, k should be independent of OMP concentration and HRT at low OMP concentrations.

The aim of this study was to assess whether k is in fact a pseudo-first order rate constant at low influent OMP concentrations. Our hypothesis, based on Michaelis–Menten theory, is that OMP influent concentration and HRT should not affect k. In order to test this, we followed a linear mixed effect modelling approach relating removal rate constants to influent OMP concentration and HRT, using a monitoring dataset including a large number of OMPs (n = 58) and WWTPs (n = 14). In our regression models, we also accounted for relevant WWTP conditions and physicochemical OMP properties that could affect k as well. We performed a systematic model selection approach (all subsets modelling) to identify the most parsimonious regression models explaining k. If k is indeed a constant, these models should not include influent concentration and HRT as predictors. To our knowledge, this is the first study that systematically examines the relationship between k and WWTP influent OMP concentration and HRT, while correcting for other relevant variables.

2. Materials and methods

2.1 Data

We quantified removal rate constants based on a dataset gathered by Evenblij et al. (2020),²¹ covering 14 WWTPs in the East of the Netherlands. They sampled WWTP influent and effluent in February and July 2018 in a period of dry weather. Three 48 hour composite samples were taken over a period of approximately 10 days. The OMP concentrations were measured with positive ionization liquid chromatography–mass spectrometry.²¹ We excluded influent concentrations that were under the limit of detection (LOD). In case effluent concentrations were under the LOD, we set them to half the threshold concentrations.^5,22 The influent concentrations in the dataset spanned 5 orders of magnitude, from 1.14 × 10⁻⁵ μmol L⁻¹ for fipronil to 4.90 μmol L⁻¹ for acetaminophen. Based on the concentration data, we calculated removal rate constants (k) based on the fraction of OMP removed over time (eqn (1), ESI† S1):

C_e = C_i·e^−k HRT (1)

where k is the removal rate constant (h⁻¹), C_i is the influent OMP concentration (μmol L⁻¹), C_e is the effluent OMP concentration (μmol L⁻¹), and HRT is the hydraulic retention time (in hours). The hydraulic retention time was reported by Evenblij et al. (2020) and varied from 0.6 to 4.2 days. The dataset allowed us to calculate 4330 k values (eqn (1)) across 58 OMPs and 14 WWTPs. Calculated k values ranged from −0.35 h⁻¹ for quetiapine to 0.57 h⁻¹ for acetaminophen (Fig. 1) and were approximately normally distributed (Fig. S2†). The negative removal rates in our dataset (23% of all data points) reflect cases where the effluent concentration was higher than the influent concentration.

Fig. 1 Box plots of OMP-specific removal rate constants k (h⁻¹) ordered by median k-value. The shown boxes span the interquartile range (25–75 percentiles), while whiskers correspond to minimum and maximum values, and horizontal solid line to median values.

From Evenblij et al. (2020), we also retrieved WWTP conditions that were measured at the same time as the OMP concentrations and that were previously shown to influence the removal of OMPs in wastewater (Table 1). Temperature and pH were measured in influent wastewater. Furthermore, sludge retention time (SRT) and flow rate (Q) were reported. When WWTP variables were reported as a range, we determined the midpoint ((max–min)/2) and included this in our dataset. Furthermore, we collected a selection of physicochemical properties of the OMPs based on possible mechanisms that could affect k, as reported in literature and summarised in the introduction (Table 1). We determined the speciation state of the OMPs at pH 7 with Marvin sketch and speciated SMILES strings were generated (https://chemaxon.com/marvin). Subsequently, we calculated the descriptors (mentioned in Table 1) with Chemaxon (https://www.chemaxon.com) and MOPAC2016 (https://openmopac.net) through the OCHEM platform.²³ Molecular structures were optimised with Corina (https://wwww.mol-net.de).

Table 1 Environmental variables and physicochemical OMP properties included in the analysis, including a rationale (with references), and the median and range of each variable in the dataset used in this study (n = 2960)

Variable (abbreviation, unit)	Rationale	Median (min–max)	Data source
Environmental conditions
a https://www.epa.gov/tsca-screening-tools/epi-suitetm-estimation-program-interface. b https://go.drugbank.com/. c https://pubchem.ncbi.nlm.nih.gov/. d https://www.chemaxon.com. e https://openmopac.net.
Sludge retention time (SRT, d)	A higher SRT is expected to increase removal by affecting microbial community species composition and metabolic capacity to biotransform^9,24	23.5 (1.9–87.9)	Evenblij et al. (2020)^21
Influent temperature (Ti, °C)	Increase in temperature might increase OMP removal^25,26	13.5 (5.0–25.1)	Evenblij et al. (2020)^21
Influent pH (pH, dimensionless)	pH affects speciation state of the OMP and could therefore influence OMP availability and sorption^10,27	7.7 (7.4–8.8)	Evenblij et al. (2020)^21
Flow rate (Q, m^3)	Flow rate is related to the size of the plant and number of people connected, which affects OMP load^5	7963 (671–51 255)	Evenblij et al. (2020)^21

---

Physicochemical properties
Water solubility (S, mg L^−1)	Increased solubility influences OMP availability and sorption^5,6,15,16	31.14 (2.8 × 10^−4–1.0 × 10^6)	EPISuite^a
Octanol water partition coefficient (log Kow, dimensionless)	Increased Kow increases sorption^15,16	0.75 (−4.1–6.1)	Drugbank,^b Pubchem^c
Strongest acidic pKa (pKa, dimensionless)	Influences OMP availability and reactivity^15,16	4.85 (−3.3–16.1)	Chemaxon^d
Strongest basic pKb (pKb, dimensionless)	Influences OMP availability and models reactivity^15	0 (−7.7–12.3)	Chemaxon^d
van der Waals' surface area, calculated at pH 7.4 (A, Å^2)	Influences binding characteristics and other processes sensitive to steric interactions^15	420.7 (157.4–1199.0)	Chemaxon^d
Hydrogen bond donor, calculated at pH 7.4 (HBD, dimensionless)	Influences electrostatic interactions between molecules that determine chemical reactivity and/or binding interactions^15,28	1 (0–7)	Chemaxon^d
Hydrogen bond acceptor, calculated at pH 7.4 (HBA, dimensionless)	Influences electrostatic interactions between molecules that determine chemical reactivity and/or binding interactions^15,28	4 (1–14)	Chemaxon^d
Dipole moment (v, Debye)	Charge separation in OMPs may influence binding characteristics, interaction with the cell membrane, and/or bioavailability^15,16,28	10.7 (0.5–42.4)	MOPAC^e
Energy of the highest occupied molecular orbital (EHOMO, eV)	Influences nucleophilic and electrophilic reactivity of a compound, indicates ability to donate protons easily^15,16,28,29	−9.1 (−3.3–−3.8)	MOPAC^e
Energy of the lowest occupied molecular orbital (ELUMO, eV)	Influences nucleophilic and electrophilic reactivity of a compound, indicates ability to donate protons easily and may influence sorption and biotransformation.^15,16,28,29	−0.6 (−5.1–4.8)	MOPAC^e
E LUMO − EHOMO (ΔEL–H, eV)	Influences nucleophilic and electrophilic reactivity of a compound and indicates an OMPs stability^15,28	8.1 (4.9–11.7)	MOPAC^e
Final heat of formation (Hf, kcal mol^−1)	Enthalpy of formation of the products affects reactivity^28	−96.2 (−891.8–209.6)	MOPAC^e

---

2.2 Modelling

To assess if and how k is related to influent OMP concentration and HRT, we adopted a linear mixed effect (LME) modelling approach accounting for other variables that may affect k (Table 1).³⁰ Prior to model fitting, we removed incomplete records (i.e., 1370 observations with a missing value for at least one of the included environmental variables or physicochemical OMP properties), leaving 2960 observations for the modelling. We further assessed the skewness of all potentially explanatory variables (Table 1). As a threshold, we considered a skewness of −1 or +1.³¹ If the skewness exceeded the threshold, we used the log-transformed variable in case this sufficiently reduced skewness. When a variable also included negative numbers, we cube root-transformed it. In order to handle collinearity and prevent difficulty in separating out the independent contribution of variables to explained variance, we conducted a stepwise variance inflation factor (VIF) analysis on all possible fixed effect variables (i.e., the OMP influent concentration C_i, HRT and the moderators included in Table 1). A high VIF value indicates a high collinearity with another variable or a combination of variables. During each step, we discarded the variable with the highest VIF value until all variables had a VIF value below 3.³² This resulted in the removal of the energy of the highest occupied molecular orbital (E_HOMO), van der Waals' surface area (A), strongest basic pK_b, hydrogen bond donor (HBD) and water solubility (S) (Table S1†). After excluding these variables, 12 variables remained for the model fitting (Table S1†). Next, we scaled all remaining variables to zero-mean and unit-variance to prevent non-convergence issues in the modelling.

We tested the optimal random effect structure based on a model including all possible fixed effect variables, following recommendations by Zuur et al. (2009).³³ We included OMP and WWTP as a random effect to account for non-independence of observations and to include the variation caused by unknown OMP properties and WWTP conditions that can affect k and were not included in our model, such as possible variation caused by different microbial communities in the 14 WWTPs. We tested two random effect structures: 1) crossed random intercepts for OMP and for WWTP, to account for non-independence of observations of the same chemical or from the same WWTP; and 2) a random intercept for WWTP and a random slope for OMP influent concentration, the latter to allow the relationship between k and influent concentration to vary between OMPs. We fitted the models with restricted maximum likelihood and subsequently selected the best random effect structure based on Akaike's information criterion (AIC).²³ Next, we performed model selection on the fixed effects by adopting an all-subsets modelling approach,²⁴ testing all possible combinations of fixed effect variables, while keeping the best-supported random effect structure, which included a random intercept for WWTP, and a random slope for influent concentration per OMP. Thus, we used the following full-model structure as a basis for the fixed effects selection (eqn (2)):

k = log C_i + HRT + log k_ow + pK_a + log HBA + v + E_LUMO + ΔE_L–H + H_f + log SRT + log Q + T_i + pH + (log C_i|OMP) + (1|WWTP) (2)

We identified the best-supported model based on AIC, using the maximum likelihood, and refitted it based on restricted maximum likelihood for coefficient estimation.³³ Further, we assessed the importance of the variables in the models within 2 AIC units from the best-supported model (ΔAIC < 2), based on Akaike weights.²⁵ The variable importance is based on both the prevalence of a variable in the top set of models (ΔAIC < 2) and the AIC weights of these models and is a measure between 0 and 1, where 0 indicates that the variable is included in none of the fitted models, while 1 means a variable is included in all fitted models.

We performed all data analyses in the R environment (R version 4.3.0).²⁶ To calculate the skewness of all variables we used the moments package²⁷ and for the VIF analysis we used the USDM package.²⁸ For the LME full model construction we used lme4 (ref. 30) and to test all possible model combinations we used the MuMIn package,²⁴ specifically the function “dredge”. We used MuMIn also to calculate marginal and conditional R² values. We made graphs with the packages ggplot2, ggeffects, sjPlot and forcats.

3. Results and discussion

3.1 Best supported model

The best-supported model (lowest AIC) describing the removal rate constant k included the scaled influent OMP concentration (log C_i) and hydraulic retention time (HRT) as follows (eqn (3)):

k = 0.035 + 0.045 log C_i − 0.017HRT + (log C_i|OMP) + (1|WWTP) (3)

Confidence intervals for fitted coefficients are shown in Table 2. Residual plots of the final model showed no indication of nonlinearity or heteroscedasticity (Fig. S3 and S4†). The fixed and random effects together explained 68% of the variation in k according to the conditional R². The two fixed effect variables (HRT and log C_i) explained 27% of the variation in k in our dataset, judged from the marginal R², while the random effects explained 41% of the variation in k.

Table 2 Confidence intervals of intercept and coefficients of the best supported model with the lowest AIC

	Estimate	2.5%	97.5%
Intercept	0.035	0.020	0.050
Coefficient log Ci	0.045	0.034	0.055
Coefficient HRT	−0.017	−0.023	−0.010

---

The best-supported model indicates that influent OMP concentration has the largest influence on k, judged from the fitted standardized coefficients, followed by the HRT (Fig. 2). In general, we found a positive relationship between OMP concentration and k, i.e. with an increase in OMP concentration, there was an increase in k (eqn (3), Fig. 2). The relationship between k and HRT was negative, i.e. with an increase in HRT there was a decrease in k (Fig. 2).

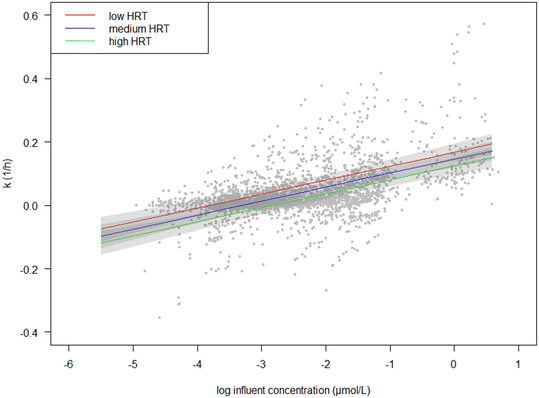Fig. 2 Estimated marginal effect of log C_i (μmol L⁻¹) on the predicted k (h⁻¹) in the best-supported model (lowest AIC; eqn (3)). HRT was held constant at low, medium and high values (5, 50 and 95% percentiles, corresponding with 0.6, 1.7 and 2.7 hours, respectively) to show the effect of HRT on the marginal effect of log C_i.

3.2 Influent OMP concentration and k

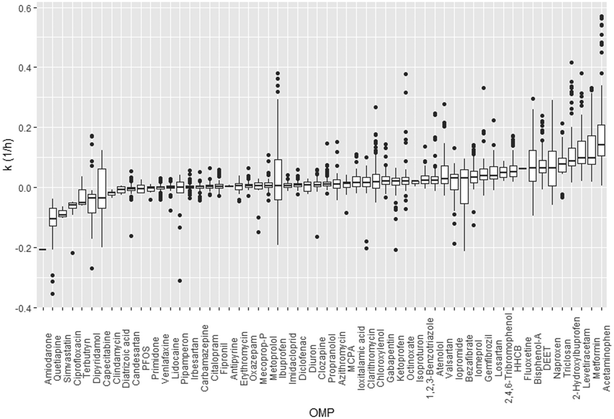
For most OMPs (n = 56) we found a positive relationship between k and influent OMP concentration, with varying slope coefficients depending on the OMP (0.01–0.15, Fig. 3, Table S2†). Positive relationships may reflect adaptation of the microbial community to previous OMP exposure, resulting in a higher activity. Adaptation may include changes in microbial community composition, phenotypic adaptation by individual microorganisms (e.g. enhanced gene transcription due to induction processes), or genetic adaptation by individual cells via mutations, horizontal gene transfer or recombination events.^4,29,34 When influent OMP concentrations are low, adaptation might not take place. Instead, other processes could affect the removal at low concentrations, such as limited mass transfer and a lack of gene induction. For a few OMPs, i.e. atrazine, 2-methyl naphthalene and toluene, several studies showed that a slow mass transfer across the cell membrane was responsible for slow biotransformation rates.^35–38 For OMPs 3-phenyl propionic acid (3-PPA) and sulfamethoxazole, threshold concentrations for the induction of genes were found that likely prevented the removal of OMPs at low concentrations.^39,40 In line with our results, a recent study by Rich and Helbling (2023) indicated that for specific OMPs (propranolol, clindamycin, lidocaine and gemfibrozil) influent concentrations in a single WWTP are an important factor in controlling microbial community activity.⁴¹ For other OMPs (n = 112), Rich and Helbling (2023) did not identify influent OMP concentration as a driver for microbial activity. The difference with our study is that we included multiple WWTPs (n = 14), with likely different adapted microbial communities that could cause a positive relationship between influent OMP concentration and k. For several OMPs (ibuprofen, diclofenac, carbamazepine, fluoxetine, citalopram, erythromycin, atenolol, iomeprol, iopromide, bezafibrate), we found positive correlations of influent OMP concentration and k, while previous studies found negative correlations (Table S3† and references therein). These differences might be explained by the time microorganisms had to adapt to increased OMP exposure and the concentrations used in the experiments. When performing bioreactor or bottle incubations in a limited amount of time, increased OMP exposure likely leads to short-term adaptation processes (e.g. microbial community changes and phenotypic adaptation), opposed to WWTPS where microorganisms have longer adaptation periods.⁴²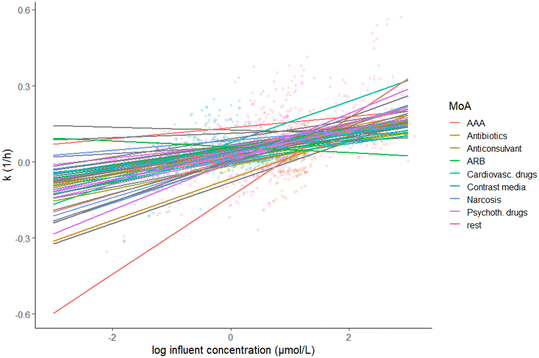

Fig. 3 The relationship between k (h⁻¹) and standardised log influent OMP concentration (μmol L⁻¹) per OMP, given a mean value for HRT across the observations. Confidence intervals are not shown for readability. OMPs are classified according to their mode of action (MoA) (Table S2,† according to Posthuma et al. (2019)⁴³ supplemented with other literature). Abbreviations: AAA = analgesics, anti-inflammatory drugs and antipyretics; ARB = angiotensin II receptor blocker, Cardiovasc. drugs = cardiovascular drugs; Psychoth. drugs = psychotherapeutic drugs, “rest” includes OMPs for which no MoA was available and OMPs with MoAs that were less frequent in our dataset (n < 3). See Fig. S9† for values of deviations from main model intercept and concentration slope per OMP.

For 2-hydroxyibuprofen and valsartan we found a negative relationship between influent concentration and k. Helbling et al. (2012) showed that biotransformation of valsartan by activated sludge may take place via cometabolism,⁴⁴ which could explain a lack of a concentration effect. A decrease in k with increasing OMP concentration could also be an indication that the OMP is toxic, as enzyme availability is likely not an issue for OMPs in such low concentrations (C < k_m, ESI† S1). When an OMP is toxic to an organism this leads to a reduction of metabolic activities of a cell,⁴⁵ including biotransformation. Interestingly, while we found a negative relationship with concentration for 2-hydroxyibuprofen (−0.01), we found the strongest positive relationship for its parent compound ibuprofen (0.15). This indicates that 2-hydroxyibuprofen might be more toxic than ibuprofen. We did not find evidence of toxic effects of valsartan and 2-hydroxyibuprofen on activated sludge biotransformation in literature. Further research efforts should investigate this. A negative relationship between k and influent OMP concentration has been reported for antibiotics (e.g. trimetoprim or sulfametoxazole) in previous studies.^6,46 However, for the antibiotics in our dataset (azithromycin, ciprofloxacin, clarithromycin, clindamycin, erythromycin) we found positive relationships between k and influent OMP concentration. The antibiotics occurred in very low concentrations (<2 μg L⁻¹) in our study. Other studies that included antibiotics (Table S3†) studied much higher concentrations (up to 10⁵ μg L⁻¹) and did find negative relationships between removal rate and concentration.⁴⁶ It seems that the concentrations of antibiotics included in this study either did not lead to toxic effects yet or some species are resistant to the toxic effects.

3.3 Hydraulic retention time

Next to influent OMP concentration, hydraulic retention time was included as a fixed effect in the best-supported model (eqn (3)). With increasing HRT, k decreased. Previous studies have shown that the HRT of OMPs may enhance the RE of specific OMPs such as metformin, carbamazepine, hydrochlorothiazide and sotalol.^12,17 It is hypothesized that this is caused by a longer exposure of the OMP to the microorganisms.⁴⁷ However, a negative relationship between k and HRT was unexpected, as the removal rate is assumed independent of HRT (ESI† S1). Possibly, a larger HRT might favour back-transformation, which can increase OMP concentrations again and result in a lower k.⁴⁸ Back-transformation could be responsible for the large amount of calculated negative k values (23%). This indicates that back-transformation of metabolites into parent compounds might be an important and overlooked process in WWTPs that contributes to the formation of OMPs.

3.4 Other variables affecting k

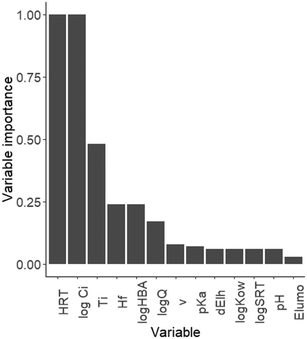
Our results revealed that both HRT and influent OMP concentration (log C_i) were the most influential parameters explaining variability in k, while other WWTP conditions and physicochemical OMP properties had much less explanatory power (Fig. 4, Table S4†). We found 25 models within 2 AIC units from the lowest AIC value (Table S4†). The variable importance analysis showed that HRT and log influent OMP concentration were consistently selected in each of the 25 models (variable importance of 1.00, Fig. 4). This increases confidence in our conclusion that k is dependent on influent OMP concentration and HRT and that the assumption of k being a constant at low influent concentrations, based on Michaelis–Menten theory, can be rejected.

Fig. 4 Importance of variables that were included in models within 2 AIC units from the best-supported model, based on Akaike weights and prevalence. Abbreviations: HRT = hydraulic retention time, C_i = influent OMP concentration, SRT = sludge retention time, T_i = influent temperature, H_f = final heat of formation, HBA = hydrogen bond acceptor, pK_a = strongest acidic pK_a, v = dipole moment, d_Elh = HOMO LUMO energy gap, E_LUMO = energy of the lowest occupied molecular orbital, K_ow = octanol–water partition coefficient, Q = flow rate.

Opposed to other studies, physicochemical properties were not included in the best-supported model (eqn (3)) and only considered of minor importance in all models within 2 AIC units from the best-supported model. Hydrogen bond acceptor and final heat of formation had a variable importance of 0.24 (ΔAIC < 2; Fig. 4) and could affect OMP reactivity and likely influence biotransformation.^15,49 The main difference between our study and other studies that related OMP removal to physico-chemical properties,^7,13,14 is that we included multiple k values per OMP, instead of a single average value. This results in a larger variability in k, hence less explanatory power of physico-chemical OMP properties, which are fixed per OMP.

In addition, WWTP variables other than HRT were not included in our best-supported model and only temperature was considered moderately important in all models (within 2 AIC units from the best-supported model), with a variable importance of 0.5 (Fig. 4). Although our analysis indicates temperature is quite important, the slope coefficient and thus effect on k, is relatively small (<0.002; Table S4†). The positive relationship between removal rate and temperature is in line with the findings of multiple previous studies reporting that temperature affects the removal of OMPs (e.g. atenolol, ketoprofen, carbamazepine and sotalol).^{12,42,50–52} Flow rate (log Q) was of minor importance in our top set of models, with a variable importance of 0.17, and has been correlated to RE previously.⁵

The remaining variables that we tested (eqn (2), Table 1) were considered of low importance, with a variable importance below 0.08, and were only included once or twice and in models that were less supported by the data (i.e., with a higher AIC). We hypothesize that instead of physicochemical properties and WWTP variables, microorganism activity is responsible for variability in k. In our best-supported model, the random intercepts for WWTP showed that 3 out of 14 WWTPs included in our dataset show a higher OMP removal, with a deviation from the intercept (0.035) of 0.02 (Nijkerk and Heino) and 0.03 (Beilen; Fig. S6†). This could reflect differences in microbial community composition, which are also driven by substrates such as organic carbon and nutrients.⁵³ Microorganisms that grow well on higher organic carbon and nutrient inputs, could also cometabolise more OMPs.⁵⁴

4. Conclusions and implications

Our findings show that Michaelis–Menten theory has limitations for calculating k in activated sludge WWTP systems, as we found that k is not constant, but instead depends by OMP concentration and HRT. We hypothesize that microorganism activity, which was not included in this study, is responsible for this variability in k. Identification of microbial species and genes responsible for biotransformation, as well as disentangling processes such as biotransformation and sorption, may help in explaining variability in k. However, given the complexity to quantify and disentangle microbial activity parameters, influent concentration could serve as a proxy for adaptation mechanisms, and the relationship between k and concentration has the potential to improve fate predictions of OMPs in activated sludge WWTPs. For that purpose, we recommend further model development, based on more observations from a wider range of OMPs and WWTPs, as well as validation based on independent data. The increase in k with increasing concentration, as we found for the majority of the OMPs investigated, indicates that the removal of OMPs in activated sludge WWTPs could be optimized by increasing OMP concentrations in influent or in side streams of the WWTP. Concentrating OMPs in influent could be achieved by decoupling rain water from sewers or by treating wastewater decentralized at specific sources such as hospitals, which contain higher concentrations of antibiotics and contrast media.^55,56 Concentrating OMPs in side streams could be achieved by first treating wastewater with chemical or mechanical methods (adsorbents or membranes) and secondly treating it with microorganisms, such as microbial-assisted adsorbent regeneration for example.^57,58 Chemical and mechanical methods (e.g. adsorbents, UV, ozone, membranes) can achieve a higher removal of OMPs in WWTPs, however these methods can also lead to environmental burden shifts as they require electricity and resources leading to global warming, eutrophication and acidification.^59,60 Activated sludge wastewater treatment requires less energy and resources, and leads to lower environmental impacts. By combining chemical or mechanical methods with (biological) activated sludge, OMP removal can be optimized while environmental burden shifts are minimized.

Data availability statement

Data for this paper, including all variables in Table 1, are available at DANSEASY at https://doi.org/10.17026/dans-zh3-evwu. The R script used for data analysis is available upon request.

Author contributions

MH, RvZ, AS and TvB conceptualised the study, TvB and DM curated data, TvB and AS analysed the data, TvB made visualisations, TvB and AS wrote the article, all authors contributed to reviewing and editing of the article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was supported by the NWO-domain TTW [Grant number 15759], The Netherlands. The authors would like to thank Juan Gallego-Zamorano, Selwyn Hoeks, Jelle Hilbers and Melina de Jonge for advice on modelling and programming. Furthermore, we would like to thank Jiaqi Wang for her help with determining speciation states of OMPs.

References

1. S. L. Gould, M. J. Winter, W. H. Norton and C. R. Tyler, The potential for adverse effects in fish exposed to antidepressants in the aquatic environment, Environ. Sci. Technol., 2021, 55(24), 16299–16312.
2. D. J. Duarte, R. Oldenkamp and A. M. Ragas, Modelling environmental antibiotic-resistance gene abundance: A meta-analysis, Sci. Total Environ., 2019, 659, 335–341.
3. M. Pomies, J.-M. Choubert, C. Wisniewski and M. Coquery, Modelling of micropollutant removal in biological wastewater treatments: a review, Sci. Total Environ., 2013, 443, 733–748.
4. A. B. Rios-Miguel, T. J. van Bergen, C. Zillien, A. M. Ragas, R. van Zelm, M. S. Jetten, A. J. Hendriks and C. U. Welte, Predicting and improving the microbial removal of organic micropollutants during wastewater treatment: A review, Chemosphere, 2023, 138908.
5. M. Douziech, I. R. Conesa, A. Benítez-López, A. Franco, M. Huijbregts and R. van Zelm, Quantifying variability in removal efficiencies of chemicals in activated sludge wastewater treatment plants–a meta-analytical approach, Environ. Sci.: Processes Impacts, 2018, 20(1), 171–182.
6. Y. Wang, K. Fenner and D. E. Helbling, Clustering micropollutants based on initial biotransformations for improved prediction of micropollutant removal during conventional activated sludge treatment, Environ. Sci.: Water Res. Technol., 2020, 6(3), 554–565.
7. T. M. Nolte, G. Chen, C. S. van Schayk, K. Pinto-Gil, A. J. Hendriks, W. J. Peijnenburg and A. M. Ragas, Disentanglement of the chemical, physical, and biological processes aids the development of quantitative structure-biodegradation relationships for aerobic wastewater treatment, Sci. Total Environ., 2020, 708, 133863.
8. B. G. Plósz, K. H. Langford and K. V. Thomas, An activated sludge modeling framework for xenobiotic trace chemicals (ASM-X): Assessment of diclofenac and carbamazepine, Biotechnol. Bioeng., 2012, 109(11), 2757–2769.
9. S. Achermann, P. Falås, A. Joss, C. B. Mansfeldt, Y. Men, B. Vogler and K. Fenner, Trends in Micropollutant Biotransformation along a Solids Retention Time Gradient, Environ. Sci. Technol., 2018, 52(20), 11601–11611.
10. T. Urase, C. Kagawa and T. Kikuta, Factors affecting removal of pharmaceutical substances and estrogens in membrane separation bioreactors, Desalination, 2005, 178(1–3), 107–113.
11. L. J. Carter, J. L. Wilkinson and A. B. Boxall, Evaluation of existing models to estimate sorption coefficients for ionisable pharmaceuticals in soils and sludge, Toxics, 2020, 8(1), 13.
12. M. Oosterhuis, F. Sacher and T. L. Ter Laak, Prediction of concentration levels of metformin and other high consumption pharmaceuticals in wastewater and regional surface water based on sales data, Sci. Total Environ., 2013, 442, 380–388.
13. K. Acharya, D. Werner, J. Dolfing, M. Barycki, P. Meynet, W. Mrozik, O. Komolafe, T. Puzyn and R. J. Davenport, A quantitative structure-biodegradation relationship (QSBR) approach to predict biodegradation rates of aromatic chemicals, Water Res., 2019, 157, 181–190.
14. K. Mansouri, T. Ringsted, D. Ballabio, R. Todeschini and V. Consonni, Quantitative structure–activity relationship models for ready biodegradability of chemicals, J. Chem. Inf. Model., 2013, 53(4), 867–878.
15. E. Zvinavashe, A. J. Murk and I. M. Rietjens, Promises and pitfalls of Quantitative Structure− Activity Relationship approaches for predicting metabolism and toxicity, Chem. Res. Toxicol., 2008, 21(12), 2229–2236.
16. L. Mamy, D. Patureau, E. Barriuso, C. Bedos, F. Bessac, X. Louchart, F. Martin-Laurent, C. Miege and P. Benoit, Prediction of the fate of organic compounds in the environment from their molecular properties: a review, Crit. Rev. Environ. Sci. Technol., 2015, 45(12), 1277–1377.
17. A. B. Rios-Miguel, M. S. M. Jetten and C. U. Welte, Effect of concentration and hydraulic reaction time on the removal of pharmaceutical compounds in a membrane bioreactor inoculated with activated sludge, Microb. Biotechnol., 2021, 14(4), 1707–1721.
18. H. Birch, K. K. Sjøholm, A. Dechesne, C. Sparham, R. van Egmond and P. Mayer, Biodegradation Kinetics of Fragrances, Plasticizers, UV Filters, and PAHs in a Mixture–Changing Test Concentrations over 5 Orders of Magnitude, Environ. Sci. Technol., 2021, 56(1), 293–301.
19. S. B. Svendsen, H. El-Taliawy, P. N. Carvalho and K. Bester, Concentration dependent degradation of pharmaceuticals in WWTP effluent by biofilm reactors, Water Res., 2020, 186, 116389.
20. R. Schwarzenbach, P. Gschwend and D. Imboden, in Environmental Organic Chemistry, Wiley, USA, 2005, pp. 387–458.
21. H. Evenblij, E. Schuman and M. Kuiper, Verwijderingsrendementen van medicijnresten op 18 RWZI's, Water Matters, 2020, 10, 28–31.
22. E. Sinclair and K. Kannan, Mass loading and fate of perfluoroalkyl surfactants in wastewater treatment plants, Environ. Sci. Technol., 2006, 40(5), 1408–1414.
23. H. Akaike, B. N. Petrov and F. Csaki, Second International Symposium on Information Theory, Akademia Kiado, 1973.
24. K. Barton, MuMIn: Multi-Model Inference, https://r-forge.r-project.org/projects/mumin/, 2009.
25. K. P. Burnham and D. R. Anderson, A practical information-theoretic approach, in Model Selection and Multimodel Inference, 2004, vol. 2.
26. RCoreTeam, R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria, 2023.
27. J. Karvanen, Estimation of quantile mixtures via L-moments and trimmed L-moments, Comput. Stat. Data Anal., 2006, 51(2), 947–959.
28. B. Naimi, N. A. Hamm, T. A. Groen, A. K. Skidmore and A. G. Toxopeus, Where is positional uncertainty a problem for species distribution modelling?, Ecography, 2014, 37(2), 191–203.
29. B. A. Poursat, R. J. van Spanning, P. de Voogt and J. R. Parsons, Implications of microbial adaptation for the assessment of environmental persistence of chemicals, Crit. Rev. Environ. Sci. Technol., 2019, 49(23), 2220–2255.
30. D. Bates, M. Maechler, B. Bolker, S. Walker, R. H. B. Christensen, H. Singmann, B. Dai, G. Grothendieck, P. Green and M. B. Bolker, Package ‘lme4’, Convergence, 2015, 12(1), 2.
31. J. F. Hair, W. C. Black, B. J. Babin, R. E. Anderson and R. L. Tatham, in Multivariate data analysis, Pearson Prentice Hall, New Jersey, humans: Critique and reformulation…, 6th edn, 2006.
32. R. Johnston, K. Jones and D. Manley, Confounding and collinearity in regression analysis: a cautionary tale and an alternative procedure, illustrated by studies of British voting behaviour, Quality Quant., 2018, 52, 1957–1976.
33. A. F. Zuur, E. N. Ieno, N. J. Walker, A. A. Saveliev and G. M. Smith, Mixed effects models and extensions in ecology with R, Springer, 2009, vol. 574.
34. A. B. Rios Miguel, M. S. M. Jetten and C. U. Welte, The role of mobile genetic elements in organic micropollutant degradation during biological wastewater treatment, Water Res.: X, 2020, 9, 100065.
35. B. N. Ehrl, M. Gharasoo and M. Elsner, Isotope Fractionation Pinpoints Membrane Permeability as a Barrier to Atrazine Biodegradation in Gram-negative Polaromonas sp. Nea-C, Environ. Sci. Technol., 2018, 52(7), 4137–4144.
36. K. Kundu, S. Marozava, B. Ehrl, J. Merl-Pham, C. Griebler and M. Elsner, Defining lower limits of biodegradation: atrazine degradation regulated by mass transfer and maintenance demand in Arthrobacter aurescens TC1, ISME J., 2019, 13(9), 2236–2251.
37. M. Kampara, M. Thullner, H. H. Richnow, H. Harms and L. Y. Wick, Impact of Bioavailability Restrictions on Microbially Induced Stable Isotope Fractionation. 2. Experimental Evidence, Environ. Sci. Technol., 2008, 42(17), 6552–6558.
38. S. Marozava, A. H. Meyer, A. Pérez-de-Mora, M. Gharasoo, L. Zhuo, H. Wang, O. A. Cirpka, R. U. Meckenstock and M. Elsner, Mass Transfer Limitation during Slow Anaerobic Biodegradation of 2-Methylnaphthalene, Environ. Sci. Technol., 2019, 53(16), 9481–9490.
39. K. Kovar, V. Chaloupka and T. Egli, A Threshold Substrate Concentration Is Required to Initiate the Degradation of 3-Phenylpropionic Acid in Escherichia coli, Acta Biotechnol., 2002, 22(3–4), 285–298.
40. R. Yan, Y. Wang, J. Li, X. Wang and Y. Wang, Determination of the lower limits of antibiotic biodegradation and the fate of antibiotic resistant genes in activated sludge: Both nitrifying bacteria and heterotrophic bacteria matter, J. Hazard. Mater., 2022, 425, 127764.
41. S. L. Rich and D. E. Helbling, Daily Monitoring at a Full-Scale Wastewater Treatment Plant Reveals Temporally Variable Micropollutant Biotransformations, Environ. Sci. Technol., 2023, 57(28), 10404–10414.
42. P. Meynet, R. J. Davenport and K. Fenner, Understanding the dependence of micropollutant biotransformation rates on short-term temperature shifts, Environ. Sci. Technol., 2020, 54(19), 12214–12225.
43. L. Posthuma, J. van Gils, M. C. Zijp, D. van De Meent and D. de Zwart, Species sensitivity distributions for use in environmental protection, assessment, and management of aquatic ecosystems for 12 386 chemicals, Environ. Toxicol. Chem., 2019, 38(4), 905–917.
44. D. E. Helbling, D. R. Johnson, M. Honti and K. Fenner, Micropollutant biotransformation kinetics associate with WWTP process parameters and microbial community characteristics, Environ. Sci. Technol., 2012, 46(19), 10579–10588.
45. V. H. Edwards, The influence of high substrate concentrations on microbial kinetics, Biotechnol. Bioeng., 1970, 12(5), 679–712.
46. Z. Wei, W. Li, D. Zhao, Y. Seo, R. Spinney, D. D. Dionysiou, Y. Wang, W. Zeng and R. Xiao, Electrophilicity index as a critical indicator for the biodegradation of the pharmaceuticals in aerobic activated sludge processes, Water Res., 2019, 160, 10–17.
47. E. Fernandez-Fontaina, F. Omil, J. M. Lema and M. Carballa, Influence of nitrifying conditions on the biodegradation and sorption of emerging micropollutants, Water Res., 2012, 46(16), 5434–5444.
48. L. Gonzalez-Gil, M. Carballa, P. F. Corvini and J. M. Lema, Reversibility of enzymatic reactions might limit biotransformation of organic micropollutants, Sci. Total Environ., 2019, 665, 574–578.
49. A. Pirovano, M. A. Huijbregts, A. M. Ragas, K. Veltman and A. J. Hendriks, Mechanistically-based QSARs to describe metabolic constants in mammals, ATLA, Altern. Lab. Anim., 2014, 42(1), 59–69.
50. S. Kahl, S. Kleinsteuber, J. Nivala, M. van Afferden and T. Reemtsma, Emerging Biodegradation of the Previously Persistent Artificial Sweetener Acesulfame in Biological Wastewater Treatment, Environ. Sci. Technol., 2018, 52(5), 2717–2725.
51. T. E. Ten Hulscher and G. Cornelissen, Effect of temperature on sorption equilibrium and sorption kinetics of organic micropollutants-a review, Chemosphere, 1996, 32(4), 609–626.
52. P. Ramin, F. Polesel, A. L. Brock and B. G. Plósz, The impact of temperature on the transformation of illicit drug biomarkers in wastewater, Sci. Total Environ., 2018, 644, 1612–1616.
53. L. Wu, D. Ning, B. Zhang, Y. Li, P. Zhang, X. Shan, Q. Zhang, M. R. Brown, Z. Li and J. D. Van Nostrand, Global diversity and biogeography of bacterial communities in wastewater treatment plants, Nat. Microbiol., 2019, 4(7), 1183–1195.
54. D. M. Kennes-Veiga, L. Gónzalez-Gil, M. Carballa and J. M. Lema, Enzymatic cometabolic biotransformation of organic micropollutants in wastewater treatment plants: A review, Bioresour. Technol., 2022, 344, 126291.
55. A. Mendoza, J. Aceña, S. Pérez, M. L. De Alda, D. Barceló, A. Gil and Y. Valcárcel, Pharmaceuticals and iodinated contrast media in a hospital wastewater: a case study to analyse their presence and characterise their environmental risk and hazard, Environ. Res., 2015, 140, 225–241.
56. G. K. Paulus, L. M. Hornstra, N. Alygizakis, J. Slobodnik, N. Thomaidis and G. Medema, The impact of on-site hospital wastewater treatment on the downstream communal wastewater system in terms of antibiotics and antibiotic resistance genes, Int. J. Hyg. Environ. Health, 2019, 222(4), 635–644.
57. M. Fu, J. Wang, B. Heijman and J. P. van der Hoek, Removal of organic micropollutants by well-tailored granular zeolites and subsequent ozone-based regeneration, J. Water Process Eng., 2021, 44, 102403.
58. A. Melo-Guimarães, F. J. Torner-Morales, J. C. Durán-Álvarez and B. E. Jiménez-Cisneros, Removal and fate of emerging contaminants combining biological, flocculation and membrane treatments, Water Sci. Technol., 2013, 67(4), 877–885.
59. S. M. Rahman, M. J. Eckelman, A. Onnis-Hayden and A. Z. Gu, Comparative life cycle assessment of advanced wastewater treatment processes for removal of chemicals of emerging concern, Environ. Sci. Technol., 2018, 52(19), 11346–11358.
60. H. Wenzel, H. F. Larsen, J. Clauson-Kaas, L. Høibye and B. N. Jacobsen, Weighing environmental advantages and disadvantages of advanced wastewater treatment of micro-pollutants using environmental life cycle assessment, Water Sci. Technol., 2008, 57(1), 27–32.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ew00377b

---