Open Access Article
Open Access ArticleSolid–liquid separation of lignocellulosic sugars from biomass by rotating ceramic disc filtration†
Patrick O.
Saboe‡
 a,
Yudong
Li
a,
Yudong
Li
 b,
Emily G.
Tomashek‡
b,
Emily G.
Tomashek‡
 c,
Eric C. D.
Tan
c,
Eric C. D.
Tan
 b,
Xiaowen
Chen
b,
Louis A.
Chirban
c,
Yian
Chen
c,
Daniel J.
Schell
b,
Eric M.
Karp§
c and
Gregg T.
Beckham
b,
Xiaowen
Chen
b,
Louis A.
Chirban
c,
Yian
Chen
c,
Daniel J.
Schell
b,
Eric M.
Karp§
c and
Gregg T.
Beckham
 *c
*c
aStrategic Energy Analysis Center, National Renewable Energy Laboratory, Golden, CO 80401, USA
bCatalytic Carbon Transformation and Scale-up Center, National Renewable Energy Laboratory, Golden, CO 80401, USA
cRenewable Resources and Enabling Sciences Center, National Renewable Energy Laboratory, Golden, CO 80401, USA. E-mail: gregg.beckham@nrel.gov
First published on 25th October 2024
Abstract
In many biomass conversion processes, the separation of cellulosic sugars from residual, lignin-rich solids is a critical step, and achieving high recovery yields of sugars by conventional tangential crossflow and vacuum filtration is challenged by the presence of biomass solids, which rapidly foul filters, resulting in decreased throughput. Considering the performance limitations of traditional filtration methods, dynamic filtration, which generates high shear at the membrane surface to decrease fouling, is emerging as a viable alternative for demanding solid–liquid separations. For high solids separations, there is little available information regarding the performance, limitations, and energy consumption of dynamic filtration. To that end, here we characterized the performance of a dynamic filtration module, specifically a rotating ceramic disc (RCD) filter, for the aseptic recovery of cellulosic sugars from biomass solids following pretreatment and enzymatic hydrolysis. We show how RCD rotational velocity and percent biomass solids impact the filter throughput. Additionally, we used computational fluid dynamics (CFD) simulations to estimate the shear rate at the membrane surface and to visualize hydrodynamic profiles within the module. With the combined CFD simulations and experimental results, we estimated the energy demand and operating expenses for a viable dynamic filtration system operating with a lignocellulosic feed slurry. Our results indicate that an RCD filter can achieve ≥95% recovery of sugars and produce a retentate slurry containing 12 wt% insoluble solids with low energy consumption (a 2.2-fold improvement over cross-flow filtration) and low operating costs ($0.06 per kg sugars). These results show a viable path towards operationally reliable, energy efficient, and cost-effective separations of sterilized cellulosic sugars from biomass solids and highlight the potential of dynamic filtration systems for challenging solid–liquid separations.
Introduction
The production of cellulosic sugars from lignocellulosic biomass commonly proceeds through a variety of saccharification pathways that generate soluble carbohydrates in the presence of biomass solids, which typically comprise residual lignin and unreacted polysaccharides.1–7 Many subsequent pathways for the conversion of the resulting cellulosic sugars to biofuels or biochemicals rely on biological or catalytic transformations that mandate a solid–liquid separation (SLS) step, which for biological transformations also requires strict sterility, typically down to 0.2 μm filtration to remove whole cells. However, lignocellulosic slurries are challenging to clarify because of the high moisture content and slow settling rate of biomass particles.8–11Filtration is a non-thermal, low energy, and scalable solution for solids separations and sterilization in many applications, including in the food and pharmaceutical industries12 and in wastewater treatment13,14 However, there remains a need to identify viable filtration conditions for processing biorefinery slurries including from pretreatment,15,16 enzymatic hydrolysis,16,17 consolidated bioprocessing (CBP),18 and anaerobic digestion (AD).19 Filtration of these slurries by traditional cross-flow filtration is often challenged by membrane fouling and is ultimately limited to slurries containing less than ∼5 wt% insoluble solids.20,21 Strategies to mitigate the impact of membrane fouling include the application of cleaning solutions,22 backwashing,22 addition of inorganic filter aids,23 and the addition of polyelectrolyte flocculants.11,24 These methods are primarily a means to clean conventional membranes or focused on adding exogenous, usually sacrificial components to aid filtration.
Conversely, the use of a high shear rate at the membrane surface via dynamic filtration could offer a more direct means to address challenging SLS problems,25 and indeed, early-stage research suggests that dynamic filtration can improve both throughput and recovery in high-solids containing slurries.21,24–26 Dynamic filtration systems generate a high shear rate (between 104 and 105 s−1) at the membrane surface that decreases membrane fouling and results in higher average permeate flux.24 The two most common types of dynamic filtration modules are vibratory membranes with parallel plates and rotating ceramic disc (RCD) filters that are single or double shafted.26 Relevant dynamic filtration studies include the processing of fermentation broth,25,27 juice, wine, and dairy solutions, wastewater effluents,24,26 and alkaline pretreated liquor from NaOH-based biomass pretreatment.28 Most often, experimental studies and computational fluid dynamics (CFD) simulations of dynamic filtration to date have been conducted with Newtonian fluids,29 non-Newtonian fluids with cellular suspended solids,24 and activated sludge with total suspended solids (TSS) up to 2 g L−1.30 However, many biomass slurries are non-Newtonian with insoluble solids present (up to 15 wt%) and the advantages, hydrodynamics, and performance of dynamic filtration remains unclear for SLS applications within the biorefinery, including the separations of pretreated, enzymatically-digested lignocellulose residual solids from liberated, soluble cellulosic sugars in water.
To that end, here we assessed the feasibility of an RCD filter to perform SLS on a process stream obtained from enzymatic hydrolysis of pretreated corn stover. We first characterized the rheology of the slurry by measuring the viscosity as a function of shear rate. We then determined the throughput (flux) of an RCD filter operating with 3 wt% insoluble solids as a function of disc rotation velocities (300–1200 rpm) and insoluble solids content in the retentate slurry (8–13 wt%). To show the hydrodynamics within the module operating with solids present and to estimate the local shear rate and average filtration energy demand, CFD simulations were performed with an experimentally parameterized viscosity model across the experimental operational range. By combining the experimental and CFD simulation results, we developed an open-source filtration process model to calculate mass and energy balances for a 95% recovery extent of soluble sugars from the solids-rich lignocellulosic hydrolysate stream. Lastly, we show how the target sugar recovery impacts operating expenses, while providing insight into the water consumption and operating range of RCD filtration. The results suggest that RCD filtration is a viable, cost-effective, and energy efficient SLS method for this critical biorefining application.
Results
Preparation and rheology of DDR-EH slurry
We used deacetylated and disc refined (DDR) enzymatic hydrolysate (DDR-EH) generated from alkaline pretreated corn stover as the exemplary stream for SLS demonstrations.31,32 Briefly, dried, milled corn stover was deacetylated in a 1900 L paddle mixer at 92 °C for 2 hours with a loading of 80 kg NaOH per tonne of biomass. The deacetylated biomass was acidified to a pH of 3.0 with H2SO4 and then dewatered via a screw press prior to being sent to an Andritz pilot plant (Springfield, OH) for disc-refining. The deacetylated and refined biomass then underwent enzymatic hydrolysis in a 1900-L paddle reactor at 50 °C with 25 mg protein per g cellulose total enzyme loading at a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of Novozymes Ctec3
1 ratio of Novozymes Ctec3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Htec3 and at an initial insoluble solids loading of 15 wt%. The hydrolysis was completed in 72 hours and the slurry was frozen for future use. The resulting DDR-EH used in this study contained 15 wt% total solids with 3.0 wt% insoluble solids, 73 g L−1 glucose, and 34 L−1 xylose (Table S1†). Table 1 shows results from compositional analysis performed on the milled corn stover and the solids fraction of DDR-EH.
Htec3 and at an initial insoluble solids loading of 15 wt%. The hydrolysis was completed in 72 hours and the slurry was frozen for future use. The resulting DDR-EH used in this study contained 15 wt% total solids with 3.0 wt% insoluble solids, 73 g L−1 glucose, and 34 L−1 xylose (Table S1†). Table 1 shows results from compositional analysis performed on the milled corn stover and the solids fraction of DDR-EH.
| wt% lignin | wt% glucan | wt% xylan | wt% galactan | wt% arabinan | wt% total ash | |
|---|---|---|---|---|---|---|
| Corn stover | 16.0 | 32.3 | 17.2 | 1.7 | 3.6 | 12.1 |
| DDR-EH solids | 53.6 | 17.0 | 7.2 | 1.5 | 1.8 | 9.9 |
To determine the impact of shear on the rheology of the DDR-EH hydrolysate, we measured the dynamic viscosity as a function of shear rate using a vane spindle equipped on a Brookfield viscometer. Rheological properties including yield stress and viscosity have been previously reported for DDR-EH via a roughed parallel plate technique.33 However, large biomass particles present in the slurry (up to 3 mm)33 reduce the accuracy of this technique because the parallel plate configuration tends to eject particles from between plates, effectively changing the composition of the slurry. The use of a vane geometry to obtain dynamic rheology information for slurries containing insoluble solids is recommended, as sieving is not required and the slurry properties remain homogeneous during measurements.34,35
Fig. 1 shows the viscosity as a function of the shear rate from the vane spindle measurements. As expected, the hydrolysate exhibits non-Newtonian shear-thinning properties. For context, the viscosity of water is 0.001 Pa s, olive oil is 0.084 Pa s at 20 °C,36 honey ranges from 0.42 to 23 depending on temperature and water content,37 and glycerol is 1.4 Pa s at 20 °C.38 A power law model was used to fit the viscosity data (eqn (1) and Table 2). For eqn (1), the power law coefficient, K, was estimated as the slope and the power law exponent, n, was estimated from the y-intercept from a log–log plot of shear rate as a function of viscosity. The K and n parameters were then plotted as a function of wt% insoluble solids, with the result that K and n exhibit a power law trend with respect to wt% insoluble solids (Fig. S1 and eqn (S1), (S2)†).
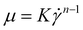 | (1) |
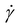 is the shear rate (1 s−1).
is the shear rate (1 s−1).
 | ||
| Fig. 1 The dynamic viscosity of DDR-EH is shown as a function of shear at 3, 6, 9, and 12 wt% insoluble solids. The curve fits are based on eqn (1) using the corresponding power law coefficients and exponent listed in Table 2. | ||
| wt% insoluble solids | K | n |
|---|---|---|
| 3 | 0.359 | 0.154 |
| 6 | 0.922 | 0.053 |
| 9 | 2.59 | 0.017 |
| 12 | 5.16 | 0.011 |
The above results provide a method to estimate the viscosity at a specific shear rate and at a given wt% insoluble solids. Within the CFD simulations, we used the experimentally parameterized viscosity model to estimate the viscosity within the RCD module at 3, 6, 9, and 12 wt% insoluble solids at 200–1200 rpm (vide infra).
SLS of hydrolysate using RCD filtration
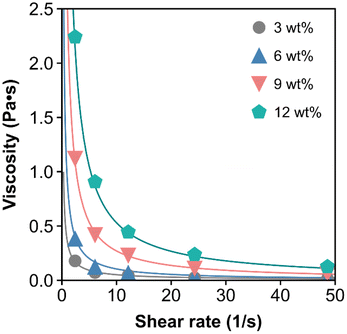
Using the prepared DDR-EH slurry as the feed material, we then performed RCD filtration with a single disc Andritz dynamic crossflow (DCF) module, which is shown in Fig. 2. The demonstrations resulted in a clarified permeate and a retentate containing concentrated insoluble solids. A microfiltration membrane with a 0.2 μm pore size was chosen to remove suspended and insoluble solids, including potential intact microbial cells, with the intention to study this process as it would be practiced industrially to produce cellulosic sugars in sterile conditions. The measured permeate contained soluble components including glucose (73 g L−1), xylose (34 g L−1), and a low concentration of acetic acid (2.26 g L−1) and lactic acid (1.4 g L−1) (Table S1†).To first investigate the impact of disc velocity on membrane performance, the disc was operated at 300, 600, and 1200 rpm. At each velocity, 500 mL of hydrolysate with 3 wt% insoluble solids was fed to the vessel, and dead-end filtration was performed by keeping the retentate valve closed during operation. Fig. 3A shows the flux measured at each rotational velocity. As expected, the highest sustained flux occurred at a disc velocity setting of 1200 rpm. However, all conditions show that membrane flux declined by 50% over the initial minute of filtration. We used the classical cake formation model,39 which assumes that the suspended solids form a porous layer on the membrane surface (eqn (S3)†) to fit data over the first minute. The cake formation coefficient (Kcf) for conditions 1200, 600, and 300 rpm is 0.0022, 0.0025, and 0.0032 respectively, indicating that as the disc velocity increases, the extent of membrane fouling decreases. The cake formation model is plotted on Fig. 3A for the 600 rpm condition. Reduced fouling at 1200 rpm motivated further investigation for the performance of the module in continuous mode at this disc velocity.
 | ||
| Fig. 3 (A) Batch filtration results showing the flux decline at 300, 600, and 1200 rpm over a few minutes. The gray line corresponds to the cake filtration model39 at the 600 rpm condition. The flux is reported in LMH (liters per square meter per hour, L m−2 h−1). (B) Continuous filtration throughput results at 1200 rpm producing 8, 11, and 13 wt% insoluble solids in the retentate slurry. (C) Continuous filtration throughput with a single backflush event at ∼60 min. The favorable flux return after backflushing indicates reversible fouling. For this demonstration, the RCD was producing 13 wt% insoluble solids in the retentate slurry. Each experiment was performed in (B) and (C) was performed with 10 L of feed material and generated 8 L of permeate after each run as shown in (D) for a single run. (D) Photo of 2 L of slurry retentate (left) and 8 L of permeate (3 bottles, right) samples collected from a single continuous RCD filtration demonstration. | ||
We measured the flux of the RCD filter operating in continuous mode at 1200 rpm, where 10 L of DDR-EH at 3 wt% insoluble solids were fed to the disc module and concentrated to 8, 11, or 13 wt% insoluble solids in the retentate slurry, which was set by adjusting the flow rate of the retentate flowrate (a lower retentate flow results in a higher concentration of solids in the retentate). At each retentate slurry concentration (8, 11, and 13 wt%), we measured flux during the filtration process (Fig. 3B).
Next, we investigated if the initial flux of the membrane could be restored after an hour of filtration time with a backflush with 50 mL of water for 1 minute. Backwashing was effective in restoring the operational flux to the initial flux (Fig. 3C). These results indicate that membrane fouling is reversible and that flux may be effectively mitigated over longer durations with commonly employed fouling mitigation methods such as backwashing. A photo of the retentate and permeate generated from a single continuous filtration demonstration is shown in Fig. 3D.
Computational fluid dynamics (CFD) simulations of RCD filtration
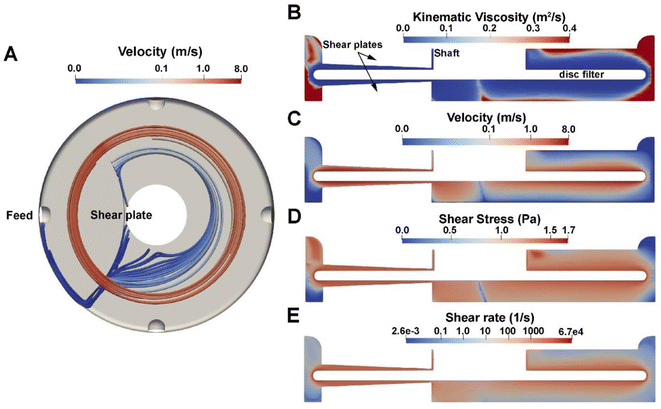
Based on the results presented above, both disc velocity and insoluble solids in the retentate impact the extent of fouling and throughput of the RCD filter. To understand the impact of disc velocity and insoluble solids on the hydrodynamics and minimum energy demand of the RCD filter, we use CFD simulations to estimate shear rate, fluid velocity, and filtration energy demand across the range of tested experimental conditions. To accomplish this, a 3D geometry was developed based on the dimensions of our RCD filter (Andritz DCF 152/S, as shown in Fig. 2). This filter has one ceramic disc with two shear plates or islands on both the front and back sides of the housing that are adjacent to the feed port of the module. In the simulation, we modeled the shear response of the hydrolysate slurry using the power law viscosity model (eqn (1)). With the experimentally parameterized viscosity model, we can approximate, with high fidelity, the hydrolysate slurry as a homogeneous fluid to reduce computational complexity by avoiding modeling the interaction of fluid and fine particle suspension. The governing equations for hydrolysate flow within the module are provided in the Materials and methods section and the files used to perform simulations are accessible on GitHub (see Notes section).To understand the flow behavior inside the module at various operating conditions, CFD simulations were conducted across the range of 200 to 1200 rpm and across the range of 3 to 12 wt% insoluble solids within the module. Fig. 4 shows the simulation result of the RCD operated at 1000 rpm with 6 wt% insoluble solids. Fig. S2† shows the shear stress in the module at 6 wt% insoluble solids in the module and between 200 and 1200 rpm, and Fig. S3† shows the shear stress in the module at 3, 6, 9, and 12 wt% insoluble solids and at 1000 rpm. Due to membrane rotation, the hydrolysate at regions close to the membrane experiences high velocity and high shear stress, significantly higher than near the walls of the module. Thus, the viscosity of the hydrolysate near the membrane surface is much lower than at regions farther away from discs. The existence of the shear plates contributes to the increased shear for hydrolysate in the gap between the disc and the shear plate island. We can see from Fig. 4A that the hydrolysate entering the gap accelerates to a higher velocity as it passes through the gap.
Another important result from the CFD simulation is the energy demand needed to spin the membrane in the presence of hydrolysate. The energy demand reported here is derived from the governing computational equations as provided in the materials and methods section (eqn (2)–(10)). Specifically, energy demand (power consumption) was calculated using eqn (10) with the normal pressure moment and tangential viscous moment being calculated using eqn (8) and (9). The estimated energy demand does not include the mechanical energy inefficiency of the system due to friction loss and/or heat loss within the module, and it also does not include the power inefficiency of the motor. As expected, the energy required for the filtration process is estimated to increase with increasing rotation velocity and wt% insoluble solids, as shown in Fig. 5. At 9 wt% insoluble solids within the module and at 1000 rpm, the energy demand is 17 W m−2 (∼0.24 kW h per m3 of permeate).
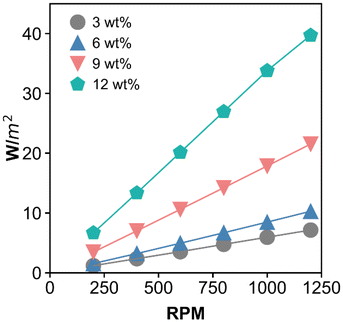 | ||
| Fig. 5 The impact of disc rotation velocity and insoluble solids content within the module on the minimum energy demand per square meter of membrane area. The power consumption is calculated from eqn (8)–(10) (see Materials and methods) which then divided the membrane area to derive the energy demand per unit area. | ||
Comparison to cross-flow filtration
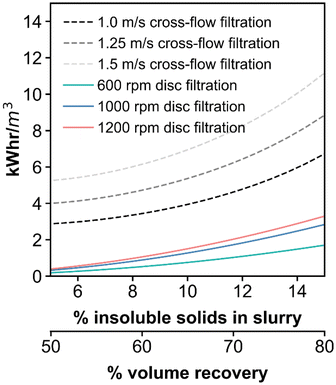
Based on the findings above, the energy consumption of RCD filtration, related to spinning the disc, was as compared to the pumping energy consumption of traditional cross-flow filtration for the same DDR-EH feed. CFD results at 600, 1000, and 1200 rpm were translated to kW h per cubic meter of permeate by dividing the energy per square meter results (Fig. 5) by flux (LMH) to give consumption in units of kW h per cubic meter. Energy consumption results from CFD were fit by a power law over the experimental insoluble solids content range to estimate the energy consumption between 5 and 15% insoluble solids in the retentate slurry (Fig. 6). We chose a flux value of 30 LMH for both the RCD and the cross-flow case for this comparison as a conservative estimate and to normalize the energy consumption across the two cases with a constant flux value. Results show that the energy savings associated with RCD filtration is 74 to 79% relative to cross-flow filtration.For the cross-flow case, energy consumption was calculated at a cross-flow velocity of 1.0, 1.25, and 1.5 m s−1. A minimum cross-flow velocity of 1.0 m s−1 was chosen as at this velocity the wall shear rate at the filter entrance is 1000 1 s−1 which is recommended for microfiltration. A detailed description of the governing equations used to calculate the pumping energy consumption are shown in the ESI section entitled ‘Energy consumption equation list for cross-flow filtration’.† Briefly, the shear-rate was calculated using the Rabinowitsch–Mooney relationship for a tubular membrane module with a diameter of 3.5 mm. The pressure drop along the length of a tubular filtration module was calculated via the Darcy–Weisbach equation, with a Fanning friction factor calculated from the modified Reynolds number estimate for non-Newtonian fluids defined by Metzner and Reed.28 The pumping energy was then calculated based on the volumetric flow rate, pressure drop, and with a pumping efficiency of 0.6 (an efficiency value of 0.6 was also applied to the RCD energy consumption as a motor efficiency). Cross-flow filtration energy demand ranges from 4.8 at 1.0 m s−1 to 8.2 kW h m−3 at 1.5 m s−1. Results indicate that the operating the RCD at a retentate slurry concentration of 12% insoluble solids, has an estimated energy consumption that ranges from 1.0 kW h m−3 at 600 rpm to 2.1 kW h m−3 at 1200 rpm. Energy savings is visualized across a large experimental window in Fig. 6. Volume recovery corresponds to the percent volume of feed recovered as permeate. With respect to additional process energy requirements, the energy demand associated with backwashing the membranes was not incorporated into the comparison for either case. Backwash energy demand is dependent on several factors including solids loading, flux, frequency, etc. leading to a large range of reported energy demands. For example, the backwash energy demand is reported to range from 0.07 to 1.35 kW h m−3 for anaerobic membrane bioreactors.40
Two-stage filtration and process model
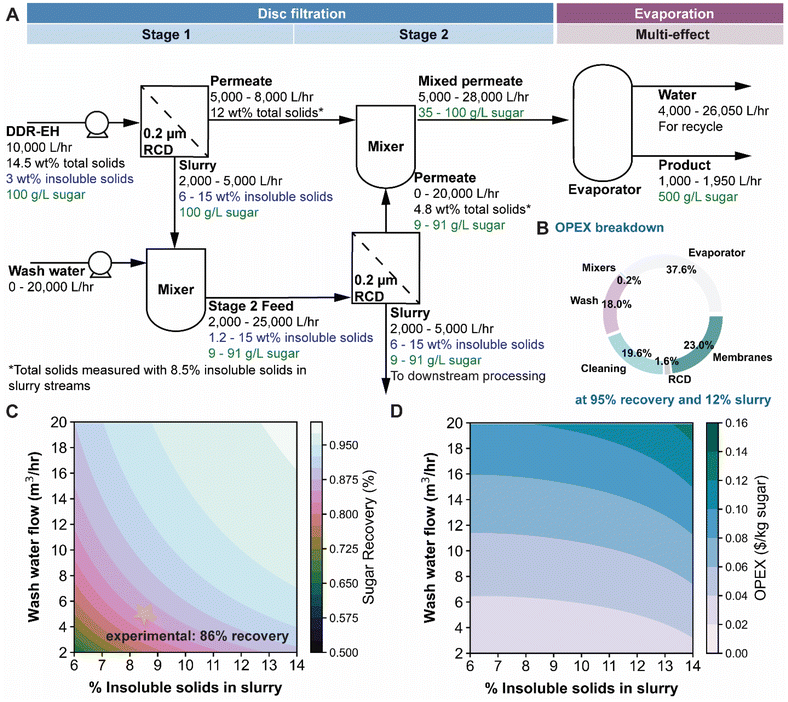
We then developed and validated a process model against experimental data to estimate the sugar recovery and operating cost of the SLS unit operation. A two-stage experimental filtration (following the block flow diagram in Fig. 7A) was performed to serve as a validation for a process model that estimates sugar recovery. Two liters of DDR-EH was filtered by the RCD filter, producing a retentate with 8.24 wt% insoluble solids (Table S2†) from the first stage. As expected, the results show that microfiltration maintains the feed sugar concentration in the permeate and that the insoluble solids are concentrated by the filter. Note that the soluble solids pass through the membrane and have a concentration of 12.1 wt% in the permeate. We used particle size analysis across slurry samples to determine show the average size of the particles (Table S2 and Fig. S4†). Particle size did not change upon filtration (permeate samples did not scatter visible light). A second filtration stage was implemented by first diluting the retentate from the first stage from 8.2 wt% insoluble solids to 3.6 wt% insoluble solids (Table S2†). The diluted sample was then fed to the RCD filter to concentrate the insoluble solids to 8.5 wt%. The combined two-stage filtration achieved an overall sugar recovery of 86 wt% within the permeate.Expanding on the above experimental results, we used process modelling to predict the sugar recovery and OPEX as a function of insoluble solids content in the retentate slurry and dilution (Fig. 7). Our process model boundary encompasses an SLS via RCD filtration and a multi-effect evaporator to concentrate sugars to 500 g L−1. The process was modeled in Python and is accessible on GitHub (see Notes section). All assumptions and equations used are described in the ESI.† Briefly, the Python code completes a water, sugar, and insoluble solids mass balance over the system. We set the sugar inlet concentration at 3% insoluble solids and 100 g L−1 cumulative soluble sugars based on experimental data (Table S2†). In the process model, the term ‘sugar’ corresponds to the summation of soluble sugars including glucose, xylose, galactose, and arabinose measured in our DDR-EH. A second stage of RCD filtration was modeled to recover additional sugars from the slurry retentate generated from stage 1. Prior to the second RCD unit, the slurry is mixed with a water wash stream, which reduces the insoluble solids content to a processable level (below <15 wt%) in the second RCD unit. Because of the hygroscopic nature of the hydrolysate flocs, it is assumed that the insoluble solids entrain soluble sugars, decreasing the recovery after mixing in accordance with the wash dispersion model,41 and to treat this, an experimental correlation was used to determine the reduced sugar recovery associated with entrainment.41 After the permeate streams are combined, a multi-effect evaporator with integrated mechanical vapor recompression was modeled to concentrate sugars in the permeate streams to achieve a final concentration of 500 g L−1 (50 wt%) of sugars. We scaled the process model to a small demonstration-scale by using a feed flow rate of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 L h−1 (45.5 dry tons per day).42,43 Based on our above RCD filtration results, we assumed that the SLS process could be operated continuously to produce a slurry containing from 6 to 15 wt% insoluble solids in the retentate slurry streams from stage 1 and stage 2 filtration. Under these operating conditions, the first RCD filter concentrates the feed by 2.0 to 5.0-fold and achieves a sugar recovery of 50% to 80% respectively. After the second stage of filtration, a sugar recovery of >95% can be achieved. We determined the minimum operating expenses (OPEX) as a summation of energy and material costs per kg of sugar recovered. The OPEX presented below are associated with the estimated membrane replacement cost, process water costs (Table S2†), cleaning costs,44 and energy costs for the evaporator, RCD, and slurry mixer.45 Labor costs, cleaning and maintenance costs, and insurance were not factored into the OPEX estimate. Evaporation operating expenses were accounted for by solving the electrical and heating demand of an evaporator in Aspen Plus. The OPEX breakdown of the system operating at 12 wt% insoluble solids in the retentate slurry and 95% sugar recovery is shown in Fig. 7B – with an overall OPEX of $0.06 per kg of recovered sugar. As shown in Fig. 7C, the recovery from the process improves as the wash flow rate and solids content are increased. Fig. 7C shows the experimental two stage sugar recovery result based on Table S2† data. The model output for sugar recovery matches the experimental sugar recovery result (86% sugar recovery) at 8.5% insoluble solids in the retentate and when scaled to the process model flowrate. Fig. 7D shows that the overall OPEX increases as the wash water flow and solids content increase. The increased operating cost at higher wash water is due to the cost of using process water and the additional evaporation energy required. The increased operating cost at higher solids content is due to the lower flux observed as solids content increases, resulting in increased membrane area and overall membrane cost.
000 L h−1 (45.5 dry tons per day).42,43 Based on our above RCD filtration results, we assumed that the SLS process could be operated continuously to produce a slurry containing from 6 to 15 wt% insoluble solids in the retentate slurry streams from stage 1 and stage 2 filtration. Under these operating conditions, the first RCD filter concentrates the feed by 2.0 to 5.0-fold and achieves a sugar recovery of 50% to 80% respectively. After the second stage of filtration, a sugar recovery of >95% can be achieved. We determined the minimum operating expenses (OPEX) as a summation of energy and material costs per kg of sugar recovered. The OPEX presented below are associated with the estimated membrane replacement cost, process water costs (Table S2†), cleaning costs,44 and energy costs for the evaporator, RCD, and slurry mixer.45 Labor costs, cleaning and maintenance costs, and insurance were not factored into the OPEX estimate. Evaporation operating expenses were accounted for by solving the electrical and heating demand of an evaporator in Aspen Plus. The OPEX breakdown of the system operating at 12 wt% insoluble solids in the retentate slurry and 95% sugar recovery is shown in Fig. 7B – with an overall OPEX of $0.06 per kg of recovered sugar. As shown in Fig. 7C, the recovery from the process improves as the wash flow rate and solids content are increased. Fig. 7C shows the experimental two stage sugar recovery result based on Table S2† data. The model output for sugar recovery matches the experimental sugar recovery result (86% sugar recovery) at 8.5% insoluble solids in the retentate and when scaled to the process model flowrate. Fig. 7D shows that the overall OPEX increases as the wash water flow and solids content increase. The increased operating cost at higher wash water is due to the cost of using process water and the additional evaporation energy required. The increased operating cost at higher solids content is due to the lower flux observed as solids content increases, resulting in increased membrane area and overall membrane cost.
To determine if the use of flocculant could decrease OPEX, we modified our two-stage MF model to include the use of flocculate and considered that flocculates can increase the throughput. As previously observed, entrainment of soluble products scales to the third of the floc size, resulting in additional entrainment as flocculates are known to increase the size of the floc.8,41 While the operating costs of the flocculant case (Fig. S5†) are similar (or lower in some cases) than the baseline non-flocculate case due to the reduced membrane area required (estimated as 20-fold less), it is apparent that the recovery is limited to 91–94% due to additional entrainment of sugar in the slurry. However, we find that the recovery for both cases is highly sensitive to the solids loading with higher solids content reducing the wash water requirements.
Discussion
SLS of lignocellulosic biomass is a common processing step in biorefineries to produce cellulosic sugars. Within several biorefinery process models, SLS is typically specified with ∼95% sugar recovery via filtration methods.42,46 However, many of the filtration data sets in the literature are limited to batch vacuum filtration experiments that are difficult to translate into continuous process models. In this work, we aimed to bridge this gap by demonstrating continuous filtration of a hydrolysate at industrially relevant solids loadings. We also developed a continuous process and process model that can be used in holistic biorefinery models to improve cost estimates of dynamic filtration systems.The results presented above highlight the potential of RCD filtration to achieve high sugar recovery (95%) from a corn stover hydrolysate slurry at a relatively low operating cost (<$0.06 per kg sugar) without the addition of filter aids and flocculants. Results show that a single-stage RCD filter can obtain 81% sugar recovery operating at 13 wt% insoluble solids loading and a two-stage RCD filter system obtains a sugar recovery of up to 98%. These results are in a similar range as previous reports completed using traditional methods. For example, Burke et al. used batch dead-end vacuum filtration and a polyelectrolyte flocculant to achieve 83% sugar (without washing) from a ponderosa pine hydrolysate.47 Sievers et al. used batch dead-end vacuum filter, polyelectrolytes flocculant, and wash water to achieved up to a 95% recovery of sugars from corn stover hydrolysate.8 Kinnarinen et al. used a dead-end filter with filter aids to achieve a sugar recovery of 91.4 to 94.7% over 10 minutes of operation time from enzymatic hydrolysis of cardboard waste.23
Our results also show that the throughput of an RCD filter is 120 to 40 LMH, with decreasing flux as the insoluble solids loading is increased, corresponding to a capacity of ∼15 to 3 kg solids per h m2. A capacity in the range of 1–3 kg h−1 m−2 has been previously reported for dead-end filtration methods.8 The use of flocculants has been shown to increase the throughput of the filter up to 40-fold due to an increase in floc size and porosity of the cake on the membrane surface.8 The use of filter aids or flocculants may become needed if an envisioned process is to produce >13 wt% insoluble solids in the retentate because of the excessive fouling that is expected above this solids loading.48 However, filter aids and flocculants are expected to decrease the percent sugar recovery due to increase sugar entrainment in the cake (Fig. S5†).
The shear stress distribution on the membrane surface has been identified as a critical factor for dynamic filtration as higher shear stress on the membrane surface contributes to the prevention of membrane fouling.49 In many previous reports, the average shear rate over the membrane surface is estimated as a solution of the Navier–Stokes equation with the use of a constant velocity coefficient parameter that accounts for the surface pressure and fluid velocity variation along the radius of the membrane.50–52 Because of the complex geometry and time dependence of velocity, CFD simulations enable precise estimation of the shear stress distribution on the membrane surface as well as the normal force. The mechanical energy predicted from CFD simulations includes contributions from both normal pressure force and tangential shear force, shown below in eqn (6) and (7) (see Materials and methods). It is the tangential shear force on the membrane surface that helps prevent membrane fouling. The normal force on the other hand produces additional transmembrane pressure difference apart from the static pressure difference which also benefits the filtration process by increasing the flux.
Challenges for RCD filtration for SLS applications in the biorefinery include the potential for high capital cost relative to non-dynamic systems and the need to replace membrane materials throughout the lifetime of the plant. Regarding capital cost, dynamic filtration modules are currently built at a relatively small scale (<150 m2). Information on capital cost is highly limited to a few units of small capacity made by a few manufacturers including Andritz and Novoflow. Cost information provided by Novoflow reveals that a unit with 60 m2 of membrane area cost $525![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in 2024. Cost improvements and further scale-up of the technology are necessary to gain industrial traction against traditional cross-flow and vacuum filtration technologies. Regarding membrane lifetime, the presence of silica in biomass hydrolysates would likely wear on the membrane surface and reduce the lifespan of the material. To account for the reduced lifetime due to abrasion of the membranes at a high shear rate, we set the lifetime of the membrane to be 5 years rather than the typical 20 to 30 years lifetime generally stated for ceramic membranes by manufacturers and in the literature.28
000 in 2024. Cost improvements and further scale-up of the technology are necessary to gain industrial traction against traditional cross-flow and vacuum filtration technologies. Regarding membrane lifetime, the presence of silica in biomass hydrolysates would likely wear on the membrane surface and reduce the lifespan of the material. To account for the reduced lifetime due to abrasion of the membranes at a high shear rate, we set the lifetime of the membrane to be 5 years rather than the typical 20 to 30 years lifetime generally stated for ceramic membranes by manufacturers and in the literature.28
Conclusion
Bioprocessing is rich with examples of slurries containing suspended and insoluble biomass solids such as the case for downstream processing after fermentation, wastewater treatment, anaerobic digestion, lignocellulosic hydrolysis, and lignin depolymerization. Processing solids is challenging as downstream equipment including filtration modules typically rapidly foul, leading to low throughput. In this work, we demonstrated and characterized RCD filtration with high solids in a continuous mode. We then modeled a disc module by CFD and developed mass and energy balances across a simple filtration and evaporation system to obtain concentrated sugars at 500 g L−1 and used sensitivity analysis over a range of solids loading to understand the economic drivers of the process and achievable sugar recovery. Operating at an insoluble solid content of 12 wt% in the retentate slurry at a disc velocity of 1200 rpm is advantageous over cross-flow filtration with at least a 2-fold energy reduction and achieves a high recovery of sugars (95%) with low OPEX ($0.06 per kg sugar).Materials and methods
Preparation of hydrolysate
Air dried corn stover provided by Idaho National Laboratory (INL) was milled at the National Renewable Energy Laboratory (NREL) using a knife mill (Jordan Reduction Solutions, Model 14 × 20, Birmingham, Alabama) to pass through a 19 mm (3/4-inch) round hole rejection. The size reduced corn stover was pretreated following the Deacetylation and Disc Refining (DDR) method described previously.32 Briefly, the milled corn stover was deacetylated using a dilute (0.1 M) NaOH solution at 92 °C for 2 hours with a chemical loading of 80 kg NaOH per tonne of biomass. The deacetylated biomass was then dewatered via a screen filter and washed to remove solubilized acetate and lignin. The washed solids were further acidified to a pH of 3.0 with sulfuric acid to preserve the material. The material was then dewatered in a screw press prior to being sent to an Andritz pilot plant (Springfield, OH) for disc-refining. The disc refining was carried out using a 36′′ disc refiner (Sprout, Model 401) with a set of Durametal fine-bar sector plates (plate pattern 36104) at an energy consumption of approximately 200 kW h per tonne of biomass. The deacetylated and disc refined biomass then underwent enzymatic hydrolysis in the 1900-L paddle reactor at 50 °C with 25 mg protein per g cellulose total enzyme loading at a ratio of Novozymes Ctec 3 to Htec 3 of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and an initial solid loading of 15% (w/w). The hydrolysis was completed in 72 hours and frozen for future use.
1 and an initial solid loading of 15% (w/w). The hydrolysis was completed in 72 hours and frozen for future use.
Liquor and compositional analysis
Chemical analysis of the DDR-EH samples was performed as described in Sluiter et al.53 Compositional analysis of the biomass samples was performed as described in Sluiter et al.54Dynamic viscosity
The dynamic viscosity of hydrolysate was measured using a DV2T Brookfield viscometer. DDR-EH samples containing 4 to 20 wt% insoluble solids were prepared by sampling the retentate during dynamic microfiltration.Dynamic microfiltration
The Andritz DCF 152/S was used to demonstrate SLS and consists of a 0.25 kW motor, one 152 mm ceramic membrane disc, and associated piping, feed tank (15 L), pressure tank, and chiller/heater. We selected a pore size of 0.2 μm (from Andritz) to remove insoluble solids, suspended solids, and bacterial contaminants. The membrane area on the Andritz DCF 152/S is 0.034 m2. During the experiments, the system was operated with a 1 bar transmembrane pressure (TMP). We used 10 L feed samples (containing 3 wt% insoluble solids) and adjusted the rpm of the motor to determine an optimum disc velocity. Between experiments, the membrane was rinsed with 1% NaOH solution for 1 hour. Because some clogging of the ¼ inch outer diameter (OD) feed line occurred during our initial batch experiments, we installed a ½ inch OD feed line between the feed vessel and the DCF 152/S module and additionally used a stainless-steel mesh with ¼ inch openings to remove string and other large objects from the EH slurry. Backwashing was performed with water at 50 mL min−1 for 1 min.Particle size analysis
Particle size analysis was performed using an Anton Paar PSA 1190 particle size analyzer. All samples were run in water using a full 450 mL reservoir. Parameters for all samples were set to fast pump and fast stir speed. A measurement time of 45 seconds, obscuration limits set to 5%–30%, and the Franhofer Reconstruction mode was used. One small drop of Igepal CO-630 (Sigma Aldrich-542334) was added to the water reservoir to aid in breaking up agglomerations. Instrument performance was verified using White House Scientific PS314 particle size standard. Anton Paar Kalliope Professional Version 3.2.5 software was used for data analysis.Computational methods
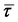 ) is computed using the local hydrolysate viscosity. The turbulence dissipation via the Reynolds stress (
) is computed using the local hydrolysate viscosity. The turbulence dissipation via the Reynolds stress (![[R with combining overline]](https://www.rsc.org/images/entities/b_i_char_0052_0305.gif) ) is computed using the shear-stress transport k − ω model.55
) is computed using the shear-stress transport k − ω model.55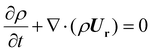 | (2) |
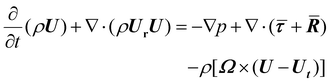 | (3) |
| Vr = U − Ur = Ut + Ω × r | (4) |
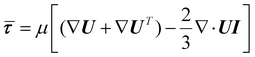 | (5) |
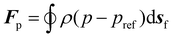 | (6) |
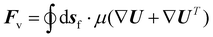 | (7) |
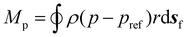 | (8) |
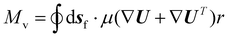 | (9) |
| P = Mω | (10) |
To compute the membrane energy demand, we first compute the fluid shear rate close to the disc. Due to the interaction of hydrolysate with the RCD filter, a normal pressure force (Fp) and a tangential viscous force (Fv) are experienced by the membrane surface which can be computed using eqn (6) and (7). We can also compute the torque using eqn (8) and (9). The power consumption for rotation motion is then calculated using eqn (10).
Nomenclature
Latin symbols
| F p | Normal pressure force vector |
| F v | Tangential viscous force vector |
| K | Power law coefficient |
| K cf | Cake formation coefficient |
| M p | Normal pressure moment |
| M v | Tangential viscous moment |
| n | Power law exponent |
| P | Power consumption |
| p | Pressure (Pa) |
| p ref | Reference pressure (Pa) |
![[R with combining overline]](https://www.rsc.org/images/entities/i_char_0052_0305.gif)
| Reynolds stress |
| s f | Face area vector |
| t | Time |
| U | Absolute velocity vector |
| U r | Relative velocity vector |
| U t | Translational velocity vector |
| U T | Transpose of the absolute velocity vector |
| V r | Velocity of the moving frame relative to the stationary frame |
Greek symbols
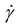
| Shear rate (1 s−1) |
| μ | Apparent viscosity (Pa s) |
| ρ | Density (kg m−3) |
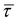
| Viscous stress tensor |
| Ω | Rotation velocity of the membrane (rpm) |
| ω | Angular velocity of the membrane |
Notes
Python codes are available on GitHub.com (NREL-SEPCON – https://github.com/NREL-SEPCON).Author contributions
Conceptualization: POS, DS, EMK, and GTB, experimentation and computation: POS, YL, XC, YC, and ECDT, visualization: POS, supervision: DS, EMK, and GTB, writing: POS, YL, and GTB.Data availability
Data points for all main text figures are available in numerical form within Data S1.† An ESI† is available to support the research conclusions of the main text.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was authored by the National Renewable Energy Laboratory, operated by Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. The research reported in this paper was sponsored by the U.S. Department of Energy (DOE), Energy Efficiency and Renewable Energy Office, Bioenergy Technologies Office (BETO) under the BETO Bioprocessing Separations Consortium via Contract No. DE-AC36-08GO28308 and under the BETO Solid Lignin Recovery (SLR) project via contract No. DE-AC36-08GO28308 with the National Renewable Energy Laboratory. We thank Lauren Valentino at Argonne National Laboratory for her leadership in the Separations Consortium. We thank Laura Hollingsworth for the critical review of the manuscript. The views expressed in the article do not necessarily represent the views of the U.S. Department of Energy or the U.S. Government. The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.References
- G. W. Huber, S. Iborra and A. Corma, Chem. Rev., 2006, 106, 4044–4098 CrossRef CAS PubMed.
- M. Besson, P. Gallezot and C. Pinel, Chem. Rev., 2014, 114, 1827–1870 CrossRef CAS PubMed.
- X. Zhang, K. Wilson and A. F. Lee, Chem. Rev., 2016, 116, 12328–12368 CrossRef CAS PubMed.
- J. D. McMillan and G. T. Beckham, Microb. Biotechnol., 2017, 10, 40–42 CrossRef PubMed.
- S. Y. Lee, H. U. Kim, T. U. Chae, J. S. Cho, J. W. Kim, J. H. Shin, D. I. Kim, Y.-S. Ko, W. D. Jang and Y.-S. Jang, Nat. Catal., 2019, 2, 18–33 CrossRef CAS.
- J. Keasling, H. Garcia Martin, T. S. Lee, A. Mukhopadhyay, S. W. Singer and E. Sundstrom, Nat. Rev. Microbiol., 2021, 19, 701–715 CrossRef CAS PubMed.
- L. R. Lynd, G. T. Beckham, A. M. Guss, L. N. Jayakody, E. M. Karp, C. Maranas, R. L. McCormick, D. Amador-Noguez, Y. J. Bomble, B. H. Davison, C. Foster, M. E. Himmel, E. K. Holwerda, M. S. Laser, C. Y. Ng, D. G. Olson, Y. Román-Leshkov, C. T. Trinh, G. A. Tuskan, V. Upadhayay, D. R. Vardon, L. Wang and C. E. Wyman, Energy Environ. Sci., 2022, 15, 938–990 RSC.
- D. A. Sievers, J. J. Lischeske, M. J. Biddy and J. J. Stickel, Bioresour. Technol., 2015, 187, 37–42 CrossRef CAS PubMed.
- A. A. Kiss, J. Grievink and M. Rito-Palomares, J. Chem. Technol. Biotechnol., 2015, 90, 349–355 CrossRef CAS.
- A. A. Kiss, J.-P. Lange, B. Schuur, D. W. F. Brilman, A. G. J. van der Ham and S. R. A. Kersten, Biomass Bioenergy, 2016, 95, 296–309 CrossRef CAS.
- M. J. Biddy, R. Davis, D. Humbird, L. Tao, N. Dowe, M. T. Guarnieri, J. G. Linger, E. M. Karp, D. Salvachúa, D. R. Vardon and G. T. Beckham, ACS Sustainable Chem. Eng., 2016, 4, 3196–3211 CrossRef CAS.
- F. Lipnizki, Membrane Technology: Volume 3: Membranes for Food Applications, 2010, 3, 1–24 Search PubMed.
- A. D. Stickland, S. J. Skinner, R. G. Cavalida and P. J. Scales, Sep. Purif. Technol., 2018, 198, 31–37 CrossRef CAS.
- Z. J. Ren and K. Pagilla, Pathways to Water Sector Decarbonization, Carbon Capture and Utilization, IWA Publishing, 2022 Search PubMed.
- N. Mosier, C. Wyman, B. Dale, R. Elander, Y. Y. Lee, M. Holtzapple and M. Ladisch, Bioresour. Technol., 2005, 96, 673–686 CrossRef CAS PubMed.
- D. B. Hodge, M. N. Karim, D. J. Schell and J. D. McMillan, Bioresour. Technol., 2008, 99, 8940–8948 CrossRef CAS PubMed.
- C. M. Payne, B. C. Knott, H. B. Mayes, H. Hansson, M. E. Himmel, M. Sandgren, J. Ståhlberg and G. T. Beckham, Chem. Rev., 2015, 115, 1308–1448 CrossRef CAS PubMed.
- L. R. Lynd, A. M. Guss, M. E. Himmel, D. Beri, C. Herring, E. K. Holwerda, S. J. Murphy, D. G. Olson, J. Paye, T. Rydzak, X. Shao, L. Tian and R. Worthen, Industrial biotechnology: microorganisms, 2017, vol. 1, pp. 365–394 Search PubMed.
- A. Abbassi-Guendouz, D. Brockmann, E. Trably, C. Dumas, J.-P. Delgenès, J.-P. Steyer and R. Escudié, Bioresour. Technol., 2012, 111, 55–61 CrossRef CAS PubMed.
- J. J. Stickel, B. Adhikari, D. A. Sievers and J. Pellegrino, J. Chem. Technol. Biotechnol., 2018, 93, 2181–2190 CrossRef CAS.
- Y. Li, M. R. Bilad and I. F. J. Vankelecom, J. Membr. Sci., 2014, 452, 165–170 CrossRef CAS.
- A. Bokhary, A. Tikka, M. Leitch and B. Liao, J. Membr. Sci. Res., 2018, 4, 181–197 CAS.
- T. Kinnarinen, M. Golmaei and A. Häkkinen, Ind. Eng. Chem. Res., 2013, 52, 14955–14964 CrossRef CAS.
- M. Cheng, X. Xie, P. Schmitz and L. Fillaudeau, Sep. Purif. Technol., 2021, 265, 118293 CrossRef.
- M. Galbe, L. Pilcher and C. Roslander, Separation of Solid Residues after SSF and SHF in Fuel Ethanol Production from Spruce, Dept. of Chemical Engineering1, Lund University, 2001.
- M. Y. Jaffrin, J. Membr. Sci., 2008, 324, 7–25 CrossRef CAS.
- C. Nurra, C. Torras, E. Clavero, S. Ríos, M. Rey, E. Lorente, X. Farriol and J. Salvadó, Bioresour. Technol., 2014, 163, 136–142 CrossRef CAS PubMed.
- P. O. Saboe, E. G. Tomashek, H. R. Monroe, S. J. Haugen, R. L. Prestangen, N. S. Cleveland, R. M. Happs, J. Miscall, K. J. Ramirez, R. Katahira, E. C. D. Tan, J. Yan, N. Sun, G. T. Beckham and E. M. Karp, Green Chem., 2022, 24, 3152–3166 RSC.
- W. Zhang, W. Liang and X. Xie, J. Water Process Eng., 2022, 49, 1–13 Search PubMed.
- A. Pinilla, J. C. Berrio, E. Guerrero, J. P. Valdés, D. Becerra, P. Pico, L. Vargas, S. Madsen, T. R. Bentzen and N. Ratkovich, J. Water Process Eng., 2020, 36, 1–10 Search PubMed.
- Y. Chen, M. A. Stevens, Y. Zhu, J. Holmes and H. Xu, Biotechnol. Biofuels, 2013, 6, 8 CrossRef CAS PubMed.
- X. Chen, E. Kuhn, E. W. Jennings, R. Nelson, L. Tao, M. Zhang and M. P. Tucker, Energy Environ. Sci., 2016, 9, 1237–1245 RSC.
- X. Chen, N. Crawford, W. Wang, E. Kuhn, D. Sievers, L. Tao and M. Tucker, ACS Sustainable Chem. Eng., 2019, 7, 1633–1641 CrossRef CAS.
- J. J. Stickel, J. S. Knutsen, M. W. Liberatore, W. Luu, D. W. Bousfield, D. J. Klingenberg, C. T. Scott, T. W. Root, M. R. Ehrhardt and T. O. Monz, Rheol. Acta, 2009, 48, 1005–1015 CrossRef CAS.
- L. Rosgaard, P. Andric, K. Dam-Johansen, S. Pedersen and A. S. Meyer, Appl. Biochem. Biotechnol., 2007, 143, 27–40 CrossRef CAS PubMed.
- J.-P. Bonnet, L. Devesvre, J. Artaud and P. Moulin, Eur. J. Lipid Sci. Technol., 2011, 113, 1019–1025 CrossRef CAS.
- S. Yanniotis, S. Skaltsi and S. Karaburnioti, J. Food Eng., 2006, 72, 372–377 CrossRef.
- M. L. Sheely, Ind. Eng. Chem., 1932, 24, 1060–1064 CrossRef CAS.
- Y. S. Polyakov and A. L. Zydney, J. Membr. Sci., 2013, 434, 106–120 CrossRef CAS.
- N. Martins-West, A. Martin-Ryals, B. Maxwell and L. Schideman, Front. Bioeng. Biotechnol., 2023, 11, 1242927 CrossRef PubMed.
- D. A. Sievers, L. Tao and D. J. Schell, Bioresour. Technol., 2014, 167, 291–296 CrossRef CAS PubMed.
- R. E. Davis, N. J. Grundl, L. Tao, M. J. Biddy, E. C. Tan, G. T. Beckham, D. Humbird, D. N. Thompson and M. S. Roni, Process Design and economics for the conversion of lignocellulosic biomass to hydrocarbon fuels and coproducts: 2018 biochemical design case update; biochemical deconstruction and conversion of biomass to fuels and products via integrated biorefinery pathways, National Renewable Energy Lab.(NREL), Golden, CO (United States), 2018 Search PubMed.
- S. Kim and B. E. Dale, Biofuels, Bioprod. Biorefin., 2016, 10, 819–832 CrossRef CAS.
- K. Gruskevica and L. Mezule, Membranes, 2021, 11, 131 CrossRef CAS PubMed.
- L. Yu, J. Ma and S. Chen, Bioresour. Technol., 2011, 102, 1012–1018 CrossRef CAS PubMed.
- S. S. Bhagwat, Y. Li, Y. R. Cortés-Peña, E. C. Brace, T. A. Martin, H. Zhao and J. S. Guest, ACS Sustainable Chem. Eng., 2021, 9, 16659–16669 CrossRef CAS.
- D. R. Burke, J. Anderson, P. C. Gilcrease and T. J. Menkhaus, Biomass Bioenergy, 2011, 35, 391–401 CrossRef CAS.
- D. B. Hodge, M. N. Karim, D. J. Schell and J. D. McMillan, Appl. Biochem. Biotechnol., 2009, 152, 88–107 CrossRef CAS PubMed.
- T. Zsirai, H. Qiblawey, M. J. A-marri and S. Judd, J. Membr. Sci., 2016, 516, 56–63 CrossRef CAS.
- A. Brou, L. Ding, P. Boulnois and M. Y. Jaffrin, J. Membr. Sci., 2002, 197, 269–282 CrossRef CAS.
- L. Li, L. Ding, Z. Tu, Y. Wan, D. Clausse and J.-L. Lanoisellé, J. Membr. Sci., 2009, 342, 70–79 CrossRef CAS.
- C. Torras, J. Pallares, R. Garcia-Valls and M. Y. Jaffrin, Desalination, 2009, 235, 122–138 CrossRef CAS.
- A. Sluiter, B. Hames, R. Ruiz, C. Scarlata, J. Sluiter and D. Templeton and et al., National Renewable Energy Laboratory, Golden, 2006, 11, 65–71.
- J. B. Sluiter, R. O. Ruiz, C. J. Scarlata, A. D. Sluiter and D. W. Templeton, J. Agric. Food Chem., 2010, 58, 9043–9053 CrossRef CAS PubMed.
- F. R. Menter, AIAA J., 1994, 32, 1598–1605 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: See SLS_ESI.docx and SLS_Data_S1.xlsx. See DOI: https://doi.org/10.1039/d4gc04533e |
| ‡ Current address: LanzaTech, Skokie, IL 60077. |
| § Current address: Crysalis Biosciences, Louisville, CO 80027. |
| This journal is © The Royal Society of Chemistry 2024 |