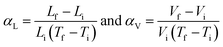Open Access Article
Open Access ArticleMultifunctional single-component organic molecular materials: ferroelectricity, negative thermal expansion, and polymorphism
Sanjay
Dutta
 ,
Lalita
Negi
,
Lalita
Negi
 and
Parthapratim
Munshi
and
Parthapratim
Munshi
 *
*
Multifunctional Molecular Materials Laboratory, Department of Chemistry, School of Natural Sciences, Shiv Nadar Institution of Eminence Deemed to be University, Delhi NCR, Uttar Pradesh 201314, India. E-mail: parthapratim.munshi@snu.edu.in
First published on 26th July 2024
Abstract
Organic materials with multifunctional properties, such as ferroelectricity, negative thermal expansion, and the phenomenon of polymorphism, have gained enormous interest from material scientists due to their unusual characteristics and unique applications. Moreover, research on single-component systems with such unusual properties is on the rise despite the necessity of satisfying strict criteria for designing such materials. This highlight provides an overview of the evolution of research on purely organic molecular ferroelectrics and thermo-responsive materials and the importance of studying polymorphism in such materials. Starting from their basics to the role of crystallographic symmetry in designing and characterizing, the mechanisms these special classes of materials follow, and the possible use of various techniques for advancing these research areas are discussed here. This highlight is expected to advance materials science research and to motivate novice researchers to explore these key research areas.
1. Introduction
Solid state science has made tremendous progress towards discovering multifunctional materials, among which ferroelectrics (FEs)1–3 have been at the forefront. Simultaneously, thermo-responsive materials with unusual negative thermal expansion (NTE) properties have gained massive interest from material scientists due to their unique characteristics.4–7 Moreover, polymorphism8 has also drawn the attention of researchers as it plays a crucial role in governing material properties.In this highlight, we aim to provide an overview of the research on purely organic molecular ferroelectrics and thermo-responsive materials and the role of polymorphism in such unusual materials. Initially, we introduce ferroelectricity and NTE properties, their applications, and the phenomenon of polymorphism. Then, we discuss the role of crystallography in designing and characterizing such materials and understanding their properties. Subsequently, we elaborate on the mechanisms these special classes of materials follow. After that, we focus on purely organic materials, especially the single-component systems. Before concluding, we discuss the possible use of various techniques for advancing these key research areas.
Ferroelectric is not related to the metal Fe (iron) as its name suggests, but it is analogous to ferromagnetism.9 Like ferromagnetic systems, FE materials consist of multiple domains comprised of electric dipoles. Domains10 are small regions within the FE crystal where a group of electric dipoles are aligned in the same direction. Under the application of a strong external electric field (E), these domains line up along its direction, resulting in net polarization (P). This leads to separation of the positive and negative poles, similar to the magnetic dipoles in iron, where the north and south poles are created under a strong magnetic field. FEs are usually accompanied by temperature-triggered structural changes to undergo a reversible ferroelectric–paraelectric phase transition, resulting in the generation and vanishing of spontaneous polarization (Ps). The net polarization in the FE materials is reversed or reoriented upon applying E. Moreover, due to their electrical bi-stability, ferroelectrics experience electrical displacement and display a hysteresis loop between P and E (Fig. 1). These characteristics are paramount for fabricating storage devices such as FeFET2,3 and FeRAM.2,3 Ferroelectrics can also be used as capacitors because these materials obey the Curie–Weiss law, and the dielectric constant rises rapidly during the ferroelectric to paraelectric transition, known as the Curie temperature (Tc).1 The parameters that define the characteristics of FE materials are Ps, remnant polarization, Pr, and the coercive field, Ec (Fig. 1). The Ps value represents the maximum polarization induced in a FE material at a high E. The Pr value indicates the amount of polarization the material can retain after removing E, i.e. at E = 0 kV cm−1. Ec is the electric field required to reverse the polarization direction, i.e. to bring the net polarization of the material to zero (P = 0 μC cm−2). The figure of merit of FE materials is assessed based on their Ps, Pr, and Ec values. Higher values of Ps and Pr and lower values of Ec signify superior characteristics of FE materials. Materials with low Ec find application in low-voltage FE devices.11
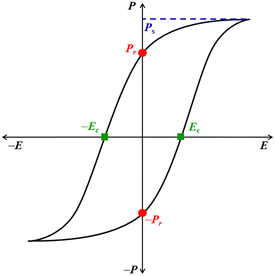 | ||
| Fig. 1 Typical hysteresis loop (P vs. E) of a ferroelectric material and its associated characterization parameters. | ||
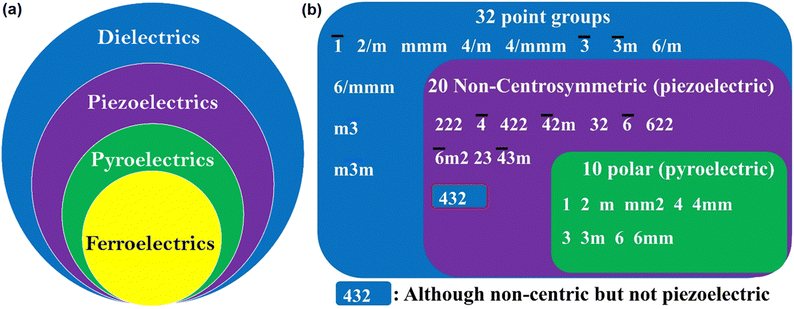
As shown in Fig. 2a, FEs are the lowest sub-group of dielectrics. They can be used in many applications due to their cross-correlation phenomena, such as piezoelectricity,1 pyroelectricity1 and second harmonic generation (SHG).12,13 In piezoelectric materials, due to electro-mechanical coupling, stress changes the electric P, and conversely, E produces strain.1,14 Thus, these materials find application in ultrasonic motion sensors, actuators, transducers, inkjet printers, and mechanical harvesters. The thermo-electric coupling leads to pyroelectric behaviour, resulting in the change in P due to uniform heating and cooling. This effect has been used in infrared detection, thermal imaging and energy harvesting.1,15 Furthermore, the polar nature of FE materials also leads to electro-optic effects such as SHG, terahertz light emission and photovoltaic effects.
FEs had come to the foray of research as early as 1920 when J. Valasek discovered ferroelectricity in sodium potassium tartrate salt (KNaC4H4O6), also known as Rochelle salt.16,17 However, for the next two decades, no FEs were discovered. Consequently, the research community presumed it was the biggest serendipity of nature until the discovery of potassium dihydrogen phosphate (KH2PO4; KDP) as a H-bonded FE in 1935.18 Subsequently, the inorganic oxide barium titanate (BaTiO3) with perovskite structure was discovered as FE material in 1945,19 which triggered the research in this important area. Thus, in the following years, the other perovskite structures20 such as lead zirconate titanate (Pb(ZrxTi1−x)O3), bismuth ferrite (BiFeO3), and lithium niobate (LiNbO3) came to the picture. These inorganic ferroelectrics have been a subject of active research for over 50 years and are used in many industrial and technological applications.
The usual phenomenon of expansion of solids with an increase in temperature is known as positive thermal expansion (PTE), which has been exploited in solid-state chemistry. Due to change in temperature, solid materials may exhibit interesting properties leading to important applications such as heat-stimulated infrared detectors in pyroelectric materials,15 and the generation of thermo-responsive switching materials.21,22 However, the expansion of solids upon heating hinders its applicability: for example, in large construction elements such as railway tracks, roads, bridges, and containers of liquefied natural gas and small precision devices such as fibre optic systems, organic light-emitting diodes (OLEDs), organic field-effect transistors (OFET), thin-films, catalyst supports, etc.6,23,24 Nevertheless, the applications of multifunctional materials require not only robust physical phenomena but also controlled thermal expansion behaviour, as it enhances both lifetime and reliability. The effect of expansion upon heating can be correlated to the asymmetric shape of the Lennard-Jones potential energy well of a diatomic molecule (Fig. 3). Higher vibrational levels get populated as the molecule is heated up, and the gap between the molecules increases.6
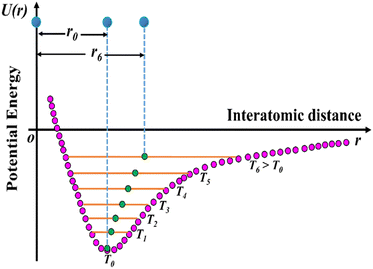 | ||
| Fig. 3 Schematic diagram of the potential energy well of paired atoms (adapted and modified from ref. 6). | ||
The thermal expansion in solids is formally quantified with the coefficient of thermal expansion (CTE), α, which can be calculated using the following equation:
Thermal expansion directions are identified by considering the principal axes, the set of orthogonal axes, X1, X2 and X3, along which thermal expansion varies linearly.25 Thermal expansion is a directional property and depends on the symmetry of the crystal system. For cubic systems, expansion is isotropic in all three directions. Hence αV = 3αL. However, for the non-orthogonal system, the expansion is anisotropic and has different magnitudes of thermal expansion along the principal axes. The volumetric expansion, αV, can be calculated by adding α1, α2, and α3, which are the CTE along each principal axis that are perpendicular to each other.
For inorganic compounds, the magnitude of αV lies in the range of 0–20 M K−1, and for molecular materials, it usually lies in the range of 100–300 M K−1.25 There are several techniques for monitoring thermal expansion in a solid. However, calculating the CTE using unit-cell parameters obtained via single-crystal X-ray diffraction (SCXRD) is one of the most commonly used methods. PASCal26 and Win_Strain27 are widely used to calculate the CTE for non-orthogonal crystal systems.
Contraction and expansion of materials upon heating and cooling, respectively, is termed NTE, a counter-intuitive phenomenon.4–7 This special class of materials with such unusual properties can counter the PTE characteristics of the material.28 However, the limited availability of NTE materials hinders the steady progress in this area of research. Thermal contraction was first documented in 1907 in quartz and silicates. Later, in 1948, NaZr2(PO4)3 (NZP)29 was reported to have an anisotropic NTE of αL = −0.4 M K−1 in the temperature range of 298–1273 K. The isotropic NTE effect was first discovered in 1996 by Sleight et al.30 in ZrW2O8, which has a CTE value of −9 M K−1 over a wide temperature range of 0.3 to 1050 K. This has led to the significant progress of NTE-based studies in solid-state chemistry. Ice is another popular example of NTE material which displays NTE below 75 K due to low-energy transverse vibrational modes.31 The emergence of the NTE phenomenon provides an excellent opportunity to control both physical and thermo-responsive properties simultaneously, especially in the case of functional materials such as dielectric, piezoelectric, pyroelectric, magnetic and optical materials. Usually, NTE characteristics are noticed in inorganic systems. Most isotropic NTEs are found in open framework structures such as AM2O8,32 AM2O7,33 A2M3O12,34 zeolites35–37 and ruthenium-based fluorides.38–40 These materials experience NTE due to the transverse vibration of the bridging atom, which includes oxygen and fluorine. The other mechanisms driving the NTE phenomenon are magnetic transition,41 charge transfer,42,43 and spontaneous volume ferro-electrostriction,44,45 which are primarily prominent in inorganic functional materials.
NTE in FE materials is not uncommon.6 However, the coexistence of FE and NTE has been reported predominantly in inorganic oxides,46–48 benzo[18]crown-6 based metal complexes,49 and dabcoHCl·3H2O.50 The report on the dabco complex demonstrated that the NTE occurs due to the rotation of water molecules, and the supramolecular architecture involving linear N–H+⋯N bonds led to the FE behaviour. However, its anhydrous polar form divests these unusual properties. The NTE effect in FE materials generally involves multiple competing mechanisms, which are material-specific and depend on the complexity of the structural, electronic, and thermodynamic factors. NTE and FE properties are directional and are linked to temperature. While the anisotropy in a crystal structure is essential for the emergence of NTE and FE characteristics, the temperature variation can lead to a non-uniform response of the material due to the asymmetric arrangement of atoms in the crystal lattice. Moreover, under an external E, the macroscopic P reversal occurs in FE materials due to the reorientation of electric dipoles, which induces strain in the lattice with an increase or decrease in temperature, leading to lattice contraction or expansion. Furthermore, with the temperature change, the FE materials undergo structural phase transitions, which may trigger lattice softening in specific directions, leading to NTE along those directions. Further elucidation of the origin of the coexistence of these intriguing phenomena warrants more studies on versatile systems and delving into the role of microscopic interactions.
Polymorphism,8 the phenomenon of the existence of a compound in multiple solid forms, has been widely studied in molecular materials for tuning their properties as it can significantly influence the material properties.51–55 Polymorphs exhibit differences in structural, thermodynamic, and other physical properties. Often, polymorphs are categorised based on their molecular conformation, packing, colour, thermodynamic stability, etc. Accordingly, polymorphism is classified as conformational polymorphism, which arises due to the existence of different conformers of the same molecule; packing polymorphism, which arises due to the difference in molecular packing of the polymorphs in their crystal lattice; colour polymorphism, which arises due to the difference in the colour of the polymorphic crystals, etc. Therefore, polymorphic materials can display distinct properties even with the slightest changes in their crystal structures.56–58 Although polymorphs occur frequently in molecular crystals, their existence in organic materials with exotic properties is scarce.54,59,60 Some of us have recently demonstrated that polymorphic forms exhibit distinct multifunctional properties. In the case of 2-(4-(trifluoromethyl)-phenyl)-1H-phenanthro[9,10-d]imidazole, it exhibits FE and NTE properties in its various crystal forms – trimorphs and hydrates (Fig. 4).61 One of the two polar forms exhibits FE characteristics, and the other displays a large reversible NTE below room temperature (RT). Further, the non-centrosymmetric hydrated form also experiences NTE below RT, but the centrosymmetric forms divest these properties. The other polymorphic materials with FE or NTE characteristics in organic materials have been highlighted in the following sections.
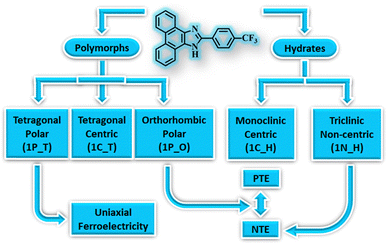 | ||
| Fig. 4 Multifunctional properties of polymorphic and hydrated forms of 2-(4-(trifluoromethyl)-phenyl)-1H-phenanthro[9,10-d]imidazole, a purely organic material. | ||
2. Ferroelectricity
2.1. Crystallographic perspective
In materials science, crystallographic symmetry plays a critical role in identifying the structural phases of the solids and helps derive their structure–property relationships. The two basic symmetry operations in crystallography, rotation (n) and reflection (m) define the symmetry of a point in space. In crystallography, 32 point groups and 230 space groups defining the microscopic and macroscopic properties of the crystalline materials62 are distributed among the 14 Bravais lattices and seven crystal systems, from higher to lower symmetry as cubic, hexagonal, rhombohedral (trigonal), tetragonal, orthorhombic, monoclinic and triclinic. Out of 32-point groups, 11 are centrosymmetric, and the remaining 21 are non-centrosymmetric (Fig. 2b). The 21 non-centrosymmetric point groups are further classified into 10 polar point groups and the rest into non-polar point groups. The lack of centre of inversion has a paramount effect on material properties, leading to numerous important physical properties in solid state science such as SHG, piezoelectricity, pyroelectricity and most importantly, ferroelectricity.63,64 FE materials must crystallize in one of the 10 polar point groups, and the corresponding paraelectric (PE) phase at a higher temperature must belong to one of the 32-point groups with a higher symmetry than the FE phase, as listed in Fig. 2b. However, introducing homochirality in a molecule can enhance the probability of a material crystallising in the polar space group. The chiral molecules crystallize in chiral point groups. There are 11 chiral point groups, of which five are polar, so there is an increased probability (5/11 vs. 10/32) that the molecule will crystallize in the polar point group.65Based on the Curie symmetry principle,66 the symmetry of the FE phase should be a maximal subgroup of the higher symmetric PE phase along which the direction of Ps exists. In light of this group-to-subgroup relationship, Aizu has identified 88 combinations of point groups for the PE to FE phase transition.67 If the PE phase crystallizes in the centrosymmetric point group, the FE is considered reversible, where Ps can be reversed under E. If the PE phase exists in the polar point group, then the FE is termed reorientable FE, where the direction of Ps is reoriented instead of reversing. Reorientable ferroelectrics are rare and fall into the category of relaxor-type FE. Moreover, under the guidance of the Curie symmetry-breaking principle, based on the point group symmetry of the known phase (PE), the symmetry and polarization direction of the other phase (FE) can be deduced using the Aizu relationship. Further, point group symmetry of the FE phase and its corresponding jump from the low temperature and low symmetric phase to the high temperature and high symmetry PE phase during symmetry breaking defines the number of allowed directions the Ps vector can have in FEs. These are then classified as (1) uniaxial (Rochelle salt, tri-glycine sulphate, LiNbO3, etc.) and (2) multiaxial (BaTiO3, PZT, etc.). In the former case, the Ps vector can reorient itself only in two polarization directions under E. For the latter case, the polarization vector can reorient itself in more than two polarization directions. As mentioned above, the point group of the FE phase is a subgroup of the PE phase. Point groups in the PE phase have various isomorphic subgroups whose polar direction corresponds to the direction of Ps, and the maximal one comprising the most symmetry elements along the polarization direction is the FE point group. Therefore, the number of polarization directions in the FE phase can be defined as n = NPE/NFE, where NPE and NFE represent the sum of symmetry elements in the PE and FE point groups, respectively. Thus, when n = 2, the FEs are uniaxial with only two opposite polarization directions, and more than two polarization directions characterize multiaxial FEs. The greater the symmetry change between the PE and FE phase, the higher the equivalent polarization directions a FE material will have. For example, in the case of LiNbO3, both the PE space group, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c (NPE = 4), and the FE space group, R3c (NFE = 2), belong to the trigonal crystal system. Closer lattice symmetries lead to the arousal of uniaxial nature.68 Similarly, diisopropylammonium bromide, a molecular FE with a high Tc (426 K) and a large Ps (23 μC cm−2), is also uniaxial with an Aizu notation of 2/mF2.69 FE transitions from a cubic crystal system to one with much lower symmetry are generally multiaxial, and the n value can be as high as 48. For instance, in BaTiO3, which is a multiaxial system, the successive phase transitions from cubic Pm
c (NPE = 4), and the FE space group, R3c (NFE = 2), belong to the trigonal crystal system. Closer lattice symmetries lead to the arousal of uniaxial nature.68 Similarly, diisopropylammonium bromide, a molecular FE with a high Tc (426 K) and a large Ps (23 μC cm−2), is also uniaxial with an Aizu notation of 2/mF2.69 FE transitions from a cubic crystal system to one with much lower symmetry are generally multiaxial, and the n value can be as high as 48. For instance, in BaTiO3, which is a multiaxial system, the successive phase transitions from cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (NPE = 48) to tetragonal P4mm (NFE = 8) at 393 K, to orthorhombic Amm2 (NFE = 4) at 278 K, and then to R3m (NFE = 6) at 183 K lead to multiaxial ferroelectric behaviour with 6, 12, and 8 equivalent polarization directions.
m (NPE = 48) to tetragonal P4mm (NFE = 8) at 393 K, to orthorhombic Amm2 (NFE = 4) at 278 K, and then to R3m (NFE = 6) at 183 K lead to multiaxial ferroelectric behaviour with 6, 12, and 8 equivalent polarization directions.
2.2. Ferroelectricity mechanisms
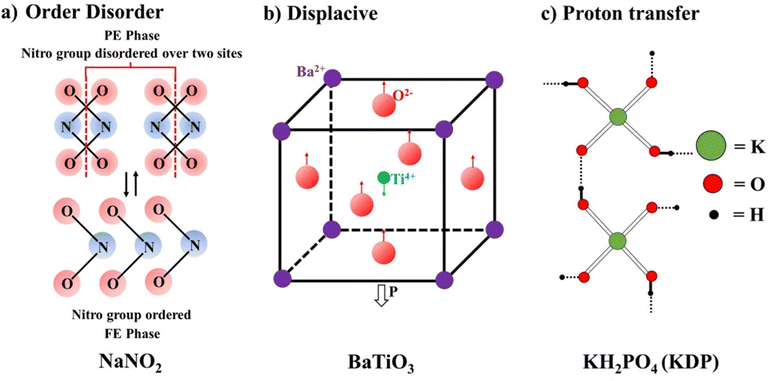
Based on the type of chemical bonding, the ferroelectrics are classified as H-bonded ferroelectrics, e.g. KH2PO4, Rochelle salt, tri-glycine sulphate, etc., and inorganic oxides having a perovskite structure, e.g. BaTiO3, PZT, etc. The third classification is based on the (1) order–disorder, (2) displacive, and (3) proton transfer mechanisms.Further, an optically controlled polarization switching mechanism has been explored in the domain of inorganic FEs. Various photo-excited electronic effects, such as flexoelectric and photovoltaic, have been studied to gain photocontrol in such materials. Light-driven effects, such as the flexoelectric effect due to photoexcitation of electronic effects to control optical polarization, have been seen in the case of SrTiO3.74 Some specific organic molecules have recently been exploited to generate polarization using light as a stimulus.75
2.3. Organic ferroelectrics
Though the first FE material, Rochelle salt16,17 is an organic salt, the past century has seen the dominance of inorganic ceramics, and the number of FEs that have come to the fore are mainly inorganic oxides and polymeric systems. Traditionally, inorganic ceramics have been used for many practical electronic applications due to their superior FE characteristics and robust piezoelectric behaviour. However, using inorganic compounds containing heavy elements has become a serious global concern, especially regarding health and the environment. Thus, the scientific community was forced to look for alternatives, leading to the resurgence of organic FEs in the past few decades due to their benign nature, mechanical flexibility, lightweight, environmental friendliness, cost-effective production and easy processing.76–81 Further, organic electronics provide design flexibility to tune the properties and enhance their performance and durability. Accordingly, organic FE devices can be portable, flexible, wearable, biocompatible and usable as economical medical devices.The order–disorder mechanism in multicomponent systems led to a significant development of molecular FEs. Sachio et al. developed several multicomponent FEs based on acid–base supramolecular co-crystals with heteronuclear hydrogen bonds, which undergo the abovementioned mechanism. Some examples are phenazine-chloranilic acid,82 and binary combinations of 2,5-dihalo-3,6-dihydroxy-p-benzoquinones with bases such as phenazine,83 5,5-dimethyl bipyridine,84 and 2,3-di(2-pyridinyl)pyrazine.85 The ferroelectricity in these systems amounts to the degree of proton transfer, which strongly depends on the acidity and basicity of the conformers. Based on the combination, there could be two types of supramolecular systems, neutral and ionic. Harada et al. used globular-shaped molecules to design molecular FEs, especially in plastic crystals.86,87 The globular molecular structure in plastic crystals can easily undergo order–disorder transition due to the low rotational barrier, which led to the development of some multiaxial FEs such as tetramethylammonium tetrachloroferrate(III)87 and tetramethylammonium bromotrichloroferrate(III).87
Further, Xiong et al. developed a metal-free perovskite-based order–disorder type FE.88 Typically, perovskites have a three-dimensional (3D) ABX3 structure in which the A cations are located in the 3D corner-sharing framework of BX6 octahedra (B represents the other cation, and X is an anion). Such perovskites represent one of the most pursued forms of isotropic ferroelectrics. The globular-shaped molecules based on DABCO derivatives have been used to design such molecular FEs. MDABCO-NH4I3 is one such derivative, which displays FEs with multiaxial characteristics above RT. In this case, the large organic cations (MDABCO), small NH4+, and halide anions (I−) occupy the A−, B−, and X-sites, respectively. The B-site cations are also involved in the NH⋯X hydrogen bonds with the surrounding X-site anions. The phase transition involves a cubic PE structure and a rhombohedral FE structure at 448 K, accompanied by a large off-centred displacement of the A- and B-site ions. This leads to a multiaxial nature with the Aizu notation67 of 432F3, having eight polarization axes along [111]. The high Ps of 22 μC cm−2 is observed due to the synergistic effect of two distinct mechanisms, ionic displacement and order–disorder orientation. The other examples are diisopropylammonium bromide,69 diisopropylammonium chloride70 and guanidinium perchlorate89 with Ps of 23, 8.9 and 8.4 μC cm−2, respectively.
Furthermore, efforts have been made to discover proton transfer mechanism-based organic FEs via database mining.90 The study also proposed density functional theory-based prediction of Ec in such systems.
Finally, the development of isotropic molecular FEs65,91 eased the fabrication of thin film devices. Conventional organic FEs with highly anisotropic crystal structures cannot work unless their crystal orientation leads to a uniaxial polarization in the desired direction. In contrast, the nearly isotropic characters of possible polarization vectors guarantee efficient switching, even in randomly oriented crystals such as polycrystalline thin films and compacted pellets.
2.4. Single-component organic ferroelectrics
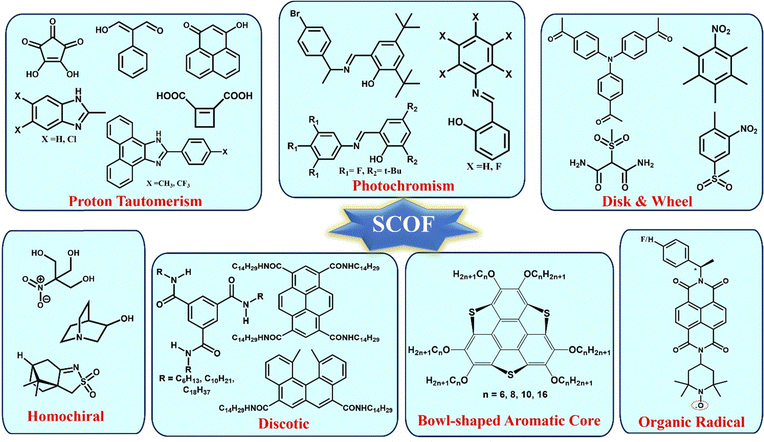
The multicomponent systems comprised of salts66,71,92 and co-crystals81,93 have certain disadvantages, which can be overcome through single-component organic ferroelectrics (SCOFs). The concern regarding salt systems is that they often contain metal ions, which leads to toxicity. However, the addition of metal ions may enhance Ps and Tc. Co-crystals, although benign, suffer from lower thermal stability and shelf life, hindering their applicability. These challenges have been overcome in the case of SCOFs. However, in the case of SCOFs, due to the thermal robustness of their FE phase, the Tc is usually hidden beyond its thermal stability. Various types of SCOFs reported in the literature are summarized below (Fig. 6).![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O). Squaric acid undergoes tautomerization between the keto and enol forms (Fig. 7a), exhibiting strong coupling between the proton and π-electron system. This type of prototropic system reinforces intra or intermolecular hydrogen bonds synergistically with the augmentation of the π-system delocalization, defined as the resonance-assisted H-bond (RAHB).98–100 The FE systems developed under this principle are defined as proton tautomerization type ferroelectrics, and the corresponding mechanism is known as the proton tautomerism mechanism (PTM)80 as illustrated in Fig. 7b.
O). Squaric acid undergoes tautomerization between the keto and enol forms (Fig. 7a), exhibiting strong coupling between the proton and π-electron system. This type of prototropic system reinforces intra or intermolecular hydrogen bonds synergistically with the augmentation of the π-system delocalization, defined as the resonance-assisted H-bond (RAHB).98–100 The FE systems developed under this principle are defined as proton tautomerization type ferroelectrics, and the corresponding mechanism is known as the proton tautomerism mechanism (PTM)80 as illustrated in Fig. 7b.
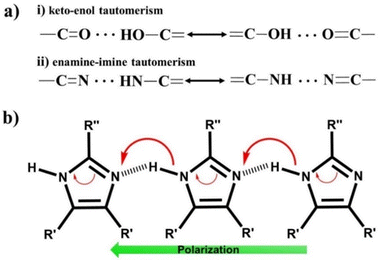 | ||
| Fig. 7 (a) Tautomeric system and (b) proton tautomerism mechanism in enamine-imine based single-component organic ferroelectrics. | ||
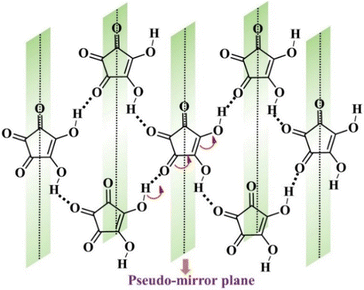
In addition to proton tautomerization, the other prime factors for designing FE systems are the presence of inherent molecular symmetry higher than C1101 and the ability of a polar structure to have hidden pseudosymmetry, which persists in the PE phase. The concept of pseudosymmetry in single-component systems is based on the intrinsic mechanism of ferroelectricity, where there is a subtle deviation of the polar structure in the FE state from the centrosymmetric structure, thus ensuring easier polarization switching. This principle has been utilised in the past by Zikmund et al.102 to predict the potential FE candidate. They discovered weak ferroelectricity in cyclohexane-1,1α-diacetic acid.103 The hidden pseudosymmetry in the proton transfer type FEs can be identified by the global crystal symmetry of the proton whose position defines the crystal polarity. Local psuedosymmetries in the crystal structures can be identified using the ADDSYM option in the PLATON program.95 Thus, based on this initial hypothesis, researchers started to explore systems consisting of tautomeric units to characterize them as FEs. The breakthrough study in this direction was achieved in 2010 when Sachio et al. discovered croconic acid (CA) as a FE material.77 CA is a black organic dye,104 a 5-member ring of oxocarbon acids (H2CnOn) that is strongly acidic because its conjugate base (C5O52−) dianion formation is favoured due to delocalization of the π-electron within the ring. This amphoteric nature of CA leads to strong RAHB98–100 formation, thus resulting in keto–enol type of proton tautomerism and contributing to a large molecular dipole moment, which gives rise to the net polarization of 30 μC cm−2 in its crystal form. In addition to the enhanced polarization, low Ec and robust thermal stability (∼450 K) observed in CA77 can be correlated to the strong coupling between the proton and the π-electron cloud. The concept of hidden pseudosymmetry in the case of CA is illustrated in Fig. 8. The pseudo-mirror symmetry, which orthogonally crosses the pentagon of the CA ring, leads to the formation of the hypothetical PE phase (protons in disorder state) with space group Pcam, one of the minimal supergroups of the polar space group Pca21 of the FE phase. The other systems comprised of β-diketone enol O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–OH moieties as a simpler prototype for the FE tautomerism are 2-phenylmalondialdehyde and 3-hydroxyphenalenone.78
C–OH moieties as a simpler prototype for the FE tautomerism are 2-phenylmalondialdehyde and 3-hydroxyphenalenone.78
Ferroelectricity was also discovered in imidazole-based derivatives comprised of the enamine unit (Fig. 7b). These enamine–imine motifs in imidazole exhibit amphoteric behaviour, thus forming a proton D–A type molecular assembly based on linear N–H⋯N hydrogen bonds. Imidazole-based SCOFs were reported in the cases of two benzimidazole derivatives, namely, 2-methylbenzimidazole79 and 5,6-dichloro-2-methylbenzimidazole.79 Further, Fraser et al. discovered ferroelectricity in halogen-substituted imidazoles, where they confirmed the ferroelectricity based on local polarization switching using the piezo force microscopic (PFM) technique.105
Recently, some of us reported SCOF in an enamine-based motif, 2-(p-tolyl)-1H-phenanthro[9,10-d]imidazole, which exists in three polymorphic forms.54 The polar crystal form of this environmentally benign material not only displays a notable Ps of 3.0 μC cm−2, a highly stable (98%) Pr of 3.9 μC cm−2, and low Ec (6.2 kV cm−1), it perseveres the FE phase up to a record-high temperature of ∼521 K (Fig. 9a). Subsequently, the crystal undergoes an irreversible phase transition to form non-polar (1N, P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21c) and centrosymmetric (P21/n) polymorphs having distinct molecular packing in their crystal lattices. These polymorphic transformations suggested that the material loses its FE characteristics beyond ∼521 K and remains non-ferroelectric. Nevertheless, this was the thermally most stable purely organic FE crystal then. Moreover, the Ec achieved in this case is much lower (6.2 kV cm−1) than those reported for the well-known CA (14 kV cm−1) and chloro derivative of benzimidazole (60 kV cm−1) at 373 K. Our study demonstrated that the migration from benzimidazoles to phenanthroimidazoles with extended benzene rings helps maintain the FE phase at a much higher temperature. Further, the study highlighted that although the PTM triggers the generation of polarization and the polarity switching via RAHB, the low value of Ec is achieved due to the relative displacements between the two crystallographically independent molecules in its crystal lattice. This study was the first to report displacive type FE in SCOF. Otherwise, it usually occurs in inorganic oxides.
21c) and centrosymmetric (P21/n) polymorphs having distinct molecular packing in their crystal lattices. These polymorphic transformations suggested that the material loses its FE characteristics beyond ∼521 K and remains non-ferroelectric. Nevertheless, this was the thermally most stable purely organic FE crystal then. Moreover, the Ec achieved in this case is much lower (6.2 kV cm−1) than those reported for the well-known CA (14 kV cm−1) and chloro derivative of benzimidazole (60 kV cm−1) at 373 K. Our study demonstrated that the migration from benzimidazoles to phenanthroimidazoles with extended benzene rings helps maintain the FE phase at a much higher temperature. Further, the study highlighted that although the PTM triggers the generation of polarization and the polarity switching via RAHB, the low value of Ec is achieved due to the relative displacements between the two crystallographically independent molecules in its crystal lattice. This study was the first to report displacive type FE in SCOF. Otherwise, it usually occurs in inorganic oxides.
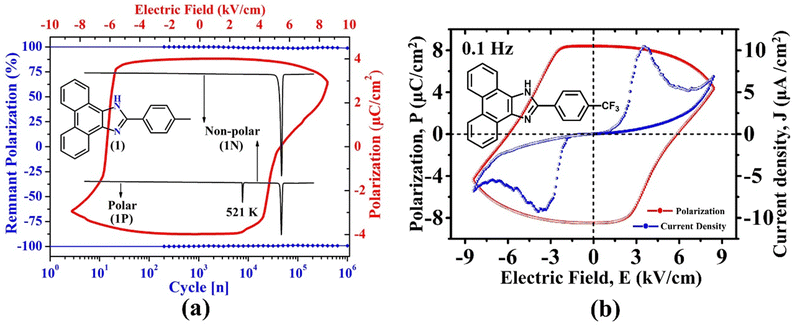 | ||
| Fig. 9 (a) Depiction of ferroelectricity, thermal stability and phase transition behaviour in 2-(p-tolyl)-1H-phenanthro[9,10-d]imidazole.54 (b) Ferroelectric loop (P vs. E) and the corresponding fatigue measurements in 2-(4-(trifluoromethyl) phenyl)-1H-phenanthro[9,10-d]imidazole.61 | ||
Further, the Ps was computationally calculated using Berry phase formalism and the DFT method with the generalized gradient approximation in the Perdew–Burke–Ernzerhof (PBE) form as implemented in the Vienna ab initio simulation package (VASP). The estimated Ps of ∼3.8 μC cm−2 compares well with that obtained from the P–E loop measurement at RT.
Furthermore, some of us discovered that the tetragonal polymorphic form (1P_T, P41) of 2-(4-(trifluoromethyl)phenyl)-1H-phenanthro[9,10-d]imidazole,61 a triflate-substituted phenanthro-imidazole, is a SCOF (Fig. 9b). In this case, the in-crystal polarization reversal measurement resulted in a Ps of ∼4.6 μC cm−2, a Pr of ∼8.3 μC cm−2 and an Ec of ∼5.8 kV cm−1 with the least leakage current. Further, based on the first-principles calculations discussed above, the Ps was predicted to be 3.1 μC cm−2, which agrees well with the experimental value. In addition to the polar FE form, this system exhibits two more polymorphs: orthorhombic polar form (1P_O, Pca21) and tetragonal centrosymmetric form (I41/a). However, the FE measurements on the pellet of 1P_O did not result in any meaningful polarization switching loop. Moreover, the Ps value estimated using VASP is also nominal (0.2 μC cm−2). Therefore, the in-crystal ferroelectric measurements were carried out only in the case of the 1P_T form.
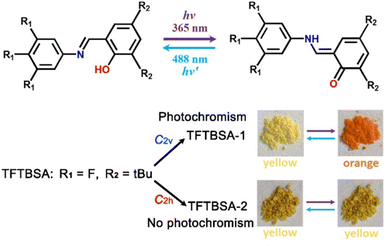 | ||
| Fig. 10 Conversion of the enol form to the trans-keto form and vice versa upon UV light irradiation (up) and photochromic and non-photochromic behaviour of the polymorphic forms TFTBSA-1 and TFTBSA-2, respectively. tBu = tert-butyl. Reprinted (used in part) with permission from ref. 75. Copyright 2021 American Chemical Society. | ||
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), where each molecule is located on the pseudo-inversion symmetry. This leads to an easy Ps switching simply by the molecular disk rotation. Although the PMNB crystal exhibits a large Pr of ∼6 μC cm−2, it experiences a very high Ec (∼100 kV cm−1) at RT and a frequency of 1 Hz along the c-axis. In the case of wheel-type FEs, the axially asymmetric substituents are used as a wheel or rotary knob. The molecules are designed in tetragonal-shaped substituents –RXYZ or triangular-shaped substituents –RXY fashion to induce a large dipole moment upon introduction of an electron-donating atom or group X and electron-withdrawing atom or group Y. Recently, 2-(methylsulfonyl)-malonamide (MSMA)114 has been reported as a wheel-type FE (Fig. 6). MSNA experiences a net polarization of 7.3 μC cm−2, a Pr of 3.8 μC cm−2, and a high Ec of ∼100–160 kV cm−1 at 3–30 Hz. Both PMNB and MSMA crystals exhibit a nearly temperature-independent relative permittivity at near RT, indicating the absence of a Tc.
), where each molecule is located on the pseudo-inversion symmetry. This leads to an easy Ps switching simply by the molecular disk rotation. Although the PMNB crystal exhibits a large Pr of ∼6 μC cm−2, it experiences a very high Ec (∼100 kV cm−1) at RT and a frequency of 1 Hz along the c-axis. In the case of wheel-type FEs, the axially asymmetric substituents are used as a wheel or rotary knob. The molecules are designed in tetragonal-shaped substituents –RXYZ or triangular-shaped substituents –RXY fashion to induce a large dipole moment upon introduction of an electron-donating atom or group X and electron-withdrawing atom or group Y. Recently, 2-(methylsulfonyl)-malonamide (MSMA)114 has been reported as a wheel-type FE (Fig. 6). MSNA experiences a net polarization of 7.3 μC cm−2, a Pr of 3.8 μC cm−2, and a high Ec of ∼100–160 kV cm−1 at 3–30 Hz. Both PMNB and MSMA crystals exhibit a nearly temperature-independent relative permittivity at near RT, indicating the absence of a Tc.
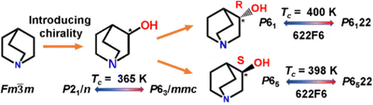 | ||
| Fig. 11 Scheme representing the introduction of homochirality in 3-quinuclidinol. Reprinted (used in part) with permission from ref. 118. Copyright 2020 American Chemical Society. | ||
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds and display FE switching.121 In the case of the hexacolumnar DLC phase above 295 K, the inversion of the dipole moment due to the conformational change of the hydrogen bond along the π-stacking column under E leads to the generation of FE switching (Fig. 12). Further, the authors used non-π-planar helicene cores bearing two −CONHC14H29 chains (Fig. 6), forming discotic molecular assemblies with 2D intermolecular interactions to achieve superior FE properties and enhance the practical utility of such systems.122 They have successfully measured excellent FE properties (Pr and Ec values of 10.7 μC cm−2 and 10.8 kV cm−1, respectively) in rac-N,N′-di(tetradecyl)-1,12-dimethyl-N5,N8-ditetradecylbenzo[c]phenanthrene-5,8-dicarboxamide which forms high-density and well-oriented ferroelectric domains in a 2D hydrogen-bonding network layer.
C hydrogen bonds and display FE switching.121 In the case of the hexacolumnar DLC phase above 295 K, the inversion of the dipole moment due to the conformational change of the hydrogen bond along the π-stacking column under E leads to the generation of FE switching (Fig. 12). Further, the authors used non-π-planar helicene cores bearing two −CONHC14H29 chains (Fig. 6), forming discotic molecular assemblies with 2D intermolecular interactions to achieve superior FE properties and enhance the practical utility of such systems.122 They have successfully measured excellent FE properties (Pr and Ec values of 10.7 μC cm−2 and 10.8 kV cm−1, respectively) in rac-N,N′-di(tetradecyl)-1,12-dimethyl-N5,N8-ditetradecylbenzo[c]phenanthrene-5,8-dicarboxamide which forms high-density and well-oriented ferroelectric domains in a 2D hydrogen-bonding network layer.
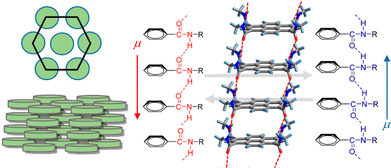 | ||
| Fig. 12 Schematic illustration of discotic hexacolumnar mesophase (left) and H-bonded 1D columnar structure with dipole (μ) inversion through the collective conformational change of the chain along the π-stacking direction (right). Reprinted (used in part) with permission from ref. 121. Copyright 2015 American Chemical Society. | ||
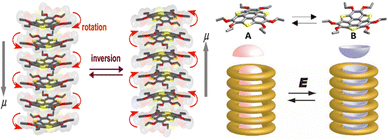 | ||
| Fig. 13 Schematic of the dipole inversion mechanism coupled with inversion of bowl-shaped (from A (up) to B (down)) conformation and skew rotation and a schematic model of the bowl-to-bowl structural inversion upon application of an electric field E, where molten –OCnH2n+1 chains surround the polar bowl column. The grey arrows indicate the dipole moment direction in each system (adapted and modified from ref. 125). | ||
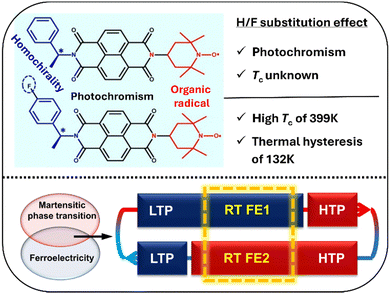 | ||
| Fig. 14 Effects of H/F substitution in NDI derivatives (top) and the combination of martensitic phase transition and ferroelectricity in S-/R-F NDI derivatives with two different ferroelectric phases at room temperature (bottom). LTP and HTP represent the low-temperature phase and high-temperature phase, respectively. RT FE1 and RT FE2 represent different ferroelectric phases at room temperature (adapted and modified from ref. 132). | ||
Additionally, biodegradable ferroelectricity is reported in the molecular crystals of 2,2,3,3,4,4-hexafluoropentane-1,5-diol (HFPD), a single-component system that exhibits a large piezoelectric response.133 The study demonstrated that the crystals can flexibly be made into thin, strain-sensing films. Moreover, HFPD exhibited promising biocompatibility with biological cells and desirable biodegradation and biosafety in physiological environments. Thus, it was envisaged that the material may find application in transient implantable electrochemical devices.
2.5. Advance methodologies to study H-bonded FEs
Conventionally, FE characterization techniques include X-ray diffraction for phase and structural analysis, P–E loop measurements to determine the macroscopic polarization and switching behaviour, and PFM experiment to visualize the domain structure and switching pattern based on amplitude and phase measurements to know the local FE behaviour. For H-bonded FEs, in addition to the conventional methodologies, advanced techniques such as neutron diffraction134 and high-resolution single-crystal X-ray diffraction experiments can be employed to understand better the FE mechanisms, especially for the order–disorder and PTM-type FEs. Charge density analysis using high-resolution X-ray and neutron diffraction data allows deriving accurate topological properties of electron densities. While neutron diffraction pinpoints the position of hydrogen atoms, high-resolution X-ray diffraction provides an opportunity to measure the degree of polarization of electron densities, which are crucial for PTM-type FEs. Moreover, neutron data allow the accurate determination of the atomic displacement parameters and lead to the efficient resolution of atomic disorders. In addition, E-dependent X-ray and neutron diffraction experiments may help monitor the dynamics of the proton due to FE switching and the corresponding π-electron delocalization. Recently, Fancher et al. performed an E-dependent neutron diffraction study on KDP crystals, a H-bonded FE.135 The study demonstrates that the macroscopic polarization reorientation is instigated by a collective change in the H-bond, leading to the reversal of the spontaneous dipole. Additionally, the decrease of secondary extinction near the Ec suggested that the inversion of macroscopic polarization is due to the nucleation and the successive growth of the new domains. Moreover, Kobayashi et al. observed electric field-induced antipolar–polar transition, along with colossal electrostriction in 2-trifluoromethyl-naphthimidazole crystals by performing an E-dependent synchrotron X-ray diffraction experiment.136 These few studies based on advanced techniques provided crucial insights towards the improved understanding of the FE mechanisms in H-bonded FEs.3. Negative thermal expansion
3.1. Mechanism of NTE
The NTE phenomenon is generally noticed in inorganic systems. Most isotropic NTE is reported in open framework structures such as AM2O8,80 AM2O7,81 A2M3O12,82 zeolites83–85 and ruthenium-based fluorides.86–88 These materials experience the NTE effect due to the transverse vibration of the bridging atom, which includes oxygen and fluorine. The other mechanisms driving the NTE phenomenon are magnetic transition,89 charge transfer90,91 and spontaneous volume ferro-electrostriction,92,93 which are mostly prominent in inorganic functional materials. The possible NTE mechanisms in inorganic solids and molecular materials are summarized in the following sections.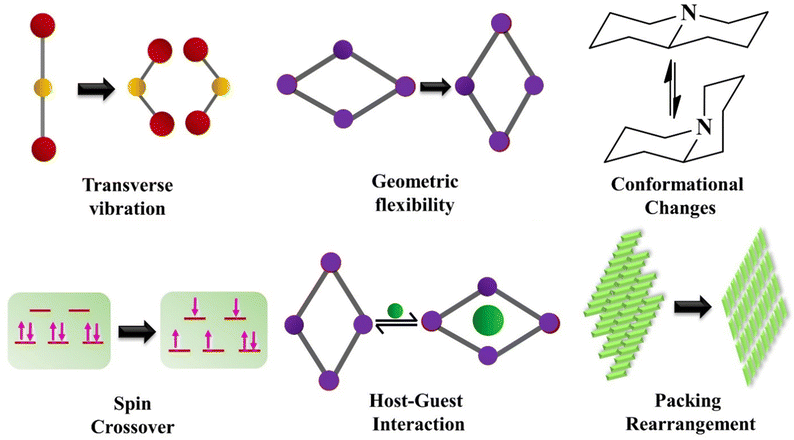 | ||
| Fig. 15 Various mechanisms leading to negative thermal expansion (NTE) behaviour in molecular materials. | ||
Williams et al.139 used the cyanide molecule as the bridging agent in Zn(CN)2 to enhance the NTE (αL = −18 M K−1) below 180 K compared to inorganic oxides such as ZrW2O8 with single-atom-supported RUM structures. The enhanced NTE effect in the case of diatom-supported RUMs is due to larger degrees of freedom. RUMs supported by a single atom are face-constrained, where an adjacent polyhedron influences the rotation of a polyhedron. However, for the diatom-supported RUMs, the polyhedron can rotate independently. Two neighbouring squares can rotate along the same or opposite directions, contributing to NTE.
Geometrical flexibility is commonly observed in the case of MOFs prepared from extended ligands, resulting in a larger void within the crystal lattice and leading to a flexible structure (Fig. 15). One of the well-known examples of flexible MOFs is MIL-53,147 which undergoes large pore (lp) and narrow pore (np) transformation upon inclusion of the guest molecule. This effect is called the breathing effect due to chemical stimuli. Further, geometrical flexibility due to temperature as a stimulus has been observed in guest-free aluminium-based MIL-53, where np to lp transformation happens above 300 K, and upon cooling, it undergoes a reversible process with a large thermal hysteresis. Furthermore, it has been observed that materials with fence-like structures undergo geometrical flexibility due to scissor-like motion.148 Perdeuterated methanol monohydrate149 is a simple molecular crystal which shows remarkable thermo-responsive behaviour with colossal anisotropic thermal expansion with αb = 462(4) M K−1, αc = 93(4) M K−1, and αa = −61(4) M K−1, along the b-, c-, and a-axis, respectively, at 155 K due to scissor-like motion. With the rise in temperature, the dynamic molecular motion of the scissor-jack-like structures leads to contraction in the orthogonal direction and expansion in the other direction.
Two salts of imidazole, imidazolium terephthalate (IMD-TPH) and imidazolium 4-hydroxybenzoate (IMD-HBC), were reported to have uniaxial NTE and biaxial PTE characteristics.150,151 The unusual behavior of the salts was elucidated based on their fencing and scissor-like motion of the 2D H-bonded network, respectively. Upon changing the imidazole with 4-methylimidazole, salt 4-methylimidazolium-4-hydroxybenzoate (4-MIMD-HBC) exhibited unusual biaxial NTE owing to the scissor-like motion with the variation of temperature.152
In organic molecular crystals, the conformational changes and packing rearrangements lead to the structures crystallizing in polymorphic forms, which often display distinct thermo-responsive effects, as was the case for the dimorphic 4,4′-methylenebis(2,6-dimethylaniline).157 The two forms crystallize in triclinic and monoclinic crystal systems and exhibit distinct thermal properties due to the striking molecular packing differences. While one polymorph experiences regular PTE, the other undergoes anisotropic NTE. Panda et al.158 observed distinct thermo-responsive behaviour in two packing polymorphs of thermo-salient crystals of (phenylazophenyl) palladium hexafluoroacetylacetonate. The α-form with head-to-head molecular stacking exhibits a uniaxial NTE of −79.2 M K−1 along the c-axis and a biaxial PTE of 260.4 and 39.4 M K−1 along the a- and b-axis. However, the β-form with head-to-tail molecular stacking shows the usual PTE.
3.2. NTE in single-component organic materials
A recent study based on a literature survey highlighted that organic materials have received great attention in the area of NTE. The study revealed that about 30% of the molecular crystals show uniaxial NTE, whereas about 5% show biaxial NTE characteristics.162 However, NTE characteristics in the case of purely organic systems are scarce. Recently, the development of organic materials with thermo-responsive properties7 has been emphasized due to certain advantages such as flexibility, benign nature, and environmental friendliness. The benign nature of the organic system allows it to adapt to physiological conditions. Thus, organic NTE materials can be utilized in dental filling. Additionally, molecular materials in their condensed phase are held together via weak interactions, such as H-bonds, coordination bonds, and weak van der Waals interactions (such as π⋯π interaction, halogen bonds, etc.).153–155 Weak interactions are highly sensitive to temperature. Therefore, a high PTE is expected for organic materials163 in the direction of weak interactions.164–166 Recently, the role of weak intermolecular interactions in controlling thermal expansion in molecular materials has been highlighted on a few occasions. The weak interactions provide enough flexibility due to a large degree of freedom, which results in some intriguing thermo-responsive and mechano-responsive behaviours such as NTE, breathing effect, and negative linear or area compressibility.Switching of uniaxial PTE to NTE in two compounds, 1,4-bis(S-3-butyn-2-ol)-benzene and 2,6-bis(S-3-butyn-2-ol)-naphthalene, with similar packing, was reported in 2018.166 The study claimed that the molecular packing arrangement and transverse vibration of some of the atoms led to this switching phenomenon. The report highlighted that the shortening of molecular length with the increase in temperature occurs due to the high thermal vibration of atoms. Very recently, Koshima et al. studied the switching of axial NTE to PTE in an enol form of N-3,5-di-tert-butylsalicylide-3-nitroaniline.167 The material also exhibits photo actuation as it undergoes photoisomerization upon light irradiation.
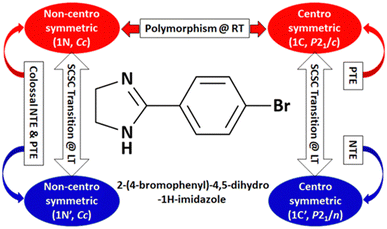 | ||
| Fig. 16 Polymorphism, phase transition, and unusual thermal expansion characteristics in halogen derivatives of 4-phenyl substituted imidazoline.168 | ||
Further, some of us reported polymorphism and hydration-driven thermo-responsive behaviour in 2-(4-(trifluoromethyl)-phenyl)-1H-phenanthro[9,10-d]imidazole (Fig. 4).61 One of the three polymorphs, the orthorhombic form 1P_O, undergoes anisotropic reversible switching from NTE (−55 M K−1) to PTE (25 M K−1) along the cell edge b at below RT (∼210 K). Moreover, while the non-centrosymmetric hydrated polymorph (1N_H, space group P1) exhibits NTE in the temperature range of 100–280 K, the centrosymmetric hydrated polymorph (space group P1) shows the usual PTE behaviour. During heating, reversible biaxial NTE (−38 M K−1 and −11 M K−1) and PTE (187 M K−1) characteristics are also noticed for 1N_H. The mechanism of NTE was investigated via molecular packing analysis in the crystal lattice as a function of temperature. In the case of 1P_O, with Z′ = 2, the A (pink) and B (red) molecules stack along [010] (Fig. 17a). The interplanar distances between the two A molecules (dA) and that between the two B molecules (dB) vary synchronously with the variation of temperature, leading to the contraction and the expansion of cell edge b and the decrease and increase of the interplanar distances dA and dB before and after the switching temperature (∼210 K), respectively (Fig. 17b). Along cell edge b, with the increase in temperature, the molecules come closer to each other (the distances dA and dB decrease) until ∼210 K. Therefore, cell edge b experiences NTE. After that, it switches to PTE when the molecules go apart (distances dA and dB increase). This synergistic decrease and increase of dA and dB with temperature leads to the anisotropic expansion and switching from NTE ↔ PTE along cell edge b upon heating and cooling, respectively. For 1N_H, the NTE and PTE arise due to the variation of the dihedral angles Φ and Ψ, as shown in Fig. 17c and d. The molecular planes intersect in an open bookcase-like fashion, and the opening and closing of the bookcase with temperature result in the expansion and contraction of the cell edges. While Φ controls the variation of the cell edge c, Ψ controls that of cell edges a and b. Upon heating, while the increase in Φ leads to the expansion of cell edges a and b, the corresponding decrease in Φ leads to the contraction of cell edge c.
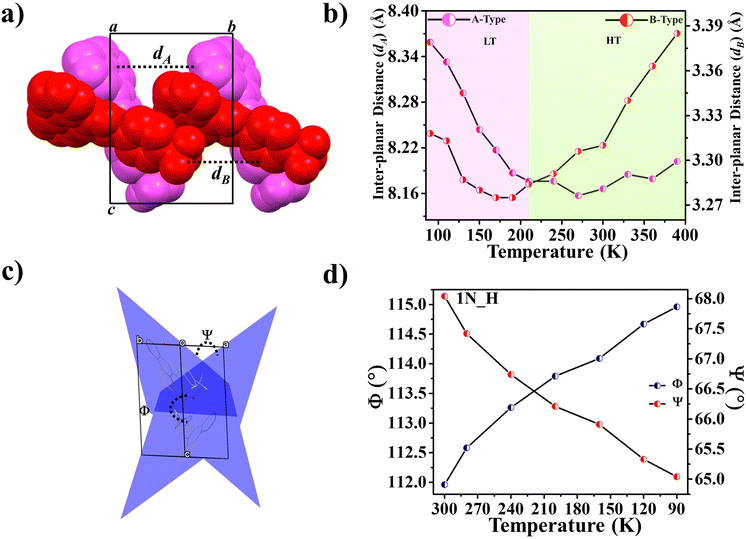 | ||
| Fig. 17 For 1P_O (Fig. 4), (a) stacking of molecules A (pink) and B (red) along [010] and (b) variation of inter-planar distances dA and dB with temperature. For 1N_H (Fig. 4), (c) dihedral angles Φ and Ψ between the molecular planes passing through the adjacent molecules A and B, forming an open bookcase-like geometry while viewing down [110] and (d) the variation of Φ and Ψ with temperature.61 | ||
3.3. NTE accompanied by order–disorder phase transformation
In the last few decades, the phase transition in molecular crystals has become an interesting topic of scientific investigation. The phase transitions are of particular interest as these studies provide the details of changes in molecular arrangements in the crystal structure and can be compared through variable temperature X-ray diffraction (VTXRD) and differential scanning calorimetry studies. Using SCXRD and PXRD techniques, the phase transition can be monitored at variable temperatures (VT). VTXRD is an ideal technique for studying disordered systems as it allows distinguishing between static and dynamic disorders. The static disorder will remain the same at VT, while the dynamic disorder may disappear. However, a limited database is available for this type of phase transition, and most of the reports belong to inorganic and multicomponent organic materials. In 2014, Shang et al. reported order–disorder-induced NTE in two ammonium Mg-formate frameworks. A few materials from the ZrW2O8 family are known to undergo order–disorder transition and show NTE.169 Chen et al. reported H-bond driven order–disorder phase transition in an inorganic NLO material, [Ag(NH3)2]2SO4.170 The order–disorder phase transition is reversible at 356 K and is associated with weak H-bonds in the crystal structure.The role of water molecules in inducing the NTE effect has been demonstrated on a few occasions. In the crystal structure of monohydrate dipeptide, tryptophylglycine (TrpGly·H2O), the NTE effect in the helical direction (c-axis) occurs due to the increasing order of water molecules enclosed in the helices.124 Szafranski reported that 1,3-diazabicyclo[2.2.2]-octane hydrochloride trihydrate (dabcoHCl·3H2O) undergoes a phase transition at 260 K and displays very strong NTE along the a- and c-axis (−529 and 33.3 M K−1, respectively) at its HT phase. At 300 K, it experiences a large αV of −386 M K−1, possibly the highest value in a molecular crystal, and the NTE occurs due to the rotation of rigid water molecules (Fig. 18).50,146
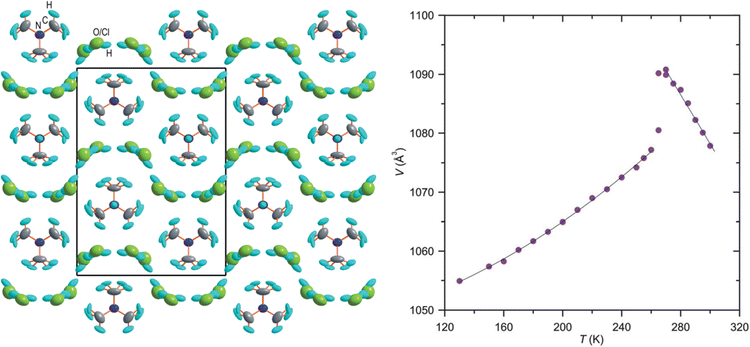 | ||
| Fig. 18 The crystal structure of the orthorhombic form of dabcoHCl·3H2O at 270 K, viewed along [100], showing the H-bonded disordered H2O molecules and Cl− anions (left). Temperature dependence of the unit-cell volume of dabcoHCl·3H2O (right). Reprinted (used in part) from ref. 50. | ||
Reports of NTE induced by order–disorder phase transition in single-component organic molecular crystals are extremely rare in the literature. Takahashi et al. reported two polymorphic forms of 2,4-dinitro anisole α and β. In the case of the β polymorph, the disordered atoms in the nitro group becomes ordered at LT (261 K) and shows small biaxial NTE (−31 and −15 M K−1).171 However, the α polymorph exhibits usual PTE behaviour. Very recently, some of us reported the thermal expansion behaviour of 2-((3,5)bis(trifluoromethyl)phenyl)-4,5-dihydro-1H-imidazole.172 This lightweight material undergoes an iso-symmetric dynamic order–disorder phase transition at LT (<150 K) (Fig. 19). Interestingly, the material exhibits PTE, near ZTE, and NTE along its respective crystallographic axes (Fig. 20) because it experiences a scissor-jack-like motion with temperature variation. The N–H⋯N hydrogen bonds in the crystal structure act as a hinge to the scissor-jack and restrict the thermal expansion along the b-axis, leading to near ZTE behaviour. The HT (298–200 K) and the LT (125–100 K) phases display uniaxial NTE with CTE of −65 and −135 M K−1 along X1 and biaxial PTE along X2 and X3, respectively. The material also exhibits a rare phenomenon of negative area expansion with CTE of −18 and −61 M K−1 for the HT and LT phases, respectively.
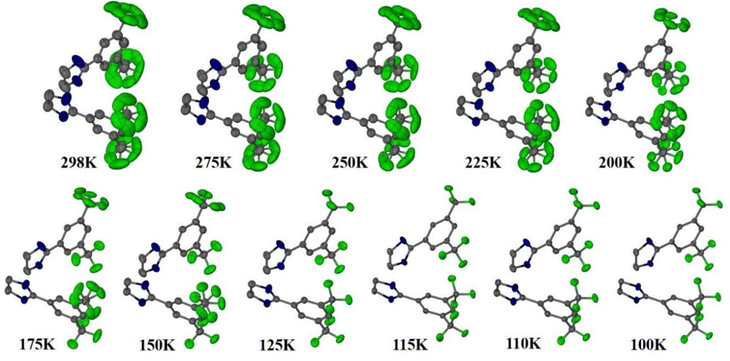 | ||
| Fig. 19 Crystal structures of 2-((3,5)bis(trifluoromethyl)phenyl)-4,5-dihydro-1H-imidazole showing the transition from its disordered phase to ordered phase. H-atoms are omitted for clarity.172 | ||
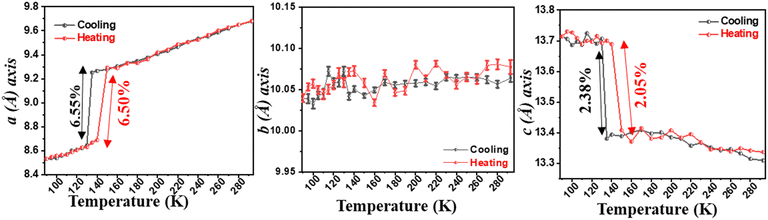 | ||
| Fig. 20 Variation of unit-cell lengths with temperature. The error bars highlighting the near ZTE behaviour are included for the b-axis.172 | ||
4. Conclusions and outlook
In this highlight, we provided an overview of the evolution of research on purely organic molecular crystals with multifunctional properties, FE and NTE, and the occurrence of polymorphism in such materials.Initially, we covered the basics of FE and NTE properties and the origin of the coexistence of these intriguing phenomena. Subsequently, we introduced the polymorphism phenomenon and its role in governing molecular properties. Further, we highlighted the crucial role of crystallographic symmetries in designing the FE materials. Furthermore, we discussed the underlying mechanisms behind the unusual FE and NTE characteristics in these special classes of materials and the importance of crystallographic techniques in characterizing FE and NTE materials. Subsequently, we focused on purely organic materials, especially the single-component organic molecular crystals, and discussed a few important cases in detail. In many cases, we discussed the existence of polymorphic forms of the FE and NTE materials and the relationship of polymorphism with the FE and NTE characteristics. We also discussed the techniques typically used for characterising FE and NTE materials and the possibility of implementing various advanced experimental techniques and theoretical approaches to advance these key research areas in materials science.
Here, we emphasized the use of organic materials and the advantage of single-component systems and summarized various principles for designing SCOFs. It was evident from the highlight that there is plenty of scope for discovering new single-component FE and NTE materials. Although the co-existence of FE and NTE properties in an organic material is yet to be discovered, we discussed that the NTE characteristic has been observed in the two polymorphic forms of a SCOF, which was a step closure to combining the FE and NTE characteristics in a single system. We expect that this highlight will guide and motivate the researchers to design such materials for practical applications in the future.
Lastly, we highlighted that due to their benign nature, flexibility, lightweight, cost-effective production, easy processing, and least toxicity, organic materials with FE and unusual thermal expansion properties are preferred over inorganic materials for application in flexible, wearable, biocompatible, reusable, economical medical devices. We envisage that this highlight will encourage scientists to explore organic materials for preparing electronic devices with precise control of thermal expansion and superior memory and energy storage capacity, e.g., sensor-based non-expansive memory devices. Further research on multifunctional organic materials is expected to yield intelligent materials for environmentally friendly applications, which may fulfil our societal needs.
Author contributions
PM has conceptualized and written the highlight. SD had written the original draft. LN contributed to the negative thermal expansion part. All the authors have contributed to editing the highlight.Data availability
No primary research results, software, or code have been included, and no new data were generated or analyzed as part of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Shiv Nadar Institution of Eminence, Delhi NCR, India, for research facilities, infrastructure, funding, and research assistantship to SD and LN. This work is supported by research grants (CRG/2018/004694 and CRG/2023/008038) from SERB, Govt. of India.References
- M. E. Lines and A. M. Glass, Principles and Applications of Ferroelectrics and Related Materials, Oxford University Press, Oxford, 2001 Search PubMed.
- J. F. Scott, Ferroelectric Memories, Springer Berlin, Heidelberg, 2000 Search PubMed.
- J. F. Scott, Science, 2007, 315, 954–959 CrossRef PubMed.
- J. S. O. Evans, J. Chem. Soc., Dalton Trans., 1999, 0, 3317–3326 RSC.
- K. Takenaka, Sci. Technol. Adv. Mater., 2012, 13, 013001 CrossRef PubMed.
- J. Chen, L. Hu, J. Deng and X. Xing, Chem. Soc. Rev., 2015, 44, 3522–3567 RSC.
- Z. Liu, Q. Gao, J. Chen, J. Deng, K. Lin and X. Xing, Chem. Commun., 2018, 54, 5164–5176 RSC.
- J. Bernstein, Strength from Weakness: Structural Consequences of Weak Interactions in Molecules, Supermolecules, and Crystals, Springer Netherlands, Dordrecht, 2002, pp. 247–260 Search PubMed.
- T. Miyazaki and H. Jin, The Physics of Ferromagnetism, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, vol. 158 Search PubMed.
- A. K. Tagantsev, L. E. Cross and J. Fousek, Domains in Ferroic Crystals and Thin Films, Springer New York, New York, NY, 2010 Search PubMed.
- Y. Noda, T. Yamada, K. Kobayashi, R. Kumai, S. Horiuchi, F. Kagawa and T. Hasegawa, Adv. Mater., 2015, 27, 6475–6481 CrossRef PubMed.
- M. Fiebig, V. V. Pavlov and R. V. Pisarev, J. Opt. Soc. Am. B, 2005, 22, 96 CrossRef CAS.
- N. E. Sherstyuk, E. D. Mishina, S. D. Lavrov, A. M. Buryakov, M. A. Marchenkova, A. S. Elshin and A. S. Sigov, Ferroelectrics, 2015, 477, 29–46 CrossRef CAS.
- K. Uchino, Ferroelectric Devices, CRC Press, 2018 Search PubMed.
- G. Sebald, D. Guyomar and A. Agbossou, Smart Mater. Struct., 2009, 18, 125006 CrossRef.
- J. Valasek, Phys. Rev., 1920, 15, 505–564 CrossRef.
- J. Valasek, Phys. Rev., 1921, 17, 475–481 CrossRef CAS.
- G. Busch and P. Scherrer, Naturwissenschaften, 1935, 23, 737 CrossRef CAS.
- G. H. Kwei, A. C. Lawson, S. J. L. Billinge and S. W. Cheong, J. Phys. Chem., 1993, 97, 2368–2377 CrossRef.
- G. H. Haertling, J. Am. Ceram. Soc., 1999, 82, 797–818 CrossRef.
- P. Theato, B. S. Sumerlin, R. K. O’Reilly and T. H. Epps, III, Chem. Soc. Rev., 2013, 42, 7055 RSC.
- Y.-J. Kim and Y. T. Matsunaga, J. Mater. Chem. B, 2017, 5, 4307–4321 RSC.
- W. Miller, C. W. Smith, D. S. Mackenzie and K. E. Evans, J. Mater. Sci., 2009, 44, 5441–5451 CrossRef CAS.
- R. H. Baughman, Science, 2002, 297, 787–792 CrossRef CAS PubMed.
- R. S. Krishnan, R. Srinivasan and S. Devanarayanan, Thermal expansion of crystals: international series in the science of the solid state, 2013 Search PubMed.
- M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329 CrossRef CAS.
- R. M. Hazen and L. W. Finger, Am. Sci., 1984, 72, 143–150 Search PubMed.
- X. Yang, X. Cheng, X. Yan, J. Yang, T. Fu and J. Qiu, Compos. Sci. Technol., 2007, 67, 1167–1171 CrossRef CAS.
- R. Roy, D. K. Agrawal and H. A. McKinstry, Annu. Rev. Mater. Sci., 1989, 19, 59–81 CrossRef CAS.
- T. A. Mary, J. S. O. Evans, T. Vogt and A. W. Sleight, Science, 1996, 272, 90–92 CrossRef CAS.
- K. Röttger, A. Endriss, J. Ihringer, S. Doyle and W. F. Kuhs, Acta Crystallogr., Sect. B: Struct. Sci., 1994, 50, 644–648 CrossRef.
- S. E. Tallentire, F. Child, I. Fall, L. Vella-Zarb, I. R. Evans, M. G. Tucker, D. A. Keen, C. Wilson and J. S. O. Evans, J. Am. Chem. Soc., 2013, 135, 12849–12856 CrossRef CAS PubMed.
- V. Korthuis, N. Khosrovani, A. W. Sleight, N. Roberts, R. Dupree and W. W. J. Warren, Chem. Mater., 1995, 7, 412–417 CrossRef CAS.
- J. S. O. Evans, T. A. Mary and A. W. Sleight, J. Solid State Chem., 1997, 133, 580–583 CrossRef CAS.
- D. A. Woodcock, P. Lightfoot, L. A. Villaescusa, M.-J. Díaz-Cabañas, M. A. Camblor and D. Engberg, Chem. Mater., 1999, 11, 2508–2514 CrossRef CAS.
- D. A. Woodcock, P. Lightfoot, P. A. Wright, L. A. Villaescusa and M. A. Camblor, J. Mater. Chem., 1999, 9, 349–351 RSC.
- P. Lightfoot, D. A. Woodcock, M. J. Maple, L. A. Villaescusa and P. A. Wright, J. Mater. Chem., 2001, 11, 212–216 RSC.
- B. K. Greve, K. L. Martin, P. L. Lee, P. J. Chupas, K. W. Chapman and A. P. Wilkinson, J. Am. Chem. Soc., 2010, 132, 15496–15498 CrossRef CAS PubMed.
- L. Hu, J. Chen, A. Sanson, H. Wu, C. Guglieri Rodriguez, L. Olivi, Y. Ren, L. Fan, J. Deng and X. Xing, J. Am. Chem. Soc., 2016, 138, 8320–8323 CrossRef CAS PubMed.
- L. Hu, J. Chen, J. Xu, N. Wang, F. Han, Y. Ren, Z. Pan, Y. Rong, R. Huang, J. Deng, L. Li and X. Xing, J. Am. Chem. Soc., 2016, 138, 14530–14533 CrossRef PubMed.
- M. van Schilfgaarde, I. A. Abrikosov and B. Johansson, Nature, 1999, 400, 46–49 CrossRef.
- Y. W. Long, N. Hayashi, T. Saito, M. Azuma, S. Muranaka and Y. Shimakawa, Nature, 2009, 458, 60–63 CrossRef PubMed.
- M. Azuma, W. Chen, H. Seki, M. Czapski, S. Olga, K. Oka, M. Mizumaki, T. Watanuki, N. Ishimatsu, N. Kawamura, S. Ishiwata, M. G. Tucker, Y. Shimakawa and J. P. Attfield, Nat. Commun., 2011, 2, 347 CrossRef PubMed.
- J. Chen, K. Nittala, J. S. Forrester, J. L. Jones, J. Deng, R. Yu and X. Xing, J. Am. Chem. Soc., 2011, 133, 11114–11117 CrossRef CAS PubMed.
- J. Chen, F. Wang, Q. Huang, L. Hu, X. Song, J. Deng, R. Yu and X. Xing, Sci. Rep., 2013, 3, 2458 CrossRef PubMed.
- Z. Pan, Y.-W. Fang, T. Nishikubo, L. Hu, S. Kawaguchi and M. Azuma, Chem. Mater., 2022, 34, 2798–2803 CrossRef CAS.
- Q. Li, K. Lin, Z. Liu, L. Hu, Y. Cao, J. Chen and X. Xing, Chem. Rev., 2022, 122, 8438–8486 CrossRef CAS PubMed.
- P. Hu, J. Chen, X. Sun, J. Deng, X. Chen, R. Yu, L. Qiao and X. Xing, J. Mater. Chem., 2009, 19, 1648 RSC.
- S. Li, K. Takahashi, R.-K. Huang, C. Xue, K. Kokado, N. Hoshino, T. Akutagawa, S. Nishihara and T. Nakamura, Chem. Mater., 2023, 35, 2421–2428 CrossRef CAS.
- M. Szafrański, J. Mater. Chem. C, 2013, 1, 7904–7913 RSC.
- G. H. Roche, D. Flot, J. J. E. Moreau, O. J. Dautel, J.-S. Filhol and A. van der Lee, Cryst. Growth Des., 2021, 21, 3850–3863 CrossRef CAS.
- K. K. Jha, S. Dutta and P. Munshi, Cryst. Growth Des., 2018, 18, 1126–1135 CrossRef CAS.
- A. Kumar, J. Chauhan, K. D. Dubey, S. Sen and P. Munshi, Mol. Pharmaceutics, 2022, 19, 1008–1018 CrossRef CAS PubMed.
- S. Dutta, V. Vikas, A. Yadav, R. Boomishankar, A. Bala, V. Kumar, T. Chakraborty, S. Elizabeth and P. Munshi, Chem. Commun., 2019, 55, 9610–9613 RSC.
- G. Gupta, Y. Gupta, A. Kumar, R. Bhowal and P. Munshi, Cryst. Growth Des., 2024, 24, 646–656 CrossRef CAS.
- W. C. McCrone, Polymorphism, in Physics and Chemistry of the Organic Solid State, ed. D. Fox, M. M. Labes and A. Weissberger, Wiley-Interscience, New York, 1965, ch. 8, vol. 2, pp. 725–767 Search PubMed.
- K. K. Jha, S. Dutta, V. Kumar and P. Munshi, CrystEngComm, 2016, 18, 8497–8505 RSC.
- D. Gentili, M. Gazzano, M. Melucci, D. Jones and M. Cavallini, Chem. Soc. Rev., 2019, 48, 2502–2517 RSC.
- H. Chung and Y. Diao, J. Mater. Chem. C, 2016, 4, 3915–3933 RSC.
- R. Bu, H. Li and C. Zhang, Cryst. Growth Des., 2020, 20, 3561–3576 CrossRef.
- S. Dutta, Vikas, V. Thangavel and P. Munshi, ACS Appl. Electron. Mater., 2021, 3, 3633–3640 CrossRef CAS.
- G. B. A. M. Glazer, Space Groups for Solid State Scientists, Elsevier, 2013 Search PubMed.
- V. Wadhawan, Introduction to Ferroic Materials, CRC Press, 2000 Search PubMed.
- H. Schmid, J. Phys.: Condens. Matter, 2008, 20, 434201 CrossRef.
- H.-Y. Zhang, Y.-Y. Tang, P.-P. Shi and R.-G. Xiong, Acc. Chem. Res., 2019, 52, 1928–1938 CrossRef CAS PubMed.
- P. P. Shi, Y. Y. Tang, P. F. Li, W. Q. Liao, Z. X. Wang, Q. Ye and R. G. Xiong, Chem. Soc. Rev., 2016, 45, 3811–3827 RSC.
- K. Aizu, Phys. Rev. B: Solid State, 1970, 2, 754–772 CrossRef.
- S. C. Abrahams, E. Buehler, W. C. Hamilton and S. J. Laplaca, J. Phys. Chem. Solids, 1973, 34, 521–532 CrossRef CAS.
- D.-W. Fu, H.-L. Cai, Y. Liu, Q. Ye, W. Zhang, Y. Zhang, X.-Y. Chen, G. Giovannetti, M. Capone, J. Li and R.-G. Xiong, Science, 2013, 339, 425–428 CrossRef CAS PubMed.
- D.-W. Fu, W. Zhang, H.-L. Cai, J.-Z. Ge, Y. Zhang and R.-G. Xiong, Adv. Mater., 2011, 23, 5658–5662 CrossRef CAS PubMed.
- Z. S. Yao, K. Yamamoto, H. L. Cai, K. Takahashi and O. Sato, J. Am. Chem. Soc., 2016, 138, 12005–12008 CrossRef CAS PubMed.
- H. Y. Ye, Y. Zhang, D. W. Fu and R. G. Xiong, Angew. Chem., Int. Ed., 2014, 53, 6724–6728 CrossRef CAS PubMed.
- S. Koval, J. Kohanoff, J. Lasave, G. Colizzi and R. L. Migoni, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 184102 CrossRef.
- T. F. Nova, A. S. Disa, M. Fechner and A. Cavalleri, Science, 2019, 364, 1075–1079 CrossRef CAS PubMed.
- Y.-Y. Tang, J.-C. Liu, Y.-L. Zeng, H. Peng, X.-Q. Huang, M.-J. Yang and R.-G. Xiong, J. Am. Chem. Soc., 2021, 143, 13816–13823 CrossRef CAS PubMed.
- S. Horiuchi and Y. Tokura, Nat. Mater., 2008, 7, 357–366 CrossRef CAS PubMed.
- S. Horiuchi, Y. Tokunaga, G. Giovannetti, S. Picozzi, H. Itoh, R. Shimano, R. Kumai and Y. Tokura, Nature, 2010, 463, 789–792 CrossRef CAS PubMed.
- S. Horiuchi, R. Kumai and Y. Tokura, Adv. Mater., 2011, 23, 2098–2103 CrossRef CAS PubMed.
- S. Horiuchi, F. Kagawa, K. Hatahara, K. Kobayashi, R. Kumai, Y. Murakami and Y. Tokura, Nat. Commun., 2012, 3, 1306–1308 CrossRef PubMed.
- S. Horiuchi, K. Kobayashi, R. Kumai and S. Ishibashi, Nat. Commun., 2017, 8, 1–9 CrossRef PubMed.
- A. S. Tayi, A. Kaeser, M. Matsumoto, T. Aida and S. I. Stupp, Nat. Chem., 2015, 7, 281–294 CrossRef CAS PubMed.
- S. Horiuchi, F. Ishii, R. Kumai, Y. Okimoto, H. Tachibana, N. Nagaosa and Y. Tokura, Nat. Mater., 2005, 4, 163–166 CrossRef CAS PubMed.
- S. Horiuchi, R. Kumai and Y. Tokura, J. Mater. Chem., 2009, 19, 4421 RSC.
- K. Kobayashi, S. Horiuchi, S. Ishibashi, F. Kagawa, Y. Murakami and R. Kumai, Chem. – Eur. J., 2014, 20, 17515–17522 CrossRef CAS PubMed.
- S. Horiuchi, R. Kumai and Y. Tokura, J. Am. Chem. Soc., 2013, 135, 4492–4500 CrossRef CAS PubMed.
- J. Harada, T. Shimojo, H. Oyamaguchi, H. Hasegawa, Y. Takahashi, K. Satomi, Y. Suzuki, J. Kawamata and T. Inabe, Nat. Chem., 2016, 8, 946–952 CrossRef CAS PubMed.
- J. Harada, N. Yoneyama, S. Yokokura, Y. Takahashi, A. Miura, N. Kitamura and T. Inabe, J. Am. Chem. Soc., 2018, 140, 346–354 CrossRef CAS PubMed.
- H.-Y. Ye, Y.-Y. Tang, P.-F. Li, W.-Q. Liao, J.-X. Gao, X.-N. Hua, H. Cai, P.-P. Shi, Y.-M. You and R.-G. Xiong, Science, 2018, 361, 151–155 CrossRef CAS PubMed.
- M. Szafranski, J. Phys. Chem. B, 2011, 115, 8755–8762 CrossRef CAS PubMed.
- S. Seyedraoufi, E. D. Sødahl, C. H. Görbitz and K. Berland, Phys. Rev. Mater., 2024, 8, 054413 CrossRef.
- Y. Y. Tang, P. F. Li, W. Q. Liao, P. P. Shi, Y. M. You and R. G. Xiong, J. Am. Chem. Soc., 2018, 140, 8051–8059 CrossRef CAS PubMed.
- T. Vijayakanth, A. K. Srivastava, F. Ram, P. Kulkarni, K. Shanmuganathan, B. Praveenkumar and R. Boomishankar, Angew. Chem., Int. Ed., 2018, 57, 9054–9058 CrossRef CAS PubMed.
- R. A. Wiscons, N. R. Goud, J. T. Damron and A. J. Matzger, Angew. Chem., Int. Ed., 2018, 57, 9044–9047 CrossRef CAS PubMed.
- R. C. Haddon and A. A. Lamola, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 1874–1878 CrossRef CAS PubMed.
- D. Semmingsen and J. Feder, Solid State Commun., 1974, 15, 1369–1372 CrossRef CAS.
- G. A. Samara and D. Semmingsen, J. Chem. Phys., 1979, 71, 1401–1407 CrossRef CAS.
- Y. Moritomo, Y. Tokura, H. Takahashi and N. Mōri, Phys. Rev. Lett., 1991, 67, 2041–2044 CrossRef CAS PubMed.
- G. Gilli, F. Bellucci, V. Ferretti and V. Bertolasi, J. Am. Chem. Soc., 1989, 111, 1023–1028 CrossRef CAS.
- P. Gilli, V. Bertolasi, V. Ferretti and G. Gilli, J. Am. Chem. Soc., 1994, 116, 909–915 CrossRef CAS.
- G. Gilli and P. Gilli, J. Mol. Struct., 2000, 552, 1–15 CrossRef.
- R. R. Choudhury and R. Chitra, Cryst. Res. Technol., 2006, 41, 1045–1048 CrossRef.
- Z. Zikmund, P. Vaněk, M. Havránková, B. Březina, M. Člermák and M. Vásša, Ferroelectrics, 1994, 158, 223–228 CrossRef.
- J. Kroupa, P. Vaněk, R. Krupková and Z. Zikmund, Ferroelectrics, 1997, 202, 229–234 CrossRef.
- D. Keil, H. Hartmann and C. Reichardt, Liebigs Ann. Chem., 1993, 935–939 CrossRef.
- M. Owczarek, K. A. Hujsak, D. P. Ferris, A. Prokofjevs, I. Majerz, P. Szklarz, H. Zhang, A. A. Sarjeant, C. L. Stern, R. Jakubas, S. Hong, V. P. Dravid and J. F. Stoddart, Nat. Commun., 2016, 7, 13108 CrossRef PubMed.
- H. Peng, J.-C. Qi, X.-J. Song, R.-G. Xiong and W.-Q. Liao, Chem. Sci., 2022, 13, 4936–4943 RSC.
- M.-M. Russew and S. Hecht, Adv. Mater., 2010, 22, 3348–3360 CrossRef PubMed.
- W.-Q. Liao, Y.-L. Zeng, Y.-Y. Tang, H. Peng, J.-C. Liu and R.-G. Xiong, J. Am. Chem. Soc., 2021, 143, 21685–21693 CrossRef PubMed.
- W. Liao, B. Deng, Z. Wang, T. Cheng, Y. Hu, S. Cheng and R. Xiong, Adv. Sci., 2021, 8, 2102614 CrossRef PubMed.
- Z. Wang, C. Huang, J. Liu, Y. Zeng and R. Xiong, Chem. – Eur. J., 2021, 27, 14831–14835 CrossRef PubMed.
- Y.-Y. Tang, Y.-L. Zeng and R.-G. Xiong, J. Am. Chem. Soc., 2022, 144, 8633–8640 CrossRef PubMed.
- Y. Du, C.-R. Huang, Z.-K. Xu, W. Hu, P.-F. Li, R.-G. Xiong and Z.-X. Wang, JACS Au, 2023, 3, 1464–1471 CrossRef PubMed.
- H. Zhang, H. Jiang, Y. Zhang, N. Zhang and R. Xiong, Angew. Chem., Int. Ed., 2022, 61, e202200135 CrossRef PubMed.
- S. Horiuchi, R. Kumai and S. Ishibashi, J. Mater. Chem. C, 2021, 9, 13739–13747 RSC.
- P.-F. Li, W.-Q. Liao, Y.-Y. Tang, W. Qiao, D. Zhao, Y. Ai, Y.-F. Yao and R.-G. Xiong, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 5878–5885 CrossRef PubMed.
- Y. Ai, Y.-L. Zeng, W.-H. He, X.-Q. Huang and Y.-Y. Tang, J. Am. Chem. Soc., 2020, 142, 13989–13995 CrossRef PubMed.
- P.-F. Li, Y. Ai, Y.-L. Zeng, J.-C. Liu, Z.-K. Xu and Z.-X. Wang, Chem. Sci., 2022, 13, 657–664 RSC.
- H.-Y. Liu, H.-Y. Zhang, X.-G. Chen and R.-G. Xiong, J. Am. Chem. Soc., 2020, 142, 15205–15218 CrossRef PubMed.
- C. F. C. Fitié, W. S. C. Roelofs, M. Kemerink and R. P. Sijbesma, J. Am. Chem. Soc., 2010, 132, 6892–6893 CrossRef PubMed.
- C. F. C. Fitié, W. S. C. Roelofs, P. C. M. M. Magusin, M. Wübbenhorst, M. Kemerink and R. P. Sijbesma, J. Phys. Chem. B, 2012, 116, 3928–3937 CrossRef PubMed.
- H. Anetai, Y. Wada, T. Takeda, N. Hoshino, S. Yamamoto, M. Mitsuishi, T. Takenobu and T. Akutagawa, J. Phys. Chem. Lett., 2015, 6, 1813–1818 CrossRef CAS PubMed.
- H. Anetai, T. Takeda, N. Hoshino, H. Kobayashi, N. Saito, M. Shigeno, M. Yamaguchi and T. Akutagawa, J. Am. Chem. Soc., 2019, 141, 2391–2397 CrossRef CAS PubMed.
- T. Akutagawa, H. Koshinaka, D. Sato, S. Takeda, S.-I. Noro, H. Takahashi, R. Kumai, Y. Tokura and T. Nakamura, Nat. Mater., 2009, 8, 342–347 CrossRef CAS PubMed.
- D. Miyajima, F. Araoka, H. Takezoe, J. Kim, K. Kato, M. Takata and T. Aida, Science, 2012, 336, 209–213 CrossRef CAS PubMed.
- S. Furukawa, J. Wu, M. Koyama, K. Hayashi, N. Hoshino, T. Takeda, Y. Suzuki, J. Kawamata, M. Saito and T. Akutagawa, Nat. Commun., 2021, 12, 768 CrossRef CAS PubMed.
- D. Bordeaux, J. Bornarel, A. Capiomont, J. Lajzerowicz-Bonneteau, J. Lajzerowicz and J. F. Legrand, Phys. Rev. Lett., 1973, 31, 314–317 CrossRef.
- C.-R. Huang, Y. Li, Y. Xie, Y. Du, H. Peng, Y.-L. Zeng, J.-C. Liu and R.-G. Xiong, Angew. Chem., Int. Ed., 2021, 60, 16668–16673 CrossRef CAS PubMed.
- S. K. Park and Y. Diao, Chem. Soc. Rev., 2020, 49, 8287–8314 RSC.
- L. Li, P. Commins, M. B. Al-Handawi, D. P. Karothu, J. M. Halabi, S. Schramm, J. Weston, R. Rezgui and P. Naumov, Chem. Sci., 2019, 10, 7327–7332 RSC.
- D. P. Karothu, R. Ferreira, G. Dushaq, E. Ahmed, L. Catalano, J. M. Halabi, Z. Alhaddad, I. Tahir, L. Li, S. Mohamed, M. Rasras and P. Naumov, Nat. Commun., 2022, 13, 2823 CrossRef CAS PubMed.
- A. Piecha-Bisiorek, A. Białońska, R. Jakubas, P. Zieliński, M. Wojciechowska and M. Gałązka, Adv. Mater., 2015, 27, 5023–5027 CrossRef CAS PubMed.
- N. Zhang, W. Sun, Y. Zhang, H.-H. Jiang, R.-G. Xiong, S. Dong and H.-Y. Zhang, Nat. Commun., 2023, 14, 5854 CrossRef CAS PubMed.
- H. Y. Zhang, Y. Y. Tang, Z. X. Gu, P. Wang, X. G. Chen, H. P. Lv, P. F. Li, Q. Jiang, N. Gu, S. Ren and R. G. Xiong, Science, 2024, 383, 1492–1498 CrossRef CAS PubMed.
- https://neutrons.ornl.gov/topaz .
- C. M. Fancher, C. M. Hoffmann, X. P. Wang, L. L. Daemen and A. J. Schultz, APL Mater., 2021, 9, 021111 CrossRef CAS.
- K. Kobayashi, S. Horiuchi, S. Ishibashi, Y. Murakami and R. Kumai, J. Am. Chem. Soc., 2018, 140, 3842–3845 CrossRef CAS PubMed.
- J. S. O. Evans, T. A. Mary and A. W. Sleight, J. Solid State Chem., 1998, 137, 148–160 CrossRef CAS.
- S. Margadonna, K. Prassides and A. N. Fitch, J. Am. Chem. Soc., 2004, 126, 15390–15391 CrossRef CAS PubMed.
- D. J. Williams, D. E. Partin, F. J. Lincoln, J. Kouvetakis and M. O’Keeffe, J. Solid State Chem., 1997, 134, 164–169 CrossRef CAS.
- A. E. Phillips, A. L. Goodwin, G. J. Halder, P. D. Southon and C. J. Kepert, Angew. Chem., 2008, 120, 1418–1421 CrossRef.
- A. E. Phillips, G. J. Halder, K. W. Chapman, A. L. Goodwin and C. J. Kepert, J. Am. Chem. Soc., 2010, 132, 10–11 CrossRef CAS PubMed.
- K. W. Chapman, P. J. Chupas and C. J. Kepert, J. Am. Chem. Soc., 2006, 128, 7009–7014 CrossRef PubMed.
- S. G. Duyker, V. K. Peterson, G. J. Kearley, A. J. Ramirez-Cuesta and C. J. Kepert, Angew. Chem., Int. Ed., 2013, 52, 5266–5270 CrossRef PubMed.
- D. J. Cram and J. M. Cram, Science, 1974, 183, 803–809 CrossRef PubMed.
- M. Zakrzewski, M. A. White and W. Abriel, J. Phys. Chem., 1990, 94, 2203–2206 CrossRef CAS.
- H. Birkedal and D. Schwarzenbach, Angew. Chem., Int. Ed., 2002, 41, 754–756 CrossRef CAS.
- C. Serre, F. Millange, C. Thouvenot, M. Noguès, G. Marsolier, D. Louër and G. Férey, J. Am. Chem. Soc., 2002, 124, 13519–13526 CrossRef CAS PubMed.
- L. D. DeVries, P. M. Barron, E. P. Hurley, C. Hu and W. Choe, J. Am. Chem. Soc., 2011, 133, 14848–14851 CrossRef CAS PubMed.
- A. D. Fortes, E. Suard and K. S. Knight, Science, 2011, 331, 742–746 CrossRef CAS PubMed.
- B. Dwivedi, A. Shrivastava, L. Negi and D. Das, Cryst. Growth Des., 2019, 19, 2519–2524 CrossRef CAS.
- L. Negi, S. Kumar, B. Dwivedi and D. Das, Cryst. Growth Des., 2021, 21, 1428–1433 CrossRef CAS.
- S. Chuskit, T. Sethi, P. Harsha and D. Das, Cryst. Growth Des., 2023, 23, 1336–1342 CrossRef CAS.
- H. T. Chifotides and K. R. Dunbar, Acc. Chem. Res., 2013, 46, 894–906 CrossRef CAS.
- S.-L. Li, T. Xiao, C. Lin and L. Wang, Chem. Soc. Rev., 2012, 41, 5950 RSC.
- J. Borges and J. F. Mano, Chem. Rev., 2014, 114, 8883–8942 CrossRef CAS PubMed.
- D. Das, T. Jacobs and L. J. Barbour, Nat. Mater., 2010, 9, 36–39 CrossRef CAS.
- S. Bhattacharya and B. K. Saha, CrystEngComm, 2014, 16, 2340 RSC.
- M. K. Panda, T. Runčevski, S. Chandra Sahoo, A. A. Belik, N. K. Nath, R. E. Dinnebier and P. Naumov, Nat. Commun., 2014, 5, 4811 CrossRef CAS.
- A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313 RSC.
- S. Brooker, Chem. Soc. Rev., 2015, 44, 2880–2892 RSC.
- B. R. Mullaney, L. Goux-Capes, D. J. Price, G. Chastanet, J.-F. Létard and C. J. Kepert, Nat. Commun., 2017, 8, 1053 CrossRef PubMed.
- D. Das, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2021, 77, 309–310 CrossRef CAS.
- J. F. Nye and R. B. Lindsay, Phys. Today, 1957, 10, 26 CrossRef.
- A. L. Kitaigorodsky, Molecular crystals and molecules, Elsevier, 2012, vol. 29 Search PubMed.
- J. D. Dunitz and A. Gavezzotti, Chem. Soc. Rev., 2009, 38, 2622 RSC.
- L. Negi, A. Shrivastava and D. Das, Chem. Commun., 2018, 54, 10675–10678 RSC.
- S. Hasebe, Y. Hagiwara, T. Ueno, T. Asahi and H. Koshima, Chem. Sci., 2024, 15, 1088–1097 RSC.
- S. Dutta and P. Munshi, J. Phys. Chem. C, 2020, 124, 27413–27421 CrossRef CAS.
- C. Lind, Materials, 2012, 5, 1125–1154 CrossRef CAS PubMed.
- Y.-C. Yang, X. Liu, X.-B. Deng, L.-M. Wu and L. Chen, JACS Au, 2022, 2, 2059–2067 CrossRef CAS PubMed.
- H. Takahashi and R. Tamura, CrystEngComm, 2015, 17, 8888–8896 RSC.
- Vikas, L. Negi and P. Munshi, Cryst. Growth Des., 2024, 24, 2533–2541 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |