Open Access Article
Open Access ArticleUnlocking the potential of self-healing and recyclable ionic elastomers for soft robotics applications†
S.
Utrera-Barrios
 *a,
N.
Steenackers
bc,
S.
Terryn
bc,
P.
Ferrentino
*a,
N.
Steenackers
bc,
S.
Terryn
bc,
P.
Ferrentino
 c,
R.
Verdejo
a,
G.
Van Asche
c,
R.
Verdejo
a,
G.
Van Asche
 b,
M. A.
López-Manchado
b,
M. A.
López-Manchado
 a,
J.
Brancart
a,
J.
Brancart
 b and
M.
Hernández Santana
b and
M.
Hernández Santana
 *a
*a
aInstitute of Polymer Science and Technology (ICTP), CSIC, Juan de la Cierva 3, 28006 Madrid, Spain. E-mail: sutrera@ictp.csic.es; marherna@ictp.csic.es
bPhysical Chemistry and Polymer Science (FYSC), Department of Materials and Chemistry (MACH), Vrije Universiteit Brussel (VUB), Pleinlaan 2, B-1050 Brussels, Belgium
cBrubotics, Vrije Universiteit Brussel (VUB) and Imec, Pleinlaan 2, B-1050 Brussels, Belgium
First published on 17th November 2023
Abstract
In the field of soft robotics, current materials face challenges related to their load capacity, durability, and sustainability. Innovative solutions are required to address these problems beyond conventional strategies, which often lack long-term ecological viability. This study aims to overcome these limitations using mechanically robust, self-healing, and recyclable ionic elastomers based on carboxylated nitrile rubber (XNBR). The designed materials exhibited excellent mechanical properties, including tensile strengths (TS) exceeding 19 MPa and remarkable deformability, with maximum elongations (EB) over 650%. Moreover, these materials showed high self-healing capabilities, with 100% recovery efficiency of TS and EB at 110 °C after 3 to 5 h, and full recyclability, preserving their mechanical performance even after three recycling cycles. Furthermore, they were also moldable and readily scalable. Tendon-driven soft robotic grippers were successfully developed out of ionic elastomers, illustrating the potential of self-healing and recyclability in the field of soft robotics to reduce maintenance costs, increase material durability, and improve sustainability.
New conceptsThis study exploited mechanically robust, self-healing, and recyclable ionic elastomers based on carboxylated nitrile rubber (XNBR), a widely commercially available product, for soft robotic applications. The developed materials combine reprocessability and elasticity, offer superior performance under demanding conditions, and embody a sustainable approach. Zinc oxide (ZnO) and magnesium oxide (MgO) were used as crosslinking agents, semi-reinforcing fillers, and processing aids, thereby streamlining the production process. An exhaustive analysis was conducted on the impact of both oxides on the behavior of the material. The conclusions drawn suggest that the mechanical performance, repairability, and recyclability are influenced by factors such as the nature of the cation (Zn2+ or Mg2+), concentration, free volume, crosslink density, and binding energy. Broadband dielectric spectroscopy was used for the first time to ascertain the optimal temperature for the healing protocol, which differs from conventional trial-and-error methods. Using an optimized compound, the feasibility of manufacturing tendon-driven soft robotic grippers was demonstrated, thereby unlocking the potential of ionic elastomers for this application. This study sets a precedent for the development of sustainable and efficient materials without intricate synthesis processes, signifying a pivotal step towards the adoption of such rubbers in the field of soft robotics. |
1. Introduction
The 4th industrial revolution requires a significant increase in the use of robotic automation, with the goal of improving productivity and efficiency. Among robotic automations, soft robots are particularly well-suited for applications that require real and safe human–robot collaboration and manipulation of fragile or sensitive objects.1 The outstanding compliance of soft robots allows them to flexibly deform and adapt their shapes upon contact with objects, making them ideal candidates for delicate handling tasks such as electronic components and food items. However, the load capacity of soft grippers remains a significant challenge due to the inherent properties of soft materials, characterized by a Young's modulus below 1 GPa.2 Several approaches have been explored to address this limitation, including the reinforcement of the elastic structure with high-strength fibers3,4 or using variable stiffness technology, such as particle jamming,5–7 soft actuator coupling,8,9 and stiffness-controlled materials.10 Unfortunately, these methods tend to complicate soft gripping systems and do not always provide a sustainable solution for soft robotics.The lifetime of soft robots and their lack of recyclability are additional key concerns that should be addressed before achieving economically and environmentally viable industrial implementation.11,12 Typically, soft robotic parts are predominantly fabricated from elastomers, such as silicones and polyurethanes. These elastomers are vulnerable to sharp objects causing cuts, tears, and punctures. Furthermore, fatigue can lead to microdamage, which may quickly amplify to larger-scale issues. Overloading is another frequently challenge due to the inherent low mechanical strength of such materials.12 In addition, most commercial elastomers also present significant challenges when it comes to reprocessing and recycling due to their permanently crosslinked structure.13 This combination of non-optimal recyclability and limited lifetime hampers their overall sustainability.14 However, the integration of self-healing and recyclable polymers presents a viable solution, enabling recovery from macroscopic damage, reducing maintenance requirements, minimizing environmental impact, and extending their operational lifecycle.12
Self-healing materials represent a cutting-edge area of research in materials science and engineering.15–18 Self-healing is understood as the ability of materials to repair damage and restore their structural and functional integrity autonomously or through external stimuli.19 Self-healing materials using Diels-Alder (DA) chemistry have already been proposed as potential components for soft robotics. Terryn et al.20 developed robust soft pneumatic actuators using DA networks based on furan-functionalized Jeffamine JT5000 (poly(propylene glycol) bis(2-aminopropyl ether)) with furfuryl glycidyl ether (FGE) and 1,1′-(methylenedi-1,4-phenylene)bismaleimide (DPBM). Tailored mechanical properties, including a tensile strength (TS) of ∼1.20 MPa and elongation at break (EB) of ∼150%, were achieved. This study demonstrated the practical use of these actuators in a soft hand for social robotics and a soft gripper for delicate items. Moreover, the actuators were capable of fully recovering from severe damage via a heating–cooling cycle (up to 90 °C in 40 min).
Cerdan et al.21 introduced a novel approach for enhancing the performance of soft robotics by incorporating humins, a byproduct of biorefinery processes, into a similar DA polymer network, based on a furan-functionalized diamine Jeffamine D400 with FGE and a low-viscous aliphatic bismaleimide (BMI-689). The researchers observed that blending humins with the DA polymer network improved the self-healing efficiency of the material, but with relatively low mechanical properties (with TS of ∼0.30 MPa and EB of ∼134%). However, these properties are counteracted by the irreversible polycondensation of humins during the thermal healing step, which enhances the strength of the material. A soft robotic gripper developed from this polymer demonstrated improved functional performance recovery upon heating (at 60 °C for 1 h) and stiffness-tunable features via humin thermal crosslinking.
Recently, Costa Cornellà et al.22 introduced a sustainable solution for soft robotics using self-healing elastomers derived from castor oil. A three-step sustainable synthesis process was presented. In the first step, castor oil (CO) was reacted with different renewable cyclic anhydrides (maleic anhydride, itaconic anhydride, and succinic anhydride). At this stage, carboxylic acid units were introduced as chain terminals in addition to two carbonyl groups that can act as hydrogen bond acceptors. In the second step, three anhydride-functionalized CO were reacted with FGE to introduce furan groups into the polymer structure. Finally, the DA cycloaddition reaction was completed using BMI-689. The variation of the different anhydrides, as well as the concentration between the diene (furan) and dienophile (bismaleimide), resulted in mechanical properties that could be adjusted (with a TS of up to ∼4 MPa). Importantly, they could also recover up to 487% of the EB, and the first 100% strain was achievable within 60 s at room temperature. These materials can be reprocessed and recycled, and they exhibit hydrolytic degradability at the end of their lifespan, thereby significantly reducing waste.
Other self-healing polymers based on different dynamic chemistries including hydrogen bonding23–25 or disulfide metathesis26,27 and extrinsic mechanisms,28 have also been used in soft robotics.12 Despite these advancements, the potential application of well-established general-purpose self-healing rubber remains unexplored. In addition, the mechanical performance of the materials available in the current state-of-the-art has its limitation. This includes low moduli, low fracture stress and non-negligible viscous effects. This stems from the low bond energy of the reversible crosslinks, that leads to breaking of the bonds at low stresses. Although the resulting self-healing soft robotics can generate large deformations, their payload is very limited. For soft robots to be competitive they need to be able to withstand forces that are comparable to traditional rigid robotics. In addition, they have to be controlled, in position or force. Time-dependent behaviors that result from viscous effects in their materials largely complicate their control, or make them impossible to control. In addition, viscous losses in the material lead to a decrease in efficiency of the soft robot. Hence, there is a clear need for self-healing elastomers in soft robotics that combine excellent (dynamic) mechanical properties with a self-healing capacity.
In this context, ionic elastomers based on general-purpose rubbers present a promising avenue in the field of soft robotics because they are a unique class of polymeric materials that combine the processability of thermoplastics with the elasticity of rubber. These elastomers have excellent mechanical and chemical resistances to non-polar solvents and exhibit excellent wear resistance. High strength materials that can exhibit large strains leads to high toughness is desired in soft robotics applications. In addition, an elastic response is demanded in soft robotics, as high viscous effects lead to slower dynamics of soft robotic actuators, difficult control and energy losses.
Here, three ionic elastomers based on XNBR were designed using a metal oxide, zinc oxide (ZnO) or magnesium oxide (MgO), as crosslinking agent, semi-reinforcing filler, and processing aid, all at once. All the materials were thoroughly characterized to evaluate their rheometric, thermal, and mechanical properties, as well as their molecular structure and dynamics. After characterization, the material with the best overall performance was used for the fabrication of tendon-driven soft robotic grippers. The simplicity in the selection of a widely available rubber, recipe design and straightforward manufacturing technique not only promotes ease of execution, but also ensures potential scalability.
2. Materials and methods
2.1. Materials
The selected elastomeric matrix was Krynac X 750, a cold-polymerized, non-staining stabilized, solid XNBR, kindly supplied by Arlanxeo. The technical details of the material can be found in ESI† S1 and its chemical composition is visually represented in Fig. 1a. Zinc oxide (ZnO, ExpertQ®, specific density: 5.47 g cm−3, particle size: <5 μm) and magnesium oxide (MgO, Pharmpur®, specific density: 3.58 g cm−3, particle size: < 150 μm), for analysis, ACS, Reag. Ph Eur, supplied by Scharlau, were used as crosslinking agents during the compounding process. The scheme of the fundamental crosslinking unit between the carboxylic groups of XNBR and the metal oxides (i.e., ion pair) is shown in Fig. 1a. The crosslinking density was evaluated using toluene (Merck, ACS Reagent, ≥99.5%). The assembly of tendon-driven soft robotic grippers required the use of polytetrafluoroethylene (PTFE, 3 M) tubing with an internal diameter of 1 mm and an external diameter of 2 mm, along with polyamide filaments (nylon) measuring 0.5 mm in diameter. Rigid parts of the gripper were 3D printed in black PLA of RS components. All the materials and chemicals were used as received without further purification.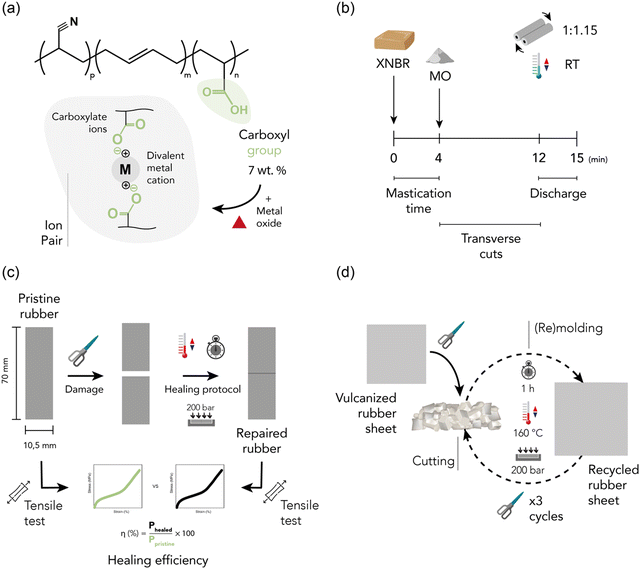 | ||
| Fig. 1 (a) Structure of XNBR and ion pairs, (b) mixing, (c) self-healing, and (d) recycling protocol. | ||
2.2. Processing
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.15. This process was carried out in three main steps, as shown in Fig. 1b. First, the rubber underwent a 4 min mastication process to enhance its plasticity and facilitate the incorporation of ingredients. The metal oxide (MO) was then incorporated, and numerous transverse cuts were made to promote the homogenization of the blend. At the 12 min mark, the discharge phase began, involving transverse roll passing for complete homogenization. After mixing for 15 min, the blend was removed from the mill, cooled in a refrigerator, and left for a minimum of 24 h before the initial characterization. Three different recipes, listed in Table 1 and expressed in parts per hundred rubber (phr), were prepared to analyze the impact of the MO based on three factors: (a) varying content of the MO (1.25 phr of MgO vs. 10 phr of MgO), (b) equivalent crosslink density (10 phr of ZnO vs. 1.25 phr of MgO), and (c) equal MO content (10 phr of ZnO vs. 10 phr of MgO). The specific contents were carefully selected through pre-optimization.
1.15. This process was carried out in three main steps, as shown in Fig. 1b. First, the rubber underwent a 4 min mastication process to enhance its plasticity and facilitate the incorporation of ingredients. The metal oxide (MO) was then incorporated, and numerous transverse cuts were made to promote the homogenization of the blend. At the 12 min mark, the discharge phase began, involving transverse roll passing for complete homogenization. After mixing for 15 min, the blend was removed from the mill, cooled in a refrigerator, and left for a minimum of 24 h before the initial characterization. Three different recipes, listed in Table 1 and expressed in parts per hundred rubber (phr), were prepared to analyze the impact of the MO based on three factors: (a) varying content of the MO (1.25 phr of MgO vs. 10 phr of MgO), (b) equivalent crosslink density (10 phr of ZnO vs. 1.25 phr of MgO), and (c) equal MO content (10 phr of ZnO vs. 10 phr of MgO). The specific contents were carefully selected through pre-optimization.
| Ingredient | 1.25MgO | 10MgO | 10ZnO | Role |
|---|---|---|---|---|
| XNBR | 100 | 100 | 100 | Rubber matrix |
| ZnO | — | — | 10 | Crosslinking agent |
| MgO | 1.25 | 10 | — | Crosslinking agent |
The curing properties of the rubber compounds were evaluated using a moving-die rheometer (MDR 2000, Monsanto). The torque increment was recorded at 160 °C for 60 min, with a frequency of 1.7 Hz and an oscillation arc of 0.5°. The optimal curing time (t90) was determined as the point at which 90% of the maximum torque (MH) was achieved. Minimum torque (ML) and scorch time (ts1) of the elastic component (S′) were also recorded. Subsequently, rubber sheets with a thickness of 2 mm were cured using an automatic press (P 200 P, Collin) at 160 °C and 200 bar at t90. The material was cooled inside the press to prevent the formation of bubbles in the vulcanized product. The selected pressure was maintained and cold water was circulated for 5 min. After at least 24 h of molding, the final samples were cut for characterization.
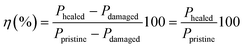 | (1) |
2.3. Characterization
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2013 standard. Tests were conducted in a universal testing machine (3366, Instron) with a 50 kN load cell at room temperature. The clamps were initially set 35 mm apart and the crosshead speed was 200 mm min−1. The stresses at various strain values (“modulus”) were measured at 100 (M100) and 300% (M300) strains, as well as the stress and strain at the breaking point, referred to as TS and EB.
2013 standard. Tests were conducted in a universal testing machine (3366, Instron) with a 50 kN load cell at room temperature. The clamps were initially set 35 mm apart and the crosshead speed was 200 mm min−1. The stresses at various strain values (“modulus”) were measured at 100 (M100) and 300% (M300) strains, as well as the stress and strain at the breaking point, referred to as TS and EB.
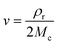 | (2) |
The Flory–Rehner expression considering the affine model was required to calculate ρrMc−1 according to eqn (3):
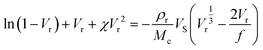 | (3) |
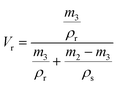 | (4) |
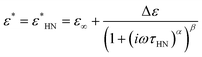 | (5) |
It is important to mention that the analysis of the dielectric property data in this research required prior use of the first-order approximation of the Kramers–Kronig relation. Different relaxation processes, especially at high temperatures, can be complex to analyze because their contribution and ionic conductivity can overlap in ε′′. An elegant way to remove Ohmic conduction from the measured loss spectra is to use a logarithmic derivative, which transforms the real part ε' into an imaginary part εder′′ that is solely based on relaxation phenomena.30–32 Thus, εder′′ lacks an Ohmic conduction term. This approximation is based on eqn (6):
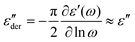 | (6) |
2.4. Assembly and actuation of the soft robotic gripper
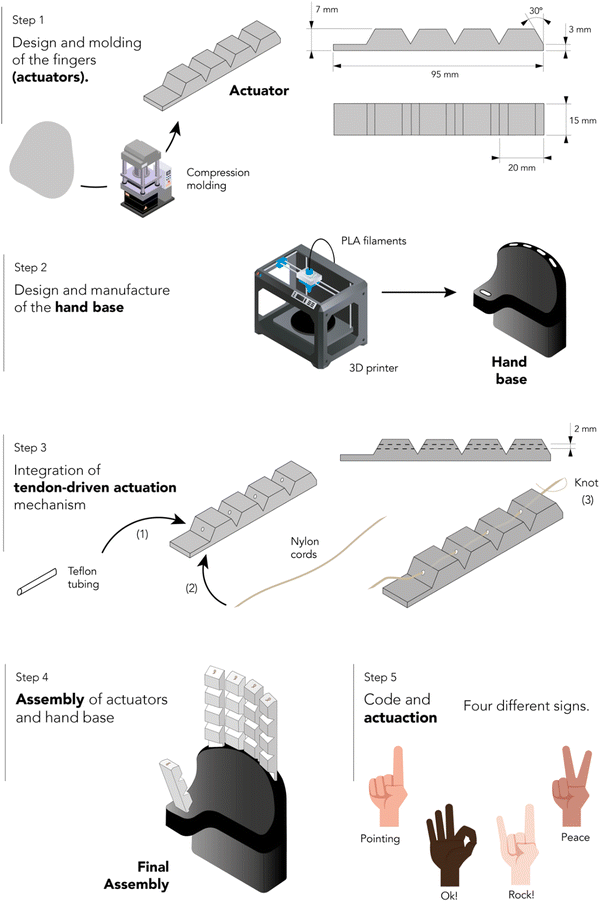
A tendon-driven soft robotic gripper prototype imitating a human hand was designed. This part of the study entailed two main stages: assembly and validation testing. The assembly and actuation process consisted of five steps. Fig. 2 shows a schematic representation of this procedure.Step 1: design and molding of the fingers (actuators). The rubber compound with optimal mechanical strength, self-healing efficiency, and recyclability was selected for compression molding of the five actuators using a hydraulic press and an aluminum mold at 160 °C and 15 bar. An additional time of 8 min was added to t90 to ensure proper vulcanization of the piece (+1 min for each mm of thickness in addition to the curing curve impellers). Two distinct sizes were prepared: a smaller variant with three phalanges for thumb simulation, and a larger variant with four phalanges for the other fingers.
Step 2: design and manufacture of the hand base. The base, corresponding to the palm of the hand and a portion of the forearm, was designed using a commercial CAD/CAE engineering software Autodesk Inventor. This piece was subsequently produced using additive manufacturing techniques with black PLA filaments on a fused filament fabrication 3D printer (Ultimaker 2).
Step 3: integration of tendon-driven actuation mechanism. The tendon-driven actuation mechanism was then embedded in the five actuators. A commercial nylon cord with a diameter of 0.5 mm was threaded through small PTFE tubes with an inner diameter of 1 mm, which were inserted into each phalanx. The cords were fixed to the top of the finger using a manually tied knot.
Step 4: assembly of actuators and hand base. Both parts were assembled and affixed firmly to a wooden base. The cords of the tendon-driven actuation mechanism were connected to servo motors (Dynamixel) that pulled the strings to generate the bending motion. The elastic energy stored in the actuators facilitates the return to its original position upon the release of pressure on the cords.
Step 5: code and actuation. Instructions for finger movements were controlled using an Arduino Uno. The Arduino code contains different predefined movements of the fingers.
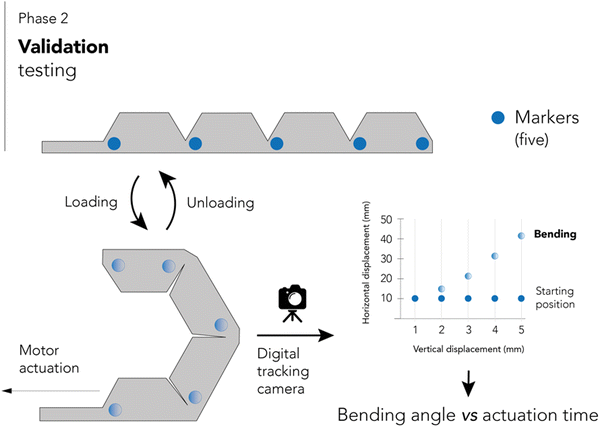
After assembly and code development, the second phase involved validation testing. A RGBD camera tracks the deformation of five marks placed on the side of a larger actuator (four phalanges). The camera recorded the position of each mark according to different movement instructions, thus generating a bending angle-time graph. For movement tracking, the actuator was positioned horizontally with the top tip facing the right, and actuation was executed in the direction towards a 90° angle with respect to the horizontal. Fig. 3 shows a schematic representation of this phase.
3. Results and discussion
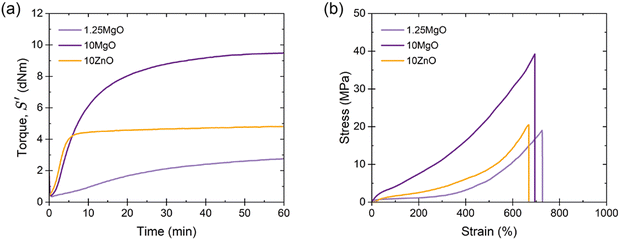
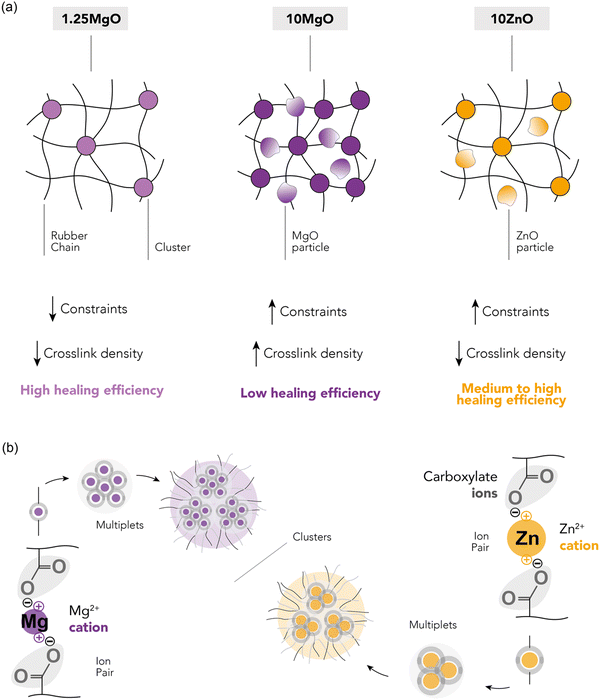
Three XNBR-based compounds were prepared using ZnO and MgO as vulcanizing agents, as described in the experimental section. The recipes were designed to investigate three key parameters: (i) increasing the content of the same MO (1.25MgO and 10MgO), (ii) equal crosslink density (1.25MgO and 10ZnO) and (iii) equal MO contents (10MgO and 10ZnO).The XNBR/MO system was selected to promote the formation of ionic crosslinks through the interaction between the carboxyl groups in the main chain of rubber and the divalent metal cations in the chosen MO (Mg2+ and Zn2+). The vulcanization process, which converts rubber from a plastic to an elastic state, facilitates the creation of a 3D network, which is fundamental for elasticity. This network was formed by ionic interactions. During vulcanization, the ionization and subsequent neutralization of ions leads to the formation of metal salt coordination, known as an “ion pair”, which serves as the functional unit of crosslinking. These ion pairs can aggregate into larger structures, referred to as “multiplets” and “clusters”. The latter forms a separate phase containing trapped chains, thereby influencing the mechanical behavior of the material. Given the relationship between crosslinking and mechanical performance, the initial step in the characterization involved the analysis of the curing (Fig. 4a) and stress–strain curves (Fig. 4b). The elastic component of the torque (S′) as a function of time was monitored to track the progress of the vulcanization reaction. Table 2 summarizes the curing and mechanical properties of the compounds.
| Property | 1.25MgO | 10MgO | 10ZnO |
|---|---|---|---|
| Note: the curing parameters (ts1, t90, ML and MH) were obtained in a moving die rheometer. The mechanical properties (M100, M300, TS and EB) were determined through a uniaxial tensile test. The crosslink density (υ) was obtained from equilibrium swelling measurements. | |||
| Scorch time, ts1 (min) | 15.22 | 2.56 | 1.83 |
| Curing time, t90 (min) | 44.92 | 26.45 | 7.32 |
| Minimun torque, ML (dNm) | 0.35 | 0.42 | 0.41 |
| Maximun torque, MH (dNm) | 2.76 | 9.48 | 4.81 |
| ΔM = MH − ML (dNm) | 2.41 | 9.01 | 4.40 |
| Cure rate index, CRI = 100/(t90 − ts1) (min−1) | 3.37 | 4.18 | 18.21 |
| Peak cure rate, PCR (dNm min−1) | 0.068 | 0.84 | 1.06 |
| Stress at 100% strain, M100 (MPa) | 0.5 ± 0.2 | 3.9 ± 0.6 | 1.7 ± 0.1 |
| Stress at 300% strain, M300 (MPa) | 1.5 ± 0.3 | 10.5 ± 0.5 | 4.0 ± 0.1 |
| Tensile strength, TS (MPa) | 19 ± 2 | 39 ± 1 | 21 ± 5 |
| Elongation at break, EB (%) | 741 ± 24 | 705 ± 12 | 664 ± 45 |
| Crosslink density, υ (×10−5 mol cm−3) | 3.57 ± 0.02 | 7.8 ± 0.2 | 3.69 ± 0.03 |
The curing curves revealed that increasing the MgO content from 1.25 phr to 10 phr resulted in a slight increase in the minimum torque (ML) from 0.35 to 0.42 dNm. However, a significant increase was observed in the maximum torque (MH), from 2.76 to 9.48 dNm, as well as in the curing rate index (CRI) and the peak cure rate (PCR, maximum slope of the S′ curve). A higher MgO content provided a higher probability of encountering carboxyl groups for the formation of an ion pair, leading to a more efficient curing process and faster cure rate. This enhanced curing efficiency resulted in increased torque, viscosity, and crosslink density, and improved mechanical performance with higher stress at low (M100) and medium strains (M300), an increase in tensile strength (TS) from 19 to 39 MPa, and a minor reduction (∼4%) in elongation at break (EB).
When comparing compounds with equal crosslink densities, it was found that 10ZnO exhibited higher MH, CRI, and PCR than its 1.25MgO counterpart. This was attributed to the excess ZnO in the recipe. According to stoichiometric calculations, ∼6 phr of ZnO is required to saturate all the carboxyl groups in XNBR. This could result in an excess of ZnO, which acts as a semi-reinforcing filler. The reinforcing character of ZnO has been widely reported in the rubber-related literature.33,34 Long before its recognition as a sulfur vulcanization activator in the early 1920s, ZnO was already used as a non-black filler in rubber compounds.35 Its semi-reinforcing characteristic has been described in natural rubber (NR),36 chlorinated natural rubber (Cl-NR),37 and styrene-butadiene rubber (SBR).38 Additionally, in a previous study by the authors,39 this effect in XNBR was demonstrated, finding a medium increase in mechanical performance when ZnO was incorporated above stoichiometric ratio. This explains why 10ZnO behaved as a stiffer material with higher M100 and M300 values. However, the TS values remained close to approximately 19 MPa for 1.25MgO and 21 MPa for 10ZnO because of their equal crosslink densities.
With similar MO contents, MgO exhibited superior mechanical properties compared to ZnO, as evidenced by the ultimate state of cure (ΔM), M100, M300, and TS, but a slower cure rate. The improved mechanical performance can be attributed to the nature of the cations. Smaller cations (lower ionic radii, r), such as Mg2+, can form stronger bonds due to electrostatic attraction (higher forces, F) between charged ions (Coulomb's law, F ∝−1r2). The generally accepted smaller ionic radius of Mg2+ (0.65 Å) compared to that of Zn2+ (0.74 Å)40–42 results in stronger ionic interactions and better mechanical performance. Another important consideration in this context is the electronic configuration of both cations. The electronic configuration of Mg2+ is [He] (1s22s22p6), whereas that of Zn2+ is [Ar]3d10 (1s22s22p63s23p63d10). Although both cations have their outermost orbital filled, in the case of Zn2+, the ligands bind to an outer shell of the ions, leading to a reduced electrostatic strength due to the greater distance from the nucleus. Similar effects were described in XNBR modified with 2,6-diaminopyridine (DAP) by Das et al.43 The effect of several metal salts, such as cobalt(II) nitrate hexahydrate (Co(NO3)26H2O, Co2+), nickel(II) nitrate hexahydrate (Ni(NO3)26H2O, Ni2+), and zinc(II) nitrate hexahydrate (Zn(NO3)26H2O, Zn2+), was explored. With smaller ionic radii, such as Ni2+ (0.69 Å), double TS was achieved compared to Zn2+. This outcome was attributable to the unique electronic configurations and size of the cations.
In contrast, the faster curing of the compounds with ZnO could be attributed to the higher affinity of the carboxyl groups to form interactions with the divalent cation. Similar results were reported by Dudev and Lim,44 who computed the formation free energies of Zn2+ and Mg2+ using different gas-phase ligands. They found that the formation free energies of compounds with Zn2+ were always lower (by 24–77 kcal mol−1) than those with Mg2+. This implies that the ligands (in which carboxylate groups are included) prefer Zn2+ to Mg2+. However, they also claimed that Zn complexes are more stable than Mg compounds, but this seems to differ from our initial observations based on the better mechanical performance of MgO compounds.
The FTIR spectra analysis provided further insight into the crosslinking process and its impact on the chemical structure of the rubber compounds. ESI† S2 shows the ATR spectra of the prepared samples as well as that of XNBR (without additives) as a reference. Every band related to the chemical structure of the rubber backbone was clearly discerned. At high wavenumbers, 2922 cm−1 and 2849 cm−1, the doublet corresponding to the vibration of the methylene (–CH2) in the polymer backbone was identified, while the medium-intensity band at 2237 cm−1 was correlated with the cyano group (–CN) in the acrylonitrile monomer. The bands at 967 cm−1 and 916 cm−1 were attributed to the out-of-plane vibrations of the –CH near the double bonds (–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–) of the trans configuration of butadiene and –CH
CH–) of the trans configuration of butadiene and –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, respectively.45 These bands remained constant after vulcanization, indicating the structural integrity of the rubber.
CH2, respectively.45 These bands remained constant after vulcanization, indicating the structural integrity of the rubber.
Of particular interest in ionic elastomers based on carboxyl groups is the band at 1698 cm−1, corresponding to the carbonyl (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) stretching of the acid. This band is directly related to the vulcanization process with metal oxides. Depending on the vulcanization system used, any shift in this signal indicates the successful formation of ionic interactions and their nature. In this case, a shift up to 1586 cm−1 was observed in 10MgO, i.e., in the presence of the Mg2+ cation (magnesium carboxylate salt), and up to 1588 cm−1 in 10ZnO, i.e., in the presence of the Zn2+ cation (zinc carboxylate salt). This change corresponds to the asymmetric carbonyl stretching of the coordination.46–49 Interestingly, in the case of 1.25MgO, a new broad band centered at 1616 cm−1 was observed, with a shoulder peak at 1580 cm−1. This suggested the occurrence of ionization of the carboxyl groups and coordination with the metal cation, even though the MgO content was below stoichiometric saturation (∼3.25 phr, 1
O) stretching of the acid. This band is directly related to the vulcanization process with metal oxides. Depending on the vulcanization system used, any shift in this signal indicates the successful formation of ionic interactions and their nature. In this case, a shift up to 1586 cm−1 was observed in 10MgO, i.e., in the presence of the Mg2+ cation (magnesium carboxylate salt), and up to 1588 cm−1 in 10ZnO, i.e., in the presence of the Zn2+ cation (zinc carboxylate salt). This change corresponds to the asymmetric carbonyl stretching of the coordination.46–49 Interestingly, in the case of 1.25MgO, a new broad band centered at 1616 cm−1 was observed, with a shoulder peak at 1580 cm−1. This suggested the occurrence of ionization of the carboxyl groups and coordination with the metal cation, even though the MgO content was below stoichiometric saturation (∼3.25 phr, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio). This indicated the possibility of higher-order coordination, such as hexacoordinated (1
2 ratio). This indicated the possibility of higher-order coordination, such as hexacoordinated (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio), which would explain the saturation effect even at a lower MgO content.48 Additionally, after vulcanization, new peaks appeared at 1420 cm−1 for the compounds with MgO, and at 1417 cm−1 for those with ZnO, associated with the symmetric carbonyl stretching of the coordination.50 These results confirmed the formation of the metal salts during vulcanization.
3 ratio), which would explain the saturation effect even at a lower MgO content.48 Additionally, after vulcanization, new peaks appeared at 1420 cm−1 for the compounds with MgO, and at 1417 cm−1 for those with ZnO, associated with the symmetric carbonyl stretching of the coordination.50 These results confirmed the formation of the metal salts during vulcanization.
To gain further insight into the structural differences and their impact on the performance of the ionic elastomers, BDS was performed. Fig. 5a–c show 3D plots of the conduction-free dielectric loss with respect to temperature and frequency.
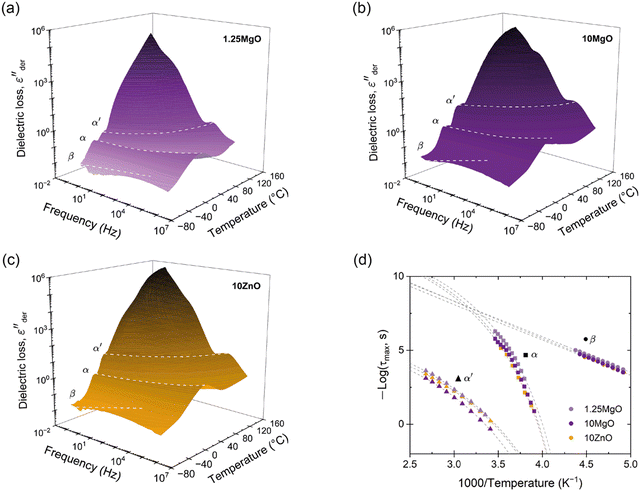 | ||
| Fig. 5 3D plots of conduction-free dielectric loss (εder′′) with respect to temperature and frequency for (a) 1.25MgO, (b) 10MgO and (c) 10ZnO. (d) Activation plot of the ionic elastomers. | ||
Three distinct relaxations were revealed: (1) β, at low temperatures, associated with short-range motions; (2) α, or segmental relaxation, associated with cooperative motions of the polymer chains as a result of the glass transition, and (3) α′, or ionic relaxation, at high temperatures, associated with the separated phase formed by the ionic clusters and the trapped rubber chains. When the ionic transition temperature is reached, a process known as ion-hopping is activated, which temporarily releases the ionic bonds and thus the trapped chains, providing maximum mobility to the system.51–53 The latter two relaxations have been previously reported in the literature for XNBR46,54 and other rubber ionomer systems.53,55,56 Additionally, several attempts have been made to understand the morphology of ionic aggregates beyond the cluster concept introduced by Eisenberg57,58 and generally accepted to explain the aggregation in ionomers. For example, Basu et al.59 demonstrated that not all Zn compounds can form this characteristic separate structure in XNBR, which is achieved with some metal oxides such as ZnO, and a lamellar-like configuration manifests within this cluster-like aggregation. However, under the specific processing conditions described in this study, the prepared ionic elastomers retain the amorphous character typical of most rubbers. This is evidenced by the absence the first-order transitions (crystallization and/or melting) in conventional differential scanning calorimetry (DSC) and thermogravimetric analysis (TGA) tests (See ESI† S3). Undoubtedly, the formation of this distinct phase (metal carboxylate salt) is pivotal for understanding the unique mechanical behavior of ionic elastomers.
The three identified relaxations can be well described by the HN formalism, as shown in eqn (5). This approach enabled the generation of an activation plot (Fig. 5d), which was essential for understanding the molecular dynamics of the prepared materials. To analyze the activating behavior, the data points were fitted using two distinct functions: a Vogel–Fulcher–Tammann–Hesse (VFTH) for the α and α′ relaxations, and Arrhenius for the β relaxation. The dashed lines in each dataset point represent the fitting results obtained using these functions, as described by eqn (7) (VFTH) and eqn (8) (Arrhenius):
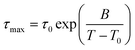 | (7) |
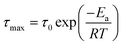 | (8) |
| Parameter | 1.25MgO | 10MgO | 10ZnO |
|---|---|---|---|
| β relaxation | |||
| Activation energy, Ea (kJ mol−1) | 46 ± 1 | 48 ± 1 | 45 ± 1 |
| α relaxation | |||
| B | 1477 ± 30 | 1552 ± 30 | 1574 ± 29 |
| Vogel temperature, T0 (K) | 204 ± 1 | 204 ± 1 | 204 ± 1 |
| Fragility strength, D | 7.2 ± 0.1 | 7.6 ± 0.2 | 7.7 ± 0.1 |
| Fragility index, m | 98 ± 1 | 94 ± 2 | 93 ± 1 |
| α′ relaxation | |||
| B | 1932 ± 36 | 1843 ± 24 | 1743 ± 14 |
| Vogel temperature, T0 (K) | 183 ± 2 | 191 ± 2 | 189 ± 1 |
| Fragility strength, D | 10.6 ± 0.2 | 9.6 ± 0.2 | 9.2 ± 0.1 |
| Fragility index, m | 72 ± 1 | 77 ± 2 | 80 ± 1 |
The results of this study revealed some interesting findings. In terms of the β relaxation, no substantial variation in the activation energy value (46 kJ mol−1, 48 kJ mol−1 and 45 kJ mol−1) was observed. β relaxation is not usually reported or discussed in recent studies on XNBR-based ionomers,29,46,54,60,61 neither by DMA nor by BDS. However, the few available research attributes its origin to rotational motions of side groups.62 Additionally, recent investigations on non-carboxylated nitrile rubber (NBR) have associated its behavior with the local non-cooperative motions of the macromolecule.63 In this context, Fritzsche et al.62 reported an increase in the activation energy of β relaxation with increasing the filler content in rubber composites (i.e., with increasing constraints); however, no further explanation was given beyond the uncertainties inherent to the linear region. In our case, it seems that intramolecular and/or intermolecular interactions within the polymer chains (i.e., van der Waals forces, electrostatic forces, and hydrogen bonds) were not affected by the presence of agglomerates (increasing MO content). However, further exploration is required to gain a deeper understanding of this relaxation behavior.
For the α relaxation, no significant variations in the parameters derived from the VFTH fit were observed, indicating that the segmental relaxation, which involves the mobility of rubber segments that neither participate in the ionic interaction nor are in its vicinity, remains unaltered. This supports the model of a separate ionic phase with its own thermal transition.
In contrast, the results for α′ relaxation showed a stark contrast. To gain further insight into the analysis, the fragility index (m) was calculated as a measure of the stiffness of the polymer backbone associated with each relaxation according to eqn (9):
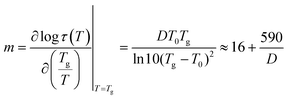 | (9) |
An increase in the Vogel temperature (T0) was observed in the compounds containing higher MO contents (10MgO and 10ZnO). This observation corresponds to a decrease in flexibility attributable to excess oxides, a hallmark of materials exhibiting fragile behavior. These materials are characterized by heightened cooperativity, a distinct deviation from Arrhenius behavior, lower D values, and high m values, which are related to the higher apparent activation energy necessary for their molecular motions.
Instead, 1.25MgO demonstrated a behavior with lower cooperativity, where the activation of its molecular dynamics was more readily facilitated. This is reflected in the higher D values and diminished m. These results hold significant implications, as they may aid in predicting self-healing behavior. When subjected to identical conditions, 1.25 MgO is expected to exhibit a superior healing response, achieving higher efficiencies than 10ZnO and 10MgO owing to its enhanced flexibility and mobility. These findings highlight the critical interplay between rubber composition, molecular dynamics, and self-healing capability in the development of advanced functional materials.
A more nuanced investigation was carried out using BDS. This step forward in the examination involved identifying the α′ relaxation process at a constant frequency of 100 Hz in the temperature-sweep domain, as shown in Fig. 6a. This approach allowed the identification of the temperature associated with the maximum ionic relaxation, that is, the ionic transition temperature. This critical value sets the lower limit of the temperature employed in the self-healing protocol, thereby offering a crucial parameter for efficient material healing. According to the acquired data, the ionic transition temperature was identified to be ∼55 °C for the compounds with equivalent crosslink density (1.25MgO and 10ZnO). However, a higher temperature around ∼65 °C was observed for 10MgO. At this chosen frequency, the relaxation temperature seems to be predominantly influenced by the crosslink density and, consequently, the number of the ionic interaction.
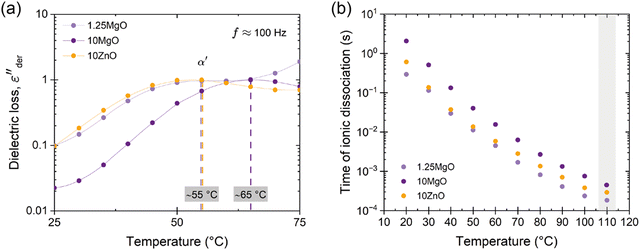 | ||
| Fig. 6 (a) Conduction-free dielectric loss (εder′′) with respect to temperature at 100 Hz. (b) Time of ionic dissociation of the prepared compounds. | ||
From these observations, a subsequent analysis was performed, plotting the variation in ionic dissociation time (obtained from the τmax values associated with each α′ relaxation) against temperature, as shown in Fig. 6b. This led to the discovery that the optimum temperature at which the ionic dissociation times among all composites approach each other equivalently (with negligible differences of around 1–2 × 10−3 s between them) is 110 °C. Based on these BDS findings, an insightful turn towards self-healing optimization was made. By embracing this approach, the traditional trial-and-error optimization process was avoided, offering a thorough analysis of the ionic dissociation times of the compounds. The insights derived from the BDS determined 110 °C as the minimum temperature for the self-healing process. This temperature selection is grounded not in conjecture but in the understanding of the molecular dynamics of the materials under specific conditions. This represents a potentially transformative approach for optimizing healing protocols in future studies. Thus, the focus has now shifted to the study of the healing process.
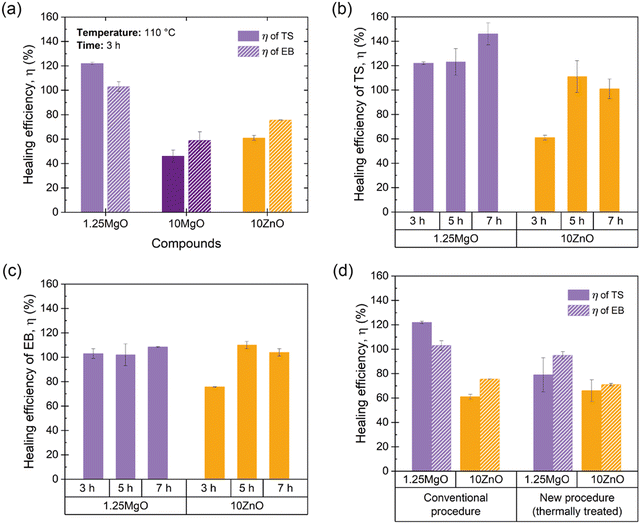
The healing capabilities of the compounds were calculated with respect to M300, TS and EB at 110 °C during 3 h (ESI† S4 and Fig. 7a). On the other hand, ESI† S5 shows the stress–strain curves of the prepared compounds, where the typical hyperelastic behavior of these materials in the pristine and healed state was observed. It is observed that all the ionic elastomers were able to fully recover their M300 values after the healing protocol. This is an interesting result from the point of view of recovering functionalities, since most commercial applications of these materials usually work at lower strains. As for the properties at the breaking point, the behavior is different. As the MgO content increased, there was a marked decrease in repairability.64–67 This demonstrates an antagonistic relationship between MgO content and healing capability. Specifically, 10MgO exhibited a lower efficiency of 46% in TS and 59% in EB compared with 1.25MgO, which achieved values above 100% in both cases, surpassing its pristine state. This effect correlates well with the stiffness of the compounds. To further elaborate on this, the study was complemented by DMA measurements. ESI† S6 shows the storage (E′) and loss (E′′) moduli of the three prepared ionic elastomers. At the healing temperature (110 °C), a remarkable increase (over a decade) in the E′ values of 10MgO was observed, indicating a higher stiffness and low diffusivity (i.e., constraints). This high stiffness and low diffusivity would be responsible for the considerable decrease in self-healing efficiency. Similar results were reported by Tierney and Register51 for ethylene-methacrylic acid (E/MAA) ionomers with Na+ cations. They found that excess acidic groups (below the stoichiometric ratio) accelerate the ion-hopping mechanism through a “plasticizing” effect of the ionic units, generating a reduction in viscosity. This implies that the diffusivity of the ionic group decreases significantly as the level of neutralization increases. All these factors will be key to the study of phenomena such as self-healing and recycling.
At equal crosslink densities, 10ZnO reached healing efficiencies of 61% in TS and 76% in EB. The presence of excess ZnO could decrease the free volume available for the motions of the XNBR chains, acting as barriers to mobility and reducing repair efficiency, due to a slowing down of the ion-hopping mechanism. This finding highlights that crosslink density alone is not the sole influence on the molecular dynamics in the self-healing process. Factors such as the free volume, steric hindrance, neutralization degree, and binding energy also play pivotal roles.
Comparing the two compounds with equal MO contents (10MgO and 10ZnO), a better self-repairing capacity was observed in the compound with ZnO, which could be explained by its lower crosslink density and ionic interaction nature (higher ionic radius, lower ionic interaction), requiring less intense conditions to achieve higher efficiencies. Similar results have been reported previously. Hirasawa et al.68 studied the effects of different cations on the ionomer structure of poly(ethylene-co-methacrylic acid) (EMAA). The ionic interaction strengths of different cations (Na+, K+, Mg2+, Zn2+, Co2+, Cu2+, and Mn2+) were correlated with the melt flow rate (MFR) at different degrees of neutralization. It was found that the MFR decreased (viscosity increased) with increasing neutralization (i.e., crosslink density). This decrease was considerably higher for alkaline and alkaline earth metal salts than for the transition metal salts. This result shows that the ionic interaction in the ionomers is stronger in Mg2+ than in Zn2+, as evidenced by the increase in viscosity in the molten state. In this context, a higher viscosity will result in lower chain interdiffusion and thus a lower self-healing capacity, as demonstrated by the results of this investigation. Fig. 8a and b provide a schematic summary of the differences observed between the ionic networks and a simplified depiction of the Eisenberg model applied to the MO (assuming equal coordination numbers).
Considering these findings and the requirement to determine the optimal healing time, 10MgO was excluded from the subsequent stage of time optimization. Fig. 7b and 8c present the efficiency results with respect to TS and EB by extending the healing protocol time to 5 and 7 h. The results reveal that at 5 h, 10ZnO is capable of fully heal (efficiencies up to 100% in TS and EB). Concurrently, 1.25MgO can achieve complete repair (efficiencies above 100%) at all the time intervals studied.
At this point in the study, one intriguing aspect to be discussed relates to the possibility of achieving healing efficiencies exceeding 100%. This raises a compelling question: How can a material that has undergone total macroscopic damage and subsequent repair exhibit performance surpassing that of the pristine samples? The influence of the healing protocol, notably the applied temperature, on material properties plays a significant role beyond healing. To comprehend the extent of this effect, in a previous study by the authors,67 a new procedure was proposed, whereby pristine specimens were subjected to heat treatment under the same healing protocol but without inducing macroscopic rupture with a razor blade. The application of temperature to the pristine material induced an increase in the crosslink density, potentially leading to an enhancement in the mechanical properties of the material. Bearing this in mind, from a physical and comparative standpoint, it could be considered reasonable to employ the heat-treated material rather than the pristine material as the reference point for calculating healing efficiency. The newly calculated efficiency value was more realistically focused on the damage, thus suppressing the effect of the temperature. Nevertheless, in the aforementioned study, the repair mechanism was based on disulfide bond exchange, which is a dynamic but covalent mechanism that is inherently different from ionic interactions. This brings us to an interesting question: does temperature influence ionic interactions in the same way as it affects sulfur bonds? To answer this question, the new procedure was applied to the samples prepared in the current study. The efficiencies of 1.25MgO and 10ZnO (at 110 °C for 3 h) were recalculated (Fig. 7d). In the case of TS, 79% (1.25MgO) and 66% (10ZnO) were obtained, and for EB, 95% (1.25MgO) and 71% (10ZnO) were obtained. This is still an outstanding (successful repair) but more realistic numerical result for the damage recovery process without considering the thermal effect.
To contextualize the significance of these findings, it is important to compare the present results on mechanical properties and self-healing efficiency with recent studies (last 3 years) on healable ionic elastomers. However, it is crucial to point out that making direct comparisons between self-healing studies is not always entirely fair, essentially because there are no international standards. As the authors noted in a previous critical review, this is one of the major issues to be resolved in the field.19 Objective assessments require that vulcanization processes, self-healing mechanisms and protocols (time, temperature, pressure, etc.), and variables in mechanical tests (sample size and shape, crosshead speed, temperature, etc.) be equivalent.
In the light of these considerations, in terms of mechanical properties and self-healing efficiency, the designed ionic elastomers exhibited competitive values when compared to the available literature. But beyond the numerical results, the simplicity of the process introduced, the use of low-cost ingredients and the optimization of repair conditions place this development in an advantageous position. Zainol et al.69 developed XNBR compounds using the same zinc-carboxylate metal–ligand interaction, but with zinc thiolate (ZT) and dicumyl peroxide (DCP) in their recipes. Employing a considerably higher amount of ZT (30 phr), a TS of up to 8 MPa was achieved, coupled with a healing efficiency of 98%, at a higher temperature (150 °C), but with a reduced repair time (just 10 min).
Naskar et al.70 prepared self-healable and extremely stretchable ionic elastomer based on the dynamic metal–ligand coordination between 1-(3-aminopropyl)imidazole (API ligand) and Zn2+ metal ion moieties incorporated onto the XNBR rubber backbone, with zinc chloride (ZnCl2). With 3 phr of Zn2+ metal ion, an excellent healing performance of 91.2% was achieved at room temperature after 24 h, with the tensile strength of 5.7 MPa.
Recently, Das et al.71 investigated the ionic crosslinking of XNBR with Ni–cysteine and Zn–cysteine complexes. Compared to the Ni–cysteine compound, the XNBR cured with the Zn–cysteine complex exhibited outstanding extensibility, recyclability, and a tensile strength of 3.8 MPa, value which is distinctly lower to that of the ZnO- and MgO-based compounds prepared in the present study. However, they reported an impressive healing efficiency of 89.5% after 24 h at room temperature. This stands in contrast with our study, which requires shorter times but higher temperatures.
In contrast to zinc-carboxylate metal–ligand coordination, Wagje and Das72 delved into alternate metal cations. In their research, XNBR was crosslinked through a copper (I)-carboxylate metal–ligand interaction using anhydrous copper chloride (CuCl). Employing 20 phr of CuCl, the best mechanical performance was obtained, with a TS of 5.41 MPa and 251% EB. However, this blend could not self-repair under the conditions tested. Conversely, at lower CuCl content (5 phr), TS was reduced to 1.95 MPa, while the self-healing efficiencies reached up to 75% following a 70 °C and 48 h protocol. This underscores the balance between mechanical strength and self-healing ability. In our current study, this trade-off is addressed, producing materials with both superior mechanical properties and high self-healing efficiencies, a result of meticulously optimized repair conditions.
It is a fact that the studies mentioned highlight the multifaceted nature of approaches in the field of ionic elastomers and the versatility of methodologies that can be employed. The available research underscore the critical importance of content optimization to ensure the best balance between mechanical strength and self-healing efficiency. Moreover, while these recent investigations offer a vast wealth of knowledge, a key distinction is evident: their focus wasn't predominantly application-oriented. In contrast, our research prioritizes this aspect for soft robotics applications, ensuring not only scientific rigor but also practical applicability. Furthermore, as evident from the variety in crosslinking agents and their costs, there's an imperative to consider the feasibility of scalability in material designs. Our work addresses this by striving for simplicity and cost-effectiveness, but a comprehensive life cycle assessment (LCA) for these particular compounds is still necessary to gain a clearer understanding of the material's sustainability and the devised process.
The recyclability of the developed compounds was also analyzed to provide sustainability to the soft actuator. The evolution of different mechanical properties (M300, TS and EB) and crosslink densities with recycling cycles was followed. The results of 10ZnO have been previously reported73 by the authors and can be found in ESI† S7, while Fig. 9 shows the values of 1.25MgO and 10MgO. With each recycling cycle, an increase in the crosslink density was determined by swelling, with a notable decrease in the volume of solvent absorbed in the recycled samples, which could be associated with the redistribution of ionic aggregates into smaller structures around the matrix. Compounds with the same crosslink density (1.25MgO and 10ZnO) showed promising behavior, with 10ZnO retaining approximately 75% of its initial properties and 1.25MgO successfully retaining both properties (TS and EB), even after R3. Nonetheless, 10MgO exhibits a limited recyclability. A noticeable decrease in TS recovery with recycling cycles was observed, also not being able to reach 300% elongation at R2 and R3. However, its net TS and EB recovery values remain above 12 MPa and 200% strain, respectively, which may be useful in several rubber applications.
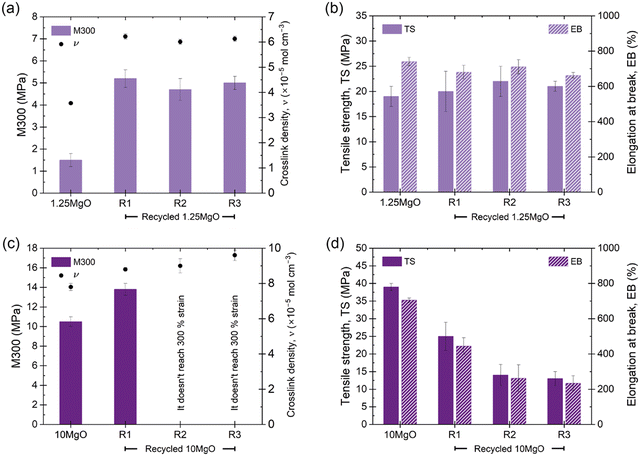 | ||
| Fig. 9 Evolution of the mechanical properties (M300, TS, and EB) and crosslink density of (a) and (b) 1.25MgO and (c) and (d) 10MgO through three recycling cycles. | ||
The final choice for manufacturing soft robotic grippers considers the balance between mechanical performance, healing capability, and recyclability. While 10MgO exhibited exceptional mechanical performance, its limitations in self-healing and recycling make it less suitable for long-term durability and sustainability. The high stiffness of 10MgO may also hinder its use for handling delicate products. 10ZnO showed good mechanical performance and healing ability, but longer healing times and recycling difficulties after the third cycle that may pose challenges in applications where quick repairs and consistent recyclability are crucial. However, this can be compensated by its shorter vulcanization time. 1.25MgO is another suitable choice. Despite having a slightly lower mechanical performance compared to other compounds, it still possesses competitive values when considering the most elastomeric materials used in soft robotics. In addition, it has a slower curing rate; however, its faster healing and ability to maintain its properties through multiple recycling cycles can significantly extend the lifespan of the robotic hand, reduce maintenance costs, and improve sustainability. Fig. 10a shows the final assembly of the soft robotic gripper developed using the optimized compound in this study.
 | ||
| Fig. 10 (a) Final assembly of gripper and (b) actuation of four programmed positions (pointing, ok, rock, and peace signs). | ||
Following the assembly process detailed earlier, the precision of the soft robotic gripper to perform intricate movements was confirmed. It was successfully actuated to form distinct gestures like the universally recognized “pointing”, “ok”, “rock!” and “peace” signs. These positions not only show the soft robot's ability to mimic human hand movements but also underscore the efficacy of using the ionic elastomer with its optimum flexibility and elastic response for the adequate performance. ESI† S8 shows a video representation of the motion achieved on the soft robot hand.
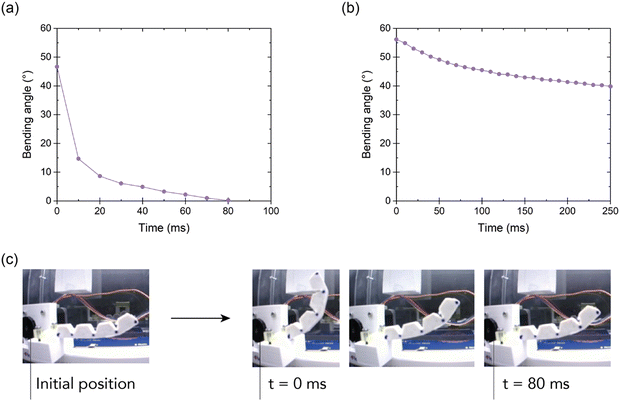
For the validation stage, two experimental tests were conducted using a motion tracking setup. These tests included a response test (Fig. 11a) and a stress relaxation test (Fig. 11b) at the system level, where the bending angle was followed as a function of time. In the response test, the actuator was initially bent to a 50° angle, after which the tension on the tendon was completely released (Fig. 11c). Next, the response of the actuator was investigated via tracking how fast it recovers to its initial (unbent) position. This test gives information about the dynamics of the selected material in this soft robotics application. It can be observed that only after 80 milliseconds, the actuator reaches back its initial position. Quick responses like these are crucial in soft robotic grippers as they guarantee rapid grasping actions, ultimately resulting in increased throughput in industrial applications.
In a second experiment, a stress relaxation test was performed on the soft bending actuator level by bringing it in a 55° bending angle by tensioning the tendon. Subsequently, the bending angle was monitored over time while maintaining the tendon in a fixed position. Due to stress relaxation in the material, the bending angle is slightly reduced over time. After 250 milliseconds the angle is reduced to 40°. Although this dynamic effect can be partially mitigated by the adaptability of the soft gripper, it is undesired in gripper applications where high position accuracy is requested. This effect results from the viscoelastic behavior of the ionic elastomer. Reversible/dynamic polymer networks in general suffer from a viscoelastic behavior, which impacts applications. Although the materials have a relatively low loss modulus at room temperature (ESI† S6), the experiments on the actuator level point out that the viscous component is far from negligible. Therefore, future work should focus on minimizing these viscous effects, as they can have an impact on the controllability of soft robotic systems. Our approach aids in the sustainable creation of soft robotic parts using healable and recyclable materials and also ensures they have the capability to fast perform with precision, a key requirement in practical real-world applications.
4. Conclusions
This investigation delves into the potential of XNBR-based compounds employing ZnO and MgO as vulcanizing agents, effectively demonstrating how a single ingredient can drastically influence the mechanical and physical properties of rubber while concurrently addressing issues of sustainability and recyclability. The research found that higher MO content increases vulcanization efficiency, leading to a higher cure rate and degree of crosslinking, and thus enhanced mechanical performance. A comparative analysis of equal crosslink densities revealed that excess ZnO imparts stiffness owing to its function as a semi-reinforcing filler. In contrast, equal MO contents induced superior mechanical properties in the MgO compound compared to ZnO owing to the stronger electrostatic attraction of its smaller cations. A significant innovation in this study is the use of BDS to determine the optimal temperature for a self-healing protocol, diverging from the traditional trial-and-error approaches typically employed for optimization. The compound with just 1.25 phr of MgO boasts the highest self-healing performance, achieving a healing efficiency of TS up to 79% and EB up to 95% at 110 °C within 3 h using an updated and fairer method for determining the repair efficiency. The selected ionic rubber also maintained full recyclability (100% recovery of the maximum mechanical properties) through three recycling cycles. Despite exhibiting the lowest tensile strength among the prepared compounds, 1.25MgO still delivered an impressive 19 MPa of TS, coupled with an EB exceeding 700%, which are an outstanding values in the field of soft matter. These findings have significant implications for the selection of elastomeric materials in areas such as soft robotics, where load capacity, sustainability, resilience, self-healing, and recycling abilities are crucial. The research successfully assembled a soft robotic gripper, demonstrating the practical application of these findings. This study significantly advances our understanding of the behavior and properties of XNBR-based compounds, particularly within the scope of ionic elastomers. It unlocks the potential of this behavior in advanced applications, such as soft robotics, where the usage of conventional ionic rubbers is no longer just a possibility, but a tangible reality.Author contributions
S.U.-B.: conceptualization, methodology, formal analysis, investigation, data curation, writing—original draft, writing—review and editing, visualization; N.S.: methodology, software, formal analysis, investigation, writing—review and editing; S.T.: conceptualization; methodology, resources, writing—review and editing, visualization; P.F.: methodology, software, investigation; R.V.: conceptualization, writing—review and editing, visualization, project administration, funding acquisition; G.V.A.: resources, funding acquisition; M.A.L.-M.: conceptualization, writing—review and editing, visualization, funding acquisition; J.B.: conceptualization; methodology, formal analysis, resources, writing—review and editing, supervision; M.H.S.: conceptualization, formal analysis, resources, data curation, writing—review and editing, visualization, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the State Research Agency of Spain (AEI) for the research contract (PID2019-107501RB-I00/AEI/10.13039/501100011033) and M. Hernández Santana for the Ramón y Cajal contract (RYC-2017-22837). The authors acknowledge the Spanish National Research Council (CSIC) for the iLink+ contract (LINKA20325) and S. Utrera-Barrios for the predoctoral contract (PIE-202060E183). The authors acknowledge the Fonds Wetenschappelijk Onderzoek (FWO) for the personal grants of S. Terryn (1100416N) and J. Brancart (12E1123N). All authors also acknowledge Arlanxeo for kindly providing XNBR and the PTI+ SusPlast from CSIC for their support.References
- X. Chen, X. Zhang, Y. Huang, L. Cao and J. Liu, J. Field Rob., 2022, 39, 281–311 CrossRef
.
- D. Rus and M. T. Tolley, Nature, 2015, 521, 467–475 CrossRef CAS PubMed
.
- L. Chen, C. Yang, H. Wang, D. T. Branson, J. S. Dai and R. Kang, Mech. Mach. Theory, 2018, 130, 109–122 CrossRef
.
- C. Yang, R. Kang, D. T. Branson, L. Chen and J. S. Dai, Mech. Mach. Theory, 2019, 139, 526–541 CrossRef
.
- E. Brown, N. Rodenberg, J. Amend, A. Mozeika, E. Steltz, M. R. Zakin, H. Lipson and H. M. Jaeger, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 18809–18814 CrossRef CAS
.
- Y. Wei, Y. Chen, T. Ren, Q. Chen, C. Yan, Y. Yang and Y. Li, Soft Robot., 2016, 3, 134–143 CrossRef
.
- P. Jiang, Y. Yang, M. Z. Q. Chen and Y. Chen, Bioinspiration Biomimetics, 2019, 14, 036009 CrossRef PubMed
.
- L. A. T. Al Abeach, S. Nefti-Meziani and S. Davis, Soft Robot., 2017, 4, 274–284 CrossRef PubMed
.
- H. Al-Fahaam, S. Nefti-Meziani, T. Theodoridis and S. Davis, Soft Robot., 2018, 5, 576–591 CrossRef
.
- Y. F. Zhang, N. Zhang, H. Hingorani, N. Ding, D. Wang, C. Yuan, B. Zhang, G. Gu and Q. Ge, Adv. Funct. Mater., 2019, 29, 1806698 CrossRef
.
- F. Hartmann, M. Baumgartner, M. Kaltenbrunner, F. Hartmann, M. Baumgartner and M. Kaltenbrunner, Adv. Mater., 2021, 33, 2004413 CrossRef CAS PubMed
.
- S. Terryn, J. Langenbach, E. Roels, J. Brancart, C. Bakkali-Hassani, Q. A. Poutrel, A. Georgopoulou, T. George Thuruthel, A. Safaei, P. Ferrentino, T. Sebastian, S. Norvez, F. Iida, A. W. Bosman, F. Tournilhac, F. Clemens, G. Van Assche and B. Vanderborght, Mater. Today, 2021, 47, 187–205 CrossRef CAS
.
- L. Imbernon and S. Norvez, Eur. Polym. J., 2016, 82, 347–376 CrossRef CAS
.
- E. Roels, S. Terryn, F. Iida, A. W. Bosman, S. Norvez, F. Clemens, G. Van Assche, B. Vanderborght and J. Brancart, Adv. Mater., 2022, 34, 2104798 CrossRef CAS PubMed
.
- S. Utrera-Barrios, R. Verdejo, M. A. López-Manchado and M. Hernández Santana, Mater. Horiz., 2020, 7, 2882–2902 RSC
.
- A. M. Wemyss, C. Bowen, C. Plesse, C. Vancaeyzeele, G. T. M. Nguyen, F. Vidal and C. Wan, Mater. Sci. Eng., R, 2020, 141, 100561 CrossRef
.
- N. Wang, X. Yang and X. Zhang, Nat. Commun., 2023, 14, 1–10 Search PubMed
.
- Y. Wang, R. Shu and X. Zhang, Angew. Chem., Int. Ed., 2023, 62, e202303446 CrossRef CAS PubMed
.
- S. Utrera-Barrios, R. Verdejo, M. Á. López-Manchado and M. Hernández Santana, Int. J. Mol. Sci., 2022, 23, 4757 CrossRef CAS PubMed
.
- S. Terryn, E. Roels, J. Brancart, G. Van Assche and B. Vanderborght, Actuators, 2020, 9, 34 CrossRef
.
- K. Cerdan, J. Brancart, E. Roels, B. Vanderborght and P. Van Puyvelde, Polymers, 2022, 14, 1657 CrossRef CAS PubMed
.
- A. C. Cornellà, S. Kashef Tabrizian, P. Ferrentino, E. Roels, S. Terryn, B. Vanderborght, G. Van Assche and J. Brancart, ACS Sustainable Chem. Eng., 2023, 11, 3437–3450 CrossRef
.
- J. Cao, C. Zhou, G. Su, X. Zhang, T. Zhou, Z. Zhou and Y. Yang, Adv. Mater., 2019, 31, 1900042 CrossRef PubMed
.
- M. Guo, Y. Wu, S. Xue, Y. Xia, X. Yang, Y. Dzenis, Z. Li, W. Lei, A. T. Smith and L. Sun, J. Mater. Chem. A Mater., 2019, 7, 25969–25977 RSC
.
- Y. Gao, X. Fang, D. Tran, K. Ju, B. Qian and J. Li, R Soc. Open Sci., 2019, 6 DOI:10.1098/RSOS.182145
.
- J. Deng, X. Kuang, R. Liu, W. Ding, A. C. Wang, Y. C. Lai, K. Dong, Z. Wen, Y. Wang, L. Wang, H. J. Qi, T. Zhang and Z. L. Wang, Adv. Mater., 2018, 30, 1705918 CrossRef PubMed
.
- Q. He, Z. Wang, Y. Wang, Z. Song and S. Cai, ACS Appl. Mater. Interfaces, 2020, 12, 35464–35474 CrossRef CAS PubMed
.
- P. Zhang and G. Li, Polymer, 2015, 64, 29–38 CrossRef CAS
.
- M. Gaca, J. Pietrasik, M. Zaborski, L. Okrasa, G. Boiteux and O. Gain, Polymers, 2017, 9, 645 CrossRef PubMed
.
- M. Wübbenhorst and J. Van Turnhout, J. Non Cryst. Solids, 2002, 305, 40–49 CrossRef
.
- J. Van Turnhout and M. Wübbenhorst, J. Non Cryst. Solids, 2002, 305, 50–58 CrossRef CAS
.
- W. H. H. Woodward, ACS Symp. Ser., 2021, 1375, 3–59 CrossRef CAS
.
- H. L. Fisher, J. Chem. Educ., 1942, 19, 522–530 CrossRef CAS
.
-
C. Chandrasekaran, Essential rubber formulary: formulas for practitioners, William Andrew Publishing, Norwich, NY, 2007 Search PubMed
.
- S. Maghami, W. K. Dierkes and J. W. M. Noordermeer, Rubber Chem. Technol., 2016, 89, 559–572 CrossRef CAS
.
- N. González, M. Del Àngels Custal, D. Rodríguez, J. R. Riba and E. Armelin, Mater. Res., 2017, 20, 1082–1091 CrossRef
.
- K. Parvathi and M. T. Ramesan, J. Polym. Res., 2023, 30, 1–15 CrossRef
.
- J. Araujo-Morera, M. A. López-Manchado, R. Verdejo and M. Hernández Santana, Polymer, 2022, 238, 124399 CrossRef CAS
.
- S. Utrera-Barrios, R. V. Manzanares, J. Araujo-Morera, S. González, R. Verdejo, M. Á. López-Manchado and M. H. Santana, Polymers, 2021, 13, 3234 CrossRef CAS PubMed
.
- R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef
.
- Z. Liu, G. Shao, W. Chen, L. Shen, Y. Cheng, X. Liang and W. Xiang, Opt. Mater. Express, 2018, 8, 2532–2541 CrossRef CAS
.
- R. M. DuChanois, M. Heiranian, J. Yang, C. J. Porter, Q. Li, X. Zhang, R. Verduzco and M. Elimelech, Sci. Adv., 2022, 8, 9436 CrossRef PubMed
.
- M. Das, S. Pal and K. Naskar, eXPRESS Polym. Lett., 2020, 14, 860–880 CrossRef CAS
.
- T. Dudev and C. Lim, J. Phys. Chem. B, 2001, 105, 4446–4452 CrossRef CAS
.
-
G. Socrates, Infrared and Raman characteristic group frequencies: tables and charts, John Wiley & Sons, 2004 Search PubMed
.
- A. Laskowska, M. Zaborski, G. Boiteux, O. Gain, A. Marzec and W. Maniukiewicz, eXPRESS Polym. Lett., 2014, 8, 374–386 CrossRef CAS
.
- S. M. Krzemińska, A. A. Smejda-Krzewicka, A. Leniart, L. Lipińska and M. Woluntarski, Polym. Test., 2020, 83, 106368 CrossRef
.
- B. A. Brozoski, M. M. Coleman and P. C. Painter, Macromolecules, 1984, 17, 230–234 CrossRef CAS
.
- P. C. Painter, B. A. Brozoski and M. M. Coleman, J. Polym. Sci., Polym. Phys. Ed., 1982, 20, 1069–1080 CrossRef CAS
.
- Z. Song, J. Wang, Q. Tao, Y. Yu, H. Zhang, C. Hu, H. Cen, X. Zheng, T. Hu and C. Wu, J. Appl. Polym. Sci., 2022, 139, 52041 CrossRef CAS
.
- N. K. Tierney and R. A. Register, Macromolecules, 2002, 35, 6284–6290 CrossRef CAS
.
- I. Mora-Barrantes, M. A. Malmierca, J. L. Valentin, A. Rodriguez and L. Ibarra, Soft Matter, 2012, 8, 5201–5213 RSC
.
- Y. Miwa, J. Kurachi, Y. Kohbara and S. Kutsumizu, Commun. Chem., 2018, 1 CAS
.
- S. Salaeh, A. Das and S. Wießner, Polymer, 2021, 223, 123699 CrossRef CAS
.
- Y. Miwa, J. Kurachi, Y. Sugino, T. Udagawa and S. Kutsumizu, Soft Matter, 2020, 16, 3384–3394 RSC
.
- L. Zhang, H. Wang, Y. Zhu, H. Xiong, Q. Wu, S. Gu, X. Liu, G. Huang and J. Wu, ACS Appl. Mater. Interfaces, 2020, 12, 53239–53246 CrossRef CAS PubMed
.
- A. Eisenberg, Macromolecules, 1970, 3, 147–154 CrossRef CAS
.
- A. Eisenberg, B. Hird and R. B. Moore, Macromolecules, 1990, 23, 4098–4107 CrossRef CAS
.
- D. Basu, A. Das, K. W. Stöckelhuber, D. Jehnichen, P. Formanek, E. Sarlin, J. Vuorinen and G. Heinrich, Macromolecules, 2014, 47, 3436–3450 CrossRef CAS
.
- T. Chatterjee, S. Hait, A. B. Bhattacharya, A. Das, S. Wiessner and K. Naskar, Polym.-Plast. Technol. Mater., 2019, 59, 141–153 Search PubMed
.
- S. M. R. Paran, G. Naderi, H. Mosallanezhad, E. Movahedifar, K. Formela and M. R. Saeb, Polymers, 2020, 12, 1192 CrossRef CAS PubMed
.
- J. Fritzsche, A. Das, R. Jurk, K. W. Stöckelhuber, G. Heinrich and M. Klüppel, eXPRESS Polym. Lett., 2008, 2, 373–381 CrossRef CAS
.
- D. Basu, S. S. Banerjee, S. Chandra Debnath, M. Malanin, L. Amirova, P. Dubois, G. Heinrich and A. Das, Polymer, 2021, 212, 123309 CrossRef CAS
.
- M. Hernández, A. M. Grande, W. Dierkes, J. Bijleveld, S. Van Der Zwaag and S. J. García, ACS Sustainable Chem. Eng., 2016, 4, 5776–5784 CrossRef
.
- A. M. Grande, R. Martin, I. Odriozola, S. van der Zwaag and S. J. Garcia, Eur. Polym. J., 2017, 97, 120–128 CrossRef CAS
.
- Y. Zhang, J. Zheng, W. Ma, X. Zhang, Y. Du, K. Li, Y. Liu, G. Yu and Y. Jia, Eur. Polym. J., 2022, 175, 111394 CrossRef CAS
.
- J. Araujo-Morera, S. Utrera-Barrios, R. D. Olivares, R. Verdugo Manzanares, M. Á. López-Manchado, R. Verdejo and M. Hernández Santana, Macromol. Mater. Eng., 2022, 2200261 CrossRef CAS
.
- E. Hirasawa, Y. Yamamoto, K. Tadano and S. Yano, J. Appl. Polym. Sci., 1991, 42, 351–362 CrossRef CAS
.
- M. H. Zainol, Z. M. Ariff, M. F. Omar, T. M. Ping and R. K. Shuib, J. Appl. Polym. Sci., 2022, 139, e51948, DOI:10.1002/APP.51948
.
- M. Das, A. Baran Bhattacharya, R. Parathodika and K. Naskar, Eur. Polym. J., 2022, 174, 111341 CrossRef CAS
.
- M. Das, T. K. Sreethu, S. Pal and K. Naskar, ACS Appl. Polym. Mater., 2022, 4, 6414–6425 CrossRef CAS
.
- S. W. Wajge and C. Das, Polym. Adv. Technol., 2023, 34, 998–1007 CrossRef CAS
.
- S. Utrera-Barrios, R. Verdugo Manzanares, A. M. Grande, R. Verdejo, M. Á. López-Manchado and M. Hernández Santana, Mater. Des., 2023, 233, 112273 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: (S1) Product data for Krynac X 750 supplied by Arlanxeo; (S2) IR spectra of the ionic elastomers; (S3) DSC and TGA results; (S4) healing efficiency based on M300 values of the ionic elastomers; (S5) stress–strain curves of the ionic elastomers in pristine and healed state (healing protocol: 110 °C, 3 h, rectangular specimens); (S6) storage (E′) and Loss moduli (E′′) by DMA; (S7) evolution of the mechanical properties (M300, TS, and EB) and crosslink density of 10ZnO through three recycling cycles; (S8) video of the actuation. See DOI: https://doi.org/10.1039/d3mh01312j |
| This journal is © The Royal Society of Chemistry 2024 |