Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing the role of surface termination in the adsorption of azupyrene on copper†
Benedikt P.
Klein‡
ab,
Matthew A.
Stoodley
 ab,
Dylan B.
Morgan
ab,
Dylan B.
Morgan
 b,
Luke A.
Rochford
a,
Leon B. S.
Williams
ade,
Paul T. P.
Ryan§
af,
Lars
Sattler
g,
Sebastian M.
Weber
g,
Gerhard
Hilt
g,
Thomas J.
Liddy
ah,
Tien-Lin
Lee
a,
Reinhard J.
Maurer
b,
Luke A.
Rochford
a,
Leon B. S.
Williams
ade,
Paul T. P.
Ryan§
af,
Lars
Sattler
g,
Sebastian M.
Weber
g,
Gerhard
Hilt
g,
Thomas J.
Liddy
ah,
Tien-Lin
Lee
a,
Reinhard J.
Maurer
 *bc and
David A.
Duncan
*bc and
David A.
Duncan
 *a
*a
aDiamond Light Source, Harwell Science and Innovation Campus, Didcot, OX11 0DE, UK. E-mail: david.duncan@diamond.ac.uk
bDepartment of Chemistry, University of Warwick, Gibbet Hill Road, Coventry, CV4 7AL, UK. E-mail: r.maurer@warwick.ac.uk
cDepartment of Physics, University of Warwick, Gibbet Hill Road, Coventry, CV4 7AL, UK
dSchool of Chemistry, University of Glasgow, University Avenue, Glasgow, G12 8QQ, UK
eSchool of Physics and Astronomy, University of Glasgow, University Avenue, Glasgow, G12 8QQ, UK
fDepartment of Materials, Imperial College London, Prince Consort Rd, SW7 2AZ, UK
gInstitut für Chemie, Carl von Ossietzky Universität Oldenburg, Carl-von-Ossietzky-Straße 9-11, 26111 Oldenburg, Germany
hSchool of Chemistry, University of Nottingham, University Park, Nottingham, NG7 2RD, UK
First published on 26th February 2024
Abstract
The role of the inorganic substrate termination, within the organic–inorganic interface, has been well studied for systems that contain strong localised bonding. However, how varying the substrate termination affects coordination to delocalised electronic states, like that found in aromatic molecules, is an open question. Azupyrene, a non-alternant polycyclic aromatic hydrocarbon, is known to bind strongly to metal surfaces through its delocalised π orbitals, thus yielding an ideal probe into delocalised surface-adsorbate interactions. Normal incidence X-ray standing wave (NIXSW) measurements and density functional theory calculations are reported for the adsorption of azupyrene on the (111), (110) and (100) surface facets of copper to investigate the dependence of the adsorption structure on the substrate termination. Structural models based on hybrid density functional theory calculations with non-local many-body dispersion yield excellent agreement with the experimental NIXSW results. No statistically significant difference in the azupyrene adsorption height was observed between the (111) and (100) surfaces. On the Cu(110) surface, the molecule was found to adsorb 0.06 ± 0.04 Å closer to the substrate than on the other surface facets. The most energetically favoured adsorption site on each surface, as determined by DFT, is subtly different, but in each case involved a configuration where the aromatic rings were centred above a hollow site, consistent with previous reports for the adsorption of small aromatic molecules on metal surfaces.
Introduction
The organic/inorganic interface is important for various modern device applications in a wide range of fields, such as organic semiconductors, gas sensing and medical devices.1–6 Molecular adsorption at this interface controls important properties such as band alignment, charge carrier injection barriers and growth templating.1,4,5,7 These properties are governed by an interplay of competing interactions at this interface: the interaction across layers between the inorganic substrate and adsorbed organic overlayer; the interaction between molecules in the organic layer; molecular distortions induced by adsorption; anchoring of the individual molecules to the inorganic substrate; etc. Thus, elucidating the role that each of these interactions play at the organic/inorganic interface is key to systematic improvement in device design, and requires the study of model systems. In particular in quantitative structural determination, there has been a strong focus on understanding how organic molecules or metal organic complexes interact with different metallic substrates. Indeed, there have been several exhaustive studies probing the different adsorption heights for such species above the (111) surface of different coinage metals.8–16 There have been, however, far fewer studies into how the interaction at the organic/inorganic interface changes with surface termination.Several studies have indicated that the interaction between the metal surfaces and molecular adsorbates follow similar rules that can be found within coordination chemistry,17–20 which would give the naïve impression that one can consider the interaction at the inorganic/organic interface to be determined simply by the individual atoms that directly bond to one another. However, some effects at the organic/inorganic interface are purely surface driven, which has been shown in the few studies comparing adsorption on different surface terminations. For example, when formate (dehydrogenated formic acid) adsorbs on Cu surfaces, it has an identical coordination number across different surface terminations, but the Cu–O bond length is dependent on the substrate.21 Namely, on the (111) and (110) surface, formate adsorbs with both of its oxygen atoms off-atop neighbouring Cu atoms (i.e. singly coordinated), yet adsorption on the (110) surface results in a significant decrease (0.09 ± 0.05 Å) in the Cu–O bond length compared to the (111) surface. This result was anticipated – the surface Cu atoms in the (110) surface are under coordinated compared to the Cu atoms in the (111) surface (6-fold vs. 9-fold), and thus are expected to more strongly interact with molecular species. The (100) termination, the third low index surface termination of fcc crystals, is expected to sit in the middle of these two substrates, in terms of interaction strength, as its surface Cu atoms are each 8-fold coordinated.
However, in the case of formate, the bonding between the surface and the molecule is very directional, featuring a strong bond between individual atoms in the surface and individual atoms in the molecule, which dominates the total adsorbate and substrate interaction. Yet, many systems of interest at the organic/inorganic interface consist of large aromatic molecules where the bonding between the substrate and adsorbates is far more delocalised. Rather than considering only the interaction found in these “localised bonds” one must also consider the “delocalised bonding” interaction between surface valence/conduction band and molecular orbitals, both of which are delocalised over multiple atoms. Quantitative studies comparing the adsorption of such large aromatic molecules on different low index surface terminations of the same metal, however, are few and far between.
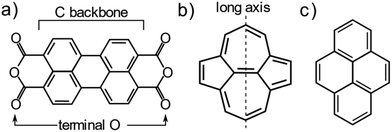
One system that is particularly well studied in the literature is PTCDA (Peryleno[3,4-cd:9,11-c′d′]dipyran-3,5,10,12-tetrone, shown schematically in Fig. 1a), a large aromatic molecule with terminal oxygen atoms (indicated in Fig. 1a). The adsorption structure of this molecule has been quantitatively determined on the three low index terminations of Ag14,22 as well as the (111) and (100) terminations of Cu.13,23 The adsorption height of the carbon backbone (indicated in Fig. 1a) of the molecule, as determined by normal incidence X-ray standing waves (NIXSW), was found to be very similar for the Ag(111) and Ag(100) surfaces but decreased significantly (∼0.3 Å) on the Ag(110) surface. However, separating the localised and delocalised contributions to the molecule-metal bond that this molecule forms is challenging. In addition to the delocalised bonding of the C backbone, that is dominated by long-range dispersion interactions, there is clear localised bonding between the terminal O atoms in the molecule and the Ag atoms at which they are anchored. Furthermore, due to differing lattice matching, the registry between the Ag atoms and the O atoms varies between the (111) and the other two terminations. Thus, it is not possible to draw direct conclusions about the role of the surface termination from the PTCDA work.
To disentangle the direct effects of the surface termination on delocalised bonding more clearly and to elucidate how the surface termination will affect interactions with large aromatic molecules, a different model molecule is required. In particular, this molecule should interact strongly with the underlying substrate, but bond to the surface via delocalised molecular orbitals rather than through localised bonds. Non-alternant polycyclic aromatic hydrocarbons (PAH) offer such properties. Non-alternant PAHs without heteroatoms contain only carbon and hydrogen, thus no highly reactive functional groups or lone pairs that would lead to localised bonds. While alternant PAHs tend to interact weakly with metallic surfaces, non-alternant PAHs, e.g. those containing 5- and 7-membered aromatic rings, have been previously shown to bond strongly to the underlying surface.24–27 Azulene, the non-alternant isomer of naphthalene, adsorbs ∼0.7 Å closer to the Cu(111) surface than naphthalene; possesses a 0.8 eV larger adsorption energy; and exhibits significant electronic hybridisation with the metallic states of the underlying Cu.25 Similarly, azupyrene (Fig. 1b) also electronically hybridises with the Cu(111) surface and exhibits a greater adsorption energy than its alternant counterpart pyrene (Fig. 1c).28 Due to its size and symmetry, the azupyrene molecule (compared to azulene) represents a more suitable model system to probe the role of the surface termination in delocalised bonding.
Azupyrene is a molecular semiconductor with a dipole-forbidden HOMO to LUMO transition, but that still has a comparably narrow optical band gap (2.54 eV).29 This forbidden transition means that, although it is optically active for absorption of photons, it does not fluoresce and could have applications in organic photovoltaics. In thick films the HOMO is found at a binding energy of 2.10 eV,29 therefore the LUMO is close to the Fermi edge. Hence, there could also be applications for this molecule as an exciton barrier at the electrode interface for a variety of organic semiconducting devices. Thus, beyond yielding a purely fundamental insight into the interaction between aromatic molecules and metallic surfaces, studying azupyrene on copper surfaces is of specific interest for future potential utilisation in organic semiconductors.
In this work, we quantitatively compare the adsorption height of azupyrene on the three different low index surface facets of Cu: Cu(111), Cu(110) and Cu(100). Utilising the NIXSW technique and density functional theory (DFT) calculations using a hybrid functional (HSE06)30 with non-local many-body dispersion (MBD-NL)31 we elucidate the adsorption geometry of the azupyrene across all three terminations. Overall, we find that there is little difference in the adsorption height between the Cu(111) and Cu(100) substrates, but a measurable decrease in adsorption height on the Cu(110) surface.
Experimental methods
The experimental measurements were performed in one of the permanent endstations mounted on the I09 beam line32 at Diamond Light Source (UK). Soft X-ray photoelectron spectroscopy (SXPS) and normal incidence X-ray standing wave (NIXSW) data were acquired using an EW4000 HAXPES (Scienta) hemispherical energy analyser. The analyser was mounted perpendicular to the incident photons, in the plane of the photon polarisation (linear horizontal). Clean Cu(111), Cu(110) and Cu(100) samples were prepared by repeated sputtering (pAr = 5 × 10−5 mbar, U = 1 kV) and annealing (T = 800–1000 K) cycles. Their cleanliness was assessed by SXPS and low energy electron diffraction (LEED). On occasion, after annealing to substrate temperatures greater than ∼900 K, a small Sn or Sb contaminant was observed on the surface of the crystal, however this contaminant had no obvious effect on the NIXSW results for the azupyrene layer and is thus assumed to not play any role in the molecular adsorption. For the NIXSW measurements, the reflectivity was acquired simultaneously to the photoelectron yield using a fluorescent plate that is mounted inside the port through which the incident photons pass. The measured reflectivity curve was used to define the position of the Bragg energy, as well as the broadening present in the system due to imperfections in the monochromator or the copper single crystals. The Cu(111), (220) and (200) reflections were employed at photon energies of ∼2990 eV, ∼4860 eV and ∼3440 eV for the NIXSW measurements of the Cu(111), (110) and (100) samples, respectively. The non-dipolar effects in the NIXSW measurement33 were addressed using a so-called “backwards-forwards Q-parameter”,34 which was calculated theoretically35 using the angle between photon polarisation and the median photoelectron intensity emission angle (θ = 18°). The NIXSW data were acquired over multiple spots on the sample (5 for the (111), 3 for the (110) and 3 for the (100) surface) and the summation of these data were analysed to obtain the results herein. Before acquisition of the NIXSW measurement a reflectivity measurement was performed to ascertain the crystalline quality of the spot on the sample, and to adjust the photon energy region such that the same energy range, relative to the Bragg energy, was acquired in each position. The individual photoelectron energy distribution curves of the NIXSW measurements were fitted with a convolution of a Gaussian and a Doniach-Sunjic36 line shape. A Gaussian error function, that shared the same Gaussian width as the peak, was used to model the step in the photoelectron intensity before and after the peak, while a straight line was used to model the background variation. The uncertainty in the coherent fraction and coherent position (and thus the mean adsorption height) is the standard error, taken at two standard deviations, from the fitting of the NIXSW photoelectron yield profiles, weighted by the standard error in the fitting of the individual spectra in the NIXSW data.Sub-monolayers of azupyrene were deposited onto the copper samples, which were held at room temperature, using a specially designed “line of sight” doser, described in greater detail in ref. 37. During deposition, the azupyrene was heated to 55–70 °C using either a warm-water bath or a Peltier heater. The azupyrene was synthesised as described in ref. 29. Previous UV/Vis spectroscopy, fluorescence spectroscopy temperature programmed desorption (TPD) and non-contact atomic force microscopy (nc-AFM) measurements on the (111) surface have not indicated the presence of any contaminant molecule.28,29,37 Notably, prior nc-AFM measurements indicate that the azupyrene adsorbs intact onto the (111) surface and TPD measurements demonstrate that the molecule remains intact on this surface up to a temperature of ∼500 K.
Computational methods
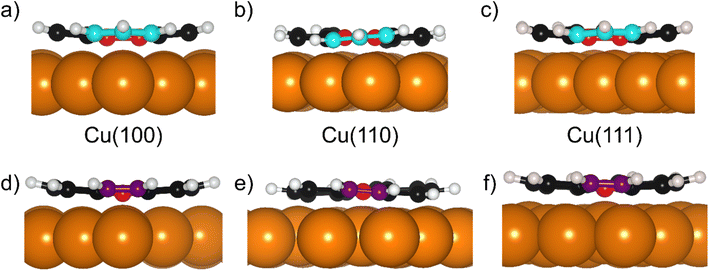
Periodic density functional theory calculations were performed with the all-electron numeric atomic-orbital code FHI-aims.38 The HSE06 hybrid functional30 was used with an exchange screening parameter of 0.11 bohr−1, together with the non-local many-body dispersion correction (MBD-NL) with the damping parameter set to 0.81.31 The Cu lattice constants were determined by performing Birch Murnaghan fits, as is detailed in §3 of the ESI.† The k-grid was set to 4 × 4 × 1 and this was used for all copper facets as the employed unit cells covered similar surface areas. The molecules were adsorbed on 6-layer Cu slabs with a large vacuum layer added perpendicular to the surface to reach a total slab thickness of 100 Å. A ‘light’ basis set was used for the lower 4 Cu layers, while a ‘tight’ basis set was used for the topmost 2 Cu layers and the C and H atoms (2020 default basis definitions). For all Cu-atoms, a frozen core approximation was employed, which included the Cu 1s, 2s, and 2p orbitals. The electronic convergence parameters were set to 1 × 10−5 e Å−3 for the electron density, 1 × 10−3 eV for the KS-eigenvalues and 1 × 10−6 eV for the total energy. Scalar relativistic effects were considered by employing the atomic ZORA correction.38 The structures were optimised until a force threshold of 0.01 eV Å−1 was reached. For Cu(111) a 5 × 5 supercell was used, for Cu(110) a 4 × 5 supercell was used, and for Cu(100) a 5 × 5 supercell was used. To determine reliable DFT adsorption heights, we performed an extensive adsorption site search by testing 7 adsorption configuration for azupyrene on Cu(100), 12 configurations on Cu(110), and 7 for Cu(111) (see §4 in the ESI† for details). This adsorption site search was performed using the PBE + MBD-NL method. The most stable adsorption structures, determined by PBE + MBD-NL, were then the starting points for structure relaxations with the HSE06 + MBD-NL functional, which were used for all analyses present herein. The best adsorption site for the adsorption of azupyrene on Cu(111) is in agreement with literature, where a similar search was reported using PBE + D3.28Results
Soft X-ray photoelectron spectroscopy (SXPS)
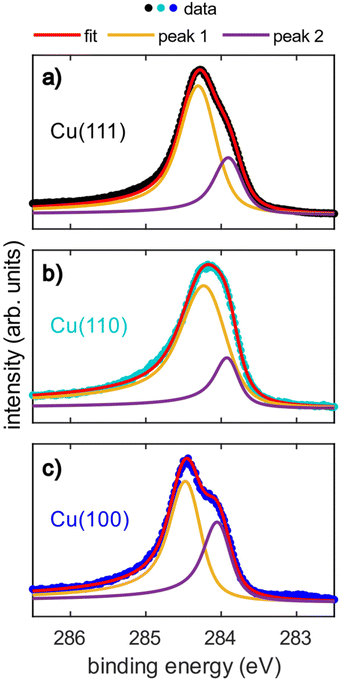
The acquired SXPS data (hν = 430 eV) for azupyrene on Cu(111), Cu(110) and Cu(100) are shown in Fig. 2. The Cu(111) SXPS data agree well with those previously published for this system,28 though our results are measured at higher spectral resolution. The spectra for Cu(111) and Cu(100), Fig. 2a and c, show a primary peak with a clearly resolved shoulder feature at lower binding energy, while for Cu(110), a single broad feature is observed. Fitting of these data revealed that the breadth of the Cu(110) spectra could not be fitted well with a single peak, suggesting that the shoulder observed from the (100) and (111) surfaces is still present. Note that due to the relatively small binding energy shift between the two peaks in all three spectra, a unique fit is not possible, however illustrative fits that indicate the two features are presented in Fig. 2. As a unique fit was not possible for these data, the SXPS will only be primarily discussed in general terms below. The clear similarities between these C 1s SXP spectra on the different surface terminations demonstrate that the azupyrene molecule adsorbs intact on the (100) and (110) surface, as has been previously observed on the (111) surface.28 Were the molecule to have partially decomposed upon adsorption additional features in the spectrum would be expected, for example a Cu–C organometallic peak at an even lower binding energy than the shoulder feature.39 There is no evidence in the spectra shown in Fig. 2 of any significant decomposition.All spectra exhibit an asymmetrical tail at higher binding energy, reminiscent of the asymmetrical loss features observed in metallic systems.28,40 This asymmetric loss feature is approximately similar for the adsorption on Cu(111) and Cu(100) (Doniach-Sunjic asymmetry parameter α = 0.12 and 0.14, respectively) and significantly more pronounced on Cu(110) (α = 0.17). Recent ultra-violet spectroscopy (UPS) and near-edge X-ray absorption fine structure (NEXAFS) measurements28 have indicated a significant hybridisation between the azupyrene molecular orbitals and the delocalised electrons of the underlying Cu(111) surface. As such, the asymmetrical line shape of the C 1s SXP spectra have also been assigned to loss features from shake-up excitation within the hybridised metallic-molecular electronic states.28 Therefore the larger asymmetry in the C 1s spectra of azupyrene on Cu(110) indicates a greater degree of hybridization of the molecular orbitals with the substrate's electronic bands.
The (110) C 1s spectra is shifted to a slightly lower binding energy (∼0.2 eV) than the (111) or (100) spectra, and the binding energy shift between the two peaks is slightly smaller (∼0.1 eV). The shift in XPS binding energies therefore cannot easily be rationalised by any naïve interpretations relying upon expected strength of interaction between the different substrates, e.g. an increase in interaction from Cu(111) to Cu(100) to Cu(110). It is possible that the increased hybridisation with the underlying substrate has resulted in this subtle change in the spectral line shape. Both the increased hybridisation and the subtle change in lineshape could also arise from the greater electronic corrugation found on the (110) surface, compared to the (100) and (111) surfaces. The localised dipoles formed by Smoluchowski smoothing41,42 may alter the degree of hybridisation between the substrate and the molecule, resulting in the smaller binding energy shift between the two features than is observed for the two other substrates. This is discussed further in the DFT section. The relative area of the shoulder seems to be at the lowest on the (110) surface, however a satisfactory fit was possible assuming the relative area of the shoulder was consistent across all surfaces (e.g. Fig. S1 in the ESI†). Any possible difference in the relative area could be attributed to diffractive effects, as, at these kinetic energies (∼150 eV), Cu is an effective backscatterer of electrons,43 thus subtle differences in atomic registry could result in significant (20–40%)44–46 variations in the photoemission intensity. Such an explanation would also explain why these shoulders are completely absent in the hard X-ray photoelectron spectroscopy (HAXPES) measurements (see Fig. S2 in the ESI†), as backscattering effects are very weak at large (>1 keV) kinetic energies.47
Normal incidence X-ray standing waves (NIXSW)
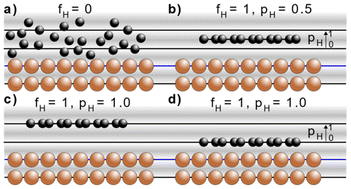
The NIXSW technique48,49 exploits the X-ray standing wave formed by the interference between the incident and reflected waves around the Bragg condition for a given reflection H = (h, k, l). The standing wave's period matches the interplanar spacing dH between the Bragg diffraction planes.50 For a monoatomic face centred cubic crystal lattice, like that of Cu, the Bragg diffraction planes will be coincident with the atomic planes of the substrate. The standing wave's phase, and thus the location of its maximum intensity, varies as the photon energy is scanned through the Bragg condition. When the phase is π, the maximum intensity is halfway between Bragg diffraction planes; when the phase is zero the maximum intensity is coincident with the Bragg diffraction planes. Any atom within this standing wavefield will therefore experience a varying electromagnetic field intensity as a function of its position between these diffraction planes. This variation in intensity will result in a characteristic absorption profile, which can be acquired by monitoring the relative photoelectron yield. The measured profile is then fitted uniquely, using dynamical diffraction theory,51 by two dimensionless parameters: the coherent fraction, fH, and the coherent position, pH. These, respectively, can be considered to correspond to the degree of order and the mean position of the absorber atoms relative to the Bragg diffraction planes, as shown in Fig. 3a–d.49 When the origin of coordinate system is chosen to be the Bragg diffraction plane closest to the surface (see Fig. 3) the coherent position is related to the mean adsorption height (hH) by:| hH = (n + pH)·dH, | (1) |
The C 1s NIXSW data from Cu(111), Cu(110) and Cu(100) are shown in Fig. 4. Despite the clear shoulder present in the Cu(111) and Cu(100) SXPS data, the NIXSW results were obtained using a single peak fitting of the data. The poorer photon energy resolution at the elevated energies required to generate the NIXSW (see Fig. S2a–c in the ESI†), meant that no unique two peak fit of the data could be achieved. The resulting coherent fractions, coherent positions and mean adsorption heights are detailed in Table 1. Within the uncertainties of the measurement, it is not possible to discriminate between the adsorption heights of azupyrene on Cu(111) and Cu(100), where the difference is only 0.01 ± 0.05 Å. Between adsorption on the Cu(111) and (110) surface, there is a statistically significant height difference of 0.06 ± 0.04 Å.
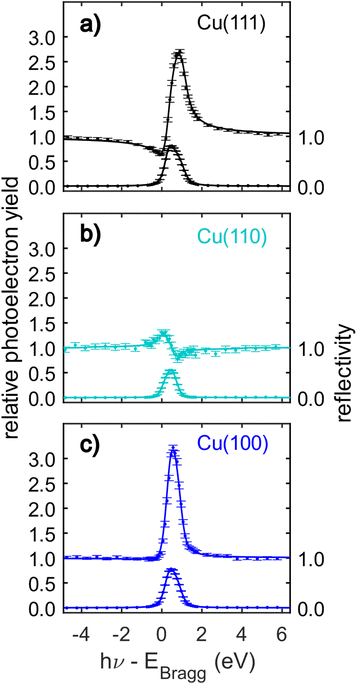 | ||
| Fig. 4 C 1s normal incidence X-ray standing waves (NIXSW) data of azupyrene adsorbed on (a) Cu(111), (b) Cu(110) and (c) Cu(100). The data were acquired from the following reflections, with their respective Bragg energies: (111), EBragg = 2978 eV; (220), EBragg = 4863 eV; (200), EBragg = 3439 eV. The corresponding coherent fractions, coherent positions and resulting mean adsorption heights obtained from fitting the data are detailed in Table 1. | ||
| NIXSW | DFT (HSE06 + MBD-NL) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| H | d H (Å) | f H | p H | h H (Å) | h H (Å) | h COM (Å) | E ads (eV) | E ads/Cu (eV) | ||
| Azupyrene | Cu(111) | 111 | 2.087 | 0.72(3) | 0.07(1) | 2.24(3) | 2.19 | 2.23 | −2.92 | −0.12 |
| Cu(110) | 220 | 1.278 | 0.74(4) | 0.71(2) | 2.18(3) | 2.07 | 2.13 | −3.36 | −0.17 | |
| Cu(100) | 200 | 1.807 | 0.70(5) | 0.24(2) | 2.23(4) | 2.18 | 2.20 | −3.46 | −0.14 | |
The observed differences in adsorption height are far smaller than those observed for PTCDA on the different terminations of Ag. This discrepancy is unlikely to be caused by a difference between Cu and Ag; between PTCDA on Cu(111)13 and Cu(100)23 larger differences of 0.22 ± 0.03 Å and 0.34 ± 0.05 Å were also observed for the carbon and oxygen atoms, respectively. Indeed, these results could indicate that the large differences observed for PTCDA on both Cu and Ag surfaces are driven by the localised bonding interaction between the oxygen and metal atoms, notably the difference in the local coordination site of the O atoms, that results in a significant convex curvature of the adsorbed molecule.
Considering the measured coherent fractions of the azupyrene molecule on the three surfaces, they are similar across all surfaces between 0.70 and 0.74. It should be noted that the Bragg planes responsible for the formation of the X-ray standing wave field are differently spaced for the three facets. The d-spacing for the (220) reflection is d220 = 1.278 Å, significantly smaller than that of either (111) (d111 = 2.087 Å) or (200) reflections (d200 = 1.808 Å). Therefore, a given spread in adsorption heights would yield a smaller coherent fraction using the (220) reflection, than the (111) or (200). If the reduction of the coherent fraction would be solely caused by a thermal vibration of the molecules and modelled with a Debye–Waller factor, then the required root mean squared vibrational amplitudes (rmsVib) would be 0.27 Å for Cu(111), 0.24 Å for Cu(100), and 0.16 Å for the Cu(110) data. A rmsvib of 0.16 Å is not unreasonable, suggesting that the azupyrene on Cu(110) may well adsorb with all C atoms at effectively the same adsorption height. For the (111) and (100) surface, the vibrational amplitudes required to explain the low coherent fraction with a single adsorption height are too large, and likely suggest the presence of C atoms at different adsorption heights.52
To better understand the experimental results, in the following we turn to DFT calculations. Though DFT calculations for azupyrene on the (111) surface have previously been reported in the literature,28 there are no such data present for the (110) and (100) surfaces.
Density functional theory calculations
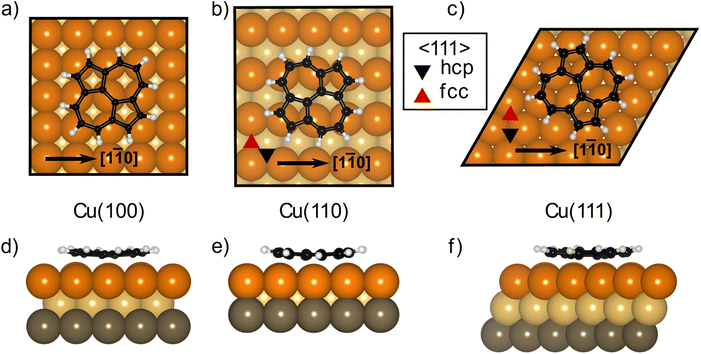
The DFT calculations in the previously published work for azupyrene on Cu(111)28 predicted an adsorption height of 2.44 Å, almost 0.2 Å greater than the height measured with NIXSW. These calculations were performed using the GGA functional PBE and the D3(BJ) dispersion correction.53–55 Standard Generalized Gradient Approximation exchange correlation functionals, such as the PBE functional,56 do not capture long-range dispersion interactions and fail to describe physisorption at metal surfaces.57 Pairwise dispersion corrections such as the Grimme D3 method54 or the surface-screened Tkatchenko-Scheffler vdW method58 have shown good performance in the prediction of the adsorption height of weakly physisorbed systems, such as benzene and azobenzene on Ag(111)59,60 or naphthalene on Cu(111) and Ag(111),24 and more strongly bound systems such as azulene and PTCDA on coinage metal surfaces.24,61,62 However, the pairwise dispersion correction approach is known to overestimate the adsorption energy, whereas the self-interaction error inherent in PBE can lead to a misrepresentation of induction effects and Pauli repulsion in the adsorption geometry. The non-local many-body dispersion method was developed to overcome the former effect and was shown to improve the description of molecule-metal interfaces.31,63,64 Recently, PBE + MBD-NL provided an accurate prediction of the adsorption height of 7,7,8,8-tetracyanoquinodimethane (TCNQ) on Ag(100) when compared to XSW measurements.65 Replacing the PBE functional with the range-separated hybrid functional HSE06,30 combined with the MBD method, was able to fully resolve the adsorption structure and energetics of benzene on Ag(111).59The optimised HSE06 + MBD-NL structures were used for all further analysis and are presented in Fig. 5 and 6. The most stable adsorption site on Cu(100) has the molecular centre directly atop a surface Cu atom and the long axis of the molecule (indicated on Fig. 1b) rotated by 45° relative to the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction. On Cu(110), the most favourable adsorption site has the centre of the molecule above a long-bridge site along the [001] direction, while the molecular long axis is rotated by 45° with respect to that direction. On Cu(111), the centre of the molecule is again located above a bridge site and the long axis of the molecule is rotated by 50° relative to the [1
0] direction. On Cu(110), the most favourable adsorption site has the centre of the molecule above a long-bridge site along the [001] direction, while the molecular long axis is rotated by 45° with respect to that direction. On Cu(111), the centre of the molecule is again located above a bridge site and the long axis of the molecule is rotated by 50° relative to the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction of that bridge site. For both the (100) and (111) surface, though the adsorption site of the molecular centre differs (atop and bridge sites, respectively), the centre of the 7- and 5-membered rings lie above hollow sites. Similar adsorption configurations have been experimentally observed for benzene on Ru(0001),66 Ni(111)67 and Co(0001),68 as well as furan on Pd(111).69 At first glance, on the (110) surface, it would appear as though the molecule has adsorbed in a different configuration, however the (110) surface is far more corrugated than the (111) or (100) surfaces. As such, every surface unit cell can almost be considered to contain two 〈111〉 steps. If this conceit is considered, the molecular rings lie above hcp hollow sites of the tilted 〈111〉 planes, as indicated in Fig. 5b. With this in mind, it would appear that on all surfaces the molecular rings are adsorbing such that they are above hollow sites, and that the differing adsorption site of the molecular centre for the (100) surface, compared to the (110) and (111) surfaces, is to facilitate this configuration. The subtle difference in the registry of the molecular rings on the (110) surface, may be the origin of the differences observed in the SXPS (see Fig. 2). As the molecule is unable to adsorb above a (110) hollow site, it must adsorb above a tilted 〈111〉 hollow site. This will likely affect the hybridisation of the molecular orbitals with the delocalised metallic electrons in the substrate. Furthermore, the atomic corrugation present in the (110) surface also has a consequence for the electronic potential. Specifically, Smoluchowski smoothing41,42 will result in small dipoles between the rows of Cu atoms, with an increased electron density in the direction of these tilted 〈111〉 planes.
0] direction of that bridge site. For both the (100) and (111) surface, though the adsorption site of the molecular centre differs (atop and bridge sites, respectively), the centre of the 7- and 5-membered rings lie above hollow sites. Similar adsorption configurations have been experimentally observed for benzene on Ru(0001),66 Ni(111)67 and Co(0001),68 as well as furan on Pd(111).69 At first glance, on the (110) surface, it would appear as though the molecule has adsorbed in a different configuration, however the (110) surface is far more corrugated than the (111) or (100) surfaces. As such, every surface unit cell can almost be considered to contain two 〈111〉 steps. If this conceit is considered, the molecular rings lie above hcp hollow sites of the tilted 〈111〉 planes, as indicated in Fig. 5b. With this in mind, it would appear that on all surfaces the molecular rings are adsorbing such that they are above hollow sites, and that the differing adsorption site of the molecular centre for the (100) surface, compared to the (110) and (111) surfaces, is to facilitate this configuration. The subtle difference in the registry of the molecular rings on the (110) surface, may be the origin of the differences observed in the SXPS (see Fig. 2). As the molecule is unable to adsorb above a (110) hollow site, it must adsorb above a tilted 〈111〉 hollow site. This will likely affect the hybridisation of the molecular orbitals with the delocalised metallic electrons in the substrate. Furthermore, the atomic corrugation present in the (110) surface also has a consequence for the electronic potential. Specifically, Smoluchowski smoothing41,42 will result in small dipoles between the rows of Cu atoms, with an increased electron density in the direction of these tilted 〈111〉 planes.
For all optimised structures, we calculate the average carbon adsorption height with respect to the projected bulk terminated surface (hH), which is directly comparable to the NIXSW data, and the height of the molecular center-of-mass (COM) with respect to the average height of the Cu atoms in the first layer (hCOM). Both numbers are tabulated together with the experimental data in Table 1.
To assess the coverage dependence of the adsorption height, we performed structure relaxations of azupyrene on Cu(111) in both the 4 × 4 and 5 × 5 unit cell with a single molecule in the unit cell, therefore simulating different coverages. The results for those calculations can be found in Table S4 of the ESI.† We find that by increasing the coverage from the 5 × 5 to 4 × 4 cell (which roughly corresponds a change of coverage by 30% of a saturated molecular layer),28 the adsorption height increases by 0.04 Å. This is within the experimental error and is significantly smaller than that which was predicted for azulene on the same surface.24 The 5 × 5 cell for the Cu(111) substrate has a comparable coverage to the structures on Cu(110) and Cu(100) and is thus preferred in the following discussion.
The deviation between the experimental and theoretical adsorption height on the (111) and (100) surface is 0.05 Å, only slightly outside the experimental uncertainty of 0.03 Å and 0.05 Å, respectively (see Table 1). The agreement is worse for the (110) surface, though a difference between experiment and theory of only 0.11 Å would usually be considered excellent and is only notable in comparison with the near perfect agreement found on the other two surface terminations.
To directly compare the DFT-derived adsorption heights of the molecule on the different facets, however, it is more intuitive to compare the hCOM values, that consider both the surface relaxation, as well as the adsorption height of the hydrogen atoms. The largest surface relaxation is observed for Cu(110) (−0.05 Å) followed by Cu(111) (−0.03 Å), and finally Cu(100) (−0.01 Å). The DFT calculations predict a trend of decreasing COM adsorption height that is consistent with the naïvely expected reactivity of each surface: 2.23 Å on Cu(111), 2.20 Å on Cu(100), and 2.13 Å for Cu(110). On all three surfaces, these COM adsorption heights of the azupyrene molecule are similar to the sum of the covalent radii of Cu and C (2.2 Å) and far smaller than the sum of the van der Waals radii (3.1 Å).
The slight difference between the two definitions of the DFT derived adsorption heights do not alter the overall trend in adsorption height, which is Cu(111) ≳ Cu(100) > Cu(110). Therefore both NIXSW results and DFT calculations agree that the adsorption height for adsorption on the Cu(111) and Cu(100) surfaces are similar, and that the adsorption height on the Cu(110) surface is smaller than on the other two surfaces.
Analysis of the DFT structures also shows that the molecule adsorbs in a slightly distorted configuration across all surfaces. On the Cu(111) and Cu(100) surfaces the central two C atoms are, on average, 0.17/0.18 Å lower in adsorption height than the outer C atoms and 0.43/0.43 Å lower than the H atoms, as shown in Fig. 6a, d/c, f (respectively). This distortion was also found in the previous DFT study of azupyrene on Cu(111), as well as in the experimental non-contact atomic force microscopy data.28 On the (110) surface, the deformation differs subtly, as shown in Fig. 6b and e. In the DFT structure, the central two C atoms are at an average adsorption height which is only 0.02 Å lower than the average outer C atom and 0.15 Å lower than the average H atom. However, the height of the individual outer atoms varies significantly and some of the outer C and H atoms are closer to the surface than the central C atoms. Therefore, no clear distinction between outer and central carbon atoms is possible on the Cu(110) surface, while on the (111) and (100) surface the consistent displacement of the central C atoms below the outer C atoms is present. This distinguishable difference between two groups of carbon atoms may also help explain the shoulder observed in the C 1s SXPS data for the (111) and (100) surface (Fig. 2). In a side view of the structures, facing either the 5- or 7-membered rings, it is clear that on the (110) surface both types of rings have subtly twisted, with respect to the surface plane, as can be observed in Fig. 6b and e. This twist is not present in either the 7- or 5-membered rings on the (100) surface, but, upon close inspection, is present in the 7-membered rings on the (111) surface. The twist of the ring, with respect to the surface plane, is less than 5° on both surfaces, but would inversely follow the general trend in the prominence of the shoulder in the C 1s SXP spectra: the twist is clearest on the (110) surface, where the shoulder is least prominent; the twist is not present on the (100) surface, where the shoulder is most prominent.
These predicted distortions are not large enough to considerably affect the measured coherent fractions. Specifically, the predicted DFT structures would result in a coherent fraction of 0.97 for the Cu(111) surface, 0.96 for Cu(100) and 0.93 for Cu(110). Considering these small distortions, to fully explain the measured coherent fractions a surprisingly large rmsvib of 0.26 Å and 0.22 Å would still be required for the Cu(111) and Cu(100) surfaces, respectively. This could suggest that the distortion in the centre of the molecule is somewhat larger than predicted or that the molecule may occupy multiple sites (either dynamically or statically) on the surface with similar, though slightly different adsorption heights.
The DFT-derived adsorption energies (Eads, Table 1) are, on the first glance, inconsistent with the trend in the adsorption heights. The adsorption energies of azupyrene adsorbed on Cu(110) and Cu(100) are similar, while the one for Cu(111) is far smaller. Indeed, the adsorption energy (Eads) of azupyrene on Cu(100) is larger than on Cu(110), even though the adsorption height on Cu(110) is significantly lower. However, if we consider the adsorption energy per surface atom in the first Cu layer (Eads/Cu), the situation is different. Here, the adsorption energies increase going through the series: Cu(111), Cu(100), Cu(110), following the trend that would be naïvely expected and roughly agreeing with the trend in the adsorption heights.
Ultimately the agreement between the DFT optimised structures and the available experimental evidence is exceptional, a further demonstration that HSE06 + MBD-NL can be considered the current gold standard for hybrid organic/inorganic interface predictions.
Conclusion
We have determined the adsorption height of azupyrene on the Cu(111), Cu(110) and Cu(100) surfaces using normal incidence X-ray standing waves and density functional theory. Compared to similar studies across different surface terminations (e.g. PTCDA on facets of Cu and Ag),13,14,16,22,23 the observed differences are relatively small (0.06 ± 0.04 Å between Cu(111) and Cu(110)), though are comparable to those measured for formate on the same surfaces (0.09 ± 0.05 Å).21 While the significant differences in adsorption height for PTCDA above the different surface terminations cannot be easily deconvoluted between the localised and delocalised bonding components due to the presence of strong O-metal bonds, azupyrene contains no hetero atoms and reactive functional groups. The interaction of the azupyrene molecule with the surface is instead mediated via the only partly localised π-orbitals.28 Thus, the comparison of azupyrene and PTCDA indicates that strong differences in the adsorption structure on different surface facets are primarily down to direct atomic coordination and that far smaller structural effects are observed when the interaction is mediated over more delocalised electronic states, as for example aromatic π-electron systems.Still, our experiments show that azupyrene is adsorbed closer to the Cu(110) surface compared to the Cu(111) and Cu(100) surfaces. This finding is in agreement with other experimental indications for a stronger interaction with the Cu(110) surface, such as the stronger asymmetry of the C 1s peak. It is interesting that the observed adsorption height differences for azupyrene on Cu(111) and Cu(110) are similar, though smaller, than those observed for formate on the same surfaces. Apparently, once the different interaction mechanisms have been disentangled, the effect of the surface termination on delocalised interactions is on a similar, if possibly smaller, scale than that of localised bonds. Density functional theory calculations using the HSE06 hybrid functional and a non-local many-body dispersion correction predicted the measured adsorption height in all systems with high accuracy, particularly for the (111) and (100) surfaces. As in experiment, the calculations show a smaller adsorption height on the Cu(110) surface. These results suggest that, for relatively strongly bound adsorbates, though the substrate effects on the delocalised interactions with different surface facets are subtle, they can be well modelled with state-of-the-art many-body-dispersion-inclusive hybrid DFT calculations. Yet, strongly bound systems tend to be the least dynamical – when anchored strongly to the substrate, thermal vibrations and dynamical site jumping is dampened. Thus, weakly bound systems, like alternant PAHs, could provide a more challenging benchmark for DFT calculations.
Author contributions
The experimental investigation was performed by BPK, MAS, LAR, LBSW, PTPR, TJL, and DAD under the supervision of DAD and TLL. The formal analysis of the experimental data was performed by BPK, LBSW and DAD. The theoretical investigation and formal analysis were performed by BPK, MAS and DBM under the supervision of RJM. The azupyrene molecule was synthesised by LS and SMW under the supervision of GH. The study was conceptualised, and the methodology designed by BPK, RJM and DAD. The article was originally drafted by DAD and was reviewed and edited by BPK, MAS, DBM, TLL and RJM.Data availability
All input and output files of electronic structure calculations have been deposited in the NOMAD database (https://nomad-lab.eu/nomad-lab/) where they are accessible via a permanent DOI: https://10.17172/NOMAD/2024.02.28-1.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Diamond Light Source for access to beamline I09 (NT27138-2, SI25379-4 and NT33709-1). B. P. K. acknowledges support from the DFG under the Walter Benjamin fellowship programme (KL 3430/1-1). M. A. S. acknowledges support from the Analytical Science CDT. D.B.M. acknowledges support from the EPSRC-funded HetSyS CDT (EP/S022848/1). T. J. L. acknowledges support from the Sustainable Hydrogen CDT at the University of Nottingham. R. J. M. acknowledges financial support via a UK Research and Innovation Future Leaders Fellowship (MR/S016023/1) and a Frontier research grant (EP/X014088/1). D. A. D. acknowledges financial support via a New Investigator Award from the Engineering and Physical Sciences Research Council (EP/X012883/1). We acknowledge computational resources from ARCHER2 UK National Computing Service which was granted via the EPSRC-funded HEC Materials Chemistry (EP/R029431/1, EP/X035859/1) and HPC-CONEXS (EP/X035514/1) consortia.References
- Y. Gao, Mater. Sci. Eng., R, 2010, 68, 39–87 CrossRef.
- A. Kaushik, R. Kumar, S. K. Arya, M. Nair, B. D. Malhotra and S. Bhansali, Chem. Rev., 2015, 115, 4571–4606 CrossRef CAS PubMed.
- C. V. S. Batista, L. Merces, C. A. R. Costa, D. H. S. de Camargo and C. C. B. Bufon, Adv. Funct. Mater., 2022, 32, 2108478 CrossRef CAS.
- G. Koller, R. I. R. Blyth, S. A. Sardar, F. P. Netzer and M. G. Ramsey, Appl. Phys. Lett., 2000, 76, 927–929 CrossRef CAS.
- L. A. Rochford, D. S. Keeble, O. J. Holmes, G. J. Clarkson and T. S. Jones, J. Mater. Chem. C, 2014, 2, 6056–6060 RSC.
- S. K. Ramakrishnan, J. Zhu and C. Gergely, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2017, 7, e1277 CrossRef.
- T. Bauert, L. Zoppi, G. Koller, A. Garcia, K. K. Baldridge and K.-H. Ernst, J. Phys. Chem. Lett., 2011, 2, 2805–2809 CrossRef CAS.
- I. Kröger, B. Stadtmüller, C. Kleimann, P. Rajput and C. Kumpf, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195414 CrossRef.
- G. Heimel, S. Duhm, I. Salzmann, A. Gerlach, A. Strozecka, J. Niederhausen, C. Bürker, T. Hosokai, I. Fernandez-Torrente, G. Schulze, S. Winkler, A. Wilke, R. Schlesinger, J. Frisch, B. Bröker, A. Vollmer, B. Detlefs, J. Pflaum, S. Kera, K. J. Franke, N. Ueno, J. I. Pascual, F. Schreiber and N. Koch, Nat. Chem., 2013, 5, 187–194 CrossRef CAS PubMed.
- D. G. de Oteyza, A. El-Sayed, J. M. Garcia-Lastra, E. Goiri, T. N. Krauss, A. Turak, E. Barrena, H. Dosch, J. Zegenhagen, A. Rubio, Y. Wakayama and J. E. Ortega, J. Chem. Phys., 2010, 133, 214703 CrossRef CAS PubMed.
- I. Kröger, B. Stadtmüller, C. Stadler, J. Ziroff, M. Kochler, A. Stahl, F. Pollinger, T.-L. Lee, J. Zegenhagen, F. Reinert and C. Kumpf, New J. Phys., 2010, 12, 083038 CrossRef.
- A. Gerlach, F. Schreiber, S. Sellner, H. Dosch, I. A. Vartanyants, B. C. C. Cowie, T. L. Lee and J. Zegenhagen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 239902 CrossRef.
- A. Gerlach, S. Sellner, F. Schreiber, N. Koch and J. Zegenhagen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 045401 CrossRef.
- A. Hauschild, R. Temirov, S. Soubatch, O. Bauer, A. Schöll, B. C. C. Cowie, T. L. Lee, F. S. Tautz and M. Sokolowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125432 CrossRef.
- A. Yang, A. Franco-Cañellas, M. Sato, B. Wang, R.-B. Wang, H. Koike, I. Salzmann, P. K. Thakur, T.-L. Lee, L. Liu, S. Kera, A. Gerlach, K. Kanai, J. Fan, F. Schreiber and S. Duhm, Phys. Rev. B, 2016, 94, 155426 CrossRef.
- S. K. M. Henze, O. Bauer, T. L. Lee, M. Sokolowski and F. S. Tautz, Surf. Sci., 2007, 601, 1566–1573 CrossRef CAS.
- D. I. Sayago, J. T. Hoeft, M. Polcik, M. Kittel, R. L. Toomes, J. Robinson, D. P. Woodruff, M. Pascal, C. L. A. Lamont and G. Nisbet, Phys. Rev. Lett., 2003, 90, 116104–116104 CrossRef CAS PubMed.
- P. S. Deimel, R. M. Bababrik, B. Wang, P. J. Blowey, L. A. Rochford, P. K. Thakur, T.-L. Lee, M.-L. Bocquet, J. V. Barth, D. P. Woodruff, D. A. Duncan and F. Allegretti, Chem. Sci., 2016, 7, 5647–5656 RSC.
- K. Flechtner, A. Kretschmann, H.-P. Steinrück and J. M. Gottfried, J. Am. Chem. Soc., 2007, 129, 12110–12111 CrossRef CAS PubMed.
- W. Hieringer, K. Flechtner, A. Kretschmann, K. Seufert, W. Auwärter, J. V. Barth, A. Görling, H.-P. Steinrück and J. M. Gottfried, J. Am. Chem. Soc., 2011, 133, 6206–6222 CrossRef CAS PubMed.
- D. Kreikemeyer-Lorenzo, W. Unterberger, D. A. Duncan, M. K. Bradley, T. J. Lerotholi, J. Robinson and D. P. Woodruff, Phys. Rev. Lett., 2011, 107, 046102 CrossRef CAS PubMed.
- O. Bauer, G. Mercurio, M. Willenbockel, W. Reckien, C. H. Schmitz, B. Fiedler, S. Soubatch, T. Bredow, F. S. Tautz and M. Sokolowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 235431 CrossRef.
- S. Weiß, I. Krieger, T. Heepenstrick, S. Soubatch, M. Sokolowski and F. S. Tautz, Phys. Rev. B, 2017, 96, 075414 CrossRef.
- B. P. Klein, J. M. Morbec, M. Franke, K. K. Greulich, M. Sachs, S. Parhizkar, F. C. Bocquet, M. Schmid, S. J. Hall, R. J. Maurer, B. Meyer, R. Tonner, C. Kumpf, P. Kratzer and J. M. Gottfried, J. Phys. Chem. C, 2019, 123, 29219–29230 CrossRef CAS.
- B. P. Klein, N. J. van der Heijden, S. R. Kachel, M. Franke, C. K. Krug, K. K. Greulich, L. Ruppenthal, P. Müller, P. Rosenow, S. Parhizkar, F. C. Bocquet, M. Schmid, W. Hieringer, R. J. Maurer, R. Tonner, C. Kumpf, I. Swart and J. M. Gottfried, Phys. Rev. X, 2019, 9, 011030 CAS.
- S. R. Kachel, B. P. Klein, J. M. Morbec, M. Schöniger, M. Hutter, M. Schmid, P. Kratzer, B. Meyer, R. Tonner and J. M. Gottfried, J. Phys. Chem. C, 2020, 124, 8257–8268 CrossRef CAS.
- B. P. Klein, S. E. Harman, L. Ruppenthal, G. M. Ruehl, S. J. Hall, S. J. Carey, J. Herritsch, M. Schmid, R. J. Maurer, R. Tonner, C. T. Campbell and J. M. Gottfried, Chem. Mater., 2020, 32, 1041–1053 CrossRef CAS.
- B. P. Klein, A. Ihle, S. R. Kachel, L. Ruppenthal, S. J. Hall, L. Sattler, S. M. Weber, J. Herritsch, A. Jaegermann, D. Ebeling, R. J. Maurer, G. Hilt, R. Tonner-Zech, A. Schirmeisen and J. M. Gottfried, ACS Nano, 2022, 16, 11979–11987 CrossRef CAS PubMed.
- B. P. Klein, L. Ruppenthal, S. J. Hall, L. E. Sattler, S. M. Weber, J. Herritsch, A. Jaegermann, R. J. Maurer, G. Hilt and J. M. Gottfried, ChemPhysChem, 2021, 22, 1065–1073 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Hermann and A. Tkatchenko, Phys. Rev. Lett., 2020, 124, 146401 CrossRef CAS PubMed.
- T.-L. Lee and D. A. Duncan, Synchrotron Radiat. News, 2018, 31, 16–22 CrossRef.
- C. Fisher, R. Ithin, R. Jones, G. Jackson, D. Woodruff and B. Cowie, J. Phys.: Condens. Matter, 1998, 10, L623 CrossRef CAS.
- F. Schreiber, K. A. Ritley, I. A. Vartanyants, H. Dosch, J. Zegenhagen and B. C. C. Cowie, Surf. Sci., 2001, 486, L519–L523 CrossRef CAS.
- V. Nefedov, V. Yarzhemsky, I. Nefedova, M. Trzhaskovskaya and I. Band, J. Electron Spectrosc. Relat. Phenom., 2000, 107, 123–130 CrossRef CAS.
- S. Doniach and M. Sunjic, J. Phys. C: Solid State Phys., 1970, 3, 285 CrossRef CAS.
- B. P. Klein, M. A. Stoodley, M. Edmondson, L. A. Rochford, M. Walker, L. Sattler, S. M. Weber, G. Hilt, L. B. S. Williams, T. L. Lee, A. Saywell, R. J. Maurer and D. A. Duncan, Appl. Phys. Lett., 2022, 121, 191603 CrossRef CAS.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- J. P. Calupitan, T. Wang, A. Pérez Paz, B. Álvarez, A. Berdonces-Layunta, P. Angulo-Portugal, R. Castrillo-Bodero, F. Schiller, D. Peña, M. Corso, D. Pérez and D. G. de Oteyza, J. Phys. Chem. Lett., 2023, 14, 947–953 CrossRef CAS PubMed.
- D. J. Morgan, Surface and Interface Analysis, 2023, n/a Search PubMed.
- R. Smoluchowski, Phys. Rev., 1941, 60, 661–674 CrossRef CAS.
- M. Methfessel, D. Hennig and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 4816–4829 CrossRef CAS PubMed.
- D. P. Woodruff, P. Baumgärtel, J. T. Hoeft, M. Kittel and M. Polcik, J. Phys.: Condens. Matter, 2001, 13, 10625 CrossRef CAS.
- D. Duncan, M. Bradley, W. Unterberger, D. Kreikemeyer-Lorenzo, T. Lerotholi, J. Robinson and D. P. Woodruff, J. Phys. Chem. C, 2012, 116, 9985–9995 CrossRef CAS.
- M. Kittel, M. Polcik, R. Terborg, J. T. Hoeft, P. Baumgärtel, A. M. Bradshaw, R. L. Toomes, J. H. Kang, D. P. Woodruff, M. Pascal, C. L. A. Lamont and E. Rotenberg, Surf. Sci., 2001, 470, 311–324 CrossRef CAS.
- D. Duncan, P. Casado Aguilar, M. Paszkiewicz, K. Diller, F. Bondino, E. Magnano, F. Klappenberger, I. Píš, A. Rubio and J. Barth, J. Chem. Phys., 2019, 150, 094702 CrossRef CAS PubMed.
- D. P. Woodruff, Surf. Sci. Rep., 2007, 62, 1–38 CrossRef CAS.
- D. Woodruff, Rep. Prog. Phys., 2005, 68, 743 CrossRef CAS.
- The X-Ray Standing Wave Technique, ed. J. Zegenhagen and A. Kazimirov, World Scientific, 2011 Search PubMed.
- M. J. Bedzyk and G. Materlik, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 6456–6463 CrossRef CAS PubMed.
- B. W. Batterman, Phys. Rev., 1964, 133, A759 CrossRef.
- D. P. Woodruff and D. A. Duncan, New J. Phys., 2020, 22, 113012 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- R. J. Maurer, V. G. Ruiz, J. Camarillo-Cisneros, W. Liu, N. Ferri, K. Reuter and A. Tkatchenko, Prog. Surf. Sci., 2016, 91, 72–100 CrossRef CAS.
- V. G. Ruiz, W. Liu, E. Zojer, M. Scheffler and A. Tkatchenko, Phys. Rev. Lett., 2012, 108, 146103 CrossRef PubMed.
- W. Liu, F. Maaß, M. Willenbockel, C. Bronner, M. Schulze, S. Soubatch, F. S. Tautz, P. Tegeder and A. Tkatchenko, Phys. Rev. Lett., 2015, 115, 036104 CrossRef PubMed.
- R. J. Maurer, W. Liu, I. Poltavsky, T. Stecher, H. Oberhofer, K. Reuter and A. Tkatchenko, Phys. Rev. Lett., 2016, 116, 146101 CrossRef PubMed.
- J. Banerjee, S. Behnle, M. C. E. Galbraith, V. Settels, B. Engels, R. Tonner and R. F. Fink, J. Comput. Chem., 2018, 39, 844–852 CrossRef CAS PubMed.
- A. Baby, M. Gruenewald, C. Zwick, F. Otto, R. Forker, G. van Straaten, M. Franke, B. Stadtmüller, C. Kumpf, G. P. Brivio, G. Fratesi, T. Fritz and E. Zojer, ACS Nano, 2017, 11, 10495–10508 CrossRef CAS PubMed.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- R. J. Maurer, V. G. Ruiz and A. Tkatchenko, J. Chem. Phys., 2015, 143, 102808 CrossRef PubMed.
- B. Sohail, P. J. Blowey, L. A. Rochford, P. T. P. Ryan, D. A. Duncan, T. L. Lee, P. Starrs, G. Costantini, D. P. Woodruff and R. J. Maurer, J. Phys. Chem. C, 2023, 127, 2716–2727 CrossRef CAS PubMed.
- C. Stellwag, G. Held and D. Menzel, Surf. Sci., 1995, 325, L379–L384 CrossRef CAS.
- G. Held, M. P. Bessent, S. Titmuss and D. A. King, J. Chem. Phys., 1996, 105, 11305–11312 CrossRef CAS.
- K. Pussi, M. Lindroos, J. Katainen, K. Habermehl-Ćwirzeń, J. Lahtinen and A. P. Seitsonen, Surf. Sci., 2004, 572, 1–10 CrossRef CAS.
- M. K. Bradley, J. Robinson and D. P. Woodruff, Surf. Sci., 2010, 604, 920–925 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr04690g |
| ‡ Current address: Research Center for Materials Analysis, Korea Basic Science Institute, 169–148 Gwahak-ro, Yuseong-gu, Daejeon 34133, Republic of Korea. |
| § Current address: Institute of Applied Physics, TU Wien, Wiedner Hauptstraße 8–10, 1040 Vienna, Austria. |
| This journal is © The Royal Society of Chemistry 2024 |