Tunable abundant valley Hall effect and chiral spin–valley locking in Janus monolayer VCGeN4†
Kang
Jia
 ab,
Xiao-Jing
Dong
ab,
Xiao-Jing
Dong
 b,
Sheng-Shi
Li
b,
Sheng-Shi
Li
 a,
Wei-Xiao
Ji
a,
Wei-Xiao
Ji
 a and
Chang-Wen
Zhang
*ab
a and
Chang-Wen
Zhang
*ab
aSchool of Physics and Technology, Institute of Spintronics, University of Jinan, Jinan, Shandong 250022, People's Republic of China. E-mail: ss_zhangchw@ujn.edu.cn
bSchool of Physics and Physical Engineering, Qufu Normal University, Qufu, Shandong 273100, People's Republic of China
First published on 27th March 2024
Abstract
It is both conceptually and practically fascinating to explore fundamental research studies and practical applications of two-dimensional systems with the tunable abundant valley Hall effect. In this work, based on first-principles calculations, the tunable abundant valley Hall effect is proved to appear in Janus monolayer VCGeN4. When the magnetization is along the out-of-plane direction, VCGeN4 is an intrinsic ferromagnetic semiconductor with a valley feature. The intriguing spontaneous valley polarization exists in VCGeN4 due to the common influence of broken inversion and time-reversal symmetries, which makes it easier to realize the anomalous valley Hall effect. Furthermore, we observe that the valley-non-equilibrium quantum anomalous Hall effect is driven by external strain, which is located between two half-valley-metal states. When reversing the magnetization, the spin flipping makes the position of the edge state to change from one valley to another valley, demonstrating an intriguing behavior known as chiral spin–valley locking. Although the easy magnetic axis orientation is along the in-plane direction, we can utilize an external magnetic field to transform the magnetic axis orientation. Moreover, it is found that the valley state, electronic and magnetic properties can be well regulated by the electric field. Our works explore the mechanism of the tunable abundant valley Hall effect by applying an external strain and electric field, which provides a perfect platform to investigate the spin, valley, and topology.
I. Introduction
Valley (a novel degree of freedom of carriers except spin and charge) and relevant manipulations have become popular topics recently,1,2 and they feature the appearance of extreme values in energy band structures.3,4 Good valley systems should possess degenerate and inequivalent valley properties in the inequivalent K points within the momentum space.5,6 For valley systems, eliminating the degeneracy to realize valley polarization (VP) is regarded as one essential question in valleytronics.7,8 Some attractive approaches have been put forward to produce VP, such as static magnetic fields,9,10 magnetic proximity effects,11,12 optical pumping,13 and magnetic doping.14,15 However, there are many challenges in these means. For instance, the valley properties of host systems are usually submerged by the magnetic proximity effect, and clusters are formed in the process of magnetic doping and hence impurity scattering increases. Antiferromagnetic (AFM) materials (for instance, MnPS3 and MnPSe3) have been investigated as valley systems by first-principles calculations.16 Lately, since spontaneous VP has hopefully come into being, a method of coupling between ferromagnetic (FM) ordering and valleys has been considered,17–19 stimulating the exploration of the anomalous valley Hall effect (AVHE), and these series of systems are referred to as ferrovalley (FV) materials,17 which are widely researched. Several two-dimensional (2D) FV materials with in-plane (IP) magnetization have been found in the 2D transition-metal dichalcogenide (TMD) family, comprising CeI2,20 ScBrI,21 ScI2,22 and LaBrI23 monolayers. Nevertheless, the spontaneous VP of FV materials cannot appear for IP magnetization. For the sake of achieving spontaneous VP, it is noteworthy that an external magnetic field can induce the magnetization direction from the IP to out-of-plane (OOP) orientation, which is vital for the exploration of spintronic and valleytronic nanodevices.In order to find good 2D FV materials with OOP magnetization, many researchers have conducted very fascinating studies. So far, several systems have been explored employing first-principles calculations.24–28 Many halogen materials have attracted wide attention, such as RuCl2,25 FeClBr,26 OsBr2,27 and RuBr2,28 because their magnetic and electronic properties can be controlled by substituting different halide atoms. Most notably, through applying strain and varying the electronic correlation effect, topological phase transitions can be achieved in RuClBr,29 RuCl2,25 OsClBr,30 VCSiN4,31 and RuBr2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 monolayers. Inspired by many research studies on valleytronics and spintronics,32–39 the combinations of topological properties and FV states in many materials possibly trigger fresh physics and phenomena.
28 monolayers. Inspired by many research studies on valleytronics and spintronics,32–39 the combinations of topological properties and FV states in many materials possibly trigger fresh physics and phenomena.
Recently, one novel 2D system of the MSi2N4 (M = Mo, W) family has been experimentally synthesized by the chemical vapor deposition (CVD) method,40 and researchers found that this method can be utilized to synthesize numerous analogous 2D systems. This materials family possesses lots of intriguing characters, containing topology, VP, transport, and magnetism.41–49 Ultrathick MoSi2N4(MoN)4 has also been recently obtained experimentally50 and ultrathick MA2N4(M′N)-intercalated monolayers have also been proposed,51 which arouse wide public concern. It is discovered that 2D Janus TMD monolayers have been synthesized in experiment.52 As is known to all, TMD and SiN layers are combined to obtain the MSi2N4 family. So, we boldly forecast that the preparation of the Janus MSi2N4 family can be realized. For the Janus MSi2N4 family, because the middle TMD layer is sandwiched by two diverse layers, the mirror symmetry is broken. The spontaneous OOP dipole has a crucial influence on spin, electronic, valley, and topology properties.
In this work, we found that Janus monolayer VCGeN4 is an intrinsic FM semiconductor with a valley feature, and the interesting tunable abundant valley Hall effect is observed in VCGeN4. Significantly, for OOP magnetization, VP can spontaneously appear on account of breaking of the inversion and time-reversal symmetries, beneficial for exploring the AVHE. Moreover, the valley-nonequilibrium quantum anomalous Hall effect (VQAHE) can be induced between two half-valley-metal (HVM) states by external strain. When reversing the magnetization, the edge state is simultaneously transformed, which indicates that VCGeN4 shows an attractive behavior known as chiral spin–valley locking. Our studies enrich systems with the tunable abundant valley Hall effect and offer a fine candidate in spintronic and valleytronic nanodevices.
II. Computational details
Based on density functional theory (DFT), all calculations were performed in the Vienna ab initio simulation package (VASP)53–55 by employing the projector-augmented-wave (PAW) method. The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional56 was utilized to describe the correlation functional. The kinetic energy cutoff, force, and energy convergence criterion were 500 eV, 0.01 eV Å−1, and 10−6 eV, respectively. Γ-center Monkhorst–Pack grids of 19 × 19 × 1 and 19 × 11 × 1 were adopted for the unit cell and rectangle supercell, respectively. The PBE+U method57 was applied for the treatment of the 3d orbitals of V atoms and the U value was set to 3.2 eV.58,59 The band structure from the PBE+U method was compared with that from the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional.60 In order to prevent the influences of adjacent layers, a vacuum space of approximate 25 Å was used. The phonon dispersion was acquired using a 3 × 3 × 1 supercell in the PHONOPY code.61,62 For acquiring the edge state and Berry curvature, the maximally localized Wannier functions were calculated using the WANNIER90 package.63,64III. Results and discussion
It is known that the MSi2N4 family has four phases (α, β, γ, and δ phases) by referring to previous research.65 We build the four phases of VCGeN4 and calculate their energies (see Table S1†). It is found that the α phase is the ground state. In the subsequent discussion, the various properties of the α phase are explored. The crystal structure of VCGeN4 is exhibited in Fig. 1(a) and (b). It shows a hexagonal lattice and the space group of P3m1 (no. 156). Each unit cell includes four N atoms, one C atom, one V atom, and one Ge atom, which are stacked with seven atomic layers in the order of N–C–N–V–N–Ge–N. Each inner V atom is surrounded by six neighboring N atoms, constituting a trigonal prismatic structure, and this VN2 layer is sandwiched by C–N and Ge–N bilayers. VCGeN4 can be obtained by changing the Ge (C) atom of one of the two GeN (CN) bilayers in monolayer VGe2N4 (VC2N4) with the C (Ge) atom. The lattice constant of VCGeN4 is optimized to 2.85 Å. The phonon dispersion is investigated. As is displayed in Fig. 1(c), all branches are positive in the entire Brillouin zone (BZ), confirming that the VCGeN4 is dynamically stable.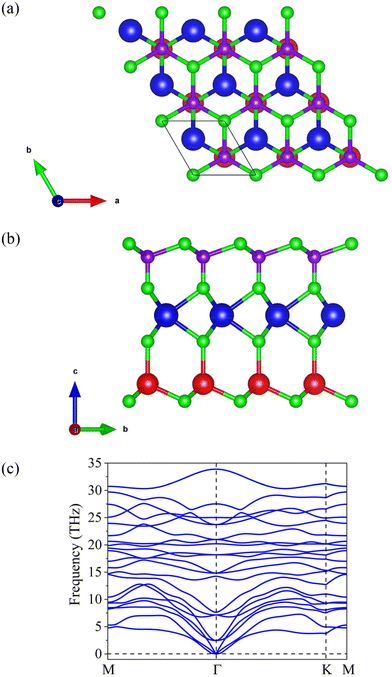 | ||
| Fig. 1 (a) Top and (b) side views of VCGeN4. The green, purple, blue, and red balls denote N, C, V, and Ge elements, respectively. (c) Phonon dispersion of VCGeN4. | ||
To research the stability of VCGeN4, the cohesive energy is first calculated, which is defined as Ecoh = (EV + EC + EGe + 4EN − EVCGeN4)/7. Here, EV, EC, EGe, and EN are the total energies of the isolated V, C, Ge, and N atoms, while EVCGeN4 is the total energy of the VCGeN4 unit cell. The obtained Ecoh is 4.08 eV per unit cell. The relative large and positive value is comparable to those of theoretical and experimental 2D materials, such as CeI2 (3.14 eV per unit cell),20 phosphorene (3.48 eV per unit cell),66 and Cu2Ge (3.17 eV per unit cell),67 indicating that it is possible to synthesize VCGeN4 in the laboratory. The formation energy is also obtained from Eform = (μV + μC + μGe + 4μN − EVCGeN4)/7, where μV, μC, μGe, and μN are the energies of per V, C, Ge, and N atom in the related stable bulk phases, respectively. The Eform is 2.62 eV per unit cell, which implies that the synthesis of VCGeN4 is an exothermic reaction.
Then, we perform Ab initio molecular dynamics (AIMD) simulations to evaluate the thermal stability of VCGeN4 at room temperature. As shown in Fig. S1,† the total energy fluctuates around the equilibrium values and no destruction is found in the final configuration, which suggests good thermal stability. Moreover, the mechanical properties of VCGeN4 are investigated. Because of the hexagonal symmetry, VCGeN4 has two independent elastic constants (C12 and C11), and the acquired C12 and C11 values are 142.08 Nm−1 and 226.54 Nm−1, respectively. The Cij values of VCGeN4 meet the Born criteria (C11 > 0 and C11–C12 > 0),68–70 confirming the mechanical stability. In short, all these calculations jointly demonstrate that VCGeN4 has excellent structural stability.
The magnetic properties of VCGeN4 are discussed. Our calculation results illustrate that VCGeN4 stabilizes into the FM configuration, and the AFM state is 153 meV higher in energy than its FM state using a rectangle supercell (see Fig. S2†). For VCGeN4, the bonding angle of V–N–V is 88.7°, close to 90°. In accordance with the Goodenough–Kanamori–Anderson rules,71–73 such a structural trait prefers the FM state, consistent with our conclusions. The stable FM coupling is prohibited for the 2D isotropic Heisenberg model, on account of the Mermin–Wagner theorem.74 Nevertheless, the long-range magnetic order is protected by finite magnetic anisotropy. Hence, the stability of FM configuration in VCGeN4 is strongly related to its MAE, which mainly includes the magnetocrystalline anisotropy (MCA) energy EMCA and the magnetic shape anisotropy (MSA) energy EMSA. The EMCA and EMSA are induced by the SOC effect and the dipole–dipole (D–D) interaction, respectively. The D–D interaction can be written as
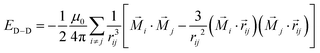 | (1) |
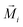
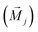 is the local magnetic moment and
is the local magnetic moment and 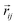 represents vectors which connect sites j and i. The EMCA is defined as the energy discrepancy between the IP and OOP magnetizations: EMCA = Ex/y − Ez. The calculated EMCA of VCGeN4 is −48 μeV. The EMSA is obtained by the energy discrepancy with the magnetization orientation rotating from the IP direction to the OOP direction. The calculated EMSA is −28 μeV, hence the MAE of VCGeN4 is −76 μeV. The negative (positive) MAE represents that the easy magnetic axis is parallel (perpendicular) to the plane. The calculated MAE (−76 μeV) means that the easy magnetic axis direction is along the IP, which indicates that there is no energy barrier for the rotation of the magnetic axis in the xy plane.20 Therefore, VCGeN4 is regarded as a 2D XY magnet.20 For 2D XY magnets with typical triangle lattice structures, the Berezinskii–Kosterlitz–Thouless (BKT) magnetic transition has been determined at a crucial temperature TC. Monte Carlo simulations are utilized to estimate the crucial temperature TC = 1.335J/kB, where kB and J are the Boltzmann constant and the nearest-neighbor (NN) exchange parameter, respectively. The J is determined by the energy difference between the AFM state energy EAFM and FM state energy EFM. According to the AFM and FM configurations, the corresponding energies of AFM and FM states can be acquired from the following equations:
represents vectors which connect sites j and i. The EMCA is defined as the energy discrepancy between the IP and OOP magnetizations: EMCA = Ex/y − Ez. The calculated EMCA of VCGeN4 is −48 μeV. The EMSA is obtained by the energy discrepancy with the magnetization orientation rotating from the IP direction to the OOP direction. The calculated EMSA is −28 μeV, hence the MAE of VCGeN4 is −76 μeV. The negative (positive) MAE represents that the easy magnetic axis is parallel (perpendicular) to the plane. The calculated MAE (−76 μeV) means that the easy magnetic axis direction is along the IP, which indicates that there is no energy barrier for the rotation of the magnetic axis in the xy plane.20 Therefore, VCGeN4 is regarded as a 2D XY magnet.20 For 2D XY magnets with typical triangle lattice structures, the Berezinskii–Kosterlitz–Thouless (BKT) magnetic transition has been determined at a crucial temperature TC. Monte Carlo simulations are utilized to estimate the crucial temperature TC = 1.335J/kB, where kB and J are the Boltzmann constant and the nearest-neighbor (NN) exchange parameter, respectively. The J is determined by the energy difference between the AFM state energy EAFM and FM state energy EFM. According to the AFM and FM configurations, the corresponding energies of AFM and FM states can be acquired from the following equations:| EFM = E0 − (6J + 2A)S2 | (2) |
| EAFM = E0 + (2J − 2A)S2 | (3) |
| J = (EAFM − EFM)/8S2 | (4) |
The obtained J is 19.13 meV when S = 1 and the TC is calculated to be 296 K.
The electronic and topological states of 2D materials are influenced by the magnetic anisotropy.25–30,75 It is widely known that the magnetization belongs to pseudovectors. For the OOP FM system, the horizontal mirror symmetry of the system can be maintained, but all vertical mirrors are broken. The maintained horizontal mirror symmetry permits a non-vanishing Chern number and spontaneous VP.75 Although the easy magnetic axis orientation of VCGeN4 is along the IP, we can apply an external magnetic field to transform the magnetic axis orientation, which brings new ideas to our research. The effect of different electronic correlations (U values) on the electronic properties of the VCGeN4 is explored to acquire the accurate electronic structures. As shown in Fig. S3,† for 0.0 eV ≤ U ≤ 2.0 eV and 2.5 eV ≤ U ≤ 4.0 eV, VCGeN4 exhibits indirect and direct band-gap semiconductor features, respectively. In particular, when the U value increases to 3.2 eV (see Fig. 2(b)), the band structure is very consistent with that obtained using the HSE06 functional (see Fig. S4†). It is seen that the band gap of 0.95 eV obtained using the HSE06 functional is larger than that obtained by the PBE+U method. The U = 3.2 eV is chosen to discuss the valley and topology in the following exploration.
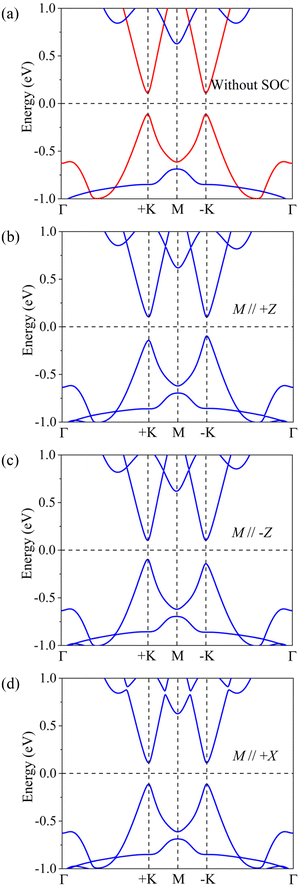
The spin-polarized energy band structures of VCGeN4 are plotted in Fig. 2. Because of the exchange interaction, Fig. 2(a) exhibits an evident spin splitting, and VCGeN4 is a narrow direct-band-gap semiconductor with a band-gap value of 0.22 eV. The conduction band minimum (CBM) and valence band maximum (VBM) are located at the −K and +K points, which are offered by the spin-up channels. For both the valence band (VB) and the conduction band (CB), the energies of the +K and −K valleys are degenerate. Some materials have valleys only in the CB or VB. Notably, degenerate valleys are formed in both the CB and VB, indicating that VCGeN4 is a potential valleytronic semiconductor. The d orbitals of V atoms lie in the trigonal prismatic crystal fields and the d orbitals can split into dxz + dyz, dxy + dx2−y2 and low-lying dz2 orbitals. According to the orbital-projected band structure (see Fig. 3), for the spin-up channels, the only one electron occupies the dz2-controlled top VB. It is expected that each V atom has the magnetic moment of 1μB, which accords with our calculated value of 1.2μB.
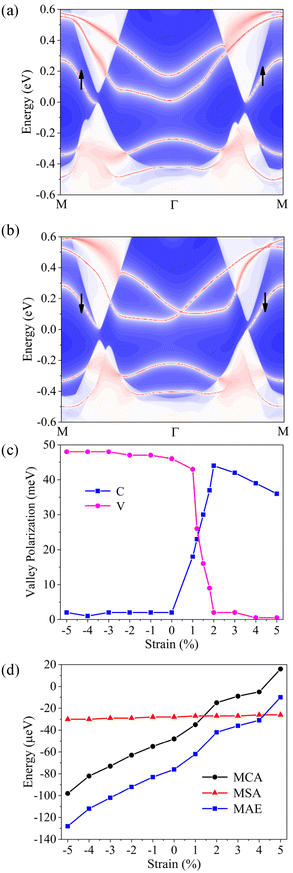
When involving the SOC and OOP magnetic anisotropy, as shown in Fig. 2(b), we find that the VP is induced. For the top VB, the energy in the +K valley is smaller than that of the −K valley and the spontaneous VP is 46 meV, while the VP of the bottom CB is 2 meV. When the magnetization of V is reversed, as shown in Fig. 2(c), the VPs of both the VB and CB are flipped and the valleys are contributed by the spin-down channels. Fig. 2(b) and (c) indicate that VCGeN4 is still a direct-band-gap semiconductor and the band-gap value is 0.20 eV. According to Fig. 2(d), the VP cannot be found with IP magnetic anisotropy.
The underlying physics of spontaneous VP in VCGeN4 can be comprehended to the combined influence of magnetic exchange interaction and SOC. When involving magnetic exchange interaction but excluding SOC, because of the broken time-reversal symmetry, the spin splitting of energy band structures in the −K and +K valleys is Δ−Kmag = Δ+Kmag (Δ−K(+K) = E−K(+K)↑ − E−K(+K)↓, where ↓ and ↑ represent spin-down and spin-up channels, respectively.) Moreover, when excluding magnetic exchange interaction but considering SOC, the spin splitting also appears in the −K and +K valleys. However, due to the inversion symmetry breaking and time-reversal symmetry protecting, the signs of the valley splitting in the −K and +K valleys are opposite, but the absolute values are the same, namely Δ−KSOC = −Δ+KSOC. Hence, when taking into account both magnetic exchange interaction and SOC, the spin splitting is Δ−Kmag+ Δ−KSOC in the −K valley and Δ+Kmag+ Δ+KSOC in the +K valley, respectively, resulting in the interesting spontaneous VP.
As described above, for VCGeN4, the VP of the VB is 46 meV, nevertheless, that in the CB is inconspicuous. The difference is relevant to the situation that valleys in the VB and CB are dominated by different orbitals. As shown in Fig. 3, it can be found that the −K and +K valleys in the CB are contributed by V-dz2 orbitals, while the −K and +K valleys in the VB are mainly dominated by dxy + dx2−y2 orbitals. We calculate the total and partial density of states (DOS) of VCGeN4. As shown in Fig. S5,† the bottom CB primarily consists of dz2 orbitals of V and the top VB is mainly composed of dxy + dx2−y2 orbitals of V and minority pz orbitals of N, which is in agreement with the orbital-resolved band structure (see Fig. 3). Because of the significant role of SOC in the VP, in order to obtain the underlying physics, a simple model is employed:
ĤSOC = λ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) ·Ŝ = Ĥ0SOC + Ĥ1SOC ·Ŝ = Ĥ0SOC + Ĥ1SOC | (5) |
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) is the orbital angular momentum and Ŝ is the spin angular momentum. Ĥ1SOC and Ĥ0SOC represent the interactions between opposite spin states and between the same spin states, respectively. It can be seen that the −K and +K valleys in the CB and VB only consist of the spin-up channel, while the spin-down channel lies far away from the −K and +K valleys. Hence, Ĥ1SOC can be ignored here. Considering Ĥ0SOC, it can be shown by the polar angles θ and ϕ:
is the orbital angular momentum and Ŝ is the spin angular momentum. Ĥ1SOC and Ĥ0SOC represent the interactions between opposite spin states and between the same spin states, respectively. It can be seen that the −K and +K valleys in the CB and VB only consist of the spin-up channel, while the spin-down channel lies far away from the −K and +K valleys. Hence, Ĥ1SOC can be ignored here. Considering Ĥ0SOC, it can be shown by the polar angles θ and ϕ: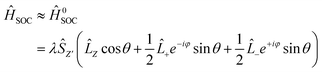 | (6) |
For the OOP magnetization orientation (θ = 0°), the ĤSOC can be written as
Ĥ0SOC = λŜZ·![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) Z = α Z = α![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) Z Z | (7) |
Because the symmetry of VCGeN4 is C3v, we chose the following basis functions
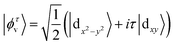 | (8) |
| |φτc〉 = |dz2〉 | (9) |
| Eτc = 〈φτc|Ĥ0SOC|φτc〉 | (10) |
| Eτv = 〈φτv|Ĥ0SOC|φτv〉 | (11) |
Consequently, the VP between valleys is given by
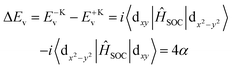 | (12) |
| ΔEc = E−Kc − E+Kc = 0 | (13) |
In accordance with these discussions, the discrepancy of the VP can be clearly comprehended. In particular, if the magnetization orientation is not taken into account, the VP of the VB can be written as ΔEv = 4α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (θ = 90° and 0° represent IP and OOP orientations, respectively), which explains that the VP cannot be observed for the IP orientation (see Fig. 2(d)).
θ (θ = 90° and 0° represent IP and OOP orientations, respectively), which explains that the VP cannot be observed for the IP orientation (see Fig. 2(d)).
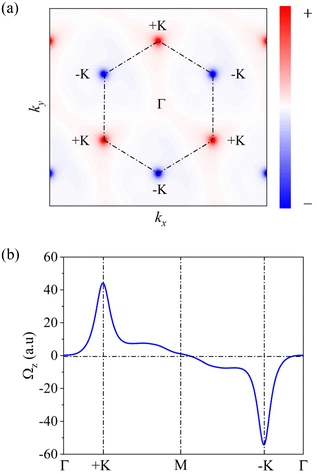
After verifying the spontaneous VP of VCGeN4, then the Berry curvature Ω(k) is investigated to evaluate its electronic transport features, which is obtained by utilizing the following Kudo formula:76
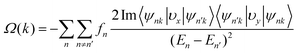 | (14) |
It is well known that epitaxial strain is an effective tool in the manipulation of the topological, magnetic, and electronic properties of 2D systems. Here, biaxial strain is introduced into VCGeN4. The strain is defined as ε = (a − a0)/a0, where a (a0) is the strained (unstrained) lattice constant. In our work, we take into account a rational strain range of −5% ≤ ε ≤ 5%. The positive (negative) ε value refers to the tensile (compressive) strain. We utilize a rectangle supercell to compare the energy discrepancy between different magnetic configurations (AFM and FM) under strain. According to Fig. S6,† the FM ground state is very stable in the investigated strain range. The band structures of some representative ε values without SOC are exhibited in Fig. S7.† When −5% ≤ ε ≤ −3% and 4% ≤ ε ≤ 5%, VCGeN4 is an indirect-gap semiconductor. For −2% ≤ ε ≤ 3%, VCGeN4 has the direct-gap semiconductor character, so this strain range will be emphatically explored in the following research. Both the +K and −K valleys in the CB and VB are occupied by the spin-up states.
Because the symmetry of 2D systems can be affected by the direction of magnetic anisotropy, which can have important impact on the electronic and topological states. First, we assume that the magnetocrystalline direction of VCGeN4 is along the OOP for the considered strain range. The band structures of some representative ε values are shown in Fig. S8† and the global band-gap versus strain is displayed in Fig. 6. The consequences indicate that the band-gap obviously varies in various strains. In particular, when ε = 1% or 1.4%, the system turns into the HVM state, where two valleys are semiconductor and metallic, respectively, and has 100% VP, which is similar to the semi-metallic behaviour with 100% spin polarization in spintronics. Because the SOC is always involved in the calculations, the perfect 100% spin polarization can be obtained in the HVM state with the identical spin channel. For traditional semi-metals, it is notable that spin-down and spin-up states are usually mixed because of the SOC. For −2% ≤ ε ≤ 1%, the global band-gap gradually decreases with increasing strains and the HVM state vanishes, while the VP remains in the VB. In particular, when 1.4% ≤ ε ≤ 3%, the VP remains in the CB, and as the strain increases, the global band-gap increases. We can observe some little band gaps between ε = 1% and 1.4%.
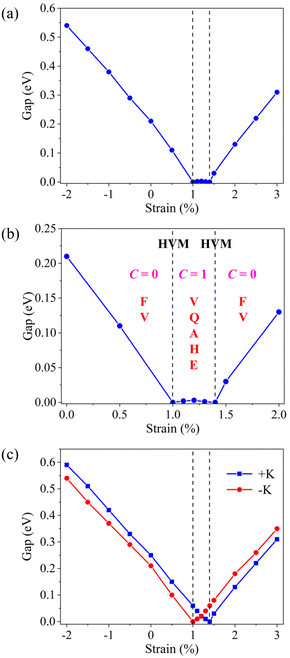 | ||
| Fig. 6 (a) The global band gaps with OOP magnetization as a function of strain and (b) phase diagram exhibited with different strains. (c) Band gaps in the +K and −K valleys as a function of strain. | ||
As previously mentioned, the diverse VP behavior can be attributed to the contribution in the +K and −K valleys of the CB and VB from diverse orbital components. In all strain regions, the dxy + dx2−y2 or dz2 orbitals of V atoms primarily occupy the +K and −K valleys in the CB and VB. The orbital-resolved band structures of ε = 0.5%, 1.2%, and 2% are shown in Fig. S9.† When 1.4% < ε < 5%, the dz2 orbitals occupy the +K and −K valleys of the VB, but the two valleys of the CB are from dxy + dx2−y2 orbitals (such as ε = 2%). For 1% < ε < 1.4%, the orbital features in the −K valley are not varied, and the dxy + dx2−y2 (dz2) orbitals occupy the +K valleys in the VB (CB) (such as ε = 1.2%). When −5% < ε < 1%, we can acquire the opposite distributions (such as ε = 0.5%) in contrast to the situations of 1.4% < ε < 5%.
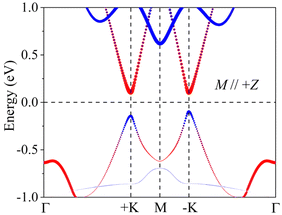
As the ε changes, the two-time inversions of orbital compositions can be observed together with the emergence of two HVM states, which indicates that topological phase transition may occur. The ε = 1.2% is chosen as an instance to prove our consideration. As plotted in Fig. 7(a), a nontrivial chiral edge state connects the VB and CB, demonstrating that VCGeN4 features a VQAHE and has a unit Chern number (C). On account of the VBM and CBM being contributed by spin-up channels, the chiral edge state has 100% spin polarization and spin-up character. While the magnetization orientation of V is flipped, the chiral edge state can be transformed correspondingly, which is analogous to the flipping of VP. According to Fig. 7(b), the edge state with spin-down channels and opposite chirality can cross the bulk band gap and connect the CB and the VB. In addition, the spin flipping makes the position of edge state to shift from one valley to another valley, indicating a pattern known as chiral spin–valley locking.
Because the variations of electronic states are closely connected with the transition of Ω(k), the Ω(k) distributions for ε = 0.5%, 1.2%, and 2% are plotted in Fig. S10.† According to Fig. S10(a) and (d),† for ε = 0.5%, Ω(k) has opposite signs with unequal absolute values in the +K and −K valleys for FV states, demonstrating the classic valley-contrasting traits. Under ε = 1.2%, both the absolute value and sign of Ω(k) in the −K valley are changed (see Fig. S10(b) and (e)†) on account of the appearance of topological phase transition. That is to say, the magnitudes of Ω(k) are inconsistent and the signs are consistent in the two valleys for 1% < ε < 1.4%. Such a situation of Ω(k) can bring about non-zero C and non-trivial topological properties. C = 1 can be obtained by 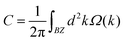 , which is analogous to the nontrivial chiral edge states (see Fig. 7(a) and (b)). When ε > 1.4%, the VQAHE state transforms into the FV state, leading to the sign variation of Ω(k) in the +K valley (for instance, under ε = 2%, see Fig. S10(c) and S10(f)†). All in all, we can observe the sign-reversal Ω(k) in two valleys with increasing strain.
, which is analogous to the nontrivial chiral edge states (see Fig. 7(a) and (b)). When ε > 1.4%, the VQAHE state transforms into the FV state, leading to the sign variation of Ω(k) in the +K valley (for instance, under ε = 2%, see Fig. S10(c) and S10(f)†). All in all, we can observe the sign-reversal Ω(k) in two valleys with increasing strain.
Tellingly, VCGeN4 can realize spontaneous VP when the magnetization direction is along the OOP, and the VP in the top VB and bottom CB is observed (see Fig. S8† and Fig. 7(c)). When 1.4% < ε < 5%, a noticeable VP can be observed in the bottom CB, but these in the top VB is almost be ignored. Nevertheless, compared with the circumstance of 1.4% < ε < 5%, the distribution of the VP for −5% < ε < 1% is opposite. We can account for these consequences utilizing the distribution of different orbitals (dxy + dx2−y2 and dz2 orbitals of V atoms). For 1% < ε < 1.4%, the VP can be discovered in the VB and CB, and VCGeN4 features a VQAHE in this region.
The situations of the magnetocrystalline direction along IP are explored. Some representative electronic structures are displayed in Fig. S11† and the band gaps versus strain are shown in Fig. S12.† When −2% ≤ ε ≤ 3%, with increasing strain, the band gap initially decreases and drops to 0, afterwards reopens and goes up. The band gap is closed in approximate ε = 1.2%, and we cannot observe spontaneous VP and the VQAHE state. For −2.5% ≤ ε ≤ 3.25% (except ε = 1.2%), VCGeN4 is a direct-band-gap semiconductor. When −5% < ε < −2.5% and 3.25% < ε < 5%, VCGeN4 is an indirect-band-gap semiconductor. For ε = 1.2%, VCGeN4 has a semi-metal character. In brief, VCGeN4 is a conventional semi-metal or FM semiconductor.
Then, the influence of strain on MAE is discussed. The MCA energy, MSA energy, and MAE vs. strain are plotted in Fig. 7(d). According to Fig. 7(d), for −5% ≤ ε ≤ 5%, the variation of MSA energy (−30 μeV < EMSA < −26 μeV) is relatively stable and the negative MAE can be found all the time, manifesting that the magnetocrystalline direction of VCGeN4 is always along the IP in the investigated strain range. Nevertheless, we can adjust the magnetization from the IP to OOP via making use of an external magnetic field to overcome the energy barrier, which will come into being intriguing electronic and topological states. For instance, when ε = 1.2%, the energy barrier of around 58 μeV corresponds to the application of an external magnetic field of about 0.29–0.58 T. Moreover, in order to comprehend the underlying physics of different MAEs, the atom-projected MCA energy without strain is obtained (see Fig. 8(a)). It is discovered that the IP MCA energy is mainly contributed by the p and d orbitals of the V atom (see Fig. 8(b) and (c)). The summations of orbital interaction lead to the MCA energy, and the p and d orbitals of V in VCGeN4 offer values of −6.74 μeV per f.u. and −38.62 μeV per f.u., respectively.
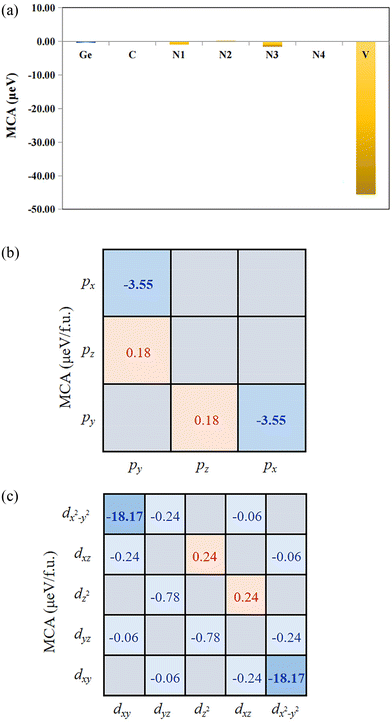 | ||
| Fig. 8 (a) Atom-resolved MCA energy and orbital-resolved MCA energies of (b) V-p and (c) V-d for VCGeN4. | ||
The electric field is always applied to tune the electronic and magnetic features.78,79 Therefore, we explore the influence of the electric field with a magnitude of 0.1–0.6 V Å−1. The magnetic interactions are discussed under the electric field. It is found that VCGeN4 maintains the FM state within an investigated electric field range (see Fig. S13†), and the increasing electric field can enhance the FM coupling. Fig. S14(a)† shows the obtained results of MCA energy, MSA energy, and MAE with the electric field. It is discovered that the MCA energy, MSA energy, and MAE of VCGeN4 are always negative, which shows that the easy magnetic axis direction is always along the IP. According to Fig. S14(b),† due to the enhancement of FM coupling with the electric field from 0.1 V Å−1 to 0.6 V Å−1, the TC monotonically increases.
The electronic structures of VCGeN4 under an electric field E are investigated. For OOP magnetization, the variations of the global band gap, the VP for the VB and CB versus E, and the band structures at the representative E are shown in Fig. S14(c), S14(d), and S15,† respectively. It is found that VCGeN4 is intrinsically a FV system for E between 0.1 V Å−1 and 0.6 V Å−1. The band gap increases with increasing E (when 0.1 V Å−1 ≤ E ≤ 0.6 V Å−1). As shown in Fig. S14(d) and S15,† within the discussed E section, the VP of the VB is noteworthy, but the VP of the CB is inconspicuous, which can be understood by the situation of V-d orbitals. Fig. S16† presents the Ω(k) of VCGeN4 under E = 0.1 V Å−1 with SOC. It is found that the Ω(k) dominantly emerges in the +K and −K valleys with unequal absolute values and opposite signs. Our works demonstrate that many characteristics of 2D materials can well regulated by the electric field, such as the valley state and electronic and magnetic properties.
IV. Conclusion
In summary, via first-principles calculations, the tunable abundant valley Hall effect is reported in VCGeN4. VCGeN4 is an intrinsic ferromagnetic semiconductor and has a valley feature. For OOP magnetization, arising from the breaking of inversion and time-reversal symmetries, the VP can spontaneously occur, motivating the exploration of charge, spin, and the AVHE. In addition, under tensile strain, band inversion can be realized in the +K and −K valleys, which induces the VQAHE. In particular, the valley feature can be maintained with an external strain and electric field, manifesting that the tunable abundant valley Hall effect exists in VCGeN4. All discoveries greatly enrich the tunable abundant valley Hall effect and point out a promising material for investigating the tunable abundant valley Hall effect in experiment.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (grant no. 52173283), the Taishan Scholar Program of Shandong Province (grant no. ts20190939), and the Independent Cultivation Program of Innovation Team of Jinan City (grant no. 2021GXRC043).References
- K. F. Mak, D. Xiao and J. Shan, Light-valley interactions in 2D semiconductors, Nat. Photonics, 2018, 12, 451–460 CrossRef CAS.
- D. Xiao, G. B. Liu, W. Feng, X. Xu and W. Yao, Coupled spin and valley physics in monolayers of MoS2 and other group VI dichalcogenides, Phys. Rev. Lett., 2012, 108, 196802 CrossRef PubMed.
- K. F. Mak, K. L. McGill, J. Park and P. L. McEuen, The valley Hall effect in MoS2 transistors, Science, 2014, 344, 1489–1492 CrossRef CAS PubMed.
- S. Wu, J. Ross, G. B. Liu, G. Aivazian, A. Jones, Z. Y. Fei, W. G. Zhu, D. Xiao, W. Yao, D. Cobden and X. D. Xu, Electrical tuning of valley magnetic moment through symmetry control in bilayer MoS2, Nat. Phys., 2013, 9, 149–153 Search PubMed.
- J. R. Schaibley, H. Y. Yu, G. Clark, P. Rivera, J. S. Ross, K. L. Seyler, W. Yao and X. D. Xu, Valleytronics in 2D materials, Nat. Rev. Mater., 2016, 1, 16055 Search PubMed.
- S. A. Vitale, D. Nezich, J. O. Varghese, P. Kim, N. Gedik, P. Jarillo-Herrero, D. Xiao and M. Rothschild, Valleytronics: opportunities, challenges, and paths forward, Small, 2018, 14, 1801483 CrossRef PubMed.
- Q. Y. Zhang, S. Yang, W. B. Mi, Y. C. Cheng and U. Schwingenschlogl, Large spin-valley polarization in monolayer MoTe2 on top of EuO (111), Adv. Mater., 2016, 28, 959–966 CrossRef CAS PubMed.
- G. Pacchioni, Valleytronics with a twist, Nat. Rev. Mater., 2020, 5, 480 CrossRef CAS.
- G. Aivazian, Z. R. Gong, A. Jones, R. L. Chu, J. Yan, D. G. Mandrus, C. W. Zhang, D. Cobden, W. Yao and X. Xu, Magnetic control of valley pseudospin in monolayer WSe2, Nat. Phys., 2015, 11, 148–152 Search PubMed.
- D. MacNeill, C. Heikes, K. F. Mak, Z. Anderson, A. Kormanyos, V. Zolyomi, J. Park and D. Ralph, Breaking of valley degeneracy by magnetic field in monolayer MoSe2, Phys. Rev. Lett., 2015, 114, 037401 CrossRef CAS PubMed.
- D. Zhong, K. Seyler, X. Y. Linpeng, R. Cheng, N. Sivadas, B. Huang, E. Schmidgall, T. Taniguchi, K. Watanabe, M. Mcguire, W. Yao, D. Xiao, K. M. Fu and X. D. Xu, van der Waals engineering of ferromagnetic semiconductor heterostructures for spin and valleytronics, Sci. Adv., 2017, 3, e1603113 CrossRef PubMed.
- H. S. Zhang, W. J. Yang, Y. H. Ning and X. H. Xu, Abundant valley-polarized states in two-dimensional ferromagnetic van der Waals heterostructures, Phys. Rev. B, 2020, 101, 205404 CrossRef CAS.
- H. L. Zeng, J. F. Dai, W. Yao, D. Xiao and X. D. Cui, Valley polarization in MoS2 monolayers by optical pumping, Nat. Nanotechnol., 2012, 7, 490–493 CrossRef CAS PubMed.
- Y. C. Cheng, Q. Y. Zhang and U. Schwingenschlogl, Valley polarization in magnetically doped single-layer transition-metal dichalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 155429 CrossRef.
- N. Singh and U. Schwingenschlogl, A route to permanent valley polarization in monolayer MoS2, Adv. Mater., 2017, 29, 1600970 CrossRef PubMed.
- X. Li, T. Cao, Q. Niu, J. R. Shi and J. Feng, Coupling the valley degree of freedom to antiferromagnetic order, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3738–3742 CrossRef CAS PubMed.
- W. Y. Tong, S. J. Gong, X. G. Wan and C. G. Duan, Concepts of ferrovalley material and anomalous valley Hall effect, Nat. Commun., 2016, 7, 13612 CrossRef CAS PubMed.
- C. M. Zhang, Y. H. Nie, S. Sanvito and A. J. Du, First-principles prediction of a room temperature ferromagnetic Janus VSSe monolayer with piezoelectricity, ferroelasticity, and large valley polarization, Nano Lett., 2019, 19, 1366–1370 CrossRef CAS PubMed.
- X. D. Zhou, R. W. Zhang, Z. Y. Zhang, W. X. Feng, Y. Mokrousov and Y. G. Yao, Sign-reversible valley-dependent Berry phase effects in 2D valley-half-semiconductors, npj Comput. Mater., 2021, 7, 160 CrossRef.
- K. Sheng, Q. Chen, H. K. Yuan and Z. Y. Wang, Monolayer CeI2: an intrinsic room-temperature ferrovalley semiconductor, Phys. Rev. B, 2022, 105, 075304 CrossRef CAS.
- K. Jia, X. J. Dong, S. S. Li, W. X. Ji and C. W. Zhang, Spontaneous valley polarization and valley-nonequilibrium quantum anomalous Hall effect in Janus monolayer ScBrI, Nanoscale, 2023, 15, 8395–8405 RSC.
- Z. He, R. Peng, Y. Dai, B. Huang and Y. Ma, Single-layer ScI2: A paradigm for valley-related multiple Hall effect, Appl. Phys. Lett., 2021, 119, 243102 CrossRef CAS.
- P. Jiang, L. Kang, Y. L. Li, X. Zheng, Z. Zeng and S. Sanvito, Prediction of the two-dimensional Janus ferrovalley material LaBrI, Phys. Rev. B, 2021, 104, 035430 CrossRef CAS.
- Y. M. Zang, Y. D. Ma, R. Peng, H. Wang, B. B. Huang and Y. Dai, Large valley-polarized state in single-layer NbX2 (X = S, Se): theoretical prediction, Nano Res., 2020, 14, 834–839 CrossRef.
- K. Sheng, B. K. Zhang, H. K. Yuan and Z. Y. Wang, Strain-engineered topological phase transitions in ferrovalley 2H-RuCl2 monolayer, Phys. Rev. B, 2022, 105, 195312 CrossRef CAS.
- R. Li, J. W. Jiang, W. B. Mi and H. L. Bai, Room temperature spontaneous valley polarization in two-dimensional FeClBr monolayer, Nanoscale, 2021, 13, 14807–14813 RSC.
- S. D. Guo, W. Q. Mu and B. G. Liu, Correlation-driven threefold topological phase transition in monolayer OsBr2, Front. Phys., 2021, 18, 33304 CrossRef.
- S. D. Guo, W. Q. Mu and B. G. Liu, Valley-polarized quantum anomalous Hall insulator in monolayer RuBr2, 2D Mater., 2022, 9, 035011 CrossRef CAS.
- H. Sun, S. S. Li, W. X. Ji and C. W. Zhang, Valley-dependent topological phase transition and quantum anomalous valley Hall effect in single-layer RuClBr, Phys. Rev. B, 2022, 105, 195112 CrossRef CAS.
- K. Jia, X. J. Dong, S. S. Li, W. X. Ji and C. W. Zhang, Electronic-correlation induced sign-reversible Berry phase and valley-nonequilibrium quantum anomalous Hall effect in the Janus monolayer OsClBr, Phys. Chem. Chem. Phys., 2023, 25, 15767–15776 RSC.
- K. Jia, X. J. Dong, S. S. Li, W. X. Ji and C. W. Zhang, Strain-engineering induced topological phase transitions and multiple valley states in Janus monolayer VCSiN4, J. Mater. Chem. C, 2023, 11, 10359–10369 RSC.
- W. R. Liu, X. J. Dong, Y. Z. Lv, W. X. Ji, Q. Cao, P. J. Wang, F. Li and C. W. Zhang, Magnetic anisotropy and ferroelectric-driven magnetic phase transition in monolayer Cr2Ge2Te6, Nanoscale, 2022, 14, 3632–3643 RSC.
- L. Zhang, S. F. Zhang, W. X. Ji, C. W. Zhang, P. Li, P. J. Wang, S. S. Li and S. S. Yan, Discovery of a novel spin-polarized nodal ring in a two-dimensional HK lattice, Nanoscale, 2018, 10, 20748–20753 RSC.
- S. J. Zhang, C. W. Zhang, S. F. Zhang, W. X. Ji, P. Li, P. J. Wang, S. S. Li and S. S. Yan, Intrinsic Dirac half-metal and quantum anomalous Hall phase in a hexagonal metal-oxide lattice, Phys. Rev. B, 2017, 96, 205433 CrossRef.
- S. S. Li, W. X. Ji, S. J. Hu, C. W. Zhang and S. S. Yan, Effect of Amidogen Functionalization on Quantum Spin Hall Effect in Bi/Sb(111) Films, ACS Appl. Mater. Interfaces, 2017, 9, 41443–41453 CrossRef CAS PubMed.
- Y. P. Wang, W. X. Ji, C. W. Zhang, P. Li, S. F. Zhang, P. J. Wang, S. S. Li and S. S. Yan, Two-dimensional arsenene oxide: A realistic large-gap quantum spin Hall insulator, Appl. Phys. Lett., 2017, 110, 213101 CrossRef.
- M. H. Zhang, C. W. Zhang, P. J. Wang and S. S. Li, Prediction of high-temperature Chern insulator with half-metallic edge states in asymmetry-functionalized stanene, Nanoscale, 2018, 10, 20226–20233 RSC.
- B. Wu, Y. L. Song, W. X. Ji, P. J. Wang, S. F. Zhang and C. W. Zhang, Quantum anomalous Hall effect in an antiferromagnetic monolayer of MoO, Phys. Rev. B, 2023, 107, 214419 CrossRef CAS.
- Y. T. Han, W. X. Ji, P. J. Wang, P. Li and C. W. Zhang, Strain-tunable skyrmions in two-dimensional monolayer Janus magnets, Nanoscale, 2023, 15, 6830–6837 RSC.
- Y. L. Hong, Z. B. Liu, L. Wang, T. Y. Zhou, W. Ma, C. Xu, S. Feng, L. Chen, M. L. Chen, D. M. Sun, X. Q. Chen, H. M. Cheng and W. C. Ren, Chemical vapor deposition of layered two-dimensional MoSi2N4 materials, Science, 2020, 369, 670–674 CrossRef CAS PubMed.
- Q. R. Cui, Y. M. Zhu, J. H. Liang, P. Cui and H. X. Yang, Spin-valley coupling in a two-dimensional VSi2N4 monolayer, Phys. Rev. B, 2021, 103, 085421 CrossRef CAS.
- C. Yang, Z. Song, X. Sun and J. Lu, Valley pseudospin in monolayer MoSi2N4 and MoSi2As4, Phys. Rev. B, 2021, 103, 035308 CrossRef CAS.
- J. Huang, P. Li, X. Ren and Z. X. Guo, Promising Properties of a Sub-5 nm Monolayer MoSi2N4 Transistor, Phys. Rev. Appl., 2021, 16, 044022 CrossRef CAS.
- H. Zhong, W. Xiong, P. Lv, J. Yu and S. Yuan, Strain-induced semiconductor to metal transition in MA2Z4 bilayers (M = Ti, Cr, Mo; A = Si; Z = N, P), Phys. Rev. B, 2021, 103, 085124 CrossRef CAS.
- Y. T. Ren, L. Hu, Y. T. Chen, Y. J. Hu, J. L. Wang, P. L. Gong, H. Zhang, L. Huang and X. Q. Shi, Two-dimensional MSi2N4 monolayers and van der Waals heterostructures: Promising spintronic properties and band alignments, Phys. Rev. Mater., 2022, 6, 064006 CrossRef CAS.
- Y. Yin, Q. H. Gong, M. Yi and W. L. Guo, Emerging Versatile Two-Dimensional MoSi2N4 Family, Adv. Funct. Mater., 2023, 33, 2214050 CrossRef CAS.
- C. C. Tho, S. D. Guo, S. J. Liang, W. L. Ong, C. S. Lau, L. M. Cao, G. Z. Wang and Y. S. Ang, MA2Z4 family heterostructures: Promises and prospects, Appl. Phys. Rev., 2023, 10, 041307 CAS.
- Q. Q. Wang, L. M. Cao, S. J. Liang, W. K. Wu, G. Z. Wang, C. H. Lee, W. L. Ong, H. Y. Yang, L. K. Ang, S. A. Yang and Y. S. Ang, Efficient Ohmic contacts and built-in atomic sublayer protection in MoSi2N4 and WSi2N4 monolayers, npj 2D Mater. Appl., 2021, 5, 71 CrossRef CAS.
- C. C. Tho, C. Yu, Q. Tang, Q. Wang, T. Su, Z. Feng, Q. Wu, C. V. Nguyen, W. Ong, S. Liang, S. Guo, L. Cao, S. Zhang, S. A. Yang, L. K. Ang, G. Wang and Y. S. Ang, Cataloguing MoSi2N4 and WSi2N4 van der Waals Heterostructures: An Exceptional Material Platform for Excitonic Solar Cell Applications, Adv. Mater. Interfaces, 2023, 10, 2201856 CrossRef CAS.
- Z. B. Liu, L. Wang, Y. L. Hong, X. Q. Chen, H. M. Cheng and W. C. Ren, Two-dimensional superconducting MoSi2N4(MoN)4n homologous compounds, Natl. Sci. Rev., 2023, 10, nwac273 CrossRef CAS.
- C. C. Tho, X. K. Feng, Z. L. Jiang, L. M. Cao, G. Z. Wang, C. S. Lau, S. D. Guo and Y. S. Ang, Ultrathick MA2N4(M′N) Intercalated Monolayers with Sublayer-Protected Fermi Surface Conduction States: Interconnect and Metal Contact Applications, arXiv, 2023, preprint, arXiv:2311.09057, DOI:10.48550/arXiv.2311.09057.
- A. Y. Lu, H. Zhu, J. Xiao, C. P. Chuu, Y. Han, M. H. Chiu, C. C. Cheng, C. W. Yang, K. H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M. Y. Chou, X. Zhang and L. J. Li, Janus monolayers of transition metal dichalcogenides, Nat. Nanotechnol., 2017, 12, 744–749 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS PubMed.
- P. E. Blochl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA + U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- D. Dey, A. Ray and L. P. Yu, Intrinsic ferromagnetism and restrictive thermodynamic stability in MA2N4 and Janus VSiGeN4 monolayers, Phys. Rev. Mater., 2022, 6, L061002 CrossRef CAS.
- S. D. Guo, W. Q. Mu, J. H. Wang, Y. X. Yang, B. Wang and Y. S. Ang, Strain effects on the topological and valley properties of the Janus monolayer VSiGeN4, Phys. Rev. B, 2022, 106, 064416 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- X. Wu, D. Vanderbilt and D. R. Hamann, Systematic treatment of displacements, strains, and electric fields in density-functional perturbation theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035105 CrossRef.
- A. Togo, F. Oba and I. Tanaka, First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- A. A. Mostofi, J. R. Yates, Y. S. Lee, I. Souza, D. Vanderbilt and N. Marzari, wannier90: A tool for obtaining maximally-localised Wannier functions, Comput. Phys. Commun., 2008, 178, 685–699 CrossRef CAS.
- X. Wang, J. R. Yates, I. Souza and D. Vanderbilt, Ab initio calculation of the anomalous Hall conductivity by Wannier interpolation, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 195118 CrossRef.
- L. Wang, Y. Shi, M. Liu, A. Zhang, Y.-L. Hong, R. Li, Q. Gao, M. Chen, W. Ren, H.-M. Cheng, Y. Li and X.-Q. Chen, Intercalated architecture of MA2Z4 family layered van der Waals materials with emerging topological, magnetic and superconducting properties, Nat. Commun., 2021, 12, 2361 CrossRef CAS PubMed.
- V. Vierimaa, A. V. Krasheninnikov and H. P. Komsa, Phosphorene under electron beam: from monolayer to one-dimensional chains, Nanoscale, 2016, 8, 7949–7957 RSC.
- L. M. Yang, I. A. Popov, A. I. Boldyrev, T. Heine, T. Frauenheim and E. Ganz, Post-anti-van't Hoff-Le Bel motif in atomically thin germanium-copper alloy film, Phys. Chem. Chem. Phys., 2015, 17, 17545–17551 RSC.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Mechanical properties of graphene and boronitrene, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428 CrossRef.
- S. Haastrup, M. Strange, M. Pandey, T. Deilmann, P. S. Schmidt, N. F. Hinsche, M. N. Gjerding, D. Torelli, P. M. Larsen, A. C. Riis-Jensen, J. Gath, K. W. Jacobsen, J. J. Mortensen, T. Olsen and K. S. Thygesen, The Computational 2D Materials Database: high-throughput modeling and discovery of atomically thin crystals, 2D Mater., 2018, 5, 042002 CrossRef CAS.
- M. Mazdziarz, Comment on ‘The Computational 2D Materials Database: high-throughput modeling and discovery of atomically thin crystals’, 2D Mater., 2019, 6, 048001 CrossRef CAS.
- B. Goodenough, Theory of the role of covalence in the Perovskite-type manganites [La, M(II)] MnO3, Phys. Rev., 1955, 100, 564 CrossRef.
- J. Kanamori, Superexchange interaction and symmetry properties of electron orbitals, J. Phys. Chem. Solids, 1959, 10, 87–98 CrossRef CAS.
- P. W. Anderson, New approach to the theory of superexchange interactions, Phys. Rev., 1959, 115, 2 CrossRef CAS.
- G. Benedek and G. F. Nardelli, Evidence for Resonant-Mode Sidebands in Alkali Halides, Phys. Rev. Lett., 1966, 17, 1136 CrossRef CAS.
- X. Liu, H. C. Hsu and C. X. Liu, In-Plane Magnetization-Induced Quantum Anomalous Hall Effect, Phys. Rev. Lett., 2013, 111, 086802 CrossRef PubMed.
- D. J. Thouless, M. Kohmoto, M. P. Nightingale and M. den Nijs, Quantized Hall Conductance in a Two-Dimensional Periodic Potential, Phys. Rev. Lett., 1982, 49, 405 CrossRef CAS.
- X. K. Feng, C. S. Lau, S. J. Liang, C. H. Lee, S. A. Yang and Y. S. Ang, Half-Valley Ohmic Contact: Contact-Limited Valley-Contrasting Current Injection, Adv. Funct. Mater., 2023, 2309848 CrossRef.
- S. D. Guo, X. S. Guo, G. Z. Wang, K. Cheng and Y. S. Ang, Electric-field induced magnetic-anisotropy transformation to achieve spontaneous valley polarization, J. Mater. Chem. C, 2022, 10, 16363–16369 RSC.
- S. D. Guo, Y. L. Tao, H. T. Guo, Z. Y. Zhao, B. Wang, G. Z. Wang and X. T. Wang, Possible electronic state quasi-half-valley metal in a VGe2P4 monolayer, Phys. Rev. B, 2023, 107, 054414 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr05643k |
| This journal is © The Royal Society of Chemistry 2024 |