Tri-state logic computation by activating DNA origami chains

Abstract

The invention of DNA nanotechnology has enabled molecular computation as a promising substitute for traditional semiconductors which are limited to two-dimensional architectures and by heating problems resulting from densification. Current studies of logic gates achieved using DNA molecules are predominately focused on two-state operations (AND, OR, etc.); however, realizing tri-state logic (high impedance Z) in DNA computation is understudied. Here we actively fold DNA origami chain-like hinged rods to induce conformational changes that return tri-state logic signals. We use rigid six helix-bundle (6HB) DNA origami to self-assemble a linear trimer chain as a circuit platform with functional single-stranded (ss) DNA near each semi-flexible hinge. The presence or absence of ssDNA enable and input strands allows hybridization to take place at the hinges, activating one fold (0) or two folds (1) from the straight linear geometry (defined as High-Z) of the trimer chain. We design two different tri-state logic gate platforms, buffer and inverter, with corresponding enable/input ssDNA to unambiguously return tri-state signals, characterized by Atomic Force Microscopy (AFM) and/or agarose gel electrophoresis (GEL). Our work on tri-state logic significantly enhances DNA computation beyond the current two-state Boolean logic with both research and industrial applications, including cellular treatments and living matter utilizing the biocompatibility of DNA molecules.

---

With the end of rapid growth in silicon hardware and Moore's Law there is a renewed interest in DNA computation with a view toward logic operations at the molecular level facilitated by DNA nanotechnology.^1–22 Another advantage of organic DNA computation^23–36 compared to inorganic silicon semiconductors is compatibility with living matter. So far the DNA computation community has been primarily focused on studying two-state devices essential to Boolean logic operations. In our work, we aim to introduce tri-state logic DNA computation with the outlook of implementing shared communication lines by multiple devices without causing interference. We've realized non-interference in logic computation taking advantage of the high programmability and specific binding of non-crosstalk DNA sequences.

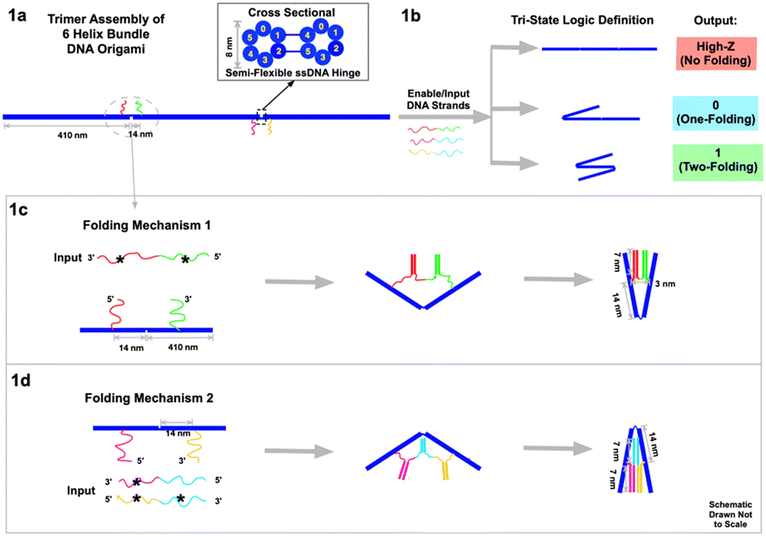
DNA nanotechnology has enabled the construction of complex nano- and micro-scale structures with nanometer-precision, including machines and motors fueled by DNA hybridization.^1–3,13 Here we design a rod-like 6HB DNA origami, 410 nm long and 8 nm thick, and then self-assemble three of them into a chain-like construct (Fig. 1a) to act as the circuit platform. The axial connection between the three 6HBs contains two semiflexible hinges, 3-base-ssDNA strands. The hinges are rigid enough to align the rods linearly yet flexible enough to be folded by DNA hybridization forces on the two ssDNA strands. These two non-complementary strands are situated on either side of each hinge, 14 nm from the hinge center. When additional ssDNA strands are added to the DNA origami trimer platform, hybridization to the strands surrounding each hinge leads to transformational changes. Depending on the complementarity of the added ssDNA, folding can be triggered at the two hinges independently. This results in three distinguishable geometries (Fig. 1b): no-folding, a single fold on either the left or the right 6HB, or two folds on both left and right. Notably, single right or left folds cannot be differentiated using AFM or gel electrophoresis data.

Fig. 1 Schematics of experimental designs. (a) The platform design for our DNA circuits is based on three six-helix bundle (6HB) DNA origami connected by two hinges and functional sticky ends. (b) The output signals of our tri-state logic gates are high impedance (no folds), zero (one fold), and 1 (two folds). (c) The folding mechanism of the first type. An input strand hybridizes to and links the sticky ends to activate the folding of a 6HB dimer hinge. Colored strands with a “*” are complementary to strands of the same color. (d) The folding mechanism of the second type. Two input (or enable) strands are required to activate folding of the 6HB dimer structure.

Two types of folding mechanism were engineered through DNA hybridization at the hinges. As a convention in this manuscript, complementary strands in all figures are denoted with the same color, and one of them is marked with a star (*). In the first mechanism (Fig. 1c), the input ssDNA consists of two segments (red*–green*) of functional sticky ends that are respectively complementary to the two sticky ends (red and green) on the two sides of the hinge. This input strand has 21-base functional sticky ends in each of the two segments, which are spaced by a neutral/non-functional 2-base T sequence. When the input ssDNA is presented to the circuit platform, it hybridizes with the two sticky ends on both sides of the hinge to fold the left two 6HB segments. After hybridization, the two 6HBs are tightly folded together at an angle between 0° and 60°, with a slight dependence on factors like thermal fluctuations of the hinges, sticky end design, AFM imaging properties, the imperfectly rigid 6HB, etc. (see ESI section 7 for discussion†). In the second type of folding mechanism (Fig. 1d), two different enable/input strands are required to complete the folding. The input magenta*–cyan is partially complementary to the left sticky ends (magenta) on the 6HB, and the input yellow*–cyan* is partially complementary to the right sticky ends (yellow). The cyan and cyan* segments of the two input strands are complementary to eventually fold the right two 6HBs. In all the experiments, the concentrations of enable/input strands are ∼50 nM, and the concentration of DNA origami, and thereby the sticky ends on them, is ∼0.5 nM. The ratio is ∼100 : 1. (For details please see the Method section.)

To close a hinge the hybridization energy must be greater than the bending energy of the hinge and the torque from the DNA force acting at points 14 nm from the hinge must be greater than the torque from the bending of the short single strands at the hinge vertex. We use a semi-flexible polymer model to obtain the bending force as a function of bending angle and rigidity. The bending energy is E_B = Kθ²/2, where K = ξ_pk_BT/L with ξ_p the persistence length and L the rod length, which results in E_B ∼ 5k_BT and a maximum torque τ = 45 pN nm. These values are comfortably smaller than the hybridization energy for our 21-base sequence ∼30k_BT and the torque from the geometry and zipping force from hybridization of 112 pN nm.

The tri-state output signals are read by the geometric changes of the 6HB trimer circuit platform. For the inputs we define the presence of the enable strand as “high”, and its absence as “low”. Similarly, the presence of the input strand is defined as “1”, and the absence of it as “0”. For the output signal, we define the no-folding linear geometry of the trimer (Fig. 1b) as “high impedance Z”. One fold, either on the left or on the right, is defined as output “0”. Two folds, on both left and right, is defined as output “1”. We use AFM to directly visualize the three geometries. Due to the strong interactions between the DNA origami and the substrate during deposition, the geometry may vary slightly from its form in free solution. We also use electrophoretic gels to monitor the different geometries. Although the molecular weights of the trimer DNA rods are essentially the same the mobilities of the folded and straight configurations are significantly different. As we have previously seen in folded DNA structures,¹³ the folded geometry has lower mobility presumably because the hook-like fold readily latches onto the gel filaments and must untangle to proceed. As a result, the linear geometry passes through fastest while the two-fold geometry is the slowest.

To test the viability of our tri-state logic computation, we constructed a prototype for “AND” operation in two-state logic (Fig. 2a). For a short version of the logic gate platform, we make a dimer by connecting two 6HB DNA origami with a pair of functional sticky ends near the hinge (Fig. 2b). The two sticky ends (magenta and blue) are not complementary to each other, while respectively partially complementary to the two input strands, magenta*–green* (input 1) and blue*–green (input 2). From the second type of folding mechanism, the folding is not activated until both input strands are present. In our experiment, output “0” is defined to be no folding when both input 1 and input 2 are absent (0 and 0). The output remains “0” when input 1 is present (1) with input 2 absent (0), or when input 1 is absent (0) with input 2 present (1). The output returns signal “1”, which is designed to be a folded dimer, when both input 1 and input 2 are present (1 and 1). Characterized by both GEL (Fig. 2d) and AFM (Fig. 2e, f and S1a–d†), the two-state AND logic gate operates as designed.

Fig. 2 Design and data of logic gate “AND”. (a) Truth table of the “AND” logic gate of the DNA circuits. (b) Design of the circuit platform with two input strands. (c) Schematics of output signals in terms of no-folding/folding. (d) Agarose gel image of the four output signals with corresponding colors. The lowest band is 6HB monomer; the middle band is not folded (straight) 6HB dimer; the upper band is folded 6HB dimer. (e) AFM images of folded dimer geometry with both input strands. Scale bar is 400 nm. (f) AFM images of not folded dimer geometry.

Our two tri-state logic gates are illustrated in Fig. 3 (buffer) and Fig. 4 (inverter). For the tri-state buffer, the DNA origami platform with enable and input strands is detailed in Fig. 3b. Note that the red sticky ends are identical on both hinges. When the enable strand is “low” (absence) and the input strand is “0” (absence), the trimer maintains the unfolded, linear geometry “High-Z” (Fig. 3d). When the enable strand is “low” (absence) and the input strand is “1” (presence), the trimer remains in the unfolded “High-Z” geometry (Fig. 3e), because the hybridization of the input strand on the right hinge does not activate any folding. When the enable strand is “high” (presence) and the input strand is “0” (absence), the left hinge is folded according to the first type of folding mechanism, however the right hinge is not folded with only one sticky end hybridized. This output is characterized as one fold, signal “0” (Fig. 3f and S2†). When the enable strand is “high” (presence) and the input strand is “1” (presence), both the hinges are folded according to the two types of folding mechanism, respectively (Fig. 3g and S3†). With 2 folds the resulting output signal is “1”. In the two-fold (output 1) scenario, the extra input and enable should form a partial duplex stem with green–green* hybridized, leaving red* and cyan* single stranded. This red* on the partial duplex stem may have occupied the red sticky ends on the left hinge before a single-stranded enable would have hybridized at the hinge. However, the local concentration of sticky ends at the hinge is 10⁵ times higher than the enable/input global concentration in the free solution, yielding more entropy gain for the green hinge sticky ends to be displaced from the partial duplex stem, to further fold the hinge. (See ESI section 6 for detailed discussion.†)

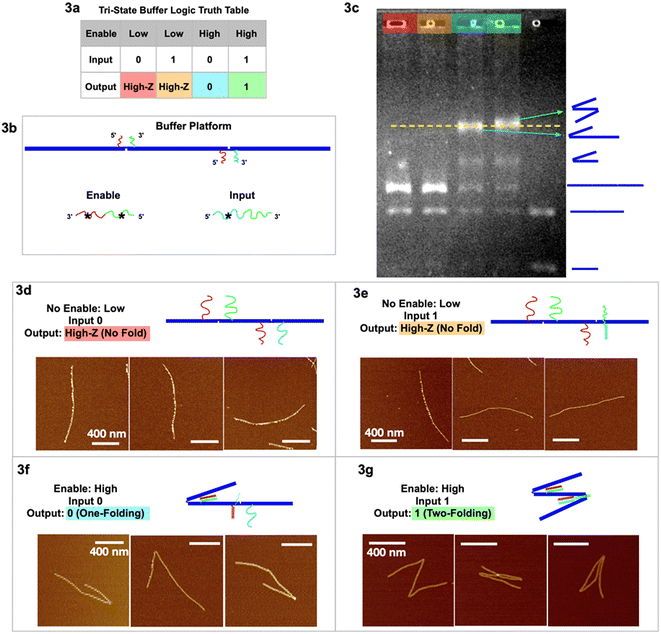Fig. 3 Tri-state logic gate, buffer. (a) Truth table. (b) Schematic of the buffer tri-state DNA circuit platform with input and enable strands. (c) Agarose gel image of the four output signals with color headings corresponding to outputs in (a), and a control sample lane with multiple geometries. (d) AFM images of output High-Z (no-folding 6HB trimer geometry) with no enable or input strands. (e) AFM images of output High-Z (no-folding geometry) with no enable but with input strands. (f) AFM images of output 0 (one fold) with enable but without input strands. (g) AFM images of output 1 (two folds) with both enable and input strands. AFM image scale bars are 400 nm. See Fig. S2 and S3† for statistics of global AFM.

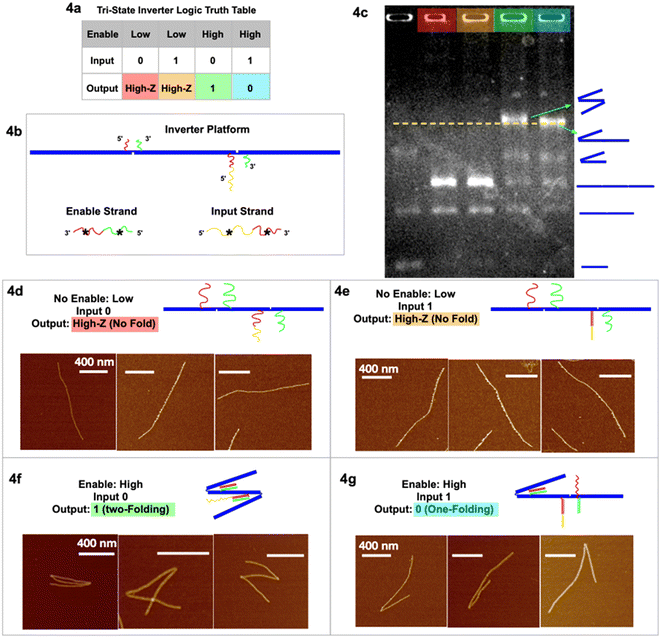Fig. 4 Tri-state logic gate, inverter. (a) Truth table. (b) Schematic of the inverter tri-state DNA circuit platform with input and enable strands. (c) Agarose gel image of the four output signals in corresponding colors, and a control sample lane with multiple geometries. (d) AFM images of output High-Z (no-folding 6HB trimer geometry) with no enable or input strands. (e) AFM images of output High-Z (no-fold geometry) with no enable but with input strands. (f) AFM images of output 1 (two-fold geometry) with enable but without input strands. (g) AFM images of output 0 (one-fold geometry) with both enable and input strands. AFM images scale bars are 400 nm. See Fig. S4 and S5† for statistics of global AFM.

The gel image (Fig. 3c) shows four sample lanes (red, orange, cyan, and green) corresponding to the four output signals in the truth table (Fig. 3a), and a control (last lane) with multiple geometries. The gel shows that the two lanes with output 0 and 1 have the highest bands (indicating the slowest mobility structures), and we believe we may see a slight difference between the two. The green output “1”, with 2 folds, is more likely to entangle with the gel filaments and therefore migrates through porous gels slower than the blue output “0” with only 1 fold. It is interesting to note that folded dimers migrate slower than not folded (straight) trimers, even though the dimer has less molecular weight than the trimer. Some lanes have more bands resulting from leftover monomers not used to form dimer or trimer structures. The statistics of global AFM images (Fig. S2 & S3†) have shown at least 70% of the targeted trimer folded according to the buffer logic, excluding monomers, dimers, and non-specific aggregations.

In the tri-state inverter logic gate (Fig. 4), the platform has been re-designed with functional sticky ends near the hinges with corresponding enable/input strands. Notably, the left sticky end on the right hinge now has two parts, red and yellow (Fig. 4c). When the enable strand is “low” (absence) and the input strand is “0” (absence), the output is the no-folding linear geometry “High-Z” (Fig. 4d). When the enable strand is “low” (absence) and the input strand is “1” (presence), the output remains no-folding “High-Z” (Fig. 4e). When the enable strand is “high” (presence) and the input strand is “0” (absence), the output returns signal “1” (two-folding), as the enable strand is able to bind at both hinges to fold the trimer twice (Fig. 4f and S5†), according to the first type of folding mechanism. When the enable strand is “high” (presence) and the input strand is “1” (presence), the enable strand is only able to fold the left hinge but not the right hinge (Fig. 4g and S4†), resulting in output “0” (one fold). At the left hinge, there was another possibility that the red* on the input strand bound the red sticky ends, while the green* on the enable strand bound the green sticky ends. However, with the same argument that there is a significantly (10⁵ times) higher local concentration of sticky ends than the global concentration of the input/enable strands, the left hinge preferred to bind to its corresponding input strand for higher Gibbs free energy. The right hinge, on introducing the input strand, is unfolded by partially unzipping the red* part of the enable strand in the process of strand displacement. With only the enable strand present, the red–red* and green–green* segments are bound and the hinge closes. In the presence of both enable and input strands we have strand displacement; the input strand segment yellow* hybridizes with the hinge segment yellow and then continues hybridizing input red* with right hinge segment red displacing enable segment red*. The right hinge sticky ends are decoupled, and the hinge opens. This is (Gibbs free) energetically favored. The final state of the right hinge is hinge red–yellow hybridized to input red*–yellow*, hinge green hybridized to enable green*. We then have dsDNA red–yellow and dsDNA green, whereas before strand displacement we had dsDNA red and green. The net gain is the hybridization of the yellow segments. Again, we have obtained the statistics of global AFM images (Fig. S4 & S5†) that show at least 70% of the targeted trimer folded according to the inverter logic, excluding monomers, dimers, and non-specific aggregations.

In conclusion, we have constructed DNA computation logic gates with DNA origami chains activated through DNA strand displacement. Our circuit gates can realize not only two-state Boolean logic, but tri-state logic as well, which is a novel addition to the DNA computation community. Our tri-state DNA circuits, both buffer and inverter gates, have been confirmed with gel electrophoresis and AFM imaging. Our work on DNA tri-state computation significantly supplements Boolean logic with both research and industrial applications, using the biocompatibilities of DNA.

Methods

Tri-state logic DNA origami platform synthesis

M13 scaffold strand and DNA staple strands were mixed at a ratio of 1 : 10 to anneal for 6HB DNA origami monomers with a final concentration of 10 nM in 1 × TAE 12.5 mM Mg²⁺ buffer. The temperature ramp was from 70 °C to 4 °C at 2 °C h⁻¹. Then all six DNA origami monomers (3 for the tri-state buffer and 3 for the inverter platform design) after annealing individually were centrifuged to purify the extra staple strands at 2.2k RCF 4 times, for 15 min each. The 1 × TAE 12.5 Mg²⁺ buffer was refilled after each time of centrifugation. This is the same and only buffer for all the following experiments reported in this article. The three different 6HB DNA origami monomers were then mixed at a ratio of 1 : 1 : 1 and incubated at 42 °C for 3 h, then ramped down to 20 °C at 2 °C h⁻¹. (The accurate control of the mixing ratio is key to obtain a high yield of the tri-state platform product.)

Adding input/enable strands to obtain output signals

The tri-state buffer and inverter 6HB DNA origami trimer platforms were then used with input/enable strands added to obtain different output signals. The ratio of the concentration of the origami platform to that of input/enable was 1 : 100, with a final concentration of origami, thereby the same concentration of sticky ends at the hinge, of 0.5 nM, and a final concentration of input/enable strands of 50 nM. Notably, in the cases where both input and enable strands were required, the two strands were added at the same time.

Reading output signals by agarose gel electrophoresis

The final products with different outputs were added to 0.8% agarose gel ran at room temperature at 50 V (relatively low to not incur significant temperature increase; otherwise, over 50 °C in the gel may distort or damage the origami structures.) Then the gel was dyed with ethidium bromide for 10 min, then washed with water for 3 min before UV imaging.

Reading output signals by atomic force microscopy

The final products with different outputs were also characterized by AFM by depositing diluted product solutions onto a mica surface, followed by DI water rinsing and air pump drying 3 times. The prepared samples on the mica were then imaged in the air mode of the AFM.

Author contributions

K. W., Q. H., M. E., B. K., P. C. and G. Z. contributed to initiation and management and performing and analyzing the experiments. K. W., P. C., and G. Z. contributed to designing the experiment, and designing the DNA sequences and DNA origami.

Conflicts of interest

We declare no conflicts of interest.

Acknowledgements

This research was primarily supported by U.S. Department of Energy (DOE) under grant DE-SC0007991 at NYU (KW, QH, GZ, PMC) for designing the experiment, designing and synthesizing the DNA sequences and origami, analyzing the data and writing the paper, and by Fairleigh Dickinson University (GZ, MRE, and BK) for performing the experiments and analyzing the data. We thank Ruojie Sha and Nadrian Seeman from the Department of Chemistry at New York University for meaningful discussions and technical support.

References

1. B. Yurke, A. J. Turberfield, A. P. Mills Jr., F. C. Simmel and J. L. Neumann, A DNA-fueled molecular machine made of DNA, Nature, 2000, 406, 605–608.
2. F. Wang, X. Zhang, X. Liu, C. Fan and Q. Li, Programming motions of DNA origami nanomachines, Small, 2019, 26, 1900013.
3. K. Lund, A. J. Manzo, N. Dabby, N. Michelotti, A. Johnson-Buck, J. Nangreave, S. Taylor, R. Pei, M. N. Stojanovic, N. G. Walter, E. Winfree and H. Yan, Molecular robots guided by prescriptive landscapes, Nature, 2010, 465, 206–210.
4. D. Schiffels, T. Liedl and D. K. Fygenson, Nanoscale structure and microscale stiffness of DNA nanotubes, ACS Nano, 2013, 7(8), 6700–6710.
5. T. Wang, D. Schiffels, S. M. Cuesta, D. K. Fygenson and N. C. Seeman, Design and characterization of 1D nanotubes and 2D periodic arrays self-assembled from DNA multi-helix bundles, J. Am. Chem. Soc., 2013, 135(27), 10178.
6. H. Chen, S. P. Meisburger, S. A. Pabit, J. L. Sutton, W. W. Webb and L. Pollack, Ionic strength-dependent persistence lengths of single-stranded RNA and DNA, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(3), 799–804.
7. P. L. Biancaniello, J. C. Crocker, D. A. Hammer and V. T. Milam, DNA-mediated phase behavior of microsphere suspensions, Langmuir, 2007, 23, 2688–2693.
8. V. T. Milam, A. L. Hiddessen, J. C. Crocker, D. J. Graves and D. A. Hammer, DNA-driven assembly of bidisperse, micron-sized colloids, Langmuir, 2003, 19, 10317–10323.
9. Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Colloids with valence and specific directional bonding, Nature, 2012, 491, 51–55.
10. W. B. Rogers and V. N. Manoharan, Programming colloidal phase transitions with DNA strand displacement, Science, 2015, 347, 639–642.
11. M. Y. B. Zion, X. He, C. C. Maass, R. Sha, N. C. Seeman and P. M. Chaikin, Self-assembled three-dimensional chiral colloidal architecture, Science, 2017, 358, 633–636.
12. H. Asanuma, X. Liang, H. Nishioka, D. Matsunaga, M. Liu and M. Komiyama, Synthesis of azobenzene-tethered DNA for reversible photo-regulation of DNA functions: hybridization and transcription, Nat. Protoc., 2007, 2, 203–212.
13. G. Zhu, M. Hannel, R. Sha, F. Zhou, M. Y. B. Zion, Y. Zhang, K. Bishop, D. Grier, N. Seeman and P. Chaikin, Microchemomechanical devices using DNA hybridization, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, 21.
14. Y. Xiong, Z. Lin, D. Mostarac, B. Minevich, Q. Peng, G. Zhu, P. Sanchez, S. Kantorovich, Y. Ke and O. Gang, Divalent multilinking bonds control growth and morphology of nanopolymers, Nano Lett., 2021, 21(24), 10547–10554.
15. M. Iwaki, S. F. Wickham, K. Ikezaki, T. Yanagida and W. M. Shih, A programmable DNA origami nanospring that reveals force-induced adjacent binding of myosin VI heads, Nat. Commun., 2015, 7, 13715.
16. J. A. Johnson, A. Dehankar, J. O. Winter and C. E. Castro, Reciprocal control of hierarchical DNA Origami-Nanoparticle Assemblies, Nano Lett., 2019, 19(12), 8469–8475.
17. P. W. K. Rothemund, Folding DNA to create nanoscale shapes and patterns, Nature, 2006, 440, 297–302.
18. C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoff, A DNA-based method for rationally assembling nanoparticles into macroscopic materials, Nature, 1996, 382, 607–609.
19. R. Schulman, B. Yurke and E. Winfree, Robust self-replication of combinatorial information via crystal growth and scission, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6405–6410.
20. Y. Tian, T. Wang, W. Liu, H. Xin, H. Li, Y. Ke, W. M. Shih and O. Gang, Prescribed nanoparticle cluster architectures and low-dimensional arrays built using octahedral DNA origami frames, Nat. Nanotechnol., 2015, 10, 637–644.
21. S. M. Douglas, H. Dietz, T. Liedl, B. Hogberg, F. Graf and W. M. Shih, Self-aseembly of DNA into nanoscale three-dimensional shapes, Nature, 2009, 459, 414–418.
22. P. Yin, H. M. Choi, C. R. Calvert and N. A. Pierce, Programming biomolecular self-assembly pathways, Nature, 2008, 451, 318–322.
23. D. Fan, J. Wang, E. Wang and S. Dong, Propelling DNA computing with materials’ power: recent advancements in innovative DNA logic computing systems and smart bio-applications, Adv. Sci., 2020, 7, 24.
24. L. Qian and E. Winfree, Scaling up digital circuit computation with DNA strand displacement cascades, Science, 2011, 332, 1196–1201.
25. H. Lv, N. Xie, M. Li, M. Dong, C. Sun, Q. Zhang, L. Zhao, J. Li, X. Zuo, H. Chen and F. Wang, DNA-based programmable gate arrays for general-purpose DNA computing, Nature, 2023, 622, 292–300.
26. S. Jia, S. Phua, Y. Nihongaki, Y. Li, M. Pacella, Y. Li, A. Mohammed, S. Sun, T. Inoue and R. Schulman, Growth and site-specific organization of micron-scale biomolecular devices on living mammalian cells, Nat. Commun., 2021, 5729.
27. Z. Lin, L. Beltran, Z. Santos, Y. Li, T. Adel, J. Fagan, A. Walker, E. Egelman and M. Zheng, DNA-guided lattice remodeling of carbon nanotubes, Science, 2022, 377, 6605.
28. M. Balter, S. Li, J. Nilsson, J. Andreasson and U. Pischel, An all-photonic molecule-based parity generator/checker for error detection in data transmission, J. Am. Chem. Soc., 2013, 135, 28.
29. D. Fan, J. Wang, E. Wang and S. Dong, A Janus-inspired amphichromatic system that kills two burds with one stone for operating a DNA janus logic pair (DJLP) library, Chem. Sci., 2019, 30, 7290–7298.
30. S. Bi, S. Yue and S. Zhang, Hybridization chain reaction: a versatile molecular tool for biosensing, bioimaging, and biomedicine, Chem. Soc. Rev., 2017, 46, 4281–4298.
31. A. Genot, J. Bath and A. Turberfield, Reversible logic circuits made of DNA, J. Am. Chem. Soc., 2011, 133, 50.
32. F. Wang, H. Lv, Q. Li, J. Li, X. Zhang, J. Shi, L. Wang and C. Fan, Implementing digital computing with DNA-based switching circuits, Nat. Commun., 2020, 11, 121.
33. F. Zhou, H. Ning, G. Zhu, L. Bershadsky, R. Sha, N. Seeman and P. Chaikin, Toward three-dimensional DNA industrial nanorobots, Sci. Robot, 2024, 8, 85.
34. G. Li, P. Chen, W. Jiang, M. Wang and H. Jiang, Amorphous Yolk-Shelled ZIF-67@Co₃(PO₄)₂ as Nonprevious Bifunctional Catalysts for Boosting Overall Water Splitting, Inorg. Chem., 2021, 60, 19.
35. Y. Ren, D. Guo, Z. Zhao, P. Chen, F. Li, J. Yao, H. Jiang and Y. Liu, Singlet Oxygen Mediated Photocatalytic Antimonite Decontamination in Water Using Nanoconfined TiO₂, Chem. Eng. J., 2022, 435, 134832.
36. H. Jiang, W. Zhang, P. Chen and Q. He, One pot Method to Synthesize a Novel La-Zr Composite with Exceptionally High Fluoride Removal Performance, J. Inorg. Organomet. Polym. Mater., 2016, 26, 285–293.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr06010a

‡ These authors contributed equally to this work.

---