Computational understanding of the coalescence of metallic nanoparticles: a mini review
Liang
Jiang†
a,
Yongxin
Guo†
a,
Zhihui
Liu
b and
Shuai
Chen
 *bc
*bc
aCollege of Automation, Wuxi University, Wuxi, 214105, China
bMaterials Genome Institute, Shanghai University, Shanghai 200444, China. E-mail: chens@shu.edu.cn
cShanghai Frontier Science Center of Mechanoinformatics, Shanghai University, Shanghai 200444, China
First published on 7th February 2024
Abstract
Metallic nanoparticles exhibit extraordinary properties that differ from those of bulk materials due to their large surface area to volume ratios. Coalescence of metallic nanoparticles has a huge impact on their properties. Remarkable progress has been made by using computational methods for understanding nanoparticle coalescence. This work aims to provide a mini review on the state-of-the-art modelling and simulation of nanoparticle coalescence. First, we will discuss the outstanding performances and coalescence behaviors of metallic nanoparticles, and list some challenges in the coalescence of metallic nanoparticles. Next, we will introduce the applications of molecular dynamics and the Monte Carlo method in nanoparticle coalescence. Furthermore, we will discuss the coalescence kinetics and mechanisms of metal nanoparticles with the same element and different elements, alloy nanoparticles and metal oxide nanoparticles. Finally, we will present our perspective and conclusion.
1. Introduction
1.1. Properties of metallic nanoparticles
Metallic nanoparticles exhibit extraordinary electronic,1 optical,2 catalytic,3 thermal,4 and magnetic properties5 that differ from those of bulk materials due to their large surface area to volume ratios. With these peculiar properties, metallic nanoparticles have been widely used in applications of solar cells,6 photodetectors,7,8 sensing,9,10 drug delivery,11etc. The properties of metallic nanoparticles are highly dependent on their shapes and size distributions, and can be modulated at the nanoscale level by tuning the nanostructures.12–15Monodisperse Pt, Pd, Au and Co particles with 10 nm diameter are stable at a temperature of more than 600 °C and have been uniformly distributed onto mixed-conducting oxide electrodes as model electrochemical cells by self-assembled nanopatterning.1 The metal catalysts activated hydrogen electrooxidation on the ceria-based electrode surface, suggesting an ideal electrode design for high-temperature electrochemical applications. A junction with an intimate interface consisting of plasmonic Ag nanoparticles and the Ag-node matrix has been synthesized via a facile one-step approach.3 The system demonstrated highly efficient visible-light photocatalytic H2 generation, outperforming most reported metal–organic framework-based photocatalytic systems.16,17
A quantitative investigation of magnetic fields generated by a cluster composed of spherical Fe3O4 nanoparticles with diameters of 30 nm ± 5 nm assembled on a dielectric non-magnetic surface has been performed.5 The results indicated that the magnetic stray field does not increase proportionally with the number of nanoparticles in the cluster, highlighting the great importance of the exact spatial arrangement of nanoparticles. The seed-mediated synthesis strategy involves adding small nanoparticle precursors into a growth solution to initiate heterogeneous nucleation. This strategy is one of the simplest and productive methodologies for synthesizing well-defined colloidal anisotropic nanostructures. Using this strategy, atomically precise gold nanoclusters, consisting of a 32-atom Au core with 8 halide ligands and 12 neutral ligands, have been generated, showing narrower size distributions and fewer impurity particle shapes.13
Based on experimental analysis and molecular dynamics simulation, monodisperse Ag nanoparticle decorated graphitic carbon nitride has been demonstrated as a decent lubricating additive of poly(phthalazinone ether sulfone ketone), which possesses reasonable friction-reducing and wear-resistant properties.18 The effects of Cu nanoparticles on frictional heating and tribological properties at various temperatures have been studied via molecular dynamics simulations.19 The results indicate that temperature distribution and surface abrasion are significantly improved by the presence of Cu nanoparticles, leading to the improvements in tribological properties. The tribological properties of Ni nanoparticles in situ prepared in rapeseed oil have been evaluated with a four-ball tribometer, and their tribomechanism has been investigated based on the characterization of the tribofilm on rubbed steel surfaces.20 The results show that Ni nanoparticles with a mass fraction of 0.3% can reduce the wear scar diameter of the steel ball by 36%.
1.2. Coalescence behaviors of nanoparticles
In practical applications, metallic nanoparticles are easily heated by the effects of electricity, light, chemical reaction, pressure, etc. It has been reported that Au nanoparticles with ∼9.6 nm radius have a strong tendency to approach and coalesce when heated to 873 K, even below their melting temperature.21 Besides, Au nanoparticles with an average diameter of 4–5 nm and a face-centered cubic (FCC) structure can form hybrid films with polystyrene, where the nanoparticle content varies from 0 to 1 wt%.4 The Au nanoparticle agglomeration deteriorates as the content increases and the interparticle distance decreases. The developed hybrid films exhibited desirable photothermal healing behavior with a photon energy source, which requires more energy with the size of defects increasing, demonstrating potential applications in functional devices with high flexibility in photothermal self-healing.Using gas-phase magnetron-sputtering aggregation experiments, Pt and Pd nanoparticles can be tuned from a growth regime with negligible nanoparticle coalescence to a coalescence regime dominated by nanoparticle-coalescence events.22 This transition has been achieved by varying both the length of the aggregation zone and the pressure difference between the aggregation and the deposition chamber. The coalescence process of the metallic glassy nanoparticles has been investigated at the atomic scale, where the viscosity of the nanoparticles through the coalescence process was measured by an in situ method.23 The results indicated that the nanoparticles possess fast dynamics at room temperature, and their viscosity exhibits a power law relationship with their size.
Coalescence of two Au nanoparticles has been observed at room temperature under a transmission electron microscope (TEM) as induced by electron beam irradiation.24 It was shown that, during irradiation, adjacent Au nanoparticles migrated close to each other. Once they came into contact, fast and massive atom transportation occurred with the creation of a neck region. On further irradiation, the two contacted nanoparticles rotated to align their crystal orientations and merged into a larger single-crystalline nanoparticle gradually. The rotation and coalescence process demonstrated an intriguing surface nanowetting ability and soft mode of atomic vibration at room temperature as driven by the beam-induced instability on non-uniformly contacted nanoparticles, which have been neglected in many existing theoretical and experimental studies.
Making good use of the coalescence and growth of metallic nanoparticles is a decent approach for bottom-up fabrication (i.e., self-assembly) of micro- and nano-sized devices.25–27 For example, the phenomenon that plasmon excitation can convert isotropic nanoparticles into anisotropic nanoprisms has already been developed into a general synthetic technique since its discovery in 2001.28 Plasmon-driven high yield conversion of Au nanoparticles into nanoplates with iodine as the inducer has been achieved.25 Interestingly, the morphology conversion has been proved as a hot hole-controlled coalescence-dominated growth process. Their results indicated that a controllable plasmon-driven nanoparticle coalescence is able to produce well-defined anisotropic metal nanostructures.
Large-scale self-assembly of monocrystalline Au nano-islands with a tunable size and separation has been achieved, paving their way for applications as efficient localized surface plasmon resonance devices.26 In their work, highly homogeneous centimeter-sized Au metasurfaces have been fabricated by one-step deposition and in situ coalescence of hot nanoparticle aerosols into a discontinuous monolayer of highly faceted monocrystals. Using a liquid cell transmission electron microscope, CoO nanoparticle rings formed via nucleation and growth tracing the perimeter of liquid droplets on the SiNx solid substrate.27 It was found that the junction of liquid droplets with a solid substrate is an attractive site for nanoparticles. Besides, coalescing droplets pushed the nanoparticles to the perimeter of the new droplet, and nanoparticles on top of the droplets rolled off toward the perimeter.
1.3. Motivation for this review on the coalescence of nanoparticles
It is obvious that metallic nanoparticles tend to coalesce when treated with electricity, light, chemical reaction, pressure, etc. in practical applications, resulting in the variation of nanoparticle distribution and morphology. It is well known that the distribution and morphology of nanoparticles have a huge impact on their electronic, optical, catalytic, and thermal properties, hence affecting their practical applications. Having a good knowledge of the coalescence of nanoparticles will undoubtedly guide the design and synthesis of metallic nanoparticles. Hence, the coalescence kinetics and mechanism of metallic nanoparticles are of great significance for both academic and industrial research and development. This is the motivation for this review to summarize the state-of-the-art research studies on the computational understanding of the coalescence of metallic nanoparticles.2. Computational methods
Direct experimental observations and measurements of coalescence of metallic nanoparticles at the nanoscale are challenging. Therefore, simulation methods at the nanoscale or atomic scale are essential to understand the coalescence kinetics and mechanisms of metallic nanoparticles. Atomistic simulations can not only capture the structural features of metallic nanoparticles but also reveal the coalescence mechanisms in detail. Molecular dynamics (MD) and Monte Carlo (MC) methods are typical atomistic simulation approaches for investigating the coalescence of metallic nanoparticles.2.1. Molecular dynamics simulations
Both MD simulation and density functional theory (DFT) calculations are computational approaches capable of simulating the movements of atoms or molecules. As compared with DFT calculations,29–32 MD simulation is suitable for longer times and larger-size scales.18,19,21 In MD simulation of metallic nanoparticles, the metal atoms in the nanoparticles interact with each other and move to energetically favorable sites, which is able to reproduce the dynamic evolution of the metallic system according to experimental conditions. The forces exerted on the metal atoms and the system energies are calculated according to the interatomic potentials. The trajectories of metal atoms are updated via solving Newton's equations of motion for each atom numerically.In MD simulation, the initial modelling of nanoparticles normally consists of the configuration of a single nanoparticle and the contact state setup between the nanoparticles. A spherical structure is considered to be a straightforward way to characterize the nanoparticles, since most of the nanoparticles are presented with a spherical feature in practice and the diameter change of the spherical nanoparticles could be utilized to depict the evolving process of the nanoparticles.21 At certain temperatures, surface atoms of the spherical nanoparticles are found to flow toward the neighbouring nanoparticles, which finally results in the approach and coalescence of nanoparticles. A polyhedral structure was also found to be adopted to simulate the evolution of the coalescence between nanoparticles.22 With the large scale of the atomic amount and long scale of the simulation time, the coalescence behavior of two truncated octahedral nanoparticles was clearly captured. Given the fact that the displacement of surface and subsurface atoms is easier to achieve than the occurrence of diffusion events in the inner part of the aggregate, the shape equilibrium of the coalescing aggregate can be well attained, while the chemical ordering is quite slow even at very high temperatures.
It has been acknowledged that the interatomic potential plays an important role in MD simulation, since the trajectory and the physical properties of atoms depend entirely on how the interaction between atoms are incorporated. Accordingly, great efforts have been made to develop the interatomic potentials to interpret the sophisticated interactions among atoms, and a series of models have been proposed, including two-body potentials, embedded-atom models for metals and bond-order potentials for covalently bonded systems. The Lennard-Jones potential,33i.e., the L-J potential, is a classical pair potential to describe the interactions between atoms with a closed valence shell. This potential simplifies the statistical mechanical formalism regarding the calculation of thermodynamic properties, and it is supposedly the most used one in MD simulations. The expression of the L-J potential could be written as follows:
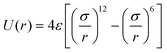 | (1) |
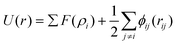 | (2) |
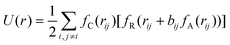 | (3) |
Besides the above empirical potentials, machine learning (ML) potentials have also been developed with the rapid development of artificial intelligence technology.43–46 For example, neural network ML potentials developed from the DeepMD-kit package (deep potentials), which are trained from a database constructed with first-principles calculations, have been demonstrated to be accurate in predicting the structural and dynamic properties of Au,47 Ti,48 and Fe49 metals, and the AgAu50 alloy. Besides, ML potentials trained using the Gaussian approximation potential framework or the spectral neighbor analysis potential approach have also proven to possess excellent accuracy.
Common integration methods to solve Newton's equations of motion are the Verlet integrator,51 Leapfrog integrator,52 and Velocity-Verlet integrator.53 The Verlet integrator only considers the position information and does not require the velocities. Only a single force evaluation per integration cycle is taken in the Verlet integrator, providing good numerical stability, as well as other properties that are important in physical systems. The Leapfrog integrator evaluates velocities at the midpoint of the position evaluations; hence it reduces the numerical error problem of the Verlet algorithm. The Velocity-Verlet integrator is similar to the Leapfrog integrator, except that the velocity and position are calculated at the same value of the time variable.
The thermodynamic ensembles are a specific variety of statistical ensembles that describe the thermodynamic equilibrium, where the macroscopic properties can be calculated from the average of every possible microscopic state. There are several different thermodynamic ensembles and one could choose an ensemble based on the desired imposed conditions along with the corresponding desired simulation output. In a microcanonical ensemble (NVE), the system maintains a constant number of atoms (N), volume (V) and energy (E). It corresponds to an adiabatic process with no heat exchange. A microcanonical MD trajectory can be viewed as an internal exchange of potential and kinetic energies, with the total energy being conserved. In an isothermal-isobaric ensemble (NPT), the number of atoms (N), pressure (P) and temperature (T) are kept constant. In this ensemble, the thermostat and barostat algorithms are required to maintain the temperature (T) and pressure (P) at a specified value, respectively. Such an ensemble corresponds to laboratory conditions open to ambient temperature and pressure. In a canonical ensemble (NVT), the number of atoms (N), volume (V) and temperature (T) are fixed. It is also called the constant temperature MD. Here, only a thermostat algorithm is required, which could maintain the constant average temperature of the simulated system.
2.2. Monte Carlo simulations
The Monte Carlo method is another commonly used approach to simulate many physical and chemical processes, such as the mixing or demixing of metallic nanoparticles which can be the end product of the diffusion and coalescence of different atomic clusters.54,55 Hybrid MC and MD simulations are always implemented by performing MC swaps of atoms following the Metropolis algorithm56 after short sequences of MD steps in the canonical ensemble, where the MD temperature is also employed in the Metropolis algorithm to determine the occurrence probability of the MC swap. The occurrence probability is calculated as:54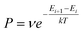 | (4) |
Kinetic Monte Carlo (kMC) is also able to simulate the time evolution of nanoparticles.57 The kMC algorithms are typically classified into two categories: one is rejection-kMC (rkMC), and the other one is rejection-free-kMC (rfkMC).58,59 A rfkMC algorithm, often called kMC, is normally utilized to simulate a process that occurs among states with calculated transition rates.60 Therefore, it is of great importance to determine the transition states and formulate the associated rates, serving as the inputs for the kMC model. At each given state, i, kMC simulation has to identify all the possible states, j, that may be transited into at the next step. The transition rate is calculated as:61
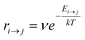 | (5) |
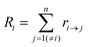 | (6) |
To determine which next state, j, is to be chosen for the transition from the current state, i, a random number U1 in the range (0,1) is generated. The state, j, that satisfies the following condition is selected:
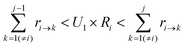 | (7) |
Meanwhile, the time of this transition can be calculated by using
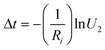 | (8) |
As compared with MD simulation, kMC simulation is capable of studying the process in a longer-time and larger-size scales. For example, MD simulation is only able to study the coalescence of several metallic nanoparticles, while kMC simulation is able to reproduce the deposition, diffusion and coalescence of many metallic nanoparticles to grow into nanoparticle films.62
3. Coalescence kinetics and mechanisms
Whether trying to prevent or exploit the coalescence of metallic nanoparticles, it is essential to have a good understanding of the kinetics and mechanisms of nanoparticle coalescence. In recent years, substantial research has been conducted to study the coalescence of metallic nanoparticles. Generally, there are three categories of coalescence according to the element type of metallic nanoparticles: (1) the coalescence of metal nanoparticles with the same element; (2) the coalescence of metal nanoparticles with different elements; (3) the coalescence of alloy nanoparticles or metal oxide nanoparticles.3.1. Coalescence of metal nanoparticles with the same element
Below the melting temperature, Au nanoparticles tend to approach and coalesce. For example, Ingham et al. reported a real-time in situ observation on the coalescence of Au nanoparticles at 250 °C and presented the aggregation and subsequent grain growth of Au nanoparticles using synchrotron small-angle X-ray scattering (SAXS) and X-ray diffraction (XRD).63 They also elucidated a more complete picture of the coalescence mechanism of metal nanocrystals by following both the particle and crystallite size dynamics (Fig. 1a and b). The results show that the grain growth stage takes significantly longer time than the particle aggregation stage.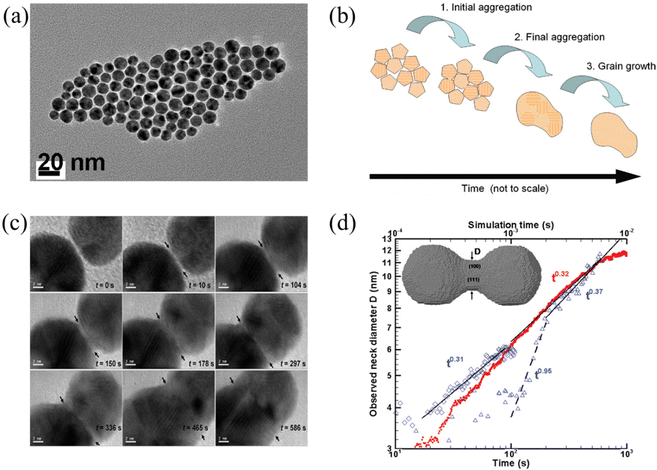 | ||
| Fig. 1 (a) TEM image of Au nanoparticles. (b) Schematic diagram showing the mechanisms of coalescence.63 These figures have been adapted from ref. 63 with permission from American Chemical Society, Copyright 2011. (c) Coalescence of two Au decahedral nanoparticles in different time. (d) Evolution of the neck diameter with time, where the experimental data are shown by blue, open symbols with time scale on the lower horizontal axis (observation 1 on diamonds, observation 2 in triangles), and the simulation data are in red solid dots with time scale on the upper horizontal axis.64 These figures have been adapted from ref. 64 with permission from American Chemical Society, Copyright 2009. | ||
Lim et al. observed the growth rate of the neck that joined two Au nanoparticles during coalescence (Fig. 1c) and made a comparison with both continuum theory and atomistic kMC simulations (Fig. 1d).64 Eventually, they found good agreement between the observations and the simulations but not with the classical continuum model due to the faceted nature of the particles. A power law fit in Fig. 1d demonstrates that the experimentally observed late-stage neck growth process has an exponent equal to 0.31 in one case (observation 1) and 0.37 in the other (observation 2), while the simulated process has an exponent of 0.32. For faceted particles, the ability of the neck to capture diffusing material is dependent on parameters (the size, composition, and roughness) that change discontinuously. This implied that the faceted structure of nanoparticles plays a crucial role in their stability to agglomeration and coalescence.
Arcidiacono et al. investigated the influence of initial temperatures and starting radii on the coalescence process of two Au nanoparticles in vacuum, with the help of MD simulations.65 They found that classical ‘neck’ theories can predict the first stage of the sintering process, when taking into account the size dependence of the melting temperature. For particles that are larger than ≈20 Å, the grain boundary diffusion was dominant in the coalescence of two nanoparticles. The MD simulations and the predictions of a macroscopic phenomenological model showed good agreement at initial temperatures near the corresponding melting point, except for the lower temperature case.
Since typical sintering of Au nanoparticles requires heating of the substrate to overcome the activation barrier for gold atom movement, Grys et al. developed a room temperature chemical process to efficiently construct Au nanoparticle films with uniform nanogaps that can be used to sequester and detect small molecules with high levels of specificity.66 In this novel sintering method, a multilayer aggregate of Au nanoparticles was prepared with a two-phase chloroform–water system, and was deposited onto substrates as needed. With a three-step process, including the definition of the nanogap size with an initial scaffolding, stripping of the scaffold molecules and stabilization of the gaps with scaffolding ligands, the nanogap spacing and facet chemistry can be fully controlled and fine-tuned. The results revealed that this method gives a reconfigurable and sensitive SERS substrate with excellent sensing capability for compounds in solution and vapors.
To understand the dominant factors of the catalytic activity and product selectivity of Au nanoparticles, Yue et al. employed in situ TEM to explore the evolution of Au nanoparticle catalysts during CO2 hydrogenation to methanol at 260 °C under ambient pressure.67 During the catalytic reactions, the surface reconstruction and shape oscillation occurred in the Au nanoparticles. The first-principles calculations indicated that the adsorption of CO2 is the main factor inducing the coalescence of Au nanoparticles, and CO and/or H2O adsorption generated by the CO2 hydrogenation cause the oscillation of the nanoparticle shape. With in situ TEM, Bekarevich et al. studied gold loading phenomena in carbon nanotubes, supposedly caused by the coalescence of gold nanoparticles.68 They found that large nanoparticles always absorb smaller nanoparticles, leading to the elongation of the encapsulated nanowire in the absence of a strong thermal gradient. In addition, the elongation process is governed by the volume ratio of encapsulated to unloaded Au.
Guo et al. proposed a new mechanism for the coalescence of Au nanoparticles in water without ligand detachment, i.e., the aggregation of the nanoparticles is induced by the twined hydrophobic chains of the ligands rather than the hydrophilic carboxyl tails.69 During coalescence, the exposed surface atoms attached to form the neck, and extended with the atomic rearrangement of the contact interface to merge the nanoparticles. Lange et al. studied the dislocation-mediated alignment processes and deformation twinning during the Au nanoparticle coalescence at low and high temperatures using MD simulations and TEM.70 They observed that rigid body rotations immediately occurred following attachment during low-temperature (500 K) simulations and low-temperature (∼315 K) TEM beam heating experiments. However, minimal rigid body rotations were observed during or immediately following attachment in high-temperature (1100 K) simulations due to the enhanced diffusion at the particles’ interface. The rotation was eventually induced by the {111} slip on planes parallel to the neck groove.
Palasantzas et al. studied the coalescence of Co nanoparticles on carbon-coated (10 nm thick) Cu grids and found that Co nanoparticles that contact with the substrate are immobile, whereas those on top of other Co particles rearrange themselves during high-temperature annealing and further coalesce.71 Lümmen et al. investigated the coalescence of Fe clusters over the course of their growth under an inert-gas atmosphere by MD simulations.72 It was found that the relaxation of the cluster shape shows an exponential decay at elevated temperatures and exhibits a regular atomic structure at lower temperatures. The transitions of the shapes are affected by the heat removal and therefore slower in the presence of a carrier gas than in a constant-energy ensemble. Ding et al. reported that the coalescence of Fe nanoclusters occurs at the temperatures lower than the cluster melting point.73 They found that the difference between coalescence and melting temperatures increases with decreasing cluster size.
Yeadon et al. explored the sintering of Cu nanoparticles on {001} copper substrate using an in situ ultrahigh vacuum TEM and demonstrated that Cu nanoparticles reorient to the same orientation as the substrate by a classical mechanism involving neck growth by surface diffusion and migration of the grain boundary upon annealing.74 Liu et al. studied the coalescence kinetics and microstructure evolution of Cu nanoparticles sintering on substrates at low temperature on a special model containing two substrate and multiple particles in between.75 It was found that, at low temperature, the dominating sintering mechanism is plastic flow caused by dislocation production and motion. They found that the dislocation-mediated alignment process is pronounced due to the pinning effect of upper and lower substrates. Furthermore, smaller-size models usually contain higher shrinkage ratio, smaller pores, more drastic crystal transformation and dislocation evolution in each stage. Buesser et al. studied the coalescence of Ag nanoparticles with various morphologies in vacuo between 400 and 1000 K by MD simulations using the EAM potential and demonstrated the formation of new crystal domains during Ag particle sintering for the first time.76 They found that the coalescence of nanoparticles is dominated by surface diffusion whereas it transitions toward plastic flow sintering near their melting point and the sintering rate of straight nanoparticle chains is much slower than that of more compact structures.
Grammatikopoulos et al. reported the MD studies on the coalescence of two or more Ta nanoparticles and obtained the parameters that influence the sintering according to their importance.77 A qualitative understanding of the mechanisms that dominate Ta nanoparticle coalescence is obtained, from simple nanoparticle reorientation in order to achieve epitaxial configuration, to atomic adsorption, neck formation, twinning within the nanoparticles and full consolidation into a single, larger nanoparticle. Temperature is identified as a dominant factor for the resultant configuration, and relative orientation (degree of crystallinity) can also have a strong impact in a more stochastic manner. Therefore, the data acquired can be used as the input for the creation of a general, element-insensitive, theoretical model of nanoparticle coalescence. Grammatikopoulos et al. also studied the mechanisms that govern Pb nanoparticle coalescence with the support of high-resolution TEM.78 The driving force for coalescence was confirmed to be surface energy minimisation, associated with dangling bond density and distribution. They also found that atomic rearrangements triggered a crystallisation wave propagating through the amorphous nanoparticles, leading to mono- or polycrystalline FCC structures.
This section reviewed the research works on the coalescence of metal nanoparticles with the same element in literature. Most research studies have focused on the coalescence of Au nanoparticles, which have been discussed initially. Interestingly, coalescence of Au nanoparticles also occurs in CO2 or water. Subsequently, research performed on other metals is summarized, including Co, Fe, Cu, Ag, Ta, Pb, etc. Below the melting temperature, surface diffusion is the dominant mass transport mechanism for nanoparticle coalescence. Typically, the surface atoms diffuse and nanoparticles form a neck initially, followed by relaxation to energetically favorable shapes. Neck formation and growth are typical features during the coalescence, which are affected by the nanoparticle size and roughness.
3.2. Coalescence of metal nanoparticles with different elements
Among a wide range of bimetallic nanoparticles, Au–Ag nanoparticles have shown great potential in the field of optics, biosensors and catalysis. Jia et al. studied the structural and thermal stability of single Au@Ag nanoparticles with different sizes and their arrays by MD simulations.79 They found that the pre-melting processes start from the surface region for both the single nanoparticles and their arrays. The melting points of Au@Ag core–shell bimetallic nanoparticles showed a feature of non-monotonicity with increasing core size at a fixed nanoparticle size. José-Yacamán et al. considered the contributions to the nanoparticle coalescence process from three points of view: these include the factors influencing nanoparticle diffusion, the nanoparticle properties relevant to diffusion, and the overall coalescence mechanism.80 The experimental evidence demonstrated the significant role of the nanoparticle liquid-like surface layer in the coalescence process based on HRTEM analysis.Goudeli et al. investigated the effects of temperature and initial particle morphology on the sintering rate, aggregation, and structure of coalescing Au–Ag nanoparticles by MD simulations.81 They observed that the sintering characteristic time is not affected by the facet orientation (Fig. 2a). It was also found that sintering equally sized Ag and Au nanoparticles results in segregated nanostructures with an Ag-enriched surface, and that the Ag surface fraction is increased with the increase of temperature (Fig. 2b). When Au nanoparticles coalesce with smaller (i.e., Ag diameter, dp,0,Ag, = 2 nm, and Au diameter, dp,0,Au = 4 nm) or larger (i.e., Ag diameter, dp,0,Ag, = 4 nm, and Au diameter, dp,0,Au, = 2 nm) Ag particles, Au embeds into Ag or a patchy Ag layer forms at the Au particle surface (Fig. 2c). Most importantly, XRD patterns during particle sintering or coalescence of Ag and Au were obtained by MD, which offer a possibility for distinction of the alloyed state of bimetallic particles (Fig. 2d).
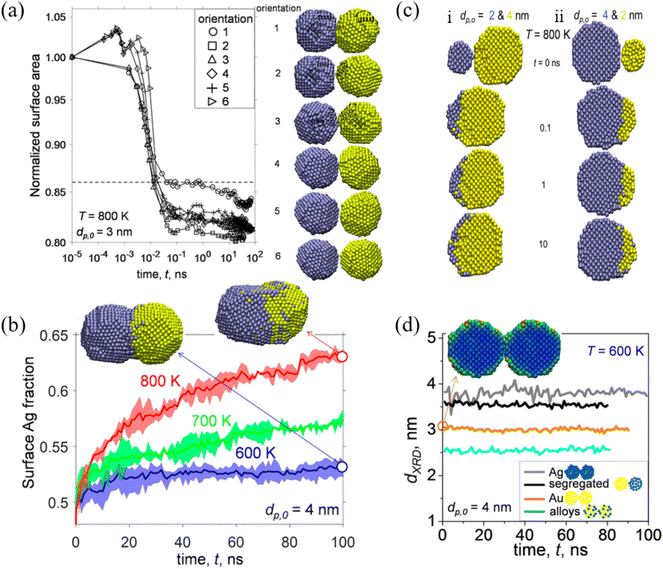 | ||
| Fig. 2 (a) Evolution of normalized surface area by coalescence of two segregated Ag−Au nanoparticles with diameter (dp,0) = 3 nm at temperature (T) = 800 K. (b) Evolution of the surface Ag fraction of coalescing Ag–Au segregated nanoparticles with dp,0 = 4 nm at T = 600 (blue line), 700 (green line), and 800 K (red line). (c) Cross-section of unequally sized Ag (blue) and Au (yellow) nanoparticles of (i) dp,0,Ag = 2 and dp,0,Au = 4 nm and (ii) dp,0,Ag = 4 and dp,0,Au = 2 nm coalescing at T = 800 K and t = 0, 0.1, 1, and 10 ns. (d) Evolution of the XRD diameter of Ag (gray lines), Au (orange lines), Ag–Au segregated (black lines), and alloyed (blue lines) nanoparticles with dp,0 = 4 nm coalescing at 600 K.81 These figures have been adapted from ref. 81 with permission from American Chemical Society, Copyright 2017. | ||
Chandross et al. developed a phenomenological model to understand the formation of a core–shell structure from the energetics of formation by MD and MMC simulations, particularly with the radii of the initial particles taken into account.82 This model indicated that relatively smaller particles of Cu and larger particles of Ag are the most energetically favorable to form a core–shell structure. This model can be used for directing synthesis routes for nanoparticles, as well as for choosing specific metallic species which are more or less likely to form such core–shell structures.
By scanning transmission electron microscopy (STEM) and electron energy-loss spectroscopy (EELS), Grammatikopoulos et al. investigated the coalescence of Ag−Cu nanoparticles and observed a remarkable difference in the shape of nanoparticles belonging to Ag- and Cu-rich samples.83 Furthermore, they employed MD and MMC simulations to demonstrate that Janus or Ag@Cu core/shell metastable structures cannot occur as a result of nanoalloy segregation. As shown in Fig. 3a, Cu@Ag core/shell structures were formed in the Cu-rich nanoparticles. However, the formation of Cu precipitates led to onion-type multi-shell structures, i.e., Ag@Cu@Ag, in the Ag-rich nanoparticles. They also found that Ag-rich configurations experienced faster or more pronounced coalescence than the Cu-rich counterparts (Fig. 3b). Besides, the heteroepitaxial diffusivity along various surfaces of both Ag and Cu nanoparticles was compared (Fig. 3c), and the differences between the sintering mechanisms of Ag- and Cu-rich nanoparticle compositions were examined. They then proposed controlled nanoparticle coalescence as a method to design unique, patterned core@partial-shell structures of mixed nanoparticles.
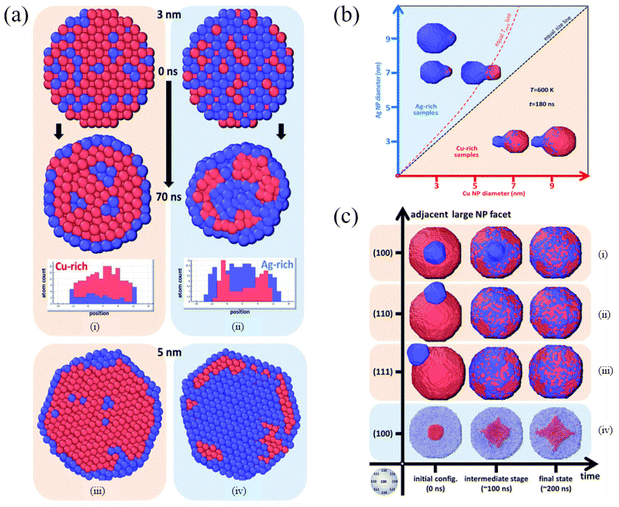 | ||
| Fig. 3 Cross-section of (a) Cu-rich (i and iii) and (b) Ag-rich nanoparticles (ii and iv), 3 nm in diameter, before and after annealing at 700 K for 70 ns. Red and blue spheres represent Cu and Ag atoms, respectively. (b) Final configurations after 180 ns of MD runs of pairs of nanoparticles sintering at 600 K. (c) Time evolution of the coalescence process at 800 K of systems comprising a 9 nm Cu nanoparticle and a 3 nm Ag nanoparticle adjacent to (100), (110) and (111) facets (i–iii, respectively) and a 9 nm Ag nanoparticle with a 3 nm Cu nanoparticle adjacent to a (100) facet (iv).83 These figures have been adapted from ref. 83 with permission from Royal Society of Chemistry, Copyright 2016. | ||
Singh et al. explored the synthesis and growth of Si−Ag hybrid nanoparticles using gas-aggregated co-sputtering experiments and MD simulations.84 The simulation results showed that Si and Ag nanoclusters nucleate separately from the corresponding supersaturated vapors, then grow and coalesce into larger nanoparticles with 15 ± 8 nm diameter, and form stable conjoined ensembles once the temperatures have reduced sufficiently to allow the formation of a stable structure. Henz et al. studied the energetic reaction of Ni and Al particles at the nanometer scale via MD simulations.85 The simulation results indicated that the reaction time is inversely related to nanoparticle size but the adiabatic temperature decreases with decreasing nanoparticle size. Besides, nanoparticle size and surface energy are important factors in determining the adiabatic reaction temperature for both systems at nanoparticle sizes of less than 10 nm diameter.
Li et al. studied the thermodynamic evolution of Ni and Au nanoparticles with different ratios of Au and Ni, as listed in Fig. 4a, through MD simulations.86 The coalescence processes of Au atoms strongly determine the final morphology of the particles, which can be used to design core–shell structure Au@Ni nanoparticles. As shown in Fig. 4b, Au atoms diffused along the surface of Ni for NP1, NP2, NP3. For NP4, NP5, NP6, and eventually Au and Ni formed alloy nanoparticles (Fig. 4bi). For larger Au particles (NP7, NP8), Au atoms encapsulated completely due to Au atom segregation (Fig. 4bi). The pair distribution function, denoted as g(r), of Au atoms (Fig. 4bii) and Ni atoms (Fig. 4biii) suggested that diverse melting modes occur during the continuous heating of Au-Ni nanoparticles.
 | ||
| Fig. 4 (a) Initial configurations of Ni-Au nanoparticle structures with different atomic ratios. (b) Cross sections through the Au-Ni nanoparticles at temperature 1173 K (i) and pair distribution function of Au atoms (ii) and Ni atoms (iii) at temperatures 1173 K, Au and Ni atoms are colored in yellow and gray respectively.86 These figures have been adapted from ref. 86 with permission from Springer Nature, Copyright 2021. | ||
Langlois et al. generated the bimetallic Cu@Ag core–shell nanoparticles via pulsed laser ablation with various chemical compositions and observed that the structure transformed to Janus-like or quasi-Janus when the amount of Ag in a particle was large.87 They reported two types of segregated configurations: a core–shell configuration for shell thicknesses under 3–4 nm, and a quasi-Janus configuration beyond a critical Ag shell thickness of 3–4 nm. Farigliano et al. studied the coalescence between small Au and Co clusters via well-tempered metadynamics to yield a core–shell structure, choosing the center of mass distance and gyration radius as their collective variables.88 It was reported that the coalescence most likely proceeds via the deformation of the core material, which is manifested by the system residing in regions with large gyration radii.
Pressure-assisted sintering (PAS) has recently gained considerable attention, since it can generate nanoparticle structures with improved mechanical properties and increased density. Using Ag-coated Cu material as a representative system, Kim and Chung conducted a detailed comparative investigation on the normal thermal sintering and PAS processes of the coalescence of nanoparticles by MD simulation.89 The results showed that the void fraction of the nanoparticle structures converges to the lower bound with the increase in sintering temperature and the coalescence of the nanoparticles is found to be more effective when pressure is applied. However, the amount of coalescence promoted by external pressure decreases substantially after a certain level and was rapidly saturated. Moreover, it was found that the surface diffusion at high temperature dominantly contributes to sintering, while both core and shell atoms contribute actively in the sintering regardless of pressure. By comparing the atomic trajectories of the core and shell materials during coalescence, it is indicated that the sintering mechanisms promoted by heat and pressure are clearly different.
In another work based on MD simulation, Zhang et al. investigated the sintering mechanisms of Cu–Ag core–shell nanoparticles, as well as the effects of shell thickness on sintering behavior.90 It was found that, compared to the sintering of Ag nanoparticles, the interface of Cu atoms plays an important role for the evolution of dislocation and stacking faults in the coalescence of Cu–Ag core–shell nanoparticles, and the surface diffusion can be activated and gradually dominates the sintering process as the temperature increases. Besides, the change of shell thickness severely affects the sintered structure. The shell with amorphous structures actively participates in the sintering process when the shell thickness is 0.5 nm. As for nanoparticles with 1 nm and 1.5 nm shells, the dislocation loops inside were involved in the sintering process. And if the nanoparticles were covered with a thicker shell, the defect on the interface brought by Cu core does not contribute to the sintering process directly.
Baletto et al. proposed a three-shell A–B–A structures (Ni/Ag, Cu/Ag, and Pd/Ag) by inverse deposition of B atoms above A cores.91 The A–B–A structures can be grown depending on the structure of the initial A core and on temperature. The growth of the intermediate B shell was triggered as the most favorable position for isolated B impurities inside A clusters, which was located one layer below the cluster surface. It provided novel possibility for controlling the chemical ordering in structures at the nanoscale level.
This section summarized the research works on the coalescence of metal nanoparticles with different elements in the literature. Most research studies have concentrated on the coalescence of Au–Ag nanoparticles or those composed of Au/Ag for the potential applications in the field of optics, biosensors and catalysis. Using the coalescence of metal nanoparticles with different elements to synthesize bimetallic nanoparticles is the typical objective of these research studies, such as A–B or A–B–A core–shell structures. Even though bimetallic core–shell structure with nanoparticles is thermodynamically unstable, sintering at relatively low temperatures can give rise to metastable structures, which eventually can be stabilized by subsequent quenching.
3.3. Coalescence of alloy nanoparticles or metal oxide nanoparticles
By adding Au during Ag nanoparticle synthesis, Sotiriou et al. systematically studied the plasmonic performance of the AgAu nanoalloy, including the effect of plasmonic resonance, release of Ag+ ions and cytotoxicity.92 They found that, unlike the mechanically mixed AgAu samples, the presence of Au in the AgAu alloy nanoparticles minimizes oxidation, which eventually decreases the antibacterial activity and toxicity of Ag. Akbarzadeh et al. studied the coalescence process of AgAu alloy nanoparticles in vacuum and on different carbon-based supports (Fig. 5a).93 The simulated results revealed that the interaction between the metallic cluster and the support surface (Fig. 5b) is relatively small, as compared to the metal–metal interactions (Fig. 5c), and the metal–metal energy of nanoalloys decreases drastically at the beginning of the coalescence and almost remains the same as the coalescence proceeds. Besides, it has been suggested that the support greatly affects the energy of clusters during the coalescence process, because the supported clusters have less energy and are stable than the clusters in vacuum.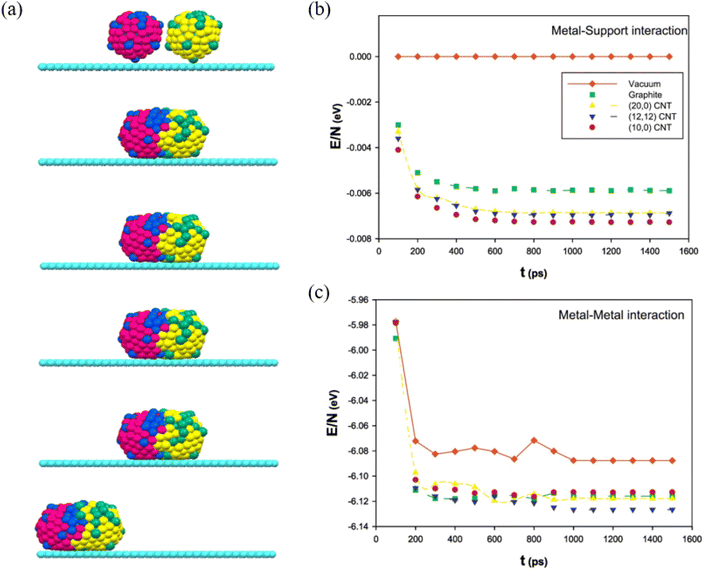 | ||
| Fig. 5 (a) The snapshots of the icosahedral AgAu nanoalloys supported on graphite after 100 ps, 200 ps, 500 ps, 1 ns, and 10 ns. (b) The metal–support and (c) The metal–metal energies of AgAu nanoalloys supported on the different surfaces during the coalescence process.93 These figures have been adapted from ref. 93 with permission from Elsevier, Copyright 2017. | ||
Lu et al. studied the thermal interactions of Cu and Ag nanoparticles using in situ STEM analysis and found that the Cu and Ag nanoparticles tend to form a Cu-core and Ag-shell structure with temperature between 150 and 300 °C, with Ag nanoparticle wetting the Cu nanoparticle on the Cu {111} surface at multiple locations followed by the diffusion of Ag atoms on the Cu surface.94 Calculations performed with the MMC algorithm, together with the experimental observations, indicated that the surface energy of Cu is much higher than that of Ag, while that of the Cu atoms is smaller, leading to their preferential location inside the core. Williams et al. developed an EAM potential for pure Ag by fitting to experimental and first-principles data, with impressive accuracy describing the properties of Ag.95 Combining with an existing EAM potential for Cu, they reconstructed the entire Cu–Ag phase diagram with MC simulations, which demonstrated satisfactory quantitative agreement with experiments. This concluded that an EAM potential fit accurately to experimental and first-principles data at 0 K can be transferable to high temperatures and can predict a simple binary phase diagram in reasonable agreement with experiments.
With an atomistic model developed within the second-moment approximation to the tight-binding model, Bochicchio et al. investigated the relation between geometry and chemical ordering in determining the nanoparticle configuration for a series of weakly miscible systems, including AgCu, AgNi, AgCo, and AuCo.96 They demonstrated that the shape and the placement of the core in the core–shell nanoparticles are strictly correlated to the overall geometric structure of the nanoparticle itself, and off-center asymmetric cores are dominant as lowest-energy structures in crystalline and decahedral motifs, while centered cores are considered for metastable configuration in icosahedral nanoparticles strongly depending on temperature. Using nanothermodynamics, Guisbiers et al. studied the phase diagrams of various polyhedral nanoparticles at sizes of 4 and 10 nm, revealing that the congruent melting point of the nanoparticles is shifted with respect to both size and composition (Fig. 6a–c).97 They suggested that segregation reveals Au enrichment at the surface of the nanoparticles (Fig. 6d), and the Cu-core/Au-shell decahedron is predicted to be the most stable structure for AuCu nanoparticles for the lowest formation energy, which was confirmed with TEM observations and MD simulations.
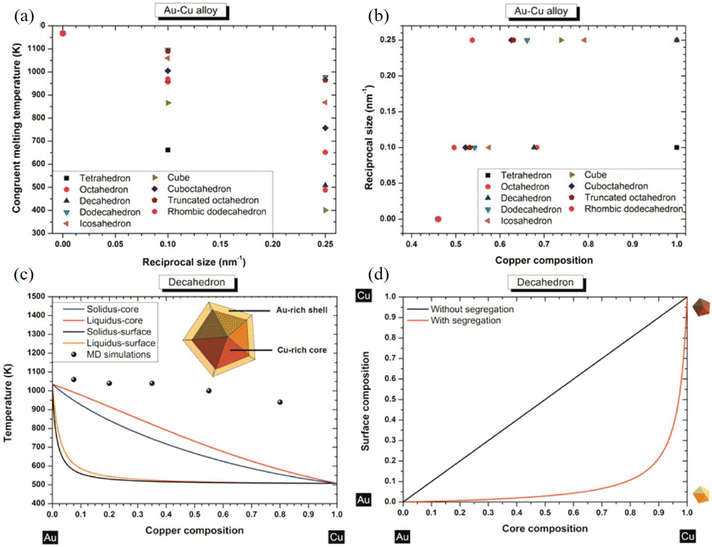 | ||
| Fig. 6 (a) Congruent melting point versus size for all the investigated shapes. (b) Congruent melting point versus composition for all the investigated shapes. (c) Phase diagram of an AuCu decahedron having 4 nm side length with and without segregation. The inset indicates a schematic cross-side view of the segregation effect into the AuCu decahedron particle. (d) Surface composition versus core composition for a AuCu decahedron having 4 nm as length side without/with segregation.97 These figures have been adapted from ref. 97 with permission from American Chemical Society, Copyright 2014. | ||
Sluiter et al. carried out the ab initio calculations to study the phase stability of superstructures based on the FCC lattice in the AuPd and AgPt alloy systems.98 They declared that, in the AuPd alloy system, compounds with the UPb prototype (Nr 40) structure are predicted to be the most stable phase, even though the experimental verification for this structure is still lacking. In the AgPt alloy system, the ground state analysis suggested that the L11 structure is predicted as the only stable compound at ambient temperature, while at very low temperature there may be a marginally stable Ag3Pt phase. Using a modified magnetron-sputtering system, Bohra et al. synthesized the NiCr alloy nanoparticles and investigated the correlation between the structures and magnetic properties of these nanoparticles.99 Direct in situ TEM and EDX analysis showed the occurrence of Cr surface segregation and precipitation into Cr satellites in the NiCr nanoparticles upon annealing. They found that the segregation of nonmagnetic Cr upon annealing can decouple magnetic nanoalloys and hence weaken their magnetic properties. Both the MD and MMC simulations revealed that it is energetically favourable for the Cr atoms to stay on the surface, resulting in the Cr segregation, and the internal stress could be released upon the Cr segregation.
Nelli et al. tuned the coalescence of PtPd alloy nanoparticles with ∼5 nm diameter from a growth regime with negligible coalescence to a coalescence-dominated regime using gas-phase magnetron-sputtering aggregation experiments.22 Furthermore, they interpreted their experimental results with MD simulations on similar-sized nanoparticles at different temperatures (500 K–700 K) and identified four different procedures when coalescence proceeds to equilibrium. These procedures occurred on a hierarchy of clearly separated time scales: (1) alignment of atomic columns; (2) alignment of close-packed atomic planes; (3) equilibration of shape; (4) equilibration of chemical ordering.
Ogata et al. investigated the stability of surface structure and space-charge distribution in free anatase and rutile nanoparticles using a variable-charge interaction potential in which atomic charges vary dynamically depending on their environment.100 It was found that the dynamic charge transfer enhances atomic diffusion in surface regions of nanoparticles at 1400 K, whereas it creates additional repulsive interparticle force through formation of a double-charge surface layer in each nanoparticle. Besides, the MD simulations also suggested that the sintering of two anatase nanoparticles is significantly promoted by the enhanced surface diffusion due to dynamic charge transfer at high temperature. Alimohammadi et al. performed MD simulations to study the sintering of nanocrystalline TiO2 with symmetric and asymmetric Wulff shapes in vacuum.101 They demonstrated that anatase nanocrystals aggregate with certain preferred orientations in vacuum, which is driven by the electrostatic forces between under-coordinated atoms on the edges between nanocrystal facet. Nevertheless, the aggregation of anatase nanocrystals rarely occurs along the direction of dipole even when the permanent dipole moment is as large as 250D, implying that higher order multipole moments are the driving force for the preferential alignment.
Buesser et al. conducted a series of MD simulations to study the sintering of 2–4 nm rutile TiO2 nanoparticles to full coalescence at 1500–2000 K.102 The simulations showed that highly mobile ions from the particle surface fill in the initially concave space between nanoparticles via surface diffusion and the final, fully coalesced, spherical-like particle with minimal displacement of inner Ti and O ions forming via grain boundary diffusion. They also revealed the significance and sequence of these two sintering mechanisms (surface diffusion and grain boundary diffusion) of TiO2. Furthermore, a faster sintering rate was present than that in the literature and nicely converged to the literature ones for increasing particle size.
This section discussed the research works on the coalescence of alloy nanoparticles and metal oxide nanoparticles in literature. Similar to section 3.2, most research studies are focused on the coalescence of alloy nanoparticles consisting of Au and Ag. Since the interactions between different metallic elements vary, surface segregation and precipitation occur during the coalescence process of alloy nanoparticles. This trend also leads to the formation of core–shell structure. For metal oxide nanoparticles, TiO2 nanoparticle is typical in sintering since it is one of the fundamental ceramics with applications in photocatalysts, capacitors, and pigments. The coalescence of TiO2 nanoparticles is mainly caused by the mobile surface ions, which is similar to the surface diffusion of atoms in the metal/alloy nanoparticles.
4. Perspective and conclusion
This work is dedicated to providing a mini review of computational approaches and applications for studying the coalescence of metallic nanoparticles. Toward this goal, we started by discussing the outstanding performances and coalescence behaviors of metallic nanoparticles, and proposing some challenges in the coalescence of metallic nanoparticles. Subsequently, we introduced the applications of molecular dynamics and the Monte Carlo method in nanoparticle coalescence. Furthermore, we summarized the coalescence kinetics and mechanisms of metal nanoparticles with the same element and different elements, alloy nanoparticles and metal oxide nanoparticles. In this section, we will present our perspective and conclusion.4.1. Coalescence of medium- and high-entropy-alloy nanoparticles
There has been an explosion of interest in the field of medium-entropy alloys (MEAs) and high-entropy alloys (HEAs) since they were first introduced in 2004, which are a novel category of multi-principal component alloys consisting of metallic elements in equal/near-equal atomic concentrations.103,104 Cantor-like HEAs, made of Al, Co, Cr, Cu, Fe, Ni, Pd, Mn, etc. and in an FCC lattice, tend to coalesce at a similar temperature to that of the conventional binary alloys. Refractory HEAs, one prominent class of HEAs consisting of refractory elements (Mo, Nb, Ta, Ti, V, W, Zr, etc.) and in a body-centered-cubic lattice, possess higher temperature resistance.The widespread interest in these materials stems from both the novelty of the concept as well as their outstanding mechanical (among other) properties, such as the uncommon balance between strength and ductility in AlCoCrFeNi2.1 and CoCuFeNiPd,105,106 ideal plasticity in AlxCoCuFeNi,107 and exceptional high temperature strength in MoNbTi and MoTaTiWZr.108,109 It has also been reported that nanoparticles play a significant role in the deformation mechanism of (FeCoNi)86-Al7Ti7, (FeCoNi)86-Al8Ti6, and Ni30Co30Fe13Cr15Al6Ti6 MEAs/HEAs.110,111 However, the coalescence kinetics/mechanism of MEA/HEA nanoparticles is rarely reported.
4.2. Coalescence of nanoparticles studied by machine learning
Although there are abundant studies focusing on the nanoparticle coalescence in recent years, current exploration on the coalescence kinetics and mechanism of metallic nanoparticles is only at the tip of an iceberg. More aspects on computational understanding of the coalescence of metallic nanoparticles still call for ML and other approaches to provide more insights. For example, using deep learning assisted atomic electron tomography,112 a full 3D atomic structure of a dumbbell-shaped Pt nanoparticle formed by a coalescence of two nanoclusters can be determined.113 The results indicated that the diffusion of interfacial atoms mainly governed the coalescence process, but other dynamic processes such as surface restructuring and plastic deformation were also involved.X-ray absorption near-edge structure (XANES) spectroscopy, SAXS, and ab initio simulations, could also be combined with ML (artificial neural network) techniques to investigate the coalescence of Cu cluster for formation of complex materials. Significant differences have been between the sizes of particle agglomerates, as probed by SAXS, and the sizes of locally ordered regions, as seen by XANES. These differences have been interpreted as evidence for the fractal, grape-cluster-like structure of the agglomerates. The huge compositional space of metals and alloys offers unlimited opportunities for academic and industrial research and development, where ML can be integrated with experimental and simulation methods to deepen the understanding of the coalescence of metallic nanoparticles.
A strong development in ML came from the rapid growth of databases, starting in the early 2000s.114 Advances in ML algorithms and data generation have created a fertile ground for computational materials science. Data-driven ML has proved to be particularly instrumental in pushing progress in a wide variety of metallic materials, including catalysts, superalloys, shape-memory alloys, metallic glasses, and high-entropy alloys. Combining high-throughput experimental techniques with high-throughput calculation/simulation approaches, massive amounts of data have been generated. Currently, the Materials Project,115 AFLOW,116 OQMD,117 and NOMAD118 repositories contain millions of calculations/simulations with hundreds of millions of structural features and extracted properties. These databases were useful to study the coalescence of metallic nanoparticles.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The contributions of Y. Guo in this paper are sponsored by the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (22KJB460039) and “Taihulight” Science and Technology Research (Basic Research) (K20221048). The contributions of S. Chen in this paper are sponsored by the National Natural Science Foundation of China (Grant No. 52301017) and Shanghai Pujiang Program (Grant No. 22PJ1403700).References
- Y. Choi, S. K. Cha, H. Ha, S. Lee, H. K. Seo, J. Y. Lee, H. Y. Kim, S. O. Kim and W. Jung, Nat. Nanotechnol., 2019, 14, 245–251 CrossRef CAS PubMed.
- V. V. Thacker, L. O. Herrmann, D. O. Sigle, T. Zhang, T. Liedl, J. J. Baumberg and U. F. Keyser, Nat. Commun., 2014, 5, 3448 CrossRef PubMed.
- Y. Liu, C.-H. Liu, T. Debnath, Y. Wang, D. Pohl, L. V. Besteiro, D. M. Meira, S. Huang, F. Yang and B. Rellinghaus, Nat. Commun., 2023, 14, 541 CrossRef CAS PubMed.
- Y. J. Cho, L. Kong, R. Islam, M. Nie, W. Zhou and K. Lu, Nanoscale, 2020, 12, 20726–20736 RSC.
- C. Iacovita, J. Hurst, G. Manfredi, P. Hervieux, B. Donnio, J. Gallani and M. Rastei, Nanoscale, 2020, 12, 1842–1851 RSC.
- B. Wu, X. Wu, C. Guan, K. F. Tai, E. K. L. Yeow, H. J. Fan, N. Mathews and T. C. Sum, Nat. Commun., 2013, 4, 2004 CrossRef PubMed.
- X. Liu, L. Gu, Q. Zhang, J. Wu, Y. Long and Z. Fan, Nat. Commun., 2014, 5, 4007 CrossRef CAS PubMed.
- A. Choudhary, G. Singh and A. M. Biradar, Nanoscale, 2014, 6, 7743–7756 RSC.
- Y. K. Choi, T. Park, D. H. D. Lee, J. Ahn, Y. H. Kim, S. Jeon, M. J. Han and S. J. Oh, Nanoscale, 2022, 14, 8628–8639 RSC.
- A. Bigdeli, F. Ghasemi, H. Golmohammadi, S. Abbasi-Moayed, M. A. F. Nejad, N. Fahimi-Kashani, S. Jafarinejad, M. Shahrajabian and M. R. Hormozi-Nezhad, Nanoscale, 2017, 9, 16546–16563 RSC.
- X. Zeng, J. Sun, S. Li, J. Shi, H. Gao, W. S. Leong, Y. Wu, M. Li, C. Liu and P. Li, Nat. Commun., 2020, 11, 567 CrossRef CAS PubMed.
- M. J. Walsh, K. Yoshida, A. Kuwabara, M. L. Pay, P. L. Gai and E. D. Boyes, Nano Lett., 2012, 12, 2027–2031 CrossRef CAS PubMed.
- L. Qiao, N. Pollard, R. D. Senanayake, Z. Yang, M. Kim, A. S. Ali, M. T. Hoang, N. Yao, Y. Han and R. Hernandez, Nat. Commun., 2023, 14, 4408 CrossRef CAS PubMed.
- M. Zheng, W. Li, M. Xu, N. Xu, P. Chen, M. Han and B. Xie, Nanoscale, 2014, 6, 3930–3933 RSC.
- Y. Chang, J. Liu, H. Liu, Y. W. Zhang, J. Gao and J. Zhao, Adv. Energy Mater., 2023, 13, 2301331 CrossRef CAS.
- M. I. Gonzalez, A. B. Turkiewicz, L. E. Darago, J. Oktawiec, K. Bustillo, F. Grandjean, G. J. Long and J. R. Long, Nature, 2020, 577, 64–68 CrossRef CAS PubMed.
- G. L. Smith, J. E. Eyley, X. Han, X. Zhang, J. Li, N. M. Jacques, H. G. Godfrey, S. P. Argent, L. J. M. McPherson and S. J. Teat, Nat. Mater., 2019, 18, 1358–1365 CrossRef CAS PubMed.
- B. Chen, M. Zhang, K. Zhang, Z. Dong, J. Li and G. Zhao, Friction, 2022, 10, 717–731 CrossRef CAS.
- C. Hu, J. Lv, M. Bai, X. Zhang and D. Tang, Friction, 2020, 8, 531–541 CrossRef CAS.
- W. Xu, G. Yang, S. Zhang, J. Xu, Y. Zhang, T. Sun, N. Song, L. Yu and P. Zhang, Friction, 2023, 1–16 Search PubMed.
- J. Wang, S. Chen, K. Cui, D. Li and D. Chen, ACS Nano, 2016, 10, 2893–2902 CrossRef CAS PubMed.
- D. Nelli, M. Cerbelaud, R. Ferrando and C. Minnai, Nanoscale Adv., 2021, 3, 836–846 RSC.
- C. Cao, K. Huang, J. Shi, D. Zheng, W. Wang, L. Gu and H. Bai, Nat. Commun., 2019, 10, 1966 CrossRef CAS PubMed.
- L. Cheng, X. Zhu and J. Su, Nanoscale, 2018, 10, 7978–7983 RSC.
- B. Huang, L. Miao, J. Li, Z. Xie, Y. Wang, J. Chai and Y. Zhai, Nat. Commun., 2022, 13, 1402 CrossRef CAS PubMed.
- Z. Fusco, M. Rahmani, R. Bo, T. Tran-Phu, M. Lockrey, N. Motta, D. Neshev and A. Tricoli, Adv. Funct. Mater., 2019, 29, 1806387 CrossRef.
- Y. Zhou, A. S. Powers, X. Zhang, T. Xu, K. Bustillo, L. Sun and H. Zheng, Nanoscale, 2017, 9, 13915–13921 RSC.
- R. Jin, Y. Cao, C. A. Mirkin, K. L. Kelly, G. C. Schatz and J. Zheng, science, 2001, 294, 1901–1903 CrossRef CAS PubMed.
- S. Yue, W. Yuan, Z. Deng, W. Xi and Y. Shen, Nano Lett., 2022, 22, 8115–8121 CrossRef CAS PubMed.
- A. Ruderman, M. B. Oviedo, S. A. Paz and E. P. Leiva, J. Phys. Chem. A, 2023, 127, 8955–8965 CrossRef CAS PubMed.
- X. Shi, W. Gao, H. Liu, Z. G. Fu, G. Zhang, Y. W. Zhang, T. Liu, J. Zhao and J. Gao, Small, 2022, 18, 2203274 CrossRef CAS PubMed.
- A. Zhang, S. Qiu, L. Zhao, H. Liu, J. Zhao and J. Gao, Laser Photonics Rev., 2024, 18, 2300742 CrossRef CAS.
- J. E. Lennard-Jones, Proc. Phys. Soc., 1931, 43, 461 CrossRef CAS.
- P. M. Morse, Phys. Rev., 1929, 34, 57 CrossRef CAS.
- R. Johnson, Phys. Rev. B: Solid State, 1972, 6, 2094 CrossRef.
- M. S. Daw and M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 6443 CrossRef CAS.
- M. Baskes, J. Nelson and A. Wright, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 6085 CrossRef CAS PubMed.
- M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 2727 CrossRef CAS PubMed.
- B.-J. Lee and M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8564 CrossRef CAS.
- B.-J. Lee, J.-H. Shim and M. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 144112 CrossRef.
- J. Tersoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 6991 CrossRef PubMed.
- K. Chenoweth, A. C. Van Duin and W. A. Goddard, J. Phys. Chem. A, 2008, 112, 1040–1053 CrossRef CAS PubMed.
- M. S. Nitol, D. E. Dickel and C. D. Barrett, Acta Mater., 2022, 224, 117347 CrossRef CAS.
- R. Jana and M. A. Caro, Phys. Rev. B, 2023, 107, 245421 CrossRef CAS.
- Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. r. Behler, G. Csányi, A. V. Shapeev, A. P. Thompson and M. A. Wood, J. Phys. Chem. A, 2020, 124, 731–745 CrossRef CAS PubMed.
- L. Zhao, Y. Chang, S. Qiu, H. Liu, J. Zhao and J. Gao, Adv. Energy Sustainability Res., 2023, 4, 2300112 CrossRef CAS.
- J.-C. Liu, L. Luo, H. Xiao, J. Zhu, Y. He and J. Li, J. Am. Chem. Soc., 2022, 144, 20601–20609 CrossRef CAS PubMed.
- T. Wen, R. Wang, L. Zhu, L. Zhang, H. Wang, D. J. Srolovitz and Z. Wu, npj Comput. Mater., 2021, 7, 206 CrossRef.
- H. Sun, C. Zhang, L. Tang, R. Wang, W. Xia and C.-Z. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2023, 107, 224301 CrossRef CAS.
- Y. Wang, L. Zhang, B. Xu, X. Wang and H. Wang, Modell. Simul. Mater. Sci. Eng., 2021, 30, 025003 CrossRef.
- L. Verlet, Phys. Rev., 1967, 159, 98 CrossRef CAS.
- P. Young, In Lecture Notes inUniversity of California, Santa Cruz, 2014 Search PubMed.
- W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637–649 CrossRef CAS.
- D. T. Gillespie, J. Comput. Phys., 1976, 22, 403–434 CrossRef CAS.
- A. F. Voter, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 6819 CrossRef CAS PubMed.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- K. Binder, D. M. Ceperley, J.-P. Hansen, M. Kalos, D. Landau, D. Levesque, H. Mueller-Krumbhaar, D. Stauffer and J.-J. Weis, Monte Carlo methods in statistical physics, Springer Science & Business Media, 2012 Search PubMed.
- A. Sadiq, J. Comput. Phys., 1984, 55, 387–396 CrossRef CAS.
- S. A. Serebrinsky, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 037701 CrossRef PubMed.
- A. F. Voter, Introduction to the kinetic Monte Carlo method, Springer, 2007 Search PubMed.
- A. Nitzan, Chemical Dynamics in Condensed Phases: Relaxation, Transfer, and Reactions in Condensed Molecular Systems, Oxford University Press, 2013 Search PubMed.
- P. Jensen and N. Combe, Comput. Mater. Sci., 2002, 24, 78–87 CrossRef CAS.
- B. Ingham, T. H. Lim, C. J. Dotzler, A. Henning, M. F. Toney and R. D. Tilley, Chem. Mater., 2011, 23, 3312–3317 CrossRef CAS.
- T. H. Lim, D. McCarthy, S. C. Hendy, K. J. Stevens, S. A. Brown and R. D. Tilley, ACS Nano, 2009, 3, 3809–3813 CrossRef CAS PubMed.
- S. Arcidiacono, N. Bieri, D. Poulikakos and C. Grigoropoulos, Int. J. Multiphase Flow, 2004, 30, 979–994 CrossRef CAS.
- D.-B. Grys, M. Niihori, R. Arul, S. M. Sibug-Torres, E. W. Wyatt, B. de Nijs and J. J. Baumberg, ACS Sens., 2023, 8, 2879–2888 CrossRef CAS PubMed.
- S. Yue, Y. Shen, Z. Deng, W. Yuan and W. Xi, Nanoscale, 2021, 13, 18218–18225 RSC.
- R. Bekarevich, M. Toyoda, K. Zhang, T. Nakata, S.-i. Taniguchi and K. Hirahara, J. Phys. Chem. C, 2017, 121, 9606–9611 CrossRef CAS.
- P. Guo and Y. Gao, Phys. Rev. Lett., 2020, 124, 066101 CrossRef CAS PubMed.
- A. Lange, A. Samanta, H. Majidi, S. Mahajan, J. Ging, T. Olson, K. van Benthem and S. Elhadj, Acta Mater., 2016, 120, 364–378 CrossRef CAS.
- G. Palasantzas, T. Vystavel, S. Koch and J. T. M. De Hosson, J. Appl. Phys., 2006, 99, 024307 CrossRef.
- N. Lümmen and T. Kraska, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 205403 CrossRef.
- F. Ding, A. Rosén and K. Bolton, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 075416 CrossRef.
- M. Yeadon, J. Yang, R. Averback, J. Bullard, D. Olynick and J. Gibson, Appl. Phys. Lett., 1997, 71, 1631–1633 CrossRef CAS.
- X. Liu, S. Li, C. Tan, C. Gao, Y. Liu, H. Ye and G. Zhang, J. Mater. Res. Technol., 2022, 17, 1132–1145 CrossRef CAS.
- B. Buesser and S. E. Pratsinis, J. Phys. Chem. C, 2015, 119, 10116–10122 CrossRef CAS.
- P. Grammatikopoulos, C. Cassidy, V. Singh, M. Benelmekki and M. Sowwan, J. Mater. Sci., 2014, 49, 3890–3897 CrossRef CAS.
- P. Grammatikopoulos, C. Cassidy, V. Singh and M. Sowwan, Sci. Rep., 2014, 4, 5779 CrossRef CAS PubMed.
- H.-H. Jia, D.-L. Bao, Y.-Y. Zhang and S.-X. Du, Chin. Phys. B, 2020, 29, 048701 CrossRef CAS.
- M. José-Yacamán, C. Gutierrez-Wing, M. Miki, D.-Q. Yang, K. Piyakis and E. Sacher, J. Phys. Chem. B, 2005, 109, 9703–9711 CrossRef PubMed.
- E. Goudeli and S. E. Pratsinis, ACS Nano, 2017, 11, 11653–11660 CrossRef CAS PubMed.
- M. Chandross, Modell. Simul. Mater. Sci. Eng., 2014, 22, 075012 CrossRef CAS.
- P. Grammatikopoulos, J. Kioseoglou, A. Galea, J. Vernieres, M. Benelmekki, R. E. Diaz and M. Sowwan, Nanoscale, 2016, 8, 9780–9790 RSC.
- V. Singh, C. Cassidy, P. Grammatikopoulos, F. Djurabekova, K. Nordlund and M. Sowwan, J. Phys. Chem. C, 2014, 118, 13869–13875 CrossRef CAS.
- B. J. Henz, T. Hawa and M. Zachariah, J. Appl. Phys., 2009, 105, 124310 CrossRef.
- B. Li, J. Li, X. Su and Y. Cui, Sci. Rep., 2021, 11, 15432 CrossRef CAS PubMed.
- C. Langlois, Z. Li, J. Yuan, D. Alloyeau, J. Nelayah, D. Bochicchio, R. Ferrando and C. Ricolleau, Nanoscale, 2012, 4, 3381–3388 RSC.
- L. M. Farigliano, S. A. Paz, E. P. Leiva and M. A. Villarreal, J. Chem. Theory Comput., 2017, 13, 3874–3880 CrossRef CAS PubMed.
- J. Kim and H. Chung, J. Mater. Sci. Technol., 2024, 184, 64–74 CrossRef.
- Z. Zhang, S. Li and Y. Liu, J. Mater. Sci., 2023, 58, 13059–13079 CrossRef CAS.
- F. Baletto, C. Mottet and R. Ferrando, Phys. Rev. Lett., 2003, 90, 135504 CrossRef CAS PubMed.
- G. A. Sotiriou, G. D. Etterlin, A. Spyrogianni, F. Krumeich, J.-C. Leroux and S. E. Pratsinis, Chem. Commun., 2014, 50, 13559–13562 RSC.
- H. Akbarzadeh, M. Abbaspour, S. Salemi and M. Hasani, J. Mol. Liq., 2017, 244, 390–397 CrossRef CAS.
- P. Lu, M. Chandross, T. J. Boyle, B. G. Clark and P. Vianco, APL Mater., 2014, 2, 022107 CrossRef.
- P. Williams, Y. Mishin and J. Hamilton, Modell. Simul. Mater. Sci. Eng., 2006, 14, 817 CrossRef CAS.
- D. Bochicchio and R. Ferrando, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165435 CrossRef.
- G. g. Guisbiers, S. Mejia-Rosales, S. Khanal, F. Ruiz-Zepeda, R. L. Whetten and M. José-Yacaman, Nano Lett., 2014, 14, 6718–6726 CrossRef CAS PubMed.
- M. H. Sluiter, C. Colinet and A. Pasturel, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 174204 CrossRef.
- M. Bohra, P. Grammatikopoulos, R. E. Diaz, V. Singh, J. Zhao, J.-F. Bobo, A. Kuronen, F. Djurabekova, K. Nordlund and M. Sowwan, Chem. Mater., 2015, 27, 3216–3225 CrossRef CAS.
- S. Ogata, H. Iyetomi, K. Tsuruta, F. Shimojo, A. Nakano, R. K. Kalia and P. Vashishta, J. Appl. Phys., 2000, 88, 6011–6015 CrossRef CAS.
- M. Alimohammadi and K. A. Fichthorn, Nano Lett., 2009, 9, 4198–4203 CrossRef CAS PubMed.
- B. Buesser, A. Grohn and S. E. Pratsinis, J. Phys. Chem. C, 2011, 115, 11030–11035 CrossRef CAS PubMed.
- J. W. Yeh, S. K. Chen, S. J. Lin, J. Y. Gan, T. S. Chin, T. T. Shun, C. H. Tsau and S. Y. Chang, Adv. Eng. Mater., 2004, 6, 299–303 CrossRef CAS.
- B. Cantor, I. Chang, P. Knight and A. Vincent, Mater. Sci. Eng., A, 2004, 375, 213–218 CrossRef.
- J. Ren, Y. Zhang, D. Zhao, Y. Chen, S. Guan, Y. Liu, L. Liu, S. Peng, F. Kong and J. D. Poplawsky, Nature, 2022, 608, 62–68 CrossRef CAS PubMed.
- S. Chen, Z. H. Aitken, S. Pattamatta, Z. Wu, Z. G. Yu, D. J. Srolovitz, P. K. Liaw and Y.-W. Zhang, Nat. Commun., 2021, 12, 4953 CrossRef CAS PubMed.
- S. Chen, P. Liu, Q. Pei, Z. G. Yu, Z. H. Aitken, W. Li, Z. Wu, R. Banerjee, D. J. Srolovitz and P. K. Liaw, Sci. Adv., 2023, 9, eadi5817 CrossRef CAS PubMed.
- F. Wang, G. H. Balbus, S. Xu, Y. Su, J. Shin, P. F. Rottmann, K. E. Knipling, J.-C. Stinville, L. H. Mills and O. N. Senkov, Science, 2020, 370, 95–101 CrossRef CAS PubMed.
- S. Chen, Z. H. Aitken, S. Pattamatta, Z. Wu, Z. G. Yu, D. J. Srolovitz, P. K. Liaw and Y.-W. Zhang, Mater. Today, 2023, 65, 14–25 CrossRef CAS.
- T. Yang, Y. Zhao, Y. Tong, Z. Jiao, J. Wei, J. Cai, X. Han, D. Chen, A. Hu and J. Kai, Science, 2018, 362, 933–937 CrossRef CAS PubMed.
- T. Yang, Y. Zhao, J. Luan, B. Han, J. Wei, J. Kai and C. Liu, Scr. Mater., 2019, 164, 30–35 CrossRef CAS.
- J. Lee, C. Jeong and Y. Yang, Nat. Commun., 2021, 12, 1962 CrossRef CAS PubMed.
- J. Lee, C. Jeong, T. Lee, S. Ryu and Y. Yang, Nano Lett., 2022, 22, 665–672 CrossRef CAS PubMed.
- G. L. Hart, T. Mueller, C. Toher and S. Curtarolo, Nat. Rev. Mater., 2021, 6, 730–755 CrossRef.
- A. Jain, G. Hautier, C. J. Moore, S. P. Ong, C. C. Fischer, T. Mueller, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2011, 50, 2295–2310 CrossRef CAS.
- S. Curtarolo, W. Setyawan, G. L. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang and O. Levy, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS.
- C. Draxl and M. Scheffler, MRS Bull., 2018, 43, 676–682 CrossRef.
Footnote |
| † These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |



