Size onset of metallic behavior in neutral aluminum clusters

Abstract

The excited state lifetimes of neutral (Al)_n clusters up to ∼1 nm in diameter in size, where n ≤ 43, are systematically measured with femtosecond time-resolved mass spectrometry. The onset of metallic behavior is identified as a distinct change in the relaxation behavior initiated with single ultraviolet (400 nm) photon excitation. The experimentally measured excited state lifetimes gradually decrease with size for small molecular scale clusters (n < 10) before becoming indistinguishable for larger clusters (n > 9), where the measurements are comparable to electron–lattice relaxation time of bulk Al (∼300 fs). Particularly intense, or magic, Al_n clusters do not exhibit any significant excited state lifetime behavior. Time-dependent density functional theory quantify the excited state properties and are presented to show that dynamics are strongly tied to the excited state charge carrier distributions and overlap, rather than detailed changes related to changes in the cluster's electronic and geometric structure. The consistency in excited state lifetimes for clusters larger than n = 9 is attributed to the hybridization of the s- and p-orbitals as well as increasing delocalization. Al₃ exhibits unique temporal delay in its transient behavior that is attributed to a transition from triangular ground state to linear structure upon excitation.

---

1. Introduction

Al is the third most abundant element in the Earth's crust (∼8%) making it an economical metal for use in many industries. When refined, it exhibits several useful properties, including non-magneticity and high conductivity, making it a critical material for use in electronic applications.¹ It rapidly forms a corrosion resistant oxide layer, making it a staple material utilized in aerospace, microelectronics,² semiconductor,³ metallurgical, anticorrosion,⁴ and packaging industries. Al is utilized as a back surface in photovoltaic cells, improving efficiency due to carrier recombination hindrance.⁵ Al is also utilized in modern optics as soft XUV transmission filters for blocking vis/IR light.⁶ Its low weight density makes its energy density higher than most organic compounds. Its high affinity for oxygen also enables it to be utilized as a nanoenergetic material for propulsion, pyrotechnics, and explosives.^7,8

Bulk Al is considered a free electron metal, enabling the excess energy from optically produced excited states to initially relax on the sub-100 fs timescale due to strong electron–electron scattering. The electron thermalization time in Al is faster than in other metals, measured on the few fs timescale (11 fs with 800 nm excitation).⁹ The conversion to nuclear motion (e-phonon) occurs roughly an order of magnitude slower (with a lattice response of ∼300 fs).^6,10

Scientific interest in the electronic properties of Al has only increased in recent years with the discovery of plasmon resonances in the ultraviolet region arising at the nanoscale,^11,12 which may be employed for nanophotonics, photocatalysis, and optoelectronic applications involving wide bandgap semiconductors. Al has a negative dielectric constant at UV wavelengths and a minimal loss coefficient, as opposed to the more established noble metal plasmon nanoparticles, which lose metallic character in the UV due to interband absorbance.¹³ Nanometer sized Al particles support plasmon resonances that are tunable over the UV-vis-NIR range by adjusting their size.^14,15 Nanostructures as small as 2.2 nm diameter have been synthesized¹⁶ and the onset of plasmonic activity is suggested to be between 3 and 4 nm.¹⁶ Phonon–phonon coupling is on the longer ps timescale.¹⁷ Al lacks d-band electrons, making the interband transitions greater than the Fermi energy of the metal, enabling plasmon resonances spanning the UV spectrum.

To maximize activity, a modern frontier of material science is aimed at creating ever-decreasing sizes of materials, which drives new demands to understand the electronic properties down to the molecular (cluster) scale. The structures and properties of small Al_n clusters have been the subject of many theoretical investigations^18–22 and demonstrate its spectroscopy and reactivity are enriched by the potentially multivalent character of the bonding which involves both 3p and 3s atomic character. Therefore, the stable clusters identified through mass spectrometry generally do not align with the well-known jellium model.²³ Molecular scale properties deviate from the bulk, and adjustment on the atomic level can drastically affect geometric structure, chemical properties, or electronic capabilities. Clusters provide opportunities for the production of new materials that possess properties different from the bulk.

Understanding the size transition between insulator and metallic character for Al clusters is of long-standing interest,²⁴ and particularly valuable to the semiconductor industry. However, it is not possible to apply standard measurements of metallic behavior, such as their reflectivity or conductivity, in clusters containing only a few atoms so alternative approaches are required. The transition between semiconducting and metallic behavior has been attributed, using photoelectron spectroscopy (PES), to the cluster size in which hybridization between the s- and p-orbitals occurs in various metal clusters, including Mg_n,²⁵ Hg_n,²⁶ and Al_n.²⁷ Another physical property measurement that distinguishes between bulk and metallic and non-metallic properties is identified as different relaxation behavior in optically excited states.^28–30 A strong interaction between delocalized electrons in metallic systems enables Auger-like electron–electron scattering on the fs timescale. In contrast, the lower density of states and weaker coupling between electronic states is characteristic of semiconductors and results in slower relaxation. However, molecular sized clusters may contain either discrete electronic energy levels which extend excited state relaxation mechanisms or contain a high density of states and present metallic behavior. Thus, sub-nanometer clusters have been measured to exhibit both metallic and semiconducting properties, and even transition between the two extrema with atomic precision.^31–37

Although the measurement of a physical property of a single cluster size is not always particularly valuable, a wealth of information is obtained by observing changes in behavior as the clusters grow in size. Here, we present a method for identifying the onset of metallic behavior in metal clusters by systematically measuring the excited state lifetimes of small neutral (Al)_n clusters as the they grow through a distinct change in their excited state relaxation behavior. We show that the excited state lifetimes are similar for n > 9, suggesting the onset of metallic behavior, in agreement with previous measurements of s/p hybridization,²⁷ as well as exhibiting relaxation lifetimes similar to bulk scale measurements.^11,12 A transition in excited state charge carrier distributions for the clusters is found to correlate with the metallicity noted from the relaxation dynamics.

2. Methods

2.1. Cluster production and detection

Al clusters were produced using laser vaporization in a high vacuum chamber. The neutral clusters were skimmed and measured using a previously described Wiley–McLaren type time-of-flight mass spectrometer (TOF-MS) coupled to a femtosecond laser source which ionizes the clusters for detection by a microchannel plate (MCP) detector.^38,39 Briefly, a translating Al rod is exposed to the second harmonic (532 nm) of a pulsed Nd:YAG laser for ablation. A synchronized pulse of 120 psi He gas is introduced for supersonic expansion. The resultant plasma plume is confined within a 1 × 60 mm collision cell to aid in the formation of clusters. This approach of laser vaporization efficiently produces cationic, anionic, and neutral clusters simultaneously. The clusters traverse a charged (−500 V) 2 mm diameter skimmer, which deflects the ionic clusters and allows only the neutral species to enter the femtosecond laser interaction region of the mass spectrometer. Neutral clusters are ionized by a well-defined sequence of femtosecond laser pulses and accelerated toward the detector by a 4.2 kV electrostatic field. With the skimmer charged, no ion signal is recorded without the presence of the femtosecond ionizing laser. In contrast, the cation distribution produced directly from the laser ablation can be measured by grounding the skimmer and pulsing the grids associated with the extraction region of the mass spectrometer at the appropriate time delay. An Einzel lens focuses the cluster beam as they traverse the 105 cm field-free region and separate in time based on their mass/charge ratio. A vacuum pressure of 5 × 10⁻⁷ Torr is maintained at the detector by three turbo pumps during the experiment. Laser pulses, gas pulses, and TOF discharges are synchronized using pulse generators.

2.2. Pump–probe spectroscopy

Excited state dynamics are detected with pump–probe spectroscopy. By sending the principal beam (800 nm) through a frequency doubling crystal, the second harmonic (400 nm) is generated. These two beams are spatially separated using a dichroic mirror, and the 800 nm beam traverses a programmable optical delay stage which varies the pulse in time with respect to the 400 nm beam. A single 400 nm photon (3.1 eV) “pumps” or excites the clusters to an intermediate excited state, and the 800 nm beam (1.55 eV) “probes” or ionizes the clusters for detection. The optical delay stage is translated in 50 fs increments from −600 fs to +4 ps and an average of 1000 laser shots are recorded for each mass spectrum. The spatially combined 400 nm and 800 nm beams are focused with a 50 cm focal lens to laser intensities of 1.4 × 10¹⁴ W cm⁻² and 5.6 × 10¹⁴ W cm⁻², respectively. Individual laser intensities are kept to a minimum to reduce the possibility of ionization from either individual beam and promote signal enhancement through beam synergy. A pulse width of 35 fs for the principal beam was determined by auto correlation. By scanning the intensities of mass spectra at differing time delays between the two laser pulses, the excited state lifetimes are determined. The intensity of the clusters in the mass spectrum at each time delay is related to the population remaining in the excited state. The transient signal is fit with a combination of a Gaussian function and an exponential decay function convoluted with a Gaussian instrumental response function. The fitting coefficients are extracted to represent the excited state lifetime (τ) and presented in Table S1.† No signal was recorded if the 800 nm beam served as the pump pulse (negative time delays).

2.3. Computational methods

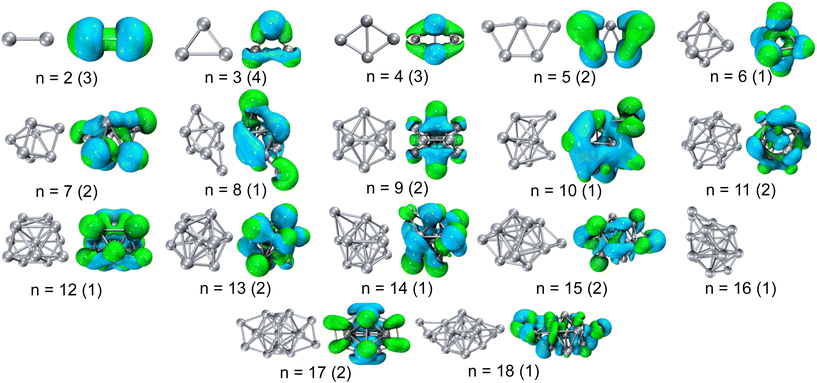
Previously calculated structures from published literature sources^18,19,21,40 were employed as starting structures for our calculations on neutral Al_n clusters. The lowest energy structure for each Al_n cluster is optimized at the density functional theory (DFT) level using CAM-B3LYP⁴¹ and the 6-311++G(3d2f, 3p2d) basis set within the Gaussian software suite. The long-range correction of CAM-B3LYP has proven essential to calculating the absorption spectra of pure metal clusters.⁴² The lowest energy clusters adopt a low spin state, except for n = 2–4 (Fig. 5), in general agreement with previous studies.²¹ There is experimental evidence that small clusters containing an even number of atoms have magnetic moments suggesting spin triplets, while clusters larger than n = 10 are low spin.⁴³ Small clusters are planar, transitioning to 3D structures at n = 6, and contain a central atom at n = 13. The vertical IPs are determined as the difference in energy between the neutral and cation electron configurations at identical (ground state) structure. The calculated IPs are in excellent agreement with previous calculations,²¹ and experimental measurements.^44–46

Time dependent (TD)-DFT calculations are performed to gain insight into the excited states for each cluster and interpret the role of the electron–hole interactions upon photoexcitation. The excited state selected for analysis contained the highest oscillator strength at the pump photon energy (3.1 eV). Several topological descriptors are calculated to quantify the spatial properties of the charge carriers, including the d (distance between centroid of the electron and hole densities), σ (root-mean-squared-deviation of the electron and the hole), Λ (percent overlap of the electron and hole wavefunctions), and total delocalization index (TDI). The formulas used for such calculations are provided in the ESI.†

3. Results and discussion

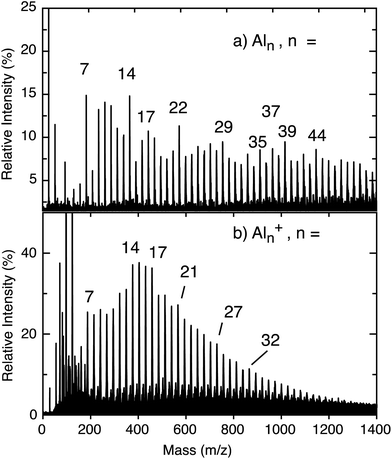
The neutral cluster distribution acquired through strong-field ionization of the neutral cluster beam by the fs laser (Fig. 1a) is different than the cation cluster distribution recorded directly from laser ablation (Fig. 1b). The cations produced directly from laser vaporization generally present a Gaussian-like distribution, but the neutral cluster distribution reveals a variety of prominent cluster sizes, in agreement with previous reports of neutral cluster distributions.^45–47 Both distributions reach a maximum cluster size of up to ∼n = 50, corresponding to a size of ∼1 nm diameter. Peak enhancements, compared to the nearest neighboring peaks, indicate high cluster stability, and highlights magic clusters. Both neutral Al₇ and Al₁₄ clusters are enhanced compared to their nearest neighboring peaks and are an indication of magic behavior. For the Al₇⁺ cluster, enhanced stability is seen as a result of containing 20 valence electrons, aligning with the jellium model. However, the jellium model generally fails to explain the relative stability in the neutral Al cluster distribution. Instead, changes in the ionization potential (IP) becomes a dominant factor for ion yield as a lower IP generally correlates to larger peak intensity. Post ionization evaporative effects can also play a role in the intensity variations. Our approach of strong-field ionizing neutral clusters demonstrates a strong sensitivity to IPs, corresponding to electron-shell openings and accounts for the relative stability of the clusters labeled in Fig. 1. The IPs decrease with cluster size,^45,46 meaning that the signal does not decay exponentially as is typical of direct cation distributions.

Fig. 1 Typical Al_n cluster distributions (a) acquired through femtosecond ionization of neutral Al clusters and (b) cation distribution Al_n clusters obtained directly through laser ablation. The Al₃O arises from the high affinity of Al to oxygen. The intensities are normalized to the Al⁺ in each respective spectra.

Transient dynamics for the neutral clusters are measured through time-resolved mass spectrometry. Experimental measurements for small Al_n clusters (n ≤ 18) are presented in Fig. 2. Table 1 presents the measured excited state lifetimes (τ) and calculated charge delocalization properties for Al_n clusters n ≤ 18. The measurements for larger clusters are similar and are presented in Fig. S1, S2 and Table S1.† Nearly all transient signals exhibit a maximum near the temporal overlap of the two laser pulses due to non-resonant ionization and decay back to their baseline signals on the femtosecond timescale. Only atomic Al⁺ contains a long-lived (≫10 ps) transient signal, reflecting the lack of an excited state coupling mechanism for relaxation in atomic systems. The lowest excited state of the Al atom corresponding to a 3s²3p (²P) to 3s²4s (²S) transition is resonant with 400 nm (3.1 eV) and has a ns lifetime.⁴⁸

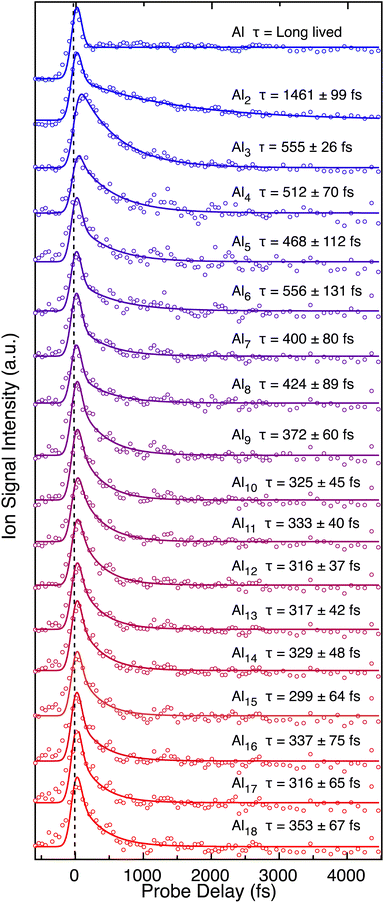Fig. 2 Transient dynamics of pure (Al)_n clusters with n < 16 following ultraviolet absorption. The vertical black dashed line is centered at t₀ to highlight the shift in signal for Al₃.

Table 1 Experimental excited state lifetimes (τ) and calculated properties for (Al)_n clusters^a

(Al)n	τ (fs)	Λ	d (Å)	σ av (Å^3)	TDI (Å^−3)	IP (eV)
a Topological descriptors for describing the character of the excited state: charge transfer character (Λ), distance between electron and hole density (d), average root mean standard deviation of the electron and hole (σav), total delocalization index (TDI), and vertical ionization potential (IP).
2	1461 ± 99	0.85	0.00	2.47	1.71	6.34
3	555 ± 26	0.74	0.42	2.75	1.74	6.37
4	512 ± 70	0.79	0.00	2.57	1.78	6.26
5	468 ± 112	0.64	0.45	3.09	1.57	6.56
6	556 ± 131	0.81	0.00	3.00	1.33	6.59
7	400 ± 80	0.74	0.32	3.04	1.25	6.16
8	424 ± 89	0.64	0.24	3.34	1.16	6.47
9	372 ± 60	0.68	0.06	3.35	1.13	6.50
10	325 ± 45	0.65	0.55	3.51	1.01	6.24
11	333 ± 40	0.64	0.49	3.74	0.92	6.29
12	316 ± 37	0.60	0.37	3.54	1.04	6.27
13	317 ± 42	0.72	0.00	3.58	0.96	6.62
14	329 ± 48	0.66	0.04	3.59	1.08	6.00
15	299 ± 65	0.61	0.26	3.84	0.86	6.01
16	337 ± 75	0.58	0.25	3.68	0.91	6.00
17	316 ± 65	0.50	0.00	3.69	1.03	6.01
18	353 ± 67	0.62	0.28	4.46	0.87	6.04

---

Al₂ exhibits a long decay (τ = 1.461 ± 0.099 ps). Al₂ spectroscopy is well known.⁴⁹ The ground state of Al₂ arises from σπ electronic configuration to give rise to a ³Π_u term, consistent with pσ bonding favored over pπ bonding. Only two electronic states are accessible upon 3.1 eV absorption, including the B state and the 2³Π_g state. Excitation to the B state is highly vibrationally excited but has roughly double the bond strength of the ground state. Multiple bonding is possible because of promotion of a 3s electron to 3p shell, giving a π² configuration, and one σ bond, giving 2 bonds. In inert matrixes, the ³Π_u term is recorded. The lack of this state in vacuum may be attributed to rapid predissociation and its short lifetime limiting fluorescence. Both states are likely to be predissociative with 1³Π_g state which is repulsive to ²P₀ and ²P₀. Thus, the ps lifetime measured is attributed to the wavepacket traversing an avoided crossing and fragmenting to ground state neutral Al atoms. At higher photon energies (∼3.4 eV), a long fluorescent lifetime (τ = ∼30 ns) has been measured for the E state,⁵⁰ demonstrating a lack of nearby available state crossings.

The anomalous transient behavior of Al₃ reaches a maximum that is delayed in time with respect to the other cluster sizes (Fig. 2). The temporal delay in signal for the Al₃ indicates a significant structural change between the neutral and cation forms, with an excited state character that transitions to align with the cation structure. Most clusters retain a nearly identical structure upon ionization as revealed by minor relaxation energy from vertical and adiabatic IPs,⁴⁴ with the exception of Al₃ as suggested by the temporal delay in the maximum transient signal recorded herein. The structure of neutral Al₃ is well known to be triangular with nearly degenerate ²A₁ and ⁴A₂ ground states.^20,51,52 Due to the small difference in energy, both are likely present in the cluster distribution. However, several excited states of the Al₃ cluster have been suggested to be linear,⁵³ matching the structure suggested for the cation's ground state.⁵¹ Using visible light, microsecond fluorescent lifetimes were recorded for relaxation back to the ground state, and attributed to a nearly linear Al₃ excited state.⁵³ No long-lived plateau is recorded herein, suggesting that a different mechanism occurs. The photoelectron spectra recorded for Al₃⁻ contains broadened peaks, which are attributed to poor Franck–Condon coupling to excited states associated with a geometry change.⁵⁴ The temporal shift in Al₃⁺ signal presents a shift in the cluster production, and a maximum signal occurs at a temporal delay of 150 fs recorded in Al₃ that likely represents a transition from the triangular ground state neutral structure into linear form on the excited state that aligns with the cation structure. The subsequent decay of τ = 555 ± 26 fs is attributed to nonadiabatic coupling, or internal conversion, that returns the system to its vibrationally excited ground state.

Al₄ is particularly weak in the mass spectra compared to its neighbors, in agreement with other experiments.⁵⁵ The geometry of neutral Al₄ is planar and spin triplet, arising from bonding of the four p electrons.^{21,22,40,56,57} The measured lifetime of Al₄ is shorter than the smaller clusters (τ = 512 ± 70 fs), and is likely due to the increased degrees of freedom and higher density of states.^40,58 In fact, the measured excited state lifetimes slowly decrease as the clusters grow from n = 3 (τ = 555 ± 26 fs) to n = 9 (τ = 372 ± 60 fs) with a nearly linear change of −28 fs per atom (obtained from the slope of a best fit line of their lifetimes). Al₆ slightly departs from the trend, with a lifetime, τ = 556 ± 131 fs, longer than neighboring clusters. However, the deviation does not appear to be significant and fits within experimental error.

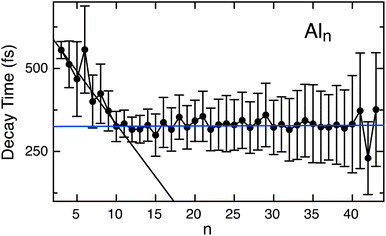
A distinct transition in the electronic relaxation behavior is identified at a cluster size of n = 9 (Fig. 3). The gradual decrease in lifetime aligns with changes in the density of electronic states revealed through photoelectron spectroscopy.^27,54,59 Smaller Al clusters (n < 9) exhibit significant energy spacings between well-defined atomic orbitals, leaving the singly occupied p orbital as the valence band. As atoms are added to the cluster, the 3s and 3p derived energy ranges broaden and overlap, where hybridization mixes their orbitals and lose distinct 3s and 3p identities at a cluster size of n = 9.²⁷ The measured lifetimes are consistent (τ ∼ 327 fs) for all larger clusters (n = 10 to 43), and are in agreement with previous values measured for bulk Al.^11,12 This consistent lifetime suggests the onset of metallic behavior occurs at n = 9, and that metallic scattering processes dominate the relaxation mechanism even in such small clusters. The orbital hybridization of larger clusters creates a large density of unoccupied states that enable rapid electron scattering processes, similar to the bulk. The energy separation between the unoccupied states is small, enabling fast e–e scattering and the relaxation operates as metallic for n > 10.

Fig. 3 Excited state lifetimes of Al_n (n = 3–43) decrease with size for n < 10, and then plateau for larger clusters reaching an average value of 327 fs. The black trend line corresponds to the fit of Al₃–Al₁₀, whereas the blue line is the fit of Al₁₁–Al₄₃.

The nearly linear decrease in lifetimes measured for small neutral clusters and consistent values recorded for the larger Al_n clusters (n > 10) is unexpected given the distinct changes in physical properties that occur upon addition of each atom. These trends suggests that the strong differences in properties such as IP and cluster geometry as they grow in size play only a minor role in relaxation dynamics. Further, despite the cluster distribution demonstrating particularly intense and stable clusters, such as Al₇⁺ and Al₁₄⁺, all clusters relax similarly to their nearest neighbors and do not show a particular magic lifetime behavior. We note that the error bars may hide subtle differences that may be related to cluster stability. For example, Al₆ exhibits a slightly longer lifetime compared to its neighboring clusters, although the reason for this is not yet clear. It is possible that the lifetime is slightly enhanced by its high O_h symmetry group or the agreement of the neutral cluster with the jellium model closing of 18 electrons. Furthermore, although only a limited number of clusters were previously examined,⁵⁹ the excited state lifetime measurements for anionic Al_n clusters are in excellent agreement with our measurements. The larger anions, including the particularly intense superatom Al₁₃⁻, also achieve a similar value of ∼300 fs. The nearly identical lifetimes between neutral and anion clusters suggests that an additional electron does not perturb the system significantly. These results also suggest that high stability attributed to the electronic or geometric symmetry of certain clusters doesn't affect their photoexcitation relaxation dynamics.

For molecular scale clusters, the energy gap between electronic states is often larger than the typical phonon energy, creating a bottleneck for the relaxation process.⁶⁰ The surprisingly fast electron–hole recombination recorded in these aluminum clusters, has been previously rationalized through a Jahn–Teller like geometric distortion that brings excited states together and enables nonradiative relaxation.⁶¹ This similarity in excited state lifetimes suggests that minor changes in electronic structure (addition of an extra electron) may not contribute to their relaxation dynamics if there are a large density of states in the frontier orbitals. Larger clusters have not been explored spectroscopically and detailed theoretical insights into their electronic structure are not available. Therefore, we limit our interpretation to understanding their excited state carrier distributions. Absorption of a 400 nm pump photon creates an electron–hole pair that strongly interact leading to the rapid relaxation. We perform TD-DFT calculations to examine the excited state charge carrier distributions following photoexcitation. These calculations suggest that dynamics are strongly tied to the excited state charge carrier distributions and overlap, rather than detailed changes of the electronic and geometric structure. Photoexcitation involves several molecular orbitals, making transition densities an efficient representation of the location and distribution of holes and electrons (Fig. 4). Deeper insights into the electronic distributions of the Al_n clusters are obtained through analysis of their topological properties (Table 1). The distance between electron and hole density centroids (d) is nearly zero in all clusters, indicating that both the electron and hole are centered on the cluster and delocalized in all directions. The Λ index quantifies the spatial overlap of electron and hole wavefunctions,⁶² and ranges between 0 and 1 to describe wavefunctions that share no common space or completely overlap, respectively. All Λ values are >0.5 in Al_n clusters, highlighting a strong overlap between electron and hole distributions as would be expected in such homogeneous systems.

Fig. 4 Lowest energy structures and spin states of neutral (Al)_n clusters calculated with DFT using CAM-B3LYP. The numbers in parenthesis correspond to the spin state of the cluster. Charge carrier transition densities of the hole (blue) and electron (green) for the excited state accessed with the pump (3.1 eV) photon. As the charge carriers spread over larger distances, the presented isovalue also decreases (0.002 for clusters Al₂–Al₄, 0.001 for Al₅–Al₉, 0.0005 for Al₁₀–Al₁₇, and 0.0004 for Al₁₈) for representation.

Excited state charge carrier delocalization values have been shown to align with changes in the excited state behavior of transition metal oxides.^31,39,63,64 Here, we quantify the spatial distribution of the charge carriers upon photoexcitation through the total delocalization index (TDI), or average of the electron/hole delocalization indexes. Smaller TDI values represent larger delocalization of the charge carriers. The TDI values calculated for Al_3–10 decrease with size, equating to increased charge delocalization spreading across the entire cluster as they grow in size (Fig. 5). A change in the trend of delocalization occurs at ∼Al₁₀, and the TDI remains nearly constant for the larger clusters (∼0.7). This transition in TDI behavior with cluster size is in excellent agreement with the trends recorded in excited state lifetimes and demonstrates a strong connection between the excited state charge carrier distributions and the excited state relaxation rates.

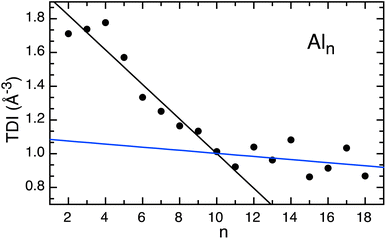Fig. 5 The total delocalization index for Al_n, (n < 18). The black trend line fits Al₃–Al₁₀, whereas the blue trend line fits Al₁₁–Al₂₀.

Below n = 10, the clusters retain a molecular character, and the changing TDI values reveal that as the cluster size increases, the charge carriers become increasingly delocalized. This result shows a significant change in the electronic behavior from photoexcitation in smaller clusters comparatively to larger clusters and highlights the onset of metallicity as cluster size increases. The clusters are sufficiently small such that electrostatic interactions between the hole and the electron are efficient for relaxation. Delocalization enables shorter excited state lifetimes and similar electronic relaxation pathways, a feature of metallic electron behavior.

Photoelectron spectra explored (Al)_n⁻ clusters up to n = 75, and suggested the ground state clusters adopt a fcc structure rather than a spherical jellium shell.⁶⁵ A wide variety of low-lying isomers may be present for neutral clusters, particularly for n > 13.⁶⁶ It has been suggested that the hybridization between the atomic s-and p-states is independent of cluster structure.⁶⁵ Therefore, it is unlikely that the inclusion of higher energy isomers will significantly change the calculated trends found in the TDI values. Furthermore, TD-DFT calculations become computationally cost prohibitive for larger clusters, and our calculations cover the size range found to be experimentally interesting and therefore provides insight to the transition in trend noted at n = 9. The metallic behavior noted in the relaxation dynamics aligns well with the TDI and therefore highlights delocalization of the charge carriers and related cluster diameter as an important feature for driving excited state relaxation in such homogeneous clusters.

4. Conclusions

The excited state dynamics of neutral Al_n clusters are measured through ultrafast time-resolved mass spectrometry and shown to align with two distinct trends. We demonstrate the power of this approach to highlight a sharp change in the collective electronic properties at a surprisingly small cluster size. The lifetimes recorded for small clusters (n < 10) decrease nearly linear with size and are attributed to molecular character, whereas the lifetimes of larger clusters are nearly identical (∼300 fs) and align with electron–lattice measurements in bulk Al and therefore suggests the onset of metallic behavior. These trends align with the charge carrier delocalization properties identified through TD-DFT calculations. These results demonstrate the evolution of electronic properties in small clusters and suggests the onset of metallic behavior occurs at the small cluster size of n = 9. The relaxation dynamics are independent of the detailed changes in the ground state electronic and geometric structure of the clusters as they change in size, enabling particularly stable clusters to exhibit nearly identical excited state dynamics as their nearest neighbors.

Author contributions

CKJ and CHR collected the experimental data. CHR and SGS performed the calculations, and SGS wrote the paper with contributions from all authors.

Data availability

The data supporting this article describing the experimental fitting coefficients have been included as part of the ESI.†

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

We gratefully acknowledge support from ASU startup funds.

References

1. H. Liu, J. Qiu, W. Zhang, M. Zhang, Z. Dou and L. Chen, Lifetime prediction and reliability analysis for aluminum electrolytic capacitors in EV charging module based on mission profiles, Front. Electron., 2023, 4, 1226006.
2. M. Wittmer, Barrier layers: Principles and applications in microelectronics, J. Vac. Sci. Technol., A, 1984, 2, 273–280.
3. D. C. Curtolo, N. Xiong, S. Friedrich and B. Friedrich, High- and Ultra-High-Purity Aluminum, a Review on Technical Production Methodologies, Metals, 2021, 11, 1407.
4. Y. Yang, A. Kushima, W. Han, H. Xin and J. Li, Liquid-Like, Self-Healing Aluminum Oxide during Deformation at Room Temperature, Nano Lett., 2018, 18, 2492–2497.
5. S. Narasimha, A. Rohatgi and A. W. Weeber, An optimized rapid aluminum back surface field technique for silicon solar cells, IEEE Trans. Electron Devices, 1999, 46, 1363–1370.
6. A. Niedermayr, M. Volkov, S. A. Sato, N. Hartmann, Z. Schumacher, S. Neb, A. Rubio, L. Gallmann and U. Keller, Few-Femtosecond Dynamics of Free-Free Opacity in Optically Heated Metals, Phys. Rev. X, 2022, 12, 021045.
7. V. K. Patel, A. Joshi, S. Kumar, A. S. Rathaur and J. K. Katiyar, Molecular Combustion Properties of Nanoscale Aluminum and Its Energetic Composites: A Short Review, ACS Omega, 2021, 6, 17–27.
8. M. Flannery, T. G. Desai, T. Matsoukas, S. Lotfizadeh and M. A. Oehlschlaeger, Passivation and Stabilization of Aluminum Nanoparticles for Energetic Materials, J. Nanomater., 2015, 2015, 1–12.
9. B. Y. Mueller and B. Rethfeld, Relaxation dynamics in laser-excited metals under nonequilibrium conditions, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035139.
10. L. Waldecker, R. Bertoni, R. Ernstorfer and J. Vorberger, Electron-Phonon Coupling and Energy Flow in a Simple Metal beyond the Two-Temperature Approximation, Phys. Rev. X, 2016, 6, 021003.
11. L. Yuan, M. Lou, B. D. Clark, M. Lou, L. Zhou, S. Tian, C. R. Jacobson, P. Nordlander and N. J. Halas, Morphology-Dependent Reactivity of a Plasmonic Photocatalyst, ACS Nano, 2020, 14, 12054–12063.
12. Y. Ekinci, H. H. Solak and J. F. Löffler, Plasmon resonances of aluminum nanoparticles and nanorods, J. Appl. Phys., 2008, 104, 083107.
13. D. Gérard and S. K. Gray, Aluminium plasmonics, J. Phys. D: Appl. Phys., 2015, 48, 184001.
14. C. Langhammer, M. Schwind, B. Kasemo and I. Zorić, Localized Surface Plasmon Resonances in Aluminum Nanodisks, Nano Lett., 2008, 8, 1461–1471.
15. A. Taguchi, Y. Saito, K. Watanabe, S. Yijian and S. Kawata, Tailoring plasmon resonances in the deep-ultraviolet by size-tunable fabrication of aluminum nanostructures, Appl. Phys. Lett., 2012, 101, 081110.
16. H. Wu, X. Cheng, H. Dong, S. Xie and S. He, Aluminum nanocrystals evolving from cluster to metallic state: Size tunability and spectral evidence, Nano Res., 2022, 15, 838–844.
17. D. Peckus, J. Henzie, T. Tamulevičius, M. Andrulevičius, A. Lazauskas, E. Rajackaitė, Š. Meškinis and S. Tamulevičius, Ultrafast relaxation dynamics of aluminum nanoparticles in solution, Phys. E, 2020, 117, 113795.
18. V. O. Kiohara, E. F. V. Carvalho, C. W. A. Paschoal, F. B. C. Machado and O. Roberto-Neto, DFT and CCSD(T) electronic properties and structures of aluminum clusters: Al_n^x (n=1–9, x=0, ±1), Chem. Phys. Lett., 2013, 568–569, 42–48.
19. B. K. Rao and P. Jena, Evolution of the electronic structure and properties of neutral and charged aluminum clusters: A comprehensive analysis, J. Chem. Phys., 1999, 111, 1890–1904.
20. S. R. Miller, N. E. Schultz, D. G. Truhlar and D. G. Leopold, A study of the ground and excited states of Al₃ and Al₃⁻. II. Computational analysis of the 488 nm anion photoelectron spectrum and a reconsideration of the Al₃ bond dissociation energy, J. Chem. Phys., 2009, 130, 024304.
21. L.-P. Tan, D. Die and B.-X. Zheng, Growth mechanism, electronic properties and spectra of aluminum clusters, Spectrochim. Acta, Part A, 2022, 267, 120545.
22. R. Fournier, Trends in Energies and Geometric Structures of Neutral and Charged Aluminum Clusters, J. Chem. Theory Comput., 2007, 3, 921–929.
23. M. Y. Chou and M. L. Cohen, Electronic shell structure in simple metal clusters, Phys. Lett. A, 1986, 113, 420–424.
24. R. L. Johnston, C. N. R. Rao and P. P. Edwards, The development of metallic behaviour in clusters, Philos. Trans. R. Soc., A, 1998, 356, 211–230.
25. O. C. Thomas, W. Zheng, S. Xu and K. H. Bowen, Onset of Metallic Behavior in Magnesium Clusters, Phys. Rev. Lett., 2002, 89, 213403.
26. K. Rademann, B. Kaiser, U. Even and F. Hensel, Size dependence of the gradual transition to metallic properties in isolated mercury clusters, Phys. Rev. Lett., 1987, 59, 2319–2321.
27. X. Li, H. Wu, X.-B. Wang and L.-S. Wang, s - p Hybridization and Electron Shell Structures in Aluminum Clusters: A Photoelectron Spectroscopy Study, Phys. Rev. Lett., 1998, 81, 1909–1912.
28. M. Aeschlimann, M. Bauer and S. Pawlik, Competing nonradiative channels for hot electron induced surface photochemistry, Chem. Phys., 1996, 205, 127–141.
29. M. Wolf, Femtosecond dynamics of electronic excitations at metal surfaces, Surf. Sci., 1997, 377–379, 343–349.
30. C. Frischkorn and M. Wolf, Femtochemistry at Metal Surfaces: Nonadiabatic Reaction Dynamics, Chem. Rev., 2006, 106, 4207–4233.
31. J. M. Garcia and S. G. Sayres, Increased Excited State Metallicity in Neutral Cr₂O_n Clusters (n < 5) upon Sequential Oxidation, J. Am. Chem. Soc., 2021, 143, 15572–15575.
32. K. Koyasu, C. Braun, S. Proch and G. Ganteför, The metal-semiconductor transition monitored by excited state lifetimes of Al₄O_m⁻ clusters, Appl. Phys. A, 2010, 100, 431–436.
33. G. B. Griffin, A. Kammrath, O. T. Ehrler, R. M. Young, O. Cheshnovsky and D. M. Neumark, Auger recombination dynamics in clusters, Chem. Phys., 2008, 350, 69–74.
34. G. B. Griffin, O. T. Ehrler, A. Kammrath, R. M. Young, O. Cheshnovsky and D. M. Neumark, Auger recombination and excited state relaxation dynamics in Hg_n⁻ (n=9–20) anion clusters, J. Chem. Phys., 2009, 130, 231103.
35. N. Pontius, M. Neeb, W. Eberhardt, G. Lüttgens and P. S. Bechthold, Ultrafast relaxation dynamics of optically excited electrons in Ni₃⁻, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 035425.
36. N. Pontius, P. S. Bechthold, M. Neeb and W. Eberhardt, Ultrafast Hot-Electron Dynamics Observed in Pt₃⁻ Using Time-Resolved Photoelectron Spectroscopy, Phys. Rev. Lett., 2000, 84, 1132–1135.
37. J. R. R. Verlet, A. E. Bragg, A. Kammrath, O. Cheshnovsky and D. M. Neumark, Time-resolved relaxation dynamics of Hg_n⁻ (11 ≤ n ≤ 16, n=18) clusters following intraband excitation at 1.5 eV, J. Chem. Phys., 2004, 121, 10015–10025.
38. J. M. Garcia, R. E. Shaffer and S. G. Sayres, Ultrafast pump–probe spectroscopy of Neutral Fe_nO_m Clusters (n, m < 16), Phys. Chem. Chem. Phys., 2020, 22, 24624–24632.
39. J. M. Garcia, L. F. Heald, R. E. Shaffer and S. G. Sayres, Oscillation in Excited State Lifetimes with Size of Sub-nanometer Neutral (TiO₂)_n Clusters Observed with Ultrafast Pump–Probe Spectroscopy, J. Phys. Chem. Lett., 2021, 12, 4098–4103.
40. F.-C. Chuang, C. Z. Wang and K. H. Ho, Structure of neutral aluminum clusters Al_n (2 ≤ n ≤ 23) : Genetic algorithm tight-binding calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 125431.
41. T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57.
42. F. Rabilloud, Assessment of the Performance of Long-Range-Corrected Density Functionals for Calculating the Absorption Spectra of Silver Clusters, J. Phys. Chem. A, 2013, 117, 4267–4278.
43. D. M. Cox, D. J. Trevor, R. L. Whetten, E. A. Rohlfing and A. Kaldor, Aluminum clusters: Magnetic properties, J. Chem. Phys., 1986, 84, 4651–4656.
44. J. Akola, H. Häkkinen and M. Manninen, Ionization potential of aluminum clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3601–3604.
45. A. Halder and V. V. Kresin, Nanocluster ionization energies and work function of aluminum, and their temperature dependence, J. Chem. Phys., 2015, 143, 164313.
46. K. E. Schriver, J. L. Persson, E. C. Honea and R. L. Whetten, Electronic shell structure of group-IIIA metal atomic clusters, Phys. Rev. Lett., 1990, 64, 2539–2542.
47. M. F. Jarrold, J. E. Bower and J. S. Kraus, Collision induced dissociation of metal cluster ions: Bare aluminum clusters, Al_n⁺ (n =3–26), J. Chem. Phys., 1987, 86, 3876–3885.
48. A. Papoulia, J. Ekman and P. Jönsson, Extended transition rates and lifetimes in AlI and AlII from systematic multiconfiguration calculations, Astron. Astrophys., 2019, 621, A16.
49. Z. Fu, G. W. Lemire, G. A. Bishea and M. D. Morse, Spectroscopy and electronic structure of jet-cooled Al₂, J. Chem. Phys., 1990, 93, 8420–8441.
50. M. F. Cai, T. P. Dzugan and V. E. Bondybey, Fluorescence Studies of Laser Vaporized Aluminum: Evidence for A³Π_u Ground State of Aluminum Dimer, Chem. Phys. Lett., 1989, 155, 430–436.
51. H. Basch, The Electronic States of Al₃, Chem. Phys. Lett., 1987, 136, 289–293.
52. J. S. Tse, Stability and potential energy surface of the three low lying electronic states of Al₃, J. Chem. Phys., 1990, 92, 2488–2494.
53. Z. Fu, G. W. Lemire, Y. M. Hamrick, S. Taylor, J.-C. Shui and M. D. Morse, Spectroscopic studies of the jet-cooled aluminum trimer, J. Chem. Phys., 1988, 88, 3524–3531.
54. C.-Y. Cha, G. Ganteför and W. Eberhardt, The development of the 3 p and 4 p valence band of small aluminum and gallium clusters, J. Chem. Phys., 1994, 100, 995–1010.
55. L. Hanley, S. A. Ruatta and S. L. Anderson, Collision–induced dissociation of aluminum cluster ions: Fragmentation patterns, bond energies, and structures for Al₂⁺ – Al₇⁺, J. Chem. Phys., 1987, 87, 260–268.
56. Y. L. Zhao and R. J. Zhang, Structures and Properties of Stable Al₄, Al₄⁺, and Al₄⁻ Comparatively Studied by ab Initio Theories, J. Phys. Chem. A, 2007, 111, 7189–7193.
57. T. H. Upton, Structural, Electronic, and Chemisorption Properties of Small Aluminum Clusters, Phys. Rev. Lett., 1986, 56, 2168–2171.
58. T. Sommerfeld, Al₄⁻ cluster anion: Electronic structure, excited states, and electron detachment, J. Chem. Phys., 2010, 132, 124305.
59. P. Gerhardt, M. Niemietz, Y. Dok Kim and G. Ganteför, Fast electron dynamics in small aluminum clusters: non-magic behavior of a magic cluster, Chem. Phys. Lett., 2003, 382, 454–459.
60. S. Xu, A. A. Mikhailovsky, J. A. Hollingsworth and V. I. Klimov, Hole intraband relaxation in strongly confined quantum dots: Revisiting the “phonon bottleneck” problem, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 045319.
61. V. V. Kresin and Yu. N. Ovchinnikov, Fast electronic relaxation in metal nanoclusters via excitation of coherent shape deformations, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 115412.
62. M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, Excitation energies in density functional theory: An evaluation and a diagnostic test, J. Chem. Phys., 2008, 128, 044118.
63. L. F. Heald, J. M. Garcia and S. G. Sayres, Oxygen Deficiencies in Titanium Oxide Clusters as Models for Bulk Defects, J. Phys. Chem. A, 2022, 126, 211–220.
64. J. M. Garcia and S. G. Sayres, Orbital-dependent photodynamics of strongly correlated nickel oxide clusters, Phys. Chem. Chem. Phys., 2022, 24, 5590–5597.
65. L. Ma, B. V. Issendorff and A. Aguado, Photoelectron spectroscopy of cold aluminum cluster anions: Comparison with density functional theory results, J. Chem. Phys., 2010, 132, 104303.
66. A. Aguado and J. M. López, Structures and stabilities of Al_n⁺, Al_n, and Al_n⁻ (n=13–34) clusters, J. Chem. Phys., 2009, 130, 064704.

---

Footnotes

† Electronic supplementary information (ESI) available: The transient dynamics measured for the larger clusters (Al₁₉–Al₄₃) are presented in Fig. S1, and additional details for the topological calculations. See DOI: https://doi.org/10.1039/d4nr02032d

‡ These authors contributed equally.

---