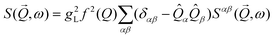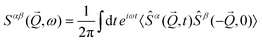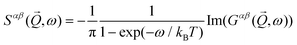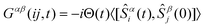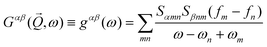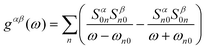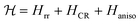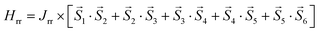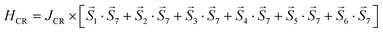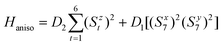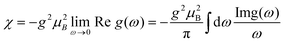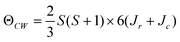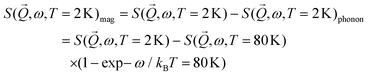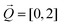Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic exchange, anisotropy and excitonic fluctuations in a [NiII7] Anderson wheel†
Emily H.
Payne
 a,
Lucinda R. B.
Wilson
a,
Lucinda R. B.
Wilson
 a,
Mukesh K.
Singh
a,
Mukesh K.
Singh
 a,
Gary S.
Nichol
a,
Gary S.
Nichol
 a,
J. R.
Stewart
b,
V.
Garcia-Sakai
a,
J. R.
Stewart
b,
V.
Garcia-Sakai
 b,
R. A.
Ewings
b,
Harry
Lane
c,
Jürgen
Schnack
b,
R. A.
Ewings
b,
Harry
Lane
c,
Jürgen
Schnack
 *d,
Chris
Stock
*c and
Euan K.
Brechin
*d,
Chris
Stock
*c and
Euan K.
Brechin
 *a
*a
aEaStCHEM School of Chemistry, The University of Edinburgh, David Brewster Road, Edinburgh, EH9 3FJ, Scotland, UK. E-mail: E.Brechin@ed.ac.uk
bISIS Pulsed Neutron and Muon Source, STF Rutherford Appleton Laboratory, Harwell Campus, Didcot, Oxon OX11 0QX, UK
cSchool of Physics and Astronomy, The University of Edinburgh, Edinburgh, EH9 3JZ, Scotland, UK. E-mail: C.Stock@ed.ac.uk
dFakultät für Physik, Universität Bielefeld, Postfach 100131, D-33501 Bielefeld, Germany. E-mail: jschnack@uni-bielefeld.de
First published on 23rd November 2023
Abstract
The solvothermal reaction of Ni(ClO4)2·6H2O with hmpH and picH in a basic MeOH solution affords [Ni7(hmp)7.55(pic)4.45](ClO4)2·6MeOH (1·6MeOH) directly upon cooling the mother liquor. The metallic skeleton of 1 describes a [NiII7] centred hexagon, commonly referred to as an Anderson wheel. Magnetic measurements reveal ferromagnetic exchange between the central Ni ion and the ring Ni ions, and antiferromagnetic exchange between neighbouring ring Ni ions. They also confirm the presence of easy-plane anisotropy for the central Ni ion, and easy-axis anisotropy for the ring Ni ions, in agreement with DFT calculations and neutron scattering. For the analysis of the latter we apply an excitonic formalism using a Green's function response theory.
Introduction
Complexes of NiII have long played a prominent role in the field of molecular magnetism, from the early studies of magneto-structural correlations in Ni dimers1 and cubes2 and the emergence of Single-Molecule Magnets (SMMs),3 to the design of molecules exhibiting very large magnetic anisotropies4 and possessing long coherence times.5 During this journey coordination chemists have developed a breadth of synthetic strategies in order to construct complexes with a variety of nuclearities and topologies. Amongst these, [Ni4] SMMs have proven to be a particularly fruitful source of information on exchange bias effects,6 antisymmetric exchange,7 quantum tunnelling,8 transverse anisotropy,9 and Berry Phase interference.10 Other common structural motifs demonstrating fascinating magnetic properties include wheels11 and discs.12 The latter offer interest from a variety of perspectives, including as molecular analogues of 2D lattices,13 model complexes to examine spin frustration14 and as robust platforms to quantitatively analyse magneto-structural correlations.15Planar heptanuclear discs conforming to centred hexagons are often referred to as Anderson or Anderson-Evans wheels,16 and are a common structure type in both polyoxometalate chemistry17 and clusters of paramagnetic 3d ions.18 A search of the Cambridge Structural Database (CSD) reveals that there are twenty nine [NiII7] Anderson wheels.19–38 Of these, fifteen have had their magnetic behaviour reported, but only five have been subject to quantitative analysis.21,26,30,36,37 This is perhaps not surprising. Given the potential for multiple (≤12) exchange interactions, and numerous g and D values, even greatly simplified models can prove computationally demanding. In general, extracting exchange coupling constants (J) has been achieved using a model which assumes just two interactions (Fig. 1), one between the central Ni ion and the Ni ions in the outer ring (Jcr) and one between neighbouring Ni ions around the ring (Jrr). However, there is no agreement regarding the nature and magnitude of these values for those complexes exhibiting competing ferro- and antiferromagnetic exchange, despite the presence of similar Ni–X–Ni angles. Some reports suggest Jcr is ferromagnetic and Jrr is antiferromagnetic, and others state Jcr is antiferromagnetic and Jrr is ferromagnetic. The only clear-cut case is when all bridges are μ2/3-N3− ions which promote ferromagnetic exchange for both Jcr and Jrr.30 Based on magneto-structural correlations developed for [Ni4O4] cubanes,2 one might expect Jcr to be ferromagnetic and Jrr antiferromagnetic in all O-bridged species given that the former are mediated by μ3-O atoms with smaller Ni–O–Ni angles than the latter, which are bridged by μ2-O atoms. Indeed, this is what is observed in a [AlIII2NiII5] Anderson wheel reported recently, where Jcr = +10 cm−1 and Jrr = −5 cm−1 (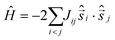 formalism).15 There is also no agreement on the sign and magnitude of the zero-field splitting (DNi) for the central or ring NiII ions. In order to investigate the magneto-structural relationship in this family of complexes further, and to unequivocally extract the relevant spin-Hamiltonian parameters, we have synthesised and characterised the complex [Ni7(hmp)7.55(pic)4.45](ClO4)2·6MeOH (1·6MeOH; Fig. 1, hmpH = 2-(hydroxymethyl)pyridine, picH = picolinic acid) using a combination of susceptibility and magnetisation measurements, magnetic neutron spectroscopy and first principles calculations. This complementary trio of techniques, employed for the first time in the analysis of [Ni7] Anderson wheels, reveals the presence of competing ferro- and antiferromagnetic exchange interactions and both easy plane and easy axis anisotropy.
formalism).15 There is also no agreement on the sign and magnitude of the zero-field splitting (DNi) for the central or ring NiII ions. In order to investigate the magneto-structural relationship in this family of complexes further, and to unequivocally extract the relevant spin-Hamiltonian parameters, we have synthesised and characterised the complex [Ni7(hmp)7.55(pic)4.45](ClO4)2·6MeOH (1·6MeOH; Fig. 1, hmpH = 2-(hydroxymethyl)pyridine, picH = picolinic acid) using a combination of susceptibility and magnetisation measurements, magnetic neutron spectroscopy and first principles calculations. This complementary trio of techniques, employed for the first time in the analysis of [Ni7] Anderson wheels, reveals the presence of competing ferro- and antiferromagnetic exchange interactions and both easy plane and easy axis anisotropy.
Experimental
Experimental procedures
All chemicals were procured from commercial suppliers and used as received (reagent grade).Synthesis of [Ni7(hmp)7.55(pic)4.45](ClO4)2·6MeOH (1·6MeOH)
Ni(ClO4)2·6H2O (0.366 g, 1 mmol) was dissolved in MeOH (20 mL), with NaOMe (0.162 g, 3 mmol) yielding a pale blue solution. To this, hmpH (0.142 mL, 1.5 mmol) was added dropwise followed by picH (0.184 g, 1.5 mmol), which resulted in a deep blue solution. The solution was stirred for 12 hours and then transferred to a Teflon-lined, stainless steel autoclave which was heated for 24 hours at 140 °C. This was then allowed to cool for a further 24 hours, yielding translucent pale blue plate-shaped crystals. Anal. calcd (%) C, 43.91; H, 3.23; N, 8.54. Found: C, 43.81; H, 3.39; N, 8.49. Yield: 56%.Note: caution should be taken when using/heating the potentially explosive perchlorate anion.
Crystallographic details
A suitable crystal with dimensions 0.48 × 0.14 × 0.04 mm3 was selected and mounted on a MITIGEN holder in Paratone oil on a Rigaku Oxford Diffraction XCalibur diffractometer. The crystal was kept at a steady T = 120.0 K during data collection. The structure was solved with the ShelXT solution program using dual methods, employing Olex2 as the graphical interface. The model was refined with ShelXL 2018/3 using full matrix least squares minimisation on F2.39–41 Three of the ligands were modelled as a disordered mixture of hmp and pic, as evidenced by a residual peak in a difference map which corresponded to the additional O site in the pic ligand. Each disorder was refined with a separate free variable. Specific occupancy values are given in the CIF; this explains the fractional values in the formula. Other than constructing an appropriate disorder model for the CH2 group the ring atoms of each hmp/pic disorder were not split as this was not justified by either the displacement ellipsoids or residual electron density peaks.Crystal data. C78H87.09Cl2N12Ni7O30.45, Mr = 2161.75, triclinic, P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (No. 2), a = 12.1951(3) Å, b = 13.4801(4) Å, c = 15.0616(4) Å, α = 110.946(3)°, β = 97.395(2)°, γ = 106.809(2)°, V = 2137.68(10) Å3, T = 120.0 K, Z = 1, Z′ = 0.5, μ(MoKα) = 1.662, 57
(No. 2), a = 12.1951(3) Å, b = 13.4801(4) Å, c = 15.0616(4) Å, α = 110.946(3)°, β = 97.395(2)°, γ = 106.809(2)°, V = 2137.68(10) Å3, T = 120.0 K, Z = 1, Z′ = 0.5, μ(MoKα) = 1.662, 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 226 reflections measured, 10
226 reflections measured, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 646 unique (Rint = 0.0441) which were used in all calculations. The final wR2 was 0.1078 (all data) and R1 was 0.0465 (I ≥ 2σ(I)). CCDC 2286832.† Powder XRD data of compound 1 (Fig. S1†) were collected on a polycrystalline powder using a Bruker D8 ADVANCE in transmission mode fitted with a LynxEye detector using Cu radiation at 40 kV, 40 mA and a Johansson monochromator, 2 mm divergence slit and 2.5° Soller slits on the incident beam side. Bruker's DIFFRAC software was used to control the diffractometer. Diffraction data were measured from 2θ = 5°–40°; step size, 0.0101°.
646 unique (Rint = 0.0441) which were used in all calculations. The final wR2 was 0.1078 (all data) and R1 was 0.0465 (I ≥ 2σ(I)). CCDC 2286832.† Powder XRD data of compound 1 (Fig. S1†) were collected on a polycrystalline powder using a Bruker D8 ADVANCE in transmission mode fitted with a LynxEye detector using Cu radiation at 40 kV, 40 mA and a Johansson monochromator, 2 mm divergence slit and 2.5° Soller slits on the incident beam side. Bruker's DIFFRAC software was used to control the diffractometer. Diffraction data were measured from 2θ = 5°–40°; step size, 0.0101°.
Magnetic thermodynamic measurements
Magnetic susceptibility and magnetisation measurements were performed on a powdered crystalline sample restrained in eicosane in the temperature and fields ranges T = 2–300 K, B = 0.1 T and T = 2–6 K, B = 0.5–7.0 T, respectively, using a Quantum Design MPMS XL SQUID magnetometer equipped with a 7 T dc magnet. The observed paramagnetic susceptibilities were corrected for diamagnetic contributions using Pascal's constants.Computational details
Density Functional Theory (DFT) calculations in the Gaussian16 suite42 have been performed to estimate the magnetic exchange interactions between the NiII centres on a [Ni5Zn2] model, constructed by replacing two NiII ions with two ZnII ions (Fig. S2a and b†) in the XRD structure of complex 1. The hybrid B3LYP functional43 together with the TZV basis set44 have been employed for the Ni and Zn atoms, the 6-31G* basis set has been used for the O and N atoms, while the 6-31G basis set has used for the C and H atoms.45 Noodleman's broken symmetry approach46 has been employed for estimating the magnetic exchange interactions. Spin configurations used to estimate the exchange coupling constants are summarised in Table S1.† Pairwise interactions have been calculated to estimate the magnetic interaction between (a) the central NiII ion and the outer ring NiII ions (Jcr), and (b) between the ring NiII ions (Jrr), in dimeric models 1A–1B (Fig. S2c and d†), respectively. We have also developed magneto-structural correlations on model 1C (Fig. S2e†) to check the dependence of the magnetic exchange interaction on the average Ni–O distance and average Ni–O–Ni angle. We have made several mono- and dimetallic models (1D–1G, Fig. S2f–i†) from complex 1 to estimate the zero field splitting parameters for each NiII centre using the ORCA software suite (version ORCA 4.0).47 The zeroth-order regular approximation (ZORA) method together with the ZORA contracted version of the basis set (ZORA-def2-TZVP for Ni, Zn and ZORA-def2-SVP for rest of the elements) have been used. The calculation further utilised the resolution of identity (RI) approximation with the auxiliary def2-TZVP and def2-SVP Coulomb fitting basis sets.48 During state-average complete active space self-consistent field (SA-CASSCF) calculations, we have included eight electrons in five d-orbitals (CAS (8 electrons/5 3d-orbitals)) in the active space. Ten triplet and fifteen singlet roots are considered during CASSCF calculations. To consider the dynamic correlation, we have performed 2nd order N-electron valence perturbation theory (NEVPT2) calculations.49 We have employed integration Grid 6 for the Ni and Zn ions, and Grid 5 for remaining elements.Neutron spectroscopy, data correction and background subtraction
Neutron spectroscopy measurements were performed on the LET (ISIS, Didcot) cold chopper spectrometer. The sample was fully protonated for these measurements, resulting in a large background from the incoherent cross section from H-atoms, as discussed below. Given the large amount of neutron incoherent scattering resulting from H and Ni, there was a significant temperature independent background in the spectroscopic data taken on LET. This primarily originated from elastic scattering leaking into inelastic channels due to instrumental effects such as finite resolution. To account for this, we have applied the principle of detailed balance to remove this background, following previous scattering studies where this has been successfully used.50 This analysis depends on the fact that at a fixed momentum and energy transfer, the measured intensities at the neutron energy gain (negative energy transfer) and energy loss (positive energy transfer) are related by the following expression with the energy transfer defined as E ≡ħω = Ei − Ef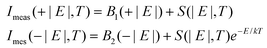 | (1) |
In our experiment on LET, data were collected at four different temperatures, T = 2, 20, 50, and 80 K. With data at ±|E| at each temperature, this gives eight data points for a given momentum Q and energy transfer |E|. Assuming temperature independent background parameters of B1 and B2 and four values of S(|E|, T = 2, 20, 50, and 80 K), this is a closed problem of fitting six parameters to eight data points for each momentum and energy transfer. To obtain the temperature independent background we performed a least-squares fit to each Q and |E| to obtain the temperature independent background parameters B1,2. We then used this to subtract off the background from the data, leaving the structure factor S(|E|, T) which can be computed theoretically and compared to first principle calculations as discussed below.
Results and discussion
Synthesis and structure
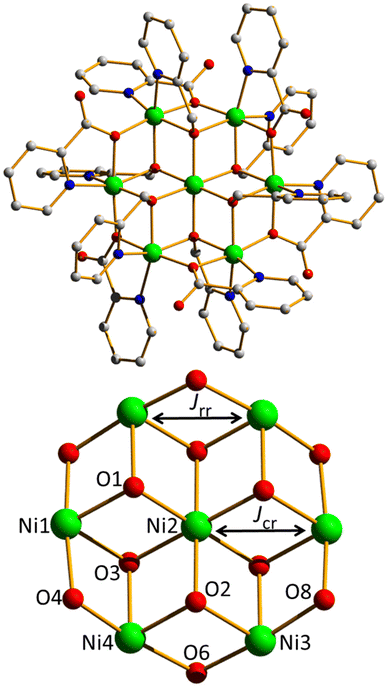
The solvothermal reaction of Ni(ClO4)2·6H2O with hmpH and picH in a basic MeOH solution affords blue plate shaped crystals of formula [Ni7(hmp)7.55(pic)4.45](ClO4)2·6MeOH (1·6MeOH) directly upon cooling the mother liquor. The crystals were found to be in a triclinic cell and structure solution was carried out in the space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . The asymmetric unit (ASU) comprises half of the formula. The metallic skeleton describes a [NiII7] centred hexagon, commonly referred to as an Anderson wheel. The central Ni ion is connected to the six ring Ni ions through a total of six μ3-O atoms deriving from the hmp ligands with Ni–O–Ni angles in range ∼96.4–99.0°. These O-atoms also provide the connectivity between neighbouring Ni ions around the inner rim of the [NiII6] ring with Ni–O–Ni angles in the range ∼97.2–98.4°. The outer rim of the ring is connected by six μ2-O atoms derived from the pic ligands with Ni–O–Ni angles in range ∼100.3–100.5°. Note the latter are larger than the former. All six NiII ions are six-coordinate and in distorted octahedral geometries. The central NiII ion possesses a {NiO6} coordination sphere, while those in the ring are {NiO4N2}. Note that the hmp/pic disorder in three of the organic ligands, as described in the crystallography details section, has no effect upon the Ni coordination spheres. The two ClO4 anions sit above and below the [Ni7] plane, with the MeOH molecules of crystallisation H-bonded to the non-bonded O-arm of the pic ligands (O⋯(H)O, ∼2.75–2.81 Å). In the extended structure this leads to a brickwork-like arrangement of cluster cations. The closest intermolecular Ni⋯Ni distances are >7.7 Å.
. The asymmetric unit (ASU) comprises half of the formula. The metallic skeleton describes a [NiII7] centred hexagon, commonly referred to as an Anderson wheel. The central Ni ion is connected to the six ring Ni ions through a total of six μ3-O atoms deriving from the hmp ligands with Ni–O–Ni angles in range ∼96.4–99.0°. These O-atoms also provide the connectivity between neighbouring Ni ions around the inner rim of the [NiII6] ring with Ni–O–Ni angles in the range ∼97.2–98.4°. The outer rim of the ring is connected by six μ2-O atoms derived from the pic ligands with Ni–O–Ni angles in range ∼100.3–100.5°. Note the latter are larger than the former. All six NiII ions are six-coordinate and in distorted octahedral geometries. The central NiII ion possesses a {NiO6} coordination sphere, while those in the ring are {NiO4N2}. Note that the hmp/pic disorder in three of the organic ligands, as described in the crystallography details section, has no effect upon the Ni coordination spheres. The two ClO4 anions sit above and below the [Ni7] plane, with the MeOH molecules of crystallisation H-bonded to the non-bonded O-arm of the pic ligands (O⋯(H)O, ∼2.75–2.81 Å). In the extended structure this leads to a brickwork-like arrangement of cluster cations. The closest intermolecular Ni⋯Ni distances are >7.7 Å.
Dc magnetic susceptibility and magnetisation measurements
Dc magnetic susceptibility (χ) and magnetisation (M) measurements were performed on a powdered microcrystalline sample of 1 in the T = 300–2 K, B = 0.1 T and T = 2–6 K, B = 0.5–7.0 T ranges, respectively. These data are shown in Fig. 2 (and Fig. S3†) in the form of the χT product versus T and M vs. B. The χT product at T = 300 K is 8.6 cm3 K mol−1, similar to the Curie constant expected for seven uncorrelated S = 1 ions with g = 2.2 (8.5 cm3 K mol−1). As temperature decreases the χT product slowly increases to a maximum value of 12.0 cm3 K mol−1 at T = 20 K, before decreasing at lower temperatures to a value of 10.5 cm3 K mol−1 at T = 2.0 K. The magnetisation data initially increase rapidly with increasing magnetic field (M = 7μB at B = 1 T and T = 2 K) T and then rise more gradually thereafter to a maximum value of M = 11μB at B = 7 T and T = 2 K. The susceptibility and magnetisation data are therefore indicative of the presence of both ferro- and antiferromagnetic exchange interactions. The susceptibility data can be simulated nicely (Fig. S3†) with an isotropic spin-Hamiltonian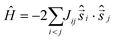 to a model that assumes just two independent exchange interactions, Jcr and Jrr, describing the interaction between the central Ni ion and ring Ni ions, and between ring Ni ions, respectively.
to a model that assumes just two independent exchange interactions, Jcr and Jrr, describing the interaction between the central Ni ion and ring Ni ions, and between ring Ni ions, respectively.
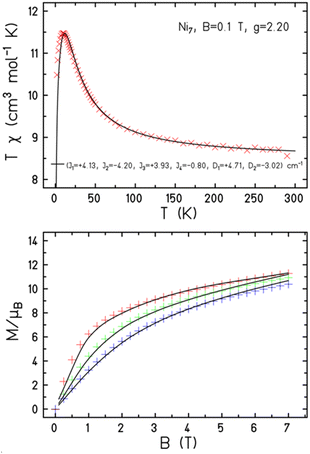 | ||
Fig. 2 Plot of the χT product vs. T (top) and M vs. B (bottom) for 1. The solid lines are a fit of the data to the model described in the text and Fig. S3.†J1, J3 = Jcr, J2, J4 = Jrr, D1 = zfs of central Ni, D2 = zfs of ring Ni. In the lower panel T = 2 K ( ), T = 4 K ( ), T = 4 K ( ), T = 6 K ( ), T = 6 K ( ). The best fit is for J1 = +4.13 cm−1, J2 = −4.20 cm−1, J3 = +3.93 cm−1, J4 = −0.80 cm−1, D1 = +4.71 cm−1, D2 = −4.02 cm−1. Uncertainties are estimated as 0.1–0.2 cm−1. ). The best fit is for J1 = +4.13 cm−1, J2 = −4.20 cm−1, J3 = +3.93 cm−1, J4 = −0.80 cm−1, D1 = +4.71 cm−1, D2 = −4.02 cm−1. Uncertainties are estimated as 0.1–0.2 cm−1. | ||
The fit can be improved by adding additional Jcr and Jrr interactions (J1–J4, Fig. S3†), permitted given the presence of just inversion symmetry in 1 (i.e. half the cluster is in the ASU). In all cases the Jcr interaction is found to be ferromagnetic and the Jrr interaction is found to be antiferromagnetic. However, this simple isotropic model does not fit the magnetization data in the full temperature and field range, particularly at high fields. Introduction of an anisotropic term 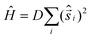 to account for the zero-field splitting associated with the octahedral NiII ions is therefore required, one for the central Ni ion with an {NiO6} coordination sphere (D1) and one for the ring Ni ions with {NiO4N2} coordination spheres (D2). The best fit of the susceptibility and magnetisation data with this model affords J1 = +4.13 cm−1, J2 = −4.20 cm−1, J3 = +3.93 cm−1, J4 = −0.80 cm−1, D1 = +4.71 cm−1 and D2 = −3.02 cm−1. Note the opposite signs of D1 and D2, positive for the central NiII ion and negative for the ring NiII ions.
to account for the zero-field splitting associated with the octahedral NiII ions is therefore required, one for the central Ni ion with an {NiO6} coordination sphere (D1) and one for the ring Ni ions with {NiO4N2} coordination spheres (D2). The best fit of the susceptibility and magnetisation data with this model affords J1 = +4.13 cm−1, J2 = −4.20 cm−1, J3 = +3.93 cm−1, J4 = −0.80 cm−1, D1 = +4.71 cm−1 and D2 = −3.02 cm−1. Note the opposite signs of D1 and D2, positive for the central NiII ion and negative for the ring NiII ions.
DFT calculations
To further support the sign and magnitude of the experimentally determined magnetic exchange interactions above, DFT calculations have been performed on a [Ni5Zn2] model created from the XRD structure of complex 1 (Fig. S2a and Table S1†). Considering symmetry and structural parameters, complex 1 has a total of five unique magnetic exchange interactions (J1 − J4, J1′ Fig. S2b†). The exchange between the central and ring NiII ions (Jcr = J1, J1′, J3) is calculated to be ferromagnetic and in the range +3.1 cm−1 ≤ Jcr ≤ +5.1 cm−1. The exchange between neighbouring ring NiII ions (Jrr = J2, J4) is calculated to be antiferromagnetic and in the range −1.6 cm−1 ≤ Jrr ≤ −6.0 cm−1. Thus, the signs and magnitudes of the DFT calculated values are in good agreement with the experimentally fitted values derived from the magnetic susceptibility and magnetisation measurements. They are also in agreement with previous magneto-structural studies performed on polymetallic NiII complexes in which larger average Ni–O–Ni angles result in an antiferromagnetic interaction and smaller average Ni–O–Ni angles result in a ferromagnetic interaction, with the crossover angle being ∼97–98°.1,2,15,51 Further DFT calculations on dimetallic models (Fig. S2c and d†) also confirm the ferromagnetic Jcr interaction (J1A = +8.2 cm−1) and antiferromagnetic Jrr interaction (J1B = −3.1 cm−1).To rationalise the magnitude and sign of the magnetic interactions, overlap integral calculations52 have been performed on the dimetallic models using the singly occupied molecular orbitals (SOMOs) of the NiII ions. Stronger overlap values between SOMOs leads to an antiferromagnetic interaction, whereas orthogonal/weak overlap values contribute to a ferromagnetic interaction. The overlap integral calculations suggest one moderate and three weak interactions for 1A and two moderate and two weak interactions for 1B. This leads to a ferromagnetic interaction for 1A and an antiferromagnetic interaction for 1B (Fig. S4 and 5†). Spin density analysis suggests strong mixing and delocalisation onto the coordinating ligand atoms followed by weak spin polarisation. The ring NiII ions have a spin density between 1.693–1.698 and the central NiII ion has a spin density of 1.735 (Fig. S6 and 7†). The smaller spin densities on the ring NiII ions can be attributed to the stronger spin delocalisation from the NiII ion to the N atom of the bridging ligand (between 0.050–0.063). As expected, the μ3-O bridging atoms have a larger spin density compared to the μ2-O bridging atoms.51 A magneto-structural correlation developed for model 1C (Fig. S2e†) with respect to the average Ni–O–Ni angle and average Ni–O distance follows the same trends observed for previously published O-bridged polymetallic NiII complexes, suggesting a strong dependence of the magnetic exchange interaction on the average Ni–O–Ni angle in particular (Fig. S8†).51
SHAPE analysis (Table S2†) suggests distorted octahedral geometries for all the NiII ions present, with the ring NiII ions [NiO4N2] being more distorted than the central NiII ion [NiO6] on account of the chelating hmp/pic ligands. For small distortions away from ideal Oh symmetry, as seen here, one would expect either easy axis or easy plane anisotropy with a magnitude of approximately |D| < 10 cm−1.52 Single ion anisotropy parameters for the four unique NiII ions present in 1 have been estimated using ab initio CASSCF/NEVPT2 calculations in the ORCA suite on model complexes 1D–1G (Fig. S2f–i†) derived from the XRD structure of complex 1.47Ab initio NEPVT2 calculations suggest easy axis anisotropy for the ring NiII ions in the range −5.4 cm−1 ≤ D2 ≤ −7.7 cm−1, and easy plane anisotropy, D1 = +7.3 cm−1, for the central NiII ion (Fig. S9 and Table S3†). The Dzz axes for Ni1–3 lie along the shortest Ni-μ3O distance, whereas for Ni4, Dzz is oriented along the longest Ni-μ3O distance (Fig. S10†). The negative and positive signs of D are thus associated with the compressed and elongated character of the octahedron, respectively.52 The calculated values are in agreement with the experimentally fitted values from the susceptibility and magnetization data, and consistent with values in the literature.52 The ground state electronic arrangements for the ring and the central NiII ions are found to be {(dyz)2 (dxz)2 (dxy)2 (dz2)1(dx2−y2)1} and {(dyz)2(dxy)2(dxz)2(dz2)1(dx2−y2)1} with the dominant spin conserved electronic transitions dxy → dx2−y2 and dxz → dx2−y2/dz2, respectively.
Excitonic magnetism
Above, a series of first principle calculations have been outlined producing a quantitative range for model parameters in the magnetic Hamiltonian of [Ni7]. In this section we validate these parameters through a comparison with magnetic neutron scattering data. We first discuss the definition of the structure factor in terms of correlations of magnetic spins. We then discuss a formalism to calculate this dynamic structure applying Green's functions formalism that links the measured neutron scattering cross section with mean field response theory. We then consider the magnetic Hamiltonian of [Ni7] and use this formalism to solve the case of an isolated [Ni7] molecule for both the excitation energy levels and their corresponding neutron intensities determined by dipolar selection rules. The intensity measured in an experiment of scattering neutrons off magnetic NiII ions is directly proportional to the structure factor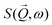 ,
, where gL is the Landé factor and f(Q) is the NiII form factor. The term
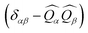 is the polarization factor, reflecting the fact that neutron scattering is only sensitive to the spin component perpendicular to the momentum transfer,
is the polarization factor, reflecting the fact that neutron scattering is only sensitive to the spin component perpendicular to the momentum transfer, 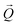 .
. 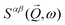 is the dynamic structure factor which is the Fourier transform of the spin–spin correlation function:
is the dynamic structure factor which is the Fourier transform of the spin–spin correlation function:where α, β = +,−, z. The dynamic structure factor
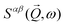 is related to the Green's response function
is related to the Green's response function 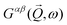 by
byTo relate the Greens function to the microscopic magnetic Hamiltonian, we note that in linear response theory, it is related to the Fourier transform of the retarded Green's function that is given by
The approach followed in previous works57 applying the Green's functions to neutron spectroscopy is to divide the magnetic Hamiltonian into two parts – a local single-ion part for the magnetic ion of interest (including terms like the crystalline electric field, spin–orbit coupling, and molecular fields), and an interion part describing interaction between magnetic ions (usually modelled in terms of a Heisenberg exchange). Here, we simplify this by considering 1 as a single ion entity with the eigenstates of the total magnetic Hamiltonian defined by {|n〉} with corresponding energy eigenvalues {ωn}. The Green's function is then reduced to the single-ion term,
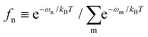 . For calculation purposes, we set ħω = E + iΓ where Γ can be physically interpreted as an energy broadening (or dampening) of the magnetic excitations sampled at an energy transfer of E. The final neutron cross section is then derived summing over all combinations of gαβ(ω). Note that in the low temperature T → 0 limit, this reduces to the simplified expression,
. For calculation purposes, we set ħω = E + iΓ where Γ can be physically interpreted as an energy broadening (or dampening) of the magnetic excitations sampled at an energy transfer of E. The final neutron cross section is then derived summing over all combinations of gαβ(ω). Note that in the low temperature T → 0 limit, this reduces to the simplified expression,where ωn0 ≡ ωn − ω0. This reduced expression avoids the need to sum over thermally excited inter-level transitions. The problem of calculating the neutron cross section then reduces to deriving the single ion response for 1. Given that each NiII ion is in a S = 1 state, from Hund's rules and the Pauli principle, each of the seven NiII sites have a three-fold multiplicity associated with different z-axis projections. This results in 1 having 37 = 2187 basis states. In this study, we have used these 2187 basis states to solve the following magnetic Hamiltonian exactly,
with Hrr, HCR, Haniso corresponding to ring, central, and anisotropic terms of the magnetic Hamiltonian. The NiII labelling and notation is schematically illustrated in Fig. S11.† These are explicitly given by,
where the indices 1–6 refer to the NiII ions on the ring and 7 the central NiII ion. This magnetic Hamiltonian divides up 1 into a problem with two exchange constants, Jrr and JCR, and two anisotropic terms, D1,2. Here we have used the result above that the spins on the outer wheel have uniaxial anisotropy while the inner spin has easy-plane anisotropy. Note that in the analysis discussed below, we have performed a fit without anisotropy, however this produces exchange constants that are unphysically large (for example JCR ∼ −4 meV = −32 cm−1) in comparison to the first principles calculations and experimental fits discussed above. To constrain the parameters used to describe the neutron response, it is important to consider the magnetic susceptibility which is related to the real part of the Green's response function and to the imaginary part via Kramers–Kronig relations.
In the high temperature paramagnetic limit the susceptibility scales as 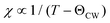 . In mean field theory, a plot of χ−1 as a function of temperature has an x-axis intercept defined by the Curie–Weiss temperature, ΘCW, and is related to the exchange constants by,
. In mean field theory, a plot of χ−1 as a function of temperature has an x-axis intercept defined by the Curie–Weiss temperature, ΘCW, and is related to the exchange constants by,
Neutron scattering
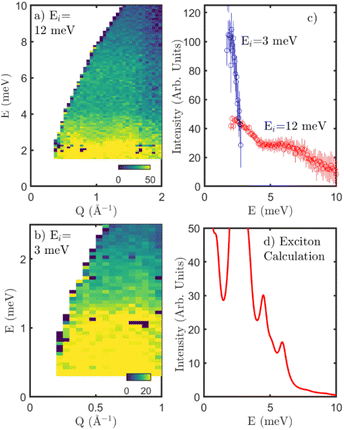
Neutron spectroscopy results from LET (ISIS) are presented in Fig. 3. Fig. 3(a and b) illustrate the background corrected data at T = 2 K using the detailed balance analysis to extract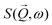 for incident energies of Ei = 12 and 3 meV. In both panels, we have corrected for a phonon background using the extracted
for incident energies of Ei = 12 and 3 meV. In both panels, we have corrected for a phonon background using the extracted 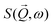 at T = 80 K by,
at T = 80 K by,thereby estimating the purely magnetic cross section at T = 2 K. The scattering in Fig. 3a and b displays a weak peak at ∼6 meV and strong scattering at low energies below ∼3 meV. This is further displayed in Fig. 3c which plots the momentum integrated intensity as a function of energy for the two experimental configurations. For comparison, the data are normalized to agree at low energy transfers. The dashed line is discussed below in terms of a parameterization of the microscopic magnetic Hamiltonian.
Parameterization
To parameterize the results, we have combined the first principles DFT results with the thermodynamic magnetic susceptibility to constrain excitonic calculations for the neutron spectroscopy results.The methodology we have used involves first fitting the high temperature magnetic susceptibility to obtain a Curie–Weiss constant thereby fixing the sum of the two exchange constants Jrr and JCR with the signs of these exchange constants fixed through the DFT first principles calculations described above. Applying the results from neutron spectroscopy and our excitonic calculations described above, we then parameterize the two excitations observed through varying the anisotropy parameters, also guided by first principles calculations.
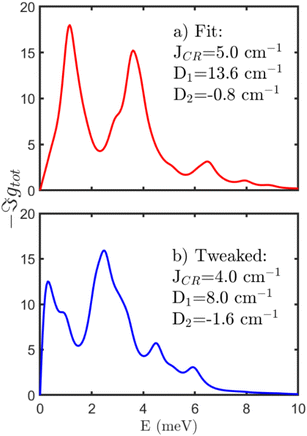
This parameterization was done by performing a least squares fit to the Ei = 12 meV data illustrated in Fig. 3. The results of this are shown in Fig. 4a. This fit produces a weak high energy peak as found in the data, however it fails to capture the significant intensity present at low-energies found in the Ei = 3 meV data in Fig. 3b and c. The parameters were then varied to bring the spectra down to lower energies while preserving a weak peak at ∼6 meV and keeping the values consistent with DFT estimates and within the constraints set by the high temperature Curie Weiss temperature (ΘCW). Based on this iterative procedure, we derive the following parameters for the microscopic magnetic Hamiltonian, Jcr = +4.0 cm−1, Jrr = −5.66 cm−1, D1 = +8.0 cm−1 and D2 = −1.6 cm−1. The results of this analysis are displayed in Fig. 3d and 4b with differences in values from Fig. 4(a) and (b) representative of the underlying error bars for the parameterized values. These are in good agreement with fits of the susceptibility/magnetization data and theoretical calculations.
Conclusions
Despite several [NiII7] Anderson wheels being previously reported, there has to date been no consensus on the magnitude and sign of the pairwise magnetic exchange interactions present, nor on the sign/magnitude of the single ion anisotropies of the constituent metal centres. In order to address this we have reported the synthesis, structure and characterization of the Anderson wheel [Ni7(hmp)7.55(pic)4.45](ClO4)2·6MeOH (1·6MeOH) through a combination of first principles calculations, magnetic susceptibility and magnetisation measurements, and neutron scattering. To the best of our knowledge this combination of techniques is employed for the first time on any [Ni7] species. To consistently describe the magnetic parameters and neutron response we applied an excitonic formalism using a Green's function response theory. The combined conclusions from these techniques and data analysis are: (a) the magnetic exchange between the central Ni ion and the ring Ni ions is ferromagnetic, (b) the magnetic exchange between the ring Ni ions is antiferromagnetic, (c) the central Ni ion possesses easy plane anisotropy, (d) the ring Ni ions possess easy axis anisotropy. Given the structural similarity between 1 and other [Ni7] in the literature, we believe these conclusions may also be valid more generally.Author contributions
EHP and LRBW performed the synthesis, and collected the PXRD/SQUID data; GSN collected and solved the single crystal XRD data; MKS performed the theoretical calculations; JS fitted the susceptibility and magnetisation data; JRS, VGS, RAE, HL and CS collected/analysed the neutron scattering data; EKB conceived the idea. All authors contributed to writing and editing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the European Union Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie grant agreement no. 832488 (MKS).References
- K. O. Joung, C. J. O'Connor, E. Sinn and R. L. Carlin, Structural and magnetic properties of dimeric di-.mu.-chloro-tetrakis(ethylenediamine)dinickel(II) chloride, Inorg. Chem., 1979, 18, 804–808 CrossRef CAS.
- (a) K. E. Andrew and A. B. Blake, The crystal structure and magnetic properties of tetra-μ3-methoxytetrakis[salicylaldehydato(ethanol)nickel(II)], J. Chem. Soc. A, 1969, 1456 RSC; J. A. Barnes and W. E. Hatfield, Low-temperature magnetic susceptibility of tetra-.mu.3-methoxy-tetrakis[salicylaldehydato(ethanol)nickel(II)], a complex with a positive exchange coupling constant, Inorg. Chem., 1971, 10, 2355–2357 Search PubMed; M. A. Halcrow, J.-S. Sun and J. C, Huffman and G. Chrsitou, Structural and Magnetic Properties of [Ni4(.mu.3-OMe)4(dbm)4(MeOH)4] and [Ni4(.eta.1,.mu.3-N3)4(dbm)4(EtOH)4]. Magnetostructural Correlations for [Ni4X4]4+ Cubane Complexes, Inorg. Chem., 1995, 34, 4167–4177 Search PubMed.
- H. Andres, R. Basler, A. J. Blake, C. Cadiou, G. Chaboussant, C. M. Grant, H.-U. Güdel, M. Murrie, S. Parsons, C. Paulsen, F. Semadini, V. Villar, W. Wernsdorfer and R. E. P. Winpenny, Studies of a Nickel-Based Single-Molecule Magnet, Chem. – Eur. J., 2002, 8, 4867–4876 CrossRef CAS.
- (a) R. Ruamps, R. Maurice, L. Batchelor, M. Boggio-Pasqua, R. Guillot, A. L. Barra, J. Liu, E.-E. Bendeif, S. Pillet, S. Hill, T. Mallah and N. Guihéry, Giant Ising-Type Magnetic Anisotropy in Trigonal Bipyramidal Ni(II) Complexes: Experiment and Theory, J. Am. Chem. Soc., 2013, 135, 3017–3026 CrossRef CAS PubMed; (b) K. E. R. Marriott, L. Bhaskaran, C. Wilson, M. Medarde, S. T. Ochsenbein, S. Hill and M. Murrie, Chem. Sci., 2015, 6, 6823–6828 RSC; (c) G. A. Craig, A. Sarkar, C. H. Woodall, M. A. Hay, K. E. R. Marriott, K. V. Kamenev, S. A. Moggach, E. K. Brechin, S. Parsons, G. Rajaraman and M. Murrie, Pushing the limits of magnetic anisotropy in trigonal bipyramidal Ni(II), Chem. Sci., 2018, 9, 1551–1559 RSC.
- (a) K. Bader, S. H. Schlindwein, D. Gudat and J. van Slageren, Molecular qubits based on potentially nuclear-spin-free nickel ions, Phys. Chem. Chem. Phys., 2017, 19, 2525–2529 RSC; (b) M. K. Wojnar, M. K. Wojnar, D. W. Laorenza, R. D. Schaller and D. E. Freedman, Nickel(II) Metal Complexes as Optically Addressable Qubit Candidates, J. Am. Chem. Soc., 2020, 142, 14826–14830 CrossRef CAS PubMed.
- E.-C. Yang, W. Wernsdorfer, S. Hill, R. S. Edwards, M. Nakano, S. Maccagnano, L. N. Zakharov, A. L. Rheingold, G. Christou and D. N. Hendrickson, Exchange bias in Ni4 single-molecule magnets, Polyhedron, 2003, 22, 1727–1733 CrossRef CAS.
- N. Kirchner, J. van Slageren, B. Tsukerblat, O. Waldmann and M. Dressel, Antisymmetric exchange interactions in Ni4 clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 094426 CrossRef.
- Y. Chen, M. D. Ashkezari, C. A. Collett, R. A. Allão Cassaro, F. Troiani, P. M. Lahti and J. R. Friedman, Observation of Tunneling-Assisted Highly Forbidden Single-Photon Transitions in a Ni4 Single-Molecule Magnet, Phys. Rev. Lett., 2016, 117, 187202 CrossRef PubMed.
- C. A. Collett, R. A. Allão Cassaro and J. R. Friedman, Precision ESR Measurements of Transverse Anisotropy in the Single-molecule Magnet Ni4, Phys. Rev. B, 2016, 94, 220402 CrossRef.
- B. C. Sheehan, R. Kwark, C. A. Collett, T. A. Costa, R. A. Allão Cassaro and J. R. Friedman, Direct spectroscopic observation of Berry-phase interference in the Ni4 single-molecule magnet, Phys. Rev. B, 2020, 102, 224428 CrossRef CAS.
- A. L. Dearden, S. Parsons and R. E. P. Winpenny, Synthesis, Structure, and Preliminary Magnetic Studies of a Ni24 Wheel, Angew. Chem., Int. Ed., 2001, 40, 151–154 CrossRef CAS PubMed.
- G. Aromí, S. Parsons, W. Wernsdorfer, E. K. Brechin and E. J. L. McInnes, Synthesis, structure and magnetic properties of a decametallic Ni single-molecule magnet, Chem. Commun., 2005, 5038–5040 RSC.
- M. I. Gonzalez, A. B. Turkiewicz, L. E. Darago, J. Oktawiec, K. Bustillo, F. Grandjean, G. J. Long and J. R. Long, Confinement of atomically defined metal halide sheets in a metal-organic framework, Nature, 2020, 577, 64–68 CrossRef CAS PubMed.
- J. N. Behera and C. N. R. Rao, A Ni2+ (S = 1) Kagome Compound Templated by 1,8-Diazacubane, J. Am. Chem. Soc., 2006, 128, 9334–9335 CrossRef CAS PubMed.
- H. W. L. Fraser, G. S. Nichol, D. Uhrín, U. G. Nielsen, M. Evangelisti, J. Schnack and E. K. Brechin, Order in disorder: solution and solid-state studies of [MIII2MII5] wheels (MIII = Cr, Al; MII = Ni, Zn), Dalton Trans., 2018, 47, 11834–11842 RSC.
- (a) J. S. Anderson, Constitution of the Poly-acids, Nature, 1937, 850 CrossRef CAS; (b) H. T. Evans, The crystal structures of ammonium and potassium molybdotellurate, J. Am. Chem. Soc., 1948, 70, 1291–1292 CrossRef CAS.
- A. Blazevic and A. Rompel, The Anderson–Evans polyoxometalate: From inorganic building blocks via hybrid organic–inorganic structures to tomorrows “Bio-POM”, Coord. Chem. Rev., 2016, 307, 42–64 CrossRef CAS.
- H. W. L. Fraser, G. S. Nichol, A. Baldansuren, E. J. L. McInnes and E. K. Brechin, Cages on a plane: a structural matrix for molecular ‘sheets’, Dalton Trans., 2018, 47, 15530–15537 RSC.
- F. H. Allen, The Cambridge Structural Database: a quarter of a million crystal structures and rising, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388 CrossRef PubMed.
- S. T. Meally, G. Karotsis, E. K. Brechin, G. S. Papaefstathiou, P. W. Dunne, P. McArdle and L. F. Jones, A family of double-bowl pseudometallocalix[6]arene discs, CrystEngComm, 2010, 12, 59–63 RSC.
- J. Zhang, P. Teo, R. Pattacini, A. Kermagoret, R. Welter, G. Rogez, T. S. A. Hor and P. Braunstein, Structural Effects of Sodium Cations in Polynuclear, Multicubane-Type Mixed Na–Ni Complexes, Angew. Chem., Int. Ed., 2010, 49, 4443–4446 CrossRef CAS PubMed.
- S. T. Meally, C. McDonald, G. Karotsis, G. S. Papaefstathiou, E. K. Brechin, P. W. Dunne, P. McArdle, N. P. Power and L. F. Jones, A family of double-bowl pseudo metallocalix[6]arene discs, Dalton Trans., 2010, 39, 4809–4816 RSC.
- W. L. Leong and J. J. Vittal, Alkali metal ion directed self-assembled Ni(II) molecular clusters, New J. Chem., 2010, 34, 2145–2152 RSC.
- S. H. Zhang, N. Li, C. M. Ge, C. Feng and L. F. Ma, Structures and magnetism of {Ni2Na2}, {Ni4} and {Ni6IINiIII} 2-hydroxy-3-alkoxy-benzaldehyde clusters, Dalton Trans., 2011, 40, 3000–3007 RSC.
- L. Q. Wei, K. Zhang, Y. C. Feng, Y. H. Wang, M. H. Zeng and M. Kurmoo, Microwave versus Traditional Solvothermal Synthesis of Ni7II Discs: Effect of Ligand on Exchange Reaction in Solution Studied by Electrospray Ionization-Mass Spectroscopy and Magnetic Properties, Inorg. Chem., 2011, 50, 7274–7283 CrossRef CAS PubMed.
- C. X. Ding, C. Gao, S. Ng, B. W. Wang and Y. S. Xie, Polynuclear Complexes with Alkoxo and Phenoxo Bridges from In Situ Generated Hydroxy-Rich Schiff Base Ligands: Syntheses, Structures, and Magnetic Properties, Chem. – Eur. J., 2013, 19, 9961–9972 CrossRef CAS PubMed.
- A. K. Ghosh, A. Bauza, V. Bertolasi, A. Frontera and D. Ray, Dinuclear and heptanuclear nickel(II) complexes: Anion coordination induced ligand arm hydrolysis and aggregation around a nickel(II) core, Polyhedron, 2013, 53, 32–39 CrossRef CAS.
- Q. P. Huang, S. H. Zhang, H. Y. Zhang, G. Li and M. C. Wu, Microwave-Assisted Synthesis, Structure and Properties of a Nano-Double-Bowl-Like Heptanuclear Nickel(II) Cluster, J. Cluster Sci., 2014, 25, 1489–1499 CrossRef CAS.
- L. Yang, Q. P. Huang, C. L. Zhang, R. X. Zhao and S. H. Zhang, Two disc-like heptanuclear clusters based on Schiff base: syntheses, structure and magnetic properties, Supramol. Chem., 2014, 26, 81–87 CrossRef CAS.
- D. I. Alexandropoulos, L. Cunha-Silva, A. Escuer and T. C. Stamatatos, New Classes of Ferromagnetic Materials with Exclusively End-on Azido Bridges: From Single-Molecule Magnets to 2 D Molecule-Based Magnets, Chem. – Eur. J., 2014, 20, 13860–13864 CrossRef CAS PubMed.
- S. H. Zhang, R. X. Zhao, G. Li, H. Y. Zhang, C. L. Zhang and G. Muller, Structural variation from heterometallic heptanuclear or heptanuclear to cubane clusters based on 2-hydroxy-3-ethoxy-benzaldehyde: effects of pH and temperature, RSC Adv., 2014, 4, 54837–54846 RSC.
- X. Yu, H. Pu and L. Y. Qing, Microwave Assisted Synthesis, and Structure of a Co-Crystal Nickel Complex with 2-ethoxy-6-methyliminomethyl-phenol, Mol. Cryst. Liq. Cryst., 2015, 607, 242–249 CrossRef CAS.
- Y. Xiao, Y. Q. Liu, G. Li and P. Huang, Microwave-assisted synthesis, structure and properties of a co-crystal compound with 2-ethoxy-6-methyliminomethyl-phenol, Supramol. Chem., 2015, 27, 161–166 CrossRef CAS.
- S. H. Zhang, G. Li, H. Y. Zhang and H. P. Li, Microwave-assisted synthesis, structure and property of a spin-glass heptanuclear nickel cluster with 2-iminomethyl-6-methoxy-phenol, Z. Kristallogr., 2015, 230, 479–484 CAS.
- Y. Xiao, Y. Qin, M. Yi and Y. Zhu, A Disc-Like Heptanuclear Nickel Cluster Based on Schiff Base: Synthesis, Structure, Magnetic Properties and Hirshfeld Surface Analysis, J. Cluster Sci., 2016, 27, 2013–2023 CrossRef CAS.
- F. Kobayashi, R. Ohtani, S. Teraoka, W. Kosaka, H. Miyasaka, Y. J. Zhang, L. F. Lindoy, S. Hayami and M. Nakamura, Syntheses, structures and magnetic properties of tetranuclear cubane-type and heptanuclear wheel-type nickel(II) complexes with 3-methoxysalicylic acid derivatives, Dalton Trans., 2017, 46, 8555–8561 RSC.
- R. Gheorghe, G. A. Ionita, C. Maxim, A. Caneschi, L. Sorace and M. Andruh, Aggregation of heptanuclear [MII7] (M = Co, Ni, Zn) clusters by a Schiff-base ligand derived from o-vanillin: Synthesis, crystal structures and magnetic properties, Polyhedron, 2019, 171, 269–278 CrossRef CAS.
- T. Zhang, L. L. Zhang, C. X. Ji, S. Ma, Y. X. Sun, J. P. Zhao and F. C. Log, Construction of Designated Heptanuclear Metal 8-hydroxyquinolates with Different Ions and Auxiliary Coligands, Cryst. Growth Des., 2019, 19, 3372–3378 CrossRef CAS.
- G. M. Sheldrick, SHELXT - Integrated space-group and crystal-structure determination, Acta Crystallogr., 2015, C71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, SHELXT - Integrated space-group and crystal-structure determination, Acta Crystallogr., 2015, A71, 3–8 CrossRef PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, Inc., Wallingford CT, 2016.
- (a) C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter, 1988, 37, 785 CrossRef CAS PubMed; (b) A. D. Becke, Density–functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS; (c) A. D. Becke, A new mixing of Hartree–Fock and local density–functional theories, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS; (d) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- (a) A. Schäfer, H. Horn and R. Ahlrichs, Fully optimized contracted Gaussian basis sets for atoms Li to Kr, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef; (b) A. Schäfer, C. Huber and R. Ahlrichs, Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef; (c) G. E. Scuseria and H. F. Schaefer III, Is coupled cluster singles and doubles (CCSD) more computationally intensive than quadratic configuration interaction (QCISD)?, J. Chem. Phys., 1989, 90, 3700–3703 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- (a) L. Noodleman and D. A. Case, Density-Functional Theory of Spin Polarization and Spin Coupling in Iron—Sulfur Clusters, Adv. Inorg. Chem., 1992, 38, 423–458 CrossRef CAS; (b) L. Noodleman and E. R. Davidson, Ligand spin polarization and antiferromagnetic coupling in transition metal dimers, Chem. Phys., 1986, 109, 131–143 CrossRef; (c) L. Noodleman, Valence bond description of antiferromagnetic coupling in transition metal dimers, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS; (d) L. Noodleman and J. G. Norman, The Xα valence bond theory of weak electronic coupling. Application to the low–lying states of Mo2Cl84−, J. Chem. Phys., 1979, 70, 4903–4906 CrossRef CAS.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 Search PubMed.
- (a) K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Auxiliary basis sets to approximate Coulomb potentials, Chem. Phys. Lett., 1995, 242, 652–660 CrossRef CAS; (b) K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Auxiliary basis sets for main row atoms and transition metals and their use to approximate Coulomb potentials, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed; (c) F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC; (d) F. Neese, Importance of Direct Spin−Spin Coupling and Spin-Flip Excitations for the Zero-Field Splittings of Transition Metal Complexes: A Case Study, J. Am. Chem. Soc., 2006, 128, 10213–10222 CrossRef CAS PubMed; (e) F. Neese and E. I. Solomon, Calculation of Zero-Field Splittings, g-Values, and the Relativistic Nephelauxetic Effect in Transition Metal Complexes. Application to High-Spin Ferric Complexes, Inorg. Chem., 1998, 37, 6568–6582 CrossRef CAS PubMed; (f) D. Maganas, S. Sottini, P. Kyritsis, E. J. J. Groenen and F. Neese, Theoretical Analysis of the Spin Hamiltonian Parameters in Co(II)S4 Complexes, Using Density Functional Theory and Correlated ab initio Methods, Inorg. Chem., 2011, 50, 8741–8754 CrossRef CAS PubMed; (g) E. Cremades and E. Ruiz, Mononuclear FeII Single-Molecule Magnets: A Theoretical Approach, Inorg. Chem., 2011, 50, 4016–4020 CrossRef CAS PubMed; (h) S. Ye and F. Neese, How Do Heavier Halide Ligands Affect the Signs and Magnitudes of the Zero-Field Splittings in Halogenonickel(II) Scorpionate Complexes? A Theoretical Investigation Coupled to Ligand-Field Analysis, J. Chem. Theory Comput., 2012, 8, 2344–2351 CrossRef CAS PubMed; (i) R. Maurice, L. Vendier and J.-P. Costes, Magnetic Anisotropy in NiII–YIII Binuclear Complexes: On the Importance of Both the First Coordination Sphere of the NiII Ion and the YIII Ion Belonging to the Second Coordination Sphere, Inorg. Chem., 2011, 50, 11075–11081 CrossRef CAS PubMed.
- (a) C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, ntroduction of n-electron valence states for multireference perturbation theory, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS; (b) C. Angeli, R. Cimiraglia and J.-P. Malrieu, n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS; (c) C. Angeli, R. Cimiraglia and J.-P. Malrieu, N-electron valence state perturbation theory: a fast implementation of the strongly contracted variant, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS.
- (a) T. Hong, M. Kenzelmann, M. M. Turnbull, C. P. Landee, B. D. Lewis, K. P. Schmidt, G. S. Uhrig, Y. Qiu, C. Broholm and D. Reich, Neutron scattering from a coordination polymer quantum paramagnet, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 094434 CrossRef; (b) C. Stock, E. E. Rodriguez and M. A. Green, Spin fluctuations and superconductivity in powders of Fe1+xTe0.7Se0.3 as a function of interstitial iron concentration, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 094507 CrossRef.
- (a) M. K. Singh and G. Rajaraman, Theoretical Studies on Hexanuclear [M3(μ3-O/OH)]2 (M = Fe(III), Mn(III), and Ni(II) Clusters: Magnetic Exchange, Magnetic Anisotropy, and Magneto-Structural Correlations, Inorg. Chem., 2019, 58, 3175–3188 CrossRef CAS PubMed; (b) M. A. Halcrow, J.-S. Sun, J. C. Huffman and G. Christou, Structural and Magnetic Properties of [Ni4(mu3-OMe)4(d bm)4(MeOH)4] and [Ni4(eta,mu3-N3)4(dbm)4(EtOH)4]. Magnetostructural Correlations for [Ni4X4]4+ Cubane Complexes, Inorg. Chem., 1995, 34, 4167–4177 CrossRef CAS; (c) K. K. Nanda, L. K. Thompson, J. N. Bridson and K. Nag, Linear dependence of spin exchange coupling constant on bridge angle in phenoxy-bridged dinickel(II) complexes, J. Chem. Soc., Chem. Commun., 1994, 1337–1338 RSC; (d) L. Ballester, E. Coronado, A. Gutierrez, A. Monge, M. F. Perpinan, E. Pinilla and T. Rico, Studies on the reactivity of S,N-derivatives of nickel with N-donor bases. Crystal structure and magnetic properties of the cubane cluster tetrakis(.mu.-hydroxo)tetrakis(.mu.-1,3-thiazolidine-2-thionato)tetrakis(pyridine)tetranickel(II)-dipyridine, Inorg. Chem., 1992, 31, 2053–2056 CrossRef CAS; (e) E. Agapaki, M. K. Singh, A. B. Canaj, G. S. Nichol, J. Schnack and E. K. Brechin, A graceful break-up: serendipitous self-assembly of a ferromagnetically coupled [NiII14] wheel, Chem. Commun., 2022, 58, 9088–9091 RSC.
- (a) A. Sarkar, S. Dey and G. Rajaraman, Role of Coordination Number and Geometry in Controlling the Magnetic Anisotropy in FeII, CoII, and NiII Single-Ion Magnets, Chem. – Eur. J., 2020, 26, 14036–14058 CrossRef CAS PubMed; (b) S. K. Singh, T. Gupta, P. Badkur and G. Rajaraman, Magnetic Anisotropy of Mononuclear NiII Complexes: On the Importance of Structural Diversity and the Structural Distortions, Chem. – Eur. J., 2014, 20, 10305 CrossRef CAS PubMed; (c) D. Lomjanský, C. Rajnák, J. Titiš, J. Moncoľ and R. Boča, Study of zero-field splitting in Ni(II) complexes with near octahedral geometry, Inorg. Chim. Acta, 2019, 491, 138–146 CrossRef; (d) T. Laluhová, J. Titiš, C. Rajnák, J. Moncoľ and R. Boča, Magnetism of pseudohalide Ni(II) complexes containing 4-methylpyridine ligands, Polyhedron, 2022, 227, 116135 CrossRef.
- P. M. Sarte, M. Songvilay, E. Pachoud, R. A. Ewings, C. D. Frost, D. Prabhakaran, K. H. Hong, A. J. Browne, Z. Yamani, J. P. Attfield, E. E. Rodriguez, S. D. Wilson and C. Stock, Spin-orbit excitons in CoO, Phys. Rev. B, 2019, 100, 075143 CrossRef CAS.
- P. M. Sarte, C. Stock, B. R. Ortiz, K. H. Hong and S. D. Wilson, Van Vleck excitons in Ca2RuO4, Phys. Rev. B, 2020, 102, 245119 CrossRef CAS.
- H. Lane, M. Songvilay, R. A. Ewings and C. Stock, Excitonic transverse and amplitude fluctuations in noncollinear and charge-ordered RbFe2+Fe3+F6, Phys. Rev. B, 2022, 106, 054431 CrossRef CAS.
- H. Lane, E. E. Rodriguez, H. C. Walker, C. Niedermayer, U. Stuhr, R. I. Bewley, D. J. Voneshen, M. A. Green, J. A. Rodriguez-Rivera, P. Fouquet, S.-W. Cheong, J. P. Attfield, R. A. Ewings and C. Stock, Metastable antiphase boundary ordering in CaFe2O4, Phys. Rev. B, 2021, 104, 104404 CrossRef CAS.
- W. J. L. Buyers, T. M. Holden and A. Perreault, Temperature dependence of magnetic excitations in singlet-ground-state systems. II. Excited-state spin waves near the Curie temperature in Pr3Tl, Phys. Rev. B: Solid State, 1975, 11, 266 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2286832. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3qi02307a |
| This journal is © the Partner Organisations 2024 |