Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A machine learning-enabled process optimization of ultra-fast flow chemistry with multiple reaction metrics†
Dogancan
Karan
a,
Guoying
Chen
a,
Nicholas
Jose
abc,
Jiaru
Bai
 b,
Paul
McDaid
d and
Alexei A.
Lapkin
b,
Paul
McDaid
d and
Alexei A.
Lapkin
 *abe
*abe
aCambridge Centre for Advanced Research and Education in Singapore, CARES Ltd. 1 CREATE Way, CREATE Tower #05-05, Singapore 138602, Singapore
bDepartment of Chemical Engineering and Biotechnology, University of Cambridge, Cambridge CB3 0AS, UK. E-mail: aal35@cam.ac.uk
cAccelerated Materials Ltd, 71-75, Shelton Street, WC2H 9JK London, UK
dPfizer Process Development Centre, RCMF, Shanbally, Ringaskiddy, P43 X336, Cork, Ireland
eInnovation Centre in Digital Molecular Technologies, Yusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Rd, Cambridge CB2 1EW, UK
First published on 4th December 2023
Abstract
Discovering the optimum process parameters of ultra-fast reactions, such as lithium–halogen exchange reactions, is typically achieved by time and resource inefficient methods including one factor at a time optimization (OFAT) or classical factorial design of experiments (DoE). Herein, we demonstrate the development of a machine learning workflow coupled with a flow chemistry platform for the optimization of the reaction conditions of a lithium–halogen exchange reaction. Flow chemistry platform allowed us to precisely control the process parameters (temperature, residence time and stoichiometry) and enabled robust and reliable data collection to train a machine learning algorithm. A Bayesian multi-objective optimization algorithm TSEMO (Thompson sampling efficient multi-objective optimization) was used to optimize the process parameters and to build process knowledge for different optimization campaigns with different mixing intensifications (capillary reactor vs. microchip reactor). The algorithm successfully identified a set of optimal conditions corresponding the trade-off between yield and impurity in different optimization campaigns. Furthermore, the optimization results and Gaussian process (GP) surrogate models within TSEMO were further analyzed to infer the operating regime of the system for different mixing intensifications (mixing controlled vs. reaction-controlled regime). The machine learning workflow has proven to be robust and data efficient, revealing rich information about the reaction studied compared to single-objective, OFAT and DoE approaches.
1. Introduction
Organolithium compounds, such as aryllithiums are powerful tools in organic synthesis due to their high reactivity and versatility.1,2 The reaction between an aryl halide and alkyl lithium is extremely fast and highly exothermic; the resulting aryllithium intermediates have short lifetimes. The reaction time scale is usually of the order of mixing time which makes these reactions difficult to control and study. When batch processing is employed, such reactions are carried out at cryogenic conditions (below −70 °C) to avoid side reactions and to prolong the lifetime of unstable aryllithium intermediates.3 However, poor mixing characteristics of batch processing can result in hotspot formation leading to formation of byproducts and low yields when highly reactive functional groups are present.4Continuous flow reactors offer a viable solution to handle fast, exothermic reactions with unstable intermediates.5,6 Flow reactors offer superior heat and mass transport properties due to high surface area to volume ratio which prevents the hot spot formation and large temperature gradients in highly exothermic reactions. In addition, precise control over the residence time within millisecond range enables the utilization of flash chemistry,7 where highly reactive and unstable intermediates can be created in situ and consumed in a subsequent step prior to their decomposition. Using flow reaction technology lithium–halogen exchange reactions can be performed under milder conditions with precise control over the process parameters such as temperature, mixing and stoichiometry, leading to improved yield and selectivity compared to their batch counterparts. These advantages offered by continuously flow reactors have been demonstrated on various lithium–halogen exchange reactions in the published reports.8–12
Despite the widespread utilization of continuous processing in lithium–halogen exchange reactions, building process knowledge and obtaining optimum process parameters are achieved by rather inefficient methods. For example, intuition-based methods such as one factor at a time optimization (OFAT)13–15 or/and 2D temperature/residence time mapping (brute-force DoE)16–18 have been widely used to identify the optimum process parameters including residence time, temperature, solvent, reaction stoichiometry, mixer type etc. These methods require an exponentially increasing number of experiments as the number of parameters increases, making them time and resource efficient. In addition, complex interactions and non-linearities between different process parameters may not be identified leading to identification of local optima. Moreover, these methods focus on fixed values of continuous variables, potentially missing the optima between these values. Furthermore, 2D temperature/residence time mapping is typically effective when prior knowledge about the reaction, such as the optimum reaction stoichiometry, is available. This constraint limits their applicability when no information is known about the reaction. Finally, even if the reaction mechanism of lithium–halogen exchange reactions is well understood, optimization through kinetic profiling and mechanistic model development are difficult due to extremely short time scales of such reactions.
Machine learning algorithm-guided process optimization of reaction conditions has become increasingly popular to overcome the limitations of DoE and intuition-based approaches. The number of machine learning methods that could be used for the optimization of chemical systems has increased drastically in recent years.19 Some of the commonly used machine learning methods are: SNOBFIT (stable noisy optimization by branch and fit),20 Nelder–Mead simplex,21 Bayesian approaches for single objective such as SOBO22 and multi objective problems including TSEMO,23 ParEGO,24 Chimera.25 In particular, TSEMO has been widely utilized to solve various multi-objective problems including optimization of reaction conditions,26–29 solvent selection,30 optimization including life-cycle assessment,31 and distributed self-driving laboratories.32
Algorithmic optimization of the process parameters of an ultra-fast lithium–halogen exchange reaction via Bayesian optimization has recently been demonstrated by Ahn and coworkers.16 A single-objective optimization approach was used, which provided limited information about the trade-offs between the conflicting objectives (yield vs. impurity) and the influence of the different process parameters on the target objectives. In addition, they covered a small decision space for the optimization since prior knowledge (reaction stoichiometry) was available from their previous work.33
In this study we developed a generic, computer-controlled flow chemistry platform combined with a machine learning workflow that enables the optimization of a lithium–halogen exchange reaction exhibiting competing reaction pathways and conflicting objectives. Our flow platform consists of commercially available parts including pumps, temperature control unit, tubings, and fittings. The flow chemistry platform is capable of precisely controlling temperature, reaction stoichiometry and residence time to sub-second scale which allowed us to collect robust and reliable data for an extremely fast and difficult to control chemistry. Using a proven ML algorithm (TSEMO), we optimize the process parameters and understand their influence on the target objectives. This work demonstrates the first example of algorithmic process optimization of an extremely fast lithium–halogen exchange reaction with conflicting objectives.
2. Experimental
2.1. Materials
Aryl bromide starting material (compound 1, in Scheme 1) was obtained from Pfizer Inc. 2 M n-butyllithium (n-BuLi) solution in cyclohexane, anhydrous tetrahydrofuran with 250 ppm BHT as inhibitor, 99.9% (THF), anhydrous methanol, 99.8% (MeOH), anhydrous hexane 95%, acetonitrile 99.9% (HPLC grade) were purchased from Sigma Aldrich and used as received. Aryl bromide was vacuum dried before the reaction to remove the trace amount of moisture adsorbed onto the solid surface. Before the reaction, moisture content of THF and aryl bromide solution was analyzed via Karl Fischer titrator (Mettler-Toledo C10SX) using Hydranal Coulomat A as the titration solution. If the moisture content was more than 50 ppm, the solutions were discarded and prepared again.2.2. Machine learning workflow
In this work, we employed the Summit34 implementation of TSEMO23 (Thompson sampling for efficient multi objective optimization) algorithm to optimize the yield vs. impurity as competing objectives (Scheme 1). TSEMO has shown to outperform most of the state-of-the-art multi-objective optimization algorithms including ParEGO, EIM-EGO, and NSGA-II.35 A small dataset is collected by using a space-filling latin hypercube sampling (semi-random, but well-spaced selection) (LHS) as training to initialize TSEMO. Within the algorithm, individual Gaussian process (GP) surrogate models are built for the two targets – yield and impurity – to approximate their response surfaces. Subsequently, the algorithm draws random samples from GPs through Thompson spectral sampling. Then, a multi-objective genetic algorithm (NSGA-II) is called to identify the Pareto front of the random samples. Finally, TSEMO suggests a set of experiments from Pareto front (of randomly selected GP samples) which aim to improve the hypervolume of the actual Pareto front (of the experimental data). The suggested experiment is performed, and the result is added to the training set. This process continues iteratively until a termination criterion is satisfied. We used hypervolume improvement as the termination criterion.Hypervolume is defined as the volume of the objective space between the current Pareto front and an anti-utopian point of [yield, impurity] = [0, 100]. The hypervolume was calculated for each experiment along the current Pareto front. To avoid premature termination, the optimization was only terminated when the hypervolume remained unchanged for 10 consecutive experiments indicating that TSEMO could not identify a better solution beyond the current Pareto front. Throughout the study, a single experiment was executed, analyzed, and processed by TSEMO before the conditions for the subsequent experiment were generated.
2.3. Reactor platform
A schematic representation of the reactor platform is shown in Fig. 1 (photographs of the experimental are given in ESI†). Aryl bromide 1, n-BuLi and THF streams were pumped via syringe pumps (Harvard apparatus PHD ULTRA push/pull) equipped with medium-pressure switch valve boxes (Harvard apparatus) to provide continuous and uninterrupted flow. 25 mL Hamilton gastight syringes were used for n-BuLi and THF while 50 mL syringes were used for aryl bromide. Methanol was delivered by a syringe-free positive displacement pump (VICI The Cheminert® M50). Anhydrous THF and n-BuLi solution was joined in a 0.5 mm ID T-mixer and mixed in a 0.6 mL static mixer (Vapourtec).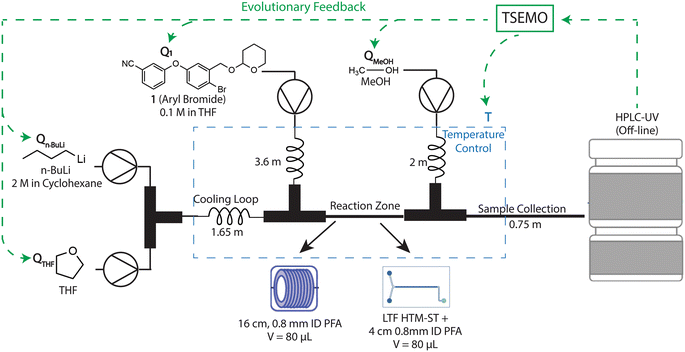 | ||
| Fig. 1 A schematic representation of rector setup to perform machine learning-driven optimization of the lithium–halogen exchange of reaction given in Scheme 1b. | ||
The dilution of the n-BuLi solution with THF served two purposes: i) to lower the freezing point of cyclohexane, ii) to reduce the flow rate difference between n-BuLi and aryl bromide pumps to prevent backflow. Cooling loops were integrated into each stream before the reaction zone. All fluid delivery lines, and cooling loops were made of 0.8 mm ID PFA tubing.
Two different reactors were employed within the reaction zone: 0.5 mm ID T-mixer equipped with 16 cm-long 0.8 mm ID PFA tubing and a commercially available microchip reactor (HTM-ST, Little Things Factory). A quench stream (MeOH) was introduced from a 0.5 mm ID T-mixer for both reactors. Subsequent to quenching, a 0.75 m long, 0.8 mm ID PFA tubing was used for sample collection. Cooling lines and reactors were fitted to a Polar Bear Plus Flow Synthesizer (Cambridge Reactor Design), which was enclosed within a glass dome, to control temperature and to minimize the influence of moisture.
2.4. Lithium–halogen exchange reaction
Before the reaction, all fluid delivery lines were purged with anhydrous hexane and dry argon to remove any trace amounts of moisture in the system. In addition, all the glass syringes were dried in an oven to remove the trace amounts of moisture adsorbed on syringe surfaces. Aryl bromide solution in anhydrous THF was prepared using Schlenk technique and loaded in syringes. Anhydrous THF and n-BuLi solution were directly loaded in syringes from the corresponding reagent bottles. During the reactions, all the solutions were kept under argon atmosphere since n-butyllithium can react with moisture in the air or atmospheric oxygen which reduces the yield.We developed an event sequence for pumps to perform the lithium–halogen exchange reaction. The event sequence helped us to reduce material consumption due to high flow rates, avoid cross contamination of reaction conditions between samples and, most importantly, prevent reactor fouling due to low solubility of the aryl-lithium intermediates. We observed that without a proper start-up or shut-down sequence, n-BuLi solution remained in cooling loop flowed to aryl bromide line, or the reagents stayed in the reaction zone for extended amounts of time which both resulted in formation of high amounts of insoluble aryl-lithium intermediates and hence reactor fouling. However, using such an event sequence resulted in dispersion along the reactor. We used the concept of residence time distribution (RTD) to analyze the dispersion behavior of the system and predict the steady state time as we will discuss in detail below.
Briefly, the sequence starts with setting the reaction temperature (T). Once the system reaches the desired temperature, n-BuLi and aryl bromide lines are purged for 30 s at 0.5 mL min−1 flow rate. Thereafter, n-BuLi and THF pumps are set to the desired flow rates based on the experimental condition (stoichiometry and residence time) while aryl bromide pump is set to 1 mL min−1. After a certain waiting time (tI), aryl bromide and MeOH pumps are also set to the desired flow rate dictated by the experimental condition. A sample is collected after the system reaches the steady state (tII). After the sample collection, n-BuLi and MeOH flow rates are set to zero while aryl bromide and THF flow rates are set to 1 mL min−1 for cleaning until all the remaining n-BuLi in cooling loop, reaction zone and sample collection zone leave the system (tIII). Finally, aryl bromide and THF flow rates are set to zero to end the sequence. Off-line analysis of the collected sample was done by UPLC-MS (Agilent 1260 Infinity II-MS).
We used an open-source lab automation package Flab (https://github.com/njoseGIT/flab) to control the pumps, the reactor and to execute the events sequence. The whole workflow was controlled by a custom written Python program which performs the optimization by TSEMO within Summit, calculates the pumps flow rates (Q1, Qn-BuLi, QTHF, QMeOH), reaction time scales (tI, tII, tIII), and volumetric consumption of the individual streams, performs the event sequence within Flab and keeps a log file. For better clarity and replicability, reader can refer to pseudo-code provided in ESI.†
3. Results and discussion
3.1. Initial exploration of decision space
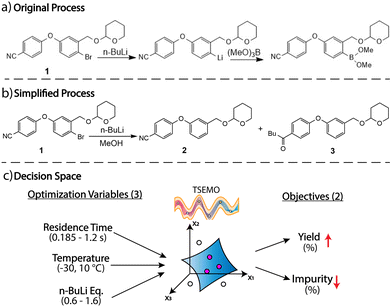
In this work, we studied the machine learning optimization of Li–Br exchange of aryl bromide 4-(4-bromo-3-(((tetrahydro-2H-pyran-2-yl)oxy)methyl)phenoxy)benzonitrile, 1. In the previous report,36 aryl-lithium intermediate of 1 is created by Li–Br exchange which is followed by the electrophilic quench by B(MeO)3 to form the corresponding aryl boronic acid ester, Scheme 1a. The key step in this process is the reaction between n-BuLi and aryl bromide 1 to create the aryl lithium intermediate. This step is extremely sensitive to mixing efficiency, residence time, temperature, stoichiometry and, hence, is difficult to control. In addition, it was reported that the molar equivalence of the electrophilic quench agent and the residence time of the quench step were not critical parameters for the process.37 Therefore, we focus our attention on the machine learning optimization of the key step in a simplified reaction as demonstrated in Scheme 1b. In this process, aryl-lithium intermediate is quenched by excess methanol to afford the protonated product 2. The only impurity for this reaction was identified as 3 which forms as a result of the reaction between n-BuLi and cyano substituent in 1.Since the formation of 2 and 3 are competing parallel reactions, it would be impossible to identify a single set of utopian conditions which correspond to maximum yield of 2 without any 3. Consequently, in this work, we set up a multi objective optimization problem where we optimized the yield (of 2, maximize) and impurity (3, minimize) as competing objectives. Three continuous variables (residence time, temperature, n-BuLi equivalence) were optimized for this multi-objective problem. It is important to stress that the residence time and the mixing efficiency were closely related in our flow rector setup. Therefore, changing residence time also changes mixing efficiency in the reactor.
The bounds of continuous variables were established based on the equipment limitations and preliminary feasibility studies such that TSEMO would not explore outside of the robust operation regime of the reactor setup. For example, the lower limit of residence time was set as 0.185 s (Q1 ~ 25 mL min−1) since pumps could not handle higher flow rates due to high pressure drop in the valve boxes. Similarly, the lower boundary of temperature (−30 °C) was the lowest temperature achievable by Polar Bear system.
The upper limits of residence time, temperature and n-BuLi were selected based on the preliminary flow experiments performed in the reactor setup. The values exceeding the upper limits shown in Scheme 1c resulted in reactor fouling due to rapid generation and accumulation of aryl-lithium intermediates in the reaction zone. Similarly, we also tested different concentrations of solution of 1 in THF (0.3–0.1 M). Concentrations of 1 higher than 0.1 M resulted in rapid clogging of the reactor due to low solubility of the lithiated intermediate. Details of preliminary experiments and observations can be found in ESI.†
3.2. Analysis of the dispersion characteristics of the system
In this section, we discuss the dispersion characteristics of the flow chemistry platform through the residence time distribution (RTD). Understanding the dispersion characteristics of the system was crucial for accurate prediction of the steady state time to collect a reliable sample and to reduce the material consumption by avoiding prolonged waiting times.As described briefly in Experimental section, each experimental run begins with the entire system, except for the aryl bromide line, filled with THF which is used to clean the reactor between experiments. Once a reaction starts, the washing solvent THF is replaced by the reaction mixture leading to dispersion due to laminar flow regime in the system. More specifically, dispersion occurs: i) within the n-BuLi cooling loop when THF is displaced by n-BuLi solution/THF mixture, ii) within the reaction zone when THF is displaced by the aryl-lithium intermediate, iii) within the sample collection tube when starting material/product mixture of 1/2/3 travels through the tubing. Similar dispersion phenomena also occur when THF is introduced to clean the reactor. In such scenario, using plug flow assumption (τ = V/Q where τ is the residence time, V is the system volume, Q is the volumetric flow rate) to estimate the total residence time of the system before sample collection would result in underestimation of the sample collection time, and hence training the machine learning algorithm with unsteady-state condition data. Therefore, we analyzed the dispersion behavior in our system by residence time distribution (RTD) theory to estimate steady state time for sample collection.
We identified the suitable dispersion model in our system based on the flow map38 by calculating Bodenstein number Bo = udt/D, where u is the superficial velocity, dt is the channel diameter, D is the molecular diffusivity, and the aspect ratio of the corresponding part of the system L/dt, where L is the tube length. To encompass the entire decision space, we used the upper and lower limits of the residence times and stoichiometric ratios given in Scheme 1. Our findings reveal that the majority of the decision space falls within the axial dispersion model to intermediate regime. For the sake of simplicity, we opted to use the axial dispersion model throughout the study. The dispersion coefficient in axial dispersion model is given by eqn (1):38
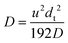 | (1) |
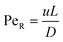 | (2) |
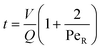 | (3) |
3.3. Algorithm-guided reaction optimization of lithium–halogen reaction
In this section we present results of three different multi-objective optimization campaigns of the Br–Li exchange reaction shown in Scheme 1b and describe how process knowledge could be obtained from the optimization results.In the first campaign, space-filling LHS was used to generate 12 training experiments to initialize the optimization. Subsequently, TSEMO designed 34 further iterations (full list of reaction conditions for all experiments is provided in ESI†) to establish a clear Pareto front (Fig. 2a). The highest yield was found to be 94.1% at the cost of 4.1% impurity. The lowest impurity was 0.25% with a much poorer yield of 59%. Between these two edge points, the Pareto front illustrates the complete trade-off between yield and impurity. The Pareto front shows that yield can be significantly increased from 59% to 94.1% at the cost of an increase in impurity from 0.25 to 4.1%. The best performing reaction conditions of different optimization campaigns in terms of maximum yield are summarized in Table 1.
 | ||
| Fig. 2 Results of the three parameter multi-objective optimization of the Br–Li exchange reaction shown in Scheme 1 in 0.8 mm ID, 16 cm long 80 μL capillary reactor with 12 training experiments. (a) The Pareto front plot of yield vs. impurity which highlights the clear trade-off between the two objectives. The tip of the Pareto plot is magnified in the inset plot for visual clarity. (b) Plot of the experimental conditions executed during the optimization with the reaction profiles. The shell color of each point denotes yield (%) whereas the core color of each point denotes per cent of impurity formed. | ||
| Entry | Reactor | # of training | τ (s) | T (°C) | n-BuLi (eq.) | Yield (%) | Imp (%) |
|---|---|---|---|---|---|---|---|
| 1 | Tube | 12 | 0.191 | −23.41 | 1.08 | 94.1 | 4.1 |
| 2 | Tube | 12 | 0.23 | −30 | 1.05 | 93.3 | 3.4 |
| 3 | Tube | 3 | 0.185 | −16.3 | 1.06 | 93.8 | 4.8 |
| 4 | Tube | 3 | 0.2 | −30 | 1.05 | 93 | 5.5 |
| 5 | Chip | 12 | 0.24 | −28.6 | 1.00 | 96 | 3.6 |
| 6 | Chip | 12 | 0.266 | −23.5 | 1.00 | 95.6 | 3.3 |
To visualize the influence of continuous variables on the target objectives, the experimental data are plotted with respect to temperature, residence time and n-BuLi equivalence where the shell and core color of the data points are correlated with yield and impurity (Fig. 2b). All the good performing experimental results (higher yield and lower impurity) are clustered around τ = 0.2 s, n-BuLi (eq.) = 1, and T < −20 °C indicating the optimum operation region of the process. Furthermore, assessing the change in yield and impurity in x, y, z axes reveal important details regarding how different operational conditions influence the reaction objectives.
The most notable change was observed when τ was increased at relatively constant n-BuLi equivalence and temperature. For example, at T = −18 °C and 0.97 molar equivalence of n-BuLi, increasing the residence time from 0.273 s to 0.98 s resulted in a dramatic decrease in yield from 86.6% to 24% while the impurity increased from 7.4% to 13.4%. However, decreasing τ below 0.23 s did not lead to a significant change in yield and impurity amount under otherwise identical conditions.
It is important to highlight that the change in the residence time of the Br–Li exchange step was achieved by changing the flow rate (Q1, Qn-BuLi, QTHF) of different streams at the constant reactor length. These observations are in line with the previous studies of lithium–halogen exchange reactions in microreactors12,14,37 where increasing the total flow rate improves the reaction yield through improved mixing and efficient utilization of highly reactive, short-lived aryl-lithium intermediates. Low flow rates (high residence times) result in incomplete mixing of 1 and n-BuLi streams, and hence lower yield. On the other hand, incomplete mixing also increases the impurity by means of formation of high n-BuLi concentration zones across the cross-section of the reactor which promotes the side reaction with the cyano substituent. Moreover, increased residence times cause unstable aryl-lithium intermediate to decompose before an electrophilic quench to form a stable product which can also result in a drop in the yield.
Increasing the molar equivalence of n-BuLi along the y axis at relatively constant τ and T first increased the product yield without a significant change in the impurity up to ∼1.08 molar equivalent of n-BuLi since more unreacted starting material could be converted to the product. However, beyond 1.08 molar equivalents of n-BuLi, the product yield started to decrease while impurity increased. For example, at τ = 0.185 s and T = −(20–25) °C, increasing the molar equivalence of n-BuLi from 1.037 to 1.1 resulted in a decrease in yield from 93.16% to 92% whereas the impurity increased from 2.5 to 8.15%. This observation suggests that the trade-off point of n-BuLi equivalence is somewhere between 1.08 to 1.1.
In lithium–halogen exchange reactions, increasing temperature promotes side reactions and leads to a faster decomposition of unstable aryl-lithium intermediates.10 Even if TSEMO primarily suggested temperature values closer to the lower limit of the decision space, it was still possible to get reasonably high yields at higher temperatures. For example, at τ = 0.24 s with 1.128 molar equivalent of n-BuLi and T = −3.5 °C, 80% yield was obtained with 18.8% impurity. The weaker dependency of the reaction objectives on temperature suggests that the reaction is physics-controlled (mixing) rather than kinetically controlled. The effect of different continuous variables on reaction objectives will be discussed in more detail in the following sections of the paper.
The reaction conditions selected by TSEMO in 34 optimization experiments showed that with respect to exploration/exploitation dilemma observed in Bayesian optimization, TSEMO in this work demonstrated a great tendency to exploitation. In contrast to the training experiments where LHS uniformly scans the decision space, TSEMO consistently proposed reaction conditions near Pareto-efficient points from the initial optimization iterations (Fig. 2a). The best-performing point was suggested as the 23rd optimization experiment. Moreover, throughout the entire 34-experiment optimization process, TSEMO only assessed residence time values greater than 0.6 seconds on three occasions, which further highlights the algorithm's tendency to efficiently exploit. Similar exploitative behavior of TSEMO algorithm has been reported in previous studies.26,28
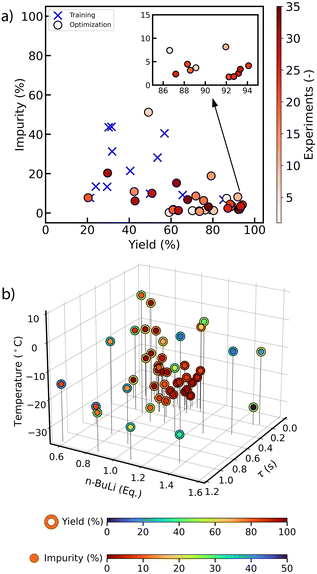
To further investigate efficiency of the algorithmic optimization of the Br–Li exchange reaction at low data regime, the optimization was repeated only with three poorly yielding training experiments. These experiments were also generated by LHS and TSEMO designed an additional 41 experiments to form a Pareto front (Fig. 3a). Similar edge points as the previous optimization campaign were observed with the highest yield of 93.8% at the cost of 4.8% impurity (Table 1). Furthermore, two optimization campaigns produced similar Pareto fronts (see Fig. 5 below) highlighting consistency between the optimization campaigns.
 | ||
| Fig. 3 Results of the three parameter multi-objective optimization of the Br–Li exchange reaction shown in Scheme 1 in 0.8 mm ID, 16 cm long 80 μL capillary reactor with three training experiments. (a) The Pareto front plot of yield vs. impurity which highlights the clear trade-off between the two objectives. The tip of the Pareto plot is magnified in the inset plot for visual clarity. (b) Plot of the experimental conditions executed during the optimization with the reaction profiles. The shell color of each point denotes yield (%) whereas the core color of each point denotes the per cent of impurity formed (%). | ||
Despite the localization of the LHS results on low yield and high impurity, the algorithm successfully identified new regions of the decision space corresponding to better results. After eight initial optimization iterations, TSEMO already generated yield and impurity values closer to Pareto front. Interestingly, the best-performing condition was suggested as the 11th experiment which was earlier than the first optimization campaign. In addition, the reaction profiles of different experimental conditions in Fig. 3b reveal that despite the lack of information regarding the upper limit of the n-BuLi equivalence compared to the original run, the algorithm only suggested two experiments beyond 1.1 equivalence of n-BuLi to explore the decision space. However, the algorithm explored the upper limits of temperature and residence time more often than in the original run.
The final optimization campaign was performed in this study to understand how mixing intensification would change the optimum reaction conditions in the decision space. For this purpose, we replaced the T-mixer capillary reactor (D = 0.8 mm, L = 16 cm) setup with a microchip reactor embedded with in-line static mixing elements (Little Things Factory, HTM-ST). It has been demonstrated that HTM-ST mixer has superior mixing properties over a T-mixer when the flow rate is higher than 8 mL min−1.39 The internal volume of the capillary reactor is 80 μL while that of microchip reactor is 60 μL. Therefore, in order to study the sole effect of the mixing characteristics of the system on target objectives, we added another 0.8 mm ID 4 cm long PFA tubing after the microchip reactor to equalize volumes of both systems at 80 μL.
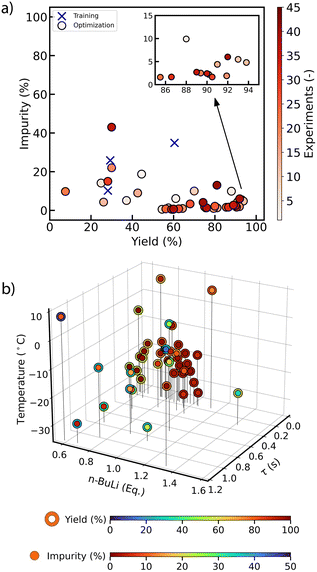
To optimize the target objectives, a similar procedure to the first optimization campaign was followed: 12 training experiments were generated by LHS and performed. Thereafter, TSEMO designed 28 more experiments to form a Pareto front (Fig. 4a). The highest yield was 96% at the cost of 3.6% impurity. The lowest impurity was 0.76% with 67% yield. The comparison between the best-performing results of the two systems (T-mixer with capillary tube vs. microchip reactor) reveals that it was possible to get a slightly higher yield and a lower impurity as a best-performing point in the microchip reactor. Interestingly, the chip system required 8% less n-BuLi to obtain a better overall performance than the T-mixer capillary reactor (Table 1 entry 1 vs. entry 5).
 | ||
| Fig. 4 Results of the three parameter multi-objective optimization of the Br–Li exchange reaction shown in Scheme 1 in HTM-ST microchip reactor with 12 training experiments. (a) The Pareto front plot of yield vs. impurity which highlights the clear trade-off between the two objectives. The tip of the Pareto plot is magnified in the inset plot for visual clarity. (b) Plot of the experimental conditions executed during the optimization with the reaction profiles. The shell color of each point denotes yield (%) whereas the core color of each point denotes the per cent of impurity formed (%). | ||
In addition, the comparison between the reaction profiles in Fig. 2b and 4b highlights several distinctions between the two systems. Notably, the target objectives were improved considerably between τ = 0.2–0.4 s in the chip system, thereby illustrating the impact of mixing intensification on the outcome of the optimization. For example, at τ = 0.39 s, T-mixer capillary reactor resulted in 65.5% yield and 9% impurity with T = −18 °C and n-BuLi = 0.9 eq. whereas the chip resulted in 82.55% yield and 10% impurity with T = −18 °C and n-BuLi = 0.97 eq. Moreover, even at very high residence times (low flow rates) the chip reactor still provided better reaction outcomes. For instance, at τ ∼ 1 s, the T-mixer capillary reactor resulted in 31.8% yield and 31% impurity with T = −25 °C and n-BuLi = 1.39 eq. whereas the chip resulted in 56.65% yield and 35% impurity with T = −15 °C and n-BuLi = 1.3 eq. Curiously, we also observed a more pronounced effect of higher temperatures on the outcome of the optimization in the chip reactor compared to the original tube setup. For example, at τ = 0.481 s and 0.808 eq. n-BuLi the T-mixer capillary reactor resulted in 50% yield and 10% impurity at T = 8.3 °C while the chip reactor resulted in 32% yield and 1.2% impurity at τ = 0.205 s and 0.805 eq. n-BuLi at the same temperature despite its superior mixing performance. The overall improvement of the target objectives at a wider range of residence times and more substantial temperature influence within the chip system suggest that the controlling mechanism of the reaction is altered, and kinetics of the reaction is more relevant in the chip system.
Finally, comparison between Pareto-efficient points of different optimizations in Fig. 5 reveals that all the optimization campaigns produced a similar Pareto front with chip reactor producing slightly better results than the T-mixer capillary reactor.
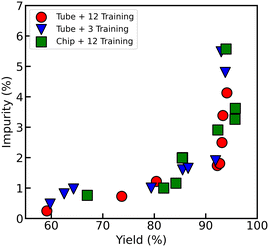 | ||
| Fig. 5 Pareto efficient points of yield vs. impurity related to optimization of Br–Li exchange reaction in Scheme 1 with different optimization campaigns. | ||
The optimization campaigns shown in Fig. 2–4 highlight the utility of the multi-objective optimization in Br–Li exchange reactions compared to single-objective and DoE approaches. For example, unlike the previous work on the machine learning optimization of Br–Li exchange reaction with single objective wherein a single optimum solution was identified,16 we identified a set of Pareto-efficient solutions (Fig. 5). Within these Pareto-efficient solutions, one objective cannot be improved without making the other one worse off, highlighting the complete trade-off between the two objectives. It is important to highlight that all the conditions along the Pareto front represent viable solutions. Depending on the specific process requirements such as impurity tolerance or downstream strategy, a specific condition can be selected from this range of solutions. On the other hand, if we applied a five-level, three-factor DoE approach to obtain process knowledge for this Br–Li exchange reaction, it would take 5 × 5 × 5 = 125 experiments to obtain a response surface for a single campaign. Consequently, more information about the process can be extracted with fewer number of experiments through multi-objective Bayesian optimization compared to DoE approach.
3.4. Sensitivity of the developed statistical models to input variables
Gaussian process (GP) surrogate models that are used in the TSEMO algorithm are not only useful during the optimization of the target objectives, but also the hyperparameters of the surrogate models can provide additional insight into the chemical system. Especially, the lengthscale hyperparameter describes importance of the input variables in the target objectives, a concept known as automatic relevance detection.40 The lower value of the lengthscale hyperparameter indicates a greater contribution of the corresponding input variable to the target objective. Lengthscales of continuous variables for the tube and the chip reactors are tabulated in Table 2.| Hyperparameter | Tube | Chip | ||
|---|---|---|---|---|
| GP1 (yield) | GP2 (impurity) | GP1 (yield) | GP2 (impurity) | |
| θ τ | 0.15 | 0.61 | 0.54 | 0.7 |
| θ T | 1.03 | 0.58 | 0.35 | 0.88 |
| θ n-BuLi | 0.31 | 0.25 | 0.38 | 0.55 |
| σ f | 0.71 | 1.16 | 1.02 | 2.01 |
| σ noise | 6.9 × 10−4 | 2.9 × 10−3 | 9 × 10−3 | 3.9 × 10−3 |
For the T-mixer capillary reactor, the residence time and n-BuLi equivalence are significantly more relevant to obtain high yield while temperature is the least relevant variable. On the other hand, n-BuLi equivalence is the most relevant parameter to obtain low impurity. These observations are in agreement with our discussion above that the reaction is mainly controlled by the physical step (mixing). In the chip reactor, temperature and n-BuLi equivalence are the most relevant parameters while residence time has a smaller contribution to achieve a high yield. Similarly, this situation further supports our argument that controlling mechanism of the reaction is altered and temperature is more important than in the T-mixer capillary reactor.
Besides the lengthscales, low output variance (σf), and noise hyperparameter (σnoise), see Table 2, indicate high quality and the consistency of the collected data which further highlights robustness of the flow reactor setup developed in this work. As a result, the trained GP surrogate models can be used to make accurate predictions of reaction conditions which are unseen by the model during the optimization. This idea is illustrated in Fig. 6. We generated 30 random experimental conditions, performed in the T-mixer/capillary reactor and analyzed the results by UPLC-MS. On the other hand, we used the GP surrogate models built within TSEMO for yield and impurity from the first optimization campaign (Fig. 2) to predict the outcome of the same 30 experiments. Since the GP models are constantly updated with every experiment, we used the models at the end of the optimization campaign (after 46 total experiments). For every point predicted, the mean and the standard deviation were calculated from the average of 1000 samples drawn from GPs (full list of reaction conditions and GP predictions for all experiments is provided in ESI†). We confirmed that the randomly generated experiments were different than the optimization experiments suggested by TSEMO. The results in Fig. 6 indicate that the GP surrogate models could predict the outcome of the unseen reaction conditions with around 5.5% mean absolute error (MAE) and 6–7% RMSE. In addition, the standard deviations of the predictions were lower near the target objectives (high yield and low impurity) as the model has more information about these regions in the decision space. The model accuracy can be further improved for process modeling purposes by performing post-optimization experiments in high-uncertainty regions.
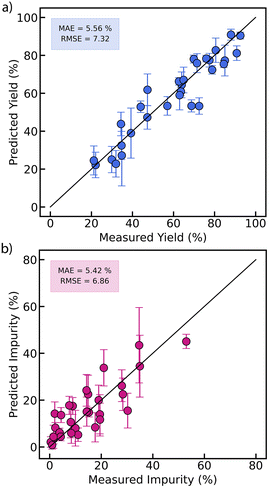 | ||
| Fig. 6 Yield (a) and impurity (b) predictions of 30 experimental conditions unseen by the Gaussian process (GP) surrogate model of the first optimization campaign (Fig. 2). The mean (data points) and the standard deviation (error bars) of the predictions were calculated from the average of 1000 samples drawn from the GPs. Black solid line represents the parity line. | ||
Finally it is worth stressing that optimizing process parameters and extracting implicit knowledge through GP surrogate models are tied to the experimental setup due to complex interactions between the chemistry and the physical setup through mixing and heat transport characteristics. In other words, the knowledge generated in this work may not be applicable to other experimental setups and physical information of the system needs to be included.
Conclusions
In conclusion we have demonstrated an optimization workflow consisting of a flow chemistry platform and multi-objective Bayesian optimization algorithm (TSEMO) towards the optimization of an ultra-fast lithium–halogen exchange reaction. The flow chemistry platform allowed precise control of temperature, stoichiometry, and residence time below the sub-second range for a difficult to control chemistry which enabled robust and reliable data collection. Three continuous variables were optimized to maximize the yield and to minimize the impurity. We applied this workflow to three different optimization campaigns with different numbers of training data sets and mixing intensifications. TSEMO was able to rapidly exploit the decision space and locate the optimum reaction conditions and trade-off zones (Pareto front) within 50 experiments. In addition, the reaction conditions suggested by TSEMO allowed us to gain insight into the effects of the different process parameters (residence time, temperature, stoichiometry, mixing efficiency) on the target objectives. Moreover, the use of Gaussian process surrogate models within TSEMO provided additional interpretability about the interactions within the system. The hyperparameters of the surrogate models could be analyzed, which infers the contribution of the input variables to the target objectives. In addition, we also demonstrated that the Gaussian process surrogate models could be used to gain additional information about the process via prediction of the unseen experimental conditions. Hence, this workflow provides a robust and data efficient approach for identifying optimum process parameters of lithium–halogen exchange reactions compared to single objective optimization, OFAT and factorial DoE methods. The analysis and design principles in this work are general and can be extended to other reactions to build process knowledge.Author contributions
DK: design of the study, performing calculations and experiments, development of the experimental system, manuscript drafting; GC: preliminary chemical system batch experiments and flow experiments; NJ: experiment automation with FLAB; JB: codes for closing the self-optimization loop PM: study conceptualization, supervision, manuscript revision; AAL: study conceptualization, supervision, funding acquisition, manuscript revision.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by Pfizer within the Pharma Innovation Programme in Singapore (PIPS) project. The project was hosted by Cambridge Centre for Advanced Research and Innovation in Singapore (CARES) whose lab is supported by the National Research Foundation Project C4T within CREATE Campus. J. Bai acknowledges financial support provided by CSC Cambridge International Scholarship from Cambridge Trust and China Scholarship Council.References
- D. M. Hodgson, Organolithiums in enantioselective synthesis, Springer Science & Business Media, 2003 Search PubMed.
- J. Clayden, Organolithiums: selectivity for synthesis, Elsevier, 2002 Search PubMed.
- A. Hafner, et al., A simple scale-up strategy for organolithium chemistry in flow mode: From feasibility to kilogram quantities, Org. Process Res. Dev., 2016, 20(10), 1833–1837 CrossRef CAS.
- M. E. Kopach, et al., Flow Grignard and lithiation: screening tools and development of continuous processes for a benzyl alcohol starting material, Org. Process Res. Dev., 2016, 20(9), 1581–1592 CrossRef CAS.
- B. Gutmann, D. Cantillo and C. O. Kappe, Continuous-flow technology—a tool for the safe manufacturing of active pharmaceutical ingredients, Angew. Chem., Int. Ed., 2015, 54(23), 6688–6728 CrossRef CAS PubMed.
- K. S. Elvira, X. C. I. Solvas, R. C. Wootton and A. J. Demello, The past, present and potential for microfluidic reactor technology in chemical synthesis, Nat. Chem., 2013, 5(11), 905–915 CrossRef CAS.
- J. I. Yoshida, Flash chemistry: flow microreactor synthesis based on high-resolution reaction time control, Chem. Rec., 2010, 10(5), 332–341 CrossRef CAS.
- B. Picard, et al., Bromine-lithium exchange on gem-dibromoalkenes part 1: batch vs microflow conditions, J. Flow Chem., 2020, 10, 139–143 CrossRef CAS.
- J. A. Newby, et al., Design and application of a low-temperature continuous flow chemistry platform, Org. Process Res. Dev., 2014, 18(10), 1211–1220 CrossRef CAS.
- A. Nagaki, Y. Ashikari, M. Takumi and T. Tamaki, Flash chemistry makes impossible organolithium chemistry possible, Chem. Lett., 2021, 50(3), 485–492 CrossRef CAS.
- H. Usutani and D. G. Cork, Effective utilization of flow chemistry: use of unstable intermediates, inhibition of side reactions, and scale-up for boronic acid synthesis, Org. Process Res. Dev., 2018, 22(6), 741–746 CrossRef CAS.
- J. Choe, J. H. Seo, Y. Kwon and K. H. Song, Lithium–halogen exchange reaction using microreaction technology, Chem. Eng. J., 2008, 135, S17–S20 CrossRef CAS.
- S. Zeibi Shirejini and A. Mohammadi, Halogen–lithium exchange reaction using an integrated glass microfluidic device: an optimized synthetic approach, Org. Process Res. Dev., 2017, 21(3), 292–303 CrossRef CAS.
- A. Hafner, M. Meisenbach and J. Sedelmeier, Flow chemistry on multigram scale: continuous synthesis of Boronic acids within 1 s, Org. Lett., 2016, 18(15), 3630–3633 CrossRef CAS.
- K. Pérez, et al., Bromine–Lithium Exchange on a gem-Dibromoalkene, Part 2: Comparative Performance of Flow Micromixers, Org. Process Res. Dev., 2020, 24(5), 787–791 CrossRef.
- G.-N. Ahn, et al., Exploring ultrafast flow chemistry by autonomous self-optimizing platform, Chem. Eng. J., 2023, 453, 139707 CrossRef CAS.
- A. Nagaki, H. Kim and J. I. Yoshida, Aryllithium compounds bearing alkoxycarbonyl groups: generation and reactions using a microflow system, Angew. Chem., 2008, 120(41), 7951–7954 CrossRef.
- A. Nagaki, D. Ichinari and J.-I. Yoshida, Three-component coupling based on flash chemistry. Carbolithiation of benzyne with functionalized aryllithiums followed by reactions with electrophiles, J. Am. Chem. Soc., 2014, 136(35), 12245–12248 CrossRef CAS PubMed.
- C. J. Taylor, et al., A Brief Introduction to Chemical Reaction Optimization, Chem. Rev., 2023, 123(6), 3089–3126 CrossRef CAS.
- N. Holmes, G. R. Akien, A. J. Blacker, R. L. Woodward, R. E. Meadows and R. A. Bourne, Self-optimisation of the final stage in the synthesis of EGFR kinase inhibitor AZD9291 using an automated flow reactor, React. Chem. Eng., 2016, 1(4), 366–371 RSC.
- D. Cortés-Borda, et al., Optimizing the Heck–Matsuda reaction in flow with a constraint-adapted direct search algorithm, Org. Process Res. Dev., 2016, 20(11), 1979–1987 CrossRef.
- The GPyOpt authors, GPyOpt: A Bayesian Optimization framework in python, 2016, https://github.com/SheffieldML/GPyOpt.
- E. Bradford, A. M. Schweidtmann and A. Lapkin, Efficient multiobjective optimization employing Gaussian processes, spectral sampling and a genetic algorithm, J. Glob. Optim., 2018, 71(2), 407–438 CrossRef.
- J. Knowles, ParEGO: A hybrid algorithm with on-line landscape approximation for expensive multiobjective optimization problems, IEEE Trans. Evol. Comput., 2006, 10(1), 50–66 Search PubMed.
- F. Häse, L. M. Roch and A. Aspuru-Guzik, Chimera: enabling hierarchy based multi-objective optimization for self-driving laboratories, Chem. Sci., 2018, 9(39), 7642–7655 RSC.
- M. I. Jeraal, S. Sung and A. A. Lapkin, A Machine Learning-Enabled Autonomous Flow Chemistry Platform for Process Optimization of Multiple Reaction Metrics, Chem.: Methods, 2021, 1(1), 71–77 CAS.
- A. D. Clayton, et al., Automated self-optimisation of multi-step reaction and separation processes using machine learning, Chem. Eng. J., 2020, 384, 123340 CrossRef CAS.
- A. M. Schweidtmann, A. D. Clayton, N. Holmes, E. Bradford, R. A. Bourne and A. A. Lapkin, Machine learning meets continuous flow chemistry: Automated optimization towards the Pareto front of multiple objectives, Chem. Eng. J., 2018, 352, 277–282 CrossRef CAS.
- P. Jorayev, et al., Multi-objective Bayesian optimisation of a two-step synthesis of p-cymene from crude sulphate turpentine, Chem. Eng. Sci., 2022, 247, 116938 CrossRef CAS.
- Y. Amar, A. M. Schweidtmann, P. Deutsch, L. Cao and A. Lapkin, Machine learning and molecular descriptors enable rational solvent selection in asymmetric catalysis, Chem. Sci., 2019, 10(27), 6697–6706 RSC.
- D. Helmdach, P. Yaseneva, P. K. Heer, A. M. Schweidtmann and A. A. Lapkin, A Multiobjective Optimization Including Results of Life Cycle Assessment in Developing Biorenewables-Based Processes, ChemSusChem, 2017, 10(18), 3632–3643 CrossRef CAS.
- M. Kraft, et al., From Platform to Knowledge Graph: Distributed Self-Driving Laboratories, 2023 Search PubMed.
- H. Kim, H. J. Lee and D. P. Kim, Integrated One-Flow Synthesis of Heterocyclic Thioquinazolinones through Serial Microreactions with Two Organolithium Intermediates, Angew. Chem., Int. Ed., 2015, 54(6), 1877–1880 CrossRef CAS.
- K. C. Felton, J. G. Rittig and A. A. Lapkin, Summit: benchmarking machine learning methods for reaction optimisation, Chem.: Methods, 2021, 1(2), 116–122 CAS.
- P. Müller, et al., Automated multi-objective reaction optimisation: which algorithm should I use?, React. Chem. Eng., 2022, 7(4), 987–993 RSC.
- T. Akama, et al., Discovery and structure–activity study of a novel benzoxaborole anti-inflammatory agent (AN2728) for the potential topical treatment of psoriasis and atopic dermatitis, Bioorg. Med. Chem. Lett., 2009, 19(8), 2129–2132 CrossRef CAS.
- H. Usutani, T. Nihei, C. D. Papageorgiou and D. G. Cork, Development and scale-up of a flow chemistry lithiation–borylation route to a key boronic acid starting material, Org. Process Res. Dev., 2017, 21(4), 669–673 CrossRef CAS.
- O. Levenspiel, Chemical reaction engineering, John Wiley & Sons, 1998 Search PubMed.
- S. Schwolow, J. Hollmann, B. Schenkel and T. Röder, Application-oriented analysis of mixing performance in microreactors, Org. Process Res. Dev., 2012, 16(9), 1513–1522 CrossRef CAS.
- C. K. Williams and C. E. Rasmussen, Gaussian processes for machine learning (no. 3), MIT Press, Cambridge, MA, 2006 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3re00539a |
| This journal is © The Royal Society of Chemistry 2024 |