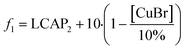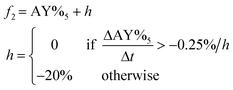Accelerating reaction optimization through data-rich experimentation and machine-assisted process development†
Jonathan P.
McMullen
 *a and
Jon A.
Jurica
b
*a and
Jon A.
Jurica
b
aProcess Research and Development, Merck & Co., Inc., P.O. Box 2000, Rahway, NJ 07065, USA. E-mail: jonathan.mcmullen@merck.com
bAnalytical Research and Development, Merck & Co., Inc., P.O. Box 2000, Rahway, NJ 07065, USA
First published on 22nd May 2024
Abstract
The field of reaction engineering is in a constant state of evolution, adapting to new technologies and the changing demands of process development on accelerated timelines. Recent advancements in laboratory automation, data-rich experimentation, and machine learning have revolutionized chemical synthesis research, bringing significant enhancements to reaction engineering. To showcase these advantages, this study introduces a machine-assisted process development workflow that uses data-rich experimentation to optimize reaction conditions for drug substance manufacturing. The workflow adopts a scientist-in-the-loop approach, ensuring valuable contributions and informed decision-making throughout the entire procedure. Two case studies are presented: a copper-catalyzed methoxylation of an aryl bromide and the global bromination of primary alcohols in gamma-cyclodextrin. In addition to identifying the optimal reaction conditions, the workflow emphasizes the importance of process knowledge. Data-driven reaction models are constructed for both case studies, showcasing how early-stage reaction data can inform late-stage process characterization and control strategies. The speed and efficiency offered by the machine-assisted approach enabled complete reaction optimization and reaction modeling in one week, approximately. This reaction data, along with other process knowledge obtained throughout development, highlight the future prospects for reaction engineering in drug substance development. As the field continues to embrace innovative technologies and methodologies, there is vast potential for further advancements in reaction engineering practices, leading to more streamlined and efficient process development and accelerating the discovery and optimization of chemical manufacturing processes.
Introduction
In drug substance process development, identifying the optimal reaction conditions is of paramount importance. The search for safe, scalable operating conditions that maximize product yield and ensure quality active pharmaceutical ingredient (API) in manufacturing demands a substantial investment of time and resources. Recently, the breadth of reaction optimization has expanded beyond standard reaction metrics and encompasses other manufacturing objectives, such as sustainability, raw material cost reduction, and process cycle time minimization. Striking a suitable balance among these diverse goals is a core responsibility of process chemists and chemical engineers, but remains challenging for numerous reasons. Beyond the technical complexities of nonlinear reaction responses, identifying the optimal conditions is further exacerbated by constraints in resources, accelerated timelines, and competing process development objectives. The confluence of these factors has spurred considerable investment in new tools and methodologies to streamline process optimization in drug substance development.Automation and data-rich experimentation (DRE) have revolutionized process development by offering enhanced capabilities at the lab benchtop.1 The integration of process analytical tools, such as on-line HPLC2,3 and in situ spectroscopy,4–7 increases the data density in each experiment, providing information on both the reaction kinetics and the overall reaction performance. Enhancements to throughput can be achieved through the utilization of parallel reactor technology, integrated with automated sampling strategies, allowing for collection of comprehensive reaction profiles.8 This enables a deeper understanding of the correlation between reaction inputs and process dynamics.9 Moreover, advancements in analytical equipment along with data analytics enable a higher throughput of off-line samples with a more straightforward visualization of results.
In recent years, the application of feedback optimization algorithms to guide experiments towards desired conditions has proven to be an effective and efficient approach to process development.10–14 This is particularly evident in scenarios with complex syntheses with multiple reaction variables. Initially implemented in flow reactor systems, where sequential experiments can be easily modified by adjusting flow rates, early examples identified local solutions to simple optimization problems.15–22 However, more recent demonstrations have showcased the use of sophisticated operations, algorithms, and multifaceted objective functions.12,23–33 To further expand this methodology in chemical synthesis research, similar approaches are required for reactions where batch operations are preferred.
When selecting a batch reaction optimization platform, careful consideration of various features is essential to ensure that the experimental hardware and chosen algorithm align with the goals of drug substance development. The choice of reactor technology should be made based on factors such as desired throughput, the physical properties of the reaction, and the required data density. Plate-based reactors may be appropriate when there is limited starting material and the aim is to optimize reaction performance across multiple solvents, bases, and catalysts.34,35 Larger reactors with overhead stirring may be more appropriate when the goal is to study the reaction with scale-up considerations. When it comes to the optimization approach, selecting an algorithm that is reputable for its experimental efficiency is obviously important.36,37 However, equally important is choosing an algorithm that aligns with the process uncertainties and the experimental workflow. Consideration should be given to size of the reaction design space, the algorithm's ability to effectively handle experimental noise, its ability to update the objective function and experimental constraints, and the suggested number of experiments with each iteration (e.g., single sequential or multiple parallel experiments). These features can be especially valuable during early process development, when flexibility and overall experimental speed are crucial.
This work presents one methodology for machine-assisted batch reaction optimization with data-rich experimentation, emphasizing important considerations in the process. To illustrate the approach, two case studies are provided: the first involves the copper-catalyzed methoxylation of an aryl bromide38 (Scheme 1), while the second focuses on the global bromination of primary alcohols in gamma cyclodextrin (Scheme 2).39 In both cases, a “scientist-in-the-loop” approach was employed to contribute valuable insights and filter the data effectively. The experimental design and algorithmic operations were carefully selected to ensure that iterations of experimentation, data acquisition, and analysis could be completed within one week, aligning with common drug substance development timelines. Furthermore, post-run data-driven reaction modeling was conducted, highlighting how the optimization process can be further utilized to extract kinetic information and provide design space details for formal process characterization.
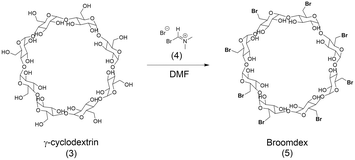 | ||
| Scheme 2 Bromination of γ-cyclodextrin via Bromo–Vilsmeier reagent (4) to produce drug substance intermediate Broomdex (5). | ||
Experimental
Automated reactor technology
All experiments were performed in an Integrity 10 reaction block that was equipped with an AmigoChem workstation for automated reaction sampling. These combined technology platforms enable 10 reactions to be operated simultaneously, independently, and with custom sampling strategies. Reactions were performed in 25 mm diameter glass tubes (Kimble, 150 mm height) with magnetic stir bar agitation and jacket control temperature. Reactions were performed under a nitrogen blanket to maintain inert conditions. The reaction jacket temperature in each experiment was determined by the optimization algorithm and manually entered in the AmigoChem operating software. To enable reaction profiling, automated sampling technology and a liquid handling arm were utilized to collect reaction samples, which were subsequently analyzed using off-line UPLC (ultra-performance liquid chromatography). Samples withdrawn from each reactor were charged to 2 mL UPLC vials that were pre-diluted with an appropriate quench and diluent.The temperature range offered by the AmigoChem workstation was considered suitable for conducting optimization investigations, and the Teflon coated stir bar ensured adequate mixing for the methoxylation's thin slurry nature and the homogeneous bromination. These cursory suitability checks instilled confidence that the optimization results would translate well to other equipment and scales. These features also made the AmigoChem the ideal system for these specific optimization investigations due the low starting material consumption per experiment, the parallel reactor technology enabling the desired experimental throughput, and the data-rich reaction sampling to enable essential kinetic and stability information to support process modeling.
Methoxylation procedure
All reactions were prepared in a nitrogen inert glove box using anhydrous solvents and reagents that were degassed in the nitrogen environment. Reactions were prepared by charging 3 g of aryl bromide (1) DABCO salt to a Kimble tube, followed copper bromide (Alfa Aesar), dimethyl formamide (Sigma Aldrich), and sodium methoxide (25 wt% in methanol, Sigma Aldrich). The amounts of copper bromide, DMF, and sodium methoxide in each experiment were determined by the optimization algorithm. Additional methanol was charged to bring the total liquid volume of each reaction to 15 mL. A magnetic stirrer was added to each reactor before being capped with an Integrity 10 Teflon reactor lid. Reactors were transported to the Integrity reaction block and interlocked with a nitrogen manifold to maintain inertion. Reactions were controlled by jacket temperature on the Integrity 10 block, each determined by the optimization algorithm.During the reaction, 40 μL samples were collected by the AmigoChem and diluted with 960 μL of a quench solution (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v acetonitrile: acetic acid solution) in a 2 mL UPLC vial. Post experiment, serial dilution (5×) of samples was performed by combining 200 μL sample with 800 μL quench. Analysis of reaction results was performed on Agilent 1200 series UPLC, using an Acquity UPLC BEH C18 column (1.7 μm × 2.1 mm × 100 mm, P/N: 186002352) with detection at 210 nm. Reaction results were reported as liquid chromatography area percentage (LCAP). See the ESI† for additional analytical information.
1 v/v acetonitrile: acetic acid solution) in a 2 mL UPLC vial. Post experiment, serial dilution (5×) of samples was performed by combining 200 μL sample with 800 μL quench. Analysis of reaction results was performed on Agilent 1200 series UPLC, using an Acquity UPLC BEH C18 column (1.7 μm × 2.1 mm × 100 mm, P/N: 186002352) with detection at 210 nm. Reaction results were reported as liquid chromatography area percentage (LCAP). See the ESI† for additional analytical information.
Bromination procedure
All reactions were prepared in a nitrogen inert glove box using anhydrous solvents and reagents that were degassed in the nitrogen environment. A starting material stock solution was prepared by adding 600 ml DMF (Sigma Aldrich) to 56.4 g (88.6 wt%, 50.0 g assay) of wet γ-cyclodextrin. This solution was then dried by constant volume distillation to <200 ppm water. A magnetic stirrer bar was added to each reactor and then the Bromo–Vilsmeier reagent (Millipore Sigma) was added followed by 10.6 mL of the cyclodextrin solution (1 g basis of cyclodextrin). Additional DMF was then added to arrive at the necessary concentration and the reactor capped with an Integrity 10 Teflon reactor lid. The amounts of the Bromo–Vilsmeier reagent and addition DMF in each experiment were determined by the optimization algorithm. Reactors were transported to the Integrity reaction block and interlocked with a nitrogen manifold to maintain inertion. Reactions were controlled by jacket temperature on the Integrity 10 block, each determined by the optimization algorithm.During the reaction, 250 μL samples were collected by the Amigochem and added to 2 mL HPLC vials containing 50 μL of water. Upon reaction completion, the samples were removed, 15 μL of 48% HBr (Thermo Scientific) added, stir bars added and placed on a tumble stirrer heated to 40 °C for 5.5 h. The samples were then cooled to room temperature, 1.5 mL of 50% DMSO (Sigma Aldrich)/Acetonitrile (Sigma Aldrich) was added and then analyzed by UPLC. See the ESI† for additional analytical information.
Scientist-in-the-loop optimization methodology
Self-optimizing systems are characterized by their ability to function autonomously, which, in theory, offers high efficiency. However, in practice, relying solely on such systems can pose unnecessary risks in reaction development, particularly when development time and material resources are limited. Experimental nuances, including sampling inaccuracies or unexpected shifts in chromatograms, may be challenging for an algorithm to independently detect. As iterative data becomes available, it may be necessary to modify the objective function for reaction optimization to address unforeseen issues, such as the emergence of a new concerning impurity. Fully automated systems, devoid of human involvement, cannot anticipate the evolving needs and judgment of a scientist, especially when there is uncertainty in the reaction and analytical outcomes. For these reasons, an optimization strategy that incorporates the scientist-in-the-loop was implemented in this work.The stable noisy optimization by Branch and Fit (SNOBFIT) algorithm developed by Huyer and Neumaier40 was implemented in this machine-assisted reaction optimization demonstration, although numerous alternative algorithms could have been considered. Because it is a black-box approach, mechanistic information is not required. The algorithm accounts for noisy measurement responses, which is a common occurrence in experimental settings, and allows the user to specify the resolution in optimization variables. Each call to the algorithm is considered an iteration, and the number of experiments reported per iteration can be tailored to suit the specific capabilities of the experimental technology employed. For instance, in the present work, 10 experiments were executed per call to the algorithm, coinciding with the parallelizability of the system, enabling 10 reactions to be conducted simultaneously per iteration. The experimental throughput played an important role in selecting the SNOBFIT algorithm as it can parallelize search experiments. In contrast, traditional Bayesian optimization approaches are typically sequential in nature, although ongoing research is addressing this limitation.41,42 Specific SNOBFIT algorithm details for both case studies, including parameter settings and implementation specifics, can be found in the ESI.†
Results and data analysis
Methoxylation optimization and analysis (case study 1)
The first demonstration focused on optimizing the reaction performance of the copper-catalyzed methoxylation reaction outlined in Scheme 1. This straightforward reaction was chosen as a means to refine the experimental workflow associated with the multi-variable optimization approach utilizing parallel reactors. While historical laboratory data was not employed to initiate the SNOBFIT algorithm, prior knowledge was utilized to determine suitable reaction variables and their corresponding lower and upper bounds. Prior to commencing the experimental phase, a maximum of 40 experiments was predetermined to enable three active rounds of optimization. This threshold was carefully selected to align with the allocation of starting materials for the optimization investigations and to ensure that the duration of the optimization process remained within the targeted timeframe of approximately one week.The optimization of the reaction conditions involved adjusting several key variables, including the reaction temperature, copper bromide loading, DMF equivalents, sodium methoxide solution equivalents, and reaction time. The lower and upper bounds for each variable can be found in Table 1. In the first call to the SNOBFIT algorithm, 10 space-filling points were generated to provide essential information for subsequent search experiments. During these initial experiments, the objective function was not formally defined yet, as the reaction outcomes under the diverse range of conditions would determine which reaction properties to exploit and which to avoid. While the SNOBFIT algorithm requested a single time measurement for each experiment, multiple measurements were taken throughout the course of each reaction. This time-series information was used to assess whether kinetic phenomena, such as reaction stalling or product degradation, should be incorporated into the objective function. Moreover, a subset of these reaction results that were of interest to the scientist were added to the optimization routine.
The reaction results of the initial call to the algorithm are provided in the ESI,† and revealed several noteworthy trends that influenced the subsequent optimization process. In general, all experiments resulted in incomplete conversion and only several experiments resulted in modest product yield. Considering this observation, the upper bounds for both temperature and reaction time were extended to explore conditions with faster kinetics and complete conversion (see Table 1 footnote). Concerning the reaction performance, the profiles did not unveil any significant issues regarding impurity generation or product degradation. Therefore, the reaction optimization procedure presented an opportunity to maximize yield and process efficiency. The ability to analyze preliminary reaction data, formulate informed objectives, and update the feasible design space are key advantages of the scientist-in-the-loop optimization method. This increased flexibility leads to more significant improvements in subsequent rounds of reaction optimization.
For this methoxylation, the optimizer aimed to maximize a two-term objective function, as outlined in Table 1. The first term represented product yield, while the second term served as an incentive to minimize catalyst usage, aligning with a common goal in reaction development. The round 1 reaction results were converted to objective function values, and are provided in Fig. 1a.
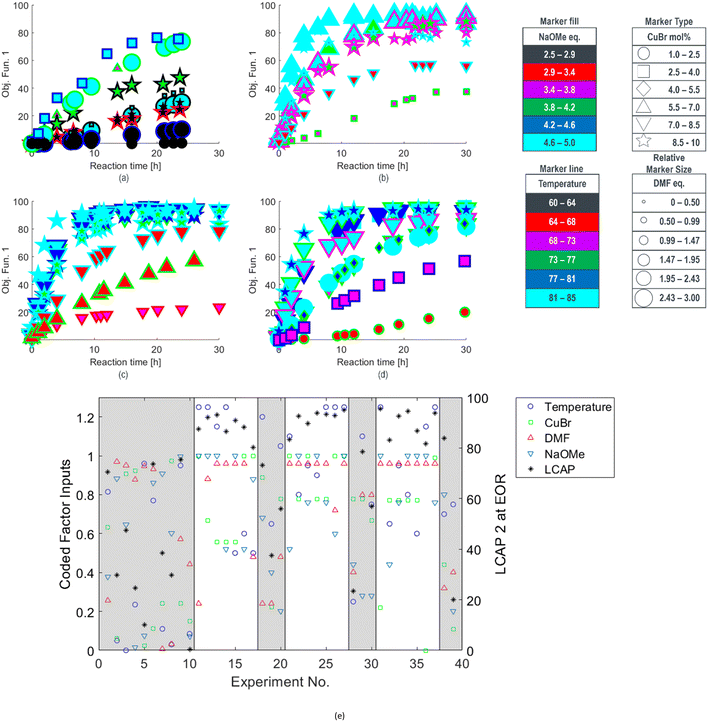 | ||
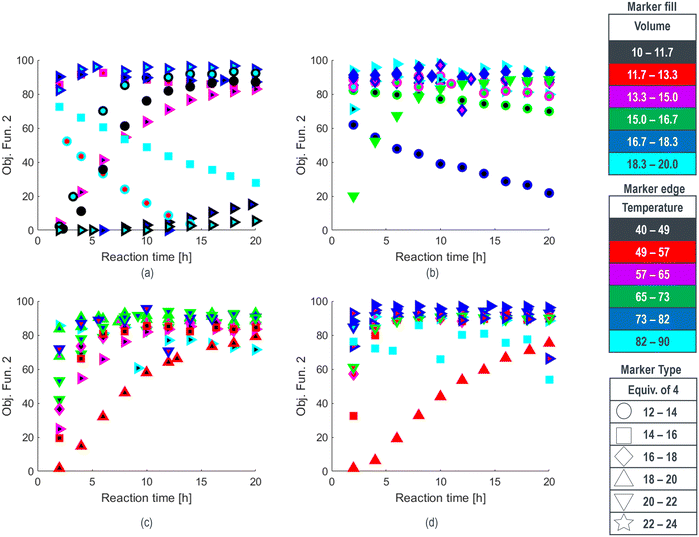
| Fig. 1 Optimization results for methoxylation investigation with objective function and experimental conditions denoted for a) the first round, b) the second round, c) the third round, and d) the fourth round, along with e) a strip chart correlating experimental coded conditions (see ESI†) with end of reaction (EOR) 2 LCAP for all runs, with grey background denoting experiments selected for space-filling design or targeted in unexplored regions. | ||
Following the initial round of experiments, subsequent iterations using the SNOBFIT algorithm actively searched for the optimal reaction conditions. Each iteration involved conducting 10 experiments with reaction temperatures, charge amounts, and reaction times specified by the algorithm. Within each iteration, seven of the 10 experiments were dedicated to searching for the local optimum, while the remaining three searched unexplored regions to better ensure that the best conditions corresponded to a global optimum. In each experiment, the requested SNOBFIT sample time was either collected or substituted with a similar time point already present in the reaction profile. Once the round of experimentation was completed, the entire reaction profile data was collected, analyzed, and utilized to calculate the objective function values. However, only the objective function value for the SNOBFIT time point and other user-selected points were inputted into the algorithm. This approach capitalized on the nearest-neighbor algorithm utilized by SNOBFIT to construct surrogate models and to perform iterative searches for optimal conditions, allowing for a more comprehensive exploration of experimental conditions and preventing bias of the sample time. Utilizing more data in the algorithm may be possible in future works through appropriate scaling of reaction variables.
The reaction results from rounds 2 to 4 of the optimization process are depicted in Fig. 1b–d, respectively. To effectively summarize the reaction performance (y-axis) over time (x-axis), the data markers are encoded with various properties, such as type, size, interior color, and outline color, to represent the multidimensional inputs of the reaction. Compared to the initial search experiments, shown in Fig. 1a, the algorithm rapidly identified an ensemble of reaction conditions during the round 2 search (Fig. 1b) that collectively exhibited faster reaction rates and higher conversions. This trend of performance improvement continued in rounds 3 and 4 (Fig. 1c and d), except for experiments intentionally targeting unexplored regions. Reaction conditions for SNOBFIT points with the maximum objective function and those yielding the highest product yield are detailed in Table 2. Furthermore, all reaction conditions and their corresponding product profiles from each experiment can be found in the (ESI†).
| Experiment | Maximum | Temperature (deg. C) | CuBr (mol%) | NaOMe (eq.) | DMF (eq.) | Time (h) | Obj. Fun. | LCAP 2 |
|---|---|---|---|---|---|---|---|---|
| 14 | Objective Function | 83 | 6.0 | 5.0 | 2.88 | 25.2 | 97.2 | 92.8 |
| 34 | LCAP 2 | 76 | 8.0 | 5.0 | 2.88 | 28 | 96.9 | 95.0 |
The end-of-reaction product LCAP and the corresponding conditions requested by the SNOBFIT algorithm are displayed in Fig. 1e. The clear background data points represent experiments directed by the algorithm, leading toward the optimal reaction conditions. In contrast, the shaded regions denote experiments selected by the algorithm for the initial space-filling design or in unexplored areas of the design space, providing comprehensive search coverage. This plot explains how the algorithm converged towards conditions at the upper ranges of temperature, DMF equivalents, and NaOMe equivalents, while identifying an appropriate CuBr loading to achieve higher conversion under these conditions. The alignment between expected trends and the performance of the algorithm in penalizing experiments with elevated CuBr levels showcases the logical nature of the operating conditions. This congruence between expectations and algorithm output is an important step in validating machine-assisted process workflows into drug substance development.
While the optimization results are directly impactful to process development, leveraging the data to build process knowledge that transcends development life cycle is just as important. One such approach is presented below by interrogating the data through machine learning practices and data-driven modeling, though alternative approaches to extract similar knowledge exist.43–48
To gain a better understanding of the reaction performance, a clustering algorithm was used to identify experimental data in the vicinity of the highest yielding run, experiment 34. From the SNOBFIT reaction dataset, 15 experiments were identified as being reasonably close to the optimal conditions using the Mahalanobis distance as a metric (see ESI† for approach and corresponding experiments). The reaction results from the set of local experiments were then modelled using functional principal component analysis (FPCA).49–53 FPCA is a branch of functional data analysis (FDA), an applied statistics discipline that involves the analysis and regression of data objects, curves, or functions rather than individual points.49 In this work, the FPCA methodology utilized the principal analysis by conditional estimation (PACE) algorithm, allowing its application to datasets with sparse or dense sampling strategies.50–52 For the sake of brevity, the discussion below is streamlined to provide a basic understanding of the modeling framework applied to the reaction results. A more detailed description of the methodology is provided in the ESI† and supported by the referenced literature.
Similar to principal component analysis (PCA), FPCA effectively reduces the dimensionality of the data by identifying functional principal components that account for longitudinal (time) variations, along with the corresponding FPC scores that elucidate the variation across experiments. Mathematically, this is provided by eqn (1), where ŷ(t) is the FPCA prediction for the reaction response time profile, μ(t) is the functional mean, ϕk(t) is a set of k eigenfunctions, also referred to as the functional principal components (FPC), and ξik is the corresponding FPC score in experiment i. To move from a descriptive model to a predictive model, the FPC scores can be treated as a separate response and regressed against the experimental input factors, as in eqn (2), where β terms are regressed coefficients, xp and xq represent indexed input factors, and NF is the number of factors.54 See ESI† for more information.
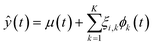 | (1) |
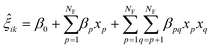 | (2) |
Using the manner described above, a FPCA model with regressed FPC scores was performed and the results are provided in Fig. 2. Statistical analysis associated with the FPC score regression is provided in the ESI.† As the results illustrate, there is excellent agreement between the experimental data, and the FPCA model using both the numerically derived FPC scores and the regressed scores (eqn (2)) for many of the experiments. While some discrepancies exist at early reaction times (e.g., experiments 16, 17, 32), the agreement improves toward the end of the reaction where conversion predictions matter most.
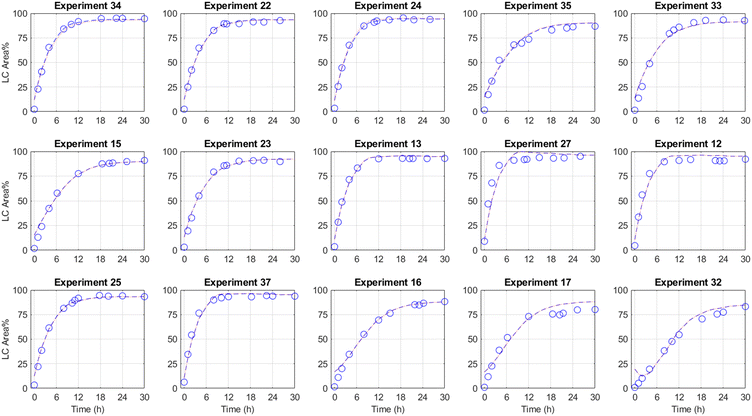 | ||
Fig. 2 Functional principal component analysis (FPCA) model for a set of methoxylation results in the local neighborhood around the optimal yield conditions (experiment 34) with experimental data ( ), FPCA model (eqn (1), ), FPCA model (eqn (1),  ), and FPCA model with regressed coefficients (eqn (2), ), and FPCA model with regressed coefficients (eqn (2),  ) overlaid. ) overlaid. | ||
Notably, as the objective is to gather this reaction optimization data in the early stages of development, these models can be utilized to identify robust operating spaces as the process matures and development progresses towards manufacturing. To demonstrate this potential, the developed FPCA model was used to estimate the product response as a function of temperature and copper bromide within the design space used for model development. As the contour profiles in Fig. 3 suggest, a wide operating space that achieves target reaction performance can be achieved by tuning the temperature, CuBr loading, and reaction time.
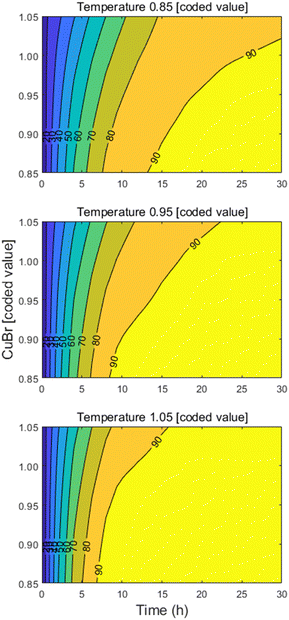 | ||
| Fig. 3 Methoxylation reaction profiles estimated through FPCA model as function of temperature and CuBr using coded values (see ESI†), keeping DMF and NaOMe equivalents at optimized values (see Table 2). | ||
Bromination optimization and analysis (case study 2)
Using a similar approach to the previous case, the bromination reaction outlined in Scheme 2 was optimized using the SNOBFIT algorithm. The algorithm was not seeded with any prior data and a total of 40 experiments were allotted for the optimization investigation. The optimization variables and the corresponding ranges are provided in Table 3. This particular reaction presented unique challenges for process development as the detection of partially brominated reaction intermediates using UPLC was limited. Additionally, there was a risk of product degradation and impurity generation due to the strongly acidic reaction conditions used. These characteristics made it an ideal candidate for machine-assisted process development as process decisions would be based on limited reaction response data.The assay yield from the initial 10 space filling experiments performed by the SNOBFIT algorithm are presented in the ESI.† Notably, these experiments demonstrated the diverse range of reaction behaviors achievable within the defined design space. This encompassed conditions with low conversions, those exhibiting fast kinetics and high conversion, as well as instances leading to rapid product degradation. Such product instability poses significant challenges for control strategies that rely on in-process quality control samples with long turnaround times. Consequently, the objective was to identify conditions that would result in high product yield while also ensuring product stability. To achieve this goal, the objective function to maximize, as outlined in Table 3 incorporated a penalty function to discourage experimental conditions in which notable product degradation was observed. Furthermore, it is noteworthy to mention the artificially low assay yield in several data points due to an imperfect sampling protocol. These data points were removed from consideration for the purposes of optimization and post-run analysis (see ESI† for specific samples). This observation emphasizes one of the critical needs for a scientist-in-the-loop machine assisted development. Objective function values for this first set of experiments are provided in Fig. 4a.
Results from optimization rounds 2–4 for the bromination are illustrated in Fig. 4b–d, respectively. In each round, the algorithm allocated seven experiments to local optimization searches and three experiments in unexplored regions to ensure the identification of the global optimum. The reaction profiles convincingly demonstrate the algorithm's effectiveness in rapidly identifying experimental conditions that result in fast kinetics, high conversion, and good stability as evident in the first set of search conditions of round 2 (Fig. 4b). Similar outcomes continued throughout the subsequent optimization rounds. Conditions corresponding to the optimal objective function are provided in Table 4. Because the penalty function was not active in this run, the optimal objective function corresponds to maximum yield in this result. See the ESI† for complete bromination optimization data.
| Experiment | Temperature (deg. C) | Volume (mL g−1) | 4 (eq.) | Time (h) | Obj. Fun. |
|---|---|---|---|---|---|
| 40 | 80 | 17.6 | 22.6 | 20 | 97.8% |
In contrast to the previous methoxylation case study, the optimization investigation in this scenario yielded limited dynamic data. Nevertheless, this data can still serve as a valuable source for generating crucial process knowledge in subsequent development stages. To demonstrate this, experimental data within a local neighborhood surrounding the optimal conditions for the assay yield at 8 hours were utilized to construct a response surface model. Through stepwise linear regression analysis of 20 experiments, a statistically significant quadratic model was derived (see ESI†). The resulting contour plot, depicted in Fig. 5, illustrates the relationship between temperature and equivalents of 4 in relation to the assay yield. This plot emphasizes the sensitive nature of the reaction and the need to strike a balance between temperature and Bromo–Vilsmeier reagent equivalents to achieve the desired conditions. Notably, at higher reaction temperatures, elevated levels of 4 were found to enhance product stability. These interesting findings were further validated through detailed characterization experiments and mechanistic studies conducted in separate research work.39
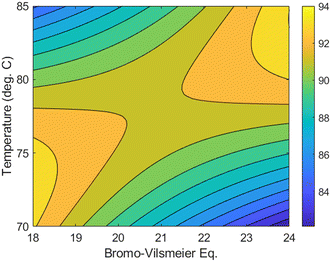 | ||
| Fig. 5 Assay yield response surface model over range of temperature and equivalents of 4 around the optimal reaction yield at 8 hours with DMF set at 15 mL g−1. | ||
Conclusions
The growth of laboratory automation and data-rich experimentation technologies, in parallel with the expansion of data science and machine learning applications into chemical synthesis, will emphasize the need for reaction engineering practices to adopt a machine-assisted process development approach. In this study, the effectiveness of such a methodology was presented for the reaction optimization of a copper-catalyzed methoxylation and a multi-substituted bromination using the SNOBFIT algorithm. A workflow was established to achieve reaction optimization in approximately one week through judicious selection of the reaction equipment, automated sampling technology, and algorithm to fit the specific reaction properties and optimization needs. The scientist-in-the-loop approach played a critical role in evaluating the results, filtering data, and making informed decisions to define the objective functions and the process constraints. This highlights the importance of human expertise in complementing and guiding the optimization process.Applying similar workflows in early drug substance programs have the promise to greatly accelerate overall process development timelines when the optimization data is leveraged throughout the research lifecycle. In this work, that data bridge was exemplified by using data-driven modeling methods. Functional principal component analysis was demonstrated as a powerful process modeling tool for the methoxylation kinetics; whereas, in the bromination case study, a more standard empirical model was established using a nearest neighbor algorithm and stepwise regression. Though beyond the scope of this individual work, the greatest gains for this approach are met when the optimization results are for long-term route development in early development are retained and leveraged in late-stage process characterization to streamline quality risk assessment and control strategy selection.
The outlook for machine-assisted process development and similar methodologies for reaction engineering are highly promising. Continued advancements in data throughput, data-rich experimentation, data engineering and analytics, as well as optimization methods, will play pivotal roles in driving significant improvements in these reaction optimization approaches. Beyond technical growth, successful implementation and sustainability of machine-assisted process development approaches require careful consideration of distribution and adoption of the technology. One barrier on this front is the initial uncertainty associated with the resource commitment, including time and material, as well as the expected gains from the optimization investigation compared to the current state. To facilitate widespread adoption, the development of numerical methods that can confidently establish tight upper and lower bounds around the expected benefits and so-called costs using minimal experimental data points will be invaluable.
Overall, with continued advancements and efforts in these areas, machine-assisted process development will continue to revolutionize reaction engineering, enabling more efficient and effective optimization strategies and driving progress in chemical manufacturing process.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Shane Stone for his experimental help with the methoxylation case study.Notes and references
- J. A. Jurica and J. P. McMullen, Automation Technologies to Enable Data-Rich Experimentation: Beyond Design of Experiments for Process Modeling in Late-Stage Process Development, Org. Process Res. Dev., 2021, 25(2), 282–291 CrossRef CAS.
- K. Zawatzky, S. Grosser and C. J. Welch, Facile kinetic profiling of chemical reactions using MISER chromatographic analysis, Tetrahedron, 2017, 73(33), 5048–5053 CrossRef CAS.
- M. Christensen, F. Adedeji, S. Grosser, K. Zawatzky, Y. Ji, J. Liu, J. A. Jurica, J. R. Naber and J. E. Hein, Development of an automated kinetic profiling system with online HPLC for reaction optimization, React. Chem. Eng., 2019, 4(9), 1555–1558 RSC.
- Y. Qin, K. A. Mattern, V. Zhang, K. Abe, J. Kim, M. Zheng, R. Gangam, A. Kalinin, J. N. Kolev, S. Axnanda, Z. E. X. Dance, U. Ayesa, Y. Ji, S. T. Grosser, E. Appiah-Amponsah and J. P. McMullen, Evolution of a Green and Sustainable Manufacturing Process for Belzutifan: Part 4—Applications of Process Analytical Technology in Heterogeneous Biocatalytic Hydroxylation, Org. Process Res. Dev., 2024, 28(2), 432–440 CrossRef CAS.
- A. Chanda, A. M. Daly, D. A. Foley, M. A. LaPack, S. Mukherjee, J. D. Orr, G. L. Reid III, D. R. Thompson and H. W. Ward II, Industry Perspectives on Process Analytical Technology: Tools and Applications in API Development, Org. Process Res. Dev., 2015, 19(1), 63–83 CrossRef CAS.
- J. Dijkmans, J. Chau, T. Maes, T. Khamiakova, S. Laps and N. Vandervoort, Generative PAT Fingerprint Approach for Verification of the Scale-Up of Pharmaceutical Processes, Org. Process Res. Dev., 2024, 28(3), 770–779 CrossRef CAS.
- Y. Miyai, A. Formosa, C. Armstrong, B. Marquardt, L. Rogers and T. Roper, PAT Implementation on a Mobile Continuous Pharmaceutical Manufacturing System: Real-Time Process Monitoring with In-Line FTIR and Raman Spectroscopy, Org. Process Res. Dev., 2021, 25(12), 2707–2717 CrossRef CAS.
- X. Li and A. L. Dunn, Development of a High-Throughput Kinetics Protocol and Application to an Aza-Michael Reaction, Org. Process Res. Dev., 2022, 26(3), 795–803 CrossRef CAS.
- C. Nunn, A. DiPietro, N. Hodnett, P. Sun and K. M. Wells, High-Throughput Automated Design of Experiment (DoE) and Kinetic Modeling to Aid in Process Development of an API, Org. Process Res. Dev., 2018, 22(1), 54–61 CrossRef CAS.
- J. A. G. Torres, S. H. Lau, P. Anchuri, J. M. Stevens, J. E. Tabora, J. Li, A. Borovika, R. P. Adams and A. G. Doyle, A Multi-Objective Active Learning Platform and Web App for Reaction Optimization, J. Am. Chem. Soc., 2022, 144(43), 19999–20007 CrossRef CAS PubMed.
- A. D. Clayton, J. A. Manson, C. J. Taylor, T. W. Chamberlain, B. A. Taylor, G. Clemens and R. A. Bourne, Algorithms for the self-optimisation of chemical reactions, React. Chem. Eng., 2019, 4(9), 1545–1554 RSC.
- P. Sagmeister, F. F. Ort, C. E. Jusner, D. Hebrault, T. Tampone, F. G. Buono, J. D. Williams and C. O. Kappe, Autonomous Multi-Step and Multi-Objective Optimization Facilitated by Real-Time Process Analytics, Adv. Sci., 2022, 9(10), 2105547 CrossRef PubMed.
- N. Aldulaijan, J. A. Marsden, J. A. Manson and A. D. Clayton, Adaptive mixed variable Bayesian self-optimisation of catalytic reactions, React. Chem. Eng., 2024, 9(2), 308–316 RSC.
- M. Christensen, Y. Xu, E. E. Kwan, M. J. Di Maso, Y. Ji, M. Reibarkh, A. C. Sun, A. Liaw, P. S. Fier, S. Grosser and J. E. Hein, Dynamic sampling in autonomous process optimization, Chem. Sci., 2024 10.1039/d3sc06884f.
- S. Krishnadasan, R. J. C. Brown, A. J. deMello and J. C. deMello, Intelligent routes to the controlled synthesis of nanoparticles, Lab Chip, 2007, 7(11), 1434–1441 RSC.
- J. P. McMullen and K. F. Jensen, An Automated Microfluidic System for Online Optimization in Chemical Synthesis, Org. Process Res. Dev., 2010, 14(5), 1169–1176 CrossRef CAS.
- J. P. McMullen, M. T. Stone, S. L. Buchwald and K. F. Jensen, An Integrated Microreactor System for Self-Optimization of a Heck Reaction: From Micro- to Mesoscale Flow Systems, Angew. Chem., Int. Ed., 2010, 49(39), 7076–7080 CrossRef CAS PubMed.
- R. A. Bourne, R. A. Skilton, A. J. Parrott, D. J. Irvine and M. Poliakoff, Adaptive Process Optimization for Continuous Methylation of Alcohols in Supercritical Carbon Dioxide, Org. Process Res. Dev., 2011, 15(4), 932–938 CrossRef CAS.
- B. J. Reizman and K. F. Jensen, Simultaneous solvent screening and reaction optimization in microliter slugs, Chem. Commun., 2015, 51(68), 13290–13293 RSC.
- D. E. Fitzpatrick, C. Battilocchio and S. V. Ley, A Novel Internet-Based Reaction Monitoring, Control and Autonomous Self-Optimization Platform for Chemical Synthesis, Org. Process Res. Dev., 2016, 20(2), 386–394 CrossRef CAS.
- B. J. Reizman, Y.-M. Wang, S. L. Buchwald and K. F. Jensen, Suzuki–Miyaura cross-coupling optimization enabled by automated feedback, React. Chem. Eng., 2016, 1(6), 658–666 RSC.
- V. Fath, N. Kockmann, J. Otto and T. Röder, Self-optimising processes and real-time-optimisation of organic syntheses in a microreactor system using Nelder–Mead and design of experiments, React. Chem. Eng., 2020, 5(7), 1281–1299 RSC.
- A.-C. Bédard, A. Adamo, K. C. Aroh, M. G. Russell, A. A. Bedermann, J. Torosian, B. Yue, K. F. Jensen and T. F. Jamison, Reconfigurable system for automated optimization of diverse chemical reactions, Science, 2018, 361(6408), 1220–1225 CrossRef PubMed.
- J. P. McMullen and B. M. Wyvratt, Automated optimization under dynamic flow conditions, React. Chem. Eng., 2023, 8(1), 137–151 RSC.
- K. Y. Nandiwale, T. Hart, A. F. Zahrt, A. M. K. Nambiar, P. T. Mahesh, Y. Mo, M. J. Nieves-Remacha, M. D. Johnson, P. García-Losada, C. Mateos, J. A. Rincón and K. F. Jensen, Continuous stirred-tank reactor cascade platform for self-optimization of reactions involving solids, React. Chem. Eng., 2022, 7(6), 1315–1327 RSC.
- D. Karan, G. Chen, N. Jose, J. Bai, P. McDaid and A. A. Lapkin, A machine learning-enabled process optimization of ultra-fast flow chemistry with multiple reaction metrics, React. Chem. Eng., 2024, 9, 619–629 RSC.
- A. Pomberger, A. A. Pedrina McCarthy, A. Khan, S. Sung, C. J. Taylor, M. J. Gaunt, L. Colwell, D. Walz and A. A. Lapkin, The effect of chemical representation on active machine learning towards closed-loop optimization, React. Chem. Eng., 2022, 7, 1368–1379 RSC.
- A. M. Schweidtmann, A. D. Clayton, N. Holmes, E. Bradford, R. A. Bourne and A. A. Lapkin, Machine learning meets continuous flow chemistry: Automated optimization towards the Pareto front of multiple objectives, Chem. Eng. J., 2018, 352, 277–282 CrossRef CAS.
- A. Slattery, Z. Wen, P. Tenblad, J. Sanjosé-Orduna, D. Pintossi, T. den Hartog and T. Noël, Automated self-optimization, intensification, and scale-up of photocatalysis in flow, Science, 2024, 383(6681), eadj1817 CrossRef CAS PubMed.
- J. Zhang, N. Sugisawa, K. C. Felton, S. Fuse and A. A. Lapkin, Multi-objective Bayesian optimisation using q-noisy expected hypervolume improvement (qNEHVI) for the Schotten–Baumann reaction, React. Chem. Eng., 2024, 9, 706–714 RSC.
- A. D. Clayton, A. M. Schweidtmann, G. Clemens, J. A. Manson, C. J. Taylor, C. G. Niño, T. W. Chamberlain, N. Kapur, A. J. Blacker, A. A. Lapkin and R. A. Bourne, Automated self-optimisation of multi-step reaction and separation processes using machine learning, Chem. Eng. J., 2020, 384, 123340 CrossRef CAS.
- A. M. K. Nambiar, C. P. Breen, T. Hart, T. Kulesza, T. F. Jamison and K. F. Jensen, Bayesian Optimization of Computer-Proposed Multistep Synthetic Routes on an Automated Robotic Flow Platform, ACS Cent. Sci., 2022, 8(6), 825–836 CrossRef CAS PubMed.
- R. Liang, X. Duan, J. Zhang and Z. Yuan, Bayesian based reaction optimization for complex continuous gas–liquid–solid reactions, React. Chem. Eng., 2022, 7(3), 590–598 RSC.
- J. W. Sawicki, A. R. Bogdan, P. A. Searle, N. Talaty and S. W. Djuric, Rapid analytical characterization of high-throughput chemistry screens utilizing desorption electrospray ionization mass spectrometry, React. Chem. Eng., 2019, 4(9), 1589–1594 RSC.
- V. Rosso, J. Albrecht, F. Roberts and J. M. Janey, Uniting laboratory automation, DoE data, and modeling techniques to accelerate chemical process development, React. Chem. Eng., 2019, 4(9), 1646–1657 RSC.
- S. Soritz, D. Moser and H. Gruber-Wölfler, Comparison of Derivative-Free Algorithms for their Applicability in Self-Optimization of Chemical Processes, Chem.: Methods, 2022, 2(5), e202100091 CAS.
- C. J. Taylor, A. Pomberger, K. C. Felton, R. Grainger, M. Barecka, T. W. Chamberlain, R. A. Bourne, C. N. Johnson and A. A. Lapkin, A Brief Introduction to Chemical Reaction Optimization, Chem. Rev., 2023, 123(6), 3089–3126 CrossRef CAS PubMed.
- F. Peng, G. R. Humphrey, K. M. Maloney, D. Lehnherr, M. Weisel, F. Lévesque, J. R. Naber, A. P. J. Brunskill, P. Larpent, S.-W. Zhang, A. Y. Lee, R. A. Arvary, C. H. Lee, D. Bishara, K. Narsimhan, E. Sirota and M. Whittington, Development of a Green and Sustainable Manufacturing Process for Gefapixant Citrate (MK-7264) Part 2: Development of a Robust Process for Phenol Synthesis, Org. Process Res. Dev., 2020, 24(11), 2453–2461 CrossRef CAS.
- S. L. Zultanski, N. Kuhl, W. Zhong, R. D. Cohen, M. Reibarkh, J. Jurica, J. Kim, L. Weisel, A. R. Ekkati, A. Klapars, D. R. Gauthier Jr. and J. M. McCabe Dunn, Mechanistic Understanding of a Robust and Scalable Synthesis of Per(6-deoxy-6-halo)cyclodextrins, Versatile Intermediates for Cyclodextrin Modification, Org. Process Res. Dev., 2021, 25(3), 597–607 CrossRef CAS.
- W. Huyer and A. Neumaier, SNOBFIT -- Stable Noisy Optimization by Branch and Fit, ACM Trans. Math. Softw., 2008, 35(2), 1–25 CrossRef.
- L. D. González and V. M. Zavala, New paradigms for exploiting parallel experiments in Bayesian optimization, Comput. Chem. Eng., 2023, 170, 108110 CrossRef.
- R. Liang, H. Hu, Y. Han, B. Chen and Z. Yuan, CAPBO: A cost-aware parallelized Bayesian optimization method for chemical reaction optimization, AIChE J., 2024, 70(3), e18316 CrossRef CAS.
- N. R. Domagalski, B. C. Mack and J. E. Tabora, Analysis of Design of Experiments with Dynamic Responses, Org. Process Res. Dev., 2015, 19(11), 1667–1682 CrossRef CAS.
- N. Klebanov and C. Georgakis, Dynamic Response Surface Models: A Data-Driven Approach for the Analysis of Time-Varying Process Outputs, Ind. Eng. Chem. Res., 2016, 55(14), 4022–4034 CrossRef CAS.
- Y. Dong, C. Georgakis, J. Mustakis, J. M. Hawkins, L. Han, K. Wang, J. P. McMullen, S. T. Grosser and K. Stone, Stoichiometry identification of pharmaceutical reactions using the constrained dynamic response surface methodology, AIChE J., 2019, 65(11), 16726 CrossRef.
- Y. Dong, C. Georgakis, J. Mustakis, J. M. Hawkins, L. Han, K. Wang, J. P. McMullen, S. T. Grosser and K. Stone, Constrained Version of the Dynamic Response Surface Methodology for Modeling Pharmaceutical Reactions, Ind. Eng. Chem. Res., 2019, 58(30), 13611–13621 CrossRef CAS.
- Y. Dong, C. Georgakis, J. Mustakis and J. P. McMullen, New Time Sampling Strategy for the Estimation of the Parameters in DRSM Models, Ind. Eng. Chem. Res., 2020, 59(28), 12792–12800 CrossRef CAS.
- K. Wang, L. Han, J. Mustakis, B. Li, J. Magano, D. B. Damon, A. Dion, M. T. Maloney, R. Post and R. Li, Kinetic and Data-Driven Reaction Analysis for Pharmaceutical Process Development, Ind. Eng. Chem. Res., 2019, 59(6), 2409–2421 CrossRef.
- P. Kokoszka and M. Reimherr, Introduction to Functional Data Analysis, CRC Press, New York, 2017 Search PubMed.
- H.-G. Müller, Functional Modelling and Classification of Longitudinal Data, Scand. J. Stat., 2005, 32(2), 223–240 CrossRef.
- F. Yao, H.-G. Müller, A. J. Clifford, S. R. Dueker, J. Follett, Y. Lin, B. A. Buchholz and J. S. Vogel, Shrinkage Estimation for Functional Principal Component Scores with Application to the Population Kinetics of Plasma Folate, Biometrics, 2003, 59(3), 676–685 CrossRef PubMed.
- F. Yao, H.-G. Müller and J.-L. Wang, Functional Data Analysis for Sparse Longitudinal Data, J. Am. Stat. Assoc., 2005, 100(470), 577–590 CrossRef CAS.
- J. P. McMullen, B. M. Wyvratt, C. M. Hong and A. K. Purohit, Integrating Functional Principal Component Analysis with Data-Rich Experimentation for Enhanced Drug Substance Development, Org. Process Res. Dev., 2024, 28(3), 719–728 CrossRef CAS.
- M. Fidaleo, Functional Data Analysis and Design of Experiments as Efficient Tools to Determine the Dynamical Design Space of Food and Biotechnological Batch Processes, Food Bioprocess Technol., 2020, 13(6), 1035–1047 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4re00141a |
| This journal is © The Royal Society of Chemistry 2024 |