DOI:
10.1039/D4RE00203B
(Paper)
React. Chem. Eng., 2024, Advance Article
Digital strategies to improve the product quality and production efficiency of fluorinated polymers: 2. Heat removal performance of reactor with internal and external cooling systems†
Received
16th April 2024
, Accepted 7th October 2024
First published on 7th October 2024
Abstract
This work aims to study the heat transfer performance of a sophisticated industrial suspension polymerization reactor, which is distinguished by its complex blade structure and capability in efficient heat removal as well as its precise control over temperature distribution through adjusting the flow ratio of cooling water in the agitator and jacket. To achieve this goal, the impact of flow ratio and agitator speed on the heat removal rate and fluid temperature gradient is systematically investigated by CFD simulation. Several indicators are developed to quantitatively assess the reactor's heat transfer capability and fluid temperature uniformity. In addition, a thorough investigation is undertaken to analyze the possible mechanisms by which these factors exert their influence on the heat transfer performance of the reactor. Finally, some strategies for optimal performance through adjusting operational parameters of this type of reactors are proposed.
1. Introduction
Suspension polymerization, which has been widely applied in the production of wide varieties of commercial polymers, such as polymethylmethacrylate (PMMA), polyvinyl chloride (PVC) and polystyrene (PSt), initially forms a suspension of monomer droplets in a continuous phase, and then polymerization in these droplets results in the generation of solid polymer beads.1,2 A major advantage of this process is that the viscosity of the reaction mixture changes little during polymerization, making it well-suited for large-scale industrial polymer production. Moreover, this process also features the advantages of easy separation of polymer particles from the reaction medium and a low content of impurities in the polymer product. Despite these benefits, the design of suspension polymerization reactors is a highly challenging task that must address numerous complex issues. Among the vast array of challenges, the control of droplet size distribution and the reaction temperature management receive an extensive research attention.3–5 The former significantly affects concentration gradients, while the latter plays a critical role in determining the rates of polymerization, the polymer chain microstructural properties and the process safety. Specifically, reaction temperatures in industrial polymerization processes typically range from 60 °C to 160 °C, depending on the polymer grade being produced. For example, lower temperatures are often used to control exothermic reactions and avoid runaway polymerization, whereas higher temperatures are employed to accelerate reaction rates and achieve the desired molecular weights. To achieve good dispersion of droplets and effective control of droplet size distribution, suspension polymerization processes normally adopt batch stirred reactors.6,7 The most widely used heat transfer measures in polymerization reactors are the external cooling jackets.8–12 Furthermore, other common methods for heat removal include employing internal cooling coils, external recirculation of cooling solution, solution evaporation for heat absorption, and passage of cooling medium through the internals coils and agitators.13–15
Although numerous studies have been undertaken regarding the heat transfer characteristics of polymerization reactors, the focus has been mainly on bulk16–18 and gas-phase19–21 polymerization reactors, with a marked scarcity of studies on suspension polymerization reactors.8–12 Additionally, these scarce studies primarily utilize numerical simulation methods, which can be broadly divided into two categories depending on whether the effect of fluid dynamics is considered. The combination of simplified reactor models, which overlook the influence of fluid dynamics, with reaction kinetics and heat transfer models can be applied in analyzing the impact of various parameters on a reactor's heat transfer performance with a high computational efficiency.8,9 Employing this approach, Wieme et al. conducted simulations on batch suspension polymerization reactors of vinyl chloride at pilot and industrial scales, exploring the possible ways for enhancing a reactor's heat removal efficiency by altering the geometry of cooling jackets and enhancing the internal heat transfer surface area.8 Han et al. studied the effect of jacket temperature and heat transfer coefficients on the heat removal capability of vinyl chloride suspension polymerization reactors and proposed methods for preventing the occurrence of thermal runaway through optimizing operating conditions and enhancing heat transfer coefficients.9 However, this simulation approach is limited in that it cannot access information on the characteristics of the internal flow field. Employing a method that integrates fluid dynamics models with reaction kinetics and heat transfer models allows for the acquisition of extensive data on the temperature, concentration and velocity fields.10–12 By applying this method, Poubel et al. assessed the impact of temperature and concentration fluctuation on kinetic variables and discovered that significant temperature and concentration gradients occurred only under special conditions, such as poorly designed operation strategies and agitation systems or extremely high reaction rates.10 Nogueira et al. adopted CFD simulation to evaluate the heat transfer performance of a designed vertically stirred tubular reactor for batch suspension polymerization of styrene, which exhibits outstanding performance in temperature control.11 Moreover, the results of Xie et al. on the methyl methacrylate suspension polymerization process in a stirred reactor suggested that it is markedly affected by reaction temperature.12 In addition to the specialized research on polymerization reactors, various cold model studies, which discount for polymerization reaction impact and without distinctive variation of system properties, still provided useful insights for heat transfer and temperature management in polymerization reactors.22–25
Overall, although some studies have been devoted to the heat transfer behaviors of suspension polymerization reactors, there are evident limitations in these studies that demand more profound exploration. Firstly, the heat transfer performance of cooling jackets has been extensively studied, while studies on other heat transfer measures are limited. Secondly, the CFD modeling of suspension polymerization reactors is mainly performed at laboratory and pilot scales, with scant reports on industrial-scale reactors. Thirdly, these studies can offer a qualitative view on the temperature distribution through temperature profiles but lack well-defined quantitative indicators to precisely assess the uniformity of temperature distribution. Fourthly, the reactor structure and type involved in previous studies are relatively conventional, highlighting a need for the development of innovative and efficient reactors.
Fluorinated polymers represent a class of important polymeric materials, widely used in numerous application areas. However, due to the great challenges in dealing with monomers and in characterizing polymers, few academic labs are still involved in research on fluorinated polymers, which has resulted in the severe scarcity of discoveries and innovations over the decades. Recently, we launched a program with a joint academic and industrial effort, aiming at the further development of high-end fluorinated polymers. The work is devoted to improve the production efficiency and product quality of fluorinated polymers via digital approaches, through combining first principle-based kinetic and transfer models with industrial production data. In the first paper of this series,2 a comprehensive kinetic model was developed for the batch process of tetrafluoroethylene (TFE) and hexafluoropropylene (HFP) bulk copolymerization. Industrial lab experiments were carried out for estimation of the model parameters, with which simulations were implemented for the industrial production operations.
This paper reports a comprehensive and in-depth investigation of the heat transfer performance of a sophisticated industrial-scale suspension polymerization reactor equipped with internal and external cooling systems by CFD simulations. Most vinyl polymerization systems are highly exothermic.26 Heat removal is critical for the product quality control, production process stability and operation safety. This research is carried out based on a detailed analysis of the characteristics and issues of an industrial TFE suspension polymerization reactor, and the manufacturing data are made available to validate the CFD simulations. The temperature control of this special reactor can be achieved by adjusting the relative flow rates of cooling agents in the agitator of the internal cooling system and in the jacket of the external cooling system. Section 2 provides a detailed description of the structure and cooling systems of the reactor and the collection method of simulation data. In sections 3, the modelling methodology, simulation settings and quantitative indicators for assessing temperature uniformity are thoroughly described. In sections 4, the impact of the flow ratio of internal cooling system to external cooling system and impeller rotation rates on heat transfer performance of the industrial-scale suspension polymerization reactor are systematically investigated.
2. Details of reactor structure, cooling systems and data collection method
2.1. Reactor structure and cooling systems
The structure and size of the studied horizontal reactor is shown in Fig. 1, and the detailed instruction for the flow pattern of cooling water in the agitator is presented in Fig. 2.
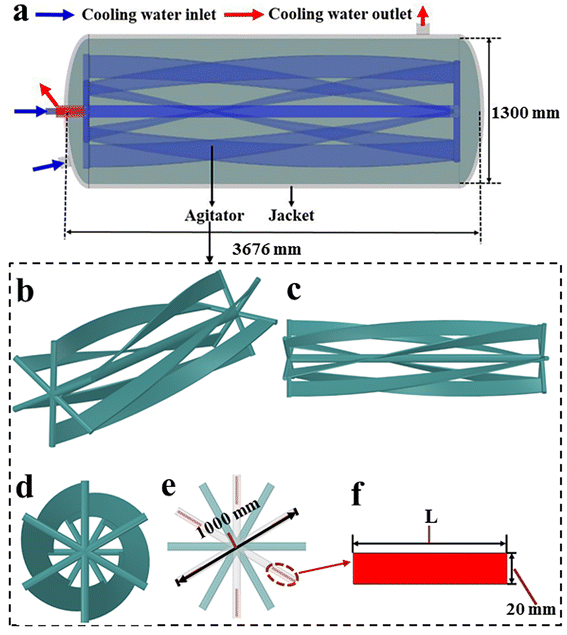 |
| | Fig. 1 Geometry details of the reactor: (a) overall structure and size, (b–d) agitator structure from various angles, and (e and f) structure and size of the agitator impeller. | |
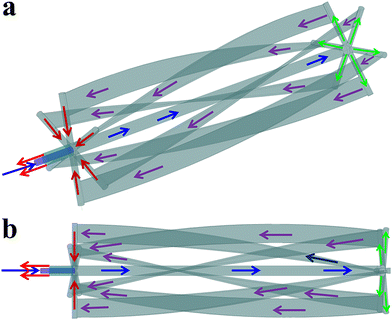 |
| | Fig. 2 The flow pattern of cooling water in the agitator from different angles. | |
As shown in Fig. 1a, the overall structure of the reactor features a length of 3676 mm, a diameter of 1300 mm, and a total volume of 4.70 m3. It can be observed that the heat can be removed by the flowing water in both internal agitator and external jacket. Fig. 1b–d clearly present the agitator structure from different angles. Fig. 1e and f display the structure and size of the agitator blade, which is formed by rotating the rectangle of length L (160 mm) and width 20 mm by 90 degrees along the axial direction.
According to Fig. 2, after entering one side of the agitator (blue arrow), the cooling water first flows along the agitator shaft until it reaches the other side of the agitator (green arrows). Then, the cooling water flows back to the entrance side of the cooling water via six draft tubes (purple arrows). Finally, the cooling water flows out through another pipeline (red arrows). The heat transfer areas of the agitator and the external cooling jacket are 9.02 m2 and 16.86 m2, respectively.
2.2. Region division for data processing
According to Fig. 3, with the exception of cooling systems, the reaction zone is divided into three regions (region 1, region 2 and region 3) based on its flow and transfer characteristics in order to quantitatively assess the temperature uniformity of different regions.
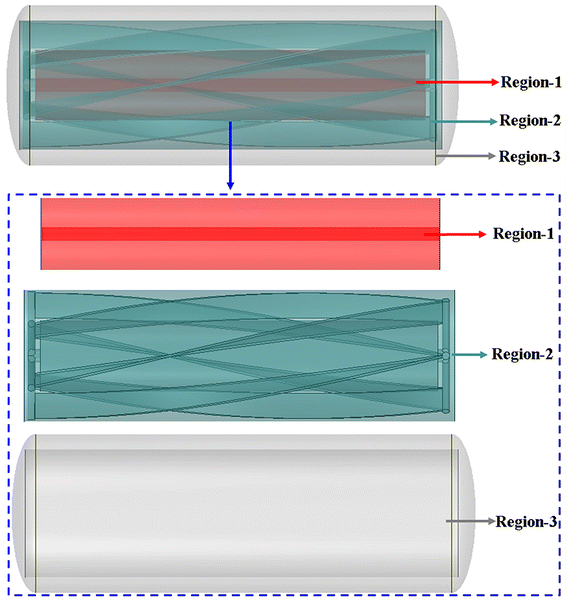 |
| | Fig. 3 The scope of region 1 (red area), region 2 (blue area) and region 3 (gray area). | |
As shown in Fig. 3, region 2 (blue area) is located in the area which is greatly affected by the motion of impeller blades. The range of region 3 (gray area) is between the cooling jacket and region 2, and the scope of region 1 (red area) is between the agitating shaft and the stirring blades that are most affected by the agitating shaft.
3. Modelling methodology
3.1. Simplified modeling strategy for suspension polymerization system
Considering the significant computational resources required for CFD simulations of industrial-scale polymerization reactors, making appropriate simplifications without substantially affecting the accuracy of research parameters is essential. Therefore, this study neglects the impact of monomer conversions, interphase interactions and reactions on the physical properties of the suspension polymerization system (e.g., density, specific heat capacity, thermal conductivity, viscosity), product properties and heat release rates. Although this simplified approach may lead to some deviations, its impact on the evaluation of the reactor's heat transfer performance is limited. It has thus been recommended for the simulation of industrial-scale polymerization reactors.27
3.2. Governing equations
The continuity equation is:| |
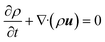 | (1) |
where ρ, t and u represent the density, time and velocity vector, respectively.
The momentum balance equation is:
| |
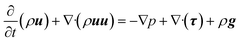 | (2) |
| |
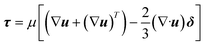 | (3) |
where
p,
τ,
ρg,
μ and
δ represent the static pressure, stress tensor, gravitational body force, molecular viscosity and unit tensor, respectively.
The energy balance equation is:
| |
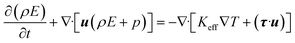 | (4) |
| |
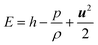 | (5) |
where
E,
Keff and
h represent the total energy of fluid per unit mass, effective heat conductivity and specific enthalpy, respectively.
3.3. Turbulence modeling
Turbulence is a prevalent phenomenon in engineering applications, marked by its intricate, transient, and three-dimensional characteristics. The creation and dissipation of eddies with varying sizes lead to fluctuations in the physical quantities within the turbulent flow field, exhibiting a pulsating behavior coupled with pronounced irregularity and randomness. The numerical simulation of turbulence is predominantly conducted through three methods: direct numerical simulation (DNS), large-eddy simulation (LES), and Reynolds-averaged Navier–Stokes simulation (RANS). DNS directly solves the Navier–Stokes (N–S) equations without introducing any additional assumptions or models, capturing all scales of turbulence information through sufficiently dense grids and time steps. RANS averages the equations of fluid motion over time, separating the flow equations into mean and fluctuating components for solution. LES, which serves as a compromise approach between DNS and RANS, spatially averages the fluid motion equations based on a certain scale of elemental volumes, precisely capturing the behavior of large-scale eddies while employing approximation or modeling approaches for the motions of small-scale eddies. Although DNS and LES can offer detailed insights into the flow field's temporal and spatial dynamics, the high computational resource requirement renders their application in addressing practical engineering issues. Given the complex structure of the industrial-scale polymerization reactor studied in this paper, the RANS is selected for turbulence simulation.
In Reynolds averaging, the variables in the N–S equations are decomposed into the mean and fluctuating components. For the velocity components:
| |
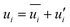 | (6) |
| |
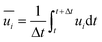 | (7) |
where
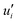
and
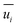
represent the fluctuating and mean velocity components, respectively. Substituting this form of velocity expression into the original momentum equation yields the following Reynolds averaged equation:
| |
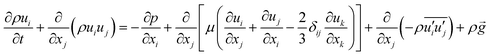 | (8) |
To close the Reynolds averaged momentum equation, the Boussinesq hypothesis for eddy viscosity,28 which correlates Reynolds stresses with gradients of mean velocity and turbulent viscosity (μt), is adopted:
| |
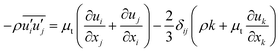 | (9) |
Subject to this hypothesis, the Reynolds averaged momentum equation is then converted to:
| |
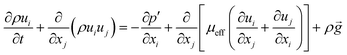 | (10) |
where
p′ is the modified pressure, which is defined by:
| |
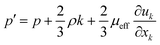 | (11) |
where
μeff is the effective viscosity, which is expressed by:
The standard
k–
ε turbulence model developed by Launder and Spalding,
29 which is widely applied in the simulation of pilot and industrial scale reactors,
30 is employed for calculating the turbulent viscosity:
| |
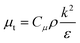 | (13) |
where
k and
ε are the turbulent kinetic energy and turbulent energy dissipation rate respectively, and
Cμ is a constant. The differential transport equations for
k and
ε in the standard
k–
ε turbulence model are:
| |
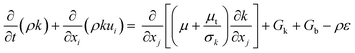 | (14) |
| |
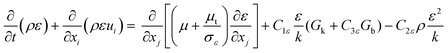 | (15) |
where
σk and
σε are the turbulent Prandtl numbers for turbulent kinetic energy and turbulent energy dissipation rate, respectively;
C1ε,
C2ε and
C3ε are model constants.
Gk and
Gb are the generation of turbulence kinetic energy due to mean velocity gradients and buoyancy, respectively, which are computed by:
| |
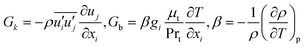 | (16) |
where Pr
t and
β represent the turbulent Prandtl number for energy (Pr
t = 0.85) and coefficient of thermal expansion, respectively. The values of
C1ε,
C2ε,
C3ε,
σk and
σε proposed by Launder and Spalding
31 are adopted in this study, which are determined by the experimental data from fundamental turbulent flows, including common shear flows such as boundary layers, mixing layers and jets:
C1ε = 1.44,
C2ε = 1.92,
C3ε = 0.99,
σk = 1.00,
σε = 1.30. These model constants demonstrate excellent performance across a broad spectrum of both wall-bound and free shear flows.
3.4. Numerical details
In this work, the 3D transient simulation is performed on the Ansys Fluent 17.2 software. A simple scheme is selected to couple the velocity and pressure, and the least-squares cell-based scheme is applied in predicting the gradients. The pressure-based solver and absolute velocity formation are used in the CFD simulation. The first-order upwind scheme is employed in solving the equations of momentum, turbulent kinetic energy, turbulent dissipation rate and energy. The grid number of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660
660![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 348 is selected for CFD simulation after carefully evaluating the balance between simulation accuracy and computational efficiency. The density, specific heat, thermal conductivity and viscosity of the reaction mixture are 998.2 kg m−3, 4182 J kg−1 K−1, 0.6 W m−1 K−1 and 0.001 Pa s, respectively.
348 is selected for CFD simulation after carefully evaluating the balance between simulation accuracy and computational efficiency. The density, specific heat, thermal conductivity and viscosity of the reaction mixture are 998.2 kg m−3, 4182 J kg−1 K−1, 0.6 W m−1 K−1 and 0.001 Pa s, respectively.
No-penetration and no-slip wall boundary conditions are employed, and the standard wall function is applied for the near wall regions. The mass flow inlet boundary and the pressure outlet boundary are used for the cooling system. The multiple reference frame (MRF) technique, which has been extensively applied in simulating the impeller rotation with high computational speed,32–34 is adopted in this work for the modeling of the rotation of impellers. Region 2 is defined as the rotating region, whereas region 3 and region 1 are assumed to be the static region. The thickness of the wall is 5.0 mm, and the stirring rate is 60 r min−1.
To accurately evaluate the heat transfer capacity of the cooling system under different conditions, the initial temperature of the reaction mixture is set to 331.65 K and the cooling water inlet temperature of both agitator and jacket are set to 301.10 K. Although the mass flow rates of cooling water in the agitator and jacket change during the CFD simulation, the total mass flow rate of cooling water remains constant at 12.0 kg s−1. The time step of transient simulation is 0.001 s, and the total time of CFD simulation is 60.0 s.
3.5. Quantitative indicators for assessing temperature uniformity
In this work, the maximum temperature difference (ΔTmax) between different regions and the average relative deviation of fluid temperature between the whole reaction zone and the local regions (ĒT) are employed as the quantitative indicators to assess the degree of temperature uniformity inside the polymerization reactor, which are calculated by:| |
ΔTmax = max(|![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 1 − 1 − ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 2|, | 2|, |![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 2 − 2 − ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 3|, | 3|, |![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 1 − 1 − ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 3|) 3|)
| (17) |
| |
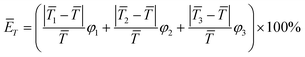 | (18) |
where ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 1,
1, ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 2,
2, ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 3 and
3 and ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) represent the average temperature of region 1, region 2 and region 3 and the whole reaction zone, respectively; φ1, φ2 and φ3 respectively denote the ratios of the volumes of region 1, region 2 and region 3 to the total reactor volume (note: φ1 + φ2 + φ3 = 1).
represent the average temperature of region 1, region 2 and region 3 and the whole reaction zone, respectively; φ1, φ2 and φ3 respectively denote the ratios of the volumes of region 1, region 2 and region 3 to the total reactor volume (note: φ1 + φ2 + φ3 = 1).
4. Results and discussion
The research in this section is divided into three parts. In section 4.1, the accuracy of CFD simulations is verified through the factory data from a company. The impacts of the flow ratio of internal and external cooling systems and those of the agitator rotation rate on the heat transfer performance of the industrial-scale suspension polymerization reactor are systematically studied in section 4.2 and section 4.3, respectively. This work provides insight into the generic heat transfer capabilities of this type of reactors.
4.1. Accuracy analysis of CFD simulations
The accuracy validation of the CFD simulation for the industrial-scale polymerization reactor (Fig. 1 and 2) is a considerable challenge because research on reactors of this structural type has not been reported. Given the lack of previous studies to confirm the precision of numerical simulations, reliance on data from manufacturing processes becomes essential for accuracy analysis. The operational data from an industrial reactor, which is employed for producing polytetrafluoroethylene (PTFE) in a batch process, and determining the structure and geometric proportion of the suspension polymerization reactor studied in this work, are used to verify the accuracy of CFD simulations. It should be noted that the cooling water flow through the industrial reactor's internal agitator accounts for less than 10% of the total cooling water flow, whereas the relative flow rate of the internal agitator's cooling water spans from 0% to 100% of the total flow in this work. Consequently, factory data can validate simulation accuracy only to a limited extent and are insufficient for a comprehensive assessment across the entire spectrum. Additionally, considering the inherent fluctuations in the operational data, such data can only serve as a reference for evaluating the simulation accuracy. According to the industrial data, the heat removal rate of the reactor (hr,i) is estimated by:| |
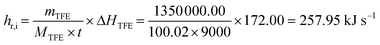 | (19) |
where mTFE, MTFE and ΔHTFE represent the amount of TFE monomer consumed during the reaction (1350 kg), its relative molecular weight (100.02), and the molar enthalpy of the reaction (172.00 kJ mol−1), respectively; t denotes the reaction time (9000 s). The flow rate of the cooling water is around 12.0 kg s−1, and the ratio of cooling water flow between the agitator and jacket is approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9. The heat removal rate by the simulation (hr,s), under the condition close to the industrial operation, is:
9. The heat removal rate by the simulation (hr,s), under the condition close to the industrial operation, is:| | |
hr,s = mrCPΔT = 284.36 kJ s−1
| (20) |
where mr, CP and ΔT represent mass, specific heat capacity, and change of temperature per unit time of the reaction mixture, respectively.
The difference between the simulation result and the operation data is 10.24%. The heat transfer rate predicted by CFD simulation exceeds that of the actual factory reactor. The discrepancy may be attributed to the actual factory reactor containing a gas phase at the reactor head space, whereas this study presumes that the reactor is completely filled with liquid, leading to a simulated heat transfer area larger than the real reactor's. Furthermore, due to the continuous dynamic changes in the physical properties of the mixture inside the industrial reactor with monomer conversion, the use of water as a substitute for the reaction mixture in this section's simulation inevitably generates a certain degree of deviation between the simulated conditions and the actual fluid properties. Despite the differences between the simulation results and factory data, the accuracy of the simulation is generally reliable.
4.2. Variation of heat transfer performance with flow ratios
Fig. 4 shows the influence of the flow ratio of internal to external cooling systems (Q1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q2) on the fluid temperature in the whole reaction zone at different times (Fig. 4a), the average fluid temperature in region 1, region 2 and region 3 (Fig. 4b), the maximum temperature difference between different regions (Fig. 4c), the average relative deviation of fluid temperature between the whole reaction zone and the local regions (Fig. 4d), and the total heat removal rates of the cooling system (hT) and the hear removal rates of the agitator (hA) and jacket (hJ) (Fig. 4e). Furthermore, the impact of flow ratio on the mean surface heat flux of jacket and agitator is presented in Fig. 5 and 6, respectively. The characteristics of fluid temperature distribution along the reactor's axial section in the vertical direction at different flow ratios are shown in Fig. 7.
Q2) on the fluid temperature in the whole reaction zone at different times (Fig. 4a), the average fluid temperature in region 1, region 2 and region 3 (Fig. 4b), the maximum temperature difference between different regions (Fig. 4c), the average relative deviation of fluid temperature between the whole reaction zone and the local regions (Fig. 4d), and the total heat removal rates of the cooling system (hT) and the hear removal rates of the agitator (hA) and jacket (hJ) (Fig. 4e). Furthermore, the impact of flow ratio on the mean surface heat flux of jacket and agitator is presented in Fig. 5 and 6, respectively. The characteristics of fluid temperature distribution along the reactor's axial section in the vertical direction at different flow ratios are shown in Fig. 7.
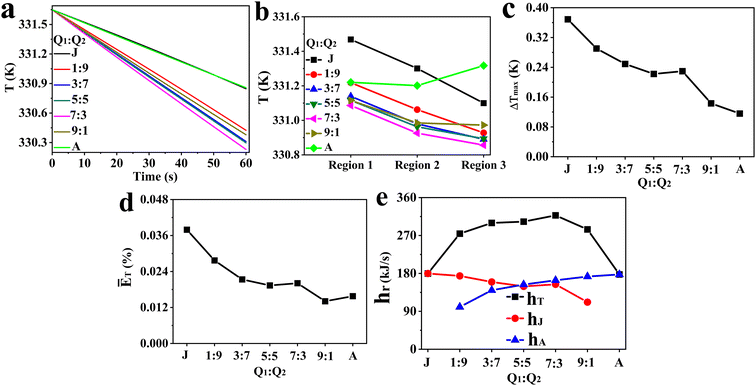 |
| | Fig. 4 Effect of Q1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q2 on (a) fluid temperature in the reaction zone at different times, (b) average fluid temperature in various regions, (c) ΔTmax, (d) ĒT, and (e) hT, hA, hJ (J and A correspond to all cooling water entering the jacket and the agitator, respectively). Q2 on (a) fluid temperature in the reaction zone at different times, (b) average fluid temperature in various regions, (c) ΔTmax, (d) ĒT, and (e) hT, hA, hJ (J and A correspond to all cooling water entering the jacket and the agitator, respectively). | |
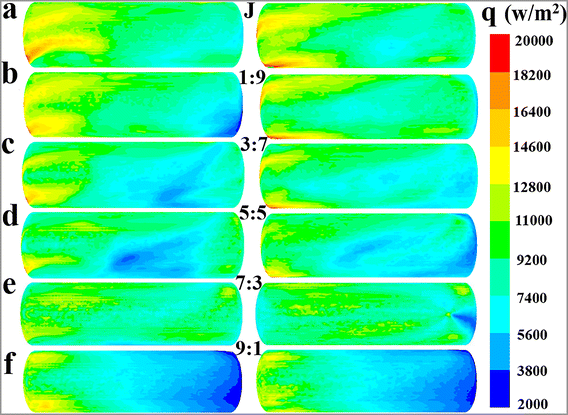 |
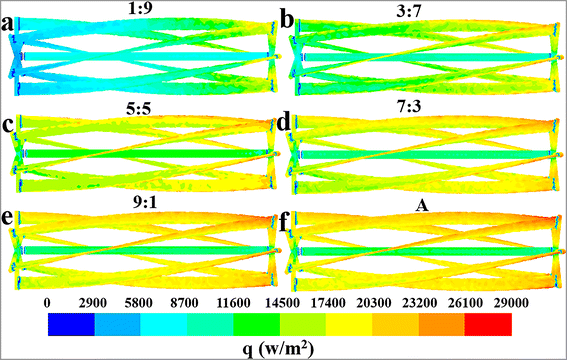
| | Fig. 5 Effect of flow ratios on the mean surface heat flux distribution characteristics of the jacket at the values of Q1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q2: (a) J, (b) 1 Q2: (a) J, (b) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, (c) 3 9, (c) 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, (d) 5 7, (d) 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, (e) 7 5, (e) 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and (f) 9 3 and (f) 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. 1. | |
 |
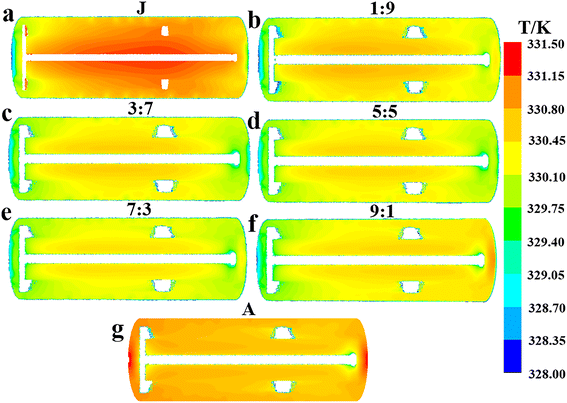
| | Fig. 6 Effect of flow ratios on the mean surface heat flux distribution characteristics of the agitator at the values of Q1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q2: (a) 1 Q2: (a) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, (b) 3 9, (b) 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, (c) 5 7, (c) 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, (d) 7 5, (d) 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, (e) 9 3, (e) 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and (f) A. 1 and (f) A. | |
 |
| | Fig. 7 Effect of flow ratios on distribution of fluid temperature along reactor's axial cross section at the Q1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q2 values: (a) J, (b) 1 Q2 values: (a) J, (b) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, (c) 3 9, (c) 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, (d) 5 7, (d) 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, (e) 7 5, (e) 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, (f) 9 3, (f) 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and (g) A. 1 and (g) A. | |
The results of Fig. 4a suggest that the heat transfer capacity of the reactor at different flow ratios is in the order 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 > 5
3 > 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 > 3
5 > 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 > 9
7 > 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 > 1
1 > 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 > J > A. Furthermore, it can be found that there is a negligible difference in heat transfer capabilities between flow ratios of (1) 5
9 > J > A. Furthermore, it can be found that there is a negligible difference in heat transfer capabilities between flow ratios of (1) 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and 3
5 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 and (2) J and A. Fig. 4b presents that the order of fluid temperature in different regions is region 1 > region 2 > region 3 when the flow ratio is clearly less than 7
7 and (2) J and A. Fig. 4b presents that the order of fluid temperature in different regions is region 1 > region 2 > region 3 when the flow ratio is clearly less than 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, the fluid temperature in region 2 and region 3 is almost identical and still lower than that of region 1 at the flow ratio up to 9
3, the fluid temperature in region 2 and region 3 is almost identical and still lower than that of region 1 at the flow ratio up to 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and there is a minimal temperature difference between region 1 and region 2, while region 3 exhibits the highest fluid temperature at the flow ratio of A. Due to significant heat exchange between fluid in different regions of the reactor under turbulent flow, the temperature in each region is influenced not only by the heat transfer rate between fluid and cooling jacket or agitator but also by the fluid circulation patterns and intensity of turbulence. This complex relationship makes it difficult to theoretically analyze the differences in heat transfer efficiency across regions. However, the heat transfer efficiency in different regions can be indirectly inferred from the temperature distribution curves in these regions. The temperature distribution curves in different regions suggest that the heat transfer rates are faster in regions closer to the external jacket when all cooling water is directed to the jacket. Conversely, the heat transfer rates in the internal fluid region (region 1) and the middle blade region (region 2) are similar, but both are higher than that in the external fluid region as the cooling water fully flows into the agitator. Additionally, the variation in temperature curves across different regions as the flow ratio changes from 1
1, and there is a minimal temperature difference between region 1 and region 2, while region 3 exhibits the highest fluid temperature at the flow ratio of A. Due to significant heat exchange between fluid in different regions of the reactor under turbulent flow, the temperature in each region is influenced not only by the heat transfer rate between fluid and cooling jacket or agitator but also by the fluid circulation patterns and intensity of turbulence. This complex relationship makes it difficult to theoretically analyze the differences in heat transfer efficiency across regions. However, the heat transfer efficiency in different regions can be indirectly inferred from the temperature distribution curves in these regions. The temperature distribution curves in different regions suggest that the heat transfer rates are faster in regions closer to the external jacket when all cooling water is directed to the jacket. Conversely, the heat transfer rates in the internal fluid region (region 1) and the middle blade region (region 2) are similar, but both are higher than that in the external fluid region as the cooling water fully flows into the agitator. Additionally, the variation in temperature curves across different regions as the flow ratio changes from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 to 7
9 to 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 suggests that raising the proportion of cooling water in the agitator and reducing it in the jacket within this range is beneficial for improving the heat transfer efficiency in all the three regions.
3 suggests that raising the proportion of cooling water in the agitator and reducing it in the jacket within this range is beneficial for improving the heat transfer efficiency in all the three regions.
Fig. 4c further quantifies the impact of flow ratios on the maximum differences of fluid temperature, revealing that the ΔTmax tends to decrease with the increase of Q1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q2, with the exception of Q1
Q2, with the exception of Q1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q2 = 7
Q2 = 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. A similar trend is observed in ĒT (Fig. 4d), where it decreases as the flow ratio increases, except at flow ratios of 7
3. A similar trend is observed in ĒT (Fig. 4d), where it decreases as the flow ratio increases, except at flow ratios of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and A. These results suggest that the temperature of the fluid region tends to rise with increasing distance from the jackets when the system relies only on the jacket for heat transfer, whereas temperature gradients between the internal and external regions can be effectively reduced through properly increasing the flow rate of cooling water in the agitator. Fig. 4e shows that an increase in the flow ratio results in a stronger heat removal capability of the agitator, whereas a weaker overall heat transfer performance of the jacket with an exception of the 7
3 and A. These results suggest that the temperature of the fluid region tends to rise with increasing distance from the jackets when the system relies only on the jacket for heat transfer, whereas temperature gradients between the internal and external regions can be effectively reduced through properly increasing the flow rate of cooling water in the agitator. Fig. 4e shows that an increase in the flow ratio results in a stronger heat removal capability of the agitator, whereas a weaker overall heat transfer performance of the jacket with an exception of the 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 flow ratio.
3 flow ratio.
Although the aforementioned analysis accurately elucidates the influence of flow ratio on the reactor's heat removal capacity and fluid temperature gradient at different conditions, it does not delve deeply into the mechanism and pathway by which the flow ratio affects heat transfer performance. Hence, this section further explores the reasons for the flow ratio's impact on heat transfer performance by taking into account distribution characteristics of the mean surface heat flux of the agitator and jacket. The heat transfer rates between the cooling medium and reaction mixture can be estimated by:
| | |
hA = KA·SA·ΔTA, hJ = KJ·SJ·ΔTJ
| (22) |
| |
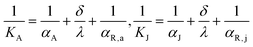 | (23) |
where
KA and
KJ represent the overall heat transfer coefficients of the fluid on both sides of the agitator and jacket;
SA and
SJ denote the heat transfer surface areas of the agitator and jacket; Δ
TA and Δ
TJ represent the temperature difference of the fluid on both sides of the agitator and jacket;
αA and
αJ denote the convective heat transfer coefficients of cooling water in the agitator and jacket;
αR,a and
αR,j represent the convective heat transfer coefficients of the reaction mixture adjacent to the agitator and jacket walls;
δ and
λ denote the thickness and thermal conductivity of the heat exchange walls, respectively. In the research of section 4.2, the values of
SA,
SJ,
δ and
λ remain constant, and the Δ
TA and Δ
TJ are identical at the initial state of CFD simulations. The convective heat transfer coefficients are influenced by fluid properties and the state of fluid motion.
35,36 However, given that the fluid properties and agitator rotation rate keep constant in this section of the study, the
αR,a and
αR,j remain virtually unchanged with the variation of flow ratio. Therefore, it can be deduced that the impact of flow ratio on heat transfer performance is largely attributed to its alteration of convective heat transfer coefficients of cooling water in the agitator and jacket.
From the observed trend where the hA increases with flow ratio (Fig. 4e), it can be inferred that the increased flow rate of cooling water in the agitator leads to a larger αA, which in turn enhances the hA. This inference is further supported by the characteristics of the agitator's surface heat flux distribution at different flow ratios, as illustrated in Fig. 6, showing that heat flux notably grows with the increased flow ratio in general. Apart from the case at a flow ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, an increase in the flow rate of the jacket cooling water typically leads to a higher hJ (Fig. 4e). Consequently, it is reasonable to deduce that this increase in the flow rate generally boosts the αJ, similar to the behavior of the agitator. Obviously, the flow ratio of 7
3, an increase in the flow rate of the jacket cooling water typically leads to a higher hJ (Fig. 4e). Consequently, it is reasonable to deduce that this increase in the flow rate generally boosts the αJ, similar to the behavior of the agitator. Obviously, the flow ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 represents a special case. In the vicinity of 7
3 represents a special case. In the vicinity of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, the total heat removal rate is at its peak, and there are marked changes in the variation trends of ΔTmax, ĒT and hA with the flow ratio.
3, the total heat removal rate is at its peak, and there are marked changes in the variation trends of ΔTmax, ĒT and hA with the flow ratio.
The distinct effect on heat transfer performance at the flow ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 can be interpreted through the heat flux distribution characteristics of the jacket at varying flow ratios, as depicted in Fig. 5. The jacket's heat flux distribution shows obvious unevenness at the flow ratios of 5
3 can be interpreted through the heat flux distribution characteristics of the jacket at varying flow ratios, as depicted in Fig. 5. The jacket's heat flux distribution shows obvious unevenness at the flow ratios of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and 9
5 and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, with the heat flux in some areas being significantly below 9200 W m−2. Conversely, the heat flux is more uniformly distributed at the flow ratio of 7
1, with the heat flux in some areas being significantly below 9200 W m−2. Conversely, the heat flux is more uniformly distributed at the flow ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and the occurrence of low heat flux areas is considerably limited. This phenomenon should be the main cause of the superior heat transfer performance at the flow ratio of 7
3, and the occurrence of low heat flux areas is considerably limited. This phenomenon should be the main cause of the superior heat transfer performance at the flow ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 compared to the ratio of 5
3 compared to the ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5. However, because the current data are not sufficient to deeply reveal the complex interplay between flow and heat transfer behaviors, the underlying mechanism of the excellent heat transfer performance at the flow ratio of 7
5. However, because the current data are not sufficient to deeply reveal the complex interplay between flow and heat transfer behaviors, the underlying mechanism of the excellent heat transfer performance at the flow ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 requires further research in future work. Comparatively, the reason for the reduced heat transfer rates at the flow ratio of A or J is quite straightforward and easy to understand, primarily due to the reduction in the heat transfer area.
3 requires further research in future work. Comparatively, the reason for the reduced heat transfer rates at the flow ratio of A or J is quite straightforward and easy to understand, primarily due to the reduction in the heat transfer area.
As shown in Fig. 7, the fluid temperature in the central area is generally higher than that in the wall region, except at the flow ratio of A. This phenomenon is particularly evident at the flow ratio of J, where all the cooling water enters the jacket for heat removal, resulting in significantly higher fluid temperature in the reactor center than in the wall region. Moreover, the temperature gradients between the fluid in the reactor's center and wall regions can be reduced by introducing cooling water into the agitator. It can be observed that the temperature gradients become quite small as the cooling water is fully channeled through the agitator for heat transfer, aligning with the variation trends of ΔTmax and ĒT across different flow ratios.
A comprehensive analysis of the heat transfer performance trends under different conditions, as reflected in Fig. 5–7, can provide theoretical guidance for determining the optimal flow ratio between the external jacket and the internal agitator. According to Fig. 5, a flow ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 allows the jacket to achieve a relatively uniform heat flux distribution. However, increasing the cooling water flow ratio in the agitator to above 9
3 allows the jacket to achieve a relatively uniform heat flux distribution. However, increasing the cooling water flow ratio in the agitator to above 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 leads to a significant unevenness in the jacket's heat flux distribution due to insufficient cooling water flow. Therefore, the flow ratio should be less than 9
1 leads to a significant unevenness in the jacket's heat flux distribution due to insufficient cooling water flow. Therefore, the flow ratio should be less than 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 considering the effect of jacket heat transfer. The results in Fig. 6 and 7 indicate that the heat transfer limitation in the agitator causes the internal region of the reactor to have a significantly higher temperature than other regions when the flow ratio is less than 3
1 considering the effect of jacket heat transfer. The results in Fig. 6 and 7 indicate that the heat transfer limitation in the agitator causes the internal region of the reactor to have a significantly higher temperature than other regions when the flow ratio is less than 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, leading to a noticeable temperature gradient. Thus, the flow ratio should be greater than 3
7, leading to a noticeable temperature gradient. Thus, the flow ratio should be greater than 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7. Furthermore, although directing all cooling water to the agitator results in a higher heat transfer rate and more uniform temperature distribution within the reactor, it also significantly reduces the heat transfer area because the jacket is no longer utilized for heat removal, leading to a substantial decrease in the overall heat transfer capacity. Hence, the cooling water proportion in the agitator should not be excessively increased solely to enhance its heat transfer capability and improve temperature uniformity, as this would neglect the important heat transfer role of the jacket.
7. Furthermore, although directing all cooling water to the agitator results in a higher heat transfer rate and more uniform temperature distribution within the reactor, it also significantly reduces the heat transfer area because the jacket is no longer utilized for heat removal, leading to a substantial decrease in the overall heat transfer capacity. Hence, the cooling water proportion in the agitator should not be excessively increased solely to enhance its heat transfer capability and improve temperature uniformity, as this would neglect the important heat transfer role of the jacket.
4.3. Variation of heat transfer performance with agitator rotation rates
This section further investigates the impact of agitator speed (n) on the heat transfer performance. Throughout the study, all the parameters except for the rotation rates remain unchanged. Although the 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 flow ratio achieves the highest heat removal rate, it does not provide optimal temperature uniformity inside the reactor. Thus, balancing the impact of flow ratio on heat transfer rate and temperature uniformity, a 5
3 flow ratio achieves the highest heat removal rate, it does not provide optimal temperature uniformity inside the reactor. Thus, balancing the impact of flow ratio on heat transfer rate and temperature uniformity, a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 flow ratio is selected for the study on agitation speed. Fig. 8 shows the impact of flow ratio on the fluid temperature in all the reaction zones at different times (Fig. 8a), average fluid temperature in region 1, region 2 and region 3 (Fig. 8b), ΔTmax (Fig. 8c), ĒT (Fig. 8d), and hT, hA and hJ (Fig. 8e). Furthermore, the impact of rotation rates on the distribution of fluid temperature and velocity along the reactor's axial cross section in the vertical direction is presented in Fig. 9 and 10a–d, respectively. The fluid velocity and velocity vector distribution characteristics in the radial cross section of the reactor's middle part when n = 30 rpm are displayed in Fig. 10e and f, respectively.
5 flow ratio is selected for the study on agitation speed. Fig. 8 shows the impact of flow ratio on the fluid temperature in all the reaction zones at different times (Fig. 8a), average fluid temperature in region 1, region 2 and region 3 (Fig. 8b), ΔTmax (Fig. 8c), ĒT (Fig. 8d), and hT, hA and hJ (Fig. 8e). Furthermore, the impact of rotation rates on the distribution of fluid temperature and velocity along the reactor's axial cross section in the vertical direction is presented in Fig. 9 and 10a–d, respectively. The fluid velocity and velocity vector distribution characteristics in the radial cross section of the reactor's middle part when n = 30 rpm are displayed in Fig. 10e and f, respectively.
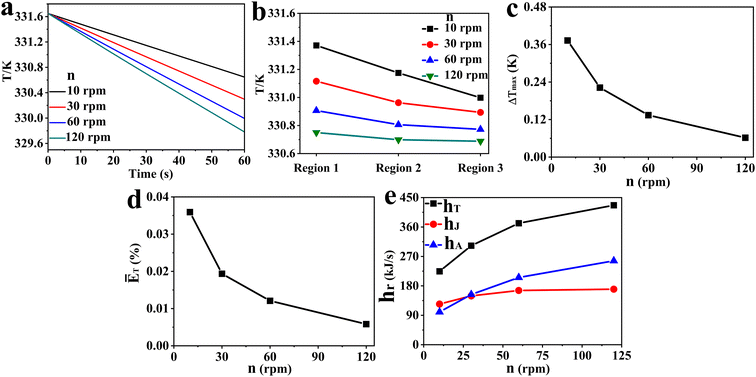 |
| | Fig. 8 Effect of agitator speeds on (a) fluid temperature in all reaction zones at different times, (b) average fluid temperature in various regions, (c) ΔTmax, (d) ĒT, (e) hT, hA, hJ. | |
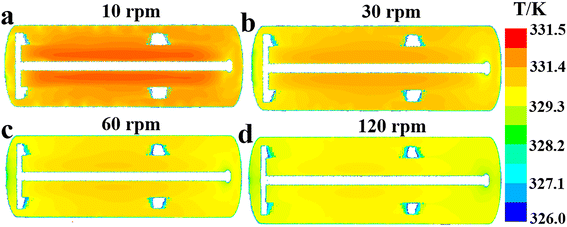 |
| | Fig. 9 Effect of agitator speed on fluid temperature distribution along the reactor's axial cross section at (a) n = 10 rpm, (b) n = 30 rpm, (c) n = 60 rpm and (d) n = 120 rpm. | |
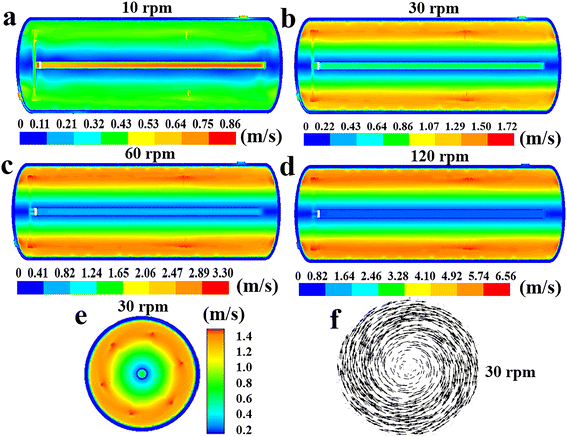 |
| | Fig. 10 Effect of agitator speed on the distribution of fluid velocity along the reactor's axial cross section at n = 10 rpm (a), 30 rpm (b), 60 rpm (c) or 120 rpm (d). (e) Fluid velocity and (f) velocity vector in the radial cross section at n = 30 rpm. | |
According to Fig. 8, the increase of agitation speed (1) enhances the heat removal rates of the agitator and jacket (Fig. 8a and e), (2) reduces the average fluid temperature in region 1, region 2 and region 3 (Fig. 8b), and (3) leads to the decrease of the ΔTmax and ĒT values (Fig. 8c and d). Increasing the rotational rate can improve the heat transfer performance of the reactor by raising heat transfer rates and promoting temperature uniformity. Fig. 9 also shows that the reactor's internal fluid exhibits an obviously higher temperature than that near the walls, whereas this temperature gradient diminishes with the increased agitator speed. The temperature in the reactor's central region is almost identical to that in the wall areas when the speed reaches 120 rpm. In addition, it is noticeable that with the increase in rotational speeds, the enhancing effect on the heat transfer rate and that on reducing temperature gradients are progressively weakened. Therefore, in practical applications, the determination of the rotational speed should be made on the basis of a careful balance between the improvement in heat transfer performance and the increase in the energy consumption caused by raising the agitation rate.
Given that the rotational speed is the only varying parameter in the study of this section, it can be deduced that the increase in speed enhances the αR,a, αR,j and αA, thereby increasing the heat removal rate of the reactor. Furthermore, as illustrated in Fig. 10, increasing the agitator rotational rate can significantly boost fluid velocities, accelerate fluid circulation within the reactor, intensify mixing of fluids in different regions, and consequently enhance the uniformity of the fluid temperature.
There are significant differences in the mechanisms by which the coolant flow ratio and the agitator speed affect the heat transfer performance of the polymerization reactor. The coolant flow ratio primarily alters the heat transfer between the coolant and the tube wall, while the rotational speed primarily changes the heat transfer rate between the reaction mixture and the tube wall as well as the overall turbulence level of the fluid. Nevertheless, there is also an interdependent relationship between the effects of the coolant flow ratio and the agitator speed on the reactor's heat transfer performance. Increasing the rotational speed can enhance the heat transfer performance to varying degrees at different coolant flow ratios, while adjusting the coolant flow ratio can achieve optimal heat transfer performance at a fixed rotational speed.
5. Conclusion
In this work, the heat transfer performance of an industrial-scale suspension polymerization reactor, which can efficiently remove the heat from polymerization reactions and control the temperature uniformity of the reaction mixture through the cooling medium in both agitator and jacket, is systematically investigated. The effects of flow ratio and agitator speed on the heat removal rate and the uniformity of fluid temperature are evaluated through the proposed quantitative indicators. Furthermore, the impact routes of these factors on the reactor's heat transfer performance are analyzed. This study provides a comprehensive insight into the characteristics of the reactor's heat transfer performance as well as an assessment of the evolution of heat transfer performance throughout the suspension polymerization process. Some significant conclusions obtained from this research are as follows:
(1) The reactor's heat transfer efficiency can be significantly enhanced and the fluid temperature uniformity can be precisely controlled through introducing cooling water in the agitator and appropriately regulating the flow ratio of cooling water in the agitator and jacket. The impact of flow ratios on the reactor's heat transfer performance is mainly due to the fact that it alters the convective heat transfer coefficients of cooling water in the agitator and jacket.
(2) The maximum heat removal rate can be achieved at the flow ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, while the flow ratios of 9
3, while the flow ratios of 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and A yield lower fluid temperature gradients. However, since the heat transfer rate at the flow ratio of A is significantly lower than those under the other conditions, the appropriate flow ratios are in the scope of 3
1 and A yield lower fluid temperature gradients. However, since the heat transfer rate at the flow ratio of A is significantly lower than those under the other conditions, the appropriate flow ratios are in the scope of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 and 9
7 and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, balancing heat transfer efficiency and temperature uniformity.
1, balancing heat transfer efficiency and temperature uniformity.
(3) The increase of agitator rotational rates can obviously boost fluid velocities, accelerate fluid circulation and intensify mixing of fluids in different regions. It improves the heat transfer performance of the reactor by raising the heat transfer rate and promoting fluid temperature uniformity. Nevertheless, it is noticeable that with the increased rotational speed, the enhancing effect of speed on heat removal rate and its effect in reducing the temperature gradient weakens progressively in the range of 10 to 120 rpm. The proposed agitation speed range is 30–90 rpm.
(4) Currently, the flow rate of cooling water through the internal agitator of industrial polymerization reactors of this type typically does not exceed 10% of the total cooling water flow, significantly restricting the full exploitation of their heat transfer capabilities. Therefore, the proportion of cooling water flow through the agitator should be properly increased in the design process to achieve superior temperature gradient control and more efficient heat removal.
Nomenclature
| Cp | Specific heat capacity [J kg−1 K−1] |
| E | Total energy of fluid per unit mass [J kg−1] |
| ĒT | Average relative deviation of temperature between the whole reaction zone and local regions |
| G | Gravitational acceleration [m s−2] |
| h | Heat removal rate [kJ s−1] |
| Keff | Effective heat conductivity [W m−1 K−1] |
| n | Rotation rate [rpm] |
| p | Pressure [Pa] |
| k | Turbulent kinetic energy [kg m2 s−2] |
| t | Time [s] |
| u | Velocity vector [m s−1] |
Greek symbols
| ε | Dissipation rate of turbulent energy [m2 s−3] |
| μ | Viscosity [Pa s] |
| ρ | Density [kg m−3] |
| δ | Unit tensor |
| φ | Volume fraction |
| σ | Turbulent Prandtl number |
Data availability
The data supporting this article have been included as part of the ESI.†
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work is sponsored by the Shanghai Sailing Program (No. 22YF1419700), the National Natural Science Foundation of China (No. U1862201), and the Open Project of Shanghai Coal Based Multigeneration Engineering Technology Research Center (GZKF-MJDLC-01).
References
- J. P. Han, Y. N. Yang, Q. Niu, Z. H. Luo and Y. N. Zhou, Chem. Eng. Sci., 2023, 275, 118753 CrossRef CAS.
- J. Ru, E. Mastan, L. Zhou, C. Shao, J. Zho, S. Wang and S. Zhu, Ind. Eng. Chem. Res., 2022, 61(40), 14813–14822 CrossRef CAS.
- O. P. Klenov, N. A. Chumakova, S. A. Pokrovskaya and A. S. Noskova, Chem. Eng. Sci., 2019, 205, 1–13 CrossRef CAS.
- G. Y. Liu and B. A. Wilhite, Chem. Eng. Sci., 2022, 258, 117758 CrossRef CAS.
- S. Y. Jiang, Z. R. Yang, J. Zhang, X. Z. Duan and X. G. Zhou, Ind. Eng. Chem. Res., 2022, 61, 14121–14131 CrossRef CAS.
- L. Xie and Z. H. Luo, Ind. Eng. Chem. Res., 2017, 56(16), 4690–4702 CrossRef CAS.
- S. H. Kim, J. H. Lee and R. D. Braatz, Comput. Chem. Eng., 2021, 152, 107391 CrossRef CAS.
- J. Wieme, T. De Roo, G. B. Marin and G. J. Heynderickx, Ind. Eng. Chem. Res., 2007, 46(4), 1179–1196 CrossRef CAS.
- J. P. Han, Y. N. Yang, C. S. Zhao, Y. H. Qian, Q. Niu, Z. H. Luo and Y. N. Zhou, Can. J. Chem. Eng., 2023, 101(9), 4927–4940 CrossRef CAS.
- W. M. Poubel, E. F. C. S. Silva, E. N. Souza and J. C. Pinto, Macromol. React. Eng., 2014, 8(4), 374–391 CrossRef CAS.
- A. L. Nogueira, M. B. Quadri, R. A. F. Machado and C. A. Claumann, Macromol. React. Eng., 2017, 11(3), 1600040 CrossRef.
- L. Xie, Q. Liu and Z. H. Luo, Chem. Eng. Res. Des., 2018, 130, 1–17 CrossRef CAS.
- M. A. Gómez, J. Collazo, J. Porteiro and J. L. Míguez, Int. J. Heat Mass Transfer, 2018, 122, 574–586 CrossRef.
- Z. M. Zhou, Z. M. Cheng and W. K. Yuan, Chem. Eng. Sci., 2005, 60(12), 3207–3215 CrossRef CAS.
- H. Pan, X. F. Liang, L. T. Zhu and Z. H. Luo, Ind. Eng. Chem. Res., 2017, 56(36), 10199–10213 CrossRef CAS.
- J. Cui, L. Ni, J. Jiang, Y. Pan, H. Wu and Q. Chen, Org. Process Res. Dev., 2019, 23(3), 389–396 CrossRef CAS.
- L. Ni, J. W. Cui, J. C. Jiang, Y. Pan, H. Wu, C. M. Shu, Z. R. Wang, S. J. Mou and N. Shi, Process Saf. Environ. Prot., 2020, 135, 294–300 CrossRef CAS.
- Y. N. Yang, Y. N. Zhou, B. Ouyang, Y. Y. Wu, X. B. Zhang and Z. H. Luo, AIChE J., 2022, 68(5), e17645 CrossRef CAS.
- M. Cai, Z. Tian, Z. Liu and B. P. Liu, Powder Technol., 2022, 407, 117647 CrossRef CAS.
- F. Dabbagh, S. Pirker and S. Schneiderbauer, AIChE J., 2021, 67, e17161 CrossRef CAS.
- H. Lei, L. T. Zhu and Z. H. Luo, Chem. Eng. Sci., 2023, 268, 118437 CrossRef CAS.
- L. Z. Wang, Y. J. Zhou and Z. B. Chen, Int. J. Chem. React. Eng., 2020, 18(3), 20190196 CAS.
- S. A. Daza, R. J. Prada, J. R. Nunhez and G. Castilho, Can. J. Chem. Eng., 2019, 97, 586–593 CrossRef CAS.
- R. Engeskaug, E. Thorbjørnsen and H. F. Svendsen, Ind. Eng. Chem. Res., 2005, 44(14), 4949–4958 CrossRef CAS.
- E. H. Abdel-Gawad, M. M. Taha, M. A. Abdel-Kawi, G. H. Sedahmed and M. A. El-Naggar, Chem. Eng. Res. Des., 2022, 178, 514–522 CrossRef CAS.
- S. Zhu and A. E. Hamielec, Polymer, 1991, 32(16), 3021–3025 CrossRef CAS.
- X. B. Zhang, K. Wang, T. Yang, S. Ma, J. Lei, Q. Xu, S. X. Ruan and Z. H. Luo, Chem. Eng. Sci., 2023, 282, 119259 CrossRef CAS.
- O. J. Hinze, Turbulence, McGraw-Hill Publishing Co., New York, 1975 Search PubMed.
- B. E. Launder and D. B. Spalding, Comput. Methods Appl. Mech. Eng., 1974, 3, 269–289 CrossRef.
- V. X. Mendoza-Escamilla, A. Alonzo-García, H. R. Mollinedo, I. González-Neria, J. A. Yáñez-Varela and S. A. Martinez-Delgadillo, Chin. J. Chem. Eng., 2018, 26(5), 942–956 CrossRef CAS.
- B. E. Launder and D. B. Spalding, Lectures in mathematical models of turbulence, Academic Press, London, England, 1972 Search PubMed.
- J. J. Wang, Y. Han, X. P. Gu, L. F. Feng and G. H. Hu, AIChE J., 2013, 59, 1066–1074 CrossRef CAS.
- S. Di, J. Xu, Q. Chang and W. Ge, Chin. J. Chem. Eng., 2016, 24(9), 1122–1134 CrossRef CAS.
- L. Xie and Z. H. Luo, Chem. Eng. Sci., 2018, 176, 439–453 CrossRef CAS.
- I. Radež, V. Hudcova and T. Koloini, Chem. Eng. J., 1991, 46(3), B83–B91 CrossRef.
- B. Triveni, B. Vishwanadham and S. Venkateshwar, Heat Mass Transfer, 2008, 44(11), 1281–1288 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  b,
Yin-Ning Zhou
b,
Yin-Ning Zhou b,
Hao Chenb,
Zheng-Hong Luo
b,
Hao Chenb,
Zheng-Hong Luo *b,
Liyang Zhou*a,
Guojun Yua,
Wenwu Liua and
Shiping Zhu
*b,
Liyang Zhou*a,
Guojun Yua,
Wenwu Liua and
Shiping Zhu *c
*c

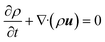
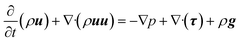
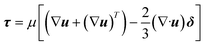
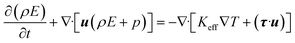
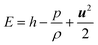
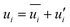
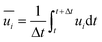
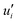 and
and 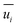 represent the fluctuating and mean velocity components, respectively. Substituting this form of velocity expression into the original momentum equation yields the following Reynolds averaged equation:
represent the fluctuating and mean velocity components, respectively. Substituting this form of velocity expression into the original momentum equation yields the following Reynolds averaged equation: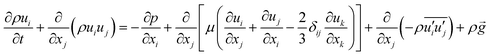
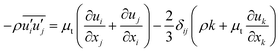
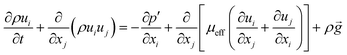
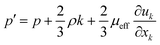
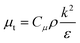
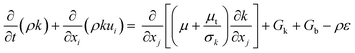
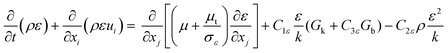
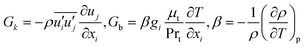
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660
660![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 348 is selected for CFD simulation after carefully evaluating the balance between simulation accuracy and computational efficiency. The density, specific heat, thermal conductivity and viscosity of the reaction mixture are 998.2 kg m−3, 4182 J kg−1 K−1, 0.6 W m−1 K−1 and 0.001 Pa s, respectively.
348 is selected for CFD simulation after carefully evaluating the balance between simulation accuracy and computational efficiency. The density, specific heat, thermal conductivity and viscosity of the reaction mixture are 998.2 kg m−3, 4182 J kg−1 K−1, 0.6 W m−1 K−1 and 0.001 Pa s, respectively.
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 1 −
1 − ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 2|, |
2|, |![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 2 −
2 − ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 3|, |
3|, |![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 1 −
1 − ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 3|)
3|)
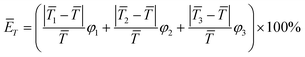
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 1,
1, ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 2,
2, ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) 3 and
3 and ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) represent the average temperature of region 1, region 2 and region 3 and the whole reaction zone, respectively; φ1, φ2 and φ3 respectively denote the ratios of the volumes of region 1, region 2 and region 3 to the total reactor volume (note: φ1 + φ2 + φ3 = 1).
represent the average temperature of region 1, region 2 and region 3 and the whole reaction zone, respectively; φ1, φ2 and φ3 respectively denote the ratios of the volumes of region 1, region 2 and region 3 to the total reactor volume (note: φ1 + φ2 + φ3 = 1).
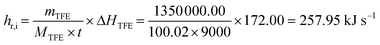
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9. The heat removal rate by the simulation (hr,s), under the condition close to the industrial operation, is:
9. The heat removal rate by the simulation (hr,s), under the condition close to the industrial operation, is:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q2) on the fluid temperature in the whole reaction zone at different times (Fig. 4a), the average fluid temperature in region 1, region 2 and region 3 (Fig. 4b), the maximum temperature difference between different regions (Fig. 4c), the average relative deviation of fluid temperature between the whole reaction zone and the local regions (Fig. 4d), and the total heat removal rates of the cooling system (hT) and the hear removal rates of the agitator (hA) and jacket (hJ) (Fig. 4e). Furthermore, the impact of flow ratio on the mean surface heat flux of jacket and agitator is presented in Fig. 5 and 6, respectively. The characteristics of fluid temperature distribution along the reactor's axial section in the vertical direction at different flow ratios are shown in Fig. 7.
Q2) on the fluid temperature in the whole reaction zone at different times (Fig. 4a), the average fluid temperature in region 1, region 2 and region 3 (Fig. 4b), the maximum temperature difference between different regions (Fig. 4c), the average relative deviation of fluid temperature between the whole reaction zone and the local regions (Fig. 4d), and the total heat removal rates of the cooling system (hT) and the hear removal rates of the agitator (hA) and jacket (hJ) (Fig. 4e). Furthermore, the impact of flow ratio on the mean surface heat flux of jacket and agitator is presented in Fig. 5 and 6, respectively. The characteristics of fluid temperature distribution along the reactor's axial section in the vertical direction at different flow ratios are shown in Fig. 7.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q2: (a) J, (b) 1
Q2: (a) J, (b) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, (c) 3
9, (c) 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, (d) 5
7, (d) 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, (e) 7
5, (e) 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and (f) 9
3 and (f) 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q2: (a) 1
Q2: (a) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, (b) 3
9, (b) 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, (c) 5
7, (c) 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, (d) 7
5, (d) 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, (e) 9
3, (e) 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and (f) A.
1 and (f) A.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q2 values: (a) J, (b) 1
Q2 values: (a) J, (b) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, (c) 3
9, (c) 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, (d) 5
7, (d) 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, (e) 7
5, (e) 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, (f) 9
3, (f) 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and (g) A.
1 and (g) A.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 > 5
3 > 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 > 3
5 > 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 > 9
7 > 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 > 1
1 > 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 > J > A. Furthermore, it can be found that there is a negligible difference in heat transfer capabilities between flow ratios of (1) 5
9 > J > A. Furthermore, it can be found that there is a negligible difference in heat transfer capabilities between flow ratios of (1) 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and 3
5 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 and (2) J and A. Fig. 4b presents that the order of fluid temperature in different regions is region 1 > region 2 > region 3 when the flow ratio is clearly less than 7
7 and (2) J and A. Fig. 4b presents that the order of fluid temperature in different regions is region 1 > region 2 > region 3 when the flow ratio is clearly less than 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, the fluid temperature in region 2 and region 3 is almost identical and still lower than that of region 1 at the flow ratio up to 9
3, the fluid temperature in region 2 and region 3 is almost identical and still lower than that of region 1 at the flow ratio up to 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and there is a minimal temperature difference between region 1 and region 2, while region 3 exhibits the highest fluid temperature at the flow ratio of A. Due to significant heat exchange between fluid in different regions of the reactor under turbulent flow, the temperature in each region is influenced not only by the heat transfer rate between fluid and cooling jacket or agitator but also by the fluid circulation patterns and intensity of turbulence. This complex relationship makes it difficult to theoretically analyze the differences in heat transfer efficiency across regions. However, the heat transfer efficiency in different regions can be indirectly inferred from the temperature distribution curves in these regions. The temperature distribution curves in different regions suggest that the heat transfer rates are faster in regions closer to the external jacket when all cooling water is directed to the jacket. Conversely, the heat transfer rates in the internal fluid region (region 1) and the middle blade region (region 2) are similar, but both are higher than that in the external fluid region as the cooling water fully flows into the agitator. Additionally, the variation in temperature curves across different regions as the flow ratio changes from 1
1, and there is a minimal temperature difference between region 1 and region 2, while region 3 exhibits the highest fluid temperature at the flow ratio of A. Due to significant heat exchange between fluid in different regions of the reactor under turbulent flow, the temperature in each region is influenced not only by the heat transfer rate between fluid and cooling jacket or agitator but also by the fluid circulation patterns and intensity of turbulence. This complex relationship makes it difficult to theoretically analyze the differences in heat transfer efficiency across regions. However, the heat transfer efficiency in different regions can be indirectly inferred from the temperature distribution curves in these regions. The temperature distribution curves in different regions suggest that the heat transfer rates are faster in regions closer to the external jacket when all cooling water is directed to the jacket. Conversely, the heat transfer rates in the internal fluid region (region 1) and the middle blade region (region 2) are similar, but both are higher than that in the external fluid region as the cooling water fully flows into the agitator. Additionally, the variation in temperature curves across different regions as the flow ratio changes from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 to 7
9 to 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 suggests that raising the proportion of cooling water in the agitator and reducing it in the jacket within this range is beneficial for improving the heat transfer efficiency in all the three regions.
3 suggests that raising the proportion of cooling water in the agitator and reducing it in the jacket within this range is beneficial for improving the heat transfer efficiency in all the three regions.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q2, with the exception of Q1
Q2, with the exception of Q1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q2 = 7
Q2 = 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. A similar trend is observed in ĒT (Fig. 4d), where it decreases as the flow ratio increases, except at flow ratios of 7
3. A similar trend is observed in ĒT (Fig. 4d), where it decreases as the flow ratio increases, except at flow ratios of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and A. These results suggest that the temperature of the fluid region tends to rise with increasing distance from the jackets when the system relies only on the jacket for heat transfer, whereas temperature gradients between the internal and external regions can be effectively reduced through properly increasing the flow rate of cooling water in the agitator. Fig. 4e shows that an increase in the flow ratio results in a stronger heat removal capability of the agitator, whereas a weaker overall heat transfer performance of the jacket with an exception of the 7
3 and A. These results suggest that the temperature of the fluid region tends to rise with increasing distance from the jackets when the system relies only on the jacket for heat transfer, whereas temperature gradients between the internal and external regions can be effectively reduced through properly increasing the flow rate of cooling water in the agitator. Fig. 4e shows that an increase in the flow ratio results in a stronger heat removal capability of the agitator, whereas a weaker overall heat transfer performance of the jacket with an exception of the 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 flow ratio.
3 flow ratio.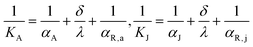
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, an increase in the flow rate of the jacket cooling water typically leads to a higher hJ (Fig. 4e). Consequently, it is reasonable to deduce that this increase in the flow rate generally boosts the αJ, similar to the behavior of the agitator. Obviously, the flow ratio of 7
3, an increase in the flow rate of the jacket cooling water typically leads to a higher hJ (Fig. 4e). Consequently, it is reasonable to deduce that this increase in the flow rate generally boosts the αJ, similar to the behavior of the agitator. Obviously, the flow ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 represents a special case. In the vicinity of 7
3 represents a special case. In the vicinity of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, the total heat removal rate is at its peak, and there are marked changes in the variation trends of ΔTmax, ĒT and hA with the flow ratio.
3, the total heat removal rate is at its peak, and there are marked changes in the variation trends of ΔTmax, ĒT and hA with the flow ratio.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 can be interpreted through the heat flux distribution characteristics of the jacket at varying flow ratios, as depicted in Fig. 5. The jacket's heat flux distribution shows obvious unevenness at the flow ratios of 5
3 can be interpreted through the heat flux distribution characteristics of the jacket at varying flow ratios, as depicted in Fig. 5. The jacket's heat flux distribution shows obvious unevenness at the flow ratios of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and 9
5 and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, with the heat flux in some areas being significantly below 9200 W m−2. Conversely, the heat flux is more uniformly distributed at the flow ratio of 7
1, with the heat flux in some areas being significantly below 9200 W m−2. Conversely, the heat flux is more uniformly distributed at the flow ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and the occurrence of low heat flux areas is considerably limited. This phenomenon should be the main cause of the superior heat transfer performance at the flow ratio of 7
3, and the occurrence of low heat flux areas is considerably limited. This phenomenon should be the main cause of the superior heat transfer performance at the flow ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 compared to the ratio of 5
3 compared to the ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5. However, because the current data are not sufficient to deeply reveal the complex interplay between flow and heat transfer behaviors, the underlying mechanism of the excellent heat transfer performance at the flow ratio of 7
5. However, because the current data are not sufficient to deeply reveal the complex interplay between flow and heat transfer behaviors, the underlying mechanism of the excellent heat transfer performance at the flow ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 requires further research in future work. Comparatively, the reason for the reduced heat transfer rates at the flow ratio of A or J is quite straightforward and easy to understand, primarily due to the reduction in the heat transfer area.
3 requires further research in future work. Comparatively, the reason for the reduced heat transfer rates at the flow ratio of A or J is quite straightforward and easy to understand, primarily due to the reduction in the heat transfer area.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 allows the jacket to achieve a relatively uniform heat flux distribution. However, increasing the cooling water flow ratio in the agitator to above 9
3 allows the jacket to achieve a relatively uniform heat flux distribution. However, increasing the cooling water flow ratio in the agitator to above 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 leads to a significant unevenness in the jacket's heat flux distribution due to insufficient cooling water flow. Therefore, the flow ratio should be less than 9
1 leads to a significant unevenness in the jacket's heat flux distribution due to insufficient cooling water flow. Therefore, the flow ratio should be less than 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 considering the effect of jacket heat transfer. The results in Fig. 6 and 7 indicate that the heat transfer limitation in the agitator causes the internal region of the reactor to have a significantly higher temperature than other regions when the flow ratio is less than 3
1 considering the effect of jacket heat transfer. The results in Fig. 6 and 7 indicate that the heat transfer limitation in the agitator causes the internal region of the reactor to have a significantly higher temperature than other regions when the flow ratio is less than 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, leading to a noticeable temperature gradient. Thus, the flow ratio should be greater than 3
7, leading to a noticeable temperature gradient. Thus, the flow ratio should be greater than 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7. Furthermore, although directing all cooling water to the agitator results in a higher heat transfer rate and more uniform temperature distribution within the reactor, it also significantly reduces the heat transfer area because the jacket is no longer utilized for heat removal, leading to a substantial decrease in the overall heat transfer capacity. Hence, the cooling water proportion in the agitator should not be excessively increased solely to enhance its heat transfer capability and improve temperature uniformity, as this would neglect the important heat transfer role of the jacket.
7. Furthermore, although directing all cooling water to the agitator results in a higher heat transfer rate and more uniform temperature distribution within the reactor, it also significantly reduces the heat transfer area because the jacket is no longer utilized for heat removal, leading to a substantial decrease in the overall heat transfer capacity. Hence, the cooling water proportion in the agitator should not be excessively increased solely to enhance its heat transfer capability and improve temperature uniformity, as this would neglect the important heat transfer role of the jacket.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 flow ratio achieves the highest heat removal rate, it does not provide optimal temperature uniformity inside the reactor. Thus, balancing the impact of flow ratio on heat transfer rate and temperature uniformity, a 5
3 flow ratio achieves the highest heat removal rate, it does not provide optimal temperature uniformity inside the reactor. Thus, balancing the impact of flow ratio on heat transfer rate and temperature uniformity, a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 flow ratio is selected for the study on agitation speed. Fig. 8 shows the impact of flow ratio on the fluid temperature in all the reaction zones at different times (Fig. 8a), average fluid temperature in region 1, region 2 and region 3 (Fig. 8b), ΔTmax (Fig. 8c), ĒT (Fig. 8d), and hT, hA and hJ (Fig. 8e). Furthermore, the impact of rotation rates on the distribution of fluid temperature and velocity along the reactor's axial cross section in the vertical direction is presented in Fig. 9 and 10a–d, respectively. The fluid velocity and velocity vector distribution characteristics in the radial cross section of the reactor's middle part when n = 30 rpm are displayed in Fig. 10e and f, respectively.
5 flow ratio is selected for the study on agitation speed. Fig. 8 shows the impact of flow ratio on the fluid temperature in all the reaction zones at different times (Fig. 8a), average fluid temperature in region 1, region 2 and region 3 (Fig. 8b), ΔTmax (Fig. 8c), ĒT (Fig. 8d), and hT, hA and hJ (Fig. 8e). Furthermore, the impact of rotation rates on the distribution of fluid temperature and velocity along the reactor's axial cross section in the vertical direction is presented in Fig. 9 and 10a–d, respectively. The fluid velocity and velocity vector distribution characteristics in the radial cross section of the reactor's middle part when n = 30 rpm are displayed in Fig. 10e and f, respectively.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, while the flow ratios of 9
3, while the flow ratios of 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and A yield lower fluid temperature gradients. However, since the heat transfer rate at the flow ratio of A is significantly lower than those under the other conditions, the appropriate flow ratios are in the scope of 3
1 and A yield lower fluid temperature gradients. However, since the heat transfer rate at the flow ratio of A is significantly lower than those under the other conditions, the appropriate flow ratios are in the scope of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 and 9
7 and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, balancing heat transfer efficiency and temperature uniformity.
1, balancing heat transfer efficiency and temperature uniformity.



