Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Deducing the conformational space for an octa-proline helix†‡
Sara M. A.
Waly
 ,
Andrew C.
Benniston
,
Andrew C.
Benniston
 * and
Anthony
Harriman
* and
Anthony
Harriman
 *
*
Molecular Photonics Laboratory, Bedson Building, School of Natural and Environmental Sciences, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK. E-mail: anthony.harriman@ncl.ac.uk
First published on 21st December 2023
Abstract
A molecular dyad, PY-P8-PER, comprising a proline octamer sandwiched between pyrene and perylene terminals has been synthesized in order to address the dynamics of electronic energy transfer (EET) along the oligo-proline chain. A simple pyrene-based control compound equipped with a bis-proline attachment serves as a reference for spectroscopic studies. The N–H NMR signal at the terminal pyrene allows distinction between cis and trans amides and, although the crystal structure for the control has the trans conformation, temperature-dependent NMR studies provide clear evidence for trans/cis isomerisation in D6-DMSO. Polar solvents tend to stabilise the trans structure for the pyrene amide group, even for longer oligo-proline units. Circular dichroism shows that the proline spacer for PY-P8-PER exists mainly in the all-trans geometry in methanol. Preferential excitation of the pyrene chromophore is possible at wavelengths in the 320–350 nm range and, for the dyad, is followed by efficacious EET to the perylene emitter. The probability for intramolecular EET, obtained from analysis of steady-state spectroscopic data, is ca. 80–90% in solvents of disparate polarity. Comparison with the Förster critical distance suggests the terminals are ca. 18 Å apart. Time-resolved fluorescence spectroscopy, in conjunction with DFT calculations, indicates the dyad exists as a handful of conformers displaying a narrow range of EET rates. Optimisation of a distributive model allows accurate simulation of the EET dynamics in terms of reasonable structures based on isomerisation of certain amide groups.
Introduction
The concept of a covalently-linked molecular dyad, whereby a well-defined connecting group spatially isolates specific donor and acceptor units, has been instrumental in the development of molecular photophysics. The most informative dyads are those where the spacer is a rigid connector maintaining close control of the geometry of the entire system by imposing a narrow distribution of separation distances and mutual orientations.1–5 In most, but not all, cases the spacer should not be electronically coupled to either donor or acceptor, nor should it operate as a relay for electron or exciton transfer between the terminals. Such dyads have led to the observation of the Marcus inverted region,6,7 and its subsequent quantum mechanical modification,8 and to recognising the limitations of Förster theory for dipole–dipole interactions at short separations.9–12 Related dyads have been designed to explore the structural demands for excitonic coupling,13 proton-coupled electron transfer,14 photochromism15 and E-type delayed fluorescence.16,17 A particular success for rigid molecular dyads has been the study of electron and exciton transfers across orthogonal spacer units.18–20 Strategies are now in place that permit photophysical measurements to be made with donor and acceptor groups at predetermined distances from ca. 120 Å to ca. 5 Å.21–24 However, intramolecular torsional perturbations are difficult to eliminate with long spacers constructed by accretion of several small units such that actual distances and orientations might not be as expected from simple molecular models.25,26 With few exceptions, these dyads are expensive to prepare and require skillful synthesis that realistically cannot be scaled-up. It is worth noting that the humble dyad has been used to construct a plethora of more exotic molecular architectures, ranging from linear oligomers to cyclic superstructures.27–31Considerable interest has been shown in the development of molecular dyads having a long, linear spacer that facilitates examination of how separation distance affects the rate of a particular chemical process.32–36 This is usually achieved by linking together several identical small spacer units, such as phenyl rings, but this does not guarantee that the spacer will adopt the fully extended conformation. An alternative route to elongated spacers is to adapt biological media to host the donor and acceptor units. This can be done, for example, using polynucleotides with intercalating reagents37 or by attaching the active chromophores to discrete sites on peptides.38 The latter procedure is particularly attractive since it allows the use of automated synthesis to assemble dyads with pre-programmed composition and length.39 One concern with this approach is that the amide connections can adopt cis and trans conformations,40 such that a unique geometry might not emerge. In the case of peptide-based spacers, rigidity is realised if the oligomer forms a helical assemblage.41
In this respect, we have considered using polyproline residues as inert spacers since proline is unlikely to perturb the electronic properties of the terminal, has good solubility in a range of solvents and is readily functionalised. Polyprolines form both right-handed and left-handed helices according to the geometry around the peptide bonds; trans conformations give rise to a left-handed helix (PPII) whereas the corresponding cis conformation favours a right-handed helix (PPI).42 Internal hydrogen bonding is insignificant in either structure. The PPII helix is relatively open and more stable than PPI,43 with interconversion between the two forms being slow due to the high activation energy for cis–trans isomerisation.44 Previous research45 has proposed that the PPII structure is sufficiently rigid for use as a “molecular ruler” in structural biology. Specifically, PPII residues have been labelled with terminal fluorophores chosen for their capacity to undergo unidirectional electronic energy transfer (EET) along the helix.46 More recent work,47 however, has raised questions about the rigidity of short polyproline residues which might invalidate their use for the determination of in situ separation distances. This uncertainty has prompted us to examine the dynamics of EET along a proline-based octamer decorated with emissive terminal chromophores. For the emitters, we have opted to use the classical pair of pyrene and perylene since these polycycles are of similar dimensions, possess well-defined transition dipole moment vectors and exhibit complimentary photophysical properties. There have been several studies of EET from pyrene to perylene, starting in 1967 (ref. 48) and including the use of a polynucleotide scaffold to provide incremental separation distances.49 The Förster critical distance50 for this pair is ca. 23 Å while the spectral overlap integral51 is reported to be ca. 2.4 × 10−14 cm6 mmol−1. Since pyrene possesses a relatively long-lived excited singlet state, these parameters should enable effective EET over considerable distances.
Our primary interest in this area is to establish if polyproline can function as a suitable spacer for directed EET. This requires that the proline-based spacer is sufficiently long to form a tight helix and that there is a unique arrangement of cis- or trans-amide linkages. A further point of concern relates to quantifying any electronic interaction between chromophore and spacer, this being a particular issue for pyrene where the photophysical properties can be manipulated by substitution.52 The minimum accretion number for formation of an oligo-proline helix53 is ca. 6 and we have opted to prepare an octamer as the basic spacer unit. For this system to be effective, it is essential that there is a narrow distribution of molecular lengths and orientations. The latter should become apparent from time-resolved fluorescence spectroscopic measurements54 made to monitor through-space EET between the terminals. Quantum chemical calculations have allowed identification of key structures in order to compare simulated rates of EET with the experimental measurements.
Results and discussion
Compound synthesis and characterisation
The linear preparation of PY-P8-PER (Scheme 1) has the advantage, relative to automated syntheses,55 that at each stage the compounds can be purified and fully characterised. Our approach started from the pyrene segment of the compound, in the form of 1-aminopyrene, reacting with the commercially available Boc protected carboxylic acid 1 using the coupling agent COMU56 and DIPEA as base57 to produce PY-P2 (ESI Pages S2–S23‡). The successful synthesis of PY-P2 was confirmed from its 1H NMR spectrum (Fig. S1‡) by the appearance of the signal for the Boc (i.e., tert-butyloxycarbonyl) methyl protons at 1.47–1.52 ppm, as well as the broad signals in the range between 1.80–5.13 ppm, which are assigned to the proline aliphatic CH2/CH protons. Confirmation of the molecular composition of PY-P2 was obtained by positive ESI mass spectrometry (CH2Cl2/CH3OH + NH4OAc) which displayed a peak at m/z = 534.2363 au corresponding to the [M + Na]+ ion and a peak at m/z = 529.2809 au corresponding to the [M + NH4]+ ion (Fig. S25‡). Deprotection of PY-P2 using 4 M HCl in 1,4 dioxane afforded PY-P2-NH in near quantitative yield. A diagnostic signal is provided by the NH proton, which was identified as a singlet at 10.99 ppm and confirmed its successful preparation (Fig. S9‡). Coupling of the carboxylic acid 1 with deprotected amino proline PY-P2-NH afforded PY-P4 in good yield (67%), before deprotection to give PY-P4-NH in excellent yield.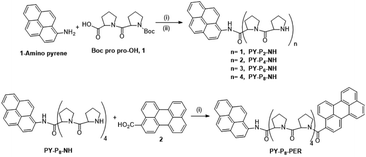 | ||
| Scheme 1 Reagents and conditions: (i) COMU, DIPEA, RT, DMF, overnight, (ii) 4 M HCl, dioxane, RT, overnight. A detailed synthetic route is given in Scheme S1.‡ | ||
By consecutive coupling of the carboxylic acid 1 and deprotected amino-proline derivatives, the octamer PY-P8-NH was prepared. At each coupling stage, the new compounds were purified and fully characterised (see ESI‡). Confirmation of the molecular composition of PY-P8-NH was obtained by positive ESI mass spectrometry (CH2Cl2/CH3OH + NH4OAc) which displayed a peak at m/z = 994.5185 au, corresponding to the [M + H]+ ion, and a peak at m/z = 1016.5005 au, corresponding to the [M + Na]+ ion (Fig. S32‡).
In the final step, the perylene carboxylic acid 2 was coupled to PY-P8-NH to produce the dyad PY-P8-PER in reasonable yield (42%). The broad signals of the 1H NMR spectrum in the region between 1.99–4.76 ppm (56 protons) are consistent with the number of proline aliphatic CH2/CH protons (Fig. S21‡). The mass spectrum displayed a peak at m/z = 1272.5894 au, consistent with the [M + H]+ ion (rmm = 1272.58), a peak at m/z = 1289.6183 au, corresponding to the [M + NH4]+ ion, (rmm 1289.62) and a peak at m/z = 1295.5768 au, corresponding to the [M + Na]+ ion (rmm 1294.58) (Fig. S33‡).
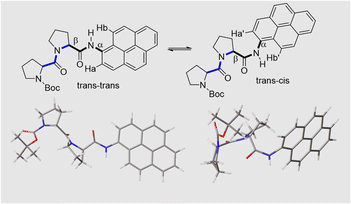
Stereochemistry at the pyrene terminal
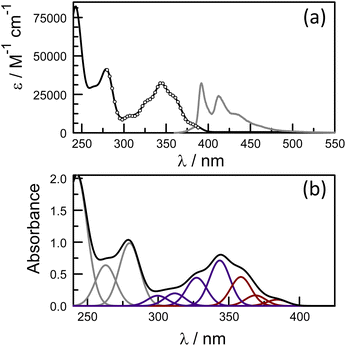
Close inspection of the 1H NMR spectrum for PY-P2 in CDCl3 indicates two peaks, with near equivalent intensities, at 10.20 ppm (53%) and 10.27 ppm (47%) (Fig. S1‡). Both peaks disappear upon a D2O shake, confirming these are associated with the amide NH-unit (Fig. S3‡). The pattern is consistent with two slowly interconverting conformers in solution. From inspection of the molecular structure, two isomers are feasible based solely on bond rotation at the pyrene-amide bond (Fig. 1). It is noted that trans to cis isomerisation modifies the chemical environment of Ha, moving it away from the CO group. Even though proton Hb is always proximal to the NH group, there is a change in the NH magnetic environment since it is within the deshielding zone of the CO subunit. Therefore, the chemical shifts for Ha/Ha′ and Hb/Hb′ are expected to differ for the two isomers. The NMR signals due to the t-butyl groups overlap and it was not possible to separate them.Due to the dynamic properties of peptide bond isomerisation,58 many nuclei offer potential as probes in NMR spectroscopy for determining both interconversion kinetics and the relative concentrations.59 Thus, selected aromatic proton resonances for PY-P2 were assigned by a combination of COSY and ROESY NMR spectra (Fig. S5–S7‡). The COSY data could be interpreted as a four-spin system, as identified in the coloured plot shown in Fig. 2. The spin system comprising two protons (blue) is clearly correlated and did not show NOE interactions to the proline protons. The three protons coloured brown are also readily identified. The two most downfield doublets (pink) are assigned to protons Hb/Hb′ since they show a strong NOE to the N–H proton as well as to several proline protons; the corresponding coupled proton is readily identified by the cross-correlation contour. The final set of protons is assigned to Ha/Ha′ (green) and as expected displays only a weak NOE to the N–H proton. The most deshielded proton is assigned as Ha (trans–trans isomer) due to the carbonyl anisotropy and hydrogen bonding effect, this being consistent with the X-ray structure discussed below.
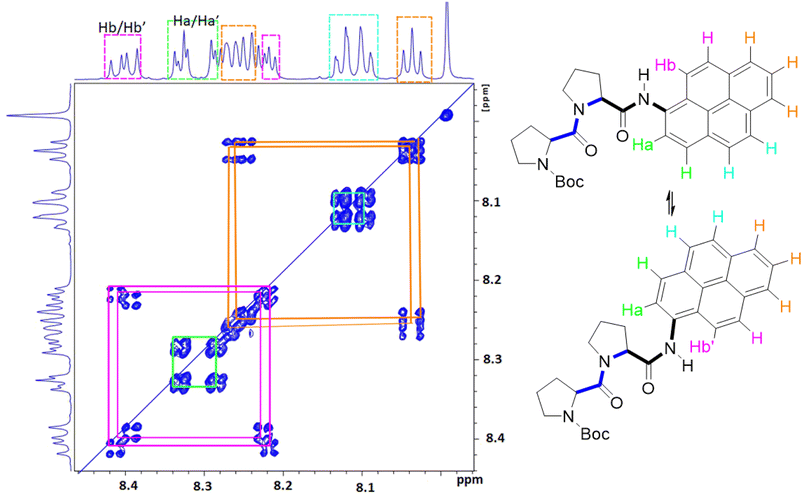 | ||
| Fig. 2 Selected COSY NMR spectrum (700 MHz, D6-DMSO) recorded for compound PY-P2 and the colour coded interpretation for the two isomers. | ||
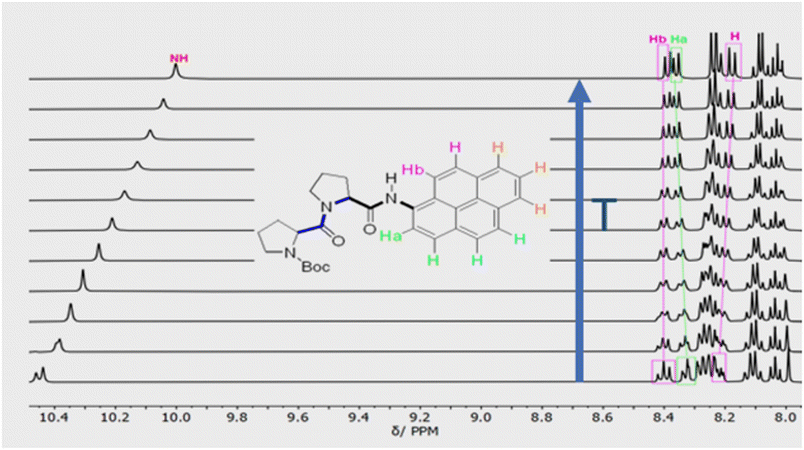
Confirmation of cis–trans isomerisation was obtained by collecting 1H NMR spectra for PY-P2 in D6-DMSO from 298 to 403 K (Fig. 3), the solvent being chosen for its low volatility. The two distinct N–H peaks at room temperature collapse into one resonance at around 323 K, which broadens and shifts upfield by around 0.47 ppm as the temperature is raised further. An additional feature is observed with increasing temperature; namely, the Ha/Ha′ protons shift upfield by ca. 0.5 ppm while the Hb/Hb′ protons shift downfield by ca. 0.4 ppm. These resonances converge and finally collapse to two doublets as expected for fast trans/cis exchange. At high temperature, the proton coupled to Hb is clearly visible as a doublet.
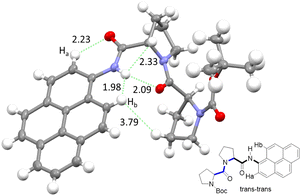
The NMR spectroscopic interpretation was validated by the collection of X-ray crystallographic data for a single-crystal of PY-P2 (Fig. 4). The solid-state structure corresponds to the trans–trans isomer. The bis-proline subunit appears to be “wrapped” around the pyrene group rather than extended as drawn in the simple chemical formula shown in Fig. 1. This feature is driven by the intramolecular hydrogen bond between the N–H amide of the pyrene and the central carbonyl group of the bis-proline. The proton assigned to Ha is evidently within the sphere of influence of the carbonyl group, as inferred from the NMR experiments. Several close contacts are identified for proton Hb, especially noting its short distance to the N–H proton of the pyrene amide. One of the proline protons resides well within the range (ca. 5 Å) needed to effect an NOE effect. Consequently, the solid-state structure appears to correlate satisfyingly well with that inferred from the NMR spectra.
By close inspection of the 1H NMR spectra for PY-P4, PY-P6, PY-P8 and PY-P8-PER in deuterated chloroform (Fig. S11, S15, S19 & S21‡), a pair of resonances at ca. 10.0 and 10.7 ppm was noted and assigned to the N–H proton at the pyrene unit for the PPI and PPII conformational structures, respectively. In the shorter oligomers, each resonance has two closely spaced peaks, consistent with cis–trans isomers at the pyrene-amide bond, as described for PY-P2. The downfield resonance corresponds to cis, while the upfield resonance relates to trans. As illustrated in Fig. S21,‡ the ratio of trans![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cis is around 3
cis is around 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (Keq = 1.5) for PY-P8-PER. When dissolved in the polar solvent D6-DMSO the spectrum is simplified with the downfield resonance reduced in intensity and a more intense signal observed at 10.35 ppm (Fig. S23‡). The trans
2 (Keq = 1.5) for PY-P8-PER. When dissolved in the polar solvent D6-DMSO the spectrum is simplified with the downfield resonance reduced in intensity and a more intense signal observed at 10.35 ppm (Fig. S23‡). The trans![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cis ratio is ca. 47
cis ratio is ca. 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (Keq ∼ 16). This observation is consistent with literature reports that in a polar solvent the trans structure (i.e., PPII) is dominant. It is noted that chemical shifts for the N–H resonance of the cis structure are comparable in CDCl3 and D6-DMSO. In contrast the N–H resonance for the trans structure is shifted upfield by around 0.3 ppm with the increase in solvent polarity. The N–H environment for the pyrene-amide would appear to not alter significantly in the cis structure. The nature of the solvent might influence any internal hydrogen bonding.
3 (Keq ∼ 16). This observation is consistent with literature reports that in a polar solvent the trans structure (i.e., PPII) is dominant. It is noted that chemical shifts for the N–H resonance of the cis structure are comparable in CDCl3 and D6-DMSO. In contrast the N–H resonance for the trans structure is shifted upfield by around 0.3 ppm with the increase in solvent polarity. The N–H environment for the pyrene-amide would appear to not alter significantly in the cis structure. The nature of the solvent might influence any internal hydrogen bonding.
Variable temperature 1H NMR spectra recorded for PY-P8-PER in D6-DMSO (Fig. S23‡) over a temperature range from 298 to 403 K were equally informative. With increasing temperature, the two N–H resonances shift upfield, which is consistent with the shift seen for PY-P2. The ratio PSII![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PSI decreased to around 22
PSI decreased to around 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (Keq ∼ 7) at 353 K. The N–H peak assigned to the trans structure is broadened, and the resonance for the cis structure is indiscernible from the background noise at around 373 K. It is inferred that the two structures are in fast exchange on the NMR timescale at this temperature.
3 (Keq ∼ 7) at 353 K. The N–H peak assigned to the trans structure is broadened, and the resonance for the cis structure is indiscernible from the background noise at around 373 K. It is inferred that the two structures are in fast exchange on the NMR timescale at this temperature.
Molecular structures calculated by DFT (B3LYP/6-311G(d,p)/PCM) methods60 for cis and trans geometries of PY-P2 in CHCl3 are shown in Fig. 1 and key structural information is given in Table 1. Further details are given in the ESI.‡ For the energy-minimised structures, the amide C–N bond is slightly shorter for the cis-isomer while the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond is longer. This suggests that the amide bond possesses somewhat more double-bond character for the cis-geometry.61 This might arise because the connecting Caryl–N bond is slightly shorter for the cis-isomer while the dihedral angle between the polycycle and the amide C–N bond is lower than for the trans-isomer (Table 2). These structural facets, especially the improved planarity, can be used to argue that the cis-isomer interacts more strongly with the polycycle. No internal hydrogen bonds could be detected for either structure. Interestingly, the second amide has the same configuration as the terminal amide, giving rise to trans,trans and cis,cis structures as the energy-minimised species (see ESI, Section S6,‡ for details). Of these, trans,trans is the lowest-energy conformer. The energy difference between trans,trans and trans,cis in CHCl3 solution is only ca. 1.3 kcal mol−1 while that between cis,cis and cis,trans is slightly smaller. The activation barriers for these isomerisation steps in CHCl3 are calculated to lie in the range of 12–15 kcal mol−1.
O bond is longer. This suggests that the amide bond possesses somewhat more double-bond character for the cis-geometry.61 This might arise because the connecting Caryl–N bond is slightly shorter for the cis-isomer while the dihedral angle between the polycycle and the amide C–N bond is lower than for the trans-isomer (Table 2). These structural facets, especially the improved planarity, can be used to argue that the cis-isomer interacts more strongly with the polycycle. No internal hydrogen bonds could be detected for either structure. Interestingly, the second amide has the same configuration as the terminal amide, giving rise to trans,trans and cis,cis structures as the energy-minimised species (see ESI, Section S6,‡ for details). Of these, trans,trans is the lowest-energy conformer. The energy difference between trans,trans and trans,cis in CHCl3 solution is only ca. 1.3 kcal mol−1 while that between cis,cis and cis,trans is slightly smaller. The activation barriers for these isomerisation steps in CHCl3 are calculated to lie in the range of 12–15 kcal mol−1.
| Parameter | PY-P2 | Pyrene | PER | Perylene |
|---|---|---|---|---|
| a Absorption band corresponding to the 0,0 transition. b Absorption maximum used to determine the solute concentration with the molar absorption coefficient (M−1 cm−1) given in parenthesis. c Taken from ref. 68. d Taken from ref. 69. e Taken from ref. 79. f Excited-singlet state lifetime extracted from a mono-exponential fit of the decay data in N2-saturated solution. Values in parenthesis refer to a fit to dual-exponential kinetics. g Triplet-excited state lifetime determined for deoxygenated solutions at low concentrations (<10 μM). h Taken from ref. 81 and 82. | ||||
| λ ABS /nm | 383 | 372 | 443 | 436 |
| λ MAX /nm | 344 (32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300) 300) |
343 (34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700)c 700)c |
NA | NA |
| ε MAX/M−1 cm−1 | 3400 | 330d | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
| λ FLU/nm | 392 | 373 | 460 | 436 |
| ΔSS/cm−1 | 130 | 70 | 830 | <30 |
| ϕ F | 0.60 | 0.58e | 0.91 | 0.87e |
| τ S | 14.5 (11.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16.0)f 16.0)f |
450f | 6.2 (4.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.6)f 6.6)f |
6.0e |
| τ T /μs | 450 | 510 | 690 | 4000h |
Stereochemistry of the polyproline spacer
Polyproline can adopt two disparate structural conformations, commonly referred to as PPI and PPII in solution and the solid state.60 The left-handed PPII structure has a helical pitch of ca. 9.0 Å with 3.0 proline residues per turn and contains all trans amide bonds; this structure is known to dominate in a polar solvent.42,43,45,62 The right-handed PPI structure, comprising all cis amide bonds, is found in less polar solvents and generates a more densely packed helix with a pitch of ca. 5.4 Å, with 3.3 proline residues per turn. A mixture of PPI and PPII structures may exist in weakly polar solvents.63In prior studies it was demonstrated64 that a PPI helix displays a negative CD band at 199 nm, with a stronger positive band at 205–215 nm. In contrast, the PPII helix has a strong negative CD band at 205–210 nm and a weak positive band at 226 nm.64 To probe the helicity of the oligo-proline spacer in PY-P8-PER, CD spectra were recorded in methanol. An example is illustrated in Fig. S50‡ and shows a strong negative band centred at around 212 nm, which is consistent with dominance of the all-trans helix. This finding is in agreement with previous studies demonstrating the stabilisation of the PPII helix in a polar protic solvent.42,65
Calculations made at the DFT (B3LYP/6-311G(d,p)) level for PY-P8-PER in CHCl3 using the PCM treatment indicate that the lowest-energy species has an all-trans alignment of the amide bonds, including the terminal pyrene-amide unit (Fig. 5). This corresponds in a crude sense to the PPII structure with some of the central proline units forming a helix, in accord with the experimental results. This arrangement places the polycycles at a centre-to-centre separation of 19 Å. The lowest energy species with the terminal amide in the cis geometry also has cis-amides at the 3- and 7-sites, with all the other amides in the trans-structure (Fig. 5). This species is less stable than the all-trans arrangement by ca. 2 kcal mol−1 and has the polycycles at a separation distance of only 15 Å (Fig. 5). A further stable structure starts with the trans,cis species, followed by an all-trans chain (Fig. S65‡). Random conformer searches, using the Monte Carlo random searching algorithm and the MMFF94 force field implemented in Spartan™ indicated that the all-cis-isomer was not to be found among the 25 lowest-energy structures. Indeed, most cis-amides occur at the 1-(i.e., the pyrene amide) or 3-sites (Fig. S63 & S64‡).
Photophysical properties of the pyrene-based terminal
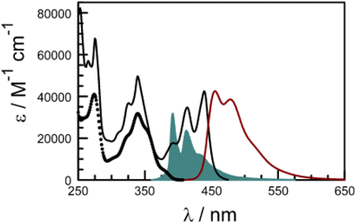
The photophysical properties of pyrene depend on the polarity of the solvent,52,66 as well as solute concentration,67 and the nature of any substituents.68 This sensitivity arises because the energy of the 1Lb state, which is below that of the 1La state, can be perturbed by structural and/or environmental changes. Most literature reports refer to the absorption band centred at around 344 nm and avoid the lower-energy transitions occurring across the wavelength range from 350 to 380 nm, where absorption is very weak (Fig. S34‡). Hara and Ware69 located the 0,0 transition as being at 372 nm with a molar absorption coefficient of 330 M−1 cm−1. To explore the effect of the amide connection on the optical properties of the pyrene chromophore, we synthesized the control compound PY-P2, which has an amide connection via the nitrogen atom at the pyrene nucleus, together with two proline residues (Scheme 1).Absorption and emission spectra were recorded for dilute CHCl3 solutions (Fig. 6) and the respective maxima (λABS and λFLU) are listed in Table 2. The lowest energy absorption transition for PY-P2 is weak but significantly stronger than that reported for pure pyrene. The 0,0 transition is located at 383 nm, corresponding to a red shift of ca. 770 cm−1 relative to pyrene under the same conditions, where the molar absorption coefficient (ε) is 3400 M−1 cm−1. At higher energy, there is a more intense absorption transition, centred at 344 nm (εMAX = 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 M−1 cm−1) which remains comparable to that found for pure pyrene. The fluorescence spectrum is resolved into vibronic components but there is little mirror symmetry with the corresponding absorption transition. The Stokes shift (ΔSS) is small and signifies that only minor geometry changes accompany evolution of the relaxed excited-singlet state while excellent agreement was observed between excitation and absorption spectra (Fig. 6). The fluorescence quantum yield (ϕF) and excited-singlet state lifetime (τS) were recorded for dilute, deoxygenated CHCl3 solutions and are also given in Table 2. Relative to pure pyrene in dilute solution, the quantum yield and lifetime recorded for PY-P2 are decreased somewhat. It was noted that the reduced chi-squared parameter (χ2 = 1.33), used as a primary indicator of the quality of the statistical fit for the lifetime,70 is too high for a satisfactory analysis (Fig. S39‡). A much improved fit (χ2 = 1.16) was obtained using a dual-exponential model71 with the longer-lived species accounting for 63% of the initial population (Table 2 and Fig. S40‡). The two derived lifetimes, however, are too similar for accurate analysis and should be taken cautiously. The mean excited-state lifetime (〈τ〉) for the pyrene donor is 14.2 ± 0.6 ns.
300 M−1 cm−1) which remains comparable to that found for pure pyrene. The fluorescence spectrum is resolved into vibronic components but there is little mirror symmetry with the corresponding absorption transition. The Stokes shift (ΔSS) is small and signifies that only minor geometry changes accompany evolution of the relaxed excited-singlet state while excellent agreement was observed between excitation and absorption spectra (Fig. 6). The fluorescence quantum yield (ϕF) and excited-singlet state lifetime (τS) were recorded for dilute, deoxygenated CHCl3 solutions and are also given in Table 2. Relative to pure pyrene in dilute solution, the quantum yield and lifetime recorded for PY-P2 are decreased somewhat. It was noted that the reduced chi-squared parameter (χ2 = 1.33), used as a primary indicator of the quality of the statistical fit for the lifetime,70 is too high for a satisfactory analysis (Fig. S39‡). A much improved fit (χ2 = 1.16) was obtained using a dual-exponential model71 with the longer-lived species accounting for 63% of the initial population (Table 2 and Fig. S40‡). The two derived lifetimes, however, are too similar for accurate analysis and should be taken cautiously. The mean excited-state lifetime (〈τ〉) for the pyrene donor is 14.2 ± 0.6 ns.
At high concentrations (>5 mM) in nonpolar solvents, pyrene forms an emissive excimer,72 which in CHCl3 solution emits at 485 nm (Fig. S37‡). This latter species, which also forms in crystals73 and condensed films,74 has been exploited as the basis of numerous disparate types of fluorescent sensor.75 In thin films, the excimer transfers excitation energy to perylene present as a dopant.74 Under similar conditions, PY-P2 shows strong self-absorption, most notably by the extinction of the emission band centred at 392 nm, but does not form an emissive excimer in observable yield (Fig. S37‡). This situation is most likely a consequence of steric blocking by the bis-proline residue preventing π-stacking of two polycycles.
Excitation of deoxygenated ethanol solutions of PY-P2 with a 4 ns laser pulse at 340 nm results in formation of the triplet-excited state, which shows a prominent differential absorption peak at ca. 425 nm.76 Less significant absorption transitions are seen at longer and shorter wavelengths (Fig. S38‡). The triplet state is quenched by molecular oxygen and undergoes bimolecular annihilation at high laser intensity (Fig. S40‡).77 At low intensity, in the absence of oxygen, the triplet state decays via first-order kinetics with a lifetime of 450 μs in dilute solution (Fig. S39‡). The fit to a first-order process is satisfactory but the derived lifetime is comparable to the interconversion time estimated from the Eyring expression so that the exponential kinetics do not rule out there being an equilibrium mixture of cis and trans isomers. Phosphorescence spectra recorded78 in an ethanol glass at 77 K allow estimation of the triplet energy as being 48 kcal mol−1 (i.e., 595 nm), which is slightly lower than that observed for pure pyrene under the same conditions.
The net conclusion is that the proline residue, and in particular the amide group, impacts somewhat on the photophysical properties of the pyrene chromophore, especially affecting the radiative rate constant. The low energy region of the absorption spectrum is intensified by way of increased mixing with the higher-lying state. The main consequence of such perturbations is that pure pyrene cannot be used as a reference compound for the EET donor. Furthermore, the apparent co-existence of two isomers is likely to complicate the dynamics of the EET event.
The perylene terminal in the dyad
Rather than use a further control compound to mimic the behaviour of the perylene terminal, it is possible to directly excite the latter and thereby bypass any EET events. Indeed, the absorption spectrum recorded for the dyad in dilute CHCl3 solution shows well-resolved transitions at λ > 400 nm which can be attributed entirely to the perylene-based chromophore (Fig. 7). There is a modest red shift of ca. 360 cm−1 for the 0,0 transition relative to pure perylene (Table 2), which can be explained in terms of increased conjugation with the appended carbonyl group. The molar absorption coefficient measured at the maximum amounts to 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 M−1 cm−1, which is similar to that reported79 for pure perylene. Fluorescence is readily detected following excitation at 420 nm and shows fine structure (Fig. 7). There is reasonable mirror symmetry with the corresponding absorption transition and a small Stokes shift (Table 2). The fluorescence quantum yield was determined to be 0.91 ± 0.05 in deoxygenated CHCl3, compared to a value of 0.87 for pure perylene under the same experimental conditions.
500 M−1 cm−1, which is similar to that reported79 for pure perylene. Fluorescence is readily detected following excitation at 420 nm and shows fine structure (Fig. 7). There is reasonable mirror symmetry with the corresponding absorption transition and a small Stokes shift (Table 2). The fluorescence quantum yield was determined to be 0.91 ± 0.05 in deoxygenated CHCl3, compared to a value of 0.87 for pure perylene under the same experimental conditions.
Time-resolved fluorescence studies with excitation at 440 nm allowed determination of the lifetime for the perylene-based excited-singlet state as being 6.2 ± 0.3 ns. Here, the decay profile gave a poor fit to a single-exponential process (χ2 = 1.45), as judged70,71,80 by the quality of the weighted residuals and their autocorrelation (Fig. S47‡). Again, a much improved fit (χ2 = 1.27) was obtained using a dual-exponential model, although the fit is still unsatisfactory (Fig. S48‡). An interesting result from this analysis is that there is a significant increase in the Stokes shift for the dyad relative to pure perylene (Table 2). This informs us that excitation of the perylene unit is followed by a some kind of geometrical relaxation in solution.
It is well known81 that intersystem crossing is quite inefficient for pure perylene, although the triplet state has been observed with an absorption maximum at ca. 515 nm and with a lifetime of ca. 4 ms.81 Laser excitation of the dyad at 420 nm, where only perylene absorbs, gave a weak transient absorption signal, centred at 520 nm (Fig. S41‡), which decayed via first-order kinetics with a lifetime of 690 μs in deoxygenated solution (Fig. S42‡). This signal is attributed to the perylene triplet-excited state. At higher laser intensities, the decay profile shows an increasing contribution from a second-order process occurring on short timescales which can be assigned to bimolecular triplet–triplet annihilation (Fig. S42‡). Indeed, both pure perylene and the perylene component of the dyad display P-type delayed fluorescence76,81 in deoxygenated fluid solution.
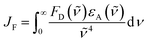 | (1) |
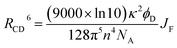 | (2) |
Electronic energy transfer
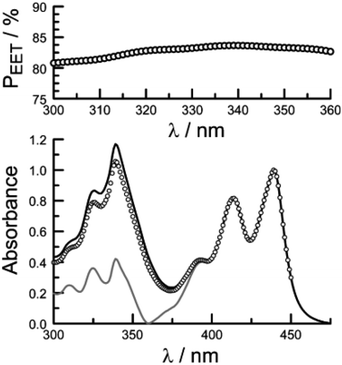
There is a thermodynamic gradient amounting to ca. 3350 cm−1 that favours EET from the singlet-excited state of pyrene to perylene in PY-P8-PER. The spectral overlap integral (JF) accompanying EET was calculated82 from eqn (1) where FD refers to the fluorescence spectrum for the pyrene donor recorded in wavenumbers and with the total intensity normalised to unity. The term εA refers to the molar absorption coefficient for the perylene acceptor with the integral being compiled between 350 and 550 nm (Fig. S44‡). The derived value, JF = 3.0 × 10−14 mmol−1 cm6, is somewhat higher than found50 for related compounds, reflecting the minor spectral shifts and broadening. With this value, eqn (2) can be used to calculate the Förster critical distance51 (RCD) for random orientations (κ2 = 0.67) of the two chromophores. Here ϕD refers to the fluorescence quantum yield for the isolated donor, n is the refractive index of the surrounding medium and NA is Avogadro's constant. The derived value is 25.4 ± 1.0 Å.Comparison of absorption spectra recorded for PY-P2 and PY-P8-PER indicates that the pyrene unit can be preferentially, but not exclusively, excited at wavelengths between 310 and 360 nm. For example, pyrene accounts for ca. 70% of the excitation intensity at 350 nm. Emission spectra recorded for PY-P8-PER in dilute methanol solution, with excitation at 350 nm, show contributions from both fluorophores, although the relative yield for perylene emission far outweighs that for pyrene. This situation is fully consistent with EET along the molecular axis, as has been demonstrated48–50 for other molecular dyads bearing the same terminals. Several methods can be used to determine the probability (PEET) for intramolecular EET in this system, while working with dilute (<2 μM) solutions ensures the absence of complications from bimolecular EET.
Firstly, excitation spectra are compared with absorption spectra recorded for PY-P8-PER in dilute solution.83 The excitation spectra were recorded by monitoring emission at 525 nm with a 1 nm slit. The absorption spectrum was recorded at the same resolution but it was still necessary to allow for a minor spectral shift to obtain accurate alignment of the peaks. The two spectra were normalised at the peak of the perylene absorption. At a qualitative level, it is apparent that photons absorbed by the pyrene chromophore lead to emission from the perylene unit since the excitation spectrum shows a clear peak centred around 340 nm. A quantitative comparison requires knowledge of the absorption spectrum for the perylene chromophore across the near-UV region. This was obtained by subtracting the spectrum for PY-P2 from that of PY-P8-PER recorded under identical conditions and adjusting to give a smooth profile. The perylene spectrum corresponds to the case where there is no EET while the absorption spectrum of the dyad corresponds to quantitative EET (Fig. 8). The excitation spectrum closely resembles the absorption spectrum of the dyad. At any given wavelength, PEET can be obtained from eqn (3) where AEX(λ), ADY(λ) and APE(λ) refer, respectively to the intensity of the excitation spectrum, the absorption spectrum measured for the dyad and the derived absorption spectrum for the perylene chromophore (Fig. 7). The mean PEET obtained in his way for PY-P8-PER in CHCl3 is 83 ± 2%. Repeating the procedure for methanol (PEET = 90 ± 4%), propan-1-ol (PEET = 85 ± 4%) and diethylether (PEET = 90 ± 6%) shows that the nature of the solvent has only a modest effect on the overall efficacy of the EET process.
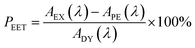 | (3) |
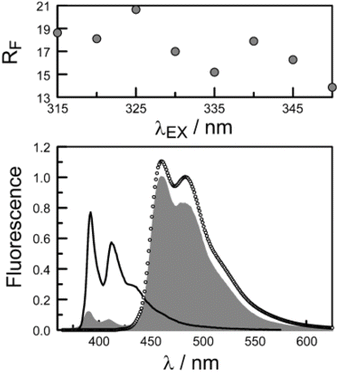
The second protocol used to determine PEET involves measuring the ratio (RF) of fluorescence signals attributable to each of the terminals following preferential excitation into the pyrene chromophore. In this case, it is necessary to know the fraction (α) of excitation light absorbed by the pyrene chromophore. The respective emission signals are obtained by integration between 350 and 440 nm for pyrene and between 450 and 550 nm for perylene (Fig. 9). The required probability is obtained from eqn (4) where ϕD and ϕA refer, respectively, to the fluorescence quantum yields for the isolated pyrene donor and the isolated perylene acceptor. Using a few different excitation wavelengths, the mean PEET derived for PY-P8-PER in chloroform was found to be 85 ± 4%. This is in excellent agreement with that obtained from the excitation spectrum. Similar values were obtained for methanol (PEET = 89 ± 3%), propan-1-ol (PEET = 84 ± 4%) and diethylether (PEET = 88 ± 6%) solutions; note, in the latter case, the dyad shows limited solubility.
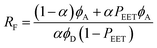 | (4) |
The derived PEET values are insensitive to the polarity and/or proticity of the solvent. At first sight, this might appear to be unexpected since the global structure of polyproline residues is known to be dependent on the nature of the solvent. However, there are certain conditions associated62–65 with such effects, most notably the need for a sufficient number of unsubstituted proline residues in the chain,53 while the presence of bulky terminals might add a further barrier to internal rotation. The rate of intramolecular EET for a through-space mechanism is known82 to be highly sensitive to the separation distance and to the mutual orientation of the chromophores. Comparison of the derived PEET values with the Förster critical distance indicates that the mean separation distance (r) between the terminals is ca. 19 Å (eqn (5)), assuming random orientation of the transition dipole moment vectors. Furthermore, the CD results (Fig. S50‡) indicate that an important fraction of the oligo-proline spacer adopts the PPII structure, which is believed64,65 to be relatively rigid in solution. This latter result is in line with the DFT calculations, which predict a major contribution from the all-trans chain. The calculations have not identified a significant fraction of the all-cis species and instead indicate that the cis-amide occurs only at a few sites along the chain. The net effect seems to be a restricted range of geometries. To examine this conclusion in more detail, time-resolved fluorescence studies were made with PY-P8-PER in solution.
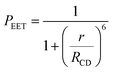 | (5) |
These latter measurements were made by time-correlated, single photon counting (TCSPC) with excitation at 330 nm. The temporal resolution of the set-up was ca. 300 ps after deconvolution of the instrument response function. Emission from pyrene could be isolated in the region of 410 nm while perylene fluorescence dominates the signal at longer (λ > 450 nm) wavelengths. Initial studies were made for PY-P8-PER in CH3OH solution, where the NMR studies predict a dominant role (i.e., ca. 90%) for the trans-isomer; we emphasise here that reference to cis or trans isomers concerns only the amide bond connected directly to the pyrene chromophore unless stated otherwise.
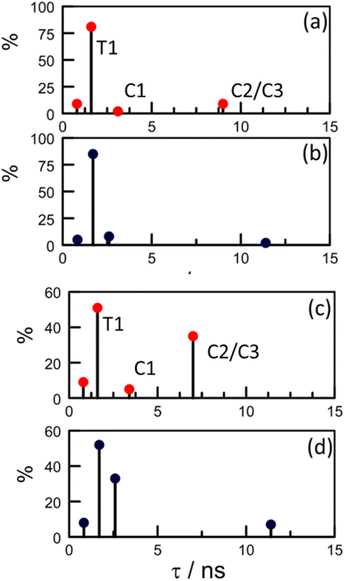
Focussing on the pyrene-based donor, the decay profile was clearly non-exponential and therefore was treated initially as the sum of exponentials (eqn (6)). Here, IF refers to the fluorescence intensity and t is the time delay from the start pulse. Analysis considers a series of j exponential decays, each with a fractional amplitude Aj and a lifetime τj. The amplitude weighted lifetime (〈τ〉) can be obtained from eqn (7). Fitting the data to dual-exponential kinetics allowed estimation of 〈τ〉 as being 2.1 ± 0.2 ns, but the quality of the fit was poor (χ2 = 1.48; Fig. S69‡). The same analysis applied to emission from the perylene unit gave 〈τ〉 as being 7.40 ± 0.09 ns (χ2 = 1.44; Fig. S49‡). Apart from the limited statistical fit, a second issue with this analysis is that the two derived lifetimes are too similar for comfort (Table 3) and, in fact, the derived parameters were found to be sensitive to the total number of counts in the peak channel (CPC) (Fig. S69–S71‡).
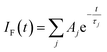 | (6) |
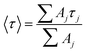 | (7) |
| Species | Solvent | DEb | Restrictedc | Initiald | Refinede |
|---|---|---|---|---|---|
| a All values are given in ns. The value given in parenthesis refers to the fractional contribution of that species. b Fit to dual-exponential kinetics. c Predicted values using only T1 and C1 to represent the molecular structure. d Distributive model using four lifetimes but with fixed parameters as listed in Table S6. e Distributive model using four lifetimes but allowing for stepwise optimisation. f Mean lifetime calculated from eqn (7). | |||||
| T1 | CH3OH | 1.6 (94%) | 1.7 (90%) | 1.7 (85%) | 1.6 (81%) |
| T2 | NA | NA | 0.83 (5%) | 0.8 (9%) | |
| C1 | 9.8 (6%) | 2.6 (10%) | 2.6 (8%) | 3.1 (2%) | |
| C2/3 | NA | NA | 11.4 (2%) | 9.0 (8%) | |
| 〈τ〉f | 2.1 | 1.8 | 1.9 | 2.0 | |
| T1 | CHCl3 | 2.0 (79%) | 1.7 (60%) | 1.7 (52%) | 1.6 (51%) |
| T2 | NA | NA | 0.83 (8%) | 0.8 (9%) | |
| C1 | 11.5 (21%) | 2.6 (40%) | 2.6 (33%) | 3.4 (5%) | |
| C2/3 | NA | NA | 11.4 (7%) | 7.0 (35%) | |
| 〈τ〉f | 4.0 | 2.1 | 2.6 | 3.5 | |
The same analysis made for PY-P8-PER in dilute CHCl3 solution, where the NMR studies indicate a mixture of trans and cis species with a slight preference for the trans-isomer, gave an unacceptable fit to dual-exponential kinetics (Fig. S72‡) and the derived lifetimes are again sensitive to the CPC (Fig. S72 & S73‡). In this case, the mean lifetime (〈τ〉 = 4.0 ± 0.18 ns) is longer than found for CH3OH, seemingly in agreement with the derived PEET values. Adding a further exponential component serves no useful purpose other than to improve the quality of the statistical fit, especially since it would need to be of similar magnitude to those already used. This situation has been encountered before by other researchers, starting with Ware et al.84 in the 1970's, and has led to the development of system-specific models.85 In our case, it was considered that the system might be better treated in terms of the computed molecular structure, assuming the cis- and trans-isomers are non-interconverting species on this timescale. The NMR studies made in CH3OH indicate a preference for the all-trans conformation but there is more structural diversity in CHCl3. Consequently, the quantum chemical studies (DFT/B3LYP/6-311G(d,p)/PCM) were applied to CHCl3 solutions (see ESI‡).
In the first instance, we considered only the lowest-energy cis- and trans-isomers and used the computed structures to calculate expected lifetimes. Thus, the centre-to-centre separation distances (r) are 19.06 Å and 14.61 Å, respectively, for trans- and cis-structures while the FRET orientation factors (κ2) for the static structures are 1.15 ± 0.05 and 0.08 ± 0.03, respectively (Fig. S57, S61 & S62‡). Using this information, the rate constant (kF) for intramolecular EET can be calculated from eqn (8) for each of the two conformers (Table S6‡).
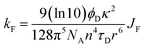 | (8) |
This simple analysis indicates that EET is less efficacious for the cis-isomer, despite the shorter r, because of the unfavourable orientation factor, but the actual disparity in kF is modest. Now, we can use the NMR results to establish the ratio of isomers present in each solvent at equilibrium and thereby predict 〈τ〉 values. For methanol, where the TCSPC data give a 〈τ〉 value of 2.1 ± 0.2 ns and NMR estimates K ≈ 9, we predict 〈τ〉 as being 1.8 ± 0.2 ns (Table 3). For CHCl3 (K ≈ 1.5) we obtain a 〈τ〉 value of 2.1 ± 0.2 ns compared to a value of 4.0 ± 0.2 ns from the dual-exponential fits (Table 3). Overall, this level of agreement is reasonable, implying that the computed structures are realistic. However, attempts to simulate the experimental decay curves using only these two structures were far from convincing, especially at longer delay times. Clearly, more species are involved!
The structural calculations project a significant contribution from a conformer having a cis-amide at the second site and with all other amides in the trans geometry (Fig. S65‡). This species has a total energy only 1–2 kcal mol−1 higher than that of the lowest energy all-trans species (T1): we refer to this new conformer as T2. Interconversion between T1 and T2 requires cis–trans isomerisation and is expected to be relatively slow but, on energetic grounds, it seems likely that T2 could contribute up to 20% of the total trans-family. The main consequence of the cis-amide at the 2-site is to fold back the pyrene unit such that r is shortened to 14.7 Å but there is a corresponding decrease in κ2 to 0.33 (Fig. S65–S68‡). The net result is that EET for T2 is expected to be somewhat faster (kF = 12 × 108 s−1) than for either T1 or C1.
The DFT calculations project the possible involvement of two additional conformers having a cis-amide at the pyrene terminal (Table 3). Both species possess an all-trans oligo-proline chain but differ in the mutual arrangement of the polycycles. The first such structure (C2; Fig. S63‡), which is ca. 2 kcal mol−1 less favourable than C1, has r ≈ 25.6 Å and returns a kF value of 0.88 × 108 s−1 (Table 3). The second species (C3; Fig. S64‡) has r ≈ 23.1 Å and gives a kF value of 0.55 × 108 s−1. Since these latter cis-species give similar kF values and are expected to be minor contributors in methanol, averaged values were used for the simulations.
Effectively, this approach doubles the number of parameters by which to simulate the experimental decay curves (Table S6‡), meaning that constraints have to be imposed. Thus, the structural landscape for PY-P8-PER in methanol is dominated by trans species. This is significant because the oligo-proline chain adopts the PPII structure, which is relatively stiff and might be expected to minimise structural fluctuations. The starting parameters for simulation of the pyrene emission decay kinetics retained the kF values calculated from the structural information (Table 3) and imposed a total trans composition of 90%. The fractional contribution of T1 was held at 85% while C2/C3 was assigned a minor role (Table S6‡). The simulated profile was obtained by convolution of these four lifetimes with an experimental instrument response function.84 After the initial minimisation, optimisation allowed the sets of parameters to vary but retaining the ratio of trans- to cis-species (Fig. S74–S76‡). The net result is an excellent fit to the experimental data with the revised parameters shown in Scheme 2. The derived 〈τ〉 is 2.0 ± 0.2 ns, which can be compared to that extracted from dual-exponential fits, where 〈τ〉 was found to be 2.3 ± 0.24 ns (Table 3).
Our NMR data obtained for CHCl3 solutions infer a significantly increased population of cis-amides and this is reflected in the starting parameters for the kinetic simulations (Table S6‡). Unlike with CH3OH, optimisation leads to a marked change in the composition and, in particular, serves to minimise the contribution of C1. Now, the cis-family is dominated by the longer-lived C2/C3 species at the expense of C1 (Scheme 2). Interestingly, the impact of T2 remains similar to that deduced for CH3OH solution but the fractional contribution of T1 falls precipitously (Table 3 and Scheme 2). After optimisation, 〈τ〉 adopts a value of 3.5 ± 0.2 ns, compared to that derived from dual-exponential fits, where 〈τ〉 is 4.1 ± 0.18 ns.
In methanol, optimisation has little effect on the lifetimes of individual species and the most significant change is the increased contribution from C2/C3 at the expense of C1 (Scheme 2). The fit is somewhat insensitive to the ratio of the trans-species such that the final composition is not particularly well defined. In CHCl3, the lifetime of C2/C3 is roughly half that predicted from the DFT structures while its relative concentration is amplified by a factor of 5-fold. The effect of moving from methanol to chloroform can be rationalised in terms of T1 being transformed into C2/C3, which would only require isomerisation at the pyrene terminal. This seems to be the only viable isomerisation available to PY-P8-PER in solution at ambient temperature.
There is a considerable gradient favouring triplet–triplet EET from pyrene to perylene, although such processes usually occur via an electron exchange mechanism86 requiring either orbital contact between the reactants or short-range super-exchange interactions.87 To eliminate the possibility of closely interacting pairs of reactants, we carried out a series of transient absorption spectral studies using 4 ns laser excitation at 340 nm. Under such conditions, with PY-P8-PER dissolved in deaerated methanol, the pyrene triplet-excited state could be detected through the appearance of the characteristic absorption band centred at 425 nm. This signal decayed via first-order kinetics with a lifetime of 415 ± 25 μs to restore the prepulse baseline (Fig. S43‡). No other transient species could be detected on the μs timescale and there is no corresponding signal in the region of 520 nm that could safely be attributed to the perylene triplet. Thus, triplet–triplet energy transfer does not occur within this system. This finding is fully consistent with a situation where the terminals are kept spatially isolated by the oligo-proline connector.
Conclusions
Our long-term ambition is to construct artificial light-harvesting antennae88 based on polyproline spacer units. These spacers need to provide structural integrity without affecting the opto-electronic properties of the light-active components or interfering with the EET events. Both the latter requisites are met by the proline octamer studied here. Furthermore, the mean PEET and RCD values can be tuned over a modest range by changing the nature of the chromophores. The main challenge, however, is controlling the rigidity of the spacer, especially in the vicinity of the chromophores. This situation is exacerbated by the observed stabilisation of the cis-isomer with weakly polar solvents such as CHCl3. On the other hand, the all-trans geometry (T1) abounds in methanol solution and the structure can be accurately modelled by DFT calculations. Here, the level of agreement between experimental and calculated EET parameters is extremely good for separation distances in the region of 20 Å. We have observed that the all-trans chain can be perturbed by inclusion of a cis-amide at either the 1 (i.e., terminal pyrene connection; C2 and C3) or 2-sites (T2). These latter conformers make a relatively minor contribution to the total population in polar solvents but provide for disparate rates of EET. Their involvement is problematic in terms of establishing a molecular ruler. However, by way of an entirely fortuitous situation, they tend to cancel out each other by returning an average lifetime not too dissimilar to that of the all-trans species. Their presence is noted only in terms of the quality of the statistical fit of the kinetic data.Our calculations do not assign a role for the corresponding all-cis species and instead the maximum contribution for cis-geometries amounts to three out of nine amides. This arrangement (C1) provides a favourable architecture for fast EET by bringing the terminals into relatively close proximity. During optimisation of the distributive model, the composition of the cis-family shifts in favour of those conformers having a single cis-amide at the pyrene connection. This allows the “tail” of the decay function to be modelled more accurately since these mono-cis structures are less amenable for intramolecular EET. In fact, the geometry of the pyrene-based amide has a significant effect on the rate of ETT and, as such, the use of polyproline spacers45,47 to validate “molecular rulers” is predicated on the availability of the all-trans chain.
This investigation introduces a new type of system-specific model by which to interpret the EET parameters. The strength of the model is the integration of NMR structural information with quantum chemical calculations. Rather than attempt to compute molecular structures in different solvents, we have relied on calculations made in CHCl3 where earlier studies have obtained good agreement between crystal structures and computed geometries for bis-proline residues.88 Refinement of the data analysis allows the composition to vary but retains the same structures. For this situation to hold, the overall geometry must be quite stiff and this is likely to be true, at least for methanol solution where the trans geometry abounds and the CD spectrum indicates helicity.
Data availability
Full details concerning synthesis and characterisation of new materials, including X-ray crystallography, are provided as part of the ESI‡ package. Steady-state and time-resolved fluorescence data are also given in the ESI,‡ together with examples of the transient absorption spectral studies. Details on the computational studies, including cartesian coordinates for key structures, are contained within the ESI.‡ Further information regarding data analysis is available from the corresponding author upon reasonable request.Author contributions
This work forms part of the Doctoral Thesis for SMAW, who performed most of the experimental work under the joint supervision of ACB and AH. ACB designed the NMR studies and was instrumental in subsequent data analysis. SMAW designed the optical spectroscopic studies and performed the relevant experiments. AH developed the distributive model and carried out the simulations. AH wrote the first version of the manuscript. All authors contributed towards preparation of subsequent drafts of the manuscript. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Newcastle University for financial support of this work. The authors express their gratitude to Dr Corinne Y. Wills (Newcastle University) and Dr Casey Dixon (Newcastle University) for advice concerning the NMR studies. The X-ray crystal structure for PY-P2 was determined by Dr Paul G. Waddell (Newcastle University) while Dr Joshua K. G. Karlsson (Newcastle University) made some of the preliminary photophysical studies with the dyad. The CD spectrum was recorded in The School of Medical Sciences at Newcastle University. The EPSRC Mass Spectrometry Unit at Swansea University is acknowledged for accurate mass measurements for all newly synthesized compounds. SMAW thanks Newcastle University (NOURS), the Newton-Mosharafa Fund, and Damietta University for financial support and for the award of a Research Studentship.References
- J. Daub, R. Engl, J. Kurzawa, S. E. Miller, S. Schneider, A. Stockmann and M. R. Wasielewski, J. Phys. Chem. A, 2001, 105, 5655–5665 CrossRef CAS; A. A. Lukas, P. J. Bushard, W. A. Weiss and M. R. Wasielewski, J. Am. Chem. Soc., 2003, 125, 3921–3930 CrossRef PubMed; M. R. Wasielewski and M. P. Niemczyk, J. Am. Chem. Soc., 1984, 106, 5043–5045 CrossRef; G. L. Closs and J. R. Miller, Science, 1988, 240, 440–447 CrossRef PubMed.
- M. Kloz, S. Pillai, G. Kodis, D. Gust, T. A. Moore, A. L. Moore, R. van Grondelle and J. T. M. Kennis, Chem. Sci., 2012, 3, 2052–2061 RSC; P. N. Liao, S. Pillai, D. Gust, T. A. Moore, A. L. Moore and P. Walla, J. Phys. Chem. A., 2011, 115, 4082–4091 CrossRef CAS PubMed; D. Kuciauskas, S. Lin, G. R. Seely, A. L. Moore, T. A. Moore, D. Gust, T. Drovetskaya, C. A. Reed and P. D. W. Boyd, J. Phys. Chem., 1996, 100, 15926–15932 CrossRef; J. L. Bahr, G. Kodis, L. de la Garza, S. Lin, A. L. Moore, T. A. Moore and D. Gust, J. Am. Chem. Soc., 2001, 123, 7124–7133 CrossRef PubMed.
- T. Kim, J. Kim, H. Mori, S. Park, M. Lim, A. Osuka and D. Kim, Phys. Chem. Chem. Phys., 2017, 19, 13970–13977 RSC; N. Aratani, D. Kim and A. Osuka, Acc. Chem. Res., 2009, 42, 1922–1934 CrossRef CAS PubMed; S. Cho, M. C. Yoon, J. M. Lim, P. Kim, N. Aratani, Y. Nakamura, T. Ikeda, A. Osuka and D. Kim, J. Phys. Chem. B, 2009, 113, 10619–10627 CrossRef PubMed; T. Asahi, M. Ohkohchi, R. Matsusaka, N. Mataga, R. P. Zhang, A. Osuka and K. Maruyama, J. Am. Chem. Soc., 1993, 115, 5665–5674 CrossRef.
- D. M. Guldi, Chem. Soc. Rev., 2002, 31, 22–36 RSC; D. M. Guldi and V. Sgobba, Chem. Commun., 2011, 47, 606–610 RSC; K. Li, D. I. Schuster, D. M. Guldi, M. A. Herranz and L. Echegoyen, J. Am. Chem. Soc., 2004, 126, 3388–3389 CrossRef CAS PubMed; J. Zirzlmeier, D. Lehnherr, P. B. Coto, E. T. Chernick, R. Casillas, B. S. Basel, M. Thoss, R. R. Tykwinski and D. M. Guldi, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5325–5330 CrossRef PubMed; I. Papadopoulos, J. Zirzlmeier, C. Hetzer, Y. J. Bae, M. D. Krzyaniak, M. R. Wasielewski, T. Clark, R. R. Tykwinski and D. M. Guldi, J. Am. Chem. Soc., 2019, 141, 6191–6203 CrossRef PubMed.
- V. Goulle, A. Harriman and J.-M. Lehn, J. Chem. Soc., Chem. Commun., 1993, 1034–1036 RSC; A. M. Brun, A. Harriman, V. Heitz and J.-P. Sauvage, J. Am. Chem. Soc., 1991, 113, 8657–8663 CrossRef CAS; V. Heitz, S. Chardon-Noblat and J.-P. Sauvage, Tetrahedron, 1991, 97, 5940–5944 Search PubMed; A. Harriman and R. Ziessel, Chem. Commun., 1996, 1707–1716 RSC; J. L. Sessler, B. Wang and A. Harriman, J. Am. Chem. Soc., 1995, 117, 704–714 CrossRef.
- M. P. Irvine, R. J. Harrison, G. S. Beddard, P. Leighton and J. K. M. Sanders, Chem. Phys., 1986, 104, 315–324 CrossRef CAS.
- G. L. Closs, L. T. Calcaterra, N. J. Green, K. W. Penfield and J. R. Miller, J. Phys. Chem., 1986, 90, 3673–3683 CrossRef CAS; M. R. Wasielewski, M. P. Niemczyk, W. A. Svec and E. B. Pewitt, J. Am. Chem. Soc., 1985, 107, 1080–1082 CrossRef; M. R. Wasielewski, Chem. Rev., 1992, 104, 435–445 CrossRef.
- M. Bixon and J. Jortner, J. Phys. Chem., 1991, 95, 1941–1944 CrossRef CAS; M. Bixon and J. Jortner, J. Phys. Chem., 1993, 97, 13061–13066 CrossRef.
- R. Ziessel, C. Goze, G. Ulrich, M. Cesario, P. Retaiileau, A. Harriman and J. P. Rostron, Chem.–Eur. J., 2005, 11, 7366–7378 CrossRef CAS PubMed; D. Bai, A. C. Benniston, J. P. Hagon, H. Lemmetyinen, N. V. Tkachenko, W. Clegg and R. W. Harrington, Phys. Chem. Chem. Phys., 2012, 14, 4447–4456 RSC.
- A. Cravcenco, C. Ye, J. Grafenstein and K. Borjesson, J. Phys. Chem. A, 2020, 125, 7219–7227 CrossRef CAS PubMed; C. A. Nijhuis, Z. Zhang, F. Adoah, C. Nickle, S. K. Karuppannan, L. Wang, J. Li, A. Tadich, B. Cowie, T. Salim, D. C. Qi, D. Thompson and E. D. Barco, Adv. Electron. Mater., 2023, 9, 2200637 CrossRef; J. Wang, T. Ding, K. Gao, L. Wang, P. Zhou and K. Wu, Nat. Commun., 2021, 12, 6333 CrossRef PubMed; D. V. Matyushov, Phys. Chem. Chem. Phys., 2023, 25, 7589–7610 RSC; E. Sobakinskaya, M. S. A. Busch and T. Renger, J. Phys. Chem. B, 2018, 122, 54–67 CrossRef PubMed; R. Ziessel, M. A. H. Alamiry, K. J. Elliott and A. Harriman, Angew. Chem., Int. Ed. Engl., 2009, 121, 2810–2814 CrossRef.
- C. P. Hsu, Z. Q. You and H. C. H. Chen, J. Phys. Chem. C, 2008, 112, 1204–1212 CrossRef CAS; S. Cho, D. Kim, H. Sumi and A. Osuka, J. Am. Chem. Soc., 2003, 125, 9668–9681 CrossRef PubMed; M. P. Debreczeny, M. R. Wasielewski, S. Shinoda and A. Osaka, J. Am. Chem. Soc., 1997, 119, 6407–6414 CrossRef.
- H. Sahoo, D. Roccatano, A. Hennig and W. Nau, J. Am. Chem. Soc., 2007, 129, 9762–9772 CrossRef CAS PubMed; M. E. Madjet, F. Muh and T. Renger, J. Phys. Chem. B, 2009, 113, 12603–12614 CrossRef PubMed; P. Brodard, S. Matzinger, E. Vauthey, O. Mongin, C. Papamicael and A. Gossauer, J. Phys. Chem. A, 1999, 103, 5858–5870 CrossRef.
- M. I. S. Rohr, H. Marciniak, J. Hoche, M. H. Schreck, H. Ceymann, R. Mitric and C. Lambert, J. Phys. Chem. C, 2018, 122, 8082–8093 CrossRef CAS; C. Lambert, T. Scherpf, H. Ceymann, A. Schmiedel and M. Holzapfel, J. Am. Chem. Soc., 2015, 137, 3547–3557 CrossRef PubMed; U. Selig, P. Nuernberger, V. Dehm, V. Settels, M. G. Sanger, B. Engels, F. Würthner and T. Brixner, ChemPhysChem, 2013, 14, 1413–1433 CrossRef PubMed; K. J. Thorley and F. Würthner, Org. Lett., 2012, 14, 6190–6193 CrossRef PubMed; P. Stachelek and A. Harriman, J. Phys. Chem. A, 2016, 120, 8104–9113 CrossRef PubMed.
- J. Chen, M. Kuss-Petermann and O. S. Wenger, Chem.–Eur. J., 2014, 20, 4098–4104 CrossRef CAS PubMed.
- L. Kortekaas, J. D. Steen, D. R. Duijnstee, D. Jacquemin and W. R. Browne, J. Phys. Chem. A, 2020, 124, 6458–6467 CrossRef CAS PubMed; X. D. Liu, C. R. Ma, A. S. Li, W. Q. Xu, Z. Y. Ma and X. R. Jia, J. Mater. Chem. C, 2019, 7, 8398–8403 RSC; S. Z. Mo, Q. T. Meng, S. L. Wan, Z. Q. Su, H. Yan, B. Z. Tang and M. Z. Yin, Adv. Funct. Mater., 2017, 27, 1701210 CrossRef; S. Fredrich, R. Gostl, M. Herder, L. Grubert and S. Hecht, Angew. Chem., Int. Ed., 2016, 55, 1208–1212 CrossRef PubMed.
- H. Heitele, P. Finckh, S. Weeren, F. Pöllinger and M. E. Michel-Beyerle, J. Phys. Chem., 1989, 93, 5173–5179 CrossRef CAS; G. L. Gaines, M. P. O'Neil, W. A. Svec, M. P. Niemczyk and M. R. Wasielewski, J. Am. Chem. Soc., 1991, 113, 719–721 CrossRef.
- A. Harriman, V. Heitz, M. Ebersole and H. Van Willigen, J. Phys. Chem., 1994, 98, 4982–4989 CrossRef CAS; X. Zhang, A. A. Sukhanov, X. Liu, M. Taddei, J. Z. Zhao, A. Harriman, V. K. Voronkova, Y. Wan, B. Dick and M. Di Donato, Chem. Sci., 2023, 14, 5014–5027 RSC.
- H. Langhals, C. Dietl, J. Dahl, R. Carlson, Y. T. Chern and P. Mayer, J. Org. Chem., 2020, 85, 11154–11169 CrossRef CAS PubMed; H. Langhals and C. Dietl, J. Org. Chem., 2022, 87, 9454–9465 CrossRef PubMed; H. Langhals, A. J. Esterbauer, A. Walter, E. Riedle and I. Pugliesi, J. Am. Chem. Soc., 2010, 132, 16772–16782 CrossRef PubMed; H. Langhals and A. Walter, J. Phys. Chem. A, 2020, 124, 1554–1560 CrossRef PubMed.
- G. J. Hedley, A. Ruseckas, A. C. Benniston, A. Harriman and I. D. W. Samuel, J. Phys. Chem. A, 2015, 119, 12665–12671 CrossRef CAS PubMed; A. Harriman, L. J. Mallon, G. Ulrich and R. Ziessel, ChemPhysChem, 2007, 8, 1207–1214 CrossRef PubMed; R. Ziessel, C. Goze, G. Ulrich, M. Cesario, P. Retailleau, A. Harriman and J. P. Rostron, Chem.–Eur. J., 2005, 11, 7366–7378 CrossRef PubMed.
- H. J. Ramesdonk, B. H. Bakker, M. M. Groeneveld, J. M. Verhoeven, B. D. Allen, J. P. Rostron and A. Harriman, J. Phys. Chem. A, 2006, 110, 13145–13150 CrossRef CAS PubMed; A. C. Benniston, A. Harriman, P. Y. Li, J. P. Rostron, H. J. Ramesdonk, M. M. Groeneveld, H. Zhang and J. W. Verhoeven, J. Am. Chem. Soc., 2005, 127, 16054–16064 CrossRef PubMed; D. Y. Liu, M. Imran, X. Xiao and J. Z. Zhao, Photochem. Photobiol. Sci., 2022, 21, 2153–2168 CrossRef PubMed.
- C. B. Winiger, S. G. Li, G. R. Kumer, S. M. Langenegger and R. Haener, Angew. Chem., Int. Ed., 2014, 53, 13609–13613 CrossRef CAS PubMed; B. Albinsson and J. Martensson, Phys. Chem. Chem. Phys., 2010, 12, 7338–7451 RSC; M. Kuss-Petermann and O. S. Wenger, Angew. Chem., Int. Ed., 2016, 55, 815–819 CrossRef PubMed.
- F. Odobel and J. Fortage, C. R. Chim., 2009, 12, 437–449 CrossRef CAS; J. Fortage, E. Goransson, E. Blart, H. C. Becker, L. Harmmarström and F. Odobel, Chem. Commun., 2007, 4629–4631 RSC; J. T. Buck, R. W. Wilson and T. Mani, J. Phys. Chem. Lett., 2019, 10, 3080–3086 CrossRef PubMed; N. Lokan, M. N. Paddon-Row, T. A. Smith, M. La Rosa, K. P. Ghiggino and S. Spieser, J. Am. Chem. Soc., 1999, 121, 2917–2918 CrossRef.
- R. Ziessel, M. Hissler and A. Harriman, Coord. Chem. Rev., 1998, 178, 1251–1298 CrossRef CAS; J. P. Collin, P. Gavina, V. Heitz and J.-P. Sauvage, Eur. J. Inorg. Chem., 1998, 1–14 CrossRef; R. H. Goldsmith, L. E. Sinks, R. F. Kelley, L. J. Betzen, W. H. Liu, E. A. Weiss, M. A. Ratner and M. R. Wasielewski, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3540–3545 CrossRef PubMed.
- J. Gierschner, Y. S. Huang, B. van Averbeke, J. Cornil, R. H. Friend and D. Beljonne, J. Chem. Phys., 2009, 130, 044105 CrossRef CAS PubMed; F. Giacalone, J. L. Segura, N. Martin, J. Ramey and D. M. Guldi, Chem.–Eur. J., 2005, 11, 4819–4834 CrossRef PubMed.
- A. A. Bothner-By, J. Dadok, T. E. Johnson and J. S. Lindsey, J. Phys. Chem., 1996, 100, 12937–12942 CrossRef.
- R. Ziessel, B. D. Allen, D. B. Rewinska and A. Harriman, Chem.–Eur. J., 2009, 15, 7382–7393 CrossRef CAS PubMed; M. A. H. Alamiry, J. P. Hagon, A. Harriman, T. Bura and R. Ziessel, Chem. Sci., 2012, 3, 1041–1048 RSC; D. Hablot, R. Ziessel, M. A. H. Alamiry, E. Bahraidah and A. Harriman, Chem. Sci., 2013, 4, 444–453 RSC.
- M. Gubelmann, A. Harriman, J.-M. Lehn and J. L. Sessler, J. Phys. Chem., 1990, 94, 308–315 CrossRef CAS; A. Harriman and J.-P. Sauvage, Chem. Soc. Rev., 1996, 25, 41–48 RSC; R. Ziessel, G. Ulrich, A. Haefele and A. Harriman, J. Am. Chem. Soc., 2013, 135, 11330–11344 CrossRef PubMed; J. Iehl, J. F. Nierengarten, A. Harriman, T. Bura and R. Ziessel, J. Am. Chem. Soc., 2012, 134, 988–998 CrossRef PubMed.
- S. Anderson, H. L. Anderson, A. Bashall, M. McPartlin and J. K. M. Sanders, Angew. Chem., Int. Ed., 1995, 34, 1096–1099 CrossRef CAS; H. L. Anderson, S. Anderson and J. K. M. Sanders, J. Chem. Soc., Perkin Trans. 1, 1995, 2231–2245 RSC; T. Tanaka and A. Osuka, Chem. Soc. Rev., 2015, 44, 943–969 RSC; Y. Nakamura, N. Aratani and A. Osuka, Chem. Soc. Rev., 2007, 36, 831–845 RSC; Y. Nakamura, S. Y. Jang, T. Tanaka, N. Aratani, J. M. Lin, K. S. Kim, D. Kim and A. Osuka, Chem.–Eur. J., 2008, 14, 8279–8289 CrossRef PubMed.
- Y. Terazono, G. Kodis, P. A. Liddell, V. Garg, T. A. Moore, A. L. Moore and D. Gust, J. Phys. Chem. B, 2009, 113, 7147–7155 CrossRef CAS PubMed; Y. Terazono, P. A. Liddell, V. Garg, G. Kodis, A. Brune, M. Hambourger, A. L. Moore, T. A. Moore and D. Gust, J. Porphyrins Phthalocyanines, 2005, 9, 706–723 CrossRef; D. Kuciauskas, P. A. Liddell, S. Lin, T. E. Johnson, S. J. Weghorn, J. S. Lindsey, A. L. Moore, T. A. Moore and D. Gust, J. Am. Chem. Soc., 1999, 121, 8604–8614 CrossRef.
- D. Holten, D. F. Bocian and J. S. Lindsey, Acc. Chem. Res., 2002, 35, 57–69 CrossRef CAS PubMed; F. R. Li, S. I. Yang, Y. Z. Ciringh, J. Seth, C. H. Martin, D. L. Singh, D. H. Kim, R. R. Birge, D. F. Bocian, D. Holten and J. S. Lindsey, J. Am. Chem. Soc., 1889, 120, 10001–10017 CrossRef.
- E. K. L. Yeow, K. P. Ghiggino, J. N. H. Reek, M. J. Crossley, A. W. Bosman, A. P. H. J. Schenning and E. W. Meijer, J. Phys. Chem. B, 2000, 104, 2596–2606 CrossRef CAS; S. H. Lee, I. M. Blake, A. G. Larsen, J. A. McDonald, K. Ohkubo, S. Fukuzumi, J. R. Reimers and M. J. Crossley, Chem. Sci., 2016, 7, 6534–6550 RSC.
- M. N. Paddon-Row, Aust. J. Chem., 2003, 56, 729–748 CrossRef CAS; M. N. Paddon-Row, Adv. Phys. Org. Chem., 2003, 38, 1–85 CrossRef; N. Lokan, M. N. Paddon-Row, T. A. Smith, M. La Rossa, K. P. Ghiggino and S. Speiser, J. Am. Chem. Soc., 1999, 121, 2917–2918 CrossRef.
- F. Barigelletti, L. Flamingni, V. Balzani, J. P. Collin, J.-P. Sauvage, A. Sour, E. C. Constable and A. M. W. C. Thompson, J. Am. Chem. Soc., 1994, 116, 7692–7699 CrossRef CAS; F. Barigelletti, L. Flamingni, V. Balzani, J. P. Collin, J.-P. Sauvage, A. Sour, E. C. Constable and A. M. W. C. Thompson, Coord. Chem. Rev., 1994, 132, 209–214 CrossRef; L. Flamigni, F. Barigelletti, N. Armardi, B. Ventura, J. P. Collin, J.-P. Sauvage and J. A. G. Williams, Inorg. Chem., 1999, 38, 661–667 CrossRef.
- J. S. Lindsey, S. Prathapan, T. E. Thompson and R. W. Wagner, Tetrahedron, 1994, 50, 8941–8968 CrossRef CAS; M. A. Miller, R. K. Lammi, S. Prathapan, D. Holten and J. S. Lindsey, J. Org. Chem., 2000, 65, 6634–6649 CrossRef PubMed; A. Ambroise, C. Kirmaier, R. W. Wagner, R. S. Loewe, D. F. Bocian, D. Holten and J. S. Lindsey, J. Org. Chem., 2002, 67, 3811–3826 CrossRef PubMed; R. S. Loewe, R. K. Lammi, J. R. Diers, C. Kirmaier, D. F. Bocian, D. Holten and J. S. Lindsey, J. Mater. Chem., 2002, 12, 1530–1552 RSC.
- A. Harriman, L. J. Mallon, K. J. Elliott, A. Haefele, G. Ulrich and R. Ziessel, J. Am. Chem. Soc., 2009, 131, 13375–13386 CrossRef CAS PubMed; A. Harriman, Chem. Commun., 2015, 51, 11745–11756 RSC.
- F. Giacalone, J. L. Segura, N. Martin, J. Ramey and D. M. Guldi, Chem.–Eur. J., 2005, 11, 4819–4834 CrossRef CAS PubMed; D. Hanss and O. S. Wenger, Eur. J. Inorg. Chem., 2009, 3778–3790 CrossRef.
- A. M. Brun and A. Harriman, J. Am. Chem. Soc., 1992, 114, 3656–3660 CrossRef CAS; A. M. Brun and A. Harriman, J. Am. Chem. Soc., 1994, 116, 10383–10393 CrossRef.
- P. K. Verma and S. K. Pal, Eur. Phys. J., 2010, 60, 137–156 Search PubMed; L. Xue, I. A. Karpenko, J. Hiblot and K. Johnsson, Nat. Chem. Biol., 2015, 11, 917–923 CrossRef CAS PubMed; A. A. Ensign, I. Jo, I. Yildirim, T. D. Krauss and K. L. Bren, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 10779–10784 CrossRef PubMed.
- M. Tokmina-Roszyk, D. Tokmina-Roszyk and G. B. Fields, Biopolymers, 2013, 100, 347–355 CrossRef CAS PubMed.
- R. B. Best, K. A. Merchant, I. V. Gopich, B. Schuler, A. Bax and W. A. Eaton, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18964–18969 CrossRef CAS PubMed; S. Doose, H. Neuweiler, H. Barsch and M. Sauer, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 17400–17405 CrossRef PubMed.
- D. W. Bolen and G. D. Rose, Annu. Rev. Biochem., 2008, 77, 339–362 CrossRef CAS PubMed.
- H. Z. Zhong and H. A. Carlson, J. Chem. Theory Comput., 2006, 2, 342–353 CrossRef CAS PubMed; P. M. Cowan and S. McGavin, Nature, 1955, 176, 501–504 CrossRef; M. Moradi, V. Babin, C. Roland and C. Sagui, J. Chem. Phys., 2010, 133, 125104 CrossRef PubMed.
- W. Taub and U. Shmueli, Nature, 1963, 198, 1165–1168 CrossRef CAS; P. Wilhelm, B. Lewandowski, N. Trapp and H. Wennemers, J. Am. Chem. Soc., 2014, 136, 15829–15832 CrossRef PubMed.
- M. Kuemin, J. Engels and H. Wennemers, J. Pept. Sci., 2010, 16, 596–600 CrossRef CAS PubMed; Y. C. Chiang, Y. J. Lin and J. C. Horng, Protein Sci., 2009, 18, 1967–1977 CrossRef PubMed; C. A. Slate, R. A. Binstead, T. J. Meyer and B. W. Erickson, Lett. Pept. Sci., 1999, 6, 61–69 Search PubMed.
- S. Dobitz, M. R. Aronoff and H. Wennemers, Acc. Chem. Res., 2017, 50, 2420–3428 CrossRef CAS PubMed; E. Sobakinskaya, M. S. A. Busch and T. Renger, J. Phys. Chem. B, 2018, 122, 54–67 CrossRef PubMed; V. Hirschfeld, H. Paulsen and C. G. Huber, Phys. Chem. Chem. Phys., 2013, 15, 17664–17671 RSC; R. B. Best, H. Hofmann, D. Nettels and B. Schuler, Biophys. J., 2015, 108, 2721–2731 CrossRef PubMed; E. Dolghih, W. Ortiz, S. Kim, B. P. Krueger, J. L. Krause and A. Roitberg, J. Phys. Chem. A, 2009, 113, 4639–4646 CrossRef PubMed.
- K. Walczewska-Szewc and B. Corry, Phys. Chem. Chem. Phys., 2014, 16, 18949–18954 RSC; E. Deplazes, D. Jayatilaka and B. Corry, Phys. Chem. Chem. Phys., 2011, 13, 11045–11054 RSC.
- B. Schuler, E. A. Lipman, P. J. Steinbach, M. Kumke and W. A. Eaton, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 2754–2759 CrossRef CAS PubMed.
- M. Tomura, E. Ishiguro and N. Mataga, J. Phys. Soc. Jpn., 1967, 22, 1117–1121 CrossRef CAS; N. Mataga, H. Obashi and T. Okada, J. Phys. Chem., 1969, 73, 370–374 CrossRef; M. Fujihara, M. Sakomura and T. Kamei, Thin Solid Films, 1989, 180, 43–50 CrossRef; A. K. Dutta, A. J. Pal and T. N. Misra, Solid State Commun., 1994, 92, 857–863 CrossRef; I. B. Berlman, C. R. Goldschmidt, Y. Tomkiewicz and A. Weinreb, Chem. Phys. Lett., 1968, 2, 657–658 CrossRef; C. R. Goldschmidt, Y. Tomkiewicz and A. Weinreb, Spectrochim. Acta, Part A, 1969, 25, 1471–1477 CrossRef; S. Müller, Y. Fritz and H.-A. Wagenknecht, ChemistryOpen, 2020, 9, 389–392 CrossRef PubMed.
- H. Kashida, T. Takatsu and H. Asanuma, Nucleic Acids Symp. Ser., 2009, 53, 29–30 CrossRef CAS PubMed; D. Lindegaard, A. S. Madsen, I. V. Asrakhova, A. D. Malakhov, B. R. Babu, V. A. Korshun and J. Wenger, Bioorg. Med. Chem., 2008, 16, 94–99 CrossRef PubMed.
- M. Masuko, S. Ohuchi, K. Sode, H. Ohtani and A. Shimadzu, Nucleic Acid Res., 2000, 28, e34 CrossRef CAS PubMed.
- S. Sindbert, S. Kalinin, H. Nguyen, A. Kienzler, L. Clima, W. Bannwarth, B. Appel, S. Müller and C. A. M. Siedel, J. Am. Chem. Soc., 2011, 133, 2463–2480 CrossRef CAS PubMed.
- Y. Niko, S. Kawauchi, S. Otsu, K. Tokumaru and G. Konishi, J. Org. Chem., 2013, 78, 3196–3207 CrossRef CAS PubMed.
- C. M. Deber, F. A. Bovey, J. P. Carver and E. R. Blout, J. Am. Chem. Soc., 1970, 92, 6191–6198 CrossRef CAS PubMed; H. Okabayashi and T. Isemura, Bull. Chem. Soc. Jpn., 1970, 43, 20–23 CrossRef; H. Okabayashi and T. Isemura, Bull. Chem. Soc. Jpn., 1970, 43, 359–361 CrossRef; D. G. McCafferty, D. A. Freisen, E. Danielson, C. G. Wall, M. J. Saderholm, B. W. Erickson and T. J. Meyer, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 8200–8204 CrossRef PubMed.
- S. Ruttinger, R. MacDonald, B. Kramer, F. Koberling, M. Roos and E. Hildt, J. Biomed. Opt., 2006, 11, 024012 CrossRef PubMed.
- A. K. Pandey, D. Naduthambi, K. M. Thomas and N. J. Zondlo, J. Am. Chem. Soc., 2013, 135, 4333–4363 CrossRef CAS PubMed.
- A. El-Faham, R. S. Funosas, R. Prohens and F. Albericio, Chem.–Eur. J., 2009, 15, 9404–9416 CrossRef CAS PubMed; A. Kumar, Y. E. Jad, B. G. de la Torre, A. El-Faham and F. Albericio, J. Pept. Sci., 2017, 23, 763–768 CrossRef PubMed.
- K. Jarowicki and P. Kocienski, J. Chem. Soc., Perkin Trans. 1, 2001, 2109–2135 RSC.
- S. Doose, H. Neuweiler, H. Barsch and M. Sauer, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 17400–17405 CrossRef CAS PubMed; M. Mutter, T. Wohr, S. Gioria and M. Keller, Biopolymers, 1999, 51, 121–128 CrossRef PubMed; M. Moradi, V. Babin, C. Toland, T. A. Darden and Z. Sagui, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 20746–20751 CrossRef PubMed; L. Q. Shi, A. E. Holliday, N. Khanal, D. H. Russell and D. E. Clemmer, J. Am. Chem. Soc., 2015, 137, 8680–8683 CrossRef PubMed.
- J. Graff, P. H. Nguyen, G. Stock and H. Schwalbe, J. Am. Chem. Soc., 2007, 129, 1179–1189 CrossRef CAS PubMed; Y. K. Kang, J. S. Jhon and H. S. Park, J. Phys. Chem. B, 2006, 110, 17645–17655 CrossRef PubMed.
- Y. K. Kang, J. Mol. Struct.: THEOCHEM, 2004, 675, 37–45 CrossRef CAS; C. Benzi, R. Improta, G. Scalmani and V. Barone, J. Comput. Chem., 2002, 23, 341–350 CrossRef PubMed; A. Flores-Ortega, A. I. Jimenez, C. Cativiela, R. Nussinov, C. Aleman and J. Casanovas, J. Org. Chem., 2008, 73, 3418–3427 CrossRef PubMed.
- V. R. Pattabiraman and J. W. Bode, Nat., 2011, 480, 471–479 CrossRef CAS PubMed.
- H. Z. Zhong and H. A. Carlson, J. Chem. Theory Comput., 2006, 2, 342–353 CrossRef CAS PubMed; E. B. Naziga, F. Schweizer and S. D. Westmore, J. Phys. Chem. B, 2013, 117, 2671–2681 CrossRef PubMed; J. A. Vila, H. A. Baldoni, D. R. Ripoll, A. Ghosh and H. A. Scheraga, Biophys. J., 2004, 86, 731–742 CrossRef PubMed.
- M. C. Huang, W. H. Chen, C. W. Huang, K. Y. Huang, J. C. Horng, M. Hayashi and I. C. Chen, RSC Adv., 2020, 10, 3493–3500 RSC.
- A. A. Adzhubei, M. J. E. Sternberg and A. A. Makarov, J. Mol. Biol., 2013, 425, 2100–2132 CrossRef CAS PubMed; B. Bochicchio and A. M. Tamburro, Chirality, 2002, 14, 782–792 CrossRef PubMed.
- L. Q. Shi, A. E. Holliday, H. L. Shi, F. F. Zhu, M. A. Ewing, D. H. Russell and D. E. Clemmer, J. Am. Chem. Soc., 2014, 136, 12702–12711 CrossRef CAS PubMed.
- A. Nakajima, Bull. Chem. Soc. Jpn., 1971, 44, 3272–3277 CrossRef CAS.
- J. B. Birks, D. J. Dyson and I. H. Munro, Proc. R. Soc. A, 1963, 275, 575–588 CAS.
- J. B. Birks, Photophysics of Aromatic Molecules, Wiley-Interscience, London, 1970 Search PubMed.
- K. Hara and W. R. Ware, Chem. Phys., 1980, 51, 61–68 CrossRef CAS; T. Yoshinaga, H. Hiratsuka and Y. Tanizaki, Bull. Chem. Soc. Jpn., 1977, 50, 3096–3102 CrossRef.
- D. V. O'Connor and D. Phillips, Time-Correlated Single Photon Counting, Academic Press, 1984, London Search PubMed.
- P. Hall and B. Selinger, J. Phys. Chem., 1981, 85, 2941–2946 CrossRef CAS.
- B. Stevens and E. Hutton, Nature, 1960, 186, 1045–1046 CrossRef CAS.
- J. B. Birks, A. A. Kazzaz and T. A. King, Proc. R. Soc. A, 1966, 291, 556–569 Search PubMed; R. D. Pensack, R. J. Ashmore, A. L. Paoletta and G. D. Scholes, J. Phys. Chem. C, 2018, 122, 21004–21017 CrossRef CAS.
- Y. Takahashi, T. Kitamura and K. Uchida, J. Lumin., 1980, 21, 425–433 CrossRef CAS.
- R. Casier and J. Duhamel, Langmuir, 2022, 38, 3623–3629 CrossRef CAS PubMed.
- G. Porter and M. W. Windsor, Discuss. Faraday Soc., 1954, 17, 178–186 RSC.
- C. Bohne, E. B. Abuin and J. C. Scaiano, J. Am. Chem. Soc., 1990, 112, 4226–4231 CrossRef CAS.
- L. Peter and G. Vaubel, Chem. Phys. Lett., 1973, 21, 158–160 CrossRef CAS.
- S. L. Murov, Handbook of Photochemistry, Marcel Dekkar, New York, 1973 Search PubMed.
- D. A. Smith, G. McKenzie, A. C. Jones and T. A. Smith, Methods Appl. Fluoresc., 2017, 5, 042001 CrossRef PubMed.
- C. A. Parker and T. A. Joyce, J. Chem. Soc. Chem. Commun., 1966, 108–109 RSC.
- W. R. Algar, N. Hildebrandt, A. S. Vogel and I. L. Medintz, Nat. Methods, 2019, 16, 815–829 CrossRef CAS PubMed.
- G. Dirks, A. L. Moore, T. A. Moore and D. Gust, Photochem. Photobiol., 1980, 32, 277–280 CrossRef CAS.
- D. R. James and W. R. Ware, Chem. Phys. Lett., 1986, 126, 7–11 CrossRef CAS; D. R. James, Y.-S. Liu, P. De Mayo and W. R. Ware, Chem. Phys. Lett., 1985, 120, 460–465 CrossRef.
- H. Lemmetyinen, N. V. Tkachenko, B. Valeur, J.-I. Hotta, M. Ameloot, N. P. Ernsting, T. Gustavsson and N. Boens, Pure Appl. Chem., 2014, 86, 1969–1998 CAS.
- G. L. Closs, P. Piotrowiak, J. M. MacInnis and G. R. Fleming, J. Am. Chem. Soc., 1988, 110, 2652–2653 CrossRef CAS.
- V. Grosshenny, A. Harriman, M. Hissler and R. Ziessel, J. Chem. Soc., Faraday Trans., 1996, 92, 2223–2238 RSC.
- S. M. Waly, J. K. G. Karlsson, P. G. Waddell, A. C. Benniston and A. Harriman, J. Phys. Chem. A, 2022, 126, 1530–1541 CrossRef CAS PubMed.
Footnotes |
| † This work is dedicated to the memory of Prof. William McFarlane (Newcastle University). Deposition reference for the crystal structure: CCDC 2283731. |
| ‡ Electronic supplementary information (ESI) available: Compound characterisation, examples of optical spectra, details of calculations, crystal structural data, TR fluorescence profiles, DFT output. CCDC 2283731. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc05287g |
| This journal is © The Royal Society of Chemistry 2024 |