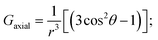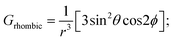Open Access Article
Open Access ArticleProbing substrate binding inside a paramagnetic cavity: a NMR spectroscopy toolbox for combined experimental and theoretical investigation†‡
Sabyasachi
Sarkar
a,
Chang-Quan
Wu
b,
Santanu
Manna
a,
Deepannita
Samanta
a,
Peter P.-Y.
Chen
 *b and
Sankar Prasad
Rath
*b and
Sankar Prasad
Rath
 *a
*a
aDepartment of Chemistry, Indian Institute of Technology Kanpur, Kanpur-208016, India. E-mail: sprath@iitk.ac.in
bDepartment of Chemistry, National Chung Hsing University, 145 Xingda Rd., South Dist., Taichung City 402, Taiwan. E-mail: pychen@dragon.nchu.edu.tw
First published on 24th September 2024
Abstract
Protein cavities often rely on the paramagnetic metal present in their active site in order to catalyse various chemical transformations in biology. The selective detection and identification of the substrate is of fundamental importance in environmental monitoring and biological studies. Herein, a covalently linked Fe(III)porphyrin dimer-based paramagnetic sensory cavity has been devised for the accurate detection and simultaneous identification of phenol (substrate) binding within the cavity that provides a unique spectroscopic signature with valuable structural and environmental information. These substrates within the paramagnetic cavity leave the fingerprints of the specific binding modes (exo vs. endo) which are well distinguished with the help of various spectroscopic studies viz. UV-vis, 1H, and 19F NMR and in their respective crystal structures also. The theoretical 19F NMR analysis plays a pivotal role in replicating the observed NMR trends with large chemical shifts of the phenolato species which in turn helps in deciphering the selective binding modes of the phenols and thereby recognizing the chemical environment within the cavity. These findings will help develop an excellent diagnostic tool for in situ monitoring of subtle conformational changes and transient interactions.
Introduction
Nature provides us with a rich toolbox of various functional micro- and nano-compartments, e.g. lipid vesicles, organelles, protein cages, virus capsids, etc. Among them, protein cages/cavities are very special and interesting types of natural nano-compartments due to their unique structural features, robustness and uniform size.1 These protein cavities often rely on the paramagnetic metal present in their active site in order to catalyse various chemical transformations as observed in the case of cytochrome P450, catalases and peroxidases to name a few.2 The selective detection and identification of substrates is of fundamental importance in environmental monitoring and biological studies. In this context, the binding of the substrate within the paramagnetic cavity sometimes provides a unique spectroscopic signature (fingerprint) that allows precise and simultaneous identification of such substrate binding in a complex mixture.3 However, metal complexes possess rich magnetic resonance properties based on paramagnetic effects of the metal centre and investigation is often complicated and challenging. Therefore, it is highly desirable to develop sensing platforms that provide outputs with effective analyte fingerprints which not only allows an accurate analysis of the complex mixture but also provides valuable structural information.Binding of the tyrosine moiety to heme is well-known in biology2 and also in model complexes.4,5 In this work, a covalently linked Fe(III)porphyrin dimer, that produces a paramagnetic cavity (Fig. 1), has been utilized to investigate preferential binding of several substituted phenols as substrates. Based on the bulk of the substituents, phenols bind either in the exo–endo or exo–exo fashion. The previous reports by Nolte and coworkers were mainly focused on the host–guest exchange of viologen guests within the porphyrin cage and determination of the binding efficiencies with the help of 1D EXSY measurements3c but utilization of paramagnetic NMR as a spectral toolbox to demonstrate the differential binding of the guests remained elusive. Herein we delineate the maiden example of the influence of the paramagnetic metal ion on substrates which has been thoroughly exploited in the 1H and 19F NMR spectral studies to reveal two different chemical environments (exo vs. endo) in solution. Moreover, these two modes of binding have been well distinguished using UV-vis spectral studies along with significant differences in the respective structural and geometrical parameters. DFT calculations have played a pivotal role in replicating the experimental 19F NMR spectra of the phenolato species that allow precise binding and identification of the substrate inside or outside of the paramagnetic cavity.
Results and discussion
Synthesis
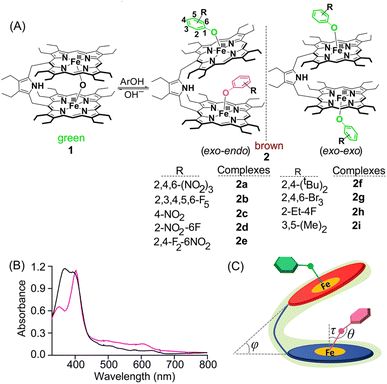
Addition of various phenols into the chloroform solution of pyrrole-bridged μ-oxo porphyrin dimer, 1, led to the generation of corresponding five-coordinate phenolato species (Fig. 1A). Fig. 1A shows the synthetic outline and the various phenolato complexes reported here along with their abbreviations used.UV-vis spectroscopy
The preferential mode of binding of various substituted phenols can be differentiated from their respective UV-vis spectra. Taking pentafluoro phenol (Fig. 1B) as a representative example, the corresponding phenolate species 2b exhibited a split Soret band at 372 and 394 nm along with three Q-bands centred at 504, 584 and 628 nm suggesting the formation of a five-coordinate complex.4,5 This Soret band splitting is possibly because of the Kasha's exciton coupling of the obliquely arranged chromophores in space.6 All the complexes having exo–endo conformations behaved similarly (Fig. S1‡). In contrast, the phenolate complex with bulky substituents such as 2,4-ditertiarybutylphenol, 2f, was found to bind in the exo–exo fashion having an intense Soret band at 403 nm along with a shoulder at 350 nm and three Q-bands centred at 492, 534 and 610 nm (Fig. 1B). Phenolate species with bulky substituents exhibited similar UV-vis spectral signatures indicating the obvious exo–exo binding mode (Fig. S2‡). The UV-vis spectra of exo–endo and exo–exo species are calculated based on time-dependent density functional theory (TD-DFT), which virtually reproduced the experimental spectra of 2b and 2f (Fig. S3 and S4‡). The most significant effect was the development of a split Soret band in the case of exo–endo and a shoulder for exo–exo species (vide supra). As shown in Fig. 1B, 2b has split Soret bands observed at 372 and 394 nm which correspond to HOMO−6 to LUMO+7 (oscillator strength f ≈ 0.37) and HOMO−5 to LUMO+6 (f ≈ 0.17), respectively (Fig. S3‡). However, for 2f, the shoulder and the Soret band observed at 350 and 403 nm are related to HOMO−6 to LUMO+1 (f ≈ 0.69) and HOMO−2 to LUMO+1 (f ≈ 1.99), respectively (Fig. S4‡). Thus, UV-vis spectra carry the hallmark of the differential binding of the substrates between exo–endo and exo–exo.Crystallographic characterization
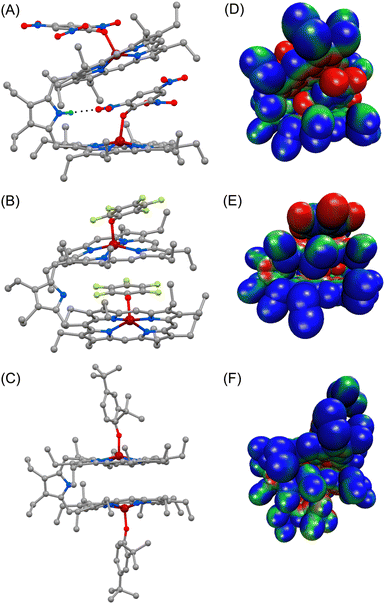
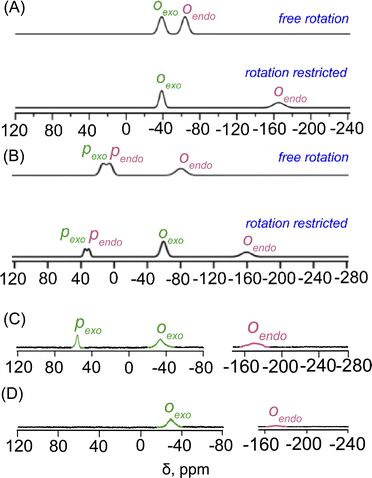
Dark brown needle-shaped crystals of 2a, 2b and 2f were grown via slow diffusion of n-hexane into dichloromethane solutions of the respective complexes in air at room temperature (Fig. 2 and S5–S7‡).7 All the complexes have two iron centres, each in a five-coordinate square-pyramidal geometry. X-ray structures of 2a and 2b clearly display exo–endo binding of the substrates, while 2f demonstrates such binding in an exo–exo mode.Differential binding of the substrate can easily be identified in the structural and geometrical parameters observed in their X-ray structures. The average Fe–Np distances for 2a and 2b are 2.060(3) and 2.062(6) Å for core I and 2.054(3) and 2.055(4) Å for core II, respectively; whereas in the case of 2f it is 2.071(13) Å (Table 1), which is within the observed range of high-spin (S = 5/2) iron(III)-porphyrinates.8,9 These values are in good accord with the previously reported Fe–Np distances for axial phenoxide coordinated iron(III)porphyrinates.4,5 The average Fe–Np distances of the endo phenolate bound Fe(III)porphyrin (core I) is longer than that of the exo phenolate bound Fe(III)porphyrin (core II) unit in the cases of 2a and 2b.
| Complex | Fe–Npa | Fe–Ob | Fe–O–Cc(θ) | ΔFe24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
Δ24e | τ | Φ | Fe⋯Feh | Ref.i | |
|---|---|---|---|---|---|---|---|---|---|---|
| a Averaged value (in Å). b Distance (in Å) of the axial ligand. c Angle (in °). d Displacement (in Å) of iron from the least–squares plane of the C20N4 porphyrinato core. e Average displacement (in Å) of atoms from the least–squares planes of C20N4 porphyrinato cores. f Tilt-angle (in °). g Inter-planar angle between the least–square planes of the C20N4 pophyrinato cores (in °). h Non-bonding distance (in Å) between two iron(III) centres in a molecule. i tw, this work. | ||||||||||
| 2a | Core I (endo) | 2.060(3) | 1.918(3) | 128.5(2) | 0.46 | 0.08 | 7.74 | 25.89 | 6.78 | tw |
| Core II (exo) | 2.054(3) | 1.911(3) | 126.7(3) | 0.42 | 0.12 | 0.90 | ||||
| 2b | Core I (endo) | 2.062(6) | 1.874(4) | 126.6(4) | 0.39 | 0.02 | 1.56 | 34.79 | 6.33 | tw |
| Core II (exo) | 2.055(4) | 1.914(4) | 121.9(4) | 0.47 | 0.16 | 0.10 | ||||
| 2f | exo | 2.071(13) | 1.818(11) | 151.55(11) | 0.47 | 0.12 | 0.04 | 2.69 | 6.21 | tw |
| [FeIII(OEP)(2,4,6-(NO2)3OPh)] | 2.049(2) | 1.930(1) | 123.87(12) | 0.40 | 0.02 | 0.66 | — | 4c | ||
However, for the exo–exo bound species, like 2f, this distance is much larger. In the case of the exo–endo dimer, the endo-bound phenolate is sandwiched between two adjacent porphyrins (Fig. 2). Indeed, the endo-phenols (C6 plane) are nearly coplanar with the pophyrinato core (exo) having a mean plane separation of 3.15 and 3.09 Å for 2a and 2b, respectively, suggesting strong π–π interactions between them. The endo binding of the substrate is further facilitated due to the H-bonding interactions between the pyrrolic N–H of the host with the O-atom of the nitro group of the endo-bound phenolate in 2a (Fig. 2A).
An interesting aspect of the differential binding of the substrate is the off-axis tilt angles (Fig. 1C) which are quite different between exo and endo binding. For example, the endo phenolate (7.74°) is much more tilted than the exo bound phenolate (0.92°) for 2a and for 2b it is 1.56° and 0.10°, respectively. But for the exo–exo species 2f, the value is very small (0.04°). The Fe–O distances observed for 2a and 2b are 1.918(3) and 1.874(4) Å for core I, respectively, while for core II the values are 1.911(3) and 1.914(4) Å. But for 2f, the value is 1.818(13) Å. These values are comparable to the Fe–O distances reported so far for iron(III)porphyrin with phenolato coordination.4,5 The Fe–O distance has been found to increase with increasing electron withdrawing substituents on the phenols; this is due to the fact that an electron withdrawing substituent with a strong inductive effect (−I) reduces the electron donating ability of the oxygen atom coordinated to the iron centre, thereby increasing the Fe–O bond length. The Fe–O–C angles for core I and core II are 128.5(2)° and 126.7(3)° in 2a and 126.6(4)° and 121.9(4)° in 2b. But for 2f, the angle is 151.55(11)°. An increase in the Fe–O–C angle leads to an increase in the s character of the phenolate oxygen atom leading to the shortening of Fe–O distance. Therefore, 2f with bulky 2,4-ditertiarybutylphenol having the maximum Fe–O–C angle resulted in the shortest Fe–O distance (Table 1) whereas 2a shows the longest Fe–O distance due to weaker binding of 2,4,6- trinitrophenol to the Fe(III) centre, owing to the very strong −I effect and resonance (−R) effects of the three electron-withdrawing nitro substituents. Interestingly, the exo and endo bound phenolate species in the exo–endo complexes have very different Fe–O–C angles: the endo bound phenols have a larger angle as compared to that of the exo bound phenolates (Table S1‡). The trends in structural and geometrical parameters of 2a, 2b and 2f were also found to correlate nicely with the theoretical ones (Table S2‡).
The porphyrin macrocycles in diheme phenolate complexes are highly distorted, while the ring is planar in the related monomeric phenolate complexes (Table 1). As evident, the interaction between two rings in diheme results in larger ring deformation of the individual porphyrin centres. This has also been reflected in the average atom displacements from the mean porphyrin plane (Δ24) and iron displacements therein (ΔFe24) (Table 1). Notably, in the exo–endo complexes, the rings are deformed to different extents. The porphyrin core with the endo bound phenolate (core I) is less distorted compared to the porphyrin core with exo bound phenolate (core II) (Fig. 4F). The average displacement of atoms from the mean porphyrin plane (Δ24) is 0.08 Å (core-I) and 0.12 Å (core-II) for 2a and 0.02 Å (core-I) and 0.16 Å (core-II) for 2b whereas for 2f, both the cores are equally distorted with a value of 0.12 Å (Fig. S8‡).
The electrostatic potentials have also been mapped onto the van der Waals surface of three representative molecules such as 2a, 2b and 2f, which show quite substantial effects of the phenols in the exo–endo and exo–exo conformers (Fig. 2D–F). The values of the electrostatic surface potential (ESP) are represented by different colours that vary from red (most negative electrostatic potential) to blue (most positive electrostatic potential); the green part represents the zero-potential regions. For 2a, the exo bound 2,4,6-trinitrophenol moiety induces the charge to the porphyrin ring to a different extent than that of the endo bound one (Fig. 2D). In contrast, 2f with bulky 2,4-ditertiarybutylphenol which prefers exo–exo mode of binding exerts very symmetrical charge distribution on two porphyrin rings (Fig. 2F).
1H and 19F NMR spectroscopy
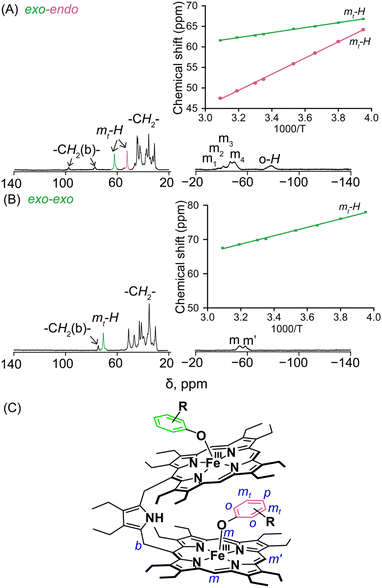
The structure and the properties of these complexes in solution can be obtained from the 1H NMR spectra.4,8–12 The solid-state structural conformations are also preserved in the solution as is reflected in their respective 1H NMR spectra. The signals are broad and situated in both upfield and downfield regions indicating π-spin delocalization from the Fe(III) centre to the phenolate moiety.4 The basic resonance pattern of the porphyrin core in the complexes is grossly similar with meso-substituted five-coordinate Fe(III)porphyrins of type [XFeIII(meso-R-OEP)].4,9,11 Due to extreme broadening of the 1H signals, 2D NMR has not been much informative. It is interesting to compare the 1H NMR spectra between the exo–endo and exo–exo conformers taking 2c and 2g as two representative examples (Fig. 3A and B).Highly deshielded methylene (spanning between 31.2 and 44.7 ppm), two downfield shifted bridging signals (at 77.3 and 97.9 ppm), four highly shielded meso signals (at −37.5, −41.4, −46.6, and −50.2 ppm), two sets of sharp meta signals (at 52.2 and 62.5 ppm) and a very broad ortho signal at −78.6 ppm have been observed in the case of 2c. Methylene peaks appeared between δ = 30.1 and 50.8 ppm in 2g; however, there have been one set of signals with two meso resonances with a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 intensity ratio at −54.1 and −59.1 ppm, one bridging signal at 74.2 ppm and one meta signal at 70.4 ppm in the complex.
1 intensity ratio at −54.1 and −59.1 ppm, one bridging signal at 74.2 ppm and one meta signal at 70.4 ppm in the complex.
Variable temperature 1H NMR studies have been performed and it was found that two meta protons of bound phenolate ions behave very differently in 2c (Fig. 3A, inset) reflecting the fact that these two signals originated from two different chemical environments which further confirms the intactness of the exo–endo conformation in solution, whereas for 2g, only one set of meta signals was found which clearly reflects the symmetrical mode of binding of the phenols in these exo–exo species (Fig. 3B, inset). Thus, the behaviour of the meta protons serves as a diagnostic tool to discriminate between these two binding modes. A schematic diagram displaying the nomenclature used for 1H NMR peak assignments is shown in Fig. 3C. The 1H NMR spectral behaviours of other exo–endo and exo–exo complexes are shown in Fig. S9 and S10.‡
In this context, the 1H NMR studies of monomeric Fe(III)porphyrins with axial phenolate coordination performed nicely by Arasasingham et. al. are worth mentioning.5e A series of substitutions varying from electron donating to electron withdrawing groups on the phenolate moiety have been utilized. The 1H NMR spectra of these protoporphyrin (IX) dimethyl esters display spectral features similar to the pattern observed here for the symmetrical exo–exo binding mode in which only one set of signals is observed.5e In contrast, the 1H NMR spectral investigation of the asymmetrical binding of catechols to the monomeric Fe(III) octaethylporphyrins investigated by Rath and co-workers4d produced two different sets of meta-proton signals similar to the dimeric complexes reported here with exo–endo binding mode. In complexes with substituted catechols, the Fe(III) centre can bind either of the two available oxygen atoms of catechol, and hence two sets of downfield shifted meta-proton signals are observed in the 1H NMR spectra which reflects the inequivalent mode of binding, a scenario somewhat similar to what we have obtained in the exo–endo mode of binding reported here in the dimeric complexes.
The Mulliken spin densities of the phenolate carbon atoms of 2c are calculated by using DFT, in which the observed spin densities are positive at the ortho and para positions but are negative at the meta position (Fig. S11‡). As a result, the ortho and para protons are shifted upfield, while the meta proton is shifted downfield, as observed in the 1H NMR spectra of the molecules. These contrasting chemical shifts with opposite signs of the spin densities for the meta protons versus the ortho/para protons (Fig. S12‡) are indicative of π-spin delocalization on the phenolate ligand.4,5c The temperature dependence of the 1H NMR signals follows the Curie law and a representative example of 2a has been shown which indicates a single spin state throughout the temperature range (Fig. S13‡).4,9–12
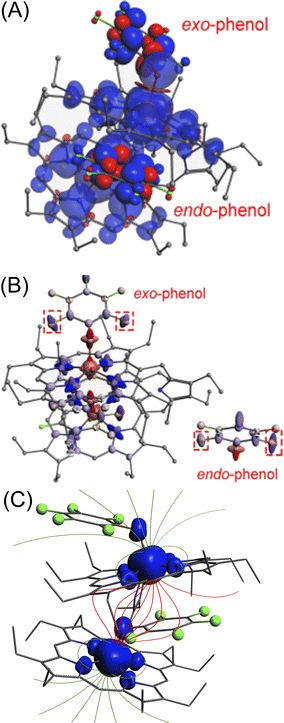
19F NMR has been a powerful probe for structural and mechanistic studies due to the presence of the 100% abundant spin 1/2 nucleus with high sensitivity and is particularly attractive for paramagnetic systems in the field of bioinorganic chemistry.13 The differential binding of the substrate inside and outside the paramagnetic cavity can easily be visualized using 19F NMR also upon using fluorinated substrates in which signals are largely upfield and downfield shifted as demonstrated for 2b, 2d, 2e and 2h (Fig. S14‡). For 2b, two sets of ortho, meta and para-F resonances and for 2d two sets of ortho-F signals, owing to exo–endo binding, have been observed. The exo and endo resonances have been assigned by comparing 19F NMR of a series of complexes containing fluorinated substrates along with DFT calculations (vide infra). For 2b, the ortho, para and meta-F signals of the exo bound phenol appear at −14.6, 29.7 and −210.2 ppm and for the endo bound phenol ortho-F resonates at −218.3, 18.7 ppm and meta-F appears at −226.5 ppm. However, para-F resonance for endo bound phenol was too broad to be detected experimentally. The calculated 19F resonances for 2b were found to match well with the experimental spectrum (Fig. 4C). Interestingly, the corresponding pentafluorophenolato complex of the cis-ethene bridged diiron(III)porphyrin dimer, however, gets stabilized in the exo–exo conformation exclusively (Fig. 4D, Scheme S1‡).4a In the case of 2d, two ortho-F resonances appear at −28.8 and −171.7 ppm for the exo and endo bound phenolates, respectively, while 2h with bulky substituent 2-ethyl-4-fluoro phenol showed only one set of para-F resonance which is in sharp contrast to that observed for the exo–endo phenols. The para-F resonance has been observed at 97.1 ppm for 2h. Therefore, 19F NMR spectroscopy serves as a powerful tool for distinguishing the exo–endo and exo–exo modes of binding.
 | ||
| Fig. 4 19F NMR spectra (at 298 K in C6D6) of (A) free pentafluoro phenol and (B) 2b. (C) DFT calculated 19F NMR spectrum of 2b. (D) 19F NMR spectrum (in CDCl3 at 298 K) of the pentafluorophenolato analogue of the cis-ethene bridged diiron(III)porphyrin dimer (exo–exo form, Scheme S1‡). (E) Schematic representation of the exo–endo conformer upon pentafluoro phenol binding. (F) Out-of-plane displacement of the porphyrin core atoms of 2b from the least–squares plane of the C20N4 porphyrinato core. The horizontal axis represents the bond connectivity between atoms. | ||
To further confirm the differential behaviour of the exo and endo19F resonances, variable temperature 19F NMR in C6D6 was performed for 2b (Fig. S15‡). As the temperature decreases, the ortho and para-F resonances of the exo bound pentafluoro phenol moiety are increasingly downfield shifted whereas its meta-F resonances are shifted in the upfield region. But the endo bound pentafluoro phenol gives different 19F resonances: one of the ortho-F resonances is increasingly downfield shifted whereas an upfield shift is observed for the other ortho-F resonance. The meta-F resonance gets increasingly upfield shifted as the temperature decreases.
Estimation of 19F NMR chemical shifts using computational studies
To understand the large upfield and downfield shifts in the 19F NMR spectra, the total NMR chemical shifts (δobs), eqn (1), including orbital (δorb), metal-centred dipolar shift (δMCdip) and contact (δcon) contributions are evaluated using density functional theory (DFT) mentioned below (detailed in the ESI‡).14,15| δobs = δorb + δMCdip + δcon | (1) |
By incorporating DFT calculations alongside NMR analysis of 2b (see details in the ESI‡), it is observed that the orbital shifts and contact shifts demonstrate similarities for the corresponding fluorine atoms in both exo-phenol and endo-phenol positions, as shown in Table 2. The contact term is highly dependent on the magnitude of the electron magnetic moment positioned at the nucleus, as expressed by eqn (2) in which Aiso is the hyperfine coupling constant, γI is the gyromagnetic ratio of the nucleus I, giso is the isotropic g factor of the spin system and μB is the Bohr magneton. In addition, two methods are usually used to evaluate the dipolar shift, namely the metal-centred point-dipole approximation, eqn (3),14c and the derivation of the anisotropic part of the hyperfine tensor from electronic structure calculation, eqn (4),14h where θ indicates the angle between the metal-nucleus (N) vector and the main axis (z-axis), Φ represents the angle between the projection of the iron-F vector on the xy plane and the x-axis, r refers to the distance between the metal and the nucleus, gani means the anisotropic part of the g-tensor, and Adip is the dipolar part of the hyperfine coupling tensor.
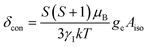 | (2) |
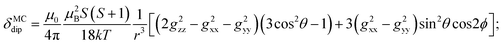 | (3) |
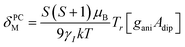 | (4) |
| ppm | o-F | m-F | p-F |
|---|---|---|---|
| a Experimental data (at 298 K) assigned for exo-phenol of 2b. b Averaged orbital shift. c Averaged contact shift within the exo-phenol. d Averaged dipolar shift within the exo-phenol according to eqn (3). e δ obs = δorb + δcon + δMCdip (Feexo). f Averaged dipolar shift within the exo-phenol according to eqn (4). g δ obs = δorb + δcon + δPCM. h Dipolar shift within the endo-phenol corresponding to Feendo and Feexo, respectively, according to eqn (3). i δ obs = δorb + δcon + δMCdip(Feendo) + δMCdip(Feexo). j Dipolar shift within the endo-phenol according to eqn (4). k δ obs = δorb + δcon + δPCM. | |||
| Experimental | |||
| δ obs (exo)a | −14.6 | −210.2 | 29.7 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| exo-Phenol | |||
| δ orb | −135.6 (−137.2, −134.0) | −152.0 (−154.7, −149.3) | −151.0 |
| δ con | 99.1 (62.3, 135.9) | −86.6 (−85.3, −87.8) | 170.3 |
| δ MCdip (Feexo)d | 21.9 (55.0, −11.2) | −3.3 (12.9, −19.5) | −4.8 |
| δ obs | −14.6 | −241.9 | 14.5 |
| δ PCM | −11.5 (−5.8, −17.1) | 1.1 (−2.5, 4.6) | −22.5 |
| δ obs | −48.0 | −237.5 | −3.2 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| endo-Phenol | |||
| o-F(1), o-F(2) | m-F(1), m-F(2) | p-F | |
| δ orb | −137.1, −133.7 | −157.2, −158.7 | −153.2 |
| δ con | 60.6, 151.0 | −65.9, −93.7 | 184.6 |
| δ MCdip (Feendo)h | −67.8, 24.8 | 24.6, 8.5 | −9.5 |
| δ MCdip (Feexo)h | −39.8, −17.6 | −11.7, 8.1 | −27.0 |
| δ obs | −184.1, 24.5 | −210.2, −235.8 | −5.1 |
| δ PCM | −107.1, −14.7 | 2.4, 31.9 | −55.6 |
| δ obs | −183.6, 2.6 | −220.7, −220.5 | −24.2 |
Drawing upon DFT-calculated Aiso values obtained from the optimized 2b structure, it's evident that exo-phenol's rotation in solution is not considered. Remarkably, a substantial difference in contact shifts is observed for the two ortho-fluorine atoms (62.3 and 135.9 ppm), while the two meta-fluorine atoms exhibit comparable values (−85.3 and −87.8 ppm). Conversely, this disparity is evident in both the o-F and m-F configurations of endo-phenol within the same computational analysis, with o-F values of 60.6 and 151.0 ppm and m-F values of −65.9 and −93.7 ppm. However, if we acknowledge that exo-phenol can rotate freely in solution due to the lack of steric hindrance, involving rotations of both its Fe–O and O-Ph single bonds, all chemical shift components for ortho- and meta-fluorine atoms can be averaged, respectively. In contrast, the endo-phenol, being positioned inside the cavity created by two Fe(III)porphyrin units along with a pyrrole-bridge, is no longer able to rotate freely in solution. Consequently, unlike the scenario with exo-phenol, the various components of the chemical shifts cannot be averaged.
Likewise, it could be posited that the spatial orientation of phenol will also significantly influence the dipolar shift. Unlike the contact shift, the dipolar shifts for the fluorine atoms in exo-phenol are primarily influenced by its Feexo centre. In contrast, endo-phenol is situated in close proximity to both Fe centres (Feendo and Feexo), resulting in all fluorine atoms experiencing dipolar shifts originating from them. This dipolar shift, as defined in eqn (3), can be evaluated using the Gaxial and Grhombic factors, along with the g values specified in the text. The corresponding Gaxial and Grhombic structural factors for the fluorine atoms in exo- and endo-phenols are illustrated in Table S3.‡ It is noteworthy that, when considering their respective coordinated Fe(III) centres, the Gaxial and Grhombic factors for both exo- and endo-phenols exhibit similarities. Unlike the exo-phenol, the non-coordinating iron centre (Feexo) significantly impacts the Gaxial and Grombic factors of the endo-phenol as well. Thus, as indicated by eqn (3), the total G factors for fluorine atoms in endo-phenol consistently far exceed those in exo-phenol. Consequently, their dipolar shifts are expected to exhibit notable distinctions, except when the values of both 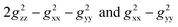 approach zero.
approach zero.
After comparing the total Gaxial and Grhombic factors for both exo- and endo-phenols in Table S3,‡ significant positive increases were observed in the Gaxial differences for all o-F (27.17 and 16.45), m-F (6.97 and 13.51), and p-F (8.06) atoms for the endo-phenol. These differences contributed to chemical shifts with either all positive or all negative values dependent on the value of 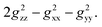 Notably, a distinct difference in values from positive to negative was observed only for o-F atoms (4.62 and −13.78) on Grhombic, which will also result in positive and negative dipolar shifts with
Notably, a distinct difference in values from positive to negative was observed only for o-F atoms (4.62 and −13.78) on Grhombic, which will also result in positive and negative dipolar shifts with 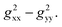
Utilizing the fitting g values (gxx = 2.10, gyy = 1.94, and gzz = 1.99) as described in the ESI,‡ the expressions 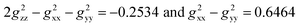 were derived. These g values in conjunction with the Gaxial and Grhombic factors in eqn (3) are applied to the dipolar shifts of exo- and endo-phenol, respectively. The dipolar shifts of exo-phenol at o-F atoms, 55.0 and −11.2 ppm, exhibit a notable difference, yet these values are averaged (21.9 ppm) to accommodate permissible rotation. Additionally, the averaged dipolar shift of the two m-F atoms is −3.3 ppm, and for the single p-F atom, it is −4.8 ppm, as depicted in Table 2. In comparison to its contact shift, the dipolar shift contributes a small amount to the paramagnetic shift. Comparing the dipolar shifts calculated using eqn (4), all these values indicate similarly small impacts on the paramagnetic shift as well. Specifically, they are −11.5 ppm (o-F), 1.1 ppm (m-F), and −22.5 ppm (p-F). For endo-phenol with restricted orientation, the dipolar shifts are revealed as follows: −107.6 ppm (−67.8 ppm from Feendo and −39.8 ppm from Feexo) and 7.2 ppm (24.8 ppm from Feendo and −17.6 ppm from Feexo) for the two o-F atoms, respectively. Comparatively, for the two m-F atoms, one exhibits a dipolar shift of 12.9 ppm (24.6 ppm from Feendo and −11.7 ppm from Feexo), while the other displays a shift of 16.6 ppm (8.5 ppm from Feendo and 8.1 ppm from Feexo). The dipolar shift for the p-F atom is −36.5 ppm (−9.5 ppm from Feendo and −27.0 ppm from Feexo). Notably, the magnitude of the overall dipolar shift in endo-phenol surpasses that of exo-phenol only when considering the influence of Feexo.
were derived. These g values in conjunction with the Gaxial and Grhombic factors in eqn (3) are applied to the dipolar shifts of exo- and endo-phenol, respectively. The dipolar shifts of exo-phenol at o-F atoms, 55.0 and −11.2 ppm, exhibit a notable difference, yet these values are averaged (21.9 ppm) to accommodate permissible rotation. Additionally, the averaged dipolar shift of the two m-F atoms is −3.3 ppm, and for the single p-F atom, it is −4.8 ppm, as depicted in Table 2. In comparison to its contact shift, the dipolar shift contributes a small amount to the paramagnetic shift. Comparing the dipolar shifts calculated using eqn (4), all these values indicate similarly small impacts on the paramagnetic shift as well. Specifically, they are −11.5 ppm (o-F), 1.1 ppm (m-F), and −22.5 ppm (p-F). For endo-phenol with restricted orientation, the dipolar shifts are revealed as follows: −107.6 ppm (−67.8 ppm from Feendo and −39.8 ppm from Feexo) and 7.2 ppm (24.8 ppm from Feendo and −17.6 ppm from Feexo) for the two o-F atoms, respectively. Comparatively, for the two m-F atoms, one exhibits a dipolar shift of 12.9 ppm (24.6 ppm from Feendo and −11.7 ppm from Feexo), while the other displays a shift of 16.6 ppm (8.5 ppm from Feendo and 8.1 ppm from Feexo). The dipolar shift for the p-F atom is −36.5 ppm (−9.5 ppm from Feendo and −27.0 ppm from Feexo). Notably, the magnitude of the overall dipolar shift in endo-phenol surpasses that of exo-phenol only when considering the influence of Feexo.
In accordance with the previously discussed orbital shifts, contact shifts, and dipolar shifts, the overall chemical shifts of the two o-F atoms in endo-phenol exhibit considerable separation. Specifically, one of them is observed at 24.5 ppm, but the other resonance is noteworthy for its extreme upfield position at −184.1 ppm. In contrast, the m-F and p-F atoms exhibit resonances comparable to those of exo-phenol, with the m-F resonating in the upfield region and the p-F resonating in the downfield region, as illustrated in Fig. 5.
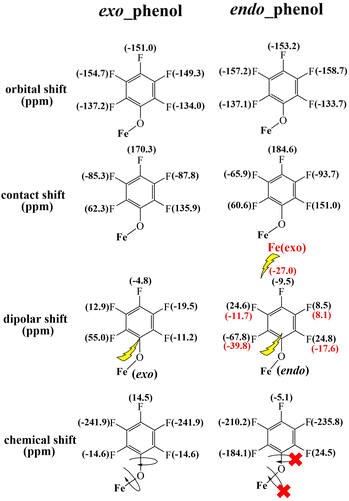 | ||
| Fig. 5 DFT-calculated orbital and contact shifts along with dipolar shifts for the exo–endo dimer 2b. | ||
The parallel scenario is observed in the DFT-calculated NMR spectra for the mono- and disubstituted fluorophenols within the exo–endo dimers, particularly (2d) and (2e), as depicted in Fig. 6. The top panel of Fig. 6A displays the calculated 19F NMR spectrum of 2d considering a potential free rotation for both exo- and endo-phenol. This spectrum displays only downfield chemical shifts similar to those observed in the o-F atoms of the exo-phenol of 2b (−40 to −70 ppm). Conversely, when considering that the phenol within the endo-monomer is anchored between two porphyrin rings, akin to the configuration observed in the endo-phenol of 2b, the calculated NMR peak of the o-F (endo) reveals at −165 ppm. This spectrum notably aligns closely with the experimental distribution, depicted in the lower panel of Fig. 6A.
In the computational analysis of 2e, assuming free rotation for both exo- and endo-phenol, the upper panel of Fig. 6B shows an overlap between the o-F (endo) and o-F (exo) peaks, located at approximately −80 ppm, with two closely situated p-F peaks (endo and exo) observed around 10 ppm. Nevertheless, this pattern deviates from the experimental results. Similar to 2b and 2d, only when endo-phenol is anchored in a preferred orientation while allowing unrestricted rotation of exo-phenol does the resulting 19F NMR spectrum replicate the distinctive upfield-downfield signals observed experimentally, as depicted in the lower panel of Fig. 6B. The DFT-calculated 19F NMR spectra align seamlessly with the experimental spectra, providing robust support for the assertion that the phenol within the endo-monomer is securely positioned between two porphyrin rings in solution (Fig. 6C and D).
In addition, Fig. 7A demonstrates that the fluorine atoms in both exo- and endo-phenol of 2b exhibit similar total spin densities. This suggests that the transfer of the high-spin iron centre to phenol through bonds is identical for both configurations. However, the real impact on the chemical shift arises not directly from these spin densities, but from the spin density on the nuclear centre, represented by 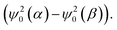 It is important to note that the nuclear spin density is significantly reduced from the total spin density and may exhibit different anisotropies due to respective spin polarization.
It is important to note that the nuclear spin density is significantly reduced from the total spin density and may exhibit different anisotropies due to respective spin polarization.
This anisotropy leads to anisotropic hyperfine constants (Axx, Ayy, and Azz). The averaged hyperfine value, Aiso = (Axx + Ayy + Azz)/3, determines the magnitude of the contact shift, as shown in eqn (2). Generally, atoms with similar total spin densities have similar Aiso. Therefore, when the dipolar shift is disregarded, the chemical shifts for exo- and endo-phenols are quite close. This approach is commonly adopted for most 1H NMR of paramagnetic species as those protons are relatively far from the metal centre.14,15 However, deviations in the hyperfine constants from Aiso result in noticeable differences in NMR chemical shifts, as described by eqn (4). Even a slight change in anisotropy can lead to a significant difference in dipolar shifts due to the spin (S). Fig. 7B highlights the distinct anisotropies of the two o-F atoms, with the size and shape of the ellipsoid representing their hyperfine tensors. This difference in anisotropy explains the observed dipolar shift differences. Magnetic field lines proposed to be induced by the spin densities of the two iron atoms are depicted in Fig. 7C.
To get more insights about the contributions of steric hindrance in the axial phenoxide complexes, geometry optimizations of 2b and 2f have been performed in exo–exo, exo–endo and endo–endo conformations. It has been observed that in the case of 2b which has smaller substituents around the periphery of the phenolato moiety, the exo–endo conformation was found to be more stable compared to endo–endo and exo–exo modes by 15.0 and 17.0 kcal mol−1, respectively in the solution phase (Fig. S16A‡). Contrastingly, for 2f with bulky substituents such as the 2,4-ditertiarybutyl group on the phenol, the exo–exo conformer was found to be the most stable followed by exo–endo and endo–endo conformers (Fig. S16B‡). Phenols containing bulky substituents stabilize the exo–exo conformation whereas, for smaller substituents, the exo–endo conformation is found to be more stable (Fig. S16‡).
Conclusions
An intricate account of structural and spectroscopic study stated here helps discriminate between different axial phenoxide binding inside and outside a paramagnetic cavity created using a pyrrole-bridged Fe(III)porphyrin dimer. The UV-vis, 1H and 19F NMR spectroscopies display very characteristic features in deciphering the phenolato binding in the exo–endo and exo–exo modes. The behaviours of the meta protons in the 1H NMR spectra serve as a crucial tool in discriminating two different types of binding modes. Moreover, the 19F NMR spectra play a pivotal role in identifying substrate binding inside or outside of the paramagnetic cavity with large chemical shifts and thereby recognizing the chemical environment of the cavity. NMR studies also reveal that the solid-state conformations remain unaltered in solution. Complexes with bulky substitution led to the stabilization of the exo–exo conformation whereas with smaller substituents exo–endo conformation is the favoured mode of binding. Computational calculations reproduce the experimentally observed modes of binding in these complexes also. These findings pave the way for making an excellent probe to develop a diagnostic tool for monitoring subtle conformational changes and transient interactions.Data availability
The data supporting this article have been included as part of the ESI.‡Author contributions
S. P. R. conceptualized and supervised the work and wrote the paper along with other coworkers. S. S., S. M. and D. S. performed all the experiments and some of the DFT calculations. C. Q. W. and P. P.-Y. C. have done the DFT calculations related to 19F NMR. The authors have analysed the results together.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank IIT Kanpur for providing all the facilities and support. The Science and Engineering Research Board (SERB), India, and SERB-STAR are gratefully acknowledged for financial support. SPR thanks SERB for giving him the Science and Technology Award for Research (SERB-STAR). Additionally, we thank the National Center for High-performance Computing (NCHC) of National Applied Research Laboratories (NARLabs) in Taiwan for providing computational resources.Notes and references
- (a) Y. Hsia, J. Bale, B. S. Gonen, D. Shi, W. Sheffler, K. K. Fong, U. Nattermann, C. Xu, P. S. Huang, R. Ravichandran, S. Yi, T. N. Davis, T. Gonen, N. P. King and D. Baker, Nature, 2016, 535, 136–139 CrossRef CAS PubMed; (b) Y.-T. Lai, E. Reading, G. L. Hura, K. –L. Tsai, A. Laganowsky, F. J. Asturias, J. A. Tainer, C. V. Robinson and T. O. Yeates, Nat. Chem., 2014, 6, 1065–1071 CrossRef CAS PubMed; (c) M. Rother, M. G. Nussbaumer, K. Rengglic and N. Bruns, Chem. Soc. Rev., 2016, 45, 6213–6249 RSC; (d) Z. Liu, J. Qiao, Z. Niu and Q. Wang, Chem. Soc. Rev., 2012, 41, 6178–6194 RSC.
- (a) D. R. Nelson, in Cytochrome P450: Structure, Mechanism and Biochemistry, ed. P. R. Ortiz de Montellano, Kluwer Academic/Plenum, New York, 2005, 3rd edn Search PubMed; (b) S. Itoh and H. Fujii, in Dioxygen-Binding in Metalloproteins and Corresponding Models, ed. E. C. Constable, G. Parkin and L. Que Jr., Elsevier, Oxford, 2021, p. 200 Search PubMed; (c) S. P. de Visser, Chem.–Eur. J., 2020, 26, 5308–5327 CrossRef CAS PubMed; (d) A. R. Baglia, J. P. T. Zaragoza and D. P. Goldberg, Chem. Rev., 2017, 117, 13320–13352 CrossRef PubMed; (e) T. L. Poulos, Chem. Rev., 2014, 114, 3919–3962 CrossRef CAS PubMed; (f) L. Que Jr and W. B. Tolman, Nature, 2008, 455, 333–340 CrossRef PubMed ;https://pubmed.ncbi.nlm.nih.gov/18800132/-full-view-affiliation-1; (g) Y. Watanabe, H. Nakajima and T. Ueno, Acc. Chem. Res., 2007, 40, 554–562 CrossRef CAS PubMed; (h) W. Nam, Acc. Chem. Res., 2007, 40, 465 CrossRef CAS; (i) I. G. Denisov, T. M. Makris, S. G. Sligar and I. Schlichting, Chem. Rev., 2005, 105, 2253–2278 CrossRef CAS PubMed; (j) B. Meunier, S. P. de Visser and S. Shaik, Chem. Rev., 2004, 104, 3947–3980 CrossRef CAS PubMed; (k) M. Sono, M. P. Roach, E. D. Coulter and J. H. Dawson, Chem. Rev., 1996, 96, 2841–2888 CrossRef CAS PubMed.
- (a) J. Novotny, S. Komorovsky and R. Marek, Acc. Chem. Res., 2024, 57, 1467–1477 CrossRef CAS PubMed; (b) A. Swartjes, P. B. White, J. P. J. Bruekers, J. A. A. W. Elemans and R. J. M. Nolte, Nat. Commun., 2022, 13, 1846–1853 CrossRef CAS PubMed; (c) A. Swartjes, P. B. White, M. Lammertink, J. A. A. W. Elemans and R. J. M. Nolte, Angew. Chem., Int. Ed., 2021, 60, 1254–1262 CrossRef CAS PubMed; (d) J. P. J. Bruekers, M. A. Hellinghuizen, A. Swartjes, P. Tinnemans, P. B. White, J. A. A. W. Elemans and R. J. M. Nolte, Eur. J. Org Chem., 2022, e202200111 CrossRef CAS PubMed; (e) J. Kretschmer, T. David, M. Dracinsky, O. Socha, D. Jirak, M. Vit, R. Jurok, M. Kuchar, I. Cisarova and M. Polasek, Nat. Commun., 2022, 13, 3179–3191 CrossRef CAS PubMed; (f) M. D. Ward, C. A. Hunter and N. H. Williams, Acc. Chem. Res., 2018, 51, 2073–2082 CrossRef CAS PubMed; (g) J. Chyba, A. Hruzikova, M. Knor, P. Pikulova, K. Markova, J. Novotny and R. Marek, Inorg. Chem., 2023, 62, 3381–3394 CrossRef CAS PubMed; (h) J. Zhang, W. Kosaka, H. Sato and H. Miyasaka, J. Am. Chem. Soc., 2021, 143, 7021–7031 CrossRef CAS PubMed; (i) J. C. Ott, E. A. Suturina, I. Kuprov, J. Nehrkorn, A. Schnegg, M. Enders and L. H. Gade, Angew. Chem., Int. Ed., 2021, 133, 23038–23046 CrossRef; (j) M. Lehr, T. Paschelke, E. Trumpf, A.-M. Vogt, C. Nather, F. D. Sonnichsen and A. J. A. McConnell, Angew. Chem., Int. Ed., 2020, 59, 19344–19351 CrossRef CAS PubMed; (k) K. Du, D. Zemerov, S. H. Parra, J. M. Kikkawa and I. J. Dmochowski, Inorg. Chem., 2020, 59, 13831–13844 CrossRef CAS PubMed; (l) Y. Zhao, G. Markopoulos and T. M. Swager, J. Am. Chem. Soc., 2014, 136, 10683–10690 CrossRef CAS PubMed.
- (a) F. S. T. Khan, S. J. Shah, S. Bhowmik, F. G. C. Reinhard, M. A. Sainna, S. P. de Visser and S. P. Rath, Dalton Trans., 2019, 48, 6353–6357 RSC; (b) F. S. T. Khan, A. K. Pandey and S. P. Rath, Chem.–Eur. J., 2016, 22, 16124–16137 CrossRef CAS PubMed; (c) S. Bhowmik, S. Dey and S. P. Rath, Chem.–Eur. J., 2013, 19, 13732–13744 CrossRef CAS PubMed; (d) A. Chaudhary, R. Patra and S. P. Rath, Eur. J. Inorg. Chem., 2010, 5211–5221 CrossRef CAS.
- (a) P. Campomanes, U. Rothlisberger, M. Alfonso-Prieto and C. Rovira, J. Am. Chem. Soc., 2015, 137, 11170–11178 CrossRef CAS PubMed; (b) A. Takahashi, T. Kurahashi and H. Fujii, Inorg. Chem., 2009, 48, 2614–2625 CrossRef CAS PubMed; (c) D. Kanamori, Y. Yamada, A. Onoda, T. Okamura, S. Adachi, H. Yamamoto and N. Ueyama, Inorg. Chim. Acta, 2005, 358, 331–338 CrossRef CAS; (d) L. Cheng, M. A. Khan, D. R. Powell, R. W. Taylor and G. B. Richter-Addo, Chem. Commun., 1999, 1941–1942 RSC; (e) R. D. Arasasingham, A. L. Balch, C. R. Cornman, J. S. de Ropp, K. Eguchi and G. N. La Mar, Inorg. Chem., 1990, 29, 1847–1850 CrossRef CAS.
- M. Kasha, H. R. Rawls and M. A. El-Bayoumi, Pure Appl. Chem., 1965, 11, 371–392 CAS.
- Crystal data for 2a: triclinic, space group P
![[1 with combining macron]](https://www.rsc.org/images/entities/i_char_0031_0304.gif) , Z = 2, a = 12.778(5) Å, b = 16.435(5) Å, c = 21.845(5) Å, α = 82.660(5)°, β = 82.881(5)°, γ = 80.640(5)°, V = 4464(2) Å3. dcalcd = 1.325 g cm−3; T = 100(2) K, goodness of fit on F2 = 1.021; R1 = 0.0699 (for I > 2σ(I)), wR2 (all data) = 0.1768. For 2b: monoclinic, space group I2/a, Z = 8, a = 34.122(3) Å, b = 14.8098(17) Å, c = 35.216(4) Å, β = 100.218(10)°, V = 17514(3) Å3. dcalcd = 1.282 g cm−3; T = 100(2) K, goodness of fit on F2 = 1.013; R1 = 0.0821 (for I > 2σ(I)), wR2 (all data)= 0.2443. For 2f: monoclinic, space group C2/c, Z = 4, a = 24.4285(14) Å, b = 17.2727(14) Å, c = 23.7474(15) Å, β = 98.248(3)°, V = 9916.5(12) Å3. dcalcd = 1.162 g cm−3; T = 100(2) K, goodness of fit on F2 = 1.061; R1 = 0.0351 (for I > 2σ(I)), wR2 (all data) = 0.0902. CCDC-2357051, 2357052 and 2357053 contain the supplementary crystallographic data of 2a, 2b and 2f, respectively, for this paper..
, Z = 2, a = 12.778(5) Å, b = 16.435(5) Å, c = 21.845(5) Å, α = 82.660(5)°, β = 82.881(5)°, γ = 80.640(5)°, V = 4464(2) Å3. dcalcd = 1.325 g cm−3; T = 100(2) K, goodness of fit on F2 = 1.021; R1 = 0.0699 (for I > 2σ(I)), wR2 (all data) = 0.1768. For 2b: monoclinic, space group I2/a, Z = 8, a = 34.122(3) Å, b = 14.8098(17) Å, c = 35.216(4) Å, β = 100.218(10)°, V = 17514(3) Å3. dcalcd = 1.282 g cm−3; T = 100(2) K, goodness of fit on F2 = 1.013; R1 = 0.0821 (for I > 2σ(I)), wR2 (all data)= 0.2443. For 2f: monoclinic, space group C2/c, Z = 4, a = 24.4285(14) Å, b = 17.2727(14) Å, c = 23.7474(15) Å, β = 98.248(3)°, V = 9916.5(12) Å3. dcalcd = 1.162 g cm−3; T = 100(2) K, goodness of fit on F2 = 1.061; R1 = 0.0351 (for I > 2σ(I)), wR2 (all data) = 0.0902. CCDC-2357051, 2357052 and 2357053 contain the supplementary crystallographic data of 2a, 2b and 2f, respectively, for this paper.. - (a) W. R. Scheidt, in The Porphyrin Handbook, ed. K. M. Kadish, K. M. Smith and R. Guillard, Academic Press, San Diego, 2000; vol. 3, p. 49 Search PubMed; (b) W. R. Scheidt and C. A. Reed, Chem. Rev., 1981, 81, 543–555 CrossRef CAS.
- (a) P. Chakraborty, N. Ghosh, N. Awasthi and S. P. Rath, Chem.–Eur. J., 2024, 30, e202400266 Search PubMed; (b) D. Lai, F. S. T. Khan and S. P. Rath, Dalton Trans., 2018, 47, 14388–14401 Search PubMed; (c) T. Guchhait, S. Sasmal, F. S. T. Khan and S. P. Rath, Coord. Chem. Rev., 2017, 337, 112–144 Search PubMed; (d) D. Sahoo, M. G. Quesne, S. P. de Visser and S. P. Rath, Angew. Chem., Int. Ed., 2015, 54, 4878–4882 CrossRef PubMed.
- (a) R. Weiss, A. Gold and J. Terner, Chem. Rev., 2006, 106, 2550–2579 Search PubMed; (b) M. Nakamura, Chem. Rev., 2006, 250, 2271–2294 Search PubMed; (c) Y. Ling and Y. Zhang, J. Am. Chem. Soc., 2009, 131, 6386–6388 CrossRef CAS PubMed; (d) D. Sakow, D. Baabe, B. Bçker, O. Burghaus, M. Funk, C. Kleeberg, D. Menzel, C. Pietzonka and M. Brçring, Chem.–Eur. J., 2014, 20, 2913–2924 Search PubMed.
- (a) H. Kalish, J. E. Camp, M. Stępień, L. Latos-Grażyński, M. M. Olmstead and A. L. Balch, Inorg. Chem., 2002, 41, 989–997 CrossRef CAS PubMed; (b) S. P. Rath, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2004, 126, 6379–6386 CrossRef CAS PubMed.
- (a) I. Bertini, C. Luchinat, G. Parigi and E. Ravera, in NMR of Paramagnetic Molecules, Elsevier, Amsterdam, 2017, 2nd edn Search PubMed; (b) F. A. Walker, in Handbook of Porphyrin Science, ed. K. M. Kadish, K. M. Smith and R. Guilard, World Scientific, Singapore, 2010, vol. 6, p. 1 Search PubMed; (c) M. Nakamura, in The Handbook of Porphyrin Science, ed. Y. Ohgo, A. Ikezaki, K. M. Kadish, K. M. Smith and R. Guilard, Word Scientific, Singapore, 2010, vol. 7, p. 1 Search PubMed; (d) G. N. La Mar, W. De, W. Horrocks and R. H. Holm, in NMR of Paramagnetic Molecules, Academic Press, New York, 1973, p. 694 Search PubMed.
- (a) L. Cosottini, S. Zineddu, L. Massai, V. Ghini and P. Turano, J. Inorg. Biochem., 2023, 244, 112236–112240 CrossRef CAS PubMed; (b) A. M. Gronenborn, Structure, 2022, 30, 6–14 CrossRef CAS PubMed; (c) D. Xie, M. Yu, R. T. Kadakia and E. L. Que, Acc. Chem. Res., 2020, 53, 2–10 CrossRef CAS PubMed; (d) Y. Huang, X. Wang, Lv. Guohua, A. M. Razavi, G. H. M. Huysmans, H. Weinstein, C. Bracken, D. Eliezer and O. Boudker, Nat. Chem. Biol., 2020, 16, 1006–1012 CrossRef CAS PubMed; (e) J. Blahut, L. Benda, J. Kotek, G. Pintacuda and P. Hermann, Inorg. Chem., 2020, 59, 10071–10082 CrossRef CAS PubMed; (f) Z. Xu, C. Liu, S. Zhao, S. Chen and Y. Zhao, Chem. Rev., 2019, 119, 195–230 CrossRef CAS PubMed; (g) K. L. Peterson, K. Srivastava and V. C. Pierre, Front. Chem., 2018, 6, 160–180 CrossRef PubMed; (h) A. E. Thorarinsdottir, A. I. Gaudette and T. D. Harris, Chem. Sci., 2017, 8, 2448–2456 Search PubMed; (i) A. A. Kislukhin, X. Hongyan, S. R. Adams, K. H. Narsinh, R. Y. Tsein and E. T. Ahrens, Nat. Mater., 2016, 15, 662–668 CrossRef CAS PubMed; (j) I. Tirotta, V. Dichiarante, C. Pigliacelli, G. Cavallo, G. Terraneo and F. B. Bombelli, Chem. Rev., 2015, 115, 1106–1129 CrossRef CAS PubMed; (k) C. Belle, C. Béguin, S. Hamman and J.-L. Pierre, Coord. Chem. Rev., 2009, 253, 963–976 CrossRef CAS.
- (a) A. Kehl, M. Hiller, F. Hecker, I. Tkach, S. Dechert, M. Bennati and A. Meyer, J. Magn. Reson., 2021, 333, 107091–107101 CrossRef CAS PubMed; (b) I. Bertini, C. Luchinat and G. Parigi, Prog. Nucl. Magn. Reson. Spectrosc., 2002, 40, 249–273 Search PubMed; (c) I. Bertini, C. Luchinat and G. Parigi, Solution NMR of Paramagnetic Molecules: Applications to Metallobiomolecules and Models, Elsevier Science Ltd., New York, 2001 Search PubMed; (d) A. Kehl, I. Bertini, C. Owens, C. Luchinat and R. S. Drago, J. Am. Chem. Soc., 1987, 109, 5208–5212 Search PubMed; (e) A. Dei, D. Gatteschi and E. Piergentili, Inorg. Chem., 1979, 18, 89–93 CrossRef CAS; (f) R. J. Kurland and B. R. McGarvey, J. Magn. Reson., 1970, 2, 286–301 CAS; (g) G. F. Kokoszka and R. W. Duerst, Coord. Chem. Rev., 1970, 5, 209–244 CrossRef CAS; (h) P. Hrobárik, R. Reviakine, A. V. Arbuznikov, O. L. Malkina, V. G. Malkin, F. H. Köhler and M. Kaupp, J. Chem. Phys., 2007, 126, 024107–024119 CrossRef PubMed; (i) A. Borgogno, F. Rastrelli and A. Bagno, Dalton Trans., 2014, 43, 9486–9496 RSC; (j) W. C. Isley III, S. Zarra, R. K. Carlson, R. A. Bilbeisi, T. K. Ronson, J. R. Nitschke, L. Gagliardi and C. J. Cramer, Phys. Chem. Chem. Phys., 2014, 16, 10620–10628 RSC; (k) A. G. Nobile, D. Trummer, Z. J. Berkson, M. Wörle, C. Copéret and P. A. Payard, Chem. Sci., 2023, 14, 2361–2368 Search PubMed; (l) A. Borgogno, F. Rastrelli and A. Bagno, Chem.–Eur. J., 2015, 21, 12960–12970 Search PubMed.
- (a) C. C. Chen, Y. W. Wu, M. Nakamura, R. J. Cheng, T. H. Tseng and P. P. Y. Chen, Dalton Trans., 2019, 48, 13820–13833 RSC; (b) R.-J. Cheng, C.-H. Ting, T.-C. Chao, T.-H. Tseng and P. P.-Y. Chen, Chem. Commun., 2014, 50, 14265–14268 Search PubMed; (c) C.-C. Chen and P. P.-Y. Chen, Angew. Chem., Int. Ed., 2012, 51, 9325–9329 CrossRef CAS PubMed.
Footnotes |
| † Dedicated to Professor Vinod K. Singh on the occasion of his 65th birthday. |
| ‡ Electronic supplementary information (ESI) available: text, figures, tables depicting detailed experimental procedures, product characterization, and DFT. CCDC 2357051–2357053. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc05432f |
| This journal is © The Royal Society of Chemistry 2024 |