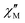A highly conducting tetrathiafulvalene-tetracarboxylate based dysprosium(III) 2D metal–organic framework with single molecule magnet behaviour

Abstract

The synthesis and whole characterization by a multitechnique approach of an unprecedented dysprosium(III) 2D metal organic framework (MOF), involving the redox-active tetrathiafulvalene (TTF)-based linker TTF-tetracarboxylate (TTF-TC), are herein reported. The single-crystal X-ray structure, formulated as [Dy₆(TTF-TC)₅(H₂O)₂₂]·21H₂O (1), reveals a complex 2D topology, with hexanuclear Dy₆ clusters as secondary building units (SBUs) interconnected by five linkers, stacked almost parallel in each layer and eclipsed along the [111] direction, leading to the formation of 1D channels filled by water molecules. The mixed valence of the TTF units is confirmed by both bond distance analysis, Raman microscopy and diffuse reflectance spectroscopy, and further supported by band structure calculations, which also predict activated conductivity for this material. Thanks to efficient TTF stacking and partial oxidation, 1 shows semiconducting behavior, with, however, a record conductivity value of 1 mS cm⁻¹ at room temperature, when compared to the previously reported TTF-based MOFs. Furthermore, temperature and magnetic field dependent ac (alternative current) magnetic susceptibility measurements demonstrate field induced slow relaxation of magnetization, accounting for two independent relaxation processes, with an energy barrier (U_eff/K) of around 12 K, typical for dysprosium carboxylate complexes. The herein reported 2D Dy-MOF provides a valuable master plan for coexistence of conducting π-TTF stacks and highly anisotropic Dy^III SMM properties.

---

Introduction

Metal organic frameworks (MOFs) are an important class of versatile networks formed by self-assembling of organic molecules (linkers) and metal ions (nodes) onto crystalline supramolecular architecture, showing intrinsic porosity. Complementing their porosity with conducting and/or magnetic properties drives the interest from the molecular level towards new technological applications.^1–4 More specifically, their crystalline structures, which exhibit highly ordered patterns, may represent challenging pathways for efficient electron transport,³ paving the way towards intriguing new applications in the fields of electrocatalysis,⁵ batteries,⁶ supercapacitors,⁷ electrochemical sensing,⁸ optoelectronics⁹ and molecular spintronics.^10,11 Most importantly, incorporation of redox activity on the linker is an emerging strategy to enhance charge transport in such supramolecular frameworks,^3,12 and among redox-active molecules, tetrathiafulvalene (TTF) and its derivatives are the most widely used for the development of organic conductors since 50 years, such as radical cation salts and charge transfer complexes, showing semiconducting, room temperature metallic and low-temperature superconducting behavior.^13–15 On the other hand, MOFs based on TTF linkers started to be developed since the discovery of the first permanent porous Zn₂(TTF-TB) (TTF-TB = tetrathiafulvalene-tetrabenzoate) conductive TTF-MOF (c-MOF) in 2012.¹⁶ To date, several TTF-MOFs have been reported and most of them behave as semiconductors with moderate to modest RT conductivity in the 10⁻⁴ to 10⁻⁹ S cm⁻¹ range.³ Conductivity in TTF materials is strongly dependent on the S⋯S intermolecular interactions and on the oxidation state, due to through space band-like charge transport mechanism; as a simple rule, high conductivity is reached when short S⋯S distances and holes are present in the structure with the possibility of generating mixed-valence oxidation states.¹⁷ Commonly, holes in TTF-based MOFs are generated by post-synthetic procedures (like iodine doping),^18,19 which show the major drawbacks of a difficult control of the final oxidation state, a reduction in porosity and crystallinity due to guest insertion and the instability of the holes generated.^19–23 Consequently, occurrence of mixed-valence states in TTF-MOFs, necessary for a highly conductive material, is scarce.²⁴ It is worth mentioning that metallic behavior in MOFs is rare and it was found only in few catecholate based networks.^25,26 Indeed the best performing c-MOFs are based on these systems, although they are still semiconductors for a very large majority of them.²⁷

On the other hand, the so-called single molecule magnets (SMMs) show superparamagnetic behavior at a molecular level^28–30 and they are among the best candidates to realize next-generation spintronic devices,³¹ particularly those based on lanthanide ions, which gave promising results, especially with Dy^III ions.³² Although several complexes have been studied, reports on slow relaxation of magnetization in lanthanide MOFs are still rare, yet under ever-growing investigation, due to the possibility of obtaining multifunctional materials with intriguing physical properties and ordered SMM centers.^33–36 Slow relaxation was already reported in several TTF–Ln complexes and more recently in TTF-MOFs.^18,21,37 The main strategy to obtain highly conducting SMMs is to combine electroactive molecules, interacting within layers and providing partially filled bands, and SMM units in a solid network. Thus, the combination of Ln-SMMs as SBU with electroactive linkers within MOFs can afford high conductivity, slow relaxation of magnetization and porosity in the same crystal lattice, as prerequisites for innovative molecular materials for spintronic devices.^10,38 Herein, we report on the synthesis and structural characterization of a 2D layered Dy^III-MOF with the TTF-based linker TTF-tetracarboxylate (TTF-TC), which exhibits a rare topology. The careful choice of the synthetic protocol allows obtaining a mixed valence of the TTF units, confirmed by single crystal X-ray structure analysis, Raman microscopy and diffuse reflectance spectroscopy. The strong orbital overlap interactions between the electroactive linkers are responsible for the remarkably high conductivity observed in the MOF, with, however, a thermally activated mechanism, supported by tight binding band structure calculations. Interestingly the herein reported c-MOF also shows field induced slow relaxation of the magnetization, due to the presence of the highly anisotropic Dy^III ions.

Results and discussion

Synthesis

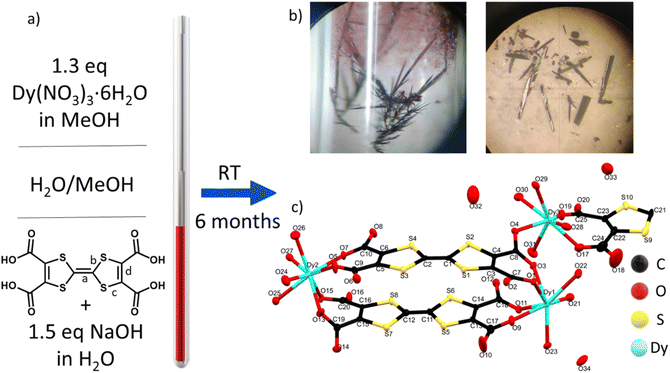
TTF-tetracarboxylate (TTF-TC) is a well-known linker used to form several CPs and MOFs with different s and d metal ions,^39,40 although no structures with lanthanide ions have been reported until now in the Cambridge structural database.⁴¹ The linker was already used in a solvothermal reaction with Ln^III to give a series of MOFs where the linker is doubly decarboxylated.³⁷ Indeed, the instability at high temperature was pointed out also by Nguyen et al. during their test on the synthesis of CPs with alkali metal ions.⁴² In their case the temperature was kept under 100 °C and for both reasons we used the same precaution during our experiments.⁴² A room temperature synthetic protocol, the layering technique, was selected for different reasons: (i) the instability of the linker under typical solvothermal conditions; (ii) it is particularly suitable for obtaining large single crystals for X-ray diffraction studies and conductivity measurements;⁴³ (iii) the prolonged reaction time under air can trigger mixed-valence and high conductivity as reported in a TTF single component conductor based on a TTF-extended dicarboxylate.⁴⁴ The layering parameters such as tube size, mixture of solvents, temperature, concentrations and pH were carefully varied in order to isolate this mixed-valence phase. In particular, [Dy₆(TTFTC)₅(H₂O)₂₂]·(H₂O)₂₁ (1) was synthesized by layering a methanol solution of the trivalent lanthanide ion on top of a water solution of TTF-TC, with addition of 1.5 eq of NaOH to partially deprotonate the linker; the base was used in order to provide better solubility while maintaining a neutral pH (checked by pH indicator paper) in order to avoid Dy₂O₃ and hydroxide precipitation, observed at higher pH. The linker in water solution was let to diffuse through a buffer of MeOH/H₂O for several months in a long and thin tube containing a solution of Dy(NO₃)₃ in MeOH on the top (Fig. 1a and b). It is well known that TTF molecules can spontaneously be oxidized under solvothermal conditions or by action of oxygen and/or a protonation–deprotonation mechanism.^24,44 In this case, thanks to the long diffusion time, the solvent mixture and the selected pH, both oxidation and full deprotonation of the linker occurred. The presence of both radical and neutral linker in the media triggered the formation of a phase in which TTF molecules do not have the same oxidation state (vide infra) affording single crystals of the MOF at the interphase (Fig. 1a and b); our attempts to obtain the MOF in shorter time and reasonable yield by other methods such as one-pot reactions at RT and high temperature, electrocrystallization and layering reactions at high temperature were not successful. Indeed, a purple microcrystalline unoxidized phase was obtained as impurity when the reaction time was reduced, by acting on the temperature and size of the tubes, and in these cases the separation of the two phases was challenging or almost impossible due to low yield of the target. The same phase was obtained in one-pot reactions, while when temperature is increased a mononuclear complex was obtained, pointing out the crucial role of the synthetic protocol in the obtainment of our target. Indeed, the thin and small tube, let undisturbed in a dark room at constant temperature for 6 months, allowed easy isolation of big crystals of the compound (around 1 mg per tube), without big effort, in a reproducible way and avoiding the risk of collecting other impurities. This slow oxidation and prolonged reaction time, even several months, revealed to be a valid strategy to induce mixed valence in TTF-MOFs and to grow suitable single crystals for conductivity measurements. We have been trying as well to decrease the reaction time by using the electrocrystallization method, but, as for the other attempts, it has not been successful until now.

Fig. 1 (a) Schematic representation of the synthetic procedure for 1; (b) optical microscope image of the crystals inside the tube and after filtration; (c) ellipsoid representation of the asymmetric unit with atom labels with 50% probability. H atoms omitted for clarity.

Crystal structure of [Dy₆(TTFTC)₅(H₂O)₂₂]·(H₂O)₂₁ (1) and topological analysis

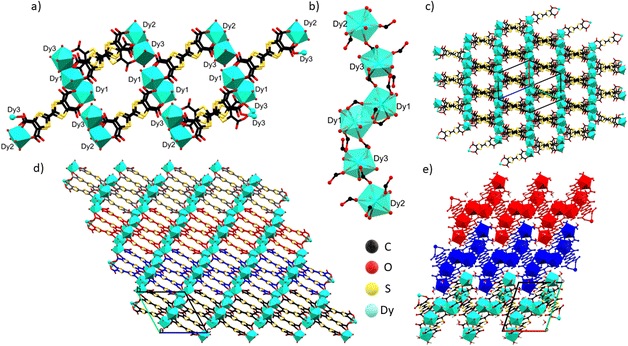
Compound 1 crystallizes in the triclinic P1̄ space group with 2.5 fully deprotonated ligands, three Dy^III cations, 11 water molecules coordinated and 10.5 uncoordinated per asymmetric unit, three of them located inside the structure and the others modeled through solvent mask (Fig. 1c). The unit formula thus corresponds to [Dy₆(TTFTC)₅(H₂O)₂₂]·21H₂O. Assuming a trivalent state of the Dy cations and fully deprotonated linkers, by stoichiometry 18 positive charges are obtained, derived from 6 Dy^III and 20 negative charges from 5 linkers, therefore, for charge compensation, two holes per formula unit are expected as a consequence of the partial oxidation of the TTF moieties. This was confirmed through structural analysis, Raman microscopy, diffuse reflectance spectroscopy and band structure calculations (vide infra). Interestingly, the three independent Dy^III ions show different types of coordination. Continuous shape measurements (CShMs) in Shape 2.1 software⁴⁵ was used to calculate deviation from the ideal polyhedron geometry with a given coordination number, and the lowest deviation value was used to assign the coordination mode: (i) Dy1 is ennea-coordinated with a Muffin (MFF-9) like geometry and C_s symmetry, the coordination sphere contains 3 O from water molecules and 6 O from carboxylate; (ii) Dy2 is octa-coordinated with a bi-augmented trigonal prism J50 (JBTPR-8) like geometry and C_2v symmetry, the coordination sphere contains 4 O from water molecules and 4 O from carboxylate; (iii) Dy3 is octa-coordinated with a Snub diphenoid J84 (JSD-8) like geometry and D_2d symmetry, and the coordination sphere contains 4 O from water molecules and 4 O from carboxylates. The three Dy^III ions show large CShM values indicating highly distorted coordination geometries. The Dy–O distances are between 2.29 and 2.49 Å, comparable to those obtained for other TTF-Dy MOFs.^18,46 A summary of selected distances, angles and shape parameters is listed in Table S1.‡ The Dy^III ions are interconnected by a complex pattern of bridging deprotonated carboxylate groups of different linker anions and arranged in a linear zigzag-like Dy₆ clusters lying along the [−111] direction. They act as secondary building units (SBUs), with a Dy01 dimer in the central position, generated after inversion operation. O1 and O2 link the two Dy01 in the central dimer by two carboxylates with a μ₂-η²: η¹ bridging mode, O3–O4 and O13–O14 link Dy1 to Dy3 and Dy3 to Dy2, respectively, by one carboxylate with a μ₂-η¹: η¹ bridging mode (Fig. 2a and b). The SBUs are linked together thanks to the tetratopic nature of the linker in a 2D polymeric layered structure and stack parallel to the a axis (Fig. 2c and d), resulting in a complex topology (vide infra). The intra Dy₆ Dy⋯Dy distances are in the 4.10–5.69 Å range (shortest within the Dy1 dimer and longest for Dy3⋯Dy2). In the packing the cations are segregated in a 2D layer at the edge of the 1D open channel, with relatively short contacts between different SBUs, e.g., 6.420 Å for Dy3⋯Dy1 (intralayer) and 6.144 Å for Dy3⋯Dy2 (interlayer), respectively (Table S2‡). Five TTF-TC anions are almost eclipsed and stacked parallel to the [111] direction inside a single 2D layer linking different SBUs and defining the 2D network. The layers are similarly eclipsed, allowing the formation of infinite 1D voids (Fig. S2a‡) and packed together thanks to both short S⋯S contacts between neighboring TTFs of two independent layers and to the “Tetris-like” disposition of the zigzag Dy₆ clusters. The latter allows multiple H-bonding interactions between water molecules and coordinated and uncoordinated O from carboxylates located at the edge of the layers (Fig. 2e and S1‡). The uncoordinated water molecules are located inside the 1D channels parallel to the stacking direction of the TTF cores. The channels have an elliptical cylinder shape, the radius of the largest spherical void is 2.6 Å (calculated with Olex2)⁴⁷ and the void space corresponds to 24.6% of the unit cell after removing uncoordinated solvent molecules inside the 1D channel from the structure. We calculated the surface area of 202.65 m² g⁻¹ by using a pore analyzer in Mercury⁴⁸ with a maximum pore aperture of 5.54 Å. Moreover, open 1D channels give a narrow pore size distribution, by Monte-Carlo simulations performed on Poreblazer4.0,⁴⁹ centered at around 5 Å, the result being in agreement with the other calculated parameters (Table S3‡). The compound, due to its connectivity and potential porosity, is well described as a 2D layered MOF with 1D open voids.

Fig. 2 (a) Crystal packing fragment highlighting the connectivity of the SBUs; (b) coordination environment in Dy₆ clusters that act as an SBU; (c) crystal packing along [111]; (d) crystal packing along the a axis, C atoms from different layers are black, blue, red and grey; (e) crystal packing along the c axis, red and blue colored atoms belong to different layers. H atoms and uncoordinated water molecules are omitted for clarity.

Thermogravimetric analysis (TGA) and elemental analysis (Experimental section) data of the bulk correspond well with the X-ray diffraction solvation findings. The TGA (Fig. S2b‡) shows a gradual weight loss of 11.5% between 25 and 100 °C, due to the evacuation of water molecules contained in the pores. The value is slightly higher than the calculated one (10.5%) and it may account for the presence of more H₂O molecules in the voids (suggested also by elemental analysis), due to the solvent mask procedure and the low crystal acquisition temperature, and/or to the simultaneous loss, in this temperature range, of water molecules weakly coordinated to Dy^III. In the range 100–265 °C a weight loss is present (broad peak of the dTGA centered at ∼215 °C) assigned to the loss of around 16 water molecules per formula unit coordinated to the metal ion. This c-MOF shows excellent stability, and the structure starts to slowly collapse at about 320 °C, with a peak in the dTGA at 400 °C. At T > 400 °C linker decomposition processes may occur.

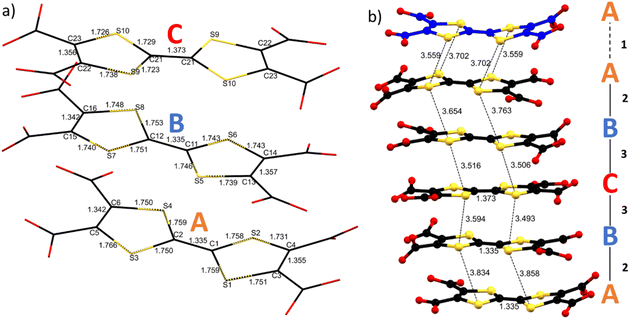
As already mentioned (vide supra), the S⋯S intermolecular interactions are the driving force for a good overlap between the 3p_z orbitals of the S atoms and formation of band-like transport in TTF-based materials. Considering the two and a half independent TTFs in the asymmetric unit, one can define three independent linkers A, B and C. The five TTFs stacking in a single layer are arranged within an ABCBA sequence giving three different types of intramolecular interactions: A–A (1), interlayer; A–B (2) and B–C (3) intralayers. Single crystal structural data show short S⋯S contact distances between 3.49 and 3.86 Å, the intralayer ones being 3.49–3.59 Å for B⋯C, and 3.86–3.65 Å for A⋯B, while the interlayer ones fall in the middle, i.e., 3.56–3.70 Å. The B–C–B trimer in the middle of the layer and A–A dimer between the layers show 4 and 2 strong S⋯S interactions respectively (distances shorter than the sum of the van der Waals radii ∼3.65 Å). The A⋯B interaction seems weaker, with only one S⋯S distance close to 3.6 Å (Fig. 3 and Table S4‡). TTF core distances are sensitive to the oxidation state of the linker.

Fig. 3 (a) Wireframe representation of the three independent TTF-TC anions in the structure with labels and distances; (b) ball and stick representation of the A–ABCBA TTF chain with the shortest S⋯S contacts, intralayer interactions straight line, interlayer dotted line.

According to molecular orbital analysis it is well known that C=C distances increase and internal C–S distances decrease upon oxidation and generally the C=C central bond shows higher sensitivity.⁵⁰ By using the equation δ = (b + c) – (a + d), we can define a δ parameter that decreases as the charge increases, analogous to the one used to determine the charge (ρ) state in other TTF salts, where a is the C=C distance between the two TTF five-membered rings; b and c are the C–S distances; d is the C=C distance within the five-membered rings (see Fig. 1).⁵¹ For TTF-TC no statistical analysis of this parameter was done due to the lack of data. Indeed, to the best of our knowledge, only one example was reported for ρ = +1 (ref. 42) and, comparing different coordination polymers, these distances seem also sensitive to the protonation state, coordination, and presence of few amounts of TTF-TC⁺˙ (see Tables 1 and S4‡). The three independent linkers in 1 show different TTF core distances suggesting non-uniform charge partition. The central linker (C) shows a higher degree of oxidation as suggested by the elongation of the C=C bond and the contraction of the C–S bonds with respect to A and B, in accordance with literature values for mono-oxidized and neutral TTFs. Indeed, δ parameters are 0.823, 0.806 and 0.729 for A, B and C respectively, close to the values obtained for TTF-TC and TTFTC⁺˙ in CPs (see Table 1 and Fig. 3 for details). Considering these values, we can assume that at least one of the two holes is mostly located in the central TTF (C). On the other hand, bond distances for A and B are in accordance with the neutral state, so by structural analysis alone it is not fully clear which is the charge repartition in the ABCBA chain, although the flat conformation of TTF (B) and slightly lower δ may be associated with a partially charged state. To understand better the connectivity of the 2D network, Topospro⁵² was used to determine the topology by using the standard representation algorithm. In this model, TTF (C), that links two Dy3 from independent clusters, and Dy2, that connects TTF (A) to TTF (B), can be described as a single edge. TTF (A) is a four-connected node and TTF (B), Dy1 and Dy3 are three-connected nodes. The result is a rare 3³4L70 topology (Fig. 4), completely different with respect to compounds involving rare earth trivalent cations and tetrathiafulvalene tetrabenzoate (TTF-TB) as the linker.⁵³ Indeed, using TopCryst⁵⁴ we found only one example with the same connectivity corresponding to a Cu^I 2D coordination network obtained by Juvenal et al.⁵⁵

Table 1 TTF bond distances (Å) and d parameter for 1 and calculated δ parameters

	a	b	b′	c	c′	d	δ	δ mean
TTF(A)1	1.335	1.759	1.758	1.731	1.751	1.355	0.810	0.823
TTF(A)2	1.335	1.750	1.759	1.75	1.766	1.342	0.836
TTF(B)1	1.335	1.746	1.743	1.743	1.739	1.357	0.794	0.806
TTF(B)2	1.335	1.753	1.751	1.74	1.748	1.342	0.819
TTF(C)	1.373	1.729	1.723	1.738	1.726	1.356	0.729	0.729

---

Fig. 4 (a) Topology representation using Topospro superimposed to the capped stick representation of a single layer; topological descriptors are labelled and for simplicity two subsets are generated, ZA and ZB corresponding to the linker and Dy^III, respectively. (b) Top view of the topology; ABCBA chain, Dy₆ and position of the 1D channel are highlighted. H atoms omitted for clarity.

Raman microscopy & UV-vis NIR diffuse reflectance

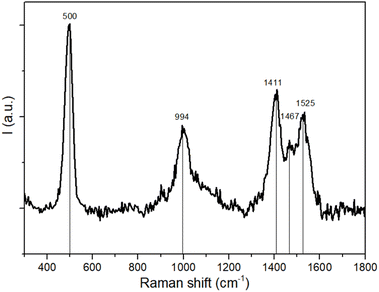
Raman spectroscopy is broadly used in the field of TTF-based materials to assign the charge state of the TTF core thanks to the strong sensitivity of C=C stretching vibration modes, red-shifted upon oxidation. For organic radical salts it is possible to obtain information about charge distribution, charge ordering and charge transfers.^56–58 Herein, the Raman spectrum shows one sharp band at 500 cm⁻¹, one band at ≈1000 cm⁻¹ and three bands between 1400 and 1600 cm⁻¹ (Fig. 5). According to the experimental and computational studies on the same linker reported in the literature, TTF-TC in the neutral state shows a single band at ≈1550 cm⁻¹ in the C=C stretching vibration mode region and bands at ≈500 cm⁻¹ and 1400 cm⁻¹, which may be assigned to the presence of TTF-TC⁺˙. So the peak at 500 cm⁻¹ can be assigned to the S–C stretching mode typical of the five-membered radical ring of TTF-TC⁺˙, the peak at 1525 cm⁻¹ to the symmetric stretching of the outer C=C bonds coupled to the central C=C stretching mode in neutral TTF-TC, and the peak at 1411 cm⁻¹ to the stretching of the C=C bond in the radical TTF-TC⁺˙. These bands are in accordance with the literature values.^59,60 The peak at ≈994 cm⁻¹ may be assigned to a ν(C–C), ν(C–S) combination mode.^61,62 The peak at 1467 cm⁻¹ suggests the presence of a +0.5 partially charged state (TTF-TC⁺˙/TTF-TC) of the linker. Indeed it is known that different bands, due to charge localization, can be present in TTF radical cation salts.⁶³ The spectra are similar to those of the series of air oxidized MOFs, where the presence of both TTF-TC⁺˙ and TTF-TC⁺˙/TTF-TC is confirmed by different spectroscopic data, with three bands in the region of the C=C stretching mode.⁶⁴ The band at 1467 falls in the middle of the others, and assuming a linear relationship between the Raman shift of the C=C stretching modes and the charge as already reported for other mixed valence systems, the linear regression fit considering ρ as a function of Raman shift gives ν = −114ρ + 1524.7 and R² = 0.9999, as a further confirmation of these assignments. The Raman spectra confirm the different charge distributions and clarify that one of the two holes in the ABCBA chain is due to the presence of the ρ = +1 linker and the other to the presence of two linkers with ρ = +0.5. It is thus reasonable to assume that the more oxidized TTF (C) has ρ = +1 charge and two of the other TTFs in the chain should have partially oxidized states. Due to the flat geometry of the ρ = +0.5 state, it can be proposed that the two TTF (B) in the ABCBA chain are partially oxidized. It results in a charge distribution of +0.5/+1/+0.5, already reported for other compounds with a rare A–B–A TTF trimer motif.⁶⁵ Consequently, TTF (A) should be in a neutral state.

Fig. 5 Micro-Raman spectrum of 1 with a He–Ne laser (λ_exc = 632.8 nm).

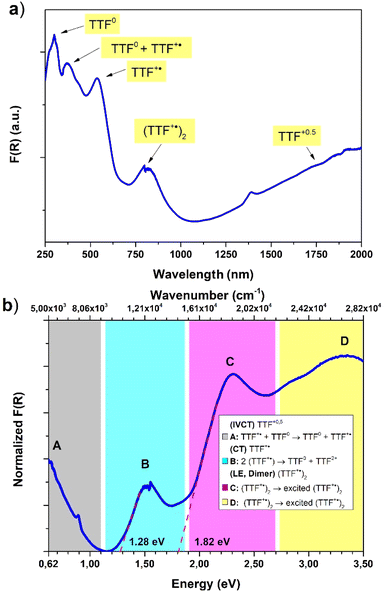
Diffuse reflectance spectroscopy was performed on a diluted sample (1% KBr w/w concentration was selected based on literature reports²⁰) to confirm the presence of different TTF oxidation states, the results being summarized in Fig. 6. Indeed, optical properties of systems based on TTF, and its different radical species formed both in solution⁶⁶ and in the solid state,⁶⁷ are well-known and corroborated by different examples and computation studies.^68–70 This characterization was also applied recently for identification of these signatures in doped TTF-MOFs.²⁰ In our case the spectrum was collected in the 250–2000 nm range where the characteristic bands are expected. In the case of the present work an optical apparatus for a lower energy region, where CT interaction of the mixed-valence system is present, was not available. These low energy bands can be correlated with conductive properties^71–73 but in some cases it is difficult to rationalize, particularly in complex mixed-valence systems; nevertheless, they can also be used to estimate the optical band gap of semiconductive radical salts with small activation energy⁷⁴ as in our case (vide infra).

Fig. 6 (a) Diffuse reflectance spectrum of 1Dy, the characteristic bands are labelled according to the text. (b) The same spectrum reported in the 0.62–3.50 eV (5000–28 200 cm⁻¹) range where characteristic TTF radical cation bands A, B, C and D are present; the inset shows our suggested assignment; note: the three different scales were used for a better comparison with previous reports.

The resulting spectrum (Fig. 6a) shows the same features of the Raman one, and it is in accordance with our charge distribution assignment:

• In the higher energy region of the spectrum, two peaks are present at around 300 nm and 370 nm. The first one can be assigned to the unoxidated TTF-TC⁰ anion, as reported for the tetra anionic sodium salt,⁷⁵ while the second one can account for two contributions: the first is ascribed to another band of the TTF-TC⁰ anion and the second is due to the intramolecular transition of TTF-TC⁺˙, as suggested by the shoulder around 400 nm and the observed red-shift compared to the unoxidated anion.^67,75

• In the medium energy region, the bands of the TTF⁺˙ radical cation are present, one at around 540 nm ascribed to an intramolecular band and another at around 800 nm ascribed to the CT band of the (TTF⁺˙)₂ dimer.^66,67,76,77

• In the lowest energy region is present a strong absorption shoulder related to the IVCT band, which is a signature of the presence of the +0.5 mixed-valence state.⁶⁷

It was not possible to determine its peak position from our data and it was estimated to be around 2500 nm (or 4000 cm⁻¹, vide infra) by the Gaussian fit procedure. These TTF characteristic bands are also present in solution but in the solid state they can be predictive about the conductive nature of the material^71,72 and can be interpreted as was made in the pioneering studies of Torrance⁶⁷ and Sugano.⁷⁶ In the region between 0.62 and 3.50 eV are present four different bands ascribed to the different radical cation species transitions labelled A, B, C and D. The D and C bands are intramolecular bands of TTF⁺˙, also named local-excitation (LE) bands;⁷⁶ their blue shifted location at around 3.3 and 2.3 eV can suggest interaction with another neighboring TTF⁺˙ through dimerization as for previously reported mixed-valence systems.^76,77 In our case, however, also the different nature of the molecules, their charge repartition and absorption of neutral TTF⁰ in the same region should be considered. The B and A bands, around 1.50 eV and 0.50 eV, respectively, are intermolecular CT bands. Band B is due to intradimer (TTF⁺˙)₂ charge transfer and band A is due to charge transfer between neutral TTF⁰ and TTF⁺˙.^67,76 The presence of the A band, also classified as an IVCT band,^78,79 is a signature of a +0.5 mixed valence state within the TTF stacks and, generally, a higher intensity compared to the B band can be an indication of relatively high conductivity.⁶⁷ The data were used to estimate the optical band gap of the sample; a Gaussian fit procedure was selected based on the characteristics of our system. Indeed, as recently pointed out by Fabrizio et al., MOFs with low DOS and localized transitions are more suitable for this data treatment⁸⁰ and it can allow the determination of band position and mid-gap states that are generally responsible for TTF MOF conductivity.⁸¹ Furthermore, the almost flat nature of the band calculated (vide infra) is in accordance with this kind of analysis.⁸⁰ On the other hand, the Tauc plot is an easier procedure and was used for all the TTF-MOFs reported in Table S7.‡ It can be a good alternative or can also be used for comparison as suggested in the work of Fabrizio et al.⁸⁰ For these reasons we have performed both analyses, according to the guidelines described in the paper. We further estimated the band gap for each band as the absorption onset of the spectra after transformation into the Kubelka–Munk function F(R) and normalization (Fig. 6b and Table 2). The latter analysis showed similar results compared to the Tauc plot as already reported in other MOFs.^82,83 The normalized data were also used for the Gaussian fit and, therefore, for the determination of band peaks corresponding in this case to the optical gap. All the results are summarized in Table 2 and Fig. 7.

Table 2 Comparison between the energy gaps determined by the different methods discussed in the text^a

Band label	Suggested assignment	Gaussian Eopt (eV)	Tauc direct Eopt (eV)	Tauc indirect Eopt (eV)	Absorption onset Eopt (eV)
a n.d. – not possible to determine from the data. b Estimated from the Gaussian fit.
A	TTF^+˙ + TTF^0 → TTF^0 + TTF^+˙	0.53^b	n.d.	n.d.	n.d.
B	2(TTF^+˙) → TTF^0 + TTF^2+	1.54	1.31	1.26	1.28
C	(TTF^+˙)2 → excited (TTF^+˙)2	2.26	1.93	1.69	1.82
D	(TTF^+˙)2 → excited (TTF^+˙)2	3.27	2.3	n.d.	n.d.

---

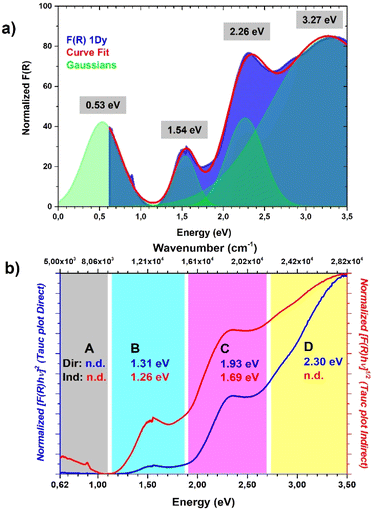Fig. 7 Comparison between (a) Gaussian fit procedure, the position of Gaussian peaks are highlighted; (b) Tauc plot direct (blue) and Tauc plot indirect, the results for each region of the spectrum are highlighted with the same color code. Further details about the Gaussian fit parameters and Tauc analysis are provided in Fig. S4.‡

The position of the band calculated by Gaussian fit (Fig. 7a and Table 2) matches with the value reported for other TTF mixed-valence systems.^76,77 Furthermore, we were able to estimate the position of the IVCT band by considering into the fit a peak out of the spectral window, only the shoulder of this band being present on the spectrum, and its maximum matches with the value obtained in other TTF-MOFs (4000 cm⁻¹ or 0.50 eV).^20,81 Furthermore, an additional CT band around 2000 cm⁻¹ (closer to our calculated and experimental energy gap) is detected for similar charge repartition (vide infra) in trimeric systems⁶⁵ and so it is expected in our case as well. The result suggests that DR in the IR region can be more suitable for the optical gap determination and for comparison with the conductivity measurements and band structure calculation results. The band gap calculated by the Tauc method and absorption onset differs from the band position calculated by Gaussian fit considering the same transition and it has lower values (Fig. 7b, S4‡ and Table 2). Indeed, it's known that these analyses can generate artifacts with errors more than 1 eV particularly when distinct bands are present.⁸⁰ When we pass from direct to indirect band gap, an increase of the lower energy band contribution is mathematical and lower band gap values were obtained for the same band. For a similar mathematical reason the band gap determined by the absorption onset falls in the middle^80,82,83 (Fig. 6b and Table 2). The values obtained for similar bands are in accordance with previously reported TTF-MOFs (see the examples reported in Table S6‡) where, as suggested by Dinca, the conductivity is mostly related to these mid-gap states caused by doping with the radical cation generated during the synthesis.⁸¹ In our case the band related to the IVCT transition is more prominent (a Gaussian peak area 3 times bigger than B peak was found, see Fig. S4‡) than that of the previously reported series of M-TTFTC MOFs, where the spectra were dominated by the B band with almost negligible contribution from A, suggesting low charge delocalization within the stacks.⁶⁴ Our material is thus more comparable to a mixed-valence TTF semiconductor with a small band gap, where the presence of not fully delocalized states along the stacks prevents high conductivity, and a small activation energy is necessary to trigger electron conduction. Indeed, Raman spectrum, optical properties, conductivity values, activation energy and band structure are in accordance with these types of systems here.^65,84,85 Generally, the comparison of the different band gap determination methods confirmed that Gaussian fit is a more precise and reproducible procedure for this class of materials both for the band gap determination and the band position. Furthermore, more information can be extrapolated, such as the peak area, which can be used for useful comparisons. On the other hand, the main drawbacks of the application of the Tauc analysis to a localized MOF system, as is the case of all reported TTF-MOFs, such as difficult determination of the gap type (direct or indirect) and artifacts due to unsuitable and arbitrary mathematical treatments, were again pointed out here.

Electronic structure of [Dy₆(TTFTC)₅(H₂O)₂₂]·(H₂O)₂₁1

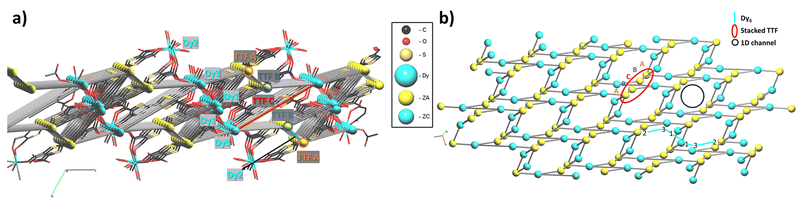
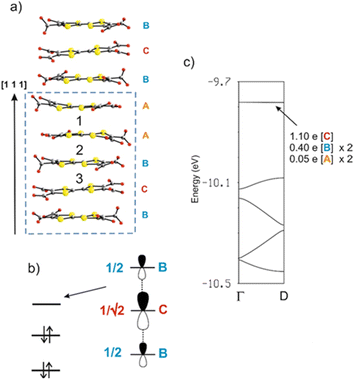
As discussed above, the crystal structure of [Dy₆(TTFTC)₅(H₂O)₂₂]·(H₂O)₂₁1 can be described as a series of parallel fully deprotonated TTF-TC chains along the [1 1 1] diagonal direction linked by Dy^III cations. Water molecules either complete the coordination of the cations or reside in the voids of the structure. Since there are no S⋯S short contacts between the donor chains, the electronic structure of 1 near the Fermi level is determined by that of an isolated chain of completely deprotonated TTF-TCs. The repeat unit of this chain contains five TTF-TCs of three different types, A, B and C, with the sequence …A–[A–B–C–B–A]–A… (vide supra). Taking into account the fully deprotonated condition of the anions and the +III oxidation state of the cations, a unit cell of the chain must contain two holes, i.e., two electrons of the π-type HOMOs (highest occupied molecular orbitals) of the anions have been formally transferred to σ-type orbitals of the carboxylates. The fact that four of the five anions (A and B) of the unit cell have the same central C=C bond length, suggest that anion C contains the two holes (i.e., the two electrons of the HOMO are missing). However, analysis of the Raman spectra advocates for the occurrence of two different charge states (vide supra). To solve this contrasting situation, we studied the electronic structure of a fully deprotonated [(TTF-TC)₅]²⁺ chain.

As shown in Fig. 8a, there are three different types of TTF-TC⋯–TTF-TC overlap: that between two A anions (type 1), those between A and B anions (type 2) and finally those between B and C anions (type 3). In order to have a hint of the strength of the HOMO⋯HOMO interactions, which are those imposing the shape of the HOMO bands and thus controlling the transport properties, we have evaluated the absolute value of the so-called HOMO⋯HOMO interaction energy (|β_HOMO–HOMO|)⁸⁶ associated with each interaction. The calculated values for the three interactions are: 0.1466 eV (A–A), 0.1816 eV (A–B) and 0.3785 eV (B–C). Since the B–C HOMO–HOMO interactions are about twice stronger than those of the others, the chains can be considered as a series of B–C–B trimeric units separated by A–A spacers, as far as the HOMO–HOMO interactions are concerned. This observation immediately clarifies the situation. The C units exhibit the longest central C=C bond, so that the two holes must be mostly located within these trimers. The upper orbital of a trimeric unit⁸⁷ is schematically shown in Fig. 8b in which the HOMO of a given donor is represented for simplicity by a p_z orbital. The numbers shown are the coefficients of every HOMO in the empty upper trimeric orbital as given by a simple Hückel-type approach. Thus, the upper trimeric orbital has as its major component the HOMO of the central anion C although the participation of the B HOMOs is by no means small. This leads naturally to the roughly +1 (C) and +1/2 (B) charges suggested by the Raman study.

Fig. 8 (a) The fully deprotonated chain of anions in [Dy₆(TTF-TC)₅(H₂O)₂₂]·21H₂O, where the different anions and interactions are labelled. (b) Schematic representation of the upper combination of the three HOMOs of a trimeric unit according to a simple Hückel treatment. For simplicity, the HOMO level of each molecule is represented by a p_z orbital. (c) Calculated band structure for the chains in (a) where Γ = (0) and D = (d*/2) where d = a + b + c. The partition of the two electrons associated with the upper empty band among the different anions of the repeat unit is shown.

The calculated band structure of the fully deprotonated [(TTF-TC)₅]²⁺ chain is shown in Fig. 8c. The five bands shown are those built from the HOMOs of the five anions and because of the electron count all bands are doubly filled except for the upper one. The partition of the two electrons associated with this orbital if it was filled (i.e., of the two holes of the repeat unit) is shown in Fig. 8c. These numbers are in excellent agreement with the previous qualitative analysis. Practically, half of the holes are associated with anion C and the rest is mostly associated with the two anions B. A quite small contribution is associated with anions A because as the HOMO–HOMO interaction associated with interaction 2 (A–B) is weak but not nil, there is a weak interaction of the B–C–B trimer with anions A and thus a weak orbital mixing. However, the mixing is too small to have any practical consequence as shown by the fact that the band is completely flat. Consequently, [Dy₆(TTFTC)₅(H₂O)₂₂]·(H₂O)₂₁1 should be a semiconductor with relatively low conductivity, when compared to classical TTF-based conductors, essentially due to the holes in the upper filled band (i.e., the fourth band from the bottom in Fig. 8c) which exhibits some dispersion. The calculated activation energy, i.e., the half-gap energy, is 0.150 eV, which is in excellent agreement with the value of 0.164 eV arising from the resistivity measurements (vide infra). In summary, the band structure calculations completely substantiate the Raman measurements and make clear the occurrence of formal charges of +1/2 and +1 in the π-type orbitals of anions B and C, respectively.

Electron transport properties

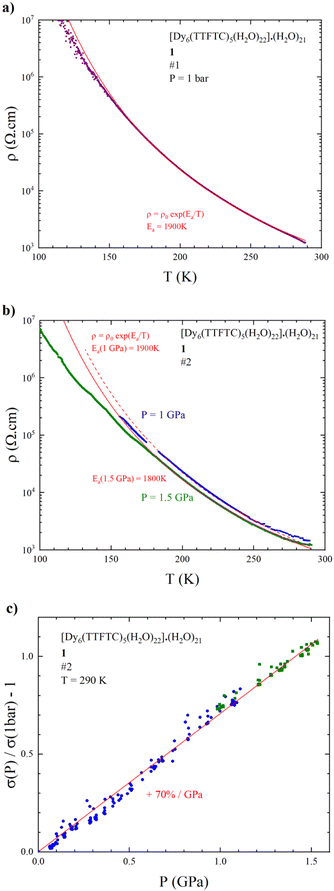
Resistivity measurements have been performed on selected single crystals of 1 as a function of temperature and/or pressure. The results indicate activated electron transport, thus confirming what was suggested by the band structure calculations. A room temperature conductivity (σ_RT) value of 1 mS cm⁻¹ was obtained for both 4 and 2-contact configurations. The 2-contact temperature dependent resistivity (ρ) data were fitted with the Arrhenius law ρ = ρ₀e^E_a^/T giving an activation energy (E_a) of 1900 K (Fig. 9a). Despite the relatively poor conductivity with respect to classical TTF-based conductors,⁸⁸ the σ_RT value obtained is relatively high in comparison to other c-MOFs. Indeed, most of the reported MOFs are poor semiconductors with σ_RT in the 10⁻³ to 10⁻⁷ S cm⁻¹ range.³ As far as we know, the σ_RT herein measured is the highest among MOFs involving TTF linkers, considering IUPAC definition of MOFs as a coordination network with potential voids,⁸⁹ surpassing the well-known Cd₂(TTFTB) obtained by Dincă et al. in 2015.⁹⁰ For comparison purpose, we have grouped in Table S6‡ TTF-based MOFs along with their RT conductivity values.

Fig. 9 Temperature dependence of the electrical resistivity of 1 (a) at ambient pressure; (b) at 1 and 1.5 GPa; the red lines represent the exponential fit giving the activation energies (E_a) indicated in the graph. (c) Pressure dependence of the normalized variation of the electrical conductivity: (σ(P) – σ(1 bar))/σ(1 bar); the red line represents the linear fit.

It is noteworthy that the use of single crystals of suitable size and stability (mechanical and thermal) for conductivity measurements is of relevant interest, since it allows reliable and reproducible conductivity measurements, which are free from artefacts compared to those on pellets, due to the different conductivity of grain boundary defects and to the anisotropy of crystals. These are also the reasons why it is the recommended way to measure and report MOFs' conductivity values. Conversely, most of the MOFs reported in Table S6‡ and in the literature were measured on pellets, highlighting once again how the synthetic strategy herein reported to obtain single crystals represents a challenge, especially in the case of c-MOFs.^3,43

Accordingly, the conductivity values in the reported TTF-MOFs range between 10⁻¹⁰ and 10⁻⁴ S cm⁻¹, thus at least one order of magnitude below our MOF 1. About the same RT conductivity value was obtained for the MIL-135(K) CP, where a fully oxidized linker was present; similar considerations about charge localization of the fully oxidized TTF-TC were discussed.⁴²

We also measured the resistivity of 1 under hydrostatic pressure. The temperature dependence of the resistivity at 1 and 1.5 GPa (Fig. 9b) shows that the activation energy decreases very slowly as pressure increases, i.e., E_a is still around 1900 K at 1 GPa and 1800 K at 1.5 GPa. This relatively weak effect on the conductive properties is confirmed by the pressure variation of the conductivity at room temperature, showing that σ_RT increases linearly with pressure with a slope of around 70%/GPa (Fig. 9c), to be compared to the Bechgaard salts (TMTSF)₂X salts (200 to 300%/GPa).

This relatively weak effect of the applied pressure is very likely due to the rigidity of the framework combined with electrostatic repulsions between the highly charged anions and cations in the MOF.

Magnetic properties

The direct current (dc) magnetic susceptibility of the hexanuclear compound 1 are shown in Fig. 10 (χ_MT vs. T plot). Magnetic measurements were performed on a microcrystalline powder sample between 2 and 300 K under an applied field of 1.0 kOe. The χ_MT value at room temperature is 80.84 cm³ K mol⁻¹. Based on the X-ray analysis, it was found that in principle two ligands in the form of the TTF-TC ligand radical were present in a Dy6 cluster. The presence of these two free radicals, if they are considered as not coupled and not delocalized, which is very likely not the case (vide supra the discussion on the electronic structure), contributes only to a small extent (0.75 cm³ K mol⁻¹) to the magnetic susceptibility compared to the six atoms of dysprosium in the cluster. In all cases, we observe a slightly lower magnetic susceptibility compared to the expected value for six non-interacting Dy^III (14.17 cm³ K mol⁻¹, S = 5/2, ⁶H_15/2, g = 4/3) ions⁹¹ and two free radicals (0.375 cm³ K mol⁻¹, S = 1/2, g = 2). The somewhat lower value of the magnetic susceptibility can also be associated with a large variation in the g-factor tensor, which is caused by a significant variation in the anisotropy of the dysprosium ion. With decreasing temperature, the χ_MT product gradually decreases down to T = 2.0 K and reaches the value of 47.60 cm³ K mol⁻¹ which can be associated with the depopulation of the M_J (Stark) sublevels of the Dy^III centers.⁹² Three coordination types of the carboxylic group are found in the compound 1-Dy. Two of these coordination modes are bridges that ensure the formation of the hexanuclear cluster. In these specific coordination modes of bridging carboxylates, a ferromagnetic as well as an antiferromagnetic interaction can be expected.⁹³ The absence of increasing segments in the χ_MT evolution with temperature is an indication in favor of dominant antiferromagnetic interactions both along the chain and within the cluster.^93,94 This is consistent with the theoretical calculations presented above (see Fig. 8b), which suggest the presence of antiferromagnetic interactions in the chain. Indeed, antiferromagnetism within a 1D arrangement of the ligand TTF has been reported.^95,96 Usually, the magnetic interactions between lanthanides connected via carboxylate have low magnitude and do not exceed the order of 1.0 cm⁻¹.^94,97,98 The evolution of the magnetization vs. field has typical shape and values corresponding to the presence of six Dy^III with significant magnetic anisotropy (Fig. 10).^{91,93,94,97–102}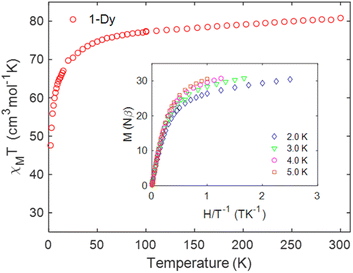

Fig. 10 Temperature dependence of the χ_MT product at 1.0 kOe for 1. Inset plots of M vs. H/T measured between 0 and 5 T at indicated temperatures.

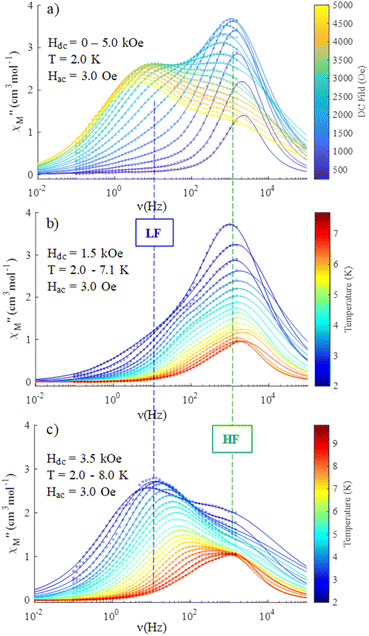
Dynamic properties of the compound were studied by measuring the temperature and field dependence ac (alternative current) magnetic susceptibility. First, no signal was observed under zero dc field at 2.0 K in the out-of-phase component (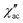) ac susceptibility (Fig. S5‡). After applying small dc fields (up to 5.0 kOe) a frequency dependent out-of-phase signal appears (Fig. S5‡). Such behavior can be the consequence of the suppression of quantum tunneling of the magnetization (QTM) and suggests the presence of field induced slow magnetic relaxation. Interestingly, two signals can be observed in the out-of-phase (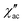) ac susceptibility as a function of the applied magnetic field, one at high frequency (HF) and one at low frequency (LF) (Fig. 11a, see also Fig. S6‡). The component at the high frequency increases with increasing static dc field and has its maximum contribution at 1.5 kOe. The second component, at low frequencies, also increases in intensity and reaches its maximum at 3.5 kOe and decreases after the magnetic field continues to increase (Fig. 11, see also Fig. S6‡). Considering the values of the real component of the ac susceptibility (χ′) at low frequencies, as well as the values of the imaginary part (χ′′) at the maxima (see Fig. S7‡), we can see that they far exceed the magnetic susceptibility values of the two radicals existing in the Dy6 cluster. Thus, we can affirm that the behaviour in the observed AC susceptibility is due to the presence of magnetic anisotropy in the Dy6 cluster.

Fig. 11 Frequency dependence of the out-of-phase susceptibility for 1: (a) field sweeping (H_dc = 0–5.0 kOe) at constant temperature T = 2.0 K; (b) temperature sweeping (T = 2.0–7.1 K) at constant applied dc field (H_dc = 1.5 kOe); (c) temperature sweeping (T = 2.0–8.0 K) at constant applied dc field (H_dc = 3.5 kOe). The circle point is experimental data, the solid line is the best fits according to the model indicated in the text. The dashed vertical lines indicate the approximate position of high and low frequency ac signals.

To investigate the nature of the two slow relaxation processes, the temperature dependence of ac susceptibility data was collected under a fixed dc field of 1.5 kOe and 3.5 kOe with variation of temperature between 2.0 and 8.0 K (with 0.3 K increment) (Fig. 11b, c, S9 and S11‡). The evaluation of the field dependence and temperature dependence of the relaxation times was achieved by fitting the out-of-phase (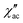 eqn (2) in the ESI‡) and in-phase ( 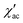eqn (1) in the ESI‡) component of ac susceptibility using a generalized Debye model for the two relaxation processes.^30,103–106

The temperature dependence of the ac susceptibility confirms the presence of two relaxation processes in 1 (Fig. 12). The two relaxation times (τ₁, τ₂) and two distribution parameters (α₁, α₂) occur along with two isothermal susceptibilities (χ_T1, χ_T2) and one common adiabatic susceptibility (χ_s) (eqn (1) and (2) in the ESI‡). Variable parameters derived from the best fits of the ac susceptibility are shown in Fig. S8, S10, and S12.‡

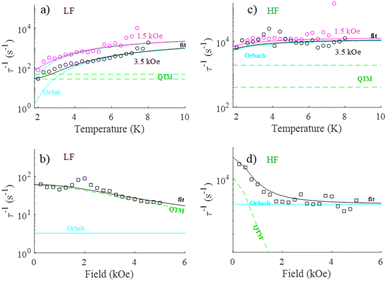Fig. 12 Temperature (a and c) and field (b and d) dependence of relaxation time for high and low frequency processes in 1. The solid lines are the best fits with the contribution of Orbach and QTM.

Both (LF and HF) relaxation processes are well defined, and the distribution parameters for the relaxation process are rather broad (α_1,2 = 0.3 ÷ 0.5) but well resolved. This is probably related to the presence of three crystallographically different Dy^III ions in the molecular structure, which can exhibit slightly different relaxation properties.¹⁰⁷ The extracted temperature and field dependence of relaxation times in 1 can be modulated based on four relaxation mechanisms specified by eqn (1):^108–11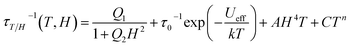1

Here, the first term represents quantum tunneling of magnetization (QTM), the second term is Orbach, third is a direct process and the last is the Raman process; H is the applied magnetic field and T is the temperature. In order to constrain the variable parameters and avoid the over-parametrization problem in the analysis, the two temperature dependences (at 1.5 and 3.5 kOe) and one field dependence (at 2.0 K) of relaxation times were fitted simultaneously¹¹⁰ (vectors of data: τ⁻¹ in s⁻¹, T in Kelvin and H in kOe). We can easily observe that for the study of the evolution of relaxation times as a function of the applied magnetic field, the values of the relaxation times are continuously decreasing (Fig. 12b and d), suggesting that the contribution of the direct process is negligible (eqn (3)). Attempts to involve the direct process in the analysis result in bringing the values of A factor to zero. For these reasons, the final expression defining the contribution of the direct process has been omitted.

To successfully reproduce the experimental relaxation data of LF and HF signals in 1, two different relaxation mechanisms: QTM and Raman (Fit B, Fig. S13‡ and Table 2) or QTM and Orbach (Fit A, Fig. 12 and Table 2) are proposed.

It should be noted that the HF signal shows a small dependence of the relaxation time on the temperature. Under this condition, we obtained for the Raman process very small values of the exponential factor n, which is not in agreement with those usually reported in the literature (n = 4–13). Consequently, for the HF data set, the study was limited to the Orbach with QTM processes, which is sufficient in order to obtain a satisfactory fit of the data. The results of the analyses are presented in Table 3.

Table 3 The variable parameters n, C, U_eff, τ₀⁻¹ and Q_i (eq-M3) for simultaneous fit of relaxation times as a function of temperature and field for 1

1	Fit	Q 1 (s^−1)	Q 2 (T^−2)	τ 0 ^−1 (s^−1)	U eff (K)	C (s^−1 K^n)	n	R
a For the dataset of 1.5 kOe. b For the dataset of 3.5 kOe.
LF	A	58.4(7)	0.09(2)	2(1) × 10^−4^a	9.5(3)^a	—	—	4.5
				3(1) × 10^−4^b	14.2(4)^b
	B	55.8(7)	0.10(3)	—	—	10.4(10)	2.7(6)	4.75
						0.4(6)	3.7(7)
HF		1.0(4) × 10^4	2(2)	6.5(1.7) × 10^−5	1.7(5)	—	—	3.21

---

Experimental section

Materials

All manipulations were performed under aerobic conditions and all chemicals purchased were of reagent grade or higher and used as received. TTF-TCH₄ was synthesized as previously reported.⁶⁴ Elemental analysis (C, H and S) was performed with a CE instruments EA 1110 CHNS. TGA was performed with an STA-6000 instrument (Mettler Toledo) under a nitrogen flux of 40 mL min⁻¹ and in the 25–800 °C temperature range (heating rate of 10 °C min⁻¹). Powder X-ray diffraction was performed on a D8 Advance diffractometer from Bruker, in the 5–40° 2θ range with 0.019754 stepwise. The sample was gently crushed and mounted on the sample holder to avoid solvent loss before other measurements; this procedure induces preferential orientation of the crystallites, but calculated Bragg peaks match with the experimental ones confirming the phase purity of the sample (Fig. S3‡). The data were corrected for the background due to the sample holder.

Synthesis

TTF-TCH₄ (3.8 mg) was dissolved in 1.0 mL of water by adding 15 μL of NaOH 1 M and was placed in the bottom of a glass tube (id: 4 mm; length: 30 cm). On top of it was carefully layered 0.5 mL of MeOH/H₂O and 6.1 mg of Dy(NO₃)₃·6H₂O dissolved in 1.0 mL of MeOH. The tube was capped with Teflon tape and parafilm® in order to avoid solvent evaporation. After 6 months, black, shining, long, rectangular crystals were collected at the interphase, decanted 3 times with H₂O/MeOH, filtered on paper, washed with H₂O and MeOH and dried in air. The synthesis was repeated in different tubes with various dimensions and the crystals were collected in a similar way. The as-reported optimized method allowed the easy separation of around 1 mg per tube of single crystals with reproducible reaction time and yields. Anal. calcd for C₅₀H₈₆Dy₆O₈₃S₂₀: C, 16.54; H, 2.39; S, 17.66. Found: C, 16.50; H 2.42; S; 17.61.

X-ray diffraction studies

X-ray single crystal diffraction data for 1 were collected at 100 K on a Bruker D8 Venture diffractometer (Mo Kα) equipped with a PHOTON II area detector. The data were indexed and processed with APEX3. The structures were solved by intrinsic phasing with the SHELXT¹¹² program and refined on F² using a full matrix least-squares algorithm with the ShelXL¹¹³ program using the Olex2 (ref. 47) graphical interface. All non-hydrogen atoms were refined anisotropically and all hydrogen atoms were placed in calculated positions and refined isotropically with a riding model. Disordered water inside the voids was modelled through a solvent mask procedure. Crystallographic data for the structure have been deposited with the Cambridge Crystallographic Data Centre, deposition number CCDC 2341521‡ (1). These data can be obtained free of charge from CCDC, 12 Union road, Cambridge CB2 1EZ, UK (e-mail: E-mail: deposit@ccdc.cam.ac.uk; or http://www.ccdc.cam.ac.uk/). The results are summarized in Table 4.

Table 4 Crystal data and structure refinement for 1

Empirical formula	C50H86Dy6O83S20
Formula weight	3631.38
Temperature (K)	100(2)
Crystal system	Triclinic
Space group	P1̄
a (Å)	12.2439(10)
b (Å)	15.9738(14)
c (Å)	16.1746(14)
α (°)	115.689(3)
β (°)	99.245(3)
γ (°)	102.148(3)
Volume (Å^3)	2670.6(4)
Z	1
ρ calc (g cm^−3)	2.258
μ (mm^−1)	4.657
F(000)	1766.0
Crystal size (mm^3)	0.21 × 0.05 × 0.01
Radiation	MoKα (λ = 0.71073)
2θ range for data collection (°)	3.85 to 51.626
Index ranges	−14 ≤ h ≤ 14, −19 ≤ k ≤ 19, −19 ≤ l ≤ 19
Reflections collected	89090
Independent reflections	10221 [Rint = 0.0747, Rsigma = 0.0392]
Data/restraints/parameters	10221/0/669
Goodness-of-fit on F^2	1.059
Final R indexes [I ≥ 2σ (I)]	R 1 = 0.0325, wR2 = 0.0684
Final R indexes [all data]	R 1 = 0.0423, wR2 = 0.0716
Largest diff. peak/hole/e (Å^−3)	1.17/−1.16
CCDC number	2341521

---

Raman microscopy

Raman spectra were carried out at room temperature on single crystals by using a micro Raman spectrometer (Horiba XploRA PLUS) equipped with a He–Ne laser (λ = 632.8 nm) in the 100–3200 cm⁻¹ range, with a 100 LWD objective (<0.25 mW μm⁻² on the crystal). A 180° reflective geometry was adopted. The samples were mounted on a glass microscope slide and the scattering peaks were calibrated against a Si standard (ν = 520.7 cm⁻¹). A typical spectrum was collected with a 200 s acquisition time and was averaged over 3 scans. No sample decomposition was observed during the experiments.

Optical properties

Diffuse reflectance (DR) spectroscopy measurements were performed under sample direct illumination in a dual-beam spectrophotometer (Agilent Technologies Cary 5000 UV-vis-NIR) equipped with a diffuse reflectance integration sphere between 250 nm and 2000 nm. The sample was ground with KBr in a 1% w/w concentration and this solid mixture directly mounted on the standard BaSO₄ sample holder. The Gaussian fit was performed using Origin9 software following the procedure reported.⁸⁰ We used the data in the 0.62–3.50 eV region that were normalized without a baseline correction. A satisfactory fit of the experimental data was obtained considering four independent peaks (A, B, C, D). Tauc plot analysis was performed following the guidelines of the same reference.

Band structure calculations

The tight-binding band structure calculations were of the extended Hückel type¹¹⁴ and a modified Wolfsberg–Helmholtz formula was used to calculate the non-diagonal H_μν values.¹¹⁵ All valence electrons were taken into account in the calculations and the basis set consisted of Slater-type orbitals of single-ζ quality for C 2s and 2p, S 3s and 3p and O 2s and 2p. The ionization potentials and exponents were taken from previous work.¹¹⁶

Single-crystal transport measurements

Before conductivity measurements, a few single crystals of 1 having no evident cracking were selected under an optical microscope and their unit cell checked with a single crystal diffractometer and crystal faces indexed to confirm that the [111] direction corresponds to the long axis of the rectangular crystals (length could exceed 1 mm). At room temperature, the electrical resistivity has been checked on several crystals both in a 4-contact configuration (applying a DC current in the range 0.1–1 μA and measuring the voltage with a Keithley 2400 source meter) and in a 2-contact configuration (applying a constant voltage (in the range 0.1–1 V) and measuring the current with a Keithley 486 picoammeter). Both configurations of measurement were in agreement and showed an ohmic behavior indicating that the resistance of the contacts is much lower than that of the single crystals. Because of the high values of the measured resistances, the temperature dependence of the resistivity was measured using the 2-contact method. High hydrostatic pressure was applied in a homemade NiCrAl clamp type cell using silicon oil (Idemitsu Daphne-oil 7373) as the pressure transmitting medium. The pressure, which is varied with a resistive manganin gauge, was measured at room temperature. Low temperature was achieved with a cryostat equipped with a 4 K pulse-tube.

Magnetic measurements

DC magnetic susceptibility data (2–300 K) were collected on powdered samples using a SQUID magnetometer (Quantum Design MPMS-XL), applying a magnetic field of 0.1 T. All data were corrected for the contribution of the sample holder and the diamagnetism of the samples estimated from Pascal's constants.^117,118 The field dependence of the magnetization (up to 5 T) was measured between 2.0 and 5.0 K. Ac magnetic susceptibility was measured between 2 and 7 K with an oscillating field magnitude of H_ac = 3.0 Oe and frequency ranging between 1 and 1488 Hz in the presence of a dc field up to H_dc = 5.0 kOe. The relaxation times were extracted from a simultaneous fit of and using the generalized Debye model.³⁰ Fitting of the variable parameters and estimation of errors was performed with a lsqcurvefit solver in MATLAB; Jacobian matrix was used to generate 95% confidence intervals on the fitted parameters.

Conclusions

We reported herein a thorough study on a redox active TTF-based Dy^III-MOF, formulated as [Dy₆(TTFTC)₅(H₂O)₂₂]·21H₂O (1), showing, to date, the highest conductivity value among the TTF-MOFs. The structural analysis of the compound revealed a complex 2D polymeric network with a rare 3³4L70 topology composed of Dy₆ clusters as SBUs and fully deprotonated TTF-TC as linkers. The mixed-valence centered on the TTF core was confirmed by a multi-technique approach involving bond distance structural analysis, Raman microscopy, diffuse reflectance spectroscopy and band structure calculations. The three independent TTF-TC molecules per asymmetric unit, TTF(A), TTF(B), and TTF(C), revealed a charge state of ρ = 0, ρ = +0.5, and ρ = +1 respectively. The electron transport properties of 1 were investigated on single crystals confirming the semiconductor behavior predicted by band structure calculations. 1 shows a σ_rt = 1 mS cm⁻¹ and small conductivity increase of 70%/GPa with the pressure very likely due to the rigidity of the coordination bond network. Furthermore, 1 exhibits frequency dependence of the in-phase and out-of-phase components of the ac susceptibility under a static DC field, indicating the presence of slow magnetic relaxation. The energy barrier (U_eff/K) of this field induced slow magnetic interaction is around 12 K, corresponding to a typical SMM behaviour for dysprosium carboxylates. This TTF-based MOF with highly anisotropic Dy^III ions, showing a rare 2D topology, provides a valuable scaffold to design highly conducting 2D MOFs combined with SMM behaviour.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article.

Author contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported in France by the CNRS and the University of Angers. This research was funded in Italy by Fondazione di Sardegna, Convenzione Triennale tra la Fondazione di Sardegna e gli Atenei Sardi, Regione Sardegna, L.R. 7/2007 annualità 2022, project VOC_3D “3D printed optical VOC sensors for indoor air quality evaluation” CUP F73C23001590007. E.C. acknowledges support from the Spanish MICIU through Grant PID2022-139776NB-C61 and the Severo Ochoa FUNFUTURE (CEX2019-000917-S) Excellence Centre distinction as well as from Generalitat de Catalunya (2021SGR01519).

Notes and references

1. H.-C. Zhou, J. R. Long and O. M. Yaghi, Chem. Rev., 2012, 112, 673–674.
2. A. E. Thorarinsdottir, T. D. Harris, Y. Cui, Y. Yue, G. Qian and B. Chen, Chem. Rev., 2020, 120, 8716–8789.
3. (a) L. S. Xie, G. Skorupskii and M. Dincă, Chem. Rev., 2020, 120, 8536–8580; (b) L. Sun, S. S. Park, D. Sheberla and M. Dincă, J. Am. Chem. Soc., 2016, 138, 14772–14782.
4. (a) S. A. Sahadevan, A. Abhervé, N. Monni, C. Sáenz de Pipaón, J. R. Galán-Mascarós, J. C. Waerenborgh, B. J. C. Vieira, P. Auban-Senzier, S. Pillet, E.-E. Bendeif, P. Alemany, E. Canadell, M. L. Mercuri and N. Avarvari, J. Am. Chem. Soc., 2018, 140, 12611–12621; (b) S. A. Sahadevan, N. Monni, A. Abhervé, D. Marongiu, V. Sarritzu, N. Sestu, M. Saba, A. Mura, G. Bongiovanni, C. Cannas, F. Quochi, N. Avarvari and M. L. Mercuri, Chem. Mater., 2018, 30, 6575–6586; (c) S. Ashoka Sahadevan, N. Monni, M. Oggianu, A. Abhervé, D. Marongiu, M. Saba, A. Mura, G. Bongiovanni, V. Mameli, C. Cannas, N. Avarvari, F. Quochi and M. L. Mercuri, ACS Appl. Nano Mater., 2020, 3, 94–104.
5. J. Wang, H. Hu, S. Lu, J. Hu, H. Zhu, F. Duan and M. Du, Nanoscale, 2022, 14, 277–288.
6. J. Liu, X. Song, T. Zhang, S. Liu, H. Wen and L. Chen, Angew. Chem., Int. Ed., 2021, 60, 5612–5624.
7. L. Niu, T. Wu, M. Chen, L. Yang, J. Yang, Z. Wang, A. A. Kornyshev, H. Jiang, S. Bi and G. Feng, Adv. Mater., 2022, 34, 2200999.
8. Y.-M. Jo, Y. K. Jo, J.-H. Lee, H. W. Jang, I.-S. Hwang and D. J. Yoo, Adv. Mater., 2023, 35, 2206842.
9. J. Liu, Y. Chen, X. Feng and R. Dong, Small Struct., 2022, 3, 2100210.
10. X. Yan, X. Su, J. Chen, C. Jin and L. Chen, Angew. Chem., Int. Ed., 2023, 62, e202305408.
11. M. Wang, R. Dong and X. Feng, Chem. Soc. Rev., 2021, 50, 2764–2793.
12. N. Monni, M. S. Angotzi, M. Oggianu, S. A. Sahadevan and M. L. Mercuri, J. Mater. Chem. C, 2022, 10, 1548–1572.
13. H. Kobayashi, H. Cui and A. Kobayashi, Chem. Rev., 2004, 104, 5265–5288.
14. P. Day and M. Kurmoo, J. Mater. Chem., 1997, 7, 1291–1295.
15. S. A. Sahadevan, A. Abhervé, N. Monni, P. Auban-Senzier, J. Cano, F. Lloret, M. Julve, H. Cui, R. Kato, E. Canadell, M. L. Mercuri and N. Avarvari, Inorg. Chem., 2019, 58, 15359–15370.
16. T. C. Narayan, T. Miyakai, S. Seki and M. Dincă, J. Am. Chem. Soc., 2012, 134, 12932–12935.
17. M. R. Bryce, J. Mater. Chem., 1995, 5, 1481–1496.
18. J. Su, T.-H. Hu, R. Murase, H.-Y. Wang, D. M. D'Alessandro, M. Kurmoo and J.-L. Zuo, Inorg. Chem., 2019, 58, 3698–3706.
19. F. Solano, P. Auban-Senzier, I. Olejniczak, B. Barszcz, T. Runka, P. Alemany, E. Canadell, N. Avarvari and N. Zigon, Chem.–Eur. J., 2023, 29, e202203138.
20. C. F. Leong, C.-H. Wang, C. D. Ling and D. M. D'Alessandro, Polyhedron, 2018, 154, 334–342.
21. J. Su, S. Yuan, J. Li, H.-Y. Wang, J.-Y. Ge, H. F. Drake, C. F. Leong, F. Yu, D. M. D'Alessandro, M. Kurmoo, J.-L. Zuo and H.-C. Zhou, Chem.–Eur. J., 2021, 27, 622–627.
22. J. Su, S. Yuan, H.-Y. Wang, L. Huang, J.-Y. Ge, E. Joseph, J. Qin, T. Cagin, J.-L. Zuo and H.-C. Zhou, Nat. Commun., 2017, 8, 2008.
23. N. Zigon, F. Solano, P. Auban-Senzier, S. Grolleau, T. Devic, P. N. Zolotarev, D. M. Proserpio, B. Barszcz, I. Olejniczak and N. Avarvari, Dalton Trans., 2024, 53, 4805–4813.
24. J. Su, N. Xu, R. Murase, Z. Yang, D. M. D'Alessandro, J. Zuo and J. Zhu, Angew. Chem., Int. Ed., 2021, 133, 4839–4845.
25. G. Skorupskii, K. N. Le, D. Leo and M. Cordova, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2205127119.
26. J. Zhang, G. Zhou, H.-I. Un, F. Zheng, K. Jastrzembski, M. Wang, Q. Guo, D. Mücke, H. Qi, Y. Lu, Z. Wang, Y. Liang, M. Löffler, U. Kaiser, T. Frauenheim, A. Mateo-Alonso, Z. Huang, H. Sirringhaus, X. Feng and R. Dong, J. Am. Chem. Soc., 2023, 145, 23630–23638.
27. G. Zhang, L. Jin, R. Zhang, Y. Bai, R. Zhu and H. Pang, Coord. Chem. Rev., 2021, 439, 213915.
28. R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143.
29. R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804–1816.
30. D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006.
31. L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186.
32. T. G. Ashebr, H. Li, X. Ying, X.-L. Li, C. Zhao, S. Liu and J. Tang, ACS Mater. Lett., 2022, 4, 307–319.
33. F. Manna, M. Oggianu, N. Avarvari and M. L. Mercuri, Magnetochemistry, 2023, 9, 190.
34. Q. Wan, M. Wakizaka and M. Yamashita, Inorg. Chem. Front., 2023, 10, 5212–5224.
35. (a) N. Monni, J. J. Baldoví, V. García-López, M. Oggianu, E. Cadoni, F. Quochi, M. Clemente-León, M. L. Mercuri and E. Coronado, Chem. Sci., 2022, 13, 7419–7428; (b) N. Monni, E. Andres-Garcia, K. Caamaño, V. García-López, J. M. Clemente-Juan, M. Giménez-Marqués, M. Oggianu, E. Cadoni, G. Mínguez Espallargas, M. Clemente-León, M. L. Mercuri and E. Coronado, J. Mater. Chem. A, 2021, 9, 25189–25195; (c) M. Oggianu, F. Bertolotti, F. Manna, F. Congiu, A. Cappai, C. Melis, G. Concas, N. Avarvari, N. Masciocchi and M. L. Mercuri, Dalton Trans., 2024, 53, 14265–14271; (d) N. Monni, S. Dey, V. García-López, M. Oggianu, J. J. Baldoví, M. L. Mercuri, M. Clemente-León and E. Coronado, Inorg. Chem. Front., 2024, 11, 5913–5923.
36. G. Huang, G. Fernandez-Garcia, I. Badiane, M. Camarra, S. Freslon, O. Guillou, C. Daiguebonne, F. Totti, O. Cador, T. Guizouarn, B. Le Guennic and K. Bernot, Chem.–Eur. J., 2018, 24, 6983–6991.
37. J.-J. Hu, Y.-G. Li, H.-R. Wen, S.-J. Liu, Y. Peng and C.-M. Liu, Dalton Trans., 2021, 50, 14714–14723.
38. G. Cosquer, Y. Shen, M. Almeida and M. Yamashita, Dalton Trans., 2018, 47, 7616–7627.
39. B. Ding, M. B. Solomon, C. F. Leong and D. M. D'Alessandro, Coord. Chem. Rev., 2021, 439, 213891.
40. H.-Y. Wang, L. Cui, J.-Z. Xie, C. F. Leong, D. M. D'Alessandro and J.-L. Zuo, Coord. Chem. Rev., 2017, 345, 342–361.
41. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., B, 2016, 72, 171–179.
42. T. L. A. Nguyen, R. Demir-Cakan, T. Devic, M. Morcrette, T. Ahnfeldt, P. Auban-Senzier, N. Stock, A. M. Goncalves, Y. Filinchuk, J. M. Tarascon and G. Férey, Inorg. Chem., 2010, 49, 7135–7143.
43. A. G. Zavyalova, D. V Kladko, I. Yu. Chernyshov and V. V Vinogradov, J. Mater. Chem. A, 2021, 9, 25258–25271.
44. Y. Kobayashi, T. Terauchi, S. Sumi and Y. Matsushita, Nat. Mater., 2017, 16, 109–114.
45. (a) D. Casanova, M. Llunell, P. Alemany and S. Alvarez, Chem.–Eur. J., 2005, 11, 1479–1494; (b) A. Ruiz-Martínez, D. Casanova and S. Alvarez, Dalton Trans., 2008, 19, 2583–2591; (c) M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, SHAPE, v2.1, 2013.
46. J. Castells-Gil, S. Mañas-Valero, I. J. Vitórica-Yrezábal, D. Ananias, J. Rocha, R. Santiago, S. T. Bromley, J. J. Baldoví, E. Coronado, M. Souto and G. Mínguez Espallargas, Chem.–Eur. J., 2019, 25, 12636–12643.
47. O. V Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
48. C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235.
49. L. Sarkisov, R. Bueno-Perez, M. Sutharson and D. Fairen-Jimenez, Chem. Mater., 2020, 32, 9849–9867.
50. T. Mori, A. Kobayashi, Y. Sasaki, H. Kobayashi, G. Saito and H. Inokuchi, Bull. Chem. Soc. Jpn., 2006, 57, 627–633.
51. P. Guionneau, C. J. Kepert, G. Bravic, D. Chasseau, M. R. Truter, M. Kurmoo and P. Day, Synth. Met., 1997, 86, 1973–1974.
52. V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576–3586.
53. L. S. Xie and M. Dincă, Isr. J. Chem., 2018, 58, 1119–1122.
54. I. Yu, K. A. P. Shevchenko, A. A. Shabalin and V. A. Blatov, Sci. Technol. Adv. Mater. Methods, 2022, 2, 250–265.
55. F. Juvenal, A. Bonnot, D. Fortin and P. D. Harvey, ACS Omega, 2017, 2, 7433–7443.
56. D. Jankowski, R. Świetlik, E. W. Reinheimer and M. Fourmigué, J. Raman Spectros., 2011, 42, 1518–1527.
57. O. Drozdova, H. Yamochi, K. Yakushi, M. Uruichi, S. Horiuchi and G. Saito, Synth. Met., 2001, 120, 739–740.
58. K. Yakushi, Crystals, 2012, 2, 1291–1346.
59. C. F. Leong, B. Chan, T. B. Faust and D. M. D'Alessandro, Chem. Sci., 2014, 5, 4724–4728.
60. P. M. Usov, C. F. Leong, B. Chan, M. Hayashi, H. Kitagawa, J. J. Sutton, K. C. Gordon, I. Hod, O. K. Farha, J. T. Hupp, M. Addicoat, A. B. Kuc, T. Heine and D. M. D'Alessandro, Phys. Chem. Chem. Phys., 2018, 20, 25772–25779.
61. Y. Lin, J. E. Eldridge, J. M. Williams, A. M. Kini and H. H. Wang, Spectrochim. Acta A Mol. Biomol. Spectrosc., 1999, 55, 839–843.
62. D. Jankowski, R. Świetlik, O. Jeannin, A. Assaf, E. W. Reinheimer and M. Fourmigué, J. Raman Spectrosc., 2013, 44, 1765–1776.
63. F. Pop, P. Auban-Senzier, A. Frąckowiak, K. Ptaszyński, I. Olejniczak, J. D. Wallis, E. Canadell and N. Avarvari, J. Am. Chem. Soc., 2013, 135, 17176–17186.
64. S. Zhang, D. K. Panda, A. Yadav, W. Zhou and S. Saha, Chem. Sci., 2021, 12, 13379–13391.
65. A. Frąckowiak, B. Barszcz, I. Olejniczak, M. Tomasik, N. Jarzyniak, R. Świetlik, P. Auban-Senzier, M. Fourmigué, O. Jeannin and F. Camerel, New J. Chem., 2020, 44, 15538–15548.
66. M. Yoshizawa, K. Kumazawa and M. Fujita, J. Am. Chem. Soc., 2005, 127, 13456–13457.
67. J. B. Torrance, B. A. Scott, B. Welber, F. B. Kaufman and P. E. Seiden, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 730–741.
68. I. Garcia-Yoldi, J. S. Miller and J. J. Novoa, J. Phys. Chem. A, 2009, 113, 484–492.
69. S. V Rosokha and J. K. Kochi, J. Am. Chem. Soc., 2007, 129, 828–838.
70. A. Coskun, J. M. Spruell, G. Barin, A. C. Fahrenbach, R. S. Forgan, M. T. Colvin, R. Carmieli, D. Benítez, E. Tkatchouk, D. C. Friedman, A. A. Sarjeant, M. R. Wasielewski, W. A. I. I. I. Goddard and J. F. Stoddart, J. Am. Chem. Soc., 2011, 133, 4538–4547.
71. G. Visentini, M. Masino, C. Bellitto and A. Girlando, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 9460–9467.
72. S. Mazumdar and Z. G. Soos, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 2810–2823.
73. F. Solano, P. Auban-Senzier, B. Barszcz, A. Frąckowiak, I. Olejniczak, P. Alemany, E. Canadell, N. Zigon and N. Avarvari, Mater. Adv., 2024, 5, 2470–2481.
74. I. Olejniczak, B. Barszcz, P. Auban-Senzier, H. O. Jeschke, R. Wojciechowski and J. A. Schlueter, J. Phys. Chem. C, 2022, 126, 1890–1900.
75. Y. Qiao, Y. Lin, S. Liu, S. Zhang, H. Chen, Y. Wang, Y. Yan, X. Guo and J. Huang, Chem. Commun., 2013, 49, 704–706.
76. T. Sugano, K. Yakushi and H. Kuroda, Bull. Chem. Soc. Jpn., 2006, 51, 1041–1046.
77. H. A. Evans, J. G. Labram, S. R. Smock, G. Wu, M. L. Chabinyc, R. Seshadri and F. Wudl, Inorg. Chem., 2017, 56, 395–401.
78. D. M. D'Alessandro and F. R. Keene, Chem. Soc. Rev., 2006, 35, 424–440.
79. P. Day, N. S. Hush and R. J. H. Clark, Philos. Trans. R. Soc. A., 2008, 366, 5–14.
80. K. Fabrizio, K. N. Le, A. B. Andreeva, C. H. Hendon and C. K. Brozek, ACS Mater. Lett., 2022, 4, 457–463.
81. L. S. Xie, E. V Alexandrov, G. Skorupskii, D. M. Proserpio and M. Dincă, Chem. Sci., 2019, 10, 8558–8565.
82. M. A. Gordillo, P. A. Benavides, C. McMillen and S. Saha, Mater. Adv., 2022, 3, 6157–6160.
83. P. Sippel, D. Denysenko, A. Loidl, P. Lunkenheimer, G. Sastre and D. Volkmer, Adv. Funct. Mater., 2014, 24, 3885–3896.
84. N. Mroweh, C. Mézière, M. Allain, P. Auban-Senzier, E. Canadell and N. Avarvari, Chem. Sci., 2020, 11, 10078–10091.
85. F. Pop, M. Allain, P. Auban-Senzier, J. Martínez-Lillo, F. Lloret, M. Julve, E. Canadell and N. Avarvari, Eur. J. Inorg. Chem., 2014, 3855–3862.
86. M. H. Whangbo, J. M. Williams, P. C. W. Leung, M. A. Beno, T. J. Emge and H. H. Wang, Inorg. Chem., 1985, 24, 3500–3502.
87. T. A. Albright, J. K. Burdett and M.-H. Whangbo, Orbital Interactions in Chemistry, John Wiley & Sons, 2013.
88. U. Geiser and J. A. Schlueter, Chem. Rev., 2004, 104, 5203–5242.
89. S. R. Batten, N. R. Champness, X.-M. Chen, J. Garcia-Martinez, S. Kitagawa, L. Öhrström, M. O'Keeffe, M. P. Suh and J. Reedijk, CrystEngComm, 2012, 14, 3001–3004.
90. S. S. Park, E. R. Hontz, L. Sun, C. H. Hendon, A. Walsh, T. Van Voorhis and M. Dincă, J. Am. Chem. Soc., 2015, 137, 1774–1777.
91. C. Benelli and D. Gatteschi, Chem. Rev., 2002, 102, 2369–2388.
92. M. L. Kahn, R. Ballou, P. Porcher, O. Kahn and J. P. Sutter, Chem.–Eur. J., 2002, 8, 525–531.
93. Y.-Z. Zheng, Y. Lan, W. Wernsdorfer, C. E. Anson and A. K. Powell, Chem.–Eur. J., 2009, 15, 12566–12570.
94. D.-D. Yin, Q. Chen, Y.-S. Meng, H.-L. Sun, Y.-Q. Zhang and S. Gao, Chem. Sci., 2015, 6, 3095–3101.
95. T. Enoki and A. Miyazaki, Chem. Rev., 2004, 104, 5449–5478.
96. T. Shikama, T. Shimokawa, S. Lee, T. Isono, A. Ueda, K. Takahashi, A. Nakao, R. Kumai, H. Nakao, K. Kobayashi, Y. Murakami, M. Kimata, H. Tajima, K. Matsubayashi, Y. Uwatoko, Y. Nishio, K. Kajita and H. Mori, Crystal, 2012, 2, 1502–1513.
97. J.-F. Chen, Y.-L. Ge, D.-H. Wu, H.-T. Cui, Z.-L. Mu, H.-P. Xiao, X. Li and J.-Y. Ge, Front. Chem., 2022, 10, 974914.
98. Y.-L. Li, Q.-Y. Liu, C.-M. Liu, Y.-L. Wang and L. Chen, Aust. J. Chem., 2015, 68, 488–492.
99. L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092–3104.
100. B. S. Sran, J. F. Gonzalez, V. Montigaud, B. Le Guennic, F. Pointillart, O. Cador and G. Hundal, Dalton Trans., 2019, 48, 3922–3929.
101. W.-H. Zhu, X. Xiong, C. Gao, S. Li, Y. Zhang, J. Wang, C. Zhang, A. K. Powell and S. Gao, Dalton Trans., 2017, 46, 14114–14121.
102. G. Lorusso, O. Roubeau and M. Evangelisti, Angew. Chem., Int. Ed., 2016, 128, 3421–3424.
103. A. Amjad, A. Figuerola, A. Caneschi and L. Sorace, Magnetochemistry, 2016, 2, 27.
104. Y.-N. Guo, G.-F. Xu, P. Gamez, L. Zhao, S.-Y. Lin, R. Deng, J. Tang and H.-J. Zhang, J. Am. Chem. Soc., 2010, 132, 8538–8539.
105. M. Grahl, J. Kötzler and I. Seßler, J. Magn. Magn. Mater., 1990, 90–91, 187–188.
106. M. Dolai, M. Ali, J. Titiš and R. Boča, Dalton Trans., 2015, 44, 13242–13249.
107. A. Zabala-Lekuona, J. M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984.
108. E. Lucaccini, L. Sorace, M. Perfetti, J.-P. Costes and R. Sessoli, Chem. Commun., 2014, 50, 1648–1651.
109. J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125–138.
110. X. Feng, J.-L. Liu, K. S. Pedersen, J. Nehrkorn, A. Schnegg, K. Holldack, J. Bendix, M. Sigrist, H. Mutka, D. Samohvalov, D. Aguilà, M.-L. Tong, J. R. Long and R. Clérac, Chem. Commun., 2016, 52, 12905–12908.
111. Y.-S. Ding, K.-X. Yu, D. Reta, F. Ortu, R. E. P. Winpenny, Y.-Z. Zheng and N. F. Chilton, Nat. Commun., 2018, 9, 3134.
112. G. M. Sheldrick, Acta Crystallogr., A, 2015, 71, 3–8.
113. G. M. Sheldrick, Acta Crystallogr., C, 2015, 71, 3–8.
114. M.-H. Whangbo and R. Hoffmann, J. Am. Chem. Soc., 1978, 100, 6093–6098.
115. J. H. Ammeter, H. B. Buergi, J. C. Thibeault and R. Hoffmann, J. Am. Chem. Soc., 1978, 100, 3686–3692.
116. K. Heuzé, M. Fourmigué, P. Batail, C. Coulon, R. Clérac, E. Canadell, P. Auban-Senzier, S. Ravy and D. Jérome, Adv. Mater., 2003, 15, 1251–1254.
117. P. Pascal, Ann. Chim. Phys., 1910, 19, 5–70.
118. O. Kahn, Molecular Magnetism, 1993.

---

Footnotes

† Dedicated to Professor Marius Andruh for his 70th birthday.

‡ Electronic supplementary information (ESI) available: Fig. S1–S11 and Tables S1–S6. CCDC 2341521. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc05763e

---