Selective optimisation of catalytic activity by tuning the structural composition in nanoparticulate CuFe₂O₄

Abstract

The tailored development of highly active and selective electrocatalysts based on abundant and non-toxic elements will be key to the rigorous implementation of sustainable processes in industry. In this context, spinel-type CuFe₂O₄ is regarded as a promising candidate. We synthesised CuFe₂O₄ nanoparticles with various Cu : Fe ratios via a microwave-assisted solvothermal route. The compositional effect on the material properties and performance in multiple electrochemical reactions, including HER, OER, ORR and CO₂RR, is investigated, in order to obtain valuable insights about those parameters that drive the improvement of catalytic activities. An increase in lattice strain and surface area is observed for compositions deviating from the ideal 1 : 2 stoichiometry, which goes in hand with an improved performance in alkaline water splitting. For the CO₂RR on the other hand, the Cu-content is determined to be the most important factor, with a Cu-excess being highly beneficial. The suitability of CuFe₂O₄ as a bifunctional water splitting catalyst was demonstrated by full cell measurements using the spinel catalyst at both the anode and cathode side at the same time. Moreover, we showed the applicability of CuFe₂O₄ in bifunctional gas-diffusion electrodes for rechargeable Zn–air batteries.

---

Introduction

Electrocatalysis represents a key technology in the energy-transition from fossil-fuel based industrial processes towards more sustainable ones. By employing electricity from renewable sources, the synthesis of a broad variety of different products becomes feasible without concomitant emissions of CO₂ and other greenhouse gases that contribute to climate change. In order to reduce the energy consumption and thus production costs, catalysts are required to improve the activity and selectivity for a reaction. To date, mainly noble metal electrocatalysts, such as Pt or Ir, have been employed. However, for sustainable catalysis to become cost-competitive to conventional carbon-based processes, the development of active and selective electrocatalysts based on earth-abundant elements is needed. In this regard, transition metal oxides have emerged as promising candidates. Thus, Ni-, Fe- and Co-based oxides can be used for the oxygen evolution reaction (OER) and the complementary hydrogen evolution reaction (HER), which represent the half reactions in electrochemical water splitting.^1–3

Besides water electrolysis for the (industrial) production of H₂, other electrochemical conversion reactions are of importance for a transition towards a sustainable energy economy, and require the development of efficient and selective catalysts. In this light, the electrocatalytic oxygen reduction reaction (ORR) is essential for operating fuel cells and metal–air batteries, which are highly attractive for sustainable energy conversion and storage.^4,5 Among earth-abundant catalysts for the ORR, especially Mn- and Co-containing oxides show an outstanding performance.^6,7

The CO₂ reduction reaction (CO₂RR), on the other hand, is offering a promising pathway for synthesising carbon containing chemicals and fuels with a higher volumetric energy density compared to H₂. More importantly, CO₂ can be captured out of the atmosphere or from industrial flue gases, which makes the CO₂RR a feasible strategy to diminish the concentration of green-house gases. Selectivity has proven to be the most important catalyst property with respect to the CO₂RR, as it determines the overall product mixture out of a wide scope of possible reduction products. Cu, especially also CuO_x-derived catalysts, is of particular interest, due to the possibility of turning excess CO₂ into valuable higher carbon (C₂₊) products.^8,9

Multifunctional earth-abundant catalysts are especially desirable since they can decrease the total amount of catalyst material required and reduce the overall production cost of the system. Additionally, they can increase the substrate scope for a system.⁶ This is especially useful, in case the target reactions occur under comparable conditions – e.g. in alkaline media – as that increases the likelihood of a catalysts's stability under the conditions applied for these reactions. Among bifunctional catalysts for OER and ORR, which are required e.g. for metal–air batteries in energy storage applications, spinel oxides are an interesting material class, due to their structural variety and variability, as well as the number of transition metal cations that can be introduced into the structure.¹⁰ Another important factor to be considered here is the fast and low-energy synthesis of spinel oxides, e.g. via co-precipitation,¹¹ or microwave assisted synthesis,^12,13 which offers the advantage of further reducing the production cost. Compared to Co and Ni, Cu is less toxic and its mining is less hazardous and politically debatable. Since the OER is usually the limiting factor in processes like water-electrolysis due to its sluggish kinetics, an aqueous alkaline environment is often chosen to improve the energy efficiency. Additionally, most earth-abundant OER and ORR catalysts are unstable in acidic media, whereas they are stable in alkaline media. This enhances the need for the development of HER and ORR catalysts that operate in an alkaline environment as well.^14,15

We recently reported on a microwave assisted aqueous synthesis of CuFe₂O₄ and its use for the electrochemical CO₂RR in a KHCO₃ electrolyte – i.e. also aqueous, if at a more neutral pH compared to the alkaline environment often tested for OER, HER and ORR.¹² The obtained CuFe₂O₄ nanoparticles are of a cubic spinel structure, although a tetragonal distortion is favoured at room temperature and at temperatures below 400 °C, indicating a kinetic control of the crystallisation process.^16,17 The material properties, especially the cation distribution in CuFe₂O₄, are influenced by the synthesis conditions and could in turn be correlated with the catalytic performance.^12,18,19

CuFe₂O₄ is a promising electrocatalyst for multiple conversion reactions. To this end, CuFe₂O₄ nanofibres on a Ni-foam substrate were used as an electrocatalyst for the OER by Silva et al., who reported on an activity surpassing that of CoFe₂O₄ and NiFe₂O₄.²⁰ Similarly, a superior OER activity was observed by Ferreira et al., for particles obtained via a proteic sol–gel synthesis.²¹ The group of Guo likewise synthesised CuFe₂O₄ nanofibres and investigated their performance for the OER and H₂O₂ reduction.²² They found an improved performance for the fibres compared to nanoparticulate analogues and an activity of CuFe₂O₄ in between that of NiFe₂O₄ and CoFe₂O₄. Moreover, CuFe₂O₄ was investigated for the ORR,²³ pointing towards a possible application as a bifunctional catalyst e.g. for metal–air batteries. Similarly, it has been applied as a catalyst for the HER in an alkaline electrolyte,^24,25 or the electrochemical CO₂RR.¹² For the alkaline HER, Belhadj et al. reported an activity of CuFe₂O₄ between that of the Ni- and Co ferrites.²⁵ Due to its semiconducting nature and small bandgap, CuFe₂O₄ has also been successfully employed for photoelectrochemical (PEC) reactions, such as PEC HER,^24,26,27 PEC OER,^28,29 or PEC CO₂RR to methanol.³⁰

We herein systematically vary the synthesis conditions for CuFe₂O₄ nanocrystals, specifically targeting different cation ratios and structural compositions. Subsequently, we employ the obtained nanoparticles for multiple electrochemical reactions, including HER, OER, ORR and CO₂RR, and identify the predominant influences of specific material properties on the resulting performance. We found that the composition only has a negligible impact on the OER activity that is mostly correlated with strain effects, whereas a high Cu-ratio is especially beneficial for the CO₂RR to CO. Furthermore, the suitability of CuFe₂O₄ as a bifunctional water splitting catalyst was demonstrated by full cell measurements using the spinel catalyst for both the anode and cathode at the same time. Additionally, we demonstrate the bifunctional OER and ORR performance of CuFe₂O₄ in gas-diffusion electrodes (GDEs) for rechargeable Zn–air batteries, elucidating the practical applicability not only for direct energy conversion and the synthesis of green fuels, but also in energy storage devices.

Experimental

Synthesis

CuFe₂O₄ was synthesised in a microwave reactor (Anton Paar, Monowave 400) for 15 min at 175 °C, based on what was previously reported.¹² The respective amounts of metal nitrates were dissolved in a mixture of 5 mL of ethylene glycol (Acros Organics, 99.5%) and 8.4 mL of ultrapure water. For stoichiometric CuFe₂O₄, 1 mmol of Fe(NO₃)₃·9H₂O (404 mg, Acros Organics) and 0.5 mmol of Cu(NO₃)₂·9H₂O (120.8 mg, Acros Organics) were used, and the exact amounts were adjusted for the other compositions. Directly before placing the reaction vial into the microwave reactor, the pH was adjusted to 12 with 3 M KOH under stirring. After reaction for 15 min at 175 °C (heating as fast as possible and cooling with compressed air), the particles were precipitated with water, washed thrice with water and once with ethanol, and dried overnight at 80 °C.

Characterisation

Prepared samples were analysed by powder X-ray diffraction (XRD) first on a Malvern PANalytical Empyrean device in Bragg–Brentano geometry, using Cu K_α radiation (λ₁ = 1.5406 Å, λ₂ = 1.54443 Å). Acceleration voltage and emission current were set to 40 kV and 40 mA, respectively. Pulse height distribution levels were adjusted to minimise sample fluorescence (8.05–11.27 keV). For Ag-XRD a STOE STADI P Mythen2 4 K diffractometer with four Dectris MYTHEN2 R 1 K strip detectors and monochromatic Ag K_α1 irradiation (λ = 0.5594 Å) was used.³¹ Crystallite sizes were estimated based on Cu-XRD patterns using the integral breadth method, i.e. dividing the height of a reflection by its area.³² Rietveld refinement was performed with FullProf, using a Thompson-Cox-Hastings pseudo-Voigt function for peak shape modelling,³³ and the structure reported by Mahmood et al. for cubic CuFe₂O₄.³⁴ Refined parameters include instrumental zero shift, scale, lattice parameters a, b, and c, the FWHM parameters Y and X, size anisotropy, isotropic B, asymmetry, and finally site occupation. Instrumental broadening was determined by measuring a LaB₆ standard (NIST SRM 660c). Following ICDD reference cards were used for the identification of observed phases: CuO-00-048-1548; CuFe₂O₄(c)-01-077-0010.

Diffuse reflectance infrared Fourier transformed (DRIFT) spectroscopy was conducted on a Bruker Alpha II spectrometer, while UV/vis/NIR measurements were conducted on a PerkinElmer Lambda 750 spectrometer, equipped with a Praying Mantis (Harrick). Spectralon was used as a white standard. For Raman spectroscopy a Horiba Jobin Yvon Raman microscope with a 11.5 W He–Ne laser (λ = 633 nm) was employed. The intensity was reduced to prevent sample heating.

X-ray photoelectron spectroscopy (XPS) was performed on a VersaProbe III Scanning XPS Microprobe from Physical Electronics (PHI) and data was evaluated using CasaXPS. Al K_α radiation was used at a beam voltage of 15 kV and power of 25 W. The spot size was 100 μm. For survey scans a time per step of 50 ms, a pass energy of 224 eV and a step size of 0.4 eV were used, while high resolution spectra were measured at a pass energy of 26 eV, step size of 0.1 eV and a step time of 50 ms. The binding energy shift was corrected using the Cu L₃M_4,5M_4,5 signal and fixing the maximum to a kinetic energy of 917.86 eV.³⁵ A Gaussian–Lorentzian line shape was assumed for the fit (GL30) after Shirley background correction. For the determination of the degree of inversion, Cu 2p spectra were approximated with two peaks with a fixed separation of 1.85 eV. For fitting the Fe 2p spectra, parameters reported for NiFe₂O₄ by Biesinger et al. were used.³⁶

For morphological characterisation, scanning electron microscopy (SEM) was performed on a Zeiss Leo 1530 instrument at an acceleration voltage of 3 kV after sputter coating with platinum (Cressington Sputter Coater 208 HR). The same instrument in combination with an ultra-dry EDX detector (Thermo Fisher Scientific NS7) was used for the energy dispersive X-ray analysis (EDX) at 20 kV. Particle surface areas were determined using the Brunauer–Emmet–Teller (BET) model on N₂ physisorption data collected on a Quadrasorb Evo device from Anton Paar QuantaTec at 77 K after degassing for 12 h at 120 °C.

Electrocatalysis

Oxygen evolution reaction (OER) and hydrogen evolution reaction (HER) experiments were performed in an H-cell with 1 M KOH as the electrolyte that was constantly purged with Ar. The measurements were conducted with a Gamry Reference 3000 potentiostat and the software Gamry frameworks. A Pt counter electrode and a reversible hydrogen reference electrode (HydroFlex, Gaskatel) were used, respectively. The cell chambers were separated by a Selemion AMV-N anion-exchange membrane (AGC group). For working electrode preparation, a catalyst ink was prepared by dispersing 10 mg of CuFe₂O₄ and 20 μL of a 5 wt% Nafion solution (Alfa Aesar) in 300 μL of iso-propanol using ultrasonication for ∼1 h. This dispersion was drop-cast (2 times 30 μL) onto 1 cm wide stripes cut out of carbon cloth (Freudenberg H2315-C2). The covered area was restricted to 1 cm² by Kapton tape. The electrodes were weighed before and after the coating with CuFe₂O₄.

At the beginning of the water splitting measurements, the open circuit potential was monitored, followed by EIS, CV, CV at different scan rates in the non-faradaic region for the determination of the ECSA, conditioning of the electrodes by 100 consecutive CV scans from −0.7 to 2 V at a scan rate of 100 mV s⁻¹ in order to remove organic residues from the synthesis, and finally 20 LSV scans (5 mV s⁻¹). Afterwards, another EIS measurement was conducted at −0.5 or 1.7 V, followed by CV for the ECSA, and finally CV over the entire region for comparison with the curves measured before the OER/HER experiment. The internal resistance was compensated for using the current interrupt method. EIS data was fit with EC-lab. For the determination of the ECSA from the double layer capacitance, a standard value for flat oxide surfaces of 40 μF cm⁻² was used.³⁷ H₂ evolution during chronoamperometry at reducing potentials was detected with a Shimadzu GC-2014 gas chromatograph. The H-cell was continuously purged with Ar at a flow rate of 25 mL min⁻².

The CO₂RR experiments were performed in a comparable H-cell setup using 0.1 M aqueous KHCO₃ as electrolyte, a Selemion anion exchange membrane, Pt as the counter, and Ag/AgCl as the reference electrode, respectively. The electrolyte was continuously purged with CO₂ (99.995 vol%, Air Liquide) at a flow rate of 20 mL min⁻¹. A Gamry Reference 3000 potentiostat was employed and the internal resistance was compensated for using the current interrupt method. Evolved gasses were analysed with a Shimadzu GC-2014 gas chromatograph, equipped with a HayeSep Q and a HayeSep R column in series, a thermal conductivity detector and a methanizer in combination with a flame ionisation detector. All potentials are converted to the RHE scale: V_RHE = V_Ag/AgCl + 0.209 + 0.059pH. The pH was around 6.8. Liquid products were analysed after chronoamperometry for 90 min and CV scans before and after the CO₂RR using HPLC (LC2010, Shimadzu). The working electrodes were prepared in the same way as for the HER/OER experiments.

For ORR experiments gas diffusion electrodes (GDE) were prepared by cutting circular pieces with a diameter of 2 cm out of carbon paper (Sigracet 29-BC) and coating them via drop casting. For the catalyst ink, 10 mg of CuFe₂O₄ were dispersed together with 20 μL of a 5 wt% Nafion solution in 300 μL of i-propanol, using ultrasonication. Subsequently, 5 times 20 μL of the dispersion was homogeneously distributed over the carbon paper electrode. After drying the electrodes were hot pressed with a N117 Nafion membrane (Ion Power) for two times 1 min at 120 °C. The membranes were pre-treated in 5 wt% H₂O₂ solutions for 30 min at 80 °C, boiled in ultrapure water, and subsequently treated with 8 wt% H₂SO₄ for 30 min at 80 °C, before storage in ultrapure water. The measurement was conducted in a home-made half-cell with a parallel flow field, based on the design of the Arenz group.³⁸ The electrode was placed on top of the flow field and fixed with a PTFE inset. The inset was filled with 20–25 mL of 4 M KOH and equipped with a Pt counter and a RHE reference electrode (Gaskatel). The working electrode area in contact with the electrolyte was 1 cm². 300 mL min⁻¹ of humidified O₂ was flushed through the cell. Before measuring 10 LSV scans at 50 mV s⁻¹ in both cathodic and anodic sweep direction, the electrodes were conditioned by performing 50 CV scans between −0.5 and 1.9 V at a scan rate of 200 mV s⁻¹. The cathodic sweeps were employed for the data evaluation herein, due to the more stable current response. The same procedure was repeated in N₂ and subtracted from the data obtained in O₂. A VSP300 potentiostat (BioLogic) was used for the measurements and the internal resistance was compensated for by 95%, using the positive feedback method.

Electrodes for Mott–Schottky measurements were prepared by electrophoretic deposition of CuFe₂O₄ on cleaned FTO substrates in acetone/iodine solutions at 15 kV. The measurements were performed in a PECC-2 cell (Zahner Elektrik), using Pt as a counter, Ag/AgCl as a reference electrode, and 0.1 M Na₂SO₄ (pH 5.6) as electrolyte. A Zennium potentiostat (Zahner Elektrik) was used and the applied potential was decreased stepwise from 0.75 to −0.75 V vs. Ag/AgCl.

For the application in a Zn–air-battery 10 mg of CuFe₂O₄ were dispersed in 300 μL of i-propanol and 20 μL of at 5 wt% Nafion-solution, and then drop-cast onto circular pieces of carbon paper (Sigracet 29-BC, 1.8 cm in diameter, 5 times 20 μL). The prepared electrodes were measured in an ECC-Air test cell (EL-CELL), using 800 μL 6 M KOH as the electrolyte, Zn foil as the counter electrode, and two glass fibre separators (EL-CELL). Humidified O₂ was flushed through the cell at a rate of approx. 20 mL min⁻¹. A Gamry Reference 3000 potentiostat was used. For comparison, a commercial Pt-GDE from De Nora Electrode Technologies (DN-Fcell Anode P1100W) was tested.

Results and discussion

Materials characterisation

The synthesis of CuFe₂O₄ was performed as previously reported, employing a microwave-assisted approach and an alkaline ethylene glycol/water mixture as solvent.¹² A synthesis duration of 15 min at 175 °C was chosen as the standard conditions and the ratio of copper to iron cations of the precursor salts Cu(NO₃)₂·3H₂O and Fe(NO₃)₃·9H₂O in the solution was varied in a range of Cu : Fe = 0.8 : 2.2 to Cu : Fe = 1.2 : 1.8. Thus, phase-pure cubic spinel ferrites could be obtained for a variety of different compositions, and only at a high copper excess of 20% (Cu : Fe – 1.2 : 1.8) based on the standard equivalent of 1.0, the emergence of a CuO by-phase becomes apparent in the Cu-X-ray diffraction (XRD) patterns (Fig. 1a). The results were further confirmed by high-resolution Ag-XRD that supported phase-purity over a wide range of different compositions (Fig. S1a†).

Fig. 1 Powder XRD patterns of CuFe₂O₄ nanoparticles with varied Cu/Fe ratios (a), Cu/Fe-ratio determined by EDX (b) and morphological characterisation with SEM (c).

All products occurred as nanoparticles of a similar size, based on scanning electron microscopy (SEM) images (Fig. 1c). A particle size of around 17 nm for stoichiometric CuFe₂O₄ was obtained, which is in good agreement with previous results derived from TEM analysis.¹² For Cu_0.8Fe_2.2O₄ and Cu_1.2Fe_1.8O₄, particle sizes of 16.5 nm and 17.5 nm were determined, respectively, suggesting a slight particle growth with increasing Cu content. This might either be attributed to the good microwave absorption properties of Cu oxides³⁹ which can result in local heating, or to the large ionic radius of Cu²⁺ compared to Fe³⁺.⁴⁰ Energy-dispersive X-ray analysis (EDX) was used for determining the actual Cu/Fe-ratio in the synthesised Cu_1±xFe_2±xO₄ demonstrating an almost ideal linear correlation of the Cu and Fe content in the prepared ferrites with the employed ratio in the precursor solution (Fig. 1b).

For all CuFe₂O₄ particles, a crystallite size of around 10 nm was determined by means of the integral breadth method. A slight decrease in the apparent size with a deviation from the ideal stoichiometric composition – especially towards an increasing Cu excess – is discernible, however (Fig. S1b†). Crystallite sizes are therefore slightly smaller than the particle sizes, but still in a range suggesting the observed nanoparticles to be single crystals, possibly with a low degree of amorphisation at the edges. However, the integral breadth method only allows for a rough estimation of particle sizes and does not allow for a differentiation between strain and size contributions to reflection broadening. Hence, Rietveld refinement was performed on the Cu-XRD patterns (Fig. S1c†). Slightly larger crystallite sizes of around 13 nm were determined. Most importantly, the decreasing crystallite size with an increasing Cu content was confirmed (Fig. 2). This can be explained by a predominant need for Fe³⁺ in building up the spinel structure, since binary Fe-based spinels can be formed (magnetite, Fe₃O₄), but on the other hand no binary Cu spinel oxides are known.

Fig. 2 Crystallite sizes determined via Rietveld refinement for CuFe₂O₄ of different compositions (a), corresponding microstrain (b), lattice parameter (c) and BET surface area (d).

The crystallite size is largest for particles with an excess of Fe in the structure. This is different from the integral breadth method, supporting an increased contribution from strain in these particles. Notably, the determined crystallite size slightly exceeds the average particle diameter for high Fe ratios. This can be an effect of the crude approximation of particle sizes from the SEM images. On the other hand, Rietveld refinement slightly overestimates crystallite sizes – at least for large deviations from the ideal stoichiometry. This is due to the chosen refinement procedure, which does not take into account changes in the Cu/Fe-ratio. We chose only to refine the occupation of octahedral and tetrahedral sites by Fe and Cu ions, respectively, under the constraint of retained stoichiometry. If we lift this constraint towards the end of the refinement for Cu, indeed consistently lower R values and particle sizes are obtained. However, the overall trend in the correlation of crystallite size and composition remains the same, and the occupation values are somewhat arbitrary (Fig. S2†). This is due to the highly similar atom form factors of Cu and Fe, making a more accurate refinement on the laboratory data impossible, as shown by a random deviation of Cu/Fe ratios based on the results for the occupation values from the composition determined by EDX. For a more accurate determination of cation distribution in the lattice, high precision synchrotron data would be required. While the absolute refined crystallite sizes might thus be slightly too large, the relative differences between samples are still meaningful, since all were treated in the same manner.

Additionally, a significant increase in microstrain with a deviation from the ideal stoichiometric composition was apparent, that coincides with an increase in the lattice parameter (Fig. 2b and c). The presence of microstrain can be considered the reason for the size underestimation by the integral breadth method. In agreement with the larger particle size of spinels containing high amounts of Cu, the BET surface area decreases with an increasing Cu-ratio (Fig. 2d) from around 200 m² g⁻¹ for Cu_0.8Fe_2.2O₄, to around 100 m² g⁻¹ for Cu_1.1Fe_1.9O₄ and those compositions with a higher Cu content.

Another important method to investigate the composition is X-ray photoelectron spectroscopy (XPS), which allows for an elemental quantification of the surface, which can be related to the bulk composition in the case of nanomaterials. XPS confirms the composition of Cu, Fe and O atoms, with trace amounts of K and organic residues from the synthesis, as can be seen in the survey spectra (Fig. S3a†). An almost linear increase of the surface Cu/Fe ratio derived from the survey spectra with an increase in the employed metal ratios is observable (Fig. S3b, Table S1†). The Cu content is slightly higher than expected, possibly due to the low intensity of the Fe 3p peak that was used for the quantification. However, it might also suggest Cu segregation at the surface and thus a deviation of the surface from the bulk structure. This would in turn support the decreased crystallite size with a simultaneously increased particle size observed for the CuFe₂O₄ particles with a high Cu content. A similar enrichment of M²⁺-ions – especially Cu²⁺ – has also been observed by the group of Sivula for spinel oxide thin films.⁴¹ The Cu 2p signals are highly similar in shape independent of the composition.

Fitting the Cu 2p spectra with two signals for Cu at tetrahedral and octahedral sites, respectively, can be used to estimate the degree of inversion – albeit neglecting multiplet splitting (Fig. 3c).^42,43 Such a fit yields a degree of inversion of around 0.7, independent of the composition, which is in good agreement with previous results (Fig. S3g†).¹² Additionally, the value is slightly below the critical degree of inversion reported for phase-transition to the tetragonal phase, which is commonly 0.75.¹⁹ Trace amounts of Cu(I) are observed, especially at a very low Cu content, which is also reflected by the relatively decreased intensity of the 2p_3/2 satellites (Fig. S3c†). The amount of Cu(I) is low in all cases, as also shown in the highly comparable Cu L₃M_4,5M_4,5 spectra, for which satisfactory fits can be obtained with the parameters given for CuO by Biesinger et al. (Fig. S3e†).³⁵ The Fe 2p spectra can be well fit with the parameters reported for NiFe₂O₄, in agreement with a crystalline spinel structure (Fig. S3f†).³⁶

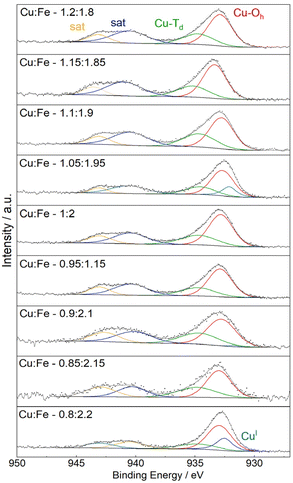Fig. 3 Fitted Cu 2p XP spectra, using two species for Cu²⁺ at octahedral and tetrahedral sites, in addition to one peak for Cu⁺ if required.

Infrared (IR) spectra of the different CuFe₂O₄ products are essentially identical (Fig. S4†), further proving the compositional integrity upon variation of the metal ratio. In addition to M–O vibrations of cations at tetrahedral (600–750 cm⁻¹) and at octahedral (400–550 cm⁻¹) sites,^44,45 respectively, the presence of organic residues from the synthesis can be detected between 1710 and 1200 cm⁻¹ and around 3000 cm⁻¹. Raman spectra show the expected weak bands for A_1g at 675 cm⁻¹, two F_2g modes at 550 cm⁻¹ and 485 cm⁻¹, an E_g mode at approx. 300 cm⁻¹ and another F_2g mode at 175 cm⁻¹ (Fig. S5†).⁴⁴ No additional peaks belonging to common by-phases such as α-Fe₂O₃ are observed.

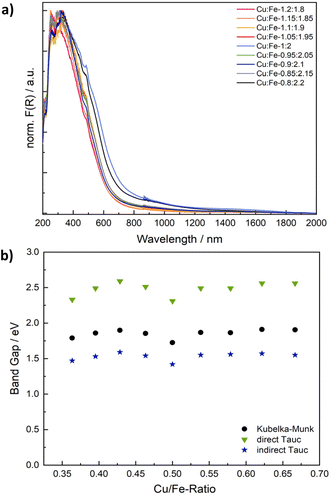
Spinel ferrites strongly absorb light in the UV to NIR range, resulting in a commonly dark brown colour. The absorption properties were examined using UV/vis/NIR spectroscopy (Fig. 4 and S6†). Although CuFe₂O₄ is a semiconductor, the observed optical transitions are – at least partially – localised and do not necessarily correlate with conventional valence to conduction band excitations. Specifically, optical absorption spectra are commonly the sum of inter-sublattice charge transfer transitions (ISCT) and intervalence charge transfer transitions (IVCT) in addition to ligand to metal charge transfer (LMCT) and crystal field transitions (Fig. S6b†).⁴⁶ The Kubelka–Munk plots of CuFe₂O₄ with different Cu/Fe-ratios exhibit essentially the same pseudo-absorption independent of the composition (Fig. 4 and S6a†). An apparent band gap of around 650–695 nm (1.8–1.9 eV) is determined, in agreement with literature reports (Table S2†).^29,41

Fig. 4 Normalised Kubelka–Munk plots showing the absorption behaviour of CuFe₂O₄ of different compositions (a) and correlation of extrapolated band gap values from Kubelka–Munk and Tauc plots with the Cu/Fe-ratio (b).

There is some debate about the character of the transition, with some groups proposing a direct band gap, whilst others are in favour of an indirect band gap.^30,47 Both the direct and the indirect Tauc plot are of reasonable appearance. While the direct Tauc plot predominantly shows the absorption visible in the range of 300 to 450 nm in the Kubelka–Munk plot, the indirect Tauc plot exacerbates the absorption towards higher wavelengths. Apparent band gap values of 2.31–2.56 eV are derived from the direct Tauc plots, whereas values of 1.42–1.59 eV in addition to a weak secondary absorption band between 0.75 to 0.88 eV are obtained from the indirect Tauc plots (Fig. S6c and d, Table S2†). Both values derived from direct and indirect Tauc plots are sometimes claimed to represent the band gap.^30,47 These values would point towards an indirect character of the band transition, albeit neglecting localisation of optical transitions. Additionally, one could choose to fit the direct Tauc plot in the region of 1.7–2.5 eV, which would result in determined values of around 2 eV, which are close to those apparent in the Kubelka–Munk plot, but only use a very small fraction of the plot. An alternative interpretation would suggest that the direct Tauc plot shows ISCT transitions between Fe³⁺ at tetrahedral sites and empty Fe³⁺ t_2g orbitals at neighbouring octahedral sites in a relatively reduced intensity, while the same transition is strongly visible in the indirect Tauc plots.^48,49 Not regarding the exact character of the optical transitions, a closer look at the apparent band gap values derived from both Kubelka–Munk and Tauc plots reveals a V-shaped correlation with the composition, with the smallest band gap determined for the ideal stoichiometry, and an increase in the band gaps apparent towards both an increasing and decreasing Cu-ratio (Fig. 3b). This effect is most likely due to the increase in microstrain going in hand with a deviation from the ideal Cu/Fe-ratio that leads to slight distortions of the electronic structure.

OER electrocatalysis

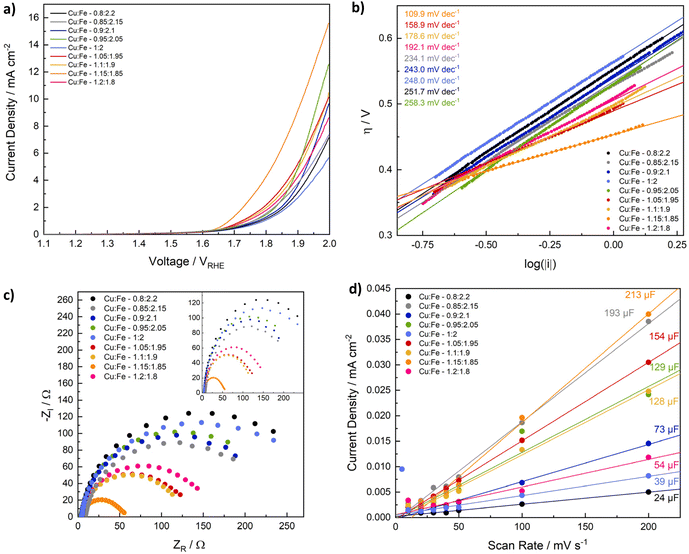
Having determined compositional and morphological differences between CuFe₂O₄ nanoparticles with different Cu/Fe-ratios, those spinel ferrites were employed for electrochemical reactions, to evaluate the influence of the composition on the catalyst-performance in the electrochemical production of different green fuels. Since CuFe₂O₄ is reportedly active for the OER, comparable to NiFe₂O₄ and CoFe₂O₄,^20,21,41 and has additionally been employed as photocathodes for the HER,²⁵ the CuFe₂O₄ nanoparticles of different composition were first tested for electrochemical water splitting in an alkaline electrolyte (1 M KOH). Specifically, electrodes were fabricated via drop-casting of the copper ferrites with Nafion as a binder on carbon fibre cloth electrodes with an exposed geometric surface area of 1 cm². HER and OER data were measured separately in an H-cell setup with a three electrode configuration (Fig. S7†).

The OER performance is generally comparable for all CuFe₂O₄ compositions, with a notable increase in the activity observed with an increasing Cu-ratio (Fig. 5a). The best performance is observed for a ratio of Cu : Fe 1.15 : 1.85, suggesting an initial increase in the activity upon introduction of Cu, until a loss of complete phase-purity, as noticed for higher Cu-ratios, results in a lower activity again for a Cu : Fe ratio of 1.2 : 1.8. A current density of 10 mA cm⁻², a commonly used figure of merit for comparing OER activities, is only achieved for samples with higher Cu content. The overpotential for the most active composition at 10 mA cm⁻² is with 684 mV still comparatively high, indicating that nanoparticulate CuFe₂O₄ has a lower OER activity compared to NiFe₂O₄, or CoFe₂O₄.^50–53 Meanwhile, overpotentials at 5 mA cm⁻² range from 589 mV to 749 mV for Cu_1.15Fe_1.85 and for stoichiometric CuFe₂O₄, respectively (Table S3†).

Fig. 5 LSV scans for the OER with CuFe₂O₄ of different composition in 1 M KOH (a), derived Tafel plots (b), Nyquist plots at 1.7 V vs. RHE after the OER (c) and double layer capacitance determined via CV at different scan rates in the non-faradaic region measured before the OER (d).

The discrepancies compared to literature reports are probably due to differences in the employed synthesis conditions that result in different material properties. Ferreira et al. obtained larger particles of tetragonal structure that were additionally subjected to ball-milling – resulting in considerably different material properties, e.g. considering strain effects.²¹ Fibres analysed by Silva et al. were likewise of tetragonal structure. Additionally, the surface area might be significantly affected by the synthesis route.²⁰ Importantly, both groups were using Ni-foam substrates instead of the more inert carbon fibre mats employed in this study.

To gain further insights into potential effects of additional metal species, we performed control experiments adding low amounts of Co- or Ni-nitrate to the electrolyte. While the influence of Ni was negligible, Co-addition resulted in a strong increase of the catalyst activity, even at 5 mg L⁻¹ of Co (Fig. S9†). During the first cycles, a notable oxidation of Co²⁺ in the electrolyte is visible, preceding the enhancement of the OER activity. Since a similar effect was observed for bare carbon cloth, the deposition of CoOOH or Co(OH)₂ species can be assumed. The overall activity is still significantly improved for the CuFe₂O₄ electrode, suggesting additional effects, such as electronic interactions between CuFe₂O₄ and the deposited Co-species. Notably, hydroxides precipitated as dark-brown solids slowly during the experiment. Thus, the total concentration of Co-ions in the solution might be reduced towards the end of the OER experiments. Although no effect is observable upon the addition of Ni to the solution, a contribution of the Ni-foam substrate as used in other studies cannot be completely ruled out as source for the different observed activities, especially in light of Ni and Ni-oxides having been shown to efficiently catalyse the OER on their own.^1,54

Interestingly, a deviation from the stoichiometric composition leads to an activity increase in all cases, similar to what was observed for the trends in microstrain and the band gap. This finding indicates that strain effects contribute to the improved performance when deviating from an ideal Cu/Fe ratio, similar to what has been reported for other electrocatalysts in literature.⁵⁵ The determined Tafel slopes range from 110 to almost 260 mV dec⁻¹ (Fig. 5b), indicating different kinetics depending on the composition. In agreement with the improved performance at high Cu-ratios, the Tafel slope is lowest for these samples, supporting faster electrode kinetics leading to a higher activity. Apart from the slope determined for Cu_1.15Fe_1.85O₄, which is around 110 mV dec⁻¹, all Tafel slopes are considerably higher than the ideal value of 120 mV dec⁻¹, i.e. the value that is commonly attributed to a rate determining one electron transfer step involving the most abundant adsorbed surface species as reactant in that step.⁵⁶ This could be an indication of adsorbates that block active sites and impede the OER performance.⁵⁷ One interpretation of the higher activity observed for higher Cu/Fe ratios would therefore be an increased amount of active sites – and thus also available surface sites – in the case of Cu-sites acting as primary reaction sites. When taking a look at the first LSV scan directly after electrode conditioning, a highly comparable activity of all samples independent of the composition is apparent, however (Fig. S8d†). This indicates dominant differences in the sample activation during the OER experiment, possibly involving changes in the cation distribution – or the in situ formation of surface FeOOH species, as generally observed for spinel-type OER catalysts.⁵⁸ The observed evolution might again be influenced by strain effects that slightly alter the electronic structure and the M–O bond lengths. Such an assumption is supported by pronounced differences in the current evolution for stoichiometric CuFe₂O₄ compared to Cu_1.15Fe_1.85O₄ (Fig. S10†).

CV curves measured before and after all other electrochemical measurements confirm an increasing activity for both the OER and the HER (Fig. S11†), and an initial activation even during the first three CV cycles. The marked activity increase during the first cycles is likely an effect of surface cleaning and removal of organic residues from the synthesis. Additionally, changes in surface composition might occur during the first cycles.⁵⁹

Another factor contributing to the significantly higher OER activity of ferrites containing larger amounts of Cu, especially Cu_1.15Fe_1.85O₄, is the much smaller charge transfer resistance (Fig. 5c). The charge transfer resistance is in line with the OER activity and the Tafel slope, and thus generally decreasing with an increasing Cu-content. This indicates that a high Cu content contributes to an increased conductivity in the semiconductor material. The Nyquist plots can be fit with two parallel circuits of capacitance and resistance in series, of which the larger corresponds to the charge transfer resistance and double layer capacitance (Fig. S12, Table S4†). A Warburg impedance was included in the fit, to account for mass transport limitations, but small in all cases.⁶⁰ The trend is less pronounced before the OER experiment, possibly due to organic residues impeding the charge transfer to the electrolyte (Fig. S12†). Additionally, it might be an effect of undergone changes in the cation distribution, since those are known to majorily impact the conductivity of CuFe₂O₄.^19,61

Another parameter known to impact the catalytic activity is the electrochemical active surface area (ECSA), that correlates the activity with the truly available surface area – and thus also the number of active sites assuming a homogeneous distribution – in contact with the electrolyte. For the determination of the ECSA, we calculated the double layer capacitance in a non-faradaic region – here 1.2–1.3 V vs. RHE (Fig. 5d). The CV scans for double layer capacitance determination were measured before and after the OER, with the shape of the curve and the centering around 0 mA cm⁻² being more stable afterwards, indicating initial contribution from additional processes, such as material changes (Fig. S13 and S14†). The ECSA is relatively small, with 0.6–5.3 cm² before, and 4–7 cm² after the OER (Table S5†). Considering average mass loadings of around 2 mg cm⁻² that equals to approx. of 0.05–0.25 m² g⁻¹, which is far lower than the measured BET surface area, but in good agreement with literature values.⁶² A smaller ECSA is expected, due to the limited surface area in contact with the electrolyte and available for the reaction, and possible discrepancies between adsorption sites for N₂ in BET measurements and active sites participating in the reaction. Before the OER, both the double layer capacitance and the ECSA are generally higher for compositions with a higher Cu-ratio – in contrast to the BET surface area – although no clear trend can be established. Notably, obtained values are highly similar after the OER, indicating, that the active species after surface reconstruction during the OER are similar. Additionally, initial differences might in part be an effect of organic residues. Due to the observed similarities, the ECSA can be assumed to play a negligible role in the different performances. The exchange current density on the other hand decreases with an increasing Cu content and increasing activity (Fig. S14†), suggesting that it is not a dominant factor determining the overall OER activity of CuFe₂O₄, either. The lower exchange current density at a high Cu-ratio might indicate Fe to be at the centre of active species.

Normalisation of current densities to the geometric surface area is debatable, due to potential blocking of active surface sites, e.g. by the Nafion binder, or by surrounding catalyst particles. We therefore also analysed the OER performance normalised to the BET surface area, the mass loading, and the ECSA (Fig. S8†). Due to the comparable ECSA for all catalysts, the general trend in OER performance is retained after normalisation. A comparison of samples after normalisation to the BET surface area is less conclusive, although a higher Cu content is still determined to be beneficial. The disruption of the previous trend can likely be explained by differences in the accessible surface area on the prepared electrode. The same is true for a normalisation to the loaded mass – here the deviations are caused by uncertainties in the determination of the very low mass loadings, due to some of the catalyst ink diffusing underneath the Kapton tape and thus not contributing to the catalytic conversion.

HER electrocatalysis

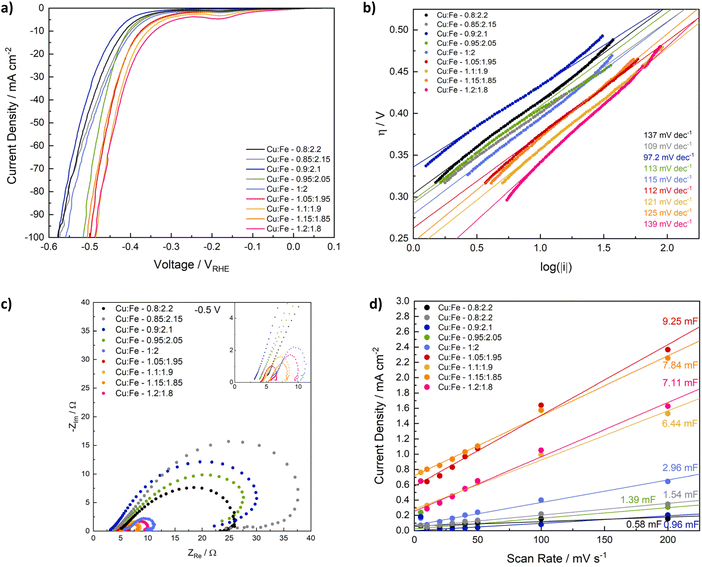
Next, we evaluated the influence of compositional variation on the activity of CuFe₂O₄ for the HER. Linear sweep voltammetry elucidates a good activity for all samples, with both the overpotential and the onset potential decreasing with an increasing Cu/Fe-ratio (Fig. 6a). Specifically, the overpotential at −10 mA cm⁻² decreases from −433 mV for Cu_0.9Fe_2.1O₄ to −342 mV for Cu_1.2Fe_1.8O₄ (Table S3†). The influence of strain effects and a CuO by-phase as observed for the OER is of less importance for the HER. Additionally, the observed differences are already apparent in the first LSV sweep (Fig. S15†), indicating that the composition – specifically the number of Cu-sites – directly affects the HER activity and not only the activation mechanism – an effect that is likely further exploited by the increased amount of Cu species at the surface observed in XPS analysis. An activation process is still visible for all samples during the initial sweeps, after which a stable activity is reached (Fig. S16†), which is also apparent in an increased negative current density in the CV curves after the HER experiment. Notably, the HER activity of samples with a high Cu ratio appears to be less affected than that of compositions with a low Cu ratio (Fig. S17†).

Fig. 6 LSV curves for the HER with CuFe₂O₄ of different composition (a), derived Tafel plots (b), Nyquist plots before the HER (c) and double layer capacitance from CVs at different scan rates measured before the HER (d).

Similar to the observation at 1.7 V, the charge transfer resistance at −0.5 V vs. RHE is significantly lower for compositions with a high Cu/Fe-ratio, compared to those containing low amounts of Cu, which is further indication of the improved conductivity with a higher Cu content (Fig. 5c). After the HER, the charge transfer resistance at −0.5 V is similar for all compositions (Fig. S18a†). It can be fit by a similar equivalent circuit as the OER data (Fig. S18, Table S6†). Before the HER, additional influences likely corresponding to corrosion, or at least changes in adsorbed surface species, are visible (Fig. 5c).⁶⁰ This may be related to the observed activation behaviour – and thus most likely to the reduction of Cu. An equivalent circuit containing additional inductive elements is needed to account for the observed loop, but did not yield satisfactory results using the simple – and often used – circuit depicted in Fig. S18.† This could be indicative of more complex phenomena and different species on the surface A qualitative discussion of differences in the charge transfer resistance is still possible.⁶³ The Tafel slope is similar for all samples and close to 120 mV dec⁻¹, suggesting similar kinetics independent of the composition, and the Volmer step to be the rate limiting one.^56,64 Interestingly, the exchange current density increases with an increasing Cu/Fe-ratio, indicating an improved electron transfer across the interface (Fig. S18b†) – this effect can likely also be attributed to the increased number of Cu-surface species.⁶⁵

The ECSA was additionally determined from CV scans between −0.1 and 0 V, i.e. closer to the relevant range for the HER. Similar to observation for electrodes employed in the OER between 1.2 and 1.3 V, both the double layer capacitance and ECSA before the electrochemical experiment are generally higher for compositions that contain more Cu (Fig. 6d, Table S5†). The differences between CuFe₂O₄ containing an excess of Cu and those samples containing less Cu are better established in this region, although the higher current densities and less defined shape of the CV curves might indicate small contributions of a faradaic current in the measurement region (Fig. S19†). After the HER, the double layer capacitance is slightly increased, but no correlation with the observed activity trend can be established (Fig. S20†), indicating that the ECSA is comparable for all samples, and small differences only have a minor contribution to the overall activity.

For a better comparison of the intrinsic activity, LSVs were also normalised to the BET surface area and the loaded mass (Fig. S21†). In general, a similar activity trend is observed as for an evaluation based on the geometric current densities. Small variations are observed that may partly be caused by differences between the apparent loaded mass and the mass fraction actually participating in the reaction, as discussed above. The LSV curves are also shown normalised to the ECSA determined after the HER, as well as to the ECSA determined after the OER at 1.2–1.3 V in Fig. S22.† No clear relation between composition and activity can be derived from the results normalised to the ECSA determined closer to the HER onset, whereas the same – if somewhat exacerbated trend as observed before clearly shows for the results normalised to the ECSA after the OER, confirming secondary contributions to the capacitive current measured between −0.1 and 0 V.

We want to note here that one should take extra caution when evaluating the ECSA of a semiconductor material. Not only do faradaic contributions have to be excluded, but a key assumption in evaluating the ECSA both via measurement of the double layer capacitance, via CV, or by EIS measurements is that the interfacial capacitance does not contain any contributions from a space charge layer in the semiconductor.³⁷ This is, however, not necessarily true for semiconducting materials. E.g. Mott–Schottky analysis is also determining the interfacial capacitance based on impedance measurements, but the interpretation of the data is fundamentally different. Here, the key assumption is that the Helmholtz layer capacitance is much larger than that of the space charge region in the semiconductor and the potential drop therefore solely occurs in the semiconductor.⁶⁶ In order to investigate the validity of using the double layer capacitance to determine the ECSA, we performed Mott–Schottky analysis on CuFe₂O₄, which was electrophoretically deposited on FTO substrates (Fig. S22†). The analysis confirms CuFe₂O₄ to be a p-type semiconductor in agreement with literature results.^67,68 The flat band potential (E_fb) is determined to be around 0.45 V vs. RHE with a slight shifting towards lower values observable for longer deposition time, likely due to a decreased contribution of any band bending at the p–n junction at the interface with the FTO substrate. At 100 Hz, the observed y-offset corresponds to a capacitance of 82 F cm⁻², that can likely be ascribed to the electric double layer.⁶⁶ The validity of the assumption of pH dependence of the flat band potential was confirmed by performing a similar experiment in 1 M KOH (Fig. S15†). The determined flat band potential is sufficiently distant from the 1.2 to 1.3 V used for the determination of the double layer capacitance only have a negligible influence on the ECSA in this region. Charging of the space charge layer might, however, contribute to the charging current measured at −0.1 to 0 V, confirming the limited suitability of that potential range for the determination of the ECSA.

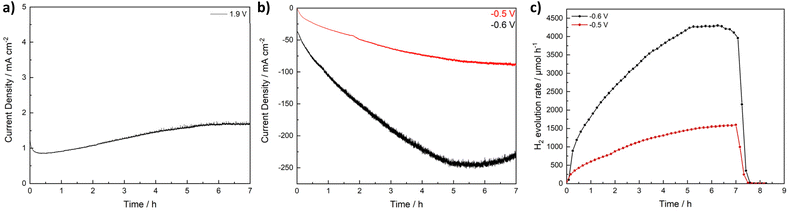
Next, we wanted to address the long-term stability of CuFe₂O₄ catalysts during the OER and the HER, respectively. Stoichiometric CuFe₂O₄ was used for an investigation of the OER performance via chronoamperometry at 1.9 V for 7 h, and at −0.5 and −0.6 V to evaluate the HER performance. A stable current associated with the OER is observed, with a slight activation visible during the first 5 h. During the evaluation of the HER activity over the course of several hours, a significant increase in the current density can be observed during the first 5 h. More than 5 times the initial activity is reached. While the activity for the OER was too low to reliably detect evolving O₂, the H₂ evolution was monitored via GC and the general shape of the H₂ evolution curve matches well with the observed current density (Fig. 7). The pronounced activation can likely be attributed to an in situ reduction of Cu in the structure, which can lead to both an increase in the conductivity and activity. While the LSV curves were overlapping after the first couple of sweeps, indicating a stable equilibrium state, the material changes during the chronoamperometry can be expected to be more extensive. The main difference thereby lies in the continuous potential variation during the LSV that allows for a partial reoxidation, which might restrict reduction and oxidation of metal species to the surface. The uninterrupted reducing potential on the other hand results in a continuous reduction.

Fig. 7 7 h chronoamperometry at 1.9 V for the OER using stoichiometric CuFe₂O₄ (a), a 7 h CA test for the HER at −0.5 V and at −0.6 V vs. RHE, respectively (b) and corresponding H₂ concentrations detected with GC (c).

To further prove this assumption, we measured XRD of the electrodes before electrochemical measurements, as well as after the OER and the HER – both for the standard measurement procedure and for the long-term experiment (Fig. S23†). While the cubic spinel structure is well retained after OER and HER experiments with the standard procedure, pronounced material changes occur during the chronoamperometric measurements both at highly reducing as well as oxidating potentials. Interestingly, the formed species are similar for both CA at 1.9 and at −0.6 V. In both cases, Fe(OH)₃ is formed, in addition to less unambiguously identifiable oxide species containing potassium from the electrolyte – especially K₃(FeO₂) and K₃CuO₂. These species might form from unstable surface species upon drying. The formation of Fe(OH)₃ might indicate FeOOH species formed upon prolonged potential application, that might contribute to the increasing activity, while the presence of K₃CuO₂ is supporting the assumption of Cu reduction.

Since CuFe₂O₄ exhibited activity for both the OER and the HER, a comparative experiment was set up using CuFe₂O₄ electrodes as both anode and cathode. After the initial conditioning protocol, first 10 LSV measurements were conducted in the OER region, followed by another 10 LSV measurements in the HER region using the same electrodes in a three-electrode configuration (Fig. S24†). The onset potential for both reactions is higher by around 0.2 mV, which can be explained by the kinetics of the reactions at the counter electrode impeding the overall current flow.

Subsequently, the cell potential was measured in a two-electrode setup for a current density of 10 mA and −10 mA at the working electrode. The cell potential increases gradually from around 2.1 to almost 2.5 V, which is around the sum of the expected 1.23 V and the overpotentials of around 800 mV for the OER and 400 mV for the HER. The potential increase is probably caused by a slow degradation of the carbon cloth electrodes at the OER side, as apparent in the development of a brown colouring of the electrolyte.

ORR electrocatalysis and Zn–air battery

For the application as a bifunctional catalyst beyond water splitting, e.g. in energy storage applications such as electrically rechargeable metal air batteries, the catalyst's activity towards the ORR is of equal importance as the OER activity. Initially, the performance of CuFe₂O₄-GDEs in the ORR was investigated by means of LSV in 4 M KOH in a half-cell setup. All CuFe₂O₄ electrodes exhibit a comparable activity (Fig. 8a). Overpotentials at 5 mA cm⁻² range between 577 mV and 646 mV, with no specific correlation between composition and activity apparent (Table S7†). The bare GDL shows basically no activity for the ORR (Fig. S25a†).

Fig. 8 ORR in 4 M KOH, measured for GDEs with CuFe₂O₄ of different composition (cathodic sweep direction) (a). Charge/discharge curves measured for Zn–air batteries using Pt- and CuFe₂O₄-GDEs and different charging/discharging rates for 10 min (b), charge/discharge polarisation curves (c), and repeated cycling tests for CuFe₂O₄, Pt, and an uncoated GDL (d). The evolution over 550 cycles of 5 min each is shown, with every 50th cycle being depicted. The number of cycles is increasing from dark to pale colours.

To then confirm the bifunctional activity of CuFe₂O₄, and thus its applicability in electrically rechargeable metal–air batteries, stoichiometric ferrite was drop-cast onto the same carbon paper GDL as used for the ORR experiments and tested in a Zn–air battery. Zn–air batteries can be readily prepared on a lab-scale using a commercial Zn-foil as anode, 6 M KOH as electrolyte, a microporous separator and as-prepared GDEs as (air-)cathode (refer to the experimental section for details). During discharge, metallic Zn is oxidised to Zn(OH)₄²⁻ at the anode, and further transforms into ZnO that precipitates on the electrode surface. Meanwhile, O₂ is reduced to OH⁻ at the air electrode (ORR). During charge, the reactions are reversed: Zn is reduced back to the metallic form while the OER is taking place.⁵ The charge–discharge potential gap can be regarded as a figure of merit to evaluate the GDE performance. As depicted in Fig. 8b, the performance of the CuFe₂O₄-GDE at various scan rates is highly comparable to that of a commercial Pt/C-GDE up until a charging rate of 40 mA s⁻¹ (16 mA cm⁻² s⁻¹), elucidating the successful function as a catalyst for both OER and ORR.

The charge/discharge polarisation curves of the CuFe₂O₄-GDE (Fig. 8c) reveal a comparable i/U characteristic to the commercial Pt/C-GDE at low charging rates. In general, the discharge polarisation curves initially show a steep voltage decrease that can be attributed to activation polarisation, followed by a steady decrease with increasing current density due to ohmic losses, as characteristic for metal–air batteries.⁶⁹ Good Zn–air battery performance is characterised by mostly constant cell voltages over a wide current density range during the charge and discharge.⁷⁰ Both activation and ohmic losses are slightly higher for CuFe₂O₄, indicating a slightly lower ORR activity in combination with a lower conductivity of the electrode. The latter can be attributed to the simple preparation of the GDE via drop-casting. Moreover, neither conductive carbon, nor PTFE were added to adjust the conductivity and wetting properties. In contrast, a similar charging voltage is reached for CuFe₂O₄, compared to the commercial Pt/C-GDE at medium current densities. While the charging voltage plateau at 2 mA cm⁻² is lower for the Pt-GDE, it is slightly higher at 4 mA cm⁻², highlighting the promising applicability of CuFe₂O₄ in GDEs for efficient charging of Zn–air batteries. Additionally, the voltage is significantly lower for CuFe₂O₄ at lower current densities, which would indicate a lower required energy input. However, in contrast to a Zn–air battery equipped with the Pt/C-GDE, the rise in cell voltage with increasing charging current rate is retarded for the CuFe₂O₄-GDE, suggesting the presence of additional obstructive phenomena, e.g. due to elevated mass transport limitations at the not yet optimised 3-phase boundary, or additional oxidation reactions at small current densities. A similar effect has been observed for other transition metal chalcogenides, e.g. MoS₂ or MnO_x, for which a positive current density before the onset of the OER is also apparent in the CV, and which has previously been ascribed to compositional changes involving redox reactions.^71–73

In order to evaluate the long-term stability of the GDE under battery operation conditions, repeated galvanostatic cycling at a current density of 50 mA cm⁻² was performed, with a charge/discharge duration of 5 min each. The discharge curves over several hundred cycles are comparable to the commercial Pt/C electrode, confirming the good ORR performance (Fig. 8d). Moreover, the stability during long-term cycling is similar. A drop in cell voltage indicating battery failure occurs roughly at the same time, which corresponds to approx. 400 cycles (∼33 h). This is probably due to the degradation of the Zn-anode. The charging characteristics on the other hand are notably different. With the Pt/C-GDE, a stable voltage of around 2.17–1.18 V is reached after only a few seconds. The voltage is increasing slightly with an increasing number of charge–discharge cycles. For the Zn–air battery equipped with a CuFe₂O₄-GDE it takes significantly longer to reach a stable voltage (∼150 s), similar to what was observed in the polarisation curves. Additionally, the charging behaviour changes during the first 200 cycles, indicating initial material changes, similar to what was observed for the HER and OER experiments. The full cycling experiment with the CuFe₂O₄ GDE and an excerpt of the first 100 cycles are depicted in Fig. S25.†

A comparison with the pristine GDL shows, that CuFe₂O₄ can in principle operate as a bifunctional catalyst with a good stability in GDEs. A comparable difference in charge and discharge plateaus of 1.03 V is reached for both Pt and CuFe₂O₄. Further investigations should aim at improving the catalytic performance of CuFe₂O₄, which can be expected to significantly enhance the suitability as a bifunctional catalyst in metal–air batteries. Additionally, the preparation technique of GDEs, for which no optimisation was attempted in this study, should be targeted in the future.

Table S8† compares the activity of our CuFe₂O₄ catalysts to related catalysts in the literature. We specifically want to stress that the most interesting finding of this study is the multifunctionality of the material, and the general possibility that our synthesis strategy offers, e.g. for tuning the activity of spinel-type oxides. It can be expected that a similar strategy can also be exploited for tuning the electrochemical performance of structurally related transition metal oxides, such as CoFe₂O₄ and NiFe₂O₄, which are known for their activity for the OER.

CO₂RR electrocatalysis

Another reaction for which CuFe₂O₄ was shown to exhibit catalytic activity is the electrochemical reduction of CO₂ to CO (and H₂). A major dependence on the structure – especially the local coordination environment of Cu in the spinel structure – was established in previous studies.¹² In order to gain insights into the influence of the Cu/Fe-ratio we used CuFe₂O₄ electrodes on carbon cloth in a comparable setup as used for the water splitting experiments (Fig. S7†), and investigated the dependence of the CO₂RR performance on the composition in a 0.1 M KHCO₃ electrolyte, at a potential of −0.69 V vs. RHE.

The current density increases with a deviation from the ideal stoichiometric composition, which might again be partially caused by strain effects. It is in the range of around 5 mA cm⁻² for the stoichiometric composition, to around 10 mA cm⁻² for samples with either a very high, or a very low Cu-content (Fig. S26a†). The CO yield on the other hand is greatly affected by the composition and increases continuously with an increasing Cu/Fe-ratio (Fig. 9a). While almost no CO₂ reduction to CO is observed for Fe-rich samples, those with a high Cu content exhibit about five times the activity (in terms of CO yield) compared to stoichiometric CuFe₂O₄ (Fig. 9b). At the same time, the faradaic efficiency for CO increases to around 13% for Cu_1.2Fe_1.8O₄, which further elucidates the tunability of the catalytic activity by a variation of the Cu/Fe-ratio. The H₂ evolution rate is lowest for the stoichiometric CuFe₂O₄, indicating a small influence of strain effects under these conditions also on the HER performance. The observed CO evolution rate and faradaic efficiency are best after 50 min of electrocatalysis. Initially, material activation and removal of organic residues – as also apparent by the higher current density during the first 20 min – is the most probable reason for the lower activity. The decreased activity after 90 min might indicate a slight deactivation, however. A normalisation of the CO yield to the active mass results in a similar activity trend, with some uncertainties due to portions of the catalyst ink diffusing underneath the Kapton tape (Fig. S26c†).

Fig. 9 CO yields for the CO₂RR experiments at −0.69 V vs. RHE conducted in 0.1 M KHCO₃ with CuFe₂O₄ of different composition (a), corresponding faradaic efficiencies (b), H₂ evolution rates (c) and FE for H₂ (d).

The selectivity calculated based on the detected gasses (in this case H₂ and CO) is comparable to the faradaic efficiency, if slightly higher, suggesting the formation of low amounts of additional products (Fig. S26b†). Small amounts of accumulated HCOOH were detected by HPLC after the experiment (Fig. S26d†), corresponding to a FE of max. 3.5%. In agreement with the higher CO₂ conversion rate generally observed at a higher Cu-ratio, the amount of HCOOH detected also increases with an increasing Cu/Fe-ratio. The sum of faradaic efficiencies is around 90% (Fig. S26e†), with the missing percentages likely being caused by inaccuracies in the quantification of the low product amounts as well as trace amounts of other products. Methane, and in selected cases also ethane, were found in almost all measurements, but in concentrations below the quantification limit.

Since CuFe₂O₄ showed some activity for the OER, which is presumably the reaction taking place at the counter electrode, a full cell testing was performed, using CuFe₂O₄ as both anode and cathode. First, the CO₂ reduction performance was investigated in a three-electrode setup, similar to the experiments with a Pt counter electrode. Both current density and gas yields are comparable to the previous runs (Fig. S27†). Subsequently, the potential at the working electrode was measured at a current density of −10 mA cm⁻² for 1 h and found to be stable at around −1 V, highlighting the good stability of CuFe₂O₄ during the investigations (Fig. S27†).

Conclusions

In this work, we demonstrated how varying the Cu/Fe-ratio in CuFe₂O₄ nanoparticles synthesised via a microwave-assisted synthesis allows for the tuning of the catalytic activity for multiple electrochemical reactions, such as ORR, OER, HER, and CO₂RR. While strain effects resulted in an improved activity for the OER with a deviation from the stoichiometric composition, in addition to an improved charge transfer resistance and lower Tafel slope, the presence of larger amounts of excess Cu proved to be beneficial for the HER activity. The ORR performance on the other hand remains mostly unaffected by the Cu content. The most significant impact of changing the Cu/Fe-ratio could be observed in the CO₂RR. Here, both the CO evolution and FE can be significantly improved by increasing the amount of Cu within the structure. All results together demonstrate how the promise of CuFe₂O₄ as a multifunctional electrocatalyst, as also demonstrated by full cell tests in water splitting and the CO₂RR, as well as preliminary tests as a bifunctional catalyst at the air electrode in Zn–air batteries. Depending on the target application, the Cu/Fe-ratio can easily be tailored with our synthetic approach and thereby adjusted for an optimum performance in the respective application.

Data availability

Data are made available at Open Science Framework, https://doi.org/10.17605/OSF.IO/G56NX. ESI is available. The authors have cited additional references within the ESI.†^35,36

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank Mirco Ade and Dr Anja Hofmann for SEM and EDX analysis, Lion Schumacher for the XPS analysis, and Dr Jana Timm and Jonas Jungmann for the N₂ physisorption measurements. Additionally, we are grateful to Dr Rameshwori Loukrakpam for assistance with the ORR measurements. Moreover, we thank the Bavarian Polymer Institute (BPI) for usage of the SEM, and XPS instruments in the KeyLabs “Device Engineering and Electron and Optical Microscopy”. J. Z. and R. M. gratefully acknowledge funding in the graduate school of the Bavarian Center for Battery Technology (BayBatt), of the University of Bayreuth.

References

1. M. Yu, E. Budiyanto and H. Tüysüz, Angew. Chem., Int. Ed., 2022, 61, e202103824.
2. A. Li, Y. Sun, T. Yao and H. Han, Chem.–Eur. J., 2018, 24, 18334–18355.
3. L. Zhang, Q. Fan, K. Li, S. Zhang and X. Ma, Sustainable Energy Fuels, 2020, 4, 5417–5432.
4. S. M. M. Ehteshami and S. H. Chan, Energy Policy, 2014, 73, 103–109.
5. K. W. Leong, Y. Wang, M. Ni, W. Pan, S. Luo and D. Y. C. Leung, Renewable Sustainable Energy Rev., 2022, 154, 111771.
6. M. S. Faber and S. Jin, Energy Environ. Sci., 2014, 7, 3519–3542.
7. Y. Wang, J. Li and Z. Wei, J. Mater. Chem. A, 2018, 6, 8194–8209.
8. S. Nitopi, E. Bertheussen, S. B. Scott, X. Liu, A. K. Engstfeld, S. Horch, B. Seger, I. E. L. Stephens, K. Chan, C. Hahn, J. K. Nørskov, T. F. Jaramillo and I. Chorkendorff, Chem. Rev., 2019, 119, 7610–7672.
9. F. Chang, M. Xiao, R. Miao, Y. Liu, M. Ren, Z. Jia, D. Han, Y. Yuan, Z. Bai and L. Yang, Electrochem. Energy Rev., 2022, 5, 4.
10. X. M. Liu, X. Cui, K. Dastafkan, H. F. Wang, C. Tang, C. Zhao, A. Chen, C. He, M. Han and Q. Zhang, J. Energy Chem., 2020, 53, 290–302.
11. S. Tao, F. Gao, X. Liu and O. T. Sørensen, Mater. Sci. Eng., B, 2000, 77, 172–176.
12. J. Zander, M. Weiss and R. Marschall, Adv. Energy Sustainability Res., 2023, 4, 2200184.
13. A. Phuruangrat, B. Kuntalue, S. Thongtem and T. Thongtem, Mater. Lett., 2016, 167, 65–68.
14. X. Ge, A. Sumboja, D. Wuu, T. An, B. Li, F. W. T. Goh, T. S. A. Hor, Y. Zong and Z. Liu, ACS Catal., 2015, 5, 4643–4667.
15. S. Wang, A. Lu and C. J. Zhong, Nano Convergence, 2021, 8, 4.
16. A. M. Balagurov, I. A. Bobrikov, V. Y. Pomjakushin, D. V. Sheptyakov and V. Y. Yushankhai, J. Magn. Magn. Mater., 2015, 374, 591–599.
17. R. Deshmukh and M. Niederberger, Chem.–Eur. J., 2017, 23, 8542–8570.
18. R. Khunphonoi, P. Khemthong, C. Luadthong, S. Kuboon, C. Kongmark, N. Viriya-empikul, P. Kidkhunthod, S. Pinitsoontorn and K. Faungnawakij, RSC Adv., 2022, 12, 15526–15533.
19. R. Zhang, Q. Yuan, R. Ma, X. Liu, C. Gao, M. Liu, C. L. Jia and H. Wang, RSC Adv., 2017, 7, 21926–21932.
20. V. D. Silva, L. S. Ferreira, T. A. Simões, E. S. Medeiros and D. A. Macedo, J. Colloid Interface Sci., 2019, 540, 59–65.
21. L. S. Ferreira, T. R. Silva, V. D. Silva, R. A. Raimundo, T. A. Simões, F. J. A. Loureiro, D. P. Fagg, M. A. Morales and D. A. Macedo, Adv. Powder Technol., 2022, 33, 103391.
22. M. Li, Y. Xiong, X. Liu, X. Bo, Y. Zhang, C. Han and L. Guo, Nanoscale, 2015, 7, 8920–8930.
23. B. J. Borah, Y. Yamada and P. Bharali, ACS Appl. Energy Mater., 2020, 3, 3488–3496.
24. S. Park, J. H. Baek, L. Zhang, J. M. Lee, K. H. Stone, I. S. Cho, J. Guo, H. S. Jung and X. Zheng, ACS Sustain. Chem. Eng., 2019, 7, 5867–5874.
25. H. Belhadj, Y. Messaoudi, M. R. Khelladi and A. Azizi, Int. J. Hydrogen Energy, 2022, 47, 20129–20137.
26. M. I. Díez-García, T. Lana-Villarreal and R. Gómez, ChemSusChem, 2016, 9, 1504–1512.
27. T. Osotchan, T. Sudyoadsuk, S. Wannapop and A. Somdee, Inorg. Chem. Commun., 2023, 151, 110631.
28. M. Einert, A. Waheed, D. C. Moritz, S. Lauterbach, A. Kundmann, S. Daemi, H. Schlaad, F. E. Osterloh and J. P. Hofmann, Chem.–Eur. J., 2023, 29(24), e202300277.
29. Y. Liu, F. Le Formal, F. Boudoire, L. Yao, K. Sivula and N. Guijarro, J. Mater. Chem. A, 2019, 7, 1669–1677.
30. K. M. Rezaul Karim, H. R. Ong, H. Abdullah, A. Yousuf, C. K. Cheng and M. M. Rahman Khan, Int. J. Hydrogen Energy, 2018, 43, 18185–18193.
31. S. L. J. Thomae, N. Prinz, T. Hartmann, M. Teck, S. Correll and M. Zobel, Rev. Sci. Instrum., 2019, 90, 043905.
32. A. R. Stokes and A. J. C. Wilson, Math. Proc. Cambridge Philos. Soc., 1942, 38, 313–322.
33. P. Thompson, D. E. Cox and J. B. Hastings, J. Appl. Crystallogr., 1987, 20, 79–83.
34. N. B. Mahmood, F. R. Saeed, K. R. Gbashi, A. Hamodi and Z. M. Jaffar, J. Mech. Behav. Mater., 2021, 30, 220–227.
35. M. C. Biesinger, Surf. Interface Anal., 2017, 49, 1325–1334.
36. M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730.
37. C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135, 16977–16987.
38. M. Inaba, A. W. Jensen, G. W. Sievers, M. Escudero-Escribano, A. Zana and M. Arenz, Energy Environ. Sci., 2018, 11, 988–994.
39. M. Samouhos, R. Hutcheon and I. Paspaliaris, Miner. Eng., 2011, 24, 903–913.
40. R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–767.
41. N. Guijarro, P. Bornoz, M. Prévot, X. Yu, X. Zhu, M. Johnson, X. Jeanbourquin, F. Le Formal and K. Sivula, Sustainable Energy Fuels, 2018, 2, 103–117.
42. T. Aghavnian, J. B. Moussy, D. Stanescu, R. Belkhou, N. Jedrecy, H. Magnan, P. Ohresser, M. A. Arrio, P. Sainctavit and A. Barbier, J. Electron Spectrosc. Relat. Phenom., 2015, 202, 16–21.
43. M. Fantauzzi, F. Secci, M. Sanna Angotzi, C. Passiu, C. Cannas and A. Rossi, RSC Adv., 2019, 9, 19171–19179.
44. M. D. P. Silva, F. C. Silva, F. S. M. Sinfrônio, A. R. Paschoal, E. N. Silva and C. W. A. Paschoal, J. Alloys Compd., 2014, 584, 573–580.
45. R. K. Selvan, C. O. Augustin, L. J. Berchmans and R. Saraswathi, Mater. Res. Bull., 2003, 38, 41–54.
46. K. R. Sanchez-Lievanos, J. L. Stair and K. E. Knowles, Inorg. Chem., 2021, 60, 4291–4305.
47. M. A. S. Amulya, H. P. Nagaswarupa, M. R. A. Kumar, C. R. Ravikumar, K. B. Kusuma and S. C. Prashantha, J. Phys. Chem. Solids, 2021, 148, 109756.
48. K. J. Kim, J. H. Lee and S. H. Lee, J. Magn. Magn. Mater., 2004, 279, 173–177.
49. M. Veis, R. Antos, S. Visnovsky, P. D. Kulkarni, N. Venkataramani, S. Prasad, J. Mistrik and R. Krishnan, Materials (Basel), 2013, 6, 4096–4108.
50. C. Simon, M. B. Zakaria, H. Kurz, D. Tetzlaff, A. Blösser, M. Weiss, J. Timm, B. Weber, U. P. Apfel and R. Marschall, Chem.–Eur. J., 2021, 27, 16990–17001.
51. V. Maruthapandian, M. Mathankumar, V. Saraswathy, B. Subramanian and S. Muralidharan, ACS Appl. Mater. Interfaces, 2017, 9, 13132–13141.
52. A. Kargar, S. Yavuz, T. K. Kim, C. H. Liu, C. Kuru, C. S. Rustomji, S. Jin and P. R. Bandaru, ACS Appl. Mater. Interfaces, 2015, 7, 17851–17856.
53. W. Bian, Z. Yang, P. Strasser and R. Yang, J. Power Sources, 2014, 250, 196–203.
54. W. J. Jiang, T. Tang, T. Tang, Y. Zhang, J. S. Hu and J. S. Hu, Acc. Chem. Res., 2020, 53, 1111–1123.
55. X. Yang, Y. Wang, X. Tong and N. Yang, Adv. Energy Mater., 2022, 12(5), 2102261.
56. T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Sci. Rep., 2015, 5, 1–21.
57. A. Kapałka, G. Fóti and C. Comninellis, Electrochem. Commun., 2008, 10, 607–610.
58. H. Ding, H. Liu, W. Chu, C. Wu and Y. Xie, Chem. Rev., 2021, 121, 13174–13212.
59. Y. J. Son, S. Kim, V. Leung, K. Kawashima, J. Noh, K. Kim, R. A. Marquez, O. A. Carrasco-Jaim, L. A. Smith, H. Celio, D. J. Milliron, B. A. Korgel and C. B. Mullins, ACS Catal., 2022, 12, 10384–10399.
60. A. C. Lazanas and M. I. Prodromidis, ACS Meas. Sci. Au, 2023, 3(3), 162–193.
61. M. Feng, A. Yang, X. Zuo, C. Vittoria and V. G. Harris, J. Appl. Phys., 2010, 107, 09A521.
62. S. Jung, C. C. L. McCrory, I. M. Ferrer, J. C. Peters and T. F. Jaramillo, J. Mater. Chem. A, 2016, 4, 3068–3076.
63. S. Feliu, Metals (Basel), 2020, 10, 1–23.
64. W. Wu, Q. Lu, G. Li and Y. Wang, J. Chem. Phys., 2023, 159, 221501.
65. A. Raveendran, M. Chandran and R. Dhanusuraman, RSC Adv., 2023, 13, 3843–3876.
66. A. Hankin, F. E. Bedoya-Lora, J. C. Alexander, A. Regoutz and G. H. Kelsall, J. Mater. Chem. A, 2019, 7, 26162–26176.
67. A. Kezzim, N. Nasrallah, A. Abdi and M. Trari, Energy Convers. Manage., 2011, 52, 2800–2806.
68. S. Bera, S. Ghosh, T. Maiyalagan and R. N. Basu, ACS Appl. Energy Mater., 2022, 5, 3821–3833.
69. D. Jiao, Z. Ma, J. Li, Y. Han, J. Mao, T. Ling and S. Qiao, J. Energy Chem., 2020, 44, 1–7.
70. J. Zhang, Q. Zhou, Y. Tang, L. Zhang and Y. Li, Chem. Sci., 2019, 10, 8924–8929.
71. T. Zhang, S. Zhang, S. Cao, Q. Yao and J. Y. Lee, Energy Storage Mater., 2020, 33, 181–187.
72. M. Wang, X. Huang, Z. Yu, P. Zhang, C. Zhai, H. Song, J. Xu and K. Chen, Nanomaterials, 2022, 12, 4069.
73. M. Xiong and D. G. Ivey, J. Electrochem. Soc., 2017, 164, A1012–A1021.

---

Footnote

† Electronic supplementary information (ESI) available: Additional figures. See DOI: https://doi.org/10.1039/d4se00968a

---