Open Access Article
Open Access ArticleDilute polyelectrolyte solutions: recent progress and open questions†
Carlos
G. Lopez‡
 *a,
Atsushi
Matsumoto
*a,
Atsushi
Matsumoto
 *b and
Amy Q.
Shen
*b and
Amy Q.
Shen
 *c
*c
aInstitute of Physical Chemistry, RWTH Aachen University, Aachen, 52056, Germany
bDepartment of Applied Chemistry and Biotechnology, Graduate School of Engineering, University of Fukui, 3-9-1 Bunkyo, Fukui City, Fukui 910-8507, Japan. E-mail: atsushi5@u-fukui.ac.jp
cMicro/Bio/Nanofluidics Unit, Okinawa Institute of Science and Technology Graduate University, 1919-1 Tancha, Onna-son, Okinawa 904-0495, Japan. E-mail: amy.shen@oist.jp
First published on 13th December 2023
Abstract
Polyelectrolytes are a class of polymers possessing ionic groups on their repeating units. Since counterions can dissociate from the polymer backbone, polyelectrolyte chains are strongly influenced by electrostatic interactions. As a result, the physical properties of polyelectrolyte solutions are significantly different from those of electrically neutral polymers. The aim of this article is to highlight key results and some outstanding questions in the polyelectrolyte research from recent literature. We focus on the influence of electrostatics on conformational and hydrodynamic properties of polyelectrolyte chains. A compilation of experimental results from the literature reveals significant disparities with theoretical predictions. We also discuss a new class of polyelectrolytes called poly(ionic liquid)s that exhibit unique physical properties in comparison to ordinary polyelectrolytes. We conclude this review by listing some key research challenges in order to fully understand the conformation and dynamics of polyelectrolytes in solutions.
1 Introduction
The field of polymer science emerged as a distinct scientific discipline in 1920, with the core concept based on the macromolecular hypothesis proposed by Staudinger.1 Since then, it has been well accepted that polymers are made of molecules covalently bonded to each other. The definition by IUPAC states that polymers are substances composed of macromolecules with a molecular weight exceeding several thousand.2 During the past century, polymer chemists have made significant advances in creating new polymer species and controlling the polymerisation process, while polymer physicists have focused on understanding the properties of polymers by using theoretical, computational, and experimental approaches. As a result, polymer-based materials are prevalent and extensively used in various industries and daily products.3Despite the significant research progress in the physics of non-ionic polymers, the properties of which (especially in dilute solutions) are relatively well understood, less advancement has been made in charged polymers. Polyelectrolytes, which received their name from Raymond M. Fuoss in 1948,4 are a class of ion-containing polymers. Historically, polymers with relatively low ion-contents (10–15%) were defined as ionomers, while polymers with very high ion-contents were defined as polyelectrolytes.5 A better definition was proposed based on the physical properties of ion-containing polymers:6 polyelectrolytes are polymers whose properties in solution are governed by electrostatic repulsion between dissociated groups along the chain, while ionomers are polymers in which the bulk properties are governed by ionic interactions (i.e., dipole interactions between ion pairs) in discrete regions of the polymer material where attractive forces dominates. In fact, some ion-containing polymers have exhibited transition from ionomer-like to polyelectrolyte-like behaviours, depending on, for example, the temperature.7 Polyelectrolytes can be further divided into two groups depending on the nature of the ionic groups.8 Weak polyelectrolytes are conventionally defined as polymers with weakly acidic or basic groups, in contrast to strong polyelectrolytes, which are composed of polymers with definitive strong acid or base groups.9–12 Note that this differs from strongly charged and weakly charged polyelectrolytes, which refer to systems with high and low densities of ionic monomers along the backbone, respectively. However, there is no universally agreed-upon threshold that defines ‘high’ versus ‘low’ charge density. Vinylic polyelectrolytes, which carry approximately one charge every 0.2–0.3 nm (e.g., PSS), and polysaccharides that have one charge per monomer unit, equating to roughly one charge every 0.5 nm, are considered as strongly charged.
Regardless of the type of polyelectrolytes, their conformation in solution is significantly influenced by the electrostatic interactions. The modelling of charged polymers is rather complicated since ions on the backbone chain are covalently bonded. For example, it is widely accepted that some counterions stay bound (condensed) in the vicinity of the chain backbone due to strong electrostatic attractions between polyions and counterions. This phenomenon is called the counterion condensation.13 As a result, the effective charge fraction on a polyelectrolyte chain in solution is not always equal to the charge density (i.e., the number of ionic monomers) of the chain. Many theoretical models with different approaches have been reported in the literature, and their predictions could explain some properties of polyelectrolyte solutions.9,10,14,15 However, many conflicting results between experimental data and theoretical predictions have been reported, even for linear polyelectrolyte chains in solutions.
The number of factors and lengthscales which control the solution properties14,16,17 is larger for charged polymers than for neutral polymers, making polyelectrolyte theory lag behind that of neutral polymers. These highly complex systems are difficult to study experimentally. For example, if we study the rheology of a neutral polymer in solution, measurements varying the polymer concentration, molar mass, solvent quality and temperature will usually suffice to understand the given system. However, for a polyelectrolyte, additional physical quantities, such as the charge density, the counterion size and its valence, the added salt concentration, and the dielectric constant of the solvent, all become relevant experimental variables. Moreover, it is not possible to define a single solvent quality, and the chemical structure of the polyelectrolyte backbone, side-chain ions and counterions have to be considered separately. In concentrated solutions, the polyelectrolyte systems exhibited fascinating dynamics18–29 which we are only beginning to understand. Their ability to form complexes with oppositely charged matter made them relevant to many industrial formulations and biological systems and is one of the main aspects of polyelectrolyte research today.30–34
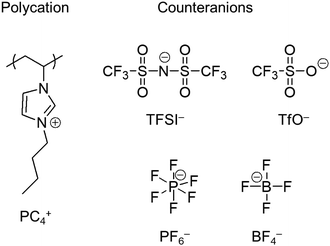
We would also like to highlight an emerging category of polyelectrolytes known as poly(ionic liquid)s or polymerized ionic liquids. In this context, poly(ionic liquid)s (PILs) denote polymers in which ionic liquid structures are covalently integrated into the repeating units.35,36 Here, ionic liquids (ILs) are molten salts consisting of cations or anions which melt below 100 °C.37Fig. 1 displays representative chemical structures of a PIL polycation and its counteranions: PIL ions are relatively large, asymmetric, and charge delocalized, making the physical properties of PILs different from those of ordinary ion-containing polymers.38 For example, PILs have exhibited glass transition at relatively low temperatures even if the charge density is high.39 This unique glass transition behaviour of PILs has led to active research in manipulating the bulk properties of PILs, e.g., their ionic conductivity and viscoelasticity, which have been extensively investigated over the past decade.40–53 The research community acquired a basic understanding of the behaviour of PILs, which function similarly to ionomers. However, the solution properties of PILs, i.e., the behaviour of PILs as polyelectrolytes, have been scarcely investigated.
In solution, PILs can release their counterions into the solvent and possess charges on their chain backbone, showing similar properties to those of ordinary polyelectrolytes, such as poly(sodium styrenesulfonate).54 In contrast to ordinary polyelectrolytes, PILs can be dissolved in solvents with a wide range of dielectric constants even if the charge density on PIL chains is high.55 Good solubility of PILs can also be obtained in pure ILs.55 The unique features of PILs in solutions have raised many interesting questions in the polyelectrolyte research community. For example, how do PILs behave in solvents with low dielectric constants?56 According to the Manning model for counterion condensation,13 the number of dissociated counterions is predicted to decrease with decreasing solvent dielectric constant. If so, PILs would behave as neutral polymers or as ionomers in low-dielectric solvents. Investigating the charge screening effects exerted by ionic liquid ions on polymerized ionic liquid chains within pure ionic liquids offers an interesting research avenue, especially considering the distinctive solvent characteristics of ionic liquids.57
Our primary aims are (1) to establish scaling laws that elucidate the relationship between the properties of polyelectrolytes and variables such as molar mass, salt concentration, and charge fraction; (2) to test the theoretical models reviewed in Section 2; and (3) to highlight experimental results which expand or challenge the current framework of polyelectrolyte physics. We provide a critical overview of several key questions in polyelectrolyte physics, with an emphasis on the experimental literature where new conclusions can be drawn by compiling and/or re-analysing existing data. We hope this perspective will complement earlier reviews in the field which have focused on the development of theory,9,15,58–62 simulations,9,63,64 and particular experimental methods, systems, or properties.65–81 This article narrows its scope to exploring the intricacies of dilute polyelectrolyte solutions.82 For experimental reviews dealing with non-dilute solutions and gels, we direct readers to ref. 14, 68 and 83–85.
This review article is structured as follows: Section 2 introduces several theoretical models proposed in the literature to represent the conformation of dilute polyelectrolyte solutions; Section 3 discusses the properties of polyelectrolytes in the dilute regime, dividing our discussion into sixteen subsections along with research questions related to the conformation and dynamics of single chains in solution; Section 4 concludes our review and highlights open questions.
2 Theoretical approaches to the conformation and dynamics of polyelectrolytes in solution
Dilute polymer solutions are defined as those in which the chains do not overlap.14,86 Considering a chain made up of N chemical monomers with an end-to-end distance R, the overlap concentration (c*) in units of number of repeating units per volume is: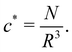 | (1) |
In this article, we use the symbol c to refer to the concentration, measured as the number of monomers per unit volume. When plotting data or quoting concentration values, it is more convenient to use concentrations in moles of monomers per volume. This is represented by ‘M’, which denotes moles of monomers per dm3. Intrinsic viscosities are in units of M−1 as opposed to the more common units of dL g−1. We also use N instead of molar masses. The following example illustrates the reason for these choices: suppose we compare the properties of polystyrene sulfonate (PSS) with Na+ and Cs+ counterions. Let us assume that the conformation of the chains is not influenced by the choice of counterion. A plot of c* or [η] vs. N will overlap for both PSS salts when expressed in units of M and M−1, respectively, thus capturing the essential physics that the chain conformation is unchanged. In contrast, a plot of c* in g L−1vs. Mw results in two separate curves for NaPSS and CsPSS because the Cs+ ion has a larger mass than the Na+ ion. A few exceptions, such as in Fig. 6, use the concentration in mass per volume (cp) as part of a dimensionless product.
2.1 Conformation in dilute salt-free solutions
| R ≃ bN for N ≤ gK. | (2) |
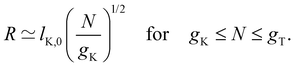 | (3) |
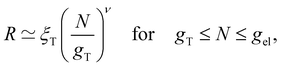 | (4) |
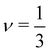 for poor solvents,
for poor solvents, 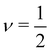 for theta solvents, and
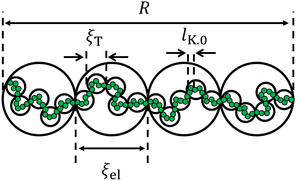
for theta solvents, and 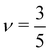 for good solvents. Here, ξT is given by eqn (3) with N = gT.
for good solvents. Here, ξT is given by eqn (3) with N = gT.
The next relevant lengthscale is the size of the electrostatic blob. This marks the distance at which the electrostatic energy is of the order of the thermal energy kBT, where kB is the Boltzmann constant and T is the absolute temperature. The Coulomb energy of an electrostatic blob is
| Uel ≃ (gelf)2e2/(ε0εrξel), | (5) |
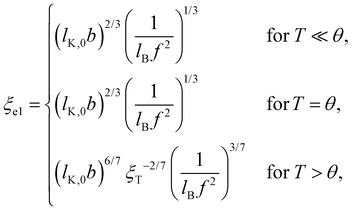 | (6) |
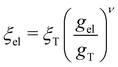 and
and 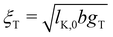 (ref. 90) under the assumption of Uel = kBT for T ≥ θ and Uel = γξel for T ≪ θ, where γ is the polymer/solvent interfacial tension, given by
(ref. 90) under the assumption of Uel = kBT for T ≥ θ and Uel = γξel for T ≪ θ, where γ is the polymer/solvent interfacial tension, given by 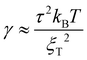 with
with 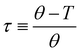 being the reduced temperature.
being the reduced temperature.
On distances larger than the electrostatic blob size, the chain is stretched, and its conformation is a pole of electrostatic blobs:
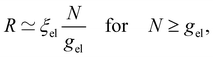 | (7) |
The conformation of polyelectrolytes is often quantified through the ‘stretching parameter’ (B), which is the ratio of the end-to-end distance of an electrostatic blob (ξel) to its fully stretched contour length:
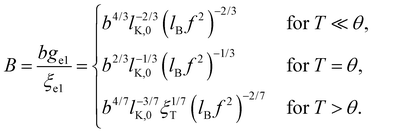 | (8) |
If the thermal blob is larger than the electrostatic blob, then eqn (3) is valid for gK ≤ N ≤ gel. Equivalently, setting ν = 1/2 in eqn (4) gives the same result. If the electrostatic blob is smaller than the Kuhn length, the equations above expect the polyelectrolyte to be in a fully stretched configuration so that R ≃ bN. This ‘rod-like’ configuration assumes no transverse fluctuations. In some cases, it was found that salt-free polyelectrolytes adopted a directed random walk configuration.98,99 In the next section, we will address the experimental evidence concerning this issue.
Polyelectrolytes having more than one dissociated charge per Kuhn segment (gK > f−1) are sometimes referred to as strongly charged polyelectrolytes. In this case, the above equations predict ξel < lK,0, so that the electrostatic blob concept should not apply. Note that if Manning condensation holds, this is always the case if lK,0 > lB and δ > 1/gK. Here, δ denotes the fraction of monomers that contain an ionic group. Some experimental evidence100 suggests that the Coulomb energy inside an electrostatic blob may significantly exceed kBT, thus adding a pre-factor to eqn (5) and making the size of electrostatic blobs larger than expected by eqn (6). This would mean that the electrostatic blob concept may apply even when there are more than one dissociated charge per bare Kuhn segment, see further discussions in Section 3.10.
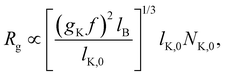 | (9) |
2.2 Conformation in dilute solutions with added salt
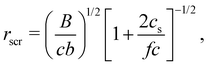 | (10) |
The screening length rscr described by eqn (10) is proportional to the Debye screening length:
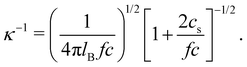 | (11) |
If the end-to-end distance R of a chain is smaller than the screening length (rscr), the chain conformation is expected to be the same as that in a salt-free solution. For R > rscr, sections of the chain with size rscr, containing gscr = rscrgel/ξel chemical monomers, repel each other with full excluded volume. The end-to-end distance of a chain is R ≃ rscr(N/gscr)0.6 for N ≥ gscr. Using the screening length from eqn (10), the dependence of the end-to-end distance on added salt concentration is given by
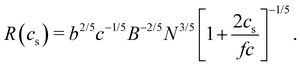 | (12) |
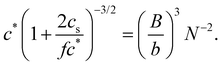 | (13) |
![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) ), the mass per unit length (ML = M0/b), and the cross-sectional chain diameter (dC).
), the mass per unit length (ML = M0/b), and the cross-sectional chain diameter (dC).
First, the properties of a polyelectrolyte chain in the absence of excluded volume (i.e. an ideal chain) were calculated using the models developed by Yamakawa and co-workers for non-ionic polymers.115,116 For the end-to-end distance:
| R0 = 2lpL − 2lp2(1 − e−L/lp), | (14) |
The influence of excluded volume was taken into account using expansion factors (α). The expansion factor αR2 = R/R0 is:
αR2 = [1 + (10![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) + 70π/9) + 70π/9)![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) 2 + 8π3/2 2 + 8π3/2![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) 3]2/15 × (0.933 + 0.067e−0.85 3]2/15 × (0.933 + 0.067e−0.85![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) –1.39 –1.39![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) 2), 2), | (15) |
![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) are:
are: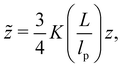 | (16) |
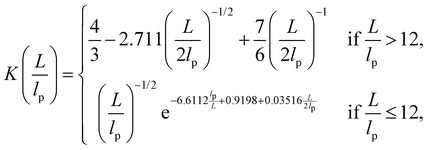 | (17) |
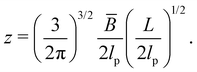 | (18) |
![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) and ML.117
and ML.117
The persistence length and excluded volume strength are separated into intrinsic and electrostatic contributions:
| lp = lp,0 + lp,e, | (19) |
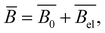 | (20) |
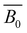 and
and 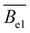 are the intrinsic and electrostatic excluded volume strengths, respectively.
are the intrinsic and electrostatic excluded volume strengths, respectively.
The non-electrostatic excluded volume is calculated as the sum of a hard-core repulsion term and an attractive term:106,118,119
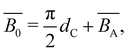 | (21) |
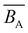 is the excluded volume strength arising from attractive contributions between Kuhn segments, see ref. 120 and 121.
is the excluded volume strength arising from attractive contributions between Kuhn segments, see ref. 120 and 121.
Approaches to estimate the 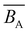 term, which is usually only relevant at very high ionic strengths, can be found in ref. 118. The added salt concentration at which
term, which is usually only relevant at very high ionic strengths, can be found in ref. 118. The added salt concentration at which 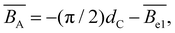 i.e.,
i.e., ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0 is referred to as the θ-salt condition because chains are not perturbed by excluded volume. Note that even at the θ-salt point, the electrostatic effect continues to influence the polymer conformation in comparison to the non-ionic scenario, primarily through the electrostatic contribution to the persistence length.
= 0 is referred to as the θ-salt condition because chains are not perturbed by excluded volume. Note that even at the θ-salt point, the electrostatic effect continues to influence the polymer conformation in comparison to the non-ionic scenario, primarily through the electrostatic contribution to the persistence length.
Experimentally, the electrostatic terms were found to vary as power-laws of the added salt concentration:
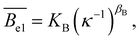 | (22) |
| lp,el = Kl(κ−1)βl. | (23) |
For the electrostatic excluded volume, Fixman and Skolnick119 predicted:
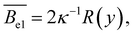 | (24) |
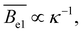 in agreement also with the scaling model of Dobrynin et al.89
in agreement also with the scaling model of Dobrynin et al.89
Note that for weakly charged polyelectrolytes, where ξel ≫ lK,0, the scaling model outlined in Section 2.2.1 indicates that the worm-like chain model should not apply because there exist two contributions to the excluded volume (non-ionic and ionic) and these perturb the chain conformation at distinct lengthscales: ξT for the non-ionic excluded volume and rscr for the ionic excluded volume. This differs from the expanded worm-like chain (WLC), where chains are modelled as having a single cross-over between Gaussian and expanded conformations.
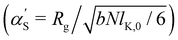 calculated by the variational procedure by Muthukumar matched the theory of Flory:133
calculated by the variational procedure by Muthukumar matched the theory of Flory:133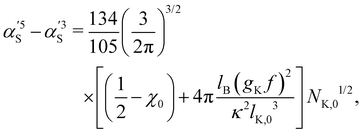 | (25) |
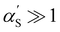 limit, the expression for the radius of gyration becomes:
limit, the expression for the radius of gyration becomes:| Rg ∝ lB1/5f2/5cs−1/5N3/5. | (26) |
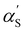 for the Rg expansion factor instead of αS.
for the Rg expansion factor instead of αS.
The Bjerrum length is included in eqn (26) in two ways: first, the explicit term lB1/5 accounts for the fact that as the dielectric constant decreases, the strength of the electrostatic repulsion between two like charges increases. According to Manning's theory, if the distance between ionic groups is smaller than lB, then f ≃ blB−1, so eqn (26) indicates Rg to be a decreasing function of lB (as shown in Fig. 24). For weakly charged polyelectrolytes, where f is independent of lB, Rg is expected to increase with lB, provided there is no shift to the ionomer regime.
2.3 Comparison of theories
![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) ≃ rscr, the expanded worm-like chain model reproduces the predictions of the scaling model for the configurational properties of polyelectrolyte chains.
≃ rscr, the expanded worm-like chain model reproduces the predictions of the scaling model for the configurational properties of polyelectrolyte chains.
Note that the conformation of polyelectrolytes is sometimes modeled as a directed random walk on lengthscales between ξel and the screening length. Under this assumption, the WLC model would not be applicable. As we will see in our review of the experimental literature, experimental evidence suggests that at least in some cases, fluctuations transverse to the stretching direction are not significant.
2.4 Dynamic properties of polyelectrolyte solutions
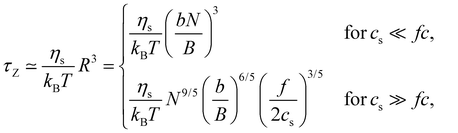 | (27) |
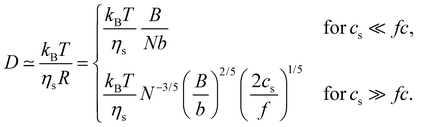 | (28) |
In the low-salt limit (fc/2cs ≪ 1), the diffusion coefficient scales as D ∝ N−1 and for cs ≫ fc/2, D ∝ N−0.6cs1/5. In salt-free solution, D may also be estimated by modelling as cylinders with length R having cross-sectional radius dC:136–138
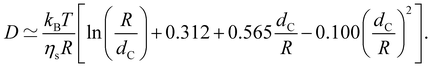 | (29) |
The intrinsic viscosity [η] of a polyelectrolyte can be given by the Flory equation: 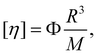 where Φ is the Flory constant, discussed in detail in Section 3.12.140 For sufficiently dilute solutions, the reduced viscosity (ηred) follows the Huggins equation:
where Φ is the Flory constant, discussed in detail in Section 3.12.140 For sufficiently dilute solutions, the reduced viscosity (ηred) follows the Huggins equation:
| ηred ≡ ηsp/c = [η] + kH[η]2c, | (30) |
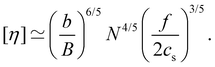 | (31) |
Extensions of the above models to account for the influence of dipolar interactions or charge induced correlations, which become more significant as the dielectric constant of the solvent is decreased, can be found in ref. 142–147 and are not discussed here due to the lack of experimental data to test these theories.
![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) and K apply equally regardless of the property being calculated.
and K apply equally regardless of the property being calculated.
2.5 Counterion condensation
Throughout Section 2, we have seen that the charge fraction f is a key factor governing the conformation and dynamics of polyelectrolytes in solution. Polyelectrolytes can be regarded as salt molecules covalently bound to each other. Therefore, one may assume that all ion pairs of a polyelectrolyte chain dissociate completely into cations and anions. However, many experimental parameters,151 such as electrophoretic mobility,152 osmotic pressure,73,153 and shear viscosity97 measurements, suggest that this scenario is valid only when the charge density δ is lower than a certain critical value which depends on the systems investigated. Instead, it is well-recognized that some of the charges on the polyelectrolyte chain are neutralised by their counterions, so that the charge fraction becomes smaller than the charge density (i.e., f < δ). This phenomenon is called the counterion condensation, paramount for discussing almost every aspect of polyelectrolytes in solution.The idea of the condensation of counterions was first introduced by Oosawa154 to explain the osmotic and activity coefficient data of polyelectrolyte solutions. Subsequently, the well-known classical counterion condensation model was proposed by Onsager and formulated by Manning.13 In the Manning model (see eqn (4) and (5) in ref. 13), we consider a single and infinitely long line charge bearing a point charge of +Zpe with a uniform distance bc between two neighboring charges, and place a free counterion of −Zce at a certain distance from the line charge. Here, Zp and Zc denote the valence of the point charge and the free counterion, respectively. With this charge configuration, the model calculates the Helmholtz free energy in order to discuss whether or not the counterion keeps dissociated from or is bound onto the line charge. Manning found that the system considered became unstable when the product of ZcZpuM is greater than unity, leading to the conclusion that a sufficient number of counterions will condense onto the line charge, effectively reducing the product of ZcZpuM to a value less than one, thereby stabilizing the system. Here, uM (= lB/bc) is the so-called Manning parameter. Consequently, the Manning model predicted that counterion condensation occurs when ZcZpuM ≥ 1. For instance, for polyelectrolytes composed of monovalent monomers (Zp = 1) and counterions (Zc = 1), condensation is predicted to occur when the charge distance bc becomes smaller than the Bjerrum length lB, i.e., uM = 1. Once the counterion condensation comes into play, the Manning model predicted the charge fraction f to be:
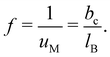 | (32) |
Manning's two-state model has been elaborated over the past half century by accounting for conditions ignored in the original model.143,144,146,147,155–166 For example, Nyquist et al.155 incorporated the chain connectivity effects on the electrostatic interaction into the two-state model, showing that the transition from the complete dissociation to the condensation regimes was broad instead of a sharp transition at uM = 1 predicted by the Manning model. The charge fraction was also found to decrease with increasing polymer concentration due to the chain contraction. Deserno et al.164 studied the effect of the salt concentration on the counterion condensation and found that the charge fraction was not largely affected by the addition of salts, and therefore, the salt effect on the counterion condensation was negligible at low cs. By considering the dielectric mismatch between the bulk solution and the local region around polyelectrolyte chains, Muthukumar144 found stronger condensation at low εr but weaker condensation at high εr than predicted by the Manning model. As a result, the Muthukumar model predicted that the dependence of f on εr was stronger than that of the Manning model. The solvent quality also made the condensation process more complex, in particular in the case of poor solvents. We refer the readers to ref. 146, 147 and 166 for more details. Reviews on this topic have also been provided by Dobrynin and Rubinstein.9,10
3 Review of experimental data
This section is structured as follows: Section 3.1 discusses the solubility of polyelectrolytes in various types of solvent media and the phase behaviour of these polyelectrolyte solutions. Sections 3.3–3.8 focus primarily on the behaviour of polyelectrolytes in salt-free solutions. Sections 3.9–3.12 examine the behaviour of polyelectrolytes in excess added salt. Special attention is paid to polystyrene sulfonate, the most widely studied polyelectrolyte system. Section 3.13 discusses the static and dynamic scattering of polyelectrolyte solutions. Section 3.14 discusses the transition between salt-free solutions, where polyelectrolytes are highly stretched, and excess salt solutions, where they behave as neutral polymers in good solvents. We conclude by discussing the ion-specific effects and underscreening in Sections 3.15 and 3.16. Sections, 3.1, 3.2 and 3.12–3.16 can be read independently from one another. For coherence, it is recommended that Sections 3.3–3.8 and 3.9–3.11 be read sequentially.3.1 Phase behaviour
In contrast, poly(ionic liquid)s exhibited excellent solubility in low dielectric solvents even if the charge density is high. Jousset et al.174 investigated the solubility of poly([(2-methacryloyloxy)ethyl]trimethylammonium 1,1,2,3,3-pentacyanopropenide) (P(M-PCP)). The P(M-PCP) did not dissolve in water but exhibited an excellent solubility in various organic solvents with a broad range of dielectric constants εr, including N-methylformamide (NMF; εr = 182), propylene carbonate (PC; εr = 65), dimethylformamide (DMF; εr = 37), acetone (AC; εr = 21), cyclohexanone (CH; εr = 16), and triethyl phosphate (TEP; εr = 11).
Marcilla et al.55 investigated the effect of the chemical structure of PILs on their solubility in five organic solvents, including an ionic liquid, 1-vinyl-3-ethylimidazolium bis(trifluoromethanesulfonyl)imide (ViEtIm-TFSI). As can be seen in Table 1, the difference in the alkyl chain length and the structure of counteranions influenced the solubility of PILs, implying the presence of ion-specific effects on the conformation and dynamics of PILs in solution. For example, acetone did not dissolve PC2-BF4 with ethyl groups but dissolved PC4-BF4 with butyl groups. Even for PILs with the same cation, methanol dissolved PC2-TfO but not PC2-BF4. Furthermore, they showed that PILs were soluble in pure ionic liquids without non-ionic solvents.
| Methanol (εr = 32, μ = 2.6 D) | Acetone (εr = 22, μ = 2.7 D) | Tetrahydrofuran (εr = 8, μ = 1.7 D) | Ethyl acetate (εr = 6, μ = 1.9 D) | ViEtIm-TFSI | ||
|---|---|---|---|---|---|---|
| (+): soluble; (−): insoluble. | ||||||
| PC2+ | BF4− | − | − | − | − | − |
| PF6− | − | + | − | − | − | |
| TfO− | + | + | − | − | + | |
| TFSI− | − | + | + | − | + | |
| PFSI− | + | + | + | + | + | |
| PC4+ | BF4− | − | + | − | − | |
| PF6− | − | + | + | + | ||
| TfO− | + | + | + | + | ||
| TFSI− | − | + | + | + | ||
| PFSI− | − | − | + | + | ||
The results in Table 1 show that the dielectric constant of the solvent cannot be used to predict the solubility of poly(ionic liquid)s. This agrees with the findings of Horne et al.,175 who showed that the capacity of solvents to swell a cross-linked network of poly(1-[(4-ethenylphenyl)methyl]-3-methylimidazolium bistriflimide) did not correlate with their dielectric constant. Instead, Horne et al. demonstrated that solvent's dipole moment (μ) showed a strong correlation with a swelling degree of polyelectrolyte gels. The data in Table 1 make it clear that the dipole moment of the solvent does not predict solubility for the systems considered. Several systems are soluble in solvents with high μ and insoluble in solvents with low μ while others show the opposite trend.
Given the limited experimental data available for ionic polymers in salt-free media,56,174,176,177 it is unlikely that solid conclusions can be drawn with regards to which parameters determine the polyelectrolyte solubility. The use of solubility parameters178–180 might help establish a framework to understand monomer and counterion solvation, but these approaches require extensive solubility datasets. Insightful work on the solubility/swelling of charged polymers can be found in the literature on ionomers and polyelectrolyte gels.176,181–191Table 1 shows that the solubility of polyelectrolytes in ionic liquids depends on the chemical nature of the ionic groups. Since ionic liquids can act as salt ions to regulate the electrostatic interaction, understanding the influence of charge screening on the solubility of these systems can be an interesting research subject.
The phase behaviour of polyelectrolytes in excess added salt can be separated into two classes: H-type behaviour, where a large concentration of the added salt is needed to cause precipitation of the polymer (salting out); and L-type behaviour, where a small concentration of added salt induces phase separation.
3.1.2.1 H-Type phase behaviour. Results by Eisenberg and co-workers,194,205,206 plotted in Fig. 3, illustrate the main phenomena observed for H-type phase behaviour. Fig. 3(a) and (b) show the influence of counterion and co-ion on the phase separation temperature (Tp) of polyvinyl sulfate in aqueous media. At high cs, the selection of the cation or anion has a profound influence on the phase behaviour of the system, in contrast to the expectation from simple treatments relying solely on electrostatic screening. The full cs–c diagram at T = 0 °C shows closed-loop behaviour, as plotted in Fig. 3(c). Data were obtained using two methods: (1) solutions were cooled below Tp and allowed to phase separate into polymer-rich and polymer-poor phases and the compositions of the two phases were evaluated. These data are plotted in circles. (2) The triangles correspond to data obtained by preparing solutions at fixed c and cs and decreasing the temperature until the solution phase separates at Tp. Plots of Tpvs. cs at fixed c were then constructed and values of cs at Tp = 0 °C obtained by interpolation. The discrepancy between the two methods arises from the polydispersity of the polymer, which leads to fractionation during phase separation in the first method. As depicted in Fig. S1 (ESI†), the inverse of the critical temperature (1/Tc), deduced from the peaks in the Tpvs. c graphs, displays a linear dependence on N−1/2. This behaviour mirrors what is observed in neutral polymer solutions, and the intercept at N−1/2 = 0 can be identified with θ−1.86,207
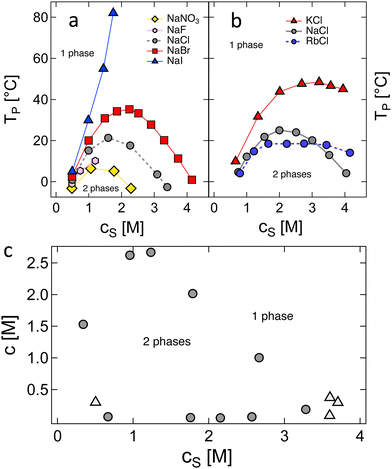 | ||
| Fig. 3 Phase behaviour of polyvinyl sulfate. (a) and (b): Phase separation temperature as a function of added salt concentration for sodium salts (a) and chloride salts (b). (c) Solubility diagram for NaPVS/NaCl/H2O system at T = 0 °C, see text for the meaning of symbols. Data are from ref. 194, 205 and 206. | ||
Buscall et al.192 studied the phase behaviour of polyacrylic acid as a function of temperature, degree of ionisation and polymer and added salt concentrations. We plot their values for the θ temperature of polyacrylic acid in Fig. 4, which illustrates the linear dependence on cs and the fraction of neutralised monomers squared (i2). The linear cs dependence was observed for other systems, see Fig. S2 (ESI†).
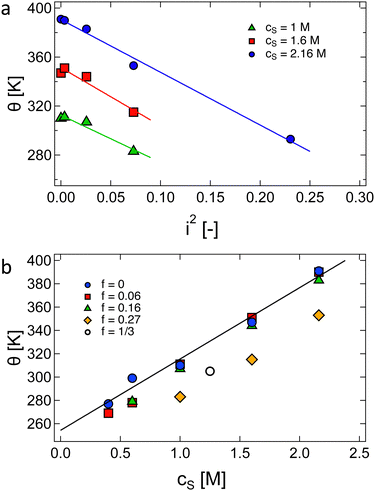 | ||
| Fig. 4 Dependence of θ temperature of polyacrylic acid in aqueous NaCl solutions as a function of (a) the degree of ionisation (i2) squared and (b) the concentration of added salt cs. Data are from ref. 192, except for the hollow circle which is from Flory and Osterheld.195 | ||
H-type behaviour192,195,197,208 can be described in terms of a Flory–Huggins theory using a χ parameter consisting of an intrinsic and an electrostatic term.9,133,201 An open question is to understand the variation of the excluded volume strength as a function of cs: increasing the ionic strength of the solvent leads to a reduction in the electrostatic term of the excluded volume (see Section 3.11), thus increasing χelec, and decreasing the solubility. The mean field approaches9 usually expect χelec ∝ f2/cs, in agreement with Muthukumar's result, but the experimental data favour a weaker scaling of 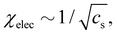 see ref. 209 and Section 3.11. The phase behaviour discussed above shows that addition of salt can also modify the non-ionic term of the solubility parameter (χ0). If χ0 decreases with increasing cs, “salting in”, a phenomenon where polyelectrolytes exhibit a re-entrant phase and/or chain expansion at high added salt, can be observed.103,201,210,211 This type of behaviour is usually found to be strongly dependent on the ion type,103,201,210–212 suggesting that solvent-mediated ion-binding to the polymer backbone plays a role, as observed earlier for polyethylene oxide,213,214 cellulose ethers215 and other systems.216 Addition of salt can also lead to a reduction of the non-ionic contribution to solubility, i.e. an increase in χ0.121
see ref. 209 and Section 3.11. The phase behaviour discussed above shows that addition of salt can also modify the non-ionic term of the solubility parameter (χ0). If χ0 decreases with increasing cs, “salting in”, a phenomenon where polyelectrolytes exhibit a re-entrant phase and/or chain expansion at high added salt, can be observed.103,201,210,211 This type of behaviour is usually found to be strongly dependent on the ion type,103,201,210–212 suggesting that solvent-mediated ion-binding to the polymer backbone plays a role, as observed earlier for polyethylene oxide,213,214 cellulose ethers215 and other systems.216 Addition of salt can also lead to a reduction of the non-ionic contribution to solubility, i.e. an increase in χ0.121
The interaction of added salts with non-ionic polymers has been studied in detail for polyethyelene oxide. In aqueous solutions, addition of electrolytes usually leads to a decrease in the solvent quality.217–219 In contrast, in polar organic solvents such as methanol, the opposite behaviour is observed.220 The mechanism underpinning these phenomena remains controversial. Generally, it is accepted that ion-binding to the backbone221–224 as well as changes in the solvent properties by the added electrolyte modify the solvent quality for the PEO chain. However, a detailed understanding of how and why their relative importance depends on solvent type remains an open question. While such effects are often not discussed when modelling the properties of polyelectrolytes, they should generally not be expected to be absent.
3.1.2.2 L-Type phase behaviour. The phase behaviour of polyelectrolytes in the presence of di-, tri- and tetra-valent ions is considered in Fig. 5. We discuss these in turn. L-Type precipitation, while usually associated with divalent and higher-valent ions,201,225 is also observed for monovalent ions with high coordination numbers notably Ag+.226,227
The critical added alkaline earth concentration 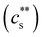 to precipitate 90% neutralised polymethacrylic acid (PMA) is plotted in Fig. 5(a). In the absence of added NaCl, the concentration of M2+ (= Mg2+, Ca2+ and Ba2+) is nearly proportional to the polymer concentration. Similar behaviour is observed for sodium polyacrylate (NaPA) with added CaCl2 for c ≳ 3 mM, see Fig. S3(a) (ESI†). The data of Sabbagh and Delsanti230 also show that for sufficiently low c,
to precipitate 90% neutralised polymethacrylic acid (PMA) is plotted in Fig. 5(a). In the absence of added NaCl, the concentration of M2+ (= Mg2+, Ca2+ and Ba2+) is nearly proportional to the polymer concentration. Similar behaviour is observed for sodium polyacrylate (NaPA) with added CaCl2 for c ≳ 3 mM, see Fig. S3(a) (ESI†). The data of Sabbagh and Delsanti230 also show that for sufficiently low c, 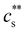 scales as ∼c−0.6. Other polyelectrolyte systems displayed this feature or a plateau in
scales as ∼c−0.6. Other polyelectrolyte systems displayed this feature or a plateau in 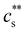 in the low c region.93,198,233,234 The phase boundary shown in Fig. 5(a) is seen to be identical for MgCl2, CaCl2, and BaCl2. If NaCl was added,
in the low c region.93,198,233,234 The phase boundary shown in Fig. 5(a) is seen to be identical for MgCl2, CaCl2, and BaCl2. If NaCl was added, 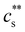 increased, a feature also observed for NaPA200,201 (see Fig. S3(b) and (c), ESI†) presumably due to the competitive binding of Na+ and M2+ to the ionic side groups. For lower degrees of neutralisation, Ikegami and Imai197 showed that Ba2+ and Ca2+ precipitate NaPA at much lower
increased, a feature also observed for NaPA200,201 (see Fig. S3(b) and (c), ESI†) presumably due to the competitive binding of Na+ and M2+ to the ionic side groups. For lower degrees of neutralisation, Ikegami and Imai197 showed that Ba2+ and Ca2+ precipitate NaPA at much lower 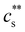 than Mg2+.235 The phase behaviour of PSS/BaCl2233,234,236,237 is discussed in Section S1 of the ESI,† where it is shown that θ depends linearly on cs, as for H-type systems.
than Mg2+.235 The phase behaviour of PSS/BaCl2233,234,236,237 is discussed in Section S1 of the ESI,† where it is shown that θ depends linearly on cs, as for H-type systems.
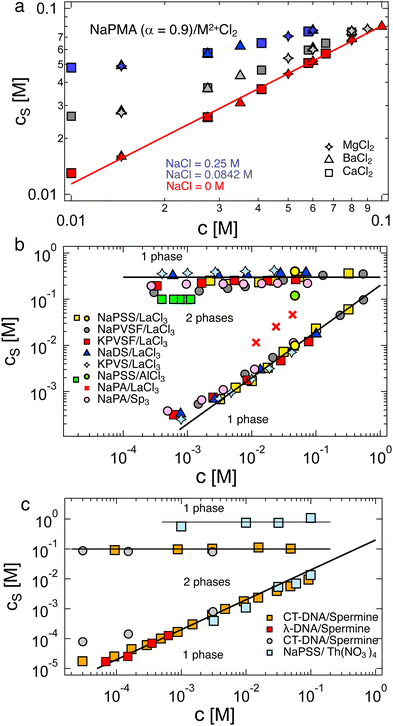 | ||
Fig. 5 (a) Added salt concentration as a function of polymer concentration for polymethacrylic acid (i = 0.9) in DI water and aqueous NaCl solutions. Line is cs = 0.57c0.85. Data are from ref. 228. (b) Added salt concentration for precipitation 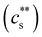 and re-dissolution (cDs) for polyelectrolytes with added trivalent salts. NaPSS/LaCl3 data are from ref. 199 (yellow squares) and ref. 229 (yellow circles), NaPSS/AlCl3 from ref. 202 (green squares) and ref. 229 (green circle) and NaPSS/LaCl3 (red crosses) from ref. 197. Sp stands for trivalent cation spermidine. All others are from ref. 230. Top line is cs = 0.3 M, bottom line is cs = 0.2c. (c) Precipitation and re-dissolution cs for DNA and PSS in the presence of tetravalent ions. NaPSS data are from ref. 199 DNA data are from ref. 231 (squares) and ref. 232 (circles). Bottom line is cs = 0.2c. and re-dissolution (cDs) for polyelectrolytes with added trivalent salts. NaPSS/LaCl3 data are from ref. 199 (yellow squares) and ref. 229 (yellow circles), NaPSS/AlCl3 from ref. 202 (green squares) and ref. 229 (green circle) and NaPSS/LaCl3 (red crosses) from ref. 197. Sp stands for trivalent cation spermidine. All others are from ref. 230. Top line is cs = 0.3 M, bottom line is cs = 0.2c. (c) Precipitation and re-dissolution cs for DNA and PSS in the presence of tetravalent ions. NaPSS data are from ref. 199 DNA data are from ref. 231 (squares) and ref. 232 (circles). Bottom line is cs = 0.2c. | ||
The phase diagrams of polyelectrolytes in the presence of trivalent ions are shown in Fig. 5(b). Phase separation occurs for 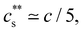 indicated by the solid line. This precipitation boundary was found to be N-independent for NaPSS/LaCl3.199 The data presented in Fig. 5(b) also show that
indicated by the solid line. This precipitation boundary was found to be N-independent for NaPSS/LaCl3.199 The data presented in Fig. 5(b) also show that 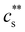 is largely insensitive to the ionic group, with acrylate, sulfonate and sulfate groups all falling onto the same curve, except for NaPA/LaCl3. This suggests that electrostatics and not ion-specific interactions are the primary driving force at play. Dubois and Boue238 found
is largely insensitive to the ionic group, with acrylate, sulfonate and sulfate groups all falling onto the same curve, except for NaPA/LaCl3. This suggests that electrostatics and not ion-specific interactions are the primary driving force at play. Dubois and Boue238 found 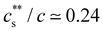 for NaPSS/LaCl3. Jan and Breedveld229 reported
for NaPSS/LaCl3. Jan and Breedveld229 reported 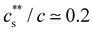 for NaPSS with added LaCl3 and CeCl3 and a higher ratio of 0.3 for AlCl3 and GaCl3; InCl3 precipitated NaPSS with N ≃ 5000 at
for NaPSS with added LaCl3 and CeCl3 and a higher ratio of 0.3 for AlCl3 and GaCl3; InCl3 precipitated NaPSS with N ≃ 5000 at 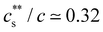 . For NaPSS with N ≃ 2500 and 600, InCl3 did not lead to precipitation. As the added salt concentration was further increased, re-dissolution of the polyelectrolytes was observed at cs = cDs. The re-entrant boundary is nearly c-independent and increases with N.199cDs was found to depend on the trivalent cation type. For NaPSS, cDs varies on the order La3+ ≃ Ce3+ > Ga3+ ≳ Al3+ > In3+. In the presence of a monovalent salt,
. For NaPSS with N ≃ 2500 and 600, InCl3 did not lead to precipitation. As the added salt concentration was further increased, re-dissolution of the polyelectrolytes was observed at cs = cDs. The re-entrant boundary is nearly c-independent and increases with N.199cDs was found to depend on the trivalent cation type. For NaPSS, cDs varies on the order La3+ ≃ Ce3+ > Ga3+ ≳ Al3+ > In3+. In the presence of a monovalent salt, 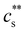 increases and cDs decreases, narrowing the two-phase region of the phase diagram.199 In some cases, re-dissolution does not occur, leading to the formation of a gel phase instead. This phenomenon is observed, for instance, when sodium carboxymethyl cellulose (NaCMC) or alginate are exposed to (Al3+ or Fe3+ ions239–243).
increases and cDs decreases, narrowing the two-phase region of the phase diagram.199 In some cases, re-dissolution does not occur, leading to the formation of a gel phase instead. This phenomenon is observed, for instance, when sodium carboxymethyl cellulose (NaCMC) or alginate are exposed to (Al3+ or Fe3+ ions239–243).
The phase diagrams of systems in the presence of tetravalent cations are plotted in Fig. 5(c). The behaviour is similar to that of the trivalent systems with  and a nearly c-independent re-entrant phase boundary. In the re-entrant region for both tri-valent and tetra-valent ions, increasing cs leads to chain expansion,229,238,244–248 presumably linked to charge-inversion, a phenomenon by which the binding of multivalent ions to the polymer backbone leads to a reversal of the net charge of the polymer backbone, see ref. 249–253 for explanations of the underlying physics and its role in biological phenomena.
and a nearly c-independent re-entrant phase boundary. In the re-entrant region for both tri-valent and tetra-valent ions, increasing cs leads to chain expansion,229,238,244–248 presumably linked to charge-inversion, a phenomenon by which the binding of multivalent ions to the polymer backbone leads to a reversal of the net charge of the polymer backbone, see ref. 249–253 for explanations of the underlying physics and its role in biological phenomena.
Understanding how the strength of binding of ions to the polyelectrolyte influences their phase behaviour remains a challenge. Experimental approaches to quantifying ion specificity are usually based on measuring relative binding constants by potentiometry (or less commonly by spectrophotometric methods254 or equilibrium dialysis255,256), and have been applied comprehensively to polyacrylic acid,257–260 see ref. 66 and 261 for overviews. The available phase data do not allow for a meaningful correlation to be established between phase behaviour and ion binding strength. Thermodynamic data on ion binding can also be obtained by isothermal titration calorimetry,202,204,262,263 which has been correlated with trends in polyelectrolyte conformational changes.264 Ion-binding and bridging265,266 mechanisms, which are important for divalent and higher-valent ions, are poorly understood. The influence of divalent salts on the conformation of polyelectrolytes has been studied extensively for sodium polyacrylate by Huber and co-workers74,264,267–273 but these datasets have not yet been comprehensively accounted for in any theoretical framework.
3.2 Viscoelasticity
The scaling assumption for calculating the dynamic properties of dilute polyelectrolytes is that chains are non-draining and can therefore be described by the Zimm model. Measuring the viscoelasticity of dilute solutions is experimentally challenging, and relatively little data exists.275 Rosser et al.274 made use of Birnboim–Schrag resonators to probe the dynamics of NaPSS in water and water/glycerol media. Fig. 6 shows the storage and loss modulus for NaPSS in an excess of 0.001 M salt solutions. The prediction of the Zimm model, following ref. 86 with a scaling exponent of ν = 0.59, shows good agreement with experimental data, thus supporting the non-draining nature of dilute polyelectrolyte coils. Note that the black lines shown in Fig. 6 do not contain any fit parameters. The validity of the Zimm model for dilute polyelectrolytes is also supported by the scaling of the diffusion coefficient and the intrinsic viscosity with the molar mass, see Section 3.9.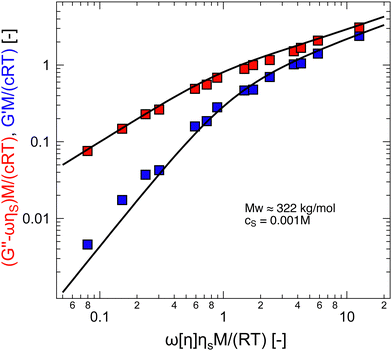 | ||
| Fig. 6 Storage and loss modulus for sodium polystyrene sulfonate in 0.001 M NaCl salt solutions. Measurements at T = 5, 15, and 25 °C were plotted into a single master-curve. Lines are the Zimm model using eqn (8.67) and (8.68) from ref. 86 with ν = 0.59. Data are from ref. 274. | ||
3.3 Dilute solution viscosity
Fuoss and co-workers4,276–284 observed that the reduced viscosity (ηred = ηsp/c) of dilute polyelectrolyte solutions in low ionic strength media increased upon dilution. Addition of a low molecular weight salt suppressed the ‘polyelectrolyte effect’ and resulted in a linear ηredvs. c trend, characteristic of non-ionic systems. The studies also showed that due to the strong non-Newtonian effect of polyelectrolyte solutions in salt-free solutions, measurements with capillary viscometers did not always capture the zero shear rate viscosity value.278,279,281,283 This important point has been neglected in a large part of the literature, see ref. 285, 286 and Section 3.4 for further discussion. It is important to note that while for sufficiently dilute solutions the shear viscosity becomes largely insensitive to the applied shear rate, the polymer contribution to the shear viscosity (η − ηs), which is the relevant quantity to determine conformational properties at infinite dilution, remains significant.287,288 An empirical function was proposed by Fuoss and co-workers to fit polyelectrolyte shear viscosity data in low ionic strength media: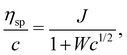 | (33) |
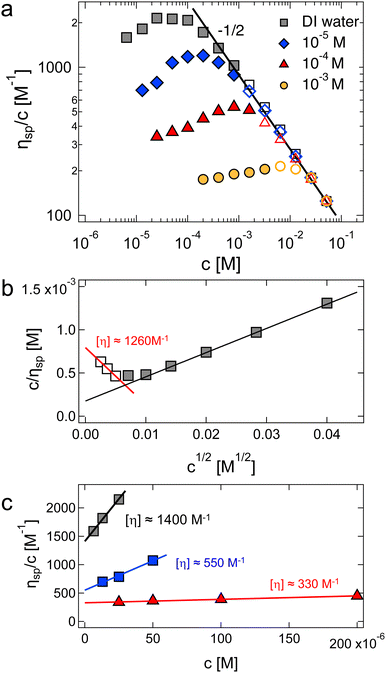 | ||
| Fig. 7 (a) Specific viscosity of NaPVS with 31% charged groups as a function of polymer concentration for different concentrations of added NaCl. Data are measured in a nitrogen atmosphere. Solid symbols represent results for dilute solutions (ηsp < 1) and hollow symbols for semidilute solutions (ηsp < 1). The solid line represents the Fuoss power-law (ηred ∝ c−1/2). (b) Inverse of reduced viscosity as a function of c1/2 for salt-free data. The black line gives an apparent intrinsic viscosity of ≃5200 M−1, see eqn (33). The red-line estimates [η] from the low-c region, corresponding to data below the viscosity maximum in plot (a). (c) Huggins plot for low concentration regime. Colours are the same as in plot (a). Data are from ref. 299. | ||
The existence of the maximum in ηred means that the extrapolation methods by Fuoss and co-workers overestimate the intrinsic viscosity of polyelectrolytes in low ionic strength media. For example, the black line shown in Fig. 7(b) (Fuoss’ method) gives [η] ≃ 5200 M−1. A more reasonable estimate based on data for concentrations below the ηred maximum gave 1260 M−1, shown by the red line, which matched the estimate from the Huggins plot shown in Fig. 7(c). This value is considerably larger than [η] ≃ 440 M−1 calculated by Nishida et al. on the basis of their model to account for inter-chain contributions to the reduced viscosity. Note also that using Nishida's method, the intrinsic viscosity was almost identical for DI water and cs = 10−4 M, in contrast to the strong cs dependence observed using the Huggins equation shown in Fig. 7(c). Other empirical methods,289–292,302,303 including an equation developed by Wolf (eqn (S3), ESI†),304–312 have been widely employed to estimate the intrinsic viscosity of polyelectrolytes in recent years.313,314 These suffer from similar problems as the Fuoss method (eqn (33)) because the fits do not produce maxima in the ηredvs. c profiles, see the ESI† (Section S5.5).
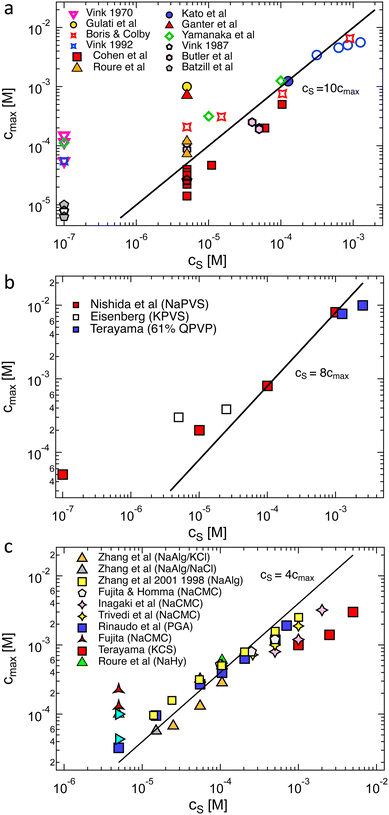
The polymer concentration at the maximum in ηred as a function of the total salt concentration in the solvent from different literature reports on NaPSS and data reported by Kato et al.316 for HPSS is plotted in Fig. 8(a). Points for which cmax > c* are shown as hollow symbols and those for which cmax < c* are shown as full symbols. For samples measured in a nitrogen atmosphere, we estimated cs ≃ 10−7 M from the self-dissociation constant of water. The value of cmax is usually found to be independent of shear rate or weakly dependent of shear rate,317 with the exception of Vink's measurements,318,319 where cmax varied strongly with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . We therefore include data measured in both the Newtonian regime and the shear-thinning regime. The latter include Cohen's297 high molar mass samples, Batzill's320 highest molar mass sample, and the two highest molar masses from Vink.321 The data from the various reports display a high degree of scatter and it is therefore not possible to establish if a fixed cmax/cs ratio exists. The data reported by Yamanaka et al. are particularly interesting: despite the very low level of residual salt due to the measurements being carried out in a nitrogen atmosphere,322,323cmax takes a higher value than for Cohen's samples. The low residual salt content of Yamanaka et al.'s samples is confirmed by their c* values, see Fig. 11. Other strong departures from the trend are observed by Boris and Colby,285 Ganter et al.298 and Gulati et al.100 in DI water. A common feature of these datasets is the high molar mass of the polymers, all of which have N > 5000. However, Batzill's samples with high N do not deviate from the overall trend. The origin of these discrepancies remains unclear.
. We therefore include data measured in both the Newtonian regime and the shear-thinning regime. The latter include Cohen's297 high molar mass samples, Batzill's320 highest molar mass sample, and the two highest molar masses from Vink.321 The data from the various reports display a high degree of scatter and it is therefore not possible to establish if a fixed cmax/cs ratio exists. The data reported by Yamanaka et al. are particularly interesting: despite the very low level of residual salt due to the measurements being carried out in a nitrogen atmosphere,322,323cmax takes a higher value than for Cohen's samples. The low residual salt content of Yamanaka et al.'s samples is confirmed by their c* values, see Fig. 11. Other strong departures from the trend are observed by Boris and Colby,285 Ganter et al.298 and Gulati et al.100 in DI water. A common feature of these datasets is the high molar mass of the polymers, all of which have N > 5000. However, Batzill's samples with high N do not deviate from the overall trend. The origin of these discrepancies remains unclear.
 | ||
| Fig. 8 Polymer concentration at maximum in the reduced viscosity as a function of monovalent added salt content for: (a) polystyrene sulfonate. Filled symbols are when cpeak < c* and hollow symbols for cpeak > c*. Data are from ref. 285, 297, 298, 316–320, 331 and 332 (b) polyvinyl sulfate and quaternised polyvinyl pyridine (degree of quaternisation = 61%). Data from ref. 299, 324 and 333 (c) carboxymethyl cellulose, sodium hyaluronate, poly(galacturonic acid), sodium alginate and potassium cellulose sulfate. Data are from ref. 290, 294, 296, 321 and 334–339. Lines are power-laws with a slope of unity, illustrating a fixed ratio between the polymer and added salt concentration. | ||
The plot of cmaxvs. cs for other flexible polyelectrolytes is shown in Fig. 8(b). A correlation is observed, except for Eisenberg's324 samples in DI water. The same plot is also shown in Fig. 8(c) for ionic polysaccharides, where the scatter is considerably smaller than for NaPSS, despite the fact that many different polymer systems are considered.325 The combined data in Fig. 8(c) suggest that cmax may follow a sublinear relationship with cs. The cs/cmax ≃ 10 and cs/cmax ≃ 4 obtained for flexible polyelectrolytes and polysaccharides, respectively, are qualitatively consistent with fcmax ≃cs since polysaccharides have typically one dissociated charge per two monomers (≃1 nm along the backbone)326–330 while PSS has one dissociated charge per five monomers.68
All data for which cs is assumed to arise solely from the self-dissociation of water clearly deviated from the trend observed for other samples, suggesting that the actual residual salt is an order of magnitude larger than our estimate. Most measurements are carried out in capillary viscometers made of glass, which likely results in contamination of the solution from ion leaching, as reported by Butler et al.331 Unfortunately, most attempts to quantify the residual salt content in polyelectrolyte solutions (usually by electrical conductivity measurements) have been performed for samples prior to their rheological measurements. This assumes that the measurement itself does not lead to contamination, which may not necessarily be the case.301
The T- and N-dependence of cmax reported by Cohen et al.340 is incompatible with 2cs ≃ fcmax as neither parameter influences f or cs significantly. In contrast, other studies341,342 have reported a much weaker temperature dependence of ηsp for NaPSS as discussed in Section S3 (ESI†). Therefore, the current experimental evidence is inconclusive and does not clearly support (nor disprove) that cmax ≃ 2cs/f.
The behaviour of ηred in dilute solution has been assigned to single chain effects58,343 (i.e. chain expansion for c < c* leads to an increase in ηred). Alternatively, several theories explain that the viscosity maximum arises primarily from intermolecular effects (the secondary electroviscous effect) and not due to chain expansion upon dilution, see ref. 344–347. Antonietti et al.344 found that many of the features observed for linear polyelectrolytes were reproduced for ionic microgels. Their results could be described by a modified Hess–Klein model.348 The authors noted that since “charge density inside the [microgel] particles is always rather high, thus suppressing pronounced Coulomb-effects”, they expected no significant electrostatic swelling and the increase of [η] upon decreasing cs was attributed to effects other than changes in particle size. They concluded that these results provided proof of the intermolecular nature of the polyelectrolyte effect. In our view, the size invariance assumption should be revised in light of recent experimental evidence.349–355 The work of Schurtenberger and co-workers349 showed that polyelectrolyte microgels display a “porcupine” morphology in low ionic strength solvents due to highly extended dangling chains on their outer surface. A discussion of mode-mode coupling approaches to polyelectrolyte solution viscosity can be found in ref. 297, 340, 347 and 356 these generally fail to capture several experimentally observed phenomena such as the molar mass dependence of cmax.
3.4 Shear rate dependence of intrinsic viscosity
The non-Newtonian characteristics of dilute polyelectrolyte solutions have been reported by many authors,321,324,335,357–361 but only a few systematic experimental studies on the subject have been published.287,288,317,362–364Fixman365 developed a theory for the non-Newtonian intrinsic viscosity of flexible polymers. The shear rate dependence on the intrinsic viscosity is expressed as:
[η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )] = [η]G(Kη )] = [η]G(Kη![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ), ), | (34) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is a reduced shear rate with:
is a reduced shear rate with: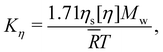 | (35) |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) is the gas constant. This is the same as the longest relaxation time predicted by the Zimm model (see eqn (8.34) of ref. 86), except for the pre-factor of 1.71.
is the gas constant. This is the same as the longest relaxation time predicted by the Zimm model (see eqn (8.34) of ref. 86), except for the pre-factor of 1.71.
In agreement with Fixman's theory, experiments show that polymers in theta solvent exhibit shear thinning and that [η](![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )/[η] for a constant Kη decreases as the excluded volume parameter z increases.366–368 A quantitative description of the shear rate dependence of [η] is still considered an open question in the rheology of dilute polymer solutions.369
)/[η] for a constant Kη decreases as the excluded volume parameter z increases.366–368 A quantitative description of the shear rate dependence of [η] is still considered an open question in the rheology of dilute polymer solutions.369
Fig. 9(a) and (b) show plots of the shear rate dependence of the relative decrease in [η] for a NaCMC polymer in aqueous solvents of varying added NaCl concentration (part a) and for a polymethacrylic acid in 0.003 M NaCl solutions of varying degrees of neutralisation (part b). In both cases, the data for different cs or i are seen to collapse onto a single mastercurve. This result is at odds with Fixman's theory as the excluded volume parameter z is expected to be an increasing function of cs and the degree of ionisation i for these systems (see Section 3.11). An analysis of data reported by Yanaki et al. for NaHy,288 provided in the ESI† (Fig. S5) shows that Fixman's theory does not quantitatively predict the dependence of [η](![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) on z. The power-law exponent for the NaCMC data is ≃−1/3. This exponent appears to work also for PMA, but since data are only available up to Kη
) on z. The power-law exponent for the NaCMC data is ≃−1/3. This exponent appears to work also for PMA, but since data are only available up to Kη![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) < 5, the −1/3 slope may not correspond to the limiting Kη
< 5, the −1/3 slope may not correspond to the limiting Kη![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≫ 1 value.
≫ 1 value.
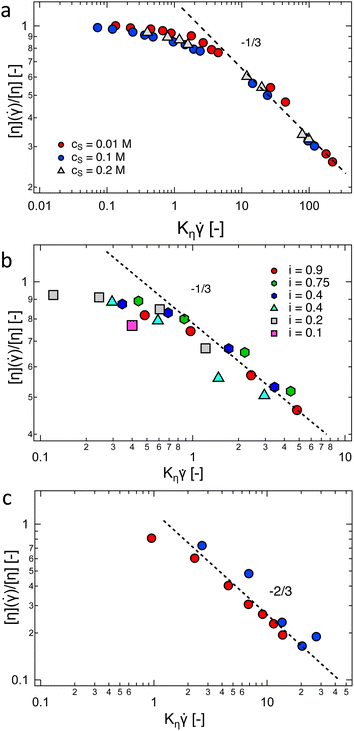 | ||
Fig. 9 Intrinsic viscosity normalised by its zero-shear value as a function of the reduced shear rate Kη![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , see eqn (35). (a) NaCMC in aqueous NaCl solutions, cs indicated on the legend. Data are from ref. 287. (b) Polymethacrylic acid in 0.003 M NaCl, neutralised with NaOH to different degrees, as indicated in the legend. Data are from ref. 362. (c) NaPSS in DI water (measurements in a nitrogen atmosphere). Data from ref. 317. Lines are power-laws with exponents indicated in the graphs. , see eqn (35). (a) NaCMC in aqueous NaCl solutions, cs indicated on the legend. Data are from ref. 287. (b) Polymethacrylic acid in 0.003 M NaCl, neutralised with NaOH to different degrees, as indicated in the legend. Data are from ref. 362. (c) NaPSS in DI water (measurements in a nitrogen atmosphere). Data from ref. 317. Lines are power-laws with exponents indicated in the graphs. | ||
In salt-free solution, the data reported by Yamanaka et al.317 for NaPSS, plotted in Fig. 9(c) display a stronger power-law of −2/3 at high shear rates, which exceeds the predictions370–372 and experimental observations373 of [η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )] ∼
)] ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1/2 for rod-like neutral polymers, but agrees with a simulation of rigid dumbbells.374
−1/2 for rod-like neutral polymers, but agrees with a simulation of rigid dumbbells.374
Simulation studies have quantified the degree of chain stretching374–378 and alignment377,379 of polyelectrolytes under shear flow. Ref. 374 and 376 indicate that for different ionic strengths, the plot shown in Fig. 9(a) should not collapse onto a single curve. The [η] vs. ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) curves are expected by Shogin and Amundsen374 to gradually transition to a power-law behaviour with a universal exponent of −2/3 at high
curves are expected by Shogin and Amundsen374 to gradually transition to a power-law behaviour with a universal exponent of −2/3 at high ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . Other studies give weaker exponents.376 Simulation studies have revealed that the dynamics of polyelectrolytes under shear display several features which are not encountered for neutral polymers: for example, Jarasree et al.378 showed that the dynamics of condensed counterions can have an influence on the tumbling of polyelectrolyte chains. Two studies noted that shear flow can promote counterion dissociation from the backbone,377,379 in agreement with the experimental results of Zhao and co-workers.380 Simulation work in elongational flows, under which a different set of transitions are expected,381 is more sparse.382
. Other studies give weaker exponents.376 Simulation studies have revealed that the dynamics of polyelectrolytes under shear display several features which are not encountered for neutral polymers: for example, Jarasree et al.378 showed that the dynamics of condensed counterions can have an influence on the tumbling of polyelectrolyte chains. Two studies noted that shear flow can promote counterion dissociation from the backbone,377,379 in agreement with the experimental results of Zhao and co-workers.380 Simulation work in elongational flows, under which a different set of transitions are expected,381 is more sparse.382
For the three systems considered, [η](![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )/[η] ≃ 0.8–0.9 for Kη
)/[η] ≃ 0.8–0.9 for Kη![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1 is found, which suggests that measurements with Kη
= 1 is found, which suggests that measurements with Kη![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≲ 1 should reasonably approximate the zero-shear rate value of the intrinsic viscosity. For the most common experimental conditions of aqueous solutions at T = 298 K, Kη ≃ 6 × 10−7[η]NM0
≲ 1 should reasonably approximate the zero-shear rate value of the intrinsic viscosity. For the most common experimental conditions of aqueous solutions at T = 298 K, Kη ≃ 6 × 10−7[η]NM0![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , which gives a critical shear rate for the onset of shear thinning of:
, which gives a critical shear rate for the onset of shear thinning of:
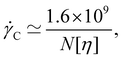 | (36) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) in s−1.300
in s−1.300
3.5 Conformation in salt-free solution at infinite dilution
The hydrodynamic radius of NaPSS in water without added salt383 as a function of the degree of polymerisation at infinite dilution is plotted in Fig. 10(a). The hydrodynamic radius is related to the diffusion coefficient of a chain via the Stokes–Einstein equation: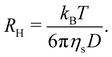 | (37) |
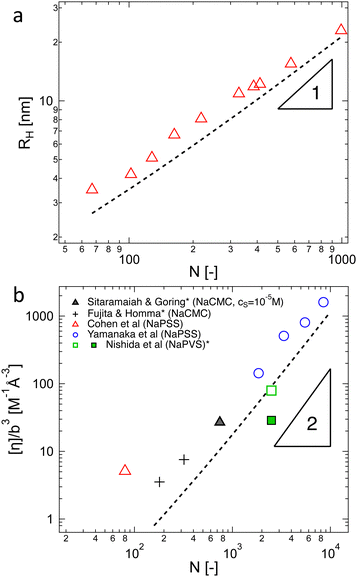 | ||
| Fig. 10 Properties of polyelectrolytes in the infinite dilution limit in DI water. (a) Hydrodynamic radius of NaPSS as a function of the degree of polymerisation, data from ref. 383. Line is the calculated hydrodynamic radius of a cylinder (eqn (37) using eqn (29) to calculate D). (b) Intrinsic viscosity for various polyelectrolytes normalised by monomer length cubed as a function of the degree of polymerisation. Data are from ref. 297, 299, 322, 323, 335 and 385. Line is the intrinsic viscosity of a cylinder calculated using Yamakawa's theory (eqn (38) with dC = 1 nm), see text for details. Points marked with an asterisk are likely affected by shear thinning. The datum by Sitaramaiah and Goring385 is for cs = 10−5 M and can be considered a lower-bound estimate for [η]. The data for NaPVS are obtained from the fit shown in Fig. 7(c) (hollow symbol) or by Nishida's method (full symbol). | ||
The intrinsic viscosity of rod-like objects of length L and cross-sectional diameter dC was calculated by Yamakawa and Yoshizaki as:
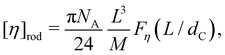 | (38) |
Following eqn (38), the intrinsic viscosity of NaPSS in deionised water is plotted as a function of N in Fig. 10(b). In order to allow comparison with other systems, we expressed [η] in units of M−1 and normalised it by b3 (b = 2.5 Å and b = 5 Å for vinyl and cellulose polymers, respectively). Note that in the c → 0 limit, polyelectrolytes are in the excess salt regime (fc < 2cs) due to the residual salt content of water. The estimation method of the residual salt concentration can be found in ref. 100, 285 and 301. In Fig. 10(b), we selected data in a sufficiently dilute solution to reach the linear ηredvs. c region and discarded intrinsic viscosity data obtained by use of fitting functions that do not yield a peak in ηredvs. c dependence. Data by Cohen et al.297,315 for high molar masses are not included as these are likely far from the zero-shear limit. Their results from ref. 315, discussed in Section S3 of ESI,† are also not included. Results reported by Yamanaka et al. for higher molar masses were measured over a wide range of shear rates and extrapolated to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0.322,323 For comparison, we included Fujita and Homma's two lowest Mw samples335 and data reported by Sitaramaiah and Goring385 for sodium carboxymethyl cellulose (NaCMC) in 10−5 M NaCl. We expect Sitaramaiah and Goring's sample to correspond to the shear thinning region. Fujita and Homma's samples are expected to be weakly influenced by shear thinning (see Fig. 10 of ref. 336). Therefore, the NaCMC data should be viewed as lower bound estimates for [η]. The intrinsic viscosity of NaPVS, estimated from the Huggins plot in Fig. 7(c) and from Nishida et al.'s method, is also included for comparison. The theoretical calculation for the intrinsic viscosity for chains in their fully extended conformation (eqn (38) with L = Nb), shown as a dashed line, under-predicted all experimental results.
→ 0.322,323 For comparison, we included Fujita and Homma's two lowest Mw samples335 and data reported by Sitaramaiah and Goring385 for sodium carboxymethyl cellulose (NaCMC) in 10−5 M NaCl. We expect Sitaramaiah and Goring's sample to correspond to the shear thinning region. Fujita and Homma's samples are expected to be weakly influenced by shear thinning (see Fig. 10 of ref. 336). Therefore, the NaCMC data should be viewed as lower bound estimates for [η]. The intrinsic viscosity of NaPVS, estimated from the Huggins plot in Fig. 7(c) and from Nishida et al.'s method, is also included for comparison. The theoretical calculation for the intrinsic viscosity for chains in their fully extended conformation (eqn (38) with L = Nb), shown as a dashed line, under-predicted all experimental results.
The data of Zhao and co-workers386 showed that the diffusion coefficients of NaPSS at extreme dilution in DI water and in 10−4 M aqueous NaCl were nearly identical, see also Fig. 31. The intrinsic viscosity of NaPVS, when estimated by Nishida's method, similarly showed no significant change for cs < 10−4 M.299 In contrast, data reported by Cohen et al.315 indicated that [η] for NaPSS (N ≃ 1600) in 10−4 M NaCl was ≃3× lower than those in DI water.387 The origin of this discrepancy is not clear to us, but it may point to an error in the estimates of [η]. The fact that Cohen's [η] value exceeded the maximum theoretical value by over an order of magnitude at low N supports this. The intrinsic viscosities shown in Fig. 10(b) for N > 100 are ≃×2 higher than the theoretical prediction. Since [η] ≃ RH3/N, this is consistent with Zhao and co-worker's data, which exceeds the theoretical prediction for RH by ≃20%. The hydrodynamic drag generated by counterions, known as the primary electroviscous effect,388,389 seems like the most likely cause for RH and [η] exceeding the theoretical values of a fully stretched rod. Experiments analogous to those presented in Fig. 10 probing the influence of the counterion size could provide confirmation of this.
The available data in the infinite dilution limit therefore suggest that NaPSS adopts a fully stretched chain conformation (B = 1) with no fluctuations perpendicular to the end-to-end vector of the chain. In contrast, measurements of the correlation length of NaPSS in dilute and semidilute solutions for 0.005 M < c < 1 M give a larger stretching parameter of B ≃ 1.8.234,390,391 An analysis of the correlation length data over a very broad concentration range234,392–395 suggests that the stretching parameter displays a weak increase with increasing concentration, which could explain this discrepancy.396 Conclusions drawn from intrinsic viscosity and/or diffusion data should be taken with caution until a more comprehensive grasp of the primary electroviscous effect is obtained. To enhance our understanding, experimental measurements similar to those depicted in Fig. 10, but conducted on polyelectrolytes with varying counterions, would be particularly valuable.
3.6 Overlap concentration in salt-free solutions
The overlap concentration of NaPSS in salt-free solution obtained by viscosity and scattering methods is compared in Fig. 11. The two estimates agreed well and showed c* ∝ N−2 in the high-N region, as expected from scaling theory. This scaling has also been reported for other systems.286,406 For N ≳ 3000, the data from Gulati et al.,100 Han et al.,301 Boris and Colby,285 and Ganter et al.298 deviated to a power-law of N−0.78, as expected in eqn (1) in the 2cs ≫ fc region. These datasets follow eqn (1) with cs ≃ 10−5 M, shown by the dashed line. This is consistent with estimates for the residual salt in NaPSS solutions, which arise due to carbonic acid dissolved from the air, of ∼10−5–10−4 M, see ref. 100, 285, 297 and 301. Vink,318 Yamanaka et al.322,323 and Batzill et al.320 measured the viscosities of NaPSS in a nitrogen atmosphere to avoid contamination from carbonic acid. Their data displayed lower c* values in the high-N region with no apparent crossover to the high salt scaling. Fitting eqn (1) and (7) to the data in the c* ∝ N−2 region gave B ≃ 2.5, which indicates that chains are significantly less extended at the overlap point than at infinite dilution. The estimate of B from c* data is close to those obtained from correlation length data in the semidilute regime.96 For N ≲ 20–30, corresponding to chains with fewer than 2–3 Kuhn segments,391 the c* data systematically deviated to lower values relative to the high-N power-law. This may be interpreted as a cross-over to the R < ξel regime, where chains are not electrostatically stretched and adopt neutral polymer conformation which is consistent with the weak variation of c* with added salt in this N range.397 Such interpretation gives ξel ≃ 3 nm. This is not entirely consistent with eqn (6), which indicates ξ ≃ lB ≃ 0.71 nm for PSS in water.407,408 Further, the ξel ≃ 3 nm value does not agree with scattering data for the chain dimensions in the semidilute regime19,391 or with the cross-sectional diameter of chains measured by the zero-average contrast method.125 The c* − N exponent has been observed to take apparent values as low as −2.5 in a recent simulation,409 which are not seen in Fig. 11(a).
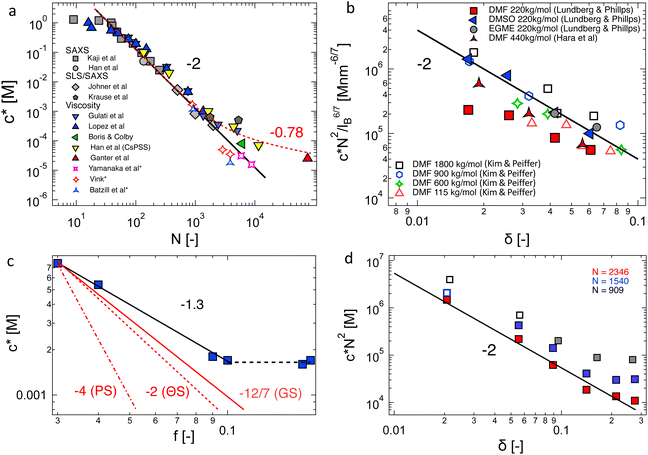 | ||
| Fig. 11 (a) Overlap concentration of NaPSS in DI water determined by scattering methods (grey symbols, data from ref. 390 as compiled in ref. 285 and 14, see also ref. 397) and using the ηsp(c*) = 1 criterion (coloured symbols from ref. 96, 100, 285, 298, 301, 318, 320 and 322). Refs marked with an asterisk are for measurements carried in a nitrogen atmosphere, which minimises carbonic acid content. Full and dashed lines are the fits at cs = 0 M, B = 2.5 and cs = 10−5 M, B = 2.5, see eqn (1). (b) Overlap concentration of lightly sulfonated polystyrene, normalised by N−2lB6/7, as expected by eqn (6c) as a function of the fraction of monomers bearing a charge, δ. Given the low degrees of sulfonation (<9%), no counterion condensation is expected and δ is expected to coincide with f. Data are from ref. 185 and 398. (c) Overlap concentration of quaternized P2VP in ethylene glycol as a function of the fraction of groups bearing a dissociated counterion, f, which was measured by conductivity. Data are from ref. 97. Red lines are scaling predictions for good solvent, theta solvent and poor solvent. (d) Overlap concentration of aminoacetalized polyvinyl acetate as a function of charged group fraction, degree of polymerisation indicated in the legend. See the text for an explanation of the hollow symbols. Data are from ref. 399. | ||
Chain shrinkage from the infinite dilution limit to the overlap concentration is consistent with the simulation work of Stevens and Kremer.98 Oostwal et al.'s data showed that the diffusion coefficient of NaPSS decreased upon dilution below c*, which also suggests chain expansion upon dilution.410 The charge fraction is known to increase with dilution below c*,80,411 and may be in part related to the differences in chain dimensions at infinite dilution and at the overlap point.412
The influence of charge fraction and solvent's Bjerrum length on the overlap concentration of lightly sulfonated ionomers in polar solvents is considered in Fig. 11(b). All estimates of c* are viscosimetric. The datasets of Kim and Peiffer398 for four degrees of polymerisation and varying charge densities (δ) in dimethylformamide (DMF) solution and that of Hara et al.172 for a single molar mass reasonably collapsed onto a single curve with a slope of −2, supporting the validity of eqn (7). Lundberg and Phillips’ data185 for a single molar mass in three solvents dimethylformamide (DMF, εr = 37), dimethyl sulfoxide (DMSO, εr = 49) and ethylene glycol monomethylether (EGME, εr = 17) also collapsed broadly and agreed with the observed trend, but the c*N2/lB6/7 values in DMF were clearly lower than in the other two solvents. Differences in solvent quality for the backbone may help explain these discrepancies because DMF is a good solvent for the PS backbone413,414 while DMSO or EGME are non-solvents for polystyrene. However, if DMSO and EGME data correspond to the T ≪ θ condition, it is not clear why poor solvent scaling (c* ∝ f−4), calculated from eqn (1) and (8) does not apply. This suggests that there are factors influencing polyelectrolyte conformation not captured in eqn (6). Further evidence for this can be seen from the fact that in cyclohexanone (εr = 18), the viscosity of NaPSS displayed ionomer behaviour while in EGME, which has a lower dielectric constant, a polyelectrolyte behaviour is apparent.
Eqn (6) was also be tested using the data of Dou and Colby97 for the intrinsic viscosity of P2VP quaternized to different degrees in ethylene glycol (EG) solutions, as shown in Fig. 11(c). The authors estimated the fraction of monomers bearing a dissociated charge from conductivity measurements. Comparing the intrinsic viscosity for P2VP in EG with the values for a theta solvent,415 we estimated that the thermal blob of the uncharged polymer contain ≃59 chemical monomers. The number of monomers in an electrostatic blob is estimated as follows:
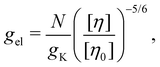 | (39) |
Matsumoto and Eguchi399 reported diluted viscosity data for aminoacetalyzed polyvinyl alcohol with different fractions of charged groups in salt-free water. As 0.1 M K2SO4 is a near theta solvent for the uncharged polymer,416 we expect water to be a marginally good solvent for the backbone and ξT ≫ ξel. The c* values normalised by N2 are plotted as a function of the fraction of charged groups in Fig. 11(d) and are consistent with the c* ∝ f−2 scaling prediction, assuming no significant counterion condensation (δ ≃ f), see the ESI,† Section S4, for the calculation of δ. The hollow points are c* obtained by extrapolating the data significantly beyond the measurement range.
Lastly, it is worth noting that plots of c* as a function of the reduced contour length Nb/B, where B is determined using scattering techniques, do not exhibit the universal behavior as predicted by the scaling model.286
We analyzed the literature data reported by Jousset et al.174 for poly([(2-methacryloyloxy)ethyl]trimethylammonium 1,1,2,3,3-pentacyanopropenide) (P(M-PCP)) and Matsumoto et al.56 for poly(1-butyl-3-vinylimidazolium bis(trifluoromethanesulfonyl)imide) (PC4-TFSI) in solvents having a broad range of dielectric constants εr ranging from 7.9 to 182. The solution viscosities of PC4-TFSI were measured as a function of shear-rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) and the
) and the ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0 limit was taken to calculate ηsp. For P(M-PCP), capillary viscometers were used, and thus, it is possible that some of the data at low c and high εr may be influenced by shear thinning. The overlap molar concentration of monomers, c*, was determined using the viscosimetric criterion outlined earlier (ηsp(c*) = 1) and plotted as a function of the solvent's Bjerrum length lB in Fig. 12. Here, when the ηsp dataset did not contain the data points crossing at ηsp = 1 over the measured c range, we extrapolated the power-law fit towards ηsp = 1.
= 0 limit was taken to calculate ηsp. For P(M-PCP), capillary viscometers were used, and thus, it is possible that some of the data at low c and high εr may be influenced by shear thinning. The overlap molar concentration of monomers, c*, was determined using the viscosimetric criterion outlined earlier (ηsp(c*) = 1) and plotted as a function of the solvent's Bjerrum length lB in Fig. 12. Here, when the ηsp dataset did not contain the data points crossing at ηsp = 1 over the measured c range, we extrapolated the power-law fit towards ηsp = 1.
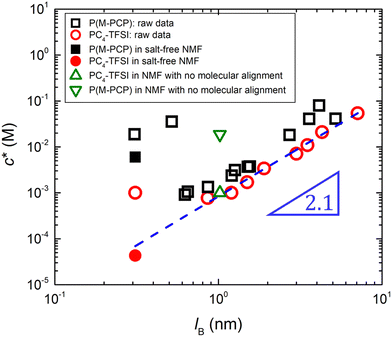 | ||
| Fig. 12 The dependence of the overlap monomer concentration c* on the Bjerrum length lB for PC4-TFSI (red circles) and P(M-PCP) (black squares) solutions without added salt. Dashed blue line is the best-fit power-law to PC4-TFSI data for lB > 0.7 nm. The full red and black points are the estimate of c* in salt-free NMF, while the hollow green points are the estimate of c* in NMF with no alignment correlations at εr = 55. Data are from ref. 56 and 174. | ||
For PC4-TFSI solutions, the value of c* initially decreased slightly with increasing lB for lB < 1 nm, beyond which it increased as c* ∝ lB2.1. It appears that the obtained exponent agrees with the scaling law of c* in poor solvents, i.e., c* ∼ lB2.0. Additional experimental evidence (for example from phase behaviour or A2 data in excess salt) is needed to establish if the various solvents considered correspond to the T ≪ θ condition.417 The observed non-monotonic dependence of c* for PC4-TFSI could be attributed to the high content of residual salts in the solvent NMF (N-methylformamide).418 Matsumoto et al. reported a residual salt concentration of 3.6 mM in NMF, which is higher than the measured c* ≃ 1 mM. Assuming f = 1 in eqn (13), we estimated the overlap monomer concentration in salt-free NMF to be c* ≃ 4.3 × 10−5 M. This estimate is included as a filled circle shown in Fig. 12 and agrees well with the trend observed for other solvents. The reduction of εr in NMF may be an alternative cause for the observed non-monotonic behaviour of c*. Dou and Colby418 have pointed out that a high dielectric constant of NMF stems from the Kirkwood correlations involving effective alignment of NMF molecules, and therefore solutes, e.g., PC4-TFSI, can randomize such a molecular alignment, leading to the reduction of εr in NMF containing polyelectrolytes. Adopting εr = 55 proposed for NMF with no alignment correlations,418 we also observed a good agreement with the trend line shown in Fig. 12 (see an open triangle at lB = 1.0 nm). However, further experimental work is required to confirm this hypothesis, for example, through dielectric relaxation spectroscopy.419
For P(M-PCP) solutions, we observed a discontinuous change in c*, as shown in Fig. 12. The value of c* increased with increasing lB for lB < 0.6 nm, exhibited a significant reduction of c* at lB ∼ 0.6 nm, increased again as lB was increased further while displaying a power-law behaviour with exponent similar to that for PC4-TFSI. Two data points at lB = 0.52 nm and lB = 0.31 nm correspond, respectively, to the c* data for P(M-PCP) in formamide (F) and in NMF having higher εr than the other solvents for lB > 0.6 nm. According to the Manning model (eqn (32)), we anticipate a more stretched configuration in F and NMF and thus a monotonic decrease of c* with respect to the decreasing lB. However, the experimental result showed a drastic change in the size of the P(M-PCP) chain when crossing lB ∼ 0.6 nm. The observed increase in c* might be explained again by considering either the presence of residual salts in NMF or the reduction of the solvent dielectric constant, as we discussed above. Note that the origin of the high εr in F is the same as that in NMF.420 Although Jousset et al. did not report the residual concentration in their NMF, the residual salt of commercial NMF grades has been reported to be as high as 0.02 M.421,422 Therefore, assuming f = 1 and cs = 0.02 M, we estimated c* in salt-free NMF, which yielded c* ≃ 6 × 10−3 M. As seen as a filled square and an inverted triangle in Fig. 12, both scenarios appear insufficient to fully account for the drastic change of c* in magnitude. We will provide a further discussion on this point in Section 3.8.1.
3.7 Counterion condensation
The estimation of the charge fraction f is not trivial because how many of the counterions on a polyelectrolyte chain are detected as dissociated counterions depends on how we measure it. As a result, the measured value of f can vary within a factor of order unity even if the same test sample is used, depending on the measurement technique applied.419 From literature reports, experimental methods using osmotic pressure,89,423–426 light scattering,423,427–429 potentiometry,80,328,430–436 ionic conductivity,326,330,437,438 and complex permittivity419 have been used to evaluate the charge fraction on a polyelectrolyte chain more accurately. Many of these data are in the semidilute regime and we do not review them here (see ref. 68 and 80, for more details). In this review, we estimated the charge fraction f based on the scaling law of c* given by eqn (13). In estimating f, we assume B for theta solvents, i.e., eqn (8b) and assume lK,0 = ξT = 2 nm for flexible polymers in the athermal solvent due to the lack of experimental data of lK,0 and ξT for the tested polyelectrolytes. Because of these assumptions, the estimated f contains uncertainties in magnitude. b was set at b = 0.25 nm for vinyl polymers.| c* ≈ N−2lB−1b16/7lK,0−30/7f−2. | (40) |
| f ≈ [c*N2lBb−16/7lK,030/7]−1/2. | (41) |
Fig. 13(a) shows the dependence of f on the degree of polymerisation N for NaPSS in salt-free aqueous solutions. Here, we did not consider data points at N < 60 from our f analysis since eqn (13) does not apply. In Fig. 13(a), we observed that the value of f was independent of N for N < 2 × 103, in good agreement with the trend predicted by the Manning counterion condensation model, i.e., f ∝ N0. It appears that f starts to decrease with increasing N for N > 2 × 103. This is probably because the overlap concentration in a salt-free solution becomes comparable to the level of the concentration of residual salts in water. The effect of residual salts in water on the measured c* is also observed in Fig. 11(a). While the N−2 power-law depicted in Fig. 11(a) shows the overlap concentration of the order of 10−5 M for NaPSS at N > 3 × 103, experimental results display overlap concentrations greater than 10−4 M. Therefore, the observed apparent decrease of f might be explained by taking the contamination of residual salts into account. In fact, when setting the overlap concentration larger than measured, the estimated f value using eqn (41) becomes larger than plotted in Fig. 13(a).
 | ||
| Fig. 13 The dependence of the charge fraction f on (a) the degree of polymerisation N for NaPSS, (b) the fraction of ionic monomers δ, (c) the molar concentration of salts cs, and (d) the Bjerrum length lB. c* data used to calculate f for plots (a)–(c) are from Fig. 11. Plot (d) uses c* data from Fig. 12. | ||
The estimated value of f in the plateau regime was much smaller than the value of f ∼ 0.2 obtained using conductivity330 and osmotic pressure89 measurements. This indicates that the charge fraction f values from eqn (41) are approximately 100 times smaller than expected. Nevertheless, the trends illustrated in Fig. 13 remain noteworthy.
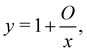 | (42) |
| y = Hx4/3, | (43) |
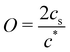 and H = (c*)2/3N4/3b2/3lK,02/3lB2/3. In the calculation, the variation of the solvent dielectric constant εr with respect to the increasing cs was also included.439
and H = (c*)2/3N4/3b2/3lK,02/3lB2/3. In the calculation, the variation of the solvent dielectric constant εr with respect to the increasing cs was also included.439
Fig. 13(c) shows that the value of f increases with increasing cs. This result suggests that the number of dissociated counterions increases with increasing cs. However, theoretical144 and simulation164 results predict a decrease in the charge fraction with the increasing cs. The apparent increase observed in Fig. 13(c) at high salt concentrations can be understood by noting that eqn (40) only applies when the screening length is larger than the electrostatic blob size, which breaks down at high cs. Beyond this limit, polyelectrolyte chains will exhibit an asymptotic decrease in chain size with respect to the increasing cs, approaching a constant end-to-end distance at high cs determined by the intrinsic (non-electrostatic) chain stiffness. Applying eqn (13) in this regime could lead to an over-prediction of f. For comparison, transference experiments for NaPA in aqueous NaCl solution showed that f is independent of cs for cs < 0.1 M.151,440,441
The procedure to estimate the f ∝ lB−1.6 relation relied on three assumptions: (1) chains adopt a rod-like conformation on distances larger than the electrostatic blob (eqn (7)); (2) the electrostatic blob size for a polyelectrolyte in theta solvent scales with the charge fraction as ξel ∝ f2/3 (eqn (6b)); (3) ξT and lK,0 do not depend on εr. The first assumption is validated by the c* ∝ N−2 scaling observed for various systems,95,285,286,404,406 as discussed in the preceding sections. The second assumption is supported by the data shown in Fig. 11(d), but has not been tested extensively. The third assumption, while difficult to test rigorously, is supported by the fact that the two PILs showed the same scaling despite their very different chemical structures. Deviations from the Manning model for ionenes in solution were reported by Popov and Hoagland on the basis of measurements of electrophoretic mobility152 and by Rodivc et al.443 from electrical conductivity and transport numbers data. In both studies, ion-solvent interactions appeared to influence the degree of counterion binding.
The Muthukumar model144 might capture the observed trend of f against lB, i.e., by considering the dielectric mismatch between the bulk and the local region around polyelectrolyte chains. However, the use of the Muthukumar model requires a priori knowledge of several material parameters, such as the dipole length of ion-pairs, the local dielectric constant, and the excluded volume parameters, which are not available in literature reports. The observed discrepancy between the experimental data and the theoretical prediction warrants more in-depth studies in the future.
3.8 Influence of solvent type on the solution viscosity
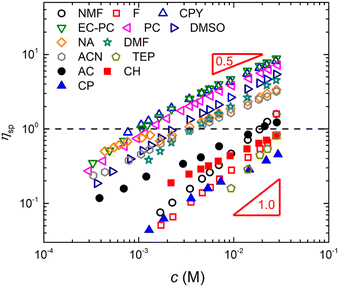 | ||
| Fig. 14 Dependence of the specific viscosity ηsp on the monomer concentration c of P(M-PCP) in various solvents with different dielectric constants εr. The solvents are triethyl phosphate (TEP: open pentagons, εr = 11), cyclopentanone (CP: filled triangles, εr = 14), cyclohexanone (CH: filled squares, εr = 16), acetone (AC: filled circles, εr = 21), acetonitrile (ACN: open hexagons, εr = 36), dimethylformamide (DMF: open stars, εr = 37), 2-nitroanisole (NA: open diamonds, εr = 44), dimethyl sulfoxide (DMSO: open right-pointing triangles, εr = 46), propylene carbonate (PC: open left-pointing triangles, εr = 65), ethylene carbonate–propylene carbonate mixture (EC–PC: open inverted triangles, εr = 86), 2-cyanopyridine (CPY: open triangles, εr = 90), formamide (F: open squares, εr = 108), and N-methylformamide (NMF: open circles, εr = 182). The values of ηsp are estimated from Fig. 2 of ref. 174. | ||
(I) For P(M-PCP) in CPY, EC–PC, PC, DMSO, DMF, and ACN solutions, ηsp followed the scalings of ηsp ∝ c0.5 and ηsp ∝ c1.0 at high and low c. The transition occurred at ηsp ∼ 1 and the exponents matched Dobrynin et al.'s predictions for the semidilute unentangled and dilute regimes. The value of ηsp for a given c increased with increasing εr, indicating that the number of dissociated counterions increased with increasing εr, as discussed in Section 3.6.2.
(II) For NA, AC, and CH solutions, ηsp displayed a single power-law dependence with respect to c over the measured c range. The power-law fit to the measured ηsp yielded the scaling of ηsp ∝ c0.55. Interestingly, the estimated power-law exponent was smaller than unity, although the tested solutions fell under the dilute concentration regime. These results suggest that the conformation of the P(M-PCP) chains depends on the concentration,56,146,444 or the influence of interchain repulsion345,346 on the solution viscosity.
(III) In the CP solutions, the measured ηsp exhibited two different power-law trends in the dilute regime. For c < 7 × 10−3 M, ηsp ∝ c1, consistent with the prediction for dilute solutions. However, at higher c, the power-law exponent became smaller. The observed trend of ηsp against c might be explained by considering the conformation change of polyelectrolytes in the dilute regime.146 Alternatively, the presence of a small amount of residual salt in the solvent could account for the decrease in the exponent at higher polymer concentrations.
(IV) In TEP solutions with the lowest εr, the value of ηsp decreased linearly with the decreasing c, showing a similar trend of ηsp for neutral polymer solutions.
(V) In F and NMF solutions with the highest εr, the value of ηsp decreased linearly with the decreasing c, suggesting that the P(M-PCP) chain behaves as a neutral polymer in F and NMF even though εr was higher than those in the other solvents. Waigh et al.444 confirmed the observed neutral polymer-like behaviour of the P(M-PCP) in NMF from its SAXS profile where no peak was detected.
For group (IV) and group (V) solvents, the value of ηsp increased linearly with increasing c, consistent with the behaviour for dilute polymer solutions. Indeed, most of the reported ηsp were smaller than one, proving that the solutions fall under the dilute regime. For TEP which has the lowest εr of the solvents studied, the measured values of ηsp were significantly smaller than those in group (I) solvents and suggest a strong counterion condensation. On the other hand, the observed neutral polymer-like behaviour of P(M-PCP) in the F and NMF is rather counter intuitive since the amount of dissociated counterions is predicted to be large in the high εr, i.e., a more stretched polyelectrolyte-like configuration of P(M-PCP) chains is expected in the F and NMF solvent.13 The apparent strong condensation in F and NMF can be recovered when the solvent contains salt impurities or alters its dielectric constant by the polymer addition. However, we showed in Section 3.6.2 that both effects could not explain the observed degree of chain shrinkage in NMF.
Jousset et al.174 reported a large increase in the specific viscosity of P(M-PCP) in NMF with increasing temperature, shown in Fig. 15. Their experiment produced two striking features: First, the overlap concentration, estimated as the point at which ηsp ≃ 1, increases by roughly an order of magnitude as the temperature increases from 40 °C to 50 °C, corresponding to a doubling of the end-to-end distance of the chains. This large change contrasts with the weak variation of the viscosity in the T = 25–40 °C and T = 50–60 °C intervals, suggesting a sharp transition. The observed transition can be explained by considering an increase in the charge fraction on the P(M-PCP) chain. However, several researchers445,446 reported a significant reduction of the dielectric constant εr of NMF with the increasing temperature, indicating an increase in the Bjerrum length of NMF. This should lower the charge density of the polyelectrolyte, which clearly did not occur in Fig. 15.
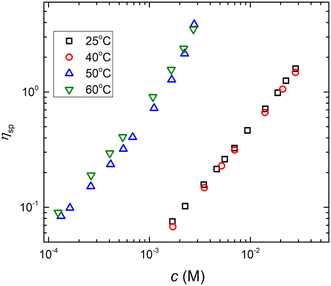 | ||
| Fig. 15 Temperature induced transition for P(M-PCP) in NMF solution. Specific viscosity ηsp is plotted as a function of monomer concentration c for P(M-PCP) in NMF at different temperatures, as indicated in the legends. Data are from ref. 174. | ||
As electrostatics alone does not seem to explain the drastic viscosity change in Fig. 15, it seems plausible that the transition may be driven by the change in solvent quality. In fact, poly(methyl methacrylate), whose chemical structure of the main chain is similar to that of P(M-PCP), is insoluble in F.174 Note that this is different from the solvent quality collapse observed for hydrophobic polyelectrolytes,147,447 as these systems display polyelectrolyte behaviour (e.g., a sub-linear exponent of ηsp with concentration and a peak in their scattering function) even in the poor solvent regime.341,448,449 It therefore appears that stronger excluded volume effects enable higher counterion dissociation and the emergence of polyelectrolyte behaviour. While it is known that solvation can influence the conformation of polyelectrolyte chains and the counterion distribution around them,450–454 the exact mechanism that leads to this sharp transition remains unclear and deserves further investigation.
The transition between polyelectrolyte behaviour and ionomer behaviour455 can be induced by varying the solvent, counterions, or charge density. It seems clear that the solvent permittivity as well as solvation of counterions,181,183,459,461 polymer backbone462 and ionic side groups184 play a role in the transition. Generally, it is observed that high solvent permittivity and good solvation of the counterions and ionic groups promote polyelectrolyte behaviour.170,459 For example, Ono et al.170 showed that an ionic polymer with large organic counterions behaved as a polyelectrolyte in non-polar media with low permittivity (εr = 5–9). A theoretical framework for the balance of dipolar attractions and electrostatic repulsion has been developed,7,463 but understanding the influence of solvation remains a challenge. For example, it has been suggested that poor solvation of ions suppresses counterion dissociation,183,461 but models to quantify these effects have not been developed. The available datasets appear to be insufficient to test simple models to quantify solvation interactions such as the use of Hansen solubility parameters. Some highly charged polyelectrolytes in low permittivity solvents (e.g. PC4-TSFI in THF56 or PAA in dioxane195,464,465) display neutral polymer behaviour, indicating that despite the large density of condensed counterions, the dipolar attraction is not significant, the reason for this is not clear to us. Analogous transitions to this polyelectrolyte-to-ionomer crossover are observed in polymer gels, for which more systematic studies on the influence of solvent parameters have been published.466–477 Finally, we note that for highly charged polyelectrolytes in intermediate or low dielectric constant solvents, an ionomer-like regime, where chains are collapsed due to dipolar or charged induced attraction have been predicted,142–147 but relatively little experimental data to test those predictions exist.421
3.9 Behaviour in excess salt solutions: scaling with cs and N
Gulati et al.100 reported the solution viscosity of NaPSS in aqueous solutions as a function of polymer concentration, molar mass and added NaCl concentration. The semidilute viscosity data showed a cross-over between the high salt exponent ηsp ∝ c5/4 and ηsp ∝ c1/2 at c ≃ 10−3 M, which suggests a residual salt concentration in DI water of cs ≃ 7.4 × 10−5 M, similar to the conductometric estimate of Han et al. (2 × 10−4 M).301 Using the cs ≃ 7.4 × 10−5 M value for the residual salt, we test eqn (13) in Fig. 16 by plotting c*[1 + fc*/(2cs)]−1.5 as a function of N, where cs includes the added NaCl and the residual salt concentration. The value of f is set to 0.2.68,91,96 This plot is seen to collapse data for different added salt concentrations except for the highest one (cs = 1 M) into a single curve following a power-law of N−2, in agreement with eqn (13). For cs = 1 M, the experimental values of c* strongly deviate downwards from the other datasets, indicating that chains are more extended than expected by eqn (13). At these high salt concentrations, where the intrinsic (non-electrostatic) contributions to chain stiffness are significant and κ−1 < ξT ≃ lB, eqn (10) and (12) overpredict the cs dependence of R, and hence of c*. | ||
| Fig. 16 Overlap concentration of NaPSS in aqueous NaCl solutions, normalised according to eqn (13). Line is power-law of −2. c* are calculated using ηsp(c*) = 1 criterion using data from ref. 100. A residual salt content of cs = 7.4 × 10−5 M was assumed.100 | ||
Fig. 17(a)–(c) show the radius of gyration, the diffusion coefficient and the intrinsic viscosity of dilute PSS as a function of molar mass in 0.5 M salt solutions. The various studies considered indicated that the PSS polymer used had a low polydispersity (Mw/Mn ≲ 1.05–1.2, see Table 2). However, due to the limited data presented in these reports, the accuracy of the polydispersity estimates could not be consistently verified.
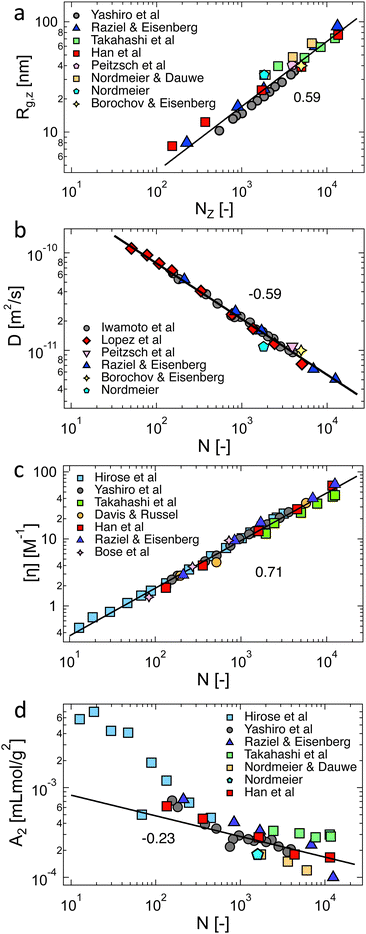 | ||
| Fig. 17 N-Dependence of (a) the radius of gyration, (b) the diffusion coefficient, (c) the intrinsic viscosity, and (d) the second virial coefficient of PSS in 0.5 M salt solution. Data are from ref. 19, 105–107, 193, 301 and 472–479, see ref. 19 for a discussion of D and [η] data. Davis and Rusell's479 values are interpolated to cs = 0.5 M. Lines for plots (a)–(c) are best-fit power laws (Rg = 0.3Nz0.59 [nm], D = 1.1 × 10−9N−0.59 [m2 s−1], [η] = 0.07N0.71 [M−1]). The line for A2 is the scaling prediction for neutral polymers in good solvents. Analogous plots for polystyrene in toluene and cyclohexane are given in the ESI† (Section S7). | ||
| Authors | M w/Mn | Ref. |
|---|---|---|
| a M z /Mw, where Mz is the z-averaged molar mass. For samples where no polydispersity is given, we assume Mz/Mw = 1.05, corresponding to sharp molar mass distribution. For samples where Mw/Mn is reported, we estimate Mz by assuming a Schulz distribution. | ||
| Bose et al. | <1.1 | 478 |
| Borochov and Eisenberg | — | 476 |
| Davis et al. | 1.05–1.05 | 479 |
| Han et al. | 1.04–1.19 | 301 |
| Hirose et al. | 1.01–1.1a | 105 |
| Iwamoto et al. | 1.01–1.1a | 105 and 106 |
| Lopez et al. | 1.04–1.09 | 19 and 100 |
| Nordmeier | ≃1.2 | 472 |
| Nordmeier and Daue | ≃1.2 | 473 |
| Peitz < 1.1 | <1.1 | 477 |
| Raziel and Eisenberg | — | 475 |
| Takahashi et al. | — | 193 |
| Yashiro et al. | 1.01–1.1a | 105 and 107 |
For experiments that use static light scattering for the determination of Rg, Mw or A2, only studies using refractive index increment measured at constant chemical potential are included.480,481 The scaling exponents observed are close to those of neutral polymers in good solvent, in agreement with the scaling theory predictions for any polyelectrolyte regardless of solvent quality.9,88,89 The Rg data display considerably more scatter than either D or [η], perhaps in part due to the larger influence of polydispersity on Rg values. The N-exponent for [η] (γη) is theoretically related to those for Rg (γR) and D (γD) as:86
| γη = 2γR − γD − 1. | (44) |
Data for the second virial coefficient are shown in Fig. 17(d). The results are from static light scattering measurements except for Hirose et al.'s dataset, where A2 values are measured from sedimentation equilibrium.105 The data are highly scattered, and it is therefore not easy to draw quantitative conclusions from them. For reference, we plot the theoretical polymer in a good solvent scaling prediction (A2 ∼ N−0.23), which is approximately obeyed for an order of magnitude in N. For N ≲ 100, a crossover to A2 ∝ N−0.8 is observed for the dataset of Hirose et al. Datasets for NaPSS by other groups in this range are not available to check whether this cross-over is the result of experimental error. For comparison, polystyrene in toluene follows a power-law of A2 ∼ N−0.27 for N ≳ 20. Deviations from a stronger power-law were observed only for oligomers (N ≃ 5–10), as shown in Fig. S19 (ESI†). This phenomenon has been assigned to the influence of chain ends.482 Data for short poly(2-acrylamido-2-methylpropanesulfonate) (NaPAMS) chains by Norisuye and co-workers109,112 reported a similar behaviour to that for the short NaPSS chains in Fig. 17(d). On the other hand, sodium hyaluronate110,483 and xanthan484,485 with a small number of Kuhn segments per chain did not display such large exponents. This implies that the presence of chain ends, rather than a transition to rod-like conformations, is the likely cause of the upturn at low N. To gain more clarity on these unusual observations, additional experimental investigations into the second virial coefficient of short flexible chains are needed. Exponents for the N-dependence of A2 in excess salt solution are found to be consistently larger than the scaling prediction (−0.23) for flexible and semiflexible polyelectrolytes. Data for NaPAMS, sodium poly(3-methacyloyloxypropane-1sulfonate) (NaPOMS), xanthan and DNA are listed in Table 3.
| System | Exponent | Ref. |
|---|---|---|
| a Data in the high N limit, see more details in Section S7 of the ESI. | ||
| Xanthan/0.1 M NaCl | −0.19 | 484 and 485 |
| NaHy/0.2 M NaCl | −0.27 | 110 and 483 |
| NaPAMS/0.1 M NaCl | −0.39 | 109 and 112 |
| NaPAMS/0.5 M NaCla | −0.31 | 109 and 112 |
| NaPOMS/0.01–5 M NaCl | −(0.27 to 0.3) | 486 |
| PS/toluene | −0.26 | 487–489 |
 | ||
| Fig. 18 Dimensions of PSS chain under different theta conditions. (a) Square of radius of gyration measured by light scattering divided by z-averaged molar mass, see Table 2 for polydispersities. Data are from ref. 105, 193, 472 and 475. The dashed line is calculated from Wang and Yu's496RH data for NaPSS with 127 < N < 5300 in 3.1 M KCl solution assuming Rg/RH = 1.32. (b) Intrinsic viscosity at the theta point divided by the square root of a weight-averaged degree of polymerisation. Data are from ref. 105, 193, 475 and 497. For Pavlov's data, N was estimated from the intrinsic viscosities in 0.2 M NaCl using an MHS relation from ref. 19. | ||
In Fig. 18(b), the intrinsic viscosity at the theta point is plotted. The [η]/N1/2 ratio is seen to be approximately independent of N for N ≳ 200. The intrinsic viscosity depends on the polydispersity more weakly than the Rg data considered in part a, and therefore may offer a more reliable estimate of the theta dimensions of the PSS chains. Data were obtained from ref. 105, 193, 475 and 497. For Pavlov et al.'s samples, the degree of polymerisation was calculated from the intrinsic viscosity in 0.2 M NaCl, using an Mark-Houwink-Sakurada (MHS) equation from ref. 19. These values agree well with Pavlov et al.'s estimates from sedimentation-diffusion using the Svedberg relationship. The data shown in Fig. 18(b) display reasonable consistency around a value of [η]/N1/2 ≃ 0.058 M−1, indicated by the dashed line. Using a value for the Flory viscosity factor of Φ = 6, see Section 3.12, the intrinsic viscosities correspond to Rg2/N ≃ 6.4 ± 0.3 Å2, in reasonable agreement with the Rg and RH data considered in part a. Based on the Rg, RH and [η] data, we judge the Rg2/N ≃ 6–10 Å2 estimate to be correct and consider Nordmeier's data as an outlier. The theta dimensions of PSS are important for the discussion on the excluded volume screening in semidilute solutions.209,391 The data of ref. 192, 195, 472 and 498 show that θ of polyelectrolytes depends linearly on the concentration of added salt, see Fig. S4 (ESI†).
The application of the variational theory to the Rg data in Fig. 21(a) was discussed in ref. 499. Eqn (25) requires three fit parameters: lK,0, f, and χ0. The Kuhn length is easily obtained as lK,0 = Rg2/Nz at the theta point. Leaving f and χ0 as free parameters, a reasonable agreement (≲30% deviation from the experimental results) was found using f = 0.24 and χ0 ≃ 0.59. The fitted values appear quite plausible: f = 0.24 is nearly identical to an estimate using ion-selective electrodes501 and the value of χ0 > 1/2 is expected due to the hydrophobic nature of the backbone. Fitting the variational theory to NaPSS data103 yielded values of f that were consistent with independent estimates from conductivity,68 but values of χ0 < 1/2, which are incompatible with the hydrophobic nature of the PSS backbone.105,193
The second virial coefficient of NaPA, plotted in Fig. 19(b), followed a power-law of A2 ∼ cs−3/5, which agreed with the scaling prediction in the high excluded volume limit (A2 ∼ Rg3/M2) until cs ≃ 0.2 M. For higher salt concentrations, as the polymer approached the theta salt conditions, a steeper decrease of A2 with cs was observed. Near the theta salt condition, a different scaling applies, and A2 does not vary as Rg3/M2. A clear example of this can be seen in Fig. 20, which compares the radius of gyration and second virial coefficients of the Li and Na salts of DNA in excess LiCl and NaCl. The LiDNA/LiCl system approaches the theta point (A2 = 0) at cs ≃ 5 M, while the NaDNA/NaCl system remains in the good solvent regime (A2 > 0) over the entire cS range considered. While Rg of the two polymers is nearly identical, the Li system shows a sharp drop in A2 as the theta point is approached. A review of second virial coefficient data for flexible,486,504–509 semiflexible,109,296,359,360,476,510–516 and rigid polyelectrolytes120,517 revealed that A2 does not follow a universal power-law with cs. Exponents both larger and smaller than −0.6 are observed in the low cs region (i.e. well below the theta salt concentration).
 | ||
Fig. 19 (a) Radius of gyration and hydrodynamic radius of sodium polyacrylate (Nw ≃ 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Nw/Nn ≃ 1.2) as a function of added NaCl concentration. Lines are the best-fit power-law lines: Rg ∝ cs−0.25 and RH ∝ cs−0.21. Eqn (12) indicates R ∝ cs−1/5. (b) Second virial coefficient for the same polymer. cs = 1.5 M corresponds to the theta condition, where A2 = 0. Data are from ref. 499. 000, Nw/Nn ≃ 1.2) as a function of added NaCl concentration. Lines are the best-fit power-law lines: Rg ∝ cs−0.25 and RH ∝ cs−0.21. Eqn (12) indicates R ∝ cs−1/5. (b) Second virial coefficient for the same polymer. cs = 1.5 M corresponds to the theta condition, where A2 = 0. Data are from ref. 499. | ||
 | ||
| Fig. 20 (a) Radius of gyration for the same systems as a function of added salt. The line is the best-fit power-law with the exponent indicated in the figure. Note that the weak exponent of Rg with cs arises due to the high rigidity of double-stranded DNA. (b) Second virial coefficient of NaDNA in aqueous NaCl solutions and LiDNA in aqueous LiCl solutions as a function of the added salt concentration. Line is the best-fit power-law to sodium data, with the exponent indicated in the figure. Data are from ref. 502 and 503. | ||
The ideal behaviour of PAA at cs = 1.5 M is illustrated in Fig. 21, which shows the ratios Rg2/Nz and RH2/Nw are independent of the degree of polymerisation, as expected for Gaussian chains. In 0.1 M NaCl solution, the chains adopt expanded coil conformations and Rg2/N ∼ RH2/N ∝ N0.2, indicated by the dashed lines. We note that the ratio ρ = Rg/RH is known to increase with excluded volume, which could explain the higher exponent observed for the Rg data compared to RH. However, the scatter in the results does not allow for a meaningful conclusion on this aspect. The data suggest that excluded volume influences Rg for shorter chain lengths more than it does RH. Weaker exponents for the Rg and RH dependence on cs are observed for published literature on polystyrene sulfonate193,472,475–477,500 and other systems including carboxymethyl cellulose,359,360,510 NaPAMS,518 and NaPOMS.486
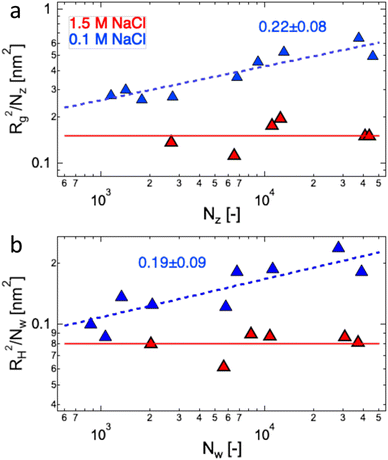 | ||
| Fig. 21 Square of (a) radius of gyration and (b) hydrodynamic radius normalised by degree of polymerisation for sodium polyacrylate at the theta salt condition (1.5 M NaCl) and below the theta salt condition (0.1 M), corresponding to the ‘good solvent’ universality class (expected exponent of 0.18). Errors in exponents are two standard deviations. Data are from ref. 499. | ||
The Huggins and Kraemers coefficients of polyelectrolytes are discussed in the ESI† (Section S5). Briefly, an analysis of literature data111,141,210,299,416,531–536 revealed that: (1) increasing the charge fraction leads to a large increase in kH in salt-free solutions and a modest decrease in kH for solutions in excess salt; (2) the Huggins coefficient shows a non-monotonic dependence on the added salt concentration; (3) kH decreases with increasing N until it reaches a constant value, which appeared to be similar to that of neutral polymers; (4) introducing hydrophobic groups leads to a large increase in kH if the added salt concentration is sufficiently high.
3.10 Behaviour in excess salt solutions: scaling with the charge density
The cs-dependence of the intrinsic viscosity of NaPA at 10% (i = 0.1) and full (i = 1) neutralisation is shown in Fig. 22(a). We plot Flory and Osterheld's data195 for NaPA with N ≃ 8170 and combine it with interpolated values based on Noda et al.'s537 and Kato et al.'s538 results. Values extrapolated from Takahashi et al.'s data,193 which cover the 160 < N < 5300 range, are also included. These results are taken at slightly different conditions (temperature and co-ion), as shown in the legend of Fig. 22(a). For both degrees of neutralisation, the experimental data agree well with the theoretical prediction in the high cs limit of the scaling and variational theories (eqn (31) and (26), [η] ∝ cs−3/5). The data at the highest cs for both degrees of neutralisation deviate downwards from the trend as the samples approach the theta points.192,539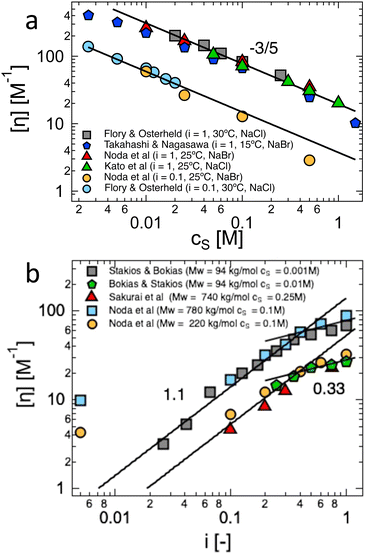 | ||
| Fig. 22 (a) Dependence of intrinsic viscosity of polyacrylic acid on added salt concentration for N ≃ 8170 (see text) for 10% ionisation (i = 0.1) and full ionisation (i = 1). Power-law of −3/5 is the scaling prediction. (b) Intrinsic viscosity vs. degree of neutralisation i. Exponents are best fit values. Data are from ref. 195, 537 and 540–543. Results reported by Bokias and Stakios542 were obtained by isoionic dilution. | ||
The dependence of the intrinsic viscosity on the degree of ionisation (i) of polyacrylic acid is plotted in Fig. 22(b). The results show two clear power-laws. For 0.02 < i < 0.3, [η] increases as i1.1. In this regime, the degree of ionisation is proportional to the fraction of monomers bearing a dissociated counterion (f). For higher degrees of ionisation, where counterion condensation sets in,11 a weaker exponent is observed. Considering f ∝ i0.3 for i > 0.3,544 the intrinsic viscosity data for i > 0.02 are consistent with a single power-law [η] ∝ f1.1 for 0.02 < i < 1. Data for different degrees of polymerisation and added salt concentrations show the same scaling exponent, which indicates that the exponent is independent of the number of electrostatic blobs in a chain. Matsumoto and Eguchi's416 intrinsic viscosity data, discussed in the ESI† (Section S4), display a weaker scaling of [η] ∝ f0.7.
At very low degrees of ionisation, the [η] ∝ f1.1 scaling breaks down as the polymer chains approach their neutral polymer dimensions. The cross-over between [η] ∼ f0 to [η] ∼ f1.1 can in principle be used to obtain an estimate of the molar mass of the electrostatic blob, but we have been unable to get consistent values from this. Similar behaviour can be observed in the data of Matsumoto and Eguchi for polyvinyl sulfate,416 as shown in Fig. S8 (ESI†). These results suggest a deficiency in the electrostatic blob model.
The [η] ∝ f1.1 scaling implies R ∼ f0.36. This exponent differs from the scaling theory exponents for good solvents (0.46), θ solvent (0.47) and poor solvent (0.73). Since NaPA has a θ point in 1.5 M NaBr, we infer water to be a poor solvent for its backbone. However, without an estimate for the size of the thermal blob, it remains ambiguous whether the behavior aligns more closely with that of a poor solvent or a θ solvent. The variational theory prediction of R ∝ f0.4 (eqn (25)) is in closer agreement with the experimental results. Note that for PAA with lK,0 ≃ 4 nm, there is more than one dissociated charge per bare Kuhn segment if i > 0.06 (assuming f ≃ i/2).11 Under these conditions, the scaling theory indicates that the electrostatic blob concept should not apply. Interestingly, no change in the exponent is observed across i = 0.12. Thus, it is possible that the electrostatic blobs are significantly larger than expected by the scaling theory, see ref. 100.
Reed et al. reported the dependence of the radius of gyration of sodium polyacrylate-co-acrylamide random co-polymers as a function of the charged group fraction (δ).545,546 In ref. 545, the refractive index increment is reported to be independent of the added salt content, in contrast to other reports for NaPA. As we only consider Rg data, which are not affected by the choice of dn/dc, we do not discuss this further. The polymer with the highest sodium acrylate content contained a fraction of δ = 0.27 charged monomers. In this regime, f ≃ δ/2 is expected.11 The radius of gyration of the co-polymers is plotted as a function of the fraction of ionisable units in Fig. 23. The exponents observed (Rg ∼ δ0.3 ∼ f0.3) are relatively close to the relationship deduced from the intrinsic viscosity data shown in Fig. 22(b). For both added salt concentrations considered, the best fit exponent is lower than the variational theory prediction by ≃0.1. The scaling theory indicates the exponent to be ≃50% larger than the experimentally observed exponent.
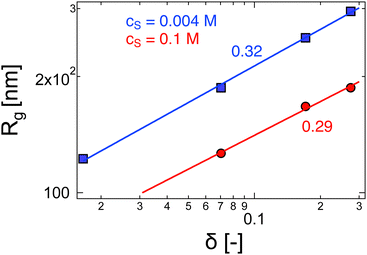 | ||
| Fig. 23 Dependence of the radius of gyration on fraction of ionic groups (δ) for polyacrylate-co-acrylamide co-polymers for two concentrations of added NaCl. Lines are best-fit power-laws, with the exponents indicated by the numbers. Data are from ref. 545 and 546. | ||
The variation of the radius of gyration on dielectric constant for quaternized PVP polyelectrolytes in different salt solutions is considered in Fig. 24, based on the results of Beer et al.103 The solvents considered differ in the quality of the solvent backbone, which may explain the scatter in the data.415,547–550 Data for the various added salt concentrations collapse well onto a single curve when normalised by cs1/5, as expected by the variational (eqn (25)) and the scaling theories (eqn (6) and (12)). Assuming Manning condensation holds (f ∝ ε), the variational theory (eqn (26)) indicates Rgcs1/5 ∝ ε0.2, which is weaker than the experimentally observed exponent. The scaling theory indicates Rgcs1/5 ∝ ε0.32 under good solvent conditions and Rgcs1/5 ∝ ε0.47 under poor solvent conditions. The poor solvent exponent matches the experimental value. The variational theory could describe the cs and ε dependence of Rg for these results, but the fitted f dependent on the solvent permittivity in an unusual way (f ∼ 0.02(ε − 16)1/2).103
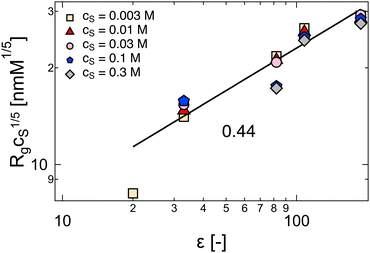 | ||
| Fig. 24 Dependence of radius of gyration multiplied by cs1/5 on the solvent dielectric constant. Data are from ref. 103. The line is the scaling prediction for good solvent. | ||
The scaling of other parameters with the charge fraction, particularly A2, is of interest to understand the nature of the electrostatic excluded volume, but the available data551–554 do not allow for any systematic conclusions to be drawn, particularly in the low charge fraction limit. The Huggins coefficient of a PVA polyelectrolyte in excess added salt was shown to be a decreasing function of charge fraction,416 see Fig. S8 (ESI†). This contrasts with the behaviour at low cs, where charged polymers display much higher kH values than neutral ones.
3.11 The expanded worm-like chain model
The expanded worm-like chain model has been used to explain the conformational and transport properties of polyelectrolytes in dilute solution in a large number of studies.105–112,118,121,477,479,483,545,555–557 Reliable fitting of the model to experimental data is made difficult by the fact that both the persistence length and the excluded volume are a function of solvent's ionic strength. Robust methods for obtaining the ideal conformation, analogous to, for example, the Stockmayer–Fixman558 plot for flexible polymers or the Bohdanecky–Bushin559,560 plot for polysaccharides, do not exist for flexible polyelectrolytes. This means that datasets covering degrees of polymerisation from a few Kuhn segments to several hundreds are usually necessary for reliable extraction of lp and![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) , the excluded volume strength. Approaches which estimate
, the excluded volume strength. Approaches which estimate ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) from A2 are in our view not reliable, because the interpenetration function is not a unique function of the excluded volume, see ref. 482 and 561.
from A2 are in our view not reliable, because the interpenetration function is not a unique function of the excluded volume, see ref. 482 and 561.
Norisuye and co-workers carried out extensive experimental light scattering and viscosimetric investigations of the conformational and hydrodynamic properties of three polyelectrolytes: NaPSS, NaPAMS and NaHy110,111,483,557 as a function of molar mass and added salt concentration. These experimental reports, in our opinion, constitute the ‘gold standard’ against which theories of dilute polyelectrolytes can be tested.562 Here, we focused on experimental work based on measurements of Rg, D and [η] instead of lP data obtained from force-extension curves, as the latter method was shown to underestimate the persistence length of neutral flexible polymers.563 The authors were able to extract the excluded volume strength and persistence length for their systems without making assumptions about the ionic strength dependence of either parameter.
An example of Norisuye's and co-workers procedure is shown in Fig. 25, which plots the intrinsic viscosity of sodium hyaluronate in 0.2 M NaCl solution as a function of degree of polymerisation, where we define the ‘monomer’ as having a molar mass of 201.5 g mol−1, corresponding to a length of ≃0.5 nm.569 The data display [η] ∝ N for short chains and [η] ∝ N0.78 at high N after a broad cross-over. The intrinsic viscosity of a worm-like chain without excluded volume, shown by the dashed line, is calculated using the procedure from ref. 384 for low molar masses and ref. 148 for higher ones. The values of lp = 4.2 nm, d = 1 nm and ML = 400 g mol−1 nm−1 are taken from ref. 483. This model provides an accurate fit to the data for N ≲ 80, but underpredicts the data for higher molar masses. As electrostatics are short-ranged, the chain conformation can be understood in terms of a ‘thermal blob’ incorporating the influence of electrostatic excluded volume.100 For NaHy in 0.2 M, nT ≃ 100, ξT,el ≃ 20 nm. Here, ξT,el refers to a thermal blob incorporating both the effects of ionic and non-ionic excluded volume, and the former is presumed to be sufficiently short-ranged. The full line shows the calculation of [η] including the excluded volume effects using ![[B with combining overline]](https://www.rsc.org/images/entities/i_char_0042_0305.gif) = 4.0 nm, as detailed in ref. 483.
= 4.0 nm, as detailed in ref. 483.
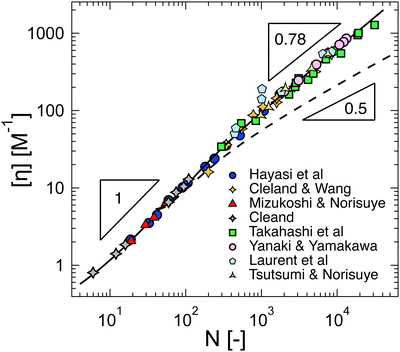 | ||
Fig. 25 Intrinsic viscosity of NaHy in 0.2 M NaCl. Full line is the fit to the WLC model with d = 1 nm, ML = 400 g mol−1 nm−1 and lp = 4.2 nm ![[B with combining overline]](https://www.rsc.org/images/entities/i_char_0042_0305.gif) = 4.0 nm, following ref. 483. The dashed line is the WLC model with the same parameters as the full line but = 4.0 nm, following ref. 483. The dashed line is the WLC model with the same parameters as the full line but ![[B with combining overline]](https://www.rsc.org/images/entities/i_char_0042_0305.gif) = 0. Data are from ref. 111, 288, 483 and 564–568. The points by Mizukoshi and Norisuye are extrapolated to cs = 0.2 M from their data in 0.02 and 0.1 M NaCl. Data from Foussiac et al. were interpolated to cs = 0.2 M. = 0. Data are from ref. 111, 288, 483 and 564–568. The points by Mizukoshi and Norisuye are extrapolated to cs = 0.2 M from their data in 0.02 and 0.1 M NaCl. Data from Foussiac et al. were interpolated to cs = 0.2 M. | ||
The fitted values of lp and the excluded volume strength for the three aforementioned systems are plotted as functions of the Debye screening length in Fig. 26. The excluded volume strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) shows a linear dependence on κ−1, with a cs-independent term
shows a linear dependence on κ−1, with a cs-independent term 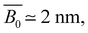 which is close to the expected value of
which is close to the expected value of  for NaHy and NaPAMS. The electrostatic part of the excluded volume is
for NaHy and NaPAMS. The electrostatic part of the excluded volume is 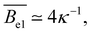 corresponding to R(y) = 2 in eqn (24). This does not agree with the theories of Fixman and Skolnik119 and matches the estimates of Odijk132 and Dobrynin et al.89 for
corresponding to R(y) = 2 in eqn (24). This does not agree with the theories of Fixman and Skolnik119 and matches the estimates of Odijk132 and Dobrynin et al.89 for 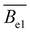 up to a pre-factor.
up to a pre-factor.
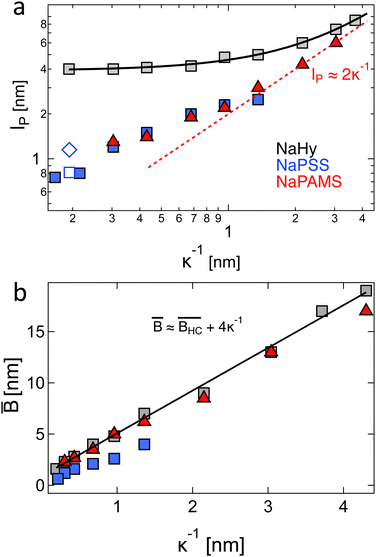 | ||
Fig. 26 (a) Persistence length for NaPSS, NaPAMS and NaHy as a function of the solvent Debye screening length. The red dashed line shows lp ≃ lp,el ≃ 2κ−1 in the low-salt limit for the two flexible systems. Full black line is lp = 4 + 0.7(κ−1)1.44 for NaHy. Hollow diamond and hollow square are calculated from Rg2/N values from Wang and Yu's496 and Takahashi et al.'s540 data in 3.1 M KCl, respectively. (b) Total excluded volume strength for the same three polyelectrolyte systems. Black line is fit to a linear function, where the intercept 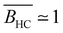 nm can be identified with the hard-core repulsion term in nm can be identified with the hard-core repulsion term in ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . Data are from ref. 105–112 and 483. . Data are from ref. 105–112 and 483. | ||
The persistence length follows a non-monotonic dependence with κ−1 and appears to approach a linear relationship in the high κ−1 limit, as expected by various theories,89 but in disagreement with the OSF model.122,123,570 Note that the scaling theory predicts lp = rscr/2 ≃ 2κ−1 for NaPSS, where we have assumed f = 0.2, in good agreement with the observed results. For NaHy, a semiflexible polylelectrolyte, there exists a region for high cs (low κ−1), where the persistence length is virtually independent of the added salt concentration because the non-electrostatic term dominates in eqn (20). In this regime, changes in chain dimensions with added salt arise from the decrease in excluded volume with increasing cs. For sufficiently rigid polyelectrolytes, such as xanthan gum, lp,0 is of the order of or larger than the contour length, and the chain dimensions are independent of cs.484,485,571
In the high-N limit, eqn (14)–(18) for the chain size of a polyelectrolyte reduce to:
R ∝ N0.59lp1/5![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) 1/5. 1/5. | (45) |
![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) ∝ κ−1 and lp ∝ κ−1 are introduced into eqn (45), Dobrynin et al.'s prediction of R ∝ cs−1/5 (eqn (12) for 2cs ≫ fcp) is recovered. A second regime is expected where lp ≃ lp,0 and
∝ κ−1 and lp ∝ κ−1 are introduced into eqn (45), Dobrynin et al.'s prediction of R ∝ cs−1/5 (eqn (12) for 2cs ≫ fcp) is recovered. A second regime is expected where lp ≃ lp,0 and 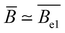 . Here, the cs dependence of the chain size is expected to approach R ∝ cs−1/10, which is consistent with the weak power-laws observed for the intrinsic viscosity of polysaccharides in the high cs regime.111,404,406 In terms of the scaling theory, this regime is analogous to rscr < ξel, where no electrostatic stiffening of the chain is expected, but electrostatic excluded volume results in chain expansion relative to the non-ionic dimensions. At sufficiently high cs, we anticipate a regime characterized by R ∝ c0s, where electrostatics does not perturb chain conformation under certain conditions, as discussed below.
. Here, the cs dependence of the chain size is expected to approach R ∝ cs−1/10, which is consistent with the weak power-laws observed for the intrinsic viscosity of polysaccharides in the high cs regime.111,404,406 In terms of the scaling theory, this regime is analogous to rscr < ξel, where no electrostatic stiffening of the chain is expected, but electrostatic excluded volume results in chain expansion relative to the non-ionic dimensions. At sufficiently high cs, we anticipate a regime characterized by R ∝ c0s, where electrostatics does not perturb chain conformation under certain conditions, as discussed below.
For strongly charged polyelectrolytes, it is possible to combine the effects of electrostatic and non-electrostatic excluded volume into a single parameter (i.e.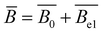 ). This approximation has been found to agree with experiments under certain conditions. It is then possible to define an effective thermal blob size:
). This approximation has been found to agree with experiments under certain conditions. It is then possible to define an effective thermal blob size:
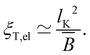 | (46) |
For sodium hyaluronate, a semiflexible polyelectrolyte, the parameters plotted in Fig. 26, setting lK = 2lp, give ξT,el ≃ 16/κ−1 for cs ≳ 0.2 M. For cs = 0.2 M, this corresponds to an effective blob size containing ≃8 Kuhn segments, each with a molar mass of ≃3.2 kg mol−1. For NaHy, the WLC model therefore indicates R ∼ c0s when Mw ≲ 26 kg mol−1 and cs ≳ 0.2 M, which is qualitatively consistent with the intrinsic viscosity data from Hayashi et al.111 However, without more detailed conformational data, it is not possible to clearly test this result. For flexible polyelectrolytes, lp contains a non-negligible electrostatic contribution over the entire cs range studied and it is therefore not clear if the R ∝ c0s applies at any added salt concentration. Most literature data for the static and hydrodynamic sizes of polyelectrolyte chains display exponents which do not clearly fall into the three regimes discussed above (R ∝ cs−0.2, R ∝ cs−0.1 and R ∝ cs0), probably because the cross-over between these are quite broad.
The expanded worm-like model conceptualizes polyelectrolytes as neutral polymers with persistence length and thermal blob size dependent on salt concentration (cs). This implies that there is a single lengthscale beyond which excluded volume perturbs the chain conformation. However, for weakly charged polyelectrolytes with large electrostatic blob sizes, two distinct length scales emerge for the onset of excluded volume effects: ξT for the intrinsic (non-electrostatic) excluded volume and rscr for the electrostatic excluded volume. For these systems, the expanded WLC model is not expected to apply.
Simulation studies on polyelectrolytes in excess salt have noted that the bond-bond orientational correlation function s(l), where l is the distance along the chain contour, follows non-exponential behaviour.28,572–574 Gubarev et al.572 found that s(l) followed a monomodal exponential decay if κ−1 < 6b (for the NaPSS/NaCl/H2O system, this would translate to cs ≳ 0.025 M) and a bimodal decay otherwise, where the short-ranged decay scaled linearly with κ−1 for high cs and the lengthscale for the second decay varied as κ−2. Non-exponential decays in s(l) were also observed for neutral polymers in good solvents.116,575,576 Several formulae have been proposed to fit the simulated results for s(l), which are sometimes interpreted as resulting from a length-scale dependent persistence length, see ref. 577 for a discussion. Quantifying the persistence length is complicated because different measurements which are equivalent for the ideal Kratky–Porod worm-like chain become different from each other when s(l) does not follow a single exponential decay.
For the EWLC model discussed above, the meaning of lp is straight-forward: it is the persistence length of the worm-like chain for a polyelectrolyte in the absence of excluded volume interactions. Yamakawa et al.'s simulation work126 showed that for non-ionic polymers with excluded volume, where s(l) follows non-exponential behaviour, the initial decay (d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[s(l)]/dl) gave the persistence length of the system. Based on a comparison of simulation data for WLCs with Debye–Huckle interactions and experimental data for NaPSS and NaHy, it was concluded that the initial decay rate in s(l) also serves as a measure of the persistence length for polyelectrolytes in excess salt.
ln[s(l)]/dl) gave the persistence length of the system. Based on a comparison of simulation data for WLCs with Debye–Huckle interactions and experimental data for NaPSS and NaHy, it was concluded that the initial decay rate in s(l) also serves as a measure of the persistence length for polyelectrolytes in excess salt.
In summary, it is not clear over what conditions the expanded WLC approach is valid for polyelectrolytes. Because s(l) cannot be measured experimentally, testing the theoretical simulation work discussed above is difficult. A theoretical derivation of form factors for such systems may allow a more rigorous comparison of experimental and simulation results.
3.12 Universal ratios
The dilute solution properties of polymers in good solvents can be characterised by a number of “universal ratios”, which, in the long N limit, are expected to take constant values independent of the chemical nature of the system. For flexible neutral polymers, these ratios have been studied and their values have been compared to theoretical predictions of renormalisation group and two-parameter theories.116,578–588 Extensive datasets are available for polystyrene and several other flexible polymers in good and theta solvents, see for example, the review of Fetters et al.589 and subsequent experimental work.487–489,531 Significantly, less attention has been paid to ionic polymers. In our view, polyelectrolytes are interesting systems to study these ratios because the range of excluded volume strengths attainable (∼κ−1) far exceeds that of neutral polymers (∼dC). Usually, five ratios are computed:579,588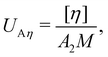 | (47) |
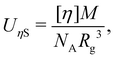 | (48) |
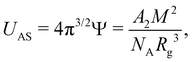 | (49) |
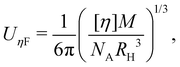 | (50) |
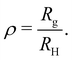 | (51) |
The second of these is related to the Fox–Flory viscosity parameter (Φ = [η]M/NAR3 ≃ UηS/63/2), and UAS is related to the well-known interpenetration function ψ (= (4π3/2)−1UAS).116,591 An additional ratio, analogous to the interpenetration function but using RH3 instead of Rg3 as the reference volume has been proposed592–594 and evaluated for polystyrene in toluene:592
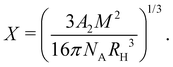 | (52) |
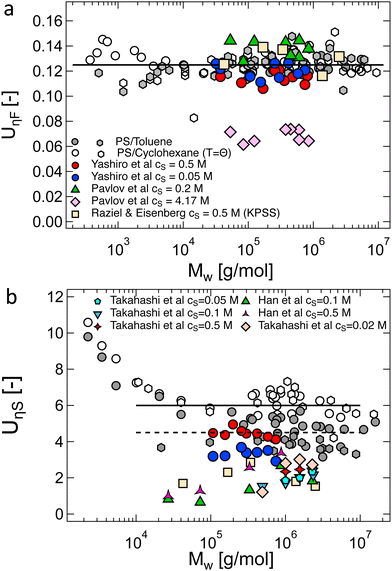 | ||
| Fig. 27 Comparison of universal ratios Uηf (top, eqn (50)) and UηS (bottom, eqn (48)) for polystyrene in good solvent (grey symbols) and theta solvent (white symbols) and NaPSS in aqueous salt solutions (other symbols). Hexagons are for interpolated values of [η] for PS. Data are from ref. 105–107, 193, 301, 475, 487–489, 497 and 590 and references listed in ref. 589. Raziel and Eisenberg's data are for KPSS in KCl solutions. (a) Full line is Uηf = 0.125. Symbols are listed in the legend. (b) Dashed and full lines in plot (a) are UηS = 6 and UηS = 4.5, respectively. Symbols are listed in the legends, see also plot (a) for symbols not listed. A plot displaying UηS over a wider molar mass range for polystyrene is included in Section S7 of the ESI.† | ||
| System | U ηF | Type | Data |
|---|---|---|---|
| PS/Tol | 0.125 ± 0.003 | F/NI (GS) | Ref. 589 and references therein |
| PS/CH | 0.129 ± 0.003 | F/NI (θ) | Ref. 589 and references therein |
| NaPSS/0.5 M NaCl | 0.114 ± 0.003 | F/I | Ref. 105–107 |
| NaPSS/0.05 M NaCl | 0.120 ± 0.004 | F/I | Ref. 105–107 |
| NaPAMS/0.05 M NaCl | 0.128 ± 0.004 | F/I | Ref. 108, 109 and 112 |
| NaPAMS/0.5 M NaCl | 0.122 ± 0.003 | F/I | Ref. 108, 109 and 112 |
| NaHy/0.2 M NaCl | 0.110 ± 0.005 | SF/I | Ref. 565 |
| PHIC/hexane | 0.115 ± 0.002 | SF/NI (GS) | Ref. 595 |
| PS stars/toluene | 0.118 ± 0.003 | F/NI (GS) | Ref. 596 and 597 |
| PS stars/cyclohexane | 0.111 ± 0.004 | F/NI (θS) | Ref. 596 and 597 |
The Fox–Flory viscosity factor for PS in good solvent takes a value of ≃25% lower than in theta solvent in the high-M limit, as indicated by the full and dashed lines shown in Fig. 27. The data for PSS display a large degree of scatter and therefore a single value for Φ cannot be determined. Studies which consider different added salt concentrations for the same PSS samples find Φ to be dependent on cs,109,193,598 a feature also observed for NaPAMS.518 The trend UηS,PS/Cycl > UηS,PS/Tol > UηS,PSS/NaCl suggests that the Flory–Fox constant decreases with increasing excluded volume strength. For Mw ≲ 2 × 104 g mol−1, the value of UηS for polystyrene shows an upturn in good and theta solvents. The data for PSS do not extend over a sufficiently broad range to check whether such ehavior also occurs. The limited data available suggest that UηS for PSS in aqueous salt solutions decreases at low Mw.
The ratio of [η] to A2M was compared as a function of molar mass for polystyrene in toluene and PSS in 0.5 M NaCl solutions, as shown in Fig. 28(a). For Mw ≳ 105 g mol−1, NaPSS and PS converge to a value of [η]/A2M ≃ 0.81. The only exception are the data from Takahashi et al.,193 which show a pronounced decrease with increasing Mw. At low molar masses, a surprising deviation was observed for Hirose et al.'s dataset,105 where [η]/A2M is seen to decrease by an order of magnitude, in contrast to PS in toluene, which shows a weak increase at low Mw. Additional studies are needed to confirm this unusual feature. As discussed above, it is possible that the large increase in A2 for low molar masses is caused by the influence of the chain ends, an effect which is observed also for polystyrene, but only for shorter oligomers.482 The data from Takahashi et al.,193 Yashiro et al.,107,109 and Han et al.301 for 0.05 M < cs < 0.1 M consistently show [η]/A2M values below those of polystyrene in toluene, even at intermediate molar masses. Understanding these differences is important because both A2M and [η]−1 are widely used as measures for the overlap concentration. For neutral polymers in good solvent, this appears to be justified but for polyelectrolytes in excess salt, the assumption appears questionable in light of the results discussed.
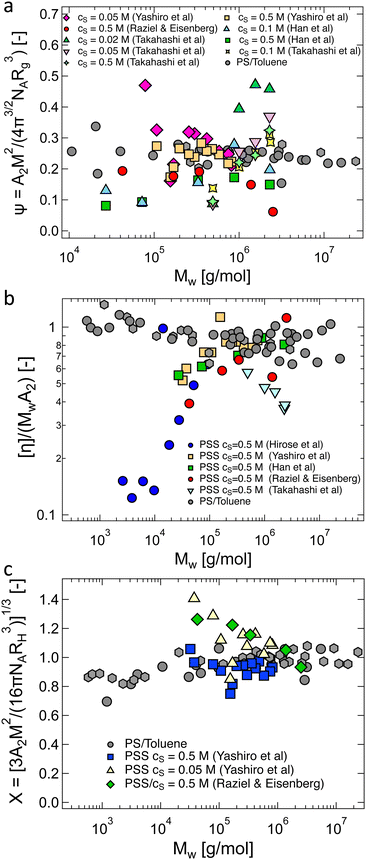 | ||
| Fig. 28 Comparison of the universal ratios UηA (a), Ψ (b) and X (c) for polystyrene in good solvent (grey symbols) and NaPSS in aqueous salt solutions (other symbols). Data are from ref. 105–107, 193, 301, 475, 487–489, 531, 590 and 599–602 and references listed in ref. 589. Raziel et al.'s data are for KPSS in KCl aqueous solution. | ||
The interpenetration function of NaPSS in NaCl and KCl solutions of different concentrations is compared to that of polystyrene in toluene in Fig. 28(b). The datasets from Norisuye and co-workers show a particularly good agreement with the polystyrene values. Despite the relatively large scatter, the value of Ψ for the PS/Tol and PSS/water/NaCl systems broadly agree. The data from Han et al. suggest a possible drop in Ψ at low molar masses, as opposed to the increase seen for PS/Tol, but this cannot be confirmed without more data for Mw < 105 g mol−1. This feature would be particularly interesting to investigate because it could provide a hint as to whether the unusual behaviour observed for [η]/A2M discussed above arises from excluded volume or hydrodynamic factors.
The ratio X (eqn (52)) is plotted as a function of Mw in Fig. 28(c). Fairly consistent results are found between the various systems, which approach a value of X ≃ 1.1 in the high Mw limit, although the number of datapoints for the PSS system is quite limited. The three lowest molar masses for Yashiro et al.'s results107 in 0.05 M NaCl suggest an increase in X with decreasing molar mass, which is the opposite of what is observed for PS/Tol. We note that other systems display values of X differently from that of polystyrene. For example, results from Murakami et al.595 for PHIC in hexane show a constant value of X ≃ 0.5 in the 66 kg mol−1 < Mw < 7200 kg mol−1 range. Sodium hyaluronate at 0.2 M NaCl also displays a somewhat lower value of X ≃ 0.8. This suggests that X may depend to some extent on backbone flexibility, meaning it should not be a universal parameter for polyelectrolytes, where flexibility is a function of cs.
The ratio ρ = Rg/RH, which is dependent on the solvent quality,603,604 can be calculated from the parameters discussed so far as:  . Considering the high M limit of the datasets in Fig. 28(b) and (c), we obtain ρ ≃ 1.5, which is in reasonable agreement with the Zimm prediction.605 A more robust estimate was made by evaluating the Rg and RH power-laws at high M, as described in Section S7 (ESI†). The results are summarised in Table 5. For NaPSS and other polyelectrolytes, ρ was observed to decrease with cs, see Fig. S25 and S26 (ESI†).
. Considering the high M limit of the datasets in Fig. 28(b) and (c), we obtain ρ ≃ 1.5, which is in reasonable agreement with the Zimm prediction.605 A more robust estimate was made by evaluating the Rg and RH power-laws at high M, as described in Section S7 (ESI†). The results are summarised in Table 5. For NaPSS and other polyelectrolytes, ρ was observed to decrease with cs, see Fig. S25 and S26 (ESI†).
A comparison of the ‘universal ratios’ of flexible neutral polymers with those of a flexible polyelectrolyte shows many similarities and also significant differences between ionic and non-ionic polymers. The only truly universal ratio appears to be UηF, which takes a constant value for all systems considered over a very wide molar mass range and for different solvent qualities, see Table 4. In general, we observe the largest discrepancies for ratios which combine excluded volume or conformational parameters with hydrodynamic parameters, e.g. UAη or Φ. In contrast, parameters combining only hydrodynamic parameters (UηF) or conformational/thermodynamic parameters (Ψ) display closer agreement between neutral polymers and polyelectrolytes.
3.13 Scattering properties of polyelectrolyte solutions
Small-angle scattering techniques are among the most powerful experimental methods for investigating the structure of polymer solutions.606 An overview of the scattering properties of polyelectrolytes in salt-free solution can be found in ref. 69, 125, 391 and 607. In excess salt, calculating the scattering contrast for X-rays and neutrons typically requires knowledge of salt-exclusion factors as discussed by Eisenberg and co-workers.481,608–610 This rigorous calculation is usually replaced by a simpler approach that approximates the salt and the solvent as a single component.19,209,234,236,611In Fig. 29(a), the form factor of TMAPSS with N = 40 (c* ≃ 1 M from Fig. 11(a)) in salt-free aqueous solution is plotted, measured by the zero-average contrast technique. The TMA counterions are contrast-matched and hence do not contribute to the coherent scattering signal.125,616 The form factor for c = 0.1 and 0.2 M agrees well, suggesting that the solutions are sufficiently diluted that the chain conformation is independent of the polymer concentration. The form factor displays a region where P(q) ∝ q−1 as expected for rigid objects. The steeper dependence in the high-q region arises from the finite lateral dimensions of the chain, and the flattening at low q corresponds to the Guinier region (qRg ≲ 1), where the P(q) ≃ 1 − q2Rg2/3. For fully stretched configurations (B = 1), the PSS chain is expected to have an effective contour length of L ≃ 10 nm. As we expect the chain to be stretched in salt-free D2O below c*, the form factor of the particle should be that of a cylinder. Using a cross-sectional radius of 0.4 nm, the form factor of a cylinder with L = 10 nm is shown as a blue line, which clearly does not fit the experimental data. If L = 5.9 nm is assumed instead, corresponding to an effective monomer size of 0.17 nm (B = 1.5), an excellent fit is obtained. This is in reasonable agreement with the value of B = 1.8 obtained from correlation length data in semidilute solutions of NaPSS.96 The high q region of the form factor of NaPSS from other studies yields effective monomer length values of 0.22–0.25 nm,96,611,613,617 while Kassapidou et al.'s125 data are an exception in this regard, and the reason remains unclear.
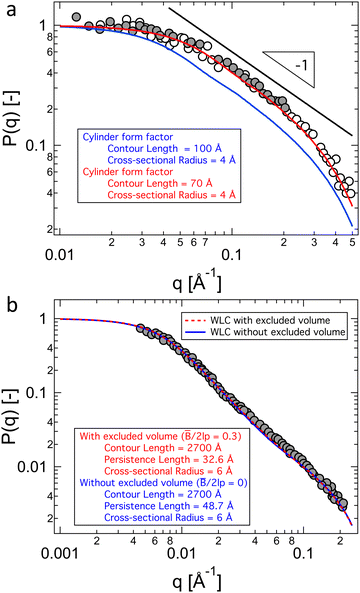 | ||
| Fig. 29 Form factor of TMAPSS in (a) salt-free aqueous solution (grey circles c = 0.2 M, white circles c = 0.1 M, c* ≃ 1 M based on Fig. 11) and (b) 0.19 M TMACl solution. Lines are fit to the cylinder form factor for (a) and to the worm-like chain form factor with and without excluded volume for (b). The fit parameters are indicated in the legend. The black line in the top panel represents the power law of −1. Cylinder form factors and WLC with excluded volume are calculated using SASView v 5.0.6. Data are from ref. 125 and 615. | ||
The form factor of TMAPSS in 0.19 M TMACl/D2O solution is shown in Fig. 29(b) using data by Ragnetti and Oberthür.615 At high-q, the form factor of a worm-like chain (or a cylinder) is
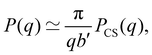 | (53) |
As PSS chains with N = 1070 in cs = 0.19 M salt solution are expected to be perturbed by the excluded volume, we next try to fit the form factor in Fig. 29(b) to an expanded worm-like chain form factor. Unfortunately, there is no analytical expression for the worm-like chain form factor with arbitrarily excluded volume (Sharp and Bloomfield developed a form factor for WLC with excluded volume,619 errors in this model are noted in ref. 618). Pedersen and Schurtenberger618 worked out the form factor of worm-like chains with a reduced binary cluster integral of ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) /(2lp) = 0.3. This value is appropriate for many polymers in good solvent systems, but if we trust the values of B and lp plotted in Fig. 26, it does not work generally for polyelectrolytes in excess salt. Specifically, for NaPSS in cs = 0.19 M, we expect
/(2lp) = 0.3. This value is appropriate for many polymers in good solvent systems, but if we trust the values of B and lp plotted in Fig. 26, it does not work generally for polyelectrolytes in excess salt. Specifically, for NaPSS in cs = 0.19 M, we expect ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) /(2lp) ≃ 0.5. Lacking a better approximation, we fit the Pedersen-Schurtenberger form factor (model 3 of ref. 618, implemented in SASView as a “flexible cylinder model”). The result is shown as a dashed red line in Fig. 29(b). The quality of the fit is identical to that of the form factor without excluded volume, but the obtained persistence length now takes a lower value of lp ≃ 3.3 nm.
/(2lp) ≃ 0.5. Lacking a better approximation, we fit the Pedersen-Schurtenberger form factor (model 3 of ref. 618, implemented in SASView as a “flexible cylinder model”). The result is shown as a dashed red line in Fig. 29(b). The quality of the fit is identical to that of the form factor without excluded volume, but the obtained persistence length now takes a lower value of lp ≃ 3.3 nm.
The fits to Ragnetti and Oberthür's data show that the form factor of a polyelectrolyte cannot, in general, be used to extract the excluded volume and persistence length simultaneously. As with the global chain properties discussed earlier (Rg, D, [η]…), P(q) for a chain in a solution of a given ionic strength must be fitted to a pair of lp and ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) values. Fitting of chains of varying molar mass with the assumption that lp and
values. Fitting of chains of varying molar mass with the assumption that lp and ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) are N-independent may allow for independently extracting these two parameters.
are N-independent may allow for independently extracting these two parameters.
Because the reduced binary cluster integral ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) /(2lp) is a function of the solution's ionic strength, it will be important for the field that forms factors for worm-like chains with arbitrarily excluded volume are developed. Some theories9 propose that dilute polyelectrolytes adopt a directed random walk conformation. As the form factor for directed random walks has not been calculated, it is difficult to test these predictions. As discussed above, simulation studies have found that, under certain conditions, the bond orientation correlation function of polyelectrolytes is bimodal. Again, no form factor is available to check when or if this is observed experimentally.
/(2lp) is a function of the solution's ionic strength, it will be important for the field that forms factors for worm-like chains with arbitrarily excluded volume are developed. Some theories9 propose that dilute polyelectrolytes adopt a directed random walk conformation. As the form factor for directed random walks has not been calculated, it is difficult to test these predictions. As discussed above, simulation studies have found that, under certain conditions, the bond orientation correlation function of polyelectrolytes is bimodal. Again, no form factor is available to check when or if this is observed experimentally.
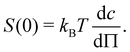 | (54) |
| Π ≃ kBTfc, | (55) |
Combining eqn (54) and (55), we get:
| S(0) ≃ f−1. | (56) |
The intermediate scattering function of polyelectrolytes, as measured by dynamic light scattering, was shown to be bimodal in solvents of low ionic strength. For some systems, it has been observed that bimodal behaviour emerges when fc/cs ≳ 0.03–0.1,103,396 but this is not always the case.422,626 The fast mode arises from the counterions, the motions of which are strongly coupled to those of the polyelectrolyte backbone.65 The slow mode is thought to have the same physical origin as the low-q upturn. The presence of the slow mode, sometimes referred to as ‘extraordinary’ behaviour, has been extensively studied65,103,396,422,627–629 and hotly debated in the literature.630,631 There exists at present no consensus about its origin.
This slow mode and low-q upturn have often been interpreted as arising from multichain clusters with a size of ∼100 nm.632 Such interpretations are considered unsatisfactory by some because it is not clear how highly incompressible systems can withstand such long-ranged concentration fluctuations. Possible explanations are that the entities responsible for the upturn are either not at equilibrium with the rest of the solution (e.g., undissolved polymer residues) or that they are non-permeable to the solution (e.g., dust particles).630,633,634 These explanations have generally been rejected on the basis of experimental tests.631,635–640
In our view, the main challenge is to reconcile the following three statements: (1) osmotic pressure and conductivity data show that eqn (55) is correct;68,424,641 (2) eqn (54) should be applied generally to two-component systems;642 (3) scattering measurements show that eqn (56) does not hold. A satisfactory account to the upturn/slow mode problem must be able to explain both the high values of S(0) and the low osmotic compressibility of the systems.
When polyelectrolyte diffusion is measured using techniques such as pulsed field gradient NMR19,301,410,643 or fluorescence photobleaching recovery,644,645 no slow mode or otherwise abnormal diffusion is apparent.631 Electrophoretic mobility measurements also do not show any abnormal behaviour.644,646,647 The viscosity of polyelectrolyte solutions also appears to be independent of the amplitude of the slow mode.648 This leads to the conclusion that whatever entities are responsible for the slow mode and low-q upturn involve only a very small number of chains and/or occupy a very small fraction of the solution volume.
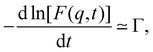 | (57) |
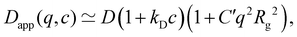 | (58) |
The variation of kD with molar mass and added salt concentration for polyelectrolytes has been reported in many literature studies.106–109,112,113,474,477,499,500,519–523 The results are compiled in the ESI,† where it is shown to be approximately proportional to the overlap concentration of the system under high excluded volume conditions, see Section S6 (ESI†). This agrees with results for neutral polymers in good solvents.651 For constant C′, the available datasets474 do not allow us to draw any clear conclusions.
In the Rg−1 ≲q ≲ (2lp)−1 region, eqn (58) does not apply and instead, the so-called q3 asymptote (Γ ∝ q3 or Dapp ∝ q) is predicted by several theories, in agreement with experimental observations for neutral polymers.116,652 The Zimm model with full hydrodynamic interactions predicts:
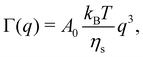 | (59) |
The apparent diffusion coefficient of DNA in NaCl and LiCl solutions normalised to its value at q = 0 is plotted as a function of qRg in Fig. 30. The datasets for different added salt concentrations approximately collapse onto a single curve. The exception is the cs = 0.005 M NaCl sample, which at intermediate qRg shows higher Dapp/D than the other samples. The Zimm prediction (eqn (59)) for good solvents (A0 = 0.0788, ρ = 1.41) is shown as a dashed line. It correctly captures the scaling of Dapp ∝ q (or equivalently Γ ∝ q3) displayed by the DNA data, although the pre-factor to the power-law is over-predicted by around 30%. For qRg ≳ 6, the Dapp/D0 data approach a plateau, which has been observed for qlK ≳ 5 for various polymer-solvent systems.116,653 Note that for the present system qlK = 5 corresponds to qRg ≃ 12–18. The plateau is seen more clearly for higher molar mass DNA samples, see for example ref. 654. The height of the plateau depends on the friction coefficient of the Kuhn segment and on the strength of the hydrodynamic interactions.591,653,654
3.14 Transition from salt-free to excess salt regimes
The preceding discussion has shown that, despite some open questions, the scaling theory largely captures the essential static and dynamic properties of polyelectrolytes in the salt-free and in excess added salt limits. We next consider the cross-over between these two regimes. The aim is to determine at which added salt concentration polyelectrolytes become flexible. The hydrodynamic radius of NaPSS in aqueous solutions at infinite polymer dilution is plotted as a function of the added salt in Fig. 31. The data of Jia et al.211 for a single NaPSS sample with Mw = 66 kg mol−1 are considered in Fig. 31(a), and a broader set of samples from different literature reports with Mw ≃ 20 kg mol−1 are compared in Fig. 31(b). At low added salt concentrations, RH ∼ c0s is observed. Such a regime is often observed in polyelectrolyte systems, such as gels.350,352 At high added salt concentrations, the scaling prediction RH ∼ cs−1/5 works for the limited added salt concentration range studied. The critical added salt concentration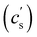 separating the two regimes can be identified from the intercept of the two power-laws or by fitting a crossover function, given in the caption. Both methods yield nearly identical results:
separating the two regimes can be identified from the intercept of the two power-laws or by fitting a crossover function, given in the caption. Both methods yield nearly identical results: 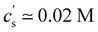 (κ−1 ≃ 2 nm) and
(κ−1 ≃ 2 nm) and 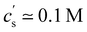 (κ−1 ≃ 1 nm) for the 66 and 20 kg mol−1 polymers, respectively.
(κ−1 ≃ 1 nm) for the 66 and 20 kg mol−1 polymers, respectively.
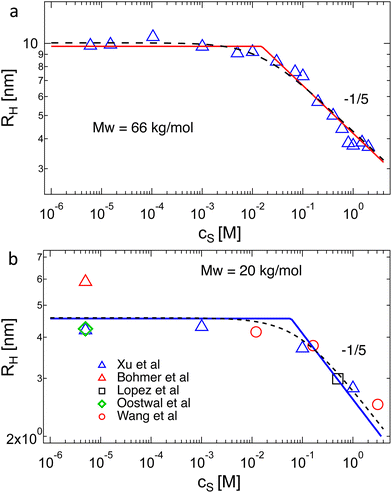 | ||
Fig. 31 Hydrodynamic radius of NaPSS in aqueous salt solutions at infinite dilution showing crossover between rod-like and flexible coil. Solid lines are fitted to RH = RH(0) for  to to 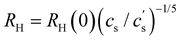 at high cs. Dashed lines are fit to crossover function at high cs. Dashed lines are fit to crossover function 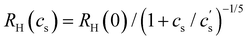 . The value of RH at low salt and the cross-over salt concentration . The value of RH at low salt and the cross-over salt concentration 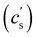 are left as fitting parameters. Data for panel (a) are from ref. 211 and for panel (b) from ref. 19, 383, 386, 410, 496 and 656. Xu et al.'s values are interpolated. are left as fitting parameters. Data for panel (a) are from ref. 211 and for panel (b) from ref. 19, 383, 386, 410, 496 and 656. Xu et al.'s values are interpolated. | ||
The scaling model predicts that chains become flexible when the screening length (eqn (10)) is of the order of the chain size. Since, as shown in Section 3.5 in the infinite dilution limit NaPSS are fully stretched in DI water, R is of the order of the contour length of the chain. Thus, we find R/κ−1 ≃ L/κ−1 ≃ 20–30, which is larger than the prediction of the Dobrynin model (rscr ≃ 3.5κ−1 for NaPSS in water).89 In order to test the scaling prediction for the flexible-to-rod transition, a study of the molar mass dependence of 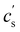 is needed. Chains become flexible when the screening length is of the order of their end-to-end distance. For longer chains, the screening length for which chains become flexible is therefore larger, corresponding to a lower value of
is needed. Chains become flexible when the screening length is of the order of their end-to-end distance. For longer chains, the screening length for which chains become flexible is therefore larger, corresponding to a lower value of 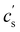 . Specifically, the scaling model predicts
. Specifically, the scaling model predicts 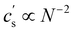 . A cursory examination of the available experimental data for NaPSS suggests they may be compatible with this prediction, but lacking more extensive datasets, no clear conclusion can be drawn at this point.
. A cursory examination of the available experimental data for NaPSS suggests they may be compatible with this prediction, but lacking more extensive datasets, no clear conclusion can be drawn at this point.
3.15 Specific ions effects on polyelectrolyte conformation
As discussed in Section 3.1, the phase behaviour of polyelectrolytes in excess added salts reveals that salt ions interact with polyelectrolytes in ways that cannot be explained by simple electrostatics.657 For example, chaotropic or hydrophobic ions may bind to non-ionic sites on the polyelectrolyte backbone because the resulting change in the structure of water is enthalpically or entropically favourable.658 In addition, Collins’ concept of matching water affinities659 and ion-pair formation can be extended to soft matter interfaces: Malikova et al.660 proposed that there can be a hydration match between counter-ions that favors ion pairing on polyelectrolytes. These solvent-mediated effects are well-known and have been studied for a variety of soft matter systems,213–215,661 but the physical origin of the observed behaviour remains controversial.662 Neutral polymers in solutions of ionic liquids are known to display associative properties,663–665 a phenomenon often attributed to interactions between the ionic liquid ions and the dipoles along the polymer backbone. Such interactions may also be important for polyelectrolytes in concentrated salt solutions.Studies by potentiometry and other methods have shown that the nature of counterions can influence the thermodynamic and transport properties of polyelectrolytes in solution,660,666–669 but a framework to understand and predict these interactions is lacking.78,662 Calorimetric techniques670–672 show a strong influence of the counterion type on the enthalpy of dilution of polystyrene sulfonate. Such data are difficult to interpret but for PSS, several authors concluded that the strength of counterion binding to the backbone increases with increasing counterion size. These trends are not clearly observed for the conformational and hydrodynamic properties of PSS. For example, the static structure factor of different alkaline salts shows only minor differences673 and the viscosity and diffusion coefficient of the sodium and cesium salts of PSS have been found to be identical.301
The importance of specific ion effects in relatively simple systems such as concentrated electrolyte solutions or neutral polymer solutions with added salts220 is recognised but poorly understood, despite important progress in recent years.662,674 As discussed in Section 3.1, polyethylene oxide is the most studied system in this regard. Depending on the solvent, addition of salt can either deteriorate solvent quality or lead to significant ion binding along the backbone, thereby inducing polyelectrolyte-like behavior. For polyelectrolyte solutions, where additional layers of complexity are present due to the importance of electrostatic screening, ion pairing, etc., it seems unlikely that a full understanding of these phenomena will be reached any time soon. It might therefore be advisable to focus part of our attention on systems where such interactions are expected to be minimised, for example, polyelectrolyte solutions in polar solvents with low hydrogen bonding. Unfortunately, experimental data for such systems are sparse. Finding polyelectrolyte/solvent/salt solutions where ion-specific are not important would be helpful, as it would allow us to work with systems for which interpretation of experimental data becomes comparatively simpler. The lack of ion-specific effects can be established if conformational or hydrodynamic properties of polyelectrolytes are found to be independent of the ion-type added.
Lacking a theoretical framework with which to interpret the influence of ion type on the conformational and hydrodynamic properties of polyelectrolytes, we limit ourselves here to introducing a few interesting results, which will hopefully draw attention to the complexity of this topic. The data of Kagawa and Fuoss210 for the intrinsic viscosity of sodium polyacrylate is plotted as a function of added salt concentration for three different monovalent salts in Fig. 32(a). At low cs, [η] is largely unaffected by the salt type but beyond cs ≃ 0.5 M, qualitatively different behaviour is observed. Particularly striking is the case of NaI, where chain re-expansion above cs ≃ 3 M is apparent. The influence of counterion radius on the hydrodynamic radius of polyvinyl sulfate and quaternised polyvinyl pyridine in excess added salt is shown in Fig. 32(b) and (c), respectively. The data from Beer et al.103 show that RH is almost independent of anion radius (Rion) in low added salt (cs = 1 mM) but decreases significantly with Rion at cs = 0.1 M. The dependence of RH on counterion size for PVS is more complicated, as it goes through a minimum. Qualitatively similar behaviour has also been observed for polyphosphates675,676 and dextran sulfate.677,678
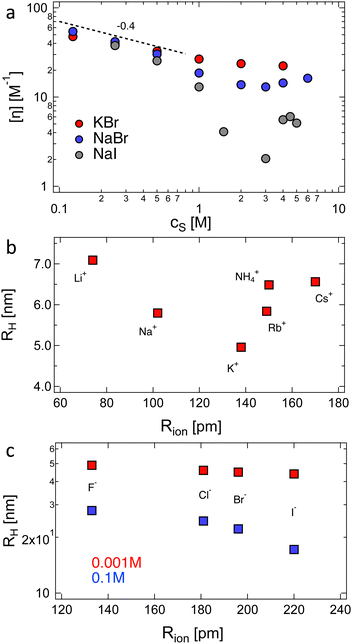 | ||
| Fig. 32 (a) Intrinsic viscosity of sodium polyacrylate as a function of added salt for different concentrations of monovalent salts. Data are from ref. 210. (b) Hydrodynamic radius of PVS in 0.5 M salt solutions of X+Cl, where X+ = Li+, Na+, K+, Rb+, Cs+ and NH4+, plotted as a function of cation radius. RH values are estimated from intrinsic viscosity using eqn (50) with UηF = 0.12. Data are from ref. 194. (c) Hydrodynamic radius of quaternised P2VP in 0.001 M and 0.1 M salt solution as a function of the anion radius. Data are from ref. 103. | ||
3.16 Charge screening in concentrated electrolyte solutions
Here, we introduce a unique charge screening behaviour observed recently for PILs in ionic liquid solutions. Ionic liquids (ILs) are a type of salts that exist in a liquid state at room temperature.37 As a result, ILs have been used as plasticizers for polymeric materials.679 In this context, the mixture of PILs and ILs could be utilized as electrolytes in batteries680 and membranes for molecular separation.681 Consequently, understanding the conformation and the polymer dynamics of PILs in IL solutions is of great importance because they are intimately related to the properties of PIL-based materials.In the previous sections, we showed that PILs behave as polyelectrolytes when dissolved in organic solvents. The physical properties of polyelectrolytes are regulated by the addition of salts because of the charge screening. Accordingly, one may intuitively assume that any charge effects are completely screened in ionic liquids because the concentration of ions is extremely high. Namely, the screening length is small enough that polyelectrolyte chains can behave as a neutral polymer in ionic liquids. However, recent experimental studies on the screening length showed that the charge screening behaviour in ionic liquid solutions was much more complicated than those predicted by the classical Debye–Hückel model.57,442,683Fig. 33 shows a typical example of the experimentally determined screening length in ionic liquid solutions, showing a non-monotonic dependence against the increasing ionic liquid concentration.682 In the plot, symbols are the screening length estimated using a surface force apparatus, while the line represents the Debye length. The surface apparatus works by measuring the force between two smooth mica surfaces as a function of separation distance, for inter-surface distances in the range ≃2–15 nm. In particular, the measured screening length increased with increasing concentration of salts in the high-salt regime, which was attributed to the charge underscreening.684 The Debye–Hückel theory predicts a monotonic decrease of the screening length with the increasing salt concentration. Note that the region where the measured screening length and the Debye–Hückel prediction disagree corresponds to κ−1 < lB. Holm and co-workers argued, on the basis of simulation work, that experimental results pointing to under-screening are likely the result of confinement effects and do not reflect the properties of ionic liquids in the bulk.685,686 This topic remains controversial,687 with several apparently conflicting results being reported over the last few years.688–693
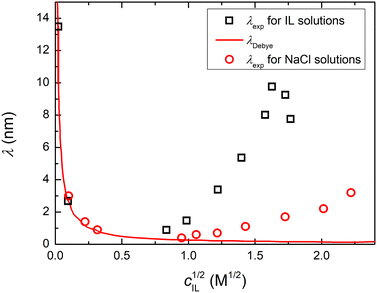 | ||
| Fig. 33 The dependence of the measured screening length λexp on the square root of the concentration cIL for an ionic liquid, 1-butyl-1-methylpyrrolidinium bis(trifluoromethanesulfonyl)imide ([C4C1 Pyrr][TFSI]), in propylene carbonate (black squares) and NaCl solutions (red circles). The red solid curve represents the screening length λDebye predicted by the Debye–Hückel theory. The λexp and λDebye are taken from Fig. 2 of ref. 682. | ||
The apparent hydrodynamic radius, measured at c = 0.01 M and scattering angle 40°, for a PIL (PC4-TFSI) in DMF solution is plotted as a function of added ionic liquid (Bmim-TFSI: 1-butyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide) concentration, cIL in Fig. 34. For cIL ≳ 1 M, the apparent hydrodynamic radius is seen to increase with increasing ionic strength. Using the scaling laws of Lee et al.,694 the screening length of the polyelectrolyte solution can be expressed as follows:
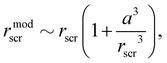 | (60) |
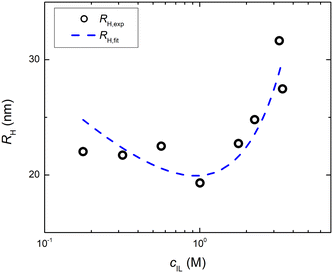 | ||
| Fig. 34 Variation of the apparent hydrodynamic radius of PC4-TFSI in DMF solution at c = 0.01 M as a function of added ionic liquid (Bmim-TFSI) concentration cIL. The line is calculated assuming RH ∝ rscr0.4, leaving the proportionality constant as a free parameter. The data are taken from ref. 57. | ||
Chain expansion at high added salt concentrations has also been observed for linear and grafted polyelectrolytes in aqueous media.211,246,695 These results have been interpreted in terms of the underscreening theory.696 A major problem for this type of interpretation is that for many polyelectrolyte systems, chain expansion is not observed at high-added salt. The most prominent example of this is NaPSS in aqueous NaCl solutions, which have been studied for cs up to 4.17 M. The results of Smith et al.682 for the screening length of concentrated electrolyte solutions expect that underscreening occurs not only for concentrated ionic liquid solutions but also for simple salts. For example, their measurements showed that λ for NaCl in water, shown in Fig. 33, increases for cs ≳ 1 M. Extensive datasets on the variation of the static and hydrodynamic sizes of NaPSS with added NaCl and KCl concentrations (up to 4.17 M) in aqueous media have been reported by several groups.105,193,475,477 These did not show any evidence of chain re-expansion in the high cs region, as would be expected from the results of Smith et al.
The curve fit shown in Fig. 34 relies on the assumptions that (1) the charge fraction on the PIL chain remains the same as that in DMF, i.e., f is independent of cIL, (2) the non-electrostatic excluded volume effect does not change with respect to the increasing cIL, (3) the scaling law of rmodscr, found by surface force measurements (2-D screening process), holds for the charge screening in polyelectrolyte systems, and (4) the solvent dynamics does not change by the addition of PILs. Unless these assumptions are justified, we cannot conclude that the charge underscreening is attributed to the increase of RH.
4 Conclusions & outstanding questions
Polyelectrolytes are ubiquitous in our daily life. The conformation and properties of polyelectrolytes are strongly influenced by the electrostatic interactions acting between charged monomers. We re-visited literature reports in the polyelectrolyte field and combined them to know the current level of understanding of the conformation and dynamics of polyelectrolyte solutions, in particular in the dilute regime. Key research challenges requiring further investigations are summarized as follows.1. The conformation of polyelectrolytes in low ionic strength solvents at infinite dilution limit is challenging to assess experimentally. This is because of the extreme dilution required for chains to be weakly interacting. Intrinsic viscosity data for polyelectrolytes in DI water or other low ionic strength solvents could serve as a valuable measure of chain conformation, but the extrapolation of the reduced viscosity to the c → 0 limit is challenging. In this regime, the technique which appears to yield the most robust results is fluorescence correlation spectroscopy (see Fig. 10a). The available RH and [η] data for NaPSS exceed the theoretical prediction for fully stretched chains, suggesting the influence of the primary electroviscous effect.
2. The overlap concentration data for various systems agrees with theoretical predictions that in dilute salt-free solutions, polyelectrolytes are highly stretched (R ∼ N). Data for NaPSS in DI water suggest that its end-to-end distance at c = c* is significantly shrunken with respect to its value at infinite dilution, in agreement with simulation work.98 Discrepancies with respect to the scaling with dielectric constant and charge fraction are observed. The data suggest deviations from Manning's condensation theory and/or the scaling calculation of the electrostatic blob may be responsible for these discrepancies but current experimental evidence does not allow us to reach a firm conclusion. Data for c* as a function of dielectric constant along with independent estimates for the fraction of free counterions, for example, based on osmometry, conductivity or dielectric spectroscopy data, would help resolve this outstanding question. Weakly charged polyelectrolytes (Ab ≫ lB), where no condensation is expected, are understudied systems. Systematic data for c* (or other conformational parameters) as a function of charge fraction, solvent permittivity and molar mass would be particularly useful to resolve open questions regarding the nature of the electrostatic blob.
3. The phenomenon of counterion condensation is key to understanding virtually every property of highly charged polyelectrolytes in solution because the charge fraction has a large influence on the conformational and thermodynamic properties of chains. Estimates for the fraction of free counterions obtained from overlap concentration data reveal two surprising trends. First, f increases with increasing added salt content (Fig. 13c). Second, the dependence of f on solvent permittivity follows a power-law of f ∝ ε1.6 (Fig. 13d), in contrast to the linear relationship predicted by the Manning model. Both findings deserve additional work using different experimental techniques such as membrane osmometry and conductivity, which provide more direct measures of counterion condensation.
4. The scaling theory's prediction for the size of the electrostatic blob was checked against viscosity and radius of gyration data for several polyelectrolyte systems. In salt-free and excess salt, the scaling prediction is partially supported by current experimental evidence, but several experimental observations (e.g., Fig. 11(c) and Fig. S8, ESI†) do not agree with the scaling predictions. Further experimental work is needed in two regards: first, systematic work on the conformational and hydrodynamic properties as a function of charge fraction in salt-free solution is at present limited to two studies,97,399 extension to other systems is vital if we are to understand the discrepancies between theory and experiment. Second, the scaling predicts ξel < lK for polyelectrolytes with more than one dissociated charge per Kuhn segment, but experimental evidence (see Fig. 12, 22(b) and 23) suggests ξel > lB. To further understand this problem, conformational and hydrodynamic data for polyelectrolytes in solvents with a broad range of dielectric constants are required.697
5. The N-scaling of the radius of gyration, diffusion coefficient and intrinsic viscosity of polyelectrolytes in excess salt agreed well with the scaling predictions. The cs scaling of these quantities showed stronger departures from theory. This is not unexpected since our understanding of the electrostatic excluded volume in polyelectrolyte solutions remains relatively thin.
6. Several experimental observations, such as the solubility of polyelectrolytes in organic media, the ionomer to polyelectrolyte crossover in solution, or the temperature induced conformational transition observed in Fig. 15 suggest that understanding the solvation of the polymer backbone, ionic groups and counterions will be critical to fully account for the behaviour of ionic polymers in solution.
7. Modelling polyelectrolytes in excess salt as expanded worm-like chains can reproduce many of their dilute solution properties, including the form-factor, radius of gyration, diffusion coefficient and intrinsic viscosity. The extracted parameters for the persistence length and excluded volume strength suggest an approximately linear variation of these two quantities with the Debye screening length. The range of applicability of this model to polyelectrolytes remains unclear, with experiments suggesting that the WLC model applies over a broader range than expected by several polyelectrolyte theories and simulations. A related question is the lengthscale at which electrostatic interactions become screened in polyelectrolyte solutions. The data analysed in this review broadly support the validity of eqn (10). However, it is of interest to note that eqn (10) appears to hold over a broader cs range than the conditions for which it was derived.
8. A comparison of several “universal ratios” for flexible neutral polymers and polyelectrolytes in excess salt revealed significant differences between the two types of systems. Only one of the ratios considered 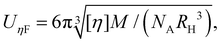 appeared to be truly universal, and may offer a way to estimate the molar mass of polyelectrolytes from diffusion and intrinsic viscosity data, which could be useful when refractive index increment values at constant chemical potential are not available. It is possible that replacing RH3 with a combination of Rg and RH, as expected by various theories, may yield a more robust universal ratio.
appeared to be truly universal, and may offer a way to estimate the molar mass of polyelectrolytes from diffusion and intrinsic viscosity data, which could be useful when refractive index increment values at constant chemical potential are not available. It is possible that replacing RH3 with a combination of Rg and RH, as expected by various theories, may yield a more robust universal ratio.
9. The transition between rod-like and flexible chain behavior was examined on the basis of diffusion data in the infinite dilution limit. The data showed departures from the predictions of the scaling model of Dobrynin et al. Here, obtaining additional datasets as a function of molar mass should provide insightful tests to theoretical ideas on screening in polyelectrolyte solutions.
10. Poly(ionic liquid)s in ionic liquid solutions exhibited an unusual upturn in the plot of the hydrodynamic radius with respect to the increasing ionic liquid concentration. This phenomenon appears to be similar to the increase in specific viscosity with increasing ionic liquid content, primarily observed for semidilute solutions. The mechanism of such counter-intuitive screening behaviour remains elusive. More generally, the topic of underscreening in concentrated electrolyte solutions is a controversial one. The dimensions of polyelectrolyte chains are highly sensitive to the screening length of the solvent media. Therefore, studying polyelectrolytes in concentrated electrolyte solutions could offer interesting insights into the underlying phenomenon.
11. Theoretical models to treat scattering data from polyelectrolyte solutions lag behind those available for neutral polymers. For example, the calculation of form factors of worm-like chains for arbitrary values of the excluded volume strength and for directed random walks will be important. Simulation work has shown that under certain conditions, polyelectrolytes display bi-modal bond-orientation correlation functions. Form factors to describe the scattering of polymer chains with these configurations are also lacking. Approximate analytical expressions for the form factors of chains with bimodal orientational correlation functions might allow experimentalists to test simulation results.
12. Several experimental results make it clear that in solutions containing monovalent salts in high concentrations, the ion type can have a large influence on the properties of polyelectrolytes. Ion-specific effects, despite being very widely studied in other contexts, have not received sufficient attention in the polyelectrolyte literature. The importance of ion-specific effects is a major hindrance to understanding basic phenomena, such as the chain conformation or phase behaviour of polyelectrolytes in concentrated salt solutions. As ion-specific effects arise largely (though not exclusively) from hydrogen bonding, work in organic solvents, especially aprotic ones, should be addressed in the future. Poly(ionic liquid)s with hydrophobic counterions, which exhibit good solubility in these systems, are good systems for such studies.
13. The importance of accurately evaluating the concentration of residual salts in polyelectrolyte solutions is of crucial importance if we are to understand their solution in low ionic strength media. Many experimental techniques may introduce residual salt ions into polyelectrolyte solutions, for example, if these come in contact with glass. Therefore, it is important to evaluate the residual salt content of samples after rheological measurements are completed, which only a few studies320 have attempted. Cohen et al. noted the importance of devising “a standard procedure for cleaning and preparing the glass surface”; yet, there remains a deficit in such standardized methods. While there are accounts of cleaning capillary viscometers using concentrated acid solutions,299,323 the implications of these practices on the results are not well-defined.
Experimental work on several of the open questions discussed above would benefit from studies of polyelectrolyte behaviour in non-aqueous solvents. While water is undoubtedly the most important polyelectrolyte solvent, experimental work in aqueous solutions is often confounded by pronounced ion-specific effects at high salt concentrations and the inadvertent presence of residual salts in low ionic strength environments. Employing organic solvents could significantly enhance our understanding of how the solvent media's dielectric constant affects polyelectrolyte behavior, an area where existing research is limited.
We hope that the subjects discussed in this article will help readers to grasp an overview of the current research progress on the conformation and dynamics of polyelectrolytes in dilute solutions. We also highlight open research questions to be answered. It is envisioned that in the not-too-distant future, many of the existing puzzles in polyelectrolyte physics will be solved, providing more accurate predictions for the solution properties of polyelectrolytes.
Appendix: nomenclature
| a | Ion diameter of salt ions |
| A 0 | Pre-factor in eqn (59), given by the Zimm model |
| A 2 | Second virial coefficient |
![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif)
| Excluded volume strength |
| Intrinsic excluded volume strength |
| Electrostatic excluded volume strength |
| Attractive contribution to excluded volume strength |
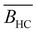
| Hard-core repulsive excluded volume strength |
| b | Length of a chemical monomer |
| B | Stretching parameter |
| b′ | Effective (z-projected) monomer size |
| b c | Distance between neighboring two point charges on a line charge |
| c | Polymer concentration (number per unit volume) |
| c max | Polymer concentration at which the reduced viscosity is maximum |
| c* | Overlap concentration |
| c IL | Concentration of ionic liquid |
| c s | Added salt concentration (number of salt molecules per unit volume) |
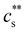
| Critical salt concentration for precipitation |
| c Ds | Critical salt concentration at re-entrant phase boundary |
| c s′ | Added salt concentration at which chains become flexible |
| C′ | Dimensional constant for Dapp in eqn (58) |
| D | Translational diffusion coefficient |
| D 0 | Translational diffusion coefficient of a worm-like chain without excluded volume |
| D app | Apparent diffusion coefficient |
| d C | Chain's cross-sectional diameter |
| e | Electrostatic unit of charge |
| f | Fraction of charged monomers bearing a dissociated charge |
| F(q,t) | Intermediate scattering function |
| F η | Function given in ref. 384 |
| G | Function given in ref. 365 |
| G′ | Storage modulus |
| G′′ | Loss modulus |
| g K | Number of chemical monomers per Kuhn segment |
| g T | Number of chemical monomers in a thermal blob |
| g el | Number of chemical monomers in an electrostatic blob |
| g scr | Number of chemical monomers in a segment of length of rscr |
| H | Function in eqn (43) |
| I(q) | Intensity of scattered light |
| i | Degree of ionisation |
| J | Dimensional constant in eqn (33) |
| K | Function in eqn (16) |
| K B | Pre-factor in eqn (22) |
| K l | Pre-factor in eqn (23) |
| K η | Product given in eqn (35) |
| k B | Boltzmann's constant |
| k D | Diffusion second virial coefficient |
| k H | Huggins constant |
| L | Contour length of chain |
| l | Distance along the chain contour |
| l B | Bjerrum length |
| l K,0 | Length of bare Kuhn monomer |
| l p | Persistence length |
| l p,e | Electrostatic persistence length |
| l p,0 | Intrinsic persistence length |
| M w | Weight averaged molar mass |
| M 0 | Molar mass of a monomer |
| M L | Mass per unit length |
| n | Refractive index of solutions |
| N | Degree of polymerisation (number of chemical monomers) |
| N A | Avogadro's constant |
| N n | Number-averaged degree of polymerisation (in number of chemical monomers) |
| N w | Weight-averaged degree of polymerisation (in number of chemical monomers) |
| N z | z-Averaged degree of polymerisation (in number of chemical monomers) |
| N K,0 | Degree of polymerisation (in number of bare Kuhn monomers) |
| O | Function in eqn (42) |
| P(q) | Form factor (by definition P(0) = 1) |
| q | Scattering wavevector |
| R | End-to-end distance of a chain |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif)
| Gas constant |
| R 0 | End-to-end distance of a WLC without excluded volume |
| R g | Radius of gyration of a chain |
| R g,0 | Radius of gyration of a chain without electrostatic effects (variational theory) |
| R H | Hydrodynamic radius |
| R ion | Counterion radius |
| r scr | Electrostatic screening length (scaling theory) |
| r modscr | Modified screening length |
| r C | Chain's cross-sectional radius |
| S(q) | Total structure factor |
| s(l) | Bond–bond orientational correlation function |
| T | Temperature |
| T p | Phase separation temperature |
| T c | Critical temperature |
| u | Ratio of Bjerrum length to monomer size (lB/b) |
| u M | Ratio of Bjerrum length to charge distance (lB/bc) |
| U el | Coulomb energy of an electrostatic blob |
| U Aη | Universal ratio given by eqn (47) |
| U ηS | Universal ratio given by eqn (48) |
| U AS | Universal ratio given by eqn (49) |
| U ηF | Universal ratio given by eqn (50) |
| W | Dimensional constant in eqn (33) |
| X | Universal ratio given by eqn (52) |
| z | Excluded volume parameter |
![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif)
| Function given by eqn (16) – scaled excluded-volume parameter |
| Z p | Valence of a side-chain ion |
| Z c | Valence of a counterion |
| α | Expansion factor (QTP theory) |
| α R | Expansion factor for end-to-end distance (αR2 ≡ R/R0) |
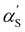
| Expansion factor in variational theory |
| α D | Expansion factor for diffusion coefficient |
| α η | Expansion factor for intrinsic viscosity |
| β l | Exponent in eqn (23) |
| β B | Exponent in eqn (22) |
| χ | Flory–Huggins solubility parameter |
| χ 0 | Intrinsic (non-electrostatic) contribution to the Flory–Huggins solubility parameter |
| χ el | Electrostatic contribution to the Flory–Huggins solubility parameter |
| δ | Fraction of monomers bearing an ionic group |
| ε 0 | Vacuum permittivity |
| ε r | Relative dielectric constant of solvents |
| Φ | Flory viscosity factor |
| Γ | Initial decay rate of intermediate scattering function |
| γ | Polymer/solvent interfacial tension |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
| Shear rate |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) C
C
| Critical shear rate for the onset of shear thinning of |
| γ η | Power-law exponent describing N-dependence of intrinsic viscosity |
| γ R | Power-law exponent describing N-dependence of radius of gyration |
| γ D | Power-law exponent describing N-dependence of diffusion coefficient |
| [η]0 | Intrinsic viscosity of WLC without excluded volume |
| [η0] | Intrinsic viscosity of non-ionic polymer |
| [η]rod | Intrinsic viscosity of rod-like objects |
| [η] | Intrinsic viscosity |
| η | Zero-shear viscosity of polymer solutions |
| η s | Viscosity of solvent |
| η sp | Specific viscosity (ηsp = (η − ηs)/ηs) |
| η red | Reduced viscosity (ηsp/c) |
| κ −1 | Debye screening length |
| λ | Screening length in electrolyte solutions |
| μ | Dipole moment of a solvent molecule |
| ν | Solvent quality exponent |
| ρ | Ratio Rg/RH |
| θ | Theta temperature |
| τ | Reduced temperature (τ ≡ T − θ/T) |
| τ Z | Longest relaxation time (Zimm model) |
| ξ T | End-to-end distance of thermal blob |
| ξ el | End-to-end distance of electrostatic blob |
| ξ T,el | Thermal blob, incorporating electrostatic contribution to excluded volume |
| Ψ | Interpenetration function |
| Π | Osmotic pressure |
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
C. G. L. acknowledges the Deutsche Forschungsgemeinschaft project GO 3250/2-1, and the Theodore von Karman Fellowship (GSO070) from the RWTH Aachen. C. G. L. thanks prof. Takaichi Watanabe for hosting his stay at the University of Okayama, during which most of the work for this manuscript was carried out, and Prof. Ralph Colby (Penn State) for many useful discussions and for providing feedback on an early version of the manuscript. We also thank Dr Max Hohenschutz (RWTH) for useful discussions and for proofreading the manuscript. A. M. acknowledges funding from the Japanese Society for the Promotion of Science (Grants-in-Aid for Early-Career Scientists, Grant No. 21K14686; Grant-in-Aid for Scientific Research(B), Grant No. 22H02139). A. Q. S. acknowledges the support of the Okinawa Institute of Science and Technology Graduate University with subsidy funding from the Cabinet Office, Government of Japan. Much of the graphical extraction of data extraction was carried out with the aid of WebPlotDigitizer.698References
- H. Staudinger, Ber. Dtsch. Chem. Ges., 1920, 53, 1073–1085 CrossRef.
- https://iupac.org/polymer-edu/what-are-polymers/ .
- A. S. Abd-El-Aziz, M. Antonietti, C. Barner-Kowollik, W. H. Binder, A. Boker, C. Boyer, M. R. Buchmeiser, S. Z. D. Cheng, F. D’Agosto, G. Floudas, H. Frey, G. Galli, J. Genzer, L. Hartmann, R. Hoogenboom, T. Ishizone, D. L. Kaplan, M. Leclerc, A. Lendlein, B. Liu, T. E. Long, S. Ludwigs, J.-F. Lutz, K. Matyjaszewski, M. A. R. Meier, K. Mullen, M. Mullner, B. Rieger, T. P. Russell, D. A. Savin, A. D. Schluter, U. S. Schubert, S. Seiffert, K. Severing, J. B. P. Soares, M. Staffilani, B. S. Sumerlin, Y. Sun, B. Z. Tang, C. Tang, P. Theato, N. Tirelli, O. K. C. Tsui, M. M. Unterlass, P. Vana, B. Voit, S. Vyazovkin, C. Weder, U. Wiesner, W.-Y. Wong, C. Wu, Y. Yagci, J. Yuan and G. Zhang, Macromol. Chem. Phys., 2020, 221, 2000216 CrossRef CAS.
- R. M. Fuoss and U. P. Strauss, J. Polym. Sci., 1948, 3, 246–263 CrossRef CAS.
- A. Eisenberg and J.-S. Kim, Introduction to ionomers, Wiley, 1998 Search PubMed.
- A. Eisenberg and M. Rinaudo, Polym. Bull., 1990, 671 CrossRef CAS.
- Q. Chen, N. Bao, J.-H. H. Wang, T. Tunic, S. Liang and R. H. Colby, Macromolecules, 2015, 48, 8240–8252 CrossRef CAS.
- L. Nova, F. Uhlik and P. Košovan, Phys. Chem. Chem. Phys., 2017, 19, 14376–14387 RSC.
- A. V. Dobrynin and M. Rubinstein, Prog. Polym. Sci., 2005, 30, 1049–1118 CrossRef CAS.
- A. V. Dobrynin, Polymer, 2020, 202, 122714 CrossRef CAS.
- A. J. Konop and R. H. Colby, Macromolecules, 1999, 32, 2803–2805 CrossRef CAS.
- S. Joly, R. Kane, L. Radzilowski, T. Wang, A. Wu, R. E. Cohen, E. L. Thomas and M. F. Rubner, Langmuir, 2000, 16, 1354–1359 CrossRef CAS.
- G. S. Manning, J. Chem. Phys., 1969, 51, 924–933 CrossRef CAS.
- R. H. Colby, Rheol. Acta, 2010, 49, 425–442 CrossRef CAS.
- M. Muthukumar, Macromolecules, 2017, 50, 9528–9560 CrossRef CAS PubMed.
- G. Chen, A. Perazzo and H. A. Stone, J. Rheol., 2021, 65, 507–526 CrossRef CAS.
- G. Chen, A. Perazzo and H. A. Stone, Phys. Rev. Lett., 2020, 124, 177801 CrossRef CAS PubMed.
- A. H. Slim, W. H. Shi, F. Safi Samghabadi, A. Faraone, A. B. Marciel, R. Poling-Skutvik and J. C. Conrad, ACS Macro Lett., 2022, 11, 854–860 CrossRef CAS PubMed.
- C. G. Lopez, J. Linders, C. Mayer and W. Richtering, Macromolecules, 2021, 54, 8088–8103 CrossRef CAS.
- A. V. Walter, L. N. Jimenez, J. Dinic, V. Sharma and K. A. Erk, Rheol. Acta, 2019, 58, 145–157 CrossRef CAS.
- L. N. Jimenez, C. D. MartiInez NarvaIez and V. Sharma, Macromolecules, 2022, 55, 8117–8132 CrossRef CAS.
- L. N. Jimenez, J. Dinic, N. Parsi and V. Sharma, Macromolecules, 2018, 51, 5191–5208 CrossRef CAS.
- C. G. Lopez, R. H. Colby and J. T. Cabral, Macromolecules, 2018, 51, 3165–3175 CrossRef CAS.
- C. Robin, C. Lorthioir, C. Amiel, A. Fall, G. Ovarlez and C. Le Coeur, Macromolecules, 2017, 50, 700–710 CrossRef CAS.
- P. Komorowska, S. Różańska and J. Różański, Cellulose, 2017, 24, 4151–4162 CrossRef CAS.
- A. Matsumoto, C. Zhang, F. Scheffold and A. Q. Shen, ACS Macro Lett., 2022, 11, 84–90 CrossRef CAS PubMed.
- F. Del Giudice, V. Calcagno, V. Esposito Taliento, F. Greco, P. A. Netti and P. L. Maffettone, J. Rheol., 2017, 61, 13–21 CrossRef CAS.
- J.-M. Carrillo, Y. Wang, R. Kumar and B. G. Sumpter, Eur. Phys. J. E: Soft Matter Biol. Phys., 2023, 46, 92 CrossRef CAS PubMed.
- E. Buvalaia, M. Kruteva, I. Hoffmann, A. Radulescu, S. Forster and R. Biehl, ACS Macro Lett., 2023, 12, 1218–1223 CrossRef CAS PubMed.
- K. Akkaoui, M. Yang, Z. A. Digby and J. B. Schlenoff, Macromolecules, 2020, 53, 4234–4246 CrossRef CAS.
- Q. Wang and J. B. Schlenoff, Macromolecules, 2014, 47, 3108–3116 CrossRef CAS.
- A. M. Rumyantsev, N. E. Jackson and J. J. De Pablo, Annu. Rev. Condens. Matter Phys., 2021, 12, 155–176 CrossRef.
- B. Ghosh, R. Bose and T. D. Tang, Curr. Opin. Colloid Interface Sci., 2021, 52, 101415 CrossRef CAS.
- S. Shah and L. Leon, Curr. Opin. Colloid Interface Sci., 2021, 53, 101424 CrossRef CAS.
- H. Ohno and K. Ito, Chem. Lett., 1998, 751–752 CrossRef CAS.
- J. Yuan and M. Antonietti, Polymer, 2011, 52, 1469–1482 CrossRef CAS.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS PubMed.
- L. N. Wong, S. D. Jones, K. Wood, L. De Campo, T. Darwish, M. Moir, H. Li, R. A. Segalman, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2022, 24, 4526–4532 RSC.
- U. H. Choi, A. Mittal, T. L. Price, M. Lee, H. W. Gibson, J. Runt and R. H. Colby, Electrochim. Acta, 2015, 175, 55–61 CrossRef CAS.
- D. S.-d la Cruz, M. D. Green, Y. Ye, Y. A. Elabd, T. E. Long and K. I. Winey, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 338–346 CrossRef.
- K. Nakamura, K. Fukao and T. Inoue, Macromolecules, 2012, 45, 3850–3858 CrossRef CAS.
- T. Inoue, A. Matsumoto and K. Nakamura, Macromolecules, 2013, 46, 6104–6109 CrossRef CAS.
- U. H. Choi, Y. Ye, D. Salas de la Cruz, W. Liu, K. I. Winey, Y. A. Elabd, J. Runt and R. H. Colby, Macromolecules, 2014, 47, 777–790 CrossRef CAS.
- M. M. Obadia, B. P. Mudraboyina, A. Serghei, T. N. T. Phan, D. Gigmes and E. Drockenmuller, ACS Macro Lett., 2014, 3, 658–662 CrossRef CAS PubMed.
- F. Fan, Y. Wang, T. Hong, M. F. Heres, T. Saito and A. P. Sokolov, Macromolecules, 2015, 48, 4461–4470 CrossRef CAS.
- Z. Wojnarowska, J. Knapik, J. Jacquemin, S. Berdzinski, V. Strehmel, J. R. Sangoro and M. Paluch, Macromolecules, 2015, 48, 8660–8666 CrossRef CAS.
- F. Fan, W. Wang, A. P. Holt, H. Feng, D. Uhrig, X. Lu, T. Hong, Y. Wang, N.-G. Kang, J. Mays and A. P. Sokolov, Macromolecules, 2016, 49, 4557–4570 CrossRef CAS.
- C. Iacob, A. Matsumoto, M. Brennan, H. Liu, S. J. Paddison, O. Urakawa, T. Inoue, J. Sangoro and J. Runt, ACS Macro Lett., 2017, 6, 941–946 CrossRef CAS PubMed.
- Z. Wojnarowska, H. Feng, Y. Fu, S. Cheng, B. Carroll, R. Kumar, V. N. Novikov, A. M. Kisliuk, T. Saito, N.-G. Kang, J. W. Mays, A. P. Sokolov and V. Bocharova, Macromolecules, 2017, 50, 6710–6721 CrossRef CAS.
- A. Matsumoto, C. Iacob, T. Noda, O. Urakawa, J. Runt and T. Inoue, Macromolecules, 2018, 51, 4129–4142 CrossRef CAS.
- E. W. Stacy, C. P. Gainaru, M. Gobet, Z. Wojnarowska, V. Bocharova, S. G. Greenbaum and A. P. Sokolov, Macromolecules, 2018, 51, 8637–8645 CrossRef CAS.
- P. Kuray, T. Noda, A. Matsumoto, C. Iacob, T. Inoue, M. A. Hickner and J. Runt, Macromolecules, 2019, 52, 6438–6448 CrossRef CAS.
- Q. Zhao, P. Bennington, P. F. Nealey, S. N. Patel and C. M. Evans, Macromolecules, 2021, 54, 10520–10528 CrossRef CAS.
- H. Chen and Y. A. Elabd, Macromolecules, 2009, 42, 3368–3373 CrossRef CAS.
- R. Marcilla, J. Alberto Blazquez, J. Rodriguez, J. A. Pomposo and D. Mecerreyes, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 208–212 CrossRef CAS.
- A. Matsumoto, R. Ukai, H. Osada, S. Sugihara and Y. Maeda, Macromolecules, 2022, 55, 10600–10606 CrossRef CAS.
- A. Matsumoto, F. Del Giudice, R. Rotrattanadumrong and A. Q. Shen, Macromolecules, 2019, 52, 2759–2771 CrossRef CAS.
- J. Barrat and J. Joanny, Adv. Chem. Phys., 1996, 94, 1–66 CrossRef CAS.
- C. Holm, J. Joanny, K. Kremer, R. Netz, P. Reineker, C. Seidel, T. A. Vilgis and R. Winkler, Polyelectrolyte theory, Springer, 2004 Search PubMed.
- A. V. Dobrynin, Curr. Opin. Colloid Interface Sci., 2008, 6, 376–388 CrossRef.
- A. Yethiraj, J. Phys. Chem. B, 2009, 113, 1539–1551 CrossRef CAS PubMed.
- S. Forster and M. Schmidt, Phys. Prop. Polym., 2005, 51–133 Search PubMed.
- J. Landsgesell, L. Nova, O. Rud, F. Uhlik, D. Sean, P. Hebbeker, C. Holm and P. Košovan, Soft Matter, 2019, 15, 1155–1185 RSC.
- K.-H. Shen, M. Fan and L. M. Hall, Macromolecules, 2021, 54, 2031–2052 CrossRef CAS.
- M. Sedlak, Langmuir, 1999, 15, 4045–4051 CrossRef CAS.
- T. Miyajima, Physical Chemistry of Polyelectrolytes, CRC Press, 2001, pp. 851–896 Search PubMed.
- U. Scheler, Curr. Opin. Colloid Interface Sci., 2009, 14, 212–215 CrossRef CAS.
- F. Bordi, C. Cametti and R. Colby, J. Phys.: Condens. Matter, 2004, 16, R1423 CrossRef CAS.
- J. Combet, P. Lorchat and M. Rawiso, Eur. Phys. J.: Spec. Top., 2012, 213, 243–265 CAS.
- C. Holm, M. Rehahn, W. Oppermann and M. Ballauff, Polyelectrolytes with Defined Molecular Architecture II, 2004, pp. 1–27 Search PubMed.
- V. M. Prabhu, Curr. Opin. Colloid Interface Sci., 2005, 10, 2–8 CrossRef CAS.
- V. Vlachy, Pure Appl. Chem., 2008, 80, 1253–1266 CrossRef CAS.
- G. Maurer, S. Lammertz and L. N. Schafer, Polym. Thermodyn.: Liquid Polymer-Containing Mixtures, 2011, pp. 67–136 Search PubMed.
- K. Huber and U. Scheler, Curr. Opin. Colloid Interface Sci., 2012, 17, 64–73 CrossRef CAS.
- M. Rubinstein and G. A. Papoian, Soft Matter, 2012, 8, 9265–9267 RSC.
- W. F. Reed, Bunsen-Ges. Phys. Chem., Ber., 1996, 100, 685–695 CrossRef CAS.
- M. Borkovec, G. J. Koper and C. Piguet, Curr. Opin. Colloid Interface Sci., 2006, 11, 280–289 CrossRef CAS.
- J. Smiatek, Molecules, 2020, 25, 1661 CrossRef CAS PubMed.
- P. Ander, Water-soluble polymers: synthesis, solution properties, and applications (ACS Symposium Series), 1991, ch. 13 Search PubMed.
- C. Wandrey, D. Hunkeler, U. Wendler and W. Jaeger, Macromolecules, 2000, 33, 7136–7143 CrossRef CAS.
- A. Zhang, X. Yang, F. Yang, C. Zhang, Q. Zhang, G. Duan and S. Jiang, Molecules, 2023, 28, 2042 CrossRef CAS PubMed.
- The monograph by Nagasawa151 provides a very good introduction to the physical chemistry of dilute polyelectrolyte solutions, including many topics not covered here, but deals primarily with studies published before 1980.
- A. Matsumoto, Nihon Reoroji Gakkaishi, 2022, 50, 43–50 CrossRef CAS.
- K. G. Wilcox, S. K. Kozawa and S. Morozova, Chem. Phys. Rev., 2021, 2, 041309 CrossRef CAS.
- F. Horkay, Gels, 2021, 7, 102 CrossRef CAS PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, New York, 2003 Search PubMed.
- P.-G. De Gennes, P. Pincus, R. Velasco and F. Brochard, J. Phys., 1976, 37, 1461–1473 CrossRef CAS.
- P. Pfeuty, J. Phys., Colloq., 1978, 39, C2–149 CrossRef.
- A. V. Dobrynin, R. H. Colby and M. Rubinstein, Macromolecules, 1995, 28, 1859–1871 CrossRef CAS.
- A. V. Dobrynin and M. Jacobs, Macromolecules, 2021, 54, 1859–1869 CrossRef CAS.
- M. Jacobs, C. G. Lopez and A. V. Dobrynin, Macromolecules, 2021, 54, 9577–9586 CrossRef CAS.
- C. G. Lopez, S. E. Rogers, R. H. Colby, P. Graham and J. T. Cabral, J. Polym. Sci., Part B: Polym. Phys., 2015, 53, 492–501 CrossRef CAS PubMed.
- W. N. Sharratt, R. O’Connell, S. E. Rogers, C. G. Lopez and J. T. Cabral, Macromolecules, 2020, 53, 1451–1463 CrossRef CAS.
- K. Salamon, D. Aumiler, G. Pabst and T. Vuletic, Macromolecules, 2013, 46, 1107–1118 CrossRef CAS.
- E. Di Cola, N. Plucktaveesak, T. Waigh, R. Colby, J. Tan, W. Pyckhout-Hintzen and R. Heenan, Macromolecules, 2004, 37, 8457–8465 CrossRef CAS.
- C. G. Lopez, F. Horkay, R. Schweins and W. Richtering, Macromolecules, 2021, 54, 10583–10593 CrossRef CAS.
- S. Dou and R. H. Colby, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 2001–2013 CrossRef CAS.
- M. J. Stevens and K. Kremer, J. Chem. Phys., 1995, 103, 1669–1690 CrossRef CAS.
- Y. Kantor and M. Kardar, Phys. Rev. Lett., 1999, 83, 745 CrossRef CAS.
- A. Gulati, M. Jacobs, C. G. Lopez and A. V. Dobrynin, Macromolecules, 2023, 56, 2183–2193 CrossRef CAS.
- M. Muthukumar, J. Chem. Phys., 1996, 105, 5183–5199 CrossRef CAS.
- M. Muthukumar, Polym. Sci., Ser. A, 2016, 58, 852–863 CrossRef CAS PubMed.
- M. Beer, M. Schmidt and M. Muthukumar, Macromolecules, 1997, 30, 8375–8385 CrossRef CAS.
- A. Katchalsky, O. Kunzle and W. Kuhn, J. Polym. Sci., 1950, 5, 283–300 CrossRef CAS.
- E. Hirose, Y. Iwamoto and T. Norisuye, Macromolecules, 1999, 32, 8629–8634 CrossRef CAS.
- Y. Iwamoto, E. Hirose and T. Norisuye, Polym. J., 2000, 32, 428–434 CrossRef CAS.
- J. Yashiro and T. Norisuye, J. Polym. Sci., Part B: Polym. Phys., 2002, 40, 2728–2735 CrossRef CAS.
- J. Yashiro and T. Norisuye, Polym. Bull., 2006, 56, 467–474 CrossRef CAS.
- J. Yashiro, R. Hagino, S. Sato and T. Norisuye, Polym. J., 2006, 38, 57–63 CrossRef CAS.
- K. Hayashi, K. Tsutsumi, F. Nakajima, T. Norisuye and A. Teramoto, Macromolecules, 1995, 28, 3824–3830 CrossRef CAS.
- K. Hayashi, K. Tsutsumi, T. Norisuye and A. Teramoto, Polym. J., 1996, 28, 922–928 CrossRef CAS.
- R. Hagino, J. Yashiro, M. Sakata and T. Norisuye, Polym. J., 2006, 38, 861–867 CrossRef CAS.
- S. Chisaka and T. Norisuye, J. Polym. Sci., Part B: Polym. Phys., 2001, 39, 2071–2080 CrossRef CAS.
- T. Ishikawa, M. Kikuchi, M. Kobayashi, N. Ohta and A. Takahara, Macromolecules, 2013, 46, 4081–4088 CrossRef CAS.
- T. Norisuye, Prog. Polym. Sci., 1993, 18, 543–584 CrossRef CAS.
- H. Yamakawa, Helical wormlike chains in polymer solutions, Springer, 1997, vol. 1 Search PubMed.
- Intrinsic viscosity and diffusion coefficient data for low molar masses are typically required to obtain precise estimates of dC and/or ML.
- R. M. Davis, Macromolecules, 1991, 24, 1149–1155 CrossRef CAS.
- M. Fixman and J. Skolnick, Macromolecules, 1978, 11, 863–867 CrossRef CAS.
- K. Kawakami and T. Norisuye, Macromolecules, 1991, 24, 4898–4903 CrossRef CAS.
- R. Davis and W. Russel, J. Polym. Sci., Part B: Polym. Phys., 1986, 24, 511–533 CrossRef CAS.
- T. Odijk, J. Polym. Sci., Polym. Phys. Ed., 1977, 15, 477–483 CrossRef CAS.
- J. Skolnick and M. Fixman, Macromolecules, 1977, 10, 944–948 CrossRef CAS.
- M. Le Bret, J. Chem. Phys., 1982, 76, 6243–6255 CrossRef CAS.
- K. Kassapidou, W. Jesse, M. Kuil, A. Lapp, S. Egelhaaf and J. Van der Maarel, Macromolecules, 1997, 30, 2671–2684 CrossRef CAS.
- H. Yamakawa, T. Yoshizaki and D. Ida, J. Chem. Phys., 2013, 139, 204902 CrossRef PubMed.
- J.-L. Barrat and J.-F. Joanny, Europhys. Lett., 1993, 24, 333 CrossRef CAS.
- Note that this condition is not met for common polyelectrolyte systems such as NaPSS or NaPAMS in water (lp,0lB)1/2 ≃ 1 nm and b/A ≃ 1.2 nm.
- R. Everaers, A. Milchev and V. Yamakov, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 8, 3–14 CrossRef CAS PubMed.
- A. V. Dobrynin, Macromolecules, 2005, 38, 9304–9314 CrossRef CAS.
- M. Fixman, J. Phys. Chem. B, 2010, 114, 3185–3196 CrossRef CAS PubMed.
- T. Odijk and A. C. Houwaart, J. Polym. Sci., Polym. Phys. Ed., 1978, 16, 627–639 CrossRef CAS.
- P. J. Flory, J. Chem. Phys., 1953, 21, 162–163 CrossRef CAS.
- K. Ghosh and M. Muthukumar, J. Polym. Sci., Part B: Polym. Phys., 2001, 39, 2644–2652 CrossRef CAS.
- K. Ghosh, G. A. Carri and M. Muthukumar, J. Chem. Phys., 2001, 115, 4367–4375 CrossRef CAS.
- If ξel ≲ lK,0, chains are rigid on all length scales, hence the dC of the chain can be used for the cylinder's cross-section. For the ξel > lK,0 case, chains can be modelled as a pole of electrostatic blobs, and ξel provides a better estimate for the cylinder's diameter.
- M. M. Tirado and J. G. de la Torre, J. Chem. Phys., 1979, 71, 2581–2587 CrossRef CAS.
- M. M. Tirado and J. G. De La Torre, J. Chem. Phys., 1980, 73, 1986–1993 CrossRef CAS.
- J. Lapham, J. P. Rife, P. B. Moore and D. M. Crothers, J. Biomol. NMR, 1997, 10, 255 CrossRef CAS PubMed.
- Note that the Flory constant depends on polymer flexibility, see for example ref. 148 and 591.
- A. Gosteva, A. S. Gubarev, O. Dommes, O. Okatova and G. M. Pavlov, Polymers, 2023, 15, 961 CrossRef CAS PubMed.
- H. Schiessel and P. Pincus, Macromolecules, 1998, 31, 7953–7959 CrossRef CAS.
- H. Schiessel, Macromolecules, 1999, 32, 5673–5680 CrossRef CAS.
- M. Muthukumar, J. Chem. Phys., 2004, 120, 9343–9350 CrossRef CAS PubMed.
- Q. Liao, A. V. Dobrynin and M. Rubinstein, Macromolecules, 2006, 39, 1920–1938 CrossRef CAS.
- J. Jeon and A. V. Dobrynin, Macromolecules, 2007, 40, 7695–7706 CrossRef CAS.
- A. V. Dobrynin and M. Rubinstein, Macromolecules, 2001, 34, 1964–1972 CrossRef CAS.
- H. Yamakawa and M. Fujii, Macromolecules, 1974, 7, 128–135 CrossRef CAS PubMed.
- H. Yamakawa and M. Fujii, Macromolecules, 1973, 6, 407–415 CrossRef CAS.
- I. Fortelný, J. Kovář, A. Živný and M. Bohdanecký, J. Polym. Sci., Polym. Phys. Ed., 1981, 19, 181–184 CrossRef.
- S. A. Rice and A. R. Dinner, Physical Chemistry of Polyelectrolyte Solutions, John Wiley & Sons, 2015, vol. 158 Search PubMed.
- A. Popov and D. A. Hoagland, J. Polym. Sci., Part B: Polym. Phys., 2004, 42, 3616–3627 CrossRef CAS.
- R. Kakehashi, H. Yamazoe and H. Maeda, Colloid Polym. Sci., 1998, 276, 28–33 CrossRef CAS.
- F. Oosawa, J. Polym. Sci., 1957, 23, 421–430 CrossRef CAS.
- R. M. Nyquist, B.-Y. Ha and A. J. Liu, Macromolecules, 1999, 32, 3481–3487 CrossRef CAS.
- E. Trizac and G. Tellez, Phys. Rev. Lett., 2006, 96, 038302 CrossRef PubMed.
- G. S. Manning, J. Phys. Chem. B, 2007, 111, 8554–8559 CrossRef CAS PubMed.
- R. Kumar, A. Kundagrami and M. Muthukumar, Macromolecules, 2009, 42, 1370–1379 CrossRef CAS PubMed.
- J.-M. Y. Carrillo and A. V. Dobrynin, Macromolecules, 2011, 44, 5798–5816 CrossRef CAS.
- P. Gonzalez-Mozuelos and M. O. de la Cruz, J. Chem. Phys., 1995, 103, 3145–3157 CrossRef CAS.
- E. Raphael and J.-F. Joanny, EPL, 1990, 13, 623 CrossRef CAS.
- E. Y. Kramarenko, A. R. Khokhlov and K. Yoshikawa, Macromol. Theory Simul., 2000, 9, 249–256 CrossRef CAS.
- G. V. Ramanathan and C. P. Woodbury, J. Chem. Phys., 1982, 77, 4133–4140 CrossRef CAS.
- M. Deserno, C. Holm and S. May, Macromolecules, 2000, 33, 199–206 CrossRef CAS.
- A. Deshkovski, S. Obukhov and M. Rubinstein, Phys. Rev. Lett., 2001, 86, 2341–2344 CrossRef CAS PubMed.
- A. V. Dobrynin, M. Rubinstein and S. P. Obukhov, Macromolecules, 1996, 29, 2974–2979 CrossRef CAS.
- M. Muthukumar, Macromolecules, 2002, 35, 9142–9145 CrossRef CAS.
- S. Liu and M. Muthukumar, J. Chem. Phys., 2002, 116, 9975–9982 CrossRef CAS.
- R. G. Winkler, M. Gold and P. Reineker, Phys. Rev. Lett., 1998, 80, 3731 CrossRef CAS.
- T. Ono, M. Ohta and K. Sada, ACS Macro Lett., 2012, 1, 1270–1273 CrossRef CAS PubMed.
- S. Ben Mahmoud, W. Essafi, A. Brulet and F. Boue, Macromolecules, 2018, 51, 9259–9275 CrossRef CAS.
- M. Hara, J. Wu and A. H. Lee, Macromolecules, 1988, 21, 2214–2218 CrossRef CAS.
- R. Barbucci, A. Magnani and M. Consumi, Macromolecules, 2000, 33, 7475–7480 CrossRef CAS.
- S. Jousset, H. Bellissent and J. C. Galin, Macromolecules, 1998, 31, 4520–4530 Search PubMed.
- W. J. Horne, M. A. Andrews, K. L. Terrill, S. S. Hayward, J. Marshall, K. A. Belmore, M. S. Shannon and J. E. Bara, ACS Appl. Mater. Interfaces, 2015, 7, 8979–8983 CrossRef CAS PubMed.
- B. Siadat, R. Lundberg and R. Lenz, Macromolecules, 1981, 14, 773–776 CrossRef CAS.
- R. Weiss, R. Lundberg and S. Turner, J. Polym. Sci., Polym. Chem. Ed., 1985, 23, 549–568 Search PubMed.
- C. M. Hansen, Hansen solubility parameters: a user's handbook, CRC Press, 2007 Search PubMed.
- M.-X. Du, Y.-F. Yuan, J.-M. Zhang and C.-Y. Liu, Macromolecules, 2022, 55, 4578–4588 CrossRef CAS.
- Y.-F. Yuan, J.-M. Zhang, B.-Q. Zhang, J.-J. Liu, Y. Zhou, M.-X. Du, L.-X. Han, K.-J. Xu, X. Qiao and C.-Y. Liu, Phys. Chem. Chem. Phys., 2021, 23, 21893–21900 RSC.
- N. Ohtani, Y. Inoue, H. Mizuoka and K. Itoh, J. Polym. Sci., Part A: Polym. Chem., 1994, 32, 2589–2595 CrossRef CAS.
- N. Ohtani, Y. Inoue, Y. Kaneko, A. Sakakida, I. Takeishi and H. Furutani, Polym. J., 1996, 28, 11–15 CrossRef CAS.
- N. Ohtani, Y. Inoue, Y. Kaneko and S. Okumura, J. Polym. Sci., Part A: Polym. Chem., 1995, 33, 2449–2454 CrossRef CAS.
- M. Hara, A. Lee and J. Wu, J. Polym. Sci., Part B: Polym. Phys., 1987, 25, 1407–1418 CrossRef CAS.
- R. Lundberg and R. Phillips, J. Polym. Sci., Polym. Phys. Ed., 1982, 20, 1143–1154 CrossRef CAS.
- S. Nomula and S. L. Cooper, Macromolecules, 2001, 34, 925–930 Search PubMed.
- G. Gebel, P. Aldebert and M. Pineri, Polymer, 1993, 34, 333–339 Search PubMed.
- Y. Nishiyama and M. Satoh, J. Polym. Sci., Part B: Polym. Phys., 2000, 38, 2791–2800 CrossRef CAS.
- Y. Fukunaga, M. Hayashi and M. Satoh, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 1166–1175 CrossRef CAS.
- N. Yasumoto, Y. Hata and M. Satoh, Polym. Int., 2004, 53, 766–771 CrossRef CAS.
- A. M. Rumyantsev, A. Pan, S. Ghosh Roy, P. De and E. Y. Kramarenko, Macromolecules, 2016, 49, 6630–6643 CrossRef CAS.
- R. Buscall and T. Corner, Eur. Polym. J., 1982, 18, 967–974 CrossRef CAS.
- A. Takahashi, T. Kato and M. Nagasawa, J. Phys. Chem., 1967, 71, 2001–2010 CrossRef.
- H. Eisenberg and G. R. Mohan, J. Phys. Chem., 1959, 63, 671–680 CrossRef CAS.
- P. J. Flory and J. E. Osterheld, J. Phys. Chem., 1954, 58, 653–661 CrossRef CAS.
- M. O. De La Cruz, L. Belloni, M. Delsanti, J. Dalbiez, O. Spalla and M. Drifford, J. Chem. Phys., 1995, 103, 5781–5791 Search PubMed.
- A. Ikegami and N. Imai, J. Polym. Sci., 1962, 56, 133–152 CrossRef CAS.
- M. A. Axelos, M. M. Mestdagh and J. Francois, Macromolecules, 1994, 27, 6594–6602 CrossRef CAS.
- M. Delsanti, J. P. Dalbiez, O. Spalla, L. Belloni and M. Drifford, Phase Diagram of Polyelectrolyte Solutions in Presence of Multivalent Salts, 1994, pp. 381–392 Search PubMed.
- R. Schweins, G. Goerigk and K. Huber, Eur. Phys. J. E: Soft Matter Biol. Phys., 2006, 21, 99–110 CrossRef CAS PubMed.
- N. Volk, D. Vollmer, M. Schmidt, W. Oppermann and K. Huber, Polyelectrolytes with Defined Molecular Architecture II, 2004, pp. 29–65 Search PubMed.
- M. Hansch, B. Hamisch, R. Schweins, S. Prevost and K. Huber, J. Chem. Phys., 2018, 148, 014901 CrossRef PubMed.
- M. Hansch, H. P. Kaub, S. Deck, N. Carl and K. Huber, J. Chem. Phys., 2018, 148, 114906 CrossRef PubMed.
- C. G. Sinn, R. Dimova and M. Antonietti, Macromolecules, 2004, 37, 3444–3450 CrossRef CAS.
- H. Eisenberg and E. F. Casassa, J. Polym. Sci., 1960, 47, 29–44 CrossRef CAS.
- H. Eisenberg and D. Woodside, J. Chem. Phys., 1962, 36, 1844–1854 CrossRef CAS.
- W. W. Graessley, Polymeric liquids & networks: structure and properties, Garland Science, 2003 Search PubMed.
- S. Kawaguchi, S. Toui, M. Onodera, K. Ito and A. Minakata, Macromolecules, 1993, 26, 3081–3085 CrossRef CAS.
- C. G. Lopez, F. Horkay, M. Mussel, R. L. Jones and W. Richtering, Soft Matter, 2020, 16, 7289–7298 RSC.
- I. Kagawa and R. M. Fuoss, J. Polym. Sci., 1955, 18, 535–542 CrossRef CAS.
- P. Jia and J. Zhao, J. Chem. Phys., 2009, 131, 231103 CrossRef PubMed.
- H. Yuan and G. Liu, Soft Matter, 2020, 16, 4087–4104 RSC.
- I. Hakem and J. Lal, EPL, 2003, 64, 204 CrossRef CAS.
- I. F. Hakem, J. Lal and M. R. Bockstaller, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 3642–3650 CrossRef CAS.
- M. Hohenschutz, P. Bauduin, C. G. Lopez, B. Forster and W. Richtering, Angew. Chem., 2022, 62, e202210208 CrossRef PubMed.
- S. Z. Moghaddam and E. Thormann, J. Colloid Interface Sci., 2019, 555, 615–635 CrossRef CAS PubMed.
- M. Ataman, Colloid Polym. Sci., 1987, 265, 19–25 CrossRef CAS.
- S. Kawaguchi, G. Imai, J. Suzuki, A. Miyahara, T. Kitano and K. Ito, Polymer, 1997, 38, 2885–2891 CrossRef CAS.
- E. Boucher and P. Hines, J. Polym. Sci., Polym. Phys. Ed., 1978, 16, 501–511 CrossRef CAS.
- R. Lundberg, F. Bailey and R. Callard, J. Polym. Sci., Part A-1: Polym. Chem., 1966, 4, 1563–1577 CrossRef CAS.
- K. Ono, H. Konami and K. Murakami, J. Phys. Chem., 1979, 83, 2665–2669 CrossRef CAS.
- F. Quina, L. Sepulveda, R. Sartori, E. B. Abuin, C. G. Pino and E. A. Lissi, Macromolecules, 1986, 19, 990–994 CrossRef CAS.
- M. Giesecke, F. Hallberg, Y. Fang, P. Stilbs and I. Furo, J. Phys. Chem. B, 2016, 120, 10358–10366 CrossRef CAS PubMed.
- C. Zhou, C. Ji, Y. Nie, J. Yang and J. Zhao, Gels, 2022, 8, 213 CrossRef CAS PubMed.
- M. Drifford and M. Delsanti, Polyelectrolyte solutions with multivalent added salts: stability, structure, and dynamics, CRC Press, 2001, pp. 157–184 Search PubMed.
- A. Ezhova and K. Huber, Macromolecules, 2014, 47, 8002–8011 CrossRef CAS.
- A. Urbanski, M. Hansch, C. G. Lopez, R. Schweins, Y. Hertle, T. Hellweg, F. Polzer and K. Huber, J. Chem. Phys., 2018, 149, 163318 CrossRef PubMed.
- I. Michaeli, J. Polym. Sci., 1960, 48, 291–299 CrossRef CAS.
- J.-S. Jan and V. Breedveld, Macromolecules, 2008, 41, 6517–6522 CrossRef CAS.
- I. Sabbagh and M. Delsanti, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 1, 75–86 CrossRef CAS.
- E. Raspaud, M. O. De La Cruz, J.-L. Sikorav and F. Livolant, Biophys. J., 1998, 74, 381–393 CrossRef CAS PubMed.
- J. Pelta, F. Livolant and J.-L. Sikorav, J. Biol. Chem., 1996, 271, 5656–5662 CrossRef CAS PubMed.
- V. M. Prabhu, Phase behavior of polyelectrolyte solutions, University of Massachusetts Amherst, 2002 Search PubMed.
- V. Prabhu, M. Muthukumar, G. D. Wignall and Y. B. Melnichenko, J. Chem. Phys., 2003, 119, 4085–4098 CrossRef CAS.
- For other carboxylate polyelectrolytes such as NaCMC, heavier alkaline earth cations exhibit much lower values of cS** (∼10 mM) than Mg2+, which exhibits H-type precipitation.93.
- V. Prabhu, M. Muthukumar, G. Wignall and Y. Melnichenko, Polymer, 2001, 42, 8935–8946 CrossRef CAS.
- S. Kanai and M. Muthukumar, J. Chem. Phys., 2007, 127, 244908 CrossRef PubMed.
- E. Dubois and F. Boue, Macromolecules, 2001, 34, 3684–3697 CrossRef CAS.
- W. N. Sharratt, C. G. Lopez, M. Sarkis, G. Tyagi, R. O’Connell, S. E. Rogers and J. T. Cabral, Gels, 2021, 7, 44 CrossRef CAS PubMed.
- R. L. Feddersen and S. N. Thorp, Sodium carboxymethylcellulose, Elsevier, 1993, pp. 537–578 Search PubMed.
- D. Ishii, D. Tatsumi and T. Matsumoto, Nihon Reoroji Gakkaishi, 2013, 40, 267–272 CrossRef.
- C. Hu, W. Lu, A. Mata, K. Nishinari and Y. Fang, Int. J. Biol. Macromol., 2021, 177, 578–588 CrossRef CAS PubMed.
- D. M. Roquero, A. Othman, A. Melman and E. Katz, Mater. Adv., 2022, 3, 1849–1873 RSC.
- P.-Y. Hsiao and E. Luijten, Phys. Rev. Lett., 2006, 97, 148301 CrossRef PubMed.
- P.-Y. Hsiao, Macromolecules, 2006, 39, 7125–7137 CrossRef CAS.
- Y. Roiter, O. Trotsenko, V. Tokarev and S. Minko, J. Am. Chem. Soc., 2010, 132, 13660–13662 CrossRef CAS PubMed.
- Y. Hou, G. Liu, Y. Wu and G. Zhang, Phys. Chem. Chem. Phys., 2011, 13, 2880–2886 RSC.
- P.-Y. Hsiao, J. Chem. Phys., 2006, 124, 044904 CrossRef PubMed.
- K. Besteman, K. Van Eijk and S. Lemay, Nat. Phys., 2007, 3, 641–644 Search PubMed.
- W. M. de Vos and S. Lindhoud, Adv. Colloid Interface Sci., 2019, 274, 102040 CrossRef CAS PubMed.
- T. T. Nguyen, A. Y. Grosberg and B. I. Shklovskii, Phys. Rev. Lett., 2000, 85, 1568 CrossRef CAS PubMed.
- A. Y. Grosberg, T. Nguyen and B. Shklovskii, RMP, 2002, 74, 329 CrossRef CAS.
- V. Perel and B. Shklovskii, Phys. A, 1999, 274, 446–453 CrossRef CAS.
- J. Mattai and J. C. Kwak, Macromolecules, 1986, 19, 1663–1667 CrossRef CAS.
- E. Nordmeier and W. Dauwe, Polym. J., 1991, 23, 1297–1305 CrossRef CAS.
- T. Tamura, N. Kawabata, S. Kawauchi, M. Satoh and J. Komiyama, Polym. Int., 1998, 46, 353–356 CrossRef CAS.
- T. Miyajima, M. Mori, S.-i Ishiguro, K. H. Chung and C. H. Moon, J. Colloid Interface Sci., 1996, 184, 279–288 CrossRef CAS PubMed.
- T. Miyajima, M. Mori and S.-i Ishiguro, J. Colloid Interface Sci., 1997, 187, 259–266 CrossRef CAS PubMed.
- Z. Iatridi, G. Bokias and J. Kallitsis, J. Appl. Polym. Sci., 2008, 108, 769–776 CrossRef CAS.
- I. Pochard, P. Couchot and A. Foissy, Colloid Polym. Sci., 1998, 276, 1088–1097 CrossRef CAS.
- T. Miyajima, Ion Exchange Solvent Extraction, 1995, 275–351 Search PubMed.
- I. Pochard, A. Foissy and P. Couchot, Colloid Polym. Sci., 1999, 277, 818–826 CrossRef CAS.
- W. R. Archer and M. D. Schulz, Soft Matter, 2020, 16, 8760–8774 RSC.
- S. Lages, R. Michels and K. Huber, Macromolecules, 2010, 43, 3027–3035 CrossRef CAS.
- A. Kundagrami and M. Muthukumar, J. Chem. Phys., 2008, 128, 244901 CrossRef PubMed.
- The ion bridging phenomenon has been studied most extensively for polyelectrolyte brushes, see ref. 699–703.
- Y. Ikeda, M. Beer, M. Schmidt and K. Huber, Macromolecules, 1998, 31, 728–733 CrossRef CAS.
- S. Lages, P. Lindner, P. Sinha, A. Kiriy, M. Stamm and K. Huber, Macromolecules, 2009, 42, 4288–4299 CrossRef CAS.
- R. Schweins, P. Lindner and K. Huber, Macromolecules, 2003, 36, 9564–9573 CrossRef CAS.
- R. Schweins and K. Huber, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 5, 117–126 CrossRef CAS.
- K. Huber, J. Phys. Chem., 1993, 97, 9825–9830 CrossRef CAS.
- G. Goerigk, R. Schweins, K. Huber and M. Ballauff, EPL, 2004, 66, 331 CrossRef CAS.
- S. Lages, G. Goerigk and K. Huber, Macromolecules, 2013, 46, 3570–3580 CrossRef CAS.
- R. W. Rosser, N. Nemoto, J. L. Schrag and J. D. Ferry, J. Polym. Sci., Polym. Phys. Ed., 1978, 16, 1031–1040 CrossRef CAS.
- The data from ref. 704 are in the semidilute non-entangled regime.
- R. M. Fuoss, Science, 1948, 108, 545–550 CrossRef CAS PubMed.
- R. M. Fuoss and U. P. Strauss, Ann. N. Y. Acad. Sci., 1949, 51, 836–851 CrossRef CAS.
- R. M. Fuoss and G. I. Cathers, J. Polym. Sci., 1949, 4, 97–120 CrossRef CAS.
- R. M. Fuoss and W. N. Maclay, J. Polym. Sci., 1951, 6, 305–317 CrossRef CAS.
- R. M. Fuoss, Discuss. Faraday Soc., 1951, 11, 125–134 RSC.
- W. N. Maclay and R. M. Fuoss, J. Polym. Sci., 1951, 6, 511–521 CrossRef CAS.
- R. M. Fuoss and D. Edelson, J. Polym. Sci., 1951, 6, 523–532 CrossRef CAS.
- U. P. Strauss and R. M. Fuoss, J. Polym. Sci., 1952, 8, 593–598 CrossRef CAS.
- T. Alfrey Jr, R. M. Fuoss, H. Morawetz and H. Pinner, J. Am. Chem. Soc., 1952, 74, 438–441 CrossRef.
- D. C. Boris and R. H. Colby, Macromolecules, 1998, 31, 5746–5755 CrossRef CAS.
- C. G. Lopez, R. H. Colby, P. Graham and J. T. Cabral, Macromolecules, 2017, 50, 332–338 CrossRef CAS.
- U. Lohmander and R. Stromberg, Makromol. Chem.: Macromol. Chem. Phys., 1964, 72, 143–158 CrossRef CAS.
- T. Yanaki and M. Yamaguchi, Chem. Pharm. Bull., 1994, 42, 1651–1654 CrossRef CAS.
- L. Yuan, T. Dougherty and S. Stivala, J. Polym. Sci., Part A-2, 1972, 10, 171–189 CrossRef CAS.
- H. Trivedi, C. Patel and R. Patel, Appl. Macromol. Chem. Phys., 1981, 95, 155–170 CAS.
- P. Liberti and S. Stivala, J. Polym. Sci., Part B: Polym. Lett., 1966, 4, 137–145 CrossRef CAS.
- J. R. Schaefgen and C. F. Trivisonno, J. Am. Chem. Soc., 1952, 74, 2715–2717 CrossRef CAS.
- Other plots, for example ηredvs. c−1/2 or ηred/c1/2vs. c1/2 were also found to work well. A discussion of these can be found in ref. 289–292 and 403.
- H. Inagaki, H. Sakurai and T. Sasaki, Bull. Inst. Chem. Res., Kyoto Univ., 1956, 34, 74–86 CAS.
- The appearance of a peak was also noted by Fuoss and Cathers for in 1 mM TBABr solvent media.278.
- H. Zhang, H. Zheng, Q. Zhang, J. Wang and M. Konno, Biopolymers, 1998, 46, 395–402 CrossRef CAS.
- J. Cohen, Z. Priel and Y. Rabin, J. Chem. Phys., 1988, 88, 7111–7116 CrossRef CAS.
- J. L. Ganter, M. Milas and M. Rinaudo, Polymer, 1992, 33, 113–116 CrossRef CAS.
- K. Nishida, K. Kaji, T. Kanaya and N. Fanjat, Polymer, 2002, 43, 1295–1300 CrossRef CAS.
- Fig. 8 of ref. 322 shows the shear rate dependence of NaPSS with a N = 5900 (×2.4 that of Nishida's sample). We expect τ ∝ N3, so that Nishida's ηred data should correspond to values 10–20% lower than the zero shear rate limit. Eqn (36) gives
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) C ≃ 103 s−1, which is on the order of the shear rate applied by capillary viscometers.
C ≃ 103 s−1, which is on the order of the shear rate applied by capillary viscometers. - A. Han, V. V. S. Uppala, D. Parisi, C. George, B. J. Dixon, C. D. Ayala, X. Li, L. A. Madsen and R. H. Colby, Macromolecules, 2022, 55, 7148–7160 CrossRef CAS.
- L. Ghimici and F. Popescu, Eur. Polym. J., 1998, 34, 13–16 CrossRef CAS.
- L. Ghimici and E. Avram, J. Appl. Polym. Sci., 2003, 90, 465–469 CrossRef CAS.
- B. A. Wolf, Macromol. Rapid Commun., 2007, 28, 164–170 CrossRef CAS.
- J. Eckelt, A. Knopf and B. A. Wolf, Macromolecules, 2008, 41, 912–918 CrossRef CAS.
- A. Eich and B. A. Wolf, ChemPhysChem, 2011, 12, 2786–2790 CrossRef CAS PubMed.
- X. Xiong and B. A. Wolf, Soft Matter, 2014, 10, 2124–2131 RSC.
- L. Ghimici, M. Nichifor, A. Eich and B. A. Wolf, Carbohydr. Polym., 2012, 87, 405–410 CrossRef CAS PubMed.
- B. A. Wolf, RSC Adv., 2016, 6, 38004–38011 RSC.
- P. Suresha, M. V. Badiger and B. A. Wolf, RSC Adv., 2015, 5, 27674–27681 RSC.
- M. V. Badiger, N. R. Gupta, J. Eckelt and B. A. Wolf, Macromol. Chem. Phys., 2008, 209, 2087–2093 CrossRef CAS.
- M. Bercea and B. A. Wolf, Int. J. Biol. Macromol., 2019, 140, 661–667 CrossRef CAS PubMed.
- A. Chatterjee and B. Das, Carbohydr. Polym., 2013, 98, 1297–1303 CrossRef CAS PubMed.
- A. Banerjee, R. De and B. Das, Carbohydr. Polym., 2022, 277, 118855 CrossRef CAS PubMed.
- J. Cohen and Z. Priel, J. Chem. Phys., 1990, 93, 9062–9068 CrossRef CAS.
- M. Kato, T. Nakagawa and H. Akamatu, Bull. Chem. Soc. Jpn., 1960, 33, 322–329 CrossRef CAS.
- J. Yamanaka, H. Araie, H. Matsuoka, H. Kitano, N. Ise, T. Yamaguchi, S. Saeki and M. Tsubokawa, Macromolecules, 1991, 24, 6156–6159 CrossRef CAS.
- H. Vink, Polymer, 1992, 33, 3711–3716 CrossRef CAS.
- H. Vink, J. Chem. Soc., Faraday Trans. 1, 1987, 83, 801–811 RSC.
- S. Batzill, R. Luxemburger, R. Deike and R. Weber, Eur. Phys. J. B, 1998, 1, 491–501 CrossRef CAS.
- H. Vink, Macromol. Chem. Phys., 1970, 131, 133–145 CrossRef CAS.
- J. Yamanaka, H. Matsuoka, H. Kitano, M. Hasegawa and N. Ise, J. Am. Chem. Soc., 1990, 112, 587–592 CrossRef CAS.
- J. Yamanaka, S. Yamada, N. Ise and T. Yamaguchi, J. Polym. Sci., Part B: Polym. Phys., 1995, 33, 1523–1526 CrossRef CAS.
- H. Eisenberg, J. Polym. Sci., 1957, 23, 579–599 CrossRef CAS.
- Note that for sodium hyaluronate, which is a co-polymer of D-glucuronic acid and N-acetyl-D-glucosamine we express the concentration in units of saccharide units, i.e. each chain segment with a length of ≃5 Å is counted as a monomer. This differs from the more usual convention of expressing molar concentration in terms of disaccharide units.
- D. Ray, R. De and B. Das, J. Chem. Thermodyn., 2016, 101, 227–235 CrossRef CAS.
- T. J. Podlas and P. Ander, Macromolecules, 1970, 3, 154–157 CrossRef CAS.
- R. L. Cleland, Biopolymers, 1968, 6, 1519–1529 CrossRef CAS PubMed.
- M. Rinaudo and M. Milas, Chem. Phys. Lett., 1976, 41, 456–459 CrossRef CAS.
- D. Truzzolillo, F. Bordi, C. Cametti and S. Sennato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011804 CrossRef CAS PubMed.
- J. A. V. Butler, A. Robins and K. Shooter, Proc. R. Soc. London, Ser. A Sci., 1957, 241, 299–310 CAS.
- I. Roure, M. Rinaudo, M. Milas and E. Frollini, Polymer, 1998, 39, 5441–5445 CrossRef CAS.
- H. Terayama, J. Polym. Sci., 1956, 19, 181–198 CrossRef CAS.
- H. Terayama, J. Polym. Sci., 1955, 15, 575–590 CrossRef CAS.
- H. Fujita and T. Homma, J. Colloid Sci., 1954, 9, 591–601 CrossRef CAS.
- H. Fujita and T. Homma, J. Polym. Sci., 1955, 15, 277–295 CrossRef CAS.
- I. Roure, M. Rinaudo and M. Milas, Bunsen-Ges. Phys. Chem., Ber., 1996, 100, 703–706 CrossRef CAS.
- M. Rinaudo, I. Roure, M. Milas and A. Malovikova, Int. J. Polym. Anal. Charact., 1997, 4, 57–69 CrossRef CAS.
- H. Zhang, H. Wang, J. Wang, R. Guo and Q. Zhang, Polym. Adv. Technol., 2001, 12, 740–745 CrossRef CAS.
- J. Cohen and Z. Priel, Macromolecules, 1989, 22, 2356–2358 CrossRef CAS.
- W. Essafi, N. Haboubi, C. Williams and F. Boue, J. Phys. Chem. B, 2011, 115, 8951–8960 CrossRef CAS PubMed.
- J. Yang, N. Liu, D. Yu, C. Peng, H. Liu, Y. Hu and J. Jiang, Ind. Eng. Chem. Res., 2005, 44, 8120–8126 CrossRef CAS.
- W. F. Reed, J. Chem. Phys., 1994, 101, 2515–2521 CrossRef CAS.
- M. Antonietti, A. Briel and S. Forster, J. Chem. Phys., 1996, 105, 7795–7807 CrossRef CAS.
- K. Nishida, K. Kaji and T. Kanaya, Polymer, 2001, 42, 8657–8662 CrossRef CAS.
- B. Ashok and M. Muthukumar, J. Phys. Chem. B, 2009, 113, 5736–5745 CrossRef CAS PubMed.
- R. Borsali, T. Vilgis and M. Benmouna, Macromolecules, 1992, 25, 5313–5317 CrossRef CAS.
- W. Hess and R. Klein, Adv. Phys., 1983, 32, 173–283 CrossRef CAS.
- S. Nojd, P. Holmqvist, N. Boon, M. Obiols-Rabasa, P. S. Mohanty, R. Schweins and P. Schurtenberger, Soft Matter, 2018, 14, 4150–4159 RSC.
- C. G. Lopez, T. Lohmeier, J. E. Wong and W. Richtering, J. Colloid Interface Sci., 2020, 558, 200–210 CrossRef PubMed.
- A. Fernandez-Nieves, A. Fernandez-Barbero, B. Vincent and F. De Las Nieves, Macromolecules, 2000, 33, 2114–2118 CrossRef CAS.
- D. Capriles-Gonzalez, B. Sierra-Martin, A. Fernandez-Nieves and A. Fernandez-Barbero, J. Phys. Chem. B, 2008, 112, 12195–12200 CrossRef CAS PubMed.
- T. Lopez-Leon and A. Fernandez-Nieves, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 011801 CrossRef CAS PubMed.
- A. Fernandez-Nieves, A. Fernandez-Barbero, B. Vincent and F. De las Nieves, J. Chem. Phys., 2003, 119, 10383–10388 CrossRef CAS.
- A. A. Polotsky, F. A. Plamper and O. V. Borisov, Macromolecules, 2013, 46, 8702–8709 CrossRef CAS.
- R. Borsali, T. A. Vilgis and M. Benmouna, Macromol. Theory Simul., 1994, 3, 73–77 CrossRef CAS.
- F. Akkerman, D. Pals and J. Hermans, Recl. Trav. Chim. Pays-Bas, 1952, 71, 56–63 CrossRef CAS.
- M. Moan and C. Wolff, Eur. Polym. J., 1973, 9, 1085–1093 CrossRef CAS.
- W. Brown and D. Henley, Macromol. Chem. Phys., 1964, 79, 68–88 CrossRef CAS.
- W. Brown, D. Henley and J. Ohman, Ark. Kemi, 1964, 22, 189–206 CAS.
- H. Eisenberg, J. Polym. Sci., 1957, 25, 257–271 CrossRef CAS.
- R. Stromberg, Non-Newtonian Flow of Dilute Polymethacrylic Acid Solutions at Different Degrees of Neutralization and Ionic Strengths, Uppsala Univ. (Sweden) Inst. of Physical Chemistry Technical Report, 1966.
- S. Pan, D. A. Nguyen, B. Dunweg, P. Sunthar, T. Sridhar and J. Ravi Prakash, J. Rheol., 2018, 62, 845–867 CrossRef CAS.
- H. Dakhil, S. Basu, S. Steiner, Y. Gerlach, A. Soller, S. Pan, N. Germann, M. Leidenberger, B. Kappes and A. Wierschem, J. Rheol., 2021, 65, 159–169 CrossRef CAS.
- M. Fixman, J. Chem. Phys., 1966, 45, 793–803 CrossRef CAS PubMed.
- T. Kotaka, H. Suzuki and H. Inagaki, J. Chem. Phys., 1966, 45, 2770–2773 CrossRef CAS.
- I. Noda, Y. Yamada and M. Nagasawa, J. Phys. Chem., 1968, 72, 2890–2898 CrossRef CAS.
- H. Suzuki, T. Kotaka and H. Inagaki, J. Chem. Phys., 1969, 51, 1279–1285 CrossRef CAS.
- R. G. Larson, J. Rheol., 2005, 49, 1–70 CrossRef CAS.
- J. G. Kirkwood and R. J. Plock, J. Chem. Phys., 1956, 24, 665–669 CrossRef CAS.
- N. Saito and M. Sugita, J. Phys. Soc. Jpn., 1952, 7, 554–559 CrossRef CAS.
- H. A. Scheraga, J. Chem. Phys., 1955, 23, 1526–1532 CrossRef CAS.
- J. T. Yang, J. Am. Chem. Soc., 1958, 80, 1783–1788 CrossRef CAS.
- D. Shogin and P. A. Amundsen, Phys. Fluids, 2020, 32, 063101 CrossRef CAS.
- R. Pamies, J. H. Cifre and J. G. De La Torre, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 1–9 CrossRef CAS.
- S. Pattanayek and J. R. Prakash, Macromolecules, 2008, 41, 2260–2270 CrossRef CAS.
- S. P. Singh and R. G. Winkler, J. Rheol., 2020, 64, 1121–1131 CrossRef CAS.
- K. Jayasree, R. Kumar Manna, D. Banerjee and P. Kumar, J. Chem. Phys., 2013, 139, 224902 CrossRef PubMed.
- C. Stoltz, J. J. de Pablo and M. D. Graham, J. Chem. Phys., 2007, 126, 124906 CrossRef PubMed.
- K. Zheng, K. Chen, W. Ren, J. Yang and J. Zhao, Macromolecules, 2022, 55, 1647–1656 CrossRef CAS.
- O. Borisov, A. Darinskii and E. Zhulina, Macromolecules, 1995, 28, 7180–7187 CrossRef CAS.
- R. Pamies, J. H. Cifre and J. G. De La Torre, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 714–722 CrossRef CAS.
- G. Xu, S. Luo, Q. Yang, J. Yang and J. Zhao, J. Chem. Phys., 2016, 145, 144903 CrossRef PubMed.
- H. Yamakawa and T. Yoshizaki, Macromolecules, 1980, 13, 633–643 CrossRef CAS.
- G. Sitaramaiah and D. Goring, J. Polym. Sci., 1962, 58, 1107–1131 CrossRef CAS.
- G. Xu, J. Yang and J. Zhao, J. Chem. Phys., 2018, 149, 163329 CrossRef PubMed.
- A similar decrease in [η] can be observed for NaPVS in DI water and 10−4 M NaCl in Fig. 4c.
- D. Izzo, M. Cloitre and L. Leibler, Soft Matter, 2014, 10, 1714–1722 RSC.
- N. Imai and K. Gekko, Biophys. Chem., 1991, 41, 31–40 CrossRef CAS PubMed.
- K. Kaji, H. Urakawa, T. Kanaya and R. Kitamaru, J. Phys., 1988, 49, 993–1000 CrossRef CAS.
- C. G. Lopez and W. Richtering, J. Chem. Phys., 2018, 148, 244902 CrossRef PubMed.
- J. Combet, F. Isel, M. Rawiso and F. Boue, Macromolecules, 2005, 38, 7456–7469 CrossRef CAS.
- J. Combet, M. Rawiso, C. Rochas, S. Hoffmann and F. Boue, Macromolecules, 2011, 44, 3039–3052 CrossRef CAS.
- K. Nishida, K. Kaji and T. Kanaya, J. Chem. Phys., 2001, 114, 8671–8677 CrossRef CAS.
- M. Drifford and J. P. Dalbiez, J. Phys. Chem., 1984, 88, 5368–5375 CrossRef CAS.
- S. Forster, M. Schmidt and M. Antonietti, Polymer, 1990, 31, 781–792 CrossRef.
- C. G. Lopez, Macromolecules, 2019, 52, 9409–9415 CrossRef CAS.
- M.-W. Kim and D. Peiffer, EPL, 1988, 5, 321 CrossRef CAS.
- M. Matsumoto and T. Eguchi, J. Polym. Sci., 1957, 26, 393–396 CrossRef CAS.
- Q. Ying and B. Chu, Macromolecules, 1987, 20, 362–366 CrossRef CAS.
- S. S. Vadodaria and R. J. English, Cellulose, 2016, 23, 1107–1121 CrossRef CAS.
- Z.-G. Wang, Macromolecules, 2017, 50, 9073–9114 CrossRef CAS.
- C. G. Lopez and W. Richtering, J. Phys. Chem. B, 2019, 123, 5626–5634 CrossRef CAS PubMed.
- C. G. Lopez, ACS Macro Lett., 2019, 8, 979–983 CrossRef CAS PubMed.
- A. Han, PhD thesis, Penn State, 2002 Search PubMed.
- C. G. Lopez, J. Rheol., 2020, 64, 191–204 CrossRef CAS.
- We assume a Kuhn segment of 2 nm and three Kuhn segments per chains, and calculate ξel assuming no excluded volume inside the electrostatic blob.
- Note that the ηsp(c*) = 1 criterion is expected to fail for short oligomeric chains, where, based on the general trends observed for electrolytes,705 the ηsp(c*) ≃ 1 point is reached well below the ‘overlap’ point.
- J. A. Bollinger, G. S. Grest, M. J. Stevens and M. Rubinstein, Macromolecules, 2021, 54, 10068–10073 CrossRef CAS.
- M. Oostwal, M. Blees, J. De Bleijser and J. Leyte, Macromolecules, 1993, 26, 7300–7308 CrossRef CAS.
- U. P. Strauss and R. M. Fuoss, J. Polym. Sci., 1949, 4, 457–472 CrossRef CAS.
- Q. Liao, A. V. Dobrynin and M. Rubinstein, Macromolecules, 2003, 36, 3399–3410 CrossRef.
- C. Tsimpris, B. Suryanarayanan and K. Mayhan, J. Polym. Sci., Part A-2, 1972, 10, 1837–1839 CrossRef CAS.
- DMF is a somewhat unusual solvent polystyrene, see ref. 559 and 706 and references therein.
- Y. Matsushita, K. Shimizu, Y. Nakao, H. Choshi, I. Noda and M. Nagasawa, Polym. J., 1986, 18, 361–366 CrossRef CAS.
- M. Matsumoto and T. Eguchi, J. Polym. Sci., 1957, 23, 617–634 CrossRef CAS.
- We are currently conducting small angle X-ray/neutron scattering experiments for PC4-TFSI in various solvents in order to evaluate the local chain conformation in a given solvent. The preliminary results found the correlation length scaled as ξ ∝ c0.5 over a wide monomer concentration (c) range. The observed scaling is similar to that for polyelectrolytes in either theta or good solvents. The data will be published elsewhere.
- S. Dou and R. H. Colby, Macromolecules, 2008, 41, 6505–6510 CrossRef CAS.
- F. Bordi, C. Cametti, J. Tan, D. Boris, W. Krause, N. Plucktaveesak and R. Colby, Macromolecules, 2002, 35, 7031–7038 CrossRef CAS.
- E. L. Bennett, I. Calisir, X. Yang, Y. Huang and J. Xiao, J. Phys. Chem. C, 2023, 127, 18669–18677 CrossRef CAS.
- S. Dou, Synthesis and characterization of ion-containing polymers, PhD thesis, Pennsylvania State University, 2007 Search PubMed.
- A. Sehgal and T. A. Seery, Macromolecules, 1998, 31, 7340–7346 CrossRef CAS.
- Z. Alexandrowicz, J. Polym. Sci., 1959, 40, 91–106 CrossRef CAS.
- W. Essafi, F. Lafuma, D. Baigl and C. Williams, EPL, 2005, 71, 938 CrossRef CAS.
- E. Raspaud, M. Da Conceicao and F. Livolant, Phys. Rev. Lett., 2000, 84, 2533 CrossRef CAS PubMed.
- P. L. Hansen, R. Podgornik and V. A. Parsegian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 021907 CrossRef CAS PubMed.
- M. Muthukumar, J. Chem. Phys., 2012, 137, 034902 CrossRef CAS PubMed.
- S. Saha, K. Fischer, M. Muthukumar and M. Schmidt, Macromolecules, 2013, 46, 8296–8303 CrossRef CAS.
- S. Saha, PhD thesis, Mainz, Univ., Diss., 2012, 2013 Search PubMed.
- M. Nagasawa and I. Kagawa, J. Polym. Sci., 1957, 25, 61–76 CrossRef CAS.
- T. J. Podlas and P. Ander, Macromolecules, 1969, 2, 432–436 CrossRef CAS.
- M. Rinaudo and M. Milas, J. Polym. Sci., Polym. Chem. Ed., 1974, 12, 2073–2081 CrossRef CAS.
- J. Tan and P. Marcus, J. Polym. Sci., Polym. Phys. Ed., 1976, 14, 239–250 CrossRef CAS.
- G. Pass, G. Phillips and D. Wedlock, Macromolecules, 1977, 10, 197–201 CrossRef CAS.
- S. Miura, M. Satoh and J. Komiyama, Polymer, 1996, 37, 1641–1646 CrossRef CAS.
- H. Maki and T. Miyajima, Macromolecules, 2011, 44, 5027–5035 CrossRef CAS.
- F. Bordi, R. Colby, C. Cametti, L. De Lorenzo and T. Gili, J. Phys. Chem. B, 2002, 106, 6887–6893 CrossRef CAS.
- T. Vuletić, S. D. Babić, D. Grgičin, D. Aumiler, J. Radler, F. Livolant and S. Tomić, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 041803 CrossRef PubMed.
- R. Buchner, G. T. Hefter and P. M. May, J. Phys. Chem. A, 1999, 103, 1–9 CrossRef CAS.
- J. R. Huizenga, P. F. Grieger and F. T. Wall, J. Am. Chem. Soc., 1950, 72, 4228–4232 CrossRef CAS.
- M. Nagasawa, I. Noda, T. Takahashi and N. Shimamoto, J. Phys. Chem., 1972, 76, 2286–2294 CrossRef CAS.
- A. Matsumoto and A. Q. Shen, Soft Matter, 2022, 18, 4197–4204 RSC.
- P. Rodič, M. Bratuša, M. Lukšič, V. Vlachy and B. Hribar-Lee, Colloids Surf., A, 2013, 424, 18–25 CrossRef.
- T. A. Waigh, R. Ober, C. E. Williams and J.-C. Galin, Macromolecules, 2001, 34, 1973–1980 CrossRef CAS.
- G. R. Leader and J. F. Gormley, J. Am. Chem. Soc., 1951, 73, 5731–5733 CrossRef CAS.
- S. J. Bass, W. I. Nathan, R. M. Meighan and R. H. Cole, J. Phys. Chem., 1964, 68, 509–515 CrossRef CAS.
- A. V. Dobrynin and M. Rubinstein, Macromolecules, 1999, 32, 915–922 CrossRef CAS.
- W. Essafi, W. Raissi, A. Abdelli and F. Boue, J. Phys. Chem. B, 2014, 118, 12271–12281 CrossRef CAS PubMed.
- W. Essafi, A. Abdelli, G. Bouajila and F. Boue, J. Phys. Chem. B, 2012, 116, 13525–13537 CrossRef CAS PubMed.
- A. Chremos and J. F. Douglas, J. Chem. Phys., 2018, 149, 163305 CrossRef PubMed.
- A. Chremos and J. F. Douglas, Soft Matter, 2016, 12, 2932–2941 RSC.
- A. Chremos and J. F. Douglas, J. Chem. Phys., 2017, 147, 241103 CrossRef PubMed.
- A. Chremos and J. F. Douglas, Gels, 2018, 4, 20 CrossRef PubMed.
- N. T. Klooster, F. Van der Touw and M. Mandel, Macromolecules, 1984, 17, 2087–2093 CrossRef CAS.
- G. Gebel, Macromolecular Complexes in Chemistry and Biology, 1994, p. 329 Search PubMed.
- A. Pedley, J. Higgins, D. Peiffer and W. Burchard, Macromolecules, 1990, 23, 1434–1437 CrossRef CAS.
- A. Young, J. Higgins, D. Peiffer and A. Rennie, Polymer, 1995, 36, 691–697 CrossRef CAS.
- R. Lundberg and H. Makowski, J. Polym. Sci., Polym. Phys. Ed., 1980, 18, 1821–1836 CrossRef CAS.
- P. K. Agarwal, R. T. Garner and W. W. Graessley, J. Polym. Sci., Part B: Polym. Phys., 1987, 25, 2095–2111 CrossRef CAS.
- D. Kawaguchi, S. Kawauchi, M. Satoh and J. Komiyama, Polymer, 1998, 39, 1387–1392 CrossRef CAS.
- R. Weiss, J. Fitzgerald, H. Frank and B. Chadwick, Macromolecules, 1986, 19, 2085–2087 CrossRef CAS.
- S. Nomula and S. L. Cooper, Macromolecules, 2001, 34, 2653–2659 CrossRef CAS.
- Z. Zhang, C. Liu, X. Cao, J.-H. H. Wang, Q. Chen and R. H. Colby, Macromolecules, 2017, 50, 963–971 CrossRef CAS.
- E. Penzel and N. Goetz, Appl. Macromol. Chem. Phys., 1990, 178, 191–200 CAS.
- S. Newman, W. R. Krigbaum, C. Laugier and P. J. Flory, J. Polym. Sci., 1954, 14, 451–462 CrossRef CAS.
- T. Ono, T. Sugimoto, S. Shinkai and K. Sada, Nat. Mater., 2007, 6, 429–433 CrossRef CAS PubMed.
- T. Ono, T. Sugimoto, S. Shinkai and K. Sada, Adv. Funct. Mater., 2008, 18, 3936–3940 CrossRef CAS.
- T. Ono, S. Shinkai and K. Sada, Soft Matter, 2008, 4, 748–750 RSC.
- K. Iseda, M. Ohta, T. Ono and K. Sada, Soft Matter, 2011, 7, 5938–5940 RSC.
- T. Ono, M. Ohta, K. Iseda and K. Sada, Soft Matter, 2012, 8, 3700–3704 RSC.
- D. Kawaguchi and M. Satoh, Macromolecules, 1999, 32, 7828–7835 CrossRef CAS.
- E. Nordmeier and W. Dauwe, Polym. J., 1992, 24, 229–238 CrossRef CAS.
- E. Nordmeier, Polym. J., 1993, 25, 1–17 CrossRef CAS.
- E. Nordmeier, Polym. J., 1993, 25, 19–30 CrossRef CAS.
- A. Raziel and H. Eisenberg, Isr. J. Chem., 1973, 11, 183–199 CrossRef CAS.
- N. Borochov and H. Eisenberg, Macromolecules, 1994, 27, 1440–1445 CrossRef CAS.
- R. M. Peitzsch, M. J. Burt and W. F. Reed, Macromolecules, 1992, 25, 806–815 CrossRef CAS.
- A. Bose, J. Rollings, J. Caruthers, M. Okos and G. Tsao, J. Appl. Polym. Sci., 1982, 27, 795–810 CrossRef CAS.
- R. Davis and W. Russel, Macromolecules, 1987, 20, 518–525 CrossRef CAS.
- R. Brussau, N. Goetz, W. Machtle and J. Stolting, Tenside, Surfactants, Deterg., 1991, 28, 396–406 CrossRef.
- H. Eisenberg, Q. Rev. Biophys., 1981, 14, 141–172 CrossRef CAS PubMed.
- H. Yamakawa, Macromolecules, 1992, 25, 1912–1916 CrossRef CAS.
- K. Tsutsumi and T. Norisuye, Polym. J., 1998, 30, 345–349 CrossRef CAS.
- T. Sato, T. Norisuye and H. Fujita, Polym. J., 1984, 16, 341–350 CrossRef CAS.
- T. Sato, T. Norisuye and H. Fujita, Macromolecules, 1984, 17, 2696–2700 CrossRef CAS.
- J. Tan and S. Gasper, J. Polym. Sci., Polym. Phys. Ed., 1975, 13, 1705–1719 CrossRef CAS.
- F. Abe, Y. Einaga, T. Yoshizaki and H. Yamakawa, Macromolecules, 1993, 26, 1884–1890 CrossRef CAS.
- K. Huber, S. Bantle, P. Lutz and W. Burchard, Macromolecules, 1985, 18, 1461–1467 CrossRef CAS.
- Y. Einaga, F. Abe and H. Yamakawa, Macromolecules, 1993, 26, 6243–6250 CrossRef CAS.
- P. Balding, R. Borrelli, R. Volkovinsky and P. S. Russo, Macromolecules, 2022, 55, 1747–1762 CrossRef CAS.
- Z. Luo and G. Zhang, Macromolecules, 2010, 43, 10038–10044 CrossRef CAS.
- A. K. Sen, S. Roy and V. A. Juvekar, Polym. Int., 2007, 56, 167–174 CrossRef CAS.
- A. K. Sen, PhD thesis, Indian Institute of Technology, Bombay (India), 2005 Search PubMed.
- Extrapolating the RH data of Serhatli et al.495 for ≃85% sulfonated PSS in 4.17 M to RH2/N ≃ 5 Å2 yields a theta temperature for their samples of 35–40°, consistent with a 1–2 °C shift of the theta point per percentage point of sulfonation.
- E. Serhatli, M. Serhatli, B. M. Baysal and F. E. Karasz, Polymer, 2002, 43, 5439–5445 CrossRef CAS.
- L. Wang and H. Yu, Macromolecules, 1988, 21, 3498–3501 CrossRef CAS.
- G. M. Pavlov, O. V. Okatova, A. S. Gubarev, I. I. Gavrilova and E. F. Panarin, Macromolecules, 2014, 47, 2748–2758 CrossRef CAS.
- A. Raziel, Excluded volume study of polyelectrolyte solutions: Potassium polystyrenesulfonate, PhD thesis, The Weizmann Institute of Science (Israel), 1971 Search PubMed.
- R. Schweins, J. Hollmann and K. Huber, Polymer, 2003, 44, 7131–7141 CrossRef CAS.
- J. Tanahatoe and M. Kuil, Macromolecules, 1997, 30, 6102–6106 CrossRef CAS.
- N. Plucktaveesak, A. J. Konop and R. H. Colby, J. Phys. Chem. B, 2003, 107, 8166–8171 CrossRef CAS.
- N. Borochov and H. Eisenberg, Biopolymers, 1984, 23, 1757–1769 CrossRef CAS PubMed.
- Z. Kam, N. Borochov and H. Eisenberg, Biopolymers, 1981, 20, 2671–2690 CrossRef CAS PubMed.
- S. P. Gasper and J. S. Tan, Water-Soluble Polymers: Proceedings of a Symposium held by the American Chemical Society, Division of Organic Coatings and Plastics Chemistry, in New York City on August 30–31, 1972, 1973, pp. 387–400.
- J. Tan and S. Gasper, Macromolecules, 1973, 6, 741–746 CrossRef CAS.
- J. Tan and S. Gasper, J. Polym. Sci., Polym. Phys. Ed., 1974, 12, 1785–1804 CrossRef CAS.
- H. Edelhoch and J. Bateman, J. Am. Chem. Soc., 1957, 79, 6093–6100 CrossRef CAS.
- R. B. Hawkins and A. Holtzer, Macromolecules, 1972, 5, 294–301 CrossRef CAS.
- H. Ochiai, M. Handa, H. Matsumoto, T. Moriga and I. Murakami, Macromol. Chem. Phys., 1985, 186, 2547–2556 CrossRef CAS.
- N. S. Schneider and P. Doty, J. Phys. Chem., 1954, 58, 762–769 CrossRef CAS.
- H. Zhang, H. Zheng, Q. Zhang, S. Gao and J. Wang, Polym. Adv. Technol., 1997, 8, 722–726 CrossRef CAS.
- K. Vanneste, D. Slootmaekers and H. Reynaers, Food Hydrocolloids, 1996, 10, 99–107 CrossRef CAS.
- D. Pals and J. Hermans, Recl. Trav. Chim. Pays-Bas, 1952, 71, 458–467 CrossRef CAS.
- T. Nicolai and M. Mandel, Macromolecules, 1989, 22, 438–444 CrossRef CAS.
- E. Sobel and J. Harpst, Biopolymers, 1991, 31, 1559–1564 CrossRef CAS PubMed.
- K. A. Strand, A. Boe, P. Dalberg, T. Sikkeland and O. Smidsroed, Macromolecules, 1982, 15, 570–579 CrossRef CAS.
- I. Morfin, W. F. Reed, M. Rinaudo and R. Borsali, J. Phys. II, 1994, 4, 1001–1019 CrossRef CAS.
- L. Fisher, A. Sochor and J. Tan, Macromolecules, 1977, 10, 949–954 CrossRef CAS.
- E. Daniel and Z. Alexandrowicz, Biopolymers, 1963, 1, 473–495 CrossRef CAS.
- J. Tanahatoe and M. Kuil, J. Phys. Chem. A, 1997, 101, 8389–8394 CrossRef CAS.
- R. Smits, M. Kuil and M. Mandel, Macromolecules, 1993, 26, 6808–6816 CrossRef CAS.
- E. Buhler and M. Rinaudo, Macromolecules, 2000, 33, 2098–2106 CrossRef CAS.
- E. Buhler, O. Guetta and M. Rinaudo, Int. J. Polym. Anal. Charact., 2001, 6, 155–175 CrossRef.
- T. Nicolai and M. Mandel, Macromolecules, 1989, 22, 2348–2356 CrossRef CAS.
- C. Pyun and M. Fixman, J. Chem. Phys., 1964, 41, 937–944 CrossRef CAS.
- H. Yamakawa, J. Chem. Phys., 1962, 36, 2995–3001 CrossRef CAS.
- M. Nagasawa and Y. Eguchi, J. Phys. Chem., 1967, 71, 880–888 CrossRef CAS.
- J. Si, N. Hao, M. Zhang, S. Cheng, A. Liu, L. Li and X. Ye, ACS Macro Lett., 2019, 8, 730–736 CrossRef CAS PubMed.
- Z. Luo and G. Zhang, Polymer, 2011, 52, 5846–5850 CrossRef CAS.
- P. M. Budd, Polymer, 1985, 26, 1519–1522 CrossRef CAS.
- F. Abe, Y. Einaga and H. Yamakawa, Macromolecules, 1993, 26, 1891–1897 CrossRef CAS.
- H. Zhou, G. Song, Y. X. Zhang, R. Dieing, L. Ma and L. Haeussling, Chin. J. Chem., 2000, 18, 322–327 CrossRef CAS.
- U. P. Strauss, N. L. Gershfeld and E. H. Crook, J. Phys. Chem., 1956, 60(5), 577–584 CrossRef CAS.
- H. Inoue, Kolloid-Zeitschrift und Zeitschrift fur Polymere, 1964, 195, 102–110 CrossRef CAS.
- G. Pavlov and A. Gosteva, Polym. Sci., Ser. A, 2022, 64, 586–590 CrossRef CAS.
- G. M. Pavlov, A. A. Gosteva, O. V. Okatova, O. A. Dommes, I. I. Gavrilova and E. F. Panarin, Polym. Chem., 2021, 12, 2325–2334 RSC.
- I. Noda, T. Tsuge and M. Nagasawa, J. Phys. Chem., 1970, 74, 710–719 CrossRef CAS.
- T. Kato, T. Tokuya, T. Nozaki and A. Takahashi, Polymer, 1984, 25, 218–224 CrossRef CAS.
- P. J. Kay and F. Treloar, Macromol. Chem. Phys., 1974, 175, 3207–3223 CrossRef CAS.
- A. Takahashi and M. Nagasawa, J. Am. Chem. Soc., 1964, 86, 543–548 CrossRef CAS.
- G. Staikos and G. Bokias, Polym. Int., 1993, 31, 385–389 CrossRef CAS.
- G. Bokias and G. Staikos, Polymer, 1995, 36, 2079–2082 CrossRef CAS.
- M. Sakurai, T. Imai, F. Yamashita, K. Nakamura and T. Komatsu, et al. , Polym. J., 1993, 25, 1247–1255 CrossRef CAS.
- These relationships are extracted from Fig. 1 of ref. 11.
- W. F. Reed, S. Ghosh, G. Medjahdi and J. Francois, Macromolecules, 1991, 24, 6189–6198 CrossRef CAS.
- W. F. Reed, Results on Polyelectrolyte Conformations, Diffusion, and Interparticle Interactions and Correlations, Macro-ion Characterization, ACS Symposium Series, ACS Publications, 1994, ch. 23, vol. 548, pp. 297–314 DOI:10.1021/bk-1994-0548.ch023.
- K. Kamide, A. Kataoka and T. Kawai, Macromol. Chem. Phys., 1970, 139, 221–253 CrossRef CAS.
- S. Arichi, Bull. Chem. Soc. Jpn., 1966, 39, 439–446 CrossRef CAS.
- S. Arichi, H. Matsuura, Y. Tanimoto and H. Murata, Bull. Chem. Soc. Jpn., 1966, 39, 434–439 CrossRef CAS.
- For example water is a non-solvent for P2VP while methanol and 1-propanol are good solvents. We are unable to find references for NMF and formamide.
- T. Orofino, Recl. Trav. Chim. Pays-Bas, 1959, 78, 434–439 CrossRef CAS.
- T. Orofino and P. Flory, J. Phys. Chem., 1959, 63, 283–290 CrossRef CAS.
- Z. Alexandrowicz, J. Polym. Sci., 1962, 56, 115–132 CrossRef CAS.
- K. McCarthy, C. Burkhardt and D. Parazak, J. Appl. Polym. Sci., 1987, 33, 1699–1714 CrossRef CAS.
- S. Ghosh, X. Li, C. E. Reed and W. F. Reed, Biopolymers, 1990, 30, 1101–1112 CrossRef CAS.
- C. E. Reed and W. F. Reed, J. Chem. Phys., 1991, 94, 8479–8486 CrossRef CAS.
- N. Mizukoshi and T. Norisuye, Polym. Bull., 1998, 40, 555–562 CrossRef CAS.
- W. Stockmayer and M. Fixman, J. Polym. Sci., Part C: Polym. Symp., 1963, 137–141 CrossRef.
- M. Bohdanecky and D. Berek, Die Makromolekulare Chemie, Rapid Communications, 1985, 6, 275–280 CrossRef CAS.
- S. Bushin, V. Tsvetkov, Y. B. Lysenko and V. Yemel’Yanov, Polym. Sci. USSR, 1981, 23, 2705–2715 CrossRef.
- F. Abe, Y. Einaga and H. Yamakawa, Macromolecules, 1994, 27, 3262–3271 CrossRef CAS.
- An exception to this are the A2 results for NaPSS and NaPAMS at low N. Their unusual behaviour should be validated by further experimental work.
- C. G. Lopez, A. Scotti, M. Brugnoni and W. Richtering, Macromol. Chem. Phys., 2019, 220, 1800421 CrossRef.
- T. C. Laurent, M. Ryan and A. Pietruszkiewicz, Biochem. Biophys. Acta, 1960, 42, 476–485 CAS.
- R. Takahashi, K. Kubota, M. Kawada and A. Okamoto, Biopolymers, 1999, 50, 87–98 CrossRef CAS.
- R. L. Cleland and J. L. Wang, Biopolymers, 1970, 9, 799–810 CrossRef CAS PubMed.
- R. L. Cleland, Biopolymers, 1984, 23, 647–666 CrossRef CAS.
- E. Fouissac, M. Milas, M. Rinaudo and R. Borsali, Macromolecules, 1992, 25, 5613–5617 CrossRef CAS.
- The fits by Tsutsumi and Norisuye,483 whose best-fit parameters for the lP, B, ML and d we adopt, were carried out using the data from ref. 111 and 483 only. The other datasets included in Fig. 25, which extend the molar mass range, are in excellent agreement with their calculation.
- A. Khokhlov and K. Khachaturian, Polymer, 1982, 23, 1742–1750 CrossRef CAS.
- T. Sato, S. Kojima, T. Norisuye and H. Fujita, Polym. J., 1984, 16, 423–429 CrossRef CAS.
- A. Gubarev, J.-M. Y. Carrillo and A. V. Dobrynin, Macromolecules, 2009, 42, 5851–5860 CrossRef CAS.
- M. Manghi and R. R. Netz, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 14, 67–77 CrossRef CAS PubMed.
- M. Ullner and C. E. Woodward, Macromolecules, 2002, 35, 1437–1445 CrossRef CAS.
- H.-P. Hsu, W. Paul and K. Binder, Macromolecules, 2010, 43, 3094–3102 CrossRef CAS.
- H.-P. Hsu, W. Paul and K. Binder, EPL, 2010, 92, 28003 CrossRef.
- P. Bacova, P. Košovan, F. Uhlik, J. Kuldova, Z. Limpouchova and K. Prochazka, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 1–10 CrossRef PubMed.
- M. Kurata and W. H. Stockmayer, Fortschritte der Hochpolymeren-Forschung, Springer, 2006, pp. 196–312 Search PubMed.
- J. Lindner, W. Wilson and J. Mays, Macromolecules, 1988, 21, 3304–3312 CrossRef CAS.
- K. Venkataswamy, A. Jamieson and R. Petschek, Macromolecules, 1986, 19, 124–133 CrossRef CAS.
- B. Dunweg, D. Reith, M. Steinhauser and K. Kremer, J. Chem. Phys., 2002, 117, 914–924 CrossRef CAS.
- M. L. Mansfield and J. F. Douglas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 021803 CrossRef PubMed.
- F. Vargas-Lara, M. L. Mansfield and J. F. Douglas, J. Chem. Phys., 2017, 147, 014903 CrossRef PubMed.
- T. Konishi, T. Yoshizaki and H. Yamakawa, Macromolecules, 1991, 24, 5614–5622 CrossRef CAS.
- K. S. Kumar and J. R. Prakash, Macromolecules, 2003, 36, 7842–7856 CrossRef CAS.
- H. Fujita, Macromolecules, 1988, 21, 179–185 CrossRef CAS.
- Y. Tsunashima, Polym. J., 1992, 24, 433–436 CrossRef CAS.
- Y. Oono and M. Kohmoto, J. Chem. Phys., 1983, 78, 520–528 CrossRef CAS.
- L. Fetters, N. Hadjichristidis, J. Lindner and J. Mays, J. Phys. Chem. Ref. Data, 1994, 23, 619–640 CrossRef CAS.
- H. Yamakawa, F. Abe and Y. Einaga, Macromolecules, 1993, 26, 1898–1904 CrossRef CAS.
- H. Yamakawa, Modern theory of polymer solutions, Harper & Row, 1971 Search PubMed.
- K. Huber, W. Burchard and A. Z. Akcasu, Macromolecules, 1985, 18, 2743–2747 CrossRef CAS.
- A. Z. Akcasu, Polymer, 1981, 22, 1169–1180 CrossRef CAS.
- A. Z. Akcasu and M. Benmouna, Macromolecules, 1978, 11, 1193–1198 CrossRef.
- H. Murakami, T. Norisuye and H. Fujita, Macromolecules, 1980, 13, 345–352 CrossRef CAS.
- N. Khasat, R. W. Pennisi, N. Hadjichristidis and L. J. Fetters, Macromolecules, 1988, 21, 1100–1106 CrossRef CAS.
- J. Roovers, N. Hadjichristidis and L. J. Fetters, Macromolecules, 1983, 16, 214–220 CrossRef CAS.
- A. Han and R. H. Colby, Macromolecules, 2021, 54, 1375–1387 CrossRef CAS.
- T. Arai, F. Abe, T. Yoshizaki, Y. Einaga and H. Yamakawa, Macromolecules, 1995, 28, 3609–3616 CrossRef CAS.
- J. Rauch and W. Kohler, J. Chem. Phys., 2003, 119, 11977–11988 CrossRef CAS.
- T. Yamada, T. Yoshizaki and H. Yamakawa, Macromolecules, 1992, 25, 377–383 CrossRef CAS.
- J. Szydlowski and W. A. Van Hook, Macromolecules, 1998, 31, 3266–3274 CrossRef CAS.
- W. Burchard and W. Richtering, Dynamic light scattering from polymer solutions, Springer, 1989, pp. 151–163 Search PubMed.
- W. Burchard, Makromolekulare Chemie, Macromolecular Symposia, 1988, pp. 1–35 Search PubMed.
- M. Rubinstein, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 2548–2551 CrossRef CAS.
- P.-G. De Gennes, Scaling concepts in polymer physics, Cornell University Press, 1979 Search PubMed.
- J. Combet, EPJ Web Conf., 2018, p. 03001 Search PubMed.
- E. F. Casassa and H. Eisenberg, J. Phys. Chem., 1961, 65, 427–433 CrossRef CAS.
- H. Eisenberg, Bunsen-Ges. Phys. Chem., Ber., 1989, 93, 350–356 CrossRef CAS.
- E. F. Casassa and H. Eisenberg, J. Phys. Chem., 1960, 64, 753–756 CrossRef CAS.
- M. N. Spiteri, PhD thesis, Universite Orsay - Paris-Sud, 1997 Search PubMed.
- K. Nishida, H. Urakawa, K. Kaji, B. Gabrys and J. S. Higgins, Polymer, 1997, 38, 6083–6085 CrossRef CAS.
- F. Boue, J. Cotton, A. Lapp and G. Jannink, J. Chem. Phys., 1994, 101, 2562–2568 CrossRef CAS.
- K. Nishida, K. Kaji, T. Kanaya and T. Shibano, Macromolecules, 2002, 35, 4084–4089 CrossRef CAS.
- M. Ragnetti and R. Oberthur, Colloid Polym. Sci., 1986, 264, 32–45 CrossRef CAS.
- We calculate P(q) by dividing the F(q) in Kassapidou's paper by 40, the degree of polymerisation of the sample.
- M. Spiteri, F. Boue, A. Lapp and J. Cotton, Phys. Rev. Lett., 1996, 77, 5218 CrossRef CAS PubMed.
- J. S. Pedersen and P. Schurtenberger, Macromolecules, 1996, 29, 7602–7612 CrossRef CAS.
- P. Sharp and V. A. Bloomfield, Biopolymers, 1968, 6, 1201–1211 CrossRef CAS PubMed.
- M. Nierlich, F. Boue, A. Lapp and R. Oberthur, Colloid Polym. Sci., 1985, 263, 955–964 CrossRef CAS.
- A. Yethiraj and C.-Y. Shew, Phys. Rev. Lett., 1996, 77, 3937 CrossRef CAS PubMed.
- A. Yethiraj, J. Chem. Phys., 1998, 108, 1184–1192 CrossRef CAS.
- E. Josef and H. Bianco-Peled, Soft Matter, 2012, 8, 9156–9165 RSC.
- Compare for example the values of lp ≃ 5 Å reported by Josef Bianco-Peled623 for alginate with the more reasonable estimates of lp ≃ 50–150 Å obtained in earlier literature.339,707–709.
- B. D. Ermi and E. J. Amis, Macromolecules, 1998, 31, 7378–7384 CrossRef CAS.
- M. Sedlak, J. Chem. Phys., 1996, 105, 10123–10133 CrossRef CAS.
- M. Schmidt, Die Makromolekulare Chemie, Rapid Communications, 1989, 10, 89–96 CrossRef CAS.
- M. Sedlak and E. J. Amis, J. Chem. Phys., 1992, 96, 826–834 CrossRef CAS.
- M. Sedlak and E. J. Amis, J. Chem. Phys., 1992, 96, 817–825 CrossRef CAS.
- W. F. Reed, Macromolecules, 1994, 27, 873–874 CrossRef CAS.
- K. S. Schmitz, Biopolymers, 1993, 33, 953–959 CrossRef CAS.
- Y. Zhang, J. F. Douglas, B. D. Ermi and E. J. Amis, J. Chem. Phys., 2001, 114, 3299–3313 CrossRef CAS.
- R. C. Michel and W. F. Reed, Biopolymers, 2000, 53, 19–39 CrossRef CAS PubMed.
- D. P. Norwood, M. Benmouna and W. F. Reed, Macromolecules, 1996, 29, 4293–4304 CrossRef CAS.
- M. Sedlak, Macromolecules, 1993, 26, 1158–1162 CrossRef CAS.
- M. Sedlak, Macromolecules, 1995, 28, 793–794 CrossRef CAS.
- M. Sedlak, J. Chem. Phys., 2005, 122, 151102 CrossRef PubMed.
- M. Sedlak, J. Chem. Phys., 2002, 116, 5246–5255 CrossRef CAS.
- M. Sedlak, J. Chem. Phys., 2002, 116, 5236–5245 CrossRef CAS.
- R. Cong, E. Temyanko, P. S. Russo, N. Edwin and R. M. Uppu, Macromolecules, 2006, 39, 731–739 CrossRef CAS.
- A. Takahashi, N. Kato and M. Nagasawa, J. Phys. Chem., 1970, 74, 944–946 CrossRef CAS.
- J. S. Higgins and H. C. Benoit, Polymers and Neutron Scattering, Oxford University Press, 1994 Search PubMed.
- M. Oostwal and T. Odijk, Macromolecules, 1993, 26, 6489–6497 CrossRef CAS.
- K. Zero and B. Ware, J. Chem. Phys., 1984, 80, 1610–1616 CrossRef CAS.
- A. Sehgal and T. A. Seery, Macromolecules, 2003, 36, 10056–10062 CrossRef CAS.
- J. P. Wilcoxon and J. M. Schurr, J. Chem. Phys., 1983, 78, 3354–3364 CrossRef CAS.
- D. Hoagland, E. Arvanitidou and C. Welch, Macromolecules, 1999, 32, 6180–6190 CrossRef CAS.
- C. G. Lopez and W. Richtering, Cellulose, 2019, 26, 1517–1534 CrossRef CAS.
- M. Schmidt, Macromolecules, 1984, 17, 553–560 CrossRef CAS.
- T. Kanematsu, T. Sato, Y. Imai, K. Ute and T. Kitayama, Polym. J., 2005, 37, 65–73 CrossRef CAS.
- W. Brown and T. Nicolai, Colloid Polym. Sci., 1990, 268, 977–990 CrossRef CAS.
- M. Doi and S. F. Edwards, The theory of polymer dynamics, Oxford University Press, 1988, vol. 73 Search PubMed.
- L. Nicholson, J. Higgins and J. Hayter, Macromolecules, 1981, 14, 836–843 CrossRef CAS.
- S.-C. Lin and J. M. Schurr, Biopolymers, 1978, 17, 425–461 CrossRef CAS.
- N. Borochov, H. Eisenberg and Z. Kam, Biopolymers, 1981, 20, 231–235 CrossRef CAS PubMed.
- U. Bohme and U. Scheler, Macromol. Chem. Phys., 2007, 208, 2254–2257 CrossRef.
- K. D. Collins, Biophys. Chem., 2012, 167, 43–59 CrossRef PubMed.
- K. I. Assaf and W. M. Nau, Angew. Chem., Int. Ed., 2018, 57, 13968–13981 CrossRef CAS PubMed.
- K. D. Collins, Q. Rev. Biophys., 2019, 52, e11 CrossRef CAS PubMed.
- N. Malikova, S. Čebašek, V. Glenisson, D. Bhowmik, G. Carrot and V. Vlachy, Phys. Chem. Chem. Phys., 2012, 14, 12898–12904 RSC.
- M. Hohenschutz, I. Grillo, O. Diat and P. Bauduin, Angew. Chem., 2020, 132, 8161–8165 CrossRef.
- K. P. Gregory, G. R. Elliott, H. Robertson, A. Kumar, E. J. Wanless, G. B. Webber, V. S. Craig, G. G. Andersson and A. J. Page, Phys. Chem. Chem. Phys., 2022, 24, 12682–12718 RSC.
- F. Lu, J. Song, B.-W. Cheng, X.-J. Ji and L.-J. Wang, Cellulose, 2013, 20, 1343–1352 CrossRef CAS.
- X. Chen, S. Liang, S.-W. Wang and R. H. Colby, J. Rheol., 2018, 62, 81–87 CrossRef CAS.
- K. Aoki, A. Sugawara-Narutaki, Y. Doi and R. Takahashi, Macromolecules, 2022, 55, 5591–5600 CrossRef CAS.
- A. Sadeghpour, A. Vaccaro, S. Rentsch and M. Borkovec, Polymer, 2009, 50, 3950–3954 CrossRef CAS.
- A. Gallegos, G. M. Ong and J. Wu, Soft Matter, 2021, 17, 9221–9234 RSC.
- K. Bohinc, D. Kovacevic and J. Požar, Phys. Chem. Chem. Phys., 2013, 15, 7210–7219 RSC.
- J. Szymczak, P. Holyk and P. Ander, J. Phys. Chem., 1975, 79, 269–272 CrossRef CAS.
- J. Požar, K. Bohinc, V. Vlachy and D. Kovačević, Phys. Chem. Chem. Phys., 2011, 13, 15610–15618 RSC.
- G. Vesnaver, M. Rudez, C. Pohar and J. Skerjanc, J. Phys. Chem., 1984, 88, 2411–2414 CrossRef CAS.
- H. Daoust and A. Hade, Macromolecules, 1976, 9, 608–611 CrossRef CAS.
- K. Kaji, H. Urakawa, T. Kanaya and R. Kitamaru, Macromolecules, 1984, 17, 1835–1839 CrossRef CAS.
- B. A. Rogers, H. I. Okur, C. Yan, T. Yang, J. Heyda and P. S. Cremer, Nat. Chem., 2022, 14, 40–45 CrossRef CAS PubMed.
- U. P. Strauss and P. D. Ross, J. Am. Chem. Soc., 1959, 81, 5299–5302 CrossRef CAS.
- U. P. Strauss, D. Woodside and P. Wineman, J. Phys. Chem., 1957, 61, 1353–1356 CrossRef CAS.
- I. Satake, M. Fukuda, T. Ohta, K. Nakamura, N. Fujita, A. Yamauchi and H. Kimizuka, J. Polym. Sci., Polym. Phys. Ed., 1972, 10, 2343–2354 CrossRef CAS.
- W. Bare and E. Nordmeier, Polym. J., 1996, 28, 712–726 CrossRef CAS.
- D. M. Correia, L. C. Fernandes, P. M. Martins, C. Garcia-Astrain, C. M. Costa, J. Reguera and S. Lanceros-Mendez, Adv. Funct. Mater., 2020, 30, 1909736 CrossRef CAS.
- T. Huang, M.-C. Long, X.-L. Wang, G. Wu and Y.-Z. Wang, Chem. Eng. J., 2019, 375, 122062 CrossRef CAS.
- A. S. Gouveia, M. Yanez, V. D. Alves, J. Palomar, C. Moya, D. Gorri, L. C. Tome and I. M. Marrucho, Sep. Purif. Technol., 2021, 259, 118113 CrossRef CAS.
- A. M. Smith, A. A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2157–2163 CrossRef CAS PubMed.
- A. Matsumoto, R. Yoshizawa, O. Urakawa, T. Inoue and A. Q. Shen, Macromolecules, 2021, 54, 5648–5661 CrossRef CAS.
- A. A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Faraday Discuss., 2017, 199, 239–259 RSC.
- J. Zeman, S. Kondrat and C. Holm, Chem. Commun., 2020, 56, 15635–15638 RSC.
- J. Zeman, S. Kondrat and C. Holm, J. Chem. Phys., 2021, 155, 204501 CrossRef CAS PubMed.
- S. A. Safran and P. Pincus, Soft Matter, 2023, 19, 7907–7911 RSC.
- E. Krucker-Velasquez and J. W. Swan, J. Chem. Phys., 2021, 155, 134903 CrossRef CAS PubMed.
- S. Kumar, P. Cats, M. B. Alotaibi, S. C. Ayirala, A. A. Yousef, R. van Roij, I. Siretanu and F. Mugele, J. Colloid Interface Sci., 2022, 622, 819–827 CrossRef CAS PubMed.
- Y. C. Fung and S. Perkin, Faraday Discuss., 2023, 246, 370–386 RSC.
- H. Jager, A. Schlaich, J. Yang, C. Lian, S. Kondrat and C. Holm, Faraday Discuss., 2023, 246, 520–539 RSC.
- J. Yang, S. Kondrat, C. Lian, H. Liu, A. Schlaich and C. Holm, Phys. Rev. Lett., 2023, 131, 118201 CrossRef CAS PubMed.
- A. Hartel, M. Bultmann and F. Coupette, Phys. Rev. Lett., 2023, 130, 108202 CrossRef PubMed.
- A. A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Phys. Rev. Lett., 2017, 119, 026002 CrossRef PubMed.
- M. Biesalski, D. Johannsmann and J. Ruhe, J. Chem. Phys., 2004, 120, 8807–8814 CrossRef CAS PubMed.
- G. Liu, D. Parsons and V. S. J. Craig, J. Colloid Interface Sci., 2020, 579, 369–378 CrossRef CAS PubMed.
- We do not consider the data in Fig. 24 and 12 to provide clear tests to the scaling electrostatic blob because in both cases, the fraction of free counterions was not established independently.
- A. Rohatgi, Webplotdigitizer: Version 4.6, 2022, https://automeris.io/WebPlotDigitizer Search PubMed.
- B. Brettmann, P. Pincus and M. Tirrell, Macromolecules, 2017, 50, 1225–1235 CrossRef CAS.
- T. H. Pial, H. S. Sachar and S. Das, Macromolecules, 2021, 54, 4154–4163 CrossRef CAS.
- J. Yu, N. E. Jackson, X. Xu, B. K. Brettmann, M. Ruths, J. J. De Pablo and M. Tirrell, Sci. Adv., 2017, 3, eaao1497 CrossRef PubMed.
- B. K. Brettmann, N. Laugel, N. Hoffmann, P. Pincus and M. Tirrell, J. Polym. Sci., Part A: Polym. Chem., 2016, 54, 284–291 CrossRef CAS.
- J. Yu, N. Jackson, X. Xu, Y. Morgenstern, Y. Kaufman, M. Ruths, J. De Pablo and M. Tirrell, Science, 2018, 360, 1434–1438 CrossRef CAS PubMed.
- D. F. Hodgson and E. J. Amis, J. Chem. Phys., 1989, 91, 2635–2642 CrossRef CAS.
- H. D. B. Jenkins and Y. Marcus, Chem. Rev., 1995, 95, 2695–2724 CrossRef CAS.
- T. Spychaj, M. Bohdanecky and D. Berek, Acta Polym., 1986, 37, 93–96 CrossRef CAS.
- B. Maciel, C. Oelschlaeger and N. Willenbacher, Colloid Polym. Sci., 2020, 298, 791–801 CrossRef CAS.
- M. Rinaudo and D. Graebling, Polym. Bull., 1986, 15, 253–256 CrossRef CAS.
- F. G. D. Banos, A. I. D. Pena, J. G. H. Cifre, M. C. L. Martinez, A. Ortega and J. G. de la Torre, Carbohydr. Polym., 2014, 102, 223–230 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00468f |
| ‡ Present address: Department of Materials Science and Engineering, Penn State University, University Park, Pennsylvania 16802, USA, E-mail: cvg5719@psu.edu |
| This journal is © The Royal Society of Chemistry 2024 |