Open Access Article
Open Access ArticleSpontaneous emergence of motion of an isotropic active particle in a Carreau fluid
Suhas
Shreekrishna
a,
Shubhadeep
Mandal
 b and
Sayan
Das
b and
Sayan
Das
 *a
*a
aMechanical Engineering Department, Birla Institute of Technology and Science, Pilani, Hyderabad Campus, Telangana 500078, India. E-mail: sayan.das@hyderabad.bits-pilani.ac.in
bMechanical Engineering Department, Indian Institute of Science, Bengaluru 560012, India
First published on 25th November 2024
Abstract
Active particles are self-propelling in nature due to the generation of a fore-aft asymmetry in the concentration of solutes around their surface. Both the surface activity and mobility play an important role in the particle dynamics. The solutes are the products of the chemical reaction between the active particle surface and suspending medium. Unlike Janus particles, isotropic active particles have been shown to undergo spontaneous self-propulsion beyond a critical particle size (or the Péclet number). Compared to Janus active particles, there is a third ingredient, namely, advection-induced instability that dictates the dynamics of such particles. The present study numerically investigates the role played by shear rate-dependent viscosity of a suspending medium in the self-phoretic dynamics of such isotropic active particles. Towards this, a non-Newtonian Carreau fluid is taken as the suspending medium. One of the important findings of this study is the presence of a second critical Péclet number beyond which the spontaneous motion of the particle ceases to exist. Even though this critical Péclet number had been previously investigated for Newtonian fluids, strong dependence of the former on the rheology of the suspending medium was not explored. The analysis also shows that a shear thinning fluid significantly reduces the maximum velocity of the particle. In addition, confinement is found to have a significant effect on the axial propulsive velocity of the particle suspended in a Carreau fluid.
1 Introduction
Studies on synthetic/artificial micron-sized active particles have been a topic of immense interest among the scientific community in the past few decades.1–3 There are, in fact, two different types of chemically active autophoretic particles, namely: chemically active Janus particles, which comprise an active as well as an inert portion of the surface of the particles. These particles self-propel as a result of the diffusophoresis of the non-uniformly distributed chemical solutes generated upon reaction of a suspending medium with the active cap.1,2,4–6 The second category of active particles is isotropically coated with a chemically active material. Even though there exists no asymmetry in the distribution of the solutes generated, it is observed that beyond a certain particle size, a hydrodynamic instability sets in that introduces a non-uniformity in the distribution of the solutes in the vicinity of the surface of the particles, hence leading to their self-diffusophoretic motion.7–9 Recent studies on active particles towards advancement in terms of physiological functions and bio-compatibility have ensured their applications in bio-medicines10 that encompass micro-surgery, in vitro delivery of drugs to target destinations11 and biological target isolation12 to name a few.Active particles in general propel as a result of the activity of the solute diffusion within a suspending medium as well as the surface mobility responsible for the development of fluid flow out of the concentration gradient of the solute in the near vicinity of the particle surface.1,13–18 The mechanism of self-propulsion of Janus particles originates from the slip flow generated due to the diffusion of solutes as a result of the surface chemical kinetics of an asymmetrically coated particle. In contrast, an isotropically coated active particle is capable of exhibiting spontaneous self-propulsion due to a hydrodynamic instability that leads to an asymmetry in the distribution of the solute. Minor perturbations in the solute concentration to an initially isotropic distribution of the solute in the vicinity of the particle cause interfacial flows resulting in solute advection. The presence of an instability further amplifies the initial perturbation and creates a polarity in the concentration along the particle surface. Thus the initial symmetry is broken and the particle self-propels in response to the slip flow generated around it. The spontaneous propulsion is a result of the non-linear interplay between the chemical and hydrodynamic fields in the vicinity of the particle, and is possible only if the strength of the solute advection overcomes any homogenizing effects or the system Péclet number (Pe) is greater than its critical value. Such a spontaneous motion of isotropic particles has been studied analytically7 as well as observed both experimentally19 and numerically.20
Michelin et al.7 were the first to show that a critical Péclet number exists at Pe = 4 across which there is a transition from a stationary isotropic particle to a self-propelled one, when the particle is suspended in a Newtonian fluid. The maximum velocity for the particle was observed approximately at Pe = 10. Subsequently, Izri et al.19 reported spontaneous motion of solubilizing water droplets suspended in an oil–surfactant medium. This study provides the experimental evidence of spontaneous motion of isotropic particles/droplets in the presence of stronger advection as compared to diffusion of solutes. Hu et al.,21 in their numerical study, investigated the phoretic motion of circular discs. They showed the different phases of motion by varying the Péclet number. As Pe increases, it was shown that the particle exhibits frequent chaotic bursts from its circular trajectory till it undergoes a fully chaotic motion. Kailasham et al.8 studied numerically the motion of isotropic spherical particles till the Péclet number becomes as high as 80. They divided the entire particle trajectory into four major regimes, namely quiescent, a steady state, stirring and a chaotic state. They showed through a spectral element method that even axisymmetric autophoretic particles can show chaotic dynamics over a longer time limiting condition. Although ballistic motion was shown to be predominant in the short time limit, sub-diffusive chaotic motion was observed at a long time limiting scenario.
The effect of confinement was thoroughly investigated by a study performed by Picella and Michelin,9 where the critical Péclet number was observed to fall as a result of an increase in the channel confinement. In another study, Desai and Michelin22 numerically investigated the near wall motion of isotropic active particles. The distance of the droplet from the wall as well as the Péclet number were two parameters based on which dipolar or quadrupolar states were identified. A numerical study on the steady state propulsion of isotropic active particles along the wall boundary was performed by the same authors.23 It was shown in this study that for a moderate Pe, chemically interactive wall repulsion as well as the velocity of the particle reduce, thus resulting in the motion of particles towards the wall with an increase in Pe. The effect of the particle shape was showcased in the numerical study by Zhu and Zhu,24 where the propulsion of isotropic elliptic active discs was taken into consideration. Recently Hu et al.25 presented the three-dimensional numerical analysis of the spontaneous motion of isotropic colloids. This study showed the gradual transition of isotropic colloids from a linear trajectory to a circular and finally to a fully chaotic motion with an increase in the Péclet number.
Most microorganisms remain suspended in complex fluids; so it is essential to have an understanding of self-propulsion in the presence of complex fluids. Synthetic active particles encounter complex fluids in applications such as in vitro and in vivo drug delivery,11,26,27 biological target capture and isolation,12etc. A significant number of studies have been dedicated towards investigating the dynamics active Janus particles in viscoelastic fluids or in other complex suspending media.28–32 A significant number of previous studies focus on the dynamics of squirmers in shear-thinning fluids, both in an unbounded medium using an asymptotic approach33–36 as well as a bounded one with the help of the lattice Boltzmann method.37,38 Li et al.29 numerically studied the role of boundaries in the swimming dynamics of a microorganism, suspended in a viscoelastic medium. They utilized a squirmer model in their analysis to show that the shear thinning behaviour of the suspending medium has a weaker wall-trapping effect on pusher type squirmers as compared to the neutral or the puller type. In a previous study by Datt et al.,33 the motion of an active particle in a second-order fluid was shown based on the distribution of surface activity. Solano et al.39 performed experiments on silica particles coated with carbon caps and suspended in a shear-thinning fluid. The particles, when illuminated, exhibited autophoretic motion which was higher than that in Newtonian fluids, thus resulting in larger translational and rotational diffusion coefficients. However, none of these studies focus on the isotropic active particles.
Even though the spontaneous motion of isotropic particles has been investigated in a Newtonian fluid,7–9,21,40 the dynamics of such particles in a complex fluid medium, such as a Carreau fluid, is still missing from the current literature. The present study looks into the combined effect of fluid rheology and channel confinement on the phoretic motion of isotropic particles due to spontaneous symmetry breaking at a finite Péclet number. Although there is not a significant change in the occurrence of the first critical Péclet number when the particle is suspended in a shear thinning (or shear-thickening) fluid, the second critical Péclet number is seen to be strongly dependent on the fluid properties. Unlike a Newtonian fluid, a Carreau fluid shows the following properties: zero-shear-rate viscosity (η0), infinite-shear-rate viscosity (η∞), the power-law index (n) and the relaxation time of the fluid (λ). The power-law index, n, signifies the extent of shear thinning (for n < 1) or shear thickening (for n > 1) behaviour. The relaxation time, λ, signifies the inverse of a characteristic shear rate at which non-Newtonian effects become significant. The present study particularly focuses on the effect of all these properties on the critical Péclet numbers as well as the phoretic velocity of the particles. When suspended in a shear thinning fluid, the particles exhibit a greater increase in their phoretic velocity due to a stronger confinement. This study uses a finite element based approach to calculate the concentration of the solutal molecules as well as the velocity components of the isotropic particles at finite Péclet numbers.
2 Problem formulation
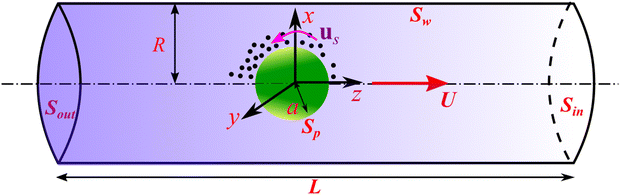
The physical system comprises an isotropic active particle of radius a which is freely suspended in a non-Newtonian Carreau fluid confined in a microchannel. A schematic of the system is presented in Fig. 1. The particle consists of an inert core and is coated uniformly over its surface by an active catalyst, which when comes into contact with the solvent molecules undergoes a chemical reaction generating solutal product molecules. Hence there is a uniform flux of these solutes from the particle surface which can be quantified by![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) .7 A positive (negative) value of
.7 A positive (negative) value of ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) would indicate emission (adsorption) of the solutes. The concentration of these solutes far away from the particle surface is taken as C∞, whereas the local concentration is denoted by C. These solute molecules interact with the particle surface via a short range potential. These interactions may be repulsive or attractive that results in the generation of a diffusiophoretic slip flow in the vicinity of the particle surface. The diffusiophoretic slip flow is dependent on the gradient of the concentration of the solute molecules, generated by the combined influence of diffusion as well as flow advection and can be expressed as
would indicate emission (adsorption) of the solutes. The concentration of these solutes far away from the particle surface is taken as C∞, whereas the local concentration is denoted by C. These solute molecules interact with the particle surface via a short range potential. These interactions may be repulsive or attractive that results in the generation of a diffusiophoretic slip flow in the vicinity of the particle surface. The diffusiophoretic slip flow is dependent on the gradient of the concentration of the solute molecules, generated by the combined influence of diffusion as well as flow advection and can be expressed as 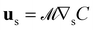 , where ∇s = (I − nn)·∇ is the surface gradient operator with n as the outward unit normal on the particle surface.4
, where ∇s = (I − nn)·∇ is the surface gradient operator with n as the outward unit normal on the particle surface.4 ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) is known as the surface mobility which indicates the strength of interaction of the solute molecules with the particle surface.4 A negative (positive) mobility signifies effective repulsive (attractive) interactions between the solute molecules and the particle surface.4
is known as the surface mobility which indicates the strength of interaction of the solute molecules with the particle surface.4 A negative (positive) mobility signifies effective repulsive (attractive) interactions between the solute molecules and the particle surface.4
The solute concentration is governed by the advection-diffusion equation
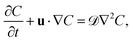 | (1) |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) represents the diffusivity of solute molecules and u is the velocity field. The above equation is subjected to the following boundary conditions at the active surface of the particle (Sp), the channel wall (Sw) and the inlet/outlet (Sin, Sout) of the channel:
represents the diffusivity of solute molecules and u is the velocity field. The above equation is subjected to the following boundary conditions at the active surface of the particle (Sp), the channel wall (Sw) and the inlet/outlet (Sin, Sout) of the channel: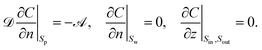 | (2) |
The first boundary condition takes into account the constant rate of flux from the active particle surface whereas the second and thrid boundary conditions denote the no-flux scenario for the inert wall and the inlet/outlet to the channel, respectively. The fluid motion is governed by the momentum equation and the continuity equation
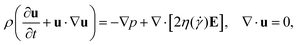 | (3) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) is a function of the shear rate
) is a function of the shear rate 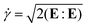 . The shear-rate dependence of viscosity is represented by the following constitutive equation41
. The shear-rate dependence of viscosity is represented by the following constitutive equation41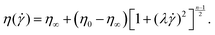 | (4) |
The fluid flow equations are subjected to the following boundary conditions along the particle surface, the channel wall and the inlet/outlet of the channel:
| u|Sp = us + U, u|Sw = 0, u|Sin,Sout = −Uez | (5) |
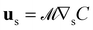 ). The channel wall is considered to be inert and thus satisfies no-slip and no-penetration conditions. Note that in the present study we focus on the axisymmetric motion in which the particle translates along the z-axis (i.e.U = Uez) and does not rotate. The translational velocity of a neutrally buoyant particle is governed by the Newton's second law of motion:
). The channel wall is considered to be inert and thus satisfies no-slip and no-penetration conditions. Note that in the present study we focus on the axisymmetric motion in which the particle translates along the z-axis (i.e.U = Uez) and does not rotate. The translational velocity of a neutrally buoyant particle is governed by the Newton's second law of motion: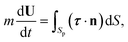 | (6) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )E is the stress tensor. The right hand side of eqn (6) represents the total hydrodynamic force on the particle. At the steady state, the total hydrodynamic force vanishes and the particle translates in a force-free manner.
)E is the stress tensor. The right hand side of eqn (6) represents the total hydrodynamic force on the particle. At the steady state, the total hydrodynamic force vanishes and the particle translates in a force-free manner.
3 Numerical solution
A closer look into the governing equations and boundary conditions reveals that the solute concentration and fluid flow are coupled to each other, and the physicochemical hydrodynamics is described by the coupled nonlinear differential equations. To identify the important dimensionless numbers, we use the following characteristic scales: length ∼ a, velocity ∼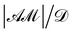 , time ∼
, time ∼ 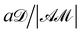 , pressure ∼
, pressure ∼ 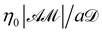 , and concentration ∼
, and concentration ∼ 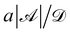 . The present system is governed by the following dimensionless numbers: Pećtlet number
. The present system is governed by the following dimensionless numbers: Pećtlet number 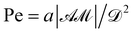 , Reynolds number
, Reynolds number 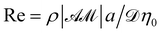 , Carreau number
, Carreau number 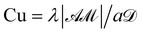 , viscosity ratio β = η∞/η0, power-law index n, dimensionless activity
, viscosity ratio β = η∞/η0, power-law index n, dimensionless activity 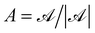 , dimensionless mobility
, dimensionless mobility 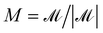 , and confinement ratio κ = a/R. The Carreau number signifies the relative importance of the characteristic strain rate imposed on the fluid to the crossover rate of strain dictated by the relaxation time of the fluid. In what follows, we solve the mathematical model and represent data in the dimensionless form.
, and confinement ratio κ = a/R. The Carreau number signifies the relative importance of the characteristic strain rate imposed on the fluid to the crossover rate of strain dictated by the relaxation time of the fluid. In what follows, we solve the mathematical model and represent data in the dimensionless form.
Exact analytical solution for this problem cannot be obtained for a wide range of parameters, thus we obtain numerical solution towards a detailed understanding of the involved fluid dynamics. The numerical solution for the above mentioned mathematical model is obtained by using the finite element software COMSOL Multiphysics. In the present study, we are primarily focused on analyzing the axisymmetric phoretic motion of the particle. To avoid continuous re-meshing of the simulation domain, we have solved the transport equations along with the boundary conditions in a reference frame which translates with the particle. The use of co-moving reference frame enables us to use a body-fitted mesh on the particle surface. The mathematical model is solved numerically with the particle situated at its center and in a computational domain of length L ≫ R. We have used the following parameters: Pe ∈ [0,50], Re = 10−3, Cu ∈ [0.01,100], β = 0.01, n ∈ [0.25,1.5], A = 1, M = 1 and κ ∈ [0.2,0.8]. The values of the parameters used in this study correspond to fluids such as Xanthan gum42 and cervical mucus.33,43 Both Boyko and Stone42 and Cordero and Lauga43 have fitted the Carreau model to the viscosity-shear rate data for Xanthan gum and human cervical mucus to obtain the property values, respectively. Based on these studies, the viscosity ratio, β, has been taken to be 0.01 or even lower values like O(10−4). For higher values of β, the fluid exhibits behavior closer to that of a Newtonian fluid.
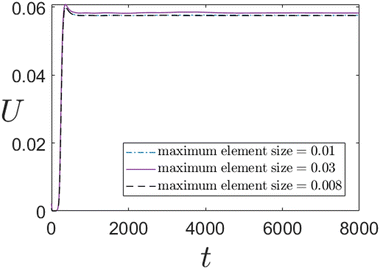
The flow field is solved for a low Reynolds number (Re = 10−3) and the Carreau constitutive model (eqn (4)) is adopted for the suspending fluid. An axisymmetric rectangular computational domain of size 100a × 20a is considered, which is discretized into approximately 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 elements. These elements are chosen as triangular (P2 − P1) elements. The mesh is generated as a uniformly growing mesh with the denser mesh near the particle surface and coarser far away from it in order to precisely capture the concentration gradient around the particle and hence the slip velocity. The reference frame is chosen to be moving with the particle and the far-field velocity is found out such that the net force acting on the particle is zero. Towards time discretization the implicit second order backward differentiation formulae (BDF) solver is utilized with a time step size of 0.01 and a relative tolerance of 10−6. The linear system of equations obtained upon discretization of the governing equations is then solved using the parallel direct sparse solver (PARDISO). The grid size independence test of the model is presented in Fig. 10 of Appendix A.
000 elements. These elements are chosen as triangular (P2 − P1) elements. The mesh is generated as a uniformly growing mesh with the denser mesh near the particle surface and coarser far away from it in order to precisely capture the concentration gradient around the particle and hence the slip velocity. The reference frame is chosen to be moving with the particle and the far-field velocity is found out such that the net force acting on the particle is zero. Towards time discretization the implicit second order backward differentiation formulae (BDF) solver is utilized with a time step size of 0.01 and a relative tolerance of 10−6. The linear system of equations obtained upon discretization of the governing equations is then solved using the parallel direct sparse solver (PARDISO). The grid size independence test of the model is presented in Fig. 10 of Appendix A.
4 Results and discussion
4.1 Motion in a Newtonian fluid
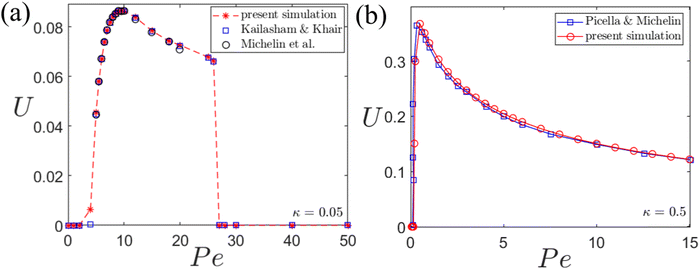
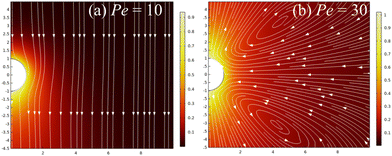
A significant number of earlier studies have focused on the spontaneous self-propulsion dynamics of isotropic particles suspended in a Newtonian fluid.7–9 The numerical model used in this analysis is validated with some of these numerical studies. Fig. 2(a) shows the variation of the dimensionless axial phoretic velocity of the isotropic particle suspended in an unbounded medium (κ = 0.05). This variation is compared with the numerically obtained results of both Michelin et al.7 and Kailasham and Khair.8 The latter had shown the variation over a wider range of Péclet numbers. The present numerical simulations show a good match with both of the above results. It can be observed from Fig. 2(a) that there are a total of three different regimes that best describe the particle dynamics. The first is the no-propulsion (NP) regime (Pe ≤ 4). In this regime, there is a radial symmetry in the solute concentration in the vicinity of the particle surface. Beyond Pe = 4, the second regime starts, which is the self-propulsion (SP) regime and can be seen to lie in the range 4 < Pe ≤ 26. Similar observations were also made from the studies by Michelin et al. as well as Kailasham and Khair.7,8 The Péclet number demarcating the first and the second regime is known as the first critical Péclet number (Pe1). In this regime a spontaneous propulsion of the particle initiates. The corresponding non-uniform ‘comet-shaped’ solute distribution as well as the streamlines can be seen in Fig. 3(a). The latter clearly indicates the unidirectional self-propulsion of particles. A maximum phoretic velocity is obtained at Pe ≈ 10 after which the particle velocity gradually reduces till Pe = 26. Finally beyond Pe = 26, the particle shows negligible self-propulsion. Even though there is a fluid flow, pumping the fluid from the poles to the equatorial region of the particle (refer to the streamlines in Fig. 3(b)), the net phoretic velocity is negligible. This can be supported by observing the solute distribution around the particle (Fig. 3(b)), which signifies a symmetric distribution of the solute across its transverse axis. This regime is thus referred to as the stirring regime (St). The particular Péclet number demarcating the self-propulsion and the stirring regime is the second critical Péclet number (Pe2).Fig. 2(b) on the other hand shows the effect of confinement on the axial phoretic velocity of the particle as a function of the Péclet number. As can be clearly seen, the first critical Péclet number is shifted from 4 to 0.01 in the presence of a confinement (κ = 0.5). For a strongly confined particle, the asymmetry in solute distribution around the particle surface is enhanced which results in an early triggering of the spontaneous motion. The numerical model used, thus predicts the same variation of axial phoretic velocity of the particle as shown by Picella et al.9 in their study.
4.2 Motion in a Carreau fluid
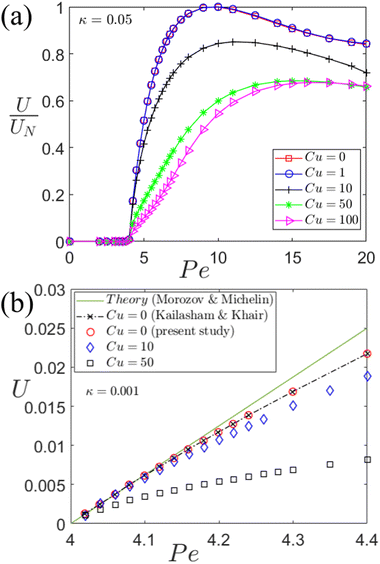
Effect of rheology. Fig. 4 shows the variation of the axial phoretic velocity with Pe for different values of the Carreau number (Cu). As Cu → 0, the suspending fluid tends to behave like a Newtonian-fluid. The axial phoretic velocity in Fig. 4(a) is normalized with respect to the maximum velocity for the case of a Newtonian fluid (Cu → 0) at Pe = 10. The figure shows the variation of the phoretic velocity when the particle is suspended in different shear-thinning fluids with varying Cu. As can be seen from the figure, the first critical Péclet number at which the motion of the particle sets in remains the same (Pe1 = 4) for all values of Cu. Hence, rheology is seen to have no effect on the first critical Péclet number when the particle is suspended in an unbounded medium. This is intuitive because the effect of rheology comes into play only when there is motion. Up to Pe1 = 4, there is no motion, and therefore, fluid rheology has no effect on the first critical Péclet number. In contrast, the maximum self-propulsion velocity (at Pe = 10) is found to reduce with an increase in the characteristic strain rate of the fluid (or Cu). However, as Cu → ∞, the point of maximum self-propulsive velocity shifts towards a higher value of the Péclet number. In addition, the magnitude of the maximum propulsive velocity also increases. This above observation can be understood by taking into consideration the rheology of the suspending fluid. The characteristic of a shear thinning fluid indicates a reduction in its viscosity due to its straining motion as the particle self-propels through the fluid. This in-turn indicates a decrease in both the thrust and drag acting on the particle. However, in shear thinning fluids, it has been observed that the decrease in thrust is much greater as compared to the drag reduction for a finite value of Cu (<100). So a decrease in the velocity, hence maximum velocity, should be expected as observed in Fig. 4(a). At very high or low strain rates (or Cu), the behavior of the suspending Carreau fluid reverts back to that of a Newtonian fluid and the swimming velocity thus increases. This can be also be observed in Fig. 4(a).
Another important observation from the same figure is the gradual decrease in the slope of the curve, that is ΔU/ΔPe, just above the first critical Péclet number. This reflects on the role of the particle size in its phoretic motion. For a particle suspended in a Newtonian fluid or as Cu → 0, an increase in its size within the corresponding range, 4 ≤ Pe ≤ 10, resulted in a significant rise in its propulsive thrust as compared to the drag. This manifests in a larger increase in its phoretic velocity as compared to the case of a particle suspended in a shear thinning fluid. On suspension in a shear thinning fluid, the rise in the propulsive thrust due to a larger particle size is counteracted by the reduction in thrust due to shear-thinning behavior of the fluid. This effectively results in a lower rate of an increase of particle propulsive velocity with an increase in the particle size till Pe = 10.
Fig. 4(b) presents the variation of the axial phoretic velocity of the particle with Pe in the vicinity of the symmetry break (Pe = 4). This variation is shown for different rheologies of the suspending medium (Cu = 0, 10, 50). Towards obtaining the phoretic velocity of the particle, the computational domain was kept quite large (R = 1000a) in order to ensure a negligible effect due to boundaries near the bifurcation, where both advection and diffusion of solutes are comparable. It is observed from Fig. 4(b) that the variation of phoretic velocity of the particle, suspended in a Newtonian fluid (Cu = 0), is linear with respect to Pe and is in agreement with the theoretical prediction (U = (Pe − 4)/16) by Morozov and Michelin20 for values of the Péclet number close to 4. However, with an increase in Cu, the variation is no longer linear and gradually deviates further away from that predicted by Morozov and Michelin20 for a Newtonian suspending medium. The deviation primary arises due to more reduction in the phoretic thrust as compared to the induced Stokes drag on the particle, when suspended in a shear-thinning fluid. This is also evident from Fig. 4(b) that shows a decrease in the rise of the phoretic velocity of the particle due to a corresponding increase in Pe.
The second critical Péclet number (Pe2). The second critical Péclet number Pe2 corresponds to the particular size of the particle at which its spontaneous propulsion comes to a stop, for a fixed solutal diffusivity and a characteristic phoretic velocity. As seen from the regime diagrams (Fig. 5), Pe2 is seen to be a strong function of the rheology of the suspending medium unlike the first critical Péclet number. A clear transition can be observed between the spontaneous self-propulsion and the stirring regime. Interestingly, as mentioned above, the occurrence of the stirring regime is seen to be dependent on the rheology of the fluid, governed by the three parameters, namely, β, Cu, and n. The primary focus of this subsection is to determine the nature of the dependence of the particle dynamics on these parameters, for different values of the Péclet number.
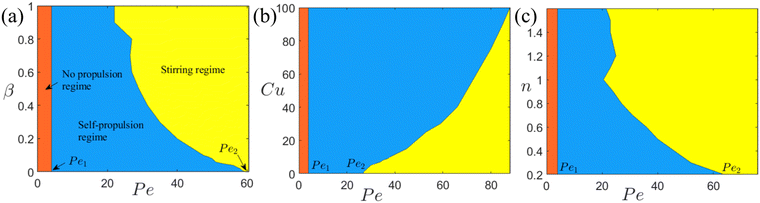 | ||
| Fig. 5 Regime diagrams indicating the effect of rheology of the suspending medium on the second critical Péclet number. The ‘red’ color regime indicates the no-propulsion (NP) regime, which is seen to be independent of the fluid rheology and hence the first critical Péclet number has a fixed value of 4.7 The ‘blue’ and ‘yellow’ colored regimes indicate the spontaneous self-propulsion (SP) regime and the stirring regime (St), respectively. (a) The effect of the viscosity ratio (β) for Cu = 30, n = 0.25, whereas (b) and (c) showcase the effect of Cu (β = 0.01, n = 0.25) and n (β = 0.01, Cu = 30), respectively. | ||
Fig. 5 showcases the three different regimes: the no-propulsion regime (NP), the spontaneous self-propulsion regime (SP) and the stirring regime (St). Depending on the values of Pe as well as β, Cu, and n, Fig. 5 presents a numerical prediction on the occurrence of the spontaneous self-propulsion of the particle. Fig. 5(a) presents the regime diagrams based on the variation of the viscosity ratio, β and the Péclet number, Pe for a fixed value of the Carreau number (Cu = 30) and the power index, (n = 0.25). Likewise, Fig. 5(b) and (c) refer to regime diagrams for the variation of Pe with Cu and n, respectively. In all of these figures, the ‘red’ region signifies the no-propulsion regime (NP), whereas the ‘blue’ and the ‘yellow’ regions signify the self-propulsion (SP) and stirring regime (St), respectively. It can be correctly observed that the first critical Péclet number (Pe1), which marks the transition from the NP regime to the SP one, is fixed at a value of 4, irrespective of the rheology of the suspending fluid. However, this is not the scenario for the case of the second critical Péclet number (Pe2). When referred to Fig. 5(a), the variation in (Pe2) is seen to be significant for lower values of β, that is, the further the rheology of the fluid drifts away from that of a Newtonian fluid (β = 1), the greater is the change (increase) in the value of the (Pe2). The nature of variation of (Pe2) with Cu (Fig. 5(b)) is just the opposite to that of figure (a). This is primarily because for a Newtonian fluid Cu → 0, thus the transition from the SP to the St regime is expected to initiate at lower Pe values. A further increase in the value of Cu inherently delays the transition. Finally, Fig. 5(c) presents the regime diagram based on the variation of the power index n. It can be inferred that shear thickening fluids (n > 1) have a significantly lesser effect on the second critical Péclet number as compared to a shear thinning fluid.
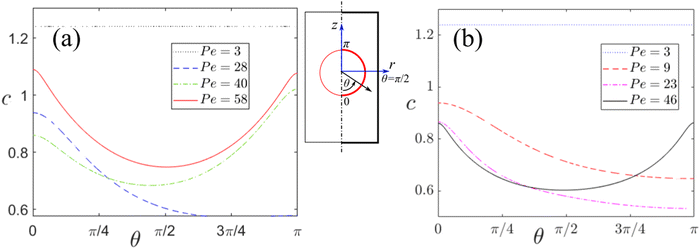
To gain a better insight into the motion characteristics of the isotropic particles, the non-dimensional solute concentration (c) at the particle interface is plotted with respect to the polar angle (θ ∈ [0,π]). It should be noted that the axis of symmetry lies at θ = 0,π. It can be observed that in the NP as well as the St regime there is no phoretic motion of the particle. However, these regimes do not signify similar particle dynamics. An explanation to this can be given if we look into Fig. 6. Fig. 6(a) and (b) present the variation of the solutal concentration along the surface of the particle suspended in a shear thinning (n = 0.25) and a shear thickening (n = 1.25) medium, respectively. As can be seen from Fig. 6(a) and (b), the variation in the solute concentration is shown for different Péclet numbers to make sure all the three different regimes are considered. As expected for the SP regime (Pe = 28, 40 in Fig. 6(a) and Pe = 9, 23 in Fig. 6(b)), the variation in c with respect to θ is asymmetric about θ = π/2. If we focus on the corresponding variation for the NP regime (Pe = 3) and the St regime (Pe = 58 in Fig. 6(a) and Pe = 46 in Fig. 6(b)), we note an interesting observation. Even though the variations of c for both the cases are symmetric about θ = π/2, ensuring no phoretic motion, there is hardly any variation of c in the NP regime. This clearly indicates that although the particle undergoes no self propulsion in the St regime (similar to the NP regime), there is clearly a convection of the fluid in the vicinity or stirring (hence the name of the regime) leading to such a symmetric distribution of the solutes along the particle interface. The inset in Fig. 6 shows the orientation of the particle with respect to the axis of symmetry. On comparison of the two figures (a) and (b) for shear thinning (n = 0.25) and shear thickening (n = 1.25) fluids, respectively, it can be inferred that the asymmetry in the variation of c in the SP regime is higher for a shear thinning fluid as compared to the shear thickening fluid, thus resulting in a greater phoretic velocity of the particle when suspended in the former fluid type.
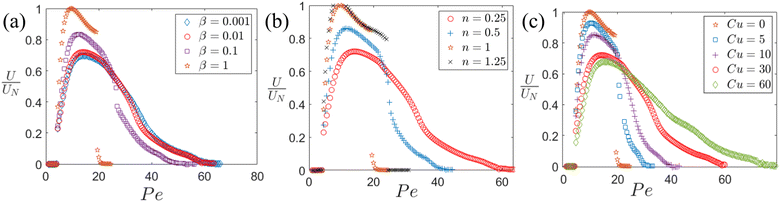
Fig. 7(a)–(c) show the variation of the normalized axial phoretic velocity with the Péclet number for different values of Cu, β and n, respectively. The primary focus for these figures is the transition of the dynamics of the particle from the SP to the St domain. In Fig. 7(a), β is varied from 0.001 to 0.9 whereas the other parameters Cu, n are kept fixed at 30, 0.25, respectively. It is seen that for lower values of β (= 0.001, 0.01, 0.1), there is a gradual transition from the SP regime to the St regime, however, for higher values (β = 0.9) there is an abrupt jump in the velocity near the second critical Péclet number resulting in a negligible phoretic velocity from a finite value. In other words, the more the rheology of the fluid deviates from a Newtoninan fluid the smoother is the transition from the SP to the St regime. In addition to this, the earliest (lowest value of Péclet number) transition from the SP to St regime occurs with a jump for a Newtonian fluid (β → 1), however, the transition occurs, without any jump, at increasingly larger values of Pe for lower values of the viscosity ratio, β. A similar observation can be made from Fig. 7(b), where a jump discontinuity is observed between regimes SP and St for a Newtonian fluid (n = 1). This jump is reduced as the fluid rheology (n = 0.25) deviates more from that of a Newtonian fluid. Interestingly, the transition occurs at the lowest value of a Newtonian fluid, whereas, for both shear-thickening (n = 1.25) and shear-thinning (n = 0.5) fluids, the transition from the SP to the St regime is seen to occur at larger values of Pe. Similar observations can also be made from Fig. 5(c). Finally, Fig. 7(c) presents the variation of the normalized phoretic velocity with Pe for different values of Cu. However, unlike Fig. 4, the primary focus here is on the second critical Péclet number. Again, similar to the other figures (b) and (c), the abruptness in reaching the stirring regime gradually decreases with an increase in Cu.
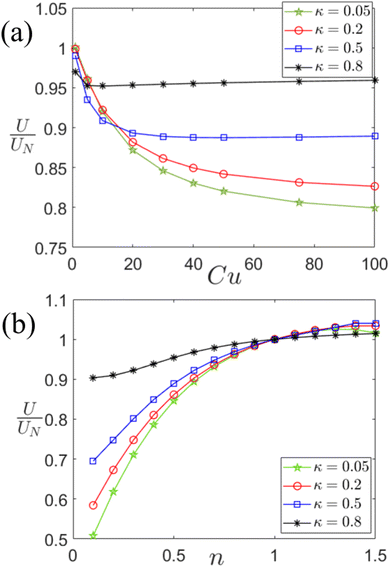
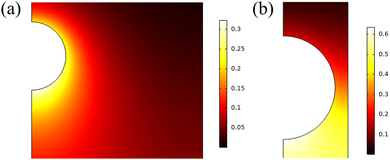
Fig. 8 represents the variation of the axial phoretic velocity of the particle as a function of both Cu and n for different confinement ratios. The phoretic velocity is normalized with respect to the corresponding velocity of the particle, suspended in a Newtonian fluid. The figures showcase the role played by the fluid rheology in phoretic motion of a confined active particle. Fig. 8(a) represents the variation of the normalized particle velocity as function of Cu for different values of κ at Pe = 10 and n = 0.5. For Cu = 0 or a Newtonian fluid, the particle exhibits the maximum velocity at Pe = 10. However, for a shear thinning fluid, the velocity of the particle is reduced significantly between 0 ≤ Cu ≤ 5 irrespective of the extent of the confinement. At higher values of Cu, the effect of channel confinement is enhanced. That is, the increase in the phoretic velocity of the particle due to the increase in the confinement ratio is significantly higher when the particle is suspended in a shear thinning fluid. In addition to this, the increase in the velocity is further enhanced as Cu increases. An explanation towards such an observation can be provided by analyzing the nature of the suspending fluid. The viscosity of a shear-thinning fluid reduces at high strain rates. Now for a strongly confined particle, the strain rate is significantly higher due to the presence of the inert wall near the particle surface. This results in lesser drag but at the same time generates a higher asymmetry in the solute distribution along the particle surface creating a larger solute concentration gradient. This manifests itself in a higher propulsive thrust on the particle as compared to a weakly confined particle. Such an observation can also be made from Fig. 9 which shows the concentration of solutes at the vicinity of the particle for Cu = 30, n = 0.5, β = 0.01, and Pe = 10. Fig. 9(a) and (b) show the solute distribution for κ= 0.2 and κ = 0.8, respectively, and the concentration gradient for the latter can be observed to be greater. A careful observation of Fig. 8(a) also shows that there is an increase in the phoretic velocity for a strongly confined particle (κ = 0.8), whereas the velocity decreases for a weakly confined particle (κ = 0.2) with Cu. This is evident because of a larger drag force as well as a lower fore-aft asymmetry for a weakly confined particle. Fig. 8(b) shows the variation of the phoretic velocity of the particle for different confinement ratios, when suspended in shear-thinning as well as a shear-thickening fluids. As n → 1, the suspending fluid tends to become Newtonian. It can be observed from the figure that as the value of n is reduced, the effect of confinement becomes more prominent for the similar reasons stated above. Interestingly, if the value of n > 1, then the fluid becomes shear-thickened and the effect of confinement reverses. Even though the confinement does not have a significant impact on the particle dynamics in this regime (n > 1), the velocity of the particle now is seen to be lower for a strongly confined particle. This is exactly opposite to what is observed for a shear thinning suspending fluid due to the increase in viscosity at higher strain rates.
5 Conclusion
The present study focuses on the spontaneous propulsion of isotropic active particles in a Carreau fluid. Towards this, an axisymmetric model of the particle is considered and a finite element based numerical approach is adopted to solve the coupled flow field and the density field equations. Upon performing a thorough analysis, it is found that rheology does not have a significant effect on the critical Péclet number, at which the propulsion of the particle sets in. However, the rheology is seen to have a significant effect on a second critical Péclet number at which the spontaneous self-propulsion of the particle comes to a stop. The maximum velocity as well as the overall variation of the phoretic velocity of the particle with Pe are also strongly dependent on the rheology of the fluid. Previously, it had been shown by Picella and Michelin9 that a strong confinement increases the overall velocity of the particle due to the generation of a thin film between the particle surface and the channel wall. Interestingly, this effect of confinement is magnified when the suspending fluid is shear-thinning (or shear-thickening). A significantly larger change in the phoretic velocity is observed due to a change in the channel confinement when the particle is suspended in a shear thinning fluid rather than a Newtonian fluid. For a shear-thickening fluid, in contrast, the phoretic velocity reduces for a stronger confinement.The present system could be experimentally realized using chemically active droplets for which the isotropic active particle serves as a canonical model.22,23,44 Chemically active droplets propel in a surfactant-rich solution by means of solubilization19,45–47 and inherently do not possess any geometric or chemical asymmetry as in the case of a typical Janus active colloid. The propulsion of an active droplet is primarily dependent on the hydrodynamic instability induced symmetry-breaking of the emission/absorption of the chemical solutes (for example surfactants) as a result of any perturbation given to the system. This, in-turn, leads to the generation of a solutal concentration gradient and hence a Marangoni stress is induced at the droplet interface that results in its propulsion. It should be noted that such a phenomenon is dependent on the advection of the solutes as opposed to their diffusion; so the Péclet number (or the droplet size) is expected to be significantly large. There have been a few experimental studies of active droplets suspended in a non-Newtonian viscoelastic medium.48,49 Hence even though the present numerical model cannot be studied experimentally, active droplets in a non-Newtonian Carreau fluid can be used for experimental studies and hence for validation. Some examples of Carreau fluids, as stated above, are blood or cervical mucus33 (biological fluids) and xanthan gum.42
Author contributions
SS was involved in performing the detailed simulations and drafting the manuscript. SD supervised SS towards the successful implementation of the work and SM formulated the overall idea and collaborated with SD to discuss about the formulation of the study and writing of the manuscript.Data availability
The authors confirm that the data supporting the findings of this study are available within the article.Conflicts of interest
There are no conflicts to declare.Appendix
The grid-independence check is carried out here to ensure the consistency of the results obtained irrespective of the element size chosen. Fig. 10 presents the transient variation of the axial phoretic velocity of the particle suspended in an unbounded medium (κ = 0.05). The suspending medium is a shear-thinning Carreau fluid with the following properties: β = 0.01, Cu = 30, n = 0.25, and Pe = 10. The variation is shown corresponding to the different maximum element sizes (0.01, 0.03, 0.008). In the numerical simulations performed, the maximum element size has been chosen as 0.01. It can be observed from Fig. 10 that there is a good match between the transient variations from the three different runs.Acknowledgements
SD gatefully acknowledges support from INSPIRE faculty grant from DST (grant no. DST/INSPIRE/04/2020/000626) and NFSG grant from BITS Pilani (NFSG/HYD/2023/H0828), Hyderabad. SM gratefully acknowledges support from DST-SERB grant no. SRG/2021/000074. The authors thank Indian Science Technology and Engineering Facilities Map (I-STEM), a Program supported by the Office of the Principal Scientific Adviser to the Govt. of India, for enabling access to the COMSOL Multiphysics 6.0 software used to carry out the numerical simulations.References
- J. R. Howse, R. A. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef PubMed
.
- J. L. Moran and J. D. Posner, Annu. Rev. Fluid Mech., 2017, 49, 511–540 CrossRef
.
- L. J. Fauci and R. Dillon, Annu. Rev. Fluid Mech., 2006, 38, 371–394 CrossRef
.
- J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef
.
- S. Das, Z. Jalilvand, M. N. Popescu, W. E. Uspal, S. Dietrich and I. Kretzschmar, Langmuir, 2020, 36, 7133–7147 CrossRef CAS PubMed
.
- W. Uspal, M. N. Popescu, S. Dietrich and M. Tasinkevych, Soft Matter, 2015, 11, 434–438 RSC
.
- S. Michelin, E. Lauga and D. Bartolo, Phys. Fluids, 2013, 25, 061701 CrossRef
.
- R. Kailasham and A. S. Khair, J. Fluid Mech., 2022, 948, A41 CrossRef CAS
.
- F. Picella and S. Michelin, J. Fluid Mech., 2022, 933, A27 CrossRef CAS
.
- B. J. Nelson, I. K. Kaliakatsos and J. J. Abbott, Annu. Rev. Biomed. Eng., 2010, 12, 55–85 CrossRef CAS PubMed
.
- R. Yang, T. Wei, H. Goldberg, W. Wang, K. Cullion and D. S. Kohane, Adv. Mater., 2017, 29, 1606596 CrossRef PubMed
.
- K. P. Yuet, D. K. Hwang, R. Haghgooie and P. S. Doyle, Langmuir, 2010, 26, 4281–4287 CrossRef CAS PubMed
.
- E. Yariv, J. Fluid Mech., 2017, 816, R3 CrossRef
.
- S. Saha, E. Yariv and O. Schnitzer, J. Fluid Mech., 2021, 916, A47 CrossRef CAS
.
- R. Brandão and E. Yariv, J. Fluid Mech., 2023, 972, R3 CrossRef
.
- R. Brandão, J. Fluid Mech., 2024, 980, A2 CrossRef
.
- R. Brandão, G. G. Peng, D. Saintillan and E. Yariv, Phys. Rev. Fluids, 2024, 9, 014001 CrossRef
.
- R. Kailasham and A. S. Khair, Soft Matter, 2023, 19, 7764–7774 RSC
.
- Z. Izri, M. N. Van Der Linden, S. Michelin and O. Dauchot, Phys. Rev. Lett., 2014, 113, 248302 CrossRef PubMed
.
- M. Morozov and S. Michelin, J. Chem. Phys., 2019, 150, 044110 CrossRef PubMed
.
- W.-F. Hu, T.-S. Lin, S. Rafai and C. Misbah, Phys. Rev. Lett., 2019, 123, 238004 CrossRef CAS PubMed
.
- N. Desai and S. Michelin, Phys. Rev. Fluids, 2021, 6, 114103 CrossRef
.
- N. Desai and S. Michelin, Phys. Rev. Fluids, 2022, 7, 100501 CrossRef
.
- G. Zhu and L. Zhu, J. Fluid Mech., 2023, 974, A57 CrossRef CAS
.
- W.-F. Hu, T.-S. Lin, S. Rafai and C. Misbah, Phys. Rev. Fluids, 2022, 7, 034003 CrossRef
.
- B. E.-F. de Ávila, P. Angsantikul, J. Li, M. Angel Lopez-Ramirez, D. E. Ramrez-Herrera, S. Thamphiwatana, C. Chen, J. Delezuk, R. Samakapiruk and V. Ramez,
et al.
, Nat. Commun., 2017, 8, 272 CrossRef PubMed
.
- S. K. Srivastava, G. Clergeaud, T. L. Andresen and A. Boisen, Adv. Drug Delivery Rev., 2019, 138, 41–55 CrossRef CAS PubMed
.
- C. Datt, G. Natale, S. G. Hatzikiriakos and G. J. Elfring, J. Fluid Mech., 2017, 823, 675–688 CrossRef CAS
.
- G. J. Li, A. Karimi and A. M. Ardekani, Rheol. Acta, 2014, 53, 911–926 CrossRef CAS PubMed
.
- M. De Corato, F. Greco and P. Maffettone, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 053008 CrossRef CAS PubMed
.
- L. Zhu, E. Lauga and L. Brandt, Phys. Fluids, 2012, 24, 051902 CrossRef
.
- A. E. Patteson, A. Gopinath and P. E. Arratia, Curr. Opin. Colloid Interface Sci., 2016, 21, 86–96 CrossRef CAS
.
- C. Datt, L. Zhu, G. J. Elfring and O. S. Pak, J. Fluid Mech., 2015, 784, R1 CrossRef
.
- H. Nganguia, K. Pietrzyk and O. S. Pak, Phys. Rev. E, 2017, 96, 062606 CrossRef PubMed
.
- K. Pietrzyk, H. Nganguia, C. Datt, L. Zhu, G. J. Elfring and O. S. Pak, J. Non-Newtonian Fluid Mech., 2019, 268, 101–110 CrossRef CAS
.
- B. van Gogh, E. Demir, D. Palaniappan and O. S. Pak, J. Fluid Mech., 2022, 938, A3 CrossRef CAS
.
- Z. Ouyang, J. Lin and X. Ku, Rheol. Acta, 2018, 57, 655–671 CrossRef CAS
.
- C. Liu, J. Lin and Z. Ouyang, Rheol. Acta, 2024, 63, 61–78 CrossRef CAS
.
- J. R. Gomez-Solano, A. Blokhuis and C. Bechinger, Phys. Rev. Lett., 2016, 116, 138301 CrossRef PubMed
.
- S. Michelin and E. Lauga, J. Fluid Mech., 2014, 747, 572–604 CrossRef
.
-
R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids, Volume 1: Fluid Mechanics, 1987 Search PubMed
.
- E. Boyko and H. A. Stone, J. Fluid Mech., 2021, 923, R5 CrossRef CAS
.
- J. R. Vélez-Cordero and E. Lauga, J. Non-Newtonian Fluid Mech., 2013, 199, 37–50 CrossRef
.
- S. Michelin, Annu. Rev. Fluid Mech., 2023, 55, 77–101 CrossRef
.
- S. Herminghaus, C. C. Maass, C. Krüger, S. Thutupalli, L. Goehring and C. Bahr, Soft Matter, 2014, 10, 7008–7022 RSC
.
- C. Jin, B. V. Hokmabad, K. A. Baldwin and C. C. Maass, J. Phys.: Condens. Matter, 2018, 30, 054003 CrossRef PubMed
.
- B. V. Hokmabad, R. Dey, M. Jalaal, D. Mohanty, M. Almukambetova, K. A. Baldwin, D. Lohse and C. C. Maass, Phys. Rev. X, 2021, 11, 011043 Search PubMed
.
- P. Dwivedi, A. Shrivastava, D. Pillai, N. Tiwari and R. Mangal, Soft Matter, 2023, 19, 3783–3793 RSC
.
- P. Dwivedi, A. Shrivastava, D. Pillai and R. Mangal, Soft Matter, 2023, 19, 4099–4108 RSC
.
| This journal is © The Royal Society of Chemistry 2024 |