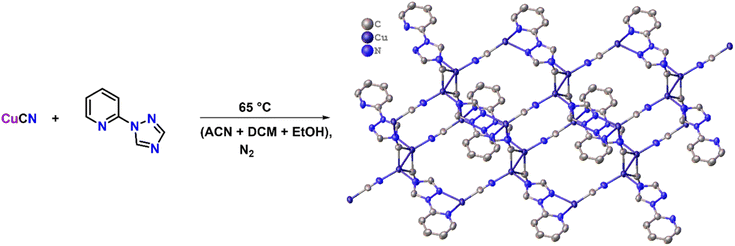
A two-dimensional semiconducting Cu(I)-MOF for binder and conductive additive-free supercapattery†
Shivendu
Mishra
a,
Mayank K.
Singh
b,
Dilip
Pandey
a,
Dhirendra K.
Rai
 *b and
Abhinav
Raghuvanshi
*b and
Abhinav
Raghuvanshi
 *a
*a
aDepartment of Chemistry, Indian Institute of Technology Indore, Simrol, Indore, Madhya Pradesh 453552, India. E-mail: r.abhinav@iiti.ac.in
bSustainable Energy and Environmental Materials (SEEM) Lab, Department of Metallurgical Engineering and Material Science, Indian Institute of Technology Indore, Simrol, Indore, Madhya Pradesh 453552, India. E-mail: dkrai@iiti.ac.in
First published on 9th January 2024
Abstract
Two-dimensional (2D) semiconductive metal–organic frameworks (MOFs) have emerged as potential electrode materials for electrochemical energy devices, combining both the merits of a battery and supercapacitor owing to their porous structure containing redox active metal centers. These electrode materials often suffer from poor conductivity and low cyclic stability and often require conductive additives. Herein, we report the synthesis of a CuCN-based semiconducting MOF (CuCN-MOF) formed from the reaction of CuCN with a nitrogen-rich multidentate 2-(1H-1,2,4-triazol-1-yl)pyridine (2TzPy) linker. The ligand with multiple binding sites along with μ2-C:N and μ3-C:C:N coordination modes of cyanide forms a 2D structure, which further generates a 3D architecture due to π–π stacking with cyanide and triazole rings of different layers. Due to the presence of redox-active Cu(I) centers, porous structure, and conducting nature, the applicability of materials has been investigated as a binder and conductive additive-free electrode material. The investigation confirms the supercapattery behavior of the material with a specific capacity of 508 C g−1 at 1 A g−1. Further, the symmetric device formed by CuCN-MOF delivers outstanding energy and power densities (maxEd = 68.175 W h kg−1, maxPd = 5.54 kW kg−1) with exceptionally high cyclic stability (96.5% up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles).
000 cycles).
Introduction
Energy consumption is rapidly increasing with the growing population. It is now necessary to move towards renewable energy sources because of depleting fossil fuels and the alarming rise in CO2 levels. The transition from fossil fuel to renewable sources needs effective energy storage systems to support the uninterrupted energy supply.1,2 Therefore, there is much interest in developing high-performance energy storage devices, such as batteries and supercapacitors. Batteries are energy storage devices having high energy density due to the involvement of charge transfer across the electrode–electrolyte interface; however, since these processes are relatively slow, batteries exhibit poor power density.3,4 On the other hand, charge storage in supercapacitors occurs due to the simple adsorption of the electrolyte ions on the electrode surface or due to surface redox reactions. Though the amount of energy stored by simple ion adsorption/desorption on the electrode surface is much less than through charge transfer processes, these processes are much faster than the charge transfer process. Therefore, supercapacitors feature low energy density but very high power density.5–8 Attempts have been made to improve the energy density of supercapacitors by invoking charge transfer-based energy storage, which has led to a wide range of supercapacitor types.Based on the charge–discharge mechanisms, supercapacitors are classified as electrical double-layer capacitors (EDLCs) and pseudocapacitors. Pseudocapacitors store charge as a result of surface redox reactions, whereas EDLCs store charge due to the accumulation of ions at the electrode/electrolyte interface, where no electron transfer is involved.9,10 Supercapacitors also offer the advantages of fast discharging, long cyclic stability, being lightweight, and simple to use.11,12 Recently, efforts have been made to combine the properties of both supercapacitors and batteries in a single electrode material to develop a new category called “supercapattery” that combines the benefits of high energy as well as high power density.13–17 This idea has led to the exploration of new types of electrode materials, such as metal oxides/sulfides, MXenes and their composites with different morphologies.18–23 In addition, efforts have also been made to develop various nanostructured porous electrode materials containing redox active metal centers to attain a greater specific surface area.24–26 Such materials offer charge storage by both double-layer formation as well as faradaic processes and, therefore, render improved energy storage performance.27 In this regard, metal–organic frameworks (MOFs) have been widely investigated as positive electrode materials for lithium and sodium ion batteries and supercapacitors due to their controllable structure, high specific surface area, and high porosity.28–32 The channeled structures of MOFs function as conduits for seamless ion transport within the electrode, facilitating high charge storage and high power density.33 It has been observed that three-dimensional (3D) MOFs formed by a 2D layer through non-covalent interaction offer high surface area and thus provide a greater electrode–electrolyte interface, resulting in improved charge storage performance.34 Moreover, the extended π-conjugation in MOFs enables them to exhibit better conductivity than other cathode materials, making them promising electrode materials.29,35–40
Among different MOFs, Cu-based MOF have been extensively explored as electrode materials because of the high natural abundance and low cost of Cu precursors. For example, Chen et al. reported a Cu(II) based 3D MOF, featuring a gravimetric capacitance of 479 F g−1 at 0.2 A g−1 with 80% capacitance retention after 2000 cycles.41 Liu et al. reported a Cu(II) based electrode material [Cu(hmt)(tfbdc)(H2O)] (hmt = hexamethylenetetramine, tfbdc = 2,3,5,6-tetrafluoroterephthalate), showing a very high specific capacitance of 1274 F g−1 at 1 A g−1 with cyclic stability of 88% after 2000 cycles.42 Our group also fabricated an rGO composite of Cu(II)-MOF, assembled using a piperazine-based tetracarboxylic linker, which shows a specific capacity of 867.09 F g−1 at 1 A g−1 with ultrahigh cyclic stability (135% capacitance after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles). The material's exceptional stability feature is attributed to the presence of the nitrogen-rich piperazine units, which increases the wettability of the electrode material.43 We observed that the similar rGO/Cu(II) MOF, formed by a tetracarboxylic linker without any nitrogen, exhibited only 83.3% capacity retention after the same number of cycles.44
000 cycles). The material's exceptional stability feature is attributed to the presence of the nitrogen-rich piperazine units, which increases the wettability of the electrode material.43 We observed that the similar rGO/Cu(II) MOF, formed by a tetracarboxylic linker without any nitrogen, exhibited only 83.3% capacity retention after the same number of cycles.44
Though the applications of Cu(II)-based MOFs are ubiquitous as electrode materials for energy storage, Cu(I)-based MOFs have rarely been explored despite the fact that electron-rich Cu(I)-complexes have a greater tendency to form clusters, which can tolerate structural changes during charging and discharging, and are therefore expected to impart improved cyclic stability.45,46 Wu et al. have reported polyoxometalate based copper(I) MOFs that showed a gravimetric capacitance of 828 F g−1 at 1 A g−1 current density.47 Recently, Zhu et al. have reported a CuCN-based MOF as an electrode material for a supercapattery with a specific capacity of 677.5 C g−1 at 1 A g−1 current density.48
In the continuation of research involving the design and synthesis of these interesting MOFs, herein, we report on the synthesis of a new 2D copper(I) cyanide-based semiconductive MOF using a 1H-1,2,4-triazole substituted pyridine ligand as a linker. The superior conductivity and the presence of Cu(I) redox-active centers in its 2D structure, which eventually transform into an interesting 3D-framework with suitable channel structure due to π–π stacking, encouraged us to investigate it as a binder and conducting additive-free electrode material in energy storage devices. Moreover, the polymer also consists of a nitrogen-rich linker, a desirable feature to derive improved charge storage performance as established previously.43 The electrochemically inactive binder and conducting additive do not play a part in the charge storage process, thus diminishing the gravimetric capacity of the device.49–53 Therefore, materials that can be cast on the current collector in neat form without compromising device cyclic stability are of much interest. The present MOF shows a specific capacity of 508 C g−1 at 1 A g−1 with excellent capacity retention of 92% after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. Additionally, the symmetrical device fabricated using the metal–organic framework (MOF//MOF) features a maximum energy density of 68.175 W h kg−1 and power density of 5.54 kW kg−1 with exceptional device stability up to 96.5% after 10
000 cycles. Additionally, the symmetrical device fabricated using the metal–organic framework (MOF//MOF) features a maximum energy density of 68.175 W h kg−1 and power density of 5.54 kW kg−1 with exceptional device stability up to 96.5% after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles.
000 cycles.
Experimental section
Synthesis of CuCN-MOF
In an oven-dried Schlenk tube, 2-(1H-1,2,4-triazol-1-yl)pyridine (2TzPy) (0.34 mmol, 50 mg) was dissolved in a mixture of solvent ACN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DCM (1
DCM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 6 mL) and stirred at 65 °C for 5 min, then CuCN (1.36 mmol, 123 mg) was dispersed in 10 mL ethanol solution. The reaction mixture was allowed to stir for a further 72 hours at 65 °C which gives a yellow precipitate. The precipitate was filtered and washed with DCM (5 mL × 2) and ACN (5 mL × 2) and dried under vacuum for 6 hours. Yield = 92%.
1, 6 mL) and stirred at 65 °C for 5 min, then CuCN (1.36 mmol, 123 mg) was dispersed in 10 mL ethanol solution. The reaction mixture was allowed to stir for a further 72 hours at 65 °C which gives a yellow precipitate. The precipitate was filtered and washed with DCM (5 mL × 2) and ACN (5 mL × 2) and dried under vacuum for 6 hours. Yield = 92%.
CuCN-MOF was dissolved in acetonitrile by heating and yellow-coloured crystals, suitable for single-crystal X-ray analysis, were obtained by keeping the solution at room temperature for several days.
Characterisation
Physicochemical characterisation
The phase purity of the coordination polymer was confirmed using an Empyrean Malvern Panalytical X-ray diffractometer with monochromatic Cu Kα (0.1540 nm) radiation in the 2θ range of 5–50°. The Brunauer–Emmett–Teller (BET) surface area and Barrett–Joyner–Halenda (BJH) pore size distribution were calculated using N2 gas adsorption–desorption on an Autosorb iQ (Quantachrome Instruments) and the data was collected using AsiQwin software. Attenuated total reflectance Fourier transform infrared spectroscopy (ATR FT-IR) was performed on a Bruker Alpha II spectrophotometer of the powdered sample in the range of 4000–400 cm−1. Morphological characterization through field emission scanning electron microscopy (FE-SEM) was done by using a JEOL JSM-7400F.Electrode fabrication for electrochemical analysis
Firstly, slurries were made by sonicating 10 mg of electrode materials in 1 mL of ethanol for 2 hours. Simultaneously, 1 × 1 cm2 of Ni-foam stripes were cut and cleaned properly before further use. Thereafter, the as-prepared slurries with a concentration of 10 mg of electrode material in 1 mL of ethanol were uniformly coated on the nickel foam with a net electrode material loading of 1 mg. The coated electrodes were dried in a vacuum for 4 hours. 1 M KOH electrolyte solution was used for all the electrochemical tests.Electrochemical studies
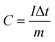 | (1) |
From the GCD curves, the following equations were used to derive the specific capacity, energy density (E), and power density (P) of the fabricated device, where, m is coated.
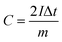 | (2) |
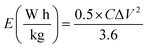 | (3) |
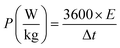 | (4) |
Results and discussion
To synthesize the CuCN-MOF, 2TzPy ligand was selected, which has three coordination sites (Scheme 1). CuCN was reacted with the ligand in a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio to get the MOF in 92%. Reaction in different metal:ligand ratios and in different sets of solvents yielded the same product, with some impurities. Crystals suitable for single crystal X-ray analysis were grown by slow evaporation of acetonitrile solution. The crystallographic parameters, selected bond lengths, and bond angles are presented in Tables S1–S3.†
1 ratio to get the MOF in 92%. Reaction in different metal:ligand ratios and in different sets of solvents yielded the same product, with some impurities. Crystals suitable for single crystal X-ray analysis were grown by slow evaporation of acetonitrile solution. The crystallographic parameters, selected bond lengths, and bond angles are presented in Tables S1–S3.†
Structural analysis
The 2D CuCN-MOF crystallizes in a triclinic system with P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group consisting of two crystallographically independent copper(I) ions, two cyanides, and a ligand in the asymmetric unit (Fig. 1a). The crystal structure analysis reveals the occurrence of a dimer [{Cu(μ3-CN)2Cu}] and monomer Cu(μ2-CN) secondary building units (SBUs) in the polymeric structure. Recently, we have reported one-dimensional Cu(I) CP with the same ligand, where only one nitrogen of the triazole ring is coordinated with the metal center.54 Interestingly, all the nitrogens are coordinated with the Cu(I) center and the polymeric structure shows the presence of two different bonding modes of cyanides; μ2-C:N and μ3-C:C:N. Though the occurrence of different coordination modes of cyanide in a single MOF is unique, μ2-C:N and μ3-C:C:N have been previously reported in CuCN-CPs by the Zhou, Xing Li, and Giordana groups.55–57 The Cu1 adopts tetrahedral geometry, coordinated by triazolyl N4, two μ3-cyanide C8 and two μ2-cyanide N5 atoms. The Cu2 also has a tetrahedral geometry, coordinated by N1 and N3 of ligand, a μ3-cyanide N6, and a μ2-cyanide C9 atom (Fig. 1b). The bridged ligand and cyanides lead to a 2D polymeric structure (Fig. S1†).
space group consisting of two crystallographically independent copper(I) ions, two cyanides, and a ligand in the asymmetric unit (Fig. 1a). The crystal structure analysis reveals the occurrence of a dimer [{Cu(μ3-CN)2Cu}] and monomer Cu(μ2-CN) secondary building units (SBUs) in the polymeric structure. Recently, we have reported one-dimensional Cu(I) CP with the same ligand, where only one nitrogen of the triazole ring is coordinated with the metal center.54 Interestingly, all the nitrogens are coordinated with the Cu(I) center and the polymeric structure shows the presence of two different bonding modes of cyanides; μ2-C:N and μ3-C:C:N. Though the occurrence of different coordination modes of cyanide in a single MOF is unique, μ2-C:N and μ3-C:C:N have been previously reported in CuCN-CPs by the Zhou, Xing Li, and Giordana groups.55–57 The Cu1 adopts tetrahedral geometry, coordinated by triazolyl N4, two μ3-cyanide C8 and two μ2-cyanide N5 atoms. The Cu2 also has a tetrahedral geometry, coordinated by N1 and N3 of ligand, a μ3-cyanide N6, and a μ2-cyanide C9 atom (Fig. 1b). The bridged ligand and cyanides lead to a 2D polymeric structure (Fig. S1†).
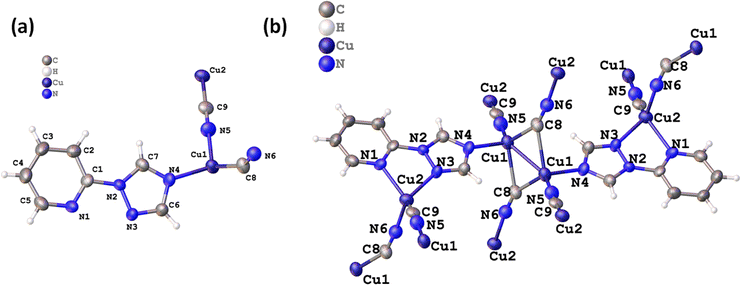 | ||
| Fig. 1 (a) Asymmetric unit of the 2D MOF, and (b) different coordination modes of CN− ions in chain propagation. | ||
The Cu1–Cu11 bond distance is 2.447(17) Å, shorter than the sum of van der Waals radii, and is close to the previously reported for Cu2–μ2C:N units.58,59 The bond lengths of Cu1–N4 and Cu1–N5 are 2.070(5) and 1.930(5), and those of Cu2–N12, Cu2–N32, and Cu2–N63 are 2.134(5), 2.153(5), and 2.004(6) Å, respectively along the symmetry operation (2) + x, 1 + y, −1 + z, (3) + x, 1 + y, + z. The bond angles between Cu and μ3-C:N: Cu1–C8–N6 and Cu11–C8–N6 are 151.4(7) and 138.9(6), respectively. Further, the bond angles between Cu and μ2-C:N: Cu2–C9–N5 and Cu1–N5–C9 are 174.5(6) and 177.4(6)° suggesting a linear arrangement. The C–N bond lengths of 1.153(9) and 1.161(8) Å for C8–N6 and C9–N5 are close to the reported C–N bond length in CuCN-MOFs.60 The bond length of Cu11–C8 is 2.281(8) whereas the Cu2–C9 bond length is 1.874(6) Å. The Cu–Cu distances between each rectangular face are shown in Fig. S2.†
Furthermore, the building blocks extend to form a 16-membered metallacycle with a zig-zag 1D chain consisting of six copper, two CN ions, and six atoms of the organic ligand, with another symmetrical zig-zag chain cross-over to form a rectangular layer with a size calculated to be 11.09 × 9.05 Å2 (Fig. S3†). These rectangular layers are separated by a distance of 4.952 and 5.072 Å (two different distances of the μ3-C:C:N unit) with a CN bridge along the a-axis. The largest metallacycle present in CuCN-MOF is a 20-membered hexagon consisting of six copper, four CN ions and six atoms of the organic ligand (Fig. S4†). The third type of cycle involves 12 atoms from four copper and four cyanides. These layers combine to form a 2D polymeric chain, where each unit forms a cuboid with one missing edge (Fig. S2a†) and three rectangular faces with a diagonal length range from 8.289 to 9.835 Å (Fig. S2b†). These cuboids stack with each other, having opposite faces connected alternatively with each side of the edge to form the 2D CuCN-MOF (Fig. 2a). This CuCN-MOF arranges in a way such that the 2TzPy unit occupies the peripheral position where the centroid distance between the pyridinic ring is 8.209 Å and the Cu(I) metal center is at the inner side of the MOF (Fig. 2b). The centroid distances between two pyridyl/triazolyl rings are the same, confirming that both the rings are in the same plane. The monolayer of the 2D MOF has multiple voids present with different sizes and the crystalline material has a density of 1.974 g cm−3. The packing arrangement of 2D CuCN-MOF is shown in Fig. S5,† where different layers are stacked by the π–π interaction between the CN anions and triazolyl rings of the 2TzPy unit with a distance of 3.215 Å (Fig. S6†). The crystal structures along the b and c axes confirm the 2D structure of the CuCN-MOF (Fig. S7†).
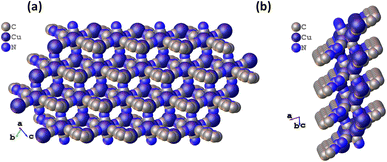 | ||
| Fig. 2 (a) The space filling model of CuCN-MOF along the a axis, and (b) space filling model along the b axis. | ||
PXRD, IR, NMR and TGA analysis
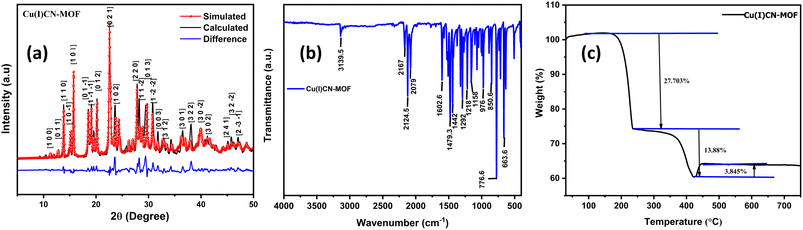
The formation of 2D CuCN-MOF was confirmed by single-crystal X-ray analysis. Further, we performed powder X-ray diffraction (PXRD) analysis to check the bulk property of the CuCN-MOF within the 2θ range of 5–50°. The experimentally observed peaks from PXRD data correspond well with the simulated pattern obtained from SCXRD analysis (Fig. 3a). This confirms the phase purity of the bulk sample, and sharp peaks suggest high crystallinity. The crystallite size calculated from PXRD data is found to be 8.9 Å. The FT-IR of the MOF shows characteristic stretching frequencies of different cyanide ions at 2167, 2124 and 2079 cm−1. The bands at 1442–1602 cm−1 correspond to the stretching frequencies of C–C and C–N of the pyridyl ring. The weak peaks at 1372, 1321, and 1292 cm−1 correspond to the ν(N–N) and ν(C–N) of the triazole ring, respectively (Fig. 3b and S9†). Further, solid-state NMR of CuCN-MOF also confirms the presence of cyanides (broad signal between 191 and 230 ppm) and ligands (112–149 ppm) (Fig. S10†). Thermal stability is an important criterion for the aptness of a complex for a particular application. TGA was performed on the CuCN-MOF at a temperature range of 25–800 °C at a flow rate of 10 °C min−1 (Fig. 3c). The TGA graph suggests the MOF's stability up to 168 °C, and a subsequent rise in temperature causes a stepwise degradation of the organic ligands up to 420 °C.BET, SEM and electrical conductivity analysis
To confirm the specific surface area and pore size distribution of the CuCN-MOF, a Brunauer–Emmett–Teller (BET) isotherm was recorded using the N2 adsorption/desorption method. Less surface area is expected for the MOF as the layers are densely packed in the crystal system by interlocking themselves between the spaces in the peripheral gaps forming a 3D arrangement. These interlocked layers are arranged in a staggered conformation in an ABAB stack sequence and minimize the effective surface area (Fig. S8†).57 The BET isotherm represents the type IV isotherm suggesting a mesoporous structure with a surface area of 8.036 m2 g−1 (Fig. S11†). The pore size distribution was obtained by the Barrett–Joyner–Halenda (BJH) method, revealing a unimodal pore size distribution of 3.42 nm, confirming the mesoporous structure (Fig. S12†).The microstructure and morphology of the 2D CuCN-MOF were characterized by field emission scanning electron microscopy (FE-SEM) (Fig. 4a–c) at various magnifications, which shows an irregular arrangement of various sheets with rough edges. Interestingly, the surface of 2D sheets of the MOF reveals a trough and crest pattern (Fig. 4c), which originates from its unique stacked crystalline structure (Fig. S8†). Such folding in the 2D sheets is advantageous from the charge storage point of view, as it facilitates the seamless diffusion of electrolytes throughout the bulk of the electrode material. Elemental mapping confirms the presence of Cu, C, and N elements in the material (Fig. 4d–f) with an appropriate ratio, which was confirmed by EDS analysis (Fig. 4g). The electrical conductivity of CuCN-MOF was measured using a two-probe direct current method, at 300 K, on pressed pellets, in the voltage range of −10 V to +10 V. The linear (I/V) graph for the MOF validates its ohmic behaviour with a conductivity value of 9.61 × 10−7 S cm−1 (Fig. S13†).
 | ||
Fig. 4 SEM images at various magnifications (a) ×3000, (b) ×5000 (c) ×15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 magnification, (d)–(f) EDS elemental mapping images, (g) EDS spectrum. 000 magnification, (d)–(f) EDS elemental mapping images, (g) EDS spectrum. | ||
Electrochemical study
To evaluate the supercapacitive efficacy of materials, cyclic voltammetry (CV), galvanostatic charge–discharge (GCD), and electrochemical impedance spectroscopy (EIS) were performed using an electrochemical workstation. In order to optimize the performance of the CuCN-MOF electrode, the working potential window was investigated methodically. To ascertain the optimal potential window (Fig. S14a–d†), cyclic voltammetry profiles of the electrode were recorded at a scan rate of 10 mV s−1 in both the positive (0.0 to 0.5 V) and the negative potential windows (−0.5 to 0.0 V). The CV and GCD investigations reveal that the electrode material exhibits similar behaviour in terms of current density and discharge time; however, in the positive potential window, well-discernible redox peaks in CV and a smaller IR drop in GCD are observed (Fig. S14†). Based on these results, all subsequent electrochemical studies were conducted within the potential window of −0.5 to 0.5 V.
Fig. 5a depicts the CV profiles of CuCN-MOF recorded in the potential range −0.5 to 0.5 V at varying scan rates. The CV profile reveals the presence of two cathodic and anodic peaks originating from Cu redox centers suggesting a battery-type behaviour of the electrode material and also giving a dual electron charge transfer mechanism within the CuCN-MOF. Based on the redox steps involving four electron transfer and the formula weight of CuCN-MOF (empirical formula C9H6Cu2N6, formula weight 325.84), its theoretical capacity is calculated to be 1184.45 C g−1. The two cathodic and anodic peaks may be attributed to the redox steps given below:
Further, as expected, the scan rate increase leads to the current rise. Interestingly, variation in scan rate does not lead to any considerable shift in the peak position, highlighting the material's low inherent resistance with insignificant structural alteration during charging and discharging, which are desirable features for cyclic stability and better rate capability.
Further, to comprehend the charge storage mechanism, the power law method was used. As per this law, the peak current response in cyclic voltammetry (CV) is related to the scan rate (ν), as described by eqn (5).
| i = aνb | (5) |
The slope of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i vs. log
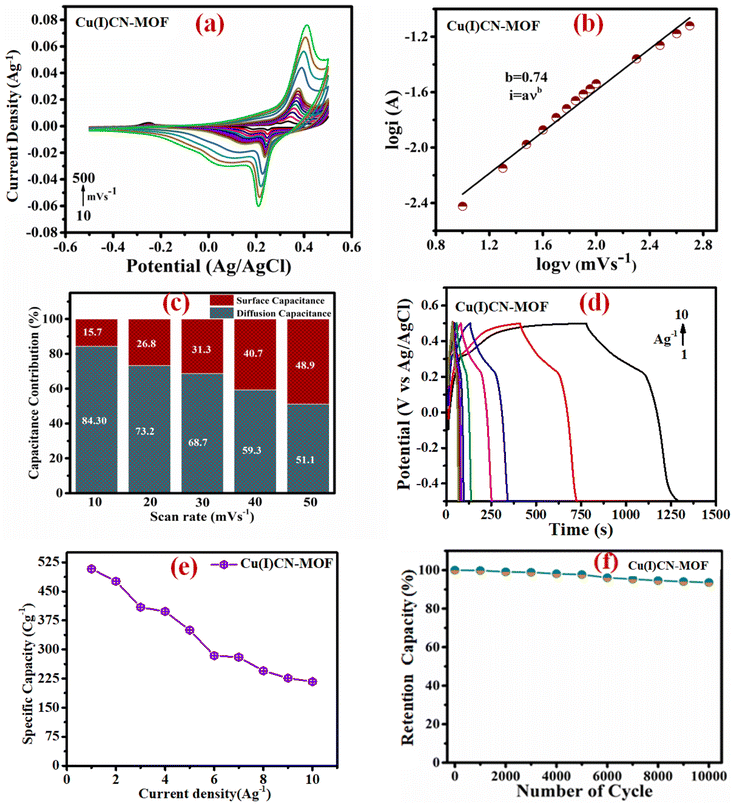
i vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ν provides the value of b, which describes the charge storage mechanism of an electrode. If b ≈ 0.5, charge storage is considered diffusion-controlled as in battery-type materials, whereas if b ≈ 1, charge storage is surface-controlled as in EDLC-type materials. The linear plot for the electrode material is shown in Fig. 5b, and the value of b was found to be 0.74. This suggests that the charge storage occurs due to the combined effect of faradaic and ion adsorption processes, suggesting a supercapattery behaviour of the material.
ν provides the value of b, which describes the charge storage mechanism of an electrode. If b ≈ 0.5, charge storage is considered diffusion-controlled as in battery-type materials, whereas if b ≈ 1, charge storage is surface-controlled as in EDLC-type materials. The linear plot for the electrode material is shown in Fig. 5b, and the value of b was found to be 0.74. This suggests that the charge storage occurs due to the combined effect of faradaic and ion adsorption processes, suggesting a supercapattery behaviour of the material.
To evaluate the quantitative partial contributions of faradaic and surface-controlled processes to the overall charge storage capacity of the material, Dunn's method has been used. Dunn's equation expresses the current at a given potential as a function of the scan rate (ν) as a combination of surface-controlled and diffusion-controlled processes, as shown in eqn (6).
| i(V) = k1ν + k2ν1/2 | (6) |
Fig. 5c depicts the bar graph displaying the percentage capacity contributions of the surface and diffusion-controlled process to the overall capacity of the electrode at various scan rates. At lower scan rates, the overall charge storage is dominated by diffusion, i.e., involving a faradaic process. However, as the scan rate increases, the diffusion-based charge storage contribution gradually decreases, whereas the charge storage due to the surface-controlled process gradually increases. At 50 mV s−1 scan rate, both charge storage mechanisms almost equally contribute to the overall capacitance of the material. The decrease in diffusion capacity with increasing scan rate can be explained by the fact that, at higher scan rates, the diffusion rate is outpaced by the scan rate, causing surface capacity to predominate. For comparison purposes, the proportion of the diffusion process to the overall CV profile of the material at 10 mV s−1 is shown in Fig. S15.†
The specific charge storage capacities of the electrode material were evaluated by galvanostatic charge–discharge (GCD) experiments at current densities ranging from 1 to 10 A g−1 within a potential window of −0.5 to 0.5 V. Fig. 5d shows the GCD profiles of the electrode at different current densities. It is observed that increasing the current density leads to a decrease in the discharging time (Fig. 5d). At 1 A g−1 current density, the calculated specific capacity of the electrode was found to be 508 C g−1. The variation of the specific capacity of the material at different current densities is depicted in Fig. 5e, showing a rapid reduction in specific capacity up to 3 A g−1, followed by a gradual decay. This is mainly due to the fact that, at low current density, the charge storage is mainly dominated by a diffusion-controlled process, which wanes rapidly due to the limitation imposed by the ion diffusion. After 3 A g−1 current density, the surface-controlled process has a significant contribution to the overall capacity, which is not much affected by the current density, resulting in a gradual reduction in the specific capacity.
The improved performances of CuCN-MOF can be explained on the basis of unique structural features. The 2D molecular structure is transformed into the supramolecular structure via π–π interaction between the layers that help in facilitating the ion transport and easing the charge transfer. Also, due to the densely packed structure and due to small bridging cyanide ligands, the redox-active centers [{Cu(μ3-CN)2Cu}] and {Cu(μ2-CN)Cu} are closer, which facilitates the electron transfer process. This structural feature overall enhances the supercapattery performances. This idea is also supported by Jin et al., who described that the high concentration of metal centers helps in the supercapacitor performances even for a nonporous coordination polymer CuAg4BHT.61
The cyclic stability of the electrode material was assessed for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 galvanostatic charge–discharge (GCD) cycles at 10 A g−1, as shown in Fig. 5f. After 10
000 galvanostatic charge–discharge (GCD) cycles at 10 A g−1, as shown in Fig. 5f. After 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, the material shows excellent capacity retention of 92%. Even though the material was used as a binder-free electrode, no trace of electrode material stripping was observed after the long cyclability experiment. This observation highlights the potential of the present coordination polymer as a binder-free electrode material for practical applications.
000 cycles, the material shows excellent capacity retention of 92%. Even though the material was used as a binder-free electrode, no trace of electrode material stripping was observed after the long cyclability experiment. This observation highlights the potential of the present coordination polymer as a binder-free electrode material for practical applications.
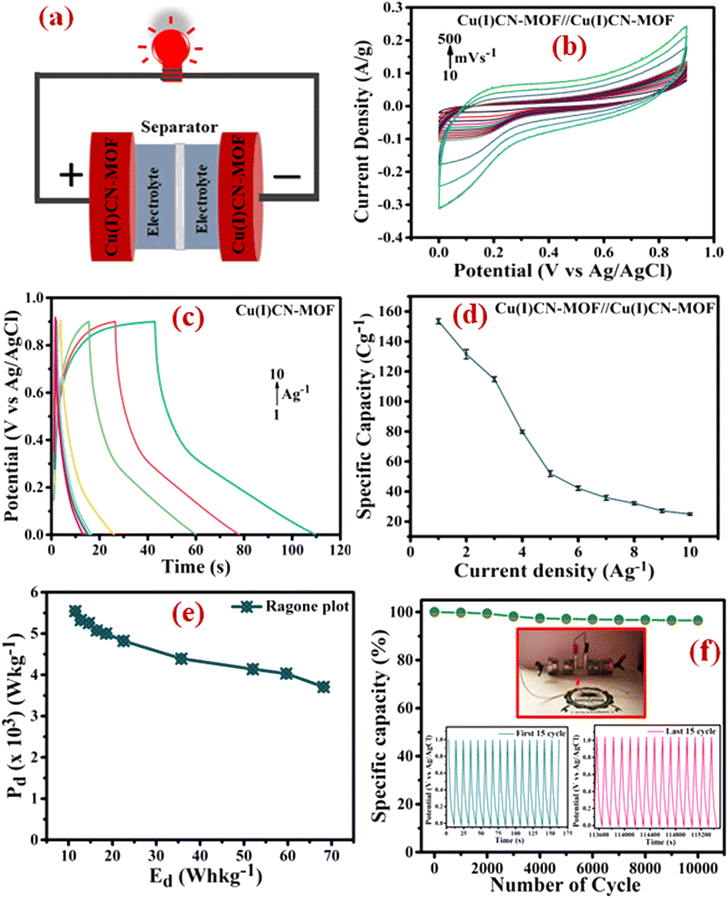
To assess the practical applicability of the electrode, a symmetric device with a cellulose membrane as a separator was assembled, as shown in Fig. 6a. Further, a Ni-foam coated CuCN-MOF electrode device was characterized in a two-electrode configuration with a 0.9 V optimal cell voltage. The CV curves of the device at various scan rates (10 to 500 mV s−1) exhibited a non-rectangular shape that retained their characteristics even at higher scan rates (Fig. 6b), indicating the device's high-rate capability. GCD experiments were conducted at various current densities (1.0 to 10 A g−1) to evaluate the specific capacity of the device (Fig. 6c). The asymmetry in the GCD curves indicates that the overall charge storage is a combination of EDLC and faradaic processes. Similar to the three-electrode configuration, the calculated specific capacity is observed to decrease upon increasing the current density. At 1 A g−1 current density, the device exhibits a specific capacity of 136.48 C g−1, which reduces to 23.0 C g−1 at 10 A g−1 (Fig. 6d). To ensure the charge storage capacity of the device is mainly because of the CuCN-MOF, we also evaluated the specific capacity of the device with bare Ni-foam as an electrode, which showed a charge storage capacity of 32 C g−1 (Fig. S16†). This confirms that CuCN-MOF is the main contributor in the charge storage device.
To analyse the energy density (Ed) and power density (Pd) of the symmetric device, a Ragone plot was constructed (Fig. 6e). The plot shows a maximum energy density of 68.175 W h kg−1 at a power density of 3.7 kW kg−1 and a maximum power density of 5.54 kW kg−1 at an energy density of 11.52 W h kg−1. Further, the cyclic stability of the device was determined by executing 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GCD cycles at a current density of 10 A g−1 within a potential window of 0–1.0 V. After 10
000 GCD cycles at a current density of 10 A g−1 within a potential window of 0–1.0 V. After 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, the device retained 96.5% of its original capacity, demonstrating exceptional cyclic stability (Fig. 6f). To demonstrate the device's practical application, two similar symmetric supercapacitor devices were connected in series to power a red light-emitting diode (LED) (inset of Fig. 6f). Overall, the energy storage device fabricated using CuCN-MOF reported in this paper exhibits outstanding electrochemical performance, including high-rate capability, cyclic stability, and energy and power densities, making it suitable for practical applications. A comparison of the performance of the present electrode material with some previously reported similar systems is summarised in Table S5.† The table clearly suggests that the binder-free electrode fabricated using CuCN-MOF presented in this work exhibits superior performance compared to most of the earlier reported MOFs in terms of cyclic stability, specific capacity, and energy and power densities.
000 cycles, the device retained 96.5% of its original capacity, demonstrating exceptional cyclic stability (Fig. 6f). To demonstrate the device's practical application, two similar symmetric supercapacitor devices were connected in series to power a red light-emitting diode (LED) (inset of Fig. 6f). Overall, the energy storage device fabricated using CuCN-MOF reported in this paper exhibits outstanding electrochemical performance, including high-rate capability, cyclic stability, and energy and power densities, making it suitable for practical applications. A comparison of the performance of the present electrode material with some previously reported similar systems is summarised in Table S5.† The table clearly suggests that the binder-free electrode fabricated using CuCN-MOF presented in this work exhibits superior performance compared to most of the earlier reported MOFs in terms of cyclic stability, specific capacity, and energy and power densities.
Conclusion
In summary, we have reported a facile one-pot synthesis of a 2D MOF using a nitrogen rich 2TzPy ligand with three different coordinating sites. The single crystal X-ray analysis shows that all the nitrogen sites are coordinated to the copper(I) metal center along with μ2-C:N and μ3-C:C:N coordination modes of cyanides, resulting in a 2D polymeric structure. Due to π–π stacking of these 2D polymer structures, it further extends to a 3D architecture, offering suitable channels to facilitate the ion transport to the bulk of the material, making it a promising electrode material. Moreover, the extended π-conjugation provided by CuCN leads to conductivity up to 9.61 × 10−7 S cm−1, suggesting the semiconductor behavior of the MOF. The electrochemical investigations suggest that the CuCN-MOF features an excellent charge storage capacity of 508 C g−1 at 1 A g−1 as a binder and conductive additive-free electrode with a cyclic stability of 92% after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. The charge storage mechanism analysis reveals that the material exhibits a supercapattery type charge storage, combining the features of battery and EDLC type electrodes. The fabricated symmetric device shows an outstanding cyclic stability of 96.5% after 10
000 cycles. The charge storage mechanism analysis reveals that the material exhibits a supercapattery type charge storage, combining the features of battery and EDLC type electrodes. The fabricated symmetric device shows an outstanding cyclic stability of 96.5% after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, with high maximum energy and power densities of 68.175 W h kg−1 and 5.54 kW kg−1, respectively. This work highlights the use of a Cu(I) MOF in developing cost-effective, highly stable, and binder and conductive additive-free electrode materials for high energy as well as high power density energy storage devices.
000 cycles, with high maximum energy and power densities of 68.175 W h kg−1 and 5.54 kW kg−1, respectively. This work highlights the use of a Cu(I) MOF in developing cost-effective, highly stable, and binder and conductive additive-free electrode materials for high energy as well as high power density energy storage devices.
Conflicts of interest
The authors declare no conflicts.Acknowledgements
SM, MKS and DP are grateful to IIT Indore for their fellowships. The Sophisticated Instrumentation Center (SIC) IIT Indore, Department of Metallurgical Engineering and Material Science and the Department of Chemistry IIT Indore are acknowledged for providing characterization facilities. We thank Prof. Preeti A. Bhobe, Department of Physics, IIT Indore, for providing the facility to record electrical conductivity.References
- B. Chen, L. Xu, Z. Xie and W.-Y. Wong, EcoMat, 2021, 3, e12106 CrossRef CAS
.
- A. González, E. Goikolea, J. A. Barrena and R. Mysyk, Renewable Sustainable Energy Rev., 2016, 58, 1189–1206 CrossRef
.
- Poonam, K. Sharma, A. Arora and S. K. Tripathi, J. Energy Storage, 2019, 21, 801–825 CrossRef
.
- K. V. G. Raghavendra, R. Vinoth, K. Zeb, C. V. V. Muralee Gopi, S. Sambasivam, M. R. Kummara, I. M. Obaidat and H. J. Kim, J. Energy Storage, 2020, 31, 101652 CrossRef
.
- Y. Jiao, J. Pei, C. Yan, D. Chen, Y. Hu and G. Chen, J. Mater. Chem. A, 2016, 4, 13344–13351 RSC
.
- B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS PubMed
.
- P. Simon, Y. Gogotsi and B. Dunn, Science, 2014, 343, 1210–1211 CrossRef CAS PubMed
.
- P. Simon and Y. Gogotsi, Nat. Mater., 2020, 19, 1151–1163 CrossRef CAS PubMed
.
- Z. Yu, L. Tetard, L. Zhai and J. Thomas, Energy Environ. Sci., 2015, 8, 702–730 RSC
.
- J. Kim, J. H. Ryu, M. Jang, S. Park, M. Kim, K. H. Lee, S. Choi, Y. Yoon, H.-K. Jung, S. S. Lee and K.-S. An, Small Methods, 2023, 7, 2201539 CrossRef CAS PubMed
.
- W. Li, J. Liu and D. Zhao, Nat. Rev. Mater., 2016, 1, 1–17 Search PubMed
.
- T. K. Ghosh and G. R. Rao, Dalton Trans., 2023, 52, 5943–5955 RSC
.
- G. Zou, Z. Tian, V. S. Kale, W. Wang, S. Kandembeth, Z. Cao, J. Guo, J. Czaban-Jóźwiak, L. Cavallo, O. Shekhah, M. Eddaoudi and H. N. Alshareef, Adv. Energy Mater., 2023, 13, 2203193 CrossRef CAS
.
- A. Khan, F. Shaheen, M. Roman, R. Ahmad, K. Mehboob and M. H. Aziz, J. Energy Storage, 2023, 58, 106317 CrossRef
.
- X. Ma, X. Wei, Z. Wei, Y. Guo, W. Wang, C. Zhang and Z.-Y. Jiang, Electrochim. Acta, 2021, 385, 138434 CrossRef CAS
.
- K. Wang, Q. Li, Z. Ren, C. Li, Y. Chu, Z. Wang, M. Zhang, H. Wu and Q. Zhang, Small, 2020, 16, 2001987 CrossRef CAS PubMed
.
- K. Karuppasamy, D. Vikraman, S. Hussain, P. Santhoshkumar, R. Bose, P. Sivakumar, A. Alfantazi, J. Jung and H.-S. Kim, Small, 2022, 18, 2107284 CrossRef CAS PubMed
.
- H. Liu, X. Liu, S. Wang, H.-K. Liu and L. Li, Energy Storage Mater., 2020, 28, 122–145 CrossRef
.
- T. Brezesinski, J. Wang, S. H. Tolbert and B. Dunn, Nat. Mater., 2010, 9, 146–151 CrossRef CAS PubMed
.
- G. Zhang and X. W. (David) Lou, Sci. Rep., 2013, 3, 1470 CrossRef PubMed
.
- M. Hu, H. Zhang, T. Hu, B. Fan, X. Wang and Z. Li, Chem. Soc. Rev., 2020, 49, 6666–6693 RSC
.
- N. M. Deyab, M. M. Taha and N. K. Allam, Nanoscale Adv., 2022, 4, 1387–1393 RSC
.
- B. L. Ellis, P. Knauth and T. Djenizian, Adv. Mater., 2014, 26, 3368–3397 CrossRef CAS PubMed
.
- R. Liu, J. Duay and S. B. Lee, Chem. Commun., 2011, 47, 1384–1404 RSC
.
- Y. Fang, X.-Y. Yu and X. W. (David) Lou, Matter, 2019, 1, 90–114 CrossRef
.
- S. Bi, H. Banda, M. Chen, L. Niu, M. Chen, T. Wu, J. Wang, R. Wang, J. Feng, T. Chen, M. Dincă, A. A. Kornyshev and G. Feng, Nat. Mater., 2020, 19, 552–558 CrossRef CAS PubMed
.
- C. Largeot, C. Portet, J. Chmiola, P.-L. Taberna, Y. Gogotsi and P. Simon, J. Am. Chem. Soc., 2008, 130, 2730–2731 CrossRef CAS PubMed
.
- B. Y. Guan, X. Y. Yu, H. B. Wu and X. W. (David) Lou, Adv. Mater., 2017, 29, 1703614 CrossRef PubMed
.
- D. Shen, Y. Sha, C. Chen, X. Chen, Q. Jiang, H. Liu, W. Liu and Q. Liu, Dalton Trans., 2023, 52, 7079–7087 RSC
.
- C. Dong and L. Xu, ACS Appl. Mater. Interfaces, 2017, 9, 7160–7168 CrossRef CAS PubMed
.
- J. Liu, M. Zheng, S. Wu and L. Zhang, Coord. Chem. Rev., 2023, 483, 215084 CrossRef CAS
.
- Y. Wu, Y. Chen, M. Tang, S. Zhu, C. Jiang, S. Zhuo and C. Wang, Chem. Commun., 2019, 55, 10856–10859 RSC
.
- S. Bi, H. Banda, M. Chen, L. Niu, M. Chen, T. Wu, J. Wang, R. Wang, J. Feng, T. Chen, M. Dincă, A. A. Kornyshev and G. Feng, Nat. Mater., 2020, 19, 552–558 CrossRef CAS PubMed
.
- K. Wang, S. Wang, J. Liu, Y. Guo, F. Mao, H. Wu and Q. Zhang, ACS Appl. Mater. Interfaces, 2021, 13, 15315–15323 CrossRef CAS PubMed
.
- T. Chen, J.-H. Dou, L. Yang, C. Sun, N. J. Libretto, G. Skorupskii, J. T. Miller and M. Dincă, J. Am. Chem. Soc., 2020, 142, 12367–12373 CrossRef CAS PubMed
.
- X. Huang, S. Zhang, L. Liu, L. Yu, G. Chen, W. Xu and D. Zhu, Angew. Chem., 2018, 130, 152–156 CrossRef
.
- Y. Chen, M. Tang, Y. Wu, X. Su, X. Li, S. Xu, S. Zhuo, J. Ma, D. Yuan, C. Wang and W. Hu, Angew. Chem., Int. Ed., 2019, 58, 14731–14739 CrossRef CAS PubMed
.
- Y. Chen, Q. Zhu, K. Fan, Y. Gu, M. Sun, Z. Li, C. Zhang, Y. Wu, Q. Wang, S. Xu, J. Ma, C. Wang and W. Hu, Angew. Chem., 2021, 133, 18917–18924 CrossRef
.
- K. Fan, C. Fu, Y. Chen, C. Zhang, G. Zhang, L. Guan, M. Mao, J. Ma, W. Hu and C. Wang, Advanced Science, 2023, 10, 2205760 CrossRef CAS PubMed
.
- K. Fan, J. Li, Y. Xu, C. Fu, Y. Chen, C. Zhang, G. Zhang, J. Ma, T. Zhai and C. Wang, J. Am. Chem. Soc., 2023, 145, 12682–12690 CrossRef CAS PubMed
.
- J. Liu, Y. Zhou, Z. Xie, Y. Li, Y. Liu, J. Sun, Y. Ma, O. Terasaki and L. Chen, Angew. Chem., Int. Ed., 2020, 59, 1081–1086 CrossRef CAS PubMed
.
- Q. Liu, X. Liu, C. Shi, Y. Zhang, X. Feng, M.-L. Cheng, S. Su and J. Gu, Dalton Trans., 2015, 44, 19175–19184 RSC
.
- S. Krishnan, A. K. Gupta, M. K. Singh, N. Guha and D. K. Rai, Chem. Eng. J., 2022, 435, 135042 CrossRef CAS
.
- M. K. Singh, A. K. Gupta, S. Krishnan, N. Guha, S. Marimuthu and D. K. Rai, J. Energy Storage, 2021, 43, 103301 CrossRef
.
- A. Schlachter and P. D. Harvey, J. Mater. Chem. C, 2021, 9, 6648–6685 RSC
.
- J. Troyano, F. Zamora and S. Delgado, Chem. Soc. Rev., 2021, 50, 4606–4628 RSC
.
- K. Wang, Z. Wang, S. Wang, Y. Chu, R. Xi, X. Zhang and H. Wu, Chem. Eng. J., 2019, 367, 239–248 CrossRef CAS
.
- Z.-R. Zhang, Z.-H. Ren, C.-Y. Luo, L.-J. Ma, J. Dai and Q.-Y. Zhu, Inorg. Chem., 2023, 62, 4672–4679 CrossRef CAS PubMed
.
- J. Kang, S. Zhang and Z. Zhang, Adv. Mater., 2017, 29, 1700515 CrossRef PubMed
.
- T. Jin, Q. Han and L. Jiao, Adv. Mater., 2020, 32, 1806304 CrossRef CAS PubMed
.
- K. Shen, S. Zhai, S. Wang, Q. Ru, X. Hou, K. San Hui, K. Nam Hui and F. Chen, Batteries Supercaps, 2021, 4, 860–880 CrossRef CAS
.
- J. Ni, X. Zhu, Y. Yuan, Z. Wang, Y. Li, L. Ma, A. Dai, M. Li, T. Wu, R. Shahbazian-Yassar, J. Lu and L. Li, Nat. Commun., 2020, 11, 1212 CrossRef CAS PubMed
.
- K. Shen, Z. Zhang, S. Wang, Q. Ru, L. Zhao, L. Sun, X. Hou and F. Chen, Energy Fuels, 2020, 34, 8987–8992 CrossRef CAS
.
- S. Mishra, D. Pandey, K. Mishra, L. Viau and A. Raghuvanshi, New J. Chem., 2023, 47, 19751–19759 RSC
.
- S.-W. Liang, M.-X. Li, M. Shao and Z.-X. Miao, Inorg. Chem. Commun., 2006, 9, 1312–1314 CrossRef CAS
.
- A. Giordana, E. Priola, G. Gariglio, E. Bonometti, L. Operti and E. Diana, Polyhedron, 2021, 198, 115059 CrossRef CAS
.
- H. Xu, B.-Y. Zhou, K. Yu, Z.-H. Su, Z.-F. Zhao, W.-L. Sun and B.-B. Zhou, New J. Chem., 2015, 39, 1301–1307 RSC
.
- X. Liu, G.-C. Guo, A.-Q. Wu, L.-Z. Cai and J.-S. Huang, Inorg. Chem., 2005, 44, 4282–4286 CrossRef CAS
.
- G.-L. Wang, M.-L. Wang, W. Zhong, M. Afzal, A. Alarifi, S. Singh, A. Kumar and J. Jin, J. Mol. Struct., 2022, 1264, 133332 CrossRef CAS
.
- Y.-L. Qin, H. Sun, Y. Jing, X.-P. Jiang, G.-F. Wang and J.-F. Qin, Acta Crystallogr., Sect. C: Struct. Chem., 2019, 75, 1517–1523 CrossRef CAS
.
- Y. Jin, S. Wu, Y. Sun, Z. Chang, Z. Li, Y. Sun and W. Xu, Mater. Horiz., 2023, 10, 3821–3829 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2245742. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3ta04708c |
| This journal is © The Royal Society of Chemistry 2024 |