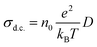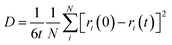Flexible doorway controlled Na⁺ ion diffusion in NaPSO glassy electrolytes from machine-learning force field simulations

Abstract

All-solid-state sodium batteries (ASSSBs), featuring nonflammable solid-state electrolytes (SSEs) and abundant sodium metal anodes, are attractive candidates for safe, cost-effective grid-scale energy storage. Recent research shows that oxygen doping increases the ionic conductivity, mechanical strength, and formability of Na₃PS_4−xO_x (NaPSO) glassy solid-state electrolytes (GSEs), offering a promising approach for developing durable, energy-dense, and affordable ASSSBs. In the Na₃PS_4−xO_x GSEs, a maximum in the Na⁺ ion conductivity is observed at the x = 0.15 composition. The Na⁺ ion conductivity decreases monotonically with further additions of oxygen. However, the limited understanding of the underlying mechanisms of Na⁺ ion motion, diffusion, and conduction in these GSEs hinders its broader application. Here, we employ machine learning force field (ML-FF) molecular dynamics (MD) simulations to investigate sodium ion (Na⁺) diffusion in NaPSO GSEs. Contrary to prior perspectives, our simulation results indicate that oxygen doping consistently reduces the free volume, which would be expected to inhibit rather than increase the Na⁺ diffusion. Interestingly, we find however, that oxygen doping also enhances the flexibility of the amorphous framework, which paradoxically facilitates Na⁺ diffusion. This dual effect results in an initial rise followed by a fall in diffusion coefficients which is consistent with the measured values of the Na⁺ ion conductivity. Our findings provide atomic-level insights into the impact of oxygen doping on Na⁺ diffusion in NaPSO glassy electrolytes, suggesting improved amorphous framework flexibility as a new strategy to enhance conductivity in solid-state electrolytes.

---

Introduction

As the global population grows, the escalating demands for sustainable and renewable energy sources in both industrial and domestic sectors has intensified the focus on developing innovative high-performance battery technologies.¹ This evolution began with lead–acid batteries, advanced through nickel–metal hydride variants, and has now culminated in the prevalent lithium-ion batteries (LIBs).^2,3 These developments have manifested notable enhancements in energy density, safety, and longevity.⁴ Nevertheless, LIBs face challenges related to resource scarcity, cost, environmental impact, and safety concerns.⁵ In response, the scientific community has begun to pivot towards an innovative paradigm: all solid state sodium batteries (ASSSBs).⁶ ASSSBs, leveraging the relative abundance and sustainable nature of sodium, offer a viable alternative with a reduced environmental impact compared to LIBs, thereby emerging as a promising candidate for large-scale energy storage applications.⁷

The structural integrity of ASSSBs hinges on three critical components: the cathode, anode, and the solid-state electrolyte (SSE).⁶ The electrodes serve as energy reservoirs, facilitating energy storage and release during charge and discharge cycles. The SEs play a paramount role in mitigating the risks such as electrical current leakage and thermal runaway, inherent in liquid electrolytes, thus enhancing both safety and battery lifespan.⁸ This component is not only a conduit for sodium ion transport but also a crucial element in preventing short circuits, ensuring efficient battery operation under high voltage conditions. An ideal SSE should exhibit excellent ionic conductivity, robust chemical stability, and high mechanical strength, a combination that researchers consistently strive for and aspire to attain in the development of sodium-ion SSEs.⁹

Inorganic SSEs for ASSSBs are broadly categorized into ceramic, glass-ceramic, and glass types. Ceramic SSEs, such as β′′-Al₂O₃ and NASICON-type oxides, exhibit high chemical stability but require high sintering temperatures and are susceptible to dendrite growth due to poor surface properties.^10–12 Glass-ceramic SSEs, like sulfide-based Na₃PS₄, mitigate dendrite growth with their softer surfaces but tend to degrade into unstable phases upon contact with sodium metal anode.^13–16 In contrast, glassy SSEs (GSEs), particularly oxysulfide types like Na₃PS_4−xO_x (NaPSO), demonstrate improved chemical stability with sodium metal but this comes at the cost of reduced sodium ion conductivity.^17,18 Given the distinct advantages of each type, a novel series of mixed oxysulfide GSEs, Na₃PS_4−xO_x (where 0 < x ≤ 0.60), have been developed.¹⁹ These GSEs not only demonstrate a superior critical current density compared to other sulfide-based sodium-ion conductive SSEs but also support high-performance room-temperature sodium-sulfur batteries, offering a promising solution for enhancing ASSSB technology.

Oxygen doped NaPSO GSEs have been identified to augment performance through several mechanisms: enhancing the glass network formation, bolstering mechanical properties, strengthening interfacial stability, and improving ionic conductivity.¹⁹ Notably, initial oxygen doping (x = 0.15) resulted in a sixfold increase in sodium-ion conductivity. However, further increase in oxygen content led to a rise in activation energy and a corresponding decrease in conductivity. This phenomenon suggests a complex relationship between the structural modifications induced by oxygen doping and the sodium-ion conductivity, necessitating further exploration at the atomic level. A comprehensive investigation into this atomic-scale mechanism is imperative to fully understand this significant increase in Na⁺ ion conductivity and for the refinement of current fabrication techniques. This could involve exploring alternative doping elements to substitute oxygen and/or experimenting with varied sintering processes. Such explorations are crucial for enhancing the performance and efficiency of sodium-ion SSEs.

Given the high computational demands of simulating diffusion events and rates at large spatial and temporal scales, especially at relatively low temperatures,²⁰ we employ machine-learning force field (ML-FF) molecular dynamics (MD) simulations to model the Na⁺ ion diffusion in amorphous NaPSO. Recent advancements in generative artificial intelligence and machine-learning interatomic potentials have demonstrated excellent capabilities in tackling complex tasks involved in resolving structure–activity relationships, reflecting the growing demand and reliability of these methods in the materials research community.^21,22 Machine learning and artificial intelligence have become powerful tools in materials science, offering new opportunities for efficiently exploring complex material behaviors while maintaining DFT-level accuracy.^20,23,24 Our findings here demonstrate that oxygen doping induces a monotonic contraction in the structure of the material, which effectively reduces the free volume, thereby impeding the diffusion of Na ions. Specifically, this contraction leads to a more constrained environment for sodium ion movement. However, moderate oxygen doping enhances the flexibility of the amorphous framework. This increased flexibility facilitates the diffusion of Na ions, countering the effects of structural contraction. The interplay of these two opposing effects—the contraction of structure reducing free volume and the enhanced flexibility aiding ion diffusion—culminates in the observed initial increase followed by a subsequent decrease in ionic conductivity in NaPSO GSEs. This study revises existing mechanisms by providing novel atomic-level insights into oxygen doping in sodium-ion GSEs. These findings are crucial for designing advanced SSEs, enhancing battery performance and safety.

Computational method

Development of the machine-learning force field

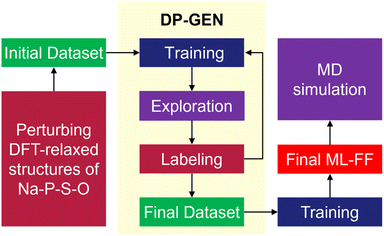
To investigate the diffusion mechanisms in amorphous NaPSO electrolyte, we have developed ML-FF techniques for Na–P–S–O systems. As shown in Fig. 1, the main training dataset for the ML-FF is generated through a concurrent learning scheme, specifically the DP Generator (DP-GEN).²⁵ This scheme iteratively enhances the quality of the model. Each iteration encompasses three sequential phases: exploration, labeling, and training.

Fig. 1 DP-GEN workflow for the construction of reliable ML-FF.

At the initial training step, all original crystal structures were sourced from the Materials Project database, extracted as conventional lattice structures.²⁶ These include pure Na₂S (fcc, hcp, Pnma), NaS₂, Na₂S₅, NaS (cubic, hexagonal), P₂O₅ (Fdd2, Pnma, R3c, P1), P₂S₅, Na₃P(SO)₂, Na₃PSO₃, Na₃PS₃O, and Na₂P₂S₂O₇. To address the non-physical overlap of pure elements observed during long MD simulations, we subsequently added S (P2₁2₁2₁, P2/c), O₂, SO₂, Na (bcc, fcc, hcp), from the Materials Project database, which significantly improved the stability of the force field. To procure a more diverse range of amorphous structures, groups of Na₂S, P₂S₅, and P₂O₅ were randomly arranged into a periodic supercell box according to their concentrations using the Packmol package.²⁷ Subsequently, structural relaxation was conducted to remove any unreasonable molecular contacts.

The initial data set used to kick-off the training and produce initial ML-FF was generated via perturbing DFT-relaxed structures of the crystal phases Na₃P(SO)₂, Na₃PSO₃, Na₃PS₃O, and Na₂P₂S₂O₇. The first iteration of exploration follows a random approach. For each crystal structure, a 2 × 2 × 2 supercell is first uniformly relaxed and compressed using scaling factors α of 0.95, 1.0, and 1.05. Subsequently, both the atomic positions and cell vectors are randomly perturbed. The magnitude of these perturbations is set to 0.01 Å for the atomic coordinates and 3% of the cell vector length for the simulation cell. A 10-step ab initio molecular dynamics (AIMD) simulation is conducted on 30 randomly perturbed structures for each crystal phase using canonical ensemble (NVT) at T = 300 K using VASP software. Atom coordinates, forces, total energies, and virial tensors of all these configurations were recorded for the training of the initial ML-FF. Starting with an initial trained ML-FF, the exploration phase employs NVT MD simulations using the large-scale atomic/molecular massively parallel simulator (LAMMPS) software.^28,29 These simulations are designed to sample pertinent configurations of various deformation processes. These processes include isotropic expansion and compression, as well as uniaxial and shear deformations in six distinct axial directions. The temperature range for these process spans from 10 to 2000 K, incorporating up to 50% strain, and is conducted over a period of 20 ps. In addition, the relevant configurations of the heating and cooling process were also collected between 10 and 2000 K using NVT Ensemble. Furthermore, we extended our simulations to cover conditions under extreme pressures, ranging from 0 to 50 000 bar, and a temperature range of 10 to 500 K, using the isobaric-isothermic (NPT) ensemble. This comprehensive process in the training ensures the ML-FF is robust and versatile, capable of accurately predicting material behavior under a wide spectrum of temperature and pressure conditions.

In this study, a comprehensive set of 95 DP-GEN iterations were conducted, resulting in the generation of 15 902 configurations. These configurations were derived from the trajectories of ML-FF MD simulations.^28,29 Selection for labeling was based on the model uncertainty of each configuration, falling within two predefined trust levels, specifically f_lo = 0.15 and f_hi = 0.35 eV Å⁻¹. This model uncertainty is quantified as the maximum standard deviation of force predictions by an ensemble of ML-FF. These models were trained using identical datasets and hyper-parameters but varied in the random seed initializing the neural network parameters. The convergence of the ML-FF was established when the proportion of visited configurations selected for labeling dropped below 1%. To meet this criterion, the entire process still required human oversight, with some exploration processes repeated until the threshold was reached.

The labeling, i.e. the ab initio calculation of energy, force, and virial, is performed with the Vienna Ab initio Simulation Package (VASP).³⁰ The Perdew–Burke–Ernzerhof (PBE) functional is used to model the exchange–correlation interaction.³¹ Additionally, the van der Waals interactions are described by the zero damping DFT-D3 method of Grimme.³² The kinetic energy cut-off of the plane waves is set to 400 eV, and the spacing of reciprocal space sampling is 0.5 Å⁻¹. The self-consistent field (SCF) iteration stops when the difference in total energy is less than 10⁻⁵ eV. Only the single-point SCF calculations were conducted for each configuration selected from DP-GEN. In addition to these parameters, a force criterion of 10⁻² eV Å⁻¹ was also employed in all simulations to refine the DFT-relaxed initial structures.

During the training phase, four distinct ML-FFs were developed using the DeePMD-kit software package.²⁹ These models shared the same hyper-parameters, differing only in the random seeds initializing their parameters. The embedding net size was set to (25, 50, 100), and the fitting net was configured to (240, 240, 240). A cut-off radius of 6 Å was established, with a smoothing parameter (rcut_smth) of 2 Å. In each training step, a minibatch – a subset of the training dataset – was used to evaluate the gradient of the loss function. This minibatch was sufficiently large to ensure that all frames included no fewer than 32 atoms. The hyper-parameters start_pref_e, start_pref_f, start_pref_v, limit_pref_e, limit_pref_f, and limit_pref_v, governing the weights of energy, force, and virial losses in the total loss function, were set to 0.02, 1000, 0.02, 1.0, 1.0, and 1.0, respectively. The learning rate was initiated at 1.0 × 10⁻³, decreasing exponentially to 3.51 × 10⁻⁸ over 5 × 10⁵ training steps during the DP-GEN iteration to enhance efficiency without compromising accuracy.³³ Ultimately, a refined deep potential model was developed based on the final training dataset. In this phase, the training step was increased to 4 × 10⁶, maintaining other parameters consistent with the earlier training step. This final deep potential model was then adopted to depict the atomic interactions within the Na–P–S–O systems in subsequent MD simulations.

MD simulations

All MD simulations were performed using the LAMMPS software, with the ML-FF deployed to describe the interatomic interactions.^28,29 The velocity Verlet algorithm is employed to integrate the equations of motion with a timestep of 1.0 fs in all MD simulations. To avoid surface effects, periodic boundary conditions are implemented in all three directions. To ensure accurate simulation of temperature and pressure, Nosé–Hoover thermostat and barostat methods were employed to control the temperature and temperature in MD simulations, with the damping constants set to 0.1 ps and 1.0 ps, respectively. For the purposes of visualization and analysis of the simulation outcomes, the Open Visualization Tool (OVITO) was utilized.³⁴

To closely mimic experimental processes and generate analogous precursors (Na₃PS_4−xO_x, with x values of 0.00, 0.15, 0.30, and 0.60), groups of Na₂S, P₂S₅, and P₂O₅ were randomly distributed in a periodic supercell box in proportion to their concentrations using the Packmol package.²⁷ All subsequent simulations were conducted five times for each composition, using five different initial structures of 1600 atoms derived from randomly generated configurations to ensure statistical reliability.

To achieve fully amorphized glassy structures, these initial configurations underwent a series of temperature treatments. Initially, they were first heated from 300 K to 1400 K over 100 ps under an NVT ensemble. They were then maintained at 1400 K for 1 ns to ensure sufficient equilibrium. This was followed by a cooling phase from 1400 K to 300 K over 500 ps, and subsequent relaxation at 300 K for 50 ps. Finally, to eliminate any residual stress from quenching, the system was further equilibrated at 300 K and 1 bar under an NPT ensemble for an additional 200 ps. To simulate the less dense structural characteristics of oxygen-free Na₃PS₄ with visible pores that is observed experimentally,¹⁹ a spherical region with a diameter of ∼1.4 nm was manually removed from the center of the fully relaxed, dense glass structure of Na₃PS₄ (Fig. S1a of ESI†). The chemical stoichiometry of the resulting porous Na₃PS₄, referred to as “P-Na₃PS₄”, was maintained by selectively removing atoms near the pore. The P-Na₃PS₄ was further equilibrated at 300 K and 1 bar under an NPT ensemble for 200 ps.

The density and the radial pair distribution (RDF) functions of the glass were computed by averaging the MD trajectory over 100 ps, following the convergence of the system's potential energy at 300 K and 1 bar. Subsequently, the bulk modulus was computed by determining the slope of the stress–strain curve under hydrostatic tension and compression, specifically within the range of ±1% strain, consistent with isostatic deformation.

The d.c. ionic conductivity of Na ions was calculated by the Nernst–Einstein relation, given as follows:

where σ_d.c. is the d.c. ionic conductivity, n₀ is the number of charge-carrier atoms per volume, e is the charge of an electron, k_B is the Boltzmann constant, T is the temperature, and D is the diffusion coefficient. The diffusion coefficient is calculated from the mean square displacement (MSD) of Na derived from MD simulations:
where t is time, N is the number of all Na atoms, and r_i is the position of i^th Na atom at time 0 and time t.

Na-MSD computations were performed across a temperature range from 333 to 423 K, at intervals of 30 K, and also at 473 K, utilizing the NPT ensemble. The duration of simulations varied depending on the temperature: 20 ns for temperatures above 390 K and extended to 50 ns for temperatures below 390 K, to ensure adequate convergence of MSD calculations at lower temperatures. It is important to note that for improved statistical accuracy, the initial 50% and the final 5% of data points from the MSD(t) curves were excluded, as these segments typically exhibit poor statistics.

Results and discussion

Accuracy test of ML-FF

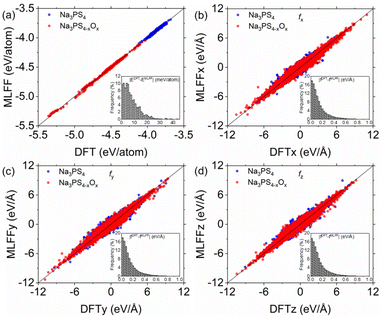
To assess the fitting performance of the ML-FF calculations, we compared its energy and force predictions against Density Functional Theory (DFT) calculations for 1300 randomly selected glassy structures from our training set. The focus of this evaluation was on the Na₃PS_4−xO_x (0 ≤ x < 4) systems, which are central to this study. As illustrated in Fig. 2, the ML-FF predictions exhibit a close correspondence with the DFT values. Quantitatively, the mean absolute error (MAE) for energies and forces in these systems are 7.47 meV per atom and 0.14 eV per Å per atom, respectively, with root-mean-square errors (RMSE) of 9.74 meV per atom and 0.21 eV per Å per atom. These accuracy levels are lower compared to those attained by previously developed ML-FFs for crystalline structures.²⁰ However, the precision is comparable to that of ML-FFs previously utilized in studies on methane hydrate decomposition and other glassy electrolytes.^35,36 This slight decrease in accuracy can be attributed to the complex nature of the larger datasets characteristic of amorphous structures, as opposed to more uniform crystalline systems.^20,23,24

Fig. 2 Benchmark test of ML-FF against DFT: comparison of (a) energies and (b–d) atomic forces for 1300 random glassy structures from Na₃PS_4−xO_x (0 ≤ x < 4). Insets show histograms of error distribution.

Structural and mechanical properties of amorphous Na₃PS_4−xO_x

Following the evaluation of the ML-FF, we applied it to MD simulations to obtain amorphous Na₃PS_4−xO_x (x = 0, 0.15, 0.30, 0.60) structures by quenching from 1400 K to ambient temperature and pressure. The calculated densities of glassy Na₃PS₄ at 2.0 g cm⁻³ are identical to the powder density of 2.0 g cm⁻³ obtained from experimental measurements at room temperature.³⁷ This close match in densities provides initial validation of the structural accuracy in the ML-FF MD.

As illustrated in Fig. 3a, the characteristic feature of the fully amorphized structures is a framework composed of PS₄³⁻ clusters interspersed with Na⁺ ions and some free S⁼ ions. The oxygen doping, predominantly substituting some S atoms of PS₄ clusters to form PS_4−xO_x (0 < x ≤ 4), appears to compact the structure due to oxygen's higher electronegativity and smaller ionic radii. This is evident from the shorter distance shift in the non-bonding peaks in the RDF shown in Fig. 3b. As the oxygen content increases, the structure becomes denser, leading to a decrease in the volume (as shown in Fig. S2†), consistent with experimental observations.¹⁹ Furthermore, the RDF of Na₃PS₄ closely aligns with previously reported results,³⁸ albeit with slight differences in relative intensity attributable to enhanced amorphization in our larger MD simulation size. Notably, the distinct peak near 6 Å, indicative of the distance between PS_4−xO_x units, is quite intense. This suggests a greater presence of independent PS_4−xO_x units, confirming a higher degree of amorphization in this study.

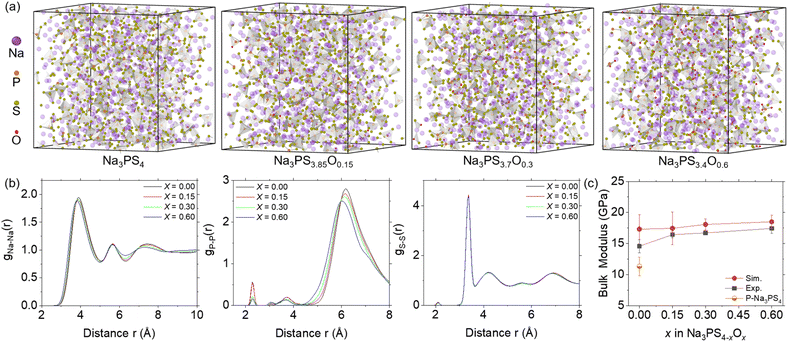Fig. 3 Structural information and bulk modulus of Na₃PS_4−xO_x (x = 0, 0.15, 0.30, and 0.60) at ambient temperature and pressure. (a) Amorphous structures of Na₃PS_4−xO_x with 1600 atoms. Oxygen doping primarily replaces some S atoms, forming PS_4−xO_x clusters that constitute the amorphous framework, interspersed with Na ions and some free S atoms. (b) Radial distribution functions (RDF) of Na–Na, P–P, and S–S pairs in glassy Na₃PS_4−xO_x, showing peak shifts to the left due to volumetric contraction from oxygen doping. (c) Bulk modulus calculated from MD and experimental data,¹⁹ with error bars indicating standard deviations (n = 5).

We also calculated the bulk modulus of these structures, performing five calculations for each composition to ensure reliability. As depicted in Fig. 3c, the simulated bulk modulus values align well with experimental results,¹⁹ increasing with oxygen content, corresponding with the increasingly compact structural features shown by the RDF. However, the simulated values are overall slightly higher due to the more idealized structures used in our simulations (free of impurities, voids, and other defects). Notably, the difference between the simulated and experimental results decreases as the oxygen concentration increases, suggesting that the experimental samples are increasingly approaching structures with theoretical density, consistent with the reported outstanding formability of NPSO.¹⁹ The larger discrepancy for x = 0 can be attributed to visible porosity and defects in the experimental samples.^19,39 Simulations of porous Na₃PS₄ (x = 0) indeed showed a significant reduction in bulk modulus, confirming this observation. These structural features and mechanical properties, accurately replicated by our trained ML-FF, validate its high precision, and make it suitable for investigating the underlying mechanisms of variations in Na ion diffusion coefficients.

Impact of oxygen doping on Na ionic conductivities

Considering the time scale limitations of MD simulations and the temperature range (298 K to 363 K) over which experimental ionic conductivities were measured,¹⁹ we simulated diffusion behaviors at temperatures of 333 K, 363 K, 393 K, 423 K, and 473 K. However, due to insufficient convergence of the mean square displacement (MSD) results for Na ions at 333 K and 363 K over extended 50 ns simulations (as detailed in Fig. S3†), reliable data could not be obtained at these temperatures. Therefore, Fig. 4 presents the comparison of simulated results at 393 K, 423 K, and 473 K with experimental results at 363 K. Notably, higher temperatures not only increase the MSD slope but also improve the smoothness of the MSD curve, suggesting that Na ions diffuse faster and more uniformly at elevated temperatures. Furthermore, the MSD results indicate the importance of simulation duration, showing stabilization only after approximately 10 ns. This suggests that MD simulations may offer more reliable insights into diffusion than AIMD methods, due to their ability to encompass larger temporal and spatial scales.²⁰ The calculated ionic conductivities of Na ions from the MSD data, compared with experimental findings, are shown in Fig. 4d as a function of the oxygen doping. The simulated conductivities exhibit an initial increase followed by a decrease, similar to the experimental results, demonstrating the efficacy of the ML-FF technique. Notably, the peak ionic conductivity at 393 K occurs at x = 0.30, whereas at 423 K and 473 K, it aligns with experimental observations at x = 0.15. This suggests that the optimum ionic conductivity might be achieved at around x = 0.20. Furthermore, the relatively flat variation at 473 K agrees with the experimental trend of converging conductivities across different compositions at higher temperatures.¹⁹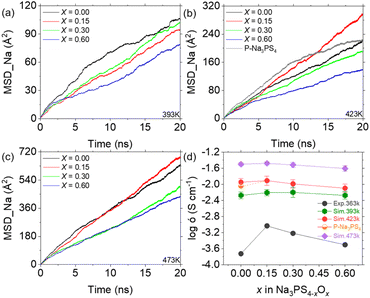

Fig. 4 MSD and ionic conductivity of Na₃PS_4−xO_x (x = 0, 0.15, 0.30, and 0.60) at various temperatures. (a–c) MSD plots of Na-ion diffusion in glassy Na₃PS_4−xO_x at 393 K (a), 423 K (b), and 473 K (c), using the stable diffusion phase between 10–19 ns for calculating reliable ionic conductivity. (d) Ionic conductivity of Na₃PS_4−xO_x at different temperatures compared with experimental results,¹⁹ showing a similar trend of initial increase followed by a decrease.

Simulations of porous Na₃PS₄ suggest that the substantial increase in conductivity from x = 0 to x = 0.15, as observed experimentally, is largely attributed to enhanced densification, in addition to the contributions from oxygen doping. This densification effectively reduces defects such as pores and interfaces, which typically impede diffusion, thus promoting Na ion diffusion. As shown in Fig. S1b,† there are no diffusion trajectories passing through the central void, demonstrating its significant obstructive effect. This elucidates the steep increase in conductivity observed at the onset of minimal oxygen doping in previous experiments.^19,39 In summary, excluding the effects of these defects, the observed rise and subsequent fall in Na ion conductivity with increasing oxygen content closely mirrors experimental outcomes. The ML-FF provides us with an opportunity to investigate the atomic mechanisms underlying this phenomenon.

Atomic mechanisms underlying conductivity variations with doping oxygen

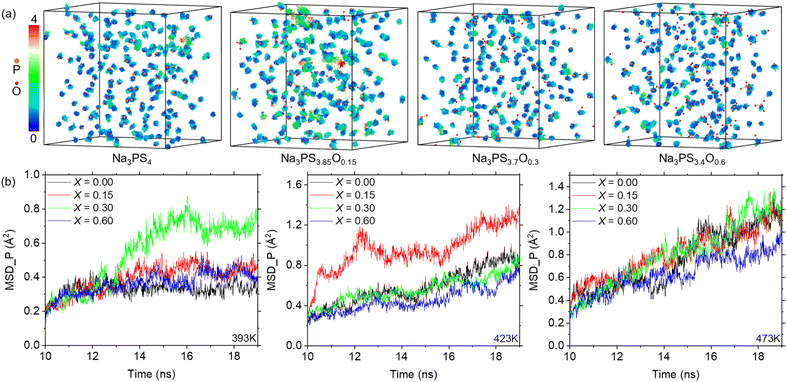
Our simulations reveal that the diffusion pathways for Na ions primarily involve shuttling between PS_4−xO_x clusters (as shown in Fig. S4†). Therefore, the size of the “doorways” formed between these clusters is a critical factor influencing the efficiency of Na ion diffusion. As indicated by computed RDF (Fig. 3b) and volume (or density) results (Fig. S2†), increasing oxygen content leads to a reduction in the structure's overall volume, consequently diminishing the size of these “doorways”. Intuitively, this reduction should uniformly hinder diffusion and thereby lower the Na⁺ ion conductivity. However, the pattern of the conductivity observed in our study and previous experimental research,¹⁹ marked by an initial increase in the ionic conductivity followed by a decrease in the ionic conductivity, strongly suggests the presence of additional factors that enhance sodium ion diffusion in these glasses. These factors seemingly counteract the limiting effect of the decreasing size of the “doorways”, pointing to a more complex underlying mechanism in Na⁺ ion transport.

This suggestion prompted a closer examination of the behavior of PS_4−xO_x clusters during diffusion, especially since oxygen doping chiefly modifies the composition of PS₄ clusters, altering the amorphous framework. The position distribution of phosphorus (P) atoms within the PS_4−xO_x clusters can serve as a proxy for the behavior of the entire framework, given that P atoms are central to these clusters. For instance, Fig. 5a illustrates the position distribution of P atoms in PS_4−xO_x clusters over a 10 ns to 19 ns timeframe at 423 K, with all Na and S atoms removed for clarity. The visual analysis of this graph distinctly shows an initial increase followed by a decrease in the mobility range of P atoms, a trend that correlates with the increasing oxygen content. Notably, this pattern aligns perfectly with the changes in Na ion conductivity calculated previously, as depicted in Fig. 4d.

Fig. 5 Position distribution and MSDs of P atoms in PS_4−xO_x clusters during 10 ns to 19 ns at different temperatures. (a) P atom position distribution in Na₃PS_4−xO_x at 423 K, with local line coloring indicating the instantaneous displacement magnitude (Å). Notably, P atoms in Na₃PS_3.85O_0.15 exhibit greater mobility, suggesting a more flexible amorphous framework in the cluster. (b) MSDs of P atoms in PS_4−xO_x clusters over the same timeframe.

The mobility of the P atoms is indicative of the amorphous framework's ability to accommodate structural changes. Unlike previous studies that employed a fixed “doorway” model to analyze ion diffusion mechanisms,^19,39–41 our simulation results here, rather, suggest that the amorphous framework actually possesses a certain degree of mobility during ion diffusion, leading to the development of a flexible “doorway” controlled ion diffusion model. Our use of ML-FF MD simulations allows for in situ dynamic studies of diffusion behaviors in SSEs and the discovery of more accurate atomic mechanisms. Oxygen doping, while compacting the structure (a conclusion corroborated by our MD results and previous experimental research), results in smaller “doorway” sizes. Nonetheless, the introduction of a few oxygen atoms disrupts the uniformity among clusters, enhancing their mobility. This is evident from Fig. 5, which shows the random distribution of oxygen atoms, indicating that these atoms do not directly affect the mobility of individual clusters. This dynamic adaptability of the “doorway” during diffusion becomes apparent (Fig. 5a).

As oxygen doping continues and the volume further decreases, this flexibility is also constrained. Fig. 5b demonstrates the MSDs of P atoms in PS_4−xO_x clusters during the same 10 ns to 19 ns period at different temperatures. Structures that exhibit larger P atom MSDs correspond to higher ionic conductivities, aligning with our previous findings (for instance, results at 393 K and 423 K as seen in Fig. 4c). When MSDs of P atom are comparable, the ionic conductivity consistently decreases with increasing oxygen content, influenced by the reduced volume, as observed at 473 K (Fig. 4c). The drastic increases in the MSD of P atoms observed under certain conditions (e.g., 13–14 ns at 393 K for x = 0.3, and 10–12 ns at 423 K for x = 0.15) suggest a significant thermal activation effect, where sufficient energy is needed to overcome the energy barrier for cluster movement. This explains the experimental trend of converging conductivities across different compositions at higher temperatures. The underlying mechanism involves higher temperatures fully unleashing the mobility of the amorphous framework in various compositions, to the extent that the limitations imposed by differing “doorway” sizes in the structures can be almost disregarded, leading to converged ionic conductivities.

Conclusions

In summary, this study has investigated the diffusion mechanisms of Na ions in NaPSO glassy electrolytes through MD simulations employing a newly developed ML-FF technique. This work challenges the previous experimental understanding, which suggests that oxygen doping non-monotonically affects Na ion conductivity by first increasing and then decreasing the free volume based on the fixed “doorway” model. Our simulations reveal that the amorphous framework possesses inherent mobility during ion diffusion, leading to the development of a flexible “doorway” model for ion diffusion. Oxygen doping disrupts the balance in the amorphous framework, enhancing its flexibility, which in turn facilitates Na ion diffusion. Coupled with the inhibitory effects from the monotonic decrease in free volume with increasing oxygen content, the diffusion coefficient exhibits an initial increase followed by a subsequent decrease. Overall, our work provides atomic-level insights into the impact of oxygen doping on Na ion diffusion in NaPSO glassy electrolytes, suggesting that enhancing the flexibility of the amorphous framework represents a novel approach for improving the conductivity of SSEs.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

Conceptualisation & project administration: Q. A., W. M. investigation and methodology: K. L., R. Z. supervision: Q. A. writing – original draft: K. L. writing – review & editing: all authors. Resources and funding acquisition: Q. A., W. M. These author contributions are defined according to the contributor roles taxonomy (CRediT).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the start-up grant from Iowa State University, and the simulations were performed at ISU High Performance Computing clusters. Work contributed by S. W. M. was supported in part by the NSF through grant DMR-1936913, by the DOE through contracts DE-EE0008852 and Battelle Memorial Institute/PNNL subcontract number 679315, and by the Iowa Department of Economic Development grant number 307352.

References

1. B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935.
2. P. P. Lopes and V. R. Stamenkovic, Science, 2020, 369, 923–924.
3. G. E. Blomgren, J. Electrochem. Soc., 2017, 164, A5019–A5025.
4. M. Winter, B. Barnett and K. Xu, Chem. Rev., 2018, 118, 11433–11456.
5. N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682.
6. J. W. Choi and D. Aurbach, Nat. Rev. Mater., 2016, 1, 16013.
7. A. Manthiram, Nat. Commun., 2020, 11, 1550.
8. E. A. Wu, S. Banerjee, H. Tang, P. M. Richardson, J.-M. Doux, J. Qi, Z. Zhu, A. Grenier, Y. Li, E. Zhao, G. Deysher, E. Sebti, H. Nguyen, R. Stephens, G. Verbist, K. W. Chapman, R. J. Clément, A. Banerjee, Y. S. Meng and S. P. Ong, Nat. Commun., 2021, 12, 1256.
9. X. Chi, Y. Liang, F. Hao, Y. Zhang, J. Whiteley, H. Dong, P. Hu, S. Lee and Y. Yao, Angew. Chem., Int. Ed., 2018, 57, 2630–2634.
10. L. Porz, T. Swamy, B. W. Sheldon, D. Rettenwander, T. Frömling, H. L. Thaman, S. Berendts, R. Uecker, W. C. Carter and Y. Chiang, Adv. Energy Mater., 2017, 7, 1701003.
11. W. Zhou, Y. Li, S. Xin and J. B. Goodenough, ACS Cent. Sci., 2017, 3, 52–57.
12. S. Kim, S. Lee, K. Jung, Y. Park, N. Cho, J. Choi and H. Kim, Bull. Korean Chem. Soc., 2015, 36, 2869–2874.
13. H. Tang, Z. Deng, Z. Lin, Z. Wang, I.-H. Chu, C. Chen, Z. Zhu, C. Zheng and S. P. Ong, Chem. Mater., 2018, 30, 163–173.
14. E. A. Wu, C. S. Kompella, Z. Zhu, J. Z. Lee, S. C. Lee, I.-H. Chu, H. Nguyen, S. P. Ong, A. Banerjee and Y. S. Meng, ACS Appl. Mater. Interfaces, 2018, 10, 10076–10086.
15. S. Wenzel, T. Leichtweiss, D. A. Weber, J. Sann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2016, 8, 28216–28224.
16. Y. Tian, T. Shi, W. D. Richards, J. Li, J. C. Kim, S.-H. Bo and G. Ceder, Energy Environ. Sci., 2017, 10, 1150–1166.
17. S. Kmiec, A. Joyce and S. W. Martin, J. Non-Cryst. Solids, 2018, 498, 177–189.
18. M. Lazar, S. Kmiec, A. Joyce and S. W. Martin, ACS Appl. Energy Mater., 2020, 3, 11559–11569.
19. X. Chi, Y. Zhang, F. Hao, S. Kmiec, H. Dong, R. Xu, K. Zhao, Q. Ai, T. Terlier, L. Wang, L. Zhao, L. Guo, J. Lou, H. L. Xin, S. W. Martin and Y. Yao, Nat. Commun., 2022, 13, 2854.
20. J. Huang, L. Zhang, H. Wang, J. Zhao, J. Cheng and W. E, J. Chem. Phys., 2021, 154, 094703.
21. Y. Liu, Z. Yang, Z. Yu, Z. Liu, D. Liu, H. Lin, M. Li, S. Ma, M. Avdeev and S. Shi, J. Mater., 2023, 9, 798–816.
22. S. Takamoto, D. Okanohara, Q.-J. Li and J. Li, J. Mater., 2023, 9, 447–454.
23. T. Hu, J. Tian, F. Dai, X. Wang, R. Wen and S. Xu, J. Am. Chem. Soc., 2023, 145, 1327–1333.
24. T. Wen, L. Zhang, H. Wang, W. E and D. J. Srolovitz, Mater. Futures, 2022, 1, 022601.
25. Y. Zhang, H. Wang, W. Chen, J. Zeng, L. Zhang, H. Wang and W. E, Comput. Phys. Commun., 2020, 253, 107206.
26. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
27. L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164.
28. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in ’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
29. H. Wang, L. Zhang, J. Han and W. E, Comput. Phys. Commun., 2018, 228, 178–184.
30. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
31. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
32. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
33. X. Wang, Y. Wang, L. Zhang, F. Dai and H. Wang, Nucl. Fusion, 2022, 62, 1–11.
34. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012.
35. K. Luo, Y. Shen, J. Li and Q. An, J. Phys. Chem. C, 2023, 127, 7071–7077.
36. R. Zhou, K. Luo, S. W. Martin and Q. An, ACS Appl. Mater. Interfaces, 2024, 16, 18874–18887.
37. M. Nose, A. Kato, A. Sakuda, A. Hayashi and M. Tatsumisago, J. Mater. Chem. A, 2015, 3, 22061–22065.
38. A. Dive, Y. Zhang, Y. Yao, S. W. Martin and S. Banerjee, Solid State Ionics, 2019, 338, 177–184.
39. Y. Kim, J. Saienga and S. W. Martin, J. Phys. Chem. B, 2006, 110, 16318–16325.
40. A. Dive, C. Benmore, M. Wilding, S. W. Martin, S. Beckman and S. Banerjee, J. Phys. Chem. B, 2018, 122, 7597–7608.
41. S. Kmiec, M. Olson, M. Kenney and S. W. Martin, Chem. Mater., 2022, 34, 9479–9491.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta05071a

---