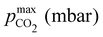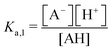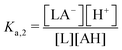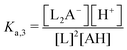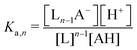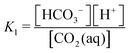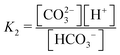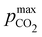Open Access Article
Open Access ArticleAcid–base concentration swing for direct air capture of carbon dioxide†
Anatoly
Rinberg
 * and
Michael J.
Aziz
* and
Michael J.
Aziz

John A. Paulson School of Engineering and Applied Sciences Harvard University Cambridge, Massachusetts, 02138, USA. E-mail: rinberg@g.harvard.edu
First published on 13th August 2024
Abstract
This work demonstrates the first experimental evidence of the acid–base concentration swing (ABCS) for direct air capture of CO2. This process is based on the effect that concentrating particular acid–base chemical reactants will strongly acidify solution, through Le Chatelier's principle, and result in outgassing absorbed CO2. After collecting the outgassed CO2, diluting the solution will result in a reversal of the acid–base reaction, basifying the solution and allowing for atmospheric CO2 absorption. The experimental study examines a system that includes sodium cation as the alkalinity carrier, boric acid, and a polyol complexing agent that reversibly reacts with boric acid to strongly acidify solution upon concentration. Though the tested experimental system faces absorption rate and water capacity limitations, the ABCS process described here provides a basis for further process optimization. A generalized theoretical ABCS reaction framework is developed and different reaction orders and conditions are studied mathematically. Higher order reactions yield favorable cycle output results, reaching volumetric cycle capacity above 50 mM for third-order and 80 mM for fourth-order reactions. Optimal equilibrium constants are determined in order to guide alternative chemical searches and synthetic chemistry design targets. There is a substantial energetic benefit for reaction orders above the first, with second- and third-order ABCS cycles exhibiting a thermodynamic minimum work for the concentrating and outgassing steps around 150 kJ per mole of CO2. A significant advantage of the ABCS is that it can be driven through well-developed and widely-deployed desalination technologies, such as reverse osmosis, with opportunities for energy recovery when recombining the concentrated and diluted streams, and extraction can occur directly from the liquid phase upon vacuum application.
1 Introduction
Carbon dioxide removal has emerged as a key component of addressing global climate change, necessary for compensating for hard-to-avoid emissions from industries such as agriculture and aviation.1,2 With global warming exceeding 1.3 °C,3 and already harming the most vulnerable and underprivileged populations on this planet, carbon removal will likely need to reach a scale of gigatonnes of CO2 per year. However, the international scientific community is in agreement that reducing greenhouse gas emissions must be prioritized to avert the worst harms of climate change.4 Some have called for decoupling emission reduction and carbon dioxide removal targets, to avoid the dangers of mitigation deterrence and the associated moral hazard, which follow from setting massive carbon dioxide removal targets of 10–20 GtCO2 per year.51.1 Direct air capture
Carbon dioxide removal spans a broad range of approaches, from land and ocean-based methods, such as reforestation, shifts in agricultural practices, and the addition of alkalinity into the ocean, to industrial methods, such as enhanced mineralization and direct air capture with carbon storage (DACCS).6,7 DACCS, in particular, is a highly energy-intensive chemical process for capturing atmospheric CO2, concentrating and compressing it, and then durably storing it in geological reservoirs or materials. Although exceptions exist, DAC methods are broadly split into two categories: one that is based on a solid sorbent and another that relies on solvent contacting. Each approach confers its own advantages. Solid sorbents, which often rely on amine polymers to react with CO2, require only low-grade heat or moisture for regeneration, and rely on minimal water usage.8 Solvent-based approaches, on the other hand, require large amounts of water, but have the advantage of decoupling contacting from regeneration allowing for continuous absorption.9In particular, electrochemical aqueous solvent DAC approaches are being investigated extensively.10–14 One type of electrochemical DAC can be driven by changing the charge state of a redox-active molecule to either directly bind with dissolved inorganic carbon (DIC) or indirectly control the hydroxide concentration in solution. Such systems have the advantage of feasibly reaching low energy of capture, below 100 kJ mol−1; however, the proposed approaches face a range of implementation challenges, such as chemical degradation, membrane stability and fouling, low kinetics of reaction.15 Other electrochemical approaches are driven through electrolysis reactions to create a stream of base and acid, for CO2 capture and subsequent neutralization, respectively.16
In contrast, the approach explored in this work, the acid–base concentration swing (ABCS), is based on a new driving method that controls the concentration of solutes in solution. No redox reaction is involved, nor is the addition or removal of acids or bases from solution. Osmotic pressure drive, such as through reverse osmosis, can be used to control the concentration of reactants in solution. In this way, though finding reversible and stable candidate reactions, as well reaching high absorption kinetics, pose challenges, the ABCS paradigm opens the exploration of new aqueous DAC chemistry.
1.2 Enhancing the alkalinity concentration swing with acid–base reactions
Our previous work, characterizing the alkalinity concentration swing (ACS), reported a process driven by concentrating an alkaline solution loaded with DIC captured from atmospheric CO2. Increasing the alkalinity and DIC concentrations together increases the solution partial pressure of CO2 and allows for CO2 collection upon vacuum application. However, the ACS, without modification, requires excessive amounts of water and has an extremely slow characteristic absorption timescale due to the requirement that it operate close to equilibrium with atmospheric CO2.We have since improved on the ACS process, by proposing the addition of a step that selects between bicarbonate and carbonate ions, which increases the volumetric cycle capacity and the absorption rate.17–19 In this work, we propose yet another modification to the ACS, the acid–base concentration swing, which introduces additional acid and base molecules into the solvent to enhance the cycle output. The relation between the alkalinity carrier, the DIC system, and the acid–base system through reaction with water, protons, and hydroxides allows for a wide range of solution state control that can be driven through osmotic pressure. The fundamental concept underlying the ABCS enhancement is the concentration-dependent charge competition between DIC anions and the added acid anions in solution. The non-conservative nature of DIC species and the ability for carbon species to be uncharged in the form of aqueous CO2 allows for shifting the equilibrium between DIC species in a favorable way as the solution is concentrated and diluted. At dilute concentrations the added acid is un-dissociated, and thereby uncharged, and the DIC anions, bicarbonate and carbonate, dominate. As the solution is concentrated, the acid anions replace bicarbonate and carbonate ions as negative charge carriers, shifting the DIC species to aqueous CO2, which therefore increases the solution partial pressure of CO2.
1.3 Non-linear chemical reactions
To develop a theoretical framework for the ABCS, we relied on past literature of non-linear chemical reactions.20,21 The ABCS efficiency increases as cooperativity and non-linearity of the underlying chemical reactions increase. Other chemical systems, such as pH oscillators,22–24 which can persist in isolated systems driven solely through chemical potential, and which exhibit complicated spatial and temporal behaviors, have been studied extensively and also rely on non-linear, cooperative reactions. The existence and wide-range of such non-linear chemical interactions suggests the potential of identifying and engineering chemical systems optimal to the ABCS.Most famously, Belousov–Zhabotisnky reactions have been studied as a model chemical oscillator based on bromine chemistry;25 however its reaction occurs at highly acidic conditions, making it inapplicable to high pH capture. The boric acid and polyol system, which we discuss later in this work, is better matched to the ABCS due to higher pKa values, and it exhibits the desired qualitative behavior required for the ABCS.26 Polyols, such as Mannitol or Sorbitol, react with boric acid reversibly to increase its acidity, or lower its effective pKa. Concentrating these molecules together will, therefore, strongly decrease the pH of the solution and enhance CO2 outgassing. Though the equilibrium constants of the boric acid and polyol system are not in the optimal range for the ABCS, the system serves as a first existence proof for non-linear acid–base systems that can be further developed or synthetically designed.
2 Acid–base concentration swing (ABCS): process description
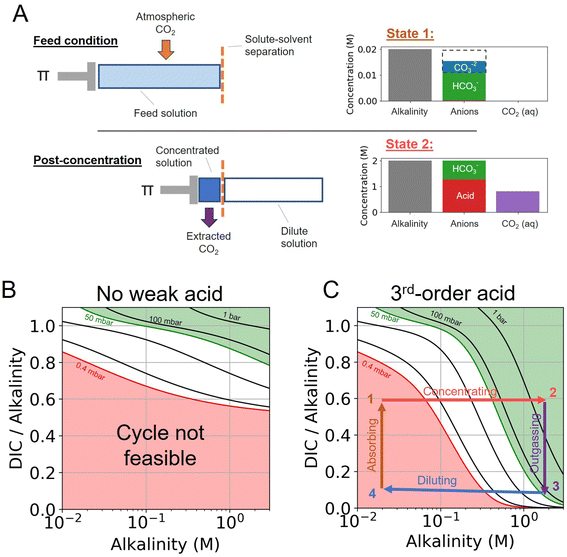
The CO2 separation processes explored in this work is based on the principle that the concentration and dilution of an alkaline solution shifts the solution partial pressure of CO2. Here, we expand on principle of the previously reported alkalinity concentration swing,27 and evaluate the addition of various weak acid and complexing agents to enhance the concentration swing mechanism.Different acid–base reaction orders will exhibit different pH scaling properties, based on Le Chatelier's Principle, as solutes are concentrated or diluted. This pH control can be combined with an alkaline aqueous system to drive CO2 absorption and outgassing. We find that the addition of higher-order acid–base reactions could be used to enhance the outgassing of CO2 by rapidly decreasing the pH of the solution as the ions in solution are concentrated. To evaluate the system analytically, we separate the system into three components (Fig. 1).
First, the alkalinity carrier: the alkalinity carriers in our system are equivalent to strong base cations (denoted by [B+] in this work), such as sodium or potassium. The alkalinity provides a positive charge in solution, but does not directly interact with any other component of the system.
Second, the acid–base system: the addition of a weak acid and/or bases, as well as non-charged complexing agents (denoted by L), can be added to solution to add proton and hydroxide sinks and sources for the DIC species to exchange with. For simplicity, we only consider acid–base species that mediate interactions through the aqueous solvent, and do not interact directly with DIC species (e.g. such as binding of CO2 and amines to form carbamates).
Third, dissolved inorganic carbon (DIC): aqueous CO2, bicarbonate, and carbonate concentration and speciation are determined for different conditions, either at fixed DIC or fixed CO2 partial pressure.
When no additional acid–base species are introduced, the system is equivalent to the alkalinity concentration swing process (Fig. 1B). There is no feasible DAC cycle possible under these conditions.
The interactions between the three components above are subject to the following two conditions: (1) charge neutrality and (2) reactions between systems are mediated through H+ and OH− or, in other words, protons and hydroxide ions are the only species exchanged between the DIC and acid–base systems.
The states of the ABCS cycle are best represented by the arrows overlaid on the DIC-to-alkalinity diagram in Fig. 1C. This is because in a plot of DIC-to-alkalinity vs. alkalinity, concentrating and diluting steps are represented simply by horizontal lines. The ABCS cycle is described succinctly as follows:
• Step 1 → 2: concentrating acids and bases – alkalinity, DIC, and acid–base system are concentrated together. Alkalinity is used as a reference concentration, and all other species concentrations are defined in relation to alkalinity.
• Step 2 → 3: CO2 outgassing – vacuum is applied and the solution CO2 partial pressure is taken to pout, thereby outgassing and collecting CO2. The collected CO2 quantity, or the volumetric cycle capacity, Cout, is defined in terms of moles of CO2 collected per volume of feed solution.
• Step 3 → 4: diluting acids and bases – the concentrated solution, having lost the extracted CO2, is diluted to its initial concentration.
• Step 4 → 1: absorbing atmospheric CO2 – diluted solution with depleted DIC concentration is exposed to atmospheric CO2 until a solution partial pressure of pin is reached.
Finally, the main driving mechanism explored in this system is osmotic pressure, resulting in concentrating and diluting the solution, or equivalently adding and removing water (Fig. 1A). This can be done through a number of mechanisms, such as reverse osmosis or capacitive deionization,28–30 which are not explored in detail here. Our previous study evaluates the work necessary to drive the concentration process.18,19,27,31 In this work, a lower bound energy analysis is conducted to establish feasibility and evaluate parameter trade-offs.
In general, alkalinity carriers can also be entirely removed if the acid–base system includes some weak base species, however this is not considered in this work. Additionally, the charge state of the acid–base system species can also be used as a basis for separation. For example, nanofiltration membrane separation can be used to separate uncharged and charged species.32,33
This work reports the first proof of principle experiment demonstrating the ABCS through a boric acid and polyol experimental system. The system is characterized and its limitations are discussed. A general ABCS theoretical framework is developed to explore requirements for a solution that absorbs CO2 in a diluted state, and then outgasses CO2 when the solution is concentrated. Requirements for the acid–base system are identified to reach adequate acidification as the solution is concentrated. In general, this work builds on the large body of research of non-linear chemical reactions,24,34 and outlines pathways for theoretical and experimental improvement of the ABCS.
2.1 ABCS chemistry: boric acid and polyol
One experimental candidate system exhibiting desired properties is a boric acid and polyol system. Boric acid, H3BO3, is a very weak acid, with an ionization constant around pKa = 9.20.26 Boric acid does not react in aqueous solution as a Brønsted acid, but instead, it behaves as a Lewis acid, binding a hydroxide to form the B(OH)4− anion: | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 1
1 or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 boron to polyol molar ratio, represented by the following two reactions:
2 boron to polyol molar ratio, represented by the following two reactions:| B(OH)3 + H2L ↔ B(OH)2L− + H2O + H+ | (2) |
| B(OH)3 + 2H2L ↔ BL2− + 3H2O + H+ | (3) |
The modified boric acid equilibrium constant, 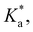 replaces Ka in eqn (1) and, as a function of the added polyol, takes the form of ref. 26:
replaces Ka in eqn (1) and, as a function of the added polyol, takes the form of ref. 26:
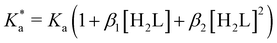 | (4) |
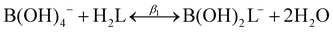 | (5) |
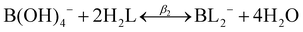 | (6) |
This reaction scheme can be converted to a system of equations and applied to the ABCS, and all the reactants in this system are commercially-available chemical species that can be studied experimentally. However, the following realizations makes this particular chemical system likely impractical to be realized in a scalable DAC process. First, the DIC system at atmospheric CO2 partial pressure buffers the pH around 9 to 10. And second, the pKa of boric acid means that much of the acid will be in a disassociated state in this pH range. This negates the cooperative effect from the polyol in the operating regime of the ABCS. In other words, if the post-absorption pH is greater than 9.3 (the boric acid pKa), then a majority of the boric acid is already in the anionic form, and the interaction with polyols will not shift its charge state significantly. To make use of the polyol and boric acid reaction as a driver of the ABCS, the CO2 absorption step would need to bring the pH of the solution below 9, which implies extremely slow absorption kinetics.
Alternatively, cycle output would improve if synthetic chemistry modifications to boric acid complexes were made to increase its pKa, preferably to 10 or higher. Ideally, however, the pKa of the weak acid is as high as possible, such that deprotonation can occur only through reaction with a complexing agent.
3 Materials and methods
3.1 Measuring solution states
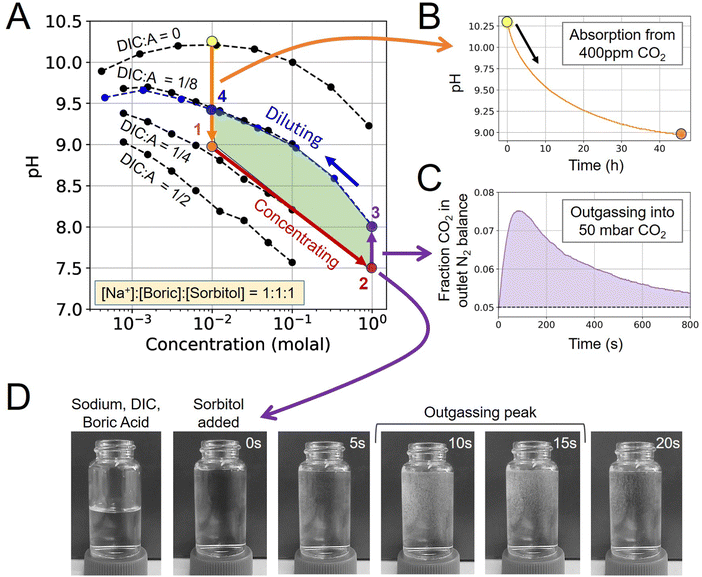
To characterize the alkalinity, DIC, and boric acid and polyol system, solution states were determined by first measuring the pH of a concentrated solution prepared by mixing dry chemicals in different ratios with diH2O. Then, taking each concentrated solution starting point and measuring the pH of the dilution series, which keeps the chemical ratios constant but reduces the concentration, allows for mapping out the pH-concentration parameter space (Fig. 2A; black dots). An Orion ROSS Micro Electrode was used to measure pH with a Thermo Orion Star A211 Benchtop pH Meter. In this work, alkalinity was introduced as sodium cations. Sodium hydroxide, sodium carbonate, sodium bicarbonate, boric acid, L-sorbitol were all purchased from Sigma-Aldrich.To map the pH-concentration parameter space, each prepared concentrated solution, at either 0.1 or 1 molal, was measured immediately after mixing, as well as 30 minutes after mixing to ensure that no significant CO2 outgassing takes place at the given concentration ratio. This ensures that the CO2 partial pressure of the prepared solution is sufficiently close to equilibrium with atmospheric conditions.
Solutions were all prepared with a fixed ratio of sodium, boric acid (B), and sorbitol (S) of: Na+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B
B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 1
S = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Four starting points were chosen with a different DIC-to-alkalinity ratio of 0, 1/8, 1/4, and 1/2. From each starting point, each solution was diluted in series by factors of 1/3 by adding diH2O.
1. Four starting points were chosen with a different DIC-to-alkalinity ratio of 0, 1/8, 1/4, and 1/2. From each starting point, each solution was diluted in series by factors of 1/3 by adding diH2O.
3.2 Absorption and outgassing
To study absorption and outgassing rates, a stirred-cell reactor (SCR) setup was assembled (ESI,† Fig. A1). Three mass flow controllers (Sierra SmartTrak 50) were installed in parallel, each connected to its own gas tank: 100% N2, 100% CO2, 0.4 mbar CO2 in N2 balance (gas tanks were purchased from AirGas). Gases were combined and mixed at a known ratio and flow rate, and bubbled through deionized water to moisten the gas feed and reduce evaporative loss. The gas line was then fed into the SCR, which was installed with conductivity, temperature, and pH probes (ThermoFisher). The SCR was placed on a stir plate and a medium-sized stir bar was spun at 200 rpm. This rpm was chosen so as not to significantly deform the solution surface, but still be fast enough to achieve a well-mixed solution condition and reach the pseudo-first order absorption regime. At 50 mL of solution loading, the gas–liquid surface area was measured to be 0.0029 m2.For each absorption experiment, 50 mL of solution was loaded into the SCR, and temperature was controlled at 25 C using a water jacket connected to a temperature-controlled water bath. Measurements were continuously recorded onto a computer for analysis. The known solution alkalinity allowed for using pH to calculate CO2 absorption. Gas flow rates were always high enough to deviate in CO2 concentration by <5% due to absorption. Conductivity measurements were used to ensure that evaporative loss was within <5%.
For outgassing experiments, the gas outlet was passed through a 10% infrared CO2 sensor (CO2Meter K30 Sensor) to measure the change in CO2 partial pressure in nitrogen balance. Outgassing into vacuum was simulated by applying a 50 mbar CO2 in N2 stream to the solution. Outgassing experiments were conducted with 10 mL of solution loaded.
3.3 Modeling ideal chemical reactions
To study the relationship between DIC, alkalinity, the weak acid system, and partial pressure, we developed an Aqueous DIC Model (ADICM), which solves the system of equations detailed in Section 4.2.1 and ESI,† Section B. In this theoretical study, we assume dilute solutions in which the activity of any non-solvent species is proportional to its concentration, and therefore chemical relations can be evaluated through concentrations and fixed equilibrium constants. We also assume that there are no solubility constraints in the tested regimes, with final alkalinity conditions being studied up to 3 M. The Python package, SciPy, was used to solve the nonlinear system of equations using the “fsolve” function.4 Results and discussion
4.1 Experimental ABCS analysis
To demonstrate the ABCS cycle, the absorption, concentrating, outgassing, and diluting steps were characterized through a combination of 400 ppm CO2 absorption experiments, solution pH measurements, and direct CO2 outgassing measurements into a headspace of 50 mbar of CO2 partial pressure.First, a solution without any pre-loaded DIC prepared at 10 mM sodium hydroxide, boric acid, and sorbitol, was exposed to 400 ppm CO2 and allowed to reach equilibrium in the absorption module (Step 4 → 1). The pH dropped from 10.27 to 8.98 (Fig. 2B). Using the mapped out pH-concentration space as reference (Fig. 2A; black dots), we infer that the DIC-to-alkalinity ratio increased from 0 to 1/4. This is equivalent to 2.5 mM of DIC loading.
For the concentrating step (Step 1 → 2), a solution was prepared at 1 molal alkalinity concentration, with a 1/4 DIC-to-alkalinity ratio or 0.25 molal DIC, to effectively simulate a concentrating step of 100×. The concentrated solution was loaded into the outgassing module and exposed to 50 mbar CO2 in N2 balance. Outgassed CO2 was measured directly in gas phase to confirm that CO2 can be extracted from this solution condition (Fig. 2C). Initial pH was measured at 7.50 and increased to 8.02 upon equilibration with 50 mbar in the outgassing module (Step 2 → 3).
The post-outgassing solution (State 3) was taken from the outgassing module and the pH of its dilution series was measured (Fig. 2A; blue dots). Based on the pH-concentration parameter space, the DIC-to-alkalinity dropped from 1/4 to 1/8, which means that roughly 0.125 molal of DIC was outgassed. The directly measured gaseous CO2 quantity was found to be within 10% of the solution measurement.
That the four steps enclose a finite area in the pH-concentration space demonstrates the first experimental evidence of the ABCS cycle. The full cycle, at the tested parameters, would have a volumetric cycle capacity, or Cout, of 1.25 mM extracted CO2 relative to the feed solution. Under these unoptimized conditions, outgassing into 50 mbar of CO2 occurred on a timescale of minutes, whereas absorption required hours at a measured average absorption flux of 0.40 μmoles m−2 s−1. In this work, because the chemical conditions are far from optimal for the absorption and cycle capacity, more detailed kinetic analysis was not pursued. However, preliminary findings suggest that absorption promoters are required to make this chemical system competitive with incumbent aqueous DAC technologies.
Finally, a visual inspection of outgassing from the concentrated solution (State 3) was performed in a 25 mL vial (Fig. 2D). Small bubbles were detected within seconds of adding sorbitol to the sodium, boric acid, and DIC solution. We note that outgassing into 50 mbar under flowing headspace exhibits different kinetics than rapid mixing in a vial under ambient conditions.
4.2 Generalized ABCS theory
Though the addition of the boric acid and polyol system represents an experimentally feasible ABCS cycle, its cycle capacity and absorption rate are impractical for a scalable DAC process. We therefore develop a theoretical model to identify optimal ABCS chemical properties. This analysis is intended to guide synthetic chemistry work and the search for different applicable chemistry systems.| (n − 1)L + AH ↔ Ln−1A− + H+ | (7) |
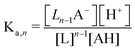 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, so [Ln−1A−] = [H+].
1 ratio, so [Ln−1A−] = [H+].
Because the driver of the ABCS is a concentrating step that increases the concentration of all the non-solvent species together, we define a concentration factor, χ, to characterize the pH-concentration scaling. Mathematically, this is expressed by: ([AH]2+ [Ln−1A−]2 = [AH]0χ). The subscript “0” represents that the total product and reactant concentration in the pre-concentrated solution (State 1) of the given species, such that: [AH]0 = [AH]1 + [Ln−1A−]1. Equivalently, [AH]0 is the initial weak acid concentration dissolved necessary to prepare State 1. The subscripts 1 and 2 correspond to the pre- and post-concentrating condition, respectively. Similarly, the initial complexing agent concentration is defined as follows: [L]0 = [L]1 + [Ln−1A−]1. We further simplify the relation by assuming that the acid and complexing species concentrations are at a ratio of θ = [L]0/[AH]0. Taking eqn (8) and incorporating the concentration factor perturbation, we derive the following relation:
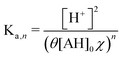 | (9) |
| pH = −(n/2)log10(θχ) + const | (10) |
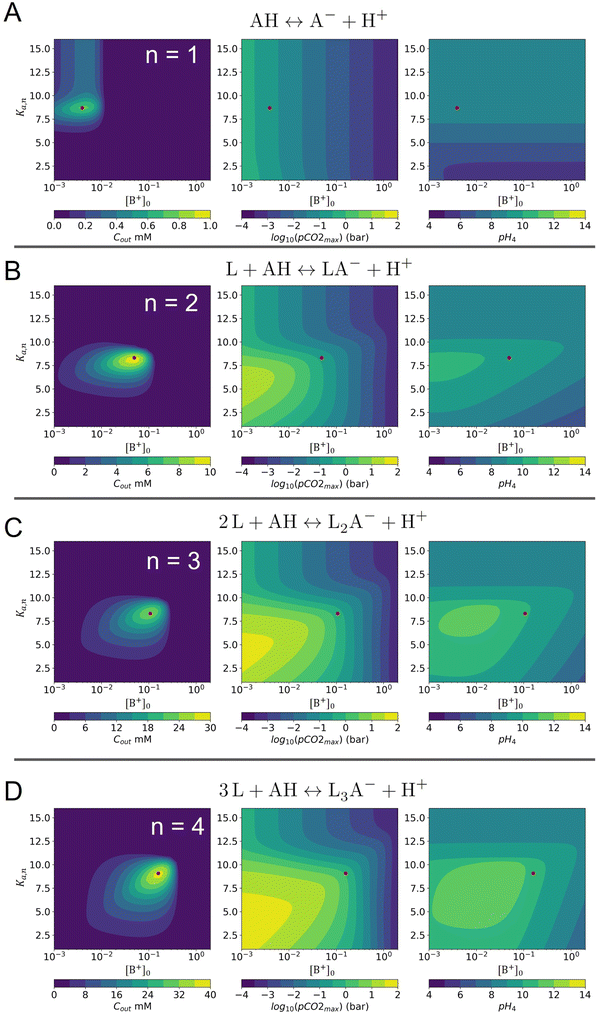
Fig. 3 plots the optimal points for each reaction order, maximizing Cout at different strong base ([B+]0) to weak acid ([AH]0) ratios. Non-intuitive Ka,n relations are revealed as reaction order and base-to-weak-acid ratios are varied. For all conditions, at the optimal point, higher reaction order and higher weak acid to base ratios increase the cycle capacity (Cout), maximum solution CO2 partial pressure post-concentration but before any extraction 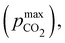 and pre-absorption pH (pH4). The output from the optimal Cout analysis is used to study ABCS operating conditions in the next section.
and pre-absorption pH (pH4). The output from the optimal Cout analysis is used to study ABCS operating conditions in the next section.
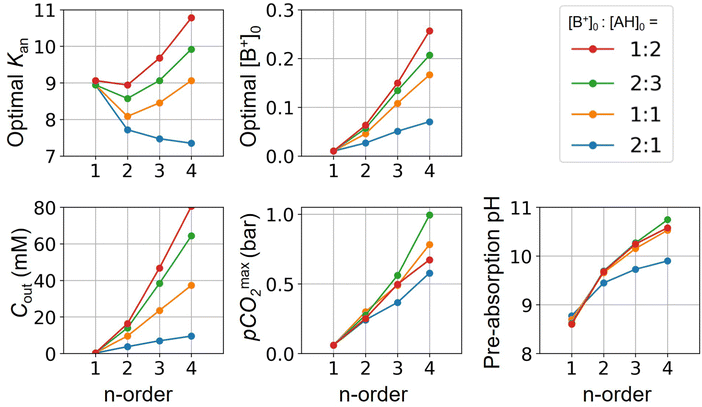 | ||
Fig. 3 ABCS optimization analysis. The optimal nth-order equilibrium constant (Ka,n) and initial strong base concentrations ([B+]0) are reported for each reaction order (1, 2, 3, and 4), and for four strong base (or alkalinity) to weak acid ratios: 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1 1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2 1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and 1 3, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The corresponding Cout, 2. The corresponding Cout, 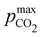 , and pH4, at each optimal point is plotted. Each optimal point corresponds to the red dot in ESI,† Fig. C2. , and pH4, at each optimal point is plotted. Each optimal point corresponds to the red dot in ESI,† Fig. C2. | ||
Whereas completely optimal conditions are unlikely to be found in existing synthetic or naturally-occurring chemical systems, this analysis serves as a guide for chemical species exploration, as well synthesis targets for chemical design.
Table 1 reports sample process conditions for different [B+]0, [AH]0, and [L]0 concentrations, and optimal pKa,n values. For a second order reaction, optimal initial concentration of 50 mM base can reach Cout around 15 mM and pH4 of 9.78. Decreasing the initial concentration to 10 mM decreases Cout to 5.8 mM, but increases pH4 to 10.38 and more than quadruples the CO2 partial pressure (compare Table 1 Examples 3 and 4).
| Example | Reaction order | [B+]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [AH]0 [AH]0 |
[B+]0 (M) | [AH]0 (M) | [L]0 (M) | pKa,n | C out (mM) | pH4 | E CO2 (kJ mol−1) | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1st order | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.01 | 0.01 | 0 | 9.0 | 0.29 | 60 | 8.71 | 1110 |
| 2 | 2nd order | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.05 | 0.05 | 0.05 | 8.0 | 9.5 | 270 | 9.62 | 165 |
| 3 | 2nd order | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
0.05 | 0.1 | 0.1 | 9.0 | 15.6 | 320 | 9.78 | 173 |
| 4 | 2nd order | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
0.01 | 0.02 | 0.02 | 9.0 | 5.8 | 1400 | 10.38 | 134 |
| 5 | 3rd order | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.1 | 0.1 | 0.2 | 8.5 | 23.3 | 540 | 10.21 | 157 |
| 6 | 3rd order | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
0.15 | 0.3 | 0.6 | 9.5 | 46.0 | 570 | 10.18 | 165 |
| 7 | 3rd order | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
0.01 | 0.02 | 0.04 | 9.5 | 7.1 | 4700 | 11.67 | 145 |
This trade-off is more substantial for third order reactions. Initial concentrations of 150 mM base outgasses 46 mM, reaches partial pressures above 500 mbar, and post-outgassing pH of 10.18. An initial strong base concentration of 10 mM, however, results in 7 mM of outgassed CO2, but more than 4.5 bar of partial pressure and pH4 of 11.67 (compare Table 1 Examples 6 and 7).
Fig. 4 plots Cout, 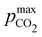 , and pH4, as functions of final alkalinity for a range of reaction orders. Each reaction order is modelled with the corresponding optimal initial strong base concentration and Ka,n, determined by maximizing Cout. Parameter map and optimization analysis is reported in ESI,† Fig. S3.
, and pH4, as functions of final alkalinity for a range of reaction orders. Each reaction order is modelled with the corresponding optimal initial strong base concentration and Ka,n, determined by maximizing Cout. Parameter map and optimization analysis is reported in ESI,† Fig. S3.
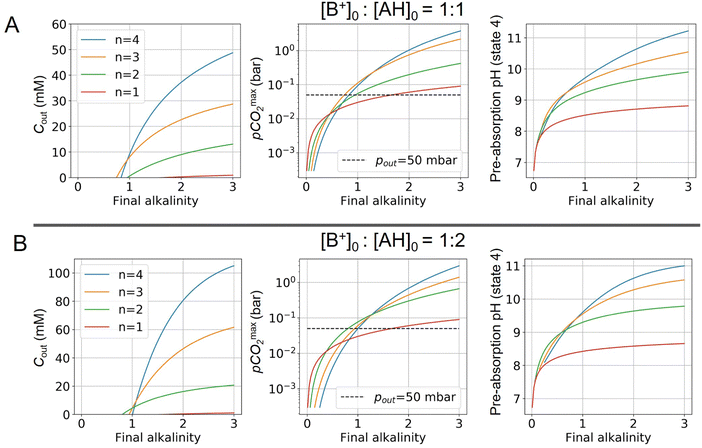 | ||
Fig. 4 ABCS process output. Cout (left), 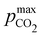 (middle), and pH4 (right) are plotted as functions of final alkalinity. (A) [B+] (middle), and pH4 (right) are plotted as functions of final alkalinity. (A) [B+]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [AH] = 1 [AH] = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; (B) [B+] 1; (B) [B+]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [AH] = 1 [AH] = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. Each reaction order is modelled with the corresponding optimal initial concentration and pKa,n, taken from Fig. 3. For all points, pin = 0.3 mbar; pout is chosen at 50 mbar and denoted with a black dashed line in the middle plots. 2. Each reaction order is modelled with the corresponding optimal initial concentration and pKa,n, taken from Fig. 3. For all points, pin = 0.3 mbar; pout is chosen at 50 mbar and denoted with a black dashed line in the middle plots. | ||
For each reaction order, Cout becomes positive at a final alkalinity around 1 M, suggesting that final alkalinity must at least exceed that concentration. Outputs of higher reaction order conditions increase relatively faster as a function of final alkalinity. Cout can reach 50 mM for reaction order 4 and 30 mM for reaction order 3, at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 base to weak acid condition (Fig. 4A). When the acid concentration is doubled (Fig. 4B), Cout is also roughly doubled for comparable parameter choices.
1 base to weak acid condition (Fig. 4A). When the acid concentration is doubled (Fig. 4B), Cout is also roughly doubled for comparable parameter choices.
When optimizing on cycle capacity, the pre-absorption pH falls between 9 and 11 (Fig. 8). Hydroxide-based absorption pathways are still relatively slow for a scalable DAC process in this pH range, suggesting that CO2 absorption promoters, such as carbonic anhydrase, will likely need to be added to the system to reach incumbent technology absorption rates that reach high pH (>12) through alkaline solutions.36,37 It is also possible that certain chemical species that exhibit cooperative acid–base reaction properties will also act as promoters. For example, even boric acid has been shown to have modest CO2 absorption enhancement properties.38
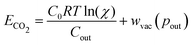 | (11) |
Table 1 reports the required minimum energy for seven representative conditions. We find that the thermodynamic minimum energy is approximately 150 kJ mol−1 for reaction orders two and three, for the example parameters and with pin = 0.3 mbar, pout = 50 mbar, and final alkalinity set to 2 M. The first order reaction, or the base ACS case, requires upwards of 1000 kJ mol−1. This suggests significant benefits when implementing a multi-order system, as compared to a first order chemical reaction. Though the cycle capacity and maximum CO2 partial pressure increase at higher reaction order, there is no significant energy difference across higher reaction orders or specific parameter choices. Based on energy costs of implementing physical reverse osmosis systems, we expect physical energy values to be at least twice the thermodynamic minimum.39
For comparison, bench scale redox electrochemical DAC processes have been shown to reach 100 kJ mol−1,15 and industrial solid sorbent and calcium-looping processes can reach required energy lower than 300 kJ mol−1.40
Importantly, whereas the values determined in this section represent an energy minimum, they also do not account for the possibility of energy recovery through the entire thermodynamic cycle. Specifically, during recombination of the concentrated and diluted streams, opportunities for energy recovery exist through forward osmosis or reverse electrodialysis,41,42 as discussed in previous works evaluating the ACS process.18,31
4.3 More effective potential acid–base systems
In Section 4.2, we discussed a theoretical framework for a cooperative acid–base system that will outgas CO2 upon concentration, and absorb atmospheric CO2 upon dilution. While the focus of the analysis was on a weak acid and uncharged complexing species, in general, other acid–base schemes can reach the same effective result.Although we do not explore this theoretical chemical scheme, the cooperative reaction between the weak acid molecules directly, without the need for a complexing agent, would result in a stronger acidification driving force per reactant (for example, AH + AH ↔ A22− + 2H+). In this case, the alkalinity carrier must still be a strong base, such as sodium or potassium.
Alternatively, an intermediate strength base and a weak acid system could achieve desired effects, while reducing the overall concentration of necessary species in solution by eliminating the need for alkalinity carriers, as well as a complexing agent. The following is an example of a second order reaction with such properties: B+ + AH ↔AB + H+. Here, B+ may come from an undissociated molecule, BOH, that is strong enough to be disassociated at pH 9–11, but also has affinity to the weak acid.
In general, although different chemical reaction pathways can be envisioned, when searching for desirable candidate chemistry schemes the following chemical and reaction properties should be satisfied: reversible reactions; solubility above 1 M; no DIC interaction; non-volatile; and non-toxic.
5 Conclusion
This experimental and theoretical analysis reveals the possibility of the ABCS as a potential approach for direct air capture of CO2. The first-ever proof of principle experiment reported here demonstrates the feasibility of using osmotic pressure and exploiting cooperative acid–base chemistry to drive a DAC cycle. However, the low cycle capacity and slow absorption kinetics in the boric acid and sorbitol system suggest that different nonlinear chemical reactants must be explored to find a potentially scalable regime.Given the guiding principles outlined above, if other reaction schemes can be identified and engineered to have high-order cooperativity then such a process could be competitive with incumbent DAC approaches. Importantly, the ABCS can be driven through reverse osmosis or capacitive deionization modules, which are technologies that are already well developed and benefit from decades of large-scale deployment. The thermodynamic minimum energy analysis suggests that whereas first-order reaction energies are exceedingly high, second- and third-order ABCS cycles are around 150 kJ mol−1. Physical implementations of these systems will likely be a factor of two or more higher, which suggests the need for energy recovery modules, such as forward osmosis, if energy consumption is to be reduced.
It is worth noting, however, that even optimal ABCS cycles still face absorption rate challenges. For third order reaction processes, absorption pH levels can reach above 11, but not above 12, which establishes an upper bound on absorption rate. By comparison, incumbent technologies have engineered their absorption modules around pH closer to 13 or 14.9 This limitation can be overcome through CO2 absorption promoters.36,43 Despite this challenge, a significant advantage of the ABCS is its simplicity. The ABCS is driven by a single concentrating step followed by an application of vacuum to extract CO2.
Data availability
Experimental measurement data for this article is plotted in its entirety in Fig. 2. The code associated with this modeling analysis in this work can be found in Anatoly Rinberg's PhD thesis (2024), Concentrating Alkalinity for Direct Air Capture of Carbon Dioxide: Using Osmotic Pressure for Concentration and Separation, at https://dash.harvard.edu/handle/1/37377926.Conflicts of interest
There are no conflicts to declare.Appendices
A Absorption and outgassing setup
A setup to measure absorption and outgassing from a candidate solution interacting with a controlled headspace gas was assembled and used for testing absorption from 0.4 mbar of CO2 and outgassing into 50 mbar of CO2 (Fig. 5).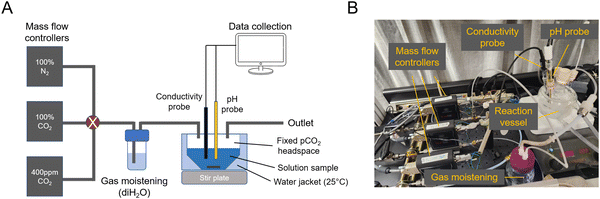 | ||
| Fig. 5 Absorption and outgassing setup. (A) Schematic of mass flow controllers and reactor vessel. (B) Image of setup. | ||
B Dissolved inorganic carbon equilibrium relations
First, it is worth understanding the pH dependence of the ACS, without any added acid–base species. The charge neutrality condition necessitates:| A = b + 2c + Kw/h − h | (B1) |
Here A, b, c, and h are the alkalinity, bicarbonate, carbonate, and proton concentrations, respectively, and the equilibrium relations between the DIC species are defined as follows:
| Hcp = a/pCO2 | (B2) |
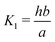 | (B3) |
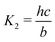 | (B4) |
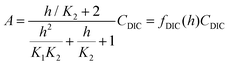 | (B5) |
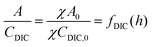 | (B6) |
This reveals that, because the χ terms cancel out, pH is invariant to concentration factor in this regime. In fact, the solution CO2 partial pressure will increase linearly with χ, but will not be further enhanced due to a shift in pH. The black line in Fig. 6C confirms this derivation. In reality, the equilibrium relations, K1 and K2, depend on the ionic strength and will result in a shift in pH as DIC solution is concentrated. Past analyses reveal that the ionic strength increases the outgassing efficiency by a factor of 30–50% depending on the regime,27 however, these effects are not considered in this work for simplicity.
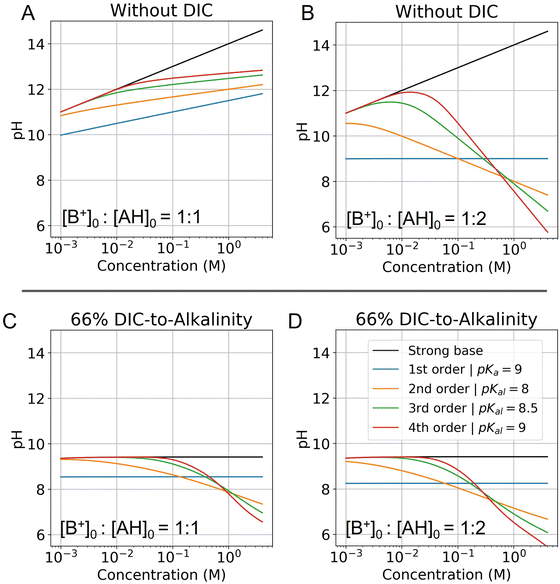 | ||
Fig. 6 Modelled pH as a function of fixed concentration. Abscissa corresponds to the concentration of the strong base in solution, and is locked to the weak acid concentration based on the corresponding ratio. (A) pH of a solution with no DIC and a base to weak acid ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is evaluated for different reaction orders (Table 2). (B) Same conditions, but at a base to weak acid ratio of 1 1 is evaluated for different reaction orders (Table 2). (B) Same conditions, but at a base to weak acid ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 is plotted. (C) Same conditions as (A) are plotted, but with the addition of 66% DIC relative to strong base concentration. (D) Same conditions as (B) are plotted, but with the addition of 66% DIC relative to strong base concentration. Optimal Ka,n is picked for each reaction order based on optimization analysis in subsequent sections. 2 is plotted. (C) Same conditions as (A) are plotted, but with the addition of 66% DIC relative to strong base concentration. (D) Same conditions as (B) are plotted, but with the addition of 66% DIC relative to strong base concentration. Optimal Ka,n is picked for each reaction order based on optimization analysis in subsequent sections. | ||
C Weak acid scaling relations
When the ratio of strong base to AH initial concentration is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. 6A), the pH increases for all reaction orders, but at varying rates, decreasing with higher reaction order. When the ratio of strong base to AH initial concentration is 1
1 (Fig. 6A), the pH increases for all reaction orders, but at varying rates, decreasing with higher reaction order. When the ratio of strong base to AH initial concentration is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (Fig. 6B), the pH first increases and then decreases as cooperative concentration effects begin to dominate. This non-monotonic effect is present only for reaction orders above 2. It further reveals that is possible to reach high pH regimes at lower concentrations, and then acidify a solution upon concentrating, which corresponds to the operating principle of ABCS.
2 (Fig. 6B), the pH first increases and then decreases as cooperative concentration effects begin to dominate. This non-monotonic effect is present only for reaction orders above 2. It further reveals that is possible to reach high pH regimes at lower concentrations, and then acidify a solution upon concentrating, which corresponds to the operating principle of ABCS.
Fig. 6C and D plots the concentration pH dependence of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 strong base to weak acid solution with the DIC system added. This shows that at a given solution loaded with DIC at lower concentration, can be concentrated and acidified, thereby increasing the partial pressure of CO2. Higher weak acid to base ratios increase acidification as a function of concentration, but also lower the concentration point at which the pH deviates from the strong base line. In general, this deviation is due to the fact that at low concentrations AH is entirely associated and uncharged, and so there is no anion to negate the strong base.
2 strong base to weak acid solution with the DIC system added. This shows that at a given solution loaded with DIC at lower concentration, can be concentrated and acidified, thereby increasing the partial pressure of CO2. Higher weak acid to base ratios increase acidification as a function of concentration, but also lower the concentration point at which the pH deviates from the strong base line. In general, this deviation is due to the fact that at low concentrations AH is entirely associated and uncharged, and so there is no anion to negate the strong base.
Finally, as with the alkalinity and DIC analysis in the previous section, a charge neutrality condition with the weak acid system can be analyzed:
| [B+] = [HCO3−] + 2[CO32−] + [Ln−1A−] + [OH−] − [H+] | (C1) |
In the conditions where hydroxide and proton concentrations are significantly smaller than those of the other non-conservative ions, the equation above simplifies to:
| A = fDIC(h)CDIC + fa,n(h)αn | (C2) |
Here, fa,n(h) is a function specific to the nth order condition relating the charge state of the acid to the pH of the solution, and α is the total concentration of the weak acid, assuming that the non-charged species, L, is of equal concentration. Adding the concentration factor perturbation, a pH-χ dependence is revealed:
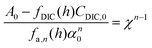 | (C3) |
Inspecting the equations confirms the concentration-dependent pH effects that are the basis of the ABCS. Fig. 6 plots the solution to the equation above for various parameter choices.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 base to weak acid ratio, alkalinity of 0.1 M corresponds to 0.1 M of weak acid. A 1
1 base to weak acid ratio, alkalinity of 0.1 M corresponds to 0.1 M of weak acid. A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio would imply that 0.1 M of alkalinity corresponds to 0.2 M of weak acid. This graphical representation projects to an ideal concentration step when moving right in a fixed DIC-to-alkalinity line, or dilution when moving left.
2 ratio would imply that 0.1 M of alkalinity corresponds to 0.2 M of weak acid. This graphical representation projects to an ideal concentration step when moving right in a fixed DIC-to-alkalinity line, or dilution when moving left.
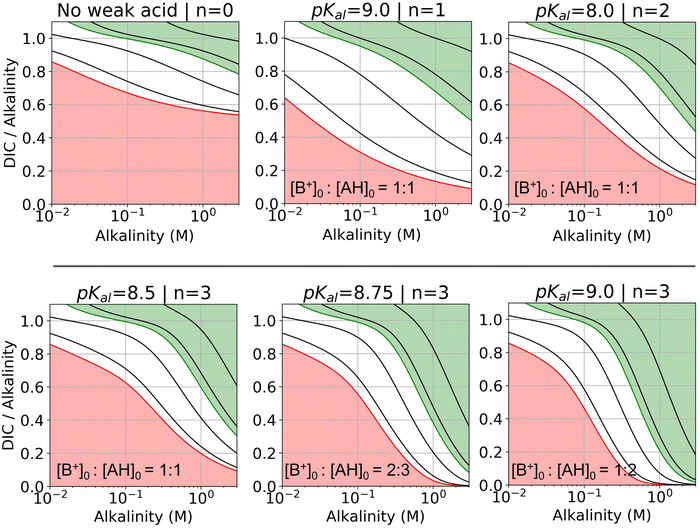 | ||
| Fig. 7 DIC-to-alkalinity diagram for different reaction orders. DIC-to-alkalinity is plotted as a function of initial strong base concentration, or equivalently [B+]0. The alkalinity to weak acid ratio is specified for each plot. Lines correspond to iso-pCO2 values, with the red line corresponding to 0.4 mbar, and the green line corresponding to 50 mbar. Black lines from bottom up correspond to: 1, 10, 100, and 1000 mbar. Red region is eligible parameter space for absorption, and green region is eligible parameter space for outgassing (given the arbitrary choice of pout = 50 mbar). Optimal Ka,n are selected based on optimization analysis in Fig. 3. | ||
For all reaction orders, increasing alkalinity concentration results in increasing CO2 partial pressure (Fig. 7). However, higher order reactions compress the iso-pCO2 lines as a function of concentration, which results in a relatively higher partial pressure increase. At higher alkalinity (above 0.1 M), higher reaction orders lowers the DIC-to-alkalinity ratio at 50 mbar (green line), which implies that even more CO2 can be outgassed upon concentration if the same amount of DIC is loaded into solution. Higher weak acid to alkalinity ratios result in further compressing of the iso-pCO2 lines and lowering the DIC-to-alkalinity ratio at 50 mbar (green line) at high concentrations. The pKa,n values for the DIC-to-alkalinity diagrams in Fig. 7 were chosen based on an analysis of optimal Cout conditions.
Fig. 8 plots Cout, 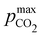 , and pH4 (pre-absorption pH), as functions of Ka,n and initial strong base concentration, [B+]0. By evaluating this parameter landscape, an optimal pKa,n and [B+]0 can be chosen to maximize the cycle capacity, Cout. Plots A, B, C, and D in Fig. 8 correspond to first, second, third, and fourth order reactions at a 1
, and pH4 (pre-absorption pH), as functions of Ka,n and initial strong base concentration, [B+]0. By evaluating this parameter landscape, an optimal pKa,n and [B+]0 can be chosen to maximize the cycle capacity, Cout. Plots A, B, C, and D in Fig. 8 correspond to first, second, third, and fourth order reactions at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 base to weak acid ratio. The red dot corresponds to the optimal parameter point where the process has the largest cycle capacity, revealing the trade-off between maximum Cout and absorption rate, which is captured by the pH4 metric. [B+]0 values that are lower than the optimal red point, can increase the post-outgassing pH by a unit or more, while decreasing the Cout value.
1 base to weak acid ratio. The red dot corresponds to the optimal parameter point where the process has the largest cycle capacity, revealing the trade-off between maximum Cout and absorption rate, which is captured by the pH4 metric. [B+]0 values that are lower than the optimal red point, can increase the post-outgassing pH by a unit or more, while decreasing the Cout value.
Acknowledgements
This research was supported by the U.S. Department of Energy Office of Fossil Energy and Carbon Management through contract DE-FE000331964 and the Harvard Climate Change Solutions Fund. We acknowledge helpful discussions with Andrew Bergman, Tommy George, Eric Fell, and Dawei Xi, as well as Professors Daniel P. Schrag, David Keith, and Jarad Mason.References
-
Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, ed. V. Masson-Delmotte, P. Zhai, A. Pirani, S. L. Connors, C. Péan and S. Berger, et al., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2021 Search PubMed
.
-
A. Bergman and A. Rinberg, The Case for Carbon Dioxide Removal: From Science to Justice, in CDR Primer, 2021. Available from: https://cdrprimer.org/read/chapter-1 Search PubMed
.
- R. A. Rohde and Z. Hausfather, The Berkeley Earth Land/Ocean Temperature Record, Earth System Sci. Data, 2020, 12(4), 3469–3479 CrossRef
. Available from: https://essd.copernicus.org/articles/12/3469/2020/.
- IPCC, Global warming of 1.5 °C, 2018.
- D. Lenzi, The ethics of negative emissions, Global Sustainability, 2018, 1, e7, DOI:10.1017/sus.2018.5
.
- J. C. Minx, W. F. Lamb, M. W. Callaghan, S. Fuss, J. Hilaire and F. Creutzig,
et al., Negative emissions—Part 1: Research landscape and synthesis, Environ. Res. Lett., 2018, 13(6), 063001, DOI:10.1088/1748-9326/aabf9b
.
- S. Fuss, W. F. Lamb, M. W. Callaghan, J. Hilaire, F. Creutzig and T. Amann,
et al., Negative emissions—Part 2: Costs, potentials and side effects, Environ. Res. Lett., 2018, 13(6), 063002, DOI:10.1088/1748-9326/aabf9f
.
- E. S. Sanz-Pérez, C. R. Murdock, S. A. Didas and C. W. Jones, Direct Capture of CO2 from Ambient Air, Chem. Rev., 2016, 116(19), 11840–11876, DOI:10.1021/acs.chemrev.6b00173
.
- D. W. Keith, G. Holmes, D. St Angelo and K. Heidel, A Process for Capturing CO2 from the Atmosphere, Joule, 2018, 2(8), 1573–1594 CrossRef CAS
. Available from: https://linkinghub.elsevier.com/retrieve/pii/S2542435118302253.
- M. Wang, H. J. Herzog and T. A. Hatton, CO2 Capture Using Electrochemically Mediated Amine Regeneration, Ind. Eng. Chem. Res., 2020, 59(15), 7087–7096, DOI:10.1021/acs.iecr.9b05307
.
- Y. Liu, H. Z. Ye, K. M. Diederichsen, T. Van Voorhis and T. A. Hatton, Electrochemically mediated carbon dioxide separation with quinone chemistry in salt-concentrated aqueous media, Nat. Commun., 2020, 11(1), 2278 CrossRef CAS PubMed
. Available from: https://www.nature.com/articles/s41467-020-16150-7.
- S. Jin, M. Wu, R. G. Gordon, M. J. Aziz and D. G. Kwabi, pH swing cycle for CO2 capture electrochemically driven through proton-coupled electron transfer, Energy Environ. Sci., 2020, 13(10), 3706–3722 RSC
. Available from: https://rsc.66557.net/en/content/articlelanding/2020/ee/d0ee01834a.
- H. Seo and T. A. Hatton, Electrochemical direct air capture of CO2 using neutral red as reversible redox-active material, Nat. Commun., 2023, 14(1), 313 CrossRef CAS PubMed
. Available from: https://www.nature.com/articles/s41467-023-35866-w.
- A. Sodiq, Y. Abdullatif, B. Aissa, A. Ostovar, N. Nassar and M. El-Naas,
et al., A review on progress made in direct air capture of CO2, Environ. Technol. Innovation, 2023, 29, 102991 CrossRef CAS
. Available from: https://www.sciencedirect.com/science/article/pii/S235218642200414X.
- T. N. D. Cao, S. W. Snyder, Y. I. Lin, Y. J. Lin, S. Negi and S. Y. Pan, Unraveling the Potential of Electrochemical pH-Swing Processes for Carbon Dioxide Capture and Utilization, Ind. Eng. Chem. Res., 2023, 62(49), 20979–20995, DOI:10.1021/acs.iecr.3c02183
.
- G. Liu, A. Yang and R. C. Darton, Numerical Modeling and Comparative Analysis of Electrolysis and Electrodialysis Systems for Direct Air Capture, ACS Sustainable Chem. Eng., 2024, 12(10), 3951–3965, DOI:10.1021/acssuschemeng.3c06259
.
- A. Rinberg and M. J. Aziz, Bicarbonate-Carbonate Selectivity through Nanofiltration for Direct Air Capture of Carbon Dioxide, ACS ES&T Eng., 2024, 4(8), 1959–1969, DOI:10.1021/acsestengg.4c00150
.
- A. Rinberg, Concentrating Alkalinity for Direct Air Capture of Carbon Dioxide: Using Osmotic Pressure for Concentration and Separation, 2024, Available from: https://dash.harvard.edu/handle/1/37377926.
- A. M. Bergman, Using Capacitive Deionization for Direct Air Capture of Carbon Dioxide: Theory and Demonstration of the Bicarbonate-Enriched Alkalinity Concentration Swing, 2024, Available from: https://dash.harvard.edu/handle/1/37377928.
- I. R. Epstein and K. Showalter, Nonlinear Chemical Dynamics: Oscillations, Patterns, and Chaos, J. Phys. Chem., 1996, 100(31), 13132–13147, DOI:10.1021/jp953547m
.
- F. Sagués and I. R. Epstein, Nonlinear chemical dynamics, Dalton Trans., 2003,(7), 1201–1217 RSC
. Available from: https://rsc.66557.net/en/content/articlelanding/2003/dt/b210932h.
- M. Orbán, K. Kurin-Csörgei and I. R. Epstein, pH-regulated chemical oscillators, Acc. Chem. Res., 2015, 48(3), 593–601 CrossRef PubMed
.
- E. Poros, V. Horváth, K. Kurin-Csörgei, I. R. Epstein and M. Orbán, Generation of pH-Oscillations in Closed Chemical Systems: Method and Applications, J. Am. Chem. Soc., 2011, 133(18), 7174–7179, DOI:10.1021/ja2010835
.
- K. Kovacs, R. E. McIlwaine, S. K. Scott and A. F. Taylor, pH oscillations and bistability in the methylene glycol–sulfite–gluconolactone reaction, Phys. Chem. Chem. Phys., 2007, 9(28), 3711–3716 RSC
. Available from: https://rsc.66557.net/en/content/articlelanding/2007/cp/b704407k.
- Controlling chaos in the Belousov—Zhabotinsky reaction | Nature. Available from: https://www.nature.com/articles/361240a0.
- M. C. C. Azevedo and A. M. V. Cavaleiro, The Acid–Base Titration of a Very Weak Acid: Boric Acid, J. Chem. Educ., 2012, 89(6), 767–770, DOI:10.1021/ed200180j
.
- A. Rinberg, A. M. Bergman, D. P. Schrag and M. J. Aziz, Alkalinity Concentration Swing for Direct Air Capture of Carbon Dioxide, ChemSusChem, 2021, 14(20), 4439–4453 CrossRef CAS PubMed
. eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/cssc.202100786.
- Ion Selectivity in Brackish Water Desalination by Reverse Osmosis: Theory, Measurements, and Implications, Environ. Sci. Technol. Lett., 2020, 71, 42–47 DOI:10.1021/acs.estlett.9b00686.
- Y. S. Oren and P. M. Biesheuvel, Theory of Ion and Water Transport in Reverse-Osmosis Membranes, Phys. Rev. Appl., 2018, 9(2), 024034, DOI:10.1103/PhysRevApplied.9.024034
.
- M. E. Suss, S. Porada, X. Sun, P. M. Biesheuvel, J. Yoon and V. Presser, Water desalination via capacitive deionization: what is it and what can we expect from it?, Energy Environ. Sci., 2015, 8(8), 2296–2319 RSC
. Available from: https://rsc.66557.net/en/content/articlelanding/2015/ee/c5ee00519a.
-
A. Rinberg, A. M. Bergman, M. J. Aziz and D. P. Schrag, Experimental Demonstration of Alkalinity Concentration Swing for Direct Air Capture of CO2. Harvard Univ., Cambridge, MA (United States), 2023. Available from: https://www.osti.gov/biblio/2248073 Search PubMed
.
- R. He, C. Dong, S. Xu, C. Liu, S. Zhao and T. He, Unprecedented Mg2+/Li+ separation using layer-by-layer based nanofiltration hollow fiber membranes, Desalination, 2022, 525, 115492 CrossRef CAS
. Available from: https://www.sciencedirect.com/science/article/pii/S0011916421005634.
- B. Van der Bruggen, A. Koninckx and C. Vandecasteele, Separation of monovalent and divalent ions from aqueous solution by electrodialysis and nanofiltration, Water Res., 2004, 38(5), 1347–1353 CrossRef CAS PubMed
. Available from: https://www.sciencedirect.com/science/article/pii/S0043135403006420.
- T. K. Gustafsson and K. V. Waller, Nonlinear and adaptive control of pH, Ind. Eng. Chem. Res., 1992, 31(12), 2681–2693 CrossRef CAS
. Available from: https://pubs.acs.org/doi/pdf/10.1021/ie00012a009.
- X. Wang, W. Conway, R. Burns, N. McCann and M. Maeder, Comprehensive Study of the Hydration and Dehydration Reactions of Carbon Dioxide in Aqueous Solution, J. Phys. Chem. A, 2010, 114(4), 1734–1740 CrossRef CAS PubMed
, Available from: https://pubs.acs.org/doi/pdf/10.1021/jp909019u.
- S. S. W. Effendi and I. S. Ng, The prospective and potential of carbonic anhydrase for carbon dioxide sequestration: a critical review, Process Biochem., 2019, 87, 55–65 CrossRef CAS
. Available from: https://www.sciencedirect.com/science/article/pii/S1359511319310037.
- A. de Oliveira Maciel, P. Christakopoulos, U. Rova and I. Antonopoulou, Carbonic anhydrase to boost CO2 sequestration: Improving carbon capture utilization and storage (CCUS), Chemosphere, 2022, 299, 134419 CrossRef CAS PubMed
. Available from: https://www.sciencedirect.com/science/article/pii/S0045653522009122.
- U. K. Ghosh, S. E. Kentish and G. W. Stevens, Absorption of carbon dioxide into aqueous potassium carbonate promoted by boric acid, Energy Proc., 2009, 1(1), 1075–1081 CrossRef CAS
. Available from: https://www.sciencedirect.com/science/article/pii/S187661020900143X.
- M. Elimelech and W. A. Phillip, The Future of Seawater Desalination: Energy, Technology, and the Environment, Science, 2011, 333(6043), 712–717 CrossRef CAS PubMed
. Available from: https://science.sciencemag.org/content/333/6043/712.
-
S. Pacala, M. Al-Kaisi, M. Barteau, E. Belmont, S. Benson and R. Birdsey, et al., Negative Emissions Technologies and Reliable Sequestration: A Research Agenda, The National Academies Press, Washington, DC, 2019 DOI:10.17226/25259
.
- Effect of Different Draw Solutions on Concentration Polarization in a Forward Osmosis Process: Theoretical Modeling and Experimental Validation. Industrial & Engineering Chemistry Research, Available from: https://pubs.acs.org/doi/full/10.1021/acs.iecr.2c03723.
- R. A. Tufa, S. Pawlowski, J. Veerman, K. Bouzek, E. Fontananova and G. di Profio,
et al., Progress and prospects in reverse electrodialysis for salinity gradient energy conversion and storage, Appl. Energy, 2018, 225, 290–331 CrossRef CAS
. Available from: https://www.sciencedirect.com/science/article/pii/S0306261918306792.
- P. C. Tseng, W. S. Ho and D. W. Savage, Carbon dioxide absorption into promoted carbonate solutions, AIChE J., 1988, 34(6), 922–931 CrossRef CAS
. eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/aic.690340604.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00251b |
| This journal is © The Royal Society of Chemistry 2024 |