Accelerating the discovery of high-mobility molecular semiconductors: a machine learning approach

Abstract

The two-dimensionality (2D) of charge transport significantly affects charge carrier mobility in organic semiconductors, making it a key target for materials discovery and design. Traditional quantum-chemical methods for calculating 2D are resource-intensive, especially for large-scale screening, as they require computing charge transfer integrals for all unique pairs of interacting molecules. We explore the potential of machine learning models to predict whether this parameter will fall within a desirable range without performing any quantum-chemical calculations. Using a large database of molecular semiconductors with known 2D values, we evaluate various machine-learning models using chemical and geometrical descriptors. Our findings demonstrate that the LightGBM outperforms others, achieving 95% accuracy in predictions. These results are expected to facilitate the systematic identification of high-mobility molecular semiconductors.

---

Molecular semiconductors are promising candidates for the development of lightweight, low-cost, and flexible optoelectronic devices.^1–3 These materials are increasingly utilised in various applications, such as light-emitting diodes (OLEDs),^4,5 field-effect transistors (OFETs),^6,7 and photovoltaic devices (OPVs).^8,9 The performance of optoelectronic devices is heavily influenced by the efficiency of charge transport processes.^10–12 Despite the critical importance of enhancing device efficiency, the discovery of high-mobility molecular semiconductors has been limited, highlighting the challenges inherent in identifying such materials. Traditional experimental trial-and-error methods have only yielded a few high-mobility materials, with further efforts primarily focused on slight modifications of existing core structures.^13,14 Also, the complex physics governing charge transport has restricted theoretical approaches to evaluating only a few materials.^15–19

Recent advances in computational frameworks and theoretical modelling have significantly improved the search for high-mobility materials. High throughput virtual screening (HTVS), a process in which large libraries of molecules are analysed using theoretical techniques and narrowed down to a small set of promising candidates for experimental verification, now enables the evaluation of vast chemical libraries.^20–25 This approach enhances the probability of identifying novel high-mobility semiconductors and provides insights into the fundamental physics governing charge transport.^26–29 Furthermore, a notable side benefit of HTVS is the generation of extensive databases containing computed physical properties of these molecules which facilitate the application of machine learning (ML) techniques to predict and optimise properties of new molecular systems.^30,31 As an example of HTVS studies, Schober et al.²⁹ devised a screening method to identify organic semiconductors with high carrier mobility by analysing electronic couplings and reorganisation energies from a large molecular crystal database. Their approach uncovered both known and novel promising materials. In another study, Nematiaram et al.²⁷ utilised transient localisation theory^32,33 to screen the Cambridge structural database (CSD)³⁴ identifying several high-mobility materials and ranking the key parameters influencing mobility. Notably, they emphasised the importance of charge transport two-dimensionality (2D), also known as band isotropy, where charge transport predominantly occurs within a two-dimensional plane. While earlier studies indicated the potential impact of isotropic bands on charge transport,^13,18,32,35 ref. 27 was the first to statistically validate this observation through large-scale calculations on existing structures.

Despite significant advancements in HTVS methods, the computation of physical properties, such as 2D, for a large number of structures remains a computationally demanding task. This limitation presents a major bottleneck in the efficient exploration of chemical space, especially as the diversity and complexity of available chemical databases continue to expand. Consequently, there is an urgent need to develop more efficient algorithms and methodologies that can accelerate these computational processes. Integrating ML models with HTVS has emerged as a promising solution to address these challenges, as ML models trained on existing datasets have shown potential in accelerating materials discovery and design.^36,37 Early attempts at employing ML for predicting charge transport-related properties have been promising,^38,39 but the rapid and efficient screening of large chemical databases to identify high-mobility materials using ML is still in its nascent stages and requires deeper exploration. Therefore, this study aims to investigate the possibility of classifying the charge transport two-dimensionality of a given crystal (into three classes of high, medium, and low) using machine learning models from its chemical and geometrical descriptors.

We utilise the database developed in ref. 27 where the charge transfer integral between HOMO orbitals of two neighbouring molecules is computed from the equation J_ij = 〈Φ_i|F̂|Φ_j〉, where Φ_i and Φ_j are the unperturbed HOMO orbitals of the two isolated distinct molecules and F̂ is the Fock operator of the dimer system. The transfer integrals are computed between all non-equivalent pairs of molecules in van der Waals contact, e.g. molecules such that at least one distance between any two atoms i and j is shorter than 1.2 × (r_i + r_j) with r_i and r_j being the van der Waals radii from ref. 40. The calculations of the transfer integrals were carried out at the B3LYP/3-21g* level of the theory, as implemented in Gaussian.⁴¹ To collect the results conveniently, to each transfer integral J, a vector R connecting the centre of mass of the molecules involved in the transfer integral is assigned. We denote by J₁ the largest transfer integral in absolute value and with J₂ the second largest transfer integral in absolute value whose corresponding R₂ is not parallel to R₁ (shown schematically in Fig. 1. The plane constructed by these two vectors is the plane of high mobility). A parameter 2D = |J₂|/|J₁| is defined to describe band isotropy. The distributions of charge transfer integrals of |J₁|, |J₂| and associated 2D values are shown in the ESI.† The distribution suggests that the dataset is notably imbalanced and can be categorised into three performance groups: (i) high-performance, which includes structures with |J₁| values of at least 0.1 eV and 2D values equal to or greater than 0.05; (ii) low-performance, which includes structures where |J₁| is less than 0.1 eV and 2D is less than 0.05; and (iii) moderate-performance, containing all other structures that do not fall into the high or low-performance categories. This classification will aid in the systematic evaluation and comparison of the structures based on their performance metrics. Building on this database, we explore a wide range of ML models including the linear and Gaussian kernel-based support vector machine (GK SVM),⁴² random forest (RF) classifier,⁴³ AdaBoost (Ada.B),⁴⁴ XGBBoost,⁴⁵ LightGBM (LGBM),⁴⁶ and logistic regression (LR)⁴⁷ as they have been promising in predicting simple molecular properties such as reorganisation energy,³⁸ and are well suited to the limited quantity of data available for this study (with the total number of sample points being 38 K). Specifically, RF mitigates overfitting by averaging outputs from multiple decision trees, providing robust predictions. XGBoost and LGBM utilise decision trees similar to RF but stand out as advanced gradient-boosting frameworks, delivering exceptional speed, scalability, and efficiency. SVM handles non-linear data effectively through its kernel functions, while AdaBoost improves classification accuracy by iteratively refining its focus on misclassified instances, compared to LR, which offers a simple approach for classification tasks. Before this investigation, several deep neural networks (DNNs) were trained on the data. However, their performance was sub-optimal as they were limited by dataset size. In future work, we plan to explore data augmentation and transfer learning techniques⁴⁸ to tackle this problem.

Fig. 1 Chemical structure of the pentacene molecule; transfer integral J between neighbouring molecules; and crystal structure illustration with the two largest transfer integrals J₁ and J₂ between molecular pairs.

For each structure (i.e. sample point), we defined a comprehensive set of descriptors (i.e. features). These descriptors include physicochemical properties such as molecular weight, molecular volume, crystal volume, and crystal density. Symmetry-related features, such as centrosymmetric and Sohncke. Bond-related features encompass the total number of bonds, specific counts of single, double, triple, and quadruple bonds, the number of aromatic bonds, the number of π-bonds, the number of cyclic bonds, and the number of rotatable bonds. Ring-related features include the total number of rings in the molecule, the number of aromatic rings, the number of fused rings, and the number of fully conjugated rings. Hydrogen bonding potential is captured by the number of hydrogen bonds. Atomic composition features include the total count of atoms in the molecule, the number of heavy atoms, and the number of unit cell molecules. Interaction-related features, such as the total number of interactions, angles between dimers, and relative distances between dimers, are also considered. We calculated correlations between parameters and retained only those with a correlation strength of less than 0.8.

Before training the model, we addressed the class imbalance in the target variable by applying oversampling to the observations. This ensured that the class distribution seen by the classifier matched the desired distribution. We achieved this by randomly oversampling examples from the minority class until the classes were balanced. The resampled dataset was then split into training and testing sets using an 80–20 split, with stratification to maintain consistent class distribution in both sets. To enhance model performance, their hyperparameters were tuned to achieve optimal performance on the training set via 5-fold cross-validation, where the training set was divided into training and validation. The search space and optimal hyperparameters for each model are given in Table 1. For the LR model, L2 regulariser was used to penalise the sum of the squares of the model parameters to prevent overfitting. The hyperparameter C controls the strength of this regularisation, with smaller values indicating stronger regularisation. The γ hyperparameter is associated with the radial basis function kernel and refers to the inverse of the radius of influence of selected samples. Number of estimators defines the maximum number of trees the RF model can use before terminating, and max depth indicates the maximum tree depth.

Table 1 Optimal hyperparameter setting for each ML model

Model	Best parameters	Parameter set
LR	C = 0.1	C = [100, 10, 1.0, 0.1, 0.01]
Ada.B	No estimators = 300	No estimators = [100, 200, 300]
Linear SVM	C = 100	C = [0.1, 1, 10, 100]
GK SVM	C = 1000, γ = 0.001	C = [0.001, 0.01, 0.1, 1.0, 10.0, 100.0, 1000.0], γ = [0.0001, 0.001, 0.01, 0.1, 1.0, 10.0]
XGBoost	Max depth = 10, min child weight = 1, learning rate = 0.3, gamma = 0.0	Max depth = [3–15], min child weight = [1–7], learning rate = [0.05–0.30], gamma = [0.0–0.4]
RF	Max depth = 18, no estimators = 187	Max depth = [1–20], no estimators = [50–500]
LGBM	Max depth = 15, no leaves = 187, learning rate = 0.2	Max depth = [3–15], no leaves = [50–500], learning rate = [0.05–0.30]

---

For each model variation, the best-performing trained model was used to predict the target variable on the test set with effectiveness measured by accuracy (the ratio of correct predictions against all predictions), precision (the ratio of positive predictions against all predicted samples), recall (the ratio of positive predictions against all the positive samples in the dataset), F1 score (the average of precision and recall), and AUC (which measures the area under the null hypothesis curve to determine if the model performs better than chance) metrics based on their averages across all folds. We run the whole training phase five times using different seeds for the random split each time. Table 2 presents the average of these five runs for each evaluation metric. In the absence of prior works for comparison, we also introduced a baseline (BL) model representing an untrained model with predictions based on random choice (i.e. 1/3 chance of predicting any of the three classes). As shown in Table 2, the best-performing model against all metrics is the LightGBM with an accuracy of 95%, with the second-best model being the Random Forest with an accuracy of 94%. Our results also indicate that the target variables have a non-linear relation with the features, as evidenced by the low performance of the linear models (e.g. an accuracy of 0.35 for Linear SVM), which is close to the accuracy of our baseline model (i.e. 0.33). Similar observations can be made for other metrics, e.g. precision, recall, etc.

Table 2 Model effectiveness reported as mean (standard deviation) of accuracy, recall, precision, F1-score, AUC across five runs

Model	Accuracy	Recall	Precision	F1-score	AUC
The highest value for each metric is highlighted in bold. We performed a paired t-test between measures obtained for each model to check the significance of the difference with the baseline and performed the same test between measures obtained for RF and LGBM. (*) and (†) denotes the fact that a model had results different from that of the baseline and that RF had results different from that of the LGBM across the five runs with the confidence levels (p < 0.05), respectively
BL	0.33	0.33	0.33	0.33	0.5
LR	0.48* (0.04)	0.48* (0.04)	0.47* (0.03)	0.48* (0.03)	0.66* (0.01)
Ada.B	0.55* (0.01)	0.55* (0.01)	0.54* (0.01)	0.55* (0.01)	0.75* (0.001)
Linear SVM	0.41* (0.07)	0.41* (0.07)	0.47* (0.09)	0.43* (0.7)	0.66* (0.04)
GK SVM	0.92* (0.001)	0.92* (0.001)	0.93* (0.001)	0.92* (0.001)	0.96* (0.002)
XGBoost	0.92* (0.01)	0.93* (0.01)	0.93* (0.01)	0.93* (0.01)	0.99* (0.01)
RF	0.94* (0.04)	0.93* (0.04)	0.93* (0.04)	0.93* (0.040)	0.99* (0.01)
LGBM	0.95*† (0.005)	0.95*† (0.005)	0.95*† (0.004)	0.95*† (0.004)	0.99*† (0.002)

---

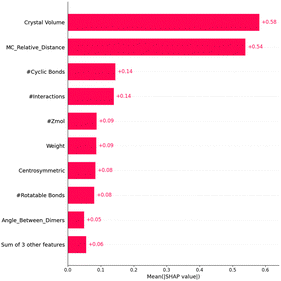
As shown in Fig. 2, SHAP analysis of feature importance for our best-performing model, LGBM, highlights that crystal volume is the most influential feature, significantly affecting lattice stability and packing density. The second most important feature, MC_relative_distance, measures the normalised spatial disparity between the centres of mass of two dimers. Calculating the absolute difference in distances and dividing by the maximum of the two provides insights into orbital overlap and intermolecular interaction strength. The number of cyclic bonds is critical in enhancing molecular rigidity, enabling stable conformations that promote efficient electron delocalisation. The number of interactions within the crystal reflects the extent of intermolecular forces stabilising arrangements conducive to charge transport. Similarly, the number of unit cell molecules (Zmol) impacts crystal density and packing efficiency. Molecular weight also contributes to lattice stability and packing, while centrosymmetry enhances symmetry-driven packing efficiencies by aligning molecular orientations. Conversely, rotatable bonds dictate molecular flexibility, affecting packing and interactions. The angle between dimers influences the alignment of molecular pairs, optimising orbital interactions. Other features, such as hydrogen bonding, aromatic rings, and Sohncke symmetry, were deemed less significant.

Fig. 2 Feature importance for LightGBM using SHAP analysis.

In conclusion, this study demonstrated the potential of ML in classifying charge transport two-dimensionality in molecular crystals. Using chemical and geometrical descriptors, our models, particularly LightGBM, achieved 95% prediction accuracy. Key descriptors influencing transport properties were identified, enabling rapid screening of molecular materials with minimal computational cost compared to traditional methods. These findings highlight ML's ability to accelerate the discovery of high-mobility molecular semiconductors, advancing organic electronics.

Data availability

The charge transfer integrals are deposited in the CSD and accessible through class CrystalPredictedProperties.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. S. R. Forrest, Nature, 2004, 428, 911–918.
2. H. Sirringhaus, Adv. Mater., 2014, 26, 1319–1335.
3. T. Nematiaram and A. Troisi, Chem. Mater., 2022, 34, 4050–4061.
4. R. Thomas, S. P. Thomas, H. Lakhotiya, A. H. Mamakhel, M. Bondesgaard, V. Birkedal and B. B. Iversen, Chem. Sci., 2021, 12, 12391–12399.
5. R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D.-G. Ha, M. Einzinger, T. Wu, M. A. Baldo and A. Aspuru-Guzik, Organic Light Emitting Materials and Devices XX, 2016, 23–30.
6. T. Hasegawa and J. Takeya, Sci. Technol. Adv. Mater., 2009, 10, 024314.
7. H. Jiang, S. Zhu, Z. Cui, Z. Li, Y. Liang, J. Zhu, P. Hu, H.-L. Zhang and W. Hu, Chem. Soc. Rev., 2022, 51, 3071–3122.
8. T. N. Aram, M. Ernzerhof, A. Asgari and D. Mayou, J. Chem. Phys., 2018, 149, 064102.
9. T. Nematiaram, A. Asgari and D. Mayou, J. Chem. Phys., 2020, 152, 044109.
10. J. Ostmeyer, T. Nematiaram, A. Troisi and P. Buividovich, Phys. Rev. Appl., 2024, 22, L031004.
11. J. S. Park, G.-U. Kim, D. Lee, S. Lee, B. Ma, S. Cho and B. J. Kim, Adv. Funct. Mater., 2020, 30, 2005787.
12. T. Nemati Aram, M. Ernzerhof, A. Asgari and D. Mayou, J. Chem. Phys., 2017, 146, 034103.
13. K. A. McGarry, W. Xie, C. Sutton, C. Risko, Y. Wu, V. G. Young Jr, J.-L. Brédas, C. D. Frisbie and C. J. Douglas, Chem. Mater., 2013, 25, 2254–2263.
14. G. Schweicher, G. Garbay, R. Jouclas, F. Vibert, F. Devaux and Y. H. Geerts, Adv. Mater., 2020, 32, 1905909.
15. H. Oberhofer, K. Reuter and J. Blumberger, Chem. Rev., 2017, 117, 10319–10357.
16. T. Nematiaram and A. Troisi, J. Chem. Phys., 2020, 152, 190902.
17. V. Coropceanu, Y. Li, Y. Yi, L. Zhu and J.-L. Brédas, MRS Bull., 2013, 38, 57–64.
18. S. Giannini, A. Carof, M. Ellis, H. Yang, O. G. Ziogos, S. Ghosh and J. Blumberger, Nat. Commun., 2019, 10, 3843.
19. D. Vong, T. Nematiaram, M. A. Dettmann, T. L. Murrey, L. S. Cavalcante, S. M. Gurses, D. Radhakrishnan, L. L. Daemen, J. E. Anthony and K. J. Koski, et al., J. Phys. Chem. Lett., 2022, 13, 5530–5537.
20. E. O. Pyzer-Knapp, C. Suh, R. Gómez-Bombarelli, J. Aguilera-Iparraguirre and A. Aspuru-Guzik, Annu. Rev. Mater. Res., 2015, 45, 195–216.
21. D. Padula, Ö. H. Omar, T. Nematiaram and A. Troisi, Energy Environ. Sci., 2019, 12, 2412–2416.
22. T. Nematiaram, D. Padula and A. Troisi, Chem. Mater., 2021, 33, 3368–3378.
23. R. Pollice, G. dos Passos Gomes, M. Aldeghi, R. J. Hickman, M. Krenn, C. Lavigne, M. Lindner-D’Addario, A. Nigam, C. T. Ser and Z. Yao, et al., Acc. Chem. Res., 2021, 54, 849–860.
24. K. Zhao, Ö. H. Omar, T. Nematiaram, D. Padula and A. Troisi, J. Mater. Chem. C, 2021, 9, 3324–3333.
25. Ö. H. Omar, M. Del Cueto, T. Nematiaram and A. Troisi, J. Mater. Chem. C, 2021, 9, 13557–13583.
26. A. Y. Sosorev, Mater. Des., 2020, 192, 108730.
27. T. Nematiaram, D. Padula, A. Landi and A. Troisi, Adv. Funct. Mater., 2020, 30, 2001906.
28. T. Nematiaram and A. Troisi, Mater. Horiz., 2020, 7, 2922–2928.
29. C. Schober, K. Reuter and H. Oberhofer, J. Phys. Chem. Lett., 2016, 7, 3973–3977.
30. Ö. H. Omar, T. Nematiaram, A. Troisi and D. Padula, Scient. Data, 2022, 9, 54.
31. Q. Ai, V. Bhat, S. M. Ryno, K. Jarolimek, P. Sornberger, A. Smith, M. M. Haley, J. E. Anthony and C. Risko, J. Chem. Phys., 2021, 154, 174705.
32. S. Fratini, S. Ciuchi, D. Mayou, G. T. De Laissardière and A. Troisi, Nat. Mater., 2017, 16, 998–1002.
33. T. Nematiaram, S. Ciuchi, X. Xie, S. Fratini and A. Troisi, J. Phys. Chem. C, 2019, 123, 6989–6997.
34. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Struct. Sci., 2016, 72, 171–179.
35. V. Dantanarayana, T. Nematiaram, D. Vong, J. E. Anthony, A. Troisi, K. Nguyen Cong, N. Goldman, R. Faller and A. J. Moulé, J. Chem. Theory Comput., 2020, 16, 3494–3503.
36. Z. Xie, X. Evangelopoulos, Ö. H. Omar, A. Troisi, A. I. Cooper and L. Chen, Chem. Sci., 2024, 15, 500–510.
37. G. Avci and K. E. Jelfs, Nat. Comput. Sci., 2024, 4, 161–162.
38. S. Atahan-Evrenk and F. B. Atalay, J. Phys. Chem. A, 2019, 123, 7855–7863.
39. V. Bhat, P. Sornberger, B. S. S. Pokuri, R. Duke, B. Ganapathysubramanian and C. Risko, Chem. Sci., 2023, 14, 203–213.
40. S. S. Batsanov, Inorg. Mater., 2001, 37, 871–885.
41. M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian 16 Revision C.01, 2016, Gaussian Inc., Wallingford CT.
42. T. Howley and M. G. Madden, Artif. Intell. Rev., 2005, 24, 379–395.
43. L. Breiman, Mach. Learn., 2001, 45, 5–32.
44. R. E. Schapire, Explaining adaboost, Springer, 2013, pp. 37–52.
45. T. Chen and C. Guestrin, Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, 2016, pp. 785–794.
46. G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, Q. Ye and T.-Y. Liu, Advances in Neural Information Processing Systems.
47. M. P. LaValley, Circulation, 2008, 117, 2395–2399.
48. S. J. Pan, Learning, 2020, 21, 1–2.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cc04200j

---