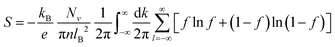Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Record thermoelectric figure of merit in Bi1−xSbx achieved by 1-D Landau level quantization†
Bin
He
a,
Xiaolong
Feng
a,
Dong
Chen
a,
Federico M.
Serrano-Sanchez
a,
Mohamed
Nawwar
 b,
Haihua
Hu
a,
Urlich
Burkhardt
a,
Berit H.
Goodge
a,
Claudia
Felser
*a,
Joseph P.
Heremans
b,
Haihua
Hu
a,
Urlich
Burkhardt
a,
Berit H.
Goodge
a,
Claudia
Felser
*a,
Joseph P.
Heremans
 *bcd and
Yu
Pan
*bcd and
Yu
Pan
 *ae
*ae
aMax Planck Institute for Chemical Physics of Solids, Dresden, 01187, Germany. E-mail: Claudia.Felser@cpfs.mpg.de; yupan2024@cqu.edu.cn
bDepartment of Materials Science and Engineering, The Ohio State University, Columbus, OH 43210, USA. E-mail: Heremans.1@osu.edu
cDepartment of Mechanical and Aerospace Engineering, The Ohio State University, Columbus, OH 43210, USA
dDepartment of Physics, The Ohio State University, Columbus, OH 43210, USA
eCollege of Materials Science and Engineering & Center of Quantum Materials & Devices, Chongqing University, Chongqing, 400044, China
First published on 4th March 2025
Abstract
Landau-level quantization confines electrons to a one-dimensional motion, generating a nearly δ-like energy distribution of the density of states that enhances the Seebeck coefficient and produces a high zT in an otherwise three-dimensional system. This mechanism is shown experimentally to create a record figure of merit of zT = 2.6 ± 0.26 at 100 K in an optimally n-type-doped single-crystalline Bi88Sb12 topological insulator, in a magnetic field of 0.4 T that is easily reached with permanent magnets. The result is confirmed to be reproducible on two samples and using two different measurement methods. The alloy is unique in that Landau levels are still distinct at 100 K. Quantization more than doubles the Seebeck coefficient and enhances the zT by a factor of 5 over the zero-field value, confirming the significant role that the quantum effect can play in thermoelectric research, especially in low-temperature cooling applications.
Broader contextAs environmental protection receives increasing attention, compressor-free techniques have gained appeal, particularly given the detrimental effects of chlorine-based cryogens on atmospheric ozone. The development of solid-state cooling devices utilizing thermoelectric materials presents an effective method for achieving cooling without compressors, because these materials can directly convert electricity into a temperature gradient. While significant advancements have been made in room temperature thermoelectric cooling devices, those designed to operate between 200 K and liquid nitrogen temperatures remain lacking. This study leverages a combination of quantum mechanics and thermoelectric principles to achieve a high figure of merit within the temperature range of 100 K to 200 K. By implementing Landau levels, we achieved synergistic optimization of transport properties that is typically attainable only in low-dimensional materials. Our findings hold great potential for application in cryogenic systems that do not rely on liquid helium. |
Main
Thermoelectric energy conversion is an all-solid-state power generation and cooling/refrigeration technology that is greenhouse-gas free, maintenance free, vibration free, and has a very high power density. However, the thermal efficiency is limited by irreversible thermodynamic losses characterized by the thermoelectric figure of merit zT = S2T/ρκ, where S is the Seebeck coefficient, T is the average temperature, ρ is the resistivity, and κ is the thermal conductivity.1 Thirty years ago, Hicks and Dresselhaus predicted that the one-dimensional (1-D) quantization of electron motion greatly enhanced zT by enhancing S,2 since the density of states of 1-D electrons is an almost δ-shaped function of energy,3 in contrast to that of three-dimensional (3-D) electrons. The present paper reports the successful embodiment of the 1-D quantum enhancement of zT in a 3-D solid using Landau-level (LL) quantization, which confines electron motion to 1-D in the direction parallel to the applied magnetic field B, while quantizing the motion in cyclotron orbits in the plane perpendicular to it. The conversion from the classic 3-D transport into 1-D Landau levels by a magnetic field is briefly summarized in Fig. 1(a). Based on this principle, we obtained an experimental zT of 2.6 ± 0.26 at 100 K and 0.4 T, five times higher than the zero-field value and comparable to those of the best performance high-temperature thermoelectric materials, in the class of precisely doped single-crystal Bi88Sb12, the first topological insulator (TI).4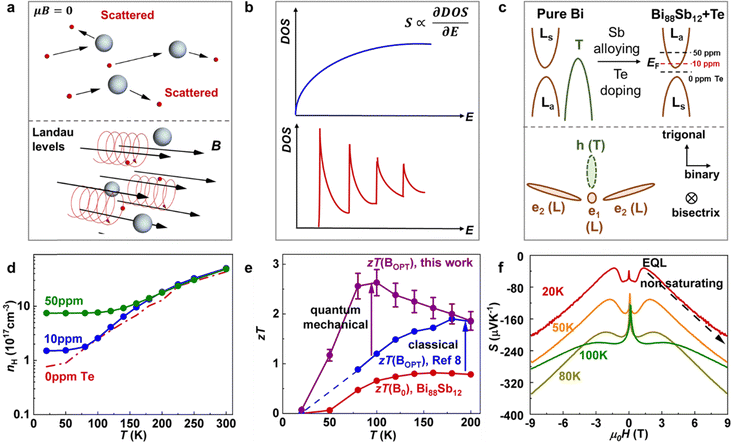 | ||
Fig. 1 Landau level quantization enhanced magneto-thermoelectric performance. (a) and (b) Scenario of electrical transport in solids with the corresponding DOS. At zero field, the electrons (red small balls) are constantly scattered. In this case, the  holds. When a strong field is applied, the electrons are subjected to the Lorentz force and move additionally in the cyclotron motion. The electrons enter the Landau levels at a high field, with the DOS being δ-shaped. (c) Upper: Band structure of pure Bi compared with that of Bi88Sb12 with doping. After alloying with Sb, the T-hole band moves far from the Fermi energy, making it possible to remove the multi-carrier effect in Bi. Further doping can effectively move the Fermi energy into the conduction band. Lower: Fermi surface of doped Bi88Sb12 viewed from the bisectrix axis, the direction of the applied magnetic field. In this view, the three electron pockets are split into two types, namely, light bisectrix (LBX) and heavy bisectrix (HBX), with the projection being close to a circle and cigar, respectively. The hole Fermi surface locates at the T point, which vanishes after alloying with Sb and electron doping. (d) Hall carrier concentrations of different doping level Bi88Sb12 samples. (e) Field enhancement of zT in Bi88Sb12. Without doping, the enhancement is maximized around 200 K, which is dominated by a classical magneto-Seebeck effect.5 After optimal doping, the Landau quantization creates δ-like DOS that gives a quantum enhancement to the zT, mainly happens near 100 K with a much higher amplitude. (f) Non-saturating Seebeck coefficient observed at high field for the 10-ppm doped crystal. The quantum limit shifts to higher fields with an increasing temperature because of a higher carrier concentration. holds. When a strong field is applied, the electrons are subjected to the Lorentz force and move additionally in the cyclotron motion. The electrons enter the Landau levels at a high field, with the DOS being δ-shaped. (c) Upper: Band structure of pure Bi compared with that of Bi88Sb12 with doping. After alloying with Sb, the T-hole band moves far from the Fermi energy, making it possible to remove the multi-carrier effect in Bi. Further doping can effectively move the Fermi energy into the conduction band. Lower: Fermi surface of doped Bi88Sb12 viewed from the bisectrix axis, the direction of the applied magnetic field. In this view, the three electron pockets are split into two types, namely, light bisectrix (LBX) and heavy bisectrix (HBX), with the projection being close to a circle and cigar, respectively. The hole Fermi surface locates at the T point, which vanishes after alloying with Sb and electron doping. (d) Hall carrier concentrations of different doping level Bi88Sb12 samples. (e) Field enhancement of zT in Bi88Sb12. Without doping, the enhancement is maximized around 200 K, which is dominated by a classical magneto-Seebeck effect.5 After optimal doping, the Landau quantization creates δ-like DOS that gives a quantum enhancement to the zT, mainly happens near 100 K with a much higher amplitude. (f) Non-saturating Seebeck coefficient observed at high field for the 10-ppm doped crystal. The quantum limit shifts to higher fields with an increasing temperature because of a higher carrier concentration. | ||
Because S, ρ, and κ are interdependent on each other, the optimization of zT has always been a challenge,6 an approach that synergistically optimizes the three transport parameters has been scarce to date. In the past few decades, the main success of high thermoelectric performance has been achieved at high temperatures (>300 K) with a variety of material engineering techniques,7 while a high-performance, low-temperature thermoelectric material remains absent except Bi1−xSbx,5,8 particularly near the liquid nitrogen temperature.9 In metal/heavily doped semiconductors, S is the energy derivative of the energy-dependent electrical conductivity σ(E).10
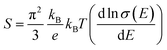 | (1) |
LL quantization achieves this and occurs in the Bi1−xSbx class of narrow-gap semiconductors at up to 100 K. Note that LLs were originally discovered less than a century ago by observing the Shubnikov–de Haas (SdH) oscillations in the end member of this class, semimetal Bi.14 In order to realize LL quantization in a Bi88Sb12 topological insulator, precise tuning of the Fermi energy into the conduction band is essential. For pristine Bi88Sb12, a strong magneto-Seebeck effect and high magneto-zT have been realized;5,8 however, there is an absence of Shubnikov–de Haas (SdH) oscillations even though the mobility is as high as 8 × 105 cm2 V−1 s−1 (at 80 K).5 We, herein, therefore performed optimal Fermi energy tuning in the conduction band by ppm-level Te doping. Owing to the high mobility and suitable Fermi energy, SdH oscillations starting from a low field (<0.1 T) at 2 K and LL quantization are observed in a single-crystalline Te-doped Bi88Sb12 topological insulator. As a consequence, the electron motion transverse to the field is then quantized onto the LLs, developing a δ-DOS (Fig. 1(b)) that meets the Mahan–Sofo criterion11 and significantly enhances the zT (80 to 160 K). This new approach based on quantum mechanical rather than classical transport greatly improves the zT of Bi88Sb12 at fields sufficiently low to be generated by a permanent magnet, which is very desirable in practical applications.
Pure Bi is a classic semimetal with an equal density of electrons and holes.15 In Bi, electrons and light holes form symmetric bands centered at the L-points of the Brillouin zone (BZ), whereas a heavy hole band is populated at the T-points.16 Alloying pure Bi with Sb results in a decrease in the lattice constant, which decreases the energy of the T-hole band and decreases the direct band gap of the L-point electrons and holes, eventually inverting these bands and creating direct-gap semiconducting topological insulators for x > 7%.17,18Fig. 1(c) shows the band structures of pure Bi and 12% Sb-alloyed Bi88Sb12. Ideally, for the pristine Bi88Sb12, the Fermi energy locates in the mid-gap. The L-point pockets of both are almost mirror images, except for the band inversion and the disappearance of the trivial band at the T-point that makes Bi88Sb12 a topological insulator.4 To locate the Fermi energy into the conduction band, n-type doping is necessary. Experimentally, we prepared multiple Bi88Sb12 single crystals by the horizontal zone melting technique with different nominal doping levels of 0, 10, and 50 ppm of Te, with the Fermi energies schematically shown as the dashed lines in the upper panel of Fig. 1(c). The actual Te concentrations in the crystal were tested by inductively coupled plasma (ICP) measurement and the results are briefly summarized in Table S1 (ESI†). After doping, the Fermi surface of n-type doped Bi88Sb12 viewed into the bisectrix axis is shown in the lower panel of Fig. 1(c). The electron pockets are slightly tilted in the Γ–L direction. Viewed along (010), the direction along which the field is applied here, the electron Fermi surface cross-sections fall into two groups: a nearly circular light bisectrix (LBX) and two elliptical anisotropic heavy bisectrices (HBXs).19,20 The T-hole band is shown as a dashed oval since it is far from the Fermi energy after doping; it does not contribute to transport below about 200 K.
Transport properties are measured along the trigonal direction with the highest mobility. The zero-field transport properties of the three crystals are summarized in Fig. S1 (ESI†). The increased Hall carrier concentrations nH in Fig. 1(d) confirm that the Fermi energies of the doped samples are shifted toward the conduction band. At 20 K, the nH increases from 7 × 1016 cm−3 in the undoped sample to 7 × 1017 cm−3 for the nominal 50-ppm crystal. For all crystals, nH increases with temperature because of the thermal excitation of the intrinsic carriers. Among the three crystals, the 10-ppm crystal is optimally doped and shows the best zT (details later). A zT-comparison between the pristine and doped Bi88Sb12 crystals is summarized in Fig. 1(e). For the 10-ppm crystal, the zT measured at zero field is shown as a red curve, labeled as zT(B0); the zT measured at optimal field (BOPT, with the highest zT at each temperature) is shown as a purple curve, labeled as zT(BOPT). Notably, zT(BOPT) is five times higher than zT(B0) at 100 K. Moreover, we compared the present result to our previous result without LL quantization, as shown by the blue curve. Obviously, there is a great enhancement of the present work compared to our previous report, and the current best zT of 2.6 at 100 K is 2.2 times higher than that of the previously reported result,8 suggesting the significance of LL quantization in zT enhancement. This high zT also provides the opportunity for thermoelectric device fabrication near liquid nitrogen temperature. At high temperatures above 100 K, the intrinsically excited carriers become dominant in transport and the quantum enhancement gradually vanishes.
Proven as a topological insulator, the quantum enhancement arises from the linear Dirac bands rather than the topological surface states. Predicted by theory,21 a non-saturating magneto-Seebeck effect is expected with the topological linear bands in the extreme quantum limit (EQL) when all carriers are on the last LL, which is exceptional compared to parabolic bands. This is observed in the present system: Fig. 1(f) reports high-field measurements of the Seebeck coefficient up to 9 T. At temperatures up to 100 K, the high-field thermopower increases linearly with the field, which has been absent in previous reports.8,22 The large, non-saturating magneto Seebeck effect provides evidence to distinguish this study from the previous ones, and highlights the importance of the quantum mechanical contribution to thermoelectric performance. The EQL increases from 1.2 T to 4.2 T in this sample because nH increases as well. The peak zT is observed at 100 K but at a field where 2 or 3 LL's are filled. This provides evidence for the quantum LL nature of the zT enhancement. Above 100 K, nH increases with T (Fig. 1(d)) due to the appearance of thermally excited holes and electrons. This reduces the peak zT, but not dramatically and the zT enhancement persists up to 180 K. Similarly, at T > 100 K, the non-saturating Seebeck coefficient vanishes progressively (ESI,† Fig. S2(b)).
Field-dependent thermoelectric transport properties
The magnetic field dependence of S, ρ, and κ with B along the bisectrix direction are given next. The 10-ppm doped sample shows the best thermoelectric performance, as summarized in Fig. 2; the undoped and 50-ppm doped samples are under- and over-doped, respectively (as summarized in Fig. S3 and S5, ESI†). For the 10-ppm crystal, a series of sample characterization studies, including the crystal quality, phase purity, compositional homogeneity, is summarized in the ESI,† Fig. S6–S8, to show its high crystal quality. Additionally, transmission electron microscopy (TEM) measurement was executed to eliminate any possible microstructure and to guarantee the bulk transport behavior. Fig. 2(a) shows the low-temperature SdH oscillations of ρ in the 10-ppm crystal. Below 10 K, they are clearly resolved starting from a very low field (<0.1 T). ρ decreases to a local minimum for 0.1 T < B < 0.5 T. At and above 1.2 T, which is shown later to be the EQL for HBX carriers, ρ increases monotonically with B. Oscillations below 1.2 T are plotted as functions of 1/B in the embedded figure. Analysis of Δρ vs. 1/B gives a period of 1.5 T−1 related to the Fermi surface area (SF) by , which gives SF = 6.35 × 1011 cm−2. The resolved Fermi surface pockets are HBX pockets, which, in elemental Bi, have an area SF = 2.37 × 1012 cm−2. The SF of the 10-ppm doped Bi88Sb12 crystal is 27% of the SF of Bi because of a smaller carrier concentration. The resolved carrier concentration n of the doped crystal is approximately 4.2 × 1016 cm−3, much lower than nH, because of the Fermi surface anisotropy.23 The n from SdH oscillations will be used exclusively here for modeling in the theoretical part. The higher-temperature in-field ρ (B) is shown in Fig. 2(b). Weak SdH oscillations can be resolved up to 100 K because of the ultra-small effective mass of the electrons.17 The negative MR observed at T < 100 K is the remnant of the SdH oscillations. Phonon scattering is then decreased by decreasing the phase space for the scattered electrons from 3-D to 1-D. A positive bipolar appears in all fields above 100 K again because of minority carrier excitation.
, which gives SF = 6.35 × 1011 cm−2. The resolved Fermi surface pockets are HBX pockets, which, in elemental Bi, have an area SF = 2.37 × 1012 cm−2. The SF of the 10-ppm doped Bi88Sb12 crystal is 27% of the SF of Bi because of a smaller carrier concentration. The resolved carrier concentration n of the doped crystal is approximately 4.2 × 1016 cm−3, much lower than nH, because of the Fermi surface anisotropy.23 The n from SdH oscillations will be used exclusively here for modeling in the theoretical part. The higher-temperature in-field ρ (B) is shown in Fig. 2(b). Weak SdH oscillations can be resolved up to 100 K because of the ultra-small effective mass of the electrons.17 The negative MR observed at T < 100 K is the remnant of the SdH oscillations. Phonon scattering is then decreased by decreasing the phase space for the scattered electrons from 3-D to 1-D. A positive bipolar appears in all fields above 100 K again because of minority carrier excitation.
Fig. 2(c) shows the field dependence of the Seebeck coefficient S(B) at various temperatures, clearly displaying SdH oscillations at 20 and 50 K and remnants at 100 K, which we will model in the next section. At T ≤ 100 K, |S| slightly increases with the field below 0.1 to 0.5 T, and then remains high up to 1 T. The low-field increase in |S| and decrease in ρ are associated with the transition from a 3-D to a 1-D LL system, when the system transitions from a scattering-limited resistivity at zero field to a largely LL-confined quasi 1-D system with μB ≫ 1. Because of the minimum in ρ and maximum in |S|, the power factor S2/ρ is maximized at low field below 100 K, as shown in Fig. 2(d). The highest power factor is achieved at 80 K, with a magnitude of over 60 mW m−1 K−2. Fig. 2(e) shows the field-dependent thermal conductivity results. At all temperatures, κ is already nearly as low as in many classical thermoelectric alloys at zero field because alloy scattering limits the lattice contribution. The field further depresses κ due to the suppression of the electronic contribution. Although the lattice contribution is dominant at low temperatures, the electronic contributions become significant at 50 K and ambipolar one above 100 K; the magnetic field can suppress the latter two and increase zT. Interestingly, both ρ and κ decrease with the field, which seems a violation of the Wiedemann–Franz law (ke = LTσ) if L is assumed to be its free electron value. We propose that the magnetic field strongly affects the Lorenz ratio L because the electron–phonon interaction is affected by the magnetic field following the same phase space argument used to explain the negative MR. As a non-magnetic material, the lattice thermal conductivity is not expected to be affected by the magnetic field. An early study showed that the Wiedemann–Franz law is obeyed at zero field with this assumption.24
The zT of the 10-ppm doped Bi88Sb12 single crystal at various temperatures and fields are calculated from the S, ρ, and κ, obtaining a remarkable value of zT of 2.6 at 100 K, 0.4 T, which is approximately five times higher than the zero-field value. Thermally excited carriers gradually reduce the overall |S| above 100 K, and the peak zT decreases. At 180 K, a zT of 2 is maintained at 1 T, which is the highest practical field achievable with permanent magnets; therefore, it is still practical for thermoelectric cooling applications.
Temperature-dependent thermoelectric transport properties
To better illustrate the figure of merit change with temperature, we replot the temperature-dependent transport properties at various set fields from 0 to 1.5 T, as shown in Fig. 3. Fig. 3(a) shows ρ(T) with the field. At 0 T, ρ increases monotonically with temperature following a doped semiconductor behavior. The lowest ρ is achieved at a finite field (from 0.1 to 0.5 T), as explained above. When the magnetic field is above 1 T, a sharp increase in ρ is observed with a decreasing temperature, which is harmful for a high zT. |S| also changes non-monotonically with T (Fig. 3(b)). |S| is the maximum when a few LLs are filled, between 0.1 and 1.5 T, and zT is the maximum in the field range where |S| is maximized and ρ is small. Fig. 3(c) shows the temperature-dependent power factors under different magnetic fields. From 0.3 T to 0.7 T, the power factor peaks at 80 K, right before the thermal excitation starts. In this range, the quantum mechanical enhancement of the Seebeck coefficient dominates the increase in the power factor. Above 1 T, the power factor reaches its maximum between 160 K and 180 K, when the classic magneto-Seebeck effect becomes crucial. Fig. 3(d) shows the temperature-dependent κ. κ decreases monotonically with applied field due to the suppression of the electronic or ambipolar contribution. The thermal excitation above 100 K can simultaneously reduce the Seebeck coefficient and elevate the thermal conductivity, as shown in Fig. 3(b) and (d), irrespective of the magnetic field. Therefore, the best zT is observed at 100 K, when a high |S| and low ρ and κ are achieved simultaneously at approximately 0.3–0.4 T, as illustrated in Fig. 3(e).The high performance of the present Te-doped Bi88Sb12 is remarkable, which is not only higher than those reported for undoped samples in the literature,7,22,25 but also comparable to the high zT values obtained for the best high-temperature materials, as illustrated in Fig. 4(e).26–31 Such a strong magneto-Seebeck effect and significantly enhanced magneto-zT, together with our previous result in undoped Bi88Sb12,8 and other topological systems like Cd3As2,32–36 highlight the great potential of magneto-thermoelectrics in topological materials for revolutionizing thermoelectric performance. The present work, wherein LL quantization and a quasi-1-D transport regime is realized in optimally doped Bi88Sb12 to reach a zT > 2.5 below 300 K, opens new avenues for high-performance thermoelectric materials’ design and thermoelectric cooling applications.
 | ||
| Fig. 4 Theory analysis and reproducibility. (a) The Landau fan diagram of the 10-ppm Te-doped Bi88Sb12. Based on the band parameters of Bi88Sb12, the fan diagram of the LBX and HBX are plotted separately in red and blue. The Fermi energy is calculated from a carrier concentration of 4.2 × 1016 cm−3. The system should enter the quantum limit at 1.2 T, which is consistent with the experimental transport data. (b) Comparison between the theoretical and experimental in-field Seebeck coefficient modeled at different temperatures and fields. Solid lines are theoretical predictions, and the dashed lines are experimental values. (c) Reproducibility of the high zT. A second crystal b is measured, with a result close to that of the original crystal a. A peak zT of 2.3 is achieved, along with a wider range of zT > 2 from 80 to 200 K. (d) Field dependent zT of b at selected temperatures, resolved from the zT calculation (solid lines) and Harman test (full circles). The raw curves of the Harman test are shown in Fig. S10 (ESI†). | ||
Theory of Landau quantization enhanced Seebeck coefficient
To prove that the enhancement of |S| in the 0.1 to 1 T range is due to LL quantization, we use the simple model reported by Skinner and Fu,21 valid when μB ≫ 1 in Bi88Sb12 with Dirac band dispersion. The carrier concentration was taken as n = 4.2 × 1016 cm−3, which was obtained from the SdH frequency. Noting that the band structure of Bi88Sb12 is almost exactly the mirror image of that of elemental Bi, except for the absence of T-point holes and the inversion of the symmetric and antisymmetric bands at the L-point of the BZ, we used the detailed LL diagram and effective masses published for the LBX and HBX Bi L-point electrons shown in Fig. 4(a).18 The calculated Seebeck coefficient is shown in Fig. 4(b). The calculations reproduced the measured field and temperature dependence of S almost quantitatively to 100 K, establishing the validity of the model and attributing the large zT to 1-D LL quantization. The slight difference may come from a finite number of minority holes as well as Fermi surface anisotropy.Reproducibility of the high thermoelectric performance
To illustrate the sample-to-sample reproducibility, we measured a second 10-ppm crystal (denoted as b) and compared it with the first crystal (denoted as a). We discovered that an unintentional slight variation in the carrier concentration resulted in the peak zT of sample b being slightly lower than that of sample a, but the high zT of sample b was achieved over a wider temperature range than that of sample a, which can be observed in Fig. 4(c). Sample b shows a peak zT of 2.3, with zT > 2 from 80 to 225 K and improved performance up to 300 K. The transport properties of sample b are shown in Fig. S4 (ESI†). Because the claim of a record zT requires the confirmation of the results using more than one measurement method,37 we also performed the Harman test on crystal b, as shown in Fig. 4(d). The Harman zT is determined by the ratio between the adiabatic resistivity ρa and isothermal resistivity ρi, via zT = ρa/ρI − 1.38 The Harman zT is plotted as full circles together with the transport-calculated zT (lines). This agreement proves the reliability of the reported enhancement in zT.Summary and outlook
In summary, a record zT of 2.6 is obtained at 100 K and 0.4 T in the 10-ppm Te-doped Bi88Sb12 single crystal, which is attributed to the LL quantization enhancement. The 1-D quantization distorts the density of states into the δ-shaped energy distribution of the density-of-states and enhances the figure of merit. This approach not only produces the high zT at cryogenic temperatures on par with the best high-temperature thermoelectric materials but also opens a new venue of research for thermoelectric cooling based on the topological materials with high magnetic field tunability. Furthermore, we highlight that precise ppm-level doping is essential for realizing the LL quantization by pushing the Fermi energy into the optimal level in the conduction band of the Bi88Sb12 topological insulator. This can be instructive for future studies in but not limited to the Bi1−xSbx system. Most importantly, we expect more studies using LL quantization to greatly enhance the thermoelectric performance in topological materials, providing a wide material platform for thermoelectric cooling applications and thermal management in the future.Methods
1. Crystal growth
The single-crystal Bi88Sb12 is grown using a traveling molten zone method.38 To achieve high-quality crystals, 99.9999% Bi is essential, and it was purified by zone melting before use. 6N Bi, Sb, and Te from Alfa Aesar are used in this study. For the doped samples, a piece of Bi containing 0.1% Te was prepared first and then further diluted to the desired Te concentration. For the Bi88Sb12 alloy, the seed and feed were prepared separately following the phase diagram. The use of the seed-feed method can minimize the super cooling effect. Pure Bi, Sb, and 0.1% Te-doped Bi were weighed by stoichiometry and loaded into quartz ampoules. The ampoules were sealed under vacuum of 3 × 10−3 mbar and loaded into a box furnace. Polycrystals were first prepared by melting the seed and feed at 700 °C, with frequent shaking of the ampoules for composition homogeneity. The ampoules were quenched to room temperature to minimize the phase segregation introduced by the super cooling procedure. In this study the seed and feed are selected as Bi96Sb4 and Bi88Sb12. The obtained seed and feed were cut to have flat ends, physically attached next to each other, and resealed in a second quartz ampoule for further single-crystal growth. A home built horizontal zone melting furnace is used for the crystal growth, and the growing process started at a speed of 1 mm per hour. The as-grown crystals were cleavable with the cleavage plane perpendicular to the trigonal axis.2. Crystal characterization
Powder diffraction was obtained using the X-ray Guinier technique (Huber G670 with Cu Kα radiation). Single-crystal Laue diffraction analysis was performed using a Bruker single-crystal diffractometer. The chemical composition of the sample was determined by point and area measurements using EDX (energy dispersive X-ray) spectroscopy in a scanning electron microscope (JSM 7800F, Jeol). At an excitation voltage of 10 kV and a beam current of 630 pA, the spectra were recorded with a silicon drift detector (SDD) (Quanta 400 EDX system, BrukerNano). The element concentrations were calculated from the intensities of the Bi M and Sb L lines using the matrix correction model eZAF (Benchmark EDS-analytical software). A series of sample characterization, including optical imaging, XRD, and SEM, are shown in ESI,† Fig. S6–S8. A cross-sectional lamella for scanning transmission electron microscopy (STEM) analysis was obtained using a standard focused ion beam (FIB) lift-out procedure with a Thermo Fisher Scientific Helios NanoLab G3 CX FIB. The STEM images were collected in a high-angle annular dark-field (HAADF) configuration on a double-aberration-corrected JEOL ARM300F instrument operating at 300 kV with a probe convergence semi-angle of 30 mrad. The STEM images are shown in Fig. S9 (ESI†).3. Transport property measurements
All transport measurements were performed using a Quantum Design Physics Property Measurement System (PPMS). The electrical transport (resistivity and Hall) was measured using the built-in electrical transport option (ETO) of the PPMS. The thermal/thermoelectric transport was measured using a one-heater, two-probe steady-state method with a breakout box. The precision voltages were measured using Keithley 2181A nanovoltmeters. In this set of experiments, we used a type-E thermocouple for thermometry, with no obvious field dependence expected down to 20 K. All field-dependent data were interpolated for zT calculation. As the resistivity and thermal conductivity were measured using the same mount, the geometrical uncertainty was limited to 15%, but it still was the dominant factor.Throughout the study, the field was parallel to the bisectrix direction (010), and an electrical/heat current was applied along the trigonal direction (001). The sign convention follows the Gerlach convention of transport coefficients, where a negative Hall slope indicates that electrons are the majority carriers.
4. Harman test of the figure of merit
The Harman39 test was performed in situ on the transport sample. We performed a DC resistance measurement under a current pulse, first reading the voltage Vi immediately after the pulse was applied when the sample was still at a constant temperature. Under the current, the sample developed a temperature gradient owing to the Peltier effect; the voltage Va was read after the gradient reached a steady state. The Harman zT was then zT = Va/Vi − 1. A Keithley 6220 current source was used for the DC current supply, and a Keithley nano-Voltmeter 2182A was used for the voltage measurement. A current of 10 mA was applied to the sample and the voltage was recorded simultaneously. A total of 200–300 time-step points were recorded until the voltage reached a steady state. LabVIEW software was used for measurement control to collect a precise isothermal voltage Vi and the time evolution of the voltage until the adiabatic value of Va. The raw curves of the Harman test are shown in Fig. S10 (ESI†).5. Theory and calculations
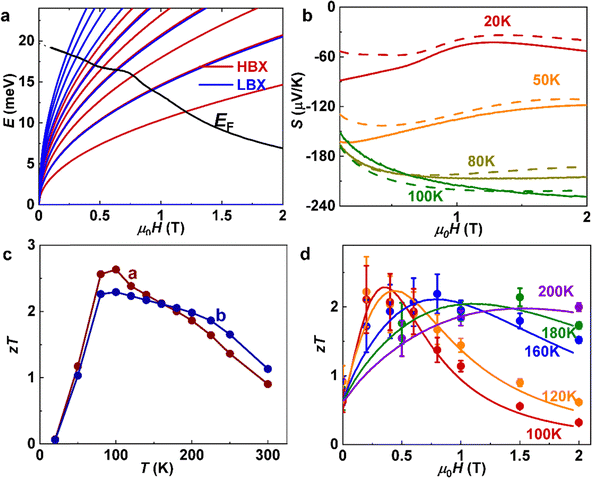
To account for the thermopower of Bi88Sb12 under magnetic fields close to the quantum limit, the system was treated in the Landau level regime. Electrons from the pockets at the L points in Bi88Sb12 were described as Dirac fermions. The Landau level diagram was then calculated asThe average Fermi velocity v was assumed as 4 × 105 m s−1, and l is the Landau level index. The Fermi level is determined from n as follows. The density of states is eBk/(4π2ℏ) on each level. For a given value of EF and the LL diagram at each field, the Fermi wavevector kF,j on each level can be derived. The sum over all levels of eBkF,i/(4π2ℏ) gives the carrier concentration in degenerate statistics; setting this equal to n gives the value of EF at each field, also plotted in Fig. 4(a). The Seebeck coefficient of the Landau level system was calculated based on the model reported by Skinner and Fu.21
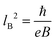 ), f is the Fermi Dirac distribution (f(ε) = {1 + exp[(ε − EF)/kBT]}−1). Nv is the degeneracy of the Fermi surface pockets. To account for the LBX and HBX in this anisotropic system, here we assign Nv to be 1 for LBX and 2 for HBX with the spin degeneracy lifted under magnetic fields. The Fermi level EF was determined by the carrier concentration n = 4.2 × 1016 cm−3, obtained by solving the quantum oscillation. As the magnetic field intensity increases, the Fermi level decreases as the density of states increases. When the magnetic field is sufficiently large, the system enters the extreme quantum limit with only the zeroth Landau level left, resulting in a non-saturating Seebeck coefficient at low temperatures.
), f is the Fermi Dirac distribution (f(ε) = {1 + exp[(ε − EF)/kBT]}−1). Nv is the degeneracy of the Fermi surface pockets. To account for the LBX and HBX in this anisotropic system, here we assign Nv to be 1 for LBX and 2 for HBX with the spin degeneracy lifted under magnetic fields. The Fermi level EF was determined by the carrier concentration n = 4.2 × 1016 cm−3, obtained by solving the quantum oscillation. As the magnetic field intensity increases, the Fermi level decreases as the density of states increases. When the magnetic field is sufficiently large, the system enters the extreme quantum limit with only the zeroth Landau level left, resulting in a non-saturating Seebeck coefficient at low temperatures.
6. Uncertainty analysis
In the transport measurement, the uncertainty in the Seebeck measurement, which is of the order of 5%, comes from the uniformity of the sample. In the temperature range of interest, particularly from 80 to 200 K, the field dependence of the thermocouple sensitivity is below 2% and is neglected. For the resistivity and thermal conductivity, the uncertainty mainly originates from the geometrical uncertainty, particularly the size of the longitudinal contacts. The magnitudes of the uncertainty in κ and ρ were estimated to be 5% each, but this geometric uncertainty was canceled out in the zT calculation. We found a 3% change in the heater resistance when it was cooled from 300 to 20 K. Additionally, a 1–3% temperature uncertainty was generated when the temperature gradient is applied to the sample. As a result, the total uncertainty in the zT calculation is estimated as 10% ± 1%.The uncertainty in the Harman method is due to the difficulty of precisely determining the initial voltage Vi. This uncertainty is larger at a low field, where it can reach 25% at 100 K. With an increasing field, this error turns smaller, with a magnitude of 10% at 1 T and 3% at 2 T. The uncertainty of the Harman method is represented by the error bars shown in Fig. 4(d).
Author contributions
B. H. and Y. P. designed this work, grew the single crystals, and performed the characterization. B. H. performed the transport measurements; B. H. and F. M. S. conducted the Harman test; U. B. performed the SEM-EDX analysis; B. H. G. performed the STEM imaging. B. H., Y. P., D. C., M. N., H. H., J. P. H., and C. F. analyzed the data; and the theoretical model was built by X. F. and J. P. H.; C. F. supervised the project. All authors were involved in writing the paper.Data availability
All datasets generated or analyzed during this study are available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was financially supported by the Deutsche Forschungsgemeinschaft (DFG) under SFB1143 (project no. 247310070) and the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter-ct.qmat (EXC 2147, project no. 390858490). Y. P. acknowledges the financial support from the National Natural Science Foundation of China (grant no. 52401263). J. P. Heremans received support from the MRSEC program of the U.S. National Science Foundation (NSF), grant number DMR 2011876. B. H. G. was supported by Schmidt Science Fellows, in partnership with the Rhodes Trust. Open Access funding provided by the Max Planck Society.References
- L. E. Bell, Science, 2008, 12, 1457–1461 CrossRef PubMed.
- L. D. Hicks and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 16631(R) CrossRef PubMed.
- J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 5888 CrossRef PubMed.
- D. Hsieh, D. Qian, L. Wray, Y. Xia, Y. S. Hor, R. J. Cava and M. Z. Hasan, Nature, 2008, 452, 970–974 CrossRef CAS PubMed.
- Y. Pan, B. He, X. Feng, F. Li, D. Chen, U. Burkhardt and C. Felser, Nat. Mater., 2025, 24, 76–82 CrossRef CAS PubMed.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- J. He and T. M. Tritt, Science, 2017, 357, eaak9997 CrossRef PubMed.
- R. Wolfe and G. E. Smith, Appl. Phys. Lett., 1962, 1, 5–7 CrossRef CAS.
- J. Mao, G. Chen and Z. Ren, Nat. Mater., 2020, 20, 454–461 CrossRef PubMed.
- M. Cutler and N. F. Mott, Phys. Rev., 1969, 181, 1336 CrossRef CAS.
- G. D. Mahan and J. O. Sofo, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 7436–7439 CrossRef CAS PubMed.
- J. P. Heremans, C. M. Thrush, D. T. Morelli and M.-C. Wu, Phys. Rev. Lett., 2002, 88, 216801 CrossRef PubMed.
- A. I. Hochbaum, R. Chen, R. D. Delgado, W. Liang, E. C. Garnett, M. Najarian, A. Majumdar and P. Yang, Nature, 2008, 461, 163–168 CrossRef PubMed.
- L. Schubnikow and W. De Haas, Nature, 1930, 126, 500 CrossRef.
- R. Hartman, Phys. Rev., 1969, 181, 1070 CrossRef CAS.
- R. D. Brown, R. L. Hartman and S. H. Koenig, Phys. Rev., 1968, 172, 598–603 CrossRef CAS.
- D. Shoenberg, Magnetic Oscillations in Metals. Cambridge University Press, 1984 Search PubMed.
- M. P. Vecchi, J. R. Pereira and M. D. Dresselhaus, Phys. Rev. B, 1976, 14, 298–316 CrossRef CAS.
- G. E. Smith and R. Wolfe, J. Appl. Phys., 1962, 33, 841–846 CrossRef CAS.
- H. J. Goldsmid, Phys. Status Solidi A, 1970, 1, 7–28 CrossRef CAS.
- B. Skinner and L. Fu, Sci. Adv., 2018, 4, eaat 2621 CrossRef PubMed.
- W. M. Yim and A. Amith, Solid-State Electron., 1972, 15, 1141–1144 CrossRef CAS.
- E. H. Putley, The Hall Effect and Relate Phenomena, Butterworth & Co. Limited, 1960 Search PubMed.
- C. Uher and H. J. Goldsmid, Phys. Status Solidi B, 1974, 65, 765 CrossRef CAS.
- V. M. Grabov and O. N. Uryupin, Proc. 16th Int Conf Thermoelectrics, 1997, 176–179.
- B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich, B. Yu, X. Yan, D. Wang, A. Muto, D. Vashaee, X. Chen, J. Liu, M. S. Dresselhaus, G. Chen and Z. Ren, Science, 2008, 320, 634–638 CrossRef CAS PubMed.
- Y. Pan and J.-F. Li, NPG Asia Mater., 2016, 8, e275 CrossRef CAS.
- Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. J. Snyder, Nature, 2011, 473, 66–69 CrossRef CAS PubMed.
- D.-Y. Chung, T. Hogan, P. Brazis, M. Rocci-Lane, C. Kannewurf, M. Bastea, C. Uher and M. G. Kanatzidis, Science, 2000, 287, 1024–1027 CrossRef CAS PubMed.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377 CrossRef CAS PubMed.
- H. Wang, X. Luo, K. Peng, Z. Sun, M. Shi, D. Ma, N. Wang, T. Wu, J. Ying, Z. Wang and X. Chen, Adv. Funct. Mater., 2019, 29, 1902437 CrossRef.
- W. Zhang, P. Wang, B. Skinner, R. Bi, V. Kozii, C.-W. Cho, R. Zhong, J. Schneeloch, D. Yu, G. Gu, L. Fu, X. Wu and L. Zhang, Nat. Commun., 2020, 11, 1046 CrossRef CAS PubMed.
- F. Han, N. Andrejevic, T. Nguyen, V. Kozii, Q. T. Nguyen, T. Hogan, Z. Ding, R. Pablo-Pedro, S. Parjan, B. Skinner, A. Alatas, E. Alp, S. Chi, J. Fernandez-Baca, S. Huang, L. Fu and M. Li, Nat. Commun., 2020, 11, 6167 CrossRef CAS PubMed.
- T. Liang, Q. Gibson, J. Xiong, M. Hirschberger, S. P. Koduvayur, R. J. Cava and N. P. Ong, Nat. Commun., 2013, 4, 2696 CrossRef PubMed.
- X. Xu, Y. Liu, G. Seyfarth, A. Pourret, W. Ma, H. Zhou, G. Wang, Z. Qu and S. Jia, Phys. Rev. B, 2021, 104, 115164 CrossRef CAS.
- W. Ouyang, A. C. Lygo, Y. Chen, H. Zheng, D. Vu, B. L. Wooten, X. Liang, J. P. Heremans, S. Stemmer and B. Liao, Adv. Mater., 2024, 36, 2311644 CrossRef CAS PubMed.
- J. P. Heremans and J. Martin, Nat. Mater., 2024, 23, 18–19 CrossRef CAS PubMed.
- D. Vu, W. Zhang, C. Şahin, M. E. Flatté, N. Trivedi and J. P. Heremans, Nat. Mater., 2021, 20, 1525–1531 CrossRef CAS PubMed.
- T. C. Harman, J. Appl. Phys., 1958, 29, 1373–1374 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ee00253b |
| This journal is © The Royal Society of Chemistry 2025 |