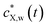Open Access Article
Open Access ArticleSorption kinetics of metallic and organic contaminants on micro- and nanoplastics: remarkable dependence of the intraparticulate contaminant diffusion coefficient on the particle size and potential role of polymer crystallinity†
Raewyn M.
Town
 *a,
Herman P.
van Leeuwen
a and
Jérôme F. L.
Duval
*a,
Herman P.
van Leeuwen
a and
Jérôme F. L.
Duval
 *b
*b
aECOSPHERE, Department of Biology, Universiteit Antwerpen, Groenenborgerlaan 171, 2020 Antwerpen, Belgium. E-mail: raewyn.town@uantwerpen.be
bUniversité de Lorraine, CNRS, LIEC, F-54000 Nancy, France. E-mail: jerome.duval@univ-lorraine.fr
First published on 28th February 2025
Abstract
We developed a mechanistic diffusion model to describe the sorption kinetics of metallic and organic contaminants on nano- and micro-plastics. The framework implements bulk depletion processes, transient fluxes, and fully adaptable particle/water boundary conditions, i.e. not only the typically assumed simple linear Henry regime, which is not applicable to many contaminant-particle situations. Thus, our model represents a flexible and comprehensive theory for the analysis of contaminant sorption kinetics, which goes well beyond the traditional empirical pseudo first or second order kinetic equations. We applied the model to the analysis of a large body of literature data on the equilibrium and kinetic features of sorption of a wide range of contaminants by diverse types and sizes of plastic particles. Results establish the paramount importance of sorption boundary conditions (Henry, Langmuir, or Langmuir–Freundlich) and reveal interesting and often overlooked sorption features that depend on the plastic particle size and the extent to which the target compound is depleted in the bulk medium. The greater degree of polymer crystallinity reported for smaller particles may underlie our findings that the intraparticulate contaminant diffusion coefficient decreases with a decreasing particle size. We establish a universal law to predict the sorption kinetics and diffusion of any compound within any plastic phase, which has far reaching importance across many domains relevant to the environment and human health.
Environmental significancePlastic particles interact with many other environmental contaminants, including inorganic compounds (e.g. metal ions) and organic compounds (e.g. pesticides and pharmaceuticals). Such interactions modify water quality and have consequences for risk assessment of plastic pollution. Notably, the rate at which contaminants are distributed within plastic particles is fundamental for understanding the potential environmental and health impacts of micro- and nano-plastics. We show that the size of plastic particles is the most important factor. |
1. Introduction
The ubiquitous presence of micro- and nano-plastic particles in the environment has raised concerns about their potential impacts on aquatic and terrestrial ecosystems. Plastic particles, together with their associated polymer additives, exert a range of adverse effects on biota at all trophic levels.1–4 In addition, plastic particles interact with and modify the chemical speciation and bioavailability of a wide range of inorganic and organic contaminants as well as other essential compounds in the environment. Knowledge of the thermodynamic and kinetic features of plastic particle interactions with essential and toxic compounds is thus fundamental for robust risk assessment of micro-/nano-plastics and determination of water quality. Conflicting reports in the literature on the potential of plastic particles to mitigate5–7 or exacerbate8–10 the bioaccumulation and/or toxicity of compounds reflect the general lack of consideration of the kinetics of the underlying processes and the involved timescales.To date, most studies have interpreted the sorption kinetics of compounds on plastic particles with empirical (pseudo-) first or second order kinetics.11–14 Although some of these empirical models also refer to intraparticulate diffusion, most do not provide a value for the pertaining diffusion coefficient.15–19 In cases where diffusion coefficients of organic compounds in plastics have been reported, there are conflicting reports on the dependence of such values on the type of organic compound or its molar mass, with the relationship depending on the nature of the polymer (amorphous vs. glassy) and its extent of hydration.20–23 Any molar mass dependence of the intraparticulate diffusion coefficient is greater for glassy, dry polymers.21
We previously developed an interpretation framework to describe the sorption kinetics of compounds on plastic particles in aqueous media by separate and coupled considerations of the transient and steady-state diffusion processes.24 This framework, built upon the empirical 2-compartment model by Bayen et al.,25 formulates the relaxation of the former diffusion process toward a steady state in the form of an ad hoc exponential decay function. It is further restricted to cases where the sorption isotherm verifies linearity, i.e. the so-called Henry sorption regime. The present work extends this approach to a fully rigorous numerical solution of the governing Fickian transfer equations that define the distribution of target compounds at the surface and in the body of plastic particles. The approach adopted herein is valid for all spatial scales and time scales, from nano to micro-sized particles, and it implements, over the time course of the sorption, the most appropriate surface sorption boundary in the form of a linear (Henry), Langmuir, or Langmuir–Freundlich isotherm. Furthermore, the extent to which the target compound is depleted in the bulk aqueous medium during the sorption process is considered. Based on this theory, which formulates the intricate coupling between bulk depletion, surface adsorption and diffusion-driven intraparticulate accumulation of contaminants over time, a robust algorithm is developed to recover consistently measured equilibrium and kinetic sorption data for contaminant/plastic systems. Our approach is successfully applied to interpret more than 100 literature data sets covering a large range of contaminants (metals and organics), polymer compositions and sizes of the plastic particles. The results demonstrate a remarkable law that connects the intraparticulate contaminant diffusion coefficient and plastic particle size regardless of the contaminant and particle chemistry considered.
2. Materials and methods
2.1 Theoretical framework
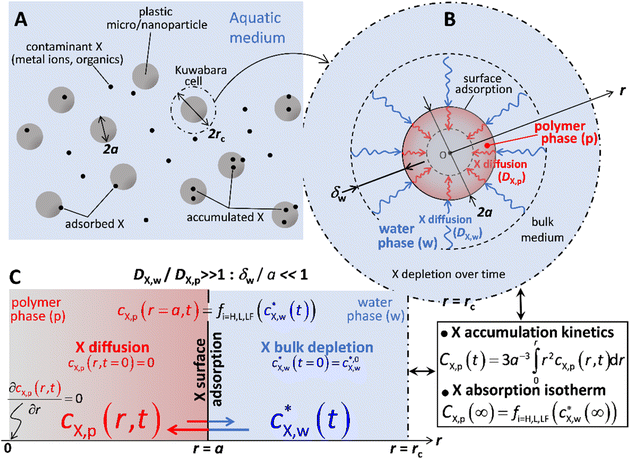
In what follows, we consider the sorption of metallic or organic contaminants, collectively denoted by X, on spherical plastic particles of radius a and volume Vp, present at a volume fraction φ in a dispersing aqueous medium (Fig. 1). We detail the expressions for spherical particles because most suitable experimental data are for this geometry. By properly accounting for geometry in the flux expressions, the theory can be applied to fibres, films, etc. To connect the relevant spatial scales of the problem, i.e. from the particle dispersion scale (Fig. 1A) to the levels of a single plastic particle (Fig. 1B) and the interface it forms with the medium (Fig. 1C), particles are distributed according to a Kuwabara representation (Fig. 1A), where they are surrounded by a virtual cell of radius rc such that the particle/solution volume ratio in that cell equates φ, leading to rc = aφ−1/3.26–28 We further adopt the radial coordinate system, r, with the origin at the particle center (Fig. 1B). Under the conditions of interest, particle dispersion is diluted so that φ ≪ 1 or rc/a ≫ 1. A glossary of symbols is reported in the ESI.†In our previous study, we showed that intraparticulate diffusion limits the overall kinetics of contaminant accumulation by plastic particles,24i.e. there is no diffusion limitation in the extraparticulate region. This property is reflected by the value of the intraparticulate diffusion coefficient of X, DX,p (m2 s−1), which is orders of magnitude lower than the one operational in the aqueous extraparticulate region, DX,w (m2 s−1).20,21 Accordingly, we consider herein that equilibrium conditions hold in the extraparticulate zone. This setting is validated by comparison with experimental data detailed below and by comparison between the relevant timescales for intra- and extra-particulate diffusion. It indicates that the experimentally observed timescales for sorption are orders of magnitude greater than those that would be operational if diffusion in the extraparticulate region is limiting.
Accordingly, the kinetics of X sorption by the plastic particles is mediated solely by the intraparticulate diffusion process, and throughout the intraparticulate accumulation, the concentration of X at the particle surface (r = a) is systematically in equilibrium with the one far from the particle. Let cX,w(a < r ≤ rc,t) denote the extraparticulate concentration of X at time t and position r. Then, we have  , where
, where 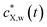 is the concentration of X in bulk medium, with
is the concentration of X in bulk medium, with  the initial concentration of X therein.
the initial concentration of X therein.  may decrease with time depending on the extent of depletion of X in the bulk medium owing to intraparticulate X accumulation and ensuing removal from the medium (Fig. 1). Equilibrium in the extraparticulate region imposes that the concentration of X on the polymer side of the particle/solution interface is related to the concentration of X at the solution side of that interface according to an equilibrium partitioning relationship (isotherm) of the form (Fig. 1C):
may decrease with time depending on the extent of depletion of X in the bulk medium owing to intraparticulate X accumulation and ensuing removal from the medium (Fig. 1). Equilibrium in the extraparticulate region imposes that the concentration of X on the polymer side of the particle/solution interface is related to the concentration of X at the solution side of that interface according to an equilibrium partitioning relationship (isotherm) of the form (Fig. 1C):
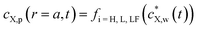 | (1) |
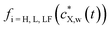 denotes the expression of Henry (i = H), Langmuir (i = L) or Langmuir–Freundlich (i = LF) surface adsorption isotherm. The nature of the isotherm obviously depends on the X contaminant-plastic particle system considered. Developed formulations of
denotes the expression of Henry (i = H), Langmuir (i = L) or Langmuir–Freundlich (i = LF) surface adsorption isotherm. The nature of the isotherm obviously depends on the X contaminant-plastic particle system considered. Developed formulations of 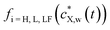 are written according to
are written according to | (2a) |
 | (2b) |
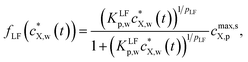 | (2c) |
The intraparticulate time-dependent concentration profile of X, cX,p(0 < r ≤ a,t) is defined by the transient Fick diffusion equation:
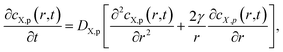 | (3) |
| cX,p(0 ≤ r ≤ a,t = 0) = 0 | (4) |
 | (5) |
This is derived from the symmetry of the concentration profile at the particle center r = 0, and the remaining boundary is provided by the surface isotherm condition given by eqn (1) and (2).
The mass balance condition of X in the Kuwabara cell of radius rc is further written as follows:
 | (6) |
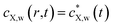 , we obtain the following equation after rearrangements:
, we obtain the following equation after rearrangements: | (7) |
The set of eqn (1)–(5) and (7) defines the time-dependent distribution of X in the particle body, cX,p(r,t), in the aqueous medium,  , and at the particle surface, cX,p(r = a, t), from the initial stage of the accumulation process to the equilibrium regime achieved at t → ∞ by the partitioning of X between the intraparticulate polymer phase and aqueous medium. At any t, the overall concentration of X within the particles, denoted as CX,p(t), results from the following spatial integral of cX,p(r,t):
, and at the particle surface, cX,p(r = a, t), from the initial stage of the accumulation process to the equilibrium regime achieved at t → ∞ by the partitioning of X between the intraparticulate polymer phase and aqueous medium. At any t, the overall concentration of X within the particles, denoted as CX,p(t), results from the following spatial integral of cX,p(r,t):
 | (8) |
The dependence of CX,p on time t featured by eqn (8) describes the X sorption kinetics on the plastic particles. For the sake of notational simplicity, we introduce the equilibrium concentrations 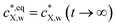 , and CeqX,p = CX,p(t → ∞). It is straightforward to verify that the X sorption isotherm must comply with the formulations:
, and CeqX,p = CX,p(t → ∞). It is straightforward to verify that the X sorption isotherm must comply with the formulations:
 | (9a,b) |
We verified that the decrease in  with time obtained from the numerical solution to eqn (1)–(5) and (7) could be properly fitted using the empirical relationship:
with time obtained from the numerical solution to eqn (1)–(5) and (7) could be properly fitted using the empirical relationship:
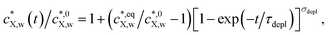 | (10) |
 | (11) |
2.2 Numerical analysis
Eqn (1)–(5) and (7) were written in terms of the reduced space and time variables![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = r/a (0 ≤
= r/a (0 ≤ ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ≤ 1) and
≤ 1) and ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = t/(βτ) (0 ≤
= t/(βτ) (0 ≤ ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ≤ 1), respectively, where τ = a2/DX,p (s) is the intraparticulate diffusion timescale and β is a factor chosen for t to cover a range of desired values. Eqn (1)–(5) and (7) were made fully dimensionless with the further introduction of the scaled concentrations
≤ 1), respectively, where τ = a2/DX,p (s) is the intraparticulate diffusion timescale and β is a factor chosen for t to cover a range of desired values. Eqn (1)–(5) and (7) were made fully dimensionless with the further introduction of the scaled concentrations  and
and ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) X,p(
X,p(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ,
,![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) = cX,p(
) = cX,p(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ,
,![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) )/cnorm;i=H,L,LFX,p, where cnorm;i=H,L,LFX,p is defined by
)/cnorm;i=H,L,LFX,p, where cnorm;i=H,L,LFX,p is defined by 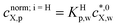 and cnorm;i=L,LFX,p = cmax,sX,p. The dimensionless forms of eqn (1)–(5) and (7) are specified by eqn (S1)–(S5) in ESI.† Knowing the particle volume fraction φ, the particle radius a and the value of γ (0 or 1), the above nondimensionalisation procedure demonstrates that X partitioning is fully determined upon specification of the model equilibrium parameters Ki=H,L,LFp,w, 1/pLF (relevant for i = LF) and cmax,sX,p (relevant for i = L, LF), and the diffusion timescale τ = a2/DX,p. Reduced eqn (S1)–(S5)† were subsequently discretized in the time domain according to the implicit Euler method31 and written as a function of the discretized concentrations denoted by
and cnorm;i=L,LFX,p = cmax,sX,p. The dimensionless forms of eqn (1)–(5) and (7) are specified by eqn (S1)–(S5) in ESI.† Knowing the particle volume fraction φ, the particle radius a and the value of γ (0 or 1), the above nondimensionalisation procedure demonstrates that X partitioning is fully determined upon specification of the model equilibrium parameters Ki=H,L,LFp,w, 1/pLF (relevant for i = LF) and cmax,sX,p (relevant for i = L, LF), and the diffusion timescale τ = a2/DX,p. Reduced eqn (S1)–(S5)† were subsequently discretized in the time domain according to the implicit Euler method31 and written as a function of the discretized concentrations denoted by ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) X,p(
X,p(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ,
,![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) =
= ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) k) =
k) = ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) (k)X,p(
(k)X,p(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) and
) and  (both dimensionless), where the integer k runs from 1 to N ≫ 1, and
(both dimensionless), where the integer k runs from 1 to N ≫ 1, and ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) k = (k − 1)Δ
k = (k − 1)Δ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) is the discretized time with Δ
is the discretized time with Δ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = 1/(N − 1) as the timestep adopted in the discretization scheme (eqn (S6)–(S10)†). The method leads in turn to the formulation of a set of N − 1 space-dependent recursive differential equations of the second order defining the concentration profiles
= 1/(N − 1) as the timestep adopted in the discretization scheme (eqn (S6)–(S10)†). The method leads in turn to the formulation of a set of N − 1 space-dependent recursive differential equations of the second order defining the concentration profiles ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) (k=2,…,N)X,p(
(k=2,…,N)X,p(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) (eqn (S7)†), with 2(N − 1) boundaries derived from eqn (1) and (5) applicable at
) (eqn (S7)†), with 2(N − 1) boundaries derived from eqn (1) and (5) applicable at ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = 1 and
= 1 and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = 0, respectively (eqn (S6) and (S9) in ESI†). Starting with the initial condition
= 0, respectively (eqn (S6) and (S9) in ESI†). Starting with the initial condition ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) (k=1)X,p(0 ≤
(k=1)X,p(0 ≤ ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ≤ 1) = 0 and
≤ 1) = 0 and ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) (k=1)X,w = 1 (eqn (S8) and (S11) in ESI†), and using the discretized form of the dimensionless mass balance condition formulated by eqn (7) (eqn (S10) in ESI†), the set of recursive differential equations was solved iteratively for k = 2, …, N using COLSYS collocation algorithm,32,33 which already proves its high efficiency in various complex modeling settings.34–36 The procedure calls for the solution {
(k=1)X,w = 1 (eqn (S8) and (S11) in ESI†), and using the discretized form of the dimensionless mass balance condition formulated by eqn (7) (eqn (S10) in ESI†), the set of recursive differential equations was solved iteratively for k = 2, …, N using COLSYS collocation algorithm,32,33 which already proves its high efficiency in various complex modeling settings.34–36 The procedure calls for the solution {![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) (k−1)X,p(
(k−1)X,p(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ),
),![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) (k−1)X,w} obtained at step k − 1 to find the concentration and bulk depletion profiles {
(k−1)X,w} obtained at step k − 1 to find the concentration and bulk depletion profiles {![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) (k)X,p(
(k)X,p(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ),
),![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) (k)X,w} at step k (see details in ESI†). After the completion of the iteration and knowledge of the intraparticulate concentration profiles at any time tk=1,…,N, the kinetics of X sorption, CX,p(t = tk=1,…,N), was evaluated by eqn (8) with the spatial integral estimated by applying the rectangle method. The convergence of the numerical results was achieved within a satisfactory delay (tens of seconds to mins) for N ≥ 1500. The robustness and validity of the adopted algorithm were further addressed by verifying that the outcomes were independent of the values adopted for N and β, and we systematically checked the expected equivalency between eqn (9a) and (9b). The full numerics was implemented in a FORTRAN program called PLASTX, which could generate all relevant outputs of the problem (including CX,p(t), CeqX,p, cX,p(r,t) and
(k)X,w} at step k (see details in ESI†). After the completion of the iteration and knowledge of the intraparticulate concentration profiles at any time tk=1,…,N, the kinetics of X sorption, CX,p(t = tk=1,…,N), was evaluated by eqn (8) with the spatial integral estimated by applying the rectangle method. The convergence of the numerical results was achieved within a satisfactory delay (tens of seconds to mins) for N ≥ 1500. The robustness and validity of the adopted algorithm were further addressed by verifying that the outcomes were independent of the values adopted for N and β, and we systematically checked the expected equivalency between eqn (9a) and (9b). The full numerics was implemented in a FORTRAN program called PLASTX, which could generate all relevant outputs of the problem (including CX,p(t), CeqX,p, cX,p(r,t) and  ) from a proper specification of the required model inputs (including τ and isotherm model descriptors).
) from a proper specification of the required model inputs (including τ and isotherm model descriptors).
2.3 Fitting of X isotherm and X sorption kinetic data
The flowchart describing the steps involved in fitting the X sorption isotherm and X intraparticulate accumulation data is shown in Fig. S1 in ESI.† The isotherm and sorption kinetic data were first selected from the literature according to the criteria detailed in the next section (step 1). The nature of the relevant isotherm (i.e. i = H, L or LF) and the corresponding parameter descriptors Ki=H,L,LFp,w, 1/pLF and/or cmax,sX,p were then evaluated by fitting the isotherm data to eqn (1) and (2) according to the Levenberg–Marquardt procedure and minimization of residues (step 2). In step 3, knowing the best isotherm type and its related theoretical descriptors (evaluated in step 2), the sorption kinetic data were fitted upon adjustment of the diffusion time scale τ using PLASTX code coupled with the freely available software PEST,37 an open source program for model parameter estimation and uncertainty analysis. We summarize in Fig. S1† the various phases of the iterative dialog between PLASTX and PEST as well as the in- and out-information fluxes exchanged between these two programs until sorption data fitting is achieved within the prescribed convergence criterion. The coupled PLASTX-PEST-based method is directly inspired by our previous work on the modeling and fitting of proton adsorption isotherms on particulate organic matter, where PEST was adopted in combination with the involved numerical evaluation of particle electrostatics.35,38 The reader is referred to ref. 35 and 38 for details on PEST implementation. Finally, we emphasize that the fitting by the coupled PLASTX-PEST codes of some of the selected X sorption kinetic data required for the adjustment of τ and of the interfacial X partition coefficient Ki=H,L,LFp,w to a value that differed from the one derived in step 1. The flexibility of PLASTX-PEST easily allows the specification of the parameters to be adjusted to reach data fitting and those fixed by the user at prescribed values (Fig. S1†).2.4 Data selection
We selected sufficiently documented literature data for which both equilibrium isotherm and sorption kinetics were reported for pristine plastic particles of spherical or approximately spherical geometry.11–13,16,39–67 The data (109 individual kinetic curves in total) correspond to the sorption of a wide variety of metal ions and organic compounds by a broad range of polymer types. The considered contaminants, (i), and polymers, (ii), include (but are not restricted to) (i) Cd(II), Cu(II), Pb(II), tetracycline, sulfamethoxazole, ciprofloxacin, atrazine, carbamazepine, triclosan, triadimefon, fluoranthene, phenanthrene, naphthalene, fluorene, etc., and (ii) polystyrene, polyvinyl chloride, polyurethane, polypropylene, polyethylene, etc. In all cases, the plastic particles were the only complexants present in the aqueous media, i.e. considering chemical speciation dynamics in the dissolved aqueous phase is immaterial for present purposes. The reader is referred to Table S1† for exhaustive lists. The results encompass cases in which the equilibrium sorption data were best described by linear (Henry), Langmuir, and Langmuir–Freundlich isotherms (see Table S1†). We excluded studies in which the particle size was not reported or only poorly documented,18,68 those which reported only kinetic data (i.e. no corresponding equilibrium isotherms),69,70 cases where very few time points were recorded in the kinetic regime,71,72 and those which exhibited gross inconsistencies between the kinetic and equilibrium data.73–75In cases where the particle size was reported as a range of radii, computations were performed for the smallest and largest values, and both results are presented in Table S1.† A density of unity was assumed for all polymers for computing particle volume fractions, φ, and for converting reported sorbed concentrations (typically given in mass units) to units of mol m−3. The uncertainty on the fitted parameters (Table S1†) was estimated by the 95% confidence intervals computed by PEST.37 The confidence limits by PEST provide only an indication of parameter uncertainty, as they rely on a linearity assumption that may not extend as far in the parameter space as the confidence limits themselves.37 The normalized root-mean-square error (NRMSE: the lower the better), derived from the sum of squared weighted residuals,24 is used as a measure of the goodness-of-fit of the model to the kinetic curves.
3. Results and discussion
3.1 Model description of experimental sorption curves
The details of the systems considered herein and the results of the data fitting, including the NRMSE values and parameter confidence intervals by PEST, are presented in Table S1.† In many cases (57 out of 109), for all types of isotherm considered, the model provided a very good fit to the kinetic data by optimizing a single parameter, namely the characteristic diffusion time, τ = a2/DX,p, from which the diffusion coefficient DX,p was derived (see Theory). In the remaining cases, allowing the thermodynamic partitioning constant KHp,w, KLp,w or KLFp,w (depending on the system) to be adjusted (together with τ) in the kinetic fitting improved the fit to the data. All the cases (with only 1 exception; see Table S1†) were fitted with γ = 1 (spherical diffusion). Because intraparticulate diffusion is the limiting step in the accumulation of X (DX,p ≪ DX,w), the almost exclusive applicability of spherical diffusion is in line with the size and shape of the particles considered herein, implying that the entire volume of the particle body is accessible to X (see brief discussion in Theory on this issue). The model considers the extent to which the target compound X is depleted in the bulk aqueous medium throughout the sorption process. Good fits to the experimental data were obtained even in cases where significant bulk depletion occurred. We highlight that in contrast to a previous study on planar polymer discs, which accounted for depletion only in the case of a linear sorption isotherm,20 our approach is applicable to any type of sorption isotherm. The power and genericity of our approach are illustrated by examples for each type of isotherm considered, for cases where there is negligible or considerable depletion of X in the bulk solution, and for systems in which satisfactory fit to the kinetic data was attained by varying only τ or by concomitant variation of both τ and Ki=H,L,LFp,w. In the case of systems described by the Langmuir isotherm (i = L), and τ the sole parameter varied in the kinetic fitting, results for the situation where bulk depletion of X is negligible (3%) are illustrated in Fig. 2, and those for considerable bulk depletion of X (87%) are shown in Fig. 3. In detail, the experimental sorption isotherms and the accumulation kinetic curves are shown together with their corresponding fits in Fig. 2A–3A and Fig. 2B–3B, respectively, while computed bulk depletion and intraparticulate concentration profiles are reported as functions of time in Fig. 2C–3C and Fig. 2D–3D, respectively.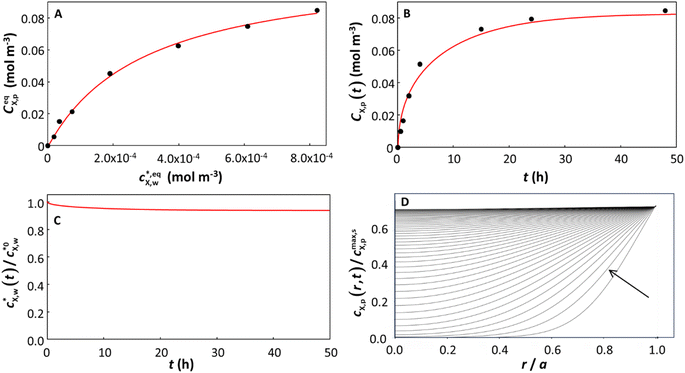 | ||
Fig. 2 Equilibrium and kinetic features of a system with low depletion of X in the bulk solution: sorption of benzophenone on polyethylene particles (a = 2.75 × 10−4 m). The panels correspond to (A) the equilibrium sorption isotherm; (B) kinetic sorption curves; (C) solution depletion profile; and (D) temporal evolution of the normalized intraparticulate concentration profiles, with the direction of increasing time indicated by the arrow. In (D), the timescale between the two plotted concentration profiles is Δt = 3588 s, starting at t = 3588 s. The condition at t = 0 (not shown) corresponds to plastic particles free of contaminants and to the initial bulk medium condition 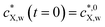 . The Langmuir isotherm best described the equilibrium data, and τ was the only parameter optimized to fit the sorption curves (see Table S1† for the pertaining parameters). The isotherm curve (A) shows the experimental data (black circles)12 and the best fit obtained according to the Langmuir sorption isotherm (eqn (1)–(2b), red curve, adjusted parameters: KLp,w and cmax,sX,p); the kinetic sorption curve (B) shows the experimental data (black circles)12 and the numerically computed values, eqn (1)–(2b), (3)–(5), (7) and (8) (red curve); and the depletion profile (C) shows the values obtained from numerical computation, eqn (1)–(2b), (3)–(5) and (7) (red curve). The maximal extent of bulk depletion is 6.3% in the kinetic sorption data, and from the fitted τ of 108.5 h, the derived diffusion coefficient is DX,p = 1.94 × 10−13 m2 s−1. . The Langmuir isotherm best described the equilibrium data, and τ was the only parameter optimized to fit the sorption curves (see Table S1† for the pertaining parameters). The isotherm curve (A) shows the experimental data (black circles)12 and the best fit obtained according to the Langmuir sorption isotherm (eqn (1)–(2b), red curve, adjusted parameters: KLp,w and cmax,sX,p); the kinetic sorption curve (B) shows the experimental data (black circles)12 and the numerically computed values, eqn (1)–(2b), (3)–(5), (7) and (8) (red curve); and the depletion profile (C) shows the values obtained from numerical computation, eqn (1)–(2b), (3)–(5) and (7) (red curve). The maximal extent of bulk depletion is 6.3% in the kinetic sorption data, and from the fitted τ of 108.5 h, the derived diffusion coefficient is DX,p = 1.94 × 10−13 m2 s−1. | ||
 | ||
Fig. 3 Equilibrium and kinetic features of a system with considerable depletion of X in the bulk solution: sorption of naphthalene on polyethylene terephthalate particles (a = 1.5 × 10−3 m). The panels correspond to (A) equilibrium sorption isotherm; (B) kinetic sorption curves; (C) solution depletion profile; and (D) temporal evolution of the normalized intraparticulate concentration profiles, with the direction of increasing time indicated by the arrow. In (D), the timescale between two plotted concentration profiles is Δt = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 021 s, starting at t = 16 021 s, starting at t = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 021 s. The condition at t = 0 (not shown) corresponds to plastic particles free of contaminants and to the initial bulk medium condition 021 s. The condition at t = 0 (not shown) corresponds to plastic particles free of contaminants and to the initial bulk medium condition 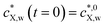 . The Langmuir isotherm best described the equilibrium data, and τ was the only parameter optimized to fit the sorption curves (see Table S1† for the pertaining parameters). The isotherm curve (A) shows the experimental data (black circles)59 and the best fit obtained according to the Langmuir sorption isotherm (eqn (1)–(2b), red curve, adjusted parameters: KLp,w and cmax,sX,p); the kinetic sorption curve (B) shows the experimental data (black circles)59 and numerically computed values, eqn (1)–(2b), (3)–(5), (7) and (8) (red curve); and the depletion profile (C) shows the values obtained from numerical computation, eqn (1)–(2b), (3)–(5), (7) (red curve). The maximal extent of bulk depletion is 87% in the kinetic sorption data, and from the fitted τ of 2225.2 h, the derived diffusion coefficient is DX,p = 2.81 × 10−13 m2 s−1. . The Langmuir isotherm best described the equilibrium data, and τ was the only parameter optimized to fit the sorption curves (see Table S1† for the pertaining parameters). The isotherm curve (A) shows the experimental data (black circles)59 and the best fit obtained according to the Langmuir sorption isotherm (eqn (1)–(2b), red curve, adjusted parameters: KLp,w and cmax,sX,p); the kinetic sorption curve (B) shows the experimental data (black circles)59 and numerically computed values, eqn (1)–(2b), (3)–(5), (7) and (8) (red curve); and the depletion profile (C) shows the values obtained from numerical computation, eqn (1)–(2b), (3)–(5), (7) (red curve). The maximal extent of bulk depletion is 87% in the kinetic sorption data, and from the fitted τ of 2225.2 h, the derived diffusion coefficient is DX,p = 2.81 × 10−13 m2 s−1. | ||
The cross-over of the intraparticulate concentration profiles shown in Fig. 3D is a consequence of depletion in the bulk medium and highlights the coupling between bulk depletion kinetics and accumulation by/diffusion within the plastic particle over time. Furthermore, in the depletive case, the presence of a gradient in the intraparticulate concentration profile at the longest experimental time (96 h; Fig. 3D) suggests that equilibrium was not attained, in line with the ongoing bulk depletion (Fig. 3C) and the ongoing increase in CX,p with time in the kinetic sorption curve (Fig. 3B).
The ESI† detailed for other contaminant/plastic particle systems has corresponding results for the linear (Henry) isotherm (non-depletive cases: KHp,w obtained from the fitting of sorption isotherm is fixed for the fitting of the kinetic sorption data, Fig. S2;†KHp,w is varied (together with τ) for the fitting of the kinetic sorption data, Fig. S3;† depletive cases: KHp,w fixed, Fig. S4;†KHp,w varied, Fig. S5†), the Langmuir isotherm (non-depletive: KLp,w varied, Fig. S6;† depletive: KLp,w varied, Fig. S7†), and the Langmuir–Freundlich isotherm (non-depletive: KLFp,w fixed, Fig. S8,† we found no examples for the case where KLFp,w is varied, nor any depletive cases for this isotherm). Also shown is the benzophenone-3/polystyrene particles system in which, for a given particle volume fraction, the extent of bulk depletion increases with decreasing particle size (Fig. S9†).12 In each case, the equilibrium sorption isotherm, kinetic sorption curve, temporal bulk solution depletion profile, and temporal evolution of the intraparticulate concentration profiles are shown.
3.2 Derived intraparticulate diffusion coefficients
To practically analyze all the data sets herein, the magnitude of the computed diffusion timescale, τ, lies in the range of 15–500 h without a clear well-defined connection to the particle radius (Fig. S10†). An illustrative example of the sorption of benzophenone-3 on a series of different-sized polystyrene particles is shown in Fig. 4. Timescales in the range of tens to hundreds of hours confirm our previous finding,24 that is intraparticulate diffusion is the process that controls the overall rate of the sorption process. If diffusion in the extraparticulate medium towards the particle surface would be the rate limiting step in surface adsorption, then the process would occur on much faster timescales, and would result in faster kinetics being observed as the particle radius decreases (it is recalled that DX,p ≪ DX,w).24 Instead, although the timescale of sorption is practically independent of particle radius (Fig. 4), the thermodynamic equilibrium parameters for a given polymer and target compound are size dependent, that is, cmax,sX,p is typically greater for smaller particle radii,12,58,76 which likely reflects the greater contribution of surface sorption relative to intraparticulate accumulation as particle size decreases.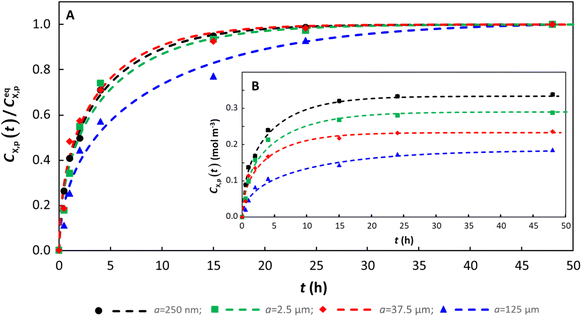 | ||
| Fig. 4 Temporal sorption of benzophenone by polystyrene particles with a range of radii, a, showing (A) normalized, CX,p(t)/CeqX,p, and (B) original data. Experimental data12 are shown as points, and the numerically computed fits to the data are shown as dashed curves (see Table S1† for parameters used in the computations). The surface area/volume ratio is a factor of 5 greater for a = 250 nm cf. a = 125 µm, and the corresponding cmax,sX,p is a factor of 1.8 greater. | ||
The experimental volume fraction, φ, used in the data sets we successfully analyzed was generally less than 5 × 10−3 (Table S1†). In cases where very high particle volume fractions were used in the measurements, there is a likelihood that plastic particle aggregates will be present, whose temporal accumulation of X will necessarily differ from that of the individual dispersed particles, i.e. the nature of the diffusion process in aggregates changes because the effective size of the object has changed. This issue can be explored by performing computations with artificially lower volume fractions. We found no suitably documented examples to robustly illustrate this point. In one case,77 the kinetic data (obtained at an experimental φ= 0.02) were better described by an artificially lower volume fraction (φ = 0.006), but the corresponding equilibrium isotherm data were obviously erroneous. Furthermore, we qualitatively expect that part of the volume fraction within particle aggregates will be inaccessible to the contaminant, resulting in an increased tendency for linear diffusion to become operational. This aspect can be investigated by comparing the fits to the data obtained for γ = 1 (spherical diffusion) versus γ = 0 (linear diffusion) (see the Theory section). Analysis of data78 obtained at an experimental φ of 0.01 provides a convincing illustration of this effect. The kinetic data are best described by linear diffusion being operational (γ = 0), Fig. S11.†
We highlight that the particle radius is not used in the fitting process. Characterization of the particle size distribution and evaluation of the colloidal stability properties of the plastic particles against aggregation are fundamental determinants of the interplay between, and the proper interpretation of, the thermodynamic and kinetic features of contaminant sorption.
The derived DX,p is found to be largely independent of the molar mass of the contaminant X in the range ca. 100 to 400 g mol−1 (Fig. S12†). All the data sets analyzed herein correspond to measurements in aqueous dispersions. There are disparate literature reports on the dependence of DX,p on molar mass depending on the crystallinity of the polymer and its degree of hydration.20–23 In the case of a polystyrene disc in aqueous media, DX,p was found to be similar (ca. 3 × 10−16 m2 s−1) for 22 compounds with molar mass in the range 180–400 g mol−1.20 Additionally, we found no trend between DX,p and the linearized (dimensionless) partition coefficient, i.e. log KHp,w or log(KLp,wcmax,sX,p) (Fig. S13†) even when a subset of the data for similar contaminants is considered (Fig. S14A† (oxy)tetracycline and Fig. S14B† metal ions). This observation supports the rationale given in the theory section regarding the insignificance of the magnitude of the equilibrium partition coefficients for the diffusional properties of the contaminants. Thus, for the data considered herein, the length scale over which the interactions between the contaminants and the polymer backbone are operative is much smaller than the particle size. We also found no trend between DX,p and cmax,sX,p (relevant for cases where Langmuir and Langmuir–Freundlich isotherms are operational, Fig. S15A (log-linear) and Fig. S15B (log–log)†).
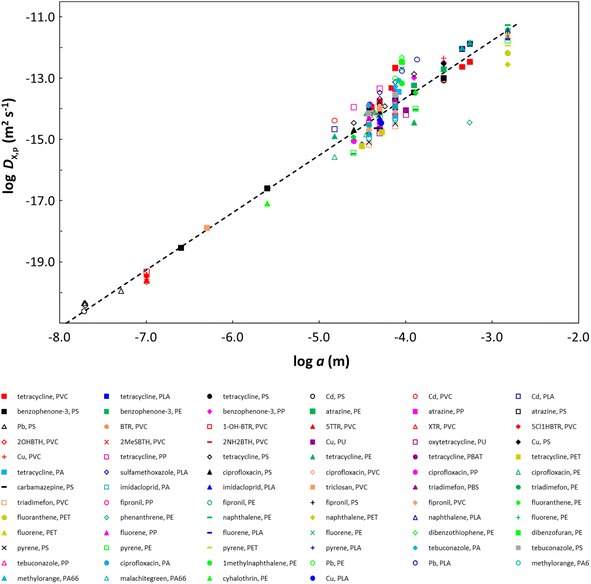
Overall, the sorption kinetics of X on plastic particles is fully determined by the diffusion timescale τ (=a2/DX,p). Thus, for a purely diffusive process, occurring without a change in the structure of the phase in which diffusion occurs, the relationship log(DX,p) = −log(τ) + 2 × log(a) is expected to hold. We can extend this reasoning to different systems defined by different particle sizes and different diffusing molecules. That is, if the structure of the phase in which diffusion takes place, and the diffusion of the target molecules therein do not differ substantially from one system to another, it means that the relationship log(DX,p) = −log(τ) + 2 × log(a) holds across systems. Because τ is rather independent of the particle radius (Fig. 4 and S10†), the consequence is that we observe a remarkable dependence of DX,p on the particle radius a (Fig. 5), i.e.DX,p increases with increasing a. The linear regression line through the log DX,pversus log a plot for all of the data (black dashed line in Fig. 5) has a slope of 1.87 and an intercept that corresponds to τ = 1.343 × 106 s, i.e. 373 h, representing the average τ value for all the data analyzed (Fig. S10†). Further support for our interpretation is provided by plotting the normalized kinetic curves for all data, i.e.CX,p(t)/CeqX,pversus [(DX,pt)1/2]/a. The results are shown in Fig. 6 for cases where the bulk depletion of the contaminant is less than 50% (to minimize non-linearity effects), which represent 75% of the analyzed data sets. The convergence of the normalized kinetic sorption curves to a common master curve (Fig. 6) underscores the lack of dependence on the kinetic timescale (τ) on the particle size a, thereby evidencing the dependence of DX,p on a.
When data are compared at the same particle radius (or film thickness), the intraparticulate diffusion coefficients reported by others for polymer spheres and films20,79–85 (determined by various means),80,86–88 and those derived via our previous explicit separation and coupling of the transient and steady-state processes,24 are of a comparable order of magnitude as those determined herein (Fig. S16†). Any differences reflect the assumptions made in the derivation of the DX,p values with regard to the pertaining spatial scale and the way in which the transient and steady-state processes are treated. We highlight that the numerical approach presented herein is the most rigorous and fundamental physicochemical model of the processes involved.
These remarkable results suggest that the diverse plastic particles considered in the analysis share similar structural properties. More explicitly, because diffusion occurs almost exclusively within the amorphous polymer zones,89,90 our findings imply that the size and distribution of the crystalline phase as well as the relative proportions of the crystalline and amorphous zones are similar across polymer types over the pertaining particle size range. The decrease in DX,p with decreasing particle radius implies a concomitant increase in polymer crystallinity, which is in line with literature reports; for example, polypropylene nanospheres exhibit 76% crystallinity, while microspheres exhibit 59% crystallinity.91 The greater scatter in the data for particle radii greater than 10 µm (Fig. 5) is in part a consequence of the greater amount of data available in this size range but may also reflect differences in the relative amounts and distribution of the crystalline and amorphous phases in larger particle bodies and across polymer types.
In support of our findings, there is a body of literature showing that for polymer thin films, DX,p decreases with decreasing film thickness,80,92–100 and for spherical particles, there is a report of DX,p decreasing with decreasing particle radius.80 In the case of thin plastic films, the decrease in DX,p with decreasing film thickness has been ascribed variously to an increasing density of the polymer chains in progressively thinner films,101 or the film thickness dependence of the distribution, orientation and size of the crystalline zones in the polymer matrix,96,98 or a reduction in the accessibility of the polymer free volume with decreasing film thickness.102 It is noteworthy that for the penetration of solvents into a dry polymer, a plot of log(DX,p) as a function of log(polymer film thickness) has a slope of approximately 2.97 In the case of spherical geometry, scrutiny of particles synthesized with a given size versus those generated by crushing of larger items might give insight into the potential relevance of factors, such as size-dependent polymer crystallinity. However, we could not find sufficient data to draw conclusions: the majority of the data we analyzed correspond to particles that were synthesized with a given size; the few cases where particles were generated by crushing of larger objects fall in a narrow size range (37 µm to 125 µm),40,43,57,62,63 and the derived DX,p values lie in the same range as those derived from non-crushed particles (Fig. 5).
The remarkable universal law that we have established enables the prediction of the sorption and release kinetics and intraparticulate diffusion of any compound in any type of polymeric particle as a function of particle size. It follows that, for the typical case of distributed particle sizes, the corresponding diffusion coefficient distribution and characteristic diffusion timescale distribution can be computed. With regard to contaminant release kinetics, our previous work,103,104 which assumed that DX,p is invariant with particle size, predicted that contaminants are released faster as the size of the plastic particles decreases, in line with the trends reported in the literature.105,106 The striking particle size dependence of DX,p identified herein provides a moderated view of the particle size dependence of contaminant release rates. Using the particle size dependence of DX,p (Fig. 5), the release rate of X from a spherical particle (eqn (11)) is indeed predicted to increase with decreasing particle size albeit less drastically than would be the case if DX,p is independent of particle size (Fig. 7).
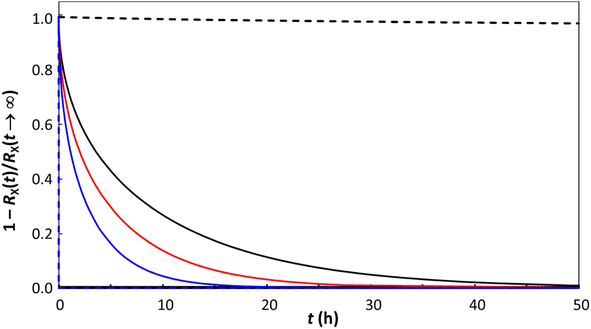 | ||
| Fig. 7 Time evolution of the release, RX, of compound X from spherical plastic particles. The curves were computed using eqn (11). Solid curves show the results for the herein identified particle size dependence of DX,p (obtained from the line of best fit through the data shown in Fig. 5) corresponding to (i) a = 10−4 m, DX,p= 2.36 × 10−14 m2 s−1, black solid curve; (ii) a = 10−6 m, DX,p= 4.19 × 10−18 m2 s−1, red solid curve; and (iii) a = 10−8 m, DX,p= 7.46 × 10−22 m2 s−1, blue solid curve. Dashed curves show the results for DX,p fixed at 4.19 × 10−18 m2 s−1 for a = 10−4 m (black dashed curve) and a = 10−8 m (blue dashed curve). | ||
4. Conclusions
The theory presented herein and applied to the analysis of contaminant sorption kinetics by plastic particles offers a flexible and comprehensive approach that goes well beyond the traditional empirical pseudo first or second order kinetic equations. We tentatively propose that the observed decrease in the intraparticulate diffusion coefficient with decreasing particle size is related to relative increases in the proportions of the crystalline zones (as well as their size and distribution) compared to the amorphous zones in smaller particles. Although, owing to the availability of sufficient experimental data, we have considered (approximately) spherical particles, we highlight that the theory is generically applicable to any type of particle (fibre, film, etc.), with proper accounting for the geometry involved in the flux expressions. Our approach provides dynamic level considerations relevant to environmental risk assessment, e.g. predicting the chemical speciation and bioavailability of contaminants associated with plastic particles, and human health, e.g. optimization of polymeric drug delivery systems and assessment of the migration of compounds in/out of plastic medical devices and food contact materials. Future work will use various strategies107,108 to extend the theory and numerical interpretative scheme to describe additional environmentally relevant scenarios, including (i) the impacts of contaminant speciation, i.e. chemical kinetic terms with the associated possibility for diffusional transport limitation in the extraparticulate phase (which may be of particular importance in soil and sediment matrices); (ii) the impact of (fully relaxed) force field interactions, while still including the fundamental transient features of the diffusional transport; (iii) time-dependent diffusional processes due to, for example, the build-up of a restricting layer of the accumulated contaminant itself,109 or aggregation concomitant with sorption; and (iv) modification of the pristine polymer interfacial zone due to e.g. the presence of biofilms.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
RMT performed this work in the framework of projects funded by the Flanders Fonds Wetenschappelijk Onderzoek, FWO (G053320N “Towards ecological risk assessment of nanoplastics: dynamic considerations” and G060920N “Novel approaches for the estimation of the use of psychoactive pharmaceuticals and illicit drugs by wastewater analysis”), and the Universiteit Antwerpen Bijzonder Onderzoeksfonds (SEP-BOF 2020 “From exposure to effects of pollutants: a dynamic mechanistic basis”).References
- V. Adam, T. Yang and B. Nowack, Toward an ecotoxicological risk assessment of microplastics: comparison of available hazard and exposure data in freshwaters, Environ. Toxicol. Chem., 2019, 38, 436–447 CrossRef CAS PubMed.
- S.-H. Nam, S. A. Kim, T.-Y. Lee and Y.-J. An, Understanding hazardous concentrations of microplastics in fresh water using non-traditional toxicity data, J. Hazard. Mater., 2023, 445, 130532 CrossRef CAS PubMed.
- H. Ranjan, S. S. Kumar, S. Priscilla, S. Swaminathan, M. Umezawa and S. S. Mohideen, Polyethylene microplastics affect behavioural, oxidative stress, and molecular responses in the Drosophila model, Environ. Sci.:Processes Impacts, 2024, 26, 2203–2214 RSC.
- P. A. Athulya, N. Chandrasekaran and J. Thomas, Polystyrene microplastics interaction and influence on the growth kinetics and metabolism of tilapia gut probiotic Bacillus tropicus ACS1, Environ. Sci.: Processes Impacts, 2024, 26, 221–232 RSC.
- T. Schell, A. Rico, L. Cherta, L. Nozal, R. Dafouz, R. Giacchini and M. Vighi, Influence of microplastics on the bioconcentration of organic contaminants in fish: is the “Trojan horse” effect a matter of concern?, Environ. Pollut., 2022, 306, 119473 CrossRef CAS PubMed.
- R. Trevisan, C. Voy, S. Chen and R. T. Di Giulio, Nanoplastics decrease the toxicity of a complex PAH mixture but impair mitochondrial energy production in developing zebrafish, Environ. Sci. Technol., 2019, 53, 8405–8415 CrossRef CAS PubMed.
- Y. Kong, Q. Zhou, R. Wang, Q. Chen, X. Xu, L. Zhu and Y. Wang, Alleviating effects of microplastics together with tetracycline hydrochloride on the physiological stress of Closterium sp, Environ. Sci.: Processes Impacts, 2024, 26, 1588–1600 RSC.
- J. Bhagat, L. Zang, H. Nakayama, N. Nishimura and Y. Shimada, Effects of nanoplastic on toxicity of azole fungicides (ketoconazole and fluconazole) in zebrafish embryos, Sci. Total Environ., 2021, 800, 149463 CrossRef CAS PubMed.
- M. Fu, J. Tan, S. Zhou, S. Ling, S. Hu, Z. Qiao, Y. Han, W. Zhang and C. Peng, Insight into bioaccumulation of decabromodiphenyl ethane in Eisenia fetida increased by microplastics, Environ. Sci. Technol., 2023, 57, 13980–13990 CrossRef CAS PubMed.
- C. Siri, Y. Liu, T. Masset, W. Dudefoi, D. Oldham, M. Minghetti, D. Grandjean and F. Breider, Adsorption of progesterone onto microplastics and its desorption in simulated gastric and intestinal fluids, Environ. Sci.: Processes Impacts, 2021, 23, 1566–1577 RSC.
- L. Gao, D. Fu, J. Zhao, W. Wu, Z. Wang, Y. Su and L. Peng, Microplastics aged in various environmental media exhibited strong sorption to heavy metals in seawater, Mar. Pollut. Bull., 2021, 169, 112480 CrossRef CAS PubMed.
- R. Cui, M.-C. Jong, L. You, F. Mao, D. Yao, K. Y.-H. Gin and Y. He, Size-dependent adsorption of waterborne benzophenone-3 on microplastics and its desorption under simulated gastrointestinal conditions, Chemosphere, 2022, 286, 131735 CrossRef CAS PubMed.
- W. Huang, J. Zhang, Z. Zhang, H. Gao, W. Xu and X. Xia, Insights into adsorption behavior and mechanism of Cu(II) onto biodegradable and conventional microplastics: effect of aging process and environmental factors, Environ. Pollut., 2024, 342, 123061 CrossRef CAS PubMed.
- H. Frost, T. Bond, T. Sizmur and M. Felipe-Sotelo, Sorption of metal ions onto PET-derived microplastic fibres, Environ. Sci.: Processes Impacts, 2024, 26, 2309–2319 RSC.
- P. Wu, Z. Cai, H. Jin and Y. Tang, Adsorption mechanisms of five bisphenol analogues on PVC microplastics, Sci. Total Environ., 2019, 650, 671–678 CrossRef CAS PubMed.
- X. Liu, J. Zhang, W. Cao, Y. Hu and W. Shen, The influence of Pb(II) adsorption on (non) biodegradable microplastics by UV/O3 oxidation treatment, J. Environ. Chem. Eng., 2022, 10, 108615 CrossRef.
- C. Hu, Y. Xiao, Q. Jiang, M. Wang and T. Xue, Adsorption properties and mechanism of Cu(II) on virgin and aged microplastics in the aquatic environment, Environ. Sci. Pollut. Res., 2024, 31, 29434–29448 CrossRef CAS PubMed.
- J. Junck, P. N. Diagboya, A. Peqini, M. Rohnke and A. During, Mechanistic interpretation of the sorption of terbuthylazine pesticide onto aged microplastics, Environ. Pollut., 2024, 345, 123502 CrossRef CAS PubMed.
- X. Guo, J. Pang, S. Chen and H. Jia, Sorption properties of tylosin on four different microplastics, Chemosphere, 2018, 209, 240–245 CrossRef CAS PubMed.
- F. C. Fischer, O. A. Cirpka, K.-U. Goss, L. Henneberger and B. I. Escher, Application of experimental polystyrene partition constants and diffusion coefficients to predict the sorption of neutral organic chemicals to multiwell plates in in vivo and in vitro bioassays, Environ. Sci. Technol., 2018, 52, 13511–13522 CrossRef CAS PubMed.
- N. B. Hatzigrigoriou, C. D. Papaspyrides, C. Joly and P. Dole, Effect of migrant size on diffusion in dry and hydrated polyamide 6, J. Agric. Food Chem., 2010, 58, 8667–8673 CrossRef CAS PubMed.
- R. M. Elder and D. M. Saylor, Robust estimates of solute diffusivity in polymers for predicting patient exposure to medical device leachables, J. Polym. Sci., 2023, 61, 2163–2180 CrossRef CAS.
- P. Dole, A. E. Feigenbaum, C. De La Cruz, S. Pastorelli, P. Paseiro, T. Hankemeier, Y. Voulzatis, S. Aucejo, P. Saillard and C. Papaspyrides, Typical diffusion behaviour in packaging polymers – application to functional barriers, Food Addit. Contam., 2006, 23, 202–211 CrossRef CAS PubMed.
- R. M. Town, H. P. van Leeuwen and J. F. L. Duval, Effect of polymer aging on uptake/release kinetics of metal ions and organic molecules by micro- and nanoplastics: implications for the bioavailability of the associated compounds, Environ. Sci. Technol., 2023, 57, 16552–16563 CrossRef CAS PubMed.
- S. Bayen, T. L. Ter Laak, J. Buffle and J. L. M. Hermens, Dynamic exposure of organisms and passive samplers to hydrophobic chemicals, Environ. Sci. Technol., 2009, 43, 2206–2215 CrossRef CAS PubMed.
- J. F. L. Duval and S. Qian, Metal speciation dynamics in dispersions of soft colloidal ligand particles under steady-state laminar flow condition, J. Phys. Chem. A, 2009, 113, 12791–12804 CrossRef CAS PubMed.
- J. F. L. Duval, Dynamics of metal uptake by charged biointerphases: bioavailability and bulk depletion, Phys. Chem. Chem. Phys., 2013, 15, 7873–7888 RSC.
- J. F. L. Duval and E. Rotureau, Dynamics of metal uptake by charged soft biointerphases: impacts of depletion, internalization, adsorption and excretion, Phys. Chem. Chem. Phys., 2014, 16, 7401–7416 RSC.
- J. F. L. Duval and H. P. van Leeuwen, Rates of ionic reactions with charged nanoparticles iin aqueous media, J. Phys. Chem. A, 2012, 116, 6443–6451 CrossRef CAS PubMed.
- J. Crank, The Mathematics of Diffusion, Clarendon Press, Oxford, 1979 Search PubMed.
- W. F. Ames, Numerical Analysis of Partial Differential Equations, Academic Press, New York, 3rd edn, 1992 Search PubMed.
- U. Ascher, J. Christiansen and R. D. Russell, Codes for Boundary-Value Problems in Ordinary Differential Equations, 1979, vol. 76, pp. 164–185 Search PubMed.
- U. Ascher, J. Christiansen and R. D. Russell, Collocation software for boundary value ODEs, ACM Trans. Math. Softw., 1981, 7, 209–222 CrossRef.
- M. Moussa, C. Caillet, R. M. Town and J. F. L. Duval, Remarkable electrokinetic features of charge-stratified soft nanoparticles: mobility reversal in monovalent aqueous electrolyte, Langmuir, 2015, 31, 5656–5666 CrossRef CAS PubMed.
- J. P. Pinheiro, E. Rotureau and J. F. L. Duval, Addressing the electrostatic component of protons binding to aquatic nanoparticles beyond the non-ideal competitive adsorption (NICA)-Donnan level: theory and application to analysis of proton titration data for humic matter, J. Colloid Interface Sci., 2021, 583, 642–651 CrossRef CAS PubMed.
- N. Lesniewska, A. Beaussart and J. F. L. Duval, Electrostatic interactions between soft nanoparticles beyond the Derjaguin approximation: effects of finite size of ions and charges, dielectric decrement and ion correlations, J. Colloid Interface Sci., 2025, 678, 808–827 CrossRef CAS PubMed.
- PEST, Model Independent Parameter Estimation and Uncertainty Analysis, https://pesthomepage.org/, (accessed November 2024).
- M. Tesfa, J. F. L. Duval, R. Marsac, A. Dia and J. P. Pinheiro, Absolute and relative positioning of natural organic matter acid-base potentiometric titration curves: implications for the evaluation of the density of charged reactive sites, Environ. Sci. Technol., 2022, 56, 10494–10503 CrossRef CAS PubMed.
- J. Fei, J. Cui, B. Wang, H. Xie, C. Wang, Y. Zhao, H. Sun and X. Yin, Co-transport of degradable microplastics with Cd(II) in saturated porous media: synergistic effects of strong adsorption affinity and high mobility, Environ. Pollut., 2023, 330, 121804 CrossRef CAS PubMed.
- X.-D. Xue, C.-R. Fang and H.-F. Zhuang, Adsorption behaviors of the pristine and aged thermoplastic polyurethane microplastics in Cu(II)-OTC coexisting system, J. Hazard. Mater., 2021, 407, 124835 CrossRef CAS PubMed.
- A. Sun, L. Xu, G. Zhou, E. Yin, T. Chen, Y. Wang and X. Li, Roles of polystyrene micro/nano-plastics as carriers on the toxicity of Pb2+ to Chlamydomonas reinhardtii, Chemosphere, 2022, 309, 136676 CrossRef CAS PubMed.
- C. Guo, L. Wang, D. Lang, Q. Qian, W. Wang, R. Wu and J. Wang, UV and chemical aging alter the adsorption behavior of microplastics for tetracycline, Environ. Pollut., 2023, 318, 120859 CrossRef CAS PubMed.
- C. Chen, X. Pang, Q. Chen, M. Xu, Y. Xiao, J. Wu, Y. Zhang, Y. Liu, L. Long and G. Yang, Tetracycline adsorption trajectories on aged polystyrene in a simulated aquatic environment: a mechanistic investigation, Sci. Total Environ., 2022, 851, 158204 CrossRef CAS PubMed.
- H. Wang, C. Qiu, Y. Song, S. Bian, Q. Wang, Y. Chen and C. Fang, Adsorption of tetracycline and Cd(II) on polystyrene and polyethylene terephthalate microplastics with ultraviolet and hydrogen peroxide aging treatment, Sci. Total Environ., 2022, 845, 157109 CrossRef CAS PubMed.
- F. Yu, C. Yang, G. Huang, T. Zhou, Y. Zhao and J. Ma, Interfacial interaction between diverse microplastics and tetracycline by adsorption in aqueous solution, Sci. Total Environ., 2020, 721, 137729 CrossRef CAS PubMed.
- F. Tong, D. Liu, Z. Zhang, W. Chen, G. Fan, Y. Gao, X. Gu and C. Gu, Heavy metal-mediated adsorption of antibiotic tetracycline and ciprofloxacin on two microplastics: insights into the role of complexation, Environ. Res., 2023, 216, 114716 CrossRef CAS PubMed.
- Y. Tian, J. Zhu, C. Ying, H. Luo, S. Zhang, L. Zhang, R. Li and J. Li, Photoaging process of polyvinyl chloride microplastics enhance the adsorption of tetracycline and facilitate the formation of antibiotic resistance, Chemosphere, 2023, 320, 137820 CrossRef CAS PubMed.
- K. Wang, T. Han, X. Chen, L. E. Rushimisha, Y. Liu, S. Yang, X. Miao, X. Li, L. Weng and Y. Li, Insights into behavior and mechanism of tetracycline adsorption on virgin and soil-exposed microplastics, J. Hazard. Mater., 2022, 440, 129770 CrossRef CAS PubMed.
- L. Wang, H. Yang, M. Guo, Z. Wang and X. Zheng, Adsorption of antibiotics on different microplastics (MPs): behavior and mechanism, Sci. Total Environ., 2023, 863, 161022 CrossRef CAS PubMed.
- F. Kong, X. Xu, Y. Xue, Y. Gao, L. Zhang, L. Wang, S. Jiang and Q. Zhang, Investigation of the adsorption of sulfamethoxazole by degradable microplastics artificially aged by chemical oxidation, Arch. Environ. Contam. Toxicol., 2021, 81, 155–165 CrossRef CAS PubMed.
- G. Liu, Z. Zhu, Y. Yang, Y. Sun, F. Yu and J. Ma, Sorption behavior and mechanism of hydrophilic organic chemicals to virgin and aged microplastics in freshwater and seawater, Environ. Pollut., 2019, 246, 26–33 CrossRef CAS PubMed.
- Y. Wang, C. Liu, F. Wang and Q. Sun, Behavior and mechanism of atrazine adsorption on pristine and aged microplastics in the aquatic environment: kinetic and thermodynamic studies, Chemosphere, 2022, 292, 133425 CrossRef CAS PubMed.
- Y. Zhang, Z. Chen, Y. Shi, Q. Ma, H. Mao, Y. Li, H. Wang and Y. Zhang, Revealing the sorption mechanisms of carbamazepine on pristine and aged microplastics with extended DLVO theory, Sci. Total Environ., 2023, 874, 162480 CrossRef CAS PubMed.
- W. Liu, T. Pan, H. Liu, M. Jiang and T. Zhang, Adsorption behavior of imidacloprid pesticide on polar microplastics under environmental conditions: critical role of photo-aging, Front. Environ. Sci. Eng., 2023, 17, 41 CrossRef CAS.
- J. Ma, J. Zhao, Z. Zhu, L. Li and F. Yu, Effect of microplastic size on the adsorption behavior and mechanism of triclosan on polyvinyl chloride, Environ. Pollut., 2019, 254, 113104 CrossRef CAS PubMed.
- M. Jiang, L. Hu, A. Lu, G. Liang, Z. Lin, T. Zhang, L. Xu, B. Li and W. Gong, Strong sorption of two fungicides onto biodegradable microplastics with emphasis on the negligible role of environmental factors, Environ. Pollut., 2020, 267, 115496 CrossRef CAS PubMed.
- W. Gong, M. Jiang, P. Han, G. Liang, T. Zhang and G. Liu, Comparative analysis on the sorption kinetics and isotherms of fipronil on nondegradable and biodegradable microplastics, Environ. Pollut., 2019, 254, 112927 CrossRef CAS PubMed.
- F. A. O. Udenby, H. Almuhtaram, M. J. McKie and R. C. Andrews, Adsorption of fluoranthene and phenanthrene by virgin and weathered polyethylene microplastics in freshwaters, Chemosphere, 2022, 307, 135585 CrossRef CAS PubMed.
- M. Lončarski, V. Gvoić, M. Prica, L. Cveticanin, J. Agbaba and A. Tubič, Sorption behavior of polycyclic aromatic hydrocarbons on biodegradable polylactic acid and various nondegradable microplastics: model fitting and mechanism analysis, Sci. Total Environ., 2021, 785, 147289 CrossRef.
- R. A. Funari, L. M. Frescura, B. B. de Menezes, A. F. de Moraes Bastos and M. B. da Rosa, Adsorption of naphthalene and its derivatives onto high-density polyethylene microplastic: computational, isotherm, thermodynamic, and kinetic study, Environ. Pollut., 2023, 318, 120919 CrossRef CAS PubMed.
- L. M. Frescura, R. A. Funari, B. B. de Menezes, A. F. de Moreas Bastos and M. B. da Rosa, Interaction of fluorene and its analogs with high-density polyethylene microplastics: an assessment of the adsorption mechanism to establish the effects of heteroatoms in the molecule, Environ. Pollut., 2023, 337, 122573 CrossRef CAS PubMed.
- C. Yang, W. Wu, X. Zhou, Q. Hao, T. Li and Y. Liu, Comparing the sorption of pyrene and its derivatives onto polystyrene microplastics: insights from experimental and computational studies, Mar. Pollut. Bull., 2021, 173, 113086 CrossRef CAS PubMed.
- N. Cui, P. Wang and N. Xu, Sorption behaviour of tebuconazole on microplastics: kinetics, isotherms and influencing factors, Environ. Technol., 2023, 44, 3937–3948 CrossRef CAS PubMed.
- Y. Yu, H. Li, J. Chen, F. Wang, X. Chen, B. Huang, Y. He and Z. Cai, Exploring the adsorption behavior of benzotriazoles and benzothiazoles on polyvinyl chloride microplastics in the water environment, Sci. Total Environ., 2022, 821, 153471 CrossRef CAS PubMed.
- K. Wang, Y. Kou, K. Wang, S. Liang, C. Guo, W. Wang, Y. Lu and Y. Wang, Comparing the adsorption of methyl orange and malachite green on similar yet distinct polyamide microplastics: uncovering hydrogen bond interactions, Chemosphere, 2023, 340, 139806 CrossRef CAS PubMed.
- T. Li, X. Cao, X. Cui, R. Zhao, H. Chen, W. Xue, Z. Cui, X. Tan and S. Ni, Competitive adsorption of lead and cadmium onto nanoplastics with different charges: two dimensional correlation spectroscopy study, Environ. Sci. Pollut. Res., 2023, 30, 72884–72899 CrossRef CAS PubMed.
- Y. Zhao, H. Chen, H. Liang, T. Zhao, B. Ren, Y. Li, H. Liang, Y. Liu, H. Cao, N. Cui and W. Wei, Combined toxic effects of polyethylene microplastics and lambda-cyhalothrin on gut of zebrafish (Danio rerio), Ecotoxicol. Environ. Saf., 2024, 276, 116296 CrossRef CAS PubMed.
- Y. Leng, W. Wang, H. Cai, F. Chang, W. Xiong and J. Wang, Sorption kinetics, isotherms and molecular dynamics simulation of 17β-estradiol onto microplastics, Sci. Total Environ., 2023, 858, 159803 CrossRef CAS PubMed.
- J. Yao, J. Wen, H. Li and Y. Yang, Surface functional groups determine adsorption of pharmaceuticals and personal care products on polypropylene microplastics, J. Hazard. Mater., 2022, 423, 127131 CrossRef CAS PubMed.
- X. Zhang, M. Zheng, L. Wang, Y. Lou, L. Shi and S. Jiang, Sorption of three synthetic musks by microplastics, Mar. Pollut. Bull., 2018, 126, 606–609 CrossRef CAS PubMed.
- M. Sun, Y. Yang, M. Huang, S. Fu, Y. Hao, S. Hu, D. Lai and L. Zhao, Adsorption behaviors and mechanisms of antibiotic norfloxacin on degradable and nondegradable microplastics, Sci. Total Environ., 2022, 807, 151042 CrossRef CAS PubMed.
- D. Rajendran, M. Kamalakannan, G. P. Doss and N. Chandrasekaran, Surface functionalization, particle size and pharmaceutial co-contaminant dependent impact of nanoplastics on marine crustacean – Artemia salina, Environ. Sci.: Processes Impacts, 2024, 26, 1130–1146 RSC.
- S. Liu, J. Huang, W. Zhang, L. Shi, K. Yi, C. Zhang, H. Pang, J. Li and S. Li, Investigation of the adsorption behavior of Pb(II) onto natural-aged microplastics as affected by salt ions, J. Hazard. Mater., 2022, 431, 128643 CrossRef CAS PubMed.
- Y. Zhang, Z. Chen, Y. Shi, Q. Ma, H. Mao, Y. Li, H. Wang and Y. Zhang, Revealing the sorption mechanisms of carbamazepine on pristine and aged microplastics with extended DLVO theory, Sci. Total Environ., 2023, 874, 162480 CrossRef CAS PubMed.
- B. Hu, Y. Li, L. Jiang, X. Chen, L. Wang, S. An and F. Zhang, Influence of microplastics occurrence on the adsorption of 17β-estradiol in soil, J. Hazard. Mater., 2020, 400, 123325 CrossRef CAS PubMed.
- N. Tang, X. Li, X. Gao, X. Liu and W. Xing, The adsorption of arsenic on micro- and nano-plastics intensifies the toxic effect on submerged macrophytes, Environ. Pollut., 2022, 311, 119896 CrossRef CAS PubMed.
- Z. Lin, Y. Hu, Y. Yuan, B. Hu and B. Wang, Comparative analysis of kinetics and mechanisms for Pb(II) sorption onto three kinds of microplastics, Ecotoxicol. Environ. Saf., 2021, 208, 111451 CrossRef CAS PubMed.
- Y. Zhou, Y. Yang, G. Liu, G. He and W. Liu, Adsorption mechanism of cadmium on microplastics and their desorption behavior in sediment and gut environments: the roles of water pH, lead ions, natural organic matter and phenanthrene, Water Res., 2020, 184, 116209 CrossRef CAS PubMed.
- F. Fornasiero, M. M. Olaya, B. Esprester, V. Nguyen and J. M. Prausnitz, Distribution coefficients and diffusivities in three polymers for nineteen aqueous nonvolatile solutes, J. Appl. Polym. Sci., 2002, 85, 2041–2052 CrossRef CAS.
- D. Klose, F. Siepmann, K. Elkharraz and J. Siepmann, PLGA-based drug delivery systems: importance of the type of drug and device geometry, Int. J. Pharm., 2008, 354, 95–103 CrossRef CAS PubMed.
- S. E. Hale, T. J. Martin, K.-U. Goss, H. P. H. Arp and D. Werner, Partitioning of organochlorine pesticides from water to polyethylene passive samplers, Environ. Pollut., 2010, 158, 2511–2517 CrossRef CAS PubMed.
- H. P. Sangam and R. K. Rowe, Migration of dilute aqueous organic pollutants through HDPE geomembranes, Geotext. Geomembr., 2001, 19, 329–357 CrossRef.
- M. Saleem, A. A. Asfour and D. De Kee, Diffusion of organic penetrants through low density polyethylene (LDPE) films: effect of size and shape of the penetrant molecules, J. Appl. Polym. Sci., 1989, 37, 617–625 CrossRef CAS.
- I. S. Voultzatis, C. D. Papaspyrides, C. J. Tsenoglou and C. Roussis, Diffusion of model contaminants in high-density polyethylene, Macromol. Mater. Eng., 2007, 292, 272–284 CrossRef CAS.
- Y. Zhou, L. Hou, H. Chen, R. Steenbakkers, K. Sehanobish, P. Wu and Q. Shi, FT-IR studies of factors affecting the diffusivity of oligo (oxyethylene) fatty acid ester in PE films: effect of temperature, ethylene oxide chain length and base resin type, Polymer, 2017, 130, 150–160 CrossRef CAS.
- J. M. Saquing, C. D. Saquing, D. R. U. Knappe and M. A. Barlaz, Impact of plastics on fate and transport of organic contaminants in landfills, Environ. Sci. Technol., 2010, 44, 6396–6402 CrossRef CAS PubMed.
- S. Seidensticker, C. Zarfl, O. A. Cirpka and P. Grathwohl, Microplastic-contaminant interactions: influence of nonlinearity and coupled mass transfer, Environ. Toxicol. Chem., 2019, 38, 1635–1644 CrossRef CAS PubMed.
- H. K. Karapanagoti and I. Klontza, Testing phenanthrene distribution properties of virgin plastic pellets and plastic eroded pellets found on Lesvos island beaches (Greece), Mar. Environ. Res., 2008, 65, 283–290 CrossRef PubMed.
- A. Peterlin, Influence of morphology on the transport properties of crystalline polymrs, Macromol. Chem., 1974, 9, 239–264 Search PubMed.
- M. Hedenqvist and U. W. Gedde, Diffusion of small-molecular penetrants in semicrystalline polymers, Prog. Polym. Sci., 1996, 21, 299–333 CrossRef CAS.
- P. Paik and K. K. Kar, Polypropylene nanosphere: particle size and crystal structure, Int. J. Plast. Technol., 2009, 13, 68–82 CrossRef CAS.
- F. Buss, J. Göcke, P. Scharfer and W. Schabel, From micro to nano thin polymer layers: thickness and concentration dependence of sorption and the solvent diffusion coefficient, Macromolecules, 2015, 48, 8285–8293 CrossRef CAS.
- V. Kislitsin and P. Choi, Thickness dependence of the diffusivity and solubility of cyclohexane in nanoscale bitumen films, ACS Omega, 2019, 4, 21578–21586 CrossRef CAS PubMed.
- D. B. Hall and J. M. Torkelson, Small molecule probe diffusion in thin and ultrathin supported polymer films, Macromol., 1998, 31, 8817–8825 CrossRef CAS.
- B. D. Vogt, C. L. Soles, H.-J. Lee, E. K. Lin and W.-L. Wu, Moisture absorption and absorption kinetics in polyelectrolyte films: influence of film thickness, Langmuir, 2004, 20, 1453–1458 CrossRef CAS PubMed.
- M. J. Galotto, A. Torres, A. Guarda, N. Moraga and J. Romero, Experimental and theoretical study of LDPE versus different concentrations of Irganox 1076 and different thickness, Food Res. Int., 2011, 44, 566–574 CrossRef CAS.
- J. P. Stanford, A. L. Maier, L. A. McDonald, P. H. Pfromm and M. E. Rezac, Kinetic and equilibrium sorption of organic liquids and vapors in Matrimid, J. Membr. Sci., 2016, 512, 29–37 CrossRef CAS.
- D. Cava, R. Catala, R. Gavara and J. M. Lagaron, Testing limonene diffusion through food contact polyethylene by FT-IR spectroscopy: film thickness, permeant concentration and outer medium effects, Polym. Test., 2005, 24, 483–489 CrossRef CAS.
- M. Roman, P. Roman, R. Verbeke, L. Gutierrez, M. Vanoppen, M. Dickmann, W. Egger, I. Vankelecom, J. Post, E. Cornelissen, K. Keesman and A. Verliefde, Non-steady diffusion and adsorption of organic micropollutants in ion-exchange membranes: effect of the membrane thickness, iScience, 2021, 24, 102095 CrossRef CAS PubMed.
- A. M. Shishatskii, Y. P. Yampol’skii and K.-V. Peinemann, Effects of film thickness on density and gas permeation parameters of glassy polymers, J. Membr. Sci., 1996, 112, 275–285 CrossRef CAS.
- M. H. Mondal, M. Mukherjee, K. Kawashima, K. Nishida and T. Kanaya, Study of thickness dependent density in ultrathin water soluble polymer films, Macromol, 2009, 42, 732–736 CrossRef CAS.
- L. Singh, C. L. Henderson and P. J. Ludovice, Characterization of property variation in ultra-thin polymer films from molecular simulation, Proc. Soc. Photo-Opt. Instrum. Eng., 2005, 5753, 1202–1211 CrossRef CAS.
- R. M. Town, H. P. van Leeuwen and R. Blust, Biochemodynamic features of metal ions bound by micro- and nano-plastics in aquatic media, Front. Chem., 2018, 6, 627 CrossRef CAS PubMed.
- R. M. Town and H. P. van Leeuwen, Uptake and release kinetics of organic contaminants associated with micro- and nanoplastic particles, Environ. Sci. Technol., 2020, 54, 10057–10067 CrossRef PubMed.
- M. E. Stack, K. Hollman, N. Mladenov, B. Harper, F. Pinongcos, K. E. Sant, C. M. Rochman, W. Richardot, N. G. Dodder and E. Hoh, Micron-size tire tread particles leach organic compounds at higher rates than centimeter-size particles: compound identification and profile comparison, Environ. Pollut., 2023, 334, 1221166 CrossRef PubMed.
- A. M. Gulizia, K. Patel, B. Philippa, C. A. Motti, L. van Herwerden and G. Vamvounis, Understanding plasticiser leaching from polystyrene microplastics, Sci. Total Environ., 2023, 857, 159099 CrossRef CAS PubMed.
- J. F. L. Duval, H. P. van Leeuwen and R. M. Town, Electrostatic effects on ligand-assisted transfer of metals metals to (bio)accumulating interfaces and metal complexes (bioavai)lability, Colloids Surf., A, 2023, 658, 130679 CrossRef CAS.
- J. F. L. Duval, Metal speciation dynamics in soft colloidal ligand suspensions. Electrostatic and site distribution aspects, J. Phys. Chem. A, 2009, 113, 2275–2293 CrossRef CAS PubMed.
- H. P. van Leeuwen, Revisited: DGT speciation analysis of metal-humic acid complexes, Environ. Chem., 2016, 13, 84–88 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4em00744a |
| This journal is © The Royal Society of Chemistry 2025 |