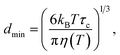Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
NMR crystallization: in situ NMR strategies for monitoring the evolution of crystallization processes
Colan E.
Hughes
 ,
Naomi V.
Ratnasingam
,
P. Andrew
Williams
,
Erwan
Benhenou
,
Rhian
Patterson
and
Kenneth D. M.
Harris
,
Naomi V.
Ratnasingam
,
P. Andrew
Williams
,
Erwan
Benhenou
,
Rhian
Patterson
and
Kenneth D. M.
Harris
 *
*
School of Chemistry, Cardiff University, Park Place, Cardiff CF10 3AT, Wales, UK. E-mail: HarrisKDM@cardiff.ac.uk
First published on 28th June 2024
Abstract
We present a discussion of the range of NMR techniques that have been utilized for in situ monitoring of crystallization processes, highlighting the opportunities that now exist for exploiting the versatility of NMR techniques to reveal insights into the changes that occur in both the solid phase and the liquid phase as a function of time during crystallization processes from solution. New results are presented from in situ NMR studies of a range of crystallization processes using the CLASSIC NMR strategy and other techniques, specifically covering the following topics: (i) crystallization of glycine from aqueous solution at low temperature, revealing the relatively long-lived existence of a pure phase of the highly meta-stable β polymorph, (ii) the complementarity of 1H→13C cross-polarization NMR and direct-excitation 13C NMR techniques in probing the evolution of the solid and liquid phases in in situ NMR studies of crystallization processes, (iii) in situ NMR studies of the process of guest exchange between a crystalline host–guest material in contact with the liquid phase of a more favourable type of guest, and (iv) systematic studies of the influence of magic-angle sample spinning on the behaviour of a crystallization system.
1. Introduction
Crystallization is a vital process in many chemical, biological and physical systems,1–7 but much still remains to be understood about fundamental aspects of crystallization mechanisms. Crystallization processes are generally governed by kinetic factors, which often result in the formation of meta-stable solid phases rather than the thermodynamically stable phase; in many cases, the crystallized phase evolves through a sequence of different solid forms, which differ in crystal structure (and may also differ in composition), before arriving at the final crystallization product. Clearly, understanding the sequence of events that occur during crystallization is a first step towards the development of deeper insights into mechanistic aspects of crystallization processes. In this regard, experimental methods that allow direct in situ monitoring of crystallization systems provide the best opportunity to understand details of the changes that occur in both the solid phase and the liquid phase as a function of time during crystallization from solution.While several experimental strategies8 (including techniques based on diffraction, microscopy and various types of spectroscopy) have been developed for in situ studies of crystallization processes, it is only in relatively recent years that solid-state NMR strategies have been developed in this field.9–13 In principle, solid-state NMR spectroscopy is a highly suitable technique for characterization of crystallization systems, as it is generally straightforward to distinguish different solid forms of a given type of molecule (such as polymorphs, hydrates, solvates and/or co-crystals) based on their high-resolution solid-state NMR spectra.
In the present paper, we focus on in situ NMR studies of the crystallization of organic materials from solution, in which the same type of molecule exists in both the solution and solid phases. In general, the crystallization processes of interest do not involve chemical transformations but instead involve the evolution of a given type of molecule from an initial solution phase to a solid phase, and in some cases with further evolution of the solid phase through a sequence of transformations between different solid forms.
In particular, we are interested in the development and application of in situ NMR strategies that exploit the selectivity of NMR to detect only the solid phase in the heterogeneous solid–liquid systems that exist during crystallization from solution, allowing the solid particles produced at an early stage of the crystallization process to be observed, and allowing the evolution of different solid phases to be monitored as a function of time. We are also particularly interested in the development of in situ NMR strategies (such as the CLASSIC NMR technique14) that yield essentially simultaneous information on the complementary changes that occur in the solid phase and in the liquid phase as a function of time during a given crystallization experiment. Such studies have been shown to lead to the discovery of new crystalline phases that arise as transient intermediates on crystallization pathways,15 to reveal the important role that amorphous solids may play as precursors to crystalline phases,16 and to enable quantitative studies of the kinetics of crystallization processes.17 A range of different types of material have been studied, with some focus on crystallization of organic molecular solids, but also encompassing processes for the formation of other types of solid, including metal–organic framework17 and cement18 materials. To date, a range of different NMR-active nuclei have been studied, primarily spin-½ nuclei (1H, 13C, 29Si and 31P) but also one case of a quadrupolar nucleus18 (27Al). Representative examples of in situ NMR studies of crystallization processes are given in Table 1, including information on relevant experimental parameters in each case.
| Crystallization process | Isotopic labelling | 1H NMR frequency | Type of in situ NMR | Time resolution | Total experiment time | Ref. |
|---|---|---|---|---|---|---|
| 1,10-Dihydroxydecane-(urea)2 co-crystal from methanol | 13C-urea (99%) | 850 MHz | Solid-state 13C NMR | 2.67 min | 11.4 h | 15 |
| Methyldiphenylphosphine oxide from toluene | — | 850 MHz | Solid-state 31P NMR | 3.2 min | 17.4 h | 15 |
| Glycine from methanol–water | 13Cα-glycine (99%) | 300 MHz | Solid-state 13C NMR | 16 min | 16.8 h | 19 |
| Glycine from H2O | 13Cα,13Cβ-glycine (99%) | 300 MHz | Solid-state 13C NMR | 26 min | 13 h | 20 |
| Glycine from D2O | ||||||
| DL-Menthol from molten liquid phase | — | 850 MHz | CLASSIC 13C NMR | 2.67 min | 2.83 h | 16 |
| Formation of MOF MFM500(Ni) from water–DMF (at 60 °C) | — | 850 MHz | CLASSIC 31P and 1H NMR | 7.1 min | 35 h | 17 |
| Hydration of CaAl2O4 | — | 850 MHz | CLASSIC 27Al NMR | 23.3 min | 21 h | 18 |
| m-Aminobenzoic acid from DMSO | — | 850 MHz | CLASSIC 13C NMR | 44.8 min | 15 h | 14 |
After giving a brief overview (Section 2) of a range of in situ NMR strategies that may be used to monitor the evolution of crystallization processes, we present new results from four separate areas of investigation (Section 3) which have been selected partly on the basis that they may stimulate discussion on specific aspects of the application of NMR methodology in this field.
2. Background to techniques
2.1 In situ solid-state NMR
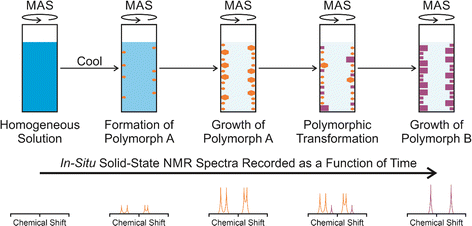
In situ solid-state NMR studies of crystallization from solution (Fig. 1) typically start from an undersaturated solution at high temperature, which is then cooled to a temperature at which the solution becomes supersaturated, and crystallization is then a thermodynamically favourable process. The emergence, growth and evolution of the solid phase are monitored as a function of time by recording the solid-state NMR spectrum of the system repeatedly during the crystallization process. The time-resolution of the in situ NMR study depends on the time to record an individual spectrum. Clearly, the time to record each spectrum must be sufficiently short to represent adequate time-resolution of the in situ study, but must be sufficiently long to ensure that the quality of the spectra recorded at each stage of the crystallization process is sufficiently high to allow the solid form(s) present to be identified. In previous in situ solid-state NMR studies, the time resolution has typically ranged from a few minutes to tens of minutes, with specific examples given in Table 1.In the case of crystallization of organic materials from solution, in situ solid-state NMR studies generally focus on recording 13C NMR spectra using the 1H→13C cross-polarization (CP) NMR technique, together with magic-angle sample spinning (MAS) and high-power 1H decoupling. The 1H→13C CP NMR technique selectively detects the solid phase in the types of heterogeneous solid–liquid systems that exist during crystallization from solution, with the liquid phase “invisible” to the measurement.
It is important to note that in situ solid-state NMR studies of crystallization are generally carried out on a relatively small scale (e.g., compared to laboratory-based crystallization experiments) as the volume of the crystallization solution is limited by the volume of the NMR rotor (ca. 25 μL for the standard liquid-state inserts used with MAS NMR rotors of 4 mm diameter; see Section 2.6.1 for more details of the liquid-state inserts). For this reason, an important consideration is to maximize the sensitivity of the experimental design in order to ensure that spectra of adequate quality can be recorded in a sufficiently short time during the crystallization process. Isotopic labelling may be essential in certain cases, and it is clearly also advantageous to measure the in situ NMR data at high magnetic field. In this regard, we note that the majority of our research in this field is carried out at the UK High-Field Solid-State NMR Facility.
In considering applications of in situ solid-state NMR methods to study materials formation processes in a wider context, it is relevant to note that there has been much activity21–27 in the study of processes in which the solid phase is produced by chemical transformations of precursor species in solution, including zeolite synthesis as a prominent example. Such processes are often carried out under hydrothermal conditions, which require the use of specialized NMR rotor technology26,28,29 to allow in situ studies to be carried out within a solid-state NMR spectrometer under the rather harsh conditions and high temperatures associated with such reactions.
2.2 In situ liquid-state NMR
In situ solid-state NMR studies of crystallization may be unfeasible when long acquisition times are required to measure the solid-state NMR spectrum (e.g., when the spin–lattice relaxation time is long); this situation is particularly problematic in the study of rapid crystallization processes. Under these circumstances, in situ liquid-state NMR may be the only viable approach to study the crystallization process, given the much faster acquisition times for liquid-state NMR. While in situ liquid-state NMR cannot reveal the identity of solid phases present during crystallization, it nevertheless provides insights into the changes in the liquid phase that arise as a consequence of crystallization. For example, analysis of the decrease in the liquid-state NMR signal intensities provides quantitative information on the decrease in the amount of dissolved species in the liquid phase as a function of time during crystallization, and changes in liquid-state NMR chemical shifts may provide insights into changes in solution-state interactions and speciation during crystallization. For in situ liquid-state NMR spectra of solutions undergoing crystallization, it is generally advantageous to record the data on a solid-state NMR spectrometer using rapid magic-angle sample spinning in order to alleviate the problem of significant line broadening that can arise (due to poor shimming) in liquid-state NMR spectra of solutions containing crystallized solid particles.We note that several liquid-state NMR studies30–34 have focused on understanding solute–solute and solute–solvent interactions in solutions with the aim of gaining insights into the modes of molecular aggregation that exist at early stages of the pathway towards crystal nucleation. In general, such studies have focused on stable solutions (i.e., saturated or undersaturated solutions) or meta-stable solutions at low degrees of supersaturation prior to crystallization, and have not actually investigated systems during the process of crystallization.
It is also relevant to mention the opportunity to use liquid-state NMR techniques to monitor the crystallization of nanocrystalline materials, as demonstrated by an in situ19F NMR study35 of crystallization of calcium fluoride (CaF2) nanocrystals. In this case, the 19F NMR spectrum of the nanocrystals contains distinct peaks from the surface and core regions, allowing the particle size to be estimated as a function of time from the relative intensities of these peaks.
2.3 CLASSIC NMR: combined liquid-state and solid-state in situ NMR studies of crystallization processes
The CLASSIC NMR (Combined Liquid- And Solid-State In situ Crystallization NMR) strategy has been developed14 to allow both in situ solid-state NMR data and in situ liquid-state NMR data to be recorded in a time-resolved manner during a given crystallization experiment. Clearly, this strategy provides the opportunity to understand the complementary changes that occur in both the solid phase and the liquid phase as a function of time during crystallization from solution. The solid-state NMR spectra reveal the time-dependent changes in the total amount of the solid phase (e.g., allowing quantitative information on crystallization kinetics to be determined) and the time-dependent changes in the identity of the solid phase (e.g., allowing polymorphic evolution to be understood), while the liquid-state NMR spectra reveal the time-dependent changes in the concentration of the solution and the time-dependent changes in solution-state speciation and intermolecular interactions that arise due to the crystallization process.The CLASSIC NMR strategy was first demonstrated14 in a study of crystallization of m-aminobenzoic acid from DMSO involving the alternating measurement of two types of NMR spectrum repeatedly during the crystallization process, specifically: (i) 1H→13C CP NMR spectra (with high-power 1H decoupling) to selectively measure the NMR signal of the solid phase, and (ii) direct-excitation 13C NMR spectra (with no 1H decoupling and a relatively short recycle delay) to selectively measure the NMR signal of the liquid phase. Following this type of experiment, the measured data are separated into a set of time-resolved 1H→13C CP NMR spectra (representing the evolution of the solid phase during the crystallization process) and a set of time-resolved direct-excitation 13C NMR spectra (representing the evolution of the liquid phase during the crystallization process).
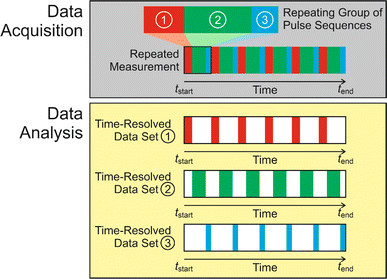
Subsequent applications have generalized the CLASSIC NMR strategy to involve a “repeating group” of more than two pulse sequences (Fig. 2), for example involving the measurement of NMR spectra for two or more different types of nucleus for the liquid phase and/or the solid phase. By careful choice of the pulse sequences in the repeating group, the CLASSIC NMR approach offers a versatile strategy to monitor time-dependent changes in both the solid and liquid phases during crystallization, with each type of spectrum yielding insights into the changes that occur in a specific aspect of the crystallization system. An important consideration, however, is the fact that the time-resolution of the in situ NMR study depends on the time to record the data for all the pulse sequences in the repeating group. Thus, a compromise must be reached between the number of different pulse sequences in the repeating group and the need to ensure that the total time to record all the spectra in the repeating group is sufficiently short to represent a suitable time-resolution for monitoring the evolution of the crystallization process as a function of time. In practice, the time resolution of CLASSIC NMR experiments may range from a few minutes to tens of minutes (specific examples are given in Table 1).
In addition to CLASSIC NMR, another strategy developed recently36,37 to allow the study of both solid and liquid phases during crystallization is a DNP-based technique in which hyperpolarized suspensions are subjected to rapid crystallization, with the hyperpolarized nuclei incorporated into the rapidly formed crystalline phase; this technique has been used to study the time-dependence of 31P NMR spectra for solute species and for the solid phase in crystallization of calcium phosphate. Another technique developed38 for the study of mixed-phase systems is SASSY (Simultaneous Solid and Solution Spectroscopy) NMR, which allows liquid-state and solid-state NMR spectra to be recorded using a single pulse sequence, with post-processing of the experimental data allowing the separate NMR spectra for the solid and liquid phases to be extracted. While SASSY NMR has been applied38 to study various mixed-phase systems, applications for in situ studies of crystallization processes have not (at the time of preparing this paper) been reported.
2.4 Measuring in situ NMR data for both liquid and solid phases in the same spectrum
In certain circumstances, it may be feasible to record NMR spectra for both the solid and liquid phases in a crystallization system using a single type of NMR measurement, with the peaks arising from the solid and liquid phases distinguished simply from their isotropic chemical shifts.10 For solid materials in which the molecules undergo significant molecular motion, the relaxation properties may be comparable to those of liquid phases, allowing signals from both the solid phase and the liquid phase to be recorded under the measurement conditions normally used to measure high-resolution liquid-state NMR spectra. Clearly, the application of this approach for in situ NMR monitoring of crystallization processes is advantageous as it allows the evolution of both the solid and liquid phases to be monitored in a strictly simultaneous manner (we recall that, in the CLASSIC NMR strategy, the solid and liquid phases are sampled at alternating time-points during the crystallization process, rather than at identical time-points). However, a disadvantage of recording the data for both phases in the same spectrum is the likelihood that the chemical shifts of some signals from the solid and liquid phases will be very similar, leading to peak overlap in the NMR spectrum and potentially obscuring information on the evolution of each phase. The approach of recording in situ NMR data for both the liquid and solid phases in a single type of spectrum is demonstrated in Section 3.2.2.5 Ex situ NMR techniques to study crystallization processes
In addition to the in situ NMR methods discussed above, an ex situ solid-state NMR strategy has been developed39 to allow the sensitivity advantages of dynamic nuclear polarization (DNP) NMR40–43 to be exploited in the study of crystallization processes. In this strategy, a crystallization solution is divided into several NMR rotors, with the crystallization process allowed to evolve simultaneously in each rotor. At specific time-points during the crystallization process, one of the rotors is inserted into the solid-state DNP NMR spectrometer and quenched rapidly to low temperature (ca. 100 K) to form a frozen solution, thus stopping the crystallization process. As the crystallization system does not evolve further after quenching, the frozen solution represents a “snap-shot” of the system at a specific time-point on the crystallization pathway. Solid-state DNP NMR spectra are recorded after quenching each frozen solution, allowing detailed information on the time-evolution of the crystallization system to be established. Applications of this ex situ solid-state DNP NMR strategy have included studies of crystallization of glycine from bulk aqueous solution,39 within confined environments in mesoporous materials,44 and in the presence of various crystallization additives.452.6 Experimental and technical considerations
The main method for temperature calibration used in our work is based on the known temperature dependence of the chemical shift difference between the two 1H NMR resonances for methanol,46–48 which allows the absolute temperature inside the NMR rotor to be determined (within the temperature range in which methanol is a liquid phase). In the first stage of the temperature calibration procedure, the 1H NMR spectrum is measured for a sample of methanol at several different values of temperature (i.e., Tsensor, as indicated by the temperature sensor) and, for each temperature, at several different values of MAS frequency (νMAS). Under each set of conditions specified by Tsensor and νMAS, the true temperature inside the NMR rotor (Ttrue) is established from the measured 1H NMR spectrum of methanol, yielding sets of values of Ttrue, Tsensor and νMAS. From numerical fitting of these data, an equation is determined expressing Ttrue as a function of Tsensor and νMAS. Thus, to carry out subsequent experiments at specific values of Ttrue and νMAS, the equation is used to determine the value of Tsensor that should be set on the temperature controller to correspond to a true sample temperature equal to Ttrue.
For calibration of temperatures outside the range in which methanol is a liquid, we have used the 207Pb NMR chemical shift for lead nitrate,49 which has a linear temperature dependence. However, as this method depends on a single resonance in the 207Pb NMR spectrum, it is necessary first to record the 207Pb NMR spectrum at a reliably known temperature (Tref), allowing all other temperatures to be determined relative to Tref.
Finally, it is reasonable to expect that temperature gradients may exist within the NMR rotor, although this issue has not yet been investigated in our work. However, as in situ NMR studies of crystallization from solution involve a fluid phase within the NMR rotor (initially a homogeneous liquid phase and subsequently a dispersion of solid particles within the liquid phase), it is plausible that the fluidity of the sample under MAS may promote efficient mixing, allowing all parts of the sample to experience the same average temperature even if a temperature gradient does exist within the rotor.
In quench cooling, the crystallization solution at the initial temperature (Tstart) of the experiment is cooled to a target temperature (Ttarget) as rapidly as possible for the cooling device used, typically without indicating a specific cooling rate. This process is essentially an uncontrolled cooling from Tstart to Ttarget, and the actual profile of temperature as a function of time is not necessarily well defined. However, this approach allows the target temperature to be reached in the shortest possible time for the cooling device used. For the typical temperature ranges used in in situ NMR studies of crystallization (e.g., for the experiments discussed in Section 3.4, Tstart = 50 °C and Ttarget = 20 °C), the process of rapid cooling usually takes less than ca. 5 min. A significant advantage of the quench cooling protocol is that, with the exception of the initial period of rapid cooling, the entire crystallization experiment is carried out at a constant temperature (Ttarget).
The controlled cooling protocol also starts from an undersaturated solution at temperature Tstart, but in this case the temperature controller is set to cool the sample at a specific cooling rate to reach the target temperature Ttarget (the lowest cooling rate in the set-up used in our experiments is ca. 0.01 °C min−1). In principle, the rate of cooling is constant throughout the cooling period, although cooling may occur more slowly on approaching Ttarget in order to avoid overshooting. In the controlled cooling experiments described in Section 3, the quoted cooling rate is the average rate during the cooling period, given by (Tstart − Ttarget)/Δtcool, where Δtcool is the time for the solution to cool from Tstart to Ttarget. Clearly, the controlled cooling protocol allows a versatile range of cooling rates to be used (recalling that certain crystallization processes may require a specific cooling schedule).
3. Results and discussion
3.1 Polymorphic evolution in the crystallization of glycine at low temperature
Crystallization of glycine (H2NCH2CO2H) has been studied extensively in polymorphism research, including the first in situ solid-state NMR studies20 of crystallization of organic materials. Three polymorphs of glycine (denoted α, β and γ) are known50–54 under ambient conditions. In terms of thermodynamic stability,55,56 the γ polymorph is the most stable and the β polymorph is the least stable. The three polymorphs are readily distinguished57 by high-resolution solid-state 13C NMR; the isotropic chemical shift for the 13C environment in the carboxylate group (α, 176.5 ppm; β, 175.5 ppm; γ, 174.5 ppm) is particularly diagnostic.Previous in situ solid-state 13C NMR studies20 showed that, on cooling a solution of glycine in water (with the water at natural isotopic abundance) from 65 °C to ambient temperature, the α polymorph was the only solid phase observed throughout the experiment (total time, 13 h). In contrast, different behaviour was observed for the same crystallization experiment carried out20 for a solution of glycine in deuterated water (D2O); while the α polymorph was again observed as the initial solid phase, a polymorphic transformation was observed after ca. 2 h from the α polymorph to the stable γ polymorph. Notably, the least stable β polymorph of glycine was not observed in these in situ solid-state 13C NMR studies of crystallization of glycine from water at ambient temperature. However, an in situ solid-state 13C NMR study19 of crystallization of glycine from a methanol–water solution reported that an essentially pure sample of the β polymorph was observed as the initial crystallization product, before starting to transform almost immediately to the α polymorph; the amount of the α polymorph then increased, with a corresponding decrease in the amount of the β polymorph until the sample was a pure phase of the α polymorph. In ex situ DNP NMR studies39 of crystallization of glycine from water, a mixture of the α and β polymorphs was observed in the early stages of the crystallization process.
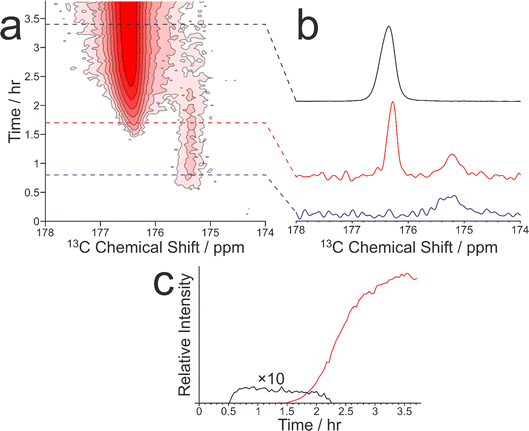
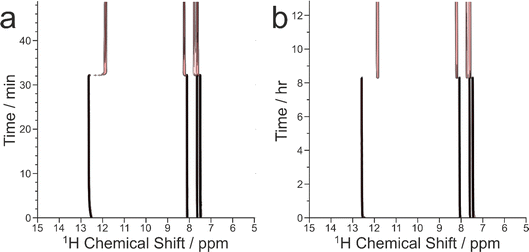
As our previous in situ solid-state 13C NMR studies of crystallization of glycine from water did not reveal conditions suitable for the formation of a pure sample of the β polymorph, we were motivated to explore the crystallization of glycine [13C-labelled (99%) in the carboxylate group; denoted 1-13C-glycine] from water (with natural isotopic abundances) at low temperatures. To allow aqueous solutions of 1-13C-glycine to be cooled to significantly lower temperatures without freezing, a small amount of glycerol was added to the crystallization solution (representing 5% by volume of the solvent) to serve as an anti-freezing agent. The solution of 1-13C-glycine in water–glycerol was cooled (in ca. 5 min) from +20 °C to −10 °C using the quench cooling protocol and then maintained at −10 °C for the remainder of the experiment. The evolution of the crystallization process was monitored by the CLASSIC NMR strategy, involving alternate recording of 1H→13C CP NMR spectra and direct-excitation 13C NMR spectra as a function of time. We focus here on the evolution of the 1H→13C CP NMR spectra as a function of time (Fig. 3). While no solid phase was observed in the early stages of the experiment, a signal at ca. 175.5 ppm appeared in the 1H→13C CP NMR spectrum at ca. 0.55 h, indicating that the initial solid phase was a pure sample of the β polymorph of glycine. Subsequently (at ca. 1.36 h), another peak also emerged at ca. 176.5 ppm, characteristic of the α polymorph of glycine. After a brief period of co-existence of these two peaks, the intensity of the peak for the α polymorph increased rapidly, while the peak for the β polymorph disappeared (Fig. 3c).
The experiment was repeated under several different cooling schedules, in each case starting from the same composition of the solution of 1-13C-glycine in water–glycerol at a temperature (20 °C or higher) at which the solution is undersaturated (in practice, our crystallization experiments started at temperatures between 20 °C and 40 °C). In all experiments involving quench cooling of the solution to either −10 °C or −15 °C, the β polymorph was produced as the initial crystallization product, which transformed subsequently to the α polymorph. In contrast, quench cooling of the solution to −5 °C instead produced the α polymorph directly as the initial crystallization product, with no evidence for the presence of the β polymorph. Furthermore, in an experiment using the controlled cooling protocol from +20 °C to −15 °C at 0.12 °C min−1, crystallization was observed to occur at +8 °C, producing the α polymorph as the crystallization product.
Clearly, the presence of glycerol allows the crystallization of glycine from aqueous solution to be extended to lower temperatures (significantly below the freezing temperature of pure water). Our in situ NMR studies indicate that, on quench cooling of a solution of glycine in water–glycerol to −10 °C or −15 °C, formation of the β polymorph is the favoured nucleation pathway, resulting in a pure sample of the β polymorph as the initial crystallization product. Clearly, this crystallization strategy represents a viable approach for producing a relatively long-lived sample of the pure β polymorph of glycine. In the results shown in Fig. 3, the β polymorph exists as a pure phase for ca. 0.81 h before the emergence and rapid growth of the α polymorph, coinciding with the rapid disappearance of the β polymorph.
Clearly, glycerol plays an important role in preventing freezing of the aqueous solution and thus allowing crystallization to take place at lower temperatures than would be possible for a solution of glycine in pure water. It is relevant to question whether, in addition to serving as an anti-freezing agent, the presence of glycerol may actually play an active role in directing the crystallization pathway to produce the β polymorph, for example through favourable interactions that promote the formation of pre-nucleation clusters and aggregates on the pathway towards nucleation of the β polymorph. However, our observation that quench cooling of a solution of glycine in water–glycerol to −5 °C produced the α polymorph tends to suggest that the critical factor in generating the β polymorph on rapid cooling to −10 °C or −15 °C is the lower temperature rather than the presence of glycerol.
It is relevant to note that a previous low-temperature in situ solid-state 13C and 15N NMR study has reported58 crystallization of glycine from an amorphous “frozen solution” formed by rapidly quenching an aqueous solution of glycine to 145 K. On subsequently warming the amorphous frozen solution to 211 K, a sharp peak appears at 173.5 ppm characteristic of a crystalline phase, which is assigned on the basis of a variety of NMR measurements, including 1H–13C HETCOR, 1H–15N HETCOR and 13C–13C dipolar build-up data, as the dihydrate phase of glycine (which was previously reported59 from in situ powder X-ray diffraction studies under the same conditions). On further increasing temperature in the in situ solid-state NMR study, the crystalline glycine dihydrate phase was observed to transform to the β polymorph of pure glycine.
3.2 Highlighting the complementarity of cross-polarization and direct-polarization NMR measurements in studying the evolution of crystallization processes
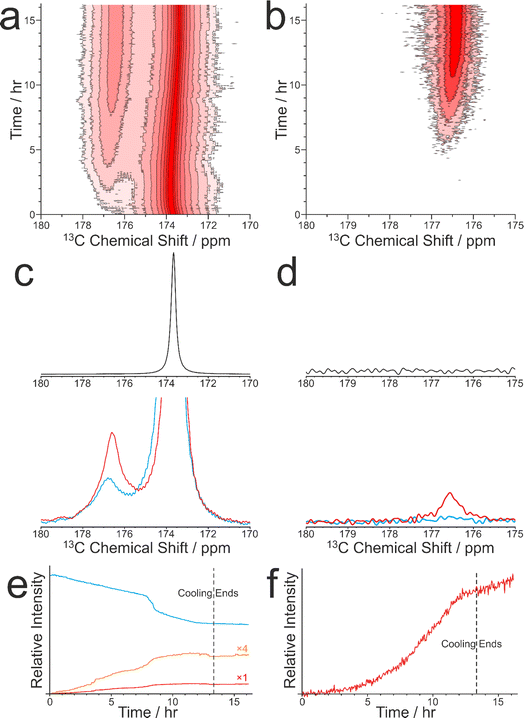
As discussed in Section 2.3, CLASSIC NMR studies of crystallization processes often involve the alternating measurement of 1H→13C CP NMR spectra and direct-excitation 13C NMR spectra to reveal information on the evolution of the solid and liquid phases during the crystallization process. However, it is important to highlight the complementarity of these techniques and to appreciate that the information that each technique provides about the evolution of the crystallization system may differ in important aspects. In this regard, we consider the results from a CLASSIC NMR study of crystallization from an aqueous solution of glycine, prepared using glycine 13C-labelled (99%) in the carboxylate group (denoted 1-13C-glycine) and water with natural isotopic abundances. The aqueous solution of 1-13C-glycine was subjected to controlled cooling from 65 °C to 20 °C over 13.3 h (at a rate of 0.056 °C min−1) and maintained at 20 °C for a further 3 h. CLASSIC NMR measurements were carried out by alternate recording of 1H→13C CP NMR spectra and direct-excitation 13C NMR spectra (in each case, high-power 1H decoupling was applied and the recycle delay was 5 s). The time resolution of the CLASSIC NMR study was 2.68 min. Under these measurement conditions, the 1H→13C CP NMR spectra contain signals only from the solid phase, whereas the direct-excitation 13C NMR spectra contain signals from both the solid and liquid phases.At the start of the crystallization process, glycine is present only in the liquid phase, giving rise to a characteristic signal in the direct-excitation 13C NMR spectra (Fig. 4a and c). However, as the experiment progresses, a peak emerges at ca. 176.5 ppm in the 1H→13C CP NMR spectra (Fig. 4b and d) indicating the formation of a solid phase, which is identified from the isotropic 13C chemical shift as the α polymorph of glycine. A relatively weak peak is also observed in the direct-excitation 13C NMR spectrum at ca. 176.5 ppm due to the solid phase [this peak is weak due to slow 13C spin–lattice relaxation of the α polymorph; the value60 of T1(13C) = 11.9 s is longer than the recycle delay (5 s) used in measuring the direct-excitation 13C NMR spectra]. Throughout the remainder of the crystallization experiment, no other peaks for solid phases are observed and the α polymorph is the only solid phase present.
We now consider the variation in the intensities of the peaks for glycine in the solution phase (from the direct-excitation 13C NMR spectra; Fig. 4e) and for the solid phase (α polymorph) of glycine (from the 1H→13C CP NMR spectra; Fig. 4f), focusing initially on the first 8 h of the experiment, during which the crystallization system is subjected to slow cooling. During this period, the intensity of the peak for glycine in the solution phase (in the direct-excitation 13C NMR spectra) decreases essentially linearly as a function of time, reflecting a decrease in the concentration of the solution phase as the amount of crystallization increases. Correspondingly, the intensity of the peak for the α polymorph of glycine (in the 1H→13C CP NMR spectra) increases as a function of time. However, in contrast to the linear decrease in the amount of glycine dissolved in the solution, the increase in the amount of the crystallized α polymorph exhibits an essentially exponential time dependence. As the loss of glycine from the solution phase results in the formation of solid glycine, an important question is why the decrease of the peak for the solution phase in the direct-excitation 13C NMR spectra and the increase of the peak for the solid phase in the 1H→13C CP NMR spectra exhibit such markedly different time dependences.
A plausible explanation for the very different time-dependences is that the 1H→13C CP NMR measurements do not necessarily detect the entire population of particles of the α polymorph within the solid phase. Our previous studies10 have estimated that, for 1H→13C CP NMR to give a signal for solid particles produced under the typical conditions used for in situ NMR studies of crystallization processes at ambient temperature, the particle volume must be larger than about 4 × 107 Å3; this volume corresponds to a minimum particle diameter of dmin ≈ 420 Å for contributing a signal in the 1H→13C CP NMR spectrum. For solid particles smaller than this critical size, the rotational correlation times are too short to give cross-polarization; therefore, these particles do not contribute to the signal in the 1H→13C CP NMR spectrum. For this reason, at the early stages of the crystallization process, when very few particles may have grown to the critical size required to give a signal in the 1H→13C CP NMR spectrum, the rate of increase of the signal in this spectrum will be significantly slower than the rate of decrease of the signal in the direct-excitation 13C NMR spectra for glycine in the solution phase. However, in subsequent stages of the crystallization process, most of the glycine lost from the solution phase will readily become incorporated in the growth of larger particles of the α polymorph, resulting in the exponentially increasing signal observed in the 1H→13C CP NMR spectra as a function of time. Potentially, a more detailed analysis of this situation could be developed in which the differences in the time-dependences of the signal for solution-phase glycine in the direct-excitation 13C NMR spectra and the signal for solid-phase glycine in the 1H→13C CP NMR spectra are used as a basis to gain more quantitative insights into the changes in the size distribution of solid particles as a function of time during the crystallization process, and such models will be explored in due course. However, in the present case, quantitative analysis of the time-dependences is complicated by the fact that the crystallization process was carried out under conditions in which the temperature of the system was decreased continuously; thus, the kinetics of relevant processes (including precipitation from the solution phase, crystal nucleation and crystal growth), all of which are temperature dependent, also become time-dependent in the context of the slow cooling experiment.
Another interesting feature concerns the behaviour of the crystallization system between about 8.1 h and 8.8 h, at which the rate of decrease in the intensity of the peak for glycine in the solution phase (in the direct-excitation 13C NMR spectra) exhibits an abrupt change to a more rapid decrease, which is not matched by an abrupt change in the rate of increase of the intensity of the peak for the solid phase in the 1H→13C CP NMR spectrum. Again, a plausible explanation is that the abrupt decrease in the amount of glycine in the solution phase may correspond to the formation of a significant amount of small solid particles that are smaller than the critical size required to contribute any significant change to the 1H→13C CP NMR spectrum.
We recall that the direct-excitation 13C NMR spectra also contain a weak peak for the solid phase (α polymorph). Interestingly, between about 8.1 h and 8.8 h, the intensity of this peak shows an abrupt increase (Fig. 4e), coinciding with the period during which the intensity of the peak for glycine in the solution phase exhibits an abrupt decrease. In this regard, the behaviour of the peak for solid-phase glycine in the direct-excitation 13C NMR spectra matches the behaviour of the peak for solution-phase glycine in the same spectra, indicating that an abrupt increase occurs in the total amount of glycine present in the solid phase (representing solid particles of all sizes) at this stage of the crystallization process. Clearly, these observations highlight the fact that, in detecting the solid phase in crystallization systems, the 1H→13C CP NMR and direct-excitation 13C NMR techniques may detect different populations of the solid particles present, depending on the distribution of particle sizes.
Finally, an important aspect for future investigation is to explore whether the use of 1H→13C CP NMR to study the solid phase as a function of time in crystallization experiments carried out under conditions of slow cooling is influenced by the gradual change in the temperature of the system. In this regard, two aspects of the temperature dependence of 1H→13C CP NMR measurements are relevant.
First, for solid particles dispersed in a liquid phase, the smallest size of particle (dmin) that can contribute to the 1H→13C CP NMR spectrum is temperature dependent. Based on our previous study,10 the value of dmin at temperature T is estimated from the following equation (assuming a spherical particle):
Second, as 1H→13C CP depends on various NMR relaxation properties of the solid phase, the intrinsic efficiency of CP is clearly temperature dependent, and will therefore vary between the initial and final temperatures in a slow-cooling crystallization experiment. A previous study63 of the temperature-dependence of the 1H→13C CP efficiency for solid glycine suggests that, for a CP contact time of 2 ms (as used in our experiment), there is only a small change in CP efficiency in the temperature range of our experiment, decreasing by ca. 5% between 65 °C and 20 °C. However, this previous study only reported the CP efficiency for the methylene 13C environment of glycine and did not specify which polymorph of glycine was studied. Clearly, to derive a more definitive understanding of this issue in the context of the CLASSIC NMR results presented here, future studies will determine the temperature dependence of the 1H→13C CP efficiency for a monophasic sample of the α polymorph of glycine as a function of temperature, including analysis of the CP efficiency for the carboxylate 13C environment.
Finally, it is clear from this discussion that slow-cooling crystallization experiments are intrinsically complex, as they involve the interplay of several different temperature dependent factors, which influence the physico-chemical properties of the crystallization solution and the kinetics of the crystallization process, as well as the sensitivity of the NMR technique used to probe the evolution of the system with time. In this regard, it is pertinent to recall (see Section 2.6.3) that in situ NMR studies of crystallization processes based on the quench cooling protocol have a significant advantage in ensuring that the majority of the crystallization process (i.e., except for the first few minutes) is carried out at constant temperature.
3.3 In situ NMR studies of guest exchange processes in solid inclusion compounds
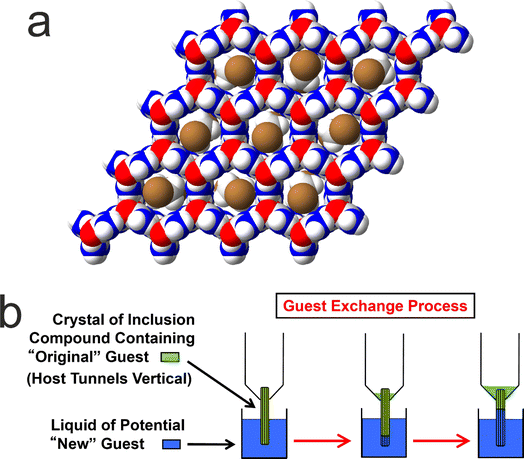
We now focus on a preliminary application of in situ NMR techniques to study guest exchange in solid host–guest materials. While this type of process does not actually involve crystallization, it nevertheless represents a process to generate new crystalline solids by the exchange of different types of molecule between a pre-formed crystalline material and a liquid phase in contact with the crystalline material. Our study to monitor the exchange of molecules between a crystalline solid and a liquid phase is focused on crystalline urea inclusion compounds,64–71 which are solid host–guest systems based on one-dimensional tunnels in a crystalline host structure constructed from a helical hydrogen-bonded arrangement of urea molecules (Fig. 5a). The types of guest molecules that form urea inclusion compounds are typically based on long-chain n-alkanes [CH3(CH2)nCH3] or terminally substituted n-alkanes, such as α,ω-dibromoalkanes [Br(CH2)mBr], as these molecules have suitable size-shape compatibility to be accommodated within the urea host tunnels, which have a diameter72 of ca. 5.5–5.8 Å. In most urea inclusion compounds, the guest molecules undergo rapid reorientational motion73–76 around the long molecular axis (in the linear conformation that the guest molecules must adopt inside the host tunnel structure), which is parallel to the host tunnel axis. As a consequence, signals from the guest molecules in urea inclusion compounds may be observed in NMR spectra recorded under conditions normally used for liquid-state NMR. For this reason, previous in situ NMR studies10 have shown that crystallization processes of urea inclusion compounds can be monitored using direct-excitation 13C NMR measurements, in which signals from molecules in both the solid and liquid phases are observed in the same spectrum and are distinguished (at least for certain 13C environments) on the basis of their isotropic 13C chemical shifts.It is relevant to note that many solid host materials, such as zeolites, find important applications in molecular separation processes, based on the selectivity of the host structure for incorporating guest molecules of specific size and shape. Such applications typically involve the selective adsorption of guest molecules within the empty host tunnel structure. However, in contrast to zeolites, the host tunnel structure in urea inclusion compounds is stable only when it is filled with a dense packing of guest molecules; the “empty” urea tunnel structure does not exist, with removal of the guest molecules from urea inclusion compounds leading to the collapse of the tunnel structure to form the pure crystalline phase of urea. For this reason, applications of urea inclusion compounds involving the selective adsorption of guest molecules within the empty host structure are clearly not viable. Nevertheless, it has been shown77,78 that guest exchange in urea inclusion compounds can occur by a mechanism that fulfils the requirement that the host tunnels remain fully occupied by guest molecules throughout the process. In particular, as shown schematically in Fig. 5b, transport of guest molecules along the host tunnels in a single crystal can be achieved by inserting new guest molecules into the tunnels at one end of the crystal (e.g., by dipping one end of the crystal into the liquid phase of the new guest), with the original guest molecules expelled from the other end of the crystal. This process is thermodynamically favoured if the urea inclusion compound containing the new guest molecules is more stable than that containing the original guest molecules.
Previous in situ studies78–80 of guest exchange in urea inclusion compounds have primarily used confocal Raman microspectrometry to monitor the type of uni-directional guest exchange process shown in Fig. 5b. In addition, bi-directional guest exchange has also been observed81 in urea inclusion compounds, in which new guest molecules enter the host tunnels at both ends of the original crystal. In this case, transport of the new guest molecules occurs in both directions along the host structure, in principle with equal probabilities of guest transport in one direction in some tunnels and in the opposite direction in other tunnels. Guest exchange has also been demonstrated82 by completely immersing the crystals containing the original type of guest molecules in the liquid phase of a potential new guest molecule, in which the guest exchange process is expected to involve bi-directional guest transport within each individual crystal.
These guest exchange processes occur by diffusion of guest molecules into and out of the ends of the host tunnels in the crystals of the urea inclusion compound, together with diffusion of the guest molecules along the host tunnels inside the crystals (as shown directly by the confocal Raman microspectrometry studies78–81). We note that, as urea is essentially insoluble in the long-chain hydrocarbons that constitute the liquid phase in the guest exchange experiments, no significant dissolution occurs when crystals of the urea inclusion compound are in contact with the liquid phase in these experiments. However, the possibility that some extent of local dissolution and/or recrystallization of the crystal surfaces may occur (e.g., at the ends of the host tunnels) cannot be ruled out, as the surface properties of the crystals under the experimental conditions of the guest exchange processes have not yet been investigated.
Here we report a preliminary CLASSIC NMR study of guest exchange in urea inclusion compounds, in which a multi-crystal sample of the urea inclusion compound containing 1,8-dibromooctane guest molecules was soaked in pure liquid tetradecane at 20 °C. From previous studies,10,83 it is known that tetradecane represents a more favourable guest molecule than 1,8-dibromooctane for inclusion in the urea tunnel structure. Thus, guest exchange is expected to occur when crystals of 1,8-dibromooctane/urea are in contact with pure liquid tetradecane. To monitor guest exchange in this case, the key diagnostic peaks in the solid-state 13C NMR spectrum are those due to the ![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) H3 group (ca. 15 ppm) and/or the
H3 group (ca. 15 ppm) and/or the ![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) H2CH3 group (ca. 25.2 ppm) of tetradecane guest molecules in the urea inclusion compound, and those due to the
H2CH3 group (ca. 25.2 ppm) of tetradecane guest molecules in the urea inclusion compound, and those due to the ![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) H2Br group (ca. 35.9 ppm) and/or the
H2Br group (ca. 35.9 ppm) and/or the ![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) H2CH2Br group (ca. 31.5 ppm) of 1,8-dibromooctane guest molecules in the urea inclusion compound. Throughout this discussion, underlining is used to indicate the specific 13C environment corresponding to a peak in the 13C NMR spectrum.
H2CH2Br group (ca. 31.5 ppm) of 1,8-dibromooctane guest molecules in the urea inclusion compound. Throughout this discussion, underlining is used to indicate the specific 13C environment corresponding to a peak in the 13C NMR spectrum.
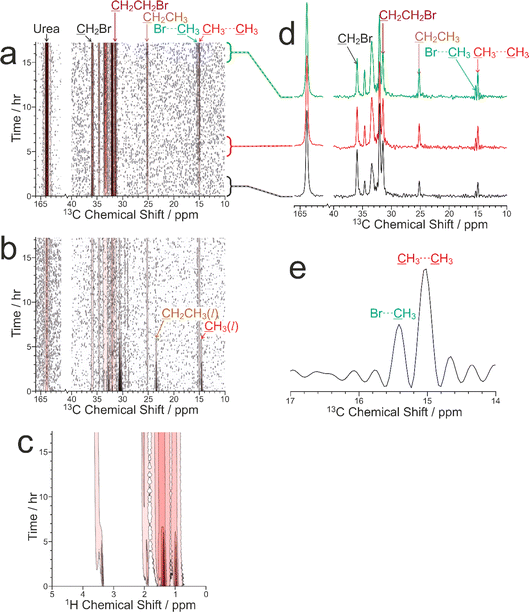
Our CLASSIC NMR study (Fig. 6) used three different pulse sequences in the repeating group to measure the following data as a function of time during the guest exchange process: (a) 1H→13C CP NMR spectra (with high-power 1H decoupling and a recycle delay of 5 s), (b) direct-excitation 13C NMR spectra (with high-power 1H decoupling and a recycle delay of 3 s), and (c) 1H NMR spectra. The time resolution of the CLASSIC NMR study was 8.75 min. While the direct-excitation 13C NMR and 1H NMR spectra are consistent with the expected changes in the liquid phase, in which the amount of tetradecane in the liquid phase decreases as a function of time and the amount of 1,8-dibromooctane in the liquid phase shows a corresponding increase, we focus primarily on the changes occurring in the crystalline phase as a function of time from analysis of the 1H→13C CP NMR spectra (Fig. 6a) and the solid-state component of the direct-excitation 13C NMR spectra (Fig. 6b).
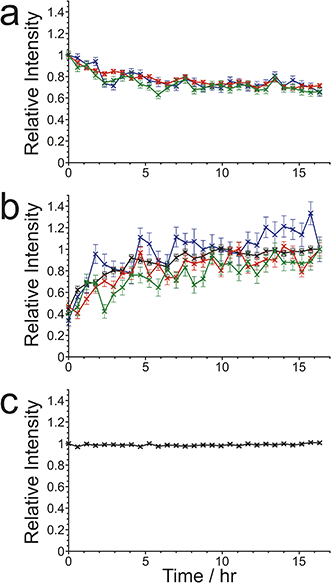
First, it is clear that guest exchange had already commenced during the period of ca. 10 min between preparing the NMR rotor (containing liquid tetradecane and the multi-crystal sample of the 1,8-dibromooctane/urea inclusion compound) and the start of data acquisition, as the first 1H→13C CP NMR spectrum recorded (see Fig. 6d) shows the presence of signals characteristic of tetradecane guest molecules in the urea inclusion compound. As time progresses, the intensities of the peaks for tetradecane guest molecules in the urea inclusion compound increase progressively (Fig. 6d and 7b). Simultaneously, the intensities of the peaks for 1,8-dibromooctane guest molecules in the urea inclusion compound decrease (Fig. 6d and 7a), with the rate of decrease mirroring the rate of increase of the peak intensities for the tetradecane guest molecules.
An important question relating to guest exchange processes of this type is whether the integrity of the crystalline host structure is maintained during the guest exchange process, which may be assessed by monitoring the peak for urea in the urea inclusion compound (163.8 ppm) as a function of time. Importantly, the intensity of this peak remains constant throughout the experiment (Fig. 7c), indicating that no degradation of the crystalline integrity of the urea host structure occurs as a consequence of guest exchange. Furthermore, there is no evidence for any change in the chemical shift of this peak nor the appearance of any new peaks arising from other solid phases containing urea during the guest exchange process [we note that the isotropic 13C chemical shift (162.6 ppm) of the pure crystalline phase of urea, which would be a plausible product of degradation of the urea inclusion compound, is significantly different from that of the urea inclusion compound].
A further interesting aspect of the solid-state 13C NMR spectra is that two isotropic peaks are observed for the CH3 group of tetradecane in the urea inclusion compound (Fig. 6d and e). These peaks arise because the isotropic 13C chemical shift for the CH3 groups of tetradecane is different depending on whether the adjacent guest molecule in the host tunnel is another tetradecane molecule, corresponding to a CH3⋯CH3 end-group interaction (15.0 ppm), or a molecule of 1,8-dibromooctane, corresponding to a CH3⋯Br end-group interaction (15.4 ppm). In contrast, the isotropic 13C chemical shifts for the CH2Br end-groups of 1,8-dibromooctane guest molecules in CH2Br⋯Br and CH2Br⋯CH3 end-group interactions in urea inclusion compounds are sufficiently close that a single peak is observed at ca. 35.9 ppm. We note that the possibility to observe different types of end-group interaction between guest molecules in crystalline urea inclusion compounds from solid-state 13C NMR spectra (not in the context of in situ studies of crystallization) has been reported previously,84,85 and methodology to use this information to derive fundamental information on the energetics of such materials has been developed.86 Clearly, deriving quantitative information on the changes in the relative amounts of the CH3⋯CH3 and CH3⋯Br end-group interactions as a function of time may provide additional insights into the structural changes that occur during the guest exchange process. However, as the relative efficiencies of 1H→13C CP for the CH3 groups in CH3⋯CH3 and CH3⋯Br end-group interactions have not yet been established, quantitative analysis of the relative intensities of the peaks in the 1H→13C CP NMR spectra for the different end-group interactions cannot be carried out at this stage. Furthermore, while individually resolved peaks are also observed in the direct-excitation 13C NMR spectra for the CH3 groups of the tetradecane guest molecules in CH3⋯CH3 and CH3⋯Br end-group interactions, the signal-to-noise ratio for these peaks is too low to allow reliable quantitative information to be obtained. Future studies will explore this aspect of the guest exchange process in more depth, allowing the analysis of the time-dependent changes in peak intensities in the in situ NMR data to be carried out on a rigorous quantitative basis.
3.4 Exploring the effect of MAS frequency on in situ NMR studies of crystallization processes
An important question relating to in situ NMR studies of crystallization from solution is whether crystallization pathways may be influenced by subjecting the crystallization system to rapid magic-angle sample spinning (MAS), as required to achieve good spectral resolution. Rapid spinning exerts a centrifugal pressure on the sample, which is estimated10 to be about 50–70 atm under typical conditions used for in situ solid-state NMR studies of crystallization processes. While such pressures are unlikely to induce polymorphic transitions directly in the solid phase (they are much lower than the values of pressure typically required to induce polymorphic transformations in organic solids87,88), the pressure generated by MAS may have a greater influence on the solution phase in crystallization systems. As MAS imposes a pressure gradient within the sample (pressure increases with distance from the rotation axis), the effect of MAS on a homogeneous solution is to introduce a density gradient and a non-uniform distribution of concentration within the solution (we recall that solubility is a function of pressure). The non-uniform nature of this crystallization environment may clearly influence crystallization processes occurring within the solution. Thus, the application of rapid MAS has the potential to influence the mechanism and/or the final outcome of crystallization processes (it is relevant to note that a solid-state transformation for which the polymorphic identity of the product obtained is influenced significantly by MAS has been reported89).As an exploratory investigation of the potential effects of MAS on crystallization processes, we focus on in situ liquid-state 1H NMR studies of co-crystal formation from a solution containing a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of benzoic acid (BA) and pentafluorobenzoic acid (PFBA) in dichloromethane-d2. This crystallization process has been studied previously10 by in situ liquid-state 1H and 19F NMR at a MAS frequency of 12 kHz. BA and PFBA form a 1
1 molar ratio of benzoic acid (BA) and pentafluorobenzoic acid (PFBA) in dichloromethane-d2. This crystallization process has been studied previously10 by in situ liquid-state 1H and 19F NMR at a MAS frequency of 12 kHz. BA and PFBA form a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal material90–92 based on a π-stacked structure with the phenyl and pentafluorophenyl rings of the BA and PFBA molecules alternating along each stack and with hydrogen-bonding between BA and PFBA molecules in adjacent stacks. In the previous in situ liquid-state 1H NMR study,10 no changes were observed in the early stages of the experiment (indicating that no crystallization occurred), but the 1H NMR spectrum changed abruptly after about 39 min, with a significant decrease in peak intensities signifying sudden dilution of the solution phase as a result of rapid crystallization. The significant lag time before crystallization occurs is consistent with slow nucleation kinetics; during this time, the supersaturated solution is “waiting” for a rare (stochastic) nucleation event, which then triggers a significant amount of rapid crystallization. The abrupt crystallization event is also associated with significant shifts in the positions of peaks in the liquid-state 1H NMR spectrum, reflecting changes in the intermolecular interactions in the solution phase.10
1 co-crystal material90–92 based on a π-stacked structure with the phenyl and pentafluorophenyl rings of the BA and PFBA molecules alternating along each stack and with hydrogen-bonding between BA and PFBA molecules in adjacent stacks. In the previous in situ liquid-state 1H NMR study,10 no changes were observed in the early stages of the experiment (indicating that no crystallization occurred), but the 1H NMR spectrum changed abruptly after about 39 min, with a significant decrease in peak intensities signifying sudden dilution of the solution phase as a result of rapid crystallization. The significant lag time before crystallization occurs is consistent with slow nucleation kinetics; during this time, the supersaturated solution is “waiting” for a rare (stochastic) nucleation event, which then triggers a significant amount of rapid crystallization. The abrupt crystallization event is also associated with significant shifts in the positions of peaks in the liquid-state 1H NMR spectrum, reflecting changes in the intermolecular interactions in the solution phase.10
In the present work, we have investigated the same crystallization system by in situ liquid-state 1H NMR, with experiments carried out using different values of MAS frequency and with all other experimental conditions identical. In these experiments, an undersaturated solution containing a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of BA and PFBA in dichloromethane-d2 at 50 °C was subjected to quench cooling (in less than ca. 5 min) to 20 °C, with the crystallization solution then maintained at 20 °C for the remainder of the experiment. We note that, in order to ensure that the crystallization experiments at different MAS frequencies are all carried out with the same true temperature of the sample (20 °C), it is critically important to apply the method for temperature calibration (which takes into account the heating effects due to MAS) described in Section 2.6.2.
1 molar ratio of BA and PFBA in dichloromethane-d2 at 50 °C was subjected to quench cooling (in less than ca. 5 min) to 20 °C, with the crystallization solution then maintained at 20 °C for the remainder of the experiment. We note that, in order to ensure that the crystallization experiments at different MAS frequencies are all carried out with the same true temperature of the sample (20 °C), it is critically important to apply the method for temperature calibration (which takes into account the heating effects due to MAS) described in Section 2.6.2.
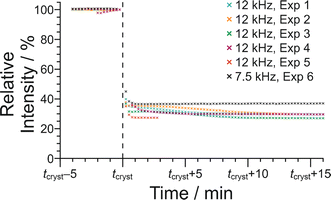
The results from the in situ liquid-state 1H NMR experiments, summarized in Fig. 8, exhibit two types of behaviour: (i) the occurrence of an abrupt crystallization event of the type observed previously (identified by a sudden decrease in the intensities of the peaks in the liquid-state 1H NMR spectrum and shifts in the peak positions, as shown in Fig. 9), or (ii) no evidence of crystallization throughout the duration of the experiment. From Fig. 8, it is clear that there is a higher probability of crystallization occurring at higher MAS frequency (νMAS). Thus, in all five experiments at νMAS = 12 kHz, the abrupt crystallization event occurred within 2.6 h of the start of the experiment, with an average time of 0.89 h. In contrast, for experiments at lower MAS frequency, crystallization was observed only in one case (at νMAS = 7.5 kHz), with the abrupt crystallization event occurring at ca. 8.3 h. For all other experiments (at νMAS = 3 kHz, 7.5 kHz, 10 kHz), no crystallization was observed within the duration of the experiment, which included experiments as long as 43 h at νMAS = 3 kHz and 25 h at νMAS = 7.5 kHz.
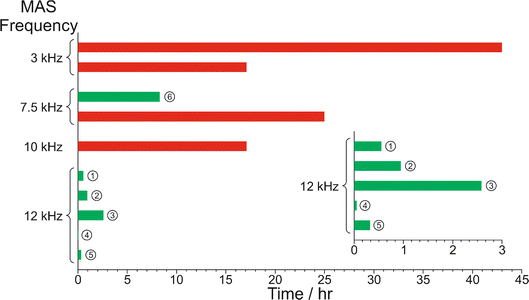 | ||
| Fig. 8 Summary of results from the in situ liquid-state 1H NMR study of crystallization of the BA–PFBA co-crystal material at different MAS frequencies. Each experiment is represented by a horizontal bar. Experiments in which crystallization was observed to occur are labelled 1–6, and are represented by a green bar; in each case, the length of the bar indicates the time at which the abrupt crystallization event occurred. Experiments in which crystallization was not observed are represented by a red bar; in each case, the length of the bar indicates the total time over which 1H NMR data were measured. More information about experiments 1–6 is given in Table 2. | ||
We now discuss the results of the experiments in which crystallization was observed to occur, specifically experiments 1–5 at νMAS = 12 kHz and experiment 6 at νMAS = 7.5 kHz, focusing on the peak for the 1H environment in the carboxylic acid group (which represents the average 1H environment due to proton exchange between BA and PFBA molecules). In this regard, it is instructive to consider the changes in both the signal intensity and the 1H NMR chemical shift for this peak as a function of time during the crystallization process, and details of the results are given in Table 2 and Fig. 10.
| Experiment | Analysis of experiments 1–5 | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | Mean | S.D. | |
| ν MAS/kHz | 12 | 12 | 12 | 12 | 12 | 7.5 | — | — |
| t cryst/min | 33.25 | 56.75 | 155 | 3.25 | 19.5 | 497.5 | — | — |
| t total/min | 49.75 | 129 | 43.5 | 21.25 | 22.25 | 769 | — | — |
| ΔIcryst/% | −60.12 | −62.21 | −63.16 | — | −64.92 | −54.99 | −62.60 | 2.00 |
| ΔIfinal/% | −70.32 | −69.76 | −72.91 | −70.43 | — | −61.35 | −70.86 | 1.40 |
| Δδcryst/ppm | −0.690 | −0.729 | −0.747 | — | −0.735 | −0.641 | −0.725 | 0.025 |
| Δδfinal/ppm | −0.782 | −0.809 | −0.839 | −0.784 | — | −0.715 | −0.804 | 0.027 |
In Fig. 10, the signal intensity is shown as a function of time in the region of the abrupt crystallization event (which occurs at time tcryst; see Table 2). In all cases, the abrupt crystallization event is associated with a sudden decrease in signal intensity, denoted ΔIcryst, which is defined as the change in peak intensity between the spectrum recorded immediately before the abrupt crystallization event and the spectrum recorded immediately after completion of this event. For a period of about 10 min after the abrupt crystallization event, a further gradual decrease in signal intensity is observed (see Fig. 10), and the intensity then remains constant for the remainder of the experiment, indicating that the crystallization system had reached equilibrium. We also consider the total decrease in signal intensity during the entire crystallization process, denoted ΔIfinal, which is defined as the change in peak intensity between the spectrum recorded immediately before the abrupt crystallization event and the final spectrum recorded at the end of the experiment. We note that experiment 4 did not give a reliable value of ΔIcryst as crystallization occurred before the sample temperature had reached 20 °C, and experiment 5 did not give a reliable value of ΔIfinal as this experiment was stopped a few minutes after the abrupt crystallization event (i.e., before the system had reached equilibrium).
For the experiments at νMAS = 12 kHz, the change in signal intensity corresponding to the abrupt crystallization event (ΔIcryst; see Table 2) is between −60.1% and −64.9% [mean value 〈ΔIcryst〉 = −62.6%; standard deviation σ(ΔIcryst) = 2.0%; based on the results from experiments 1, 2, 3 and 5], and the change in signal intensity after completing the crystallization process (ΔIfinal; see Table 2) is between −69.8% and −72.9% [〈ΔIfinal〉 = −70.9%; σ(ΔIfinal) = 1.4%; based on the results from experiments 1, 2, 3 and 4]. In contrast, for the crystallization process observed at νMAS = 7.5 kHz (experiment 6), the changes in signal intensity are significantly smaller, with ΔIcryst = −55.0% and ΔIfinal = −61.4%. These results indicate that a significantly lower amount of solid phase is produced in the crystallization process at νMAS = 7.5 kHz compared to νMAS = 12 kHz, both immediately after the abrupt crystallization event and after the crystallization system had reached equilibrium. While these conclusions are based on a relatively small number of observations, the differences in crystallization behaviour at the different MAS frequencies are nonetheless significant. Thus, the difference between the value of ΔIcryst at 7.5 kHz and the mean value 〈ΔIcryst〉 at νMAS = 12 kHz is 7.6%, which is greater than 3 times the standard deviation [σ(ΔIcryst)] in the values of ΔIcryst at νMAS = 12 kHz. Similarly, the difference between the value of ΔIfinal at νMAS = 7.5 kHz and the mean value 〈ΔIfinal〉 at νMAS = 12 kHz is 9.5%, which is greater than 6 times the standard deviation [σ(ΔIfinal)] in the values of ΔIfinal at νMAS = 12 kHz.
From the results for ΔIfinal, the fact that the amount of solid phase produced after the crystallization process had reached equilibrium is significantly higher at νMAS = 12 kHz compared to νMAS = 7.5 kHz indicates that the solubility of the BA–PFBA co-crystal at 20 °C is lower under conditions of higher MAS frequency. Furthermore, as the concentration of the supersaturated solution at 20 °C before crystallization was the same in all experiments, it follows (given the lower solubility at νMAS = 12 kHz) that the supersaturation of the solution at 20 °C before crystallization occurred would have been higher at νMAS = 12 kHz than at νMAS = 7.5 kHz, which is fully consistent with the observation from our results that crystal nucleation (which triggers the abrupt crystallization event) occurs after a significantly shorter time at νMAS = 12 kHz, resulting in the lower values of tcryst observed (see Fig. 8 and Table 2).
The 1H NMR chemical shift due to the 1H environment in the carboxylic acid groups also changes significantly at the abrupt crystallization event (see Fig. 9), moving suddenly to lower chemical shift. The change in chemical shift associated with the abrupt crystallization event, denoted Δδcryst (Table 2), is measured from the same spectra used to determine ΔIcryst (as defined above). After the abrupt crystallization event, the chemical shift continues to change gradually before reaching a constant value. The total change in chemical shift during the entire crystallization process, denoted Δδfinal (Table 2), is measured from the same spectra used to determine ΔIfinal (as defined above). As shown in Table 2, both Δδcryst and Δδfinal are significantly larger at νMAS = 12 kHz than at νMAS = 7.5 kHz. Specifically, the difference between the value of Δδcryst = −0.641 ppm at νMAS = 7.5 kHz and the mean value 〈Δδcryst〉 = −0.725 ppm at νMAS = 12 kHz is 0.084 ppm, which is greater than 3 times the standard deviation [σ(Δδcryst) = 0.025 ppm] in the values of Δδcryst at νMAS = 12 kHz. Similarly, the difference between the value of Δδfinal = −0.715 ppm at νMAS = 7.5 kHz and the mean value 〈Δδfinal〉 = −0.804 ppm at νMAS = 12 kHz is 0.089 ppm, which is greater than 3 times the standard deviation [σ(Δδfinal) = 0.027 ppm] in the values of Δδfinal at νMAS = 12 kHz.
The fact that both Δδcryst and Δδfinal depend on the MAS frequency is clearly related to the fact, discussed above, that crystallization at the higher MAS frequency (νMAS = 12 kHz) produces a solution of lower concentration both immediately after the abrupt crystallization event and after the crystallization process reaches equilibrium. Clearly, the different concentrations of the solution phases produced following crystallization at the different MAS frequencies give rise to differences in the nature and extent of the intermolecular interactions in these solutions (including hydrogen-bonding involving the carboxylic acid groups of the BA and PFBA molecules), which will have a direct consequence on the 1H NMR chemical shifts observed. Furthermore, the solution-state chemical shifts at different MAS frequencies may also be influenced directly by the pressure effects arising from MAS, including perturbations in the nature of the intermolecular interactions (for example, slight changes in average hydrogen-bond distances) resulting from the density gradients induced within the solution by the application of MAS.
Clearly, these preliminary results highlight the fact that important differences in the nature of crystallization systems may arise as a function of MAS frequency, and more detailed investigations into the fundamental origin of these effects are merited. Furthermore, these observations raise the possibility that rapid macroscopic sample spinning may have a well-defined effect on the nature of crystallization solutions and their crystallization behaviour, which suggests that the rate of sample spinning could potentially be used as an experimental variable in controlling the behaviour and outcome of crystallization processes in such cases.
4. Concluding remarks
There is now considerable scope to apply in situ solid-state NMR strategies to study the evolution of the solid phase during crystallization processes, allowing details of the formation and transformation of intermediate solid phases produced on crystallization pathways to be understood. The CLASSIC NMR strategy significantly extends the scope of in situ NMR monitoring of crystallization from solution by establishing simultaneous and complementary information on the time-evolution of both the solid and liquid phases. The results of in situ NMR studies of crystallization processes presented in this article, some of which are preliminary investigations into new aspects of this field, have been selected to stimulate discussion that may lead to improved understanding on specific aspects of the application of NMR methodology in this field. With the development of new and more powerful NMR strategies to explore the time-dependence of crystallization systems, we are confident that this field will advance significantly in the coming years.5. Methods
5.1 Instrumentation
NMR experiments were carried out on two different instruments: (a) a Bruker AVANCE III NMR spectrometer (20.0 T; 13C Larmor frequency, 213.8 MHz) at the UK High-Field (850 MHz) Solid-State NMR Facility based at the University of Warwick, and (b) a Bruker AVANCE III HD NMR spectrometer (9.4 T; 13C Larmor frequency, 100.64 MHz) at Cardiff University.5.2 Experiments in Section 3.1
The experiments reported in Section 3.1 were carried out on the Warwick instrument using an HXY 4 mm probe, with the crystallization solution [comprising 1-13C-glycine in a water–glycerol solution (5% glycerol by volume)] contained in an HR-MAS insert (made from Kel-F). The concentration of the solution was 3.17 mol dm−3. The CLASSIC NMR study was carried out by subjecting the crystallization solution to quench cooling (in about 5 min) from +20 °C to −10 °C, with a MAS frequency of 12 kHz. The CLASSIC NMR measurements involved the following pulse sequences in the repeating group: (a) 1H→13C CP NMR (CP contact time = 2 ms; high-power 1H decoupling; recycle delay = 6 s), and (b) direct-excitation 13C NMR (high-power 1H decoupling; recycle delay = 3 s). The time-resolution of the CLASSIC NMR study was 2.56 min.5.3 Experiments in Section 3.2
The experiments reported in Section 3.2 were carried out on the Warwick instrument using an HX 4 mm probe, with the crystallization solution (comprising 1-13C-glycine in water) contained in an HR-MAS insert (made from Kel-F). The concentration of the solution was 5.80 mol dm−3. The CLASSIC NMR study was carried out on subjecting the crystallization solution to controlled cooling (at a rate of 0.056 °C min−1) from 65 °C to 20 °C, with a MAS frequency of 12 kHz. The CLASSIC NMR measurements involved the following pulse sequences in the repeating group: (a) 1H→13C CP NMR (CP contact time = 2 ms; high-power 1H decoupling; recycle delay = 5 s), and (b) direct-excitation 13C NMR (high-power 1H decoupling; recycle delay = 5 s). The time-resolution of the CLASSIC NMR study was 2.68 min.5.4 Experiments in Section 3.3
The experiments reported in Section 3.3 were carried out on the Cardiff instrument using an HX 4 mm probe, with the multi-crystal sample of the 1,8-dibromooctane/urea inclusion compound soaked in pure liquid tetradecane contained in an HR-MAS insert (made from Kel-F). The CLASSIC NMR study was carried out to monitor the evolution of the guest exchange process as a function of time at 20 °C, with a MAS frequency of 10 kHz. The CLASSIC NMR measurements involved the following pulse sequences in the repeating group: (a) 1H→13C CP NMR (CP contact time = 2 ms; high-power 1H decoupling; recycle delay = 5 s), (b) direct-excitation 13C NMR (high-power 1H decoupling; recycle delay = 3 s), and (c) 1H NMR. The time-resolution of the CLASSIC NMR study was 8.75 min.5.5 Experiments in Section 3.4
The experiments reported in Section 3.4 were carried out on the Cardiff instrument using an HX 4 mm probe, with the crystallization solution [comprising benzoic acid and pentafluorobenzoic acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio) in dichloromethane-d2] contained in an HR-MAS insert (made from Kel-F). The concentration of the solution was 1.99 mol dm−3 for both benzoic acid and pentafluorobenzoic acid. In each experiment, the solution was cooled from 50 °C to 20 °C using the quench cooling protocol. The evolution of the crystallization system was monitored as a function of time at 20 °C using liquid-state 1H NMR measurements, with different MAS frequencies (3 kHz, 7.5 kHz, 10 kHz or 12 kHz) used in different experiments. The time-resolution of the in situ liquid-state 1H NMR study was 15 s.
1 molar ratio) in dichloromethane-d2] contained in an HR-MAS insert (made from Kel-F). The concentration of the solution was 1.99 mol dm−3 for both benzoic acid and pentafluorobenzoic acid. In each experiment, the solution was cooled from 50 °C to 20 °C using the quench cooling protocol. The evolution of the crystallization system was monitored as a function of time at 20 °C using liquid-state 1H NMR measurements, with different MAS frequencies (3 kHz, 7.5 kHz, 10 kHz or 12 kHz) used in different experiments. The time-resolution of the in situ liquid-state 1H NMR study was 15 s.
Data availability
Supporting experimental data for this article may be accessed at: https://doi.org/10.17035/d.2024.0325941060.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to the UK High-Field Solid-State NMR Facility for the award of significant amounts of time for our research in this field, to EPSRC and Diamond Light Source for the award of a PhD studentship (to R. P.), and to Cardiff University for support. The UK High-Field Solid-State NMR Facility was funded by EPSRC and BBSRC (contract reference PR140003), as well as the University of Warwick, including part funding through Birmingham Science City Advanced Materials Projects 1 and 2 supported by Advantage West Midlands and the European Regional Development Fund.References
- L. Addadi and S. Weiner, Phys. Scr., 2014, 89, 098003 CrossRef CAS
.
- J. J. De Yoreo, P. U. P. A. Gilbert, N. A. J. M. Sommerdijk, R. L. Penn, S. Whitelam, D. Joester, H. Zhang, J. D. Rimer, A. Navrotsky, J. F. Banfield, A. F. Wallace, F. M. Michel, F. C. Meldrum, H. Cölfen and P. M. Dove, Science, 2015, 349, aaa6760 CrossRef PubMed
.
- X. Ye, M. R. Jones, L. B. Frechette, Q. Chen, A. S. Powers, P. Ercius, G. Dunn, G. M. Rotskoff, S. C. Nguyen, V. P. Adiga, A. Zettl, E. Rabani, P. L. Geissler and A. P. Alivisatos, Science, 2016, 354, 874–877 CrossRef CAS PubMed
.
- A. G. Shtukenberg, M. D. Ward and B. Kahr, Chem. Rev., 2017, 117, 14042–14090 CrossRef CAS PubMed
.
- M. J. V. Vleet, T. Weng, X. Li and J. R. Schmidt, Chem. Rev., 2018, 118, 3681–3721 CrossRef PubMed
.
- F. C. Meldrum and C. O'Shaughnessy, Adv. Mater., 2020, 32, 2001068 CrossRef CAS
.
- N. Fellah, I. J. C. D. Cruz, B. G. Alamani, A. G. Shtukenberg, A. V. Pandit, M. D. Ward and A. S. Myerson, Cryst. Growth Des., 2024, 24, 3527–3558 CrossRef CAS
.
- N. Pienack and W. Bensch, Angew. Chem., Int. Ed., 2011, 50, 2014–2034 CrossRef CAS PubMed
.
- K. D. M. Harris, C. E. Hughes and P. A. Williams, Solid State Nucl. Magn. Reson., 2015, 65, 107–113 CrossRef CAS PubMed
.
- C. E. Hughes, P. A. Williams, V. L. Keast, V. G. Charalampopoulos, G. R. Edwards-Gau and K. D. M. Harris, Faraday Discuss., 2015, 179, 115–140 RSC
.
- K. D. M. Harris, C. E. Hughes, P. A. Williams and G. R. Edwards-Gau, Acta Crystallogr., Sect. C: Struct. Chem., 2017, 73, 137–148 CrossRef CAS
.
- M. Juramy and G. Mollica, Curr. Opin. Colloid Interface Sci., 2023, 63, 101663 CrossRef CAS
.
-
K. D. M. Harris and C. E. Hughes, in Modern NMR Crystallography: Concepts and Applications, ed. D. L. Bryce, RSC, Cambridge, 2024 Search PubMed
.
- C. E. Hughes, P. A. Williams and K. D. M. Harris, Angew. Chem., Int. Ed., 2014, 53, 8939–8943 CrossRef CAS
.
- C. E. Hughes, P. A. Williams, T. R. Peskett and K. D. M. Harris, J. Phys. Chem. Lett., 2012, 3, 3176–3181 CrossRef CAS
.
- C. E. Hughes, P. A. Williams, B. M. Kariuki and K. D. M. Harris, ChemPhysChem, 2018, 19, 3341–3345 CrossRef CAS
.
- C. L. Jones, C. E. Hughes, H. H.-M. Yeung, A. Paul, K. D. M. Harris and T. L. Easun, Chem. Sci., 2021, 12, 1486–1494 RSC
.
- C. E. Hughes, B. Walkley, L. J. Gardner, S. A. Walling, S. A. Bernal, D. Iuga, J. L. Provis and K. D. M. Harris, Solid State Nucl. Magn. Reson., 2019, 99, 1–6 CrossRef CAS PubMed
.
- C. E. Hughes and K. D. M. Harris, Chem. Commun., 2010, 46, 4982–4984 RSC
.
- C. E. Hughes and K. D. M. Harris, J. Phys. Chem. A, 2008, 112, 6808–6810 CrossRef CAS PubMed
.
- J. D. Epping and B. F. Chmelka, Curr. Opin. Colloid Interface Sci., 2006, 11, 81–117 CrossRef CAS
.
- A. Aerts, C. E. A. Kirschhock and J. A. Martens, Chem. Soc. Rev., 2010, 39, 4626–4642 RSC
.
- G. Férey, M. Haouas, T. Loiseau and F. Taulelle, Chem. Mater., 2014, 26, 299–309 CrossRef
.
- M. Haouas, Materials, 2018, 11, 1416 CrossRef PubMed
.
- S. A. Morris, G. P. M. Bignami, Y. Tian, M. Navarro, D. S. Firth, J. Čejka, P. S. Wheatley, D. M. Dawson, W. A. Slawinski, D. S. Wragg, R. E. Morris and S. E. Ashbrook, Nat. Chem., 2017, 9, 1012–1018 CrossRef CAS PubMed
.
- I. I. Ivanova, Y. G. Kolyagin, I. A. Kasyanov, A. V. Yakimov, T. O. Bok and D. N. Zarubin, Angew. Chem., Int. Ed., 2017, 56, 15344–15347 CrossRef CAS
.
- I. I. Ivanova, E. P. Andriako, I. A. Kostyukov, D. S. Zasukhin, D. A. Fedosov and D. N. Zarubin, Cryst. Growth Des., 2023, 23, 5677–5689 CrossRef CAS
.
- T. Deuchande, O. Breton, J. Haedelt and E. Hughes, J. Magn. Reson., 2006, 183, 178–182 CrossRef PubMed
.
- Z. Zhao, S. Xu, M. Y. Hu, X. Bao and J. Z. Hu, J. Phys. Chem. C, 2016, 120, 1701–1708 CrossRef CAS
.
- A. Spitaleri, C. A. Hunter, J. F. McCabe, M. J. Packer and S. L. Cockroft, CrystEngComm, 2004, 6, 489–493 RSC
.
- M. Kimura, Cryst. Growth Des., 2006, 6, 854–860 CrossRef CAS
.
- C. E. Hughes, S. Hamad, K. D. M. Harris, C. R. A. Catlow and P. C. Griffiths, Faraday Discuss., 2007, 136, 71–89 RSC
.
- C. A. Hunter, J. F. McCabe and A. Spitaleri, CrystEngComm, 2012, 14, 7115–7117 RSC
.
- A. Bērziņš, A. Semjonova, A. Actiņš and M. Salvalaglio, Cryst. Growth Des., 2021, 21, 4823–4836 CrossRef
.
- R. Mashiach, H. Weissman, L. Avram, L. Houben, O. Brontvein, A. Lavie, V. Arunachalam, M. Leskes, B. Rybtchinski and A. Bar-Shir, Nat. Commun., 2021, 12, 229 CrossRef CAS PubMed
.
- E. Turhan, C. Pötzl, W. Keil, M. Negroni, K. Kouřil, B. Meier, J. A. Romero, K. Kazimierczuk, I. Goldberga, T. Azaïs and D. Kurzbach, J. Phys. Chem. C, 2023, 127, 19591–19598 CrossRef CAS
.
- E. M. M. Weber, T. Kress, D. Abergel, S. Sewsurn, T. Azaïs and D. Kurzbach, Anal. Chem., 2020, 92, 7666–7673 CrossRef CAS
.
- R. Ghosh Biswas, R. Soong, A. Jenne, M. Bastawrous, M. J. Simpson and A. J. Simpson, Angew. Chem., Int. Ed., 2023, 62, e202216105 CrossRef CAS PubMed
.
- P. C. Vioglio, P. Thureau, M. Juramy, F. Ziarelli, S. Viel, P. A. Williams, C. E. Hughes, K. D. M. Harris and G. Mollica, J. Phys. Chem. Lett., 2019, 10, 1505–1510 CrossRef CAS PubMed
.
- Q. Z. Ni, E. Daviso, T. V. Can, E. Markhasin, S. K. Jawla, T. M. Swager, R. J. Temkin, J. Herzfeld and R. G. Griffin, Acc. Chem. Res., 2013, 46, 1933–1941 CrossRef CAS
.
- A. J. Rossini, A. Zagdoun, M. Lelli, A. Lesage, C. Copéret and L. Emsley, Acc. Chem. Res., 2013, 46, 1942–1951 CrossRef CAS PubMed
.
- L. Zhao, A. C. Pinon, L. Emsley and A. J. Rossini, Magn. Reson. Chem., 2018, 56, 583–609 CrossRef CAS
.
- I. B. Moroz and M. Leskes, Annu. Rev. Mater. Res., 2022, 52, 25–55 CrossRef CAS
.
- M. Juramy, R. Chèvre, P. C. Vioglio, F. Ziarelli, E. Besson, S. Gastaldi, S. Viel, P. Thureau, K. D. M. Harris and G. Mollica, J. Am. Chem. Soc., 2021, 143, 6095–6103 CrossRef CAS
.
- M. Juramy, P. C. Vioglio, F. Ziarelli, S. Viel, P. Thureau and G. Mollica, Solid State Nucl. Magn. Reson., 2022, 122, 101836 CrossRef CAS PubMed
.
- A. L. Van Geet, Anal. Chem., 1968, 40, 2227–2229 CrossRef CAS
.
- A. L. Van Geet, Anal. Chem., 1970, 42, 679–680 CrossRef CAS
.
- A. E. Aliev and K. D. M. Harris, Magn. Reson. Chem., 1994, 32, 366–369 CrossRef CAS
.
- A. Bielecki and D. P. Burum, J. Magn. Reson., Ser. A, 1995, 116, 215–220 CrossRef CAS
.
- G. Albrecht and R. B. Corey, J. Am. Chem. Soc., 1939, 61, 1087–1103 CrossRef CAS
.
- Y. Iitaka, Acta Crystallogr., 1960, 13, 35–45 CrossRef CAS
.
- Y. Iitaka, Acta Crystallogr., 1961, 14, 1–10 CrossRef CAS
.
- P.-G. Jönsson and Å. Kvick, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 1827–1833 CrossRef
.
- Å. Kvick, W. M. Canning, T. F. Koetzle and G. J. B. Williams, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 115–120 CrossRef
.
- G. L. Perlovich, L. K. Hansen and A. Bauer-Brandl, J. Therm. Anal. Calorim., 2001, 66, 699–715 CrossRef CAS
.
- E. V. Boldyreva, V. A. Drebushchak, T. N. Drebushchak, I. E. Paukov, Y. A. Kovalevskaya and E. S. Shutova, J. Therm. Anal. Calorim., 2003, 73, 409–418 CrossRef CAS
.
- R. E. Taylor, Concepts Magn. Reson., 2004, 22A, 79–89 CrossRef CAS
.
- P. C. Vioglio, G. Mollica, M. Juramy, C. E. Hughes, P. A. Williams, F. Ziarelli, S. Viel, P. Thureau and K. D. M. Harris, Angew. Chem., Int. Ed., 2018, 57, 6619–6623 CrossRef PubMed
.
- W. Xu, Q. Zhu and C. Hu, Angew. Chem., Int. Ed., 2017, 56, 2030–2034 CrossRef CAS
.
- M. J. Potrzebowski, P. Tekely and Y. Dusausoy, Solid State Nucl. Magn. Reson., 1998, 11, 253–257 CrossRef CAS
.
- A. Nowacka, P. C. Mohr, J. Norrman, R. W. Martin and D. Topgaard, Langmuir, 2010, 26, 16848–16856 CrossRef CAS
.
- J. Kestin, M. Sokolov and W. A. Wakeham, J. Phys. Chem. Ref. Data, 1978, 7, 941–948 CrossRef CAS
.
- W. Kolodziejski and J. Klinowski, Chem. Rev., 2002, 102, 613–628 CrossRef CAS PubMed
.
- K. D. M. Harris and M. D. Hollingsworth, Proc. R. Soc. London, Ser. A, 1990, 431, 245–269 CrossRef CAS
.
- K. D. M. Harris, J. Solid State Chem., 1993, 106, 83–98 CrossRef CAS
.
- K. D. M. Harris, J. Mol. Struct., 1996, 374, 241–250 CrossRef CAS
.
- M. D. Hollingsworth, M. E. Brown, A. C. Hillier, B. D. Santarsiero and J. D. Chaney, Science, 1996, 273, 1355–1359 CrossRef CAS
.
- S. van Smaalen and K. D. M. Harris, Proc. R. Soc. London, Ser. A, 1996, 452, 677–700 CrossRef CAS
.
- F. Guillaume, J. Chim. Phys., 1999, 96, 1295–1315 CrossRef CAS
.
- M. D. Hollingsworth, Science, 2002, 295, 2410–2413 CrossRef CAS
.
- K. D. M. Harris, Supramol. Chem., 2007, 19, 47–53 CrossRef CAS
.
- A. R. George and K. D. M. Harris, J. Mol. Graphics, 1995, 13, 138–141 CrossRef CAS PubMed
.
- M. S. Greenfield, R. L. Vold and R. R. Vold, Mol. Phys., 1989, 66, 269–298 CrossRef CAS
.
- K. D. M. Harris and P. Jonsen, Chem. Phys. Lett., 1989, 154, 593–598 CrossRef CAS
.
- F. Guillaume, C. Sourisseau and A. J. Dianoux, J. Chem. Phys., 1990, 93, 3536–3541 CrossRef CAS
.
- P. Girard, A. E. Aliev, F. Guillaume, K. D. M. Harris, M. D. Hollingsworth, A.-J. Dianoux and P. Jonsen, J. Chem. Phys., 1998, 109, 4078–4089 CrossRef CAS
.
- A. A. Khan, S. T. Bramwell, K. D. M. Harris, B. M. Kariuki and M. R. Truter, Chem. Phys. Lett., 1999, 307, 320–326 CrossRef CAS
.
- J. Marti-Rujas, A. Desmedt, K. D. M. Harris and F. Guillaume, J. Am. Chem. Soc., 2004, 126, 11124–11125 CrossRef CAS PubMed
.
- J. Martí-Rujas, K. D. M. Harris, A. Desmedt and F. Guillaume, J. Phys. Chem. B, 2006, 110, 10708–10713 CrossRef
.
- J. Martí-Rujas, A. Desmedt, K. D. M. Harris and F. Guillaume, J. Phys. Chem. B, 2007, 111, 12339–12344 CrossRef PubMed
.
- J. Martí-Rujas, A. Desmedt, K. D. M. Harris and F. Guillaume, J. Phys. Chem. C, 2009, 113, 736–743 CrossRef
.
- A. Mahdyarfar and K. D. M. Harris, J. Chem. Soc., Chem. Commun., 1993, 51–53 RSC
.
- B. A. Palmer, A. Le Comte, K. D. M. Harris and F. Guillaume, J. Am. Chem. Soc., 2013, 135, 14512–14515 CrossRef CAS PubMed
.
- M. D. Hollingsworth and N. Cyr, Mol. Cryst. Liq. Cryst., 1990, 187, 135–144 CrossRef
.
- M. D. Hollingsworth and A. R. Palmer, J. Am. Chem. Soc., 1993, 115, 5881–5882 CrossRef CAS
.
- K. D. M. Harris and P. E. Jupp, Proc. R. Soc. London, Ser. A, 1997, 453, 333–352 CrossRef CAS
.
- M. Guerain, J. Pharm. Sci., 2020, 109, 2640–2653 CrossRef CAS PubMed
.
- S. A. Moggach, S. Parsons and P. A. Wood, Crystallogr. Rev., 2008, 14, 143–184 CrossRef CAS
.
- M. Xu and K. D. M. Harris, J. Am. Chem. Soc., 2005, 127, 10832–10833 CrossRef CAS PubMed
.
- M. Gdaniec, W. Jankowski, M. J. Milewska and T. Połoñski, Angew. Chem., Int. Ed., 2003, 42, 3903–3906 CrossRef CAS
.
- D. Albesa-Jové, B. M. Kariuki, S. J. Kitchin, L. Grice, E. Y. Cheung and K. D. M. Harris, ChemPhysChem, 2004, 5, 414–418 CrossRef
.
- L. S. Reddy, A. Nangia and V. M. Lynch, Cryst. Growth Des., 2004, 4, 89–94 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2025 |