Open Access Article
Open Access ArticleA machine learning approach for dynamical modelling of Al distributions in zeolites via23Na/27Al solid-state NMR†
Chen
Lei
 a,
Carlos
Bornes
a,
Carlos
Bornes
 a,
Oscar
Bengtsson
b,
Andreas
Erlebach
a,
Oscar
Bengtsson
b,
Andreas
Erlebach
 a,
Ben
Slater
a,
Ben
Slater
 b,
Lukas
Grajciar
b,
Lukas
Grajciar
 a and
Christopher J.
Heard
a and
Christopher J.
Heard
 *a
*a
aDepartment of Physical and Macromolecular Chemistry, Faculty of Science, Charles University in Prague, 12483, Czech Republic. E-mail: heardc@natur.cuni.cz
bDepartment of Chemistry, University College London, 20 Gordon Street, London, WC1H 0AJ, UK
First published on 3rd June 2024
Abstract
One of the main limitations in supporting experimental characterization of Al siting/pairing via modelling is the high computational cost of ab initio calculations. For this reason, most works rely on static or very short dynamical simulations, considering limited Al pairing/siting combinations. As a result, comparison with experiment suffers from a large degree of uncertainty. To alleviate this limitation we have developed neural network potentials (NNPs) which can dynamically sample across broad configurational and chemical spaces of sodium-form aluminosilicate zeolites, preserving the level of accuracy of the ab initio (dispersion-corrected metaGGA) training set. By exploring a wide range of Al/Na arrangements and a combination of experimentally relevant Si/Al ratios, we found that the 23Na NMR spectra of dehydrated high-silica CHA zeolite offer an opportunity to assess the distribution and pairing of Al atoms. We observed that the 23Na chemical shift is sensitive not only to the location of sodium in 6- and 8MRs, but also to the Al–Sin–Al sequence length. Furthermore, neglect of thermal and dynamical contributions was found to lead to errors of several ppm, and has a profound influence on the shape of the spectra and the dipolar coupling constants, thus necessitating the long-term dynamical simulations made feasible by NNPs. Finally, we obtained a predictive regression model for the 23Na chemical shift in CHA (Si/Al = 35, 17, 11) that circumvents the need for expensive NMR density functional calculations and can be easily extended to other zeolite frameworks. By combining NNPs and regression methods, we can expedite the simulations of NMR properties and capture the effect of dynamics on the spectra, which is often overlooked in computational studies despite its clear manifestation in experimental setups.
1 Introduction
In aluminosilicate zeolite solid acid catalysts, the nature (Brønsted vs. Lewis), activity and selectivity of active site is intricately related to the position of Al atoms within the framework and the distribution of non-framework cations, both of which evolve during operation. Depending on the Al siting among inequivalent framework sites, and on the relative positions of Al atoms to one another, the acid site may be placed in a particular environment that can be utilized to direct the mechanism and selectivity of catalytic reactions.1–3 Although numerous studies have attempted to elucidate the Al distributions by combining experimental methods, namely solid-state NMR, FTIR and UV/vis of Co2+-exchanged zeolites,4,5 along with the support of computational calculations, we have yet to find a definitive way to identify the siting and pairing of Al atoms in zeolites.In general, solid-state NMR spectroscopy is a promising technique as it provides direct information about the chemical environment surrounding both framework atoms, such as 17O, 29Si, 27Al, as well as extraframework atoms, such as 1H, 23Na, etc.6,7 In siliceous zeolites, 29Si NMR can be used to identify the topology of different frameworks.8 In aluminosilicate zeolites, 29Si NMR is often used to identify changes in the amount of neighbouring Al atoms, as these gives rise to different 29Si chemical shifts. Unfortunately, defective species such as SiOH groups result in 29Si resonances in the same region of Si atoms surrounded by Al atoms, thus hindering the identification of Al pairs.9,1027Al solid-state NMR is routinely used to detect the coordination of Al species (4-, 5- or 6-coordinated) and provides information about the decomposition of the framework under reactive or hydrolytic stress, by tracing the formation of extraframework Lewis acid sites, and extended framework Al species.11–15 However, from the perspective of pinpointing the precise location of Al within zeolite frameworks, 1D 27Al is limited by quadrupolar broadening, which can be overcome in multiple-quantum magic-angle spinning (MQMAS) experiments. Although some studies have combined MQMAS experiments with computational calculations to predict the 27Al isotropic chemical shift at various T sites,16,17 these studies are generally unable to reproduce the dynamical effects that significantly impact the observed chemical shift, that lead to the overlap of 27Al resonances arising from crystallographically inequivalent sites.18
Multinuclear experiments have been applied to narrow down Al locations, notably the application of 27Al and 23Na NMR, which combines signals from framework Al sites with those of Na counter-cations to obtain additional structural information. Previous studies showed that 23Na NMR can provide information about the Na and Al siting on dehydrated CHA19 and FER.20 The position of both Na and Al atoms was studied on MOR with different Si/Al ratios using 2D D-HMQC 23Na–27Al experiments, which allow an increase in the resolution of 27Al dimension and observe Al species that are not observed in 1D 27Al experiments.21 All the aforementioned studies used 23Na MQMAS to remove the quadrupolar broadening inherent to 1D 23Na experiments and retrieved information about the 23Na isotropic chemical shift, quadrupolar coupling constant (CQ) and the asymmetric parameter (ηQ): values that combine to predict the position and shape of the spectrum, and can be readily compared with those obtained from DFT NMR calculations. However, such calculations are generally limited by the high cost of ab initio calculations, and thus only consider either static structural models or short molecular dynamics simulations up to tens of picoseconds, to explore a limited number of relevant Al/Na configurations.
Given that real experimental NMR spectra are measured generally around room temperature and signals are an average of data collected over a timescale of μs–s,22 static and short MD calculations represent a significant simplification of the real NMR measurements. In a recent work, we demonstrated the importance of operando modeling in predicting the 27Al chemical shift of zeolites, as thermal vibrations of the lattice, the sequence length (n) in Al–Sin–Al of the calculated model and the simulation timescale all had non-trivial effects on the chemical shift.18 In the case of an extraframework cation, such as Na+, this effect is likely to be exacerbated, owing to its larger mobility, when compared to framework Al atoms.23
The cost of accurate NMR modelling on realistic models is primarily due to two factors: the need for long timescale dynamical simulations, and the large number of NMR calculations required to obtain time-averaged results. Combining MD calculations with NMR calculations requires several orders of magnitude more computing power than to perform a single NMR calculation on a single optimized structure.24 In this regard, machine learning has recently revealed itself to be a useful tool to improve computational efficiency in materials science,25 including in NMR simulations.26–28 In particular, reactive neural network potentials (NNPs), developed to reproduce density functional accuracy in zeolites,29–32 offer a solution to the problem of high computational cost of dynamical sampling, enabling us to systematically search the Al and Na distributions in zeolites and to perform long molecular dynamics simulations to fit the experimental conditions. Such potentials have been shown to accurately describe reactive processes in zeolites, including hydrolysis, cation migration,33 water32 and encapsulated metal cluster diffusion31 and even the dynamic stability of the frameworks under various conditions/reactions.34
A further means to simplify the calculation of NMR properties is to relate some simple geometrical descriptors to the observable of interest. This has been successfully applied to the 27Al isotropic chemical shift (δiso) in low silica aluminosilicate zeolites,35 but has been shown to be a poor predictor in high silica frameworks.18,36,37 Similarly, several works have suggested an empirical correlation between 23Na δiso and Na coordination numbers and Na–O distances in crystalline and amorphous materials.38–43 Koller et al. connected the experimental 23Na chemical shifts (δiso) of sodium silicates and sodalites with the total valence of the oxygen atoms around the Na cation and Na–O distances.44 Charpentier et al.42 obtained an empirical linear function of Na–O average distance and coordination numbers from a dataset with around twenty points of sodosilicates materials, which predicted 23Na δiso with errors less than 10 ppm. Establishing a linear correlation between 23Na δiso and local structural descriptors across a large zeolite dataset can streamline the prediction of time-averaged isotropic chemical shifts, eliminating the need for computationally expensive NMR ab initio calculations. Least absolute shrinkage and selection operator (LASSO) can be used to identify important factors structural descriptors that correlate linearly with the δiso. In a recent study, we showed that a two-descriptor correlation accurately predicted the 27Al δiso of high silica zeolites, with a precision of approximately 1 ppm with respect to DFT calculations.18,45
In this study, we developed a general NNP for Na-form zeolites, to explore stable Na configurations of the various Al distributions within the dehydrated high silicon CHA framework (Si/Al = 35, 17 and 11). Numerical simulations of the NMR spectra were performed using NMR parameters obtained from DFT calculations, taking into account the effects of temperature, dynamics, and the influence of Na/Al configurations, by averaging over configurations sampled via NNP-MD. The scheme of the modeling process is shown in Fig. S1.† These calculations show that a great deal of information is contained within the combined 23Na–27Al solid-state NMR, which can be used to rule out Al distributions and identify Na locations, from a combination of chemical shift, CQ, ηQ, and homo- and heteronuclear dipolar couplings. Furthermore, using the dataset from NNP-MD, a multivariate linear regression was conducted to establish a connection between 23Na δiso and several structural descriptors. Combining the NNP and the LASSO regression, a double ML approach for the 23Na NMR δiso and 27Al NMR δiso prediction was built, which provides a way to simulate the time-averaged NMR properties of zeolites efficiently.
2 Models and methods
2.1 Model
Models of dehydrated zeolite CHA in the sodium form, with Si/Al ratios of 35, 17 and 11 (CHA(35), CHA(17) and CHA(11) respectively), with a unit cell containing 36 T sites were used. The lattice parameters were optimized for each Si/Al ratio for a representative low-energy Na/Al configuration, and then kept fixed for all subsequent Na/Al configurations throughout the study. For CHA(35) the lattice parameters are a = 13.785 Å, b = 13.702 Å, c = 14.795 Å, α = 89.802°, β = 90.164° and γ = 120.190°, for CHA(17) they are a = 13.830 Å, b = 13.633 Å, c = 14.886 Å, α = 89.803°, β = 90.346° and γ = 120.158°, and for CHA(11) the optimized values are a = 13.949 Å, b = 13.680 Å, c = 14.944 Å, α = 89.532°, β = 90.250° and γ = 121.380°.Since all T sites of siliceous CHA are symmetry equivalent, CHA(35) has a single Al environment, and three low energy Na+ configurations for isolated Al sites, one six-member ring geometry (SII) and two different eight-member ring sites (SIII and SIII′) (Fig. 1 and S2†). The complete set of Al configurations is considered systematically in CHA(17), under the restriction that they obey Löwenstein's rule.46 It should be noted that it has been suggested that this rule may not be obeyed in dehydrated H-CHA,47 but is maintained under hydrated conditions48 and in CHA in the Na-form.49 CHA(17) structures are sorted by the minimum Al–Sin–Al (n = 1, 2, 3, 4) sequence length in the configuration, and are named I, II, III, and IV, respectively. There are 9 cases with the Al–Si1–Al sequence, named as I(A)–I(I), 12 cases with the Al–Si2–Al sequence named as II(A)–II(L), 8 cases with the Al–Si3–Al sequence named as III(A)–III(H); and 2 cases with the Al–Si4–Al sequence named as IV(A) and IV(B). For each Al configuration, various possible Na location combinations were considered via an automatic generation scheme (Section 2.3) and were supplemented by relevant additional combinations of 6MR and 8MR site pairs for Na ions. Only the Na configurations found to be within 20 kJ mol−1 of the lowest energy structure for a given Al distribution are considered for NMR property calculations. Two additional cases, II(A) and II(B), with energies of 22 and 28 kJ mol−1, were considered to evaluate specific Al configurations exhibiting distinctive dynamic behaviours (II(A) with Al–Si2–Al sequence in 6MR and II(B) with Al–Si2–Al sequence in one d6r) (Fig. S3†). Na+ configurations are named by their relative energy within that Al distribution, e.g. I(A)1 denotes the lowest energy case of I(A) Al configuration. In each specific case, the location of Na+ is denoted as 6MR(mAl): Al–Sin–Al or 8MR(mAl): Al–Sin–Al, where m is the number of the Al substituted sites in the 6MR and 8MR and n defines the Al sequence length.
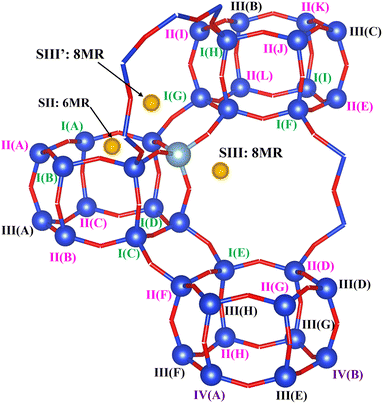 | ||
| Fig. 1 Model for the 36 T site CHA zeolite used in this work. Labels for configurations in the CHA(17) model are given. The Al configurations are named with I/II/III/IV(X), where I, II, III and IV are used to denote the shortest Al–Sin–Al sequences with n = 1, 2, 3 and 4, respectively, and X are letters to distinguish the different sites with same n. The yellow balls denote the possible locations of Na+, SII is on the 6MR window and SIII is on the 8MR window as defined in the previous work.50 | ||
Additionally, fifteen CHA(11) configurations were built to extend the analysis to lower Si/Al ratios. These configurations allow for additional Na distributions and Al sequences, including 6MR(3Al): Al–Si–Al–Si–Al, 8MR(3Al): Al–Si–Al–Si–Al and 8MR(3Al): Al–Si2–Al–Si–Al. Lastly, two MOR zeolite models with Si/Al = 11 and 7 were adopted to test the generalization to another framework (Fig. S4†).
2.2 Neural network potential
The development of robust NNPs for Na-aluminosilicate zeolites requires a structurally diverse dataset. In our previous studies,32 we created a database for protonic aluminosilicate zeolites that covers the breadth of zeolite frameworks, Si/Al ratios and water loadings for training of general NNPs for this material class. Here, the same computational approach was employed to extend the DFT dataset to Na-containing zeolites. First, 10 pure silica zeolites and a silica bilayer were used for construction of 132 initial structures (see Table S1†) varying in Si/Al and water loadings (using Materials Studio version 2022). The chosen silica zeolites (bilayer) were previously selected to encompass structurally distinct atomic environments across existing and hypothetical silica frameworks.29 All initial configurations underwent equilibration through short (10 ps) AIMD runs (PBE+D3(BJ) level) at three different temperatures (1200, 2400, 3600 K), employing the Nosé–Hoover thermostat, a 1 fs time step and with hydrogen replaced by tritium.Subsequently, the AIMD trajectories were subsampled using Farthest Point Sampling (FPS) together with the smooth overlap of atomic positions (SOAP)51 kernel as a similarity metric to reduce redundancy of similar atomic environments in the structure set. The FPS-selected subsets were then used for single-point calculations at the SCAN+D3(BJ) level. Additionally, 210 lattice deformations were applied to the 132 generated initial structures by 70 different lattice vector perturbations (see also ref. 29 for details) at three different strain rates (1.5%, 3%, and 4.5%). These deformations sampled close-to-equilibrium configurations and were also applied to 12 Na-alumino(silicate) and Na-oxide polymorphs such as NaOH and Na2O (see Table S2†).
Training and inference of the NNPs employed the SchNetPack python package52 along with the atomistic simulation environment (ASE).53 The SchNet architecture NNPs54 used six interaction blocks, a feature vector size of 128, and utilized 60 Gaussians for the expansion of pairwise distances with a cutoff radius of 6 Å. This set of parameters has been demonstrated for several related datasets to yield accurate NNPs.29,32,54 We re-trained the ensemble of six NNPs previously developed for H-aluminosilicates using the herein extended Na-aluminosilicate database. The dataset was partitioned into training (80%), validation (10%), and test sets (10%) using random splits. The ADAM optimizer with a batch size of four structures was utilized to minimize the mean squared error of energy per atom and forces. Furthermore, we used a dynamic learning rate strategy, reducing the learning rate (from 10−4 to 3 × 10−6) by factor 0.75 if the validation loss did not lower within three epochs.
The resulting NNPs showed energy and force root mean square errors (RMSE) of 5.3 meV per atom and 188 meV Å−1 for the database test set, respectively. These errors are similar to other rotationally invariant NNPs which allow DFT quality predictions as demonstrated earlier.29,32 To ascertain the NNP accuracy for MD simulations performed in this work, we recalculated energies and forces at the SCAN+D3(BJ) level for structures taken from various MD trajectories. Firstly, we used CHA(11), CHA(17), and CHA(35) resembling the structures present in the training database as test cases within the training domain (in-domain tests). Additionally, to assess the generality of the NNPs, we considered zeolite frameworks not included in the DFT database for out-of-domain tests. We conducted additional MD simulations for FER (Si/Al = 35) and MOR (Si/Al = 7 and 11) at 350 K for 1 ns. We also examined the NNP performance for a cubic unit cell of FAU (Si/Al = 3) containing 100 water molecules as a test for a water-loaded zeolite. Finally, 100 uncorrelated configurations (50 in the case of FAU) were subsampled from all MD trajectories (taken at least every 10 ps) for SCAN+D3(BJ) single-point calculations to determine energy and force errors. Generalisation tests of the NNP predictions of static DFT energetics were performed for selected cases which span pore-size, ring diameters, unit cell volume and Si/Al (CHA(11,17,35), MOR(7,11), FER(35), FAU(3)), showing energy and force errors within 4.2 meV per atom and 72 meV Å−1 in all cases. This high degree of transferability is necessary for comparisons across environments and topologies. The AIMD simulations and SCAN+D3(BJ) single-point calculations for dataset creation and NNP testing used VASP with an energy cutoff of 400 eV, standard PAW potentials and k-point grids with a linear density of at least 0.1 per Å−1.
2.3 Configuration generation
The aluminosilicate configurations were identified using a Python workflow that used a step-wise approach to sample the energy landscape. In this study, the configurations used correspond to various Si/Al ratios in a 36 T-site 1 × 1 × 1 sodium cation-compensated CHA unit cell. In the first iteration of this method, all symmetry-unique Al configurations were generated for a single aluminium atom. However, in the case of 1 defect in CHA there is only one unique T-site, so enumerating multiple Al positions is unnecessary. Next, for each potential Al location, possible sodium positions are generated by triangulating the initial positions using the position of neighbouring oxygen atoms. All possible permutations are then locally relaxed, using the NNP at constant volume (fixed cell parameters).The sodium positions were generated using a normalised vector sum that places the sodium 2.5 Å from each oxygen in the tetrahedron with a bias towards the edges. For each oxygen atom associated with an Al site, the vectors 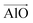 and
and 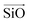 were calculated. Here
were calculated. Here 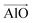 corresponds to a vector from the aluminium atom to the given oxygen atom, and
corresponds to a vector from the aluminium atom to the given oxygen atom, and 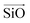 is a vector from the silicon atom bonded to the same oxygen atom being considered. From this the position of the Na+ ion was determined by taking a normalized sum of the two vectors and multiplying by a scaling factor, the resulting projection vector
is a vector from the silicon atom bonded to the same oxygen atom being considered. From this the position of the Na+ ion was determined by taking a normalized sum of the two vectors and multiplying by a scaling factor, the resulting projection vector 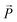 was then added to the Al position thereby defining the Na position.
was then added to the Al position thereby defining the Na position.
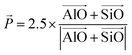 | (1) |
2.4 Density functional subsampling and molecular dynamics
Initial optimization of the unit cells was performed using the VASP 5.4 code,55,56 employing a 700 eV wavefunction cutoff with PAW potentials57 and the Perdew, Burke, Ernzerhof exchange–correlation functional,58 with Grimme's D3 dispersion correction with Becke Johnson damping.59 Energy and force convergence criteria were set to 10−6 eV and 10−2 eV Å−1, respectively, while the Brillouin zone was sampled at the Gamma point.Time-averaged structural, energetic and NMR data for each structure were generated via molecular dynamics simulations in the canonical (NVT) ensemble with the NNPs, using the ASE53 software package. Simulations were performed, starting with the geometries generated in the structure generation step, with a duration of 1 ns per run, at a temperature of 350 K with a Nosé–Hoover thermostat and a timestep of 0.5 fs, to obtain well-equilibrated trajectories. Snapshots along the MD trajectory were saved every 100 steps (50 fs).
Further subsampling of 100 configurations equally spaced along each trajectory (every 10 ps) was performed to generate a representative, uncorrelated dataset for calculation of time-averaged NMR properties at the DFT level. Magnetic shielding and electric field gradient tensors were calculated using the gauge-including projector augmented-wave method,60 as implemented in CASTEP version 18.1.61 We used the PBE functional revised for solids (PBEsol)62 and ‘on the fly’ ultrasoft pseudopotentials.63 An energy cutoff of 700 eV was used to converge the energies to within 10−8 eV per atom and the Brillouin zone was sampled at the Gamma point.
Values of time-averaged magnetic shielding σcalc, CQ and ηQ were calculated from the tensors averaged over the 100 structure dataset. Conversion of the calculated average 27Al chemical shielding (σcalc) to isotropic chemical shift (δiso) was performed using the standard linear regression relationship (eqn (2)), using the coefficients derived in previous work for high-silica aluminosilicate CHA.18
| δiso = −1.11σcalc + 609.72 | (2) |
| δiso = −0.86σcalc + 476.68 | (3) |
2.5 Spectral simulations
23Na and 27Al spectral simulations were performed using Simpson version 4.2.1.64,65 All simulations were performed at a spinning rate of 40 kHz and a magnetic field of 36 T, except for the variable magnetic field simulation in Fig. S13.† The powder pattern of each spectrum was obtained using 3384 Euler angles by considering 376 α–β pairs using the ZCW algorithm,66–68 and 9 γ angles. The σcalc, CQ and ηQ parameters used to define the simulation spin system were obtained from CASTEP NMR calculations and converted using the Simpyson python package. All spectra were obtained by considering only the central transition.Recoupling numerical simulations were performed at a spinning rate of 20 kHz and a magnetic field of 23.5 T, using 143 α–β pairs as implemented in ZCW algorithm,66–68 and 15 γ angles. 23Na–27Al D-HMQC recoupling simulations were performed using SR421 recoupling scheme,69 which has been used to recouple other quadrupolar pairs.70 Recoupling efficiency loss from frequency offset sensitivity was avoided by omitting chemical shift information in the simulation of recoupling curves.
2.6 LASSO regression
Linear regression was adopted to correlate the 23Na chemical shielding σ with geometrical descriptors, employing structural features selected by LASSO. The LASSO regression was based on 6232 DFT values of 23Na σ from MD trajectories of CHA(17). It should be noted that cutoffs to define the coordination sphere of Na in the structural features were set as 3.5, 4.0, and 5.0 Å for O, Al, and Si, respectively. Calculations of structural features and LASSO regression used ASE53 and Scikit-learn,71 respectively. Full details are provided in the ESI (Section 5).† Additionally, validation tests of the 27Al chemical shifts prediction formula from LASSO analysis in previous work18 were performed in the present Na-CHA models. The result reveals that this formula retains a high precision for the prediction of 27Al chemical shifts with a mean absolute error of 1.25 ppm (Fig. S7†).3 Results
3.1 Generation of the dataset
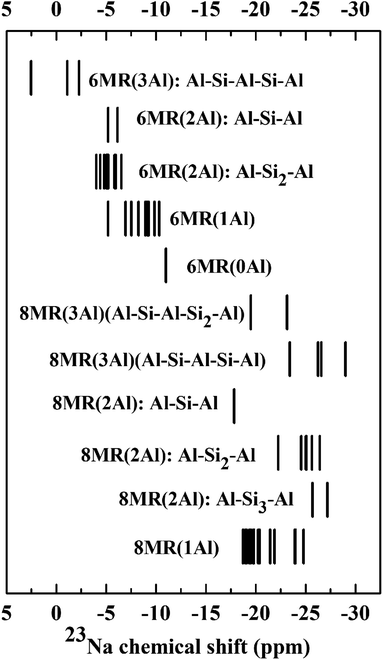
In order to determine the 23Na chemical shifts in CHA, we selected an experimentally relevant high-silicon model, CHA(17), which contains two Al atoms per unit cell, allowing Al to either form pairs or remain isolated. As it is understood that the Al distribution in zeolites is not simply under thermodynamic control, we cannot rule out Al pairing possibilities based on energetic stability.16,72 Hence, all possible Al distributions were considered within the 36 T site model of CHA(17) described in Section 2.1. For each Al distribution, a number of Na locations were produced, via the configuration generation scheme in Section 2.3.The Na/Al configurations which remained after applying a cutoff filter for energy of 20 kJ mol−1 were considered to be thermally accessible.73–76 We supplemented this dataset with configurations for the CHA(35) model, which contains only one fully isolated Al atom per unit cell, and a subset of possibilities from CHA(11), with 3 Al atoms per unit cell (see ESI† Section 2 for details). Upon determination of each Na/Al configuration and Si/Al ratio, static DFT calculations of the 23Na NMR parameters were performed and are shown in Fig. 2 and 3.
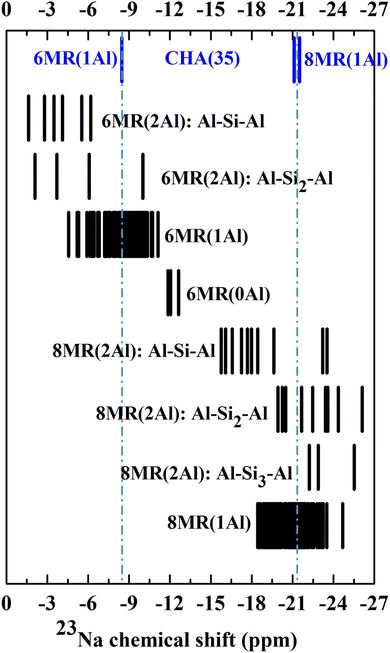 | ||
| Fig. 2 DFT 23Na chemical shifts calculated from all low energy local minima for CHA(X), (X = 35, 17) (shown in Fig. S2 and S3†). | ||
3.2 Static NMR shifts
Beginning with the single CHA(35) model, there are three significantly contributing locations for the Na ion: above the face of a 6MR (SII), with preferential bonding to the oxygen atoms which make up the AlO4 tetrahedron, and two, nearly isoenergetic locations in the 8MR site (SIII and SIII′), which are higher in energy by 8.2 and 9.1 kJ mol−1 (Fig. S2†). Na occupation of other sites is energetically uncompetitive and is discussed in the ESI Section 2.1.† The 23Na chemical shifts of isolated Na atoms in CHA(35) can be clearly separated into 6MR (−8.5 ppm) and 8MR (−21.5/−21.1 ppm) sites, as previously reported by Zhao et al.19 However, the competing 8MR locations, which are nearly-isoenergetic, can be separated neither by their chemical shift nor by CQ/ηQ, showing a difference of 0.1 MHz and 0.1 from static calculations (Table S6†), respectively.Considering the CHA(17) model, the possibilities for Na location become more complex, as we must consider the proximity of the Al atoms to each other, and the distortions to the framework. From Fig. 2 it is clear that groupings of 23Na chemical shifts can be isolated based on three factors. First, whether the Na atom lies in the 6MR (δiso ≥ −15 ppm) or the 8MR (δiso ≤ −15 ppm). Second, how many Al atoms are in the ring to which the Na is associated, 6MR(nAl) and 8MR(nAl), where n = 0, 1, 2. Third, how distant the Al atoms are, which is characterised by the length n of the shortest sequence Al–Sin–Al. With these three features, patterns emerge which may be used to narrow down the possible Al distributions observed experimentally.
We note several features which emerge from this analysis. Na atoms at 8MR sites are always more shielded (more negative δ) than those at 6MR sites. While the other modifying factors broaden the chemical shift range, we can still identify 23Na chemical shift ranges, 6MR sites between 0 and −15 ppm, and 8MR sites from −15 to −27 ppm, with no significant overlap.
Increasing the number of Al atoms in the ring to which the Na ion is bound leads to greater deshielding, and generates separated blocks of 23Na chemical shifts that can be used to identify Al distributions. For example, the 6MR(1Al) configurations form a broad block, centred at −7.9 ppm, which is close to the value observed for the comparable 6MR(1Al) configuration for CHA(35) (−8.5 ppm). The 6MR(2Al): Al–Si1–Al configurations form a block centred at −3.9 ppm, which is a measurable difference in chemical shift. The same effect occurs for 6MR(0Al) configurations, which are centred at −12.3 ppm and can therefore be expected to be distinguishable from 6MR(1Al) and 6MR(2Al) configurations.
The third modifier, the Al–Sin–Al sequence length, is the most subtle effect. We establish that for Al distributions in which the Al atoms do not share a double six ring (d6r), a sequence length of Al–Si3–Al is sufficiently long that they can be considered isolated. This was verified for both the 23Na and 27Al chemical shifts, and agrees with prior works by Dědeček on the 27Al NMR.77 It is worth noting that when both Al atoms share a d6r this rule is not followed. This can be seen clearly for the peak at −25.5 ppm for the 8MR(2Al): Al–Si3–Al configuration, which is shifted with respect to the isolated 8MR(1Al) shifts of around −21 ppm in CHA(35). There is a general tendency towards increased shielding upon lengthening the sequence, which is most closely followed by those configurations which do not share a d6r (see ESI Fig. S3† for details).
Overall, we can conclude that the 23Na chemical shift can provide considerable predictive information about the Al distribution and pairing beyond just the location of Na ions in 6- or 8MR positions.
In order to extend this analysis beyond high-silica models, we considered a subset of low-energy configurations for CHA(11). This model contains three Al sites per unit cell and thus generates additional possibilities for Na/Al environments. Fig. 3 shows the static chemical shift predictions for these configurations, from which it is clear that the trends observed for CHA(17) continue to be valid for higher Al content. Na atoms at the 6MR sites are less shielded than the 8MR sites, with no overlap between the two sets. The position of a configuration within the 6MR block is defined by the number of Al atoms in the d6r, in accordance with the CHA(17) findings. The 6MR(3Al) configuration has the lowest 23Na chemical shift, followed sequentially by 6MR(2Al), 6MR(1Al) and 6MR(0Al) sites. For 8MR sites, the analysis is complicated by the wide variety of sequence length combinations available. However, trends can be observed within structural classes. For example, in the 8MR(2Al): Al–Sin–Al class, the longer the sequence length n, the further the 23Na peaks are shifted to lower 23Na chemical shifts. Thus overall, the detailed structure of the chemical shifts reveals trends which may be used to isolate or rule out Na and Al configurations in Na-CHA.
3.3 Effect of dynamics
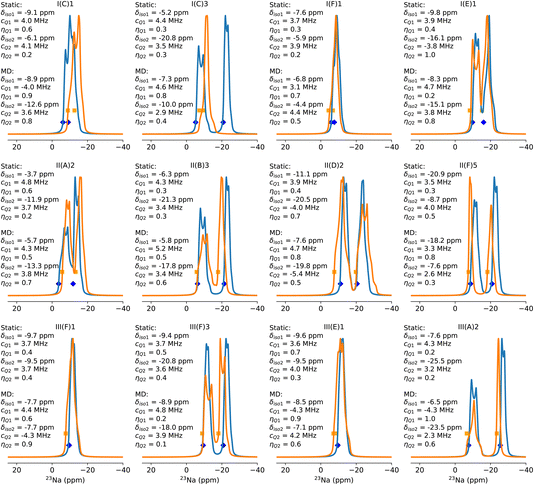
Having generated a large dataset of thermally accessible Na configurations for all CHA(35) and CHA(17) Al distributions, we next considered the effects of dynamics. The motions of the framework and the counterion that occur on the timescale of data collection may lead to a variety of effects which can manifest themselves as a change to the spectrum. Firstly, local thermal fluctuations may change the bond lengths and angles, along with other features that govern the value of the chemical shift. Secondly, the localization of thermal energy into vibrational modes of Na ions may drive reactive transformations, in which the ion moves between thermally accessible sites on a timescale shorter than the NMR acquisition time. Finally, the position and shape of the peaks may vary, due to changes in magnetic shielding and electric field gradient tensors that result from the previous effects.We tested these dynamic effects via long (1 ns) equilibrium molecular dynamics simulations applied to a representative subset of the CHA(17) Na/Al distributions, within 20 kJ mol−1 of the ground state, for all Al–Sin–Al sequence lengths, and energy barriers of some cases are calculated with the NNP NEB (nudged elastic band) method to understand their dynamic behaviors. Thus, structures involving both 6MR and 8MR initial positions for Na are included. The isotropic chemical shifts and quadrupolar parameters (CQ and ηQ) were calculated as averages over the simulations, generated from 100 snapshots via DFT, to reproduce the averaging effects observed in NMR experiments.
Fig. 4 shows the simulated static and dynamically averaged spectra for a selection of low-energy configurations. Further configurations and analysis are to be found in the ESI (Table S7 and Fig. S8†). Several effects are immediately apparent from these spectra. Firstly, the chemical shift varies between static and dynamic spectra. The change in chemical shift on moving from the static calculation to the dynamic one is usually within 3 ppm, and in most cases is to the left, implying a deshielding effect of temperature (350 K) and time averaging. However, there are exceptions, such as in the case of configuration II(A)2, where two Al substitutions in a 6MR and one Na+ at the 6MR(Al–Si2–Al) and one at the 6MR(0Al) in the same d6r. Therefore, it cannot be assumed that dynamical effects lead to a simple systematic change to the chemical shift, which would allow for a uniform correction to the shift. The same finding is true for both the quadrupolar coupling constant, CQ, and the asymmetry parameter, ηQ. In general, the value of CQ increases, but there are exceptions, including II(A)2 and one of the sodium ions in I(C)1 and I(C)3. Over the full dataset, including those configurations not included in Fig. 4, the average change in CQ is 0.2 MHz, and the average change in ηQ is 0.1. Hence, the static local minimization does not give a precise measure of these parameters at thermal equilibrium.
The combination of δiso, CQ and ηQ gives rise to the overall position and shape of the spectrum. In Fig. 4 we can characterize the effect of dynamics on the spectrum into three main classes. First is the class in which neither the shape nor the position of the peak changes significantly. Configurations I(F)1, III(F)1 and III(E)1 belong to this class. Second is the class in which the position of the peaks does not change much, but the shape of the spectrum does change. We assign configurations II(D)2, I(E)1, III(F)3, III(A)2 and II(A)2 to this class. Third is the class in which both the spectral shape and peak positions change significantly. This class includes I(C)1, I(C)3, II(B)3 and II(F)5.
We can interrogate the behaviour of the zeolites during the dynamical simulation to understand the nature of these three classes. In the first class, we observed that over the entire length of the molecular dynamics run, neither Na ion in the unit cell moved away from the initial position. The only fluctuations are short-ranged thermal vibrations, but no long-distance migrations occur. These configurations are invariably those in which both sodium ions lie in 6MRs, which for sequence length Al–Si1–Al and Al–Si3–Al tend to be the global minimum structures. In these specific cases depicted here, I(F)1 is the global minimum for the Al distribution I(F), in which Al atoms are in adjacent d6rs, one on the top face and the other on the bottom. This allows for both sodium ions to adopt 6MR sites (above and below, respectively), and this configuration outcompetes the next local minimum I(F)2, in which one sodium ion lies in an 8MR site which contains both Al atoms. Interestingly, despite their close energetic and geometric similarity, these two configurations do not interconvert on the 1 ns timescale. The reason for this lack of interconversion was determined via nudged elastic band (NEB) calculation, to be a relatively high activation barrier (see Fig. S10†). For configurations III(F)1 and III(E)1, both Al atoms are separated by three silicon atoms, and are in different d6rs. As was observed in the static calculation of chemical shifts in Section 3.2, such configurations reproduce the 23Na and 27Al chemical shifts of CHA(35), which means neither the Na nor the Al atoms interact with or influence each other. As a result, they can be considered isolated. This is the reason there is little change in the spectrum from static to dynamic calculation. The small changes observed are due solely to the effects of thermal fluctuations of the system. The same finding is observed for the spectra of the configuration with the longest sequence IV(A)I and IV(A)3, in which the spectral shape, chemical shift and Na positions do not change significantly over the simulation (ESI Fig. S8†).
In the second class, the chemical shifts do not change greatly. However, the shape of the spectra changes, owing to the effect of dynamics on the nature of the local minima adopted by the Na ions. In particular, configurations in which both 6MR and 8MR sites are adopted by sodium appear in this class. II(D)2, I(E)1, III(F)3 and III(A)2 all have such an arrangement of Na ions, and II(A)2 wherein one Na cation occupies a 6MR(0Al) site. Significant changes to both CQ and ηQ are observed for both Na ions in these configurations. Hence, the static prediction is poor for such systems, despite the ions remaining in their initial local minima throughout the simulation. Configurations II(D)2 and the ground state II(D)1 are close in energy, and they are related by a simple rotation of one Na ion from the top face of a 6MR to the nearby 8MR site. Nevertheless, the interconversion is not observed on the 1 ns timescale, which again, was found to be due to a high activation barrier (see Fig. S10†). The changes in spectral shape are primarily apparent in the Na ions at the 8MR, likely due to their higher degrees of freedom for thermal vibrations and movements. In contrast, in configuration I(E)1, the Na ion at the 6MR exhibits the most significant modification in spectral shape. Interestingly, in configuration III(F)3, changes in both peak shapes are observed even though both Na ions remain in their original local minimum at the 6- and 8MRs throughout the MD simulation.
Hence, one cannot conclude that CQ or ηQ varies in a particular way for particular locations of sodium ions, and thus we are unable to make predictions about the effects of temperature and dynamical averaging in class two configurations. In configuration III(A)2, the 6MR Na ion moves across the d6r from one face to another, and remains there for around 30% of the trajectory time, while the 8MR Na ion remains in 8MR. Although the dynamic process averages different 6MR Na configurations, the chemical shift changes only slightly, however, the asymmetric parameter ηQ changes considerably, probably due to the change of d6r face.
The final example in this class is II(A)2, which is an outlier among the considered configurations. Both sodium ions lie in 6MR sites, on the top and bottom faces of the same d6r. However, both Al atoms lie on the bottom face. Thus, one sodium ion is at a 6MR(2Al): Al–Si2–Al site and the other is at a 6MR(0Al) site. As observed in Section 3.2, these two configurations are on average, the most deshielded and shielded 6MR configurations, respectively. The 6MR(0Al) sodium lies at −11.9 ppm in the static calculation, and at −13.3 ppm from the dynamic calculation, and is therefore near to overlapping with the positions of 8MR sites. This configuration is not the most stable II(A) configuration, which has one 6MR and one 8MR sodium, but is only 22 kJ mol−1 higher. Interestingly, the configuration does not convert to the ground state II(A)1 on the timescale of the simulation, and thus represents a kinetic trap. Such configurations can be found at other Si/Al ratios, and appear to vary in relative stability to the global minimum, with Si/Al. The higher the Al content, the more stable the 6MR(0Al) configuration is, and at CHA(11) it is within 9 kJ mol−1 of the global minimum. This suggests that such configurations may play a role in the kinetics and the spectra of Na-CHA (ESI Fig. S17†).
The third class involves cases in which the sodium cations change locations on the timescale of the simulation, leading to a dynamical average of all NMR parameters that is a combination of contributions from multiple states. In the coupled cases of I(C)1 and I(C)3, we see large changes to the shape and position of peaks. I(C)1 is the global minimum, in which both Na ions adopt 6MR(1Al) sites, on either face of the same d6r, giving rise to one broad, overlapping band in the static spectrum. I(C)3 consists of one 6MR(1Al) site and one 8MR(1Al) site, and therefore has a large separation between peaks in the static spectrum. Both configurations are connected by a simple rotation of one Na+ cation from the 6MR to the 8MR site which is observed to have a fairly low barrier, as depicted in Fig. S10.† During the simulation, I(C)1 and I(C)3 configurations interchange, with I(C)1 (0 kJ mol−1) adopted more commonly than I(C)1 (15 kJ mol−1) (the trajectory is shown in ESI Fig. S9†). It is notable that despite the relatively large energetic difference between the configurations, both are occupied during the simulations, suggesting a low interconversion barrier and a highly dynamic situation, in which the final, equilibrated spectrum is a weighted average of the two configurations. Indeed, while the simulation timescale is insufficient to fully equalize the I(C)1 and I(C)3 spectra, the dynamical spectra are more similar than the static ones. The resulting changes to the calculated chemical shifts are large, with up to 11 ppm difference between the static and dynamic values. In addition, the CQ value of the mobile Na ion decreases considerably, the same behaviour is observed for I(A)1 and I(G)1 (Fig. S8†).
II(B)3 and II(F)5 are similar, but less extreme examples. In II(B)3, the configuration is relatively high in energy, at +22 kJ mol−1, and contains a 6MR and an 8MR Na ion. It converts to the ground state II(B)1 configuration during the simulation, with both Na ions in a 6MR(1Al) configuration (see Fig. S10†), but requires 750 ps to achieve this transition. Hence, it is unusually dynamically stable. For II(F)5, the sodium ions adopt a 6MR and an 8MR site, which is 19 kJ mol−1 higher in energy than the ground state (II(F)1). It also shows a surprising degree of dynamical stability. Over the course of the simulation, it is converted into another sub-optimal II(F)3 configuration, but does not reach the ground state in 1 ns. This slow interconversion may lead to contributions to the spectrum from energetically unfavourable minima.
In general, the various effects of dynamics on the locations and spectral characteristics of the sodium ions are manifestations of the interaction between nearby aluminium/sodium atoms. When the Al–Sin–Al sequence is long (n ≥ 3), the sodium atoms are not in contact with each other, and they cannot influence each other's motion, and their spectra replicate isolated configurations in high Si/Al ratios. The exception to this is when n = 3 and both Al atoms share a d6r. When the sequences are shorter (n ≤ 3), analysis is more complex, as there is interaction between aluminium atoms, but the mobility of the Na ion is dependent on the particular arrangement of Al and the identity of the ring to which the Na ion belongs.
3.4 Dipolar coupling
Most studies rely on the calculation of δiso as the only metric of comparison with experimental results. As we have shown above, CQ and ηQ are very important in describing the shape of the resonances and can aid in the identification of species present in a particular zeolite studied experimentally. Another parameter that can be experimentally extracted but is often overlooked is the interatomic distance, which can be easily compared with computational models. Although magic angle spinning averages out the dipolar coupling, which is proportional to r−3, one can reintroduce it using recoupling methods and retrieve information about interatomic distances.78,79 Even though such recoupling methods are most commonly used to recouple spin-½ or spin-½–quadrupolar pairs,80,81 one can find some examples of studies looking at the recoupling of quadrupolar–quadrupolar pairs,70,82 including zeolites.21Fig. S14–S16† show the 23Na–27Al heteronuclear, 23Na–23Na and 27Al–27Al homonuclear dipolar coupling of the models obtained from static and dynamical calculations. The dipolar coupling between 27Al–27Al pairs obtained from both static and dynamic calculations show good agreement with each other, which is expected as the framework Al atoms do not move much during dynamical simulations. On the other hand, the dipolar couplings obtained from static or dynamical calculations for 23Na–23Na pairs show a variety of results, as trajectories wherein Na atoms are very mobile show either an over/underestimation of the dipolar coupling when compared to static calculations. Our results suggest Al–Si1–Al moieties give rise to 27Al–27Al dipolar couplings above 40 Hz, while for pairs in the same 4MR (I(C) and I(G) structures) the couplings are above 90 Hz. On the other hand, our data suggests that longer Al–Sin–Al cannot be distinguished by solely analysing the recoupling between Al pairs.
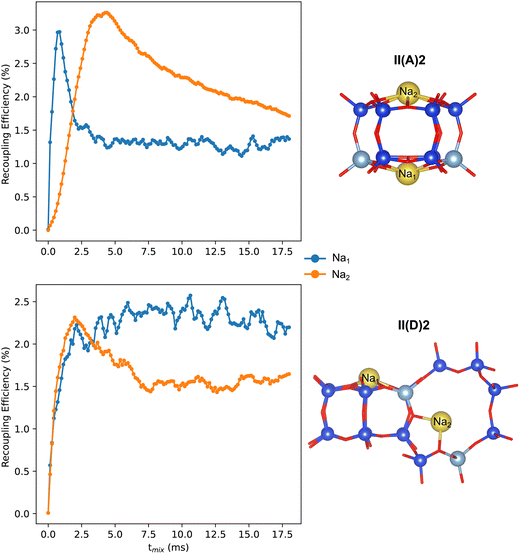
The 23Na NMR spectra obtained from Models II(A)2 and II(D)2 exhibit two resonances around −5.7 and −13.3 ppm, and −7.6 and −19.8 ppm, respectively. These resonances correspond to distinct Al and Na sitings. However, both models produce similar spectra, indicating that using only 1D spectra to determine the siting and pairing of Al can be ambiguous. We performed numerical simulations to predict the magnetization build-up curves of a recoupling experiment involving 23Na–27Al pairs. Fig. 5 shows that for model II(D)2, the magnetization of both Na atoms increases rapidly. However, in the case of model II(A)2, only the Na1 atom, which is situated close to two Al atoms, shows a rapid magnetization build-up. On the other hand, the magnetization of the Na2 atom, located at the siliceous 6MR(0Al), increases more slowly and only achieves high magnetization transfer at higher mixing times. These results suggest that recoupling methods can be used to identify Na–Al connectivities, which can help confirm or rule out particular Na/Al arrangements.
3.5 Physical interpretation of 23Na chemical shift
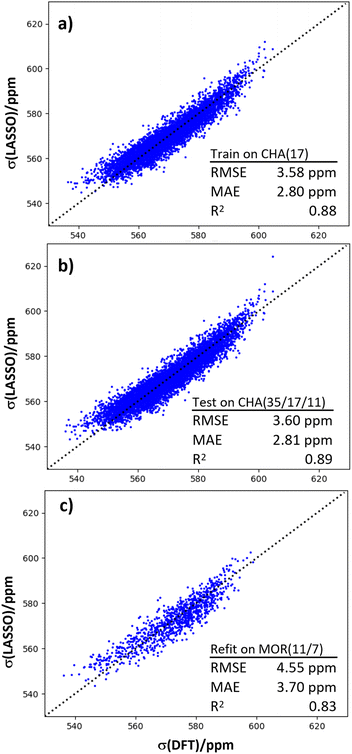
Another application of machine learning and dynamical simulations is for generating insight into the physical origins of chemical shifts. LASSO regression was used to generate a linear relationship between 23Na chemical shift and a set of local structural features (Fig. 6).We trained the LASSO model on the dynamical data generated from the CHA(17) configurations in the previous section, as described in the Models and methods section. Of an initial set of 25 parameters (Table S3†), only seven were required to fit the shifts with a mean absolute error (MAE) of around 2.5 ppm, and a high Pearson correlation coefficient of 0.88. By systematically reducing the number of parameters, LASSO aims to avoid overfitting, while maintaining physical interpretability that is not present in more sophisticated regression schemes, such as Kernel Ridge Regression.
| σ = c0 + c1CNNa–O + c2CNNa–O(Al) + c3CNNa–Si + c4dNa–O + c5dminNa–O + c6dminNa–Si + c7αO–Na–O | (4) |
Our results show the most important features are those related to Na–O distances and O–Na–O angles (Fig. S6c†). This is in agreement with the findings of Charpentier et al.42 who showed a good correlation between Na–O distance and 23Na chemical shift of various materials. It is worth noting that some features in the LASSO regression are not necessarily linearly independent, such as coordination number Na–O and average distance Na–O, and thus may be interrogated to reduce the dimensionality. Further discussion of the effect of cutoff distances and changing the feature space size can be found in the ESI Section 5.† Nevertheless, as the features in eqn (4) are all readily available from a molecular dynamics simulation, we have chosen to keep this seven parameter fit. Smaller parameter sets increase the error, while larger sets reduce the error, but at a risk of overfitting. It is worth noting that the Na–Al distance does not feature in eqn (4), nor do any parameters pertaining to the framework itself, such as Al–O bond lengths or O–Al–O angles.
Fig. 6b shows that the LASSO model trained on CHA(17) data can be applied to CHA structures with lower and higher Al content with no significant loss of precision. This generalization test shows that the parameters that control the chemical shift do not change between Si/Al = 35 and Si/Al = 11. In order to test the transferability of this expression to other topologies, we considered zeolite MOR. Mordenite is another industrially important zeolite, which can be prepared in sodium form at similar Si/Al ratios to CHA. However, it has a more complex pore structure, with both 8 and 12 rings and side pockets. We have found in previous work that the conclusions about 27Al chemical shifts drawn from CHA,18 which is a simple, rigid framework, do not necessarily translate to MOR, hence this is a stern test of the regression model. The same parameterization, with the same coefficients as for CHA gave an unsatisfactory result for a combined dataset of MOR(7) and MOR(11), with an R2 coefficient of 0.70 and an MAE value of 4.63 ppm (shown in Fig. S6f†). However, refitting the coefficients of the LASSO model, while keeping the features identical, recovered a good linear fit, as shown in Fig. 6c. This result suggests that while the particular regression for one zeolite does not straightforwardly translate to another, the features included in the fit are good for other topologies, and essentially capture the underlying relationship between structure and chemical shift.
4 Discussion
4.1 Machine learning
The neural network potentials developed within this work can accelerate the sampling of configurations while retaining the level of accuracy of the ab initio training set. We utilise NNPs for the initial sampling of configurations via an unbiased structure generation approach, which allows us to be near-exhaustive for high silica CHA but may also be extended to the more complex environments at lower Si/Al, where exhaustiveness with DFT rapidly becomes unfeasible. This is found to be necessary, owing to the large number of energetically competitive local minima of Na siting for a given Al distribution. This problem is compounded by a large number of Al distributions, of which an incomplete subset may not be chosen a priori, as total electronic energy is known in general not to be the primary governing factor for the adoption of a particular Al distribution in zeolites. We also apply the NNPs directly for long molecular dynamics simulations. In this case, the simulation of long timescales was found to be crucial, as it drove changes in Na location, and in less dynamical structures, the equilibrium bond lengths, which in turn affects the δiso, CQ, ηQ, and dipolar couplings that can be used for experimental verification of zeolite structure. The inclusion of thermal vibrations and the shift from potential to finite temperature free energy surface must therefore be taken into account when comparing calculated and experimental parameters. We further observe that these effects may be an additional tool for the identification of Al/Na distributions.Transitions between Na local minima were often found to occur on a timescale in the hundreds of picoseconds. This means the length of simulation available to ab initio dynamics (tens of ps in CHA) would provide a misleading expectation of dynamical stability of certain minima, for example, II(A)3 configuration changed to II(A)1 after about 0.5 ns, and II(B)3 changed to II(B)1 in about 0.75 ns (Fig. S10†). In addition, it is not clear from the static relative energies alone, whether a configuration is dynamically stable or not. In several cases, two nearly iso-energetic minima interconvert slowly, while more energetically separated structures swap on a shorter timescale, owing to the low barrier pathways that exist between them. As a result, long dynamics are invaluable, for which the acceleration provided by NNPs is essential.
4.2 Effect of model choice
Zeolites represent a diverse class of materials, characterized by a wide range of topological motifs, including different-sized pores and channels, as well as distinct elemental composition. These features contribute to the unique properties of zeolites, such as shape-selectivity, reactivity and dynamics. Hence, any computational model should aim to reproduce experimental data with high fidelity across a wide range of zeolite motifs. Our NNPs have demonstrated their capability to describe both the structural and dynamical behaviour of various Na-zeolites, spanning from fully siliceous frameworks to the Löwenstein rule-limited ratio of 1.For derived relationships, such as the LASSO regression for 23Na chemical shifts, such a high degree of generalization may not be assumed. We found in our generalization tests that the fit for CHA(17) may be extended to CHA(11) and CHA(35) without loss of precision. Nevertheless, at lower Si/Al, other factors may become significant. For example, Na–Al distances are reduced, Na–Na interactions may become relevant as the unit cell becomes crowded and the optimal unit cell shape and volume will vary. The high quantity of Al atoms will cause more significant distortions of the framework, which in turn will be highly distribution-dependent. In our tests, LASSO regressions re-trained on alternative frameworks show good transferability of the features, but require new coefficients to give optimal linear fits.
In addition to the Si/Al ratio, the length of the Al–Sin–Al sequence plays a significant role in the 23Na chemical shifts. This was previously found for 27Al in CHA and MOR,18 and is noted in this work to be a useful descriptor for the 23Na chemical shifts, given a particular Na configuration. The importance of sequence length is further illustrated by comparing the 23Na chemical shifts calculated for periodic models with cluster models and experimental data previously reported (refer to ESI Section 11† for more details).19
A further consideration for the model is temperature. We selected a temperature of 350 K, which aligns with typical conditions in experimental solid-state NMR, accounting for the heating effects induced by magic angle spinning. In CHA(17) we considered II(A)1 at 150, 350, and 550 K. Our simulations reveal that higher temperatures lead to increased mobility of Na ions, in particular, those at the 8MRs, consequently affecting the calculated δiso, CQ and ηQ (Fig. S12†). In principle, the activation energy for transitions and residence time profiles may be obtained from a systematic comparison of MD trajectories at various temperatures and becomes a feasible task with NNPs. Even though this was not within the scope of the current work, future studies can explore the effect of temperature, as a tunable parameter in MD simulations and experimentally, to identify Na/Al siting.
4.3 27Al NMR
Solid-state NMR of the quadrupolar nucleus 27Al is a common approach for the analysis of zeolite structure, particularly in the identification of coordination environments, which can range from three to six around the Al centre, and which is correlated with the type of acidity present. Thus, as a tool to understand catalytic activity and selectivity, 27Al NMR is useful, particularly in combination with MQMAS experiments, which suppresses the 2nd-order quadrupolar broadening of the peaks, not averaged out in standard MAS experiments, and allows direct access to isotropic chemical shifts. However, as a tool to determine the siting or distributions of Al atoms among T sites in zeolites, it is less successful, owing to the limited resolution of the 27Al chemical shift to T site location in zeolites. We calculated the 27Al solid-state NMR spectra for all CHA(17) configurations considered in this work, and have extracted the chemical shifts, CQ and ηQ values, which are given in the ESI (Fig. S11, Table S8†). However, in agreement with previous works, the position of 27Al resonances do not show significant changes with Al siting. The main effect of dynamics is to shift the peak position by only a few ppm, in agreement with findings of Vanlommel et al.,83 for models with multiple Al atoms per unit cell. However, it remains difficult to separate Al distributions by this method. Lastly, all simulations presented in this work use fully dehydrated zeolites, known to produce NMR “invisible” aluminium species. These species are often heavily distorted and thus appear as very broad resonances that are hard to observe at modest magnetic fields (Fig. S13†), however, at higher magnetic fields one should be able to observe such resonances.5 Conclusions
We have generated and verified a transferable machine-learning driven approach for the analysis of Na/Al solid state NMR in zeolites, and applied it to the industrially important small-pore zeolite CHA. Enhanced sampling of the low energy configurations of Na/Al in CHA in the sodium form showed that a great deal of information can be drawn from calculated 23Na NMR chemical shifts, which, in combination with asymmetry parameters and dipolar coupling constants, may be used to significantly narrow down the possible Al and Na distributions present in the sample. Three important factors were determined to control the chemical shift: 6MR versus 8MR position of Na, the number of Al atoms in the ring, and the length of the shortest Sin sequence between Al atoms. We also show the great importance of dynamic sampling, which affects the position and shape of peaks in the NMR spectrum as well as the dipolar coupling constants, and gives rise to an array of feasible ion migrations at a standard NMR acquisition temperature. By characterising the features which control the chemical shift, we have shown that a fitted polynomial of primarily Na–O distance and O–Na–O angle parameters can be used in combination with inexpensive ML simulations, to reproduce chemical shifts without the need for costly DFT calculations in the future.Data availability
Data for this article, including the neural network potentials, training database and error data, in addition to structures of relaxed CHA(17) isomers are contained in a zenodo database at https://doi.org/10.5281/zenodo.11120133. The data supporting this article, including full datasets of calculated static and dynamic NMR data, LASSO regression contributions and hyperparameters have been included as part of the ESI.†Author contributions
CL: investigation, data curation, writing – original draft. CB: formal analysis, data curation, visualization. OB: methodology, investigation. AE: methodology, validation, visualization, writing – original draft. BS: funding acquisition, resources. LG: funding acquisition, methodology, writing – review & editing. CJH: conceptualization, funding acquisition, project administration, supervision, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the Czech Science Foundation (LG, AE, CJH: GAČR standard project 23-07616S). Charles University Centre of Advanced Materials (CUCAM) (OP VVV Excellent Research Teams, project number CZ.02.1.01/0.0/0.0/15_003/0000417) is acknowledged. This work was supported by the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID: 90254) and ERC_CZ project LL 2104 (CJH). CB acknowledges the funding from the European Union’s Horizon Europe research and innovation program under the ERA-PF grant agreement No. 101180584. BS and OB acknowledge Dan Hewitt for contributions to the structure generation code used in the generation of CHA configurations and to Johnson Matthey for supporting OB via an EPSRC CASE studentship.Notes and references
- A. Corma, Chem. Rev., 1997, 97, 2373–2420 CrossRef CAS
.
- Z. S. J. Dědeček and B. Wichterlová, Catal. Rev. Sci. Eng., 2012, 54, 135–223 CrossRef
.
- J. Dedecek, E. Tabor and S. Sklenak, ChemSusChem, 2019, 12, 556–576 CrossRef CAS
.
- K. Mlekodaj, J. Dedecek, V. Pashkova, E. Tabor, P. Klein, M. Urbanova, R. Karcz, P. Sazama, S. R. Whittleton, H. M. Thomas, A. V. Fishchuk and S. Sklenak, J. Phys. Chem. C, 2019, 123, 7968–7987 CrossRef CAS
.
- J. Dědeček, D. Kaucký, B. Wichterlová and O. Gonsiorová, Phys. Chem. Chem. Phys., 2002, 4, 5406–5413 RSC
.
- S. Li and F. Deng, Annu. Rep. NMR Spectrosc., 2013, 78, 1–54 CrossRef CAS
.
- M. Zheng, Y. Chu, Q. Wang, Y. Wang, J. Xu and F. Deng, Prog. Nucl. Magn. Reson. Spectrosc., 2024, 140–141, 1–41 CrossRef CAS
.
- D. H. Brouwer, R. J. Darton, R. E. Morris and M. H. Levitt, J. Am. Chem. Soc., 2005, 127, 10365–10370 CrossRef CAS PubMed
.
- E. Lippmaa, M. Maegi, A. Samoson, M. Tarmak and G. Engelhardt, J. Am. Chem. Soc., 1981, 103, 4992–4996 CrossRef CAS
.
- J. Klinowski, Chem. Rev., 1991, 91, 1459–1479 CrossRef CAS
.
- M. Jin, M. Ravi, C. Lei, C. J. Heard, F. Brivio, Z. Tošner, L. Grajciar, J. A. van Bokhoven and P. Nachtigall, Angew. Chem., Int. Ed., 2023, 62, e202306183 CrossRef
.
- M. Ravi, V. L. Sushkevich and J. A. van Bokhoven, Chem. Sci., 2021, 12, 4094–4103 RSC
.
- M. Ravi, V. L. Sushkevich and J. A. van Bokhoven, J. Phys. Chem. C, 2019, 123, 15139–15144 CrossRef CAS
.
- K. Chen, S. Horstmeier, V. T. Nguyen, B. Wang, S. P. Crossley, T. Pham, Z. Gan, I. Hung and J. L. White, J. Am. Chem. Soc., 2020, 142, 7514–7523 CrossRef CAS PubMed
.
- K. Chen, Z. Gan, S. Horstmeier and J. L. White, J. Am. Chem. Soc., 2021, 143, 6669–6680 CrossRef CAS PubMed
.
- S. Sklenak, J. Dědeček, C. Li, B. Wichterlova, V. Gabova, M. Sierka and J. Sauer, Angew. Chem., Int. Ed., 2007, 46, 7286–7289 CrossRef CAS PubMed
.
- S. Sklenak, J. Dedecek, C. Li, B. Wichterlova, V. Gabova, M. Sierka and J. Sauer, Phys. Chem. Chem. Phys., 2009, 11, 1237–1247 RSC
.
- C. Lei, A. Erlebach, F. Brivio, L. Grajciar, Z. Tošner, C. J. Heard and P. Nachtigall, Chem. Sci., 2023, 14, 9101–9113 RSC
.
- Z. Zhao, Y. Xing, S. Li, X. Meng, F.-s. Xiao, R. McGuire, A.-N. Parvulescu, U. Müller and W. Zhang, J. Phys. Chem. C, 2018, 122, 9973–9979 CrossRef CAS
.
- P. Klein, J. Dedecek, H. M. Thomas, S. R. Whittleton, J. Klimes, J. Brus, L. Kobera, D. L. Bryce and S. Sklenak, J. Phys. Chem. C, 2022, 126, 10686–10702 CrossRef CAS
.
- B. Fan, W. Zhang, P. Gao, G. Hou, R. Liu, S. Xu, Y. Wei and Z. Liu, J. Phys. Chem. Lett., 2022, 13, 5186–5194 CrossRef CAS PubMed
.
- R. G. Bryant, J. Chem. Educ., 1983, 60, 933 CrossRef CAS
.
- C. Blanco and S. M. Auerbach, J. Phys. Chem. B, 2003, 107, 2490–2499 CrossRef CAS
.
- A. H. Mazurek, L. Szeleszczuk and D. M. Pisklak, Int. J. Mol. Sci., 2021, 22, 4378 CrossRef CAS PubMed
.
- S. S. Chong, Y. S. Ng, H.-Q. Wang and J.-C. Zheng, Front. Phys., 2024, 19, 13501 CrossRef
.
- P. Gao, J. Zhang, Q. Peng, J. Zhang and V.-A. Glezakou, J. Chem. Inf. Model., 2020, 60, 3746–3754 CrossRef CAS PubMed
.
- F. M. Paruzzo, A. Hofstetter, F. Musil, S. De, M. Ceriotti and L. Emsley, Nat. Commun., 2018, 9, 4501 CrossRef PubMed
.
- Z. Chaker, M. Salanne, J.-M. Delaye and T. Charpentier, Phys. Chem. Chem. Phys., 2019, 21, 21709–21725 RSC
.
- A. Erlebach, P. Nachtigall and L. Grajciar, npj Comput. Mater., 2022, 8, 174 CrossRef CAS
.
- I. Saha, A. Erlebach, P. Nachtigall, C. J. Heard and L. Grajciar, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2022-d1sj9-v3.
- C. J. Heard, L. Grajciar and A. Erlebach, Nanoscale, 2024, 16, 8108–8118 RSC
.
- A. Erlebach, M. Šípka, I. Saha, P. Nachtigall, C. J. Heard and L. Grajciar, Nat. Commun., 2024, 15, 4215 CrossRef CAS PubMed
.
- M. Bocus, R. Goeminne, A. Lamaire, M. Cools-Ceuppens, T. Verstraelen and V. Van Speybroeck, Nat. Commun., 2023, 14, 1008 CrossRef CAS
.
-
I. Batatia, P. Benner, Y. Chiang, A. M. Elena, D. P. Kovács, J. Riebesell, X. R. Advincula, M. Asta, M. Avaylon, W. J. Baldwin, F. Berger, N. Bernstein, A. Bhowmik, S. M. Blau, V. Cărare, J. P. Darby, S. De, F. D. Pia, V. L. Deringer, R. Elijošius, Z. El-Machachi, F. Falcioni, E. Fako, A. C. Ferrari, A. Genreith-Schriever, J. George, R. E. A. Goodall, C. P. Grey, P. Grigorev, S. Han, W. Handley, H. H. Heenen, K. Hermansson, C. Holm, J. Jaafar, S. Hofmann, K. S. Jakob, H. Jung, V. Kapil, A. D. Kaplan, N. Karimitari, J. R. Kermode, N. Kroupa, J. Kullgren, M. C. Kuner, D. Kuryla, G. Liepuoniute, J. T. Margraf, I.-B. Magdău, A. Michaelides, J. H. Moore, A. A. Naik, S. P. Niblett, S. W. Norwood, N. O'Neill, C. Ortner, K. A. Persson, K. Reuter, A. S. Rosen, L. L. Schaaf, C. Schran, B. X. Shi, E. Sivonxay, T. K. Stenczel, V. Svahn, C. Sutton, T. D. Swinburne, J. Tilly, C. van der Oord, E. Varga-Umbrich, T. Vegge, M. Vondrák, Y. Wang, W. C. Witt, F. Zills and G. Csányi, A Foundation Model for Atomistic Materials Chemistry, arXiv, 2024, preprint, arXiv:2401.00096, DOI:10.48550/arXiv.2401.00096
.
- E. Lippmaa, A. Samoson and M. Magi, J. Am. Chem. Soc., 1986, 108, 1730–1735 CrossRef CAS
.
- J. Kučera and P. Nachtigall, Microporous Mesoporous Mater., 2005, 85, 279–283 CrossRef
.
- S. Sklenak, J. Dedecek, C. Li, B. Wichterlova, V. Gabova, M. Sierka and J. Sauer, Phys. Chem. Chem. Phys., 2009, 11, 1237–1247 RSC
.
- S. F. Dec, G. E. Maciel and J. J. Fitzgerald, J. Am. Chem. Soc., 1990, 112, 9069–9077 CrossRef CAS
.
- P. J. Dirken, J. B. H. Jansen and R. D. Schuiling, Am. Mineral., 1992, 77, 718–724 CAS
.
- D. Heidemann, C. Hübert, W. Schwieger, P. Grabner, K.-H. Bergk and P. Sarv, Z. Anorg. Allg. Chem., 1992, 617, 169–177 CrossRef CAS
.
- X. Xue and J. F. Stebbins, Phys. Chem. Miner., 1993, 20, 297–307 CrossRef CAS
.
- T. Charpentier, S. Ispas, M. Profeta, F. Mauri and C. J. Pickard, J. Phys. Chem. B, 2004, 108, 4147–4161 CrossRef CAS
.
- J. Steinadler, O. E. O. Zeman and T. Bräuniger, Oxygen, 2022, 2, 327–336 CrossRef CAS
.
- H. Koller, G. Engelhardt, A. P. M. Kentgens and J. Sauer, J. Phys. Chem., 1994, 98, 1544–1551 CrossRef CAS
.
-
D. Willimetz, Bachelor's thesis, Charles University, 2023
.
- W. Loewenstein, Am. Mineral., 1954, 39, 92–96 CAS
.
- R. E. Fletcher, S. Ling and B. Slater, Chem. Sci., 2017, 8, 7483–7491 RSC
.
- C. J. Heard, L. Grajciar and P. Nachtigall, Chem. Sci., 2019, 10, 5705–5711 RSC
.
- M. Fant, M. Ångqvist, A. Hellman and P. Erhart, Angew. Chem., Int. Ed., 2021, 60, 5132–5135 CrossRef CAS
.
- L. J. Smith, H. Eckert and A. K. Cheetham, J. Am. Chem. Soc., 2000, 122, 1700–1708 CrossRef CAS
.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef
.
- K. T. Schütt, P. Kessel, M. Gastegger, K. A. Nicoli, A. Tkatchenko and K.-R. Müller, J. Chem. Theory Comput., 2019, 15, 448–455 CrossRef
.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef
.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS
.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- T. Charpentier, Solid State Nucl. Magn. Reson., 2011, 40, 1–20 CrossRef CAS PubMed
.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570 CrossRef CAS
.
- G. I. Csonka, J. P. Perdew, A. Ruzsinszky, P. H. T. Philipsen, S. Lebègue, J. Paier, O. A. Vydrov and J. G. Ángyán, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 155107 CrossRef
.
- J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401 CrossRef
.
- M. Bak, J. T. Rasmussen and N. C. Nielsen, J. Magn. Reson., 2000, 147, 296–330 CrossRef CAS PubMed
.
- D. W. Juhl, Z. Tošner and T. Vosegaard, Versatile NMR Simulations Using SIMPSON, Annu. Rep. NMR Spectrosc., 2020, 100, 1–59 CrossRef CAS
.
- S. K. Zaremba, Ann. Mat. Pura Appl., 1966, 73, 293–317 CrossRef
.
- H. Conroy, J. Chem. Phys., 1967, 47, 5307–5318 CrossRef
.
- V. B. Cheng, H. H. Suzukawa and M. Wolfsberg, J. Chem. Phys., 1973, 59, 3992–3999 CrossRef CAS
.
- A. Brinkmann and A. P. M. Kentgens, J. Am. Chem. Soc., 2006, 128, 14758–14759 CrossRef CAS
.
- R. W. Dorn, A. L. Paterson, I. Hung, P. L. Gor'kov, A. J. Thompson, A. D. Sadow, Z. Gan and A. J. Rossini, J. Phys. Chem. C, 2022, 126, 11652–11666 CrossRef CAS
.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Technol., 2011, 12, 2825–2830 Search PubMed
.
- O. H. Han, C.-S. Kim and S. B. Hong, Angew. Chem., Int. Ed., 2002, 41, 469–472 CrossRef CAS
.
- A. Navrotsky, O. Trofymluk and A. A. Levchenko, Chem. Rev., 2009, 109, 3885–3902 CrossRef CAS PubMed
.
- A. Navrotsky and Z.-R. Tian, Chem.–Eur. J., 2001, 7, 769–774 CrossRef CAS PubMed
.
- P. M. Piccione, C. Laberty, S. Yang, M. A. Camblor, A. Navrotsky and M. E. Davis, J. Phys. Chem. B, 2000, 104, 10001–10011 CrossRef CAS
.
- N. J. Henson, A. K. Cheetham and J. D. Gale, Chem. Mater., 1994, 6, 1647–1650 CrossRef CAS
.
- J. Dědeček, S. Sklenak, C. Li, B. Wichterlová, V. Gábová, J. Brus, M. Sierka and J. Sauer, J. Phys. Chem. C, 2009, 113, 1447–1458 CrossRef
.
- P. Hodgkinson and L. Emsley, J. Magn. Reson., 1999, 139, 46–59 CrossRef CAS
.
- G. De Paëpe, Annu. Rev. Phys. Chem., 2012, 63, 661–684 CrossRef
.
- G. Tricot, J. Trébosc, F. Pourpoint, R. Gauvin and L. Delevoye, The D-HMQC MAS-NMR Technique: An Efficient Tool for the Editing of Through-Space Correlation Spectra Between Quadrupolar and Spin-1/2 (31P, 29Si, 1H, 13C) Nuclei, Annu. Rep. NMR Spectrosc., 2014, 81, 145–184 CrossRef CAS
.
- Y. Ji, L. Liang, X. Bao and G. Hou, Solid State Nucl. Magn. Reson., 2021, 112, 101711 CrossRef CAS
.
- M. Zheng, S. Xin, Q. Wang, J. Trébosc, J. Xu, G. Qi, N. Feng, O. Lafon and F. Deng, Magn. Reson. Chem., 2021, 59, 1062–1076 CrossRef CAS
.
- S. Vanlommel, A. E. J. Hoffman, S. Smet, S. Radhakrishnan, K. Asselman, C. V. Chandran, E. Breynaert, C. E. A. Kirschhock, J. A. Martens and V. Van Speybroeck, Chem.–Eur. J., 2022, 28, e202202621 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Data supporting this article, including full datasets of calculated static and dynamic NMR data, LASSO regression contributions and hyperparameters. See DOI: https://doi.org/10.1039/d4fd00100a |
| This journal is © The Royal Society of Chemistry 2025 |