Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
SPCal – an open source, easy-to-use processing platform for ICP-TOFMS-based single event data
Thomas E.
Lockwood
 a,
Lukas
Schlatt
b and
David
Clases
a,
Lukas
Schlatt
b and
David
Clases
 *c
*c
aUniversity of Technology Sydney, Ultimo, NSW, Australia
bNu Instruments Ltd, Wrexham, UK
cNanoMicroLab, University of Graz, Graz, Austria. E-mail: David.Clases@uni-graz.at
First published on 12th November 2024
Abstract
Single particle inductively coupled plasma-mass spectrometry (SP ICP-MS) has evolved into one of the most powerful techniques for the bottom-up characterisation of nanoparticle suspensions. The latest generation of time-of-flight mass analysers offers new perspectives on single particles by rapidly collecting full mass spectra and providing information on particle composition and abundances, even in unknown samples. However, SP ICP-TOFMS is associated with vast and complex data, which can hamper its applicability and the interrogation of specific particle features. Unlocking the full potential of SP ICP-TOFMS requires dedicated, easy-to-use software solutions to navigate through data sets and promote transparent, efficient and precise processing. SPCal is an open-source SP data processing platform, which we have previously released for quadrupole-based data. In this work, we expand its reach by additionally enabling the analysis of TOF-based SP data sets. We have incorporated various tools to facilitate the handling, manipulation and calibration of large data sets and provide the required statistical fundament and models to promote accurate thresholding. Non-target screening tools are integrated to pinpoint particulate elements in unknown samples without the requirement for a priori investigations or modelling. Next to basic functions like the calibration of size and mass distributions, methods to carry out cluster analysis (PCA, HAC) provide the means to study groups of particles based on their composition and conditional data filtering allows the interrogation of particle populations by selectecting specific features.
Introduction
The properties of nanoparticles (NPs) are stipulated by a set of parameters which include size, composition, and number concentrations. These parameters are difficult to determine, and we struggle to find and study the basic traits of common entities. The growing production of engineered nanomaterials, the increasing emission of incidental particles as well as the investigation of natural entities all call for dedicated methods to pinpoint particles and to study their unique facets.1 Methods require the ability to assess NPs on a particle-to-particle basis whilst offering high matrix-tolerance and the capability to pinpoint relevant particles across a large size-scale among unobtrusive entities. This is only possible at high single particle (SP) counting rates and high levels of both selectivity and sensitivity.2 These parameters are especially important for environmental samples, where no previous knowledge on rare and abundant entities is available. Particles in such samples may contain virtually any element of the periodic table, occur at very low number concentrations and in varying compositions. Their tracing resembles the veritable search for a needle in a haystack and their detailed characterisation poses even more challenges.3Single particle inductively coupled plasma-mass spectrometry (SP ICP-MS) has become one of the most powerful techniques for counting particles and establishing models on size distributions and compositions. The concept of SP ICP-MS is based on the individual introduction of particles into a plasma, where atomisation and ionisation processes take place. Consequently, each particle disintegrates into a cloud of elemental cations, which can be extracted in discrete ion packages and detected separately as resolved pulses. In ICP-MS, the quadrupole is the most commonly used mass analyser, providing high detection power and simple operation.2,4 However, a major disadvantage of this analyser is associated with time-consuming scanning operations when analysing varying m/z. Therefore, quadrupoles can only analyse one m/z per SP at a sufficient data acquisition rate (typically ≥10 kHz). This is a significant restriction as it prevents quadrupole-based instruments from being used to study SP composition and limits non-target particle screening approaches.3
These disadvantages can be overcome with time-of-flight (TOF)-based ICP-MS. Currently, there are two manufacturers that provide commercial instruments with the capability to record full mass spectra fast enough to support the advanced study of SPs. These instruments offer a vast potential to advance our understanding of nano- and microparticles but provide extremely large and complex data sets, which are difficult to encompass and interrogate.
Currently there exists no vendor-independent or open-source data processing platform for ICP-TOFMS. While manufacturers do provide some software, many studies still replace or extend data processing capabilities using inhouse software and scripts. One recent example is a set of data processing tools that support TOFWERK instrument data sets.5
We have previously reported an open-source data processing platform named “SPCal”, which was designed for quadrupole-based SP data sets.6 It was developed and distributed with the aim to drive transparent processing, to enable more comparability and to implement state-of-the-art algorithms and (statistical) approaches, which have been developed over the recent years.
With the present work, we expand the capabilities and applicability of SPCal to enable the analysis of TOF-based SP data sets in addition to quadrupole-based data. We propose an improved platform, which incorporates dedicated statistical approaches, new models, and state-of-the-art tools to drive the interrogation of complex particle suspensions using SP ICP-TOFMS. The new software has several powerful ICP-TOF data processing features while retaining its ease-of-use for users new to SP data processing.
Experimental
Instrumentation
SPCal is designed to be vendor-independent and is compatible with various data formats. Data shown here was recorded on a Vitesse ICP-TOFMS instrument (Nu Instruments, Wrexham, UK). Data acquisition was carried out with Nu Codaq software. At least three mass spectra were binned and saved to disk at approximately 10 kHz. This raw data was directly analysed with SPCal. Raw data from Nu Instruments, exported csv and txt files, and TOFWERK HDF5 data can be imported.Data processing
Different functions, calibration pathways and tools are implemented in SPCal and fundamental ideas and concepts have previously been published elsewhere.6 Here, critical considerations are briefly summarised whilst pointing out new, ToF specific, functions and adaptations.When loading a data set, SPCal first determines which type of mass analyser has been used by checking for low integer values. If more than 75% of values below 5 counts are integers, then a quadrupole-based analyser is assumed. Integer values are taken as ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) ± 0.05 as exported quadrupole data frequently contain a small offset from true integer values. For low mean signal values, poisson and compound poisson statistics are used for quadrupole- and TOF-based data sets, respectively, to determine the critical value over which a particle is recognised. Gaussian statistics are used in both cases for increased baseline signals, when less than 5% of non-zero signal is below 5 counts. This corresponds to a mean background of around 10 counts but was found to be more resilient to high particle counts. Statistics can be stipulated if required. The critical value can be adjusted manually or by modification of the pre-set α or σ values, which both stipulate the quantiles for thresholding and as such, the probability to falsely identify a signal as a SP event. Following summaries and discussions in the Multi-Agency Radiological Laboratory Analytical Protocols (MARLAP),7 different Poisson-based methods can be used for thresholding: Currie's method, Formula A, Formula C and the Stapleton approximation. An option to carry out iterative thresholding is implemented (and suggested) to approximate the real “ionic mean”. Here, this iterative algorithm consecutively eliminates recognised SP signals from the mean signal to recalculate the mean and threshold until no new SP signals are found and thus the limit no longer decreases.
± 0.05 as exported quadrupole data frequently contain a small offset from true integer values. For low mean signal values, poisson and compound poisson statistics are used for quadrupole- and TOF-based data sets, respectively, to determine the critical value over which a particle is recognised. Gaussian statistics are used in both cases for increased baseline signals, when less than 5% of non-zero signal is below 5 counts. This corresponds to a mean background of around 10 counts but was found to be more resilient to high particle counts. Statistics can be stipulated if required. The critical value can be adjusted manually or by modification of the pre-set α or σ values, which both stipulate the quantiles for thresholding and as such, the probability to falsely identify a signal as a SP event. Following summaries and discussions in the Multi-Agency Radiological Laboratory Analytical Protocols (MARLAP),7 different Poisson-based methods can be used for thresholding: Currie's method, Formula A, Formula C and the Stapleton approximation. An option to carry out iterative thresholding is implemented (and suggested) to approximate the real “ionic mean”. Here, this iterative algorithm consecutively eliminates recognised SP signals from the mean signal to recalculate the mean and threshold until no new SP signals are found and thus the limit no longer decreases.
When loading TOF-based data sets a periodic table is displayed, from which elements/isotopes may be selected for in-depth analysis. For unknown samples, a non-target screening function is used to pinpoint particulate elements as explained in detail later. Once elements/isotopes are selected, contiguous regions of SP events are summed. In the case of ToF data, a single particle (and its composition) is described by contiguous regions of any signal for selected isotopes. Calibration pathways to determine particle number concentrations, sizes, and masses are implemented as described previously.6
Results and discussion
Critical value and background modelling
Unlike quadrupole-based ICP-MS instruments, ICP-TOFMS instruments use fast analogue-to-digital converters (ADCs) to resolve the short detection intervals at which different m/z are detected. This detection paradigm excludes an event-counting mode and exposes the probabilistic response of the electron multiplier, typically a micro-channel plate or similar detector.8 Additionally, spectra must be binned as acquisition speed exceeds rates at which data can be saved.9 These factors give rise to a single ion signal or single ion area (SIA) distribution, which is used to convert raw ADC signal to counts. Usually, only the mean of the SIA for every element is considered, although mass dependant approaches have been suggested.10 The probabilistic nature of the SIA and the binning of spectra complicate the definition of a critical value, over which a signal event is identified as SP event with sufficient accuracy. While quadrupole based SP ICP-MS data sets with low background can be described with Poisson statistics,11 SP ICP-TOFMS data requires a compound Poisson approach in which the number of binned spectra as well as the SIA distribution is known.12 While the number of binned spectra is an experimentally set parameter, determination of the SIA requires the analysis of an ionic standard. Experimental SIAs were recorded by analysing an ionic standard with low ion transmission ensuring the sporadic arrival of individual ions at the detector. The probability of a multi-ion acquisition event was calculated for each element using eqn (1), where P(0′) is the fraction of non-zero values with a multi-ion probability P(>1) below 0.1%.| P(>1) = Γ(3,P(0′)) | (1) |
Each ion that strikes the detector produces a signal that is sampled from the SIA distribution and thus the result of multiple ions is a compound Poisson sampling of the SIA. Eqn (2) describes the Poisson process of ions arriving at the detector while eqn (3) states that the signal for each ion will be defined by the gain statistics of the detector.
| k = Poisson(λ) | (2) |
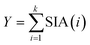 | (3) |
SPCal provides two methods to calculate thresholds for ToF data. If the single-ion signal distribution of the detector is provided, then software uses it to simulate a compound Poisson distribution with λ of the signal mean. Many values are drawn using the statistics above and the threshold can then be defined as the desired quantile of this simulation. This method will accurately predict the threshold, as it uses the true signal distribution but is slow and computationally expensive. This is compounded at low alpha values, where the number of simulations required for accuracy grows.13
The second method recognises that the SIA can be approximated with lognormal or gamma distributions.8 For this method a log-normal is chosen as the cumulative density function (CDF) is well defined, allowing easy extraction of the quantile for any given alpha value. Single-ion distributions from Nu Instruments and TOFWERKs instruments were fit using a log-normal, both having an optimal shape parameter σ of 0.47 (Fig. 1C and D). The fit is particularly accurate in the tail portion of the distribution, where the thresholding will occur. The optimal σ and μ = ln(1) − 0.5σ2 (to produce a mean value of one) were used in eqn (4) to approximate the signal produced by the SIA.
 | (4) |
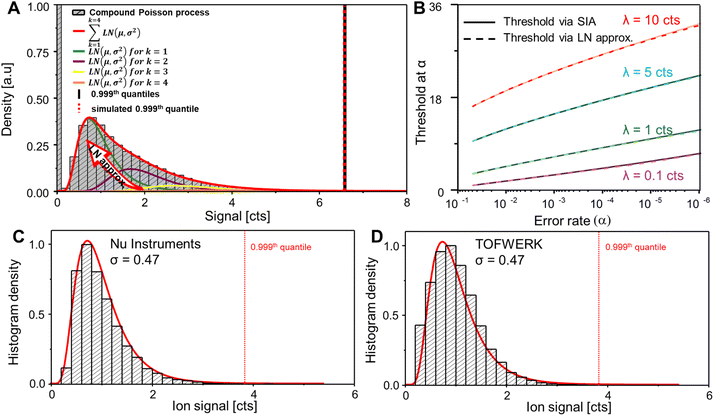 | ||
| Fig. 1 (A) shows the LN approximation to fit an ideal compound Poisson process. LNs for different k (Poisson events) are simulated and summed (red) to fit the compound Poisson distribution (bar diagram). Reproduced from (ref. 17) with permission from the Royal Society of Chemistry. (B) Shows the relation between the threshold and α error rate for different (ionic background) means. It is visible that the true SIA is fitted well by the LN approximation method. (C and D) Show real SP ICP-TOFMS data obtained from the two current vendors and the application of the LN approximation. | ||
To approximate the entire compound Poisson process, the sum of k log-normal distributions must be calculated for each possible value of k in the Poisson distribution that is greater than zero. The sum of these log-normal distributions is approximated using another log-normal with parameters from eqn (5) and (6), using the method defined by Fenton.14
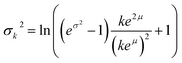 | (5) |
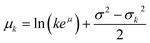 | (6) |
Finally, the cumulative distribution function (CDF) of each of these new log-normal distributions FX is then weighted by the probability from the Poisson probability mass function f. A threshold can then be calculated using eqn (7), returning the first value at which the CDF FY is greater than the desired zero-truncated quantile q0, calculated from the quantile q using eqn (8).
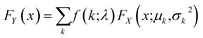 | (7) |
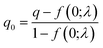 | (8) |
This method is much faster than the simulation and requires only two parameters: the signal mean and the shape parameter σ of the single-ion distribution. These factors enable iterative thresholding to better estimate detection limits in cases where the background distribution is not known, such as when particles are partially dissolved or when unknown samples are analysed.15
The log-normal (LN) approximation approach is visualised in Fig. 1A where LN distributions for different Poisson events k were created (orange, yellow, purple and green lines) and summed (red line) to fit an ideal compound Poisson process. It is visible that the simulated compound Poisson distribution approximates the compound process well and that the experimental (black vertical line) and approximated critical values (red dashed line) (0.999th percentile) predicted approximately the same value.
In Fig. 1B, thresholds at different error rates (dashed lines) were simulated and plotted to compare the LN approximation at different mean background values to a Monte Carlo simulation of the compound Poisson process (1 billion points; solid line). While threshold values were approximated well, small divergences were observed at high background levels and low error rates (e.g., λ = 10 counts) and Gaussian statistics may be more adequate to reflect these conditions more accurately. SPCal uses an automatic decision function in which compound Poisson statistics are only applied to data sets with low mean backgrounds and Gaussian statistics are called otherwise. Finally, experimental SIAs (histograms, Fig. 1C and D) were recorded for instruments from the two manufacturers and fitted using the proposed LN approximation (red line) demonstrating a high level of accordance for experimental and simulated distributions.
Non-target particle screening
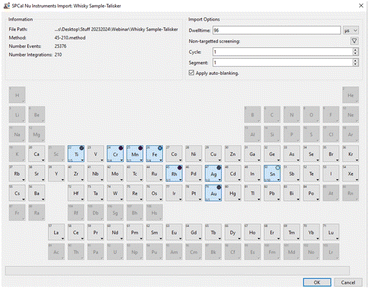
Establishing the presence and composition of particles is fundamental to analysis, and yet can be difficult to achieve in practice. In many cases, samples will have little to no a priori information and the presence of particles must be experimentally determined. In the case of environmental samples, where particle numbers are low, this requires extended analysis times and, with sequential mass analyses such as a quadrupole ICP-MS, analysis must be repeated for each element to inquire the presence of a particle.3 SP ICP-TOFMS generally allows the acquisition of all m/z in a single measurement and is therefore predestined to carry out screening approaches. However, existing SP analysis algorithms are limited in their ability to pinpoint NP events for every element in data sets that can easily exceed several gigabytes. Additionally, the SIA needs to be known for every isotope signal to define a critical value over which a particle is recognised as such. This would require a separate analysis of an ionic standard for each element. The shape parameter for the optimal log-normal fit changes slightly over the mass range from 0.43–0.49 from 45 to 238 amu. However, using the LN approximation with a sigma of 0.47 for all masses produces a maximum error of 2% in the quantile predicted for a mean signal of 1.0 at an alpha value of 1 × 10−6, compared to using the optimal shape. For elements with lower m/z, errors were approximately 5%. Therefore, SIAs for individual elements do not need to be determined in parallel and are modelled with minimal input allowing rapid and efficient thresholding. The LN approximation approach has therefore a high utility to pinpoint particulate elements in unknown samples.16 SPCal incorporates a “non-target screening” approach that rapidly defines a critical value for all recorded m/z. Compound Poisson (LN approximation) or Gaussian statistics are called depending on the mean signal of the data set. Contiguous regions above the critical value are counted and scored in parts-per-million relative to the total number of screened data points, i.e., the number of detected particles per million events. The minimum score over which elements are pinpointed and can be chosen freely (by default set to 100 ppm). The score is reported as colour code which provides an overview on particulate element abundances across the periodic table. To limit processing time, screening is limited to a user selectable number of events at the start of the data file (by default the first 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data points). Fig. 2 shows an example from a recently published study where SP data from a diluted whisky sample was processed to indicate particulate elements.16 Using a threshold of 25 ppm whilst acquiring a mass range from 45–210 amu pinpointed Ti, Fe, Ag, Sn and Au as particulate elements within seconds and without previous knowledge.
000 data points). Fig. 2 shows an example from a recently published study where SP data from a diluted whisky sample was processed to indicate particulate elements.16 Using a threshold of 25 ppm whilst acquiring a mass range from 45–210 amu pinpointed Ti, Fe, Ag, Sn and Au as particulate elements within seconds and without previous knowledge.
Calculator
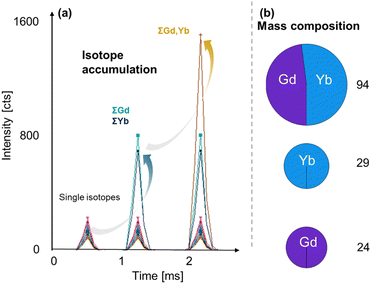
Simple arithmetic operations can be performed to investigate the sums, differences, or ratios of elements/isotopes on a per-particle basis. This has different utilities and can for example be used for standardisation (e.g., an internal ionic standard) to compensate for signal drift, for calibration (e.g., isotope dilution analysis) as well as to correct for spectral interferences mathematically. Furthermore, the signal of all isotopes of an element as well as cumulative element signals contained in a single particle can be summed up to increase signal to noise ratios as previously demonstrated by Lockwood et al.9 An example is shown in Fig. 3, where up-conversion NPs containing Gd and Yb were analysed. The single isotopes of both elements can be recorded individually as shown on the left. However, the summing of all Gd and Yb isotopes increases the overall signal for both elements, improving mass and size detection limits. Summing the element signals of Yb and Gd enhances figures of merit further.Compositional analysis
One of the fundamental benefits of simultaneous mass acquisition is the ability to determine the elemental composition of individual particles. SPCal provides a simple interface to perform clustering, adapted from Tharaud et al.,17 who used hierarchical agglomerative clustering (HAC) to classify both engineered and natural nanoparticles in the environment based on their isotopic/elemental composition. Here, events are grouped by successively merging pairs of clusters in a tree-like hierarchy. Clusters can then be separated by a minimum required distance within each cluster. HAC is implemented in the current software using a C extension and can be limited by both a minimum Euclidean distance and minimum cluster size. Prior to clustering, data can be calibrated to subsequently report mass/size compositions of elements in clusters. An example is shown for up-conversion NPs in Fig. 3b. Individual clusters can subsequently be selected to display cluster-specific plots such as histograms and scatter plots. Finally, principal component analysis is implemented to investigate composition-specific clusters visually as shown in Fig. 4f. The apparent elemental composition of particles may be affected by elemental detection limits, as lower signal elements are not detected in smaller particles.17 Compositional filtering, explained in the next section, can be used to ensure clustering is only performed on particles with sufficient mass to be detected but may obscure the true composition if element fractions vary with particle size.Conditional analysis
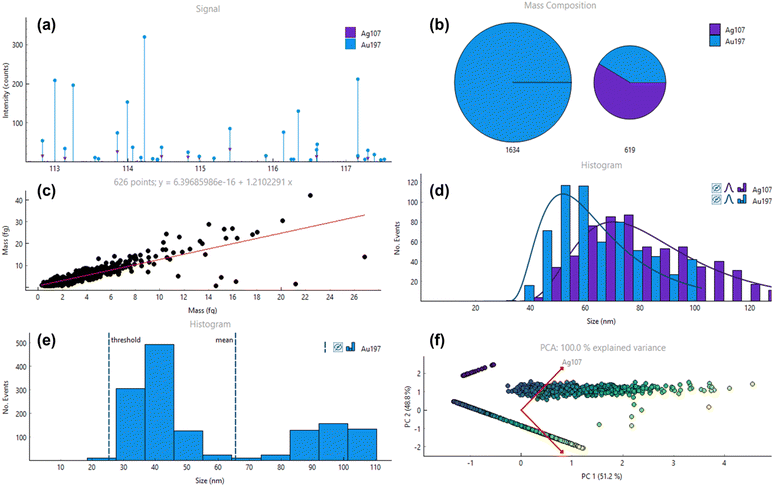
SP ICP-TOFMS provides the option to interrogate SP events based on specific features. This conditional analysis provides opportunities to select specific size, mass or signal ranges, in which particles are further interrogated as well as to limit analyses to SP events associated with a specific cluster or containing one or a specific set of elements. This is demonstrated in Fig. 4, where a mix containing small Au NPs (40 nm mean size), large Au NPs (100 nm mean size) and core–shell AuAg NPs were analysed. Fig. 4a shows the raw signals and SP events with varying signal intensity and composition. HAC was performed and identified two types of particles as expected – those which only contain Au, and which contain both Au and Ag (Fig. 4b). The second cluster was subsequently selected for more thorough analysis as shown in Fig. 4c and d, where a mass scatter plot of SP events as well as size histograms for each element fraction for this cluster were plotted, respectively. For the latter, it needs to be considered that SPCal projects size data by assuming a perfectly homogenous and spherical shape, which is not the case for the Ag shell in a AuAg core shell particle. In case of more complex particles containing substructures and exhibiting different shapes (e.g., nanorods), mass-based histograms are more adequate and can be selected instead. Fig. 4e shows a conditional analysis in which only particles without Ag were calibrated and plotted in a size histogram. This allows the resolution of 40 nm and 100 nm Au NP fractions whilst eliminating interfering Au signals from the AuAg core–shell particles. Fig. 4f shows the PCA analysis for SPCal to investigate the NP mixture and demonstrates the possibility to pinpoint three clusters. Here, a third cluster is visible, which was not picked up by the HCA due to the chosen minimum cluster size. This third cluster (top) contains only Ag without detectable fractions of Au, most likely due to synthesis impurities.Conclusions
The maturation of TOF analysers capable of single particle applications provides new paradigms for the implementation of non-target particle screening and the determination of particle compositions. However, to really exploit this technology and to bring SP analyses to the next level, we need to overcome several challenges associated with data processing. In one hand, we have vast data sets, accumulated at rates exceeding 1–2 GB min−1 and, in the other, we require new ideas, models, statistics, and filters to interrogate specific aspects and features of NPs. One of the largest challenges is the harmonisation of data analysis and processing protocols to provide transparent, reproducible, and traceable analyses across different labs, instruments and applications.SPCal is an open-source Python-based platform designed to enable the analysis of data sets recorded with instruments from various vendors. Building on software for quadrupole-based data, this work improves the underlying codebase and expands the application of SPCal to SP ICP-TOFMS. Easy handling of complex data sets and essential tools for SP analyses are accessed through a graphical user interface. Compound Poisson or Gaussian statistics are used to determine critical values and a LN approximation method was developed to quickly calculate limits, specifically to drive non-target particle screenings. Several tools to facilitate calibrations via ionic responses or transport efficiency are readily integrated to enable the calculation of particle number concentrations as well as size and mass distributions. TOF-specific tools are integrated to enable compositional (HCA, PCA) and conditional analysis, to select specific particle features and to measure isotope and element ratios in SP events.
Data availability
The code for “SPCal” can be found at https://github.com/djdt/spcal. A previous version of this software for quadrupole-based SP ICP-MS was published in 2021 (https://doi.org/10.1039/D1JA00297J). The software presented here advances on this by enabling the analysis of SP ICP-TOFMS data sets and implementing various tools and statistics. The version of the code employed for this study is version 1.2.7.Author contributions
This work was conceptualised by DC. All authors performed investigations. Software was written by TEL. TEL and DC prepared the first draft of the manuscript and all authors contributed to its creation and review.Conflicts of interest
LS works for Nu Instruments.Acknowledgements
Following the first release of SPCal, we have received feedback across various groups of the ICP-community and would like to thank the individuals for their critical thinking, constructive criticism, new ideas and suggestions. We welcome further feedback for the current platform. We further would like to acknowledge Nu Instruments and TOFWERK for access to data files to optimise data import and background modelling. The University of Graz is acknowledged for the financial support. Computational facilities were provided by the UTS eResearch High Performance Computer Cluster.References
- M. F. Hochella, D. W. Mogk, J. Ranville, I. C. Allen, G. W. Luther, L. C. Marr, B. P. McGrail, M. Murayama, N. P. Qafoku, K. M. Rosso, N. Sahai, P. A. Schroeder, P. Vikesland, P. Westerhoff and Y. Yang, Science, 2019, 363, eaau8299 CrossRef.
- B. Meermann and V. Nischwitz, J. Anal. At. Spectrom., 2018, 33, 1432–1468 RSC.
- R. Gonzalez de Vega, T. E. Lockwood, X. Xu, C. Gonzalez de Vega, J. Scholz, M. Horstmann, P. A. Doble and D. Clases, Anal. Bioanal. Chem., 2022, 414, 5671–5681 CrossRef CAS.
- D. Clases and R. Gonzalez de Vega, Anal. Bioanal. Chem., 2022, 414, 7363–7386 CrossRef CAS PubMed.
- A. Gundlach-Graham, S. Harycki, S. E. Szakas, T. L. Taylor, H. Karkee, R. L. Buckman, S. Mukta, R. Hu and W. Lee, J. Anal. At. Spectrom., 2024, 39, 704–711 RSC.
- T. E. Lockwood, R. de Vega and D. Clases, J. Anal. At. Spectrom., 2021, 36, 2536–2544 RSC.
- MARLAP, Detection and quantification capabilities, accessed 06.03.2024, https://www.epa.gov/sites/default/files/2015-05/documents/402-b-04-001c-20_final.pdf Search PubMed.
- D. J. Gershman, U. Gliese, J. C. Dorelli, L. A. Avanov, A. C. Barrie, D. J. Chornay, E. A. MacDonald, M. P. Holland, B. L. Giles and C. J. Pollock, J. Geophys. Res.: Space Phys., 2016, 121(10), 10005–10018 Search PubMed.
- T. E. Lockwood, R. de Vega, Z. Du, L. Schlatt, X. Xu and D. Clases, J. Anal. At. Spectrom., 2024, 39, 227–234 RSC.
- A. Gundlach-Graham and R. Lancaster, Anal. Chem., 2023, 95, 5618–5626 CrossRef CAS PubMed.
- M. Tanner, J. Anal. At. Spectrom., 2010, 25, 405–407 RSC.
- A. Gundlach-Graham, L. Hendriks, K. Mehrabi and D. Günther, Anal. Chem., 2018, 90, 11847–11855 CrossRef CAS.
- E. J. Chen and W. D. Kelton, Proceedings of the 1999 Winter Simulation Conference, 1999, pp. 428–434 Search PubMed.
- L. Fenton, IRE Trans. Commun. Syst., 1960, 8, 57–67 Search PubMed.
- J. Tuoriniemi, G. Cornelis and M. Hassellöv, Anal. Chem., 2012, 84, 3965–3972 CrossRef CAS PubMed.
- R. Gonzalez de Vega, T. E. Lockwood, L. Paton, L. Schlatt and D. Clases, J. Anal. At. Spectrom., 2023, 38, 2656–2663 RSC.
- M. Tharaud, L. Schlatt, P. Shaw and M. F. Benedetti, J. Anal. At. Spectrom., 2022, 37, 2042–2052 RSC.
| This journal is © The Royal Society of Chemistry 2025 |