 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Short-range order and hidden energy scale in geometrically frustrated magnets
A. P.
Ramirez
and
S. V.
Syzranov

Physics Department, University of California, Santa Cruz, California 95064, USA
First published on 10th January 2025
Abstract
In geometrically frustrated (GF) magnets, conventional long-range order is suppressed due to the presence of primitive triangular structural units, and the nature of the ensuing ground state remains elusive. One class of candidate states, extensively sought in experiments and vigorously studied theoretically, is the quantum spin liquid (QSL), a magnetically-disordered state in which all spins participate in a quantum-coherent many-body state. Randomly located impurities, present in all materials, may prevent QSL formation and instead lead to the formation of a spin-glass state. In this article, we review available data on the specific heat, magnetic susceptibility, and neutron scattering in GF materials. Such data show that a pure GF magnet possesses a characteristic “hidden energy scale” significantly exceeded by the other microscopic energy scales in the material. When cooled down to a temperature below the hidden energy scale, a GF material develops significant short-range order that dominates its properties and, in particular, dictates the spin-glass transition temperature for experimentally accessible impurity densities. We review the manifestations of short-range order in the commonly observed thermodynamics quantities in GF materials, possible scenarios for the hidden energy scale, and related open questions.
I. Introduction
In most magnetic materials at low temperatures, spins are arranged in a regular pattern, i.e. form long-range magnetic order. In some materials, however, it may be impossible to simultaneously minimize all magnetic interactions between spins, which may lead to competition between multiple magnetic states, and the material may possibly avoid long-range order.In 1973, Anderson proposed1 that the ground state of the Heisenberg model with nearest-neighbor antiferromagnetic (AF) interactions on a triangular lattice may lack magnetic order and instead display liquid-like properties with strong quantum fluctuations. Although this proposal turned out to be incorrect (the model develops the so-called 120° order2–4), it initiated a series of theoretical studies5–7 of “quantum spin liquids” (QSLs), magnetic states that lack long-range order (LRO) at T = 0 and, broadly speaking, exhibit liquid-like properties due to strong quantum fluctuations. The interest in QSLs has been driven by the possibility of numerous fundamental phenomena predicted in them, such as novel topological states, fractionalized excitations, and long-range entanglement, as well as the existence of anyon excitations in some QSLs, which can be used for robust quantum computation.
QSLs can be grouped into two theoretical categories that fit the broad description. The first includes models of spins on bipartite, e.g. honeycomb, lattices in which the interactions are tuned to prevent LRO. Spins on such lattices would be ordered antiferromagnetically if the interactions were AF and short-ranged but avoid this order due to a more complicated structure of the interactions, exemplified by the Shastry-Sutherland8 and Kitaev9 models. Despite the existence of materials such as RuCl3, considered as their approximate realizations,10,11 these materials nevertheless undergo long-range order in zero magnetic field12–15 instead of displaying clear signs of a QSL. While interesting behavior suggestive of a QSL has recently been reported in RuCl3 in sufficiently strong magnetic fields,16–18 the interpretation of the respective results as evidence for a QSL is under dispute (see, e.g., ref. 19–21).
A second class of systems, the so-called geometrically frustrated (GF) magnets, consists of materials in which the smallest structural unit in the magnetic sublattice is a triangle.22–24 Such triangles make it impossible to minimize simultaneously all nearest-neighbor AF interactions between spins. This class includes large mineral families such as the spinels, pyrochlores, magnetoplumbites, jarosites, and delafossites.25 These materials show a suppression of LRO to temperatures far below the characteristic scales of AF interactions obtained from high-temperature measurements. In the absence of LRO, strong quantum fluctuations in such materials are predicted to yield QSL states with fascinating fundamental properties, such as many-body entanglement and topological excitations.5–7,26–28 Theoretical interest in such states has been mirrored by experimental searches that have produced a large number of magnets with triangular primitive units and greatly suppressed LRO transitions.24
A. What exactly is a quantum spin liquid?
The term “spin liquid” commonly refers to a T = 0 state of a magnetic material that lacks LRO. The term “quantum spin liquid” is used to label a quantum-coherent state in which, in addition to the lack of LRO, the quantum nature of spins gives rise to qualitatively new properties. Despite some commonalities among the different QSL models, in our view, there is not a universal, commonly accepted definition of a QSL. Often, in theoretical work, a spin liquid is referred to as a QSL if it displays long-range entanglement or topological properties, such as topological order or fractionalized excitations, or can be described in terms of emergent gauge fields.The ambiguity surrounding the theoretical description of QSLs is mirrored experimentally, where there is no consensus that QSLs have been conclusively identified in specific materials. The experimental assignment of the QSL label to a particular material has relied on such features as the absence of a transition to LRO or the form of the inelastic structure factor measured by neutron scattering. These features, however, are not unique to QSLs and allow for other explanations. For example, LRO can be suppressed by many other experimental factors, e.g., dimerization,29 quenched disorder,30 low effective dimensionality,31 or combinations of these.
Numerous excellent reviews dedicated to QSLs have been written over the last decade (see, e.g., ref. 5–7 and 26–28). We refer the readers to these reviews for a detailed discussion of possible definitions of QSLs. In this article, we focus rather on the properties of GF materials, the largest class of systems in which QSLs are sought, and especially those properties that are common across classes of GF materials and thus reveal the fundamental physics of magnetic states in GF systems and their properties observable in experiment.
B. Goal of this review
The aim of this review is to outline a minimal set of existing facts that apply to all GF magnets in the hope of informing future theoretical work. Thus, we will restrict discussion to the most common experimental quantities, because such data allow for intercomparison among all GF materials. While GF magnets have been experimentally probed in many different ways, the most common quantities are the magnetic susceptibility [χ(T)], specific heat [C(T)], and the intensity of neutron scattering.Other probes include NMR and μSR. We will not consider these here because, in our view, each has a significant level of interpretive uncertainty. Each one gives good information on the internal field at the probe site, but the identity of the site is either unknown in the case of μSR32–34 or not well defined, as shown by the two distinct signals in NiGa2S4, which were interpreted as evidence of stacking faults.32
It is useful to remember what χ(T), C(T), and neutron scattering reveal about the state of a magnetic material. The susceptibility, χ(T), is a long wavelength probe that is especially useful at high temperatures for determining the spin–spin interaction strength via Curie–Weiss analysis and at low temperatures for detecting transitions, e.g., to an LRO or a spin-glass state. Most importantly for this work, χ(T) can detect non-magnetic (singlet) excitations only weakly. The specific heat, however, is sensitive to all excitations with a spin origin, including non-magnetic excitations, but also to those not spin-derived, such as phonons and charged excitations. A powerful aspect of the C(T) probe is its ability to count degrees of freedom, provided the non-spin-derived excitations are accurately determined. Neutrons, like χ(T), can probe magnetic and structural excitations and can access them over a large range of wavelengths, from mesoscopic distances down to interatomic length scales. The complementarity of these three probes is sufficient to demonstrate key universal features of GF magnets. As we argue, among those universal features is the short-range magnetic order (SRO) that forms below a certain characteristic temperature, which is significantly exceeded by the spin–spin interaction energy.
C. Materials to be discussed
The strength of geometrical frustration in a material is characterized by the ratio| f = θW/Tc, | (1.1) |
Non-GF 3D materials undergo magnetic-ordering phase transitions at temperatures Tc ∼ θW, and thus have f-ratios of order unity. By contrast, strongly GF materials avoid ordering down to very low temperatures, resulting in Tc ≪ θW and large f-ratios f ≫ 1.
In systems that undergo spin-glass and magnetic ordering transitions, the temperature Tc corresponds to the critical temperature of the respective transition. The definition, however, can be extended to the case of the freezing of the magnetic degrees of freedom that is not accompanied by any phase transition, as discussed in ref. 35.
In this review, we will focus on materials with strong geometrical frustration, corresponding to f ≳ 10, that have also been subject to magnetic vacancy studies and a full complement of the simple experimental probes mentioned above. We show that a select group of such materials develops SRO at intermediate (T ∼ |θW|/10) temperatures. We then argue that this SRO is a universal feature of all GF systems and is key to understanding ground states and their elementary excitations.
Due to the above restrictions, many GF systems will not be extensively analyzed. Most evident among the omissions is the family of paratacamite compounds related to well-known herbertsmithite [γ-ZnCu3(OH)6Cl2],36 which consists of a kagome lattice of Cu2+ spins. Herbertsmithite, and its relatives volborthite [Cu3V2O7(OH)2·2H2O],37–39 vesignieite [BaCu3V2O8(OH)2],40 kapellasite [Cu3Zn(OH)6Cl2],40,41 haydeeite [α-Cu3Mg(OH)6Cl2],42 and barlowite [Cu4(OH)6FBr]43,44 all have Cu2+ on a kagome lattice and exhibit a variety of ground states including FM and AF order. They all possess hydrogen, which is deleterious for neutron scattering, though some have been studied in their deuterated form, most importantly Herbertsmithite,36 and we will show these data below. Also, for these materials, we are unaware of systematic studies of spin vacancies, a technique that has yielded great insight into the ground state.
A second, large group of materials that eludes the present review is 4f electron systems, the frustration in which has been intensively studied especially in recent years.26 Since 4f atoms in an ionically bonded solid have exchange coupling strengths at least an order of magnitude less than 3d systems, the θW values are usually in the range of a few Kelvins or less and, thus, the interaction can be strongly influenced by dipole–dipole (long range) forces which are rarely considered for d-row transition ions. Most importantly, however, geometrical frustration addresses the physics at energy scales two or more orders of magnitude less than the mean field temperature, θW. Thus, for θW values less than 1 K, measurements of C(T) and χ(T) are needed down to 10 mK, which presents a barrier for characterization. Firstly, obtaining C(T) even down to 50 mK often requires great care to maximize thermal coupling to the sample. Secondly, commercial magnetometers only reach 300 mK. Thus, obtaining susceptibility data down to the required temperatures is considerably more difficult than for systems with larger θW values. Finally, the splitting of the total angular momentum multiplet often leads to high-mJ doublets and, while this poses no fundamental barrier to collective behavior, higher-lying multiplets often obscure the determination of effective moment from data taken above 2 K. Thus, in our view, the existing body of experimental work on 4f materials precludes the systematic intercomparison of both high and low energy scales as can be done for 3d systems.
II. Characterization of GF magnetic materials
A. Types of quenched disorder
In order to describe GF materials in the pure limit, one should understand their response to quenched disorder. One may distinguish here between two generic types of disorder: intrinsic and extrinsic.Intrinsic disorder occurs without introducing quenched randomness in the synthesis process. For example, in Y2Mo2O7, Jahn–Teller distortions of the Mo octahedra result in randomness in the spin–spin interaction and a spin-glass (SG) transition at Tg = 22 K.45,46 In some materials, different ions have to randomly occupy the same crystallographic site to ensure charge balance between cations and anions. For example, in Fe2TiO5, the Fe3+ and Ti4+ ions are randomly located on both A and B sites of the pseudo-Brookite structure.47 In NaCdCo2F7, the A site can be occupied by both Na1+ and Cd2+.48 Another example of such disorder comes from the inverse spinels, such as B(AB)O4, in which site mixing occurs between the A2+ and B3+ ions.49
Extrinsic disorder refers to foreign atoms introduced in the clean material. Often, such disorder is represented by vacancies, i.e. foreign non-magnetic atoms substituting for the magnetic atoms of the clean material. Of course, non-magnetic vacancies will be at least subtly different in atomic size and, therefore, will not bond with their neighboring cations in a manner identical to the magnetic ion, hence one expects small steric distortion around the vacancies. Extrinsic disorder may also be introduced by substitution on either a non-magnetic cation site or the anion site, which can lead to charge disorder or sterically induced randomness in the exchange interactions between magnetic ions.50
Techniques for measuring disorder at the required precision are few. In most cases, purity control consists of identifying the presence or absence of unexpected diffraction peaks in X-ray diffraction (XRD). Such a technique, however, cannot detect impurities or disorder other than by the observations of foreign crystallographic phases or broadening of the diffraction peaks. In the case of Y2Mo2O7, pair distribution function analysis of neutron and X-ray scattering was needed to determine the distribution of bond lengths responsible for interaction disorder and the observed spin glass behavior.46,51 For deviations from the stoichiometry larger than a few percent, energy-dispersive X-ray absorption can reveal impurity atoms, but its precision is limited.
B. Importance of spatial dimensionality
The role of spatial dimensionality is well-understood for non-frustrated systems exhibiting LRO and is manifested both in the critical behavior as well as the ground state and its elementary excitations.31 Effective dimensionality less than three can arise either from a crystal structure that is lamellar (2D) or fibrous (1D), or may result from a collective structural distortion such as a cooperative Jahn–Teller effect that modulates the spin–spin interaction in a uniform manner.52The role of spatial dimensionality is less well-understood for SGs. Great effort has been devoted to the question of whether or not a 2D system can transition to an SG state, and the present consensus, based on computational work, is that spin glass freezing anomalies are only observable in 3D systems.53 While certain layered materials such as Rb2(Cu,Co)F4,54 have been shown to exhibit SG behavior, such materials can be classified only as “quasi-2D”, i.e. while the intra-plane interactions are small compared to the inter-plane ones, the 3D nature of the intra-plane correlations is essential for the emergence of the SG phase.
While the consensus view is that purely 2D systems do not evince an SG transition, it is possible that the SG-transition temperature is actually strongly suppressed in quasi-2D materials, owing to their effective 2D nature at short scales. Numerous authors seeking to establish the existence of 2D QSLs in layered materials argued that the absence of an SG cusp in χ(T) for experimentally accessed temperatures rules out an SG state, which is seen as inimical to a QSL (see, for example, ref. 36 and 55–57). The SG transition in such layered systems, however, may take place at temperatures below the observed range.
C. Heisenberg vs. Ising spins
This review focuses on strongly GF systems with Heisenberg spins. Ising spins on frustrating lattices present a different and informative complement to Heisenberg spins. In early theoretical work, Wannier considered 2D Ising spins on a triangular lattice and showed that, whereas ferromagnetic spin–spin interactions lead to LRO, antiferromagnetic interactions cause a total suppression of the transition and lead to a nonzero ground-state entropy (per spin).22 The existence of such non-vanishing ground-state entropy for theoretical Ising models makes them ‘infinitely frustrated”, a situation reflected experimentally by the lack of Ising-based magnets for which the f-ratio can be defined by a measurable low-energy scale. Among the materials that have Ising spins but do not exhibit an ice-like state are Co3Mg(OH)6Cl258 and A2Co(SeO3)2, where A = K or Rb.59A possible reason behind the lack of experimental Ising GF magnets is related to the stringent conditions required to create local degeneracy. Ising spins occur due to, e.g., a distortion in the crystal field environment or due to spin–orbit coupling, i.e. a local structural anisotropy. Such anisotropy can lead to anisotropy in the spin–spin interaction and the subsequent selection of certain favored LRO states, thus destroying frustration. While the paucity of GF Ising systems is unfortunate from the perspective of comparing theory and experiment, their role in the development of quantum materials would be limited anyway due to the Ising single-ion potential well constraint at very low temperatures. (Transverse-field Ising materials are possible but present the additional requirement of a unique transverse field direction, which is more difficult to realize with a triangular motif.)
With the above caveat in hand, a special class of 3D Ising systems was pioneered by Harris, Bramwell et al., who described a formal correspondence between water ice and a class of Ising magnets which they called “spin ice”.60 The correspondence is, specifically, between two possible hydrogen atom positions around each oxygen in water ice and the two states of an Ising spin. The spin-ice materials class consists of Ising ions, such as Ho3+ or Dy3+, occupying the A-site of the pyrochlore lattice, a sublattice consisting of corner-shared tetrahedra. Ramirez et al. measured61 the specific heat of the spin ice candidate, Dy2Ti2O7, and showed that the ground-state entropy of the Dy3+ ions is close to Pauling's estimate (R/2)ln(3/2) ≈ 0.29R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2).
ln(2).
While it may seem as though the spin-ice state results purely from the frustration of interactions, several factors set spin ice apart from the Heisenberg GF systems, which are the focus of this review. First, Dy2Ti2O7 is not strongly GF because θW = 0.5 K, which is the same temperature region where the spin ice SRO sets in, thus f ≈ 1. Second, when disordered, Dy2Ti2O7 fails to exhibit an SG state.62 Third, because of the small spin–spin exchange interactions, long-range dipole–dipole interactions play an important role in determining the ground state energy.63 It is interesting to consider why Dy2Ti2O7 doesn't undergo LRO similar to other Ising systems on triangle-based lattices. This is most likely due to the non-collinear nature of the crystal field distortion of the rare-earth environment. The Ising axis for each ligand environment surrounding the Dy3+ ions connects the vertex of the tetrahedron to its center. Thus, with four distinct crystalline directions, the distortion itself is sterically frustrated, which may help to explain the relatively small number of spin-ice materials.
Unlike Ising systems, no evidence has been found for missing entropy, i.e. extensive entropy of the ground states, in the Heisenberg spin systems. While missing entropy, suggestive of spin-liquid behavior, has been reported for CuAl2O464 and CuGa2O4,65 where Cu2+ occupies the A-site of the spinel lattice, the conclusion about the missing entropy was reached based on the specific-heat extending only up to 20 K or 30 K, respectively. At the same time, the inverse susceptibility χ−1(T) in these materials deviates from linearity at a much higher temperature, implying that the remaining entropy will be found at higher temperatures.
III. Magnetic susceptibility
A. The Curie–Weiss law
The dependence of the inverse magnetic susceptibility χ(T) on temperature T for several GF materials36,66–73 with large f-ratios f > 10 is shown in Fig. 1. At sufficiently high temperatures, GF materials exhibit the Curie–Weiss behaviour of the susceptibility| 1/χ(T) ∝ T + θW, | (3.1) |
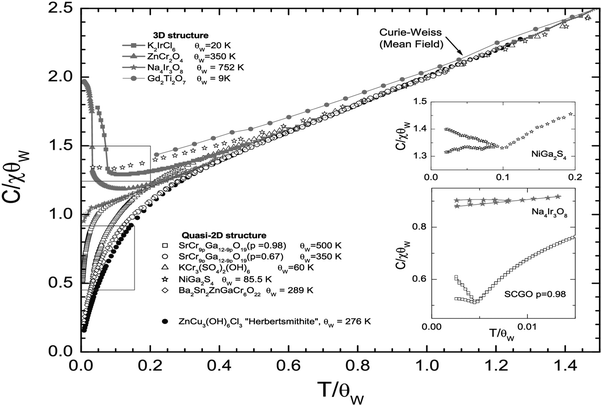 | ||
| Fig. 1 The dependence of the inverse susceptibility χ−1(T) on the temperature T for several GF materials.36,66–73 The susceptibility and the temperature are shown, respectively, in units of C/θW and θW, where C and θW are the Curie and Weiss constants. The upper and lower insets, represented by the boxes in the main frame, show, respectively, the spin-glass transitions in NiGa2S4 and Na4Ir3O8 and SrCr8.8Ga3.2O19. The dashed line shows the Curie–Weiss law. | ||
The value of θW obtained from the temperature dependence (3.1) can be used to obtain the f-ratio [cf.eqn (1.1)], which characterizes the degree of frustration. Because the dependence (3.1) implies that a material behaves effectively as free spins in the limit of high temperatures T ≫ θW, the respective value of θW is faithful only if the measured slope of 1/χ(T) matches the expected Hund's rule moment.
B. Susceptibility and glass transitions
While the linear, high-temperature behavior of the inverse susceptibility is a universal feature of GF systems, there is a dichotomy in the low-temperature behavior between GF systems that eventually undergo LRO to an AF state and those that resist ordering.At temperatures above magnetic and glass transitions, this dichotomy usually manifests in the sign of the deviation of the magnetic susceptibility from the Curie–Weiss law. When the system undergoes an AF transition, the high-temperature χ(T)−1 typically bends upward on cooling (see Fig. 1), reflecting the appearance of AF correlations. However, if the system undergoes an SG glass transition instead of developing magnetic order, χ(T)−1 typically bends downwards on cooling above the transition, a behavior that in conventional magnetic systems is referred to as a Curie tail and similar to that coming from free spins.
Such Curie tails can be explained by the presence of dilute vacancy defects. As discussed in detail in Section III C below, a vacancy defect in a GF material is equivalent to an effective spin, a “quasispin”, in terms of its magnetic susceptibility. At sufficiently high temperatures, magnetic correlations in the system are short-ranged, and the quasispins of vacancy defects can be considered non-interacting and independent of each other. Such quasispins act as effective free spins and give rise to the Curie tail. At lower temperatures, the quasispin–quasispin interactions become essential (see Section III C for a detailed discussion).
At the lowest temperatures, SG transitions are observed (see the insets in Fig. 1) even in rather pure materials, such as the triangular lattice compound NiGa2S474 and the spinel ZnCr2O4.67 In ZnCr2O4, SG freezing is even observed deep in the AF temperature regime, demonstrating that an SG state can coexist with LRO.
The novelty of SGs occurring in nearly pure GF materials was realized early in the development of GF magnetism24,45 and suggests an analogy with conventional SGs in metallic materials in which spins have densities less than 1%, far below the nearest-neighbor percolation threshold. Such materials undergo SG freezing due to the long-range nature of the RKKY interaction.75 The analogy falters, however, in the following manner. While the RKKY interaction in conventional SGs exists above the glass temperature, Tg, there is no evidence for such an interaction for GF SGs above Tg. In addition, the medium in which the GF SG state forms is comprised of a dense population of spins, whereas conventional metallic SGs have no magnetic sources in the spatial region between the spins. Thus, the physical difference between the two classes of SGs is profound,24 despite similarities in their collective, bulk behavior.76,77
C. Quasispins
Vacancy defects, the most common type of quenched disorder in GF materials, have a fundamental effect on magnetic susceptibility. It has been found that, in terms of response to a magnetic field, vacancies act as effective free spins, “quasispins”, with the Curie-like susceptibility [in units of (gμB)2/kB]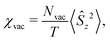 | (3.2) |
The quasispin behavior (3.2) was first identified78 in SrCr9pGa12−9pO19 (where Nvac ∝ 1 − p) and attributed to “orphan spins”, i.e. the spins of rare Cr3+ ions that are disconnected from the bulk of the spins by the vacancies. The density of such “orphan spins” is rather low and insufficient to account for the value of the Curie constant in the contribution (3.2) to the susceptibility,67 yet the “orphan spin” contribution would scale non-linearly with the defect density Nvac, in contradiction with the observed linear dependence.78
A more realistic picture of the vacancy susceptibility is the quasispin picture, in which each isolated vacancy is screened by the surrounding magnetic medium and behaves as a free spin. Such behavior should be expected in a generic material based on the fluctuation–dissipation relation χzz = 〈![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) z2〉/T if the magnetization
z2〉/T if the magnetization ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) z of a correlated region around a vacancy commutes with the system's Hamiltonian.
z of a correlated region around a vacancy commutes with the system's Hamiltonian.
The behavior and values of quasispins of vacancy defects have been a subject of intense research in a variety of systems, such as 2D Heisenberg antiferromagnets,79–83 one-dimensional spin chains and ladders79,84–90 and arrays of classical vector spins.91,92 It has been argued in ref. 90 that the variance 〈Ŝz2〉 of the quasispin of a vacancy defect and quasispin–quasispin interactions match the variance of the spins of the magnetic atom and spin–spin interactions in the vacancy-free material, as long as the presence of the vacancy does not change the short-range magnetic order around it and the magnetization along the z axis is a good quantum number. This has been confirmed84 by exact calculations for a 1D chain with nearest-neighbor and next-to-nearest-neighbor interactions, the minimal model in which vacancies exhibit quasispin behavior.
Quasispins exhibit further intriguing phenomena close to quantum phase transitions. It has been demonstrated in ref. 80 that in a material close to such a transition, the soft modes of the fluctuating order parameter renormalize the value of a vacancy quasispin and lead to an effective fractional quasispin. A fractional quasispin has been reported in numerical simulations in ref. 93 for a bilayer antiferromagnetic system in which the quantum phase transition is driven by the value of the interlayer coupling.
The generic behavior of the magnetic susceptibility in a material with dilute vacancies can be summarized by the equation
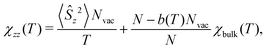 | (3.3) |
Eqn (3.3) describes the susceptibility of a GF magnet in the limit of dilute vacancies, in which the quasispins of isolated vacancies can be considered independently. With increasing the vacancy density Nvac/N, the susceptibility (3.3) receives non-linear corrections in Nvac.90
IV. Hidden energy scale and short-range order
In this section, we review available data for the properties of the glass transitions, neutron-scattering results, and thermodynamic properties of GF magnetic materials. All such data demonstrate the existence of the “hidden energy scale” in such materials, significantly exceeded by other microscopic energies, e.g. θW, in them. When a material is cooled down below such a scale, it develops significant short-range magnetic order. This scale, albeit a property of a disorder-free material, also determines the temperature of the glass transition for realistic impurity concentrations.A. Glass transition temperature vs. amount of disorder
In ref. 94, the spin-glass transition temperature Tg has been analyzed as a function of the density of vacancy defects in all frustrated materials for which the data on such transitions are available. Fig. 2 summarizes the discovered trends.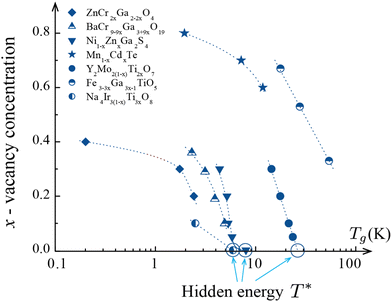 | ||
| Fig. 2 Adapted with modification from ref. 94. The glass-transition temperature as a function of vacancy density for GF magnetic materials. Extrapolation to the limit of vanishing vacancy densities reveals the hidden energy scale T*. | ||
Although the glass transition is disorder-driven, increasing the density of vacancies, which contribute to the total disorder strength, lowers the glass transition temperature. In other words, contrary to common intuition and existing models (see, e.g. ref. 75, 95 and 96), purifying the material by reducing the number of vacancies makes random spin freezing more favorable.
In the limit of vanishing density concentration, the glass transition temperature extrapolates to a scale of order T* ∼ 10 K, which we dubbed the “hidden energy scale”, in all analyzed frustrated compounds.97 This scale is significantly exceeded by the Weiss constant θW, which characterizes the strength of spin–spin interactions and is typically a few hundred Kelvin.94
Another universal trend displayed by all GF magnets is the increase of magnetic susceptibility χ(T) with increasing the vacancy concentration, as shown in Fig. 3(b) and (d). This trend, as well as the decrease of the SG transition temperature with adding impurities to a material, is opposite to the trends observed in conventional SGs (i.e. SGs in non-GF materials).75
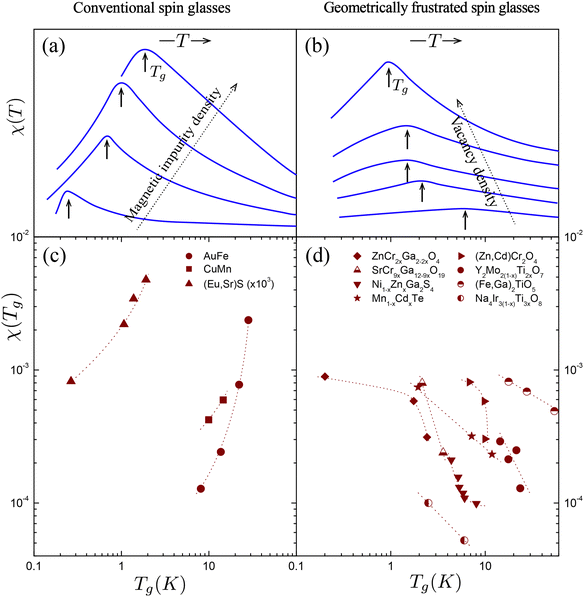 | ||
| Fig. 3 Adapted with modification from ref. 94. The behavior of magnetic susceptibility χ(T) and glass transition temperatures as a function of impurity density in conventional glasses [panels (a) and (c)] and in geometrically frustrated materials [panels (b) and (d)]. | ||
The dichotomy between conventional SGs and those in GF materials comes from the different nature of quenched randomness, degrees of freedom that undergo SG freezing, and the clean medium. Indeed, in conventional spin glasses, magnetic impurities are randomly located in a non-magnetic medium, and the SG transition consists in the freezing of the magnetic moments of those impurities. With increasing the density of magnetic impurities, the strength of interactions between them grows, and both the SG transition temperature and the susceptibility grow, as shown in Fig. 3a for the compound EuxSr1−xS.98
By contrast, in GF materials, the medium consists of magnetic atoms, while quenched disorder is dominated by randomly located vacancies, i.e. non-magnetic atoms. As discussed in Section III C, each vacancy can be associated with a quasispin. Because the quasispin contribution to the susceptibility χ(T) is more singular at low temperatures than the bulk susceptibility [cf.eqn (3.3)], it dominates the effect of changing the impurity concentration, resulting in the increase of the susceptibility with vacancy density,99 dχ(T)/dNvac > 0.
While quenched disorder is necessary for SG transitions, we argue35,94 that the temperature of SG transitions in the analyzed GF compounds is determined by the properties of the clean GF medium rather than the amount of quenched disorder for experimentally achievable amounts. As we clarify in what follows, the lowest-energy magnetic degrees of freedom have a characteristic energy of the order of the hidden energy scale T* described above and are suppressed at lower temperatures. In the presence of quenched disorder, this usually leads to spin-glass freezing at a temperature of order T*.94
The hidden energy T* being the property of the clean GF medium is consistent with its value being of the same order of magnitude (10 K) in a broad class of materials despite different microscopic details and types of disorder. Below, we present further evidence for a crossover in the properties of the clean GF medium at temperatures T ∼ T* in the neutron scattering intensity and discuss a microscopic scenario for the hidden energy scale.
B. Neutron data
As we describe in this subsection, the intensity of neutron scattering in GF materials confirms the existence of the hidden energy scale and can provide further insights into its nature.Neutrons are an essential probe for understanding conventional antiferromagnets since they scatter elastically from atomic spins and can detect staggered order, even though this order produces no net magnetic moment. In the ordered state of a magnet possessing LRO, inelastic neutron scattering can also measure the energy-wavevector relationship of spin waves and, by appropriate modeling, extract the spin–spin interaction strengths.
Because LRO is usually not seen in GF systems, information gleaned from elastic scattering is confined to broad intensity versus wavevector peaks. Such a diffuse scattering signal lies underneath sharp Bragg peaks caused by scattering of neutrons from the ionic nuclei. Most generally, magnetic scattering can be related to the generalized susceptibility, as discussed by Bramwell in ref. 25. In particular, the anisotropy in this susceptibility can reveal the nature of SRO, the prime example being the so-called “pinch points” in the diffuse scattering in spin ice.100–102 Pinch-point patterns of scattering result from the spin ice-rule expressing the lowest energy state of the four spin directions on a tetrahedron, namely two-in-two-out. We believe that such an analysis of scattering intensities will be critically important for understanding the ground state of GF systems, but the present discussion will be concerned simply with the presence or absence of the SRO revealed by such data.
Broholm et al. were first to show that a GF system, SrCr9pGa12−9pO19 (p = 0.79), exhibits a broad SRO scattering signal. They extracted a maximum spin–spin correlation length of ξ = 7 ± 2 Å from the width of the broad peak, and showed that the scattering intensity at the corresponding wavelength increases rapidly on cooling through the hidden energy scale.103 Similar data were obtained for a sample of SrCr8.9Ga3.1O19 (p = 0.97, Tg = 3.68 K) and are shown in Fig. 4a, along with the susceptibility on the same compound.104 Thus, we see that the atomic spins undergo short-range order at the hidden energy scale. In addition, it is reasonable to surmise that this is a bulk effect, i.e. the fraction of such spins is a non-negligible fraction of the total atomic spin population and, as discussed above, exists independently of the SG state.
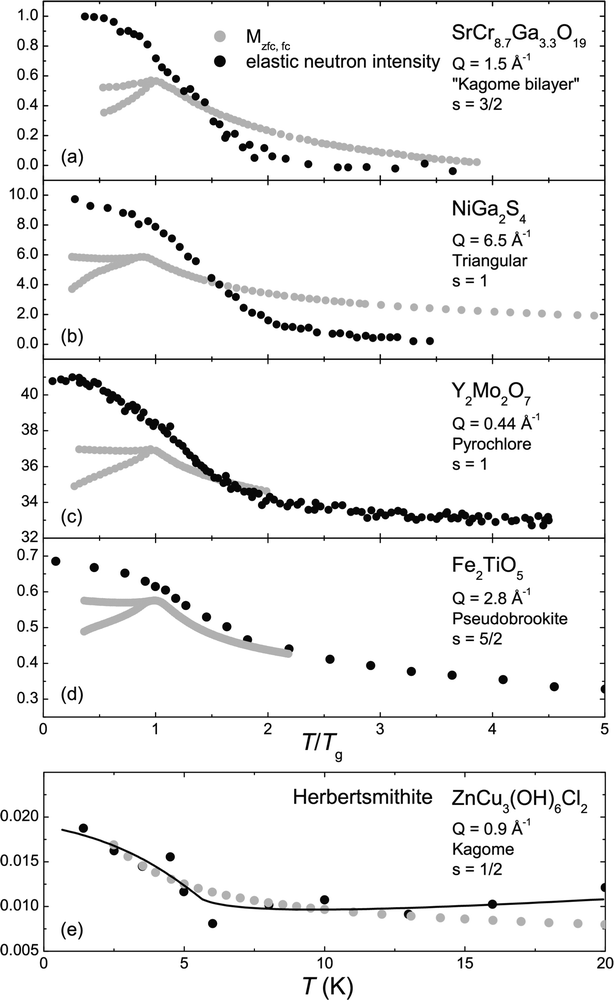 | ||
| Fig. 4 Neutron scattering intensity (black circles)36,47,104–106 and magnetic susceptibility (grey circles)36,45,47,74,104 for various GF compounds as a function of temperature. | ||
How common is such a neutron signature of SRO in GF systems? We argued previously that the hidden energy scale was a generic feature of all GF magnets94 and, fortunately, neutron scattering has now been performed on a good handful of such f > 10 materials. In Fig. 4b–e, we show data for NiGa2S4,74,105 Y2Mo2O7,45,106 Fe2TiO547 and herbertsmithite36 similar to that for SrCr9pGa12−9pO19.104 These data encompass different spin values (S = 1/2, 1, 3/2, 5/2), different lattice types (triangular, kagome, pyrochlore, hyperkagome), as well as effective spatial dimensionalities 2 and 3. We see that the growth of intensity at short wavelength is a generic feature of these systems, and always occurs in the vicinity of the SG transition, with the exception of Herbertsmithite, which has been argued to be 2D to a very good approximation (in contrast to the other lamellar materials, such as SrCr9pGa12−9pO19 and NiGa2S4, in which the interlayer coupling are more essential) and therefore will not exhibit SG freezing. Similarly to the other materials, the characteristic temperature T* ∼ 5 K at which Herbertsmithite exhibits SRO is significantly smaller than the Weiss constant θW ≈ 300 K.
We note that for SG transitions in conventional, non-GF materials, neutron scattering also shows an increase in diffuse scattering on cooling towards the glass transition temperature.75,107 In these systems, however, this magnetic scattering is caused by the degrees of freedom that undergo SG freezing. In GF systems, on the other hand, neutrons are scattered by the background spins. Neutron scattering cannot, of course, differentiate between the two scenarios, but in GF systems, it clearly evidences the SRO established by the bulk of the spins.
C. A scenario for the hidden energy scale
The data summarized in Sections IV A and IV B illustrate that the hidden energy scale is a universal property of GF magnets and is a property of the clean system. Recently, we proposed35 a scenario of the hidden energy scale.Essential to this scenario is the observation that the heat capacity C(T) in GF frustrated materials, in which data in a sufficiently large temperature range are available, display two peaks in the behavior of C(T), as shown in Fig. 5. This two-peak behavior is observed experimentally in all materials for which the heat-capacity data are available in a sufficiently broad temperature range, such as 3He atoms on graphite,108,109 NiGa2S4,72 NaYbO2,110 NaYbSe2,111 Gd3Ga5O12,112 as well as in abundant numerical simulations.113–129
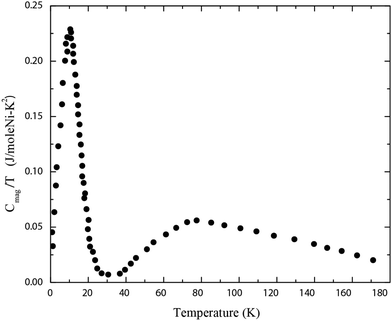 | ||
| Fig. 5 The C(T)/T vs. T dependence in NiGa2S4 obtained by digitizing the data reported in ref. 72. | ||
The temperature of the higher-energy peak is of the order of the Weiss constant θW, while the low-temperature peak is located at significantly lower temperatures of the order of the hidden energy scale T*. An important insight into the nature of both peaks is provided by the numerical simulations35,121,128 of a family of the XXZ models described by the Hamiltonian
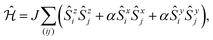 | (4.1) |
In ref. 121, it was demonstrated that the XXZ model on the kagome lattice exhibits the two-peak structure of the heat capacity for any nonzero transverse coupling [α > 0 in eqn (4.1)] but has only one peak in the Ising case (α = 0), suggesting that the transverse coupling is essential for the formation of the lower-temperature peak, while the higher-temperature peak is of the Ising origin.
The ground states of the Ising model on common frustrating lattices have extensive degeneracy (i.e. degeneracy that scales exponentially with the system size). Single spin–flip excitations have energies of the order θW ∼ ZJ, where Z and J are the coordination number and the AF coupling constant, and give rise to one peak in the heat capacity C(T). In the presence of a weak transverse coupling (0 < α ≪ 1), the degeneracy of the Ising ground states is lifted, with the respective low-energy excitations resulting in the formation of the lower-temperature peak.35,121,128 The characteristic energy of that peak is determined by the Ising instantons, the minimum sequences of pair-wise spin-exchange processes that connect similar Ising ground states to each other.
With increasing the transverse coupling, i.e. the value of the parameter α, the energies of the excitations that give rise to the lower peak of C(T) increase. However, the two peaks remain separated even for α ∼ 1.128 It has been estimated in ref. 35 that the ratio of the hidden energy scale, i.e. the temperature of the first peak, to the characteristic temperature θW of the second peak has the order of magnitude
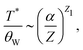 | (4.2) |
The estimate (4.2) also imposes a constraint on the generalized f-ratio, the figure of merit of frustration given by eqn (1.1) in which the temperature Tc ∼ T* is the characteristic energy scale of the freezing of the magnetic degrees of freedom that is not necessarily accompanied by a (magnetic-ordering or spin-glass) phase transition. However, in the presence of sufficient quenched disorder in 3D, the freezing out of these degrees of freedom will lead to an SG transition at a temperature T ∼ T*.
We note that while the two-peak feature is a universal property of GF magnets, only one of those peaks is usually observed due to an insufficient temperature range accessed in the measurements. In GF materials with 3d elements, the higher-temperature peak lies at temperatures θW ≳ 100 K and is rarely captured in experiments. In GF materials with significantly lower θW, such as rare-earth compounds, the lower peak may lie below the lower limit of cryogenic apparatus (∼50 mK) and may thus be inaccessible in experiments.
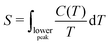 | (4.3) |
The values of the Ising ground-state entropy are known for common 2D lattices, (such as triangular22,130,131) and kagome132,133 lattices, based on analytical arguments. For other lattices, e.g. the pyrochlore lattice,61,134 the value of the entropy can be found numerically. We note that magnetism in many GF systems comes from higher spins, such as spins-1 or spins-3/2. Strictly speaking, the entropy under the lower peak in these systems has to be compared with the ground-state entropy of the respective higher-spin counterparts of the Ising model. Often, however, the ground-state entropy of such models will match the ground-state entropy of the conventional Ising model, corresponding to classical spins-1/2.
A test case for the entropy associated with the hidden energy scale is provided by NiGa2S4, a layered, effectively 2D material with a triangular lattice and the heat capacity C(T) shown in Fig. 5. The value of the entropy (4.3) under the lower peak obtained from the digitized data72 shown in Fig. 5 is given by S ≈ 0.35 per spin, which is indeed close to the value of the Ising ground-state entropy (SIsing ≈ 0.32 on the triangular lattice22,130,131).
D. Specific heat at the lowest temperatures
In the previous subsections, we described manifestations of the hidden energy scale in GF magnets, the type of excitations leading to that scale, and the total associated entropy. In this subsection, we describe the temperature and magnetic-field dependencies of the heat capacity C(T), which provide further insight into the lowest-energy excitations in GF materials.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 entropy, per mole of Cr.
4 entropy, per mole of Cr.
The family of the SCGO materials exhibits a universal trend: the quadratic behavior C(T) ∝ T2 of the lowest-temperature (T ≪ T*) heat capacity, robust on varying the concentration p of the magnetic Cr atoms. This temperature dependence is inconsistent with the linear heat capacity C(T) ∝ T generically expected to emerge in spin glasses due to tunnelling between pairs of local energy minima separated by random potential barriers.136
In a layered, i.e. effectively 2D material, the observed behavior of heat capacity may come from any linearly dispersive excitations. We note that such excitations in SCGO cannot be antiferromagnetic spin waves, since (i) no magnetic Bragg peaks are seen in neutron scattering, as expected for an AF state137 and, (ii) the characteristic energy ∼6 K of such excitations does not match the characteristic spin–spin interaction energy, which is estimated as the Weiss constant, approximately 500 K, in SCGO.138 For a sufficiently large density of the linearly-dispersive excitations, their heat capacity may mask the conventional linear contribution common in spin glasses.136
The quadratic behaviour C(T) ∝ T2 of the heat capacity has also been observed in the layered material NiGa2S4 described in Section IV C. In this material, the SRO that develops at temperatures below the hidden energy scale T*, has a correlation region of 26 Å in the plane of the layers, and possesses a non-collinear spiral structure. The non-collinearity, along with the existence of static SRO, was argued to create the conditions for the so-called Halperin–Saslow modes,139 which can be thought of as linear-dispersing hydrodynamic excitations. The theory139 of such modes was constructed for systems in which the ground state is comprised of non-collinear spins that are static but not long-range ordered, and while the theory was developed in the context of conventional spin glass, it should also apply to GF systems with SRO.140
Because the Halperin–Saslow modes are linearly dispersive, they can lead to the quadratic low-temperature dependence C(T) ∝ T2 in quasi-2D materials such as NiGa2S4 and other layered systems. A conclusive identification of the mechanism of this quadratic behaviour of the heat capacity requires further investigation.
For Ising spins on the pyrochlore lattice and the SCGO lattice,138 the magnetization in the ground states is zero. Because in the presence of weak transverse coupling between spins, the low-energy excitations are given by superpositions of such states and states obtained from them by permutations of spins, these low-energy excitations will also be non-magnetic. On these lattices, the heat capacity C(T) at low temperatures T ≲ T* will be insensitive to the magnetic field.
Other lattices, such as the triangular and kagome lattice, allow for nonzero magnetization of the ground states of the Ising model with nearest-neighbor interactions. On these lattices, the low-energy excitations will, in general, be magnetic. On the kagome lattice, magnetic low-energy excitations have been observed numerically in ref. 118, 121, 123, 125, 128, 129 and 141.
Experimentally, it has been shown that SrCr9pGa12−9pO19, NiGa2S4, and also Na4Ir3O8 all have peaks in C(T)/T that are nearly field-independent68,136,142 on Zeeman energy scales comparable to the hidden energy scale. While this field-independence is expected in SCGO and Na4Ir3O8 based on the above argument, its microscopic mechanism in the (quasi-2D) compound NiGa2S4 with a triangular lattice calls for further investigation. In this material, beyond-nearest-neighbor interactions or interlayer coupling might play a role. Such interactions are also required to prevent magnetic ordering on the triangular lattice.2–4
V. Conclusions and further directions
We have reviewed available data on the specific heat, magnetic susceptibility and neutron scattering in geometrically frustrated (GF) materials. The available data for the intensity of neutron scattering as a function of temperature and for the glass transition temperature as a function of impurity density suggest the existence of a characteristic energy scale, the “hidden energy scale” T*, which is of the order of 10 K in the analyzed materials.A. Key manifestations of the hidden energy scale
The scale T* manifests itself in spin-glass (SG) freezing at temperatures T < T* in the cleanest 3D GF materials, i.e. in materials with the smallest concentrations of the vacancy impurities, the most common form of quenched disorder in GF magnets. Cooling a material to temperatures below T* is also accompanied by an increase in the intensity of neutron scattering even in materials that do not exhibit the spin-glass transition due to the low dimensionality.The GF materials for which specific heat C(T) data are available in a sufficiently broad temperature range exhibit two peaks in the temperature dependence of the specific heat C(T). The higher-temperature peak is centered at temperatures of the order of the Weiss constant θW, while the lower-temperature peak is located near the hidden energy scale T*. Such a structure in C(T) is supported by abundant numerical simulations of small clusters of spins on geometrically frustrating lattices.
B. The origin of the hidden energy scale and spin-glass transition
The SG freezing observed at a temperature of order T* in many rather clean GF materials raises the question of whether QSLs are achievable in GF systems or always get replaced by an SG state. This question, in part, motivated the current work. While in our view, there is not a precise, commonly accepted definition of a QSL, an SG state is considered to be incompatible with a QSL.In most GF systems, the main source of quenched disorder, which is necessary for the existence of an SG state, is vacancy defects. It has remained a puzzle for a while what causes the SG transitions in the purest GF materials, with vacancy defects virtually eliminated. The existence of such SG transitions in rather clean GF systems seems to have created a school of thought that the SG transition is caused by a nearly immeasurable type of quenched disorder, and the SRO observed in, e.g. neutron scattering, is caused by this glass transition.
By contrast, the available facts summarized in this review illustrate that the short-range order (SRO) that forms at temperatures T below the hidden energy scale T* is a property of the disorder-free system. The available facts also suggest that the formation of this SRO precipitates the SG transition in the presence of weak quenched disorder.
The hidden energy scale comes from the excitations that give rise to the lower-temperature peak in C(T). In a generic XXZ model on a GF lattice, such excitations are continuously connected to superpositions of Ising ground states when this model is deformed to the Ising model. The total entropy of such excitations associated with the lower-temperature peak of C(T) matches the entropy of the ground states of the Ising model. This correspondence is illustrated by the thermodynamic data in NiGa2S4 and can be used to verify the discussed origin of the hidden energy in other GF materials.
A GF material, thus, possesses a large density of excitations at the characteristic energy T*, which are no longer activated when the material is cooled down to temperatures T ≲ T*. In the presence of quenched disorder, the freezing out of such excitations leads to a spin-glass transition. We emphasize that at such transitions, the properties of the clean medium are in the driver's seat: while quenched disorder is required for SG freezing, the transition temperature will normally be determined by a crossover in the properties of the clean GF medium upon cooling. Although an SG state can be avoided if quenched disorder is completely eliminated, currently available materials display an SG transition at a temperature of order T* for a broad range of disorder strengths.
Further theoretical advances are required to explain various details of the heat capacity C(T), for example, the observed quadratic temperature dependence C(T) ∝ T2 at T ≪ T* and the near-independence of C(T) of the magnetic field. Explaining these features will require identifying the spin structure of the lowest-energy excitations, as well as evaluating their dispersion.
C. Short-range order
The available neutron-scattering data further confirms the formation of short-range order near the hidden energy scale. This type of magnetic order is rather unusual, distinct from both the long-range magnetic order and spin-glass order, and creates new exciting possibilities for understanding and manipulating it.For example, a characteristic feature of neutron scattering in spin ice is the set of pinch points in the momentum-dependent scattering. We expect that such structure will be revealed in strongly GF systems, but only in large-q diffusive scattering. This structure should coincide with a build up of specific heat, already seen in a few systems. The two energy scales represented by the Weiss temperature and the hidden energy should also be systematically probed using specific heat. This will require measurements over a larger range of temperatures than is usually accessed.
D. Magnetic susceptibility and impurities
As we discussed in this review, the magnetic susceptibility in GF magnets follows the Curie–Weiss law, consistent with the mean-field description of magnetic materials, down to temperatures significantly lower than the Weiss constant θW. The reason for the persistence of the Curie–Weiss law in the lowest temperature range still remains to be investigated.Quenched disorder has a profound effect on the magnetic susceptibility in GF materials. The most common type of quenched disorder in GF magnets is vacancy defects. In terms of magnetic susceptibility, a vacancy defect is equivalent to an effective free spin, a “quasispin”. Such quasispins lead to the Curie-tail ∝Nvac/T contributions to χ(T) in the limit of small concentrations Nvac. At larger vacancy concentrations, the interactions between vacancy quasispins are essential.
While theoretical progress has been achieved in describing quasispins in, e.g., Ising systems, in the vicinity of quantum criticality, and in materials where vacancies do not disrupt short-range order, the values of quasispins and their interactions in generic quantum GF materials remain to be investigated. As the quasispin behavior has been investigated in terms of linear response of the magnetic susceptibility, another question that awaits further study is the response of defects to larger magnetic fields. If quasispins can display quantum behavior, this may open new intriguing opportunities for storing and manipulating quantum information using quasispins. Encoded by numerous spins around a vacancy, the quantum state of a quasispin may be expected to be well protected from local noise.
E. Vacancy defects and the spin-glass transition
Another, counter-intuitive effect of vacancy defects on a GF material is the decrease of the spin-glass transition temperature with increasing vacancy concentration. Conventional intuition and existing models of spin glasses suggest that increasing the strength of quenched disorder raises the temperature of the glass transition. Despite vacancies contribute to the total disorder strength, adding them to a clean material has the opposite effect: they suppress the transition temperature.As we discussed, in the vacancy-free limit, the glass transition takes place at a temperature of the order of the hidden energy scale T*. Introducing dilute vacancies disrupts the glass order and lowers the transition temperature. While the effect of vacancies on a non-vacancy glass transition is readily captured by an effective field theory in terms of the glass order parameter,99 the described trend still awaits a microscopic description.
Finally, while we have concentrated on analyzing the most easily accessed measurements, now that the basic spin dynamics framework is established, other more targeted spectroscopies, such as muon spin relaxation and nuclear magnetic resonance, can also be brought to bear on describing the ground states and excitations in GF materials. Of particular interest are the dynamics of excitations below the hidden energy scale, which both NMR and μSR have shown signs of ref. 32 and 143 and may help to inform the microscopic theory of low-energy states.
Data availability
The data used to generate Fig. 1, 4 and 5 are available from the cited articles, except for the data for the magnetic susceptibility in SrCr9pGa12−9pO19 with p = 0.98 and p = 0.67. The latter data are available from the authors on request. Fig. 2 and 3 have been adapted with modification from the cited articles.Conflicts of interest
The authors declare that they have no conflicts of interest.Acknowledgements
We are grateful to S. Haravifard, P. Popp, M. Sedik, S. Sun, and S. Zhu for collaborations on the topics of this review. We also appreciate useful discussions with R. Colman, P. Prelovšek, B. Sbierski, and M. Ulaga. This work has been supported by the NSF grant DMR2218130.References
- P. Anderson, Resonating valence bonds: a new kind of insulator?, Mater. Res. Bull., 1973, 8, 153 CrossRef CAS.
- B. Bernu, C. Lhuillier and L. Pierre, Signature of Néel order in exact spectra of quantum antiferromagnets on finite lattices, Phys. Rev. Lett., 1992, 69, 2590 CrossRef PubMed.
- L. Capriotti, A. E. Trumper and S. Sorella, Long-Range Néel Order in the Triangular Heisenberg Model, Phys. Rev. Lett., 1999, 82, 3899 CrossRef CAS.
- S. R. White and A. L. Chernyshev, Néel order in square and triangular lattice Heisenberg models, Phys. Rev. Lett., 2007, 99, 127004 CrossRef PubMed.
- L. Savary and L. Balents, Quantum spin liquids: a review, Rep. Prog. Phys., 2016, 80, 016502 CrossRef PubMed.
- J. Knolle and R. Moessner, A field guide to spin liquids, Annu. Rev. Condens. Matter Phys., 2019, 10, 451 CrossRef CAS.
- C. Broholm, R. J. Cava, S. A. Kivelson, D. G. Nocera, M. R. Norman and T. Senthil, Quantum spin liquids, Science, 2020, 367, eaay0668 CrossRef CAS PubMed.
- B. S. Shastry and B. Sutherland, Exact ground state of a quantum mechanical antiferromagnet, Phys. B + C, 1981, 108, 1069 CrossRef CAS.
- A. Kitaev, Anyons in an exactly solved model and beyond, Ann. Phys., 2006, 321, 2 CAS january Special Issue.
- F. Iga, A. Shigekawa, Y. Hasegawa, S. Michimura, T. Takabatake, S. Yoshii, T. Yamamoto, M. Hagiwara and K. Kindo, Highly anisotropic magnetic phase diagram of a 2-dimensional orthogonal dimer system TmB4, J. Magn. Magn. Mater., 2007, 310, e443 CrossRef CAS , proceedings of the 17th International Conference on Magnetism.
- G. Jackeli and G. Khaliullin, Mott Insulators in the Strong Spin-Orbit Coupling Limit: From Heisenberg to a Quantum Compass and Kitaev Models, Phys. Rev. Lett., 2009, 102, 017205 CrossRef CAS PubMed.
- R. D. Johnson, S. C. Williams, A. A. Haghighirad, J. Singleton, V. Zapf, P. Manuel, I. I. Mazin, Y. Li, H. O. Jeschke, R. Valenti and R. Coldea, Monoclinic crystal structure of a – RuCl3 and the zigzag antiferromagnetic ground state, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 235119 CrossRef.
- Y. Kubota, H. Tanaka, T. Ono, Y. Narumi and K. Kindo, Successive magnetic phase transitions in a-RuCl3: XY-like frustrated magnet on the honeycomb lattice, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094422 CrossRef.
- J. A. Sears, M. Songvilay, K. W. Plumb, J. P. Clancy, Y. Qiu, Y. Zhao, D. Parshall and Y.-J. Kim, Magnetic order in a-RuCl3: a honeycomb-lattice quantum magnet with strong spin–orbit coupling, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 144420 CrossRef.
- A. Banerjee, J. Yan, J. Knolle, C. A. Bridges, M. B. Stone, M. D. Lumsden, D. G. Mandrus, D. A. Tennant, R. Moessner and S. E. Nagler, Neutron scattering in the proximate quantum spin liquid a – RuCl3, Science, 2017, 356, 1055 CrossRef CAS PubMed.
- Y. Kasahara, T. Ohnishi, Y. Mizukami, O. Tanaka, S. Ma, K. Sugii, N. Kurita, H. Tanaka, J. Nasu and Y. Motome, et al., Majorana quantization and half-integer thermal quantum Hall effect in a Kitaev spin liquid, Nature, 2018, 559, 227 CrossRef CAS PubMed.
- P. Czajka, T. Gao, M. Hirschberger, P. Lampen-Kelley, A. Banerjee, J. Yan, D. G. Mandrus, S. E. Nagler and N. Ong, Oscillations of the thermal conductivity in the spin–liquid state of a-RuCl3, Nat. Phys., 2021, 17, 915 Search PubMed.
- J. Zheng, K. Ran, T. Li, J. Wang, P. Wang, B. Liu, Z.-X. Liu, B. Normand, J. Wen and W. Yu, Gapless Spin Excitations in the Field-Induced Quantum Spin Liquid Phase of a-RuCl3, Phys. Rev. Lett., 2017, 119, 227208 CrossRef PubMed.
- J. A. N. Bruin, R. R. Claus, Y. Matsumoto, J. Nuss, S. Laha, B. V. Lotsch, N. Kurita, H. Tanaka and H. Takagi, Origin of oscillatory structures in the magnetothermal conductivity of the putative Kitaev magnet a-RuCl3, APL Mater., 2022, 10, 090703 CrossRef CAS.
- J. Bruin, R. Claus, Y. Matsumoto, N. Kurita, H. Tanaka and H. Takagi, Robustness of the thermal Hall effect close to half-quantization in a-RuCl3, Nat. Phys., 2022, 18, 401 Search PubMed.
- E. Lefrancois, J. Baglo, Q. Barthélemy, S. Kim, Y.-J. Kim and L. Taillefer, Oscillations in the magnetothermal conductivity of a-RuCl3: evidence of transition anomalies, Phys. Rev. B, 2023, 107, 064408 CrossRef CAS.
- G. H. Wannier, Antiferromagnetism. the triangular ising net, Phys. Rev., 1950, 79, 357 CrossRef.
- P. W. Anderson, Ordering and antiferromagnetism in ferrites, Phys. Rev., 1956, 102, 1008 CrossRef CAS.
- A. Ramirez, Thermodynamic measurements on geometrically frustrated magnets, J. Appl. Phys., 1991, 70, 5952 CrossRef CAS.
- C. Lacroix, P. Mendels and F. Mila, Introduction to frustrated magnetism: materials, experiments, theory, Springer Science & Business Media, 2011, vol. 164 Search PubMed.
- J. R. Chamorro, T. M. McQueen and T. T. Tran, Chemistry of quantum spin liquids, Chem. Rev., 2020, 121, 2898 CrossRef PubMed.
- Y. Zhou, K. Kanoda and T.-K. Ng, Quantum spin liquid states, Rev. Mod. Phys., 2017, 89, 025003 CrossRef.
- L. Clark and A. H. Abdeldaim, Quantum spin liquids from a materials perspective, Annu. Rev. Mater. Res., 2021, 51, 495 CrossRef CAS.
- P. Merchant, B. Normand, K. Krämer, M. Boehm, D. McMorrow and C. Ruegg, Quantum and classical criticality in a dimerized quantum antiferromagnet, Nat. Phys., 2014, 10, 373 Search PubMed.
- I. Kimchi, J. P. Sheckelton, T. M. McQueen and P. A. Lee, Scaling and data collapse from local moments in frustrated disordered quantum spin systems, Nat. Commun., 2018, 9, 4367 Search PubMed.
- L. J. D. Jongh and A. R. Miedema, Experiments on simple magnetic model systems, Adv. Phys., 2001, 50, 947, DOI:10.1080/00018730110101412.
- H. Takeya, K. Ishida, K. Kitagawa, Y. Ihara, K. Onuma, Y. Maeno, Y. Nambu, S. Nakatsuji, D. E. MacLaughlin, A. Koda and R. Kadono, Spin dynamics and spin freezing behavior in the two-dimensional antiferromagnet NiGa2S4 revealed by Ga-NMR, NQR and μSR measurements, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 054429 CrossRef.
- Y. J. Uemura, A. Keren, K. Kojima, L. P. Le, G. M. Luke, W. D. Wu, Y. Ajiro, T. Asano, Y. Kuriyama, M. Mekata, H. Kikuchi and K. Kakurai, Spin Fluctuations in Frustrated Kagomé Lattice System SrCr8Ga4O19 Studied by Muon Spin Relaxation, Phys. Rev. Lett., 1994, 73, 3306 CrossRef CAS PubMed.
- D. Bono, P. Mendels, G. Collin, N. Blanchard, F. Bert, A. Amato, C. Baines and A. D. Hillier, μSR study of the quantum dynamics in the frustrated s = 3/2 kagomé bilayers, Phys. Rev. Lett., 2004, 93, 187201 CrossRef CAS PubMed.
- P. Popp, A. P. Ramirez and S. Syzranov, Origin of the hidden energy scale and the f-ratio in geometrically frustrated magnets, arXiv, 2024, preprint, arXiv:2406.12966 [cond-mat.str-el] DOI:10.48550/arXiv.2406.12966.
- J. S. Helton, K. Matan, M. P. Shores, E. A. Nytko, B. M. Bartlett, Y. Yoshida, Y. Takano, A. Suslov, Y. Qiu, J.-H. Chung, D. G. Nocera and Y. S. Lee, Spin Dynamics of the Spin-1/2 Kagome Lattice Antiferromagnet ZnCu3(OH)6Cl2, Phys. Rev. Lett., 2007, 98, 107204 CrossRef CAS PubMed.
- M. Lafontaine, A. Le Bail and G. Férey, Copper-containing minerals—I. Cu3V2O7(OH)2·2H2O: the synthetichomolog of volborthite; crystal structure determination from X-ray and neutron data; structural correlations, J. Solid State Chem., 1990, 85, 220 CrossRef CAS.
- Z. Hiroi, M. Hanawa, N. Kobayashi, M. Nohara, H. Takagi, Y. Kato and M. Takigawa, Spin-1/2 Kagomé-Like Lattice in Volborthite Cu3V2O7(OH)2·2H2O, J. Phys. Soc. Jpn., 2001, 70, 3377 CrossRef CAS.
- H. Yoshida, Y. Okamoto, T. Tayama, T. Sakakibara, M. Tokunaga, A. Matsuo, Y. Narumi, K. Kindo, M. Yoshida, M. Takigawa and Z. Hiroi, Magnetization “steps” on a kagome lattice in volborthite, J. Phys. Soc. Jpn., 2009, 78, 043704, DOI:10.1143/JPSJ.78.043704.
- M. Yoshida, Y. Okamoto, M. Takigawa and Z. Hiroi, Magnetic order in the spin-1/2 kagome antiferromagnet vesignieite, J. Phys. Soc. Jpn., 2013, 82, 013702, DOI:10.7566/JPSJ.82.013702.
- O. Janson, J. Richter and H. Rosner, Modified Kagome Physics in the Natural Spin-1/2 Kagome Lattice Systems: Kapellasite Cu3Zn(OH)6Cl2 and Haydeeite Cu3Mg(OH)6Cl2, Phys. Rev. Lett., 2008, 101, 106403 CrossRef CAS PubMed.
- R. Colman, A. Sinclair and A. Wills, Comparisons between Haydeeite, a-Cu3Mg(OD)6Cl2, and Kapellasite, a – Cu3Zn(OD)6Cl2, Isostructural S = 1/2 Kagome Magnets, Chem. Mater., 2010, 22, 5774, DOI:10.1021/cm101594c.
- T.-H. Han, J. Singleton and J. A. Schlueter, Barlowite: a spin-1/2 antiferromagnet with a geometrically perfect kagome motif, Phys. Rev. Lett., 2014, 113, 227203 CrossRef PubMed.
- X. Y. Yue, Z. W. Ouyang, J. F. Wang, Z. X. Wang, Z. C. Xia and Z. Z. He, Magnetization and esr studies on Cu4(OH)6FCl: an antiferromagnet with a kagome lattice, Phys. Rev. B, 2018, 97, 054417 CrossRef CAS.
- J. Greedan, M. Sato, X. Yan and F. Razavi, Spin-glass-like behavior in Y2Mo2O7, a concentrated, crystalline system with negligible apparent disorder, Solid State Commun., 1986, 59, 895 CrossRef CAS.
- P. M. M. Thygesen, J. A. M. Paddison, R. Zhang, K. A. Beyer, K. W. Chapman, H. Y. Playford, M. G. Tucker, D. A. Keen, M. A. Hayward and A. L. Goodwin, Orbital Dimer Model for the Spin-Glass State in Y2Mo2O7, Phys. Rev. Lett., 2017, 118, 067201 CrossRef PubMed.
- P. G. LaBarre, D. Phelan, Y. Xin, F. Ye, T. Besara, T. Siegrist, S. V. Syzranov, S. Rosenkranz and A. P. Ramirez, Fluctuation-induced interactions and the spin-glass transition in Fe2TiO5, Phys. Rev. B, 2021, 103, L220404 CrossRef CAS.
- A. Kancko, G. Giester and R. H. Colman, Structural and spin-glass properties of single crystal Jeff = 1/2 pyrochlore antiferromagnet NaCdCo2F7: correlating Tf with magneticbond-disorder, Phys. Scr., 2023, 98, 075947 CrossRef CAS.
- J. B. Goodenough, Magnetism and the chemical bond, R. E. Krieger Pub. Co., 1963 Search PubMed.
- H. Martinho, N. O. Moreno, J. A. Sanjurjo, C. Rettori, A. J. García-Adeva, D. L. Huber, S. B. Oseroff, W. Ratcliff, S.-W. Cheong, P. G. Pagliuso, J. L. Sarrao and G. B. Martins, Magnetic properties of the frustrated antiferromagnetic spinel ZnCr2O4 and the spin-glass Zn1−xCdxCr2O4 (x = 0.05, 0.10), Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 024408 CrossRef.
- C. H. Booth, J. S. Gardner, G. H. Kwei, R. H. Heffner, F. Bridges and M. A. Subramanian, Local lattice disorder in the geometrically frustrated spin-glass pyrochlore Y2Mo2O7, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R755 CrossRef CAS.
- N. Blanc, J. Trinh, L. Dong, X. Bai, A. A. Aczel, M. Mourigal, L. Balents, T. Siegrist and A. Ramirez, Quantum criticality among entangled spin chains, Nat. Phys., 2018, 14, 273 Search PubMed.
- L. A. Fernandez, E. Marinari, V. Martin-Mayor, G. Parisi and J. J. Ruiz-Lorenzo, Universal critical behavior of the two-dimensional ising spin glass, Phys. Rev. B, 2016, 94, 024402 CrossRef.
- C. Dekker, A. F. M. Arts, H. W. de Wijn, A. J. van Duyneveldt and J. A. Mydosh, Activated Dynamics in the Two-Dimensional Ising Spin-Glass Rb2Cu1−xCoxF4, Phys. Rev. Lett., 1988, 61, 1780 CrossRef CAS PubMed.
- Y. Shimizu, K. Miyagawa, K. Kanoda, M. Maesato and G. Saito, Spin liquid state in an organic mott insulator with a triangular lattice, Phys. Rev. Lett., 2003, 91, 107001 CrossRef CAS PubMed.
- Z. Ma, J. Wang, Z.-Y. Dong, J. Zhang, S. Li, S.-H. Zheng, Y. Yu, W. Wang, L. Che, K. Ran, S. Bao, Z. Cai, P. Čermák, A. Schneidewind, S. Yano, J. S. Gardner, X. Lu, S.-L. Yu, J.-M. Liu, S. Li, J.-X. Li and J. Wen, Spin-Glass Ground State in a Triangular-Lattice Compound YbZnGaO4, Phys. Rev. Lett., 2018, 120, 087201 CrossRef CAS PubMed.
- K. Kitagawa, T. Takayama, Y. Matsumoto, A. Kato, R. Takano, Y. Kishimoto, S. Bette, R. Dinnebier, G. Jackeli and H. Takagi, A spin–orbital-entangled quantum liquid on a honeycomb lattice, Nature, 2018, 554, 341 CrossRef CAS PubMed.
- M. Fujihala, X. G. Zheng, Y. Oohara, H. Morodomi, T. Kawae, A. Matsuo and K. Kindo, Short-range correlations and persistent spin fluctuations in the undistorted kagome lattice Ising antiferromagnet Co3Mg(OH)6Cl2, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 012402 CrossRef.
- R. Zhong, S. Guo and R. J. Cava, Frustrated magnetism in the layered triangular lattice materials K2Co(SeO3)2 and Rb2Co(SeO3)2, Phys. Rev. Mater., 2020, 4, 084406 CrossRef CAS.
- M. J. Harris, S. T. Bramwell, D. F. McMorrow, T. Zeiske and K. W. Godfrey, Geometrical Frustration in the Ferromagnetic Pyrochlore Ho2Ti2O7, Phys. Rev. Lett., 1997, 79, 2554 Search PubMed.
- A. P. Ramirez, A. Hayashi, R. J. Cava, R. Siddharthan and B. Shastry, Zero-point entropy in ‘spin ice’, Nature, 1999, 399, 333 CrossRef CAS.
- J. Snyder, B. G. Ueland, A. Mizel, J. S. Slusky, H. Karunadasa, R. J. Cava and P. Schiffer, Quantum and thermal spin relaxation in the diluted spin ice Dy2−xMxTi2O7 (M = Lu, Y), Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 184431 Search PubMed.
- B. C. den Hertog and M. J. P. Gingras, Dipolar interactions and origin of spin ice in ising pyrochlore magnets, Phys. Rev. Lett., 2000, 84, 3430 CrossRef CAS PubMed.
- R. Nirmala, K.-H. Jang, H. Sim, H. Cho, J. Lee, N.-G. Yang, S. Lee, R. Ibberson, K. Kakurai and M. Matsuda, et al., Spin glass behavior in frustrated quantum spin system CuAl2O4 with a possible orbital liquid state, J. Phys.: Condens. Matter, 2017, 29, 13LT01 CrossRef CAS PubMed.
- L. A. Fenner, A. S. Wills, S. T. Bramwell, M. Dahlberg and P. Schiffer, Zero-point entropy of the spinel spin glasses CuGa2O4 and CuAl2O4, J. Phys.: Conf. Ser., 2009, 145, 012029 CrossRef.
- A. H. Cooke, R. Lazenby, F. R. McKim, J. Owen, W. P. Wolf and B. Bleaney, Exchange interactions in antiferromagnetic salts of iridium II. Magnetic susceptibility measurements, Proc. R. Soc. London, Ser. A, 1959, 250, 97 CAS.
- A. D. LaForge, S. H. Pulido, R. J. Cava, B. C. Chan and A. P. Ramirez, Quasispin glass in a geometrically frustrated magnet, Phys. Rev. Lett., 2013, 110, 017203 Search PubMed.
- Y. Okamoto, M. Nohara, H. Aruga-Katori and H. Takagi, Spin-Liquid State in the S = ½ Hyperkagome Antiferromagnet Na4Ir3O8, Phys. Rev. Lett., 2007, 99, 137207 CrossRef PubMed.
- A. P. Ramirez, B. S. Shastry, A. Hayashi, J. J. Krajewski, D. A. Huse and R. J. Cava, Multiple Field-Induced Phase Transitions in the Geometrically Frustrated Dipolar Magnet: Gd2Ti2O7, Phys. Rev. Lett., 2002, 89, 067202 CrossRef CAS PubMed.
- The data for SrCr9pGa12−9pO19 with p = 0.98 and p = 0.67 is available on request.
- A. P. Ramirez, C. Broholm, S. H. Lee, M. F. Collins, L. Heller, C. Kloc and E. Bucher, Magnetism in a chromium jarosite Kagomé lattice KCr3(OH)6(SO4)2 (abstract), J. Appl. Phys., 1993, 73, 5658 CrossRef.
- S. Nakatsuji, Y. Nambu, H. Tonomura, O. Sakai, S. Jonas, C. Broholm, H. Tsunetsugu, Y. Qiu and Y. Maeno, Spin disorder on a triangular lattice, Science, 2005, 309, 1697 CrossRef CAS PubMed.
- I. S. Hagemann, Q. Huang, X. P. A. Gao, A. P. Ramirez and R. J. Cava, Geometric Magnetic Frustration in Ba2Sn2Ga3ZnCr7O22: A Two-Dimensional Spinel Based Kagomé Lattice, Phys. Rev. Lett., 2001, 86, 894 CrossRef CAS PubMed.
- Y. Nambu and S. Nakatsuji, Two-dimensional magnetism and spin-size effect in the S = 1 triangular antiferromagnet NiGa2S4, J. Phys.: Condens. Matter, 2011, 23, 164202 CrossRef PubMed.
- K. Binder and A. P. Young, Spin glasses: experimental facts, theoretical concepts, and open questions, Rev. Mod. Phys., 1986, 58, 801 CrossRef CAS.
- A. P. Ramirez, G. P. Espinosa and A. S. Cooper, Strong frustration and dilution-enhanced order in a quasi-2D spin glass, Phys. Rev. Lett., 1990, 64, 2070 CrossRef CAS PubMed.
- M. Gingras, C. Stager, B. Gaulin, N. Raju and J. Greedan, Nonlinear susceptibility measurements at the spin-glass transition of the pyrochlore antiferromagnet Y2Mo2O7, J. Appl. Phys., 1996, 79, 6170 CrossRef CAS.
- P. Schiffer and I. Daruka, Two-population model for anomalous low-temperature magnetism in geometrically frustrated magnets, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 13712 CrossRef CAS.
- A. W. Sandvik, E. Dagotto and D. J. Scalapino, Nonmagnetic impurities in spin-gapped and gapless Heisenberg antiferromagnets, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 11701 Search PubMed.
- S. Sachdev, C. Buragohain and M. Vojta, Quantum impurity in a nearly critical twodimensional antiferromagnet, Science, 1999, 286, 2479 Search PubMed.
- K. H. Höglund and A. W. Sandvik, Susceptibility of the 2D Spin-1/2 Heisenberg Antiferromagnet with an Impurity, Phys. Rev. Lett., 2003, 91, 077204 CrossRef PubMed.
- V. S. Maryasin and M. E. Zhitomirsky, Triangular antiferromagnet with nonmagnetic impurities, Phys. Rev. Lett., 2013, 111, 247201 CrossRef CAS PubMed.
- V. S. Maryasin and M. E. Zhitomirsky, Collective impurity effects in the Heisenberg triangular antiferromagnet, J. Phys.: Conf. Ser., 2015, 592, 012112 CrossRef.
- S. Sun, A. P. Ramirez and S. Syzranov, Quasispins of vacancy defects in ising chains with nearest- and next-to-nearest-neighbor interactions, Phys. Rev. B, 2023, 108, 174436 CrossRef CAS.
- S. Katsura and B. Tsujiyama, Ferro- and antiferromagnetism of dilute Ising model, Critical phenomena, National Institute of Standards and Technology, Gaithersburg, MD, 1966, pp. 219–225 Search PubMed.
- M. Wortis, Griffiths singularities in the randomly dilute one-dimensional ising model, Phys. Rev. B: Condens. Matter Mater. Phys., 1974, 10, 4665 Search PubMed.
- L. Bogani, R. Sessoli, M. G. Pini, A. Rettori, M. A. Novak, P. Rosa, M. Massi, M. E. Fedi, L. Giuntini, A. Caneschi and D. Gatteschi, Finite-size effects on the static properties of a single-chain magnet, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 064406 Search PubMed.
- S. V. Goupalov and D. C. Mattis, Magnetic susceptibilities of finite Ising chains in the presence of defect sites, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 224412 Search PubMed.
- V. Val’kov and M. Shustin, Effect of intersite repulsion on the correlation functions and thermodynamics of an Ising chain with annealed magnetic disorder, Bull. Russ. Acad. Sci.: Phys., 2016, 80, 1335 Search PubMed.
- M. Sedik, S. Sun, A. P. Ramirez and S. Syzranov, Quasispins of vacancy defects and their interactions in disordered antiferromagnets, arXiv, 2024, preprint, arXiv:2404.05845 [cond-mat.dis-nn] DOI:10.48550/arXiv.2404.05845.
- A. Wollny, E. C. Andrade and M. Vojta, Singular field response and singular screening of vacancies in antiferromagnets, Phys. Rev. Lett., 2012, 109, 177203 Search PubMed.
- A. Wollny, L. Fritz and M. Vojta, Fractional impurity moments in two-dimensional noncollinear magnets, Phys. Rev. Lett., 2011, 107, 137204 CrossRef PubMed.
- K. H. Höglund and A. W. Sandvik, Anomalous Curie Response of Impurities in Quantum-Critical Spin-1/2 Heisenberg Antiferromagnets, Phys. Rev. Lett., 2007, 99, 027205 CrossRef PubMed.
- S. V. Syzranov and A. P. Ramirez, Eminuscent phase in frustrated magnets: a challenge to quantum spin liquids, Nat. Commun., 2022, 13, 2993 CrossRef CAS PubMed.
- V. S. Dotsenko, Physics of the spin-glass state, Phys.-Usp., 1993, 36, 455 Search PubMed.
- M. Mézard, G. Parisi and M. A. Virasoro, Spin glass theory and beyond: An Introduction to the Replica Method and Its Applications, World Scientific Publishing Company, 1987, vol. 9 Search PubMed.
- With the exception of the compounds Fe3−3xGa3x−1Ti5, in which a significantly higher glasstransition temperature may be attributable to the formation of antiferromagnetic clusters (ref. 47 and 144).
- H. Maletta and W. Felsch, Insulating spin-glass system EuxSr1−xS, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 1245 CrossRef CAS.
- S. Syzranov, Effect of vacancy defects on geometrically frustrated magnets, Phys. Rev. B, 2022, 106, L140202 Search PubMed.
- C. L. Henley, The “Coulomb Phase” in Frustrated Systems, Annu. Rev. Condens. Matter Phys., 2010, 1, 179, DOI:10.1146/annurev-conmatphys-070909-104138.
- Y. Tabata, H. Kadowaki, K. Matsuhira, Z. Hiroi, N. Aso, E. Ressouche and B. Fåk, Kagomé Ice State in the Dipolar Spin Ice Dy2Ti2O7, Phys. Rev. Lett., 2006, 97, 257205 CrossRef CAS PubMed.
- T. Fennell, P. P. Deen, A. R. Wildes, K. Schmalzl, D. Prabhakaran, A. T. Boothroyd, R. J. Aldus, D. F. McMorrow and S. T. Bramwell, Magnetic Coulomb Phase in the Spin Ice Ho2Ti2O7, Science, 2009, 326, 415 CrossRef CAS PubMed.
- C. Broholm, G. Aeppli, G. P. Espinosa and A. S. Cooper, Antiferromagnetic fluctuations and short-range order in a kagomé lattice, Phys. Rev. Lett., 1990, 65, 3173 CrossRef CAS PubMed.
- J. Yang, A. Samarakoon, S. Dissanayake, H. Ueda, I. Klich, K. Iida, D. Pajerowski, N. P. Butch, Q. Huang, J. R. D. Copley and S.-H. Lee, Spin jam induced by quantum fluctuations in a frustrated magnet, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11519 CrossRef CAS PubMed.
- C. Stock, S. Jonas, C. Broholm, S. Nakatsuji, Y. Nambu, K. Onuma, Y. Maeno and J.-H. Chung, Neutron-Scattering Measurement of Incommensurate Short-Range Order in Single Crystals of the S = 1 Triangular Antiferromagnet NiGa2S4, Phys. Rev. Lett., 2010, 105, 037402 CrossRef CAS PubMed.
- J. S. Gardner, B. D. Gaulin, S.-H. Lee, C. Broholm, N. P. Raju and J. E. Greedan, Glassy Statics and Dynamics in the Chemically Ordered Pyrochlore Antiferromagnet Y2Mo2O7, Phys. Rev. Lett., 1999, 83, 211 CrossRef CAS.
- J. A. Mydosh, Spin glasses: an experimental introduction, CRC Press, 1993 Search PubMed.
- D. S. Greywall and P. A. Busch, Heat capacity of 3He adsorbed on graphite at millikelvin temperatures and near third-layer promotion, Phys. Rev. Lett., 1989, 62, 1868 Search PubMed.
- K. Ishida, M. Morishita, K. Yawata and H. Fukuyama, Low temperature heat-capacity anomalies in two-dimensional solid 3He, Phys. Rev. Lett., 1997, 79, 3451 Search PubMed.
- M. M. Bordelon, E. Kenney, C. Liu, T. Hogan, L. Posthuma, M. Kavand, Y. Lyu, M. Sherwin, N. P. Butch and C. Brown, et al., Field-tunable quantum disordered ground state in the triangular-lattice antiferromagnet NaYbO2, Nat. Phys., 2019, 15, 1058 Search PubMed.
- K. M. Ranjith, S. Luther, T. Reimann, B. Schmidt, P. Schlender, J. Sichelschmidt, H. Yasuoka, A. M. Strydom, Y. Skourski, J. Wosnitza, H. Kühne, T. Doert and M. Baenitz, Anisotropic field-induced ordering in the triangular-lattice quantum spin liquid NaYbSe2, Phys. Rev. B, 2019, 100, 224417 Search PubMed.
- P. Schiffer, A. P. Ramirez, D. A. Huse, P. L. Gammel, U. Yaron, D. J. Bishop and A. J. Valentino, Frustration induced spin freezing in a site-ordered magnet: gadolinium gallium garnet, Phys. Rev. Lett., 1995, 74, 2379 Search PubMed.
- V. Elser, Nuclear antiferromagnetism in a registered 3He solid, Phys. Rev. Lett., 1989, 62, 2405 Search PubMed.
- C. Zeng and V. Elser, Numerical studies of antiferromagnetism on a kagomé net, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 8436 Search PubMed.
- N. Elstner and A. P. Young, Spin-1/2 Heisenberg antiferromagnet on the kagomé lattice: high-temperature expansion and exact-diagonalization studies, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 6871 CrossRef CAS PubMed.
- T. Nakamura and S. Miyashita, Thermodynamic properties of the quantum Heisenberg antiferromagnet on the kagomé lattice, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 9174 Search PubMed.
- P. Tomczak and J. Richter, Thermodynamical properties of the Heisenberg antiferromagnet on the kagomé lattice, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 9004 Search PubMed.
- P. Sindzingre, G. Misguich, C. Lhuillier, B. Bernu, L. Pierre, C. Waldtmann and H.-U. Everts, Magnetothermodynamics of the spin-1/2 kagomé antiferromagnet, Phys. Rev. Lett., 2000, 84, 2953 CrossRef CAS PubMed.
- G. Misguich and B. Bernu, Specific heat of the S = 1/2 Heisenberg model on the kagome lattice: high-temperature series expansion analysis, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 014417 Search PubMed.
- G. Misguich and P. Sindzingre, Magnetic susceptibility and specific heat of the spin-1/2 Heisenberg model on the kagome lattice and experimental data on ZnCu3(OH)6Cl2, Eur. Phys. J. B, 2007, 59, 305–309 Search PubMed.
- M. Isoda, H. Nakano and T. Sakai, Specific heat and magnetic susceptibility of Ising-like anisotropic Heisenberg model on kagome lattice, J. Phys. Soc. Jpn., 2011, 80, 084704 Search PubMed.
- P. Prelovšek and J. Kokalj, Finite-temperature properties of the extended Heisenberg model on a triangular lattice, Phys. Rev. B, 2018, 98, 035107 CrossRef.
- J. Schnack, J. Schulenburg and J. Richter, Magnetism of the N = 42 kagome lattice antiferromagnet, Phys. Rev. B, 2018, 98, 094423 CrossRef CAS.
- L. Chen, D.-W. Qu, H. Li, B.-B. Chen, S.-S. Gong, J. von Delft, A. Weichselbaum and W. Li, Two-temperature scales in the triangular-lattice Heisenberg antiferromagnet, Phys. Rev. B, 2019, 99, 140404 CrossRef CAS.
- P. Prelovšek, K. Morita, T. Tohyama and J. Herbrych, Vanishing wilson ratio as the hallmark of quantum spin–liquid models, Phys. Rev. Res., 2020, 2, 023024 CrossRef.
- K. Seki and S. Yunoki, Thermodynamic properties of an S = 1.2 ring-exchange model on the triangular lattice, Phys. Rev. B, 2020, 101, 235115 Search PubMed.
- T. Hutak, T. Krokhmalskii, J. Schnack, J. Richter and O. Derzhko, Thermodynamics of the s = 1/2 hyperkagome-lattice Heisenberg antiferromagnet, Phys. Rev. B, 2024, 110, 054428 CrossRef CAS.
- M. Ulaga, J. Kokalj, A. Wietek, A. Zorko and P. Prelovšek, Finite-temperature properties of the easy-axis Heisenberg model on frustrated lattices, Phys. Rev. B, 2024, 109, 035110 CrossRef CAS.
- M. Ulaga, J. Kokalj and P. Prelovšek, Easy-axis Heisenberg model on the triangular lattice: from supersolid to gapped solid, arXiv, 2024, preprint, arXiv:2408.05034 [cond-mat.str-el] DOI:10.48550/arXiv.2408.05034.
- C.-O. Hwang, S.-Y. Kim, D. Kang and J. M. Kim, Thermodynamic properties of the triangular-lattice Ising antiferromagnet in a uniform magnetic field, J. Korean Phys. Soc., 2008, 52, 203 CrossRef.
- S.-Y. Kim, Ising antiferromagnet on a finite triangular lattice with free boundary conditions, J. Korean Phys. Soc., 2015, 67, 1517 CrossRef.
- K. Kanô and S. Naya, Antiferromagnetism. the kagomé Ising net, Prog. Theor. Phys., 1953, 10, 158 CrossRef.
- R. R. P. Singh and M. Rigol, Thermodynamic properties of kagome antiferromagnets with different perturbations, J. Phys.: Conf. Ser., 2009, 145, 012003 CrossRef.
- G. C. Lau, R. S. Freitas, B. G. Ueland, B. D. Muegge, E. L. Duncan, P. Schiffer and R. J. Cava, Zero-point entropy in stuffed spin-ice, Nat. Phys., 2006, 2, 249–253 Search PubMed.
- B. Martínez, F. Sandiumenge, A. Rouco, A. Labarta, J. Rodríguez-Carvajal, M. Tovar, M. Causa, S. Galí and X. Obradors, Magnetic dilution in the strongly frustrated kagome antiferromagnet SrGa12−xCrxO19, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 10786 CrossRef PubMed.
- P. W. Anderson, B. I. Halperin and C. M. Varma, Anomalous low-temperature thermal properties of glasses and spin glasses, Philos. Mag. A, 1972, 25, 1, DOI:10.1080/14786437208229210.
- C. Broholm, G. Aeppli, G. P. Espinosa and A. S. Cooper, Antiferromagnetic fluctuations and short-range order in a kagomé lattice, Phys. Rev. Lett., 1990, 65, 3173 Search PubMed.
- A. P. Ramirez, G. P. Espinosa and A. S. Cooper, Elementary excitations in a diluted antiferromagnetic kagomé lattice, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 2505 CrossRef CAS PubMed.
- B. I. Halperin and W. M. Saslow, Hydrodynamic theory of spin waves in spin glasses and other systems with noncollinear spin orientations, Phys. Rev. B: Condens. Matter Mater. Phys., 1977, 16, 2154 Search PubMed.
- D. Podolsky and Y. B. Kim, Halperin-saslow modes as the origin of the low-temperature anomaly in NiGa2S4, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 140402 Search PubMed.
- C. Waldtmann, H.-U. Everts, B. Bernu, C. Lhuillier, P. Sindzingre, P. Lecheminant and L. Pierre, First excitations of the spin 1/2 Heisenberg antiferromagnet on the kagomé lattice, Eur. Phys. J. B, 1998, 2, 501–507 CrossRef CAS.
- A. P. Ramirez, B. Hessen and M. Winklemann, Entropy balance and evidence for local spin singlets in a kagomé-like magnet, Phys. Rev. Lett., 2000, 84, 2957 CrossRef CAS PubMed.
- L. Limot, P. Mendels, G. Collin, C. Mondelli, B. Ouladdiaf, H. Mutka, N. Blanchard and M. Mekata, Susceptibility and dilution effects of the kagomé bilayer geometrically frustrated network: a Ga NMR study of SrCr9pGa12−9pO19, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 144447 Search PubMed.
- D. Phelan, F. Ye, H. Zheng, E. Krivyakina, A. Samarakoon, P. LaBarre, J. Neu, T. Siegrist, S. Rosenkranz and S. Syzranov, et al., The geometrically frustrated spin glass (Fe1−pGap)2TiO5, Acta Crystallogr., Sect. A: Found. Adv., 2023, 79, a247 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |
