High-throughput development of tough metallic glass films†
Yuzhou
Wu‡
ab,
Yue
Huang‡
ab,
Yebei
Wang‡
a,
Fuchao
Wang
a,
Yunhe
Gao
a,
Yingying
Sun
a,
Meichen
Jian
a,
Lijian
Song
a,
Yu
Tong
 a,
Yan
Zhang
a,
Chao
Wang
c,
Yanhui
Liu
a,
Yan
Zhang
a,
Chao
Wang
c,
Yanhui
Liu
 c,
Jun-Qiang
Wang
c,
Jun-Qiang
Wang
 *a,
Juntao
Huo
*a,
Juntao
Huo
 *a and
Meng
Gao
*a and
Meng
Gao
 *a
*a
aNingbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences, Ningbo 315201, China. E-mail: gaomeng@nimte.ac.cn; huojuntao@nimte.ac.cn; jqwang@nimte.ac.cn
bSchool of Materials Science and Chemical Engineering, Ningbo University, Ningbo 315211, China
cInstitute of Physics, Chinese Academy of Sciences, Beijing 100190, China
First published on 23rd October 2024
Abstract
Fast development of metallic glass films with high toughness has been a long-sought goal of humankind in view of their superior properties and great potential for application in the field of soft electronics. However, until now, there has been no effective experimental strategy because of the lack of suitable and precise toughness measurement technology. In the present work, we introduced a feasible route for developing tough metallic glass films using combinatorial material library preparation and high-throughput toughness measurement via nanoindentation. Based on this route, tough metallic glass films for the quaternary Zr–Ti–Cu–Al system were successfully screened out. The corresponding electron work function map was detected to uncover the physical mechanism for the composition dependence of toughness. In addition, the preliminary assessments of the screened tough metallic glass films as strain-sensing materials were also conducted. Our current research not only provides a versatile toolbox for high-throughput development of tough metallic glass films, but also exemplifies their potential as strain-sensing materials.
New conceptsStrain-sensing materials are the key materials for various soft, stretchable and wearable electronics. Metallic glass films have an excellent combination of good electrical conductivity, extremely low roughness, large elastic limit and high corrosion resistance, and exhibit competitive potential as strain-sensing materials. Herein, we present an experimental framework for high-throughput development of tough metallic glass films aiming to use them as strain-sensing materials. In this framework, one effective high-throughput toughness measurement method based on nanoindentation was applied to metallic glass films for the first time. What is more, the electric work function map was precisely detected to uncover the physical mechanism of the composition dependence of toughness. The outcome of the current research not only opens up a window for high-throughput discovery of tough metallic glass films universally and flexibly, but also inspires a new wave of research studies for the development of metallic glass films as strain-sensing materials. |
Introduction
Metallic glasses (MGs), also known as amorphous alloys, are a class of metallic alloys with a long-range disordered atomic structure.1–3 Different from traditional crystalline metals, there do not exist structural defects in MGs, such as point defects, dislocations and grain boundaries. These structural characteristics endow MGs with a series of excellent properties like large elastic strain, high strength, outstanding catalytic activity and good magnetic properties.4–8 Compared to bulk MGs, thin MG films (MGFs) with micro- and nanoscale dimensions display superior performance, such as extremely low roughness, high corrosion resistance and extremely low temperature coefficients of resistance.9–12 Especially, owing to their excellent combination of good electrical conductivity, large elastic limit and exceptional biocompatibility, MGFs have become a class of promising strain-sensing materials for soft electronics (stretchable and wearable electronics).11–16 What is more, MGFs can be formed in a broad range of compositions, providing abundant choices of adjustable properties and desirable functionalities.17,18 However, the intrinsic brittleness is the Achilles heel for the application of MGFs as strain-sensing materials.19–21 The dominant mechanical properties that are being directly related to the brittleness problem of MGs are plasticity and toughness.22,23 While the improvement of the plasticity for MGs has been extensively studied and reported,24–28 the research on fracture toughness of MGs is rare due to the multiple dependence on various internal and external factors.29,30 Until now, there have been few reports on tough MG systems, such as Pd82.5P6Si9.5Ge2 (200 MPa m1/2),31 Pt57.5Cu14.7Ni5.3P22.5 (80 MPa m1/2),32 Zr61Ti2Cu25Al12 (130 MPa m1/2),33 and Ti40Zr25Cu12Ni3Be20 (100 MPa m1/2).34 Considering the rapid replacement and upgrading for strain-sensing materials for application in stretchable and wearable electronics, these limited MGFs are obviously not enough. Therefore, it is crucial to rapidly develop more tough MGFs to meet the potential requirements for soft electronic applications.Current research and development studies of various materials including MGs heavily rely on a conventional “trial-and-error” strategy. It generally requires decades of studies to develop an optimal material for industrial applications. For MGs, the design of new systems with desirable performance is quite challenging due to the enormously large number of potential compositions available. The vastness of the combined composition-processing space makes the fast screening of new MGs based on trial-and-error experiments difficult and expensive. In contrast, one new materials genome initiative based on high throughput experiment, calculation and a big data project has been proposed.35 A high-throughput strategy has been applied to rapidly screen a series of the physical and chemical properties of MGs, such as glass forming ability,36 thermal stability,37 thermal plastic processability,38 corrosion resistance,39 mechanical properties,40,41 and catalytic activity.42 Combinatorial synthesis of material libraries has emerged as a powerful strategy for the fast development of new materials. Among various techniques employed for combinatorial synthesis, magnetron co-sputtering has proven to be a highly effective and versatile method for depositing MGFs with controlled compositions and structures.43,44
For high-throughput development of tough MGFs based on the combinatorial synthesis of material libraries, it is critical to propose one suitable experimental characterization method for toughness. For bulk MGs, toughness is usually characterized via single-edge notched three-point bending tests or compact-tension tests under tensile loading, which are not applicable for MGFs.33 For small samples, there are two other methods based on nanoindentation: the crack length-based method45,46 and the fracture initiation point characterization method.47 The crack length-based method utilizes one nanoindenter to press the sample to create a crack and then statistically analyze the crack length via SEM to calculate the toughness. However, this method faces many challenges because the crack lengths produced under different stress conditions are uncontrollable. In the fracture initiation point characterization method, the initiation of the first crack is difficult to confirm at lower stresses.48–50 In addition, the high cost and low efficiency of the above methods make them unsuitable as fast screening methods for high-throughput development of MGFs. Recently, one new toughness characterization method based on the conversion between elastic deformation energy and fracture energy during nanoindentation was adopted.51–54 This method has advantages of low cost, high efficiency and high data duplication, and can be seen as one applicable method for high-throughput development of tough MGFs.
In the present work, we propose a facile and flexible framework for high-throughput development of tough MGFs by combining the combinatorial synthesis of a material library, structural characterization, composition analyses and toughness determination (see Fig. 1a). Considering that the composition of Zr61Ti2Cu25Al12 has excellent toughness, there should exist the largest possibility to develop more new MG materials with large toughness. Meanwhile, for the applications of strain-sensing materials, the cost for the chemical elements within the MGs should be low and the Zr–Ti–Cu–Al system well meet the low-cost requirements. Thus, the MG system of Zr–Ti–Cu–Al with potential large toughness and low cost was chosen as the research object. The map of toughness within the wide composition space was determined. To clarify the physical mechanism of the dependence of toughness on the chemical composition, we utilized Kelvin peakforce microscopy (KPFM) to measure the electron work function (EWF) of the same MGF material library. It was found that the MGs with high EWF exhibit high toughness; that is, there exists one positive relationship between toughness and EWF. This result may provide a new idea to reveal the physical origin of toughness in MGs from the perspective of the electronic features. Finally, we selected three MG compositions based on the above screening results and fabricated three single-composition MGFs. For these three MGFs, we tested the electrical signal stability after different stretching cycles to check if the MGFs could be considered as strain-sensing materials. The results demonstrated that the MGF with high toughness has no surface cracks after 5000 cyclic stretching and displays high electrical signal stability, making it an excellent flexible strain sensitive material. The related assessment processes will provide effective guidance for the future applications in the field of strain-sensing materials.
Materials and methods
Fabrication of MGF material libraries and single-composition MGFs
The combinatorial MGF material libraries were fabricated via magnetron co-sputtering deposition with four different elemental sputtering targets including Zr, Ti, Cu and Al targets (99.99% purity, purchased from ZhongNuo Advanced Material, Beijing). Single crystal silicon wafers (diameter of 50 mm) were used as the substrates for the deposition, which exhibit good bonding with the MGF material library. In order to make the structure and property tests more accurate, each MGF material library was divided into 37 circular subregions with a diameter of 5 mm by placing one designed mask plate on the silicon wafer during deposition. The composition gradient of combinatorial MGF material libraries was adjusted by tuning the height and angle of the sputtering guns. The deposition time for each combinatorial MGF material library was about 2 hours. The sputtering power ranges were 50–80 W for the Zr target, 10–40 W for the Ti target, 30–50 W for the Cu target, and 20–30 W for the Al target. After the base pressure in the chamber becomes lower than 1 × 10−5 Pa, argon gas rushed into the chamber. Then, the working pressure was adjusted to 0.5 Pa. The flow rate of argon gas during deposition was set as 40 standard cubic centimeters per minute (SCCM).Single-composition MGFs were also fabricated via magnetron co-sputtering deposition with Zr, Ti, Cu and Al targets. The flexible polyethylene terephthalate (PET) was selected as the deposition substrate due to its good flexibility and low price. Meanwhile, in order to test the substrate effect, we also prepared several single-composition MGFs by using single-crystal silicon as the deposition substrate under the same conditions. The PET films with a thickness of 0.1 mm were firstly cut into several dog-bone-shaped tensile specimens for subsequent mechanical property tests. In order to obtain the totally single-composition MGFs, the PET substrate was kept rotating at a constant speed of 10 rpm during the deposition. In the current work, three compositions were chosen as single-composition MGFs: the Zr38Ti10Cu29Al23 (at%) MGF with sputtering powers of 60 W for the Zr target, 35 W for the Ti target, 45 W for the Cu target, and 25 W for the Al target; the Zr48Ti8Cu27Al17 (at%) MGF with sputtering powers of 65 W for the Zr target, 40 W for the Ti target, 45 W for the Cu target, and 24 W for the Al target; and the Zr61Ti2Cu25Al12 (at%) MGF with sputtering powers of 70 W for the Zr target, 14 W for the Ti target, 38 W for the Cu target, and 24 W for the Al target. The deposition times for three single-composition MGFs were also set as 2 hours.
For comparison, one rod-like bulk MG with a nominal composition of Zr61Ti2Cu25Al12 (at%) was prepared by arc melting pure elements and then was remelted five times to ensure homogeneity. The ingot was cast into a copper mold with cyclic cooling water to produce several rod-like samples with the dimensions of 3 mm × 15 mm (diameter × length).
Structural and compositional characterization of MGF material libraries and single-composition MGFs
The thicknesses of all of the fabricated MGFs were about 1000 nm measured using an atomic force microscope in tapping mode (AFM; Bruker ICON). The diameter of the applied silicon tip was 2 nm (Tap 525A; Bruker). The amorphous nature of the MGFs was verified via high-resolution micro-area X-ray diffraction with a Cu Kα radiation source (XRD; Bruker D8 DISCOVER). The diameter of the X-ray diffraction spot was 1 mm, and the spacing between each spot for diffraction regions in the MGF material library was about 7 mm. The surface morphology was observed using an atomic force microscope in tapping mode (AFM; Bruker ICON). The chemical compositions of the combinatorial MGF material libraries and single-composition MGFs, calibrated with bulk alloys of known compositions, were measured using an energy-dispersive X-ray spectrometer (EDS; ZEISS EVO18) attached to a scanning electron microscope (SEM; ZEISS EVO18). The microscopic structural features for different MGFs were characterized using a high-resolution transmission electron microscope (TEM; Talos F200x). The fracture morphology for different MGF samples after uniaxial tensile fracture was observed using a scanning electron microscope (SEM; ZEISS EVO18).EWF mapping of the MGF material library using a Kelvin probe force microscope
The EWF tests were performed on a Kelvin probe force microscope (KPFM) of an AFM (Bruker ICON). The tip radius of the applied platinum tip was about 25 nm and the nominal spring constant was 200 N m−1. The sensitivity coefficient of the AFM tip was determined by the thermal tuning method.55,56 The adopted mode between the probe and the surface for KPFM tests was the intermittent contact mode. The AFM probe vibrates above the sample surface and makes a brief contact with the sample surface during each vibration cycle. By measuring the contact potential difference (VCPD) between the probe and the sample, the EWF of the sample can be determined. The EWF tests were separately conducted on the 37 circular subregions. The dimensions of the testing regions were 50 μm × 50 μm, and the scanning rate was 0.995 Hz. Before the AFM tests, the contamination of the sample surface should be reduced, and all of the experiments were performed at room temperature.High throughput toughness characterization of MGF material libraries by nanoindentation
Nanoindentation tests were conducted on the MGF material libraries at room temperature (Hysitron TI980). The applied nanoindentation machine was equipped with a Berkovich diamond nanoindenter. All of the tests were done in the load-controlling mode. The displacement resolution is about 0.01 nm and the load resolution is about 50 nN. The maximum drift rate was set to be 0.05 nm s−1 before each measurement. Before the nanoindentation tests, the surface roughness of the MGF material libraries was confirmed by AFM. To avoid the errors induced by the surface morphology during nanoindentation tests, the surface roughness of the MGF material libraries needs to be below 1 nm. In order to prevent the influence of the substrate, the nanoindentation depth was set as about 100 nm, which is 10% of the thickness of the MGFs.57 Before the nanoindentation tests, the nanoindenter needs to be calibrated. For ensuring statistical significance, for each subregion of the MGF material libraries, the toughness tests were repeated 9 times with 3 × 3 arrays.Stretchability and electrical signal stability testing of single-composition MGFs
To test the stretchability of the MGFs, a series of the tensile tests were conducted on a 1 KN universal testing machine (Zwick/Roell Z1.0). The tensile specimens were the above prepared dog-bone shaped samples: samples 1, 2, and 3. For comparison, one same shaped PET tensile sample was also prepared as the reference. The applied tensile displacement rate was 0.05 m s−1 to confirm the detailed elastic strain limit for each sample. For electrical signal stability testing, a series of cyclic tensile experiments were performed on the samples 1, 2, and 3 at a fixed elastic strain of 2% with a displacement rate of 0.05 m s−1. The change in the electrical resistance of three samples during cyclic tensile testing was recorded using four-probe resistance measurements (4D Model 280). For repeatability and reliability of experimental data, both of the tensile tests and the electrical resistivity measurements for each sample were repeated three times for the error analyses. The surface morphology for each sample was observed using a scanning electron microscope (SEM; ZEISS EVO18).Results and discussion
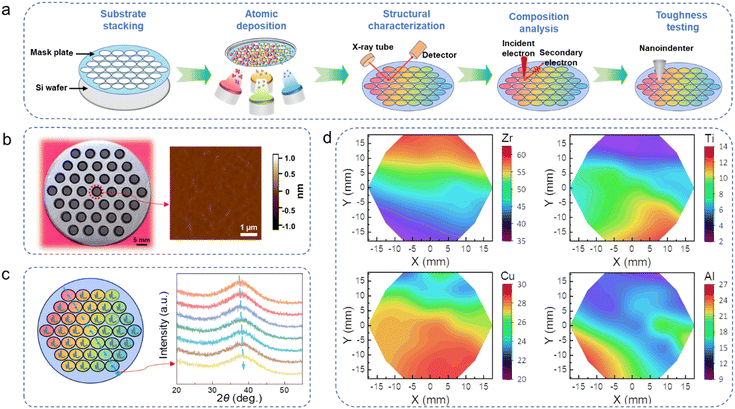
Structural and compositional analyses of the fabricated Zr–Ti–Cu–Al MGF material library
Fig. 1a schematically depicts the detailed process for high throughput development of tough MGFs in the current work. Here, we selected the Zr–Ti–Cu–Al quaternary MG system as our primary research subject in view of its low cost, good glass forming ability and potential large toughness.33,57,58 By focusing on this quaternary composition space, there is a big possibility to discover new MG compositions with high toughness. Based on the magnetron co-sputtering technique and the strategy of the substrate stacking with a mask plate and Si wafer, the Zr–Ti–Cu–Al quaternary MGF material library was fabricated. The optical picture of the MGF material library is displayed in the left part of Fig. 1b. Notably, the applied mask plate with identical dimensions successfully divides the entire MGF material library into 37 individual sub-regions, facilitating compositional refinement and subsequent property analyses. For the following structural analyses and property characterization studies, the surface morphology is one key factor. For one subregion within the MGF material library marked by a red dotted circle, the three-dimensional surface morphology was measured by using AFM, as shown in the right part of Fig. 1b. In addition, the three-dimensional surface topography corresponding to one amplified local region was also obtained and shown in Fig. S1 (ESI†). Clearly, the surface roughness of the fabricated MGF material library is 0.18 nm, which well meets the roughness requirements of the following measurements.To verify the amorphous nature of the fabricated MGF material library, a series of high-resolution micro-area XRD tests were conducted on all of the 37 subregions within the MGF material library. The detailed XRD patterns are shown in the left part of Fig. 1c. Clearly, all of the MGs corresponding to each region are amorphous. Moreover, the chemical composition distribution of the MGF material library was measured using EDS. The detailed elemental distributions for Zr, Ti, Cu and Al are shown in Fig. 1d. The compositional variation within the prepared MGF library ranges from 35 to 64 at% for Zr, 2 to 14 at% for Ti, 20 to 30 at% for Cu, and 9 to 27 at% for Al. It is obvious that the composition of the MGF material library shows a gradient distribution, consistent with the initial experimental design. In addition, at around 33°, there appears one small crystalline peak for all MGF samples. Previous research has reported that this crystalline peak belongs to the Si wafer substrate,37,42 which is reasonable considering that the thickness of the MGF material library is only about 1000 nm.
High throughput toughness characterization of the Zr–Ti–Cu–Al MGF material library based on nanoindentation
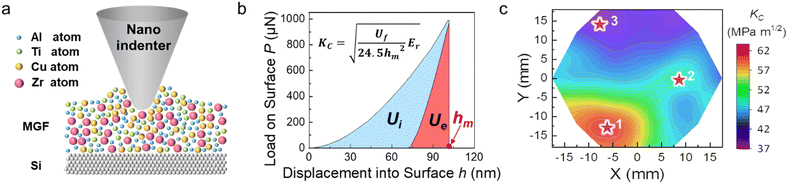
One of the main reasons for the limited research on the toughness of MGs is the lack of suitable characterization methods. In the current work, one energy conversion method based on nanoindentation was applied and it is suitable for the high-throughput toughness characterization of the MGF material library. Fig. 2a illustrates the scheme of the nanoindentation deformation on the Zr–Ti–Cu–Al MGF. Fig. 2b shows one typical nanoindentation load and a displacement P–h curve in the continuous loading mode with a loading rate of 0.3 mN s−1. The nanoindentation energy conversion method to estimate the toughness is mainly based on the energy conversion from the irreversible energy during nanoindentation to the critical fracture energy.51–54,59 The detailed calculation process is described below.According to the experimentally measured P–h curve, the total energy (Ut) and the stored elastic energy (Ue) when unloading during the nanoindentation process can be calculated. Then, the irreversible energy (Ui) can be obtained by subtracting the stored elastic energy from the total energy:59
| Ui = Ut − Ue | (1) |
| Ui = Up + Uf | (2) |
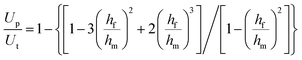 | (3) |
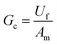 | (4) |
| Am = 24.5hm2 | (5) |
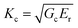 | (6) |
For the estimation of mechanical properties based on the nanoindentation, the substrate effect needs to be avoided.45,46 Here, for the calculation of toughness in eqn (6), the maximum indentation depth hm is one key parameter. Thus, to check the effect of the maximum indentation depth on the toughness, three hm values corresponding to 5%, 10%, and 15% of the thickness for the Zr38Ti10Cu29Al23 MGF library were selected. The detailed nanoindentation P–h curves with different hm values can be seen in Fig. S2 (ESI†). The values of the corresponding toughness were calculated accordingly, as shown in Fig. S3 (ESI†). It is clear that the corresponding toughnesses with different hm values are almost the same with the small error range, 50 ± 4 MPa m1/2. This result indicates that the intrinsic toughness seems to be not dependent on hm, and it confirms that the energy conversion method can give the intrinsic toughness. On the other hand, it should be noted that the toughness for hm of 15% thickness is slightly larger than those of 5% and 10% thickness. Thus, it indicates that the substrate starts to have an influence on the determination of toughness when hm starts to increase about 15% of the MGF thickness. Herein, the maximum indentation depth of 10% of the thickness was chosen for the determination of toughness for all of the MGFs via nanoindentation. To further confirm the validity of the nanoindentation energy conversion method, we also prepared one rod-like bulk MG with the reported composition of Zr61Ti2Cu25Al12 and the diameter is 3 mm. Previous research33 reported the fracture toughness of 130 MPa m1/2. According to the current method, the obtained toughness is about 132 MPa m1/2, and it is close to the above reported value (see Fig. S4, ESI†).
By using the energy conversion method, the color contours of the toughness across the Zr–Ti–Cu–Al MGF material library are displayed in Fig. 2c. Clearly, the MGFs with different chemical compositions have different toughness values, which display the obvious composition dependence. By comparing the composition diagrams in Fig. 1d, the composition region lying in the AlTi-rich side exhibits a higher toughness trend. Since the Al element among the four metallic elements has the smallest size, it is speculated that Al atoms fill the interstitial spaces between other atoms during the deposition process, leading to a denser atomic packing within the MGF sample.62 This results in significantly enhanced interatomic bonds and makes fracture less likely to occur, exhibiting a larger toughness.63 In addition, three specific compositions of Zr38Ti10Cu29Al23, Zr48Ti8Cu27Al17, and Zr61Ti2Cu25Al12 were selected to test the possibility of using them as the strain-sensing materials as discussed below. They were named as samples 1, 2, and 3, respectively. The corresponding toughness values are 64, 53, and 38 MPa m1/2. Therefore, through the current nanoindentation energy conversion method, the MGFs with high toughness in the Zr–Ti–Cu–Al quaternary system have been fast screened. Compared with traditional methods, this method significantly reduces experimental costs and shortens testing cycles. Meanwhile, since the above method does not have strict requirements for sample size and microstructure, it is not limited to MGs but is also suitable for various other materials, including crystalline metals, semiconductors, or polymer materials, which shows its promising potential for broad applications in different fields.
To further investigate the microscopic structural features of samples 1, 2 and 3, a series of high resolution TEM measurements were conducted and the detailed results are displayed in Fig. S5a, d and g (ESI†). Clearly, all of the three MGF samples are amorphous, which is consistent with the results shown in Fig. 1c. In addition, it seems that the microscopic structures for three MGFs are very similar, which makes it difficult to connect with their different toughnesses. The correlation between the microscopic structure and the toughness in MGs is still one of the hot research topics in the field of amorphous materials. On the other hand, previous research studies reported that the toughness of MGs is positive with a typical size of the fracture surface structure.64,65 Here, we also investigated the fracture morphology for MGF samples 1, 2 and 3 after tensile fracture and the detailed results are shown in Fig. S5b, e and h (ESI†). The corresponding size distributions of the typical dimple fracture structure are also shown in Fig. S5c, f and i (ESI†). First, for three samples, the typical fracture morphologies are dimple-like patterns, which imply that the fracture modes are ductile rather than brittle.65 This result is in agreement with the larger toughness values for three MGFs. Second, the average sizes for the dimple structure are: sample 1 (∼151.92 nm), sample 2 (∼100.63 nm), and sample 3 (∼96.67 nm). By comparing the corresponding toughness values, the larger the size of dimple structures for MGFs, the greater the toughness of the corresponding MGF sample, which is in agreement with previous research studies.64,65
EWF mapping of the Zr–Ti–Cu–Al MGF material library via KPFM
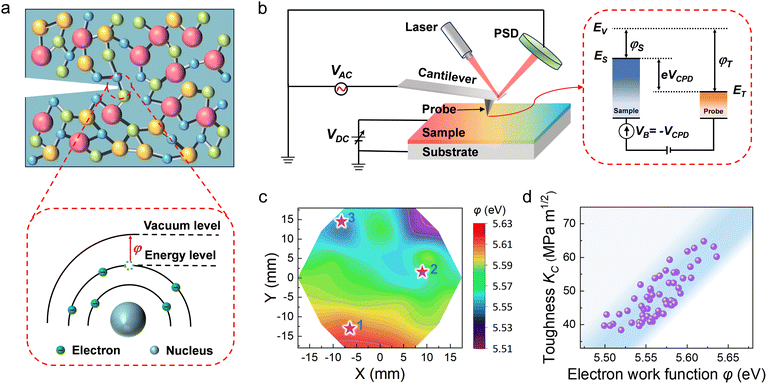
From the results in Fig. 2c, the toughness of the Zr–Ti–Cu–Al MGF material library exhibits obvious composition dependence. To reveal this dependence, we introduced the basic physical parameter of EWF. Toughness, one of the important mechanical properties of materials, is a measure of materials’ resistance to fracture. Basically, it is determined by the electron behavior that governs the atomic bond strength and ultimately the integrated mechanical properties.66 Generally, the stronger the atomic bond between atoms in a metal, the larger the toughness.53 However, there is no simple but fundamental parameters to reflect the electron behavior and the atomic bond of metallic materials. Recently, several research studies indicated that EWF largely reflects the intrinsic electron behaviors and is closely related to various mechanical properties of metals in the traditional alloys, such as the elastic modulus, the strength and the toughness.67–71 For toughness, there exists one positive correlation between the toughness and the corresponding EWF in various crystalline metals and alloys, as shown in Fig. S6 (ESI†). EWF is the minimum energy required to move electrons at the Fermi level inside a metal to its surface without kinetic energy. The fracture of alloys can be considered as a process in which atomic bonds are broken and electrons transfer from energy levels to the vacuum. From this view, it is reasonable that the higher the EWF, the stronger the atomic bond and the higher the toughness. It should be noted that EWF is influenced by the composition, the atomic packing structure and the surface conditions. Under the same surface conditions and the amorphous structure, EWF is mainly determined by its composition. Therefore, EWF can be used as an indicator to screen the optimal compositions with large fracture toughness within MGF material libraries. The correlation between the fracture and the EWF for MGFs is illustrated in Fig. 3a.Indeed, surface oxidation of the thin film samples can affect the accuracy of the toughness and EWF measurements. To address the issue of surface oxidation, we performed a series of HRTEM, EDS and XPS experiments. The element maps for sample 1 are displayed in Fig. S7 (ESI†), and the detailed proportions of each chemical element for samples 1, 2, and 3 on single crystal silicon substrate are included in Table S1 (ESI†) (EDS) and Table S2 (ESI†) (XPS). First, from Fig. S7 (ESI†), one can see that the distributions of different elements for sample 1 are uniform without any signs of element segregation. Second, the oxygen contents for samples 1, 2 and 3 are 1.27%, 1.17% and 1.41% based on the EDS results and 1.16%, 1.21% and 1.08% based on the XPS results. It is clear that the oxygen contents for all of the MGF samples are close and very low, demonstrating that the prepared films in this work exhibit good oxidation resistance. Additionally, the surface roughness results in Fig. 1b also confirm that the MGF surface is very smooth and there is no serious surface oxidation. Therefore, for the toughness and EWF measurements, the influence of surface oxidation should be negligible.
Currently, there are two methods for measuring EWF, ultraviolet photoelectron spectroscopy (UPS)72 and KPFM. Typically, the method chosen for the EWF measurements depends on the sample type, surface conditions, and measurement requirements. Compared with UPS, KPFM is a simple, rapid, high-resolution, and non-destructive technique for measuring the EWF. Moreover, KPFM is one preferable method to do the high throughput measurement in this work. Therefore, herein, we chose the KPFM method for the EWF measurements. The scheme for measuring the EWF by KPFM is depicted in Fig. 3b. When the conductive probe is grounded and contacts with the surface of the testing material, the potential difference VCPD can be quickly established. Considering that the EWF of the applied platinum probe (φT) is 5.65 eV, the EWF of the sample (φS) can be determined as follows:73
| φS = φT − eVCPD. | (7) |
Based on the above measurement principle, the EWF map for the Zr–Ti–Cu–Al MGF material library was obtained and shown in Fig. 3c. Clearly, the EWF exhibits the evident chemical composition dependence, which is similar to the toughness in Fig. 2c. It is interesting to find that the compositions on the bottom left side (Al-rich MGFs) display the maximum values of the EWF. This result is in line with the maximum values of the toughness within the almost same composition space.
What is more, the values of EWF for the samples 1, 2, and 3 were determined to be 5.62, 5.57, and 5.57 eV, which show a positive correlation with the toughness. In order to further provide a more comprehensive explanation for the correlation between the EWF and the toughness, we also prepared another Zr–Ti–Cu–Al MGF material library with different composition ranges. The corresponding chemical composition map is displayed in Fig. S8 (ESI†). Both of the values of the EWF and the corresponding toughness with the same composition are plotted in Fig. 3d. One can clearly see that there actually exists a positive correlation between toughness and EWF. The detailed physical mechanism of this positive correlation in MGs needs more experiments and simulations to clarify, which will be the focus of our future research.
These results confirm that for MGFs, the larger the EWF, the larger the toughness and the less likely fracture occurs. The physical mechanism being responsible for such correlation can be explained. It is known that the activation energies for crack initiation, which determines the fracture toughness, are closely related to the electronic state. A higher EWF corresponds to a higher stability of electrons in metallic bonds within MGFs. Thus, a larger driving force is required to change the electron state associated with a high EWF in order to achieve electronic rearrangement, which corresponds to a certain mechanical deformation. Therefore, the resistance of a metal to fracture should be, in general, consequently larger when its EWF is higher. By combining the XRD results in Fig. 1c and HRTEM results in Fig. S5 (ESI†), it implies that the electronic feature may be a more key and direct factor than the atomic structure governing the toughness of MGs. Therefore, the above results demonstrate that EWF may be considered as a promising and effective indicator to develop tough MGs, providing critical clues for element selection and material tailoring.
On the other hand, it should be noted that the parameter of EWF may be useful to study the size effect or other external treatments on the various mechanical properties of MGs. For example, for the bulk MG and MGF with the same composition, the electron states should be significantly different due to different atomic structures. Thus, there should appear one obvious change for the EWF. Thus, it is expected that this simple but fundamental parameter may lead to the development of new methodologies or supplementary approaches for designing and tailoring MG materials with improved mechanical properties on a feasible electronic base.
Preliminary assessment of tough Zr–Ti–Cu–Al MGFs as strain-sensing materials
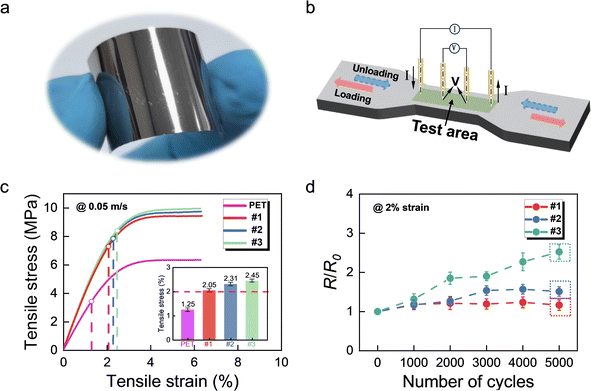
For strain-sensing materials, the large elastic strain and the good crack-resistance under cyclic deformation are the key performance metrics for determining the service life.19,21,74 In order to explore the potential applications of MGFs in the field of soft electronics, we did the preliminary assessments of the elastic strain and the crack-resistance performance in tough Zr–Ti–Cu–Al MGFs. For simplicity, we selected three screened samples 1, 2, and 3 as the research subjects considering that these three samples display significantly different toughnesses. Meanwhile, the composition of sample 3 has been previously reported and it possesses a huge toughness like that of the bulk, which is up to about 130 MPa m1/2.33 Different from the above combinatorial MGF material library, the MGFs as the strain-sensing materials were deposited on the flexible PET substrates. The choice of PET substrates is due to their good transparency, glossiness, easy availability, low cost, and excellent stretchable properties.75Fig. 4a shows the optical image of one flexible MGF for sample 1 with a thickness of about 1000 nm and an area of about 8 cm2. The fabricated MGFs demonstrate excellent flexibility by easily bending to nearly 180° without noticeable cracks. What is more, all of the MGFs are smooth and shiny, showing their low roughness and good smoothness. To verify the amorphous nature of three MGFs, XRD tests were conducted and the detailed results are shown in Fig. S9 (ESI†). Clearly, all film samples exhibit prominent broad diffraction peaks, which is the characteristic of amorphous MGs. The slight differences in peak positions are attributed to the variations in chemical compositions of different MGF samples.
For MGs, the substrate plays a key role in the structures and the properties of the deposited films.76,77 In this work, all of the preparations were conducted at room temperature, which excludes the substrate temperature effect on the MGFs. During high throughput screening of toughness, the nanoindentation tests were done on the MGF samples deposited on single-crystal silicon. In contrast, the MGF samples for the strain-sensitive materials were deposited on the soft PET substrate. To verify if the hard single-crystal silicon and the soft PET substrate affect the composition and the toughness of the prepared MGFs, a series of XPS and nanoindentation tests were conducted. The detailed values of the chemical compositions and the toughnesses for samples 1, 2 and 3 with two different substrates are shown in Fig. S10 (ESI†) and Table S2 (ESI†). Clearly, different substrates do not affect the chemical compositions and the corresponding toughnesses for all of the three MGFs. Thus, the substrate effect can be eliminated in the current work.
In order to test the elastic deformation ability and the electrical signal stability during cyclic deformation of MGFs, we designed an in situ tensile platform combined with the electrical signal measurement instrument, as illustrated in Fig. 4b. Firstly, to determine the elastic strain limit for these MGF materials, a series of uniaxial tensile tests were conducted and the displacement rate was set to be 0.05 m s−1. The detailed tensile stress–strain curves are displayed in Fig. 4c. For reference, the single PET material was also tested and this result is also included in Fig. 4c. These results clearly show that the elastic strain limits for MGF samples 1, 2, and 3 are 2.05 ± 0.07%, 2.31 ± 0.07%, and 2.45 ± 0.06%, respectively. In contrast, the elastic tensile strain limit of the PET material is only 1.25 ± 0.07%. For this lower tensile strain limit of the PET material, it tends to undergo viscoelastic deformation during stretching78 and the viscoelastic deformation strain is much larger than the elastic strain limits of the MGFs. Thus, the PET material with smaller elastic strain will not affect the elastic deformation of the MGFs and the following cyclic performance tests.
According to the above results and discussions, the parameters for the cyclic stretching tests of three MGFs are as follows: the fixed cyclic tensile strain is 2%, the stretching rate is 0.05 m s−1, and the cycle numbers are set as 1000, 2000, 3000, 4000, and 5000, respectively. The electrical signal stability of three MGFs was measured using four probe measurement methods after different cycle numbers of cyclic stretching under 2% strain. The detailed results for the relative resistivity R/R0 (R0 is the resistivity of the not deformed sample) are displayed in Fig. 4d. With the increase of the cycle number, three MGF samples display different evolution trends. For sample 1 with the largest toughness, the relative resistivity does not increase (1.17 ± 0.19 after 5000 cycles marked by the red dashed rectangle). For sample 2 with medium toughness, there is a slight increase of the relative resistivity (1.51 ± 0.12 after 5000 cycles marked by the blue dashed rectangle). In contrast, for sample 3 with the minimum toughness, there appears a gradual increase trend with the increase of the cyclic number (2.52 ± 0.13 after 5000 cycles marked by the green dashed rectangle). And the relative value changes by approximately two times after 5000 cycles, which indicates that there appears a large structure change for sample 3.
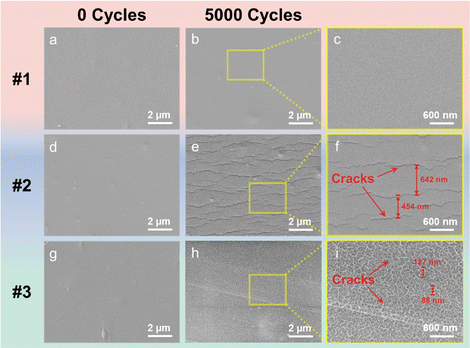
To check the detailed change for three samples, we observed the surface morphologies of three MGFs after 5000 cycles. The detailed SEM images for three MGFs are shown in Fig. 5. Before cyclic stretching, there were no noticeable cracks on the surface of all three MGFs, as shown in Fig. 5a, d and g. After 5000 cycles of cyclic stretching, multiple cracks appear on the surfaces of samples 2 and 3, while sample 1 remains smooth without cracks (see Fig. 5b, e and h). To further investigate the detailed crack morphology on the surface of the MGF samples, three local regions marked by yellow rectangles are separately selected in Fig. 5b, e and h. The amplified SEM surface morphologies are shown in Fig. 5c, f and i. One can clearly see that there actually are no significant cracks on sample 1. In contrast, there appear two kinds of different crack morphologies on samples 2 and 3. For sample 2, the cracks are long and scattered, exhibiting a stripe-like distribution, and the distance between the cracks ranges from 400 to 700 nm. The sample 3 displays the denser island-like cracks, and the distances between cracks lie around 50–200 nm. By comparing the results of the resistivity for three MGFs in Fig. 4d, different evolution behaviors of the relative resistivity for three MGFs are mainly induced by different surface morphologies during stretching tests. Sample 1 does not have the crack and thus its electrical signal stability is the best. For sample 3, 5000 cycle stretching leads to a great deal of cracks and then to the worst electrical signal stability. Therefore, the screened tough MGF sample 3 based on the current high throughput development can be used as the strain-sensing materials in view of their excellent elastic strain limit and good crack-resistance.
Conclusions
In summary, we proposed one effective high throughput strategy to fast screen MGFs with large toughness via the nanoindentation energy conversion method. A quaternary Zr–Ti–Cu–Al MGF material library was fabricated using magnetron co-sputtering technology and the corresponding toughness map displays the obvious composition dependence. Considering that the EWF represents the intrinsic atomic bonding strength, the combined EWF distribution was detected by KPFM to understand the composition dependence of toughness from the electronic perspective. It was found that there exists one positive correlation between the toughness and the EWF. A higher EWF corresponds to a higher stability of electrons in metallic bonds within MGFs, which leads to larger toughness. Finally, the preliminary assessments of the screened Zr–Ti–Cu–Al MGFs as strain-sensing materials were conducted. It was verified that the MGFs with large toughness can be used as the potential optimal strain-sensing materials due to their excellent elastic strain limit and good crack-resistance. The current high throughput development strategy is simple but effective, and will be useful for developing high-toughness MGFs aiming to apply them in soft electronics.Author contributions
Meng Gao and Yuzhou Wu conceived the idea and wrote the original manuscript. Yuzhou Wu, Yue Huang and Yebei Wang designed and conducted the experiments. Fuchao Wang, Yunhe Gao, Yingying Sun, Lijian Song and Yan Zhang evaluated the data. Meichen Jian conducted the XPS experiments. Yu Tong conducted the EDS experiments. Chao Wang and Yanhui Liu conducted the high-throughput XRD experiments. Meng Gao, Jun-Qiang Wang, and Juntao Huo supervised the work, provided resources and reviewed the manuscript. All authors contributed to the discussion and analysis of the results.Data availability
All data needed to evaluate the conclusions in the paper are presented in the paper and/or the ESI† Materials. Additional data related to this paper may be requested from the authors.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work was supported by the Zhejiang Provincial Natural Science Foundation Regional Innovation and Development Joint Foundation with Quzhou City (LZY23E010002), the National Natural Science Foundation of China (52201194, 52222105, 92163108, and 52231006), the 3315 Innovation Youth Talent in Ningbo City (2021A123G), the Youth Innovation Promotion Association CAS (2019296), the Zhejiang Provincial Natural Science Foundation of China (LR22E010004), and the Ningbo Natural Science Foundation of Ningbo City (2022J310).References
- W. H. Wang, The elastic properties, elastic models and elastic perspectives of metallic glasses, Prog. Mater. Sci., 2012, 57, 487–656 CrossRef CAS.
- M. W. Chen, A brief overview of bulk metallic glasses, NPG Asia Mater., 2011, 3, 82–90 CrossRef.
- A. L. Greer, M. B. Costa and O. S. Houghton, Metallic glasses, MRS Bull., 2023, 48, 1054–1061 CrossRef.
- J. S. Zhang, Y. O. Liu, H. Yang, Y. Ren, L. S. Cui, D. Q. Jiang, Z. G. Wu, Z. Y. Ma, F. M. Guo, S. Bakhtiari, F. Motazedian and J. Li, Achieving 5.9% elastic strain in kilograms of metallic glasses: Nanoscopic strain engineering goes macro, Mater. Today, 2020, 37, 18–26 CrossRef CAS.
- W. Q. Zhu, Z. Li, H. Shu, H. J. Gao and X. D. Wei, Amorphous alloys surpass E/10 strength limit at extreme strain rates, Nat. Commun., 2024, 15, 1717 Search PubMed.
- F. C. Li, M. X. Li, L. W. Hu, J. S. Cao, C. Wang, Y. T. Sun, W. H. Wang and Y. H. Liu, Achieving Diamond-Like Wear in Ta-Rich Metallic Glasses, Adv. Sci., 2023, 10, 2301053 CAS.
- X. Y. Jian, W. B. Zhang, Y. X. Yang, Z. L. Li, H. G. Pan, Q. S. Gao and H. J. Lin, Amorphous Cu–W Alloys as Stable and Efficient Electrocatalysts for Hydrogen Evolution, ACS Catal., 2024, 5, 2816–2827 Search PubMed.
- J. Q. Wang, L. J. Song, J. T. Huo, M. Gao and Y. Zhang, Designing Advanced Amorphous/Nanocrystalline Alloys by Controlling the Energy State, Adv. Mater., 2024, 2311406 Search PubMed.
- T. Egami, T. Iwashita and W. Dmowski, Mechanical Properties of Metallic Glasses, Metals, 2013, 3, 77–113 Search PubMed.
- P. Yiu, W. Diyatmika, N. Bönninghoff, Y. C. Lu, B. Z. Lai and J. Chu, Thin film metallic glasses: Properties, applications and future, J. Appl. Phys., 2020, 127, 0310901 Search PubMed.
- H. J. Xian, C. R. Cao, J. A. Shi, X. S. Zhu, Y. C. Hu, Y. F. Huang, S. Meng, L. Gu, Y. H. Liu, H. Y. Bai and W. H. Wang, Flexible strain sensors with high performance based on metallic glass thin film, Appl. Phys. Lett., 2017, 111, 121906 CrossRef.
- M. Liu, C. R. Cao, Y. M. Lu, W. H. Wang and H. Y. Bai, Flexible amorphous metal films with high stability, Appl. Phys. Lett., 2017, 110, 031901 CrossRef.
- J. Y. Bae, E. J. Gwak, G. S. Hwang, H. W. Hwang, D. J. Lee, J. S. Lee, Y. C. Joo, J. Y. Sun, S. H. Jun, M. R. Ok, J. Y. Kim and S. K. Kang, Biodegradable Metallic Glass for Stretchable Transient Electronics, Adv. Sci., 2021, 8, 202004029 Search PubMed.
- N. Van Toan, T. T. K. Tuoi, Y. C. Tsai, Y. C. Lin and T. Ono, Micro-Fabricated Presure Sensor Using 50 nm-Thick of Pd-Based Metallic Glass Freestanding Membrane, Sci. Rep., 2020, 10, 10108 Search PubMed.
- Q. K. Jiang, P. Liu, Y. Ma, Q. P. Cao, X. D. Wang, D. X. Zhang, X. D. Han, Z. Zhang and J. Z. Jiang, Super elastic strain limit in metallic glass films, Sci. Rep., 2012, 2, 852 CrossRef CAS.
- M. Jung, E. Lee, D. Kim, K. Kim, C. J. Yun, H. Lee, H. Kim, K. Rhie and S. Jeon, Amorphous FeZr metal for multi-functional sensor in electronic skin, npj Flexible Electron., 2019, 3, 8 CrossRef.
- S. Y. Ding, Y. H. Liu, Y. L. Li, Z. Liu, S. Sohn, F. J. Walker and J. Schroers, Combinatorial development of bulk metallic glasses, Nat. Mater., 2014, 13, 494–500 CrossRef CAS PubMed.
- S. J. Wu, Z. Q. Liu, R. T. Qu and Z. F. Zhang, Designing metallic glasses with optimal combinations of glass-forming ability and mechanical properties, J. Mater. Sci. Technol., 2021, 67, 254–264 CrossRef CAS.
- R. Qu, R. Maaß, Z. Liu, D. Tönnies, L. Tian, R. O. Ritchie, Z. Zhang and C. A. Volkert, Flaw-insensitive fracture of a micrometer-sized brittle metallic glass, Acta Mater., 2021, 218, 117219 CrossRef CAS.
- Z. X. Wang, Y. J. Yuan and B. B. An, Multiple cracking of amorphous films on ductile substrates, Int. J. Fract., 2022, 238, 17–33 CrossRef.
- J. J. Lewandowski, W. H. Wang and A. L. Greer, Intrinsic plasticity or brittleness of metallic glasses, Philos. Mag. Lett., 2005, 85, 77–87 CrossRef CAS.
- X. K. Xi, D. Q. Zhao, M. X. Pan, W. H. Wang, Y. Wu and J. J. Lewandowski, Fracture of Brittle Metallic Glasses: Brittleness or Plasticity, Phys. Rev. Lett., 2005, 94, 125510 CAS.
- P. Sharma, K. Yubuta, H. Kimura and A. Inoue, Brittle metallic glass deforms plastically at room temperature in glassy multilayers, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 024106 Search PubMed.
- S. Sohn, N. Liu, G. H. Yoo, A. Ochiai, J. Chen, C. Levitt, G. Liu, S. C. Schroers, E. T. Lund, E. S. Park and J. Schroers, A framework for plasticity in metallic glasses, Materialia, 2023, 31, 101876 CAS.
- Y. Wu, D. Cao, Y. Yao, G. Zhang, J. Wang, L. Liu, F. Li, H. Fan, X. Liu, H. Wang, X. Wang, H. Zhu, S. Jiang, P. Kontis, D. Raabe, B. Gault and Z. Lu, Substantially enhanced plasticity of bulk metallic glasses by densifying local atomic packing, Nat. Commun., 2021, 12, 6582 CAS.
- M. Gao, J. Dong, Y. Huan, Y. T. Wang and W. H. Wang, Macroscopic tensile plasticity by scalarizating stress distribution in bulk metallic glass, Sci. Rep., 2016, 6, 21929 CAS.
- Y. H. Liu, G. Wang, R. J. Wang, D. Q. Zhao, M. X. Pan and W. H. Wang, Super Plastic Bulk Metallic Glasses at Room Temperature, Science, 2007, 315, 1385–1388 CAS.
- G. Kumar, P. Neibecker, Y. H. Liu and J. Schroers, Critical fictive temperature for plasticity in metallic glasses, Nat. Commun., 2013, 4, 1536 CrossRef PubMed.
- W. Chen, H. F. Zhou, Z. Liu, J. Ketkawe, N. Li, J. Yurko, N. Hutchinson, H. J. Gao and J. Schroers, Processing effects on fracture toughness of metallic glasses, Scr. Mater., 2017, 130, 152–156 CrossRef CAS.
- J. Ketkaew, R. Yamada, H. Wang, D. Kuldinow, B. S. Schroers, W. Dmowski, T. Egami and J. Schroers, The effect of thermal cycling on the fracture toughness of metallic glasses, Acta Mater., 2020, 184, 100–108 CrossRef CAS.
- M. D. Demetriou, M. E. Launey, G. Garrett, J. P. Schramm, D. C. Hofmann, W. L. Johnson and R. O. Ritchie, A damage-tolerant glass, Nat. Mater., 2011, 10, 123–128 CrossRef CAS PubMed.
- J. Schroers and W. L. Johnson, Ductile Bulk Metallic Glass, Phys. Rev. Lett., 2004, 93, 255506 CrossRef PubMed.
- Q. He, J. K. Shang, E. Ma and J. Xu, Crack-resistance curve of a Zr–Ti–Cu–Al bulk metallic glass with extraordinary fracture toughness, Acta Mater., 2012, 60, 4940–4949 CrossRef CAS.
- X. J. Gu, S. J. Poon, G. J. Shiflet and J. J. Lewandowski, Compressive plasticity and toughness of a Ti-based bulk metallic glass, Acta Mater., 2010, 58, 1708–1720 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, Acta Mater., 2013, 1, 011002 Search PubMed.
- M. X. Li, Y. T. Sun, C. Wang, L. W. Hu, S. Sohn, J. Schroers, W. H. Wang and Y. H. Liu, Data-driven discovery of a universal indicator for metallic glass forming ability, Nat. Mater., 2021, 21, 165–172 CrossRef PubMed.
- M. X. Li, S. F. Zhao, Z. Lu, A. Hirata, P. Wen, H. Y. Bai, M. Chen, J. Schroers, Y. Liu and W. H. Wang, High-temperature bulk metallic glasses developed by combinatorial methods, Nature, 2019, 569, 99–103 CrossRef CAS PubMed.
- S. Ding, Y. Liu, Y. Li, Z. Liu, S. Sohn, F. J. Walker and J. Schroers, Combinatorial development of bulk metallic glasses, Nat. Mater., 2014, 13, 494–500 CrossRef CAS PubMed.
- J. Liu, N. Liu, M. Sun, J. Li, S. Sohn and J. Schroers, Fast Screening of Corrosion Trends in Metallic Glasses, ACS Comb. Sci., 2019, 21, 666–674 CrossRef CAS PubMed.
- S. Sarker, R. T. Kong, R. Schoeppner, L. Ward, N. A. Hasan, D. G. V. Campen, I. Takeuchi, J. Hattrick-Simpers, A. Zakutayev, C. E. Packard and A. Mehta, Discovering exceptionally hard and wear-resistant metallic glasses by combining machine-learning with high throughput experimentation, Appl. Phys. Rev., 2022, 9, 011403 CAS.
- J. H. Cao, M. Gao, Y. F. Cai, J. L. Li, Y. Wang, J. Q. Wang and J. T. Huo, Rapid screening the mechanical properties of ZrNi-based metallic glasses by high-throughput combinatorial approach, Intermetallics, 2022, 148, 107640 CrossRef CAS.
- X. Z. Liu, P. Zou, L. J. Song, B. W. Zang, B. N. Yao, W. Xu, F. S. Li, J. Schroers, J. T. Huo and J. Q. Wang, Combinatorial High-Throughput Methods for Designing Hydrogen Evolution Reaction Catalysts, ACS Catal., 2022, 12, 3789–3796 CrossRef CAS.
- K. Wieczerzak, A. Sharma, C. Hain and J. Michler, Crystalline or amorphous? A critical evaluation of phenomenological phase selection rules, Mater. Des., 2023, 230, 111994 CrossRef CAS.
- L. Lapeyre, K. Wieczerzak, C. Hain, J. Metzger, A. Sharma, A. Bensaoula, J. Michler and T. Nelis, Influence of HiPIMS pulse widths on the deposition behaviour and properties of CuAgZr compositionally graded films, Surf. Coat. Technol., 2022, 450, 129002 CrossRef CAS.
- M. Sebastiani, K. E. Johanns, E. G. Herbert and G. M. Pharr, Measurement of fracture toughness by nanoindentation methods: Recent advances and future challenges, Curr. Opin. Solid State Mater. Sci., 2015, 19, 324–333 CrossRef CAS.
- J. Chen, On the determination of coating toughness during nanoindentation, Surf. Coat. Technol., 2012, 206, 3064–3068 CrossRef CAS.
- H. Guo, C. B. Jiang, B. J. Yang and J. Q. Wang, On the fracture toughness of bulk metallic glasses under Berkovich nanoindentation, J. Non-Cryst. Solids, 2018, 481, 321–328 CrossRef CAS.
- Q. Kang, X. Fang, C. Wu, P. Verma, H. Sun, B. Tian, L. Zhao, S. Wang, N. Zhu, R. Maeda and Z. Jiang, Mechanical properties and indentation-induced phase transformation in 4H–SiC implanted by hydrogen ions, Ceram. Int., 2022, 48, 15334–15347 CrossRef CAS.
- V. Trabadelo, S. Pathak, F. Saeidi, M. Parlinska-Wojtan and K. Wasmer, Nanoindentation deformation and cracking in sapphire, Ceram. Int., 2019, 45, 9835–9845 CAS.
- S. Sinha, R. A. Mirshams, T. Wang, S. S. Nene, M. Frank, K. Liu and R. S. Mishra, Nanoindentation behavior of high entropy alloys with transformation-induced plasticity, Sci. Rep., 2019, 9, 6639 CAS.
- M. Liu, D. Hou and C. Gao, Berkovich nanoindentation of Zr55Cu30Al10Ni5 bulk metallic glass at a constant loading rate, J. Non-Cryst. Solids, 2021, 561, 120750 CAS.
- Y. Liu, Fracture toughnesss assessment of shales by nanoindentation, A Master of Science Project, 2020 Search PubMed.
- M. R. Taha, E. Soliman and M. Sheyka, Fracture toughness of hydrated cement paste using nanoindentation, Recent Advances in Fracture Mechanics of Concrete-B, 2010, 1, 105–111.
- J. Chen and S. J. Bull, Indentation fracture and toughness assessment for thin optical coatings on glass, J. Phys. D: Appl. Phys., 2007, 40, 5401–5417 CAS.
- S. Belikov, J. Alexander, C. Wall, I. Yermolenko, S. Magonov and I. Malovichko, Thermal tune method for AFM oscillatory resonant imaging in air and liquid, 2014 American Control Conference, 2014.
- H. Bückle, Use of hardness test to determine other material properties, The Science of Hardness Testing and Its Research Applications, 1973, 453–494.
- D. Wang and P. Li, Thermodynamic and mechanical properties of Cu–Zr–Al–Ti bulk metallic glasses, AIP Adv., 2018, 8, 125003 Search PubMed.
- L. Y. Chen, Z. Xue, Z. J. Xu, J. Q. Chen, R. X. He, X. P. Nie, Q. P. Cao, X. D. Wang, S. Q. Ding and J. Z. Jiang, CuZrAlTi Bulk Metallic Glass with Enhanced Glass Forming Ability, Mechanical Properties, Corrosion Resistance and Biocompatibility, Adv. Eng. Mater., 2011, 14, 195–199 CrossRef.
- J. Chen, Indentation-based methods to assess fracture toughness for thin coatings, J. Phys. D: Appl. Phys., 2012, 45, 203001 CrossRef.
- Y. T. Cheng, Z. Li and C. M. Cheng, Scaling relationships for indentation measurements, Philos. Mag. A, 2009, 82, 1821–1829 CrossRef.
- P. Klugkist, K. Rätzke, S. Rehders, P. Troche and F. Faupel, Activation Volume of 57Co Diffusion in Amorphous Co81Zr19, Phys. Rev. Lett., 1998, 80, 3288–3291 CAS.
- Y. Ma, L. Li, J. Qian, W. Qu, R. Luo, F. Wu and R. Chen, Materials and structure engineering by magnetron sputtering for advanced lithium batteries, Energy Storage Mater., 2021, 39, 203–224 CrossRef.
- E. Bitzek, J. R. Kermode and P. Gumbsch, Atomistic aspects of fracture, Int. J. Fract., 2015, 191, 13–30 Search PubMed.
- G. Wang, Y. T. Wang, Y. H. Liu, M. X. Pan, D. Q. Zhao and W. H. Wang, Evolution of nanoscale morphology on fracture surface of brittle metallic glass, Appl. Phys. Lett., 2006, 89, 121909 Search PubMed.
- G. Wang, D. Q. Zhao, H. Y. Bai, M. X. Pan, A. L. Xia, B. S. Han, X. K. Xi, Y. Wu and W. H. Wang, Nanoscale Periodic Morphologies on the Fracture Surface of Brittle Metallic Glasses, Phys. Rev. Lett., 2007, 98, 235501 CrossRef CAS PubMed.
- W. Callister and D. G. Rethwisch, Materials Science and Engineering: An Introduction, John Wiley & Sons, New York, 8th edn, 2010 Search PubMed.
- Y. Luo, Y. Tang, T. F. Chung, C. L. Tai, C. Y. Chen, J. R. Yang and D. Y. Li, Electron work function: an indicative parameter towards a novel material design methodology, Sci. Rep., 2021, 11, 11565 CrossRef CAS.
- H. B. Michaelson, The work function of the elements and its periodicity, J. Appl. Phys., 1977, 48, 4729–4733 CrossRef CAS.
- N. D. Lang and W. Kohn, Theory of Metal Surfaces: Work Function, Phys. Rev. B: Solid State, 1971, 3, 1215–1223 CrossRef.
- H. Lu, C. Ouyang, X. G. Yan, J. Wang, G. M. Hua, R. Chung and D. Y. Li, Potential application of electron work function in analyzing fracture toughness of materials, J. Mater. Sci. Technol., 2017, 33, 1128–1133 CrossRef.
- H. Lu, Z. Liu, X. G. Yan, D. Y. Li, L. Parent and H. Tian, Electron work function–a promising guiding parameter for material design, Sci. Rep., 2016, 6, 24366 CrossRef CAS.
- H. Meng, C. Liao, M. Deng, X. Xu, L. Yu and Q. Peng, 18.77% Efficiency Organic Solar Cells Promoted by Aqueous Solution Processed Cobalt(II) Acetate Hole Transporting Layer, Angew. Chem., Int. Ed., 2021, 60, 22554–22561 CrossRef CAS.
- O. Vilitis, M. Rutkis, J. Busenberg and D. Merkulov, Determination of Contact Potential Difference by the Kelvin Probe (Part I) I. Basic Principles of Measurements, Latv. J. Phys. Tech. Sci., 2016, 53, 48–57 Search PubMed.
- P. Murali, T. F. Guo, Y. W. Zhang, R. Narasimhan, Y. Li and H. J. Gao, Atomic Scale Fluctuations Govern Brittle Fracture and Cavitation Behavior in Metallic Glasses, Phys. Rev. Lett., 2011, 107, 215501 CrossRef CAS PubMed.
- A. B. Reddy, G. S. M. Reddy, J. Jayaramudu, K. Sudhakar, B. Manjula, S. S. Ray and E. R. Sadiku, Polyethylene Terephthalate-Based Blends: Natural Rubber and Synthetic Rubber, Poly (Ethylene Terephthalate) Based Blends, Compos. Nanocompos., 2015, 5, 75–98 Search PubMed.
- P. Luo, C. R. Cao, F. Zhu, Y. M. Lv, Y. H. Liu, P. Wen, H. Y. Bai, G. Vaughan, M. di Michiel, B. Ruta and W. H. Wang, Ultrastable metallic glasses formed on cold substrates, Nat. Commun., 2018, 9, 1389 CrossRef CAS PubMed.
- P. Luo, S. E. Wolf, S. Govind, R. B. Stephens, D. H. Kim, C. Y. Chen, T. Nguyen, P. Wąsik, M. Zhernenkov, B. Mcclimon and Z. Fakhraai, Nat. Mater., 2024, 23, 688–694 CrossRef CAS PubMed.
- C. E. Chou, Y. L. Liu, Y. L. Zhang, C. H. Hsueh, F. Q. Yang and S. Lee, Thermomechanical deformation of polyethylene-terephthalate artificial muscles, Polymer, 2020, 210, 123013 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh00815d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |