Open Access Article
Open Access ArticleGuided ad infinitum assembly of mixed-metal oxide arrays from a liquid metal†
Julia J. Changa,
Chuanshen Dub,
Dhanush Jamadgnia,
Alana Paulsa,
Andrew Martina,
Le Weic,
Thomas Ward‡
d,
Meng Lu c and
Martin M. Thuo
c and
Martin M. Thuo *a
*a
aNorth Carolina State University, Department of Materials Science & Engineering, Raleigh, NC 27695, USA. E-mail: mthuo@ncsu.edu
bIowa State University, Department of Materials Science & Engineering, Ames, Iowa 50011, USA
cIowa State University, Department of Electrical and Computer Engineering, Ames, Iowa 50011, USA
dIowa State University, Department of Aerospace Engineering, Ames, Iowa 50011, USA
First published on 25th November 2024
Abstract
Bottom-up nano- to micro-fabrication is crucial in modern electronics and optics. Conventional multi-scale array fabrication techniques, however, are facing challenges in reconciling the contradiction between the pursuit of better device performance and lowering the fabrication cost and/or energy consumption. Here, we introduce a facile mixed-metal array fabrication method based on guided self-assembly of polymerizing organometallic adducts derived from the passivating oxides of a ternary liquid metal to create mixed metal wires. Driven by capillary action and evaporation-driven Marangoni convection, large-area, high-quality organometallic nano- to micro-wire arrays were fabricated. Calcination converts the organometallics into oxides (semiconductors) without compromising wire continuity or array periodicity. Exploiting capillary bridges on a preceding layer, hierarchical arrays were made. Similarly, exploiting the conformity of the liquid to the mold, arrays with complex geometries were made. Given the periodicity and high refractive index of these arrays, we observe guided mode resonance while their complex band structures enable fabrication of diodes or gates. This work demonstrates a simple, affordable approach to opto-electronics based on self-assembling arrays.
New conceptsThis work captures the simplicity and power in self-assembly. By coupling surface reactions, fluid dynamics and capillary-guided and coordination geometry governed self-assembly, we fabricate well-ordered arrays of metal oxide synthons. Given the high precision of convective flows, nano- to micron-sized wires in 2D or 3D hierarchical assemblies are realized with conformal inter-layer contacts. Exploiting such an assembly enables thermal conversion of these arrays into ordered semiconductor wires that show rectification (diode) or gating (transistor) behavior without the associated prohibitive cost in microelectronic manufacturing. |
The need for device fabrication efficiency has been exacerbated by global demand for electronics. Low energy consumption, efficient fabrication, and lower cost always conflict with the pursuit for enhanced device performance.1 Arrays, the periodic arrangement of building blocks, serve as the basis of many functional devices (e.g., optical metamaterials2,3 or integrated circuits4). Fabrication of nanoarrays relies on efficient organization methods with traditional approaches falling into two main subcategories, viz: bottom-up and top-down methods.5 Bottom-up methods assemble as-synthesized building blocks into arrays based on interactions (covalent bonds,6,7 hydrogen bonds,8 and electrostatic interactions9 among others). Top-down methods construct arrays from bulk materials generally via selective abstraction (e.g., e-beam lithography,10,11 laser writing,12 and 3D printing). These strategies, however, often fail to reconcile the contradiction between precision across length scales and fabrication efficiency. Template-assisted fabrication techniques produce multi-scale arrays in high yields without compromising the quality.13 Serving as masks, stamps, or maps, templates are applied in lithographic (phase-shifting or edge lithography),14 imprinting/embossing,15,16 or self-assembly processes17,18 to produce large-area arrays. Despite enhanced efficiency realized by adopting templates, multiple post-processing steps are often necessary to impart functionality to the as-obtained patterns,19 which can introduce defects as well as increase fabrication costs. New fabrication techniques are therefore needed to continue producing high precision, functional devices at manageable costs.20–22
Liquid metal particles have great potential to reduce energy and capital costs in the fabrication of functional arrays since they can act as reservoirs for metal ions. Speciation and reformation kinetics of the passivating oxides dictate selectivity in the release of metal ions from an alloy. Surface plasticity (as captured by the Shuttleworth equation23) in liquid droplets ensures re-equilibration upon etching, hence the surface oxide is a tuneable source of metal ions. Undercooled liquid metal core–shell (ULMCS) particles present a structural and compositional complex oxide (Fig. 1(ai)), in part due to the inherent speciation,24 organization,25 and associated chemical potential gradient.26 Mechanically, the oxide shell is ultrathin (<5 nm), and thus flexible, allowing non-Hertzian contacts and capillary self-organization.26,27 Whereas ULMCS particles have been used in structural fabrication,28,29 low-temperature soldering and interconnects,30 metal soft lithography,31 and super hydrophobic coatings,32 they have not been adopted as sources of semiconductor arrays. Liquid metals, however, have been used to fabricate thin oxide films or related materials based on surface plasticity and deformability.33–35 Surface patterning through controlled sequential presentation of metal ions has, however, been observed with liquid metals through selective release onto the metal's surface.36,37 Hence, our inference that an analogous process can be achieved with ULMCS through chemical etching and far-from the surface organization of generated organometallic adducts giving synthons for semiconductor materials removed from the metal particles.
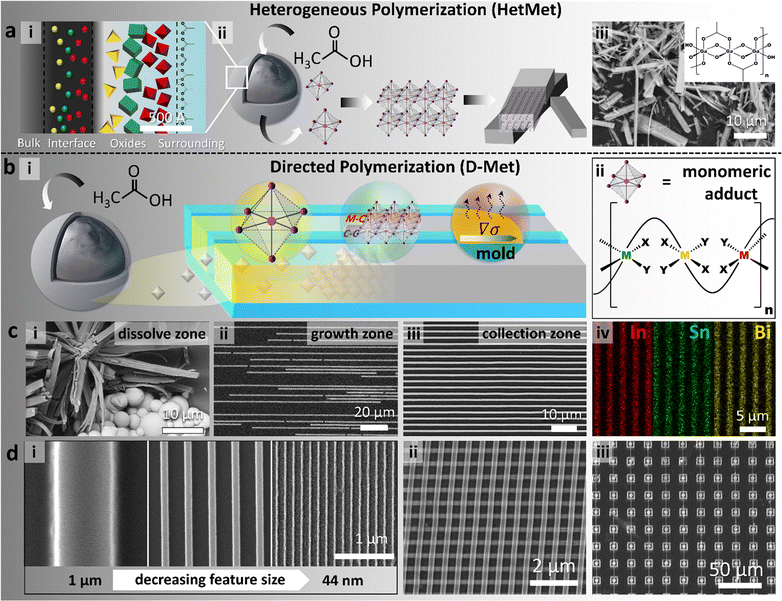 | ||
| Fig. 1 Schemes and data summary on the directed metal ligand reaction (D-Met). (a) Schematic illustration of the HetMet reaction using liquid metal particles (ii) as metal ion reservoirs, with speciation (i) in the passivating oxide governing order of release. Using gallium-rich alloys, the hydroxyacetate polymer self assembles in situ (ii) into wires (red = metal and purple = oxygen from the ligand) that are stochastically precipitated (iii). Inset: the structure of the gallium polymer showing interloping acetate ligands.38 (b) Schematic of the directed HetMet reaction (D-Met) exploits fluid dynamics and evaporation (Marangoni convection) in a confined channel to direct the assembly process away from the etch zone (i). (ii) For clarity, the monomeric adduct and resulting mixed-metals (red, green and yellow) polymeric structure analogous to (aiii) when the oxide shell is rapidly etched. (c) Experimental data showing the: (i) dissolve zone, precipitates akin to Hetmet, (ii) growth zone shows incomplete wire formation, and (iii) collection zone where wires are fully formed. (iv) Elemental mapping of arrays formed from undercooled metal alloy particles showed a homogenous distribution of three metal elements. (d) Wires derived from D-met range from: (i) nm–mm in size, (ii) ordered hierarchical multi-layers, and (iii) complex patterns. | ||
Exploiting the partial miscibility of organometallic adducts in aqueous media, steady-state kinetics ad-infinitum living polymerization was demonstrated using liquid metal particles as an infinitely large metal ion reservoir – the so-called HetMet reaction (Fig. 1a).38 This reaction led to the synthesis of ultra-large high aspect ratio self-assembled beams that were then thermally translated to graphitic-carbon-coated metal oxides with tuneable band gaps.39 Analogously, using ULMCS particles but confining the reaction in a thin liquid layer (droplet), both the localization and morphology of precipitates were controlled.32 Herein, we extend the above work by coupling the HetMet reaction with confinement and fluid dynamics to separate metal particles (ion source) from the self-assembling adducts (abbreviated as the D-Met process. Fig. 1(bi)). Restricting the dimensions of the growing adducts based on channel dimensions as well as exploiting Taylor dispersion and Marangoni flow allows us to control both the nucleation point and the rate of ion transport to the growing seed.
Results and discussion
To illustrate this ansatz, undercooled Field's metal particles (51 wt% In, 36.5 wt% Bi and 12.5 wt% Sn) were chosen as the exemplar material. ULMCS Field's metal particles were synthesized by the shearing liquid into complex particles (SLICE) method with an average diameter of 1.93 ± 1.13 μm.40 A homogenous distribution of In, Sn and Bi in the particles indicated its undercooled amorphous state (Fig. S1, ESI†). The particles were deposited on one edge of a polydimethylsiloxane template (PDMS). Introducing an acid–base pair (aqueous acetic acid) on the particles etches and chelates metal ions from the surface to give hydroxy-acetate ‘monomeric’ adducts (Fig. 1bi and ii). As previously shown,38 solubilized hydroxyacetates in situ oligomerize and, if not dispersed into the channel, stochastically precipitate around the particles (Fig. 1ci, dissolve zone). By placing ULMCS particles close to the channel inlet, Jurin's law dictates that when the liquid is poured over, rapid filling of the channel would occur with concomitant transport of the etched hydroxyacetate adducts/monomer.41 Due to high shear associated with rapid filling of the channels, Taylor dispersion drives the enrichment of formed adducts towards the end of the channel to form a seed that grows to a desired wire (Fig. 1ciii, collection zone). Adventitious precipitation along the channel can also initiate nucleation (Fig. 1cii, growth zone); however, this being a living polymerization reaction,38 we anticipate these nucleates to continue growing and merge with the growing beams from the collection zone. From energy dispersive X-ray spectroscopy (EDS), obtained arrays were composed of homogenously distributed metal organic compounds due to the usage of alloys as the metal ion source (Fig. 1civ). Evaporation, coupled with a decrease in the adduct concentration due to precipitation, leads to a surface tension gradient, ∇σ, across the liquid–air interface, which triggers Marangoni flow inside the channel following the modified Navier–Stokes equation (eqn (1) – assuming laminar flow and no external body force):| n·T·t = −t·∇σ | (1) |
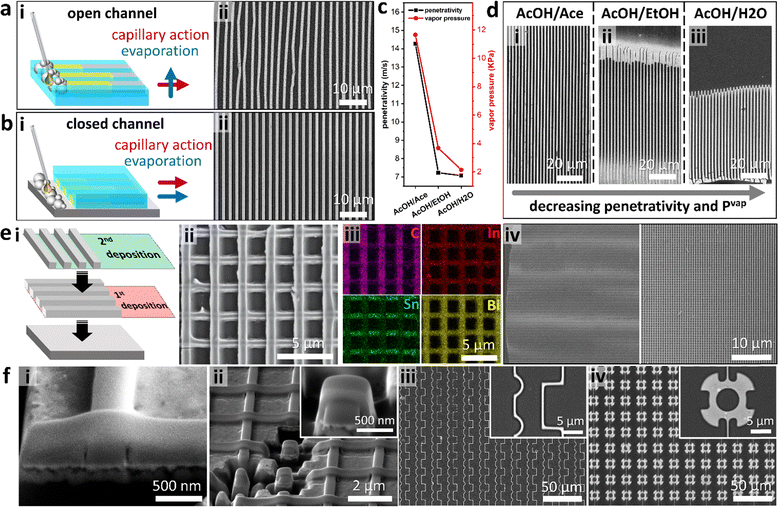
From the above discussion, we inferred that by controlling evaporation, hence the flow vector related to Marangoni convective flow, the wire array morphology could be tuned. First, we investigated the role of the direction of evaporation. When the D-Met reaction was performed directly on a PDMS mold, the directions of solvent evaporation and capillary action were perpendicular (referred to as open channel growth, Fig. 2a). Their high Reynolds number led to turbulent flow inducing deformation and non-uniformity in the size of the wires. When the grating was flipped, however, evaporation and capillary action were aligned (referred to as closed channel growth, Fig. 2b). Inducing coherence in the fluidic shear, evaporation, and associated Marangoni flow, the nucleation point is pinned to the edge of the channel (Taylor dispersion), hence uniform periodic wire arrays were obtained (Fig. 2b). By closing the channel, we significantly lower the associated Reynolds number (Re) triggering laminar flow, hence uniformity. In this configuration, the liquid–solid contact line is directly pinned on the substrate with the nucleate being deposited in its vicinity. Considering its robustness in fabricating high-quality arrays, the closed channel method was adopted for the rest of the study.
To understand the role of solvent properties on wire morphology, we compared three polar solvents with different vapor pressures. Solutions of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratios of acetic acid (AcOH) were prepared with acetone (AcOH/Ace), ethanol (AcOH/EtOH), and water (AcOH/H2O). After applying the respective solution on Field's metal particles, the channels rapidly filled with the liquid based on Washburn penetrativity (p, m s−1):42
1 volume ratios of acetic acid (AcOH) were prepared with acetone (AcOH/Ace), ethanol (AcOH/EtOH), and water (AcOH/H2O). After applying the respective solution on Field's metal particles, the channels rapidly filled with the liquid based on Washburn penetrativity (p, m s−1):42
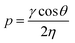 | (2) |
Coupling the low miscibility of metal oxides in polar solvents and capillary effects, we inferred that the D-Met process can be used to fabricate hierarchical layered arrays. To demonstrate hierarchical assembly, the first layer of an array is deposited and then calcined at 600 °C to form oxides; then, a second layer of the wire array is deposited on top of the 1st layer to create an orthogonal array (Fig. 2ei). This process generates a uniform layered grid array (Fig. 2eii), of which the elemental mapping is analogous to that of a single layer albeit with less carbon signals from the 1st layer due to calcination (Fig. 2eiii). As expected, the large-area fabrication of both single- and multi-layer arrays is feasible given the simplicity of D-Met (Fig. 2eiv). Using fast ion bombardment (FIB) to cut a cross-section of the intersection points on the 2-layer nanowire structures revealed conformal contact (Fig. 2fi). For brevity, we show that these cross-sections can be isolated into free standing units structurally analogous to some FinFet morphologies (Fig. 2fii). Other deposition modifications of a single layer can be achieved through careful mold design and/or controlled fluid flow to enable the generation of complex single layers. Here, we demonstrate deposition of patterns with right angle corners, curvatures, as well as micro-rotor mimicking designs (Fig. 2fiii and iv). This D-Met approach can therefore be used to create structures analogous to current technologies.
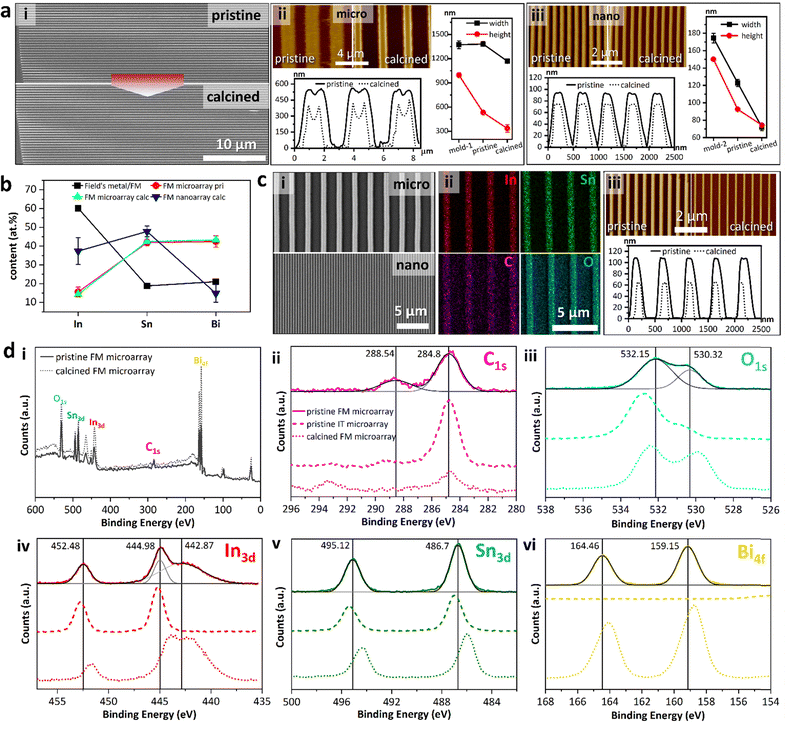
A major advantage to HetMet was the transformation of the organometallic ligand into graphitic carbon leading to tuneable bandgap metal oxides. The wire array morphology, however, might be damaged by heat treatment. Thus, we studied the array morphology change before and after aerobic calcination. The pristine Field's metal array possesses a sharp-edged feature with an aspect-ratio of up to a thousand (Fig. 3a pristine). After 1-hour calcination at 600 °C, the wires remained continuous with minor structural defects (Fig. 3a calcined). Atomic Force Microscopy (AFM) revealed a trapezoid shape of pristine microwires with averages of 1381.50 ± 29.15 nm in width (w) and 531.63 ± 17.94 nm in height (h), which were reduced to 1168.58 ± 26.88 nm and 334.43 ± 46.88 nm after the heat treatment, respectively (Fig. 2aii). Apart from a decrease in the cross-section area, the dips at the top centre of the pristine wire were intensified by heat (Fig. 2aii). Despite severe volume shrinkage caused by heat (46.79% assuming constant wire length), continuity preservation of D-Met arrays indicated unique self-assembly microstructures, which phenomenon is prominent for nano-arrays.38 We observe that the wider the wires, the more deformed they get with a significant increase in buckling. Using a smaller mold leads to lower discrepancies in beam to mold dimensions. When the mold channel dimensions are <200 nm (h = 174 nm and w = 150 nm), wires showed >70% match (h = 92 nm and w = 122 nm). Upon calcination, these narrower wires lost 24% and 43% in h and w, respectively (Fig. 3aiii).
Elemental mapping in Field's metal pristine arrays revealed homogenous distribution across both micro- and nanowires (Fig. S4, ESI†). To further investigate the composition, the ratio of different elements, relative to the alloy, were evaluated. From Field's metal (%atomic 60.1% In, 18.8% Sn and 21.1% Bi translating to %wt 51% In, 16.5% Sn and 32.5% Bi) for clarity, we discuss the composition in atomic %. Microwire arrays bearing %at composition: 15.6% In, 41.9% Sn, and 42.5% Bi were realized from Field's metal (Fig. 3b). The post-reaction particle composition was 60% In, 19% Sn and 21% Bi in line with the asymmetric etching of the components. Calcination of microwire arrays did not significantly change the composition (14.3% In, 42.4% Sn, and 43.3% Bi). For calcined Field's metal nanoarrays the atomic ratios for In, Sn and Bi were 37.4%, 47.8%, and 14.8% (Fig. 3b), respectively. We inferred that for narrower channels, the surface rich species of undercooled Field's metal particles (In and Sn) would be enriched in the obtained array as less etching of the particle was required to fill the channel compared to the micro-channels. Thus, potential control of the array composition could be achieved by careful etching. To confirm the observations above, analogous studies were repeated with undercooled indium tin (IT) particles (Fig. 3c). Both micro- and nanowire arrays were fabricated (Fig. 3ci), with uniform distribution of In, Sn, C and O.
The arrays were further characterized using the X-ray photoelectron spectrum (XPS) to investigate the electronic states of elements. The survey spectra confirmed the existence of In, Sn, Bi, C and O in both pristine and calcined arrays, with a decrease in the C signal intensity confirming the carbon loss (Fig. 3di). For pristine Field's metal microarrays, the C 1s peak at 288.54 eV was attributed to the acetate (Fig. 3dii).43 Two oxygen species are observed (Fig. 3diii) that we attribute to the acetate and bridging hydroxyls (Fig. 1aiii). Three In3d peaks were observed at 452.48, and 444.98 eV – with Bi 4d appearing as a shoulder at 442.87 eV (Fig. 3div). The arrays show In 3d5/2 peaks at slightly higher binding energies (444.98 eV and 442.87 eV) than In2O3 (444.30 eV). A broad peak at a lower binding energy grows with calcination indicating a shift to a more reduced environment.44 Sn 3d was observed at 495.12 eV and 486.70 eV, while Bi 4f peaks occurred at 164.46 eV and 159.15 eV (Fig. 3dv and vi).45,46 Analogous analysis of pristine indium tin microarrays showed In 3d5/2 peaks, albeit with the absence of the Bi3d peak at 442.87 eV (Fig. 3div). To further support the above observations, the XPS spectra of calcined FM microarrays were obtained. For all the metallic species, heat treatment induced shifts in their binding energies towards lower binding energies. Powder X-ray diffraction (PXRD) analysis of pristine arrays showed sharp peaks at the low 2θ indicating order (Fig. S5, ESI†).
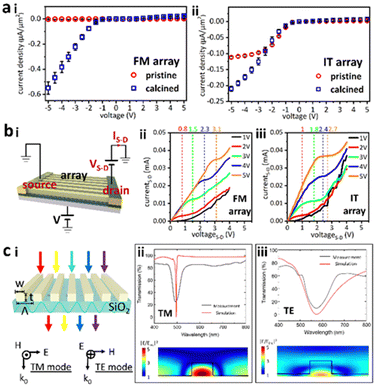
Conductivity of the arrays was then measured using two Au probes (Fig. S6, ESI†). Fig. 4ai shows the poor conductivity of pristine Field's metal microwires (expanded in Fig. S7, ESI†) making it challenging to accurately calculate their resistance. For calcined wires, the positive bias conductivity is very poor, while the negative bias resistance, R− = 4.56 × 10−2 Ω m, indicates a significant increase in charge transport. Pristine arrays from InSn particles had R− = 4.48 × 10−2 Ω m that decreased to R− = 2.22 × 10−2 Ω m when calcined (Fig. 4aii). The asymmetric conductance indicates a diode-like behaviour. To further explore this anisotropic conductance, a three-terminal field emission transistor (FET) was fabricated using the calcined wire array (Fig. 4bi). Under 1 V bias, increasing the source–drain voltage VS–D from 0 to 5 V induced an enhancement of the source–drain current IS–D following the half-exponential function. When V was set to 2 V, however, a platform formed in the IS–D–VS–D curve, which is indicative of transistor characteristics. This platform became more defined with an increase in V (Fig. 4bii). Calcined wires made from InSn particles showed a similar behavior to their Field's metal congeners, albeit with a smaller estimated threshold voltage i.e., Field's metal wires = 1.467 V vs. InSn wires = 1.267 V (Fig. 4biii).
To illustrate the potential of wire arrays in optics, an optical filter was built by fabricating pristine nanowire arrays from InSn particles onto a glass substrate (Fig. 4ci). The refractive index of the above arrays was 1.72–1.82, and an extinction coefficient in the range 0–0.09, from the 400 nm to 500 nm range (Fig. S8, ESI†). The observed refractive index was larger than that of both glass (1.5) and air (1.0) and thus satisfied the requirements for guided mode generation.47 When light incident on the sample was polarized in the transverse magnetic (TM) direction, the transmission spectrum showed a dip at 580 nm (Fig. 4cii). A transverse electric (TE) wave caused a similar transmission dip at 500 nm albeit with a larger dip width compared to the TM wave (Fig. 4ciii). The measured transmittance spectra aligned with simulation results, indicating great field trapping and enhancement inside the wire arrays (Fig. 4cii and iii).
Experimental
Synthesis of undercooled liquid metal core–shell particles
Particles were synthesized as previously reported.48 For Field's metal particles, the metal (10 g) and diethylene glycol (200 mL) were placed in a Cuisinart® (SBC-1000FR) soup maker and heated to ca. 118 °C using the built-in base heater and heating tape wrapped around the soup maker jug. Then, 2 mL glacial acetic acid was added to the blender and the mixture was sheared at ∼9000 rpm (setting 2) for 10 minutes. The resulting suspension was quenched in ethanol and allowed to equilibrate under ambient conditions. The slurry was then filtered using a Buchner funnel with a Whatman GF/F filter. The filtered particles were washed with copious amounts of ethanol, followed by an ethyl acetate rinse. The remaining particles were then harvested and stored in ethyl acetate. For InSn particles, the eutectic InSn alloy was made by mixing 10.20 g indium metal into 12.05 g molten tin, and then the alloy was cooled down to room temperature. For particle synthesis, a mixture of the 4.32 g InSn alloy, 200 mL of diethylene glycol and 1.04 g of trichloroacetic acid was preheated to 140 °C on a hot plate. After immediately transferring to a tilted Cuisinart® (SBC-1000FR) soup maker, the mixture was sheared at a speed of ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm (setting 4) for 4 minutes. The obtained particles were filtered following the same procedure as for Field's metal particles.
000 rpm (setting 4) for 4 minutes. The obtained particles were filtered following the same procedure as for Field's metal particles.
Fabrication of pristine arrays by D-Met
The AcOH/Ace activation agent applied in the D-Met process was prepared by mixing 5 mL glacial acetic acid with 5 mL acetone. AcOH/EtOH and AcOH/H2O were prepared following the same method but by replacing acetone with ethanol and deionized water, respectively. For open channel growth, the undercooled metal particle solution (ca. 1 μL) was dropped on one end of a polydimethylsiloxane (PDMS) grating with a micropipette. Then, ∼0.1 mL of the agent was deposited onto the deposited particles using a plastic pipette. Grating channels were filled with the liquid automatically. The samples were kept in ambient for ∼30 minutes until the agent dried completely. This flux-and-dry procedure was repeated two more times. Then, a substrate (Si or glass) attached by two-sided carbon tape was placed onto the above PDMS grating. After picking the grating up with tweezers, the obtained wire array was transferred onto the substrate. For wires fabricated by the close channel method, the undercooled metal particle solution (ca. 1 μL) was deposited on substrates (Si or glass). Then, the PDMS grating with channels facing down was positioned near the deposited particles. One droplet (0.1 mL) of the activation agent was dropped onto the particles and completely dried in ambient before two more flux-and-dry cycles were carried out. Then, the template was removed with the array formed directly on the substrate and was ready to use.Heat-treatment of pristine arrays
For heat-treatment, obtained pristine D-Met arrays were placed in muffle furnace (KSL1200-X, MTI Corp.) in an ambient atmosphere. The furnace was set at a ramping rate of 10 °C min−1, kept at 600 °C for an hour and then cooled down to room temperature.Fabrication of 2-layer structures
For 2-layer grid fabrication, the first layer array was produced and calcined by following above close-channel growth and heat-treatment procedures. Then, another 1 μL of undercooled metal particle solution was deposited on the same substrate, and a PDMS template was flipped onto the 1st layer with desired interlayer angles. After repeating the close-channel growth, a 2-layer structured grid array was obtained.Conductivity measurement
Two eutectic gallium indium (EGaIn) liquid metal droplets (ca. 0.04 μL) were deposited 1 mm apart onto wires along their length and served as electrodes. A Keithley 6430 Sub-Femtoamp Remote Sourcemeter was connected to the electrodes and cycling voltage (V) from −5 V to 5 V with a 0.5 V step was applied while the current (I) was recorded. A hundred I–V cycles were recorded for reaching a steady state. The conductivity setup photo was taken with a ME520TA reflective microscope.Construction of a simplified back gate field-effect transistor (FET)
A back-gate FET was constructed by connecting gold electrodes to ends of wire arrays as the source and drain electrodes. A Si substrate was used as the back-gate electrode and the intrinsic SiO2 layer on the Si substrate served as the dielectric in the FET device. A 1 to 5 V voltage was applied on the Si substrate. Under each applied voltage, the current between the source and drain was recorded versus the source-gate voltage changed from −4 to +4 V in a step of 0.1 V. The measurement was done using an HP 4155B semiconductor analyzer with a probe station.Transmission spectrum measurement
The transmission spectra of pristine arrays on glass were measured using a homebuilt device. After mounting the sample on a stage, collimated broadband light (HL-2000, OceanOptics) was applied as the light source and shone vertically on the sample. Transmitted light was collected by fiber and analyzed with an OceanOptics USB2000 spectrometer.Conclusions
By directing and confining the HetMet reaction with channels (abbreviated as D-Met), we demonstrate a robust method to autonomously organize mixed-organometallic wire arrays. The precursor organometallic, and hence metal oxide, arrays form with great structural and compositional fidelity, the latter dictated by bulk plasticity and speciation on the liquid metal oxide shell. From this work, we demonstrate that: (i) the morphology of the obtained array can be tuned by coupling fluid dynamics to surface reaction (etching) and/or self-assembly kinetics. Aligning the direction of the capillary pressure, fluidic shear, and solvent evaporation results in the deposition of high-quality wire arrays. Washburn penetrativity (p) and vapor pressure (Pvap) of the solvent significantly affect the wire morphology as larger p or Pvap gave longer wires albeit with a higher defect density. Exploiting capillarity (bridges and wetting) in D-Met enables hierarchical multilayer arrays as well as the fabrication of complex shapes. (ii) Aerobic calcination transformed pristine organometallic nanowires into respective semiconducting oxides. The wires remain continuous despite a significant volumetric change on calcination in part due to the proximal sintering of the evolving adducts. (iii) The fabricated arrays are good synthons for fabricating diodes and gates, suggesting that liquid metal particles can be used to address challenges in semiconductor arrays and microelectronics fabrication. The observed FET properties render these arrays ideal candidates for microelectronics. Coupled with a high refractive index and low extinction coefficient, these arrays are ideal for guided mode resonance devices and can be extended into waveguides given the asymmetric response in the TM and TE modes. The simplicity and low-cost nature of this method renders it ideal for large area patterning of components that can later be isolated and integrated elsewhere.Author contributions
JC and MT designed experiments; JC and MT curated the data; ML, LW, CD, and JC performed characterization, and MT supervised and raised funds for the project. All authors participated in writing the manuscript.Data availability
Authors confirm that data supporting this work are available within the article or its ESI.† A copy of the data supporting the findings herein are available from the principal investigators, [ML (electrical) and MT (all)], upon reasonable request.Conflicts of interest
Authors declare no conflict of interest.Acknowledgements
This work was supported in part by North Carolina State University, Iowa State University (patent loyalty funds), and by the National Science Foundation under Award No. 2243104.References
- V. Zhirnov, Decadal Plan for Semiconductors: New Compute Trajectories for Energy-Efficient Computing, Sandia National Lab., Albuquerque, NM, 2020 Search PubMed.
- S. Kasani, K. Curtin and N. Wu, Nanophotonics, 2019, 8, 2065–2089 Search PubMed.
- N. I. Zheludev and Y. S. Kivshar, Nat. Mater., 2012, 11, 917–924 CrossRef CAS.
- M. M. Waldrop, Nature, 2016, 530, 144–148 CrossRef CAS PubMed.
- L. F. Thompson, C. G. Willson and M. J. Bowden, Introduction to Microlithography, ACS Publications, 1983 Search PubMed.
- A. Alvarez-Fernandez, C. Cummins, M. Saba, U. Steiner, G. Fleury, V. Ponsinet and S. Guldin, Adv. Opt. Mater., 2021, 9, 2100175 Search PubMed.
- W. Dong, Y. Zhang, C. Yi, J. J. Chang, S. Ye and Z. Nie, ACS Nano, 2023, 17, 3047–3054 CrossRef CAS PubMed.
- N. Liu and T. Liedl, Chem. Rev., 2018, 118, 3032–3053 Search PubMed.
- C. Yi, H. Liu, S. Zhang, Y. Yang, Y. Zhang, Z. Lu, E. Kumacheva and Z. Nie, Science, 2020, 369, 1369–1374 CrossRef CAS PubMed.
- W. T. Chen, A. Y. Zhu, V. Sanjeev, M. Khorasaninejad, Z. Shi, E. Lee and F. Capasso, Nat. Nanotechnol., 2018, 13, 220–226 CrossRef CAS PubMed.
- J. Li, P. Yu, S. Zhang and N. Liu, Nano Lett., 2020, 20, 6845–6851 CrossRef CAS PubMed.
- J. Geng, W. Yan, L. Shi and M. Qiu, Light: Sci. Appl., 2022, 11, 189 CrossRef CAS PubMed.
- M. Guo, Z. Qu, F. Min, Z. Li, Y. Qiao and Y. Song, InfoMat, 2022, e12323 CrossRef CAS.
- J. Henzie, J. E. Barton, C. L. Stender and T. W. Odom, Acc. Chem. Res., 2006, 39, 249–257 CrossRef CAS PubMed.
- M. H. Lee, M. D. Huntington, W. Zhou, J.-C. Yang and T. W. Odom, Nano Lett., 2011, 11, 311–315 Search PubMed.
- D. Qin, Y. Xia and G. M. Whitesides, Nat. Protoc., 2010, 5, 491 Search PubMed.
- V. Flauraud, M. Mastrangeli, G. D. Bernasconi, J. Butet, D. T. Alexander, E. Shahrabi, O. J. Martin and J. Brugger, Nat. Nanotechnol., 2017, 12, 73–80 CrossRef CAS PubMed.
- Q.-Y. Lin, J. A. Mason, Z. Li, W. Zhou, M. N. O’Brien, K. A. Brown, M. R. Jones, S. Butun, B. Lee and V. P. Dravid, Science, 2018, 359, 669–672 CrossRef CAS PubMed.
- F. Yang, Q. Chen, J. Wang, J. J. Chang, W. Dong, W. Cao, S. Ye, L. Shi and Z. Nie, ACS Nano, 2022, 17, 725–734 Search PubMed.
- J. Hasler, Proc. IEEE, 2020, 108, 1283–1302 Search PubMed.
- Y. Pu, C. Shi, G. Samson, D. Park, K. Easton, R. Beraha, A. Newham, M. Lin, V. Rangan, K. Chatha, D. Butterfield, I. Member and R. Attar, IEEE J. Solid State Circ., 2018, 53, 936–948 Search PubMed.
- A. Zhou, S. R. Santacruz, B. C. Johnson, G. Alexandrov, A. Moin, F. L. Burghardt, J. M. Rabaey, J. M. Carmena and R. Muller, Nat. Biomed. Eng., 2019, 3, 15–26 CrossRef CAS PubMed.
- L.-Q. Chen, MRS Bull., 2019, 44, 520–523 CrossRef.
- R. N. Sodhi, P. Brodersen, L. Cademartiri, M. M. Thuo and C. A. Nijhuis, Surf. Interface Anal., 2017, 49, 1309–1315 CrossRef CAS.
- A. Martin, B. S. Chang, A. M. Pauls, C. Du and M. Thuo, Angew. Chem., 2021, 133, 5993–6000 CrossRef.
- A. Martin, C. Du, B. Chang and M. Thuo, Chem. Mater., 2020, 32, 9045–9055 Search PubMed.
- L. Cademartiri, M. M. Thuo, C. A. Nijhuis, W. F. Reus, S. Tricard, J. R. Barber, R. N. Sodhi, P. Brodersen, C. Kim, R. C. Chiechi and G. M. Whitesides, J. Phys. Chem. C, 2012, 116, 10848–10860 CrossRef CAS.
- B. S. Chang, R. Tutika, J. Cutinho, S. Oyola-Reynoso, J. Chen, M. D. Bartlett and M. M. Thuo, Mater. Horiz., 2018, 5, 416–422 RSC.
- A. Martin, B. S. Chang, Z. Martin, D. Paramanik, C. Frankiewicz, S. Kundu, I. D. Tevis and M. Thuo, Adv. Funct. Mater., 2019, 29, 1903687 CrossRef.
- A. Martin, B. Chang, J. Cutinho, L. Shen, T. Ward, E. W. Cochran and M. M. Thuo, Mater. Horiz., 2021, 8, 925–931 Search PubMed.
- J. J. Chang, A. Martin, C. Du, A. M. Pauls and M. Thuo, Angew. Chem., Int. Ed., 2020, 59, 16346–16351 CrossRef CAS PubMed.
- J. J. Chang, C. Du, A. Pauls and M. Thuo, Angew. Chem., Int. Ed., 2021, 60, 13929–13936 Search PubMed.
- B. J. Carey, J. Z. Ou, R. M. Clark, K. J. Berean, A. Zavabeti, A. S. Chesman, S. P. Russo, D. W. Lau, Z.-Q. Xu and Q. Bao, Nat. Commun., 2017, 8, 14482 Search PubMed.
- J. Lin, Q. Li, T.-Y. Liu, Y. Cui, H. Zheng and J. Liu, Phys. Status Solidi RRL, 2019, 13, 1900271 CrossRef.
- N. Syed, A. Zavabeti, J. Z. Ou, M. Mohiuddin, N. Pillai, B. J. Carey, B. Y. Zhang, R. S. Datta, A. Jannat and F. Haque, Nat. Commun., 2018, 9, 3618 Search PubMed.
- J. Cutinho, B. S. Chang, S. Oyola-Reynoso, J. Chen, S. S. Akhter, I. D. Tevis, N. J. Bello, A. Martin, M. C. Foster and M. M. Thuo, ACS Nano, 2018, 12, 4744–4753 Search PubMed.
- A. Martin, W. Kiarie, B. Chang and M. Thuo, Angew. Chem., Int. Ed., 2020, 132, 360–365 CrossRef.
- B. S. Chang, B. Thomas, J. Chen, I. D. Tevis, P. Karanja, S. Çınar, A. Venkatesh, A. J. Rossini and M. M. Thuo, Nanoscale, 2019, 11, 14060–14069 Search PubMed.
- B. S. Chang, A. Martin, B. Thomas, A. Li, R. W. Dorn, J. Gong, A. J. Rossini and M. M. Thuo, ACS Mater. Lett., 2020, 2, 1211–1217 CrossRef CAS.
- I. D. Tevis, L. B. Newcomb and M. Thuo, Langmuir, 2014, 30, 14308–14313 Search PubMed.
- P.-G. Gennes, F. Brochard-Wyart and D. Quere, Capillarity and wetting phenomena, Springer, New York, 2004 Search PubMed.
- E. W. Washburn, Phys. Rev., 1921, 17, 273 Search PubMed.
- H. K. Nguyen, R. Addou, K. C. Chukwu, G. S. Herman and L. Árnadóttir, J. Phys. Chem. C, 2023, 127, 11472–11480 Search PubMed.
- G. Hollinger, R. Skheyta-Kabbani and M. Gendry, J. Phys. Rev. B, 1994, 49, 11159 CrossRef CAS PubMed.
- M. A. Stranick and A. Moskwa, SnO2 by XPS, 1993.
- T. P. Debies and J. W. Rabalais, Chem. Phys., 1977, 20, 277–283 Search PubMed.
- G. Quaranta, G. Basset, O. J. Martin and B. Gallinet, Laser Photonics Rev., 2018, 12, 1800017 CrossRef.
- S. Çınar, I. D. Tevis, J. Chen and M. Thuo, Sci. Rep., 2016, 6, 21864 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh01177e |
| ‡ Current address: University of Virginia, Department of Mechanical and Aerospace Engineering, Charlottesville, VA 22904, USA. |
| This journal is © The Royal Society of Chemistry 2025 |