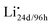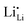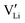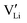Is the single-ion conductor cubic Li₇La₃Zr₂O₁₂ a binary ionic electrolyte?

Abstract

Garnet-type cubic Li₇La₃Zr₂O₁₂ (c-LLZO) is a single-ion conductor, but the dynamics of lithium dendrite initiation during one-way plating in Li|c-LLZO|Li symmetric cells demonstrate several trends that all resemble the dendrite initiation mechanisms found in binary liquid electrolytes. This Opinion article provides an analysis of the possible charge carriers and discusses the four species that coexist in c-LLZO when continued electrochemical reactions take place at the opposite interfaces of the ceramic electrolyte. The new understanding explains the possibility of significant concentration polarization before the onset of dendrites in c-LLZO, without violating commonly accepted rules and physical laws. We conclude that under Faradaic reaction conditions, c-LLZO is a binary ionic electrolyte with as the positive charge carrier and 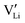the negative charge carrier, among native but neutral Li^×_Li and V^×_Li. Li ions are still the sole conducting ion, but the electrochemically generated Li vacancies significantly alter the long-range transport behavior, rendering the single-ion conductor a binary electrolyte.

---

Introduction

Garnet-type cubic Li₇La₃Zr₂O₁₂ (c-LLZO) is one of the most promising solid-state electrolytes¹ that holds the promise to enable anode-free Li metal batteries toward a higher energy density by removing the intercalation anodes, a longer cycle life by limiting ion leaching from cathodes, and enhanced safety by replacing flammable nonaqueous electrolytes and physically blocking hazardous Li dendrites. However, Li dendrite penetrations were still encountered in c-LLZO. In most reports, the critical current density² (CCD) that may induce dendrite penetration is lower than 1 mA cm⁻² for 1-mm-thick pellets, with only a few exceptions of thin-film samples, in which the CCD can reach 10 mA cm⁻². By far, dendrites in c-LLZO are being understood mainly from the defects and solid mechanics perspective. Transport-based mechanisms that have been verified in binary liquid electrolytes were rejected by the prevailing belief that single-ion conductors with a transference number near unity do not allow long-range concentration polarization. However, defects- and mechanics-based models cannot provide a satisfactory explanation for the observed thickness dependence, where thinner LLZO electrolytes allow higher CCDs and higher areal capacities. Still, micron-thick lithium phosphorus oxynitride (LiPON) electrolytes are known to work for thousands of cycles without dendrite penetration even at high current densities.³ This thickness dependence, while might be correlated with other causes, can be explained by the long-range transport mechanisms. Systematic experiments using classical electroanalytical techniques with hundreds of highly consistent c-LLZO miniature samples indeed revealed possible transport limitations in c-LLZO at the onset of dendrite penetration, where mechanical factors were excluded via control experiments.^4,5 The key question is: what are the charge carriers in the single-ion conductor c-LLZO to physically justify such similarities between single-ion-conducting solid electrolytes and binary liquid electrolytes?

Different from the thermodynamic analyses of native defects and possible charge carriers,^6,7 this Opinion article examines the scenario when continued electrochemical reactions take place at the opposite interfaces of the ceramic electrolyte. The new understanding helps resolve a few critical questions about the dendrite initiation in c-LLZO, without violating commonly accepted rules and physical laws. We conclude that under Faradaic reaction conditions, c-LLZO is a binary electrolyte with as the positive charge carrier and the electrochemically generated as the negative charge carrier, among native but neutral Li^×_Li and V^×_Li. The electrochemically generated charged vacancies have an ionic origin, as they are the uncompensated charges from the surrounding ions when Li ions are stripped away from these equilibrium positions. While Li ions are still the sole conducting ion, the presence of these effective negative charges makes c-LLZO a binary electrolyte.

Equilibrium versus electrochemically generated charged vacancies

Pioneering works⁸ have confirmed the space group Ia3̄d (no. 230) for the highly conductive c-LLZO. Using the data from Awaka et al.,⁹ a unit cell is constructed and displayed in Fig. 1a, where the available Li sites (24d and 96h) form continuous pathways that weave through the crystal along the channels defined by ZrO₆ octahedra and LaO₈ dodecahedra. For clarity, Fig. 1b displays only the available Li sites to reveal the complex 3-dimensional (3D) network, which allows high ionic flux densities during Li transport.

Fig. 1 Crystal structure of cubic Li₇La₃Zr₂O₁₂. (a) Display of the unit cell where LaO₈ dodecahedra and ZrO₆ octahedra define the Li sites and possible transport channels for Li ions. (b) Li ion sites in the cubic unit cell form a 3D network. Gold spheres are 24d sites. Pair-wise pink spheres are 96h sites. (c) Positions of Zr ions in the cubic unit cell. In this 8 per-formula-unit (pfu) unit cell of Li₇La₃Zr₂O₁₂, only 56 out of 120 available Li sites are occupied by Li ions, yielding an occupancy of only 46.7% and allowing facile Li transport.

It must be pointed out that not all 120 Li sites shown in Fig. 1b are occupied by Li ions. For the 8-per-formula-unit (8-pfu) c-LLZO unit cell, only 56 Li ions from Li₇La₃Zr₂O₁₂, or 52 Li ions from the Ta-doped LLZO (Li_6.5La₃Zr_1.5Ta_0.5O₁₂), will be distributed onto these 120 sites. Using the Kröger–Vink notation for species inside the crystal structure, we will have 56 Li ions on Li sites which appear as neutral Li^×_Li, and 64 unoccupied Li sites appear as neutral V^×_Li. In the case of Li_6.5La₃Zr_1.5Ta_0.5O₁₂, there will be 52 Li ions on Li sites (Li^×_Li), 4 Ta⁵⁺ ions on 4 Zr-sites which show one positive charge ; and 4 charged vacancies on 4 nearby Li-sites (due to local charge balance) which show one negative charge . Here, superscript × means no apparent charge, superscript ˙ means one positive charge, and the superscript prime means one negative charge. Subscript Li (or Zr) means the intrinsic crystallographic site for Li (or Zr). V is the vacancy or the empty Li-site. For species outside the crystal structure, we use the standard chemical notation with numerical superscripts for ions. The doping reaction can be written as .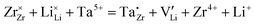

Here, we assume that the and the associated charged vacancy 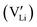are immobile and mainly help stabilize the cubic structure. Their contributions to transport are negligible. Therefore, in the following discussion, we will not discuss the roles of these structural dopants and the associated vacancies. We will only consider a stable cubic LLZO crystal structure, in which 120 Li sites are available for 52–56 Li ions to reside/visit and realize the long-range transport. As we shall see below, the actual number of Li ions at equilibrium does not undermine our analysis and conclusion.

To facilitate the discussion of transport, we can take one-half of the unit cell and “stretch and flatten” the Li-site network into a 2D plot in Fig. 2. The lone circles are 24d sites, while those form contact pairs are 96h sites (between any two 24d sites). Solid spheres represent Li-occupied sites, Li^×_24d or Li^×_96h, both of which are Li^×_Li. Open circles represent unoccupied Li sites, V^×_24d or V^×_96h, both of which may be denoted as V^×_Li. Following the simple argument of Coulombic repulsion, and based on the ab initio molecular dynamics (AIMD) simulations,^10,11 only one Li ion can be accommodated in each pair of the 96h sites. Each Li-occupied 24d site, i.e. Li^×_24d, prevents 4 Li ions from occupying the 4 neighboring 24d sites. Fig. 2a shows two slabs with two possible Li ion configurations in equilibrium. Electroneutrality is achieved locally and globally.

Fig. 2 Schematic of the defects chemistry and mobile charge carriers along the Li transport pathway in c-LLZO. (a) In equilibrium, Li ions are distributed homogeneously in the 24d and 96h sites, forming 4 types of neutral species: Li⁺ ion on 24d Li-site (Li^×_24d) and Li⁺ ion on 96h Li-site (Li^×_96h) are shown as solid blue spheres; vacant 24d Li-site (V^×_24d) and vacant 96h Li-site (V^×_96h) are shown as open blue circles. (b) When the electrochemical driving force is applied, external Li⁺ ions from the positive electrode is pushed into the crystal structure near the positive interface to form (solid pink spheres), while Li⁺ ions on a Li^×_24d/96h is stripped out of the 24d or 96h site near the negative interface to generate (pink open circles). Native defects are shown in blue. Electrochemically generated defects are in pink. Structural ions La, Zr, Ta, and O are omitted for clarity.

Existing analyses on Li transport in c-LLZO were mainly about diffusion in (near) equilibrium conditions, where short-range hopping or cooperative movement occurs within a single unit cell. Investigations on how Li ions diffuse and migrate under realistic working conditions, e.g., when a constant-flux Faradaic reaction boundary condition is implemented at the interface, are very limited. As illustrated in Fig. 2b, when the electrochemical reaction starts, one external Li ion (Li⁺_E) will be pushed into the crystal structure, likely onto an empty neutral Li site V^×_Livia, creating a positive charge among other native neutral Li^×_Li. 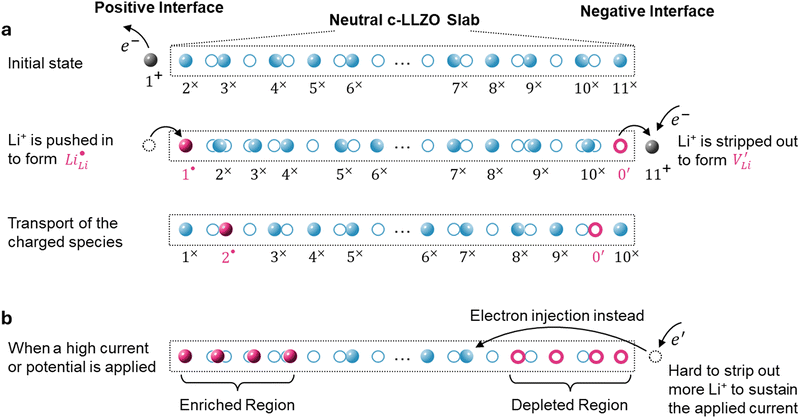Simultaneously at the opposite interface, the interfacial electrochemical potential will dislodge the Li⁺ of the neutral native Li^×_Li to make it an external Li⁺_E, leaving behind an uncompensated charged Li vacancy within the crystal structure, among other native neutral vacancies V^×_Li. This reaction can be written as . Note that these electrochemically generated charged vacancies are different from the structural Li vacancies introduced by and tightly associated with the immobile dopants. The Li⁺_E stripped out from the crystal structure will be reduced into a Li atom at the negative electrode by the electron from the external circuit. The global electroneutrality of LLZO is not violated. As such, despite that c-LLZO is still a single-ion conductor, as no other ions are moving, the existence of the charged Li vacancy and the charged Li ions on Li-site , both from the interfacial faradaic reactions, make c-LLZO a binary electrolyte. As one may immediately reflect, this binary nature determines that the transference number of Li in LLZO will not⁴ be a value close to 1.

Charge distribution near the interface

Having net charges at the ceramic interfaces is perceived to be limited within a very short Debye length λ_D, less than one Ångström,¹² or at most 1–2 nanometers,¹³ due to the very high Li concentration > 40 M in c-LLZO at room temperature. Therefore, the accumulation of charged species in c-LLZO and their migration over long distances are considered not physically probable. However, the widely used Debye length was not derived with a dynamic Faradaic boundary condition. It is always a thermodynamic result, sometimes derived under the assumption of ideally blocking electrodes held at a fixed potential. When a constant-flux Faradaic boundary condition is applied, however, the concentration distribution profiles change significantly according to the Poisson–Nernst–Planck equation.¹⁴ As such, a dynamic space charge region, which is a dynamic diffusion layer (not the diffuse layer used as a synonym for Debye length), will develop and extend toward the bulk of the electrolyte, easily exceeding the thermodynamic Debye length.

Nevertheless, the thermodynamic Debye length still tells the strong screening effects around charged species in c-LLZO. Therefore, we may assume that the charged species within each transport channel are screened from being affected by those in another channel. We can further simplify the schematics to evaluate the scenario in a single Li-ion transport channel in Fig. 3.

Fig. 3 Schematic explanations of (a) the generation and transport of at the positive interface and at the negative interface in a single Li-ion conducting channel, due to the electrochemical transfer of Li⁺ ions across the interfaces; and (b) the scenario of the generation and accumulation of and in high-current conditions.

The transport channel defined by the ZrO₆ and LaO₈ polyhedra is very narrow to fit in just one Li ion in the transverse direction. Along this 1D path, Coulombic repulsion can be adopted to estimate the energy penalty between Li ions. Pushing one external positive Li ion into an equilibrium system is equivalent to shortening the separation distance between two Li ions. Using the simple formula of Coulombic energy , where e is the elementary charge, the permittivity of vacuum, the dielectric constant of c-LLZO, and r the distance. The energy penalty to push two Li ions from an equilibrium separation of 2.7 Å to 1.7 Å is 62.6 meV. According to a recent AIMD simulation of Li dimers in vacuum,¹¹ the energy penalty for shortening the Li–Li separation from 2.7 Å to 1.7 Å is about 1500 meV. Adjusting this energy by dividing it with the dielectric constant of c-LLZO yields a value of 30 meV, close to the simple estimate from Coulombic energy. Although the accurate energy penalty requires rigorous mathematical models and realistic atomistic simulations, our simple estimates presented here are not expected to deviate by an order of magnitude. Our estimates indicate that a voltage difference of 30–60 mV will be enough to push two Li ions to reach a 1.7 Å separation. In practice, pushing in and stripping out Li⁺ in a symmetrical Li|c-LLZO|Li cell can be achieved at overpotentials (voltage differences) much lower than 30 mV. The higher the voltage differences, the more Li ions can crowd into the single channel. The potential energy stored between the crowded Li ions ( and/or Li^×_Li) then serves as the internal driving force to push one another down the 1D channel toward the negative electrode (Fig. 3a).

Symmetrically, Li⁺ will be stripped out from Li^×_Li at the negative interface, generating an equal amount of charged Li vacancies (Fig. 3). These accumulated charge carriers at the opposite interfaces of the c-LLZO, i.e.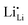 at the positive interface and 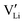at the negative interface, will be driven by the electric field to migrate toward the bulk until recombinations occur via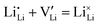. They might also miss each other and co-exist as Frenkel pairs, due to the high density of available channels and strong screening effects between channels. Therefore, these uncompensated charge carriers can travel across a distance much longer than the thermodynamic Debye length. In fact, electron holography¹⁵ and Kelvin probe atomic microscopy¹⁶ experiments have revealed that nonlinear electrical potential profiles (equivalent to the existence of net charges via Poisson's equation) can extend into single-ion conductor ceramic electrolytes for > 1 μm and even across the entire 2 mm sample thickness,¹⁶ when the battery-relevant Faradaic reactions boundary conditions are applied.^15–17 A more recent in situ experiment using a focused ion beam-scanning electron microscope (FIB-SEM) clearly revealed a bowl-shape crack that formed about 10–20 μm below the W-tip working electrode,¹⁸ yet after a certain amount of time when the outward protrusion of lithium whiskers became stalled, indicating the depletion of Li ions at the interface.

Li ion depletion and the aftermaths

As discussed above and schematically explained in Fig. 3, continued electrochemical reactions at the negative interfaces will consume the Li⁺ from the neutral Li^×_Li and produce . The negatively charged vacancies will be repelled by the electric field to move toward the bulk of the c-LLZO. Li^×_Li and will diffuse and migrate toward the negative interface and effectively lower the concentration of . However, if the interfacial reaction rate, i.e. the applied current density, is higher than the transport flux density of Li^×_Li and , the concentration of 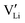near the negative interface will only increase, leading to the complete Li ion depletion in all channels. When there are no positive charges (Li ions) that can be easily stripped outward to sustain the required interfacial current density, the only way for the system to continue the galvanostatic dynamic process is to inject inward negative charges (electrons) into the electrolyte (Fig. 3b). The injection of electrons into a dielectric material will lead to either a very quick or progressive dielectric breakdown, inducing cracks in ceramics¹⁹ or fractal treeing²⁰ in polymers, similar to what have been observed in c-LLZO experiments.

Since the electron injection will only occur when there are no Li ions that can be stripped out at the immediate interface, these electrons will have to travel across a finite thickness of the depleted layer to find Li ions to reduce (Fig. 3b). This behavior explains why remote Li metal nucleation has been found in multiple experiments, but only at high-current conditions.²¹ Different from the liquid electrolyte where both the cations and anions will be depleted to create a nonconductive blanket of electrolyte covering the electrode and result in a divergent voltage response at the Sand's time, the depleted region in c-LLZO still has negative charge carriers that may move locally (Fig. 3b), exhibiting conductivity. This subtle difference explains the lack of the divergent voltage response at the onset of Li dendrite penetration in c-LLZO.^5,22

As can be seen in Table 1, reduction reactions of the Li ions and any other metal ions commonly found in doped c-LLZO will always lead to significant size/volume changes, while brittle ceramic materials cannot sustain a deformation > 5% without forming cracks. This explains why many operando experiments that inevitably employ high local current densities always see cracks accompanying dendrite penetrations. The cracks establish new ceramic|metallic interfaces inside the crystal, along which Li metal continues to plate.

Table 1 Comparisons of ionic and atomic radii and the volume expansion percentage of metal elements²³ commonly found in doped c-LLZO

Element	R ion (Å)	R atom (Å)	R increase (%)	Vol. expansion (%)
Li	0.76 (+)	1.52	100	700.54
La	1.06 (3+)	1.87	76.42	450.20
Zr	0.86 (4+)	1.60	86.05	542.70
	1.00 (2+)	1.60	60	309.07
	0.86 (4+)	1.00 (2+)	16.28	57.22
Ta	0.72 (5+)	1.70	136.11	1222.44
	0.82 (4+)	1.70	107.32	792.64
	0.72 (5+)	0.82 (4+)	13.98	47.72
Nb	0.69 (5+)	1.64	137.68	1238.41
	0.78 (4+)	1.64	110.26	828.64
	0.86 (3+)	1.64	90.70	591.35
	0.69 (5+)	0.78 (4+)	13.04	44.46
Al	0.53 (3+)	1.43	169.81	1239.70
Ga	0.62 (3+)	1.26	103.23	738.71
	0.62 (3+)	1.36 (1+)	119.35	955.46

---

In summary, when the electrochemical reaction takes place at the negative interface, positive Li ions will be stripped out of the c-LLZO, leaving behind electrochemically generated charged vacancies within the c-LLZO. The presence and the long-range transport of these electrochemically generated charged Li vacancies make c-LLZO a binary ionic electrolyte. Similar to the binary liquid electrolyte, if the actual local current density at the negative interface is higher than the ionic flux density coming through the c-LLZO, Li ions will be depleted, which is the root cause of electron injection into the c-LLZO, hence the inward lithium dendrite penetration. To establish a more accurate understanding of this binary transport in c-LLZO, the classical Nernst–Planck equation for binary liquid electrolytes^24–26 needs to be solved with the Poisson's equation,¹⁴ yet taking into account steric effect among the crowded charge carriers at the interface. Further incorporating electrostatic correlations will help capture the coordinated concomitant ion transport for a more realistic understanding. Ultimately, the transport-based understanding tells us that if solid-state electrolytes can be made thin enough (still in high quality), the dendrite penetration can be avoided by avoiding triggering the transport limitation, or equivalently, by avoiding the ion depletion and the electron injection. Performing thickness-dependent experiments on other single-ion conductor ceramic electrolytes, e.g., LATP (Li_1+x+yAl_yTi_2−ySi_xP_3−xO₁₂) and argyrodite sulfide (Li₆PS₅Cl) solid electrolytes, will provide opportunities to further validate the theoretical understanding in this Opinion article, and eventually unify the theory of dendrite initiation in all types of electrolytes.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this Opinion article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by a National Science Foundation Grant (Award No. 2203994). The author thanks Dr. William Chueh and Dr. Ju Li for helpful discussions.

References

1. V. Thangadurai, S. Narayanan and D. Pinzaru, Garnet-type solid-state fast Li ion conductors for Li batteries: critical review, Chem. Soc. Rev., 2014, 43, 4714–4727,  10.1039/C4CS00020J.
2. Y. Lu, et al., Critical Current Density in Solid-State Lithium Metal Batteries: Mechanism, Influences, and Strategies, Adv. Funct. Mater., 2021, 31, 2009925,  DOI:10.1002/adfm.202009925.
3. F. Han, et al., High electronic conductivity as the origin of lithium dendrite formation within solid electrolytes, Nat. Energy, 2019, 4, 187–196,  DOI:10.1038/s41560-018-0312-z.
4. R. Gopal, L. Wu, Y. Lee, J. Guo and P. Bai, Transient Polarization and Dendrite Initiation Dynamics in Ceramic Electrolytes, ACS Energy Lett., 2023, 8, 2141–2149,  DOI:10.1021/acsenergylett.3c00499.
5. R. Gopal and P. BaiIntrinsic Electrochemical Limits Preceding Dendrite Penetration in Ceramic Electrolytes, arXiv, 2024, preprint DOI:10.48550/arXiv.2410.02127.
6. A. G. Squires, D. O. Scanlon and B. J. Morgan, Native Defects and Their Doping Response in the Lithium Solid Electrolyte Li₇La₃Zr₂O₁₂, Chem. Mater., 2020, 32, 1876–1886,  DOI:10.1021/acs.chemmater.9b04319.
7. X. Zhan, S. Lai, M. P. Gobet, S. G. Greenbaum and M. Shirpour, Defect chemistry and electrical properties of garnet-type Li₇La₃Zr₂O₁₂, Phys. Chem. Chem. Phys., 2018, 20, 1447–1459.
8. C. A. Geiger, et al., Crystal Chemistry and Stability of “Li₇La₃Zr₂O₁₂” Garnet: A Fast Lithium-Ion Conductor, Inorg. Chem., 2011, 50, 1089–1097,  DOI:10.1021/ic101914e.
9. J. Awaka, et al., Crystal structure of fast lithium-ion-conducting cubic Li₇La₃Zr₂O₁₂, Chem. Lett., 2011, 40, 60–62.
10. K. Meier, T. Laino and A. Curioni, Solid-state electrolytes: revealing the mechanisms of Li-ion conduction in tetragonal and cubic LLZO by first-principles calculations, J. Phys. Chem. C, 2014, 118, 6668–6679.
11. J. Holland, et al., A Workflow for Identifying Viable Crystal Structures with Partially Occupied Sites Applied to the Solid Electrolyte Cubic Li₇La₃Zr₂O₁₂, J. Phys. Chem. Lett., 2023, 14, 10257–10262,  DOI:10.1021/acs.jpclett.3c02064.
12. G. Li and C. W. Monroe, Dendrite nucleation in lithium-conductive ceramics, Phys. Chem. Chem. Phys., 2019, 21, 20354–20359,  10.1039/C9CP03884A.
13. N. J. J. de Klerk and M. Wagemaker, Space-Charge Layers in All-Solid-State Batteries; Important or Negligible?, ACS Appl. Energy Mater., 2018, 1, 5609–5618,  DOI:10.1021/acsaem.8b01141.
14. M. van Soestbergen, P. M. Biesheuvel and M. Z. Bazant, Diffuse-charge effects on the transient response of electrochemical cells, Phys. Rev. E, 2010, 81, 021503,  DOI:10.1103/PhysRevE.81.021503.
15. K. Yamamoto, et al., Dynamic Visualization of the Electric Potential in an All-Solid-State Rechargeable Lithium Battery, Angew. Chem., Int. Ed., 2010, 49, 4414–4417,  DOI:10.1002/anie.200907319.
16. C. Zhu, et al., Understanding the evolution of lithium dendrites at Li_6.25Al_0.25La₃Zr₂O₁₂ grain boundaries via operando microscopy techniques, Nat. Commun., 2023, 14, 1300,  DOI:10.1038/s41467-023-36792-7.
17. K. Yamamoto, et al., Direct observation of lithium-ion movement around an in situ-formed-negative-electrode/solid-state-electrolyte interface during initial charge–discharge reaction, Electrochem. Commun., 2012, 20, 113–116,  DOI:10.1016/j.elecom.2012.04.013.
18. J. Zhao, et al., In situ Observation of Li Deposition-Induced Cracking in Garnet Solid Electrolytes, Energy Environ. Mater., 2022, 5, 524–532,  DOI:10.1002/eem2.12261.
19. C. Neusel, et al., Dielectric breakdown of alumina single crystals, J. Eur. Ceram. Soc., 2012, 32, 1053–1057.
20. T. Miyashita, Deterioration of water-immersed polyethylene-coated wire by treeing, IEEE Trans. Electr. Insul., 1971, 129–135.
21. X. Liu, et al., Local electronic structure variation resulting in Li ‘filament’ formation within solid electrolytes, Nat. Mater., 2021, 20, 1485–1490,  DOI:10.1038/s41563-021-01019-x.
22. E. Kazyak, et al., Li Penetration in Ceramic Solid Electrolytes: Operando Microscopy Analysis of Morphology, Propagation, and Reversibility, Matter, 2020, 2, 1025–1048,  DOI:10.1016/j.matt.2020.02.008.
23. N. N. Greenwood and A. Earnshaw, Chemistry of the Elements, Elsevier, 2012.
24. J. Newman and K. Thomas-Alyea, Electrochemical Systems, John WIley & Sons, Inc., 2004.
25. P. Bai, J. Li, F. R. Brushett and M. Z. Bazant, Transition of lithium growth mechanisms in liquid electrolytes, Energy Environ. Sci., 2016, 9, 3221–3229,  10.1039/c6ee01674j.
26. Y. Lee, B. Ma and P. Bai, Concentration polarization and metal dendrite initiation in isolated electrolyte microchannels, Energy Environ. Sci., 2020, 13, 3504–3513,  10.1039/D0EE01874K.

---