Magnetic Kagome materials: bridging fundamental properties and topological quantum applications

Abstract

Kagome materials, characterized by their unique lattice structure and electronic properties such as Dirac cones, flat bands, van Hove singularities, and topologically nontrivial surface states, have become a focal point in solid state chemistry and condensed matter physics. The combination of spin–orbit coupling (SOC) and magnetism in these materials leads to several notable phenomena, such as the large anomalous Hall effect and anomalous Nernst effect observed in noncollinear antiferromagnets like Mn₃Sn and Mn₃Ge and Weyl semimetal behaviour in Co₃Sn₂S₂. The interplay between charge order, superconductivity, and symmetry breaking in materials like AV₃Sb₅, LaRu₃Si₂, and CeRu₂ unveils a rich landscape of emergent quantum phenomena, in addition to the distorted Kagome lattice in HoAgGe, along with the flat band, saddle point, and Dirac cones in YMn₆Sn₆. Topological skyrmions in FeGe and the quantum Chern insulating phase in TbMn₆Sn₆ further underscore the rich physics of these materials. Therefore, Kagome materials are uniquely suited to study the interaction between topology, magnetism, and electron correlation. This review comprehensively covers the progress in topological Kagome magnets, the fundamental concepts, and the connections between their exotic properties and the Kagome lattice structure. In conclusion, several open questions and future research directions are highlighted, providing valuable insights for researchers aiming to advance this integrated field. This review serves as a reference for understanding the potential of Kagome materials and their future advancements, fostering further exploration of their complex and promising properties.

---

Pranav Negi

Pranav Negi received his MSc (2023) in Chemistry from the University of Delhi. He is currently pursuing his PhD with Dr Subhajit Roychowdhury at the Indian Institute of Science Education and Research, Bhopal (IISERB). His research interests include the synthesis of single crystals of topological quantum materials and the study of their transport properties.

Koushik Medhi

Koushik Medhi is currently a final year BS-MS student with Dr Subhajit Roychowdhury at the Indian Institute of Science Education and Research, Bhopal (IISERB). His current research interests include understanding the low thermal conductivity in perovskite and Kagome materials.

Abhinav Pancholi

Abhinav Pancholi is currently a final year BS-MS student with Dr Subhajit Roychowdhury at the Indian Institute of Science Education and Research, Bhopal (IISERB). His current research interests include synthesis of single crystals of topological quantum materials.

Subhajit Roychowdhury

Subhajit Roychowdhury obtained his PhD in chemistry from the New Chemistry Unit, Jawaharlal Nehru Centre for Advanced Scientific Research (2019) under the supervision of Prof. Kanishka Biswas and did his postdoctoral research with Prof. Claudia Felser as a Humboldt Fellow at the Max Planck Institute for Chemical Physics of Solids. He is currently an Assistant Professor at the Department of Chemistry, Indian Institute of Science Education and Research, Bhopal (IISERB). His research interests include solid-state chemistry and topological quantum materials.

---

Wider impact

In this review, we provide a comprehensive overview of magnetic Kagome materials, highlighting a selection of representative systems. Magnetic Kagome materials are at the forefront of quantum materials research, offering transformative insights for materials scientists, solid-state chemists, and physicists alike. Their unique lattice geometry gives rise to intriguing electronic properties, such as Dirac-like band structures, flat bands, and topologically nontrivial states, which can be further tuned through the interplay of magnetism and electron correlation effects. This makes them ideal platforms for investigating exotic quantum phenomena, including the anomalous Hall and Nernst effects, chiral spin textures, and magnetic Weyl semimetals. In addition to summarizing key advancements, we address open questions and future research directions, offering a roadmap for interdisciplinary collaboration. We believe that this review will serve as a foundational resource, inspiring researchers across disciplines to further unlock the potential of magnetic Kagome materials and drive innovation in energy, quantum computation, and spintronics applications.

1. Introduction

Beyond the familiar Bravais lattice, four remarkable two-dimensional lattices with high symmetry stand out: square, triangular, honeycomb, and Kagome lattices.¹ These structures are defined by the unique equivalence of their vertices, where each vertex is connected to four, six, three, and four nearest neighbours, respectively. These elegant geometric configurations not only embody fundamental principles of symmetry but also unlock insights into cutting-edge physical phenomena.^2,3 Their simplicity and versatility make them indispensable in advancing transformative technologies from spintronics and quantum computing to thermoelectrics. The Kagome lattice, first conceptualized by Syozi in 1951, is inspired by the intricate design of traditional bamboo baskets commonly found in Japan (Fig. 1).⁴ This lattice, with its distinctive interlocking geometry, carries a deeper meaning in Japanese folklore, where it symbolizes protection and containment, reflecting the strength and harmony of its woven structure. The Kagome lattice is composed of a network of corner-sharing triangles, creating a repeating star-like pattern. It can be visualized as a honeycomb lattice with additional diagonal connections across the hexagonal cells. This arrangement results in a series of interwoven triangles, forming a periodic lattice with high symmetry. The unit cell of a Kagome lattice consists of three lattice points, which distinguishes it from simpler lattice types such as triangular or square lattices.

Fig. 1 Timeline of recent developments in the field of topological Kagome magnets.

The triangular arrangement leads to frustration, where hopping electrons encounter interference paths that cancel each other out. This leads to a complete localization of electronic states at certain energies. These states do not disperse, regardless of the momentum, resulting in a flat band (FB) in the energy spectrum.^5,6 As per the tight-binding model of the Kagome lattice, a flat band emerges alongside a pair of symmetry-protected Dirac bands and van-Hove singularities (vHSs)⁵ (Fig. 2a). When spin–orbit coupling (SOC) is introduced, the linear band crossing at the K point and the quadratic band touching at the Γ point become gapped.⁷ This inclusion of SOC transforms both the Dirac and FBs into topologically nontrivial states, unlocking new realms of exotic quantum behaviour. The Kagome lattice has attracted considerable attention in quantum materials research due to its remarkable quantum properties.² Interest surged after the theoretical prediction by Wen and co-workers in 2011, which suggested the potential realization of fractional quantum Hall states at high temperatures.⁸ This groundbreaking insight has positioned the Kagome lattice as a promising platform for exploring various quantum phenomena.

Fig. 2 (a) Schematic representation of the Kagome lattice with a flat band (FB), a Dirac point (DP) and van Hove singularities (vHSs) near the Fermi level (E_F). Crystal structures of (b) Mn₃Sn, (c) Co₃Sn₂S₂, (d) Fe₃Sn₂, (e) FeGe and (f) YMn₆Sn₆.

FBs in momentum space arise from pronounced electron localization in real space and serve as fertile ground for exploring nontrivial topological phenomena, especially in strongly correlated systems.^5,6 These FBs, together with vHSs in Kagome lattices, dramatically enhance the density of states (DOS), potentially triggering robust electron correlation effects.⁹ In particular, vHSs mark critical points in the electronic band structure where the DOS diverges, paving the way for rich and tunable ground states. In van Hove filling, the interplay between these singularities and varying Coulomb interactions can give rise to emergent electronic phases such as superconductivity or spin/charge density waves (CDWs).^10–12 These effects highlight the versatility of the Kagome lattice as a platform for exploring the delicate balance between geometry, topology, and strong electron correlations.

Breaking the time-reversal symmetry, as in ferromagnetic (FM) ordering, splits the spin-degenerate bands and opens exciting possibilities for electronic behaviour. The inclusion of SOC further enriches this scenario, enabling the emergence of various gapped phases. These gaps can host massive Dirac or Weyl fermions, imprinting unique characteristics on the band structure.¹³ Symmetry breaking in Kagome systems modulates their distinctive bands, unlocking pathways to novel topological phenomena. These include a pronounced intrinsic anomalous Hall effect (AHE) and an anomalous Nernst effect (ANE), both stemming from the Berry curvature intrinsic to the broken time-reversal symmetry.^14–18 Such effects underscore Kagome materials as an ideal platform to explore the intricate interplay between magnetism, topology, and strong electron correlations, offering fertile ground for uncovering fundamentally new quantum states.

This review delves into the remarkable advances in magnetic Kagome materials, offering a comprehensive exploration of their diverse families and fascinating properties. We begin with noncollinear antiferromagnets such as Mn₃Sn and Mn₃Ge and then progress to FM systems like Co₃Sn₂S₂ and Fe₃Sn₂ and traverse through the quantum Chern insulator REMn₆Sn₆. The journey continues through topological skyrmions in FeGe, the LnTi₃Bi₄ family, charge order and superconductivity in AV₃Sb₅, LaRu₃Si₂, and CeRu₂ and culminates in the distorted Kagome lattice in HoAgGe (Fig. 1). For each class, we provide a detailed analysis of its crystal and electronic structures, magnetic properties and anomalous transport phenomena. The final sections highlight the transformative potential of magnetic Kagome materials for cutting-edge applications, including racetrack memory and quantum information technologies. We also address the challenges that lie ahead, charting a path towards the realization of novel topological quantum states that have so far eluded discovery. By integrating fundamental insights with forward-looking perspectives, this review serves as a roadmap for navigating the vibrant landscape of magnetic Kagome materials, from their intricate properties to their immense potential in shaping future quantum technologies.

2. Crystal structure

The individual crystal structure of several Kagome magnets is discussed in this section.

2.1. Mn₃X (X = Sn, Ge)

Mn₃X exhibits a hexagonal chiral antiferromagnetic (AFM) structure (space group P6₃/mmc) composed of Kagome layers of Mn atoms in the ab-plane.^17,19 These layers form a breathing-type arrangement and are stacked along the c-axis²⁰ (Fig. 2b).

2.2. Co₃Sn₂S₂

The compound Co₃Sn₂S₂ was first synthesized in the late 20th century. In 1978 and 1988, Zebel et al. and Natarajan et al. prepared Co₃Sn₂S₂ crystals, respectively.^21,22 Their work focused primarily on understanding the crystal structure of Co₃Sn₂S₂ and its relationship with bulk transport properties, laying the foundation for future studies. A significant theoretical milestone occurred in 2011, when Wan et al. and Xu et al. predicted magnetic Weyl fermions in materials such as HgCr₂Se₄ and Y₂Ir₂O₇.^23,24 Despite the theoretical promise, the experimental realization of magnetic Weyl semimetals remained elusive for years.

In 2018, groundbreaking work conducted by Wang et al. and Liu et al. independently identified Co₃Sn₂S₂ as a magnetic Weyl semimetal.^14,25 This half-metallic ferromagnet exhibited the long-sought magnetic Weyl fermion behaviour. Subsequent studies confirmed the existence of bulk Weyl nodes, surface Fermi arcs, and other unique features of the magnetic Weyl semimetal phase in Co₃Sn₂S₂, sparking intense interest in its topological and magnetic properties.^15,26 These discoveries have positioned Co₃Sn₂S₂ at the forefront of quantum materials research, bridging the fields of magnetism and topology with profound implications for condensed matter physics.

The compound Co₃Sn₂S₂ belongs to the shandite family and crystallizes in a rhombohedral lattice with the space group R3̄m.²⁷ Its crystal structure consists of CoSn₄S₂ octahedral blocks stacked in a hexagonal close-packed sequence along the c-axis. Each cobalt atom is coordinated by four tin atoms and two sulphur atoms to form a distorted octahedron. Within the structure, the Co and S atoms occupy the Wyckoff positions 9e and 6c, respectively.²⁵ The CoSn₄S₂ octahedra are interconnected in two ways: by face-sharing along the ab-plane and corner-sharing along the c-axis. Furthermore, in the Co–Sn layers, the Co atoms form a perfect Kagome lattice, characterized by corner-sharing triangles of Co atoms (Fig. 2c). There are two distinct Sn sites in the structure.¹⁸ One set of Sn atoms, designated as Sn (2), are located at the centres of the Kagome hexagons and occupy the Wyckoff position 3a. The other set, designated as Sn (1), is located between the Co–Sn bilayers, connecting adjacent Co–Sn (2) layers, and occupies the Wyckoff position 3b. In addition, the S atoms are located above and below the Co–Sn (2) layers, completing the structural arrangement.

2.3. Fe₃Sn₂

The crystal structure of Fe₃Sn₂ consists of alternating Fe–Sn bilayers and Sn layers stacked along the c-axis.¹³ Within each Fe–Sn bilayer, the iron atoms are arranged in two Kagome layers characterized by two types of equilateral triangles that differ in their Fe–Fe bond lengths: 0.2732 nm for the larger triangles and 0.2582 nm for the smaller ones.²⁸ The tin atoms are located at the centres of the hexagons formed by the Kagome layers (Fig. 2d). In addition, the smaller triangles of Fe atoms in the two Kagome layers align to form interconnected octahedral structures composed of iron atoms. Separating successive Fe–Sn bilayers is a distinct Sn layer in which the tin atoms form a two-dimensional network. This network features six-membered rings that share edges, similar to the structural arrangement found in graphene. This unique combination of Kagome bilayers and Sn layers contributes to the distinctive electronic and magnetic properties of Fe₃Sn₂.

2.4. REM₆X₆

The REM₆X₆ family of compounds (where RE represents a rare earth element, M is a transition metal, and X is a group IV element) are characterized by a unique double Kagome lattice of M atoms. Structurally, these compounds can be viewed as modified versions of the centrosymmetric CoSn-type structure (Table 1).²⁹ In the CoSn-type arrangement, alternating layers of Sn-centred Co Kagome lattices and Sn honeycomb lattices generate large hexagonal voids that can accommodate cationic atoms. When rare earth (RE) atoms occupy these voids, the Sn atoms in the Kagome layers are displaced from the centres of the Co–Kagome lattices, resulting in a doubling of the unit cell along the c-axis and making adjacent voids inaccessible. The placement of RE atoms at either 0 or 1/2 along the z-axis introduces various ordering patterns, contributing to the structural diversity of 166 compounds. The combination of these structural features allows for a multitude of possible configurations, making this family a “compound generating machine.”

While there are excellent reviews of the entire REM₆X₆ family,^30,31 in this review article we will focus specifically on the REMn₆Sn₆ series and explore its unique structural, magnetic and physical properties.

Kagome lattice structures of rare earth metals have gained considerable attention because of their intriguing electronic and magnetic properties. One series of such interesting materials is REMn₆Sn₆. Most of the REMn₆Sn₆ compounds crystallize in a centrosymmetric structure.^32–34 Kagome planes consist of Mn₃Sn units sandwiched between two distinct layers of Sn₃ and Sn₂RE (Fig. 2e). This sequence, [Mn₃Sn] [Sn₃] [Mn₃Sn] [Sn₂RE], results in the Sn honeycombs occupied by RE atoms being relatively anionic, while the other honeycombs are more cationic. This charge difference promotes coherent electron transfer between the two types of honeycombs, thereby electrostatically stabilizing the RE cations.³² As a result, REMn₆Sn₆ compounds form pristine Mn Kagome layers.^32,35,36

REMn₆Sn₆ (RE = Sc, Y, Gd, Lu) compounds have a hexagonal HfFe₆Ge₆-type structure (space group P6/mmm), while only SmMn₆Sn₆ is isotypical with the YCo₆Ge₆ structure (space group P6/mmm), a disordered variant of HfFe₆Ge₆.^{30–33,35,37–40} Apart from HfFe₆Ge₆ and YCo₆Ge₆ structures, some REMn₆Sn₆ (RE = Pr, Nd, Sm) compounds also crystallize in lower symmetry orthorhombic close packing, isostructural with HoFe₆Sn₆ (space group Immm), which is a stacking variant composed of slabs of the HfFe₆Ge₆ type and of the YCo₆Ge₆ type.^30,41–43 Depending on the synthesis conditions, SmMn₆Sn₆ can adopt different crystal structures. At the lower annealing temperature of 723 K, it crystallizes in the orthorhombic HoFe₆Ge₆ type structure.⁴⁴ On the other hand, the symmetry increases to the hexagonal YCo₆Ge₆ type when the annealing temperature is increased to 973 K.⁴⁴

Table 1 Structural and magnetic properties of REMn₆Sn₆

Composition	Space group	Structure type	Lattice parameter (Å)			Magnetism	TN/Tc (K)	Ref.
			a	b	c
ScMn6Sn6	P6/mmm	HfFe6Ge6	5.474	5.474	8.973	AFM	384	40 and 45
YMn6Sn6	P6/mmm	HfFe6Ge6	5.512	5.512	8.984	AFM	335	40 and 46
PrMn6Sn6	Immm	HoFe6Sn6	9.075	28.976	5.577	FIM	340	42
NdMn6Sn6	Immm	HoFe6Sn6	9.066	28.924	5.566	FIM	340	42
SmMn6Sn6 (phase 1)	Immm	HoFe6Sn6	9.077	28.825	5.547	FIM	380	42
SmMn6Sn6 (phase 2)	P6/mmm	YCo6Ge6	5.552	5.552	4.526			40
GdMn6Sn6	P6/mmm	HfFe6Ge6	5.521	5.521	9.007	FIM	449	40
TbMn6Sn6	P6/mmm	HfFe6Ge6	5.519	5.519	9.004	FIM	425	40
DyMn6Sn6	P6/mmm	HfFe6Ge6	5.515	5.515	8.996	FIM	405	40
HoMn6Sn6	P6/mmm	HfFe6Ge6	5.508	5.508	8.993	FIM	391	40
ErMn6Sn6	P6/mmm	HfFe6Ge6	5.509	5.509	8.992	AFM	337	40
TmMn6Sn6	P6/mmm	HfFe6Ge6	5.506	5.506	8.988	AFM	337	40
YbMn6Sn6	P6/mmm	HfFe6Ge6	5.553	5.553	9.043	FIM	300	37
LuMn6Sn6	P6/mmm	HfFe6Ge6	5.496	5.496	8.985	AFM	345	40

---

2.5. FeGe

FeGe crystallizes in a hexagonal structure with the space group P6/mmm in which the magnetic Fe atoms form Kagome planes separated by nonmagnetic Ge honeycomb layers⁴⁹ (Fig. 2f). This unique structural arrangement gives rise to intriguing magnetic properties.

2.6. LnTi₃Bi₄

The Ti-based Kagome lattice, LnTi₃Bi₄ (Ln representing the rare earth elements), has recently attracted considerable interest owing to its wide range of magnetic properties and remarkable chemical versatility (Table 2).^47,50

Table 2 Structural and magnetic properties of LnTi₃Bi₄

Ln	Properties						Ref.
	a (Å)	b (Å)	c (Å)	Magnetism	TN/TC (K)	Ms (μB)
La	5.95	10.35	25.11	NM	—	—	47
Ce	5.91	10.32	24.99	AFM	3	1.5	47
Pr	5.90	10.32	24.93	—	9	2.3	47
Nd	5.89	10.32	24.91	FM	9	2.5	47
Sm	5.87	10.31	24.79	FM	23	0.4	47
Eu	5.97	10.38	25.37	FM	11	7.9	47
Gd	5.86	10.30	24.73	AFM	13	7.5	47
Yb	5.91	10.36	24.87	NM	—	—	47
Tb	5.84	10.30	24.65	AFM	24	9.3	48

---

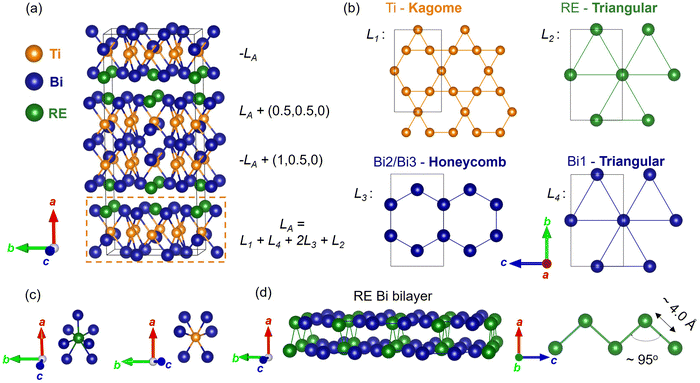
The LnTi₃Bi₄ compound differs significantly from the Kagome prototypes AV₃Sb₅ (A = K, Rb, Cs) and REM₆X₆ due to its more intricate crystal structure.⁴⁷ LnTi₃Bi₄ has a layered crystal structure with the orthorhombic space group Fmmm. Notably, the LnTi₃Bi₄ family incorporates structural elements from the REM₆X₆ Kagome prototypes. Viewed along the c-axis, the LnTi₃Bi₄ structure is composed of alternating layers in the sequence X₄–M₃–AX₂–[AX₂–M₃–X₄–M₃–AX₂]–AX₂–AX₂–M₃–X₄, with the bracketed segment resembling the motif observed in the HfFe₆Ge₆ structure (Fig. 3). Unlike AV₃Sb₅ or ATi₃Bi₅, LnTi₃Bi₄ has double Kagome layers in its unit cell.

Fig. 3 (a) Crystal structure of Ln(RE)Ti₃Bi₄. (b) Kagome network of Ti (L₁), triangular lattice of RE (L₂), honeycomb (L₃) and triangular lattice of Bi (L₄). (c) The coordination environment of RE and Ti. (d) The REBi bilayer and Ln–Ln zigzag chains.

Within the unit cell of LnTi₃Bi₄, five distinct sublattices can be identified: (1) the Kagome lattice formed by Ti atoms, (2) Ln-based zigzag chains, (3) two Bi honeycomb-like arrangements, (4) a Bi triangular lattice, and (5) a triangular lattice of Ln atoms (Fig. 9). The Kagome layers in this structure experience additional anisotropic distortions that lower the symmetry from hexagonal to orthorhombic. This contrasts with the D_6h symmetry typically seen in Kagome systems like AV₃Sb₅. The Ln zigzag chains, aligned along the a-axis, impose quasi-one-dimensional properties on the LnBi₂ layers, further reducing the crystalline symmetry to D_2h.⁵⁰ This symmetry reduction, driven by lattice distortions, has significant implications for the electronic structure of the Kagome lattice, influencing features such as Dirac cones and FBs.

Interestingly, the Ti Kagome lattice and the Bi triangular lattice in LnTi₃Bi₄ exhibit bond equivalencies and deviate from the bc plane, as shown in Fig. 3. This results in a distortion of the TiBi layer, which manifests itself as both in-plane and out-of-plane displacements. These structural complexities underline the distinctiveness of LnTi₃Bi₄ and its properties. Fig. 9d also highlights the Ln zigzag chains, which run parallel to the a-axis and feature nearest neighbour Ln–Ln intrachain distances of approximately 4 Å. The Ln atoms are nine-coordinate, with Ln–Bi bond lengths ranging from 3.3 to 3.6 Å.⁴⁷ The Bi honeycomb and Ti Kagome lattices are anticipated to exhibit fascinating topological features, while the Ln triangular lattice introduces geometric frustration. Each of these structural motifs contributes to the potential for exploring magnetism and topological properties in LnTi₃Bi₄, establishing it as a compelling candidate for the study of unique material behaviours.

2.7. Distorted Kagome

Most of the intensive research efforts mentioned above have focused on the ideal Kagome lattice. However, a promising next step in this field is to explore distortions of the Kagome lattice, which, despite their realization in certain magnetic compounds, remain experimentally unexplored. In contrast to the standard Kagome lattice, distorted variants could accommodate a much richer range of physical phenomena.

For instance, when the two distinct types of triangles in a typical Kagome lattice are rotated in opposite directions, the resulting structure breaks inversion symmetry, giving rise to a non-centrosymmetric lattice. This structural change causes the doubly degenerate Dirac cone characteristic of the pristine Kagome lattice to split into a pair of Weyl points, potentially opening exotic physics and new avenues for experimental investigation.

HoAgGe is a member of the RAgGe series (R = Tb–Lu) and adopts a hexagonal ZrNiAl-type structure (space group P6̄2m) in which the Ho atoms are arranged in triangular coordination with an interatomic distance of 3.686 Å.^51–53 The Ho atoms form a distorted Kagome lattice in the ab-plane. The lattice distortion arises from the substructure, which consists of two distinct types of triangles that rotate by the same angle (∼15.58°) but in opposite directions around the c-axis. This rotation breaks the inversion symmetry, resulting in a non-centrosymmetric structure. Despite breaking the spatial inversion symmetry of an individual Kagome layer, the overall space group of the three-dimensional crystal remains unchanged. Considering only the Ho³⁺ ions, this distortion reduces the D_6h symmetry of the Kagome lattice to D_3h, while preserving the local easy axes of the Ho³⁺ moments. The combination of strong local easy-axis anisotropy and FM nearest neighbour (NN) interactions between the Ho³⁺ moments gives rise to “1-in-2-out” or “2-in-1-out” ice rules on the distorted Kagome lattice.⁵³

Recently, Schoop and co-workers successfully synthesized orthorhombic Cs₂Ni₃S₄ (space group Fmmm) by soft chemical processing, stabilizing a layered structure with two-dimensional Kagome-like nickel networks in the ab-plane. Unlike an ideal Kagome lattice, the corner-sharing Ni triangles in Cs₂Ni₃S₄ exhibit a slight distortion, with two sides measuring 2.913 Å, while the third side is slightly longer at 2.963 Å, making the triangles isosceles instead of equilateral. The structure consists of stacked S–Ni–S layers along the c-axis, with Cs atoms occupying the interlayer spaces. Within these layers, Ni atoms adopt a square-planar coordination with sulphur, which contributes to the structural stability and electronic properties of the material.⁵⁴

3. Electronic band structure

The individual crystal structure of several Kagome magnets is discussed in this section.

3.1. Mn₃Sn

Nakatsuji and co-workers investigated the electronic structure of Mn₃Sn using angle-resolved photoemission spectroscopy (ARPES) and density functional theory (DFT) calculations to reveal the presence of magnetic Weyl fermions, characterized by Weyl nodes near the Fermi energy (E_F) resulting from the non-collinear magnetic order and the time-reversal symmetry breaking⁵⁵ (Fig. 4a–c). The SOC plays a pivotal role by lifting degeneracies along nodal rings, leaving intact Weyl nodes with opposite chiralities, which are distributed over high-symmetry points in momentum space. The ARPES data, supported by DFT calculations, show significant band renormalization and damping effects due to strong electron correlations in the Mn 3d orbitals, with a bandwidth reduction by a factor of five. The band structure analysis identifies nodal rings without SOC, which evolve into Weyl nodes when SOC is introduced, preserving band crossings in certain directions. These Weyl points arise along highly symmetric lines, such as K–M–K, where the intersection of electron and hole bands creates type-II Weyl fermions. The experimental ARPES intensity maps align well with theoretical predictions, confirming the existence of flat electron and hole bands that facilitate high intensity near the Weyl points.⁵⁵ The magnetic texture in Mn₃Sn strongly influences the electronic structure, leading to orthorhombic features even within the hexagonal symmetry.

Fig. 4 (a) Calculated band structure of Mn₃Sn around M and M′ points.⁵⁵ (b) ARPES intensity plot near the Fermi level.⁵⁵ (c) The band dispersion along the line of high symmetry for different hυ values from 50 to 170 eV and the corresponding energy distribution curves (EDCs).⁵⁵ (d) Hall conductivity as a function of field at 300 K in Mn₃Sn.¹⁷ (e) Hall conductivity as a function of temperature at zero magnetic field.¹⁷ (f) Nernst signal and magnetization as a function of field at 300 K in Mn_3.06Sn_0.94.⁵⁶ (g) Nernst signal as a function of temperature at 300 K in Mn_3.06Sn_0.94.⁵⁶ (a)–(c) Are reproduced with permission from ref. 55. (d) and (e) Are reproduced with permission from ref. 17. (f) and (g) Are reproduced with permission from ref. 56.

The tunability of Weyl node positions by small magnetic fields provides direct control of the Berry curvature, opening avenues for manipulation of topological properties. These findings are complemented by magnetotransport measurements that confirm the chiral anomaly as a bulk signature of Weyl physics, as evidenced by a positive longitudinal magnetoconductance (LMC) and negative transverse magnetoconductance (TMC) under parallel electric and magnetic fields.⁵⁵ Together, the ARPES and electronic structure results underscore the unique ability of Mn₃Sn to host magnetic Weyl fermions, driven by the intricate interplay of geometric frustration, SOC, and correlation effects, marking a significant advance in the understanding of topological excitations in correlated electron systems.

3.2. Co₃Sn₂S₂

Magnetic Weyl semimetals (WSMs), which break time reversal symmetry, offer a rich platform for studying the interplay between magnetism, electron correlations, and topological orders. The interplay of crystal field, SOC, and ferromagnetism lifts the band degeneracy, creating three pairs of Weyl points per Brillouin zone, as confirmed by ARPES and theoretical calculations¹⁵ (Fig. 5a and b). Scanning tunnelling microscopy (STM) studies revealed chiral edge states localized to step edges on Kagome terraces and quantum well-like states confined to narrow terraces (Fig. 5c), showing linear energy dispersion with velocities around 5 × 10⁴ m s⁻¹.⁵⁷ These findings align with theoretical models of WSMs as layered stacks of Chern insulators coupled by interlayer interactions. Numerical simulations confirmed that these edge states emerge as hybridized modes localized at exposed terraces or steps and decay into the bulk, consistent with the observed spatial confinement of 1.5 nm.⁵⁸ Experimental and simulated data agree on the dependence of chiral edge states on terrace geometry, terrace width, and interlayer coupling strength. The identified surface states merge into bulk features at Weyl points, providing a deeper understanding of TRS-breaking WSMs (Fig. 5d).

Fig. 5 (a) Calculated band structure of Co₃Sn₂S₂ with and without SOC.¹⁴ (b) Plot of the second derivative of the intensity from ARPES data with the corresponding bulk calculations.²⁵ (c) Scanning tunneling microscopy and spectroscopy (STM/S) data at 4 K showing the edge state on the Co₃Sn plane.⁵⁸ (d) Dispersions between (i) the theoretically computed topological surface states (TSS) along the path and [(ii)–(vi)] the experimentally observed TSSs.¹⁵ (e) Connectivity of intra-Brillouin zone (BZ) Fermi arcs and the breaking of time-reversal symmetry at the Sn-terminated surface in Co₃Sn₂S₂.²⁶ (a) Is reproduced with permission from ref. 14. (b) Is reproduced with permission from ref. 25. (c) Is reproduced with permission from ref. 58. Creative Commons license: https://creativecommons.org/licenses/by/4.0/. (d) Is reproduced with permission from ref. 15. (e) Is reproduced with permission from ref. 26.

These Fermi arcs, which connect Weyl nodes of opposite chirality in momentum space, provide a signature of the bulk topology. While the existence of Fermi arcs is topologically protected, their specific connectivity and spatial properties can vary depending on the details of the surface termination. Morali et al. have investigated how three distinct terminations of the Co₃Sn₂S₂(001) surface – tin (Sn), cobalt (Co) and sulphur (S) – affect the Fermi arc structure and connectivity, shedding light on the interplay between bulk topology and surface potentials (Fig. 5e).²⁶ Using scanning tunnelling microscopy and spectroscopy (STM/STS) alongside ab initio calculations, the study reveals that the surface potential imposed by different terminations profoundly affects the Fermi arc behaviour. On the Sn-terminated surface, Fermi arcs exhibit intra-Brillouin zone connectivity, connecting Weyl nodes within the same Brillouin zone, while on the Co-terminated surface, they connect Weyl nodes across adjacent Brillouin zones through hybridization with non-topological surface bands, forming a unique inter-Brillouin zone connectivity. The S-terminated surface presents a different scenario, where Fermi arcs overlap extensively with bulk states, reducing their topological protection and making them difficult to observe directly.

Optical spectroscopy and theoretical calculations show that the electronic kinetic energy derived from experiments is significantly reduced compared to single-particle ab initio predictions.⁵⁷ This discrepancy arises due to many-body interactions, indicating band narrowing and a flattened electronic band near the Fermi energy. The Coulomb interaction strength is estimated to be U ≈ 4 eV, which is confirmed by DFT plus dynamical mean-field theory (DFT+DMFT). Despite the electronic correlations, Co₃Sn₂S₂ retains its Weyl semimetallic state, characterized by Weyl cones and surface Fermi arcs. Furthermore, the electronic correlations induce a FB connecting the Weyl cones, which is evidenced by specific optical conductivity features.

Recently, Beidenkopf and co-workers identified a triangular distortion on the Kagome surface of Co₃Sn₂S₂ that flattens the band dispersion near the saddle points to form a higher order van Hove singularity (HOvHS) with an algebraically divergent DOS.⁵⁹ This emergent singularity is pinned at the Fermi energy and causes a Pomeranchuk instability, leading to the formation of nematic electronic states. These states spontaneously break the rotational symmetry of the Kagome lattice while preserving the translational symmetry, manifesting in distinct wavefunction redistributions across the Fermi surface. By linking HOvHS formation to nematicity, the research unveils new pathways for engineering exotic quantum states in correlated materials, suggesting that Kagome metals such as Co₃Sn₂S₂ are fertile ground for exploring symmetry-breaking instabilities and unconventional electronic phases. This study uncovers a novel mechanism for generating HOvHS in Kagome materials, highlighting the transformative role of lattice distortions in shaping electronic properties.

3.3. Fe₃Sn₂

Theoretical predictions suggest that in materials with broken time-reversal symmetry, such as FM systems, Kagome lattices can support Dirac electronic states with Berry curvature-induced phenomena.⁶⁰ Fe₃Sn₂, a bilayer Kagome compound with FM order, offers a platform to study these properties.

In Fe₃Sn₂, the Kagome planes are stacked in a bilayer fashion, with interlayer coupling adding complexity to the electronic structure. Breaking the time-reversal symmetry by FM order splits the spin-degenerate Dirac bands, while spin–orbit coupling induces a mass gap of about 30 meV at the Dirac points, transforming the electronic states into massive Dirac fermions.¹³ These massive Dirac fermions are crucial for generating the Berry curvature of the material, which drives phenomena such as the anomalous Hall effect (AHE).

ARPES is used to map experimentally the band structure of Fe₃Sn₂ with high resolution in momentum and energy. Low temperature measurements (∼20 K) reveal two Dirac cones at the K and K′ points of the Brillouin zone, in agreement with theoretical predictions¹³ (Fig. 6b). The ARPES spectra confirm the presence of a 30 meV energy gap at the Dirac points. The massive Dirac fermions in Fe₃Sn₂ give rise to a significant Berry curvature, which is concentrated around the gapped Dirac points. This curvature dominates the intrinsic anomalous Hall conductivity (AHC) of the material, which has been experimentally observed to persist up to 300 K.

Fig. 6 (a) Magnetic force microscopic images of first-order spin-reorientation phase transition in Fe₃Sn₂.⁶¹ (b) ARPES data measured in Fe₃Sn₂, showing two Dirac points, Dirac circle and two electron pockets.¹³ (c) The de Haas–van Alphen effect in Fe₃Sn₂ as a massive Dirac model.⁶² (a) Is reproduced with permission from ref. 61. (b) Is reproduced with permission from ref. 13. (c) Is reproduced with permission from ref. 62. Creative Commons license: https://creativecommons.org/licenses/by/4.0/.

Furthermore, ARPES measurements reveal a nearly dispersionless FB about 0.2 eV below the Fermi level, extending over significant parts of the Brillouin zone along the Γ–K and Γ–M directions.⁶³ These flat bands originate primarily from Fe–Sn layers, as confirmed by band calculations. DFT analysis showed that Fe₃Sn₂ has several nearly flat bands associated with Fe d-orbitals. These bands dominate the density of states (DOS) near the Fermi level, enabling high temperature ferromagnetism. The calculated magnetic moment of 2.04μ_B per Fe atom is in good agreement with experimental measurements, validating the model.

Ye et al. studied the de Haas–van Alphen (dHvA) effect in Fe₃Sn₂, uncovering quasi two-dimensional (2D) massive Dirac states and their modulation by the orientation of the FM moment⁶² (Fig. 6c). The dHvA effect reveals Fermi surface pockets corresponding to bulk Dirac states with effective masses and band areas that vary systematically with the direction of the magnetic moment. The study identifies two quasi-2D Dirac bands whose behaviour is consistent with a massive Dirac model incorporating a Kane–Mele type SOC. The effective masses of the Dirac fermions were determined from the temperature dependence of the dHvA oscillation amplitudes. The α₁ and α₂ pockets have effective masses of 0.59m_e and 2.5m_e, respectively, where m_e is the electron mass. These values are consistent with a massive Dirac model and suggest a highly anisotropic Fermi surface, in agreement with previous spectroscopic observations.

Recently, Yao et al. identified Weyl nodes in Fe₃Sn₂.⁶⁴ Unlike many other materials where Weyl nodes exist above or below the Fermi level, in Fe₃Sn₂ their proximity provides an opportunity to directly influence transport phenomena. The study revealed that Fe₃Sn₂ hosts Weyl nodes at or near the Fermi level. These nodes arise from the crossing of majority and minority spin bands and are highly sensitive to the direction of the magnetization. Eight pairs of Weyl nodes were identified for magnetization along the y-axis, while ten and six pairs were observed for magnetization along the x- and z-axes, respectively. Fe₃Sn₂ preserves inversion symmetry but breaks time-reversal symmetry due to its FM nature. Magnetization along different axes introduces different levels of symmetry, affecting the band structure and the presence of Weyl nodes. For example, y-axis magnetization preserves mirror symmetry, resulting in specific nodal line structures. In contrast, x- and z-axis magnetization breaks certain symmetries, leading to more complex distributions of Weyl points.

3.4. REMn₆Sn₆

REMn₆Sn₆ exhibits complex band structure characterized by topological FBs, vHSs and Dirac points. These features are influenced by the magnetic interactions within the Kagome lattice, which introduce novel topological states and quantum phases (Fig. 7).^30,31 REMn₆Sn₆ hosts a variety of magnetic orders that significantly affect the electronic bands near the Fermi level. For example, YMn₆Sn₆ has in-plane FM ordering of the Mn layer combined with helical AFM ordering along the c-axis.⁶⁵ This results in a non-degenerate magnetic state due to the FM state with large SOC leading to the emergence of spin polarized Dirac bands. These bands along with FBs and vHSs contribute to the distinct electronic properties of YMn₆Sn₆.^46,65 DFT and dynamical mean field theory (DMFT) calculations by Li et al. reveal the existence of FBs throughout the entire Brillouin zone touching a quadratic band at the Γ′ point, which emerges from a Dirac band at the K point and forms a saddle point at M⁴⁶ (Fig. 7d).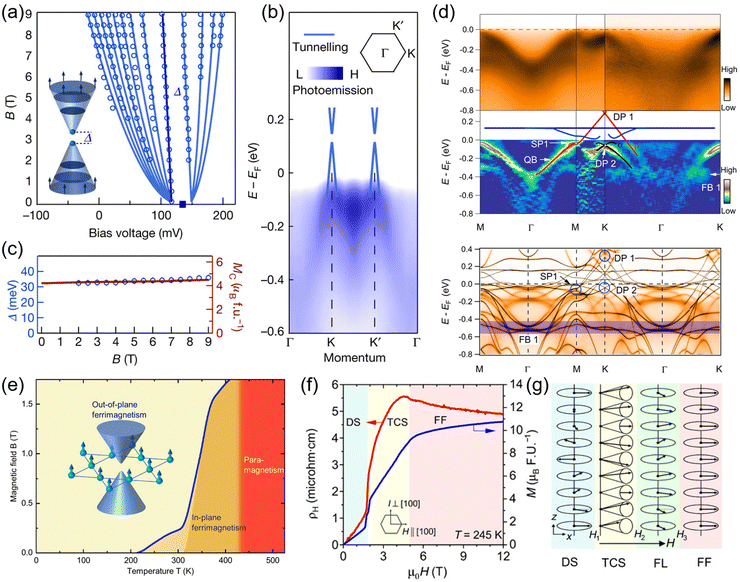

Fig. 7 (a) Fitting of the Landau fan data with the spin polarised and the Chern gapped Dirac dispersions.⁶⁷ (b) Experimental band dispersions of TbMn₆Sn₆ using STM and ARPES.⁶⁷ (c) Dirac gap size and out-of-plane magnetization as a function of the magnetic field.⁶⁷ (d) Upper panel: photoemission intensity plots along the Γ–M–K–Γ path and the corresponding second derivative plots of YMn₆Sn₆. Lower panel: theoretical ARPES spectra in the ferromagnetic state with spin–orbit coupling, highlighting the presence of Dirac points, a saddle point, and a flat band.⁴⁶ (e) Magnetic phase diagram of TbMn₆Sn₆ along the B//c-axis.⁶⁶ (f) The variation of Hall resistivity and magnetization for YMn₆Sn₆ with the magnetic field at 245 K.⁶⁵ (g) Schematic representation of different magnetic structures with the applied field in YMn₆Sn₆.⁶⁵ (a)–(c) Are reproduced with permission from ref. 67. (d) Is reproduced from ref. 46. Creative Commons license: https://creativecommons.org/licenses/by/4.0/. (e) Is reproduced from ref. 66. Creative Commons license: https://creativecommons.org/licenses/by/4.0/. (f) and (g) Are reproduced with permission from ref. ⁶⁵.

One of the key features of REMn₆Sn₆ is the presence of Chern gapped Dirac fermions^36,66,67 (Fig. 7a and e). Their existence has been studied by transport measurements of quantum oscillations with a non-trivial Berry phase as well as a large intrinsic AHE. The first experimental evidence for these gapped Dirac fermions in TbMn₆Sn₆ was provided by STM⁶⁷ (Fig. 7b). The Dirac cone energy and gap size decrease as one moves from Gd to Er, highlighting the tunability of these topological features through magnetic exchange coupling between rare earth 4f and transition metal 3d electrons.³⁶ In ErMn₆Sn₆, ARPES measurements by Dhakal et al. indicate the presence of Dirac-like states both above and below the Fermi level, with a FB located approximately 400 meV above the Fermi level.³⁴ The presence of Dirac cones at the K point with SOC opens the gap at this point, contributing to the AHE.

For TbMn₆Sn₆, a linear band crossing at the K point with a 15 meV gap was observed above the Fermi level at 215 meV, considering SOC.³⁵ TbMn₆Sn₆ is metallic and shows the AHE. Yin et al. initially associated it with a 2D like SOC gapped Dirac cone near the Fermi level at the K point⁶⁷ (Fig. 7c). However, Jones et al. calculated the Berry curvature and found that the AHE originates from other regions of the Brillouin zone.⁶⁸ Later, Lee et al. analysed the band structures of REMn₆Sn₆ and discovered that the quasi 2D Dirac cone lies over 0.7 eV above the Fermi level, higher than that reported by Yin et al., and computationally demonstrated that the observed AHE in REMn₆Sn₆ has a 3D character, not related to the quasi 2D Dirac cone.^67,69

3.5. LnTi₃Bi₄

The LnTi₃Bi₄ family of Kagome metals, characterized by distorted bilayer Kagome lattices, exhibit a unique electronic structure defined by twofold rotational symmetries (C_2x and C_2z).⁵⁰ These symmetries arise from lattice distortions that break the sixfold rotational symmetry (C_6z) while preserving the twofold symmetry (C_2z). Several bands cross the Fermi level (E_F), which is consistent with the metallic nature of LnTi₃Bi₄. The defining features of the valence electronic structure of LnTi₃Bi₄ are: (i) linear Dirac-like states, (ii) multiple vHSs, and (iii) double FBs^47,50,70,71 (Fig. 8a and b). These FBs arise due to destructive wavefunction interference within the Ti–Kagome lattice, with interlayer coupling contributing to bonding–antibonding splitting. The electronic structure of LnTi₃Bi₄, particularly in compounds such as NdTi₃Bi₄ and YbTi₃Bi₄, displays pronounced anisotropy^70,72 (Fig. 8c–f). This anisotropy is evident when comparing band dispersions along high-symmetry cuts, such as Γ–M–K′–Γ and Γ–M′–K–Γ, where the Γ–M and Γ–K directions serve as twofold rotation axes.⁷⁰ The DOS near EF is dominated by Ti and Bi orbitals, with distinct Fermi surface pockets, including a circular pocket at Γ, hexagonal symmetry pockets along Γ–M, and triangular and circular pockets near the K point. Orbital projected DFT calculations attribute the FBs primarily to the Ti d_xy and Ti d_x²−y² orbitals.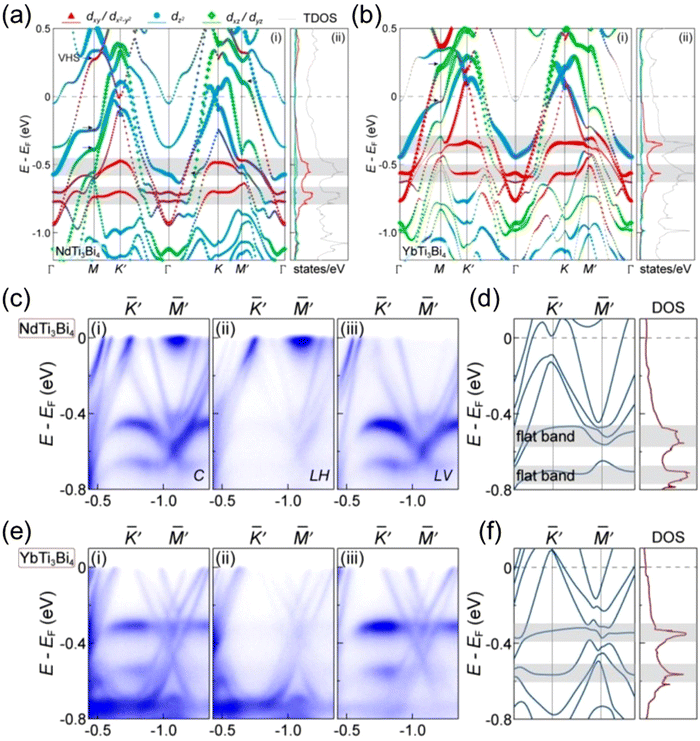

Fig. 8 Orbital resolved electronic band structures of (a) NdTi₃Bi₄ and (b) YbTi₃Bi₄. Experimental band dispersions of (c) NdTi₃Bi₄ and (e) YbTi₃Bi₄. DFT calculated band structure of (d) NdTi₃Bi₄ and (f) YbTi₃Bi₄.⁵⁰

In YbTi₃Bi₄, the vHS near E_F includes one at ∼150 meV above E_F and two at ∼250 meV below E_F, associated with Ti d_xy, d_x²−y², and d_z² orbitals.⁷¹ While vHSs in other Kagome metals (e.g., AV₃Sb₅) are associated with charge ordering and superconductivity, the vHSs in YbTi₃Bi₄ are further from E_F, possibly explaining the absence of such phenomena. In EuTi₃Bi₄, however, the vHS bands exhibit opposite concavities along orthogonal directions, manifesting as hole-like along Γ–M (M′) and electron-like along K–M (M′). The anisotropic vHS distribution inhibits Fermi surface nesting, which explains the absence of charge density wave phenomena.⁷³

High-resolution ARPES and theoretical calculations revealed robust surface states (SS1 and SS2) connecting different bulk vHS bands in EuTi₃Bi₄. These states persist across magnetic transitions and exhibit resilience to time-reversal symmetry breaking due to effective symmetries introduced by the crystal structure. In particular, SS2 results from SOC induced band inversion and shows nontrivial topological features.⁷³

At low temperatures, ARPES measurements revealed unusual band splitting below the magnetic ordering temperature, highlighting the interplay between magnetism and the electronic structure. This magnetic coupling introduces novel phenomena that further enrich the potential of LnTi₃Bi₄.

The electronic complexity of LnTi₃Bi₄, driven by its bilayer Kagome lattice, anisotropic vHS, and robust topological surface states, makes it a fertile platform for exploring emergent phases of matter. Its unique interplay of anisotropy, strong correlation effects, and magnetism positions it as a promising material for advancing our understanding of quantum phenomena.

3.6. Distorted Kagome

In contrast to conventional Kagome materials, which exhibit dispersionless flat bands resulting from purely geometric frustration, Cs₂Ni₃S₄ exhibits low dispersion bands near the Fermi level. The flat bands in Cs₂Ni₃S₄ originate from the Ni-based Kagome lattice, with primary contributions from the Ni d_xy and S p_x/p_y orbitals. These bands have a very low bandwidth (∼0.4 eV), similar to quasi-flat bands found in other Kagome materials. A tight-binding model considering only Ni d_xy orbitals reproduces the expected Kagome band structure, including a characteristic Kagome flat band. However, hybridization with S p_x/p_y orbitals reduces the bandwidth of the entire Kagome-derived band manifold to ∼0.3 eV, further flattening the band structure. In contrast to purely localised Kagome-flat bands, the bands in Cs₂Ni₃S₄ exhibit an extended quantum metric, suggesting potential relevance for correlated electron phenomena. The weak dispersion of these bands is due to the formation of molecular orbitals between Ni d and S p states. Consequently, doping or oxidation can shift the Fermi level into these flat bands, potentially inducing strong electron correlation effects.⁵⁴

4. Magnetic properties

4.1. Mn₃X (X = Sn, Ge)

Mn₃X exhibits a hexagonal chiral antiferromagnetic (AFM) structure (space group P63/mmc) composed of Kagome layers of Mn atoms in the ab-plane with an ordering temperature of 430 K and 365 K for Mn₃Sn and Mn₃Ge, respectively.^17,19 These layers form a breathing-type arrangement and are stacked along the c-axis²⁰ (Fig. 2b). Neutron diffraction reveals that the magnetic moments of Mn atoms form an inverse triangular spin configuration with a 120° in-plane alignment.^74–76 This spin arrangement leads to a small net FM moment due to slight canting, reducing the crystal symmetry to orthorhombic. The weak FM moment is approximately 0.003μ_B per Mn and 0.007μ_B per Mn for Mn₃Sn and Mn₃Ge, respectively.⁷⁷ This magnetic configuration influences the transport properties of the materials and is crucial for studying their topological features.

4.2. Co₃Sn₂S₂

Co₃Sn₂S₂ is a FM half-metal that exhibits long-range FM ordering below its Curie temperature of about 175 K.^15,18,25,26 The magnetism arises primarily from the Co atoms, which exhibit a spin polarization leading to a magnetic moment of approximately 0.33μ_B per Co atom along the crystallographic c-axis. X-ray magnetic circular dichroism (XMCD) studies have shown that this magnetic moment is predominantly spin derived, with negligible contribution from the orbital moment.⁷⁸

Isothermal magnetization (M–H) measurements along the H‖c orientation at low temperatures reveals a distinct hysteresis with significant coercivity, confirming the hard magnetic nature of Co₃Sn₂S₂.¹⁸ This behaviour is further enhanced by the magneto-crystalline anisotropy of the material, which strongly favours the c-axis as the magnetic easy axis, ensuring robust magnetic properties.

Interestingly, spatially resolved angle resolved photoemission spectroscopy (μ-ARPES) combined with DFT calculations has unveiled the presence of an in-plane AFM minority phase embedded in the predominantly FM matrix.⁷⁸ This interplay of FM and AFM phases adds complexity to the magnetic behaviour of the material and provides deeper insights into its electronic structure. The combination of strong magnetism, anisotropy and unique magnetic phases makes Co₃Sn₂S₂ a compelling material for both fundamental research and advanced spintronic applications.

4.3. Fe₃Sn₂

Fe₃Sn₂ is characterized by a high Curie temperature (T_c ≈ 640 K) and an exceptionally large orbital magnetic moment relative to the spin magnetic moment (m_orb/m_spin ≈ 0.22), which is approximately five times larger than that observed in elemental iron.⁷⁹ This enhancement is attributed to significant SOC effects. The Kagome bilayer geometry of Fe₃Sn₂ contributes to a strong bilayer coupling (J_bi ≈ −37.5 meV), which dominates over the in-plane nearest neighbour exchange interactions (J₁ ≈ −25 meV). This coupling results in distinct acoustic and optical spin-wave modes, whose intensities and dispersions are influenced by the out-of-plane momentum component.⁷⁹

Spin waves in Fe₃Sn₂ exhibit substantial damping, a phenomenon attributed to interactions with electron–hole pairs and the redistribution of Weyl fermions near the Fermi level. These interactions highlight a strong coupling between the spin and charge degrees of freedom of the material. Advanced techniques, including resonant inelastic X-ray scattering (RIXS), X-ray absorption spectroscopy (XAS), and magnetic circular dichroism (MCD), were used to investigate these properties. Zhang et al. revealed that the unique magnetic properties of Fe₃Sn₂ arise from its AB-stacked bilayer Kagome structure and robust SOC.⁷⁹

The damping of spin waves, which is particularly pronounced at higher momenta, highlights the significant electron–magnon coupling in this material. This behaviour emphasises the hybridized nature of the electronic and magnetic excitations and demonstrates the interplay between the Kagome bilayer structure and the intrinsic SOC effects of the material.

4.4. REMn₆Sn₆

REMn₆Sn₆ compounds have diverse magnetic properties due to the presence of magnetic Mn and RE elements and their different types of magnetic coupling, mainly inter- or intra-layer exchange interaction between the RE elements and the Mn Kagome lattice and long-range magnetic interaction (RKKY-type) between RE–RE layered structures.^30,31 In all Mn planes, the crystallographically equivalent Mn–Mn nearest neighbours are ferromagnetically coupled within the plane, with this coupling occurring across the Sn₃ layers.^{33–35,45,65,80,81} However, along the c-axis, distinct interplanar Mn–Mn bonds display AFM interactions across the [Sn₂RE] layers. Consequently, the magnetic properties of REMn₆Sn₆ are highly sensitive to the specific RE element chosen, as it plays a crucial role in modulating the balance between FM and AFM exchange interactions.

For nonmagnetic RE elements (Sc, Y, and Lu), the absence of transferred FM interaction between Mn layers across [Sn₂RE] layers makes the Mn Kagome sublattice magnetically more frustrated, leading to a complex AFM spiral structure.^31,36,69,81 The interlayer magnetic interaction between nearest and second nearest neighbour Mn Kagome lattices exhibits a transition to incommensurate AFM ordering. Below this transition, in the absence of magnetic field, the in-plane Mn layer moment changes its orientation with respect to each other, resulting in spiral structure along the c-axis. The spiral structures of ScMn₆Sn₆, YMn₆Sn₆ and LuMn₆Sn₆ were reported with transition temperatures 300 K, 333 K and 208 K respectively.^30,31,38 Ghimire et al. reported that in YMn₆Sn₆, the in-plane magnetic field along the Kagome layer can distort the magnetic state to a transverse conical spiral phase (TCS), fan like state and a forced FM state with increasing magnetic field.⁶⁵

For magnetic RE elements, the magnetic order and anisotropy are mainly dependent on the Mn–RE interaction.^36,46 From an orbital perspective, the hybridization between Mn-3d and RE-5d orbitals always favours antiparallel coupling, leading to parallel coupling with RE-4f spin in REMn₆Sn₆. For heavy RE elements, according to Hund's rule, the overall coupling is negative and RE moment order antiparallel with respect to Mn leads to ferrimagnetic (FIM) ordering.³¹ However, the interaction of RE (Er and Tm) is too weak leading to independent ordering of Mn and Er/Tm sublattices in an AFM manner.^34,36,40 The helical AFM structures have been reported for ErMn₆Sn₆ (above 75 K) and TmMn₆SN₆ (below 324 K).³⁸ In addition, the magnetic ordering of Er and Tm sublattices in ErMn₆Sn₆ and TmMn₆Sn₆ introduces a second transition with FIM (∼75 K) and AFM ordering (∼58 K) respectively.³⁰

For REMn₆Sn₆ (RE = Pr, Nd, Sm) all compounds are ferrimagnetically ordered with a Curie temperature (T_c) slightly above room temperature.⁴² Weitzer et al. reported a significant contribution of the magnetic moment coming from the Mn atoms to the total magnetization, which is below the expected magnetization for full FM alignment, suggesting the presence of AFM interactions or a more complex structure.⁴²

For heavy RE (= Gd–Ho), REMn₆Sn₆ compounds have FM layers of both RE and Mn atoms, featuring FM Mn–Mn inter-sublattice exchange and strong AFM Mn–RE inter-sublattice coupling.^30,36,40 This results in a collinear FIM behaviour below the Curie transition temperature (376 K to 435 K). Magnetic order is in-plane for RE = Gd, while additional spin reorientation occurs for RE = Tb, Dy, and Ho. In TbMn₆Sn₆ the magnetic order aligns along the c-axis at low temperatures but deviates at room temperature. For RE = Ho and Dy, a conical magnetic structure forms with the order tilted 45°–50° from the c-axis below 180 K-240 K.³⁹ For YbMn₆Sn₆, the FM transition occurs around 300 K and a FIM transition at 30 K.³⁷ The ordered Yb atoms at low temperatures can induce Yb magnetic ordering and the AFM coupling of Yb and Mn moments can give rise to a FIM state.

4.5. LnTi₃Bi₄

The evolution of magnetism in the titanium-based Kagome metals LnTi₃Bi₄ progresses through distinct magnetic states depending on the choice of the lanthanide ion (Ln), ranging from nonmagnetic to AFM and FM behaviour.⁴⁷ This variation arises from the interplay between the Kagome lattice, quasi-1D Ln zigzag chains, and the magnetic properties of the lanthanide ion. The Kagome lattice introduces electronic features such as Dirac points, FBs, and vHSs, while the Ln chains dictate the magnetic interactions. This combination results in a rich magnetic landscape, providing a platform to study anisotropic magnetism and emergent phenomena.

4.5.1. Nonmagnetic behaviour. The nonmagnetic behaviour of LnTi₃Bi₄ is observed where nonmagnetic ions, such as La³⁺, occupy the Ln site. LaTi₃Bi₄ serves as a nonmagnetic reference compound for the LnTi₃Bi₄ family, providing insight into the intrinsic electronic structure of the Kagome lattice.⁴⁷

In LaTi₃Bi₄, the Kagome-derived electronic features dominate. Dirac-like band crossings near the Fermi level and FBs slightly below it characterizes the electronic structure. The absence of magnetic moments in the Ln site ensures no magnetic ordering, simplifying the system to a purely electronic Kagome lattice with negligible magnetic contributions. This makes LaTi₃Bi₄ an ideal material for isolating the effects of lattice distortion and electronic topology without the interference of magnetism.

In YbTi₃Bi₄, ytterbium adopts the nonmagnetic divalent state (Yb²⁺), characterized by a fully filled f-shell configuration. The material exhibits an exceptionally low saturation magnetization of approximately 0.01μ_B per Yb²⁺, which is consistent with contributions from a small fraction of magnetic impurity spins or a minor presence of trivalent Yb³⁺ ions.⁴⁷

Temperature-dependent magnetization measurements reveal exceedingly weak responses, reflecting the absence of intrinsic magnetic ordering in YbTi₃Bi₄. Similarly, LaTi₃Bi₄ displays an even lower saturation magnetization of about 0.005μ_B per La³⁺ under an applied field of 7 T.

4.5.2. Antiferromagnetism. The introduction of magnetic Ln ions, such as Ce³⁺, Tb³⁺ or Gd³⁺ adds magnetic degrees of freedom to LnTi₃Bi₄. This leads to AFM ordering, where magnetic moments on adjacent Ln sites align in opposite directions.
4.5.2.1. CeTi₃Bi₄. CeTi₃Bi₄ exhibits a relatively simple AFM ground state. Magnetic measurements show a metamagnetic transition around 1 T, indicating a spin flip process from an AFM to a field polarized state. At low fields, a plateau in the magnetization emerges around 2 K.^47,82

The saturation magnetization is approximately 1.5μ_B, 70% of the expected value for Ce³⁺. This discrepancy could be due to strong crystal field effects or incomplete spin polarization. Curie–Weiss analysis confirms the magnetic moment of Ce³⁺, yielding an effective moment of 2.7μ_B, close to the theoretical value of 2.53μ_B. Heat capacity measurements display a sharp lambda anomaly at 3 K, consistent with the AFM transition.

4.5.2.2. GdTi₃Bi₄. GdTi₃Bi₄, a newly discovered member of the LnTi₃Bi₄ family, exhibits a much more complex magnetic behaviour. At zero field, GdTi₃Bi₄ adopts an AFM ground state with a Néel temperature (T_N) of about 13 K.^47,83

Magnetization measurements reveal multiple metamagnetic transitions: at H‖[100], transitions occur at critical fields H_C1 ≈ 2 T, H_C2 ≈ 3 T, and H_C3 ≈ 3.5 T. At H‖[001], similar transitions are observed, with H_C1 ≈ 1.5 T, H_C2 ≈ 3.5 T, and H_C3 ≈ 4.5 T. These transitions correspond to successive spin-flop processes, where the AFM order partially aligns with the applied field. At higher fields, the magnetic moments eventually become fully aligned, resulting in a field-polarized state. The saturation magnetization (∼7.5μ_B) agrees well with the Gd³⁺ magnetic moment (g_J = 7μ_B).

Heat capacity measurements reveal a double peak near T_N, attributed to competing magnetic interactions. This behaviour mirrors similar phenomena in other Gd-based intermetallics, such as Gd₃Ru₄Al₁₂, where sinusoidal magnetic order transitions into three-dimensional helical order.⁸⁴ The complex AFM phase diagram of GdTi₃Bi₄ makes it a promising candidate for the study of exotic spin textures, such as skyrmions.

4.5.2.3 TbTi₃Bi₄. Two distinct magnetic transitions occur, with a Néel temperature (T_N1) at 20.4 K and a lower transition (T_N2) at 3 K. These transitions correspond to changes in the AFM ordering of Tb spins, as confirmed by magnetization and specific heat measurements.^47,48,85

For magnetic fields applied along different crystallographic axes, distinct magnetic anisotropies emerge. Along the a-axis, the magnetization shows hysteresis and features a prominent 1/3 magnetization plateau, indicating spin frustration and noncollinear magnetic textures within the Tb zigzag chains. A weaker 2/3 magnetization plateau also appears, suggesting complex spin interactions. Along the b and c axes, the magnetization is linear, highlighting the quasi-1D Ising-like nature of Tb spins constrained by crystal electric fields.

Magnetic interactions in TbTi₃Bi₄ combine FM coupling along the zigzag chains (a-axis) with AFM interactions between the chains. This results in a highly anisotropic magnetic behaviour, with strong quantum fluctuations contributing to the observed frustration. These characteristics make TbTi₃Bi₄ an excellent candidate for investigating exotic magnetic textures and their interplay with electronic properties, including potential skyrmion phases in finite fields.

4.5.3. Ferromagnetism. Ferromagnetism in LnTi₃Bi₄ arises when Ln ions such as Eu²⁺, Nd³⁺ or Sm³⁺ possess strong magnetic moments that align parallel to each other under low external fields.
4.5.3.1. EuTi₃Bi₄. EuTi₃Bi₄, with Eu²⁺ (S = 7/2), exhibits robust FM behaviour. Unlike the AFM compounds, EuTi₃Bi₄ has an out-of-plane [001] magnetic easy axis, distinguishing it as the sole LnTi₃Bi₄ member with this anisotropy.^47,73

Magnetic measurements reveal a transition at ∼11 K, characterized by a sharp rise in magnetization. The saturation magnetization reaches 7μ_B, consistent with the spin-only moment of Eu²⁺. Curie–Weiss analysis confirms this, with an effective paramagnetic moment of 7.9μ_B, close to the theoretical value of 7.93μ_B.

Specific heat measurements reveal a lambda anomaly at the magnetic transition, with an entropy recovery consistent with the expected R ln(8) for Eu²⁺. The magnetization anisotropy is significant, with an order of magnitude difference between the in-plane and out-of-plane responses. Curiously, the in-plane magnetization shows an unusual peak, suggesting complex spin arrangements.

4.5.3.2. SmTi₃Bi₄. SmTi₃Bi₄, another FM compound, exhibits strong in-plane anisotropy. The magnetic easy axis is aligned with the [010] direction. Magnetic measurements reveal a transition at ∼23 K, with a saturation magnetization consistent with the Sm³⁺ moment. Importantly, SmTi₃Bi₄ is a hard magnet in this series, as indicated by isothermal magnetization measurements.^47,86

Rotation dependence studies show a rapid decrease in magnetization for directions deviating from [010]. The strong in-plane anisotropy and higher transition temperature distinguish SmTi₃Bi₄ from EuTi₃Bi₄.

Throughout the LnTi₃Bi₄ series, magnetic anisotropy plays a pivotal role, driven by the quasi-1D Ln zigzag chains. These chains induce anisotropic magnetic interactions, with the direction of the easy axis varying depending on the Ln ion. In AFM compounds, the anisotropy is manifested in the direction dependent critical fields for metamagnetic transitions. In FM systems, anisotropy determines the direction of spontaneous magnetization and affects the magnetic transition temperature.

The Kagome lattice contributes indirectly by influencing the electronic structure that mediates magnetic interactions. The slight distortion of the Kagome lattice and its impact on the DOS near the Fermi level can affect the exchange interactions, further complicating the magnetic behaviour. Future studies could further explore doping, substitution, and pressure effects to tune the magnetic and electronic properties of these intriguing materials.

4.5.4. HoAgGe. Two distinct magnetic transitions occur, with a Néel temperature (T_N1) at ∼11 K and a lower transition (T_N2) at ∼7 K.^53,87,88 These transitions correspond to changes in the AFM ordering of the Ho spins, as confirmed by magnetization and specific heat measurements. Magnetic entropy confirms the Kagome spin-ice rule through short-range correlations persisting above the ordering temperatures. The magnetic structure is dictated by Ising-like Ho³⁺ moments confined to the ab-plane. Previous neutron studies on single crystals of HoAgGe by Gegenwart and co-workers revealed the observation of a partially ordered state at 10 K in which Ho moments form clockwise or counterclockwise hexagons around triangles in the Kagome lattice, with one-third of the moments remaining disordered.⁵³ This partially ordered state obeys the Kagome spin-ice rule, with two spins pointing in and one pointing out (or vice versa) for each triangle. At lower temperatures (T < 7 K), all Ho moments align into a long-range ordered state with alternating clockwise and counterclockwise hexagons, forming a √3 × √3 ground state, i.e. a fully ordered state below 7 K is observed.

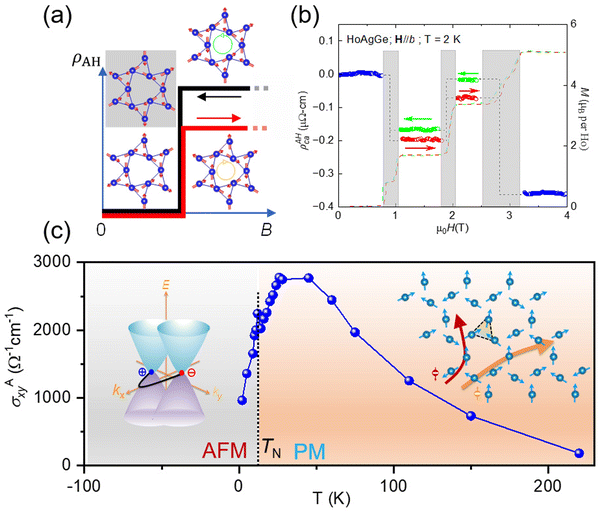
Under applied magnetic fields, HoAgGe undergoes metamagnetic transitions, characterized by discrete spin flips that preserve the ice rule. These transitions lead to the formation of distinct magnetization plateaus at fractional values of the saturation magnetization, such as 1/3, 1/6, 2/3, and 5/6. These plateaus correspond to field-induced shifts between different spin configurations, which reflect changes in the magnetic structure as a function of the applied field.^53,87,88 The occurrence of these transitions is driven by the interplay between magnetic dipolar interactions, crystal electric fields (CEF), and the external magnetic field.

The discovery of Kagome spin-ice behaviour in HoAgGe establishes it as the first metallic system to exhibit such a state.⁵³ The metallic nature introduces unique opportunities to study interactions between conduction electrons and frustrated magnetism, potentially leading to exotic phenomena like AHEs and magnetoelectric coupling.

5. Key physical properties

5.1. Anomalous Hall effect

The anomalous Hall effect (AHE) is a bulk property that arises from the Berry curvature of all occupied electronic states and requires comprehensive calculations over the entire Brillouin zone rather than focusing on a single point.^89–91 This effect is particularly significant in topological magnetic materials where the Hall resistivity can be decomposed into three components: normal Hall resistivity (ρ^N), anomalous Hall resistivity (ρ^A) and topological Hall resistivity (ρ^T).^91,92

ρ^H = ρ^N + ρ^A + ρ^T = R_OH + R_S4πM + ρ^T

where R_O is the normal Hall resistivity coefficient, which is defined by the number of carriers, and R_S is the anomalous Hall resistivity coefficient. The third term results from a nontrivial spin texture with non-zero chirality and Berry phase, which generates the topological Hall effect (THE). In the high field saturation region, the THE vanishes and the AHE dominates, simplifying the above equation to ρ^H = R_OH + R_S4πM.

5.1.1. AHEs in antiferromagnets: Mn₃X systems. The AHE typically arises in FM systems due to their finite net magnetization. However, Mn₃X, a hexagonal antiferromagnet with a non-collinear spin structure, defies this convention by exhibiting a significant AHE even at room temperature.^17,93 This antiferromagnet has a 120° inverse triangular spin configuration within a Kagome lattice framework, which generates a very weak net magnetization per Mn atom. This unique configuration enables Mn₃X to exhibit an AHE comparable to FM metals, which is driven by its intrinsic Berry curvature rather than magnetization.

The AHE in Mn₃Sn was characterized by measuring the Hall resistivity (ρ_H) and Hall conductivity (σ_H) at various magnetic field orientations and temperatures.¹⁷ Notably, Mn₃Sn exhibited a hysteretic Hall resistivity at 300 K, with a pronounced jump in ρ_H of approximately 6 μΩ cm in response to small magnetic fields (∼300 Oe) (Fig. 4d). This large, field-tunable AHE was observed over a broad temperature range from 100 K to 400 K (Fig. 4e), indicating its stability under technologically relevant conditions. The Hall conductivity reached values of ∼20 Ω⁻¹ cm⁻¹ at 300 K and nearly 100 Ω⁻¹ cm⁻¹ at 100 K, which is extraordinary for an antiferromagnet.¹⁷ Temperature dependent studies of σ_H highlighted the robustness of the AHE in Mn₃Sn. However, below 50 K, additional contributions to the AHE (100 Ω⁻¹ cm⁻¹ at 5 K) emerged due to spin canting along the c-axis in the low temperature phase. This transition enhanced the Hall response, possibly incorporating a THE component associated with spin chirality.

Similarly, Nayak et al. obtained a large AHC of ∼500 Ω⁻¹ cm⁻¹ at 2 K and ∼50 Ω⁻¹ cm⁻¹ at room temperature in Mn₃Ge, with significant anisotropy across different crystallographic planes; the xz-plane shows the largest anomalous Hall conductivity (AHC), while the xy-plane shows negligible values due to symmetry constraints (Table 3).⁹³ Moreover, Mn₃Ge exhibits a large spin Hall effect (∼1100 ħ e⁻¹ Ω⁻¹ cm⁻¹), comparable to platinum, originating from the Berry curvature mechanism.

The origin of the AHE lies in the chiral nature of the spin structure in Mn₃X. The inverse triangular configuration breaks the in-plane hexagonal symmetry, enabling the generation of the Berry curvature in momentum space. This curvature contributes to a fictitious magnetic field that governs the Hall response. In addition, the weak FM component of Mn₃X allows for the easy manipulation of the spin texture using small magnetic fields, facilitating the reversal of the sign of the Hall effect.

5.1.2. Co₃Sn₂S₂: a Kagome Weyl semimetal with a giant AHE. Co₃Sn₂S₂, with its quasi-2D Kagome lattice and strong out-of-plane magnetization, emerges as a prime candidate for realizing a large intrinsic AHE. The AHC in Co₃Sn₂S₂ reaches 1130 Ω⁻¹ cm⁻¹ at 2 K, significantly higher than typical FM materials (Table 3).¹⁴ The anomalous Hall angle (AHA) reaches a huge value of 20%. Theoretical calculations suggest that these values stem from Berry curvature hotspots near Weyl nodes and gapped nodal lines.

Thakur et al. investigated the preservation of topological properties in Co₃Sn₂S₂ upon Ni substitution, highlighting the robustness of such properties to lattice distortions and chemical changes, a key aspect of topological materials.⁹⁴ The saturation magnetization and Curie temperature decrease with increasing Ni content due to (i) increased Co–Co distances in the Kagome lattice weakening the magnetic coupling, (ii) the nonmagnetic nature of Ni atoms disrupting magnetic interactions between Co atoms, and (iii) a reduction in exchange splitting due to Ni substitution, yet the AHC remains largely intrinsic and in agreement with theoretical predictions.

Co₃Sn₂S₂ is notable for its robust AHE properties, which are attributed to Weyl nodes located near the Fermi level acting as sources of strong Berry curvature. While the intrinsic AHE is significant, the extrinsic contributions from impurity scattering can also enhance the total AHE. Liu and co-workers have investigated how Fe doping at cobalt sites can tune both intrinsic and extrinsic contributions to achieve record-breaking AHC and AHA values.⁹⁵ Fe atoms replace Co atoms in the Kagome lattice, introducing asymmetric scattering that enhances the extrinsic component of the AHE. Fe has one less valence electron than Co, which slightly shifts the Fermi energy without significantly altering the intrinsic Berry curvature contributions. This approach preserves the intrinsic AHC while leveraging extrinsic effects for additional enhancement. As a result, Fe doping increases the AHC to 1850 Ω⁻¹ cm⁻¹ and AHA to a record 33%, surpassing values reported for other AHE materials⁹⁵ (Fig. 9b). These improvements are due to the synergistic contributions of intrinsic and extrinsic mechanisms, separated by the Tian-Ye-Jin (TYJ) scaling model.

Fig. 9 (a) Negative magnetoresistance induced by a chiral anomaly.¹⁴ (b) AHC as a function of Fe concentration in Co_3–xFe_xSn₂S₂.⁹⁵ Anomalous Hall resistivity as a function of magnetic field in (c) pristine and (d) Cl doped Co₃Sn₂S₂ single crystals.⁹⁶ (e) Anomalous Hall resistivity of both crystals as a function of temperature.⁹⁶ (f) Anomalous Hall conductivity (AHC) of both crystals as a function of temperature.⁹⁶ (a) Is reproduced with permission from ref. 14. (b) Is reproduced with permission from ref. 95.

Pristine Co₃Sn₂S₂, characterized by Weyl nodes approximately 60 meV above the Fermi energy, offers limited electrical mobility and magnetoresistance (MR) due to the substantial energy difference between the Weyl points and the Fermi level (Fig. 9a). Chlorine doping, targeting the sulphur sites, shifts the Fermi energy by 15 meV closer to the Weyl points without altering the magnetic structure, as verified by ARPES and DFT calculations.⁹⁶ The resistivity drops fivefold in the FM phase, and the MR increases from 17% in undoped samples to 155% in doped ones at 9 T, accompanied by an electron mobility of 4000 cm² V⁻¹ s⁻¹ – twice that of pristine Co₃Sn₂S₂. Electrical transport measurements show that chlorine doping enhances both electron and hole mobilities, aligning the electronic carrier concentration closer to theoretical predictions for Weyl semimetals. Magnetotransport studies highlight a temperature dependent AHE with notable enhancements in the AHC (Fig. 9c–f). At 40 K, the AHC peaks at 1680 Ω⁻¹ cm⁻¹, approximately 30% higher than that in undoped samples, which is attributed to the proximity of the Fermi level to the Weyl points. The enhanced AHC arises from a mixed contribution of intrinsic and extrinsic mechanisms, analysed using scaling laws that separate skew scattering and side-jump effects. Chlorine doping reduces resistivity and enhances carrier lifetimes, leading to pronounced skew scattering contributions below 60 K, while intrinsic effects dominate at higher temperatures.

Compared to other AHE materials, such as FM transition metals and Heusler compounds, Co₃Sn₂S₂ stands out due to its large intrinsic AHC and AHA. This distinction underscores the advantages of Weyl semimetals with topologically nontrivial band structures for achieving a giant AHE.

5.1.3. Fe₃Sn₂: nonlinear AHE and skyrmion correlations. The AHC (σ^A_xy) of Fe₃Sn₂ reaches ∼400 Ω⁻¹ cm⁻¹ at 5 K and is linked to topologically enhanced Berry curvature near small gap regions and avoided band crossings near the Fermi level Table 3.⁹⁷ A sudden increase in σ^A_xy at ∼100 K corresponds to a spin reorientation transition, where the magnetization shifts from the c-axis to the ab-plane, causing significant Fermi surface modifications that amplify the Berry curvature. This behaviour contrasts with polycrystalline Fe₃Sn₂, where grain boundary scattering introduces inhomogeneity, resulting in a different scaling index.⁹⁸

Wang et al. observed a giant THE of ∼2.01 μΩ cm at 300 K and 0.76 T in Fe₃Sn₂, highlighting its correlation with skyrmion states and non-collinear spin textures driven by magnetic frustration.⁹⁹ This giant THE occurs at low magnetic fields (<1.3 T) and disappears when the field aligns the Fe moments, confirming its origin in real-space topological spin textures.

Recently, Wu and co-workers investigated a novel nonlinear Hall effect governed by quantum geometric properties of Bloch electrons in the Kagome magnet Fe₃Sn₂.¹⁰⁰ They experimentally observed and theoretically explained the magneto-nonlinear Hall effect (mNLHE), where the Hall response is nonlinear in both electric and magnetic fields, unlike conventional Hall effects. This discovery links the response to the Berry curvature, an intrinsic geometric property of the electronic band structure, and highlights its dominant orbital origin, termed anomalous orbital polarizability (AOP). Theoretical models identify Weyl nodes within 10 meV of the Fermi level as hotspots for large AOP values, linking the nonlinear response to topological features of the band structure.

5.1.4. AHEs in REMn₆Sn₆ compounds. Recent studies have reported the observation of AHEs in REMn₆Sn₆ compounds Table 3.^30,31 The AHC and its angular dependence have been found to be strongly correlated with the magnetic structure and electronic topology in these materials.³⁵ For AFM REMn₆Sn₆ compounds, the zero-field AHE is not explicitly observed in their Hall resistivity. The THE has been detected in AFM REMn₆Sn₆, which is attributed to the frustrated interlayer exchange interactions leading to strong magnetic fluctuations.¹⁰¹ The THE appears only in the transverse conical spiral (TCS) magnetic phase at elevated temperatures⁶⁵ (Fig. 7f). However, in the polarized FM state at high fields (B > B_sat), the topologically non-trivial spin structure cannot be maintained, and the topological contribution to the Hall effect disappears, leaving the AHE as the dominant contribution. YMn₆Sn₆ exhibits metallic behaviour with weak anisotropy. A relatively large intrinsic AHE was observed in YMn₆Sn₆, with AHC reaching 45 Ω⁻¹ cm⁻¹ in one direction and 300 Ω⁻¹ cm⁻¹ in another, comparable to the FIM TbMn₆Sn₆. TmMn₆Sn₆ has a more complex magnetic structure due to its double magnetic sublattices and possesses a non-collinear magnetic structure with a transition temperature of 350 K.¹⁰¹ The THE was also observed by Liu et al. in TmMn₆Sn₆, like the case of YMn₆Sn₆, which is attributed to the presence of the TCS magnetic structure and non-zero chirality.

ErMn₆Sn₆ exhibits complex magnetic behaviour, lying between the FIM and AFM states.³⁶ Below 100 K, a small magnetic field triggers a metamagnetic transition, causing a sharp jump in the magnetization. At low temperatures, the ρ^H shows a slight linear increase with the field, without saturation, up to 9 T for both H‖ab plane and H‖c axis configurations (Fig. 7f). However, between 200 and 300 K, ρ^H increases rapidly with the field for H‖c, surpassing the critical field for the metamagnetic transition. A narrow hysteresis in ρ^H is observed in the AFM phase when the field is applied along the ab-plane, but not for the c-axis. The ordinary Hall coefficient (R_O) is negative for H‖ab and positive for H‖c at 200 K, possibly due to changes in the electronic structure. THE contribution is minimal compared to AHE contribution in both configurations.^41,102

FIM REMn₆Sn₆ compounds exhibit a tunable electronic and magnetic state, making them ideal for exploring large AHEs. Notably, GdMn₆Sn₆ shows a significant intrinsic contribution to Hall conductivity, supported by Fermi surface calculations and resistivity anisotropy, indicating a 3D electronic structure.¹⁰³ HoMn₆Sn₆ shows a remarkable AHE due to Berry curvature, with a spin reorientation transition at lower temperatures. The AHE is primarily driven by an intrinsic mechanism, although the extrinsic side-jump mechanism becomes significant near the spin reorientation transition.³³ GdMn₆Sn₆ shows an intrinsic AHC of 223 Ω⁻¹ cm⁻¹, comparable to that of Fe₃Sn₂, attributed to reduced dimensionality, while HoMn₆Sn₆ and YbMn₆Sn₆ exhibit AHCs of 120 Ω⁻¹ cm⁻¹ and 32 Ω⁻¹ cm⁻¹, respectively. NdMn₆Sn₆ and SmMn₆Sn₆ also exhibit large intrinsic AHCs (∼100–200 Ω⁻¹ cm⁻¹) below room temperature, highlighting the tunability of the Berry curvature over different rare earth elements. Overall, the intrinsic AHC in Kagome magnets such as REMn₆Sn₆ remains robust to temperature, demonstrating the stability of the Berry curvature in the occupied state.

5.1.5. GdTi₃Bi₄ and TbTi₃Bi₄: AHEs in zig-zag chain magnets. The AHE in GdTi₃Bi₄ arises from its intricate magnetic textures and electronic structure.⁸³ This material features one-dimensional zigzag Gd spin chains within a Kagome lattice framework, which introduces unique magnetic and transport phenomena. At low temperatures, GdTi₃Bi₄ exhibits two successive metamagnetic transitions under an external magnetic field, accompanied by distinct anomalies in Hall resistivity and magnetization.

The zigzag Gd chains result in an orthorhombic crystal structure with reduced symmetry, contributing to the emergence of complex spin textures. At the first metamagnetic transition, the formation of striped domain walls with reversed magnetic chirality is observed. These domain walls are associated with abrupt jumps in the Hall resistivity, indicating a significant contribution of domain wall skew scattering to the AHE.

In the intermediate magnetic field regime, corresponding to a one-third magnetization plateau, the material exhibits homogeneous magnetic textures, potentially indicative of a skyrmion phase. This phase is characterized by chiral spin arrangements and could explain the observed AHE even in the absence of domain walls. Such behaviour aligns with theoretical predictions and experimental findings in other skyrmion-hosting systems, underscoring the topological origin of the AHE in this field range.

TbTi₃Bi₄ demonstrates an exceptionally large AHE, with an AHC reaching a record high value of 6.2 × 10⁵ Ω⁻¹ cm⁻¹ at 2 K, among the highest reported for any magnetic material Table 3.⁸⁵ The AHE originates from the coupling between the Tb spin textures and the electronic bands of the Kagome lattice, with contributions from noncollinear spin configurations and spin chirality.

The anomalous Hall resistivity displays a pronounced hysteresis consistent with the metamagnetic transitions, highlighting the influence of magnetic phase boundaries on transport properties. With decreasing temperature, the AHE becomes more prominent, peaking in the magnetic plateau regime associated with the 1/3 magnetization plateau. The strong AHE in this regime suggests a chiral magnetic texture, possibly skyrmions, stabilized by the frustrated zigzag chains.

Angle-dependent Hall resistivity measurements reveal additional complexity, with distinct hysteresis loops evolving as the magnetic field orientation changes. This behaviour reflects the interplay between the quasi-1D zigzag chain magnetism and quasi-2D electronic structure of the Kagome lattice. The AHC and AHA reach maximum values of 4.3 × 10⁵ Ω⁻¹ cm⁻¹ and 79%, respectively, surpassing known skyrmion-hosting materials.

These results emphasise the crucial role of mixed dimensionality in TbTi₃Bi₄, where the interplay between quasi-1D and quasi-2D structures regulates the coupling between magnetism and electronic band topology, providing a platform for future spintronic applications.

5.1.6. AHE in a distorted Kagome lattice, HoAgGe. The study of the electrical resistivity of HoAgGe single crystals provides critical insight into the electronic transport properties of the material, especially in relation to their magnetic transitions and spin configurations.

The temperature dependent resistivity, measured along the c-axis in zero magnetic field, shows typical metallic behaviour at high temperatures. At low temperatures, two distinct anomalies emerge: (i) a sharp peak in the resistivity is observed at this temperature, associated with the onset of AFM ordering. This behaviour arises due to the suppression of spin disorder scattering as the Ho³⁺ spins align into an ordered state. (ii) A subtle shoulder-like feature in the resistivity indicates a spin reorientation transition. This shift in the spin configuration slightly perturbs the electronic scattering mechanisms and marks a second magnetic phase transition.^87,88

The magnetic field dependent resistivity of HoAgGe has been measured with magnetic fields applied along both the a/b and c axes. The results reveal distinct differences in the transverse (B‖a/b) and longitudinal (B‖c) MR and AHE.^87,88

5.1.7. Transverse configuration (B‖a/b). At low temperatures (T < 1.95 K) the resistivity increases significantly, reaching up to 100% of its zero-field value at 14 T.⁸⁸ This large positive MR cannot be attributed solely to the ordinary Lorentz force and indicates complex electron scattering mechanisms influenced by spin configurations and magnetic transitions. Furthermore, the MR shows a jump at the metamagnetic transitions between the 1/3 and 2/3 plateaus and between the 2/3 plateau and the saturated state. In the middle of the 1/3 and 2/3 plateaus, the MR hysteresis persists, reflecting a uniform magnetic order within each plateau but different transport properties for the near-degenerate states¹⁰⁴ (Fig. 10a). Similarly, the AHE shows a clear hysteresis as a function of the magnetic field (Fig. 10b, Table 3). A significant feature is the contrasting behaviour between increasing and decreasing field sweeps, with the AHE plateau values differing depending on the direction of the sweep. Within each plateau, the hysteresis indicates the existence of near-degenerate states with identical net magnetization but different Berry curvatures, leading to variations in the intrinsic contribution to the AHE.¹⁰⁴ At higher temperatures or weaker fields, thermal activation overcomes the kinetic barriers and suppresses the hysteresis. The disappearance of hysteresis above 5–7 K reflects the reduced stability of discrete plateaus and the merging of near-degenerate states.

Fig. 10 (a) Schematic representation of the emergent time-reversal-like degenerate states, resulting in finite field hysteresis of the anomalous Hall resistivity in the distorted Kagome lattice of HoAgGe.¹⁰⁴ (b) Observation of finite hysteresis in the field-dependent AHE, while the hysteresis in the field dependence of the magnetization vanishes at 2 K.¹⁰⁴ (c) Temperature variation of the AHC below and above the Néel temperature.⁸⁷ (a) and (b) Are reproduced with permission from ref. 104.

Table 3 Physical properties of Kagome materials

Materials	Transition temperature	Topological phenomena	Properties	Ref.
FM: ferromagnetic; AFM: antiferromagnetic; SC: superconductor; AHC: anomalous Hall conductivity; ANE: anomalous Nernst effect; CDW: charge density wave; PDW: pair density wave; AHE: anomalous Hall effect; THE: topological Hall effect; vHS: van Hove singularity; FB: flat band; FIM: ferrimagnetic.
Mn3Sn	Noncollinear AFM (∼430 K)	Weyl semimetal	AHC (∼100 Ω^−1 cm^−1 at 100 K), ANE (∼0.6 μV K^−1 at 200 K)	17 and 56
Mn3Ge	Noncollinear AFM (∼365 K)	Weyl semimetal	AHC (500 Ω^−1 cm^−1 at 2 K)	93
Co3Sn2S2	FM (∼175 K)	Weyl semimetal	AHC (∼1130 Ω^−1 cm^−1 at 2 K), ANE (∼3–5 μV K^−1 at 80 K)	14, 18 and 105
Fe3Sn2	Noncollinear FM (∼640 K)	Massive Dirac point, skyrmion	AHC (∼400 Ω^−1 cm^−1 at 5 K), spin reorientation, magneto-nonlinear Hall effect, spin wave propagation and quantum information application	97, 100, 106 and 107
AV3Sb5 (A = K, Cs, Rb)	SC (∼0.9–2.5 K)	Dirac semimetal	CDW, PDW, nematic order, symmetry breaking	9, 30, 108 and 109
LaRu3Si2	SC (∼7 K)	Unconventional superconductor	Nodeless Kagome superconductor	110–113
CeRu2	SC (∼6 K) with magnetic order (T ∼40 K)	Unconventional superconductor	Strong electronic correlations, nodeless superconductivity	114–117
REMn6Sn6	FM: RE = Yb	Chern gapped Dirac fermions, FBs near Fermi level	AHC (∼100–300 Ω^−1 cm^−1)	30, 31, 118 and 119
	AFM: RE = Sc, Y, Tm, Lu, Er		ANE (∼2–2.4 μV K^−1)
	FIM: Gd, Tb, Dy, Ho, Pr, Nd, Sm
FeGe	Collinear AFM (∼400 K)	Magnetic skyrmions	CDW, spin reorientation, Racetrack memory applications	49 and 120–122
LnTi3Bi4	FM: Ln = Eu, Nd, Sm	Linear Dirac-like state, multiple vHSs, double FBs	AHC: ∼6.2 × 10^5 Ω^−1 cm^−1 at 2 K for Ln = Tb	85
	AFM: Ln = Ce, Tb, Gd
	NM: Ln = La, Yb
HoAgGe	Noncollinear AFM (∼11 K)	Time reversal like degeneracy, Weyl semimetal	Distorted Kagome lattice, spin ice, plateaus in magnetization, MR and AHE, THE	87, 88 and 104
Cs2Ni3S4	Nonmagnetic	Flat band	Correlated insulating state	54

---

The hysteretic behaviour of the AHE and MR in HoAgGe reveals a complex interplay of symmetry, spin configurations, and transport phenomena.¹⁰⁴ These findings highlight the role of Berry curvature and kinetic barriers in shaping transport properties and provide insights into the exotic physics of Kagome spin ices and frustrated systems more broadly.

In addition, the transverse MR follows a field dependence between B² and linear behaviour, deviating from conventional metallic systems. This unusual dependence is likely due to the coexistence of uncompensated electron and hole carriers, as well as spin scattering effects.⁸⁸

Below the Néel temperature (T_N ≈ 11 K), HoAgGe exhibits an AFM spin-ice configuration with noncoplanar spins that create scalar spin chirality, leading to a large intrinsic AHE characterized by an AHC of 700 Ω⁻¹ cm⁻¹ at 2 K, one of the highest reported for AFM systems⁸⁷ (Fig. 10c). This large AHC arises from the Berry curvature generated by Weyl points near the Fermi level due to SOC and time-reversal symmetry breaking. Surprisingly, the AHC remains significant at temperatures up to 45 K, with a maximum value of 2800 Ω⁻¹ cm⁻¹ driven by spin-cluster induced skew scattering. This extrinsic contribution arises from noncoplanar spin fluctuations enhanced by the distorted Kagome lattice geometry. The topological Hall resistivity reaches ∼1.6 μΩ cm at 2 K and 3 T, highlighting the contribution of real-space Berry curvature from noncoplanar spin structures. The THE disappears at high fields, where the spins align and noncoplanar textures disappear. The THE is most pronounced at low temperatures and decreases as thermal fluctuations disrupt spin chirality.

The findings demonstrate that structural distortions in Kagome lattices can enhance topological transport phenomena, such as the AHE and THE, by tuning Berry curvature and spin textures. HoAgGe serves as a model system for studying the interplay between magnetism, lattice geometry, and topology, offering insights into the design of materials with robust topological responses for spintronic and quantum applications.

5.2. Anomalous Nernst effect

The anomalous Nernst effect (ANE) is the thermoelectric counterpart of the AHE, both of which are directly influenced by the Berry curvature of a material's electronic structure. The ANE, characterized by the generation of a transverse voltage in response to a temperature gradient, is conventionally associated with magnetization in FM materials.¹⁸ In magnetic Weyl semimetals, the ANE and AHE are topologically driven, making them essential tools for probing the nature of charge carriers and intrinsic magnetic properties.

Interestingly, Ikhlas et al. observed a significant ANE in Mn₃Sn despite its negligible net magnetization (∼0.002μ_B per Mn). A transverse thermopower of ∼0.35 μV K⁻¹ was observed at room temperature (Fig. 4f), peaking at ∼0.6 μV K⁻¹ around 200 K (Fig. 4g).⁵⁶ The ANE in Mn₃Sn exhibits hysteresis with field sweeps, indicating its robustness and independence from conventional magnetization scaling laws. Combined first-principles calculations and experimental observations confirmed that the Kagome lattice structure of Mn₃Sn induces a chiral magnetic order, locally breaking time-reversal symmetry and reducing crystal symmetry from sixfold to twofold. This structure induces a significant Berry curvature at the Fermi energy (E_F), which governs the ANE.

Co₃Sn₂S₂ is particularly interesting because its Weyl points are close to the Fermi level, and its magnetic Kagome lattice promotes strong SOC, which enhances Berry curvature effects.^15,26 The Nernst effect has been less studied compared to the Seebeck effect, mainly because most devices require an external magnetic field. This dependence is a practical challenge for thermoelectric applications. Materials with intrinsic magnetization, particularly hard magnetic materials, offer a promising avenue for realizing zero-field Nernst devices.

Co₃Sn₂S₂ is identified as a hard magnetic material with a Curie temperature of ∼177 K and significant coercivity at low temperatures. The anomalous Nernst thermopower (S^A_xy) of Co₃Sn₂S₂ was measured as a function of temperature at the zero magnetic field.¹⁸ A peak S^A_xy of about 3 μV K⁻¹ was observed at 80 K. In contrast to the AHE, which is determined by the Berry curvature of all occupied bands, the Nernst effect is sensitive to the Berry curvature near E_F. The band structure influenced by SOC showed the presence of Weyl points and nodal lines. The Berry curvature, associated with these features, was identified as a key factor contributing to the transverse thermoelectric response.

Recently, Yang et al. studied the ANE of Bridgman-grown Co₃Sn₂S₂.¹⁰⁵ Below T_C, the ANE exhibits a strong temperature dependence, with S^A_xy reaching a maximum of ∼5 μV K⁻¹ at 70 K, a value significantly larger than that observed in conventional FM metals. The corresponding anomalous transverse thermoelectric conductivity (σ^A_xy) peaks at ∼10 A K⁻¹ m⁻¹, surpassing other magnetic semimetals by one to two orders of magnitude. The findings highlight the role of the Berry curvature near the Weyl points in enhancing the ANE.

Furthermore, YMn₆Sn₆ exhibits a high Néel temperature (∼340 K), making it an exceptional candidate for room temperature applications.⁶⁵ Its electronic structure with Dirac points and FBs near the Fermi level gives rise to a significant Berry curvature, which drives the large ANE. At 300 K, the ANE reaches approximately 2 μV K⁻¹.¹¹⁸ Notably, the ANE mechanism in YMn₆Sn₆ diverges from the magnetization-dependent linear scaling observed in conventional ferromagnets, emphasizing the role of the intrinsic Berry curvature rather than the magnetic moment magnitude. Magnetization studies reveal complex spin structures, including distorted spiral (DS), TCS, and fan-like (FL) states, each corresponding to distinct magnetic transitions that are influenced by applied magnetic fields (Fig. 7g). These magnetic transitions are reflected in the magneto-Seebeck and Nernst thermopower measurements, which demonstrate a strong field dependence, especially around the transition points. The entropy changes associated with these transitions highlight the coupling between magnetic and charge dynamics, further enhancing the thermoelectric performance of the material. DFT calculations confirm the presence of an intrinsic Berry curvature near the Fermi level and accurately reproduce the experimental AHC and ANE results, reinforcing the topological nature of the material.

Recently, Madhogaria et al. also investigated the thermal and thermoelectric transport properties of ScMn₆Sn₆.¹¹⁹ Thermal Hall effect, ANE and thermal conductivity measurements revealed the role of Berry curvature in both momentum and real space topologies. ScMn₆Sn₆ exhibits multiple magnetic phases like YMn₆Sn₆, with the TCS phase playing a pivotal role in the observed phenomena. The anomalous signals, including a large Nernst coefficient of ∼2.21 μV K⁻¹ at room temperature, are attributed to the interplay between the unique spin textures of the material and its electronic band structure characterized by Dirac points, vHSs, and FBs. Unlike skyrmion systems, ScMn₆Sn₆ exhibits topological Nernst and thermal Hall effects due to the spin chirality of the TCS phase, confirming its potential as a non-skyrmion topological material. In addition, the Seebeck coefficient, thermal conductivity, and magnetization measurements underline a strong coupling between magnetic transitions and transport properties, which is further supported by DFT calculations.

5.3. Spin reorientations in Fe₃Sn₂

Wu et al. identified a low-temperature spin reorientation transition at about 80 K through magnetization and AC susceptibility measurements, which was attributed to changes in magnetic anisotropy rather than spin glass behaviour, as confirmed by neutron powder diffraction (NPD) data.¹⁰⁶ This transition is closely related to the material's “breathing”-like Kagome lattice structure, characterized by two distinct Fe–Fe bond lengths that evolve with temperature, leading to a symmetric, ideal Kagome lattice at higher temperatures. The lattice constant ratio c/a decreases monotonically with temperature, correlating with changes in anisotropy that drive the spin reorientation. Thermal properties reveal significant anharmonic lattice vibrations above 280 K, as observed by heat capacity measurements and Raman spectroscopy, suggesting that anharmonicity plays a crucial role in the non-monotonic thermal conductivity and high temperature lattice behaviour of the material. Phonon dispersion analysis highlights distinct contributions from Fe and Sn atoms, with evidence of strong anharmonicity affecting thermal and magnetic properties. The heat capacity of the material exceeds the Dulong-Petit limit at high temperatures, implicating contributions from intrinsic anharmonicity, electronic, and thermal expansion effects, while phonon–phonon scattering dominates the observed phonon softening in Raman spectra. The study resolves prior debates on the nature of the low temperature magnetic state, emphasizing that the spin reorientation, rather than a structural transition, underpins the magnetic anomalies.

Using temperature- and frequency-dependent infrared spectroscopy, Biswas et al. investigated how spin reorientation at low temperatures influences the electronic structure of the material, revealing optical fingerprints of Dirac fermions, FBs and spin-induced phenomena.¹²³ Previous studies have shown that spins reorient with temperature even in the absence of external fields, but the implication for the electronic structure remains unclear. They have addressed this gap using advanced optical measurements.^124–126 The optical conductivity reveals two-step absorption features characteristic of Dirac fermions. These correspond to two distinct Dirac cones below the Fermi energy. Temperature dependent measurements show that these features are largely unaffected by spin reorientation, confirming the robustness of Dirac nodes buried in the electronic structure.

Low energy optical absorption peaks correlate with FBs and their associated vHSs. A strong low-energy absorption feature (∼100 cm⁻¹) evolves significantly with temperature and saturates below 150 K.¹²³ Magnetic susceptibility measurements confirm spin reorientation in this region, with spins aligning in the Kagome plane. This reorientation opens a gap (∼12 meV) at specific Weyl nodes, in agreement with theoretical predictions. The experimental observation of a spin reorientation induced band gap at Weyl nodes provides crucial insights into the dynamic control of topological states by magnetic manipulation.

Recently, Soh and co-workers have shown that spin reorientation transition in Fe₃Sn₂ is first order in nature, analogous to liquid–gas transitions, with a critical endpoint in the field-temperature phase space, using techniques such as magnetometry and variable temperature magnetic force microscopy (MFM)⁶¹ (Fig. 6a). The transition involves abrupt changes in the magnetic easy axis, with spins realigning from the c-axis to the Kagome plane as the temperature decreases. Nucleation and growth processes during the transition have been imaged and show that new magnetic phases form at the domain walls of the high temperature phase and later migrate to the domain centres. The coexistence of phases and dense domain patterns contributes to an inhomogeneous electronic structure, which affects the electrical conductivity of the material. The study provides a direct visualization of the transition, resolving ambiguities in prior reports about the order of the spin reorientation. The nucleation and self-organization observed in Fe₃Sn₂ are influenced by disorder and structural imperfections. Additionally, the thermal hysteresis observed between cooling and warming cycles confirms the first order nature of the transition. The complex domain evolution and its dependence on the thermal history suggest a significant coupling between magnetic and electronic properties, potentially influencing magnetotransport in Fe₃Sn₂. Small-angle neutron scattering (SANS) data show that the magnetic scattering is nearly isotropic in the low temperature (LT) phase, whereas it becomes anisotropic in the high temperature (HT) phase, reflecting the presence of mesoscopic stripe-like magnetic domains.⁶¹

As discussed above, the material exhibits spin reorientation with decreasing temperature, with the magnetic easy axis gradually tilting from the c-axis to the ab-plane. The uniaxial magnetic anisotropy (UMA) varies with temperature and influences the evolution of the magnetic domain structures. Using Lorentz transmission electron microscopy (LTEM), Zhang and co-workers observed the evolution of magnetic domains over a wide temperature range (130–300 K).¹²⁷ In the zero magnetic field, Fe₃Sn₂ forms stripe-like domains with out-of-plane magnetization. Upon cooling, these stripes transform into vortex-like domains as the spin texture changes. Micromagnetic simulations confirm that these transformations are governed by the UMA and exchange interactions. Applying an external magnetic field perpendicular to the Kagome plane induces a progression from stripe domains to isolated skyrmionic bubbles. The transformation involves intermediate states, such as dumbbell-shaped domains, before stabilizing as skyrmionic bubbles at higher fields (∼800 mT). These bubbles exhibit variable spin textures, characterized by Bloch lines and topological spin structures. The use of transport of intensity equation (TIE) analysis reveals helicity and vorticity variations within these bubbles, demonstrating their adaptability under external stimuli. The skyrmionic bubbles observed in Fe₃Sn₂ include both trivial and topologically nontrivial configurations.

MR measurements reveal peaks corresponding to transitions from stripe domains to skyrmionic bubbles and from bubbles to saturation states. The critical fields shift with temperature, enabling the construction of a magnetic phase diagram that maps the skyrmion formation region. The skyrmionic states persist up to 400 K, suggesting potential applicability at even higher temperatures.

5.4. Magnetism and charge density waves in FeGe

At room temperature, FeGe exhibits an A-type collinear AFM order with a Néel temperature (T_N) of approximately 400 K. In this state, the Fe spins within each Kagome layer are ferromagnetically aligned, but the layers themselves are antiferromagnetically coupled along the crystallographic c-axis. As the temperature decreases, the magnetic structure undergoes significant changes. Below ∼60 K, the Fe spins reorient into a double-cone configuration, introducing a canted AFM order.⁴⁹ This spin reorientation indicates a complex interplay of magnetic anisotropies. At 30 K, FeGe experiences an additional magnetic phase transition that further modifies its magnetic structure.^128,129 When a magnetic field is applied along the c-axis, FeGe undergoes a spin-flop transition at a critical field of about 7 T at low temperatures. Beyond this field, the Fe spins predominantly align in the Kagome plane, highlighting the tunable magnetic behaviour of the material. This combination of structural and magnetic features makes FeGe a compelling system for studying the interplay between Kagome lattice geometries and complex magnetic phases.

In 2022, Teng et al. demonstrated the emergence of a short-range charge density wave (CDW) below T_CDW ≈ 100 K in FeGe where it coexists with the AFM order of the material.⁴⁹ Unlike copper oxides and nickelates, where the CDW typically precedes or parallels the magnetic order, the CDW in FeGe enhances the AFM moment and induces an AHE, suggesting a coupling mechanism distinct from previously studied systems. ARPES experiments highlight vHSs near the Fermi level at specific high-symmetry points of the Brillouin zone, such as the M and L points (Fig. 11a). Two vHSs (vHS1 and vHS2) have been identified at the M point: vHS1 is slightly above the Fermi level, while vHS2 is located below it. A third vHS (vHS3) is found at the L point, also above the Fermi level (Fig. 11b). These vHSs and the quasi-straight sections of the Fermi surface provide evidence for nesting-driven instabilities that are likely to contribute to the formation of the CDW. Yi and co-workers identified a dispersion kink (Fig. 11e) in the ARPES data near 30 meV, attributed to electron–phonon interactions, which was further confirmed by inelastic neutron scattering (INS) measurements.¹³⁰

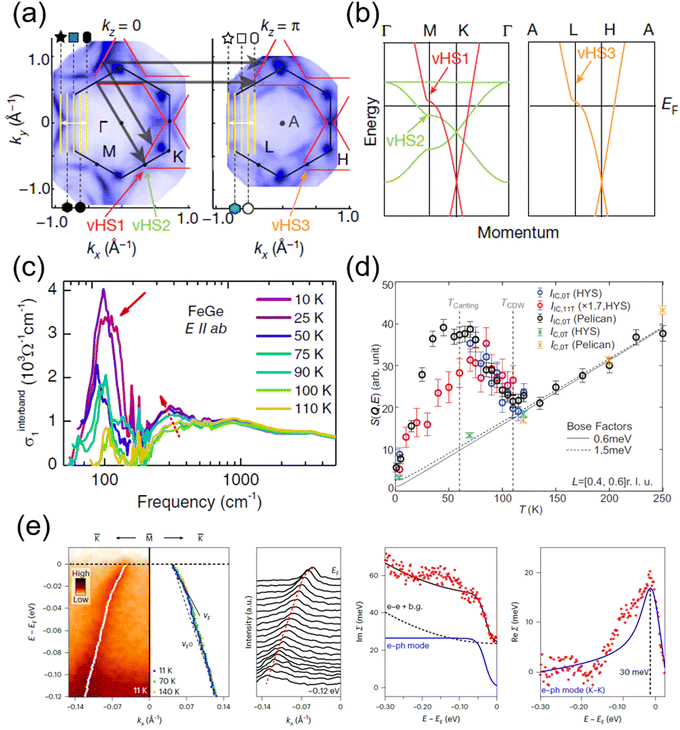Fig. 11 (a) ARPES data showing the experimental observation of vHSs in FeGe.⁴⁹ (b) Schematic of the locations of vHSs in the electronic structure.⁴⁹ (c) Experimental observation of interband transfers below 100 K.¹³¹ (d) Low energy spin structure and excitations as a function of temperature and field.¹³² (e) Experimental observation of a dispersion kink and a bosonic mode at 30 meV.¹³⁰ (a) and (b) Are reproduced with permission from ref. 49. (c) Is reproduced with permission from ref. 131. (d) Is reproduced with permission from ref. 132. (e) Is reproduced with permission from ref. 130.

Using advanced X-ray scattering techniques and theoretical calculations, the study identifies a unique 2 × 2 × 2 superstructure in the A-type antiferromagnetic (A-AFM) phase of FeGe, characterized by charge superlattice peaks along the c-axis and phonon anomalies distinct from conventional electron–phonon coupling.¹³³ Magnetic exchange interactions in FeGe modulate the band structure, bringing the vHSs close to E_F and enabling nesting conditions conducive to CDW formation. The CDW order, in turn, enhances the magnetic moment in the AFM phase, indicating a strong coupling between these orders. Furthermore, X-ray diffraction and diffuse scattering (DS) experiments revealed the presence of a multi-q CDW phase with propagation vectors associated with the nesting of vHSs and magnetic symmetry points.¹³⁴ A precursor phase with quasi-long-range bond orientation order is identified above the CDW transition temperature, characterized by anisotropic diffuse scattering and structural dimerization of Ge atoms. The observed CDW is found to emerge from a topological melting process mediated by defect unbinding, resembling a Kosterlitz–Thouless-like transition. Subires et al. proposed that the CDW transition is an order–disorder phenomenon influenced by lattice frustration and spin-phonon coupling.¹³⁴

Utilizing infrared spectroscopy supported by DFT calculations revealed that the 100 K structural phase transition, previously associated with CDW instability, instead results in a distinct band reconstruction without a conventional CDW gap opening.¹³¹ This transition manifests as temperature-dependent spectral weight redistribution in the low-energy optical conductivity, showing new interband transitions below 100 K rather than the high-energy shifts typical of CDW materials (Fig. 11c). Despite structural distortions like trihexagonal rearrangements and partial dimerization of Ge atoms, no clear gap signature is observed, challenging the conventional understanding of CDWs in Kagome systems. This identifies strong electronic correlations as a key factor differentiating FeGe from other Kagome systems such as AV₃Sb₅ and ScV₆Sn₆, where distinct CDW gaps are observed.^135–138

The absence of a CDW gap is also observed in the optical spectra, suggesting a unique mechanism that differs from conventional CDW materials. This study identifies low energy spectral weight shifts driven by a trihexagonal distortion of the Fe–Kagome planes and partial dimerization of in-plane Ge1 atoms (Fig. 11d). This transition induces band splitting rather than gap opening, which is confirmed by shifts in interband optical conductivity and Fano resonance broadening, indicating strong electron–phonon coupling.¹³⁹

At temperatures below 60 K, the system enters an incommensurate magnetic phase characterized by a double-cone AFM structure along the c-axis and gapless incommensurate spin excitations.¹³² These excitations persist at higher temperatures, suggesting the dominant role of itinerant electrons and Fermi surface nesting rather than local exchange interactions in driving the incommensurate order. Furthermore, single-crystal X-ray diffraction and scanning tunnelling microscopy (STM) experiments revealed a unique 2 × 2 CDW in FeGe, which persists below the spin canting transition temperature (∼60 K) without a corresponding long-range structural modulation. The authors attribute this phenomenon to a competition between the CDW and the canted AFM order, which dynamically influences the underlying crystal structure.¹³²

Using de Haas–van Alphen (dHvA) quantum oscillation measurements and first-principles calculations, the study reveals key insights into the Fermi surface (FS) topology of this material.¹⁴⁰ Measurements under high magnetic fields (up to 45.2 T) uncover four distinct cyclotron orbits, including one associated with the 2 × 2 folded Brillouin zone, with light cyclotron masses indicating weak electron correlation effects. The angular dependence of the dHvA frequencies further demonstrates the three-dimensionality of the FS. Notably, experimental observations and DFT calculations confirm that the FS largely retains its unreconstructed character despite the presence of CDWs, suggesting a limited influence of short-range CDW on FS morphology.

Recently, Santi and co-workers have investigated the effect of pressure on the charge density wave states in the Kagome metal FeGe.¹⁴¹ Using high-pressure X-ray diffraction and DFT, they showed that the system transitions from a 2 × 2 CDW phase at low pressures to a quasi-long range √3 × √3 CDW order at higher pressures above 15 GPa. This evolution is characterized by changes in the propagation vectors and structural modulation within the lattice, with the √3 × √3 phase becoming the stable ground state at high pressure.

This establishes FeGe as a rare platform where strong electron correlations, magnetic order, and topology converge, opening new avenues for exploring emergent quantum states in Kagome lattice systems.

6. Superconductivity in Kagome-lattice systems

6.1. AV₃Sb₅

The Kagome superconductors AV₃Sb₅ (A = K, Rb, Cs) exhibit an intricate interplay between charge density waves (CDWs), superconductivity, and symmetry breaking, making them an ideal platform for studying correlated electron phenomena.^9,30,108,109

These compounds crystallize in a P6/mmm space group, featuring a Kagome lattice of vanadium atoms.¹⁴² Within this structure, Sb1 atoms occupy the centers of the V hexagons, while Sb2 atoms form antimony layers that are sandwiched between the V Kagome layers and A-site cation layers (Fig. 12a). Despite minor differences across the series, their band structures remain qualitatively similar, with the Fermi level primarily dominated by the d-orbitals of vanadium atoms in the Kagome net (Fig. 12b and c).^108,143 These multiorbital materials host a range of van Hove singularities (vHSs) at the M-points of the Brillouin zone, originating from d_xy, d_yz, and d_xz orbitals, with both m-type and p-type vHSs lying close to the Fermi energy (E_F).^11,144 Additionally, a Dirac crossing at the K-point is observed below E_F.¹⁴²

Fig. 12 (a) Crystal structure of AV₃Sb₅. (b) Electronic band structure of AV₃Sb₅.¹¹ (c) Fermi surface mapping of CsV₃Sb₅.¹⁴³ (d) Temperature dependence of resistivity, showing the superconducting transition at low temperature.¹⁴⁵ (e) Temperature dependence of heat capacity, showing the CDW peak at 94 K for CsV₃Sb₅.¹⁴⁵ (f) Temperature–pressure phase diagram of AV₃Sb₅.¹⁴⁶ (b) Is reproduced with permission from ref. 11. (c) Is reproduced with permission from ref. 143. (d) and (e) Are reproduced with permission from ref. 145. (f) Is reproduced with permission from ref. 146.

A prominent feature of AV₃Sb₅ is the presence of a CDW transition at T_CDW ≈ 80–110 K, where a (2 × 2 × 2 or 2 × 2 × 4) superlattice modulation forms, significantly reconstructing the Fermi surface and affecting superconductivity (Fig. 12d and e).^{145,147–153} Unlike conventional CDWs, which are primarily driven by electron–phonon interactions, the CDW state in AV₃Sb₅ appears to be electronic in origin, with experimental evidence suggesting the importance of Fermi surface nesting, van Hove singularities, and strong electronic correlations in stabilizing this ordered phase. A striking characteristic of the CDW state in AV₃Sb₅ is the breaking of time-reversal symmetry (TRS), as revealed by zero-field muon spin relaxation (μSR) experiments, which detect spontaneous internal magnetic fields below T_CDW.^109,154,155 This result suggests the formation of a chiral flux phase, where loop currents circulate within the Kagome lattice, producing local magnetic fields without net magnetization.^156–159 The emergence of such a time-reversal symmetry breaking (TRSB) state is highly unusual in a nonmagnetic material and points to a possible orbital current-driven charge order, making AV₃Sb₅ fundamentally different from conventional CDW systems. This chiral charge order also has significant implications for superconductivity, as the existence of spontaneous currents could induce an unconventional pairing mechanism, potentially leading to topological superconductivity. Beyond TRSB, the CDW phase in AV₃Sb₅ also breaks inversion and rotational symmetry (C₆ → C₂), as demonstrated by STM and X-ray diffraction experiments, which reveal a bond order pattern that modifies the electronic structure and introduces anisotropic transport properties.^160–162

The interplay between CDW order and superconductivity in AV₃Sb₅ is another crucial aspect of its phase diagram, as pressure-dependent studies have shown that suppressing the CDW state enhances superconductivity, suggesting a competition between these two orders (Fig. 12f).^{146,150,163–165} This behavior is evident in resistivity and magnetotransport measurements, where the superconducting transition temperature (T_C ≈ 2–3 K) increases under pressure as the CDW state weakens. Despite this apparent competition, the coexistence of CDW order and superconductivity raises intriguing questions, particularly since TRSB is observed in both the charge-ordered and superconducting states, implying that superconductivity in AV₃Sb₅ may also be unconventional.^{150,154,166–169} The presence of van Hove singularities near the Fermi level in AV₃Sb₅ further enhances the CDW instability, as density functional theory (DFT) calculations and angle-resolved photoemission spectroscopy (ARPES) confirm that flat bands and Dirac points contribute to the electronic reconstruction at T_CDW.^{144,170–174} The exact nature of the CDW phase remains a topic of debate, as different experimental techniques have provided evidence for both unidirectional and chiral charge orders, suggesting the possibility of multiple competing CDW phases.^175–179 Additionally, optical and Raman spectroscopy studies indicate that electron–phonon coupling alone cannot account for the observed CDW transition, reinforcing the argument that electronic interactions and momentum-space instabilities drive the charge ordering in AV₃Sb₅.^180–183 The observation of TRSB, inversion symmetry breaking, and rotational symmetry breaking makes AV₃Sb₅ unique among Kagome superconductors, as it hosts an intricate electronic order that strongly influences its superconducting properties. The competition between charge order and superconductivity, coupled with the presence of spontaneous currents and broken symmetries, provides strong evidence that AV₃Sb₅ may host topological superconductivity and exotic quantum phases. These findings place AV₃Sb₅ at the forefront of modern condensed matter research, offering a rich playground for exploring unconventional superconductivity, correlated electronic states, and spontaneous symmetry-breaking phenomena in Kagome lattice systems.

6.2. LaRu₃Si₂

In addition to the well-studied AV₃Sb₅ series, LaRu₃Si₂ stands out as a layered Kagome lattice superconductor with the highest known T_c (∼7 K) among the Kagome systems.^109–112 Muon spin rotation (μSR) measurements reveal a single s-wave superconducting gap, confirming that the superconducting state is fully gapped without nodes and remains robust under hydrostatic pressures up to 2 GPa, indicating stability against external perturbations.¹¹³ The band structure calculations highlight the electronic features of the Kagome lattice, including flat bands, Dirac points, and van Hove singularities near the Fermi level, which are key to enhancing electronic correlations and superconductivity. A crucial finding is that electron–phonon interactions alone cannot fully account for the observed T_c, as theoretical calculations predict a much lower T_c (∼1.2 K) than the experimentally observed value, suggesting that additional electronic interactions derived from the Kagome lattice play a dominant role. Notably, LaRu₃Si₂ does not exhibit a charge density wave (CDW) state, which distinguishes it from the well-known AV₃Sb₅ Kagome superconductors that display strong CDW ordering. The absence of a competing CDW phase allows superconductivity in LaRu₃Si₂ to develop without suppression, contributing to its robust superfluid density and stable superconducting gap under pressure.

Furthermore, the study finds that LaRu₃Si₂ has a high DOS at the Fermi level, largely due to the narrow Kagome bands and the proximity of van Hove singularities, which may enhance pairing interactions beyond conventional Bardeen–Cooper–Schrieffer (BCS) mechanisms.¹¹³ A comparative analysis of the T_c to superfluid density ratio (T_c/λ_eff⁻²) places LaRu₃Si₂ closer to unconventional superconductors, rather than to conventional phonon-mediated BCS superconductors. This suggests that additional electronic interactions, possibly from Kagome flat bands or van Hove singularities, contribute to the superconductivity enhancement. Guguchia and co-workers also found that under pressure, neither the T_c nor the superfluid density changes significantly under pressure, suggesting that LaRu₃Si₂ is already in an optimal superconducting state at ambient pressure.¹¹³ The findings collectively establish LaRu₃Si₂ as a moderately coupled, nodeless Kagome superconductor, where superconductivity is likely enhanced by electronic correlations originating from the Kagome lattice rather than conventional phonon interactions.

6.3. CeRu₂

CeRu₂ is a rare system in which superconductivity (T_c ≈ 6 K) coexists with magnetic order (T ≈ 40 K).^{109,114–116} Density functional theory (DFT) calculations show that Ru atoms form a Kagome lattice in the [111] direction and host flat bands near the Fermi surface, indicating strong electronic correlations and possible flat-band magnetism.¹⁸⁴ C. Mielke III et al. presented a detailed study focusing on its superconducting gap structure and magnetic behavior using muon spin rotation (μSR) spectroscopy.¹¹⁷ The superconducting order parameter follows an anisotropic s-wave gap symmetry, confirming nodeless superconductivity. The superfluid density (λ⁻²) and the T_c/λ⁻² ratio show that CeRu₂ behaves more like an unconventional superconductor than a conventional BCS superconductor. In addition to superconductivity, the μSR experiments identify three distinct magnetic anomalies at T₁ ≈ 110 K, T₂ ≈ 65 K, and T₃ ≈ 40 K, suggesting complex magnetic interactions.¹¹⁷ Notably, these magnetic features are enhanced under an applied magnetic field, reinforcing the magnetic origin of these transitions.

By systematically varying the Ru content (CeRu_2−x, with x = 0.10, 0.24), L. Z. Deng et al. found that the superconducting critical temperature (T_c) and upper critical field (H_c2) can be tuned, establishing a link between Ru stoichiometry and superconducting properties.¹¹⁷ High pressure experiments reveal an unusual phase diagram, where superconductivity initially weakens with increasing pressure up to ∼28 GPa, but then resurges beyond this threshold, accompanied by the emergence of a secondary superconducting transition. Above 75 GPa, both T_c and the magnetic transition temperature decrease, indicating competition between magnetism and superconductivity. Interestingly, at extreme pressures (∼141 GPa), T_c saturates, hinting at a pressure-driven stabilization of the superconducting state.

CeRu₂ is unique due to the coexistence of superconducting and magnetic states, as compared to other Kagome superconductors such as AV₃Sb₅ and LaRu₃Si₂. The findings suggest that charge order, magnetism, and topology play a crucial role in the superconducting state, providing a foundation for exploring exotic pairing mechanisms and correlated electron phenomena in Kagome superconductors.

6.4. Others

Resistivity, magnetization, specific heat, and muon spin rotation (μSR) spectroscopy establish that Re₂Zr is a moderately coupled, type-II superconductor with T_C ≈ 6.65 K.¹⁸⁵ Crystal structure analysis reveals that Re atoms form a distorted Kagome lattice, which is known to host exotic electronic states, including flat bands and Dirac cones. Zero-field μSR measurements detect spontaneous internal magnetic fields below T_C, providing strong evidence for broken time-reversal symmetry in the superconducting state, suggesting the presence of an unconventional superconducting order parameter.

Recently, Cava and co-workers discovered superconductivity in LaIr₃Ga₂, a novel Kagome lattice superconductor with T_C ≈ 5.2 K.¹⁸⁶ Unlike previously studied Kagome superconductors such as LaRu₃Si₂, which exhibits a distorted Kagome lattice, LaIr₃Ga₂ features a perfectly ordered Kagome lattice composed of 5d Ir atoms, known for strong SOC. Structural characterization by single crystal X-ray diffraction confirms that LaIr₃Ga₂ adopts a CeCo₃B₂-type structure (space group P6/mmm), with Kagome layers of Ir atoms sandwiched between La and Ga layers.¹⁸⁷ Magnetization, resistivity, and heat capacity measurements confirm bulk superconductivity, with an upper critical field ≈4.71 T and a lower critical field ≈7.1 mT, classifying it as a type-II superconductor. Heat capacity analysis suggests weakly coupled BCS superconductivity with a Sommerfeld coefficient γ ≈ 15 mJ mol⁻¹ K⁻², indicating moderate electron correlations.¹⁸⁶ Electronic structure calculations reveal Dirac points, flat bands, and spin–orbit induced band splitting near the Fermi level, confirming the dominant role of Ir 5d states. The presence of SOC-driven electronic states makes LaIr₃Ga₂ a promising platform for exploring topological superconductivity and exotic quantum phases in Kagome materials.

7. Applications of Kagome magnets

7.1. Racetrack memory

Hard disk drives have achieved remarkable data storage densities, but their dependence on intricate and fragile mechanical components highlights the need for solid-state alternatives that can offer equivalent or even greater storage capacities. Racetrack memory is an emerging candidate in this domain, encoding information in a magnetic nanoribbon where data are stored as a sequence of magnetic domains, either up or down, separated by domain walls (DWs).^188,189 These domain walls can be electrically manipulated via spin torque, enabling efficient reading and writing of data. However, to realize its full potential as a competitive technology, racetrack memory faces critical challenges. These include reducing the critical currents required for domain wall motion, ensuring high operational velocities, and mitigating the adverse effects of material defects. Skyrmions, nanoscale magnetic vortices with topological protection, have emerged as a promising solution to these challenges, offering robust, energy-efficient, and high-density data storage options for racetrack memory systems.

A recent study conducted by Yu et al. demonstrated the stabilization of skyrmion crystals (SkX) in FeGe films across a broad range of temperatures and magnetic fields, particularly when the film thickness is reduced below the skyrmion lattice constant (Fig. 13a and b).¹²⁰ This achievement is crucial for enabling room temperature operation of skyrmion-based racetrack memory devices. Skyrmions, being significantly smaller than conventional domain walls, allow for increased storage densities while maintaining high energy efficiency due to their low depinning currents.^190–193 This facilitates smooth and reliable motion of skyrmions along racetracks driven by spin transfer torque (STT).¹⁹⁴ Furthermore, the study emphasises the importance of film thickness in skyrmion stabilization, showing that thinner films expand the SkX phase diagram, whereas thicker films limit its stability. FeGe, with its high helical transition temperature (280 K) and strong Dzyaloshinskii–Moriya interaction (DMI), proves to be an excellent material for stabilizing skyrmions at low magnetic fields (∼0.1 T) and near room temperature, making it suitable for integration into standard operating environments.

Fig. 13 (a) The variation of the skyrmion lattice with the external magnetic field at T = 260 K and (b) the variation of the skyrmion lattice with the temperature at B = 0.1 T in FeGe.¹²⁰ (c) Schematic representation of the fundamental mechanism underlying the formation of wavepacket precursors.¹⁰⁷ (a) and (b) Are reproduced with permission from ref. 120.

A further advance in skyrmion research has been the ability to control the helicity, or the in-plane swirling direction of magnetization, of skyrmion bubbles. A recent study conducted by Wang and co-workers demonstrated that helicity reversal can be achieved using current pulses with densities ranging from 10⁹ to 10¹⁰ A m⁻² and pulse widths between 100 ns and 1 μs.¹²¹ Unlike conventional DMI-stabilized skyrmions with fixed helicity, skyrmionic bubbles possess helicity as a binary degree of freedom, enabling energy efficient current induced switching. This feature was experimentally validated using in situ Lorentz transmission electron microscopy (LTEM) and computational simulations. The helicity reversal is driven by local pinning effects and dipole–dipole interactions with transient distortions and reformation of spin textures during the switching process. The nanotrack devices have been designed to isolate topologically stable skyrmionic bubbles, ensuring reliable helicity control under controlled conditions.

By leveraging geometrically confined systems, it has also been demonstrated that skyrmions can be stabilized over a wide temperature range (100–630 K), further enhancing their applicability in practical racetrack memory devices.¹²² The findings provide valuable insights into optimizing skyrmion dynamics by tailoring pinning centres and current parameters, addressing challenges such as the skyrmion Hall effect and ensuring precise control of skyrmion motion. These advances pave the way for the integration of skyrmion-based elements into racetrack memories, enabling robust, low-energy manipulation of topological spin textures. Due to their high density, energy efficiency, and operational stability, skyrmions have the potential to revolutionize data storage and processing technologies, making racetrack memory a viable solid-state alternative to traditional storage systems.

7.2. Spin wave propagation and quantum information application

Spin waves, which are collective oscillations of electron spins, are increasingly seen as a promising means to transport spin-based quantum information over macroscopic distances.¹⁹⁵

Recently, Orenstein and co-workers explored the propagation of spin wavepackets in the Kagome ferromagnet Fe₃Sn₂, emphasizing its potential for advancing spin-based quantum information transport (Fig. 13c).¹⁰⁷ Time-resolved magneto-optic Kerr effect (TR-MOKE) microscopy is a powerful technique used to excite and detect spin wavepackets with high spatial and temporal resolution. TR-MOKE microscopy uncovers the phenomenon of spin wave “precursors,” where magnetization signals propagate over 20 μm in less than 100 ps – far exceeding the expected time based on the group velocity.¹⁹⁶ These precursors arise from the interplay between long-range magnetic dipole interactions and the unique biaxial magnetic anisotropy of Fe₃Sn₂, which produces a saddle-point magnetostatic spin-wave (MSW) dispersion relation distinct from uniaxial systems. This dispersion leads to anisotropic propagation, with forward modes along certain directions and backward modes in others, governed by the alignment of wavevectors relative to the magnetization. The observed dynamics reveal a transition from Gaussian to non-Gaussian wavepacket profiles at larger separations, highlighting contributions from both propagating and non-propagating modes. Unlike conventional spin waves dominated by short-range exchange interactions, the behaviour here is dictated by magnetostatic interactions, showcasing a novel regime of spin transport. Additionally, the study demonstrates how optical excitation launches coherent wavepackets with spatially and temporally resolved properties, offering insights into spin dynamics in low-dimensional magnetic systems. These findings underscore the promise of Fe₃Sn₂ for spintronic applications, particularly in enabling ultrafast, long-range transmission of spin information in FM systems. By bridging the gap between experimental observations and theoretical modelling, the research contributes to a deeper understanding of magnetostatic wave behaviour in Kagome lattices and paves the way for the exploration of similar effects in other quasi-2D magnetic materials, reinforcing the role of Fe₃Sn₂ as a model system for ultrafast spin transport in quantum technologies.

Spin information in Fe₃Sn₂ travels over distances of more than 20 μm in less than 100 ps, with effective velocities far exceeding those inferred from neutron scattering experiments. This ultrafast transport is attributed to magnetostatic interactions, which dominate over short-range exchange effects. The findings highlight the potential of Fe₃Sn₂ for enabling high-speed spintronic applications.

The ability to rapidly and efficiently transmit spin information over macroscopic distances positions Fe₃Sn₂ as a promising material for spintronic applications. Lee et al. demonstrated the feasibility of utilizing magnetostatic waves for long-range quantum information transport in FM systems. The findings also provide insights into the design of materials and devices that exploit the interplay between magnetic anisotropy and spin wave dispersion.

8. Future outlook

Topological Kagome magnets have recently emerged as a fascinating class of quantum materials, offering fertile ground for exploring the interplay between magnetism, topology, and electronic correlations. The unique lattice geometry of Kagome structures—characterized by corner-sharing triangles-enables these materials to host fascinating phenomena, including flat electronic bands, Dirac fermions, vHSs and robust spin-polarized states. This has spurred extensive research into their fundamental properties and potential technological applications. Here, we summarize the research progress on a few representative topological Kagome materials and their use in cutting-edge applications, including racetrack memory and quantum information technologies. Despite significant progress in understanding and harnessing their properties, many challenges and opportunities lie ahead.

Recent research has predominantly centred on properties such as AHC and the THE in three-dimensional bulk Kagome materials, primarily due to the strong interlayer interactions in these systems. However, materials within the LnTi₃Bi₄ family present a unique opportunity as they can be readily exfoliated down to a few layers or even a monolayer. This characteristic makes them particularly intriguing for investigating topological properties in the two-dimensional limit, potentially uncovering novel physical phenomena. To advance this field, high-throughput computational screening combined with machine learning offers a powerful approach for systematically discovering new Kagome magnets. Machine learning algorithms can also aid in predicting optimal synthesis conditions, thereby minimizing the reliance on traditional trial-and-error experimentation. Recent high-throughput first-principles calculations and machine learning approaches have led to the prediction of several novel Kagome materials with intriguing superconducting, charge density wave, and magnetic properties.

Wang and co-workers predicted that Kagome materials adopting the AV₃Sb₅-type prototype, specifically CsM₃Te₅ (M = Ti, Zr, Hf), exhibit superconducting critical temperatures ranging from 3.5 K to 8 K. Calculated formation energy and phonon dispersion confirm the thermodynamic and dynamic stability of these compounds, indicating their feasibility for experimental synthesis.¹⁹⁷

Beyond superconductivity, new materials such as NaZr₃As₅, MgNi₆Ge₆, HfNi₆In₆ and ScNb₆Sn₆ have been predicted to be dynamically stable and potentially host charge density wave (CDW) phases, adding to the growing list of exotic electronic materials in the Kagome family.^198,199

In the realm of magnetic Kagome materials, high-throughput density functional theory combined with atomistic spin dynamics simulations has led to the discovery of stable Co₃Pb₂S₂ and Co₃Tl₂S₂, which are predicted to exhibit ferromagnetic order with Curie temperatures of about 329 K and 266 K, respectively – significantly higher than that of Co₃Sn₂S₂ (∼170 K), making them promising candidates for room temperature applications.²⁰⁰

Theoretical approaches play a crucial role in predicting the magnetic ground states and calculating the magnetic moments of atoms within the Kagome sublattice across various compounds.²⁰¹ Recently, Jovanovic and Schoop demonstrated the effectiveness of combining chemical heuristics, local symmetry analysis, and density functional theory (DFT) based calculations to predict band structures in Kagome materials, offering deeper insights into their distinctive magnetic properties.²⁰² While computational methods provide rapid predictions of material structures and characteristics, experimental validation remains essential to accurately assess the true potential of these materials. The synergy between theory and experiment is essential for refining structure–property relationships, ensuring that computational predictions align with real-world observations.

Despite the rapid advancement of computational techniques, relatively few studies have experimentally validated or refuted theoretical predictions.^203–205 While theoretical tools accelerate discoveries, they must be closely integrated with experimental methodologies to enhance predictive accuracy. Experimental validation involves a systematic approach, beginning with solid-state synthesis using techniques such as arc melting, solid-state reaction, and high-temperature annealing. High quality single crystals are grown using flux methods, Bridgman, or chemical vapor transport methods, allowing for precise structural and physical property investigations. X-ray diffraction (XRD) and single crystal XRD confirm phase purity and structural integrity.

To explore superconducting behavior, low temperature electrical resistivity, magnetic susceptibility, and specific heat measurements are performed using instruments such as a Physical Property Measurement System (PPMS) and a SQUID magnetometer, as exemplified by the experimental verification of superconductivity in AV₃Sb₅ compounds. CDW phenomena are examined through heat capacity, temperature-dependent XRD, Raman spectroscopy, and ARPES, which reveal structural distortions and electronic band modifications.

For magnetic Kagome materials, magnetization and transport experiments are crucial for characterizing magnetic transitions and topological properties. Techniques such as AHE measurements, neutron diffraction, and muon spin relaxation (μSR) are utilized to probe magnetic ordering and Berry curvature effects. The integration of material synthesis, structural characterization, transport measurements, and advanced spectroscopic techniques provides a comprehensive framework for the experimental realization and understanding of novel Kagome materials, ultimately bridging the gap between theoretical predictions and practical applications.

Achieving the quantum Hall effect (QHE) at high temperatures in Kagome magnets represents a pivotal challenge and opportunity in the field. The QHE, typically observed at cryogenic temperatures, arises from topologically protected edge states and strong magnetic interactions. To achieve this phenomenon at high temperatures, advances in material design, strain engineering, and electronic structure tuning are essential. Realizing the QHE at high temperatures will enable transformative applications in quantum technologies, including fault-tolerant quantum computing and ultra-sensitive magnetic sensors, unlocking the full potential of Kagome magnets.

Theoretically, it has been proposed that a two-dimensional Kagome lattice, when time-reversal symmetry is broken due to magnetic ordering, could host a quantum anomalous Hall effect (QAHE) if the electron filling lies within an energy gap.²⁰⁶ Despite these insights, experimental efforts to isolate a magnetic 2D Kagome layer and achieve quantized AHC have not yet been successful. Moving forward, the identification of suitable 2D magnetic Kagome materials is key to realizing this theoretical scenario, opening the door to groundbreaking advances in the study of topological quantum phenomena.

The Kagome lattice has attracted considerable attention in quantum materials research after the theoretical prediction by Wen and co-workers in 2011 about the potential realization of fractional quantum Hall states at high temperatures. However, the experimental realization is still in its infancy state. The discovery of cleaner flat-band Kagome magnets is crucial for the realization of the fractional quantum Hall effect (FQHE), as these systems enhance electron interactions due to their high DOS. The recent discovery of a charge density wave in FeGe is a promising development in the quest to uncover charge ordering in other topological Kagome magnets.

The exploration of moiré superlattices in twisted two-dimensional (2D) materials has paved the way for the discovery of exotic correlated and topological states. While much of the focus has been on nonmagnetic systems like twisted bilayer graphene, where moiré patterns result in flat electronic bands and a variety of correlated phases, recent developments have extended these ideas to Kagome materials, revealing intriguing phenomena. For instance, a twisted bilayer of Kagome lattices can produce emergent FBs akin to those seen in magic-angle twisted bilayer graphene. The potential for groundbreaking discoveries is further heightened with the study of twisted magnetic Kagome lattices, as they introduce the interplay between magnetization textures and topological surface states.²⁰⁷ Experimental investigations in this area could significantly advance our understanding of correlated and topological phases in moiré systems, offering unprecedented opportunities for innovation.

Achieving magnetic topological superconductivity in Kagome magnets involves harnessing their unique lattice geometry, intrinsic magnetism, and topological properties. One key strategy is to induce superconductivity via the proximity effect by coupling Kagome magnets to conventional superconductors while preserving their magnetic and topological characteristics. Alternatively, intrinsic superconductivity can be realized by leveraging FBs, which enhance electron correlations, and by doping or applying pressure to tune the electronic filling and magnetic interactions. The natural breaking of time-reversal symmetry in these materials, due to their magnetic ordering, can further enable chiral superconducting states. These approaches provide a promising pathway for engineering magnetic topological superconductivity for quantum applications.

Topological Kagome magnets represent a rapidly evolving frontier in condensed matter physics and materials science. While significant challenges remain in synthesis, understanding of correlated phenomena, and device integration, the future holds immense promise. Advances in synthesis techniques, computational tools, and interdisciplinary collaboration will pave the way for realizing robust topological and magnetic properties under ambient conditions. Moreover, the unique features of Kagome magnets-from FBs and Dirac points to novel quantum states-make them ideal candidates for transformative applications in spintronics, quantum computing, and beyond. Addressing these challenges and capitalizing on the emerging opportunities will unlock the full potential of Kagome magnets in the coming decades.

Data availability

No primary research results or codes have been included. No new data have been generated or analysed as part of this review.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work is supported by IISER Bhopal.

References

1. C. Kittel, Introduction to Solid State Physics, Wiley, Hoboken, NJ, 8th edn, 2004.
2. Q. Wang, H. Lei, Y. Qi and C. Felser, Acc. Mater. Res., 2024, 5, 786–796.
3. N. Chowdhury, K. I. A. Khan, H. Bangar, P. Gupta, R. S. Yadav, R. Agarwal, A. Kumar and P. K. Muduli, Proc. Natl. Acad. Sci., India, Sect. A, 2023, 93, 477–495.
4. I. Syozi, Prog. Theor. Phys., 1951, 6, 306–308.
5. M. Kang, S. Fang, L. Ye, H. C. Po, J. Denlinger, C. Jozwiak, A. Bostwick, E. Rotenberg, E. Kaxiras, J. G. Checkelsky and R. Comin, Nat. Commun., 2020, 11, 4004.
6. M. Kang, L. Ye, S. Fang, J. S. You, A. Levitan, M. Han, J. I. Facio, C. Jozwiak, A. Bostwick, E. Rotenberg, M. K. Chan, R. D. McDonald, D. Graf, K. Kaznatcheev, E. Vescovo, D. C. Bell, E. Kaxiras, J. van den Brink, M. Richter, M. Prasad Ghimire, J. G. Checkelsky and R. Comin, Nat. Mater., 2020, 19, 163–169.
7. K. Sun, Z. Gu, H. Katsura and S. Das Sarma, Phys. Rev. Lett., 2011, 106, 236803.
8. E. Tang, J. W. Mei and X. G. Wen, Phys. Rev. Lett., 2011, 106, 236802.
9. J. X. Yin, B. Lian and M. Z. Hasan, Nature, 2022, 612, 647–657.
10. W. S. Wang, Z. Z. Li, Y. Y. Xiang and Q. H. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 115135.
11. Y. Hu, X. Wu, B. R. Ortiz, S. Ju, X. Han, J. Ma, N. C. Plumb, M. Radovic, R. Thomale, S. D. Wilson, A. P. Schnyder and M. Shi, Nat. Commun., 2022, 13, 2220.
12. Y. Luo, Y. Han, J. Liu, H. Chen, Z. Huang, L. Huai, H. Li, B. Wang, J. Shen, S. Ding, Z. Li, S. Peng, Z. Wei, Y. Miao, X. Sun, Z. Ou, Z. Xiang, M. Hashimoto, D. Lu, Y. Yao, H. Yang, X. Chen, H. J. Gao, Z. Qiao, Z. Wang and J. He, Nat. Commun., 2023, 14, 3819.
13. L. Ye, M. Kang, J. Liu, F. von Cube, C. R. Wicker, T. Suzuki, C. Jozwiak, A. Bostwick, E. Rotenberg, D. C. Bell, L. Fu, R. Comin and J. G. Checkelsky, Nature, 2018, 555, 638–642.
14. E. Liu, Y. Sun, N. Kumar, L. Muechler, A. Sun, L. Jiao, S. Y. Yang, D. Liu, A. Liang, Q. Xu, J. Kroder, V. Süβ, H. Borrmann, C. Shekhar, Z. Wang, C. Xi, W. Wang, W. Schnelle, S. Wirth, Y. Chen, S. T. B. Goennenwein and C. Felser, Nat. Phys., 2018, 14, 1125–1131.
15. D. F. Liu, A. J. Liang, E. K. Liu, Q. N. Xu, Y. W. Li, C. Chen, D. Pei, W. J. Shi, S. K. Mo, P. Dudin, T. Kim, C. Cacho, G. Li, Y. Sun, L. X. Yang, Z. K. Liu, S. S. P. Parkin, C. Felser and Y. L. Chen, Science, 2019, 365, 1282–1285.
16. J. Kübler and C. Felser, EPL, 2014, 108, 67001.
17. S. Nakatsuji, N. Kiyohara and T. Higo, Nature, 2015, 527, 212–215.
18. S. N. Guin, P. Vir, Y. Zhang, N. Kumar, S. J. Watzman, C. Fu, E. Liu, K. Manna, W. Schnelle, J. Gooth, C. Shekhar, Y. Sun and C. Felser, Adv. Mater., 2019, 31, 1806622.
19. J. F. Qian, A. K. Nayak, G. Kreiner, W. Schnelle and C. Felser, J. Phys. D: Appl. Phys., 2014, 47, 305001.
20. E. Krén, J. Paitz, G. Zimmer and É. Zsoldos, Phys. B, 1975, 80, 226–230.
21. M. Zabel, S. Wandinger and K. J. Range, Z. Naturforsch., B, 1979, 34, 238–241.
22. S. Natarajan, G. V. S. Rao, R. Baskaran and T. S. Radhakrishnan, J. Less-Common Met., 1988, 138, 215–224.
23. X. Wan, A. M. Turner, A. Vishwanath and S. Y. Savrasov, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205101.
24. G. Xu, H. Weng, Z. Wang, X. Dai and Z. Fang, Phys. Rev. Lett., 2011, 107, 186806.
25. Q. Wang, Y. Xu, R. Lou, Z. Liu, M. Li, Y. Huang, D. Shen, H. Weng, S. Wang and H. Lei, Nat. Commun., 2018, 9, 3681.
26. N. Morali, R. Batabyal, P. K. Nag, E. Liu, Q. Xu, Y. Sun, B. Yan, C. Felser, N. Avraham and H. Beidenkopf, Science, 2019, 365, 1286–1291.
27. P. Vaqueiro and G. G. Sobany, Solid State Sci., 2009, 11, 513–518.
28. Q. Wang, S. Sun, X. Zhang, F. Pang and H. Lei, Phys. Rev. B, 2016, 94, 075135.
29. D. C. Fredrickson, S. Lidin, G. Venturini, B. Malaman and J. Christensen, J. Am. Chem. Soc., 2008, 130, 8195–8214.
30. Y. Wang, H. Wu, G. T. McCandless, J. Y. Chan and M. N. Ali, Nat. Rev. Phys., 2023, 5, 635–658.
31. X. Xu, J. X. Yin, Z. Qu and S. Jia, Rep. Prog. Phys., 2023, 86, 114502.
32. B. Lv, R. Zhong, X. Luo, S. Ma, C. Chen, S. Wang, Q. Luo, F. Gao, C. Fang, W. Ren and Z. Zhong, J. Alloys Compd., 2023, 957, 170356.
33. H. Zeng, G. Yu, X. Luo, C. Chen, C. Fang, S. Ma, Z. Mo, J. Shen, M. Yuan and Z. Zhong, J. Alloys Compd., 2022, 899, 163356.
34. G. Dhakal, F. Cheenicode Kabeer, A. K. Pathak, F. Kabir, N. Poudel, R. Filippone, J. Casey, A. Pradhan Sakhya, S. Regmi, C. Sims, K. Dimitri, P. Manfrinetti, K. Gofryk, P. M. Oppeneer and M. Neupane, Phys. Rev. B, 2021, 104, L161115.
35. L. Gao, S. Shen, Q. Wang, W. Shi, Y. Zhao, C. Li, W. Cao, C. Pei, J. Y. Ge, G. Li, J. Li, Y. Chen, S. Yan and Y. Qi, Appl. Phys. Lett., 2021, 119, 092405.
36. W. Ma, X. Xu, J. X. Yin, H. Yang, H. Zhou, Z. J. Cheng, Y. Huang, Z. Qu, F. Wang, M. Z. Hasan and S. Jia, Phys. Rev. Lett., 2021, 126, 246602.
37. L. Jiang, F. R. Fan, D. Chen, Q. Mu, Y. Wang, X. Yue, N. Li, Y. Sun, Q. Li, D. Wu, Y. Zhou, X. Sun and H. Liang, J. Phys.: Condens. Matter, 2024, 36, 315701.
38. G. Venturini and B. Malaman, J. Magn. Magn. Mater., 2015, 377, 159–171.
39. Y. Lee, R. Skomski, X. Wang, P. P. Orth, Y. Ren, B. Kang, A. K. Pathak, A. Kutepov, B. N. Harmon, R. J. McQueeney, I. I. Mazin and L. Ke, Phys. Rev. B, 2023, 108, 045132.
40. B. Malaman, G. Venturini and B. Roques, Mater. Res. Bull., 1988, 23, 1629–1633.
41. W. Ma, X. Xu, Z. Wang, H. Zhou, M. Marshall, Z. Qu, W. Xie and S. Jia, Phys. Rev. B, 2021, 103, 235109.
42. F. Weitzer, A. Leithe-Jasper, K. Hiebl, P. Rogl, Q. Qi and J. M. D. Coey, J. Appl. Phys., 1993, 73, 8447–8450.
43. J. Han, G. K. Marasinghe, J. B. Yang, W. J. James, M. Chen, W. B. Yelon, P. L. Héritier, I. Dubenko and N. Ali, J. Phys.: Condens. Matter, 2004, 16, 5407–5417.
44. B. Malaman, G. Venturini, B. Chafik El Idrissi and E. Ressouche, J. Alloys Compd., 1997, 252, 41–49.
45. H. Zhang, C. Liu, Y. Zhang, Z. Hou, X. Fu, X. Zhang, X. Gao and J. Liu, Appl. Phys. Lett., 2022, 121, 202401.
46. M. Li, Q. Wang, G. Wang, Z. Yuan, W. Song, R. Lou, Z. Liu, Y. Huang, Z. Liu, H. Lei, Z. Yin and S. Wang, Nat. Commun., 2021, 12, 3129.
47. B. R. Ortiz, H. Miao, D. S. Parker, F. Yang, G. D. Samolyuk, E. M. Clements, A. Rajapitamahuni, T. Yilmaz, E. Vescovo, J. Yan, A. F. May and M. A. McGuire, Chem. Mater., 2023, 35, 9756–9773.
48. K. Guo, Z. Ma, H. Liu, Z. Wu, J. Wang, Y. Shi, Y. Li and S. Jia, Phys. Rev. B, 2024, 110, 064416.
49. X. Teng, L. Chen, F. Ye, E. Rosenberg, Z. Liu, J. X. Yin, Y. X. Jiang, J. S. Oh, M. Z. Hasan, K. J. Neubauer, B. Gao, Y. Xie, M. Hashimoto, D. Lu, C. Jozwiak, A. Bostwick, E. Rotenberg, R. J. Birgeneau, J. H. Chu, M. Yi and P. Dai, Nature, 2022, 609, 490–495.
50. Y. Hu, C. Le, L. Chen, H. Deng, Y. Zhou, N. C. Plumb, M. Radovic, R. Thomale, A. P. Schnyder, J. X. Yin, G. Wang, X. Wu and M. Shi, Phys. Rev. B, 2024, 110, L121114.
51. B. Gibson, R. Pöttgen, R. K. Kremer and K. R. A. Ziebeck, J. Manage. Eng., 1996, 12, 34–39.
52. E. Morosan, S. L. Bud’ko, P. C. Canfield, M. S. Torikachvili and A. H. Lacerda, J. Magn. Magn. Mater., 2004, 277, 298–321.
53. K. Zhao, H. Deng, H. Chen, K. A. Ross, V. Petříček, G. Günther, M. Russina, V. Hutanu and P. Gegenwart, Science, 2020, 367, 1218–1223.
54. G. Villalpando, M. Jovanovic, B. Hoff, Y. Jiang, R. Singha, F. Yuan, H. Hu, D. Călugăru, N. Mathur, J. F. Khoury, S. Dulovic, B. Singh, V. M. Plisson, C. J. Pollak, J. M. Moya, K. S. Burch, B. A. Bernevig and L. M. Schoop, Sci. Adv., 2024, 10, eadl1103.
55. K. Kuroda, T. Tomita, M. T. Suzuki, C. Bareille, A. A. Nugroho, P. Goswami, M. Ochi, M. Ikhlas, M. Nakayama, S. Akebi, R. Noguchi, R. Ishii, N. Inami, K. Ono, H. Kumigashira, A. Varykhalov, T. Muro, T. Koretsune, R. Arita, S. Shin, T. Kondo and S. Nakatsuji, Nat. Mater., 2017, 16, 1090–1095.
56. M. Ikhlas, T. Tomita, T. Koretsune, M. T. Suzuki, D. Nishio-Hamane, R. Arita, Y. Otani and S. Nakatsuji, Nat. Phys., 2017, 13, 1085–1090.
57. Y. Xu, J. Zhao, C. Yi, Q. Wang, Q. Yin, Y. Wang, X. Hu, L. Wang, E. Liu, G. Xu, L. Lu, A. A. Soluyanov, H. Lei, Y. Shi, J. Luo and Z. G. Chen, Nat. Commun., 2020, 11, 3985.
58. S. Howard, L. Jiao, Z. Wang, N. Morali, R. Batabyal, P. Kumar-Nag, N. Avraham, H. Beidenkopf, P. Vir, E. Liu, C. Shekhar, C. Felser, T. Hughes and V. Madhavan, Nat. Commun., 2021, 12, 4269.
59. P. K. Nag, R. Batabyal, J. Ingham, N. Morali, H. Tan, J. Koo, A. Consiglio, E. Liu, N. Avraham, R. Queiroz, R. Thomale, B. Yan, C. Felser and H. Beidenkopf, arXiv, 2024, preprint, arXiv:2410.01994 DOI:10.48550/arXiv.2410.01994.
60. I. I. Mazin, H. O. Jeschke, F. Lechermann, H. Lee, M. Fink, R. Thomale and R. Valentí, Nat. Commun., 2014, 5, 4261.
61. K. Heritage, B. Bryant, L. A. Fenner, A. S. Wills, G. Aeppli and Y. Soh, Adv. Funct. Mater., 2020, 30, 1909163.
62. L. Ye, M. K. Chan, R. D. McDonald, D. Graf, M. Kang, J. Liu, T. Suzuki, R. Comin, L. Fu and J. G. Checkelsky, Nat. Commun., 2019, 10, 4870.
63. Z. Lin, J. H. Choi, Q. Zhang, W. Qin, S. Yi, P. Wang, L. Li, Y. Wang, H. Zhang, Z. Sun, L. Wei, S. Zhang, T. Guo, Q. Lu, J. H. Cho, C. Zeng and Z. Zhang, Phys. Rev. Lett., 2018, 121, 096401.
64. M. Yao, H. Lee, N. Xu, Y. Wang, J. Ma, O. V. Yazyev, Y. Xiong, M. Shi, G. Aeppli and Y. Soh, arXiv, 2018, preprint, arXiv:1810.01514 DOI:10.48550/arXiv.1810.01514.
65. N. J. Ghimire, R. L. Dally, L. Poudel, D. C. Jones, D. Michel, N. T. Magar, M. Bleuel, M. A. McGuire, J. S. Jiang, J. F. Mitchell, J. W. Lynn and I. I. Mazin, Sci. Adv., 2020, 6, eabe2680.
66. X. Xu, J. X. Yin, W. Ma, H. J. Tien, X. B. Qiang, P. V. S. Reddy, H. Zhou, J. Shen, H. Z. Lu, T. R. Chang, Z. Qu and S. Jia, Nat. Commun., 2022, 13, 1197.
67. J. X. Yin, W. Ma, T. A. Cochran, X. Xu, S. S. Zhang, H. J. Tien, N. Shumiya, G. Cheng, K. Jiang, B. Lian, Z. Song, G. Chang, I. Belopolski, D. Multer, M. Litskevich, Z. J. Cheng, X. P. Yang, B. Swidler, H. Zhou, H. Lin, T. Neupert, Z. Wang, N. Yao, T. R. Chang, S. Jia and M. Zahid Hasan, Nature, 2020, 583, 533–536.
68. D. C. Jones, S. Das, H. Bhandari, X. Liu, P. Siegfried, M. P. Ghimire, S. S. Tsirkin, I. I. Mazin and N. J. Ghimire, Phys. Rev. B, 2024, 110, 115134.
69. Y. Lee, R. Skomski, X. Wang, P. P. Orth, Y. Ren, B. Kang, A. K. Pathak, A. Kutepov, B. N. Harmon, R. J. McQueeney, I. I. Mazin and L. Ke, Phys. Rev. B, 2023, 108, 045132.
70. M. I. Mondal, A. P. Sakhya, M. Sprague, B. R. Ortiz, M. Matzelle, B. Ghosh, N. Valadez, I. Bin Elius, A. Bansil and M. Neupane, arXiv, 2023, preprint, arXiv:2311.11488 DOI:10.48550/arXiv.2311.11488.
71. A. P. Sakhya, B. R. Ortiz, B. Ghosh, M. Sprague, M. I. Mondal, M. Matzelle, I. Bin Elius, N. Valadez, D. G. Mandrus, A. Bansil and M. Neupane, Commun. Mater., 2024, 5, 241.
72. L. Chen, Y. Zhou, H. Zhang, X. Ji, K. Liao, Y. Ji, Y. Li, Z. Guo, X. Shen, R. Yu, X. Yu, H. Weng and G. Wang, arXiv, 2023, preprint, arXiv:2307.02942 DOI:10.48550/arXiv.2307.02942.
73. Z. Jiang, T. Li, J. Yuan, Z. Liu, Z. Cao, S. Cho, M. Shu, Y. Yang, J. Ding, Z. Li, J. Liu, Z. Liu, J. Liu, J. Ma, Z. Sun, Y. Guo and D. Shen, arXiv, 2023, preprint, arXiv:2309.01579 DOI:10.48550/arXiv.2309.01579.
74. T. Nagamiya, S. Tomiyoshi and Y. Yamaguchi, Solid State Commun., 1982, 42, 385–388.
75. S. Tomiyoshi, J. Phys. Soc. Jpn., 1982, 51, 803–810.
76. P. J. Brown, V. Nunez, F. Tasset, J. B. Forsyth and P. Radhakrishna, J. Phys.: Condens. Matter., 1990, 2, 9409–9422.
77. T. Chen, T. Tomita, S. Minami, M. Fu, T. Koretsune, M. Kitatani, I. Muhammad, D. Nishio-Hamane, R. Ishii, F. Ishii, R. Arita and S. Nakatsuji, Nat. Commun., 2021, 12, 572.
78. S. A. Ekahana, S. Okamoto, J. Dreiser, L. Roduit, G. D. Jakub, A. Hunter, A. Tamai and Y. Soh, arXiv, 2024, preprint, arXiv:2401.15602 DOI:10.48550/arXiv.2401.15602.
79. W. Zhang, T. C. Asmara, Y. Tseng, J. Li, Y. Xiong, Y. Wei, T. Yu, C. W. Galdino, Z. Zhang, K. Kummer, V. N. Strocov, Y. Soh, T. Schmitt and G. Aeppli, Nat. Commun., 2024, 15, 8905.
80. J. Han, W. B. Yelon, W. J. James, G. K. Marasinghe, I. Dubenko and N. Ali, Int. J. Mod. Phys. B, 2001, 15, 3223–3227.
81. H. Wang, L. Jiang, Z. Zhou, R. Wang, A. Wang, Y. Chai, M. He, G. Han, J. Ying, X. Lu, Y. Pan, G. Wang, X. Zhou and X. Chen, Phys. Rev. B, 2023, 108, 155135.
82. P. Park, B. R. Ortiz, M. Sprague, A. P. Sakhya, S. A. Chen, M. D. Frontzek, W. Tian, R. Sibille, D. G. Mazzone, C. Tabata, K. Kaneko, L. M. DeBeer-Schmitt, M. B. Stone, D. S. Parker, G. D. Samolyuk, H. Miao, M. Neupane and A. D. Christianson, arXiv, 2024, preprint, arXiv:2412.10286 DOI:10.48550/arXiv.2412.10286.
83. E. Cheng, N. Mao, X. Yang, B. Song, R. Lou, T. Ying, S. Nie, A. Fedorov, F. Bertran, P. Ding, O. Suvorov, S. Zhang, S. Changdar, W. Schnelle, R. Koban, C. Yi, U. Burkhardt, B. Büchner, S. Wang, Y. Zhang, W. Wang and C. Felser, arXiv, 2024, preprint, arXiv:2409.01365 DOI:10.48550/arXiv.2409.01365.
84. M. Hirschberger, T. Nakajima, S. Gao, L. Peng, A. Kikkawa, T. Kurumaji, M. Kriener, Y. Yamasaki, H. Sagayama, H. Nakao, K. Ohishi, K. Kakurai, Y. Taguchi, X. Yu, T. Arima and Y. Tokura, Nat. Commun., 2019, 10, 5831.
85. E. Cheng, K. Wang, Y. Hao, W. Chen, H. Tan, Z. Li, M. Wang, W. Gao, D. Wu, S. Sun, T. Ying, S. Nie, Y. Li, W. Schnelle, H. Chen, X. Zhou, R. Koban, Y. Chen, B. Yan, Y. Yang, W. Wu, Z. Liu and C. Felser, arXiv, 2024, preprint, arXiv:2405.16831 DOI:10.48550/arXiv.2405.16831.
86. Z. Zheng, L. Chen, X. Ji, Y. Zhou, G. Qu, M. Hu, Y. Huang, H. Weng, T. Qian and G. Wang, Sci. China: Phys., Mech. Astron., 2024, 67, 267411.
87. S. Roychowdhury, K. Samanta, S. Singh, W. Schnelle, Y. Zhang, J. Noky, M. G. Vergniory, C. Shekhar and C. Felser, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, 2401970121.
88. N. Li, Q. Huang, X. Y. Yue, S. K. Guang, K. Xia, Y. Y. Wang, Q. J. Li, X. Zhao, H. D. Zhou and X. F. Sun, Phys. Rev. B, 2022, 106, 014416.
89. N. Kumar, S. N. Guin, K. Manna, C. Shekhar and C. Felser, Chem. Rev., 2021, 121, 2780–2815.
90. B. A. Bernevig, C. Felser and H. Beidenkopf, Nature, 2022, 603, 41–51.
91. N. Nagaosa, J. Sinova, S. Onoda, A. H. MacDonald and N. P. Ong, Rev. Mod. Phys., 2010, 82, 1539–1592.
92. S. Roychowdhury, K. Samanta, P. Yanda, B. Malaman, M. Yao, W. Schnelle, E. Guilmeau, P. Constantinou, S. Chandra, H. Borrmann, M. G. Vergniory, V. Strocov, C. Shekhar and C. Felser, J. Am. Chem. Soc., 2023, 145, 12920–12927.
93. A. K. Nayak, J. E. Fischer, Y. Sun, B. Yan, J. Karel, A. C. Komarek, C. Shekhar, N. Kumar, W. Schnelle, J. Kübler, C. Felser and S. S. P. Parkin, Sci. Adv., 2016, 2, 1501870.
94. G. S. Thakur, P. Vir, S. N. Guin, C. Shekhar, R. Weihrich, Y. Sun, N. Kumar and C. Felser, Chem. Mater., 2020, 32, 1612–1617.
95. J. Shen, Q. Zeng, S. Zhang, H. Sun, Q. Yao, X. Xi, W. Wang, G. Wu, B. Shen, Q. Liu and E. Liu, Adv. Funct. Mater., 2020, 30, 2000830.
96. B. He, M. Yao, Y. Pan, K. E. Arpino, D. Chen, F. M. Serrano-Sanchez, S. Ju, M. Shi, Y. Sun and C. Felser, Commun. Mater., 2024, 5, 275.
97. Q. Wang, S. Sun, X. Zhang, F. Pang and H. Lei, Phys. Rev. B, 2016, 94, 075135.
98. T. Kida, L. A. Fenner, A. A. Dee, I. Terasaki, M. Hagiwara and A. S. Wills, J. Phys.: Condens. Matter, 2011, 23, 112205.
99. Q. Wang, Q. Yin and H. Lei, Chin. Phys. B, 2020, 29, 017101.
100. L. Wang, J. Zhu, H. Chen, H. Wang, J. Liu, Y. X. Huang, B. Jiang, J. Zhao, H. Shi, G. Tian, H. Wang, Y. Yao, D. Yu, Z. Wang, C. Xiao, S. A. Yang and X. Wu, Phys. Rev. Lett., 2024, 132, 106601.
101. C. Liu, H. Zhang, Z. Li, Y. Yan, Y. Zhang, Z. Hou and X. Fu, Surf. Interfaces, 2023, 39, 102866.
102. K. Fruhling, A. Streeter, S. Mardanya, X. Wang, P. Baral, O. Zaharko, I. I. Mazin, S. Chowdhury, W. D. Ratcliff and F. Tafti, Phys. Rev. Mater., 2024, 8, 094411.
103. T. Asaba, S. M. Thomas, M. Curtis, J. D. Thompson, E. D. Bauer and F. Ronning, Phys. Rev. B, 2020, 101, 174415.
104. K. Zhao, Y. Tokiwa, H. Chen and P. Gegenwart, Nat. Phys., 2024, 20, 442–449.
105. H. Yang, W. You, J. Wang, J. Huang, C. Xi, X. Xu, C. Cao, M. Tian, Z. A. Xu, J. Dai and Y. Li, Phys. Rev. Mater., 2020, 4, 024202.
106. P. Wu, J. Song, X. Yu, Y. Wang, K. Xia, B. Hong, L. Zu, Y. Du, P. Vallobra, F. Liu, S. Torii, T. Kamiyama, Y. Xiong and W. Zhao, Appl. Phys. Lett., 2021, 119, 082401.
107. C. Lee, Y. Sun, L. Ye, S. Rathi, K. Wang, Y. M. Lu, J. Moore, J. G. Checkelsky and J. Orenstein, Proc. Natl. Acad. Sci. U. S. A., 2023, 121, 2220589120.
108. S. D. Wilson and B. R. Ortiz, Nat. Rev. Mater., 2024, 9, 420–432.
109. Z. Guguchia, R. Khasanov and H. Luetkens, npj Quantum Mater., 2023, 8, 41.
110. H. Barz, Mater. Res. Bull., 1980, 15, 1489–1491.
111. J. M. Vandenberg and H. Barz, Mater. Res. Bull., 1980, 15, 1493–1498.
112. B. Li, S. Li and H. H. Wen, Phys. Rev. B, 2016, 94, 094523.
113. C. Mielke, Y. Qin, J. X. Yin, H. Nakamura, D. Das, K. Guo, R. Khasanov, J. Chang, Z. Q. Wang, S. Jia, S. Nakatsuji, A. Amato, H. Luetkens, G. Xu, M. Z. Hasan and Z. Guguchia, Phys. Rev. Mater., 2021, 5, 034803.
114. S. B. Roy and P. Chaddah, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 11100–11102.
115. S. Kittaka, T. Sakakibara, M. Hedo, Y. Ōnuki and K. Machida, J. Phys. Soc. Jpn., 2013, 82, 123706.
116. H. Sugawara, T. Yamazaki, N. Kimura, R. Settai and Y. Õnuki, Phys. B, 1995, 206–207, 196–198.
117. C. Mielke III, H. Liu, D. Das, J. X. Yin, L. Z. Deng, J. Spring, R. Gupta, M. Medarde, C. W. Chu, R. Khasanov, Z. M. Hasan, Y. Shi, H. Luetkens and Z. Guguchia, J. Phys.: Condens. Matter, 2022, 34, 485601.
118. S. Roychowdhury, A. M. Ochs, S. N. Guin, K. Samanta, J. Noky, C. Shekhar, M. G. Vergniory, J. E. Goldberger and C. Felser, Adv. Mater., 2022, 34, 2201350.
119. R. P. Madhogaria, S. Mozaffari, H. Zhang, W. R. Meier, S. H. Do, R. Xue, T. Matsuoka and D. G. Mandrus, Phys. Rev. B, 2023, 108, 125114.
120. X. Z. Yu, N. Kanazawa, Y. Onose, K. Kimoto, W. Z. Zhang, S. Ishiwata, Y. Matsui and Y. Tokura, Nat. Mater., 2011, 10, 106–109.
121. Z. Hou, Q. Zhang, X. Zhang, G. Xu, J. Xia, B. Ding, H. Li, S. Zhang, N. M. Batra, P. M. F. J. Costa, E. Liu, G. Wu, M. Ezawa, X. Liu, Y. Zhou, X. Zhang and W. Wang, Adv. Mater., 2020, 32, 1904815.
122. C. D. Batista, S. Z. Lin, S. Hayami and Y. Kamiya, Rep. Prog. Phys., 2016, 79, 084504.
123. A. Biswas, O. Iakutkina, Q. Wang, H. C. Lei, M. Dressel and E. Uykur, Phys. Rev. Lett., 2020, 125, 076403.
124. G. Le Caer, B. Malaman and B. Roques, J. Phys. F, 1978, 8, 323–336.
125. B. Malaman, D. Fruchart and G. Le Caer, J. Phys. F, 1978, 8, 2389–2399.
126. G. Le Caer, B. Malaman, L. Haggstrom and T. Ericsson, J. Phys. F, 1979, 9, 1905–1919.
127. Z. Hou, W. Ren, B. Ding, G. Xu, Y. Wang, B. Yang, Q. Zhang, Y. Zhang, E. Liu, F. Xu, W. Wang, G. Wu, X. Zhang, B. Shen and Z. Zhang, Adv. Mater., 2017, 29, 1701144.
128. J. Bernhard, B. Lebech and O. Beckman, J. Phys. F, 1984, 14, 2379–2393.
129. J. Bernhard, B. Lebech and O. Beckman, J. Phys. F, 1988, 18, 539–552.
130. X. Teng, J. S. Oh, H. Tan, L. Chen, J. Huang, B. Gao, J. X. Yin, J. H. Chu, M. Hashimoto, D. Lu, C. Jozwiak, A. Bostwick, E. Rotenberg, G. E. Granroth, B. Yan, R. J. Birgeneau, P. Dai and M. Yi, Nat. Phys., 2023, 19, 814–822.
131. M. Wenzel, E. Uykur, A. A. Tsirlin, S. Pal, R. M. Roy, C. Yi, C. Shekhar, C. Felser, A. V. Pronin and M. Dressel, Phys. Rev. Lett., 2024, 132, 266505.
132. L. Chen, X. Teng, H. Tan, B. L. Winn, G. E. Granroth, F. Ye, D. H. Yu, R. A. Mole, B. Gao, B. Yan, M. Yi and P. Dai, Nat. Commun., 2024, 15, 1918.
133. H. Miao, T. T. Zhang, H. X. Li, G. Fabbris, A. H. Said, R. Tartaglia, T. Yilmaz, E. Vescovo, J. X. Yin, S. Murakami, X. L. Feng, K. Jiang, X. L. Wu, A. F. Wang, S. Okamoto, Y. L. Wang and H. N. Lee, Nat. Commun., 2023, 14, 6183.
134. D. Subires, A. Kar, A. Korshunov, C. A. Fuller, Y. Jiang, H. Hu, D. Călugăru, C. McMonagle, C. Yi, S. Roychowdhury, C. Shekhar, J. Strempfer, A. Jana, I. Vobornik, J. Dai, M. Tallarida, D. Chernyshov, A. Bosak, C. B. A. Bernevig and S. Blanco-Canosa, arXiv, 2024, preprint, arXiv:2408.04452 DOI:10.48550/arXiv.2408.04452.
135. E. Uykur, B. R. Ortiz, O. Iakutkina, M. Wenzel, S. D. Wilson, M. Dressel and A. A. Tsirlin, Phys. Rev. B, 2021, 104, 045130.
136. M. Wenzel, B. R. Ortiz, S. D. Wilson, M. Dressel, A. A. Tsirlin and E. Uykur, Phys. Rev. B, 2022, 105, 245123.
137. D. W. Kim, S. Liu, C. Wang, H. W. Nam, G. Pokharel, S. D. Wilson, J. H. Cho and S. J. Moon, Phys. Rev. B, 2023, 108, 205118.
138. T. Hu, H. Pi, S. Xu, L. Yue, Q. Wu, Q. Liu, S. Zhang, R. Li, X. Zhou, J. Yuan, D. Wu, T. Dong, H. Weng and N. Wang, Phys. Rev. B, 2023, 107, 165119.
139. Z. Chen, X. Wu, S. Zhou, J. Zhang, R. Yin, Y. Li, M. Li, J. Gong, M. He, Y. Chai, X. Zhou, Y. Wang, A. Wang, Y. J. Yan and D. L. Feng, Nat. Commun., 2024, 15, 6262.
140. K. Tang, H. Zhou, H. Li, S. Pan, X. Wu, H. Li, N. Zhang, C. Xi, J. Zhang, A. Wang, X. Wan, Z. Xiang and X. Chen, Phys. Rev. Res., 2024, 6, 013276.
141. A. Korshunov, A. Kar, C. Y. Lim, D. Subires, J. Deng, Y. Jiang, H. Hu, D. Călugăru, C. Yi, S. Roychowdhury, C. Shekhar, G. Garbarino, P. Törmä, C. Felser, B. A. Bernevig and S. Blanco-Canosa, arXiv, 2024, preprint, arXiv:2409.04325 DOI:10.48550/arXiv.2409.04325.
142. B. R. Ortiz, L. C. Gomes, J. R. Morey, M. Winiarski, M. Bordelon, J. S. Mangum, I. W. H. Oswald, J. A. Rodriguez-Rivera, J. R. Neilson, S. D. Wilson, E. Ertekin, T. M. McQueen and E. S. Toberer, Phys. Rev. Mater., 2019, 3, 094407.
143. C. Li, X. Wu, H. Liu, C. Polley, Q. Guo, Y. Wang, X. Han, M. Dendzik, M. H. Berntsen, B. Thiagarajan, Y. Shi, A. P. Schnyder and O. Tjernberg, Phys. Rev. Res., 2022, 4, 033072.
144. M. Kang, S. Fang, J. K. Kim, B. R. Ortiz, S. H. Ryu, J. Kim, J. Yoo, G. Sangiovanni, D. Di Sante, B. G. Park, C. Jozwiak, A. Bostwick, E. Rotenberg, E. Kaxiras, S. D. Wilson, J. H. Park and R. Comin, Nat. Phys., 2022, 18, 301–308.
145. B. R. Ortiz, S. M. L. Teicher, Y. Hu, J. L. Zuo, P. M. Sarte, E. C. Schueller, A. M. M. Abeykoon, M. J. Krogstad, S. Rosenkranz, R. Osborn, R. Seshadri, L. Balents, J. He and S. D. Wilson, Phys. Rev. Lett., 2020, 125, 247002.
146. C. C. Zhu, X. F. Yang, W. Xia, Q. W. Yin, L. S. Wang, C. C. Zhao, D. Z. Dai, C. P. Tu, B. Q. Song, Z. C. Tao, Z. J. Tu, C. S. Gong, H. C. Lei, Y. F. Guo and S. Y. Li, Phys. Rev. B, 2022, 105, 094507.
147. H. Chen, B. Hu, Y. Ye, H. Yang and H. J. Gao, Chin. Phys. B, 2022, 31, 097405.
148. F. H. Yu, T. Wu, Z. Y. Wang, B. Lei, W. Z. Zhuo, J. J. Ying and X. H. Chen, Phys. Rev. B, 2021, 104, L041103.
149. Y. Hu, X. Wu, B. R. Ortiz, X. Han, N. C. Plumb, S. D. Wilson, A. P. Schnyder and M. Shi, Phys. Rev. B, 2022, 106, L241106.
150. L. Zheng, Z. Wu, Y. Yang, L. Nie, M. Shan, K. Sun, D. Song, F. Yu, J. Li, D. Zhao, S. Li, B. Kang, Y. Zhou, K. Liu, Z. Xiang, J. Ying, Z. Wang, T. Wu and X. Chen, Nature, 2022, 611, 682–687.
151. A. Tsirlin, P. Fertey, B. R. Ortiz, B. Klis, V. Merkl, M. Dressel, S. Wilson and E. Uykur, SciPost Phys., 2022, 12, 049.
152. T. Kato, Y. Li, K. Nakayama, Z. Wang, S. Souma, F. Matsui, M. Kitamura, K. Horiba, H. Kumigashira, T. Takahashi, Y. Yao and T. Sato, Phys. Rev. Lett., 2022, 129, 206402.
153. X. Chen, X. Zhan, X. Wang, J. Deng, X.-B. Liu, X. Chen, J. G. Guo and X. Chen, Chin. Phys. Lett., 2021, 38, 057402.
154. C. Mielke, D. Das, J. X. Yin, H. Liu, R. Gupta, Y. X. Jiang, M. Medarde, X. Wu, H. C. Lei, J. Chang, P. Dai, Q. Si, H. Miao, R. Thomale, T. Neupert, Y. Shi, R. Khasanov, M. Z. Hasan, H. Luetkens and Z. Guguchia, Nature, 2022, 602, 245–250.
155. L. Yu, C. Wang, Y. Zhang, M. Sander, S. Ni, Z. Lu, S. Ma, Z. Wang, Z. Zhao, H. Chen, K. Jiang, Y. Zhang, H. Yang, F. Zhou, X. Dong, S. L. Johnson, M. J. Graf, J. Hu, H. J. Gao and Z. Zhao, arXiv, 2021, preprint, arXiv:2107.10714 DOI:10.48550/arXiv.2107.10714.
156. C. Guo, C. Putzke, S. Konyzheva, X. Huang, M. Gutierrez-Amigo, I. Errea, D. Chen, M. G. Vergniory, C. Felser, M. H. Fischer, T. Neupert and P. J. W. Moll, Nature, 2022, 611, 461–466.
157. H. D. Scammell, J. Ingham, T. Li and O. P. Sushkov, Nat. Commun., 2023, 14, 605.
158. X. Feng, K. Jiang, Z. Wang and J. Hu, Sci. Bull., 2021, 66, 1384–1388.
159. J. W. Dong, Z. Wang and S. Zhou, Phys. Rev. B, 2023, 107, 045127.
160. V. Scagnoli, L. J. Riddiford, S. W. Huang, Y. G. Shi, Z. Tu, H. Lei, A. Bombardi, G. Nisbet and Z. Guguchia, J. Phys.: Condens. Matter, 2024, 36, 185604.
161. Y. Xiang, Q. Li, Y. Li, W. Xie, H. Yang, Z. Wang, Y. Yao and H. H. Wen, Nat. Commun., 2021, 12, 6727.
162. H. Li, H. Zhao, B. R. Ortiz, T. Park, M. Ye, L. Balents, Z. Wang, S. D. Wilson and I. Zeljkovic, Nat. Phys., 2022, 18, 265–270.
163. F. Du, S. Luo, B. R. Ortiz, Y. Chen, W. Duan, D. Zhang, X. Lu, S. D. Wilson, Y. Song and H. Yuan, Phys. Rev. B, 2021, 103, L220504.
164. Z. Zhang, Z. Chen, Y. Zhou, Y. Yuan, S. Wang, J. Wang, H. Yang, C. An, L. Zhang, X. Zhu, Y. Zhou, X. Chen, J. Zhou and Z. Yang, Phys. Rev. B, 2021, 103, 224513.
165. Q. Wang, P. Kong, W. Shi, C. Pei, C. Wen, L. Gao, Y. Zhao, Q. Yin, Y. Wu, G. Li, H. Lei, J. Li, Y. Chen, S. Yan and Y. Qi, Adv. Mater., 2021, 33, 2102813.
166. X. Wu, T. Schwemmer, T. Müller, A. Consiglio, G. Sangiovanni, D. Di Sante, Y. Iqbal, W. Hanke, A. P. Schnyder, M. M. Denner, M. H. Fischer, T. Neupert and R. Thomale, Phys. Rev. Lett., 2021, 127, 177001.
167. R. Tazai, Y. Yamakawa, S. Onari and H. Kontani, Sci. Adv., 2022, 8, eabl4108.
168. C. C. Zhao, L. S. Wang, W. Xia, Q. W. Yin, J. M. Ni, Y. Y. Huang, C. P. Tu, Z. C. Tao, Z. J. Tu, C. S. Gong, H. C. Lei, Y. F. Guo, X. F. Yang and S. Y. Li, arXiv, 2021, preprint, arXiv:2102.08356 DOI:10.48550/arXiv.2102.08356.
169. Z. Guguchia, C. Mielke, D. Das, R. Gupta, J. X. Yin, H. Liu, Q. Yin, M. H. Christensen, Z. Tu, C. Gong, N. Shumiya, M. S. Hossain, T. S. Gamsakhurdashvili, M. Elender, P. Dai, A. Amato, Y. Shi, H. C. Lei, R. M. Fernandes, M. Z. Hasan, H. Luetkens and R. Khasanov, Nat. Commun., 2023, 14, 153.
170. H. Luo, Q. Gao, H. Liu, Y. Gu, D. Wu, C. Yi, J. Jia, S. Wu, X. Luo, Y. Xu, L. Zhao, Q. Wang, H. Mao, G. Liu, Z. Zhu, Y. Shi, K. Jiang, J. Hu, Z. Xu and X. J. Zhou, Nat. Commun., 2022, 13, 273.
171. S. Cho, H. Ma, W. Xia, Y. Yang, Z. Liu, Z. Huang, Z. Jiang, X. Lu, J. Liu, Z. Liu, J. Li, J. Wang, Y. Liu, J. Jia, Y. Guo, J. Liu and D. Shen, Phys. Rev. Lett., 2021, 127, 236401.
172. R. Lou, A. Fedorov, Q. Yin, A. Kuibarov, Z. Tu, C. Gong, E. F. Schwier, B. Büchner, H. Lei and S. Borisenko, Phys. Rev. Lett., 2022, 128, 036402.
173. J. Zhao, W. Wu, Y. Wang and S. A. Yang, Phys. Rev. B, 2021, 103, L241117.
174. M. Kang, S. Fang, J. Yoo, B. R. Ortiz, Y. M. Oey, J. Choi, S. H. Ryu, J. Kim, C. Jozwiak, A. Bostwick, E. Rotenberg, E. Kaxiras, J. G. Checkelsky, S. D. Wilson, J. H. Park and R. Comin, Nat. Mater., 2023, 22, 186–193.
175. T. Park, M. Ye and L. Balents, Phys. Rev. B, 2021, 104, 035142.
176. Y. P. Lin and R. M. Nandkishore, Phys. Rev. B, 2021, 104, 045122.
177. M. H. Christensen, T. Birol, B. M. Andersen and R. M. Fernandes, Phys. Rev. B, 2022, 106, 144504.
178. H. Tan, Y. Liu, Z. Wang and B. Yan, Phys. Rev. Lett., 2021, 127, 046401.
179. H. Miao, H. X. Li, W. R. Meier, A. Huon, H. N. Lee, A. Said, H. C. Lei, B. R. Ortiz, S. D. Wilson, J. X. Yin, M. Z. Hasan, Z. Wang, H. Tan and B. Yan, Phys. Rev. B, 2021, 104, 195132.
180. G. Liu, X. Ma, K. He, Q. Li, H. Tan, Y. Liu, J. Xu, W. Tang, K. Watanabe, T. Taniguchi, L. Gao, Y. Dai, H. H. Wen, B. Yan and X. Xi, Nat. Commun., 2022, 13, 3461.
181. S. Wu, B. R. Ortiz, H. Tan, S. D. Wilson, B. Yan, T. Birol and G. Blumberg, Phys. Rev. B, 2022, 105, 155106.
182. D. Wulferding, S. Lee, Y. Choi, Q. Yin, Z. Tu, C. Gong, H. Lei, S. Yousuf, J. Song, H. Lee, T. Park and K. Y. Choi, Phys. Rev. Res., 2022, 4, 023215.
183. E. Uykur, B. R. Ortiz, S. D. Wilson, M. Dressel and A. A. Tsirlin, npj Quantum Mater., 2022, 7, 16.
184. L. Z. Deng, M. Gooch, H. X. Liu, T. Bontke, J. Y. You, S. Shao, J. X. Yin, D. Schulze, Y. G. Shi, Y. P. Feng, G. Chang, Q. M. Si and C. W. Chu, arXiv, 2022, preprint, arXiv:2204.00553 DOI:10.48550/arXiv.2204.00553.
185. M. Mandal, A. Kataria, P. K. Meena, R. K. Kushwaha, D. Singh, P. K. Biswas, R. Stewart, A. D. Hillier and R. P. Singh, Phys. Rev. B, 2025, 111, 054511.
186. X. Gui and R. J. Cava, Chem. Mater., 2022, 34, 2824–2832.
187. H. C. Ku, G. P. Meisner, F. Acker and D. C. Johnston, Solid State Commun., 1980, 35, 91–96.
188. S. S. P. Parkin, M. Hayashi and L. Thomas, Science, 2008, 320, 190–194.
189. A. Fert, V. Cros and J. Sampaio, Nat. Nanotechnol., 2013, 8, 152–156.
190. T. H. R. Skyrme, Nucl. Phys., 1962, 31, 556–569.
191. S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii and P. Böni, Science, 2009, 323, 915–919.
192. W. Münzer, A. Neubauer, T. Adams, S. Mühlbauer, C. Franz, F. Jonietz, R. Georgii, P. Böni, B. Pedersen, M. Schmidt, A. Rosch and C. Pfleiderer, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 041203.
193. X. Z. Yu, Y. Onose, N. Kanazawa, J. H. Park, J. H. Han, Y. Matsui, N. Nagaosa and Y. Tokura, Nature, 2010, 465, 901–904.
194. A. Brastaas, G. Bauer and P. Kelly, Phys. Rep., 2006, 427, 157–255.
195. Y. Kajiwara, K. Harii, S. Takahashi, J. Ohe, K. Uchida, M. Mizuguchi, H. Umezawa, H. Kawai, K. Ando, K. Takanashi, S. Maekawa and E. Saitoh, Nature, 2010, 464, 262–266.
196. R. L. Dally, D. Phelan, N. Bishop, N. J. Ghimire and J. W. Lynn, Crystals, 2021, 11, 307.
197. J. G. Si, L. T. Shi, P. F. Liu, P. Zhang and B. T. Wang, Phys. Rev. B, 2022, 106, 214527.
198. X. W. Yi, X. Y. Ma, Z. Zhang, Z. W. Liao, J. Y. You and G. Su, Phys. Rev. B, 2022, 106, L220505.
199. X. Feng, Y. Jiang, H. Hu, D. Călugăru, N. Regnault, M. G. Vergniory, C. Felser, S. Blanco-Canosa and B. A. Bernevig, arXiv, 2024, preprint, arXiv:2409.13078 DOI:10.48550/arXiv.2409.13078.
200. H. K. Singh, A. Sehrawat, C. Shen, I. Samathrakis, I. Opahle, H. Zhang and R. Xie, Acta. Mater., 2023, 242, 118474.
201. V. Meschke, P. Gorai, V. Stevanović and E. S. Toberer, Chem. Mater., 2021, 33, 4373–4381.
202. M. Jovanovic and L. M. Schoop, J. Am. Chem. Soc., 2022, 144, 10978–10991.
203. P. Singh, T. Del Rose, A. Palasyuk and Y. Mudryk, Chem. Mater., 2023, 35, 6304–6312.
204. Y. Jiang, S. Jia, S. Chen, X. Li, L. Wang and X. Han, Materials, 2022, 15, 3149.
205. A. Mantravadi, R. A. Ribeiro, S. L. Bud’ko, P. C. Canfield and J. V. Zaikina, Inorg. Chem., 2024, 63, 24697–24708.
206. L. Muechler, E. Liu, J. Gayles, Q. Xu, C. Felser and Y. Sun, Phys. Rev. B, 2020, 101, 115106.
207. F. Crasto de Lima, R. H. Miwa and E. Suárez Morell, Phys. Rev. B, 2019, 100, 155421.

---

Footnote

† Equal contribution.

---