Open Access Article
Open Access ArticleMachine learning-guided discovery of gas evolving electrode bubble inactivation†
Jack R.
Lake‡
a,
Simon
Rufer‡
 a,
Jim
James
b,
Nathan
Pruyne
b,
Aristana
Scourtas
a,
Jim
James
b,
Nathan
Pruyne
b,
Aristana
Scourtas
 bc,
Marcus
Schwarting
d,
Aadit
Ambadkar
b,
Ian
Foster
cd,
Ben
Blaiszik
bc,
Marcus
Schwarting
d,
Aadit
Ambadkar
b,
Ian
Foster
cd,
Ben
Blaiszik
 *bc and
Kripa K.
Varanasi
*bc and
Kripa K.
Varanasi
 *a
*a
aDepartment of Mechanical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA. E-mail: varanasi@mit.edu
bGlobus, University of Chicago, 5801 S Ellis Ave, Chicago, IL 60637, USA. E-mail: blaiszik@uchicago.edu
cData Science and Learning Division, Argonne National Laboratory, 9700 S Cass Ave, Lemont, IL 60439, USA
dDepartment of Computer Science, University of Chicago, 5801 S Ellis Ave, Chicago, IL 60637, USA
First published on 8th October 2024
Abstract
The adverse effects of electrochemical bubbles on the performance of gas-evolving electrodes are well known, but studies on the degree of adhered bubble-caused inactivation, and how inactivation changes during bubble evolution are limited. We study electrode inactivation caused by oxygen evolution while using surface engineering to control bubble formation. We find that the inactivation of the entire projected area, as is currently believed, is a poor approximation which leads to non-physical results. Using a machine learning-based image-based bubble detection method to analyze large quantities of experimental data, we show that bubble impacts are small for surface engineered electrodes which promote high bubble projected areas while maintaining low direct bubble contact. We thus propose a simple methodology for more accurately estimating the true extent of bubble inactivation, which is closer to the area which is directly in contact with the bubbles.
Introduction
Electrochemical gas-evolving electrode (GEE) design is relevant for a multitude of industrial applications including water electrolysis for renewable Hydrogen production,1,2 the Chlor-alkali process for chlorine production,3,4 and electrochemically mediated CO2 capture.5–7 The negative effects of bubbles can be significant and have been reported to incur energy penalties of up to ∼10% for water electrolysis,8,9 ∼20% for the chlor-alkali process,10 and ∼25% for electrochemically mediated amine regeneration.11,12 The Chlor-alkali process accounts for approximately 2% of annual electricity usage in the United States,13 and Hydrogen generation and CO2 capture are poised to grow significantly, further motivating the study of bubbles on GEEs.14–20 Bubbles of gaseous product adhered to catalysts lead to catalyst inactivation, increasing activation overpotentials. Bubbles cause further losses from impeding mass transport and ionic conduction and induce concentration variability near the electrode surface.8,21 A wide range of studies exist that investigate GEEs, including the impacts of concentration overpotential22 and generated concentration gradients around bubbles,23 bubble nucleation models,24 and active methods to enhance the departure of bubbles by using ultrasonic25 or magnetic26,27 fields. Recent works have summarized current progress and methods for the study and mitigation of adhered bubbles on electrodes along with the formation of micro- and nanobubbles.10,28–30 However, the fundamental means by which bubbles inactivate the surface of GEEs and cause changes to current density is an open area of research which holds promise for optimizing these systems. Currently, the prevailing understanding is that the projected area underneath a bubble (the ‘bubble projected area’) has a small but nonzero activity, but that this activity is small enough that it can be acceptably treated as fully inactive and not at all contributing to the reaction.31–33 Such works thus calculate the area inactivated by a bubble as πR2, where R is the bubble radius, which is equivalent to the orthogonal projection of the bubbles maximal extent.31–33 However, recent experiments have shown that the area underneath the bubble may actually be substantially active,34 and thus the extent of bubble inactivation remains an open question. With the goal of gaining a more fundamental understanding of bubble inactivation in this work, we employ surface engineering techniques to systematically modulate the bubble–electrode interaction and use a Machine Learning (ML) approach to detect bubbles and collect data to quantify the effects of bubble coverage. We use the Oxygen Evolution Reaction (OER) as our model system.Significant research has used surface engineering to advantageously alter the interactions between bubbles and electrode surfaces. These approaches have focused on altering electrode surface chemistry, surface roughness, or both to modulate a GEE's surface wettability and investigate the performance impacts.35 For example, prior work has focused on the wettability impacts caused by altering the surface chemistry of nickel porous foams36 and patterned hydrophobically modified electrodes37 using polytetrafluoroethylene (PTFE), and others have altered electrode wettability by modulating the roughness of GEEs by using micropatterning.38 Other surface modification methods have been demonstrated in attempt to enhance performance of GEEs, such as promoting bubble nucleation away from the GEE active surface39 and advantageous bubble manipulation via capillarity.40 While the above approaches attempt to improve performance, the fundamental limitations arising from the extent of bubble passivation are not well understood, precluding the systematic engineering and optimization of bubble–electrode interactions. Along these lines, our prior work shows how electrochemically-active surface area (ECSA), which is a common metric for describing active area, is not necessarily the best predictor of performance due to bubble passivation.34 Generally, the use of metrics which do not consider bubble passivation could lead to lower performance and inefficient usage of precious material catalysts. In this work, we aim to develop a fundamental understanding of the mechanisms by which bubbles passivate electrodes to better quantify active electrode area. We leverage surface engineering to systematically control bubble–electrode interactions to isolate and study the most relevant passivation mechanisms.
Accurate data of bubble sizes, positions, and states over time is needed to perform quantitative analyses of bubble inactivation. Traditional image analysis techniques such as the Hough transform41–45 suffer from inaccuracies due to blurriness and shadowing caused by departing bubbles and other visual complexities of the electrode environment. Moreover, changes in the lighting conditions or optical properties of the electrode or bubbles between experiments require re-initialization and tuning of the data collection algorithms. To facilitate facile collection of accurate data, we trained a deep convolutional neural network (CNN) to detect electrochemical bubbles adhered to the electrode. This Machine Learning (ML) approach outperforms traditional image analysis techniques, has the potential to generalize across electrodes, and will be open-sourced for use.
Here, we use the ML-based bubble detection scheme to quantify the extent to which bubbles cover and contact GEE surfaces, and in using an engineered electrode surface to systematically alter these bubble characteristics, we elucidate the extent of inactivation. Our findings indicate that the projected area of the bubbles is not entirely inactivated, as is currently assumed by state-of-the-art electrode–bubble interaction models.31–33 We go on to determine a methodology to quantify the bounds of bubble inactivation, finding the directly contacted bubble area to be a better approximation. These new findings provide an alternative framework by which to approach how GEEs should be designed to limit electrocatalyst inactivation during operation. By minimizing direct contact of bubbles with GEEs, rather than bubble projected area, new approaches and architectures for optimizing gas evolving electrochemical systems can emerge. More broadly, our findings can provide a framework for the optimal utilization of precious catalyst materials by minimizing unused catalyst area caused by bubble passivation. These findings are particularly important for porous electrodes and other novel architectures with high active material loadings which are otherwise prone to increased passivation by gas bubbles.46,47
Adhered electrochemical bubbles on smooth electrodes
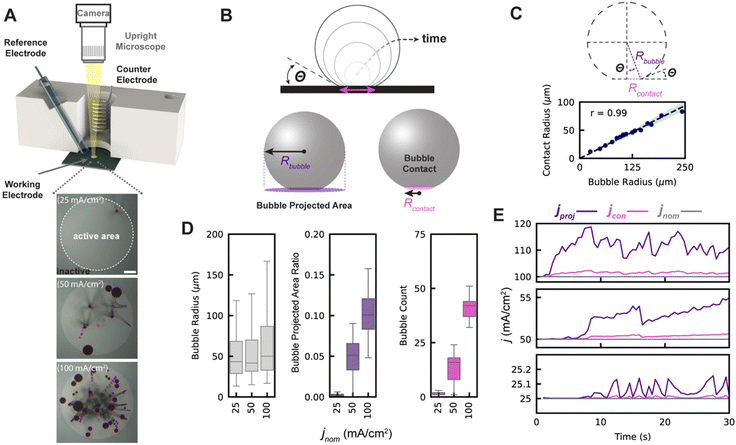
To measure the impacts of adhered gas bubbles on GEEs, bubbles arising from platinum-catalyzed oxygen evolution in a 0.5 M H2SO4 electrolyte (no non-air gas saturation was performed) was observed from a top-down perspective (Fig. 1A, top). A circular active Pt working electrode of 3 mm in diameter was patterned via photolithography, surrounded by an inactive region of silicon nitride (Fig. 1A, bottom). The focus of this study is on current density operation between 25 and 100 mA cm−2 on a geometric basis, beginning with the onset of bubble generation and approaching a range high enough to be of relevance for commercial electrochemical device operation, like for alkaline water electrolyzer operation48 where bubble effects are industrially significant. Chronopotentiometric experiments and data collection are limited to a 30–60 seconds duration as defects begin to occur on the smooth platinum, changing the surface properties and resulting in uncontrolled bubble nucleation in areas not predetermined by the subsequently discussed surface engineering process, which makes it difficult to accurately assess the relationship between projected area and contact area.The nominal current density, jnom, is defined as the total current passing through the working electrode, Itot, divided by the working electrode's geometric area, A:
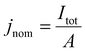 | (1) |
In this work, we will denote the actual relative bubble inactivation as ψ, such that the actual current density for the working electrode during experiments is defined as:
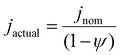 | (2) |
As such, ψ represents the true fractional portion of the electrode area between 0 and 1 that is inactivated at a given time due to the presence of adhered bubbles. Prior works suggest that ψ should be the bubble projected area: that is, the ratio of the shadowed area of adhered bubbles on the surface of the electrode to the total electrode geometric surface area49 as shown in Fig. 1B. Here, we denote the bubble projected area ratio as ϕ, and it can be calculated given the radius Rbubble, i of each of n bubbles on the surface at a given time: 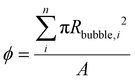 . We separately define the bubble contact area ratio between the contact area of adhered bubbles on the electrode surface to the electrode's total geometric surface area as shown in Fig. 1B, and denote it as
. We separately define the bubble contact area ratio between the contact area of adhered bubbles on the electrode surface to the electrode's total geometric surface area as shown in Fig. 1B, and denote it as 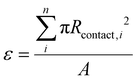 . This bubble contact represents the physical lower-bound of bubble inactivation, as catalyst regions in contact with the gas phase cannot facilitate a reaction. We aim to experimentally determine whether the inactivated area is appropriately approximated by the bubble projected area by performing a number of current-controlled experiments under different degrees of both bubble projected area and bubble contact area and measuring the resultant electrochemical potential fluctuations. Two additional current densities can be defined based on either the bubble projected area or the contact area, as follows:
. This bubble contact represents the physical lower-bound of bubble inactivation, as catalyst regions in contact with the gas phase cannot facilitate a reaction. We aim to experimentally determine whether the inactivated area is appropriately approximated by the bubble projected area by performing a number of current-controlled experiments under different degrees of both bubble projected area and bubble contact area and measuring the resultant electrochemical potential fluctuations. Two additional current densities can be defined based on either the bubble projected area or the contact area, as follows:
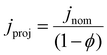 | (3) |
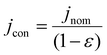 | (4) |
As demonstrated in prior work,34 adhered gas bubbles that grow on extremely smooth surfaces such as those used in this study do not experience pinning. Thus, an adhered bubble's contact line advances at a constant contact angle (θ) as the bubble grows, as shown graphically in Fig. 1B. By using high-magnification imaging from a side-view to image the contact lines of bubbles on our smooth electrodes, we confirm a linear relationship between bubble radius and contact line radius, Rcontact = Rbubble![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ), where θ = 22° as shown in Fig. 1C. The bubble contact area on our smooth electrode can therefore be indirectly computed given any bubble's radius, and the contact and projected area are related in this case as ε = ϕ
sin(θ), where θ = 22° as shown in Fig. 1C. The bubble contact area on our smooth electrode can therefore be indirectly computed given any bubble's radius, and the contact and projected area are related in this case as ε = ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. This transform enables the simultaneous tracking of both bubble projected area and contact area given only the size of the bubble, which is measured by the ML detection system.
θ. This transform enables the simultaneous tracking of both bubble projected area and contact area given only the size of the bubble, which is measured by the ML detection system.
Using this experimental setup, we filmed the electrode from above and applied our ML-based bubble detection algorithm to capture relevant bubble metrics for each of the experiments at 25, 50, and 100 mA cm−2 (see ESI Video 2A and B†). Fig. 1D shows the distributions of adhered bubble size, bubble projected area, and number of adhered bubbles over the course of each 30 seconds experiment, with data collection beginning at the start of the experiment. Each bubble which appears in the 30 seconds experiment is given a unique identifier, and each bubble is counted only once in each boxplot. We find that as the nominal current density is increased, the median and range of bubble size and bubble count also increase. This leads to two effects, which are shown in Fig. 1E: (i) as current density increases, jproj and jcon deviate more significantly from the nominal current density, and (ii) variations in jproj and jcon are greater at higher current densities.
We note that because the contact and projected area cannot be decoupled on smooth electrodes, it is difficult to isolate and assess the individual contributions of bubble contact and projected area to inactivation. Though chemical alteration of the surface energy could change the contact angle and decouple contact and projected area, such changes also affect electrocatalytic properties and introduce significant complexity. We alternatively chose to alter the morphologies of our electrodes to include small microscale ‘nanotextured spots’ with nanoscale roughness that promote the preferential nucleation of gas bubbles and pin their contact lines, decoupling contact area from bubble projected area. This approach also advantageously provides a greater degree of control over bubble nucleation and interactions, enabling our ML bubble detection algorithm to work more effectively. The ML algorithm is described next, followed by the results and analysis for the nanotextured spot electrodes.
Deep learning for bubble detection
To understand key relationships between bubble nucleation, growth, and departure for time series experiments, we developed a supervised ML pipeline, and trained neural network models to label individual bubbles across video frames. The ML pipeline involves data collection, manual image labeling, model training and validation, hyperparameter optimization, and inference. A training set of manually labelled images was taken from videos of GEE bubble evolution on both smooth and nanotextured spot grid-nucleated surfaces. In all, over 1000 annotated instances of bubbles across 22 images selected randomly from 9 separate videos were used during model training. Classical data augmentation strategies such as blurring, sharpening, rotating, cropping, and contrast enhancement techniques were used to augment the dataset.We trained two model architectures commonly used for object detection and tracking, Mask R-CNN50,51 and Faster R-CNN,52,53 to recognize bubbles and which is used to generate the bubble labels in all figures of this manuscript. A graphical representation of the model architectures is shown in Fig. 2A. The models were initialized with weights aggregated from the COCO dataset.54 Models were first fine-tuned by using images of bubble evolution on smooth surfaces, then further tuned by using a set of labeled images of bubble evolution on grid-nucleated surfaces. We also benchmarked our supervised methods against an implementation based on Hough circles, to serve as a classical computer vision baseline55 (see ESI section 7†). Training, inference, and benchmarks were run on an NVIDIA A100 GPU, with 70% of annotated images used for training, 20% for validation, and 10% for testing.
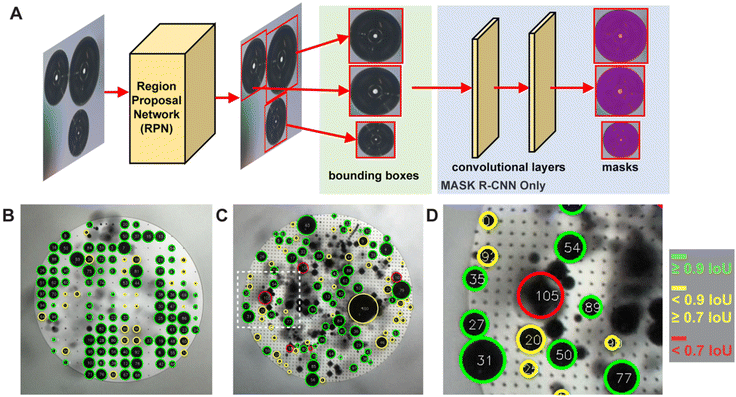 | ||
| Fig. 2 (A) Diagram of the high-level ML architecture used for bubble identification. Note that the Mask R-CNN architecture has additional convolutional layers to produce the masks, while the Faster R-CNN does not. (B) Image of b200 grid-nucleated surface with oxygen bubble nucleation annotated with predictions and intersection over union (IoU) scores. Green denotes the highest IoUs (≥0.9) while red denotes the lowest (<0.7). Bubble predictions were generated by using the Faster R-CNN V2 architecture. See Table S1† for overall mAP and IoU results per model architecture. (C) Image of b50 grid-nucleated surface with oxygen bubble nucleation, also annotated with predictions and IoU scores. (D) Subset of inset (B) highlighting bubble predictions with various IoU scores. Note that Bubble 105, with an IoU < 0.7, is a false positive detection of bubbles after they have detached from the surface. Only attached bubbles are considered valid predictions. Low-scoring predictions are frequently false positives or tiny bubbles. | ||
The model performance was further improved via hyperparameter optimization (HPO), with optimal parameters determined by the Asynchronous Successive Halving Algorithm (ASHA).56 The model with the highest mean average precision (mAP) and intersection over union (IoU) scores was selected for data collection inference. mAP scores measure the precision in the predictions of overall bubble detections, and IoU scores measure the overlap of the predicted bounding boxes with the ground truth bubble annotations (i.e., the “tightness” of the match). Examples of segmented image frames are shown in Fig. 2B–D and a table detailing model performance versus is included in ESI Table 1.† Additional details regarding hand-labeling, minimum detectable bubble size, computer vision methods, augmentation strategies, model architectures, model training, and evaluation can be found in the ESI sections 6 and 7.†
Nanotextured spot grid patterned electrodes to control adhered bubbles
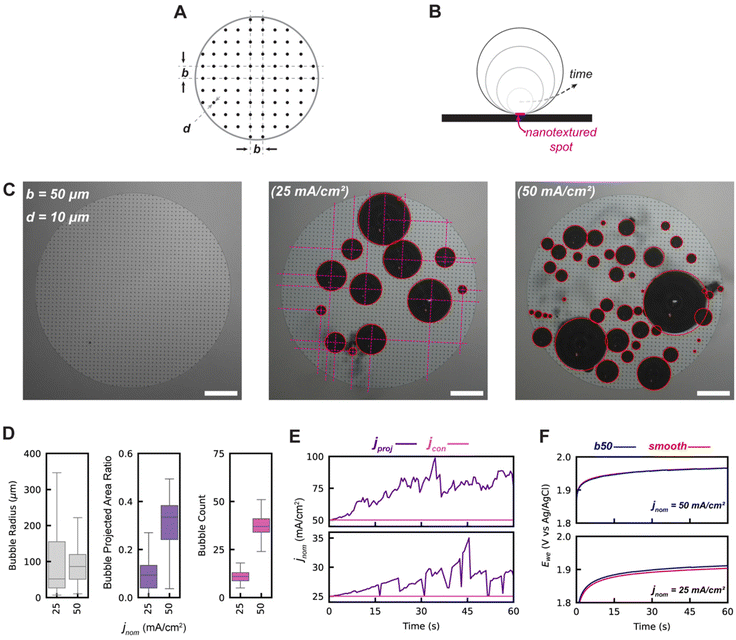
To maximize the bubble projected area while minimizing the bubble contact, surface engineering of regularly spaced nucleation-promoting nanotextured spots on the 3 mm electrode was envisioned, as shown graphically in Fig. 3A. The design parameters for these electrodes are the spacing between adjacent nanotextured spots, designated by b, and the diameter of each nanotextured spot, designated by d. The initially designed nanotextured spot electrode used a spacing b = 50 μm and a diameter d = 10 μm. At the low and moderate current densities of 25 and 50 mA cm−2, we demonstrate that bubbles preferentially nucleate and grow almost exclusively at nanotextured spot locations, as shown in Fig. 3C. The utility of nanotextured spots for investigating the impacts of adhered bubbles are primarily due to their ability to (1) spatially control the location of adhered bubbles by promoting nucleation at these nanotexture regions by lowering the free energy barrier to do so, and (2) decouple the linear relationship between bubble projected area and bubble contact that is observed for smooth electrodes. This second benefit is shown graphically in Fig. 3B, as an adhered bubble's contact line is effectively pinned to the edges of the nanotextured spot, keeping its contact area constant while the bubble radius grows and the bubble projected area increases. By virtue of this approach, the bubble projected area and bubble contact become decoupled, and the bubble projected area far exceeds the bubble contact. The bubble contact is now solely a function of the number of bubbles adhered to the working electrode's surface, defined as ε = nAns where n is the number of bubbles adhered to the electrode surface and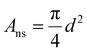 is the geometric area of a single nanotextured spot. The high degree of control and repeatability offered by using this approach makes it an ideal way to understand the way that bubble projected area and contact area are related to the dynamics of a GEEs electrochemical performance.
is the geometric area of a single nanotextured spot. The high degree of control and repeatability offered by using this approach makes it an ideal way to understand the way that bubble projected area and contact area are related to the dynamics of a GEEs electrochemical performance.
As shown in Fig. 3D, the b50 nanotextured spot electrodes have a significantly greater number of adhered bubbles and a greater bubble projected area ratio when compared to the smooth electrodes (Fig. 1D) due to the increased pinning afforded by the nanotextured spots. Moreover, bubble contact areas remain small as the bubble contact is constrained to only the nanotextured spot, thus effectively decoupling the projected and contact bubble areas as intended. As shown in Fig. 3E, this preferential promotion of bubble coverage allows for bubble projected area derived current densities jproj to approach twice that of the contact derived current density jcon, which remains effectively equivalent to the nominal current density.
It is of particular interest to note that the measured potentials required to maintain equivalent nominal current densities are almost identical in both the smooth and b50 nanotextured spot electrode cases, as shown in Fig. 3F, despite the b50 surface having a roughly 7-fold greater bubble projected area. Even with the addition of the nanotextured spots, the electrochemically active surface area (ECSA) for both the smooth control surfaces and these b50 nanotextured spot electrodes are within approximately 1% of one another, owing to the minimal surface fraction that is occupied by the nanotextured spot patterns. These results support the hypothesis that bubble projected area may not be the primary driver of inactivation.
The b50 nanotextured spot electrode successfully validated the morphological strategy for decoupling bubble contact and projected area. However, operation at current densities higher than 50 mA cm−2 was not practical due to rapid coalescence-induced bubble departure which obfuscated the surface and decreased IOU scores as shown in Fig. 2D (see ESI Video 3†). Increasing the spacing parameter b and thus lowering the density of nanotextured spots was expected to reduce the rate of coalescence-induced departure such that accurate data could be collected at higher bubble coverages which accentuate the effects of bubble coverage.
Optimizing nucleation grid promoting electrodes to maximize projected area
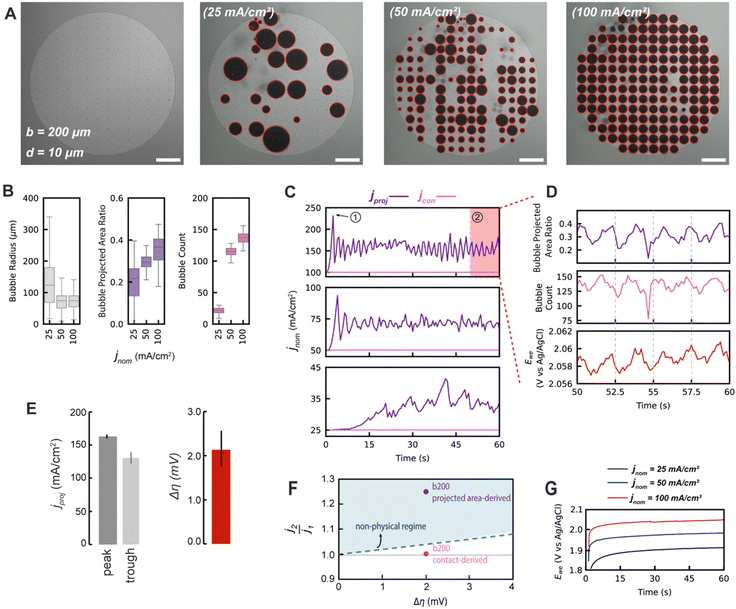
To lower the density of nanotextured spots on the working electrode, a spacing parameter of b = 200 μm was used, lowering the number density of nanotextured spots by an order of magnitude relative to the b50. This b200 nanotextured spot electrode design was intended to enable regular release of bubbles of a maximum diameter that is approximately equivalent to the spacing size. This is because at high occupancy of bubbles on nanotextured spots, the primary mechanism by which most bubbles will depart becomes coalescence-induced departure. As bubbles encounter a neighboring bubble, coalescence will occur which will transfer surface energy to potential energy via a ‘jump’ in the resulting coalesced bubble, as has been previously studied57 (see ESI Video 1†).As shown visually in Fig. 4A, at moderate and high current densities of 50 and 100 mA cm−2, there is a high degree of bubble occupancy on the b200 electrodes. As shown in Fig. 4B, the median bubble counts adhered to the electrode at a given time are between 100 and 150, close to the total number of nanotextured spots for the b200 design (164), demonstrating the high occupancy. This results in high bubble projected area ratios ranging between approximately 0.2 and 0.5. Additionally, the ability of the nanotextured spot electrodes to control the bubble sizes at high current densities is demonstrated by the tightly controlled distributions of bubble radii centered near b/2 in Fig. 4B.
These electrodes periodically shed groups of bubbles via coalescence-induced departure, creating regular fluctuations in the bubble projected area which is especially pronounced at the highest nominal current density tested of 100 mA cm−2. This behavior manifests in the significant and sustained fluctuations of the bubble projected area-derived current density, as shown in Fig. 4C. These periodic trends are highlighted for the final 10 seconds for the 100 mA cm−2 b200 electrode case in Fig. 4D. The current fluctuations are tightly temporally aligned with the fluctuations in measured potential of the working electrode, Ewe. The average peak and trough values of jproj over this period are roughly 163 mA cm−2 and 131 mA cm−2, and correspond to a fluctuation in Ewe of only approximately 2 mV as shown in Fig. 4E. These relative changes of ∼25% in jproj are unexpectedly large given the ∼0.1% change in Ewe. We therefore seek to propose physical arguments to justify that these small measured changes in Ewe could not be responsible for such large changes in current density, as would be required if the bubble projected area-derived current density were actually an accurate descriptor of the actual current density.
Physical arguments for most relevant bubble inactivation metric
To obtain a physical upper limit for fluctuations in actual current densities achievable for a given fluctuation in measured potential, the Butler–Volmer model in the upper limit of the Tafel Regime was used: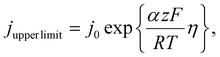 | (5) |
This equation represents the upper limit of a current density that is achievable for a given absolute overpotential, as it only considers activation losses at the electrode, neglecting the relevant effects of mass transport or ohmic losses that also limit the current achievable for a real GEE, especially when operating at high reaction rates (note that all potentials are not iR-corrected). Neglecting mass transport and ohmic losses is a conservative assumption, as these effects are positively correlated with bubble coverage. For a complete justification of this assumption, please see the ESI section 5.† To apply this physical upper limit to the experimentally observed current and potential fluctuations, we form a ratio between the peak and trough conditions of the electrode shown in Fig. 4D. This ratio relates how a change in overpotential would cause relative increases in the actual current density if activation losses were the sole source of loss in the system, ignoring all other effects, as shown in the following equation:
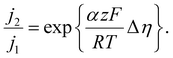 | (6) |
Here, j2 and j1 represent the peak and trough actual current densities during fluctuations of the electrode under test, and Δη represents the difference in overpotential between those two conditions (i.e., Δη = η2 − η1). Observing these relative changes conveniently eliminates the exchange current density, which can vary by orders of magnitude depending on the conditions of the reaction and materials used. Instead, we only require a reasonable value for the transfer coefficient, whose value is less variable and can be found in literature to be approximately 0.5 for Pt-catalyzed OER at high overpotentials.59
We plot the fluctuations of the overpotential during the b200 100 mA cm−2 experiment against the fluctuations of different current density metrics and compare them with the upper physical limit imposed by the Butler–Volmer kinetics in Fig. 4F to assess the viability of the metrics. When the bubble contact-derived current density fluctuations and corresponding changes in overpotential are plotted against the upper-limit model in Fig. 4F, we see these points fall below the model. This implies that the reaction is not operating in a purely kinetically-limited regime, which is sensible given that there are other losses due to mass transport and ohmic effects. However, the data considering bubble projected area-derived current densities fall above the physical upper bound. This is a non-physical result, as it implies that the electrode is able to induce greater changes in actual current densities for a given change in overpotential than a purely kinetically limited reaction. The small fluctuations observed in overpotentials despite marked changes in bubble projected area indicate that physical inactivation of the entire bubble projected area of an electrode is not possible.
We therefore propose that the actual inactivation of the electrode's surface ψ must lie somewhere between the contact area fraction ε and Kϕ, rather than the bubble projected area metric ϕ. Here, K represents an experimental factor which is less than 1, and is the maximum possible fraction of the bubble projected area which is active. The K factor can be determined by interrogating the limiting condition when 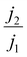 reaches its highest physically allowable value,
reaches its highest physically allowable value, 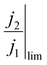 (i.e. on the dashed blue line of Fig. 4F). In our case, a 2 mV fluctuation corresponds to a maximum
(i.e. on the dashed blue line of Fig. 4F). In our case, a 2 mV fluctuation corresponds to a maximum 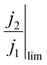 of 1.04. The following expression relates K and
of 1.04. The following expression relates K and 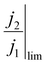 :
:
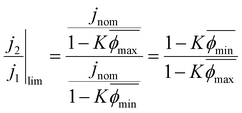 | (7) |
Here, 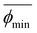 and
and 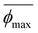 correspond to the average trough and peak bubble projected area ratios respectively. Eqn (7) can be combined with eqn (6) to yield the K factor as a function of fundamental quantities, the fluctuation in potential due to bubble inactivation Δη, and the peak and trough bubble projected area ratios only:
correspond to the average trough and peak bubble projected area ratios respectively. Eqn (7) can be combined with eqn (6) to yield the K factor as a function of fundamental quantities, the fluctuation in potential due to bubble inactivation Δη, and the peak and trough bubble projected area ratios only:
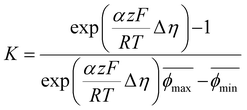 | (8) |
In our case, K = 0.24, again suggesting that the majority of the area underneath electrochemical bubbles is active.
Taken together, we suggest that the recently introduced bubble-induced electrochemically active surface area (BECSA)34 be defined relative to its ECSA as BECSA = ECSA × (1 − ψ), where ψ is bounded as ε < ψ < Kϕ. When the bubble contact on a surface is described by a constant contact angle θ, ψ can be further defined as (sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)ϕ < ψ < Kϕ. The K factor is undoubtedly a function of many physical conditions such as electrode chemistry and morphology, pressure, electrolyte chemistry, and can be estimated for other systems with the same methodology demonstrated herein. We believe utilizing BECSA with the appropriate K factor to calculate the actual current density provides a more accurate representation of the dynamic current densities of a GEE during operation, and help to better understand the inactivating effects of bubbles.
θ)ϕ < ψ < Kϕ. The K factor is undoubtedly a function of many physical conditions such as electrode chemistry and morphology, pressure, electrolyte chemistry, and can be estimated for other systems with the same methodology demonstrated herein. We believe utilizing BECSA with the appropriate K factor to calculate the actual current density provides a more accurate representation of the dynamic current densities of a GEE during operation, and help to better understand the inactivating effects of bubbles.
Conclusions
We have systematically studied the dynamic relationship between bubble projected area and bubble contact on both smooth and surface engineered Pt Oxygen evolving electrodes and used these studies to form a more fundamental understanding of the degree to which bubbles inactivate GEEs. To enable this work, we developed a machine learning based bubble detection algorithm to collect large datasets in a facile manner without the need for human intervention to annotate bubbles adhered on the electrode surface. This tool can be useful not only for scientists studying electrochemically generated bubbles, but also for those studying other adhered bubbles. While pristinely smooth electrodes cause a bubble's radius and its contact to be linearly related to the contact angle formed at the electrode, surface engineered electrodes were shown as a useful way to decouple this relationship. Nucleation promoting nanotextured spot arrays were demonstrated to both control where bubbles nucleated spatially and limit the contact of bubbles to nanotextured spot areas, allowing for increased bubble projected area while maintaining minimal bubble contact for electrodes under test. An optimized version of these nanotextured spot engineered electrodes was demonstrated to produce periodically fluctuating bubble projected area as adhered bubbles of a controllable size were regularly released via coalescence-induced departure with neighbors. Future work may focus on further improving the ability of electrodes to facilitate rapid bubble departure.61 Our kinetic model shows that assuming the bubble projected area is fully inactivated leads to non-physical results. The K factor defined herein is a physical property of any given electrode and its condition, and can be used to estimate the true extent of bubble inactivation. It can be easily determined with our methodology which requires only a chronoamperometric potential trace along with temporal bubble coverage data. Thus, an important new GEE design paradigm emerges that can focus primarily on minimizing the direct contact between adhered bubbles and an electrode, as opposed to the conventional bubble projected area metric. This new perspective brings with it important implications for the fabrication of more efficient high-active area electrode architectures and may afford a decreased dependence on precious catalyst materials.Notes
This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.Data availability
All videos of bubble evolution and labeled images for network training are made available on the Materials Data Facility.60Github repository including training codes: https://github.com/differentiate-catalysis/catalyst-bubble-detection/tree/main.
Data and figures are available upon reasonable request from the corresponding authors.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Professors Rafael Gomez-Bombarelli and Yang Shao-Horn for useful discussions. This work was carried out in part through the use of MIT.nano facilities. This material is based upon work supported by the Department of Energy, Advanced Research Projects Agency-Energy (ARPA-E), under Award Number DE-AR0001220.References
- M. Chatenet, B. G. Pollet, D. R. Dekel, F. Dionigi, J. Deseure, P. Millet, R. D. Braatz, M. Z. Bazant, M. Eikerling, I. Staffell, P. Balcombe, Y. Shao-Horn and H. Schäfer, Water Electrolysis: From Textbook Knowledge to the Latest Scientific Strategies and Industrial Developments, Chem. Soc. Rev., 2022 10.1039/d0cs01079k
.
- M. El-Shafie, Hydrogen Production by Water Electrolysis Technologies: A review, Results Eng., 2023, 20 DOI:10.1016/j.rineng.2023.101426
.
- L. N. Zhang, R. Li, H. Y. Zang, H. Q. Tan, Z. H. Kang, Y. H. Wang and Y. G. Li, Advanced Hydrogen Evolution Electrocatalysts Promising Sustainable Hydrogen and Chlor-Alkali Co-Production, Energy Environ. Sci., 2021 10.1039/d1ee02798k
.
- A. Kumar, F. Du and J. H. Lienhard, Caustic Soda Production, Energy Efficiency, and Electrolyzers, ACS Energy Lett., 2021 DOI:10.1021/acsenergylett.1c01827
.
- M. C. Stern, F. Simeon, H. Herzog and T. A. Hatton, Post-Combustion Carbon Dioxide Capture Using Electrochemically Mediated Amine Regeneration, Energy Environ. Sci., 2013, 6(8), 2505–2517, 10.1039/C3EE41165F
.
- A. M. Zito, L. E. Clarke, J. M. Barlow, D. Bim, Z. Zhang, K. M. Ripley, C. J. Li, A. Kummeth, M. E. Leonard, A. N. Alexandrova, F. R. Brushett and J. Y. Yang, Electrochemical Carbon Dioxide Capture and Concentration, ACS Chem. Rev., 2023, 123(13), 8069–8098, DOI:10.1021/acs.chemrev.2c00681
.
- F. Sabatino, M. Mehta, A. Grimm, M. Gazzani, F. Gallucci, G. J. Kramer and M. Van Sint Annaland, Evaluation of a Direct Air Capture Process Combining Wet Scrubbing and Bipolar Membrane Electrodialysis, Ind. Eng. Chem. Res., 2020, 59(15) DOI:10.1021/acs.iecr.9b05641
.
- A. Angulo, P. van der Linde, H. Gardeniers, M. Modestino and D. Fernández Rivas, Influence of Bubbles on the Energy Conversion Efficiency of Electrochemical Reactors, Joule, 2020, 4(3), 555–579, DOI:10.1016/J.JOULE.2020.01.005
.
- A. E. Angulo, D. Frey and M. A. Modestino, Understanding Bubble-Induced Overpotential Losses in Multiphase Flow Electrochemical Reactors, Energy Fuels, 2022, 36(14), 7908–7914, DOI:10.1021/ACS.ENERGYFUELS.2C01543
.
- A. Angulo, P. van der Linde, H. Gardeniers, M. Modestino and D. Fernández Rivas, Influence of Bubbles on the Energy Conversion Efficiency of Electrochemical Reactors, Joule, 2020, 555–579, DOI:10.1016/j.joule.2020.01.005
.
- T. Alan Hatton, M. Rahimi, F. Zucchelli and M. Puccini, Improved CO2 Capture Performance of Electrochemically Mediated Amine Regeneration Processes with Ionic Surfactant Additives, ACS Appl. Energy Mater., 2020, 3(11), 10823–10830, DOI:10.1021/ACSAEM.0C01859/SUPPL_FILE/AE0C01859_SI_001.PDF
.
- M. Wang, M. Rahimi, A. Kumar, S. Hariharan, W. Choi and T. A. Hatton, Flue Gas CO2 Capture via Electrochemically Mediated Amine Regeneration: System Design and Performance, Appl. Energy, 2019, 255, 113879, DOI:10.1016/J.APENERGY.2019.113879
.
- Advanced Chlor-Alkali Technology, U.S. Dept. of Energy, Office of Energy Efficiency and Renewable Energy. https://www1.eere.energy.gov/manufacturing/industries_technologies/imf/pdfs/1797_advanced_chlor-alkali.pdf (accessed 2021–12–03).
-
J. Dukovic and C. W. Tobias, Influence of Attached Bubbles on Potential Drop and Current Distribution at Gas-Evolving Electrodes, in Proceedings - The Electrochemical Society, The Electrochemical Society, 1986, vol. 86–12, pp. 122–147, DOI:10.1149/1.2100456
.
-
H. Vogt, Gas-Evolving Electrodes, in Comprehensive Treatise of Electrochemistry, Springer US, Boston, MA, 1983, pp. 445–489, DOI:10.1007/978-1-4615-6690-8_7
.
- C. Gabrielli, F. Huet, M. Keddam, A. Macias and A. Sahar, Potential Drops Due to an Attached Bubble on a Gas-Evolving Electrode, J. Appl. Electrochem., 1989, 19(5), 617–629, DOI:10.1007/BF01320636
.
- H. Vogt, The Rate of Gas Evolution at Electrodes—II. An Estimate of the Efficiency of Gas Evolution on the Basis of Bubble Growth Data, Electrochim. Acta, 1984, 29(2), 175–180, DOI:10.1016/0013-4686(84)87044-9
.
-
R. Wüthrich, C. Comninellis and H. Bleuler, Bubble Evolution on Vertical Electrodes under Extreme Current Densities, in Electrochimica Acta, Pergamon, 2005, vol. 50, pp. 5242–5246, DOI:10.1016/j.electacta.2004.12.052
.
- A. Taqieddin, M. R. Allshouse and A. N. Alshawabkeh, Mathematical Formulations of Electrochemically Gas-Evolving Systems, J. Electrochem. Soc., 2018, 165(13), E694–E711, DOI:10.1149/2.0791813jes
.
- D. Zhang and K. Zeng, Evaluating the Behavior of Electrolytic Gas Bubbles and Their Effect on the Cell Voltage in Alkaline Water Electrolysis, Ind. Eng. Chem. Res., 2012, 51(42), 13825–13832, DOI:10.1021/IE301029E
.
- X. Zhao, H. Ren and L. Luo, Gas Bubbles in Electrochemical Gas Evolution Reactions, Langmuir, 2019, 35(16), 5392–5408, DOI:10.1021/ACS.LANGMUIR.9B00119/ASSET/IMAGES/LARGE/LA-2019-00119Z_0003.JPEG
.
- C. Gabrielli, F. Huet and R. P. Nogueira, Fluctuations of Concentration Overpotential Generated at Gas-Evolving Electrodes, Electrochim. Acta, 2005, 50(18), 3726–3736, DOI:10.1016/j.electacta.2005.01.019
.
- Y. B. Vogel, C. W. Evans, M. Belotti, L. Xu, I. C. Russell, L. J. Yu, A. K. K. Fung, N. S. Hill, N. Darwish, V. R. Gonçales, M. L. Coote, K. Swaminathan Iyer and S. Ciampi, The Corona of a Surface Bubble Promotes Electrochemical Reactions, Nat. Commun., 2020, 11(1), 1–8, DOI:10.1038/s41467-020-20186-0
.
- Z. Lu, L. Zhang, R. Iwata, E. N. Wang and J. C. Grossman, Transport-Based Modeling of Bubble Nucleation on Gas Evolving Electrodes, Langmuir, 2020, 36(49), 15112–15118, DOI:10.1021/acs.langmuir.0c02690
.
- S. D. Li, C. C. Wang and C. Y. Chen, Water Electrolysis in the Presence of an Ultrasonic Field, Electrochim. Acta, 2009, 54(15), 3877–3883, DOI:10.1016/J.ELECTACTA.2009.01.087
.
- H. B. Liu, D. Zhong, J. Han, L. M. Pan and Y. Liu, Hydrogen Bubble Evolution from Magnetized Nickel Wire Electrode, Int. J. Hydrogen Energy, 2019, 44(60), 31724–31730, DOI:10.1016/j.ijhydene.2019.10.063
.
- H. b. Liu, Q. Hu, L. m. Pan, R. Wu, Y. Liu and D. Zhong, Electrode-Normal Magnetic Field Facilitating Neighbouring Electrochemical Bubble Release from Hydrophobic Islets, Electrochim. Acta, 2019, 306, 350–359, DOI:10.1016/j.electacta.2019.03.140
.
- X. Zhao, H. Ren and L. Luo, Gas Bubbles in Electrochemical Gas Evolution Reactions, Langmuir, 2019, 35(16), 5392–5408, DOI:10.1021/acs.langmuir.9b00119
.
- Q. Chen, J. Zhao, X. Deng, Y. Shan and Y. Peng, Single-Entity Electrochemistry of Nano- and Microbubbles in Electrolytic Gas Evolution, J. Phys. Chem. Lett., 2022, 13(26), 6153–6163, DOI:10.1021/ACS.JPCLETT.2C01388
.
- H. Ren, S. R. German, M. A. Edwards, Q. Chen and H. S. White, Electrochemical Generation of Individual O2 Nanobubbles via H2O2 Oxidation, J. Phys. Chem. Lett., 2017, 8(11), 2450–2454, DOI:10.1021/ACS.JPCLETT.7B00882/ASSET/IMAGES/LARGE/JZ-2017-00882J_0004.JPEG
.
- H. Vogt, The Quantities Affecting the Bubble Coverage of Gas-Evolving Electrodes, Electrochim. Acta, 2017, 235, 495–499, DOI:10.1016/j.electacta.2017.03.116
.
- H. Vogt, The Actual Current Density of Gas-Evolving Electrodes—Notes on the Bubble Coverage, Electrochim. Acta, 2012, 78, 183–187, DOI:10.1016/J.ELECTACTA.2012.05.124
.
- J. Dukovic and C. W. Tobias, The Influence of Attached Bubbles on Potential Drop and Current Distribution at Gas–Evolving Electrodes, J. Electrochem. Soc., 1987, 134(2), 331–343, DOI:10.1149/1.2100456
.
- J. R. Lake, Á.M Soto and K. K. Varanasi, Impact of Bubbles on Electrochemically Active Surface Area of Microtextured Gas-Evolving Electrodes, Langmuir, 2022, 38(10), 3276–3283, DOI:10.1021/acs.langmuir.2c00035
.
- Z. Li, R. Hu, J. Song, L. Liu, J. Qu, W. Song and C. Cao, Gas–Liquid–Solid Triphase Interfacial Chemical Reactions Associated with Gas Wettability, Adv. Mater. Interfaces, 2021, 8(6), 2001636, DOI:10.1002/ADMI.202001636
.
- R. Iwata, L. Zhang, K. L. Wilke, S. Gong, M. He, B. M. Gallant and E. N. Wang, Bubble Growth and Departure Modes on Wettable/Non-Wettable Porous Foams in Alkaline Water Splitting, Joule, 2021, 5(4), 887–900, DOI:10.1016/J.JOULE.2021.02.015
.
- C. Brussieux, P. Viers, H. Roustan and M. Rakib, Controlled Electrochemical Gas Bubble Release from Electrodes Entirely and Partially Covered with Hydrophobic Materials, Electrochim. Acta, 2011, 56(20), 7194–7201, DOI:10.1016/j.electacta.2011.04.104
.
- T. Fujimura, W. Hikima, Y. Fukunaka and T. Homma, Analysis of the Effect of Surface Wettability on Hydrogen Evolution Reaction in Water Electrolysis Using Micro-Patterned Electrodes, Electrochem. Commun., 2019, 101, 43–46, DOI:10.1016/j.elecom.2019.02.018
.
- P. Peñas, P. van der Linde, W. Vijselaar, D. van der Meer, D. Lohse, J. Huskens, H. Gardeniers, M. A. Modestino and D. F. Rivas, Decoupling Gas Evolution from Water-Splitting Electrodes, J. Electrochem. Soc., 2019, 166(15), H769–H776, DOI:10.1149/2.1381914jes
.
- Z. Long, Y. Zhao, C. Zhang, Y. Zhang, C. Yu, Y. Wu, J. Ma, M. Cao and L. Jiang, A Multi–Bioinspired Dual–Gradient Electrode for Microbubble Manipulation toward Controllable Water Splitting, Adv. Mater., 2020, 32(17), 1908099, DOI:10.1002/adma.201908099
.
- K. Ando, Y. Uchimoto and T. Nakajima, Concentration Profile of Dissolved Gas during Hydrogen Gas Evolution: An Optical Approach, Chem. Commun., 2020, 56(92), 14483–14486, 10.1039/D0CC05695B
.
- P. A. Kempler, Z. P. Ifkovits, W. Yu, A. I. Carim and N. S. Lewis, Optical and Electrochemical Effects of H 2 and O 2 Bubbles at Upward-Facing Si Photoelectrodes, Energy Environ. Sci., 2021, 14(1), 414–423, 10.1039/D0EE02796K
.
- M. Suvira and B. Zhang, Effect of Surfactant on Electrochemically Generated Surface Nanobubbles, Anal. Chem., 2021, 93(12), 5170–5176, DOI:10.1021/ACS.ANALCHEM.0C05067/ASSET/IMAGES/LARGE/AC0C05067_0005.JPEG
.
- J. T. Davis, D. E. Brown, X. Pang and D. v. Esposito, High Speed Video Investigation of Bubble Dynamics and Current Density Distributions in Membraneless Electrolyzers, J. Electrochem. Soc., 2019, 166(4), F312–F321, DOI:10.1149/2.0961904JES/XML
.
- X. Yang, F. Karnbach, M. Uhlemann, S. Odenbach and K. Eckert, Dynamics of Single Hydrogen Bubbles at a Platinum Microelectrode, Langmuir, 2015, 31(29), 8184–8193, DOI:10.1021/ACS.LANGMUIR.5B01825/SUPPL_FILE/LA5B01825_SI_001.PDF
.
- T. Kadyk, D. Bruce and M. Eikerling, How to Enhance Gas Removal from Porous Electrodes?, Sci. Rep., 2016, 6(1), 1–14, DOI:10.1038/srep38780
.
- S. J. Gross, K. M. McDevitt, D. R. Mumm and A. Mohraz, Mitigating Bubble Traffic in Gas-Evolving Electrodes via Spinodally Derived Architectures, ACS Appl. Mater. Interfaces, 2021, 13(7), 8528–8537, DOI:10.1021/ACSAMI.0C20798/ASSET/IMAGES/LARGE/AM0C20798_0009.JPEG
.
-
A. Keçebaş, M. Kayfeci and M. Bayat, Electrochemical Hydrogen Generation, in Solar Hydrogen Production: Processes, Systems and Technologies, Academic Press, 2019, pp. 299–317, DOI:10.1016/B978-0-12-814853-2.00009-6
.
- H. Vogt and R. J. Balzer, The Bubble Coverage of Gas-Evolving Electrodes in Stagnant Electrolytes, Electrochim. Acta, 2005, 50(10), 2073–2079, DOI:10.1016/J.ELECTACTA.2004.09.025
.
- K. He, G. Gkioxari, P. Dollár and R. Girshick, Mask R-CNN, in Proceedings of the IEEE international conference on computer vision, 2017, pp. 2961–2969.
-
Y. Li, S. Xie, X. Chen, P. Dollar, K. He and R. Girshick, Benchmarking Detection Transfer Learning with Vision Transformers, 2021, DOI:10.48550/arxiv.2111.11429
.
- S. Ren, K. He, R. Girshick and J. Sun, Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks, arXiv, 2015, preprint, arXiv:1506.01497, DOI:10.48550/arXiv.1506.01497.
- X. Sun, P. Wu and S. C. H. Hoi, Face Detection Using Deep Learning: An Improved Faster RCNN Approach, Neurocomputing, 2018, 299, 42–50, DOI:10.1016/J.NEUCOM.2018.03.030
.
- T. Y. Lin, M. Maire, S. Belongie, J. Hays, P. Perona, D. Ramanan, P. Dollár and C. L. Zitnick, Microsoft COCO: Common Objects in Context, in Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 2014, vol. 8693 LNCS(PART 5), pp. 740–755, DOI:10.1007/978-3-319-10602-1_48/COVER.
- H. Yuen, J. Princen, J. Illingworth and J. Kittler, Comparative Study of Hough Transform Methods for Circle Finding, Image Vis. Comput., 1990, 8(1), 71–77, DOI:10.1016/0262-8856(90)90059-E
.
- L. Li, K. Jamieson, A. Rostamizadeh, E. Gonina, J. Ben-tzur, M. Hardt, B. Recht and A. Talwalkar, A System for Massively Parallel Hyperparameter Tuning, Proc. Mach. Learn. Res., 2020, 2, 230–246 Search PubMed
.
- Á. Moreno Soto, T. Maddalena, A. Fraters, D. van der Meer and D. Lohse, Coalescence of Diffusively Growing Gas Bubbles, J. Fluid Mech., 2018, 846, 143–165, DOI:10.1017/jfm.2018.277
.
-
A. Bard and L. Faulkner, Electrochemical Methods Fundamentals and Applications, John Wiley & Sons, Inc., 2nd edn, 2001 Search PubMed
.
- M. Bockris and A. K. M. Shamshul Huq, The Mechanism of the Electrolytic Evolution of Oxygen on Platinum, Proc. R. Soc. London, Ser. A, 1956, 237(1209), 277–296 Search PubMed
.
- J. Lake, S. Rufer, J. James, N. Pruyne, A. Scourtas, M. Schwarting, A. Ambadkar, I. Foster, B. Blaiszik and K. K. Varanasi, Labeled Dataset of Hydrogen and Oxygen Bubbles Evolving on Electrodes, Materials Data Facility, 2023, DOI:10.18126/9pj2-hpef.
- A. Bashkatov, S. Park, C. Demirkir, J. Wood, M. T. M. Koper, D. Lohse and D. Krug, Performance Enhancement of Electrocatalytic Hydrogen Evolution through Coalescence-Induced Bubble Dynamics, J. Am. Chem. Soc., 2024, 146(14), 10177–10186, DOI:10.1021/jacs.4c02018
.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional experimental details, figures, materials, and methods, including: (1) materials, (2) experimental setup and imaging, (3) electrochemical measurements, (4) Pt working electrode fabrication & characterization, (5) mass transport and ohmic effects, (6) generating ground truth data, (7) deep learning methodologies. See DOI: https://doi.org/10.1039/d4nr02628d |
| ‡ Authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2025 |