 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
What makes β-NaYF4:Er3+,Yb3+ such a successful luminescent thermometer?
Markus
Suta

Inorganic Photoactive Materials, Institute of Inorganic Chemistry, Heinrich Heine University Düsseldorf, Universitätsstraße 1, 40225 Düsseldorf, Germany. E-mail: markus.suta@hhu.de
First published on 21st January 2025
Abstract
Luminescence thermometry has emerged as a promising approach for remote, non-invasive temperature sensing at the nanoscale. One of the simplest approaches in that regard is single-ion luminescence Boltzmann thermometry that exploits thermal coupling between two radiatively emitting levels. The working horse example for this type of luminescence thermometry is undoubtedly the green-emitting upconversion phosphor β-NaYF4:Er3+,Yb3+ exploiting the thermal coupling between the two excited 2H11/2 and 4S3/2 levels of Er3+ for this purpose. Within this tutorial article, I would like to give a theoretically motivated account on the underlying reasons for the experimentally recorded success of this material for Boltzmann thermometry referring to time-resolved data on both the bulk and nanocrystalline material. Guidelines are established and both advantages and potential pitfalls in β-NaYF4:Er3+,Yb3+ for luminescence thermometry are given.
Introduction
Remote temperature sensing by means of a luminescence signal (luminescence thermometry) has revolutionized phosphor research and has been one of its dominating areas since the early 2000s.1–6 Among the various possibilities to use temperature-dependent luminescence for calibration in thermometry, self-referenced ratiometric thermometry is one of the simplest approaches.4 It exploits the fact the luminescence intensity ratio (LIR) of thermally coupled, radiatively emitting excited states from the same electron configuration follows Boltzmann's law thus enabling an appealingly simple calibration of such an optical thermometer. A representative example of this concept are the green-emitting 2H11/2 and 4S3/2 levels of the Er3+ ion discussed within this work. Usually, the energy splitting between thermally coupled electronic states should be in the order of the thermal energy kBT to be probed (kB is Boltzmann's constant), which is roughly 102–103 cm−1 for temperatures around room temperature and 101–102 cm−1 for cryogenic temperatures. The trivalent lanthanoid ions with the intraconfigurational 4fn–4fn transitions (n = 2 for Pr3+ to n = 12 for Tm3+) in the ultraviolet (UV), visible, and near infrared (NIR) range are naturally suited for that purpose because the low linewidth of the related emission lines allows to spectrally resolve such low energy gaps.7 Thus, thermal coupling between different spin–orbit levels of the lanthanoids is useful for thermometry at around room temperature and above,7,8 while thermal coupling between different crystal field states is required for cryogenic temperature measurements exploiting single-ion Boltzmann thermometry.9–11 Although it is often argued in literature that the energy gap should not exceed 2000 cm−1 for effective thermometry, it should be noted that this statement depends on the temperature of interest, and energy gaps beyond 2000 cm−1 can be easily exploited if the intrinsic non-radiative coupling between excited states is sufficiently strong or temperatures are high enough.12–14 This is usually encountered in so-called crossover luminescent thermometers that probe thermal coupling between excited states of different electronic configurations such as Pr3+,15–19 selected divalent lanthanoid ions,14,20–23 or thermally activated delayed fluorescent emitters.24–27 In the context of this tutorial article, only the case of classic ratiometric Boltzmann luminescent thermometers will be considered.Although the electronic structure of the trivalent lanthanoids formally offers a rich variety of possibilities for luminescent thermometry, the prominent upconversion phosphor β-NaYF4:Er3+,Yb3+ stands out in this regard.28,29 In this phosphor, NIR excitation of the Yb3+ ions at 980 nm leads to bright green upconverted emission from the thermally coupled excited 2H11/2 and 4S3/2 levels of Er3+. Probably, also the excellent size and habitus control of nanocrystalline β-NaYF4:Er3+,Yb3+ without significant loss in its upconversion performance has additionally contributed to the huge recorded success of that compound in the field.30,31
Er3+ was established as one of the pioneering ratiometric luminescent thermometers with various milestones, first in fluoridic ZBLAN fibers in 1990,32 then in BaTiO3 in 2004,33 and finally as nanocrystalline β-NaYF4:Er3+,Yb3+ in 2009.34 Since then, the latter compound has been constantly exploited as the working horse example for tests of luminescence thermometry in real-case applications including catalysis and microflow reactors,35–39 probing of Brownian motion,40,41 thermal imaging of microelectronic circuits,42 plasmonic heating43,44 and heat transfer along lipid bilayers.45,46 Other examples include temperature monitoring within a mitochondrium,47 pushing of the single nanothermometric level within a heated nanowire,48 or recording of density fluctuations of water.41 The established success of this upconversion phosphor for thermometry even allowed to shed light on potential biases in luminescence nanothermometry.49–52 But what makes this phosphor stand out compared to many other lanthanoid-activated inorganic compounds that leads to this constantly recorded experimental success? Based on recently established theoretical guidelines for Boltzmann thermometers,8 I would like to elaborate on the consequences for Er3+ and demonstrate from thermodynamic and kinetic viewpoints – using both measured and reported data – why β-NaYF4:Er3+,Yb3+ is actually such a successful luminescent Boltzmann thermometer and what practical issues can potentially arise when it is used in its nanocrystalline rather than microcrystalline form.
Results and discussion
Synthesis
A microcrystalline sample of the nominal composition β-NaY0.80Er0.02Yb0.18F4 (hereafter simply referred to as β-NaYF4:Er3+,Yb3+) has been prepared by a conventional solid-state chemical route. For that purpose, Y2O3 (99.999%, Chempur), Er2O3 (99.999%, Chempur) and Yb2O3 (99.99%, smart-elements) were dissolved in the respective stoichiometric amounts in 6 mL concentrated HCl (37%, Fisher Scientific) upon heating at around 100 °C until the solution became completely transparent. After that, the solvent level was carefully reduced at 80 °C and gradually diluted with distilled H2O. Subsequently, the pH was increased to 5 by dropwise addition of aqueous, concentrated NH3 (28–30 wt%, Thermo Scientiifc) solution. Finally, an excess of saturated (NH4)2CO3 (98%, Thermo Scientific) solution was added resulting in a precipitation of the basic rare earth carbonates. The dried colourless residue was reacted with 3 eq. NH4HF2 (98%, Thermo Scientific) at 120 °C for 1 h, thoroughly mixed with additional 3 eq. NH4HF2 and reacted at 150 °C before final reaction with 2 eq. NaBF4 (98%, Chempur) at 500 °C under a N2 atmosphere. According to X-ray powder diffraction, it was phase pure, although some reflections are shifted compared to the reflections of the database pattern of β-NaYF4 (ICSD: 51916) based on the presence of the smaller Er3+ and Yb3+ ions that change the lattice constants of the prepared compound.Characterization
The sample purity was assessed by means of X-ray powder diffraction on a X'Pert diffractometer (Malvern Panalytical, Cu Kα radiation) working with Bragg–Brentano geometry. The powdered sample was measured in reflection mode on an Al sample holder. Steady-state and time-resolved photoluminescence were measured on a FLS1000 photoluminescence spectrometer (Edinburgh Instruments) equipped with a 450 W Xe lamp, Czerny-Turner double grating monochromators (focal length 2 × 325 mm, blazed at 400 nm and 500 nm, respectively) in both the excitation and emission compartment, and a thermoelectrically (−20 °C) cooled PMT-980 detector (Hamamatsu). A continuous-wave laser with variable power density emitting at λ = 980 nm (PhotonTec, estimated power density of the unfocused beam for the experiments in this work: ∼5.5 mW cm−2) was used as an excitation source, while the luminescence decay of the green emission was recorded with a VPL-510 laser (Edinburgh Instruments; λex = (515 ± 5) nm, 70 mW average incident power, variable temporal pulse width, repetition rate f = 125 Hz). Upconversion emission spectra were corrected for the grating efficiency and detector sensitivity. Temperature-dependent luminescence spectra were acquired with a Linkam Scientific THMS600 cell (accuracy ± 0.1 °C) between 77 K and 823 K.Thermodynamic assessment
In its dynamic working range, the LIR, R21(T), between two emission peaks with intensities I20 and I10 for the transitions from two thermally coupled excited levels |2〉 and |1〉 to a common ground level |0〉 of a luminescent Boltzmann thermometer follows the simple calibration law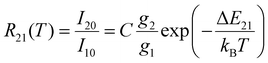 | (1) |
For a better mechanistic understanding of luminescent Boltzmann thermometers, it is advisable to use microcrystalline instead of nanocrystalline samples to avoid an impact of surface-attached ligands or surrounding solvent molecules to non-radiative transitions. Typically, the two green-emitting spin–orbit levels 2H11/2 = |2〉 and 4S3/2 = |1〉 of the Er3+ ion are probed for luminescence Boltzmann thermometry.14 In the host β-NaYF4, they are separated by an energy gap of ΔE21 = (650 ± 10) cm−1 according to high-resolution excitation spectra of a representative microcrystalline sample at 77 K (see Fig. 1(a)), in good agreement to earlier reports.52,53 It is noteworthy that many publications report varying values for this energy gap,35–39,54,55 but photoluminescence excitation spectra offer an unambiguous reference for this value that can be related to the estimated gap according to a Boltzmann fit of the temperature-dependent LIR (see Fig. 1(b) and (c)). Given that value for ΔE21, it can be estimated that the thermodynamic optimum operating temperature range for an Er3+-based Boltzmann thermometer, in which it works with highest possible statistical precision,8 is given by
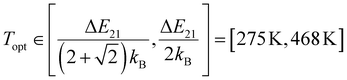 | (2) |
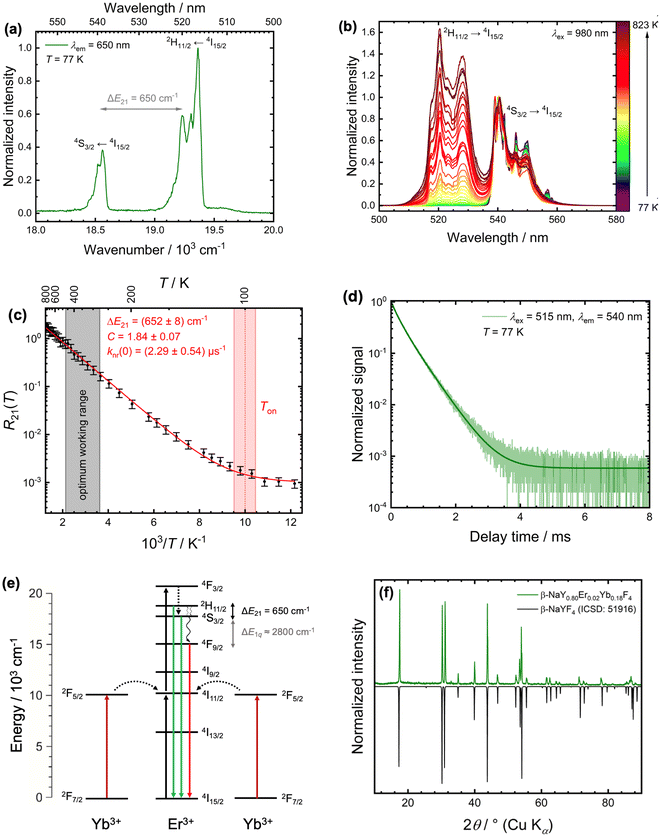 | ||
| Fig. 1 Characteristics of microcrystalline β-NaYF4:2 mol%Er3+,18 mol%Yb3+ for luminescence Boltzmann thermometry. (a) High-resolution photoluminescence excitation spectra at T = 77 K (plotted against wavenumbers) upon monitoring the red 4F9/2 → 4I15/2-based emission at λem = 650 nm. The effective energy gap between the 4S3/2 and 2H11/2 level is indicated. (b) Temperature-dependent upconversion spectra of β-NaYF4:2 mol%Er3+,18 mol%Yb3+ upon near infrared excitation (λex = 980 nm) between 77 K and 823 K. The spectra were normalized with respect to the emission peak at 540 nm. (c) Plot of the LIR of the two green emission bands of Er3+ against reciprocal temperature in the measured temperature range. Integration ranges were between 510 nm and 533 nm as well as 533 nm and 555 nm, respectively. The red line corresponds to a fit according to eqn (1) with an offset term related to knr(0). Both the estimated onset temperature Ton and the optimum working range according to eqn (2) are indicated. (d) Luminescence decay curve of the 4S3/2 → 4I15/2-based emission (λem = 540 nm, spectral bandwidth Δλ = 1.5 nm) upon direct excitation into the 2H11/2 level (λex = 515 nm) at T = 77 K. The solid line represents an effective triexponential fit and gives an intensity-weighted average decay time of 〈τ〉 = 0.41 ms. (e) Schematic energy level scheme for the cooperative upconversion process between Yb3+ and Er3+. Solid, straight arrows depict absorption (upward) or emission (downward) pathways. Relevant nonradiative processes in this work are indicated by curly black arrows. (f) Powder X-ray diffraction pattern (Cu Kα radiation) of as-synthesized microcrystalline β-NaYF4:2 mol%Er3+,18 mol%Yb3+ compared to a diffraction pattern derived from single-crystal structure data of β-NaYF4 (ICSD: 51916). | ||
In that temperature range, there is a compromise between high relative sensitivity Sr(T) and appreciable signal-to-noise ratio of the emission peaks stemming from both excited levels. Thus, Er3+ is particularly suited as a luminescent thermometer for biologically relevant temperatures, which nicely coincides with its application in upconversion phosphors for bioimaging applications.56 In the optimum temperature range according to eqn (2), the relative sensitivities of the Er3+-based Boltzmann thermometer vary between Sr(T = 275 K) = 1.24% K−1 and Sr(T = 468 K) = 0.43% K−1. It should be noted, however, that the relative sensitivity does not fully determine the performance of a luminescent thermometer, but rather the overall expected relative statistical uncertainty, which will be addressed below.
A second important feature relates to the radiative transition rates of both involved emission lines. Usually, the low intensity of the higher energetic emission poses a fundamental limitation to the precision of any luminescent Boltzmann thermometer as its intensity is typically dominated by the thermal population of the higher excited level and thus, the exponential Boltzmann factor of eqn (1). However, an additionally beneficial factor for the overall precision of the luminescent Boltzmann thermometer can be the pre-constant Cg2/g1 based on the motivation that a LIR should be in the order of 10° in a regarded temperature range for highest precision.
In the case of Er3+, it is g2 = 12 and g1 = 4, if thermalization between the different Stark states in a ligand field is assumed (which is given in the optimum temperature range according to eqn (2)). It has been demonstrated that a thermodynamically advisable value for Cg2/g1 should be8
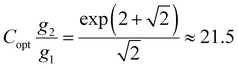 | (3) |
The electronic pre-constant C is connected to the spontaneous emission rates A20 and A10 for the radiative transitions |2〉 → |0〉 and |1〉 → |0〉,
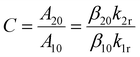 | (4) |
In the case of Er3+ in β-NaYF4, careful diffuse reflectance measurements on microcrystalline powders allow an estimate for the exponential pre-constant for Er3+ of Cg2/g1 = 18.9, which is close to the optimum value for highest precision according to eqn (3). In contrast, Judd–Ofelt calculations rather yield a value of Cg2/g1 = 7.7 indicating that the range of possible C values in literature can vary significantly.57,58 Such high values for the exponential prefactor mean that the intensity of the higher energetic 2H11/2 → 4I15/2-based emission of Er3+ at around 525 nm shows a higher spontaneous radiative emission rate or oscillator strength. This fact becomes particularly prominent at higher temperatures, at which the 2H11/2 → 4I15/2-based emission at around 525 nm is even more intense than the 4S3/2 → 4I15/2-based emission at around 540 nm (see Fig. 1(b)). Such a feature is very uncommon for most other thermometrically exploited lanthanoid ions such as Nd3+, Gd3+, or Eu3+, for which it is generally A20 ≲ A10 and thus, Cg2/g1 < 101. It should be noted that photonic effects can additionally affect this pre-constant and have to be taken into account for nanothermometers in the vicinity e.g., mirroring surfaces.52 In this particular compound, an exponential pre-factor of Cg2/g1 = 5.52 ± 0.21 is estimated, although the error range is probably even larger given that it is in principle estimated from an extrapolation of the LIR formally infinite temperatures. The overall unusually high value (partially related to the high J degeneracy of the 2H11/2 level) electronically contributes to an appreciable signal-to-noise ratio from both green emission band and thus, enhances the overall precision of the Er3+-based luminescent thermometer.
In its optimum performance range (see eqn (2)) and with an intensity of the 4S3/2 → 4I15/2-based emission of I10 = 106 cts, the minimum expected relative uncertainty σT/T of the Er3+-related luminescent thermometer is constantly below 0.08% according to8
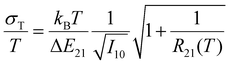 | (5) |
Kinetic assessment
So far, it has been demonstrated that the green-emitting 2H11/2 and 4S3/2 levels of Er3+ fulfil many of the required conditions for thermodynamically motivated optimum performance as a single-ion luminescent Boltzmann thermometer in the physiological temperature range with high statistical precision. Besides this thermodynamic motivation, the kinetic interplay between radiative decay of the lower energetic excited 4S3/2 level and non-radiative coupling between the excited levels is relevant for the dynamic working range of any single ion as a luminescent Boltzmann thermometer.8,61In the case of Er3+, the radiative decay rate (corrected for reabsorption effects) of the 4S3/2 level in β-NaYF4:0.1 mol%Er3+ is k1r = 1.55 ms−1, in good agreement with earlier calculations.57,62 This competition poses a natural, kinetically induced onset temperature Ton for such a luminescent Boltzmann thermometer below which the two excited states decouple and thermal equilibrium is not sustained anymore since the nonradiative absorption rate cannot compete with radiative decay of the lower energetic excited level anymore.8,61 The nonradiative transitions among 4fn spin–orbit levels is most dominantly governed by the energy gap law of multiphonon transitions.63 It was demonstrated that the energy gap ΔE21 is ideally bridged by no more than p = 2 vibrational modes to ensure that the onset temperature for thermal equilibrium is below the optimum range as defined in eqn (2).8 This is clearly given in the case of β-NaYF4:Er3+,Yb3+ with a cutoff phonon energy of ħωcut = 450 cm−1 (ref. 64) and the respective energy gap of ΔE21 = (650 ± 10) cm−1. If nonradiative thermal coupling involves p = 2 effective phonon modes of energy ħωeff = ΔE21/p, the expected onset temperature Ton for Boltzmann behaviour of the LIR can be derived as8
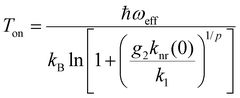 | (6) |
Fig. 1(c) depicts the temperature-dependent LIR of the two green emission bands of Er3+ in the representative microcrystalline β-NaYF4:2 mol%Er3+, 18 mol% Yb3+ sample (see Synthesis section for more details) between 77 K and 823 K obtained upon excitation with 980 nm to eliminate background for higher accuracy. From the estimated onset temperature of Ton = (100 ± 5) K according to the recorded LIR between the 2H11/2- and 4S3/2-based emission bands in the green range and an average decay rate of k1 = 2.43 ms−1 (see Fig. 1(d)), an intrinsic nonradiative transition rate of knr(0) = (2.29 ± 0.54) μs−1 governing the coupling the 2H11/2 and 4S3/2 level can be estimated from eqn (6). The value appears reasonable given the fact that detection of the luminescence decay trace of the 4S3/2-based emission of Er3+ in β-NaYF4 at 77 K (see Fig. 1(d)) upon excitation into the 2H11/2 level does not reveal any rise component even if the pulse width is decreased to 0.1 μs and the decay is regarded in a μs time range. This implies that the feeding of the 4S3/2 level proceeds faster than 1 μs, matching the upper estimate for knr(0). Compared to many other lanthanoid ions with similar two-phonon nonradiative transitions between their excited levels such as Eu3+, the intrinsic nonradiative coupling between the excited levels of Er3+ is unusually strong and indicates an induced electric dipolar nature of the respective nonradiative transition.8 A measure for that can be the relevant matrix elements for induced electric dipolar transitions as originally suggested by Judd and Ofelt.65,66 For the 2H11/2 ↔4S3/2 transition, they read ∥〈U(k)∥〉2 (∥〈U(2)∥〉2 = 0.000, ∥〈U(4)∥〉2 = 0.2002, ∥〈U(6)∥〉2 = 0.0097) according to Carnall et al.,53 which are higher than for most other thermometrically relevant nonradiative transitions within the trivalent lanthanoids. For comparison, a respective two-phonon non-radiative transition rate between the 5D1 and 5D0 levels of Eu3+ in e.g., LaPO4 or LaBO3 is in the order of only 101 ms−1 and indicates a magnetic dipolar transition,67 as was also originally proposed by Weber.68
According to the energy gap law, it could be questioned why no host compound with higher cutoff phonon energies resonant to the energy gap ΔE21 such as aluminates, vanadates, phosphates, or borates could be more recommendable for Er3+ as a luminescent Boltzmann thermometer. The reason for that point lies in the special electronic landscape of the Er3+ ion. Besides the two thermally coupled green emitting levels, there is also a red-emitting lower energetic 4F9/2 level ca. 2800 cm−1 below the 4S3/2 level (see Fig. 1(e)). Thus, even if a higher cutoff phonon energy may accelerate the nonradiative thermal coupling between the green-emitting 2H11/2 and 4S3/2 levels of Er3+, competitive nonradiative multiphonon relaxation from the 4S3/2 level to the 4F9/2 level also becomes more effective thus increasing the total decay rate k1 of the 4S3/2 level that the nonradiative absorption rate to the 2H11/2 level has to compete with. An example demonstrating this problem is YVO4:0.1 mol%Er3+. This compound has a higher cutoff phonon energy of ħωcut = 890 cm−1 resulting in a higher decay rate of k1 = 102 ms−1 of the 4S3/2 level in that host due to faster non-radiative relaxation to the lower energetic 4F9/2 level.69 In contrast, no phonon modes with an energy of 650 cm−1 are present in xenotime-type YVO4 excluding a resonant one-phonon process for the non-radiative coupling between the 2H11/2 and 4S3/2 level of Er3+ in that host.70,71 Consequently, the onset temperature for thermalization between those two green-emitting levels in YVO4:0.1 mol%Er3+ is only at Ton = 135 K,69 even above the respective value in β-NaYF4:Er3+(Yb3+). The non-radiative coupling strength between the 2H11/2 and 4S3/2 level can be estimated by knr(0) ≈ 7 μs−1 in YVO4:0.1 mol%Er3+ based on the reported spectroscopic data, in the same order of magnitude as for β-NaYF4:Er3+,Yb3+.
Thus, at high temperatures, nonradiative multiphonon relaxation from the 4S3/2 = |1〉 to the red-emitting 4F9/2 = |q〉 level can become a general limitation for β-NaYF4:Er3+,Yb3+ as a luminescent Boltzmann thermometer. However, given a mutual energy gap of ΔE1q ≈ 2800 cm−1, it can be derived from the thermal occupation of phonons that the onset temperature for stimulated (and thus, thermally accelerated) nonradiative relaxation from the 4S3/2 to the red-emitting 4F9/2 level is about8
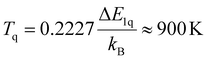 | (7) |
This makes Er3+ formally suited as a classic Boltzmann thermometer over a wide temperature range between 77 K and 900 K in β-NaYF4. Another high-temperature limitation in this host is the phase transition to the cubic fluorite-type α polymorph, which occurs, however, at around 1050 K in the bulk compound and may be even at lower temperatures in nanocrystalline NaYF4.72
Difference between microcrystalline and nanocrystalline samples and other practical problems
Another practical aspect is the usage of nanocrystalline core-only β-NaYF4 instead of a microcrystalline powder. In that case, the surface-attached organic ligands or, alternatively, surrounding solvent molecules with X–H vibrational modes (X = C, N, O) dominate the nonradiative transitions within the Er3+ ion. While this fact accelerates the relaxation pathway from the green-emitting 4S3/2 to the red-emitting 4F9/2 level (one of the major reasons why core-only β-NaYF4:Er3+,Yb3+ nanocrystals often show more dominant red upconverted emission upon NIR excitation),62,73 the thermometrically relevant nonradiative 2H11/2 ← 4S3/2 absorption transition is not significantly enhanced. As a consequence, the expected minimum onset temperature Ton for Boltzmann-type luminescence thermometry with Er3+ is generally higher in nanocrystalline β-NaYF4 than in the analogous microcrystalline samples. Reported values for the average decay rate k1 of the 4S3/2 level of core-only β-NaYF4:0.1 mol%Er3+ nanocrystals in various solvents are maximally k1 = 3 ms−1 including the photonically induced enhancement due to the refractive index n of the solvent.62 Assuming that there is a resonant vibrational mode that would allow a one-phonon bridging of the energy gap of ΔE21 = (650 ± 10) cm−1, it can be estimated from eqn (2) that the onset temperature could be even decreased to Ton = 88 K taking into account that the non-radiative coupling becomes stronger by around an order of magnitude to knr(0) ≈ 10 μs−1 according to the energy gap law.63In practice, however, higher activator fractions are used in nanocrystalline β-NaYF4 for brighter upconversion emission upon NIR excitation. A competitive depopulation channel in such a case is cross-relaxation. It has been demonstrated that both at higher Er3+ and Yb3+ contents in β-NaYF4, the 4S3/2 level decays faster due to additional cross-relaxation based on an interaction with neighbouring Er3+ or Yb3+ ions. This is also the reason for the faster decay observed in the presented microcrystalline sample of β-NaYF4:Er3+,Yb3+ (see Fig. 1(d)) and can be quantitatively assessed with the shell model of energy transfer.62,74 In the following, I want to show that the choice of the right activator fractions is a compromise between the performance as a bright upconversion phosphor and the dynamic working range as a Boltzmann luminescent thermometer. Higher Er3+ and Yb3+ fractions and the consequent faster decay of the 4S3/2 level (higher decay rate k1) will lead to an increase of the expected onset temperature (see eqn (6)). Similar effects are known from e.g., Nd3+.75,76 Therefore, it is generally recommended to use core–shell nanostructures and keep track of activator concentrations to limit internal cross-relaxation effects between Er3+ ions or between Er3+ and Yb3+ ions. For example, in core–shell nanocrystals of β-NaYF4:2 mol%Er3+, the average decay rate of the 4S3/2 level increases to around k1 = 4 ms−1,62 while in the case of respective β-NaYF4:2 mol%Er3+,18%Yb3+ nanocrystals, it even increases to k1 = 5 ms−1.62 These values result in expected onset temperatures of Ton = 106 K and Ton = 109 K, respectively, still much below the optimum performance range according to eqn (2) assuming a similar non-radiative coupling rate as in microcrystalline samples. If, in addition, core-only nanocrystals are used, the respective decay rate increases to k1 = 8 ms−1 (2 mol% Er3+) and k1 = 10 ms−1 (2 mol% Er3+, 18 mol% Yb3+),62 resulting in maximum expected onset temperatures of Ton = 115 K and Ton = 118 K, respectively. Thus, although the additional quenching pathways in nanocrystalline upconversion phosphors can lead to a difference in the onset temperature of up to around 18 K, the effect is still not practically problematic if Er3+ is used as a Boltzmann thermometer in its optimum performance range at physiological temperatures (see eqn (2)). Yet, it is important to bear these effects in mind once lower temperatures are supposed to be measured with the green-emitting levels of Er3+ (although not thermodynamically recommendable). Overall, Er3+ is a particularly robust Boltzmann thermometer whose intrinsic electronic properties make it stand out compared to many other lanthanoid-based luminescent thermometers and support a unique, wide dynamic working range. The host compound β-NaYF4 combines many beneficial features that make Er3+ perform almost at optimum theoretically suggested conditions both from a thermodynamic and kinetic perspective.
Conclusions
The upconversion phosphor β-NaYF4:Er3+,Yb3+ is one of the working horse examples of a Boltzmann luminescent thermometer with a huge experimentally recorded success. In this tutorial work, it is demonstrated by recently developed thermodynamic and kinetic guidelines what makes Er3+ a primary candidate for Boltzmann thermometry. The green-emitting 2H11/2 and 4S3/2 levels of Er3+ are particularly suited for temperature measurements slightly above room temperature (between 275 K and 468 K) with highest possible statistical precision. The special feature of a higher spontaneous emission rate of the higher energetic 2H11/2 level in the Er3+ ion leads to a favourable electronic pre-factor C that ensures a LIR of the green emission bands close to 1 and is additionally beneficial for high readout precision. Besides those thermodynamic aspects, a unique property of Er3+ among the trivalent lanthanoid ions is the high non-radiative coupling strength between the 2H11/2 and 4S3/2 levels of knr(0) = (2.29 ± 0.54) μs−1, much stronger than for most other lanthanoid ions. This extraordinarily high value stems from an induced electric dipolar nature of the nonradiative transition and renders a particularly wide dynamic working range of Er3+ as a Boltzmann thermometer. It results in very low onset temperatures for thermal coupling of the green-emitting levels in the range of Ton = (100 ± 5) K. The host compound β-NaYF4 with its low cutoff phonon energy of only 450 cm−1 is beneficial for a limitation of the nonradiative multiphonon relaxation of the 4S3/2 level into the red-emitting 4F9/2 level, even if already two phonon modes need to be consumed to bridge the energy gap of 650 cm−1 between the two green-emitting levels.Two major competitive processes could potentially increase the onset temperature for Boltzmann behaviour of the LIR of the green emission bands of Er3+. One of them is the previously indicated nonradiative relaxation pathway to the red-emitting 4F9/2 level, which is more prominent in nanocrystalline (particularly core-only) β-NaYF4:Er3+,Yb3+ due to the higher-energetic X–H (X = C, N, O) functional groups of surface-attached ligands or, alternatively, the surrounding solvent molecules. The other competitive pathway is cross-relaxation based on an interaction with neighbouring Er3+ and/or Yb3+ ions. Both described pathways effectively increase the total decay rate of the 4S3/2 level and thus, the onset temperature Ton. It was demonstrated, however, that the respective onset temperatures for realistic values of typical activator concentrations in upconversion phosphors still remain below 120 K. Overall, Er3+ combines many of the theoretically suggested optimum conditions for a single-ion luminescent thermometer. Especially the strong intrinsic coupling between the two green-emitting 2H11/2 and 4S3/2 levels makes this ion particularly robust towards many disturbing excited state decay pathways and ensures that β-NaYF4:Er3+,Yb3+ is one of the widest-range Boltzmann luminescent thermometers among all lanthanoid-activated inorganic compounds.
Data availability
Source data generated in this study, which are presented in the main text, are provided as a Source Data files via the Zenodo repository under accession code https://doi.org/10.5281/zenodo.14738155. Source data is also available from the corresponding author upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support by a materials cost allowance of the Fonds der Chemischen Industrie e.V. and the “Young College” of the North-Rhine Westphalian Academy of Sciences, Humanities, and the Arts is gratefully acknowledged by the author.References
- S. W. Allison and G. T. Gillies, Rev. Sci. Instrum., 1997, 68, 2615–2650 CrossRef.
- S. F. Collins, G. W. Baxter, S. A. Wade, T. Sun, K. T. V. Grattan, Z. Y. Zhang and A. W. Palmer, J. Appl. Phys., 1998, 84, 4649–4654 CrossRef.
- P. R. N. Childs, J. R. Greenwood and C. A. Long, Rev. Sci. Instrum., 2000, 71, 2959–2978 CrossRef.
- S. A. Wade, S. F. Collins and G. W. Baxter, J. Appl. Phys., 2003, 94, 4743–4756 CrossRef.
- V. K. Rai, Appl. Phys. B, 2007, 88, 297–303 CrossRef CAS.
- A. H. Khalid and K. Kontis, Sensors, 2008, 8, 5673–5744 CrossRef CAS.
- C. D. S. Brites, S. Balabhadra and L. D. Carlos, Adv. Opt. Mater., 2019, 7, 1801239 CrossRef.
- M. Suta and A. Meijerink, Adv. Theory Simul., 2020, 3, 2000176 CrossRef CAS.
- R. Marin, D. A. Gálico, R. Gayfullina, J. O. Moilanen, L. D. Carlos, D. Jaque and M. Murugesu, J. Mater. Chem. C, 2022, 10, 13946–13953 RSC.
- G. Brunet, R. Marin, M.-J. Monk, U. Resch-Genger, D. A. Gálico, F. A. Sigoli, E. A. Suturina, E. Hemmer and M. Murugesu, Chem. Sci., 2019, 10, 6799–6808 RSC.
- S. Zanella, M. Aragon-Alberti, C. D. S. Brites, F. Salles, L. D. Carlos and J. Long, Angew. Chem., 2023, 135, e202306970 CrossRef.
- M. D. Dramićanin, J. Appl. Phys., 2020, 128, 040902 CrossRef.
- M. Suta, Opt. Mater.: X, 2022, 16, 100195 Search PubMed.
- B. Bendel and M. Suta, J. Mater. Chem. C, 2022, 10, 13805–13814 RSC.
- C. D. S. Brites, K. Fiaczyk, J. F. C. B. Ramalho, M. Sójka, L. D. Carlos and E. Zych, Adv. Opt. Mater., 2018, 6, 1701318 Search PubMed.
- M. Sójka, J. F. C. B. Ramalho, C. D. S. Brites, K. Fiaczyk, L. D. Carlos and E. Zych, Adv. Opt. Mater., 2019, 7, 1901102 CrossRef.
- M. Sójka, C. D. S. Brites and E. Zych, J. Mater. Chem. C, 2020, 8, 10086–10097 RSC.
- P. Bolek, J. Zeler, C. D. S. Brites, J. Trojan-Piegza, L. D. Carlos and E. Zych, Chem. Eng. J., 2021, 421, 129764 CrossRef.
- M. Sójka, W. Piotrowski, L. Marciniak and E. Zych, J. Alloys Compd., 2024, 970, 172662 Search PubMed.
- T. Zheng, M. Sójka, M. Runowski, P. Woźny, S. Lis and E. Zych, Adv. Opt. Mater., 2021, 9, 2101507 CrossRef.
- M. Sójka, M. Runowski, T. Zheng, A. Shyichuk, D. Kulesza, E. Zych and S. Lis, J. Mater. Chem. C, 2022, 10, 1220–1227 RSC.
- Z. Cao, X. Wei, L. Zhao, Y. Chen and M. Yin, ACS Appl. Mater. Interfaces, 2016, 8, 34546–34551 CrossRef PubMed.
- L. Cui, Z. Dong, D. Yu, Y. Wang and A. Meijerink, Sci. Adv., 2024, 10, eado7737 CrossRef PubMed.
- J. C. Fister, D. Rank and J. M. Harris, Anal. Chem., 1995, 67, 4269–4275 CrossRef.
- C. Baleizão, S. Nagl, S. M. Borisov, M. Schäferling, O. S. Wolfbeis and M. N. Berberan-Santos, Chem. – Eur. J., 2007, 13, 3643–3651 CrossRef PubMed.
- A. Steinegger, I. Klimant and S. M. Borisov, Adv. Opt. Mater., 2017, 5, 1700372 CrossRef.
- A. Steinegger and S. M. Borisov, ACS Omega, 2020, 5, 7729–7737 CrossRef CAS PubMed.
- N. Menyuk, K. Dwight and J. W. Pierce, Appl. Phys. Lett., 1972, 21, 159–161 CrossRef CAS.
- K. W. Krämer, D. Biner, G. Frei, H. U. Güdel, M. P. Hehlen and S. R. Lüthi, Chem. Mater., 2004, 16, 1244–1251 CrossRef.
- L. Wang and Y. Li, Chem. Mater., 2007, 19, 727–734 CrossRef CAS.
- F. Wang, Y. Han, C. S. Lim, Y. Lu, J. Wang, J. Xu, H. Chen, C. Zhang, M. Hong and X. Liu, Nature, 2010, 463, 1061–1065 CrossRef CAS.
- H. Berthou and C. K. Jörgensen, Opt. Lett., 1990, 15, 1100–1102 CrossRef CAS PubMed.
- M. A. R. C. Alencar, G. S. Maciel, C. B. de Araújo and A. Patra, Appl. Phys. Lett., 2004, 84, 4753–4755 CrossRef CAS.
- F. Vetrone, R. Naccache, A. Zamarrón, A. J. de la Fuente, F. Sanz-Rodríguez, L. M. Maestro, E. M. Rodríguez, D. Jaque, J. G. Solé and J. A. Capobianco, ACS Nano, 2010, 4, 3254–3258 CrossRef CAS.
- R. G. Geitenbeek, P. T. Prins, W. Albrecht, A. van Blaaderen, B. M. Weckhuysen and A. Meijerink, J. Phys. Chem. C, 2017, 121, 3503–3510 CrossRef CAS.
- R. G. Geitenbeek, A. E. Nieuwelink, T. S. Jacobs, B. B. V. Salzmann, J. Goetze, A. Meijerink and B. M. Weckhuysen, ACS Catal., 2018, 8, 2397–2401 CrossRef PubMed.
- T. Hartman, R. G. Geitenbeek, G. T. Whiting and B. M. Weckhuysen, Nat. Catal., 2019, 2, 986–996 CrossRef.
- R. G. Geitenbeek, J. C. Vollenbroek, H. M. H. Weijgertze, C. B. M. Tregouet, A. E. Nieuwelink, C. L. Kennedy, B. M. Weckhuysen, D. Lohse, A. van Blaaderen, A. van den Berg, M. Odijk and A. Meijerink, Lab Chip, 2019, 19, 1236–1246 RSC.
- I. K. van Ravenhorst, R. G. Geitenbeek, M. J. van der Eerden, J. Tijn van Omme, H. H. Peréz Garza, F. Meirer, A. Meijerink and B. M. Weckhuysen, ChemCatChem, 2019, 11, 5505–5512 CrossRef.
- C. D. S. Brites, X. Xie, M. L. Debasu, X. Qin, R. Chen, W. Huang, J. Rocha, X. Liu and L. D. Carlos, Nat. Nanotechnol., 2016, 11, 851–856 CrossRef PubMed.
- F. E. Maturi, R. S. R. Filho, C. D. S. Brites, J. Fan, R. He, B. Zhuang, X. Liu and L. D. Carlos, J. Phys. Chem. Lett., 2024, 15, 2606–2615 CrossRef.
- T. P. van Swieten, T. Van Omme, D. J. Van Den Heuvel, S. J. W. Vonk, R. G. Spruit, F. Meirer, H. H. Pérez Garza, B. M. Weckhuysen, A. Meijerink, F. T. Rabouw and R. G. Geitenbeek, ACS Appl. Nano Mater., 2021, 4, 4208–4215 CrossRef.
- Z. Ye, D. K. Bommidi and A. D. Pickel, Adv. Opt. Mater., 2023, 11, 2300824 CrossRef.
- B. Harrington, Z. Ye, L. Signor and A. D. Pickel, ACS Nanosci. Au, 2023, 4, 30–61 CrossRef.
- A. R. N. Bastos, C. D. S. Brites, P. A. Rojas-Gutierrez, C. DeWolf, R. A. S. Ferreira, J. A. Capobianco and L. D. Carlos, Adv. Funct. Mater., 2019, 29, 1905474 CrossRef.
- A. R. N. Bastos, C. D. S. Brites, P. A. Rojas-Gutierrez, R. A. S. Ferreira, R. L. Longo, C. DeWolf, J. A. Capobianco and L. D. Carlos, Nanoscale, 2020, 12, 24169–24176 RSC.
- X. Di, D. Wang, J. Zhou, L. Zhang, M. H. Stenzel, Q. P. Su and D. Jin, Nano Lett., 2021, 21, 1651–1658 CrossRef PubMed.
- K. Wiwatowski, K. Sulowska, R. Houssaini, A. Pilch-Wróbel, A. Bednarkiewicz, A. Hartschuh, S. Maćkowski and D. Piątkowski, Nanoscale, 2023, 15, 10614 RSC.
- A. D. Pickel, A. Teitelboim, E. M. Chan, N. J. Borys, P. J. Schuck and C. Dames, Nat. Commun., 2018, 9, 4907 CrossRef.
- A. D. Pickel and C. Dames, J. Appl. Phys., 2020, 128, 045103 CrossRef.
- T. P. van Swieten, A. Meijerink and F. T. Rabouw, ACS Photonics, 2022, 9, 1366–1374 CrossRef.
- S. J. W. Vonk, T. P. van Swieten, A. Cocina and F. T. Rabouw, Nano Lett., 2023, 23, 6560–6566 CrossRef.
- W. T. Carnall, H. Crosswhite and H. M. Crosswhite, Technical Report: Energy level structure and transition probabilities in the spectra of the trivalent lanthanides in LaF3, Argonne National Lab, 1978 (report no.: ANL-78-XX-95). DOI:10.2172/6417825.
- A. M. Kaczmarek, M. Suta, H. Rijckaert, A. Abalymov, I. Van Driessche, A. G. Skirtach, A. Meijerink and P. Van der Voort, Adv. Funct. Mater., 2020, 30, 2003101 CrossRef.
- D. T. Klier and M. U. Kumke, RSC Adv., 2015, 5, 67149–67156 RSC.
- G. Chen, H. Qiu, P. N. Prasad and X. Chen, Chem. Rev., 2014, 114, 5161–5214 CrossRef.
- G. Yao, C. Link, Q. Meng, P. S. May and M. T. Berry, J. Lumin., 2015, 160, 276–281 CrossRef.
- P. Villanueva-Delgado, D. Biner and K. W. Krämer, J. Lumin., 2017, 189, 84–90 CrossRef.
- P. Rühl, D. Wang, F. Garwe, R. Müller, M. Haase, K. W. Krämer, W. Paa, R. Heintzmann, S. H. Heinemann and H. Stafast, J. Lumin., 2021, 232, 117860 CrossRef.
- T. P. van Swieten, T. van Omme, D. J. van den Heuvel, S. J. W. Vonk, R. G. Spruit, F. Meirer, H. H. P. Garza, B. M. Weckhuysen, A. Meijerink, F. T. Rabouw and R. G. Geitenbeek, ACS Appl. Nano Mater., 2021, 4, 4208–4215 CrossRef PubMed.
- R. G. Geitenbeek, H. W. de Wijn and A. Meijerink, Phys. Rev. Appl., 2018, 10, 064006 Search PubMed.
- F. T. Rabouw, P. T. Prins, P. Villanueva-Delgado, M. Castelijns, R. G. Geitenbeek and A. Meijerink, ACS Nano, 2018, 12, 4812–4823 CrossRef PubMed.
- L. A. Riseberg and H. W. Moos, Phys. Rev., 1968, 174, 429–438 CrossRef.
- M. M. Lage, R. L. Moreira, F. M. Matinaga and J.-Y. Gesland, Chem. Mater., 2005, 17, 4523–4529 CrossRef.
- B. R. Judd, Phys. Rev., 1962, 127, 750–761 CrossRef.
- G. S. Ofelt, J. Chem. Phys., 1962, 37, 511–520 CrossRef.
- T. P. van Swieten, J. M. Steenhoff, A. Vlasblom, R. de Berg, S. P. Mattern, F. T. Rabouw, M. Suta and A. Meijerink, Light: Sci. Appl., 2022, 11, 343 CrossRef PubMed.
- M. J. Weber, Phys. Rev., 1967, 157, 262–272 CrossRef.
- J. A. Capobianco, P. Kabro, F. S. Ermeneux, R. Moncorgé, M. Bettinelli and E. Cavalli, Chem. Phys., 1997, 214, 329–340 CrossRef CAS.
- C. Z. Bi, J. Y. Ma, J. Yan, X. Fang, D. Z. Yao, B. R. Zhao and X. G. Qiu, Eur. Phys. J. B, 2006, 51, 167–171 CrossRef CAS.
- A. Sanson, M. Giarola, B. Rossi, G. Mariotto, E. Cazzanelli and A. Speghini, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 21430 CrossRef.
- O. Greis and J. M. Haschke, Chapter 45: Rare earth fluorides, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner Jr. and L. Eyring, 1982, vol. 5, pp. 387–460 Search PubMed.
- M. J. J. Mangnus, V. R. M. Benning, B. Baumgartner, P. T. Prins, T. P. van Swieten, A. J. H. Dekker, A. van Blaaderen, B. M. Weckhuysen, A. Meijerink and F. T. Rabouw, Nanoscale, 2023, 15, 16601–16611 RSC.
- F. T. Rabouw, S. A. den Hartog, T. Senden and A. Meijerink, Nat. Commun., 2014, 5, 3610 CrossRef PubMed.
- M. Suta, Ž. Antić, V. Ðorđević, S. Kuzman, M. D. Dramićanin and A. Meijerink, Nanomaterials, 2020, 10, 543 CrossRef CAS PubMed.
- A. Skripka, A. Benayas, C. D. S. Brites, I. R. Martín, L. D. Carlos and F. Vetrone, Nano Lett., 2020, 20, 7648–7654 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |

