 Open Access Article
Open Access ArticleTunable assembly of confined Janus microswimmers in sub-kHz AC electric fields under gravity†
Carolina van Baalena,
Laura Alvarez b,
Robert W. Style
b,
Robert W. Style a and
Lucio Isa
a and
Lucio Isa *a
*a
aLaboratory for Soft Materials and Interfaces, Department of Materials, ETH Zürich, Vladimir-Prelog-Weg 5, 8093 Zürich, Switzerland. E-mail: lucio.isa@mat.ethz.ch
bUniv. Bordeaux, CNRS, CRPP, UMR 5031, F-33600 Pessac, France. E-mail: laura.alvarez-frances@u-bordeaux.fr
First published on 1st April 2025
Abstract
Active systems comprising micron-sized self-propelling units, also termed microswimmers, are promising candidates for the bottom-up assembly of small structures and reconfigurable materials. Here we leverage field-driven colloidal assembly to induce structural transformations in dense layers of microswimmers driven by an alternating current (AC) electric field and confined in a microfabricated trap under the influence of gravity. By varying the electric field frequency, we realize significant structural transformations, from a gas-like state at high frequencies to dynamically rearranging dense crystalline clusters at lower frequencies, characterized by vorticity in their dynamics. We demonstrate the ability to switch between these states on-demand, showing that the clustering mechanism differs from motility-induced phase separation. Our results offer a valuable framework for designing high-density active matter systems with controllable structural properties, envisioned to advance the development of artificial materials with self-healing and reconfiguration capabilities.
1 Introduction
Unlike steady-state equilibrium or driven matter, active systems comprise autonomous units that constantly self-propel by locally converting energy from the imbalance of a specific thermodynamic quantity, such as temperature, chemical or ionic concentration, yielding a range of distinctive features. The collective translation of such self-propelling units can lead to the formation of coherent patterns and self-organization—an essential characteristic for the proper functioning of many biological systems across various length scales, ranging from the antipredatory function of large bird flocks,1 down to the enhanced colonization abilities of swarming motile bacteria,2 and the dynamic actin-myosin cytoskeleton critical to numerous aspects of cell physiology.3 Particularly interesting from a physics as well as material science perspective is the study of microscopic active matter, which has uncovered a variety of new behaviors unattainable in equilibrium systems.Microscopic active systems can display non-trivial density profiles and critical fluctuations, even at densities much lower than the bulk jamming density found in passive systems. In such systems, the self-propelling units, often referred to as microswimmers or active particles, may undergo dynamic clustering akin to a liquid–gas phase separation4–10 or crystallization11–17 at relatively low particle densities and in the absence of any temperature changes or attractive inter-particle interactions, making microswimmers promising candidates for the bottom-up assembly of small structures and reconfigurable materials that can change their properties on demand.
Numerical studies have shown that microswimmer self-assembly can arise through self-trapping driven by the interplay of out-of-equilibrium collisions and finite reorientation times. This mechanism is fundamentally governed by microswimmer density, self-propulsion velocity, and rotational diffusion.7,8,18 Although attractive inter-particle interactions are not required, they can facilitate the onset of collective motion and expand the range of dynamic structures achievable.7,19,20 Indeed, different experiments have demonstrated the existence of various collective states of synthetic microswimmers, including polar liquid states,21,22 turbulence,23 swarms,24 and living crystals.15,17 Nonetheless, experimentally achieving a wide range of on demand controlled structures remains a challenging task, in particular, due to the need for a single experimental system with controlled microswimmer densities, as well as in situ control over the microswimmers' self-propulsion speed and interaction potential.
In this manuscript, we utilize gravity and electric field-driven colloidal assembly to achieve controlled structural organization and self-propulsion dynamics in dense layers of colloidal microswimmers. By varying the frequency of the applied electric field, we induce structural transitions spanning gas-like states to self-assembled motile crystallites, accompanied by emergent vorticity at lower field frequencies. Furthermore, we demonstrate the ability to switch between these states on demand by modulating the field frequency. This approach enables the creation of a high-density active matter system with strong, tunable interactions, distinct from prior studies emphasizing assembly driven primarily by motion persistence.15,17
2 Results
2.1 Confined active colloidal monolayers under gravity
We examine the behavior of metallo-dielectric Janus spheres confined in an inclined microfabricated chamber under an applied electric field, focusing on how frequency modulation affects their structural organization and dynamics. Our samples comprise a suspension of Pd-capped SiO2 Janus spheres (diameter 2R = 3 μm) residing between two parallel electrodes held at a distance of 2h = 30 μm using a spacer (Fig. 1a). The bottom electrode integrates a microfabricated rectangular 1.0 × 0.6 mm2 (L × W) chamber with a funneling inlet at the top (details on the sample preparation can be found in Section 5). Once assembled, we place the experimental cell at an angle of α = 45°, yielding a gravitational force perpendicular (F⊥) and parallel (F‖) to the laboratory frame (Fig. 1b). Under the action of gravity, the particles slide on the bottom electrode and down into the opening of the microfabricated chamber (Fig. 1c). After approximately 3 hours, denoted as t = 0, a dense sediment has formed at the bottom of the chamber (Fig. 1c). Over the course of the entire experiment, we keep the experimental cell at α = 45°, which not only allows us to collect the microswimmers before turning the activity on, but also enables studying high-density active monolayers under slight compression. We connect the top and bottom electrodes to an electric field generator, producing an AC field with a chosen amplitude and frequency in the direction perpendicular to the electrodes. The rapidly alternating field causes a partial buildup of the ionic double layer near the electrodes and simultaneously polarizes the metallo-dielectric Janus spheres, yielding a gradient in the electric field where the particle meets the electrode. The latter causes the formation of hydrodynamic flows,25–27 which are of different magnitude and direction on the Pd side of the Janus particle, i.e. due to better polarizability of Pd compared to SiO2, resulting in the propulsion of the Janus spheres with their SiO2 face in front.28 As we will describe later, the frequency of the applied AC field also affects interparticle interactions mediated by EHD flows.We allow the active system to evolve for 9 min under a fixed applied peak-to-peak voltage of Vpp = 4 V (corresponding to a field strength of 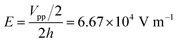 ) and varying frequency from f = 800 Hz to f = 200 Hz (Videos S1–S4, ESI†). It is worth noting that the chamber boundaries exhibit strong repulsion upon activation of the AC field, driven by outward hydrodynamic flows. These flows arise from electric field gradients at the interface of the electrode and the chamber material printed on it, resulting from their differing electrical properties.29 Therefore particles do not enter a region of approximately 30 μm from the walls of the chamber, hence they cannot escape through the top hole over the course of the experiment, and the chamber thus effectively acts as a trap. As shown qualitatively in Fig. 1e–h, applying different electric field frequencies results in markedly distinct structural features of the active colloidal monolayers. At a frequency of f = 800 Hz, the microswimmers explore the entire space of the trap, with an average probability density P(ρ) as a function of height z that decays gradually from the bottom of the trap to the top (Fig. 1i). At f = 500 Hz, the structure of the microswimmers' monolayer appears similar, but with a higher particle density at the bottom of the trap. Decreasing the frequency further to f = 300 Hz results in increasing particle densities at the bottom, and finally at f = 200 Hz only a dense sediment is left at the bottom of the trap, while no free swimming particles remain in the top part, as quantitatively apparent from the sharp drop in P(ρ) versus z. To understand if the changing structure of the monolayers can be a result of changes in the self-propulsion velocities of the microswimmers, we measure their free swimming velocities in the absence of gravity, i.e. above a horizontal substrate (i.e. α = 0°), as shown in Fig. 1j. Upon decreasing the frequency of the electric field from f = 800 Hz to f = 500 Hz, the mean self-propulsion velocities of the microswimmers remain approximately constant at around v ≈ 20 μm s−1. However, further reducing the frequency from f = 500 Hz to f = 200 Hz, causes a marked decline in the mean self-propulsion velocity to v ≈ 7 μm s−1. The sedimentation force acting on a single microswimmer, as approximated from the buoyant weight of a 3 μm SiO2 sphere, is Fg ≈ 0.22 pN in our experiment. In contrast, the observed self-propulsion velocities at frequencies f = 800, 500 and 300 Hz correspond to active forces, obtained from Stokes' drag, of Fs ≈ 0.51, 0.49, and 0.37 pN, respectively. Thus, at these frequencies, the average self-propulsion force is sufficient to enable microswimmers to overcome gravitational forces and swim upwards. A minor effect of gravity becomes discernible at these frequencies, as evidenced in the polar plot in Fig. 1k. Here, we show the mean instantaneous velocities measured in the top part of the trap (i.e., at α = 45°) as a function of the swimming direction for f = 800, 500 and 300 Hz, revealing self-propulsion velocities approximately ∼3 μm s−1 higher in the downward direction compared to the upward direction. Conversely, at f = 200 Hz, the average self-propulsion force of the microswimmers falls below the threshold needed to swim upwards (Fs ≈ 0.18 pN), which explains the absence of microswimmers in the top part of the trap at this frequency. The pronounced changes in the suspension microstructure with decreasing field frequency, however, cannot be solely attributed to variations in microswimmer persistence, as we will discuss in Sections 2.2–3.
) and varying frequency from f = 800 Hz to f = 200 Hz (Videos S1–S4, ESI†). It is worth noting that the chamber boundaries exhibit strong repulsion upon activation of the AC field, driven by outward hydrodynamic flows. These flows arise from electric field gradients at the interface of the electrode and the chamber material printed on it, resulting from their differing electrical properties.29 Therefore particles do not enter a region of approximately 30 μm from the walls of the chamber, hence they cannot escape through the top hole over the course of the experiment, and the chamber thus effectively acts as a trap. As shown qualitatively in Fig. 1e–h, applying different electric field frequencies results in markedly distinct structural features of the active colloidal monolayers. At a frequency of f = 800 Hz, the microswimmers explore the entire space of the trap, with an average probability density P(ρ) as a function of height z that decays gradually from the bottom of the trap to the top (Fig. 1i). At f = 500 Hz, the structure of the microswimmers' monolayer appears similar, but with a higher particle density at the bottom of the trap. Decreasing the frequency further to f = 300 Hz results in increasing particle densities at the bottom, and finally at f = 200 Hz only a dense sediment is left at the bottom of the trap, while no free swimming particles remain in the top part, as quantitatively apparent from the sharp drop in P(ρ) versus z. To understand if the changing structure of the monolayers can be a result of changes in the self-propulsion velocities of the microswimmers, we measure their free swimming velocities in the absence of gravity, i.e. above a horizontal substrate (i.e. α = 0°), as shown in Fig. 1j. Upon decreasing the frequency of the electric field from f = 800 Hz to f = 500 Hz, the mean self-propulsion velocities of the microswimmers remain approximately constant at around v ≈ 20 μm s−1. However, further reducing the frequency from f = 500 Hz to f = 200 Hz, causes a marked decline in the mean self-propulsion velocity to v ≈ 7 μm s−1. The sedimentation force acting on a single microswimmer, as approximated from the buoyant weight of a 3 μm SiO2 sphere, is Fg ≈ 0.22 pN in our experiment. In contrast, the observed self-propulsion velocities at frequencies f = 800, 500 and 300 Hz correspond to active forces, obtained from Stokes' drag, of Fs ≈ 0.51, 0.49, and 0.37 pN, respectively. Thus, at these frequencies, the average self-propulsion force is sufficient to enable microswimmers to overcome gravitational forces and swim upwards. A minor effect of gravity becomes discernible at these frequencies, as evidenced in the polar plot in Fig. 1k. Here, we show the mean instantaneous velocities measured in the top part of the trap (i.e., at α = 45°) as a function of the swimming direction for f = 800, 500 and 300 Hz, revealing self-propulsion velocities approximately ∼3 μm s−1 higher in the downward direction compared to the upward direction. Conversely, at f = 200 Hz, the average self-propulsion force of the microswimmers falls below the threshold needed to swim upwards (Fs ≈ 0.18 pN), which explains the absence of microswimmers in the top part of the trap at this frequency. The pronounced changes in the suspension microstructure with decreasing field frequency, however, cannot be solely attributed to variations in microswimmer persistence, as we will discuss in Sections 2.2–3.
We note that changing the applied field strength provides an additional handle to modify the structural properties of the active monolayers, as shown in Fig. 1l. Increasing the applied peak-to-peak voltage from Vpp = 2 to 5 V at a fixed frequency of f = 200 Hz slightly decreases the overall density of the sediment and yields an increasing number of voids within it. We also observe an increasing mobility of the particles within the structures upon increasing the applied peak-to-peak voltage, which is likely responsible for the less compact structure observed at Vpp = 5 V compared to Vpp = 4 V. Nevertheless, in what remains, we will focus on the effect of modulating the frequency of the electric field, which allows for a greater range of distinct structural features.
2.2 Structural features
Having described the qualitative features of our system, we start by quantitatively investigating its structural properties. At the highest frequency, i.e. f = 800 Hz, the microswimmers are dispersed throughout the entire trap, and the system shows features analogous to the active gas-like state observed for suspension of Pt-capped catalytically active Janus particles under a gravity field.30–32 Notably, after 9 min of equilibration at 800 Hz (Fig. 1i), the average density profile in the center of the particle trap decays exponentially with height, analogous to ref. 30–32 and theoretically discussed by ref. 33–35 (S1, ESI†). Moreover, throughout the entire trap, the structure of the suspension is disordered, as visually apparent from zoomed-in snapshots of the active gas-like monolayer with particles color coded according to their local orientation ψ6 (Fig. 2a). This is further quantitatively displayed in Fig. 2e, which shows a spatial correlation of the local orientation G6(r/2R) that decays over length scales on the order of the particle diameter (orange data). Consequently, the sixfold symmetry in the system is low, characterized by the high probability of low values of the absolute value of the hexagonal order parameter |ψ6| (Fig. 2f). Upon reducing the frequency of the AC electric field to f = 500 Hz, clear differences appear in the structural properties of the system. As shown in Fig. 2b, clusters emerge with orientations that remain correlated over larger length scales (Fig. 2e). Nonetheless, the overall order of the system remains low, as shown by the corresponding probability distribution of the absolute value of the hexagonal order parameter (Fig. 2f). Instead, at even lower frequencies, i.e. f = 300 Hz and f = 200 Hz, the probability distributions of the absolute value of the hexagonal order parameter show a shift towards higher values. Additionally, the color-coded snapshots in Fig. 2c and d show manifestation of crystalline clusters, i.e. crystallites, comprising hexagonally assembled particles with strong orientational order that appear structurally similar to the “living crystals” observed in experiments focusing on the assembly of photocatalytic and thermophoretic microswimmers, which are formed through motion persistence.15,17 Moreover, aside from the few single free-swimming microswimmers at f = 300 Hz, the structures formed at the bottom of the trap at f = 300 Hz and f = 200 Hz are essentially entirely composed of connected crystallites comprising hexagonally packed microswimmers. Consequently, G6 only starts to decay significantly after ∼10 particle diameters, indicating the characteristic size of the crystalline domains at low f. Finally, associated with the emergence of the crystallites, voids correspondingly emerge in the structures at f = 300 Hz and f = 200 Hz, as highlighted in Fig. 2g. Namely, upon decreasing f, the distributions of void sizes shift from mainly containing small voids with sizes <50 μm at f = 800 Hz towards including void sizes >500 μm at f = 300 Hz and f = 200 Hz.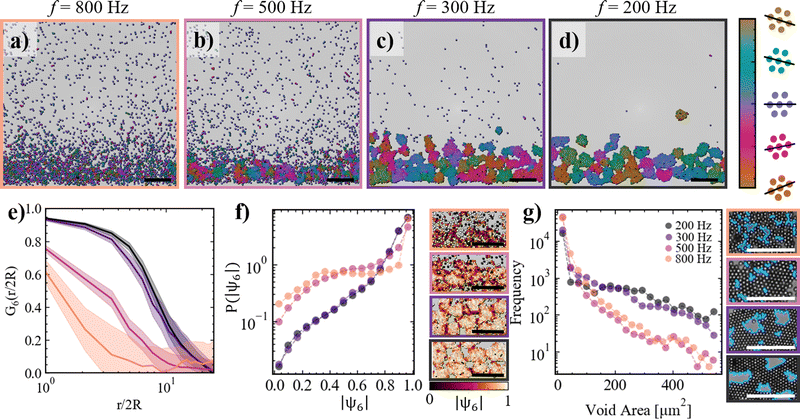 | ||
| Fig. 2 Static structural information of microswimmer monolayers at different frequencies. (a)–(d) Snapshots of the system after 9 min of equilibration at different frequencies at Vpp = 4 V. Particles are color-coded according to their local orientation. The frame color-coding corresponds to Fig. 1e–h. (e) Correlation function of the local orientation versus distance normalized by the particle size for the different f. (f) Distribution of the absolute value of the hexagonal order parameter ψ6 (left) and typical snapshots, with particles color-coded according to the absolute value of ψ6. (g) Distribution of void sizes (left) and typical snapshots of identified voids (right). Scale bars: 50 μm. | ||
2.3 Dynamical features
Having examined the static structural features of our system, we now turn our attention to their dynamic properties, exploring how microswimmer motion and clustering behavior evolve with decreasing electric field frequency. At a frequency of f = 800 Hz, in the gas-like state, the direction of motion of individual microswimmers appears uncorrelated, as visually apparent in Fig. 3a, where particles are color-coded according to their direction of motion.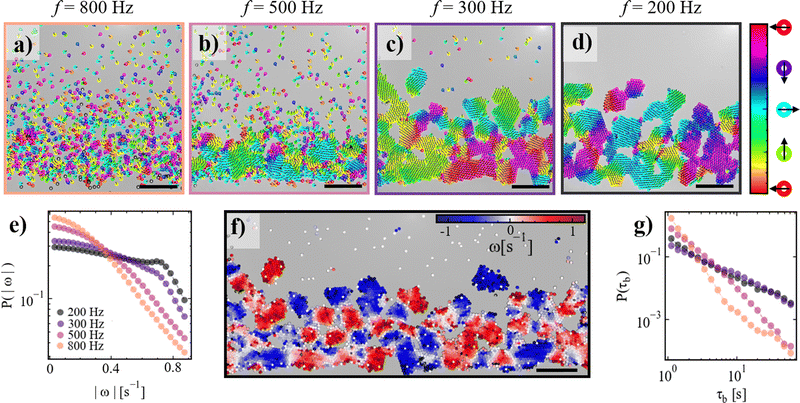 | ||
| Fig. 3 Dynamics of microswimmer monolayers: the presence of vorticity. (a)–(d) Snapshots of the system after 9 min of equilibration at different frequencies at Vpp = 4 V, particles are color-coded according to their direction of motion extracted from the velocity vector. The arrows indicating the direction of motion in (b)–(d) show the presence of vortices. Frame colorcoding corresponds to Fig. 1a–d. (e) Probability distributions of the absolute vorticity at different frequencies (see Section 5.1 for details on the calculation). (f) Snapshot of a larger field of view corresponding to (c), color-coded according to the local vorticity values. (g) Probability distributions of the bond duration of particles at different frequencies. Note that for lower frequencies bond durations exceed the timescale of the experiment, hence the true distribution is not fully displayed. Scale bars: 50 μm. | ||
Decreasing the frequency to f = 500 Hz leads to the emergence of collective motion within the system. Specifically, Fig. 3b illustrates vortex-like dynamics at this frequency, marking a significant shift from the uncorrelated motion observed at f = 800 Hz. Similarly, at lower frequencies (f = 300 Hz, Fig. 3c, and f = 200 Hz, Fig. 3d), the crystallites in the system also exhibit vortex-like behavior, indicating the prevalence of rotational dynamics across these frequencies.
To quantify this behavior, we calculate the vorticity ω [s−1] of the microswimmers at different frequencies and analyze the probability distribution of the absolute vorticity (Fig. 3e). At f = 800 Hz, the probability distribution exhibits a sharp peak at |ω| = 0, which gradually decays to zero at approximately |ω| ≈ 0.9 s−1. Reducing the frequency to f = 500 Hz slightly decreases the peak probability at |ω| = 0 and extends the tail of the distribution. At f = 300 Hz, this extension becomes significantly more pronounced, reflecting an increase in rotational activity. Further lowering the frequency to f = 200 Hz results in the emergence of a secondary peak around |ω| ≈ 0.7 s−1, marking a substantial enhancement of rotational motion within the system.
Remarkably, the state of our system at frequencies f ≤ 300 Hz shares similarities with previous experiments involving active chiral Quincke rollers,36,37 magnetically rotating colloidal rods,38 and spinning starfish embryo crystals.11 However, unlike those systems, the active agents in our study lack intrinsic chirality or spinning behavior. The spontaneous vortical dynamics of hexagonally packed aggregates comprising randomly oriented Janus particles has been numerically predicted using a pusher-type squirmer model,39 where vorticity arises from microswimmer orientation and the geometry of the hexagonally packed aggregates. Fig. 3f shows a representative spatial map of vorticity for the low-frequency case, highlighting regions of correlated vorticity associated with crystallites rotating almost rigidly. Neighboring crystallites tend to rotate in opposite directions, as evidenced by the alternating blue and red regions in the figure. This cogwheel-like behavior likely results from hydrodynamic interactions, where a rotating crystallite's flow field drags its neighbor into phase-locked counter-rotation, as also reported in ref. 39.
To further assess the rigidity of these structures, we analyze the distribution of bond durations, defined as the duration of geometrical contact between neighboring particles, across different frequencies (Fig. 3g). At higher frequencies (f = 800 Hz and f = 500 Hz), bonds are predominantly short-lived, with the distribution falling to zero within the 1-minute measurement time frame. As the frequency decreases, the average bond duration increases markedly. At f = 300 Hz and f = 200 Hz, a significant fraction of bonds persist beyond the measurement time frame, highlighting the emergence of stable, coordinated assemblies that remain intact over extended periods.
2.4 On-demand crystallisation
A key feature of the system is its ability to undergo on-demand reconfiguration by adjusting the frequency of the AC electric field. In Fig. 4, we demonstrate the “condensation” of an active colloidal monolayer by rapidly lowering the frequency from f = 800 Hz to f = 200 Hz. Fig. 4a shows the immediate evolution of the monolayer after this frequency drop. Following the frequency reduction, small clusters form almost instantaneously and grow over time, as reflected by the cluster size distributions P(Sc) shifting to larger values (Fig. 4b). Clusters initially formed in the upper region of the trap sediment downward, as shown by their trajectories in Fig. 4c. The sedimentation speed increases with the growing size of the clusters (Fig. 4d), and they continue to fall until they merge with the fully connected structure at the bottom of the trap. After approximately 1.5 minutes, the resulting monolayer exhibits similar structural and dynamical features as those seen in systems equilibrated for 9 minutes at f = 200 Hz.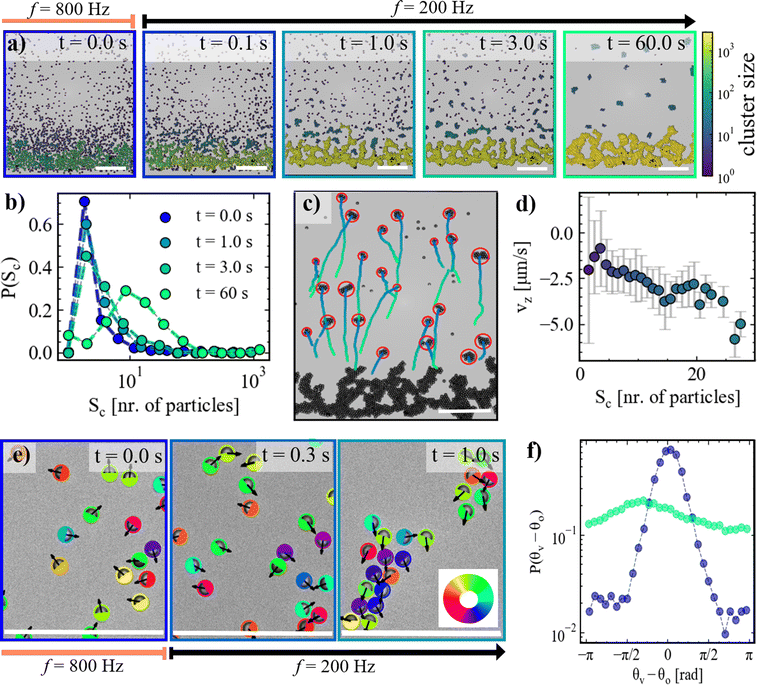 | ||
| Fig. 4 Condensation of microswimmers under gravity by switching the frequency of the AC electric field. (a) Snapshots of the system at different times after switching the frequency from 800 Hz to 200 Hz. Particles are color-coded according to the size of the cluster they belong to. (b) Cluster size distributions at 0, 1, 3, and 60 seconds after switching the AC field frequency from 800 Hz to 200 Hz. (c) Trajectories of clusters formed upon switching the frequency of the electric field (increasing time from blue to green). (d) Sedimentation speed of clusters as a function of their size. Error bars represent the standard deviation over at least 20 measurements. (e) High magnification snapshots of the system at different times after switching the frequency from 800 Hz to 200 Hz. Particles are color-coded according to their orientation, with the cap artificially colored. Black arrows indicate the direction of the velocity vector for each particle. See Fig. S2 (ESI†) for the corresponding raw images. (f) Probability distributions of the difference between the cap orientation and the orientation of the velocity vector 5 seconds before (blue) and 5 seconds after (mint green) switching the AC electric field. Scale bars: 50 μm. | ||
To gain a deeper understanding of the particle-level mechanisms driving cluster formation, we analyze the orientation of the microswimmer caps (Video S5, ESI†). In Fig. 4e, high-magnification images show the metallic caps of the Janus microswimmers color-coded by their orientations (θ0), with the direction of motion indicated by black arrows extracted from the velocity vector (θv). At f = 800 Hz (first panel, t = 0.0 s), interparticle interactions are minimal, and the difference between θ0 and θv is small, as seen in the black arrows that are mostly perpendicular to the caps. This is corroborated by the narrow normal distribution of θv–θ0 centered around zero (dark blue data in Fig. 4f). After switching the frequency to f = 200 Hz, we observe that the orientation of the caps and the black arrows begin to deviate from perpendicularity and particles are drawn together, regardless of their cap orientation (second panel in Fig. 4e). Consequently, the particles form clusters in which they assume random orientations, as shown in the last panel of Fig. 4e. The difference between θ0 and θv after switching to f = 200 Hz is shown by the green data in Fig. 4f. The distribution broadens to larger values, and the peak has shifted to around π/2 due to the downward sedimentation of the clustered Janus particles. Thus, the formation of motile clusters in this system appears unrelated to motion persistence or to the occurrence of collisions between the microswimmers, and instead appears to stem from attractive colloidal inter-particle interactions resulting from EHD flows around the Janus microswimmers, as discussed in more detail in Section 3.
We probe the frequency-driven changes in the nature of the fluid flows around the Janus microswimmers by adding small (2R = 200 nm) polystyrene (PS) tracer particles to the experimental system (Fig. 5). At f = 800 Hz, the Janus microswimmer moves at a relatively high self-propulsion speed, while drawing tracer particles (yellow) toward the silica hemisphere and releasing them from the metallic hemisphere. Notably, a fraction of the tracer particles accumulates near the metallic hemisphere (Fig. 5b), likely due to positive dielectrophoresis (pDEP) arising from the strong electric field gradient generated by the potential difference between the metallic hemisphere and the electrode surface.40 When the frequency is reduced to f = 200 Hz, the microswimmer slows down, and the tracer particles are attracted towards the Janus microswimmer, where they distribute around its entire circumference (Fig. 5c). This isotropic distribution indicates that contractile fluid flows towards the Janus microswimmer become more pronounced and evenly distributed as the frequency decreases.40
3 Discussion
Our investigation reveals the complex dynamics and structural transformations of metallo-dielectric Janus microswimmers under confinement within a rectangular trap and subjected to a perpendicularly oriented AC electric field. By systematically adjusting the AC field frequency, we demonstrate that the self-propulsion of these microswimmers, as well as their assembly into varying structural forms, can be finely controlled. Specifically, we observe a frequency-dependent progression from a gas-like state of independent microswimmers to densely packed, motile crystallites exhibiting collective motion with pronounced vorticity as the frequency decreases from f = 800 Hz to f = 200 Hz.In prior studies, the assembly behavior of metallo-dielectric Janus microswimmers under perpendicular AC electric fields has been investigated primarily in the MHz frequency regime. These studies report the formation of self-assembled chains,24 swarms,24 and long-ranged repulsive states.24,41 Additionally, the formation of 2D networks under parallel high-frequency AC electric fields has also been observed (e.g., ref. 42 and 43). In such high-frequency AC electric fields, inter-particle interactions are predominantly governed by dipolar interactions, which arise from the differing polarization coefficients of the dielectric and metallic hemispheres of the Janus particles.
In contrast to these earlier studies, our experiments focus on the sub-kHz frequency range, where the applied frequency is several orders of magnitude lower than those typically associated with electric field-induced dipolar interactions.24,44 In this regime, particle assembly under a perpendicular AC electric field is governed by a complex interplay of frequency-dependent hydrodynamic effects.26,27,45–47 Specifically, induced-charge electroosmotic (ICEO) flows dominate in the kHz range. ICEO arises from the interaction between the applied electric field and the electric double layer (EDL) induced on the surface of the polarizable Janus particle. The characteristic timescale for this process is described by the particle charge relaxation time, τp = k−1R/D, where k−1 is the Debye length, R is the particle radius, and D is the ionic diffusion coefficient. For our experimental conditions, τp corresponds to a frequency of approximately 4.4 kHz (detailed calculations can be found in S4, ESI†). At frequencies below this threshold, the EDL on the particle has sufficient time to fully develop, enabling the nonlinear fluid flows associated with ICEO.
As the frequency decreases further into the sub-kHz range, electrohydrodynamic (EHD) flows begin to dominate near conducting surfaces, such as the bottom electrode in our experiments. The emergence of EHD flows is governed by the electrode charge relaxation time, τe = k−12h/D, where now instead of the particle radius R, the distance between the two electrodes 2h becomes the relevant length scale. For our setup, τe corresponds to a frequency of approximately 200 Hz (detailed calculations can be found in S4, ESI†). At frequencies approaching this value, the EDL at the electrode has sufficient time to fully form, creating a strong interaction with the distorted electric field near the particle. This interaction generates localized field gradients that drive fluid motion characteristic of EHD flows.
The transition from ICEO to EHD flows is evident in our experiments, where we observe a sharp decline in microswimmer self-propulsion velocity at frequencies below 500 Hz. Tracer experiments (Fig. 5a) further support this transition, showing an accumulation of tracer particles around the entire circumference of the Janus microswimmer. This behavior is driven by strong inward convective flows, which are a hallmark of EHD near conducting surfaces.40
Interestingly, we observe crystallization for bare silica spheres (i.e., without the Pd coating) across all explored frequencies (see Fig. S3, ESI†). This contrasts with the behavior of the Janus particles, highlighting the competitive roles of ICEO and EHD flows in assembly dynamics. The metallic cap of the Janus microswimmer plays a crucial role in ICEO, as the disparity in polarizability between the metallic and dielectric hemispheres enhances ICEO flows around the more polarizable metallic hemisphere. This intensified ICEO flows disrupt crystallization at higher frequencies, delaying its onset to lower frequencies. In the absence of the metallic cap, ICEO is diminished, allowing crystallization to occur even at higher frequencies. These observations are consistent with our experimental findings and underscore the intricate coupling between hydrodynamic flows and particle surface properties.
4 Conclusion
In conclusion, our study demonstrates the tunable dynamics of dense monolayers of AC field-driven Janus microswimmers in the sub-kHz regime. We present a versatile experimental platform in which particle density is controlled, while microswimmer self-propulsion speed and inter-particle interactions can be tuned by varying the AC electric field frequency. At high frequencies, particles remain in a gas-like state, whereas decreasing the frequency drives their assembly into motile crystallites with emergent vorticity and collective motion. At low frequencies, the isotropic orientation of particles within these self-assembled crystallites indicates that long-range EHD flows dominate over alignment interactions, highlighting the potential of frequency-dependent EHD flows as a powerful tool for controlling clustering and internal structure in colloidal active matter systems.By enabling dynamic control over both self-propulsion and assembly, our findings open up exciting possibilities for designing reconfigurable, high-density active systems with potential applications in smart materials, self-healing systems, and soft robotics. Additionally, our study lays the groundwork for further investigations into systems comprising mixtures of particles with varying self-propulsion speeds and inter-particle interactions. Finally, exploring the factors that govern the characteristic size of clusters at low frequencies will be a promising avenue for future research and the competition between the different components of electrohydrodynamic flows calls for further theoretical and numerical studies, as the low-frequency behavior of Janus active particles remains largely unexplored.
5 Materials and methods
5.1 Janus particles
Metallo-dielectric Janus microswimmers are fabricated by drop-casting an aqueous suspension of SiO2 spheres (R = 2.96 μm, SiO2-R-LSC84, microparticles GmbH) on a plasma-cleaned microscopy slide, followed by depositing a thin (2 nm) Cr adhesion layer and a 6.5 nm Pd layer. The resulting metallo-dielectric Janus particles were dispersed in 1 mL MilliQ water by ultrasonicating for 20 min, washed three times with a 1% surfactant (Pluronic-127, Sigma Aldrich) solution by centrifugation and supernatant replacement, and finally concentrated by sedimentation and supernatant removal to yield a suspension of ∼2 mg particles per mL. Note that we do not remove the surfactant in order to prevent sticking to the electrodes of the experimental cell over the course of the experiment. Hence, experiments are carried out in the presence of 1% Pluronic-127.5.2 Preparation of the experimental cell
Prior to each experiment, a particle traps was microfabricated on top of an indium tin oxide (ITO) coated glass substrate (resistivity ≈ 400 Ω) using two-photon polymerization of a photosensitive resin (Nanoscribe Photonic Professional GT, IP-S), followed by 20 minutes developing in propylene glycol methyl ether acetate (PGMEA, Sigma Aldrich), rinsing with isopropyl alcohol (IPA, Sigma Aldrich), and finally one min exposure to UV light (365 nm @ 3 W cm−2, Nitecore GEM10UV) to ensure full curing of the structure. To assemble the experimental cell, a round, h = 30 μm thick double sided adhesive spacer (no. 5603, Nitto) was placed around the microfabricated structure. The resulting well was filled with 1.5 μL of the Janus particle suspension, and finally, the cell was closed by sticking another ITO coated substrate on top of the assembly (ITO coated side down). The ITO-coated substrates, i.e. the electrodes, were then connected to a function generator (National Instruments Agilent 3352X, USA) that generates an AC electric field with a frequency ranging from f = 200–800 Hz, and an applied peak-to-peak voltage of Vpp = 4 V, corresponding to a field of E = Vpp/h ≈ 133 V mm−1, unless stated otherwise. The entire sample cell was placed at an angle of α = 45° degrees with respect to the optical table, and imaged in bright-field transmission mode using a custom-build optical setup comprising an infinity-corrected low magnification (M PLAN APO 20×, Optem) or high magnification (Plan Apo Infinity Corrected 50×, Mitutoyo) long-working-distance objective connected to a CMOS camera (Orca Flash4.0 V3, Hamamatsu). Images of 2048 × 2048 pixels were taken at a frame rate of 30 frames per second.5.3 Data analysis
From the experimental videos, particles were tracked using a centroid finding algorithm48 implemented in Python (Trackpy v0.4.249).5.4 Hexagonal order parameter
From the obtained particle coordinates, we determine the hexagonal order parameter, ψ6, and subsequently the phase of ψ6 as follows. First, we identify for each particle i the number of nearest neighbors in the first shell (N), and calculate the angles between the reference particle and each of the j-th neighbors, θj. The value of ψ6 is then calculated by taking the average of the complex exponential of six times these angles:
 | (1) |
| phase(ψ6) = arg(ψ6) | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) denotes the argument (or angle) of the complex number in the complex plane.
) denotes the argument (or angle) of the complex number in the complex plane.
5.5 Vorticity
The vorticity of the microswimmers was computed by first calculating the velocity gradients and then deriving the vorticity from these gradients. First, we identify for each particle i the neighbors j in the first two surrounding shells. Then, assuming the displacement of the neighbors with respect to particle i is given by the sum of a translation and a rotation, the velocity gradients were derived by solving the system:| B = A·J | (3) |
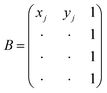 are the initial positions of the neighbors augmented with an additional column of ones to facilitate the inclusion of translational components. The matrix
are the initial positions of the neighbors augmented with an additional column of ones to facilitate the inclusion of translational components. The matrix 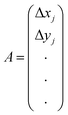 contains the displacements after time step Δt, and
contains the displacements after time step Δt, and  is the Jacobian matrix. To obtain the velocity gradients, eqn (3) was solved for J by calculating the dotproduct of B and the inverse of matrix A, A+. Finally, the vorticity ω was calculated as the difference between the partial derivatives of the velocity components:
is the Jacobian matrix. To obtain the velocity gradients, eqn (3) was solved for J by calculating the dotproduct of B and the inverse of matrix A, A+. Finally, the vorticity ω was calculated as the difference between the partial derivatives of the velocity components:
 | (4) |
5.6 Janus microswimmer cap orientation
The cap orientation of individual microswimmers was extracted from high-magnification images using a custom code written in Matlab. In brief, we first find the center of each particle using a centroid finding algorithm.48 We then apply a bandpass filter to the original image with a passband frequency range of 2–7 pixels, which yields the caps of the Janus particles to appear as bright blobs. Subsequently, circular regions were cropped around the particle center, and the brightness center was obtained by weighing the intensity of the pixels in the corresponding crop with the distance from the center position. Finally, the center and the brightness center were connected to obtain the orientation of the two-dimensional Janus particle.Author contributions
Author contributions are defined based on the CRediT (Contributor Roles Taxonomy) and listed alphabetically. Conceptualization: L. A., L. I., C. v. B. Formal analysis: C. v. B. Funding acquisition: L. I. Investigation: L. A., C. v. B. Methodology: L. A., R. W. S., C. v. B. Project administration: L. I. Software: C. v. B. Supervision: L. I. Validation: C. v. B. Visualization: C. v. B. Writing – original draft: C. v. B. Writing – review and editing: L. A., L. I., R. W. S., C. v. B.Data availability
The data supporting this article have either already been included as part of the ESI,† or will be included upon publication.Conflicts of interest
The authors declare that they have no conflicts of interest.Acknowledgements
We acknowledge Roberto Piazza, Stefano Buzzaccaro, Chantal Valeriani and Nuno Araujo for useful discussions, and Moritz Röthlisberger for preliminary experiments. C. v. B. acknowledges funding from the European Unions Horizon 2020 MSCA-ITN-ETN, project number 812780. L. I. acknowledges funding from the European Research Council (ERC) under the European Unions Horizon 2020 Research and Innovation Program grant agreement no. 101001514.References
- F. Zoratto, D. Santucci and E. Alleva, Rendiconti Lincei, 2009, 20, 163–176 Search PubMed.
- S. Lai, J. Tremblay and E. Déziel, Environ. Microbiol., 2009, 11, 126–136 CAS.
- M. F. Olson, Actin-myosin cytoskeleton regulation and function, Cells, 2022, 12(1), 9 CrossRef PubMed.
- J. Bialké, H. Löwen and T. Speck, Europhys. Lett., 2013, 103, 30008 CrossRef.
- A. G. Thompson, J. Tailleur, M. E. Cates and R. A. Blythe, J. Stat. Mech.: Theory Exp., 2011, 2011, P02029 CrossRef.
- D. Levis and L. Berthier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062301 CrossRef.
- G. S. Redner, A. Baskaran and M. F. Hagan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012305 CrossRef.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef.
- T. Speck, J. Bialké, A. M. Menzel and H. Löwen, Phys. Rev. Lett., 2014, 112, 218304 Search PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- T. H. Tan, A. Mietke, J. Li, Y. Chen, H. Higinbotham, P. J. Foster, S. Gokhale, J. Dunkel and N. Fakhri, Nature, 2022, 607, 287–293 CrossRef CAS PubMed.
- A. P. Petroff, X.-L. Wu and A. Libchaber, Phys. Rev. Lett., 2015, 114, 158102 CrossRef PubMed.
- X. Chen, X. Yang, M. Yang and H. Zhang, Europhys. Lett., 2015, 111, 54002 CrossRef.
- A. Petroff and A. Libchaber, New J. Phys., 2018, 20, 015007 CrossRef.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936–940 Search PubMed.
- E. S. Bililign, F. Balboa Usabiaga, Y. A. Ganan, A. Poncet, V. Soni, S. Magkiriadou, M. J. Shelley, D. Bartolo and W. T. Irvine, Nat. Phys., 2022, 18, 212–218 Search PubMed.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 Search PubMed.
- J. Tailleur and M. E. Cates, Phys. Rev. Lett., 2008, 100, 218103 CrossRef CAS PubMed.
- J. Martin-Roca, R. Martinez, L. C. Alexander, A. L. Diez, D. G. Aarts, F. Alarcon, J. Ramrez and C. Valeriani, J. Chem. Phys., 2021, 154, 164901 CrossRef CAS PubMed.
- E. Sesé-Sansa, G.-J. Liao, D. Levis, I. Pagonabarraga and S. H. Klapp, Soft Matter, 2022, 18, 5388–5401 Search PubMed.
- A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95–98 Search PubMed.
- M. Driscoll, B. Delmotte, M. Youssef, S. Sacanna, A. Donev and P. Chaikin, Nat. Phys., 2017, 13, 375–379 Search PubMed.
- H. Karani, G. E. Pradillo and P. M. Vlahovska, Phys. Rev. Lett., 2019, 123, 208002 CrossRef CAS PubMed.
- J. Yan, M. Han, J. Zhang, C. Xu, E. Luijten and S. Granick, Nat. Mater., 2016, 15, 1095–1099 CrossRef CAS PubMed.
- T. M. Squires and M. Z. Bazant, J. Fluid Mech., 2006, 560, 65–101 CrossRef.
- W. Ristenpart, I. A. Aksay and D. Saville, J. Fluid Mech., 2007, 575, 83–109 CrossRef CAS.
- M. Z. Bazant and T. M. Squires, Phys. Rev. Lett., 2004, 92, 066101 CrossRef PubMed.
- S. Gangwal, O. J. Cayre, M. Z. Bazant and O. D. Velev, Phys. Rev. Lett., 2008, 100, 058302 CrossRef PubMed.
- C. van Baalen, S. Ketzetzi, A. Tintor and L. Isa, arXiv, 2025, preprint, arXiv:2501.00660 DOI:10.48550/arXiv.2501.00660.
- J. Palacci, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2010, 105, 088304 Search PubMed.
- F. Ginot, I. Theurkauff, D. Levis, C. Ybert, L. Bocquet, L. Berthier and C. Cottin-Bizonne, Phys. Rev. X, 2015, 5, 011004 CAS.
- F. Ginot, A. Solon, Y. Kafri, C. Ybert, J. Tailleur and C. Cottin-Bizonne, New J. Phys., 2018, 20, 115001 CrossRef CAS.
- J. Vachier and M. G. Mazza, Eur. Phys. J. E: Soft Matter Biol. Phys., 2019, 42, 1–11 CrossRef CAS PubMed.
- M. Enculescu and H. Stark, Phys. Rev. Lett., 2011, 107, 058301 CrossRef.
- G. Szamel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012111 CrossRef.
- B. Zhang, A. Sokolov and A. Snezhko, Nat. Commun., 2020, 11, 4401 CrossRef CAS PubMed.
- B. Zhang, H. Yuan, A. Sokolov, M. O. de la Cruz and A. Snezhko, Nat. Phys., 2022, 18, 154–159 Search PubMed.
- J. Mecke, Y. Gao, C. A. Ramrez Medina, D. G. Aarts, G. Gompper and M. Ripoll, Commun. Phys., 2023, 6, 324 Search PubMed.
- Z. Shen, A. Würger and J. S. Lintuvuori, Soft Matter, 2019, 15, 1508–1521 CAS.
- A. Boymelgreen and G. Yossifon, Langmuir, 2015, 31, 8243–8250 CAS.
- D. Nishiguchi and M. Sano, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 052309 Search PubMed.
- H. Schmidle, S. Jäger, C. K. Hall, O. D. Velev and S. H. Klapp, Soft Matter, 2013, 9, 2518–2524 CAS.
- S. Gangwal, O. J. Cayre and O. D. Velev, Langmuir, 2008, 24, 13312–13320 CAS.
- J. Zhang, J. Yan and S. Granick, Angew. Chem., Int. Ed., 2016, 128, 5252–5255 Search PubMed.
- X. Yang, S. Johnson and N. Wu, Adv. Intell. Syst., 2019, 1, 1900096 CrossRef.
- X. Yang and N. Wu, Langmuir, 2018, 34, 952–960 CAS.
- A. Boymelgreen, G. Yossifon and T. Miloh, Langmuir, 2016, 32, 9540–9547 CAS.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- D. B. Allan, T. A. Caswell, N. C. Keim, C. M. van der Wel and R. W. Verweij, Trackpy v0.4.2, 2019, https://zenodo.org/record/3492186 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental videos and corresponding description. See DOI: https://doi.org/10.1039/d4sm01511h |
| This journal is © The Royal Society of Chemistry 2025 |


