Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Chain dynamics in polyisoprene stars with arms linked by dynamic covalent bonds to the central core†
Beatriz Robles-Hernández *ab,
Nikolaos Patelis
*ab,
Nikolaos Patelis c,
Arantxa Arbe
c,
Arantxa Arbe b,
Konstantinos Ntetsikas
b,
Konstantinos Ntetsikas c,
Saibal Bhaumik
c,
Saibal Bhaumik c,
Nikos Hadjichristidis
c,
Nikos Hadjichristidis *c,
Ángel Alegría
*c,
Ángel Alegría ab and
Juan Colmenero
ab and
Juan Colmenero bd
bd
aDepartamento de Polímeros y Materiales Avanzados: Física, Química y Tecnología (UPV/EHU), 20018 San Sebastián, Spain. E-mail: beatriz.robles@ehu.eus
bCentro de Física de Materiales (CFM-MPC), CSIC-UPV/EHU, Paseo Manuel de Lardizabal 5, E-20018 Donostia San Sebastián, Spain
cPolymer Synthesis Laboratory, Chemistry Program, KAUST Catalysis Center, Physical Science and Engineering Division, King Abdullah University of Science and Technology (KAUST), 23955 Thuwal, Saudi Arabia. E-mail: Nikolaos.Hadjichristidis@kaust.edu.sa
dDonostia International Physics Center (DIPC), Paseo Manuel de Lardizabal 4, E-20018 San Sebastián, Spain
First published on 31st March 2025
Abstract
Although the use of dynamic covalent bonding (DCB) is a promising method to obtain easily recyclable polymer networks, there are many aspects of the incorporation of dynamic covalent bonding into polymer systems that remain poorly understood. In order to gain insight into the fundamentals of these materials, well-controlled model systems are required. Here, we present the synthesis of polyisoprene (PI)-based 3-arm stars containing vinylogous urethane DCBs as linkers of the PI arms to the core of the star. The dynamics of these 3-arm stars, with three different arm sizes, is studied by broadband dielectric spectroscopy. A conventional (static) 3-arm PI star of intermediate size has also been synthesized and studied, and all results are directly compared with those of a linear PI chain. A prominent intermediate relaxation between those identified as the slower normal mode and the faster α-relaxation of PI is found in the stars containing DCBs. This relaxation, which becomes more significant as the molecular mass of the PI arms decreases, seems to originate from the dynamic bond exchange that occurs at the level of the star's core. On the other hand, the arm retraction dynamics responsible for the normal mode relaxation do not show significant differences with respect to that observed in the static star.
1 Introduction
Polymers with dynamic covalent bonds (DCBs) have attracted increasing scientific interest due to their reversible bond formation and the broad range of features and functionalities they present, like shape memory, self-healing, responsiveness, improved stretchability, high toughness, malleability, and re-processability, among others.1–6 Furthermore, replacing permanent chemical bonds with dynamic bonds transforms regular thermosets into reconfigurable materials known as covalent adaptable networks (CANs).2,6–17In terms of their interaction nature, DCBs are a unique class of bonds that merge the dynamic properties of supramolecular chemistry with the stability of covalent interactions.18,19 These bonds can reversibly break and reform in response to external stimuli (temperature, light, pH, etc.) through associative (new bonds form along with the breaking of old ones) or dissociative (bonds break first, followed by new bond formation) exchange mechanisms.6,20 In this regard, imine and vinylogous urethane bonds are among the most extensively studied associative DCBs.18,20,21 They are formed through the condensation reaction between amines and carbonyl or acetoacetate groups, respectively. However, the stability of imine bonds under certain conditions can be a limitation, leading to the development of vinylogous urethanes as an alternative.22 These bonds exhibit enhanced stability due to their conjugated structure, where the enamine and keto forms are stabilized by intramolecular hydrogen bonding. Unlike conventional urethanes, vinylogous urethanes have increased reactivity, allowing for thermally induced transamination reactions with or without a catalyst via Michael addition–elimination or iminium-based pathways.20,23
Extensive studies on small model molecules have provided critical insights into the dynamic behavior of CANs and vinylogous urethanes.22–25 However, model dynamic polymers, well-defined in terms of molecular architecture, composition, and molecular weight with low dispersity, are essential for understanding the structure–property relationships and dynamics within the family of dynamic polymer materials. Anionic polymerization has been one of the most reliable methods for synthesizing model complex macromolecular architectures with static bonds, such as diblocks, stars, grafts, rings, etc., serving as benchmark systems for a detailed quantitative analysis.26–35 Consequently, anionic polymerization and post-functionalization reactions36,37 can serve as a synthetic pathway for dynamic model polymers. Despite this progress, a notable gap remains in the synthesis and study of model polymers incorporating DCBs. Polymers with DCBs present relaxation mechanisms with different timescales and length scales, making it possible to tune their viscoelastic properties. A deep understanding at a molecular level of the role played by the DCB in the macroscopic properties is still missing, while there is no clear understanding of the influence of the segmental relaxation in the bond exchange mechanism yet.14
In that sense, broadband dielectric spectroscopy (BDS) is a well-suited technique due to its sensitivity to dipole fluctuations, which allows unraveling the dynamics at a molecular level. This is of particular interest for studying the bond exchange process of the DCBs and how that process affects the dynamics of the whole chain.38 To this end, a thorough investigation can help to understand the role played by the dynamics of the bonds in the structure–property relationship in CANs. For this purpose, the synthesis and characterization of polyisoprene (PI)-based vitrimers (associative CANs) with imine dynamic bonds has been reported, providing new insights into the vitrimer's dynamics, and highlighting the necessity of model polymers.39 Using PI chains of different lengths and varying the cross-link concentration, model polymers with a constant chain length between dynamic linkages were obtained. In a complete structural study carried out in those vitrimers, a clustering of the cross-linkers was observed by X-ray diffraction.40 Besides, in a dielectric study, the fluctuation of the dipole moment of the cross-linker was detected. Interestingly, the fluctuation of those dipoles occurs in a concerted way with the PI segments close to the chain ends. Furthermore, type-A polymers41 like PI present a net dipole moment related to the chain end-to-end vector, allowing the observation of the so-called normal mode (NM) by dielectric spectroscopy, which involves the entire chain motion. In the case of the PI vitrimers with imine dynamic bonds, the full reorientation of the end-to-end vector is hindered, but limited fluctuations of the chain ends presumably occur inside the clusters of cross-linkers.42
Macromolecular architectures incorporating DCBs, such as stars, are ideal systems for simplifying the topological complexity introduced by DCBs in CANs. Additionally, recent studies have shown that PI star polymers with static bonds, when used as additives in isofrictional blends with linear PI, effectively reduce the mixture's viscosity through the constraint release mechanism.43,44 Thus, star polymers through DCBs represent a promising new class of rheological agents, enhanced by the dynamic character of their core.
Considering these factors, we present, for the first time, the synthesis of 3-arm star PI model dynamic polymers via anionic polymerization followed by post-functionalization reactions and vinylogous urethane chemistry, by varying the arm molecular weight (2, 5, and 11 kg mol−1) and we address their dynamics using BDS. Three relaxation processes are detected in the melt state: slow and fast relaxations corresponding to the NM and the α-relaxation respectively, and an intermediate mode attributed to the dipolar fluctuation of the DCB. Additionally, one model 3-arm star PI through static bonds was synthesized and used as a reference for comparative analysis.
2 Materials and methods
2.1 Materials
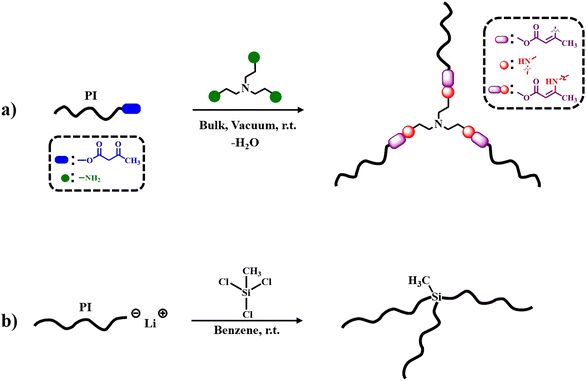
The synthesis and characterization of the 3-arm star PI polymers is extensively described in the Results section. The materials and instrumentation used for the synthesis and characterization of the samples are detailed in ESI.† The synthetic procedure of the final dynamically bonded PI stars is represented in Scheme 1a. The trifunctional cross-linker links the flexible PI chains via DCBs. The synthesis route for the 3-arm star PI with static covalent bonds is depicted in Scheme 1b. Additionally, a linear PI was used for reference, synthesized by anionic living polymerization as described in the ESI of ref. 45. All the experiments were performed within a month from the synthesis date. To confirm that the properties of the samples remained unchanged, size exclusion chromatography (SEC) experiments were performed before and after the experiments.2.2 Methods
When conducting dielectric measurements in rubber-like materials, the thickness of the sample capacitor is affected by diverse factors, such as the normal force applied to ensure good electric contact, which changes with temperature due to thermal expansion. To overcome this problem and be able to compare the dielectric permittivity of the DCB stars with those reported for linear PI,46,47 the values of the complex dielectric permittivity were re-scaled by comparing the residual high-frequency permittivity ε∞ at a temperature well below the glass transition temperature (190 K), assuming that at that temperature the physical mechanism contributing to ε∞ is mainly the induced polarisation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ/2)/λ, where θ is the scattering angle. Reciprocal space calibration was done using silver behenate as standard. Samples were placed in transmission geometry, with a sample-to-detector distance of 0.5 m, covering a Q-range between 0.05 and 0.9 Å−1 by combining 9 different detector positions with a 3 × 3 detector scan profile. Measurements under vacuum in isothermal conditions were performed employing a Linkam Scientific Instruments THMS600 temperature controller with temperature stability of 0.1 K. Measuring times were of 400 s for each scan.
sin(θ/2)/λ, where θ is the scattering angle. Reciprocal space calibration was done using silver behenate as standard. Samples were placed in transmission geometry, with a sample-to-detector distance of 0.5 m, covering a Q-range between 0.05 and 0.9 Å−1 by combining 9 different detector positions with a 3 × 3 detector scan profile. Measurements under vacuum in isothermal conditions were performed employing a Linkam Scientific Instruments THMS600 temperature controller with temperature stability of 0.1 K. Measuring times were of 400 s for each scan.3 Results
3.1 Synthesis and characterization
For the first time, model dynamic 3 arm-star PI [d-(PI)3], was synthesized through anionic polymerization27,28,30 and vinylogous urethane chemistry22,25 as depicted in Scheme 1. Additionally, a 3-arm star PI [(PI6k)3] with static covalent bonds was synthesized according to the literature29,48 and served as a reference for comparison in the BDS dynamic study. Specifically, three different ω-hydroxy functionalized polyisoprenes (PI-OH) were synthesized with molecular weights of 2, 5, and 11 kg mol−1 (Table S1, ESI†). Standard high vacuum techniques and custom-made glass apparatuses were employed to synthesize well-defined PI-OH polymers. s-BuLi initiated the isoprene polymerization in a benzene solution at room temperature while ethylene oxide and methanol served as end-capping and terminating agents, as depicted in Scheme S1a (ESI†). Subsequently, the reaction of PI-OH with tert-butyl acetoacetate produced ω-acetoacetate functionalized polyisoprenes (PI-AcAc) (Table S2 and Scheme S2, ESI†). Following this, three d-(PI)3 with PI arm molecular weights of 2, 5, and 11 kg mol−1, were synthesized by the condensation reaction of PI-AcAc with tris(2-aminoethyl)amine (TAEA) in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.02 molar ratio, in bulk under vacuum at room temperature (Table 1 and Scheme 1a). Additionally, one 3-arm star PI with Mn (PI-arm) ∼ 6 kg mol−1, labeled as (PI6k)3, was synthesized via static covalent bonds (Table 1, Scheme 1b and Scheme S1b, ESI†). Initially, isoprene was anionically polymerized with s-BuLi in benzene at room temperature to generate the living PI6k arm. A coupling reaction was followed between methyltrichlorosilane and the living PI arm in a 1
1.02 molar ratio, in bulk under vacuum at room temperature (Table 1 and Scheme 1a). Additionally, one 3-arm star PI with Mn (PI-arm) ∼ 6 kg mol−1, labeled as (PI6k)3, was synthesized via static covalent bonds (Table 1, Scheme 1b and Scheme S1b, ESI†). Initially, isoprene was anionically polymerized with s-BuLi in benzene at room temperature to generate the living PI6k arm. A coupling reaction was followed between methyltrichlorosilane and the living PI arm in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.95 molar ratio of PI arm to –Cl, forming the 3-arm star PI. The pure 3-arm star PI6k, free from the unreacted PI arm, was isolated using the fractionation technique. Furthermore, the dynamic associative behavior of the PI macromolecular architectures was experimentally investigated and confirmed by reacting d-(PI2k)3 with aniline as illustrated in Scheme S3 (ESI†).25 All linear precursors (PI-OH, PI-AcAc, and PI arm) and the corresponding 3-arm star PI were characterized by SEC, 1H NMR and FT-IR analysis. All the PI-OH exhibited low dispersity (Đ = Mw/Mn ≤ 1.06) and Gaussian molecular weight distribution, as shown in Fig. S1a (ESI†). The specific conditions and use of Schlenk techniques for the acetoacetylation of PI-OH yielded well-defined PI-AcAc, free from dimer byproducts, as indicated by the SEC traces in Fig. S1b (ESI†). The SEC trace corresponding to the PI6k arm, of the (PI6k)3, shows a small side peak to the left of the main peak corresponding to dimers formed during the aliquot termination with methanol under air. The SEC trace of the fractionated (PI6k)3 star reveals a well-defined product free of unreacted PI arm (Fig. S2, ESI†).
0.95 molar ratio of PI arm to –Cl, forming the 3-arm star PI. The pure 3-arm star PI6k, free from the unreacted PI arm, was isolated using the fractionation technique. Furthermore, the dynamic associative behavior of the PI macromolecular architectures was experimentally investigated and confirmed by reacting d-(PI2k)3 with aniline as illustrated in Scheme S3 (ESI†).25 All linear precursors (PI-OH, PI-AcAc, and PI arm) and the corresponding 3-arm star PI were characterized by SEC, 1H NMR and FT-IR analysis. All the PI-OH exhibited low dispersity (Đ = Mw/Mn ≤ 1.06) and Gaussian molecular weight distribution, as shown in Fig. S1a (ESI†). The specific conditions and use of Schlenk techniques for the acetoacetylation of PI-OH yielded well-defined PI-AcAc, free from dimer byproducts, as indicated by the SEC traces in Fig. S1b (ESI†). The SEC trace corresponding to the PI6k arm, of the (PI6k)3, shows a small side peak to the left of the main peak corresponding to dimers formed during the aliquot termination with methanol under air. The SEC trace of the fractionated (PI6k)3 star reveals a well-defined product free of unreacted PI arm (Fig. S2, ESI†).
| Sample | Mna (g mol−1) | Đa main peak | 1,4 microstructureb (mol%) | 3,4 microstructureb (mol%) | Tgc (K) |
|---|---|---|---|---|---|
| a From SEC (THF, 35 °C, calibrated with PI standards).b Determined by 1H NMR spectroscopy (500 MHz, chloroform-d, 25 °C).c From the inflection point of reversing heat flow curve obtained from modulated DSC measurements, determined from cooling cycles. | |||||
| d-(PI2k)3 | 5500 | 1.04 | 89.7 | 10.3 | 211.3 |
| d-(PI5k)3 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
1.07 | 92.2 | 7.8 | 212 |
| d-(PI11k)3 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
1.13 | 92.4 | 7.6 | 212.3 |
| (PI6k)3 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
1.02 | 93.0 | 7.0 | 210 |
The formation of well-defined 3-arm star PI via vinylogous urethane bonding was challenging due to the system's dynamic chemistry (Scheme 1). To ensure that no unreacted PI-AcAc remained and to promote catalyst-free transamination within the system,22 a 2% excess of TAEA was used in all cases, producing a small number of mono and di-arm star PI chains with free –NH2 functionality, as shown in Scheme S4 (ESI†). The formation of d-(PI)3 was verified by the appearance of the high molecular weight traces in the SEC chromatograph, as depicted in Fig. 1. A minor right-side peak appeared in the chromatogram for all three d-(PI)3, which can be attributed to the one-arm structure, as illustrated in Scheme S4 (ESI†). Noticeably, in the case of the d-(PI11k)3, the system appeared to reach equilibrium after about 10 days, with only minor changes thereafter. According to SEC, besides the main peak corresponding to the d-(PI11k)3, two additional peaks on the right are attributed to the two-arm and one-arm structures. An explanation for that could be that the higher steric hindrance of the PI11k-AcAc (Mn = 11 kg mol−1) restricts the complete formation of the 3-arm star, compared to the lower molecular weight of d-(PI2k)3 and d-(PI5k)3. The dynamic behavior of the vinylogous urethane architectures was examined using SEC. d-(PI2k)3 was mixed with an excess of aniline at room temperature, where no change was detected in the SEC traces after 24 hours due to the slow kinetics of the transamination reaction. However, upon heating to 130 °C, the d-(PI2k)3 peak almost disappeared, with a small peak appearing corresponding to the 2-arm structure, along with the main peak of d-PI2k-Ph as shown in Fig. S3 and Scheme S3b (ESI†).
 | ||
| Fig. 1 SEC traces of 3-arm star PI [d-(PI)3] with molecular weight of PI-AcAc (a) 2 kg mol−1, (b) 5 kg mol−1, and (c) 11 kg mol−1 in THF at 35 °C. | ||
Subsequently, 1H NMR analysis was conducted, confirming the success of the synthetic steps in this study. The PI-OH spectrum shows a characteristic peak at 3.60 ppm (designated as a in Fig. S5, ESI†) for the terminal –CH2–OH protons (2H). A signal appeared at 5.13 ppm (1H) corresponding to the olefinic protons of the PI backbone (1H), and a multiplate at 4.7–4.68 ppm attributed to the vinyl group protons (–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2). Additionally, the 1,4 microstructure of PI precursors was estimated to range from 90% to 93%. The successful acetoacetylation of PI2k-OH was confirmed by the disappearance of the –CH2–OH protons signal at 3.60 ppm (assigned as a) and the appearance of three new signals: –CH2–O– at 4.07 ppm (assigned as b, m), (O
CH2). Additionally, the 1,4 microstructure of PI precursors was estimated to range from 90% to 93%. The successful acetoacetylation of PI2k-OH was confirmed by the disappearance of the –CH2–OH protons signal at 3.60 ppm (assigned as a) and the appearance of three new signals: –CH2–O– at 4.07 ppm (assigned as b, m), (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–CH2–C
C–CH2–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) at 3.43 ppm (assigned as c, s) and (O
O) at 3.43 ppm (assigned as c, s) and (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–CH3) at 2.27 ppm (assigned as d, s), as shown in Fig. S6a (ESI†). Similar spectra were observed for PI5k-AcAc and PI11k-AcAc as shown in Fig. S7a and S8a (ESI†). The condensation reaction of PI-AcAc and TAEA was also analyzed by 1H NMR, confirming the formation of vinylogous urethane bonds and the successful synthesis of d-(PI)3 (Fig. S6b, ESI†). In more detail, the d-(PI2k)3 spectrum shows the disappearance of the characteristic peaks of PI2k-AcAc at 3.43 ppm and 2.27 ppm. Additionally, some new proton signals are observed and assigned as follows: two multiplates appear at 8.69–8.57 ppm, attributed to the nitrogen proton (–CH2–NH–) (designated as h), two signals appear at 4.53–4.43 ppm corresponding to the (O
C–CH3) at 2.27 ppm (assigned as d, s), as shown in Fig. S6a (ESI†). Similar spectra were observed for PI5k-AcAc and PI11k-AcAc as shown in Fig. S7a and S8a (ESI†). The condensation reaction of PI-AcAc and TAEA was also analyzed by 1H NMR, confirming the formation of vinylogous urethane bonds and the successful synthesis of d-(PI)3 (Fig. S6b, ESI†). In more detail, the d-(PI2k)3 spectrum shows the disappearance of the characteristic peaks of PI2k-AcAc at 3.43 ppm and 2.27 ppm. Additionally, some new proton signals are observed and assigned as follows: two multiplates appear at 8.69–8.57 ppm, attributed to the nitrogen proton (–CH2–NH–) (designated as h), two signals appear at 4.53–4.43 ppm corresponding to the (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–CH
C–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) proton (designated as j), and a multiplet at 3.90 ppm that assigned to (H2C–CH2–O–C
C) proton (designated as j), and a multiplet at 3.90 ppm that assigned to (H2C–CH2–O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) (designated as k). Furthermore, a multiplet signal shows at 3.25 ppm, attributed to (N–CH2–CH2–NH) (designated as g), with another multiplet at 2.68 ppm assigned to (N–CH2–CH2–NH) (designated as f). d-(PI5k)3 and d-(PI11k)3 show similar 1H NMR spectra to that of d-(PI2k)3 (Fig. S7 and S8b, ESI†), confirming the successful synthesis across all molecular weights. Fig. S9 (ESI†) shows the 1H NMR spectrum of the 3-arm PI star synthesized through static covalent bonds, (PI6k)3, similar to the precursor of PI6k-arm. The peak at 5.13 ppm (designated as a) corresponds to the olefinic protons of the PI backbone, while the peaks at 4.7−4.68 ppm (designated as b) are assigned to the vinyl group protons (–C
O) (designated as k). Furthermore, a multiplet signal shows at 3.25 ppm, attributed to (N–CH2–CH2–NH) (designated as g), with another multiplet at 2.68 ppm assigned to (N–CH2–CH2–NH) (designated as f). d-(PI5k)3 and d-(PI11k)3 show similar 1H NMR spectra to that of d-(PI2k)3 (Fig. S7 and S8b, ESI†), confirming the successful synthesis across all molecular weights. Fig. S9 (ESI†) shows the 1H NMR spectrum of the 3-arm PI star synthesized through static covalent bonds, (PI6k)3, similar to the precursor of PI6k-arm. The peak at 5.13 ppm (designated as a) corresponds to the olefinic protons of the PI backbone, while the peaks at 4.7−4.68 ppm (designated as b) are assigned to the vinyl group protons (–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2). A comparison of the integrations of these signals reveals that the microstructure of the star (PI6k)3 consists of 93% 1,4 units and 7% 1,3 units.
CH2). A comparison of the integrations of these signals reveals that the microstructure of the star (PI6k)3 consists of 93% 1,4 units and 7% 1,3 units.
Along with SEC and 1H-NMR, FT-IR analysis was conducted at all steps of the synthesis. The FT-IR spectrum of PI2k-OH displays a broad signal at 3330 cm−1 corresponding to the O–H stretching band, and two peaks at 1643 cm−1 and 1663 cm−1, attributed to the –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C– vibrations of the PI backbone49 as shown in Fig. S10 (ESI†). The acetoacetylation of PI2k-OH was also confirmed via FT-IR (Fig. S11, ESI†). More specifically, the t-butyl acetoacetate precursor exhibits two characteristic signals at 1712 cm−1 and 1738 cm−1, corresponding to the ketone and ester carbonyl groups, respectively.22 Similar signals (1722 cm−1 and 1738 cm−1) appeared in the case of PI2k-AcAc confirming the effective functionalization by t-butyl acetoacetate. Furthermore, the formation of d-(PI2k)3 through vinylogous urethane chemistry is confirmed firstly by the near disappearance of the –NH2 bands of TAEA at 3350 cm−1 and 3270 cm−1, a weak residual signal remains attributed to the 2% excess of TAEA, and second from the disappearance of the acetoacetate vibrational band at 1722 cm−1 and 1738 cm−1. Additionally, two new bands emerge at 1601 cm−1, and 1645 cm−1 attributed to the C
C– vibrations of the PI backbone49 as shown in Fig. S10 (ESI†). The acetoacetylation of PI2k-OH was also confirmed via FT-IR (Fig. S11, ESI†). More specifically, the t-butyl acetoacetate precursor exhibits two characteristic signals at 1712 cm−1 and 1738 cm−1, corresponding to the ketone and ester carbonyl groups, respectively.22 Similar signals (1722 cm−1 and 1738 cm−1) appeared in the case of PI2k-AcAc confirming the effective functionalization by t-butyl acetoacetate. Furthermore, the formation of d-(PI2k)3 through vinylogous urethane chemistry is confirmed firstly by the near disappearance of the –NH2 bands of TAEA at 3350 cm−1 and 3270 cm−1, a weak residual signal remains attributed to the 2% excess of TAEA, and second from the disappearance of the acetoacetate vibrational band at 1722 cm−1 and 1738 cm−1. Additionally, two new bands emerge at 1601 cm−1, and 1645 cm−1 attributed to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups of the vinylogous urethane (Fig. 2). The FT-IR analysis was primarily conducted on the 2 kg mol−1 samples due to the lower molecular weight for enhanced signal clarity. Similar results were obtained for the 5 and 11 kg mol−1, as depicted in Fig. 2. It is worth noting that initial evidence suggests that these systems remain stable for approximately 50 days when stored under a dynamic vacuum at room temperature. However, side reactions occurred beyond this period, forming static covalent bonds, and the system gradually nearly lost its dynamic character. The system remains fully stable when stored in a non-polar solvent (cyclohexane, benzene) under vacuum at −20 °C. Additional experiments and studies are required to elucidate the long-term transformations of this complex system.
O groups of the vinylogous urethane (Fig. 2). The FT-IR analysis was primarily conducted on the 2 kg mol−1 samples due to the lower molecular weight for enhanced signal clarity. Similar results were obtained for the 5 and 11 kg mol−1, as depicted in Fig. 2. It is worth noting that initial evidence suggests that these systems remain stable for approximately 50 days when stored under a dynamic vacuum at room temperature. However, side reactions occurred beyond this period, forming static covalent bonds, and the system gradually nearly lost its dynamic character. The system remains fully stable when stored in a non-polar solvent (cyclohexane, benzene) under vacuum at −20 °C. Additional experiments and studies are required to elucidate the long-term transformations of this complex system.
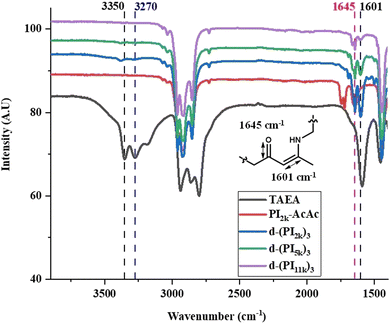 | ||
| Fig. 2 FT-IR spectra of the linear precursor PI2k-AcAc, TAEA, and the 3-arm PI stars [d-(PI)3] through vinylogous urethane chemistry. | ||
3.2 Dielectric study
The dielectric response of the DCB stars with a Mn of 5 kg mol−1 per arm at a temperature about 42 K above Tg is shown in Fig. 3. In this temperature range the main relaxation components are well within the experimental frequency window. Data corresponding to a linear PI of Mn = 6 kg mol−1 (LPI6k) as well as those corresponding to the PI 3-arm star with static covalent bonds of the same Mn [(PI6k)3] are also included for comparison. As can be observed, while the dielectric spectra of LPI6k and (PI6k)3 show two well-resolved relaxation processes, the signal measured for the DCB stars is more complex. In the linear PI and statically bonded star, it is known that the high-frequency process is due to the segmental relaxation (also known as α-relaxation) and the low-frequency one is attributed to the end-to-end vector reorientation of the PI chains (normal mode, NM),50,51 and is related with the so-called arm retraction in the case of the stars. In the DCB stars, besides these two relaxation processes detected at similar frequencies, there is a pronounced increase in the intensity of the signal at intermediate frequencies, so large that it appears as a third peak in the spectra. This particularity in the spectra was also found in mono- and di-functionalized linear polyisoprenes bearing hydroxyl (OH–) end-group(s), where a third peak in the frequency range between the segmental process and the global chain relaxation was observed, attributed to the relaxation of segments in the vicinity of the H-bonded groups.52In Fig. 4 we show a comparison of the DCB stars with different molecular weight per arm. It can be observed that the intensity of the mid-frequency relaxation process increases as the Mn of the arm decreases, that is, with the volume fraction of functional cores: the d-(PI11k)3 spectrum shows 3 clear peaks of similar height, while in the d-(PI5k)3 the intensity of the central peak increases and the normal mode one—which shifts toward higher frequencies as the chain shortens53—is visible as a low-frequency shoulder of that central peak; in the d-(PI2k)3 the signal of the mid-frequency relaxation is even more intense, to the point that the NM and the α-relaxation are both hidden by this peak. The correlation between the intensity of the mid-frequency process and the volume fraction of functional cores in the samples suggests that this relaxation mode is associated with the dipole reorientation of the functional cores.
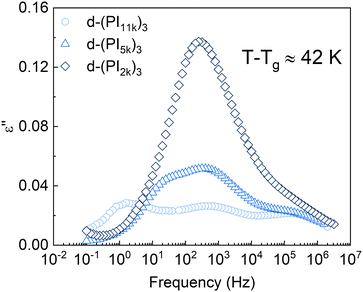 | ||
| Fig. 4 Imaginary component of the dielectric permittivity for the different PI stars. For each sample, the selected temperature is about 42 K above its calorimetric Tg. | ||
To gain insight into the molecular origin of the relaxation components observed in these stars, we analyzed the dependence with the temperature of the characteristic frequencies obtained from the maxima of the peaks by simple inspection. We selected the d-(PI11k)3 since, as already mentioned, in this sample the peaks corresponding to the three relaxation processes are better resolved (see Fig. 4). The obtained frequencies are represented in Fig. 5a (empty symbols) as a function of the reciprocal temperature. The temperature dependence of the frequencies follows the Vogel–Fulcher–Tamman (VFT) law:54
 | (1) |
 , with
, with  .
.
 | ||
| Fig. 5 Arrhenius plot of (a) the three peak maxima for the d-(PI11k)3 star and (b) the peak maxima for the main components of each recorded spectrum (see text for details). Empty symbols correspond to the values obtained from visual inspection of the loss curves. Solid symbols correspond to the results obtained from the BDS data analysis using eqn (2). Lines correspond to the VFT description of these frequencies (see legend). | ||
For the NM, the values of D and T0 were fixed to those used for the α-relaxation, and f∞ was allowed as a fitting parameter. This provides a good description of the main part of the data set. Finally, we have found that the same type of approach also delivers a reasonable description of the intermediate relaxation associated with the DCB fluctuations (see Fig. 5a). These results indicate that the time-temperature superposition would also work as a good approximation in this type of material, suggesting that the DCB exchange is slaved to the segmental mobility, which also controls the temperature dependence of the normal mode relaxation.
This analysis can be extended to the other DCB stars considering only those components showing a clear peak in the recorded spectrum, meaning that in the case of d-(PI2k)3 and d-(PI5k)3 only a single peak is tracked. The values obtained in this way are shown in Fig. 5b. In this plot we have included as lines those used to describe the data already shown in panel a. An overall similar behavior is found for all the characteristic frequencies, confirming that the results obtained for d-(PI11k)3 can be extended to the whole set of samples investigated, at least within the present level of accuracy in the determination of the characteristic frequencies.
A complete description of the relaxation curves is required to properly resolve the characteristics of the three different relaxation contributions for each polymer and thus, go beyond the previous semi-quantitative analysis. To this end, the dielectric relaxation data have been described as a superposition of three relaxation processes plus a term to account for DC conductivity, σDC, and other low-frequency effects:
 | (2) |
For the low-frequency mode, we used the Rouse-like description of the normal mode50 where each mode contributes as a Cole–Cole relaxation process:55–58
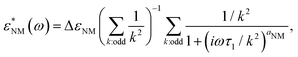 | (3) |
The other two relaxation processes (α-relaxation and DCB relaxation) have been described using the Havriliak–Negami (HN) function or its mirrored version (mHN),60–62 depending on the direction of the asymmetrical broadening of the corresponding relaxation peak. In the case of the HN function, the peak may broaden asymmetrically toward higher frequencies, and it reads
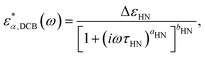 | (4) |
 | (5) |
The mirrored version of the HN equation can be written as62
 | (6) |
In addition, some assumptions were made to limit the number of free parameters in the fitting process: (i) the relaxation time of the maximum of the α-relaxation peak was fixed from the value determined in the linear PI after taking into account the differences in Tg values (see Table 1), as obtained from differential scanning calorimetry (DSC) (see ESI† for details); (ii) the ratio of the dielectric strengths ΔεNM/Δεα was fixed to the value obtained for the static star (PI6k)3; (iii) for each sample, the dielectric strength ratio ΔεDCB/Δεα was assumed to remain temperature independent.
The description obtained with these assumptions, together with the corresponding data at a given temperature, is shown in Fig. 6 for the three samples and, as can be seen, this fitting strategy provides a very good description of the rather complex relaxation curves. The parameters obtained from the fits for the data at 250 K are collected in Table 2.
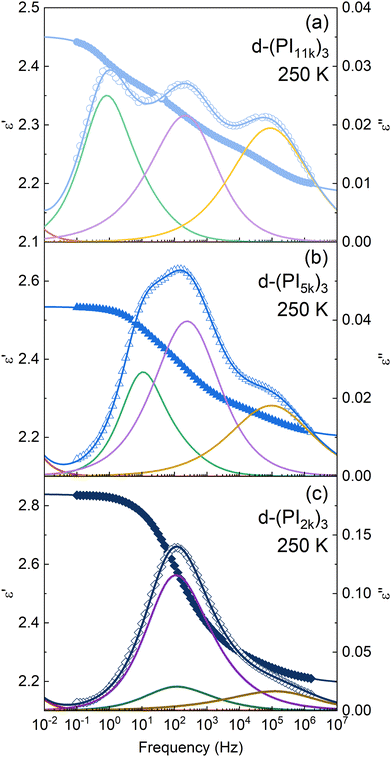 | ||
| Fig. 6 Dielectric permittivity as a function of frequency for 3-arm stars with a molecular weight of (a) 11 kg mol−1, (b) 5 kg mol−1, and (c) 2 kg mol−1 per arm, at 250 K. Solid symbols account for the measured real component and open symbols for the imaginary one. Fittings to eqn (2) are represented by solid lines: blue lines for the whole dielectric response; the resolved relaxation components (only for the imaginary part of the dielectric permittivity) are also depicted: normal mode (green), α-relaxation (yellow) and DCB-component (purple). Red lines account for the conductivity. | ||
| Sample | α-relaxation | DCB-relaxation | Normal mode | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Δεα | fmaxα (Hz) | aαa | bαa | ΔεDCB | fmaxDCB (Hz) | aDCB | bDCB | ΔεNM | fNM (Hz) | aNMa | |
| a These parameters are constant with temperature, as well as the ratios Δεα/ΔεNM and Δεα/ΔεDCB.b The mirrored version of the HN function (eqn (6)) was used to describe this peak. | |||||||||||
| d-(PI2k)3 | 0.094 | 111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 950 |
0.53b | 0.57 | 0.47 | 112.95 | 0.67 | 0.66 | 0.085 | 100 | 0.62 |
| d-(PI5k)3 | 0.092 | 89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 929 929 |
0.5b | 0.88 | 0.162 | 244.85 | 0.60b | 0.89 | 0.082 | 10 | 0.8 |
| d-(PI11k)3 | 0.094 | 81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774 774 |
0.5 | 1 | 0.091 | 215.10 | 0.64b | 0.68 | 0.085 | 0.75 | 0.74 |
The components contributing to the overall fitting curve obtained in this way allow a more accurate determination of the characteristics of each relaxation process, namely, peak frequencies and dielectric relaxation intensities. In particular, the peak frequencies determined from the fittings can be compared with those previously obtained from direct data inspection (see filled symbols in Fig. 5). This comparison shows that in the samples where the relaxation components are overlapping, there are some discrepancies. On the contrary, in the case of the d-(PI11k)3 sample, when inspecting the values of the characteristic frequencies obtained by this type of fitting at several temperatures, the preliminary conclusions are fully confirmed (see Fig. 5a).
Regarding the dielectric strengths of the components obtained from the analysis, the data collected in Table 2 show that the relaxation intensities associated with the polymer dynamics are approximately the same for all the samples, within the experimental uncertainties. This could be expected due to the small amount of DCBs in all these systems (less than ≈2% wt). In this situation, the type and concentration of PI dipoles in the material remain essentially constant. On the contrary, important differences exist when considering the DCB component, with a clear correlation with the DCB concentration.
Fig. 7 shows the variation of the dielectric relaxation intensities of the DCB component as a function of the reciprocal of the arm mass, which is proportional to the volume fraction of DCB. A rather linear behavior with zero intersection is found, supporting the procedure used in the dielectric data fitting. From the slope of the fitting line, we can estimate the corresponding effective dipole moment μeffDCB, by assuming54,70 μeffDCB ≈ (ε0kBT ΔεDCB/n)1/2, where ε0 is the vacuum permittivity, n is the dipole number density and kB is the Boltzmann constant. From this equation, we obtain μeffDCB ≈ 2.0 D for each dynamic covalent bond of the 3-arm stars. We can compare this dipole moment with that obtained for the two parts of the DCB, namely, the acetate moiety (1.72 D for methyl acetate71) and the amine one (0.92 D for dymethyl amine71). As can be seen, the value obtained is close to that expected for the DCB.
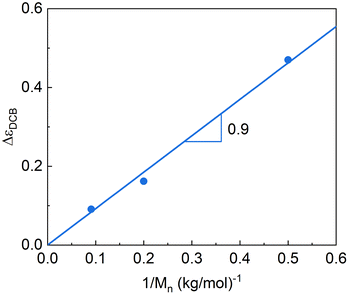 | ||
| Fig. 7 Dielectric strengths of the DCB relaxation component as a function of the inverse of the arm Mn. The line corresponds to a simple proportionality law. | ||
4 Discussion
To make a flawless comparison of the values of the frequencies corresponding to different samples, the small differences in the glass transition temperature are relevant and must be considered. Thus, using d-(PI11k)3 as a reference, the frequency values of the other samples were corrected by a factor derived from the VFT equation, valid for small temperature changes in Tg:
fcorr ≈ fmeas![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[ΔTg D T0/(T − T0)2], exp[ΔTg D T0/(T − T0)2],
| (7) |
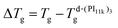 (at 250 K this results in fcorr = fmeas
(at 250 K this results in fcorr = fmeas![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[0.216 ΔTg]). In this way, the frequency values obtained in samples with higher Tg values (slower relaxation) are shifted to higher values, and vice versa. Fig. 8a shows the resulting values as a function of the molecular weight of the PI arm at 250 K. These results show that the frequency of α-relaxation (yellow symbols) remains almost constant, as expected for the compensation for the Tg values.
exp[0.216 ΔTg]). In this way, the frequency values obtained in samples with higher Tg values (slower relaxation) are shifted to higher values, and vice versa. Fig. 8a shows the resulting values as a function of the molecular weight of the PI arm at 250 K. These results show that the frequency of α-relaxation (yellow symbols) remains almost constant, as expected for the compensation for the Tg values.
Let's now start comparing how the characteristic frequencies of the other relaxation processes are modified as the molecular mass of the PI arms changes. Focusing the attention on the molecular weight dependence of the NM frequencies, we can observe in Fig. 8a (green symbols), that our high-molecular weight data follow a power law behavior with an exponent around 3.5, which has already been observed for conventional PI star polymers,72,73 and also for linear polymers above the critical molecular weight, which for PI is around 7 kg mol−1.46,47 Below that molecular weight, the NM relaxation time follows a power law with an exponent of 2, in agreement with the Rouse theory.50 The present results have been compared with published ones from linear47 and star44,74 PI polymers using the α-relaxation frequency as a reference, as depicted in Fig. 8b. For the high-molecular weight samples, no differences are observed in this comparison with respect to the behavior of conventional PI stars within uncertainties. For the shortest arms investigated (d-(PI2k)3 sample), we recall that the NM relaxation is masked (see Fig. 6c) by a much stronger DCB contribution to the dielectric relaxation, which gives rise to large uncertainties in the NM peak frequency determination. Within these uncertainties, the dynamics of these short arms—well below the entanglements threshold—is close to Rouse behavior, as reported for linear chains and other small stars.75 In summary, from this comparison, we can conclude that the presence of DCB in the star polymers seems to have little effect on the arm retraction dynamics—the molecular mechanism associated with the normal mode relaxation of conventional stars.
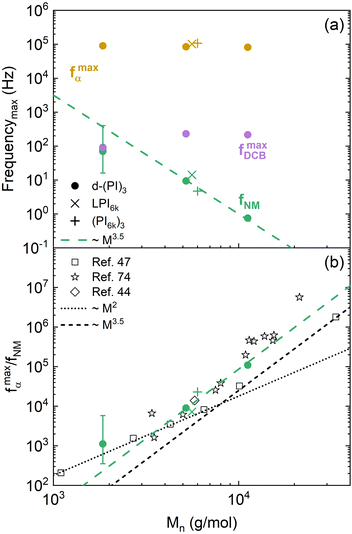 | ||
| Fig. 8 (a) Characteristic frequencies of the relaxation components as a function of the arm Mn at 250 K. The dashed line corresponds to a power law with an exponent 3.5. (b) Comparison of the molecular weight dependence of the ratio of segmental relaxation and normal mode characteristic frequencies for different PI-based architectures: solid symbols for present work samples, open symbols for literature values (squares: linear chains;47 diamond: 8-arm star;44 stars: stars with various number of arms74). | ||
Moving to the DCB-related dynamics, their characteristic frequencies are markedly slower than those of the PI α-relaxation, but show a similar temperature dependence. This latter result suggests a direct link between the PI segmental dynamics and the DCB reorientation event. On the other hand, when comparing the DCB frequency values of different samples (see Fig. 8a, purple symbols), we found that they are essentially the same for the d-(PI5k)3 and d-(PI11k)3 samples, but for the d-(PI2k)3 sample, the frequency is significantly lower. This difference is beyond uncertainty. It can be noticed already in the raw data, as observed in Fig. 6. Indeed, for d-(PI5k)3 the DCB is the main peak of the three relaxation processes, with an intensity 5.5 times that of the NM relaxation. Therefore, the position of its maximum is well determined by the global spectrum. Given the difference in intensities between the NM and the DCB peaks (supported by the results shown in Fig. 7), the position of the former barely affects the maximum of the latter. Moreover, only in this sample, the NM frequency is close to that of the DCB. In principle, we do not see a clear connection between these two features. Motivated by these findings, we had a closer inspection into the calorimetric response of the three samples. In Fig. 9 the DSC curves obtained during cooling for all 3-arm stars are directly compared. Again in this observable, the different behavior of the sample with lowest molecular weight is manifested. The glass transition seems to be more extended; in particular, there are indications of vitrification starting at higher temperatures than in the other samples.
In all the systems we would expect that the PI segments close to the DCBs would have a slower dynamics than those further along the chain approaching the arm end, giving rise to a gradient of mobility along the arm. Since fmaxDCB and, in particular, the ratio fmaxDCB/fmaxα are smaller for the d-(PI2k)3 sample, these effects would be more pronounced for this sample. In this picture, we can assume that there is a local Tg associated with the slower PI segments with timescales close to those of the DCB relaxation. According to eqn (7), a reduction in frequency by about 3 decades, as observed in Fig. 8a, would correspond to a shift in Tg values of about 30 K. This corresponds well with the temperature range in which significant differences in the DSC trace are observed when comparing, for instance, d-(PI2k)3 and d-(PI11k)3 samples, as can be seen in Fig. 9. In the latter case, the number of PI segments involved in the mobility gradient would be relatively small and can be used as a good reference for the more homogeneous PI segmental dynamics. In addition, we note the minimal differences found between d-(PI5k)3 and d-(PI11k)3 samples. Thus, the d-(PI2k)3 sample presents significantly slower DCB dynamics and clearly more heterogeneous dynamics of the PI segments.
To look for a possible origin of this different behavior in the samples, we investigated their structural properties at the mesoscale. Clusterization of cross-linkers with DCBs has been reported for polyethylene vitrimers76 and also for telechelic polymer vitrimers based on both PI and polybutadiene,40,42,77 and could have an important impact on the dynamics of the system.
Small-angle X-ray diffraction (SAXS) results on the 3-arm stars (see Fig. 10) point toward significant clustering in the particular case of the d-(PI2k)3 sample, with the presence of a broad but very clear low-angle diffraction peak. The peak position Qmax ≈ 0.15 Å−1 corresponds to distances between clusters of about 2π/Qmax = 4.2 nm. This is in the range of the average end-to-end distance of linear PI with the mass of the arm.78 A coincidence between the inter-cluster distance and the bulk chain dimension was also found in the PI telechelic vitrimers case.40,42 In those materials it would be the consequence of the conservation of Gaussian conformation of the chains despite being connected to clusters at their ends, emphasizing the role of conformational entropy. However, this condition would not necessarily predetermine the inter-cluster distance in the present systems, with one end of each arm free. Experiments at different temperatures showed no significant dependence on the temperature of this distance. A simple model to describe the situation would consider the material as an ensemble of effective micelles, each of the micelle composed of N stars, where the core containing the N triamines is nano-segregated from the PI arms. This could be considered as an equivalent star with a larger core and more arms. In a crude approach to estimating N, we can assume a cubic lattice where each cube of side L (L would be the inter-cluster distance) has the volume of one of these micelles, i.e., L3 = N(vcross + nvarm). Here, vcross ≈ 0.24 nm3 and varm ≈ 3.4 nm3 are the estimated volumes of a cross-linker molecule and a PI-arm, respectively, and n = 3 is the number of arms in the d-(PI2k)3 sample. This yields about 7 stars/micelle, i.e., we would have an effective melt of 21-arm stars with dynamically active cores. For the other two samples, signatures of nanostructuration are not evident. Thus, cross-linkers would not be aggregated—or, at least, would be associated in a much lesser extent—in d-(PI5k)3 and d-(PI11k)3.
This structural peculiarity of d-(PI2k)3 could explain the differences observed regarding the DCB dynamics and the calorimetric traces. In this sample, the crosslinkers would be confined within nanodomains. This would cause more hindered (and thereby slower) mobility of the crosslinkers and consequently slower reorientations of the DCBs than in the other samples. Nanostructuration would thus enhance the gradient of mobility in d-(PI2k)3. On the other hand, let us remind that the concentration of crosslinkers—and thereby also of slowed-down PI segments linked to them—is highest in this sample. Thus, the contribution of the motions of these entities to the specific heat is also the largest. As argued above, these contributions would be slower if the entities are in the nanodomain cores than if they are more randomly distributed in the sample. This would rationalize the observed significant extension of the calorimetric glass transition to higher temperatures, most likely due to confined dynamics of entities inside the inner regions of the clusters.
We now discuss the nature of the DCB relaxation. The fact that the values of the effective dipole moments obtained for the intermediate relaxation components are close to those expected for the complete reorientation of the dipolar entities involved in the DCB would suggest that a complete reorientation of the polar group at the core of the stars can occur on timescales that can be several orders of magnitude faster than those corresponding to normal mode relaxation, particularly in the case of the bigger stars. Interestingly, the ratio between the DCB and α-relaxation peak frequencies is around 400, a value similar to that reported for PI-based telechelic vitrimers42 (see Fig. S15, ESI†). In such systems, imine DCBs were present instead of the vinylogous urethane bonds linking the moieties in the present samples but the same TAEA triamine was used as crosslinker. In light of these results, one could consider that dynamic bond exchange is already active at temperatures a few degrees above Tg and does not involve the whole arm fluctuations. The fact that the DCB peak frequencies observed in Fig. 5 are similar in all samples, and equal in the samples where no clusterization is resolved, suggests that the bond exchange reaction could take place within the core of each star, i.e., it is an intra-molecular process. This would explain why the NM relaxation of the longest arms is essentially insensitive to the presence of DCB at the core. According to this interpretation, the dynamic bond exchange in the core of the stars would be limited only by the hindered mobility of the directly attached PI chain-portion, so dynamic bond exchange would take place as long as the motions of these PI chain-portions are possible. The timescale difference between the DCB and the segmental dynamics reorientation corresponds to that expected between the end-to-end fluctuations and the segmental dynamics for an entire linear PI chain of about 20 repeat units, suggesting that this could be the size of such a chain portion. On the other hand, apparently, in the close vicinity of other cores—within the nanodomains—the DCB exchange slows down probably due to confined dynamics of the crosslinkers.
Last, we compare the present results on the stars with those obtained on model PI vitrimers,42 where all the chain ends are connected to trifunctional crosslinkers, forming networks. Noteworthy, despite the DCB chemistry not being the same, the timescale of the DCB relaxation in the vitrimers is comparable to that in the stars (see Fig. S15, ESI†), and also shows a temperature dependence similar to that of the segmental dynamics. In fact, the larger dipole associated with the vinylogous urethane bond in the stars enhances the dielectric signal of the DCB-related relaxation and allows establishing this coincidence beyond uncertainties. On the contrary, the slower relaxation detected in the vitrimers showed a distinct temperature dependence with respect to the other two processes, consistent with that found in other dynamic covalent network systems. This suggests that the validity of the time-temperature superposition for the normal mode in the stars is due to the fact that we are not dealing with networks but with polymers with star architecture. In addition, the slowest process observed in the vitrimers is extremely broad—much broader than the stars' normal mode—reflecting the complexity and variety of processes involved in the chain end-to-end relaxation within the clusterized network.
Conclusions
In this study, we successfully synthesized three well-defined dynamic 3-arm PI stars (PI-arm 2, 5, and 11 kg mol−1) for the first time via vinylogous urethane bonding. Tris(2-aminoethyl)amine (TAEA) served as the core, with three linear PI-AcAc arms attached through a condensation reaction between the three primary amino groups of the core and the acetoacetate groups of the PI arms. The synthesis was confirmed using SEC, 1H NMR, and FT-IR. The dynamic behavior of these stars was further evaluated through a transamination reaction with an excess of aniline at elevated temperatures, revealing their adaptability and dynamic nature.Comparing the dielectric relaxation of dynamic 3-arm PI stars with that of conventional (static) ones, we observed that, in addition to the usual α - and NM relaxation processes, a new intermediate and relatively strong relaxation mode emerges, whose intensity increases linearly with the concentration of dynamic bonds in the core of the stars. The peak frequency of this component is about 400 times lower than that characterizing the PI segmental dynamics. In the particular case of the stars with shorter arms, the frequency of this relaxation process—associated with the DCB dipole fluctuation—is 2.5 times slower than in the other stars with longer arms. This difference could be related to the presence of a segregated clustering of the cores for the shortest arm stars, as inferred from the SAXS experiments. Probably for the same reason, the glass transition range as observed by MDSC extends to higher temperatures in this sample, indicating a greater dynamic heterogeneity of structural arrest in this case. Finally, the larger scale chain dynamics detected by the NM relaxation in the dynamically bonded 3-arm stars is similar to that of conventional stars. This means that the arm retraction dynamics is not affected by the dynamic character of the bonds, and consequently the bond exchanges that take place below room temperature would be restricted to those that occur in the core, i.e. the would be intramolecular (or intracluster) events.
Author contributions
Conceptualization: N. H., J. C., A. A., A. A.; investigation: B. R., A. A., A. A., N. P, K. N., S. B.; analysis: B. R., A. Alegría, N. P., K. N, S. B.; methodology: A. A., A. A., J. C., N. H.; supervision: A. A., A. A., J. C., N. H.; writing – original draft: B. R., A. Alegría, N. P., K. N., S. B.; writing – review and editing: N. H., J. C., A. Arbe funding acquisition: N. H., J. C., A. A., A. A.Data availability
The data that support the findings of this study will be available upon request to the corresponding authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
B. R., A. A., A. A., and J. C. gratefully acknowledge the Grant PID2021-123438NB-I00 funded by MCIN/AEI/10.13039/501100011033 and by ERDF A way of making Europe, the Grant IT-1566-22 from Eusko Jaurlaritza (Basque Government) and the Open Access funding from the University of the Basque Country. N. P., K. N., S. B., and N. H. gratefully acknowledge support from the King Abdullah University of Science and Technology (KAUST) (BAS/1/1342-01-01).Notes and references
- R. J. Wojtecki, M. A. Meador and S. J. Rowan, Nat. Mater., 2011, 10, 14–27 CrossRef CAS PubMed.
- C. J. Kloxin and C. N. Bowman, Chem. Soc. Rev., 2013, 42, 7161–7173 RSC.
- Y. Yang and M. W. Urban, Chem. Soc. Rev., 2013, 42, 7446–7467 RSC.
- N. Roy, B. Bruchmann and J. M. Lehn, Chem. Soc. Rev., 2015, 3786–3807 RSC.
- F. García and M. M. Smulders, J. Polym. Sci., Part A: Polym. Chem., 2016, 54, 3551–3577 CrossRef PubMed.
- P. Chakma and D. Konkolewicz, Angew. Chem., Int. Ed., 2019, 58, 9682–9695 CrossRef CAS PubMed.
- C. J. Kloxin, T. F. Scott, B. J. Adzima and C. N. Bowman, Macromolecules, 2010, 43, 2643–2653 CrossRef CAS PubMed.
- W. Zou, J. Dong, Y. Luo, Q. Zhao and T. Xie, Adv. Mater., 2017, 29, 1606100 CrossRef PubMed.
- G. M. Scheutz, J. J. Lessard, M. B. Sims and B. S. Sumerlin, J. Am. Chem. Soc., 2019, 141, 16181–16196 CAS.
- J. M. Winne, L. Leibler and F. E. D. Prez, Polym. Chem., 2019, 10, 6091–6108 RSC.
- M. K. McBride, B. T. Worrell, T. Brown, L. M. Cox, N. Sowan, C. Wang, M. Podgorski, A. M. Martinez and C. N. Bowman, Annu. Rev. Chem. Biomol. Eng., 2019, 10, 175–198 CrossRef CAS PubMed.
- V. Zhang, B. Kang, J. V. Accardo and J. A. Kalow, J. Am. Chem. Soc., 2022, 144, 22358–22377 CrossRef CAS PubMed.
- S. Samanta, S. Kim, T. Saito and A. P. Sokolov, J. Phys. Chem. B, 2021, 125, 9389–9401 CAS.
- M. L. Martins, X. Zhao, Z. Demchuk, J. Luo, G. P. Carden, G. Toleutay and A. P. Sokolov, Macromolecules, 2023, 56, 8688–8696 CAS.
- L. Li, X. Peng, D. Zhu, J. Zhang and P. Xiao, Macromol. Chem. Phys., 2023, 224, 2300224 CAS.
- H. Feng, S. Wang, J. Y. Lim, B. Li, W. Rusli, F. Liu, N. Hadjichristidis, Z. Li and J. Zhu, Angew. Chem., Int. Ed., 2024, 63, e202400955 CAS.
- X. Fan, J. Zheng, J. C. C. Yeo, S. Wang, K. Li, J. K. Muiruri, N. Hadjichristidis and Z. Li, Angew. Chem., Int. Ed., 2024, 63, e202408969 CAS.
- Dynamic Covalent Chemistry, ed. W. Zhang and Y. Jin, Wiley, 2017 Search PubMed.
- P. T. Corbett, J. Leclaire, L. Vial, K. R. West, J. L. Wietor, J. K. Sanders and S. Otto, Chem. Rev., 2006, 3652–3711 CAS.
- T. Jadhav, B. Dhokale, Z. M. Saeed, N. Hadjichristidis and S. Mohamed, ChemSusChem, 2024, 17, e202400356 CAS.
- M. E. Belowich and J. F. Stoddart, Chem. Soc. Rev., 2012, 41, 2003–2024 CAS.
- W. Denissen, G. Rivero, R. Nicolaÿ, L. Leibler, J. M. Winne and F. E. D. Prez, Adv. Funct. Mater., 2015, 25, 2451–2457 CAS.
- P. Haida, G. Signorato and V. Abetz, Polym. Chem., 2022, 13, 946–958 CAS.
- W. Denissen, M. Droesbeke, R. Nicola, L. Leibler, J. M. Winne and F. E. D. Prez, Nat. Commun., 2017, 8, 1–7 Search PubMed.
- P. Haida, V. Abetz, P. Haida and V. Abetz, Macromol. Rapid Commun., 2020, 41, 2000273 CAS.
- N. Hadjichristidis and A. Hirao, Anionic Polymerization: Principles, Practice, Strength, Consequences and Applications, 2015, pp. 1–1082 Search PubMed.
- N. Hadjichristidis, H. Iatrou, S. Pispas and M. Pitsikalis, J. Polym. Sci., Part A: Polym. Chem., 2000, 38, 3211–3234 CrossRef CAS.
- K. Hong, D. Uhrig and J. W. Mays, Curr. Opin. Solid State Mater. Sci., 1999, 4, 531–538 CrossRef CAS.
- N. Hadjichristidis, M. Pitsikalis, S. Pispas and H. Iatrou, Chem. Rev., 2001, 101, 3747–3792 CrossRef CAS PubMed.
- K. Ntetsikas, V. Ladelta, S. Bhaumik and N. Hadjichristidis, ACS Polym. Au, 2023, 3, 158–181 CAS.
- J. Colmenero and A. Arbe, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 87–113 CAS.
- J. Colmenero, J. Polym. Sci., Part B: Polym. Phys., 2019, 57, 1239–1245 CAS.
- G. Polymeropoulos, G. Zapsas, K. Ntetsikas, P. Bilalis, Y. Gnanou and N. Hadjichristidis, Macromolecules, 2017, 50, 1253–1290 CrossRef CAS.
- B. M. Erwin, M. Cloitre, M. Gauthier and D. Vlassopoulos, Soft Matter, 2010, 6, 2825–2833 RSC.
- E. V. Ruymbeke, K. Orfanou, M. Kapinstos, H. Iatrou, M. Pitsikalis, N. Hadjichristidis, D. J. Lohse and D. Vlassopoulos, Macromolecules, 2007, 40, 5941–5952 CrossRef.
- M. A. Gauthier, M. I. Gibson and H. A. Klok, Angew. Chem., Int. Ed., 2009, 48, 48–58 CrossRef CAS PubMed.
- P. Theato and H. A. Klok, Functional Polymers by Post-Polymerization Modification: Concepts, Guidelines, and Applications, Wiley-VCH, 2013 Search PubMed.
- M. Tress, K. Xing, S. Ge, P. Cao, T. Saito and A. Sokolov, Eur. Phys. J. E: Soft Matter Biol. Phys., 2019, 42, 133 CAS.
- S. Bhaumik, K. Ntetsikas, N. Patelis, K. Peponaki, D. Vlassopoulos and N. Hadjichristidis, Macromolecules, 2024, 57, 1751–1760 CrossRef CAS.
- A. Arbe, A. Alegra, J. Colmenero, S. Bhaumik, K. Ntetsikas and N. Hadjichristidis, ACS Macro Lett., 2023, 1595–1601 CAS.
- W. H. Stockmayer, Pure Appl. Chem., 1967, 15, 539–554 Search PubMed.
- A. Alegra, A. Arbe, J. Colmenero, S. Bhaumik, K. Ntetsikas and N. Hadjichristidis, Macromolecules, 2024, 57, 5639–5647 Search PubMed.
- P. M. D. Molina, A. Alegría, J. Allgaier, M. Kruteva, I. Hoffmann, S. Prévost, M. Monkenbusch, D. Richter, A. Arbe and J. Colmenero, Phys. Rev. Lett., 2019, 123, 187802 Search PubMed.
- P. M. D. Molina, A. Alegra, J. Allgaier, M. Kruteva, I. Hoffmann, S. Prévost, M. Monkenbusch, D. Richter, A. Arbe and J. Colmenero, Macromolecules, 2020, 53, 5919–5936 Search PubMed.
- R. Lund, L. Willner, A. Alegría, J. Colmenero and D. Richter, Macromolecules, 2008, 41, 511–514 CAS.
- C. Riedel, A. Alegría, P. Tordjeman and J. Colmenero, Macromolecules, 2009, 42, 8492–8499 CAS.
- C. Riedel, A. Alegría, P. Tordjeman and J. Colmenero, Rheol. Acta, 2010, 49, 507–512 CrossRef CAS.
- K. Ntetsikas, D. Moschovas, G. Zapsas, I. Moutsios, K. Tsitoni, G. M. Manesi, A. F. Nabiullin, N. Hadjichristidis, D. A. Ivanov and A. Avgeropoulos, Polym. Chem., 2021, 12, 2712–2721 RSC.
- D. Chen, H. Shao, W. Yao and B. Huang, Int. J. Polym. Sci., 2013, 937284 Search PubMed.
- P. E. Rouse, J. Chem. Phys., 1953, 21, 1272–1280 CrossRef CAS.
- K. Adachi and T. Kotaka, Prog. Polym. Sci., 1993, 18, 585–622 CrossRef CAS.
- A. Pipertzis, K. Ntetsikas, N. Hadjichristidis and G. Floudas, Macromolecules, 2022, 55, 10491–10501 CrossRef CAS.
- D. Boese and F. Kremer, Macromolecules, 1990, 23, 829–835 CrossRef CAS.
- Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schönhals, Springer-Verlag Berlin Heidelberg, 2003 Search PubMed.
- S. Arrese-Igor, A. Alegra and J. Colmenero, Phys. Rev. Lett., 2014, 113, 078302 CrossRef CAS PubMed.
- S. Arrese-Igor, A. Alegra and J. Colmenero, ACS Macro Lett., 2014, 3, 1215–1219 CrossRef CAS PubMed.
- T. Gambino, A. M. D. Ilarduya, A. Alegra and F. Barroso-Bujans, Macromolecules, 2016, 49, 1060–1069 CrossRef CAS.
- J. Ochs, D. E. Martnez-Tong, A. Alegria and F. Barroso-Bujans, Macromolecules, 2019, 52, 2083–2092 CrossRef CAS.
- H. Yosbida, H. Watanabe, K. Adachi and T. Kotaka, Macromolecules, 1991, 24, 2981–2985 CrossRef.
- S. Havriliak and S. Negami, J. Polym. Sci., Part C, 1966, 14, 99–117 CrossRef.
- S. Havriliak and S. Negami, Polymer, 1967, 8, 161–210 CrossRef CAS.
- C. J. F. Böttcher and P. Bordewijk, Theory of Electric Polarization, Vol. 2: Dielectrics in Time-Dependent Fields, Elsevier, 1973 Search PubMed.
- R. Diaz-Calleja, Macromolecules, 2000, 33, 8924 CrossRef CAS.
- G. Floudas, S. Paraskeva, N. Hadjichristidis, G. Fytas, B. Chu and A. N. Semenov, J. Chem. Phys., 1997, 107, 5502–5509 Search PubMed.
- C. Lorthioir, A. Alegra, J. Colmenero and B. Deloche, Macromolecules, 2004, 37, 7808–7817 CrossRef CAS.
- L. D. Valle-Carrandi, A. Alegra, A. Arbe and J. Colmenero, Macromolecules, 2012, 45, 491–502 Search PubMed.
- A. Alegra, R. Lund, F. Barroso-Bujans, A. Arbe and J. Colmenero, Colloid Polym. Sci., 2014, 292, 1863–1876 Search PubMed.
- S. A. Kim, R. Mangal and L. A. Archer, Macromolecules, 2015, 48, 6280–6293 Search PubMed.
- N. Neubauer, R. Winkler, M. Tress, P. Uhlmann, M. Reiche, W. K. Kipnusu and F. Kremer, Soft Matter, 2015, 11, 3062–3066 CAS.
- C. J. F. Böttcher, Theory of Electric Polarization, Vol. 1: Dielectrics in Static Fields, Elsevier, 1973 Search PubMed.
- R. Johnson, NIST 101. Computational Chemistry Comparison and Benchmark Database [online], 2022, https://cccbdb.nist.gov, Release 22, May 2022. Accessed September 2024 Search PubMed.
- D. Boese, F. Kremer and L. J. Fetters, Polymer, 1990, 31, 1831–1837 CAS.
- P. Kardasis, A. Oikonomopoulos, G. Sakellariou, M. Steinhart and G. Floudas, Macromolecules, 2021, 54, 11392–11403 CAS.
- D. Boese, F. Kremer and L. J. Fetters, Macromolecules, 1990, 23, 1826–1830 CAS.
- D. Vlassopoulos, G. Fytas, B. Loppinet, F. Isel, P. Lutz and H. Benoit, Macromolecules, 2000, 33, 5960–5969 CAS.
- R. G. Ricarte, F. Tournilhac, M. Cloitre and L. Leibler, Macromolecules, 2020, 53, 1852–1866 CAS.
- A. Alegría, A. Arbe, J. Colmenero, N. Patelis, S. Bhaumik, M. Zhou and N. Hadjichristidis, Macromolecules, 2025 DOI:10.1021/acs.macromol.4c03035.
- L. J. Fetters, D. J. Lohse, D. Richter, T. A. Witten and A. Zirkel, Macromolecules, 1994, 27, 4639–4647 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details on materials, instrumentation, synthetic methods, and dielectric characterization of linear PI and static PI stars. See DOI: https://doi.org/10.1039/d5sm00091b |
| This journal is © The Royal Society of Chemistry 2025 |