Open Access Article
Open Access ArticleTargeted modifications in ionic liquids – from understanding to design†
Frederik
Philippi
 and
Tom
Welton
and
Tom
Welton
 *
*
Department of Chemistry, Molecular Sciences Research Hub, Imperial College London, White City Campus, London W12 0BZ, UK. E-mail: t.welton@ic.ac.uk
First published on 12th March 2021
Abstract
Ionic liquids are extremely versatile and continue to find new applications in academia as well as industry. This versatility is rooted in the manifold of possible ion types, ion combinations, and ion variations. However, to fully exploit this versatility, it is imperative to understand how the properties of ionic liquids arise from their constituents. In this work, we discuss targeted modifications as a powerful tool to provide understanding and to enable design. A ‘targeted modification’ is a deliberate change in the structure of an ionic liquid. This includes chemical changes in an experiment as well as changes to the parameterisation in a computer simulation. In any case, such a change must be purposeful to isolate what is of interest, studying, as far as is possible, only one concept at a time. The concepts can then be used as design elements. However, it is often found that several design elements interact with each other – sometimes synergistically, and other times antagonistically. Targeted modifications are a systematic way of navigating these overlaps. We hope this paper shows that understanding ionic liquids requires experimentalists and theoreticians to join forces and provides a tool to tackle the difficult transition from understanding to design.
Introduction
Ionic liquids are liquid salts. The term usually implies a low melting point, often around or below room temperature. They are now well established as a separate class of solvents, distinctively different from conventional molecular solvents.1–5 Ionic liquids have reached virtually every area of science and technology where solvents are required – from large scale industrial processes6–8 and battery electrolytes9–13 to pharmaceuticals,14–16 from metal deposition17,18 to protein crystallisation.19–21One reason for this wide spread is the sheer number of possible ionic liquids.6,22 Every ionic liquid has at least two constituents, cation and anion, which can be chosen independently. Different types of ions and variations thereof allow for near limitless fine tuning of properties. For example, the choice of a cation involves the choice of a type such as imidazolium, phosphonium or guanidinium. Each of these cation types itself can be modified by changing side chain lengths, substitution patterns, functional groups, etc. The properties of the resulting ionic liquids are diverse and can thus be tailored to a given application.
Michael Freemantle recognised the potential of ionic liquids to serve as what he called ‘designer solvents’ in a visionary article in 1998.23 The term ‘designer solvents’ captures the high expectations of the community that ionic liquids can be optimised and adapted to meet the practical requirements of many diverse applications.24–32 In this context, ionic liquids are also referred to as ‘neoteric solvents’. Neoteric solvents such as ionic liquids or supercritical CO2 are those that emerged at the end of the 20th century, with the prospect to solve the challenges of the 21st.33–36 In some cases, functional groups can be covalently attached to an ionic liquid. Such ‘task specific ionic liquids’ actively participate on a molecular level rather than just providing a supporting solvent, for example by coordinating a metal or by providing an active site for a reaction.37–42
To fulfil all these ambitious expectations, we require a thorough understanding of how the properties of an ionic liquid arise from its molecular structure. This is the basic idea behind the search for structure–property relationships: ionic liquids with systematic structural variations are characterised (experimentally and/or theoretically), and the observed changes are then rationalised using chemical concepts.43–49 However, few properties are shared by most ionic liquids, such as a negligible vapour pressure or good thermal and chemical stability.24,50 At the same time, some ionic liquids have undesirable properties, such as high viscosity or low biodegradability.22,51–54 Practical implementations of ionic liquids must aim to exploit the advantages and overcome the issues.
A thorough understanding of structure–property relationships paves the way for the design of new derivates and ionic liquids without having to rely on trial and error. However, in the real world, structure–property relationships are rarely independent of each other. An example is the relationship between side chain length (structure) and melting points (property) in 1-alkyl-3-methylimidazolium ionic liquids, Fig. 1.55,56 Increasing the length of the alkyl side chains reduces Coulombic interactions and introduces configurational entropy, thus decreasing the melting points.56 At the same time, longer alkyl side chains lead to increased van der Waals interactions, eventually leading to an increase in melting point and the formation of a wax. Thus, ionic liquids are always a compromise, a sweet spot between high melting ‘conventional’ salt and highly viscous oil or wax.
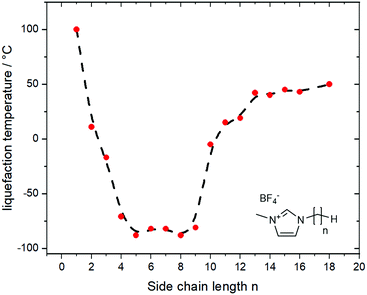 | ||
| Fig. 1 The thermal transitions for imidazolium ionic liquids show an irregular behaviour with increasing length of the side chain. Data from ref. 56, the dashed line is a guide for the eye. | ||
It is important that experimental and theoretical studies consider the dependencies between underlying concepts if they are to be used as design elements. To this end, it is advantageous to choose the objects of study in a way that isolates one underlying concept. We will use the term ‘targeted modification’ for this approach. An example of a targeted modification would be the replacement of an element with a heavier isotope to isolate the influence of mass on molecular properties. Naturally, targeted modifications have some degree of ambiguity, since they depend on the researcher to choose an appropriate underlying concept. The length of a side chain has often been used as a key variable for ionic liquids and could be regarded as such a choice. However, volume, shape, mass and flexibility all depend on the length of the side chain. One needs to be aware of the multiple dependencies where it is not possible to eliminate these. Theoretical methods such as classical MD simulations are at an advantage, since they allow for targeted modifications beyond what is experimentally feasible, such as changing the mass of any atom or molecule without changing other interactions.
In this work, ‘targeted’ is not intended to suggest the pursuit of specific applications, since such an application driven interpretation is already encompassed in the concept of task specific ionic liquids. Due to the diversity of ionic liquids and their potential applications, the fine tuning of properties for these must be done on a case-by-case basis. The reader interested in (industrial) applications is referred to the literature, including a recently published book.6,14,38,57–60 Instead, we focus on a general methodology to enable purposeful design, using properties of general importance such as viscosity or thermal transitions as our examples.
Many studies intuitively use (targeted) modifications to understand existing and design new ionic liquids. In this work, we present important concepts which guide the design of ionic liquids and demonstrate how targeted modifications have been used successfully to further our understanding of this design process. In addition, we identify gaps in the literature and discuss the limits of targeted modifications. Naturally, we cannot cover the whole body of literature on ionic liquids, thus our selection is representative, not exhaustive. Where bulk dynamics are relevant, we will use viscosity or diffusion coefficients vicariously for other transport properties, focusing on room temperature behaviour.
Electrostatics and coulombic compaction
The common denominator shared by all ionic liquids is the inevitable dominance of Coulombic interactions.61 The electrostatic forces obey Coulomb's inverse-square law and are thus of considerably longer range than, e.g., dispersion interactions, whose dependency is 1/R6.62 Since the charge carriers in ionic liquids are mobile, charge neutrality is fulfilled even at a relatively short distances. The charge of an ion in the bulk ionic liquid is largely screened within a few nanometres,63–65 but the exact nature and range of electrostatic screening in ionic liquids is still a subject of current investigation.66–73Two major effects of the charged nature of ionic liquids can be identified. First, the bulk ionic liquid experiences a compaction as a direct consequence of the strong electrostatic forces.74,75 This compaction is equivalent to an increase of pressure or a decrease in molar volume, and is thus expected to dampen the dynamics within the ionic liquid. It is indeed well known that viscosity increases with pressure for most liquids.76–78 This problem is related to the broader concept of density scaling, that is, the dynamics of glass forming liquids scale not only with temperature T, but also with density ρ.79–82 Thus, transport properties such as viscosity, electrical conductivity, or self-diffusion scale with ργ/T, an approach that has been found to work well for ionic liquids.83–86 The parameter γ is specific for a given material; however different transport properties for the same material often reveal a common scaling parameter γ.84,85,87
Apart from the compaction, the second mechanism by which electrostatic forces influence the properties of ionic liquids is the requirement of charge neutrality. In terms of static properties, this leads to the formation of the shell structure found in ionic liquids, confining ions to an ion cage formed of oppositely charged ions.63,88–90 In terms of dynamic properties, the charge neutrality condition in combination with momentum conservation give rise to correlated dynamics.91 In other words: the net movement of one ion in a given direction must eventually be compensated for by the net movement of a like-charge ion in the opposite direction or the net movement of an oppositely charged ion in the same direction, or a combination of both.
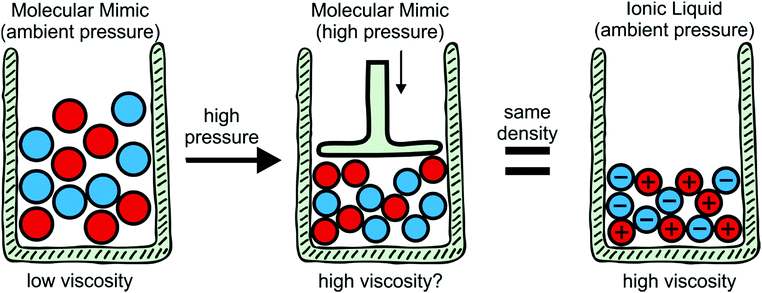
To explore the influence of electrostatics, ionic liquids can be compared to neutral analogues, for which we will use the term ‘molecular mimics’ coined by Niemann et al.92 The concept is illustrated in Fig. 2 and 3. The ions in an ionic liquid are replaced with neutral, (valence) isoelectronic analogues. For example, the central nitrogen atom in the bis(trifluoromethanesulfonyl)imide anion shown in Fig. 3a could be replaced with oxygen, leading to triflic anhydride as a possible molecular mimic. Similarly, replacement of the central nitrogen atom in an ammonium ionic liquid with carbon or silicon leads to synthetically accessible molecular mimics (Fig. 3c).
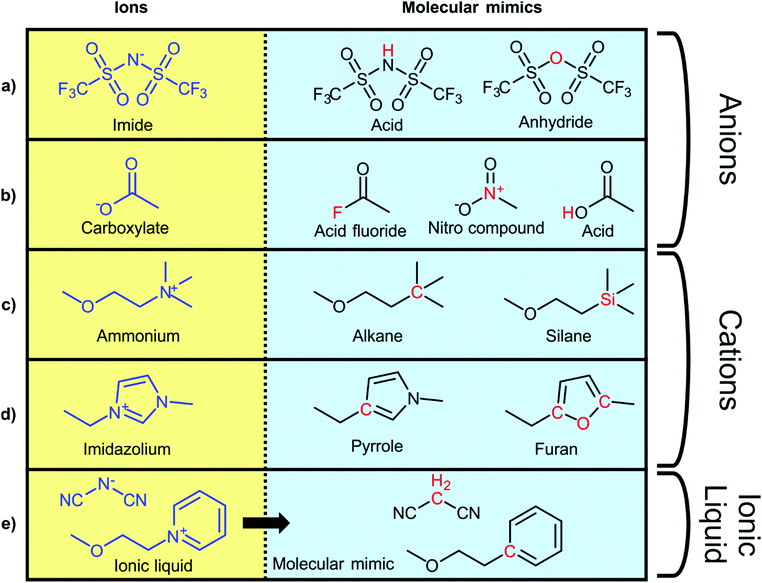 | ||
| Fig. 3 Typical ionic liquid ions (left) and their targeted modifications to yield molecular mimics (right). | ||
However, the motifs required to stabilise the negative charge in an anion – such as fluorination and delocalisation – also render their molecular mimics highly reactive. Similar problems arise with some molecular mimics of cations, such as the examples shown for imidazolium in Fig. 3d. Preliminary experiments in our group showed that in many cases, the two components of the molecular mimic of an ionic liquid do not mix (such as triflic anhydride with butylbenzene or methyltripentyl silane) or react immediately (such as triflic anhydride with 2,5-dimethylfuran or N-butylpyrrole). It is thus not always feasible to use a binary molecular mimic for an ionic liquid, in which case it is still possible to resort to theoretical methods such as molecular dynamics simulations.93
In some cases, the addition of a molecular mimic for one of either the cation or anion will suffice to answer a specific scientific question. For example, Niemann et al. have used 2-phenylethanol as the molecular mimic of N-(2-hydroxyethyl)pyridinium to investigate competition between hydrogen bonding and electrostatic interactions in an ionic liquid.92 The anion in this work was tetrafluoroborate, whose obvious molecular mimics are gaseous at ambient conditions (tetrafluoromethane or silicon tetrafluoride). In a similar approach, Zaitsau et al. used amines as molecular mimics of ammonium ionic liquids to quantify the contributions of Coulomb interactions, hydrogen bonding, and dispersion interactions to the overall interaction energy in the bulk ionic liquid.94
Despite the difficulties, the concept of binary molecular mimics has been applied successfully by Shirota and Castner.75 The ionic liquid and the corresponding binary molecular mimic used in their work are shown in Fig. 3e. By means of optical Kerr effect spectroscopy, Shirota and Castner obtained lifetimes for reorientational relaxation. They observed that the ratio of the longest lifetimes matched the predicted ratio from the Stokes–Einstein–Debye theory well, thus corroborating a hydrodynamic interpretation of reorientational relaxation in ionic liquids.75
The specific volume of the ionic liquid in Fig. 3e is reduced by approximately 16% compared to its binary molecular mimic, at the same time the viscosity is higher by a factor of 29 for the ionic liquid.75 The question arises as to what degree compaction contributes to this increase in viscosity. This would require the measurement of transport properties in a binary molecular mimic at a pressure which leads to the same molar volume as the corresponding ionic liquid, Fig. 2. To the best of our knowledge, such a study has not yet been published. Using ethanol as an example liquid, reducing the specific volume by 16% requires pressures of approximately 4 kbar.95 Viscosities can be measured at significantly higher pressures,76 thus the proposed approach appears to be feasible and will be pursued in future work.
Size and mass of ions
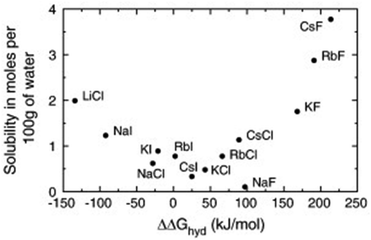
Not only the absolute values of size and mass have to be considered for ionic liquids, but also their relation. The concept is best illustrated using the simple alkali halides as examples. Fig. 4 shows the solubility of different alkali halides in water in relation to the free enthalpy of hydration of the ions.96 Salts composed of ions of similar size are poorly soluble and tend to associate in solution, whereas those of different size tend to dissolve well.96,97 The explanation of this general trend is not straightforward even for alkali metal halides and involves an interplay of electrostatics, entropic contributions and dispersion forces.96–98It is challenging to separate the pure geometrical influence of size, since a change in size is coupled to changes in mass, dispersion interactions, functionalisation, etc. In general, larger ions reduce electrostatic interactions and introduce entropy into the melt, thus lowering the melting points of ionic liquids.99 There are several approaches based on ion volumes that can be used to provide an educated guess as to whether a given ion combination will form an ionic liquid (at room temperature) or not.99,100 Some cations, like phosphonium or ammonium, are benign in the regard that their size can be modified via the side chain length without changing the character of the ion significantly. However, especially for anions, small changes in the structure can lead to significant changes in specific interactions. For example, qualitative differences in hydrogen bonding and π–π stacking (of the cation) were reported for the analogous series [SCN]−, [N(CN)2]−, and [B(CN)4]−, all paired with [C2C1im]+.101
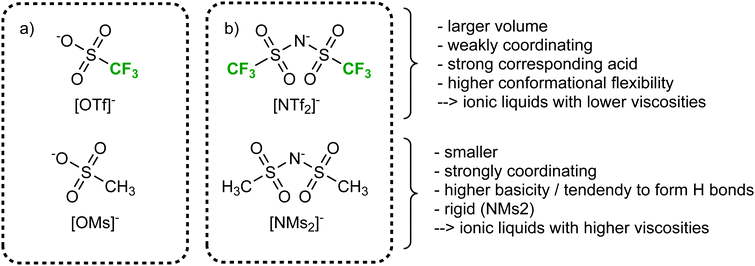
More so than size, the absolute mass can be modified experimentally by using isotopologues. Barthen et al. used this concept to isolate the impact of ion mass on ionic liquids’ viscosities.102 To this end, they determined the change in viscosity for partial deuteration of 4 different ionic liquids, Fig. 5. A clear trend is visible despite the very small changes in mass. However, it must be kept in mind that the influence of mass on transport properties is often obscured by other effects. For example, the viscosity of [C2C1im][NTf2] (1-ethyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide, 34 mPa s)103 is considerably lower than that of [C2C1im][NMs2] (1-ethyl-3-methylimidazolium bis(methanesulfonyl)imide, 787 mPa s),103 despite the mass of the [NTf2]− ionic liquid being higher by 38%. The weakly coordinating properties of the fully fluorinated anion are in this case more important than size and mass.103,104 Due to the greater basicity, [NMs2]− is a better hydrogen bond acceptor, thus forming stronger hydrogen bonds with the cation. In addition, the [NTf2]− anion has a much higher intrinsic flexibility than [NMs2]−,105 an effect that will be discussed in the next section.
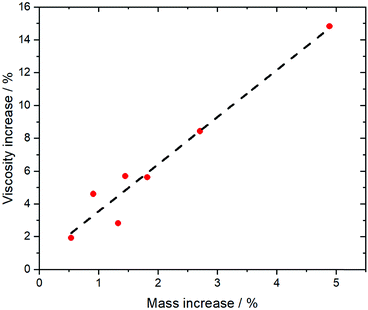 | ||
| Fig. 5 The comparison of isotopologues with different mass reveals a correlation between viscosity and mass for a variety of different ionic liquids. Experimental data points from ref. 102, the dashed line is a linear fit. | ||
A larger change in mass can be achieved with heavier analogues, i.e. by comparing valence isoelectronic cations or anions. However, a problem with this approach is that the change in mass is not isolated from other factors. A good example is the study of [C4C1im][XF6] ionic liquids with X = P, As or Sb by Shirota et al.106 The authors observed that the viscosity decreased from 290 mPa s for [C4C1im][PF6] to 134 mPa s for [C4C1im][SbF6]. They attributed this decrease – despite the higher mass – to the larger volume of the anions. Another factor that might have contributed to the higher fluidity of the heavy analogues is the higher polarisability of the anions,107 which we will discuss in the section ‘polarisability, ‘dipole moments’ and charge asymmetry’.
Notwithstanding the experimental difficulties, the influences of size and mass can be investigated in isolation with the help of simulations. To name an example related to the previous paragraph, the mass of the [PF6]− anion can be increased artificially in a simulation without changing any other parameter. In doing so, it was observed that the diffusion of [PF6]− in [C2C1im][PF6] decreased as expected, apart from a small initial increase for a very small mass change.108 The diffusion coefficient of the anion decreased by only 40% for a 20-fold increase in mass, which corresponds to an artificial molecular weight of the anion of 2900 Da.108 It is immediately evident why such a small response to the mass of the anion is outweighed by other factors such as size, given that [SbF6]− is only 1.6 times heavier than [PF6]−. Similarly, Butler and Müller-Plathe used MD simulations of [C4C1im][PF6] in which they artificially changed the ion volumes to demonstrate a clear relation between low viscosities and large volumes of both cation and anion.109
We will now focus on a selection of theoretical studies that use molecular dynamics simulations to investigate the influence of size (and mass) disparity. Spohr et al. compared simulations of charged and uncharged Lennard Jones fluids with two particle types of different size.110 They observed that viscosity decreases (and diffusion increases) with greater difference in size, keeping other parameters constant, Fig. 6.110,111 This effect was much more pronounced for the ionic liquid compared to the uncharged Lennard Jones fluid. The implications for ionic liquids are clear. Increased dynamics can be expected if ions of different size are used, but the effect will wear off eventually when another phenomenon such as dispersion interactions between long side chains begins to dominate the dynamics.
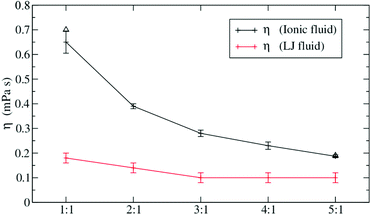 | ||
| Fig. 6 Size differences can fluidize ionic liquids. The effect is less pronounced for the (uncharged) Lennard-Jones fluid. Reprinted from ref. 110, with the permission of AIP Publishing. | ||
Structural effects are also evident in simulations of ionic liquids with significant size differences. A study of a binary Yukawa‡ ionic fluid with a size ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of the two constituents showed that the larger particles crystallised upon cooling during the simulation.112 Below this ‘freezing point’, the smaller particles remained mobile, showing regular diffusion at higher temperature and a hopping mechanism at lower temperature.112 Such curious phase behaviours find application in solid state materials, such as ionic organic plastic crystals.113–115 Although Spohr et al. did not encounter such a crystallisation of the larger particles during their simulation, they observed that the liquid structure is dominated by the larger particles.110 The combined effects of size and charge displacements will be discussed in the section ‘polarisability, ‘Dipole moments’ and charge asymmetry’.
1 of the two constituents showed that the larger particles crystallised upon cooling during the simulation.112 Below this ‘freezing point’, the smaller particles remained mobile, showing regular diffusion at higher temperature and a hopping mechanism at lower temperature.112 Such curious phase behaviours find application in solid state materials, such as ionic organic plastic crystals.113–115 Although Spohr et al. did not encounter such a crystallisation of the larger particles during their simulation, they observed that the liquid structure is dominated by the larger particles.110 The combined effects of size and charge displacements will be discussed in the section ‘polarisability, ‘Dipole moments’ and charge asymmetry’.
Ionic liquids are strongly correlated systems, and these (cross) correlations are further complicated by dependencies on size and mass. Non-negligible cross correlations are widely accepted as the reason for deviations from the Nernst–Einstein relation in ionic liquids, assuming integer charges on ions.91,116,117 However, different – and not necessarily mutually exclusive – interpretations of these deviations exist, such as ion aggregation or the presence of dynamical heterogeneities.110,118–123 In terms of the time evolution of the velocity correlation functions, both effects of relative mass and relative size have been found to be important, even for neutral binary liquids.124,125 Lighter and smaller particles show pronounced backscattering, an effect which is also caused by the shell structure in ionic liquids, with ions rattling in a cage of counterions.88,126
With the design of ionic liquids in mind, it would be interesting to investigate the magnitude of cross contributions for systems similar to the ones of Butler and Müller-Plathe109 as well as Spohr et al.110 A central issue with the interpretation of distinct diffusion coefficients is their reference frame dependence, which can be avoided by using quantities such as the relative mean molecular velocity cross correlation coefficients that do not show a reference frame dependence.126–129 Finally, technical details such as ion size dependency123 or slow convergence of the cross contributions125 need to be included in any investigation of these effects.
Conformations and conformational flexibility
The vast majority of ionic liquids are composed of ions that can exist in different conformations. Flexible groups such as (alkyl) side chains in cations are ubiquitous design elements used to lower melting points and accelerate the dynamics in ionic liquids.31,74,99,130–133 However, side chains of different length are of limited use to probe the influence of conformational equilibria due to the competing effects of size and mass as well as dispersion interactions. We will thus focus on isostructural analogues which differ markedly in their conformational properties, but not in their size. We will first present examples involving cations (Fig. 7), followed by those involving anions (Fig. 10).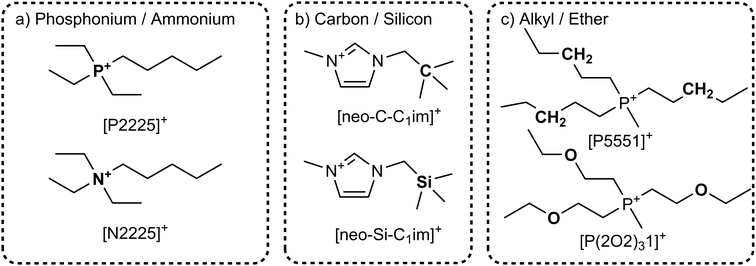 | ||
| Fig. 7 Isostructural cation analogues serve as a targeted modification to probe the effects of conformation and conformational flexibility. All ionic liquids have [NTf2]− as anion.138,140,143 | ||
Phosphonium and ammonium ionic liquids offer this similarity, with a wide variety of ionic liquid precursors and even ionic liquids readily available to the synthetic chemist. Phosphonium ionic liquids are in general less viscous than their ammonium counterparts, which is one of the many advantages that have drawn attention to the class of phosphonium ionic liquids.134–137Fig. 7a shows typical examples of ionic liquids based on triethylphosphine and triethylamine.138 For the five pairs of phosphonium/ammonium functionalised ionic liquids, the ammonium ionic liquids are more viscous by a factor of 1.7 to 2.0.138 The higher conformational flexibility of phosphonium ionic liquids has been identified as the root cause for this difference between phosphonium and ammonium ionic liquids.139–141 Of central importance appears to be the C–P–C–C (C–N–C–C) dihedral angle corresponding to rotation around the P–C (N–C) bonds. The ab initio energy barrier for this rotation is found to be approximately 10 kJ mol−1 higher for ammonium ions compared to phosphonium ions.139,140
In addition to the higher conformational flexibility of the phosphonium cations, it has also been reported that the positive charge is more localised on the phosphonium centre.139,142 Scarbath-Evers et al. used molecular dynamics simulations to differentiate between these effects and observed that the localised charge in phosphonium ionic liquids acts in the opposite direction to the higher conformational flexibility, decreasing the dynamics.139 Thus, given the current state of knowledge, conformational flexibility is the dominant cause for the improved dynamics of phosphonium based ionic liquids compared with ammonium based ionic liquids.
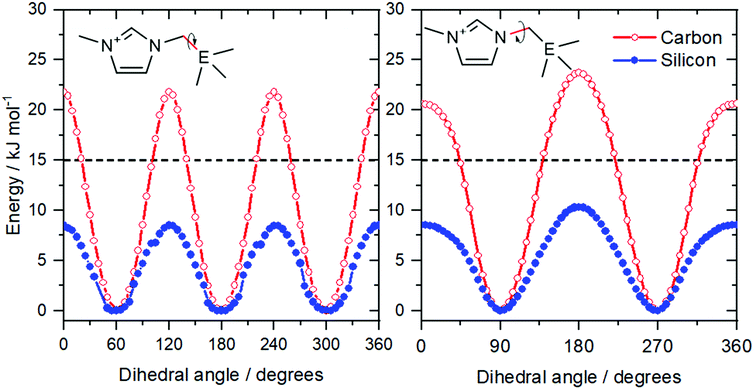
Shirota and Castner applied the concept of isostructural analogues to the side chain of imidazolium ionic liquids, Fig. 7b.143 This approach is very similar to the comparison of phosphonium and ammonium ionic liquids; the quaternary carbon is replaced by the heavier silicon. The resemblance to the case of phosphonium vs. ammonium is striking: the viscosities were 98 mPa s for [neo-Si-C1im][NTf2] and 161 mPa s for [neo-C-C1im][NTf2], i.e. the viscosity of the lighter analogue is higher by a factor of 1.6.143 Again, this effect is attributed to the higher conformational flexibility of silicon compounds.74,144
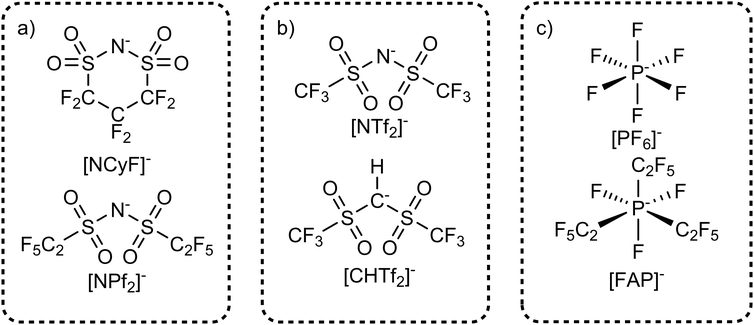
The higher flexibility of the silicon analogues can be shown with a straightforward calculation of the potential energy as a function of the dihedral angles defining the ion geometry, see Fig. 8 and ESI.† The barriers for rotation around the N–C and C–E bonds are higher for the lighter element. The energy difference between barrier heights is approximately 10 kJ mol−1, in line with the observations for phosphonium vs. ammonium. Furthermore, the barriers for the two analogues are well separated by the 15 kJ mol−1 line, which we have introduced to identify rigid (barrier above the threshold) and flexible (barrier below the threshold) ions.105,140
Ether groups are well-known as a design element to improve the properties of ionic liquids, in particular to achieve lower viscosities.145–147 Taking the example in Fig. 7c, the viscosity of the purely alkyl functionalised ionic liquid [P5551][NTf2] is a factor of 6 higher than the viscosity of the ether functionalised ionic liquid [P(2O2)31][NTf2].140 A number of thorough studies can be found that report similar effects for a variety of other cation structures such as ammonium (including cyclic), pyridinium, and imidazolium cations.147–150
Similar to phosphonium or silicon functionalisation, ether groups are another structural motif whose beneficial properties are often attributed to their high conformational flexibility.151–154 However, for ether groups, this is only one side of the coin. Equally important to the conformational flexibility is the preferred conformer geometry. Several groups have reported evidence that ether side chains tend to coil up towards the positively charged part of a cation, Fig. 9.140,155–158 Similarly, for imidazolium ionic liquids, ether groups in a (sufficiently long) side chain tend to coordinate to hydrogen atoms of the imidazolium ring, with both intra- and intermolecular interactions observed.159,160 The presence of these two overlapping phenomena, i.e. changes in both flexibility and geometry, lead to the rich diversity of ether functionalised ionic liquids, but also to a somewhat irregular behaviour.
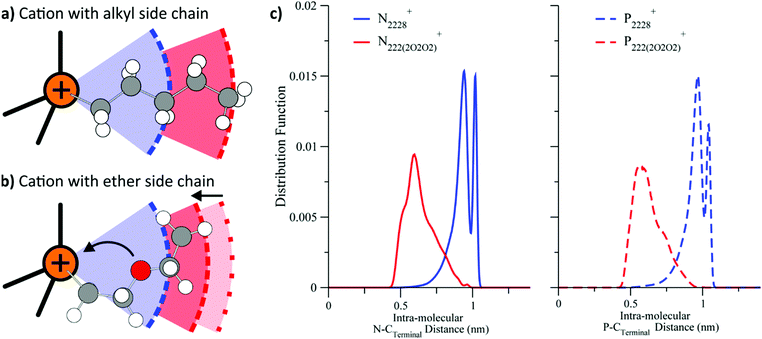 | ||
| Fig. 9 Cations with alkyl side chains (a) prefer a linear conformation, whereas those with ether side chains (b) coil.140 (c) For both ammonium and phosphonium ionic liquids, the distance between terminal carbon and quaternary centre is reduced considerably when ether groups are introduced in the side chain.156 (a) and (b) adapted from ref. 140 – Published by the PCCP Owner Societies. (c) Reprinted with permission from ref. 156. Copyright 2013 American Chemical Society. | ||
The concept of conformational flexibility is equally important for anions, the best example being [NTf2]−, introduced as an anion for ionic liquids by Pierre Bonhôte in 1996.161 The [NTf2]− anion can exist in two different conformations, cis and trans.162 These two conformers are close in energy (difference ≈kT at 25 °C), and separated by a small barrier (≈2kT at 25 °C).162 The conformational equilibrium in [NTf2]− and its relation to macroscopic properties is well documented by both theoretical105,163,164 and experimental165–172 approaches.
The interconversion between the cis and trans conformers can be prevented experimentally by formally connecting the trifluoromethyl end groups to form a cyclic anion such as [NCyF]−, Fig. 10a. The [NCyF]− anion is an analogue of [NTf2]− which is effectively locked into a cis conformation, thus lacking the flexibility of [NTf2]−. Some internal structural freedom – comparable to cyclohexane – can be expected, however reorganisation of one end group relative to the other is naturally not possible. The effect of this increased rigidity is evident in the physical properties of ionic liquids containing this anion. A viscosity of 174 mPa s has been reported for [C4C1im][NCyF], whereas the viscosity of [C4C1im][NTf2] is only 48 mPa s.173 The higher viscosity of [C4C1im][NCyF] is not caused by its higher mass compared to [C4C1im][NTf2], which becomes clear when comparing [C4C1im][NCyF] with the heavier [C4C1im][NPf2] (NPf2 = N(SO2C2F5)2, also known as BETI). The viscosity of [C4C1im][NPf2] is 104 mPa s, significantly lower than that of [C4C1im][NCyF]. The impact of the rigidity of the cyclic anion on macroscopic transport has also been shown for [C2C1pyrr][NCyF], specifically for the ionic conductivity.174 Compared to [C2C1pyrr][NPf2], [C2C1pyrr][NCyF] is more conductive by a factor of 83.174
 | ||
| Fig. 10 Targeted modifications which influence the conformational flexibility via (a) ring closure, (b) degrees of freedom for hybridization, (c) introducing flexible groups. | ||
A disadvantage of using cyclic analogues is that only the ‘cis-like’ conformer is present; thus the observed effects might also be a characteristic of said conformer. For example, it is well known that the ‘dipole moment’§ of cis-[NTf2]− is higher than that of trans-[NTf2]−.175,176 Studies using cyclic analogues are a valuable and needed addition to those with the common [NTf2]− anion and bear the potential to reveal both the influence of conformational flexibility and the characteristic effects of a particular conformer – provided that a separation of those contributions can be made. Future studies might also include the five- and even the four-membered ring, both of which are stable anions that are yet to be used in ionic liquids.177,178
The conformational flexibility of [NTf2]− is sensitive to seemingly small changes in its structure. The electronic structure of [NTf2]− allows for rehybridisation involving the central nitrogen atom (imide group), which leads to the high geometrical flexibility of this ion.105 Thus, the flexibility is lost when the central nitrogen atom (imide) is replaced with a methanide group, Fig. 10b. The effect is clearly seen in the potential energy surface, Fig. 11, and can be used to experimentally demonstrate the difference between rigid and flexible anions.105 The [NTf2]− anion, Fig. 11a, has a flat potential energy surface where cis and trans can easily interconvert to each other. The dashed line drawn at 15 kJ mol−1 encompasses minima and paths connecting these minima in a continuous basin. In contrast, the potential energy surface of the [CHTf2]− anion in Fig. 11b shows minima for cis and trans which are separated by large barriers (compared to the thermal energy). However, both conformers – cis and trans – are still present, which is a clear difference over the use of cyclic analogues.
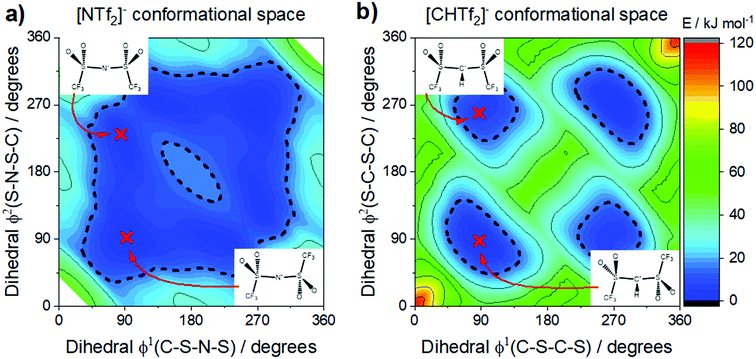 | ||
| Fig. 11 The [NTf2]− anion (a) is extremely flexible, easily changing between cis and trans conformers. In contrast, replacing the imide nitrogen with a methanide group leads to the rigid [CHTf2]− anion (b), which experiences a high barrier for cis–trans interconversion. (a) and (b) adapted from ref. 140 – Published by the PCCP Owner Societies. | ||
The structural variation between [NTf2]− and [CHTf2]− is minimal, the degree of fluorination is the same, and the change in mass and size is negligible. Thus, changes in the macroscopic properties can be rationalised with the higher conformational flexibility of [NTf2]− compared to the rigid analogue, [CHTf2]−. The impact on the viscosities of the respective ionic liquids with the [P5551]+ cation is shown in Fig. 12a.140 At room temperature, the viscosity of the ionic liquid with the rigid [CHTf2]− anion is almost twice as high as the viscosity of [P5551][NTf2], similar to the relative viscosities of [C4C1im][NCyF] and [C4C1im][NTf2]. The effect is also observed for other anions of similar structure, for example comparing the ionic liquid [C4C1im][NMsTFA] (rigid anion, viscosity 292 mPa s) to [C4C1im][NTfAc] (flexible anion, viscosity 149 mPa s),105 it is thus not limited to the methanide motif.
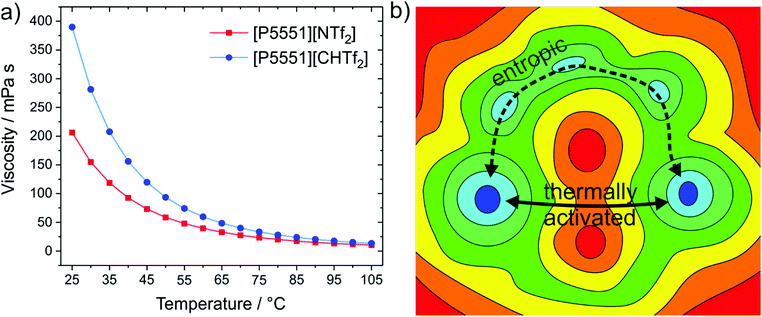 | ||
| Fig. 12 (a) The ionic liquid with the more rigid anion, [P5551][CHTf2], has an almost twofold viscosity at room temperature compared to the ionic liquid with flexible anion, [P5551][NTf2].140 (b) The viscosity difference decreases with increasing temperature, which can be explained with basin theory, as more and more pathways become thermally activated.180,378 | ||
The influence of conformational flexibility decreases with increasing temperature, which is an important observation. The factor by which [P5551][CHTf2] is more viscous than [P5551][NTf2] decreases from 1.9 (at 25 °C) to 1.3 (at 100 °C).140 The higher the temperature, the more thermal energy is available to enable more and more mechanisms of structural relaxation.179,180 Basin theory provides the framework for this rationalisation of viscous flow using the intuitive concept of the potential energy landscape.179–182 The potential energy surface is the potential energy as a function of the degrees of freedom of the system. It is thus a rugged high-dimensional surface. Viscous flow, i.e. structural relaxation, requires the bulk system to pass from one preferred structure to another. The possible preferred structures are connected by different paths involving barriers of different height, see the ‘thermally activated’ process in Fig. 12b. Higher temperatures allow the system to explore a greater proportion (of the high energy region) of the potential energy surface. At lower temperatures, other pathways might still be feasible, see the ‘entropic’ process in Fig. 12b. Thus, conformational flexibility can be seen as a ‘last resort’ to enable viscous flow of a glass-forming ionic liquid at low temperatures before the systems becomes non-ergodic, and is an important consideration for applications around room temperature.171,183
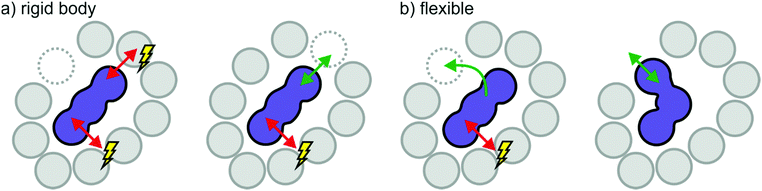
Effects of size, shape, and flexibility are necessarily connected. A large, rigid ion needs a sufficiently large gap to pass through when moving through the cage of counterions in the bulk. Depending on the shape of the ion, a relatively small gap can be passed through if the orientation is right. Thus, it is easier for a prolate (rugby ball-shaped) ion to move along its axis, Fig. 13a, whereas movement perpendicular to this axis exposes a larger surface area and thus provides more resistance. Hole theory considers the static size of ions in relation to the probability to find a sufficiently large hole, thus offering quantitative prediction of dynamic properties.184–186 On the other hand, a flexible ion with the same size and shape can sample its surroundings and dynamically adapt to available gaps, Fig. 13b. This molecular level reasoning is the basis for the ‘slithering’ mechanism of diffusion of [NTf2]− like anions.163,165,166 The entropic process in Fig. 12b thus corresponds to the flexible ion in Fig. 13. When [CHTf2]− is used instead of [NTf2]−, the potential energy surface will be qualitatively similar, but the barriers are much higher – thus the previously entropic processes involving conformational changes become thermally activated.
Naturally, experimental approaches are limited by synthetic accessibility, while theoretical methods can and should be used to fill the gaps. An elegant and straightforward way to investigate the influence of conformational flexibility in isolation is to change the barrier height for interconversion between conformers artificially in an MD simulation. Increasing the cis-trans barrier in [C2C1im][NTf2], above 15 kJ mol−1, led to a decrease in diffusion by 40–50%.163 This change in mobility agrees well with the experimental findings presented above.
Another important example of the use of conformational flexibility is the [FAP]− anion, a hydrolytically and electrochemically more stable analogue of the simpler [PF6]−, Fig. 10c.187 The use of [FAP]− instead of [PF6]− considerably lowers the viscosity of ionic liquids. For example, the viscosity of [C6C1im][PF6] is 548 mPa s, whereas that of [C6C1im][FAP] is only 74 mPa s – despite the much higher volume of the latter.188 Formally, this change translates to an increase in fluidity by a factor of approximately two per pentafluoroethyl side chain, again in line with results from other systems. A crucial difference between these two anions is that the [PF6]− anion is relatively rigid, whereas the pentafluoroethyl side chains in the [FAP]− anion can rotate around the P–C bonds, leading to increased conformational flexibility. However, other parameters such as size and mass, fluorination, coordination tendency, and symmetry change as well going from [PF6]− to [FAP]−.189 Thus, this comparison alone would not be a convincing argument for conformational flexibility. Experimentally, it would be beneficial to have at hand the [P(CF3)6]− anion, which will have a similar mass and coordination tendency compared to [FAP]−. However, the syntheses of such compounds are involved, and the [P(CF3)6]− anion might not even be sufficiently stable.187,190
Notwithstanding experimental obstacles, the contribution of conformational flexibility within the [FAP]− anion can be isolated by means of MD simulations. Kowsari and Ebrahimi performed such simulations, comparing [C4C1im][FAP] with [C4C1im][PF6]. The authors determined a variety of dynamic properties from classical molecular dynamics simulations, including a simulation of [C4C1im][FAP] where the anion was simulated as a rigid body using QSHAKE constraints.191 The diffusion coefficients from the mean squared displacement, Fig. 14, clearly show the acceleration of translational dynamics of both cation and anion when the [FAP]− anion is allowed to be flexible. The diffusion of ions in [C4C1im][FAP] with a rigid anion is comparable to or even slower than in [C4C1im][PF6].
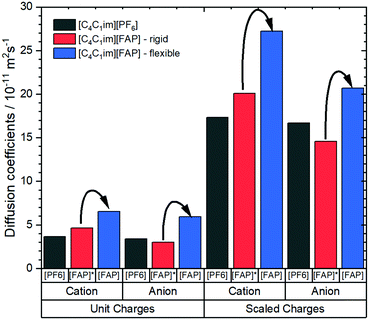 | ||
| Fig. 14 Diffusion coefficients of [C4C1im][PF6] and [C4C1im][FAP] obtained from molecular dynamics simulations.191 The simulations were set up with scaled vs. unit charges and flexible vs. rigid anions. Arrows indicate the increase in diffusion when the FAP anion is allowed to be flexible, regardless if charges are scaled or not. | ||
The experimental increases in fluidity at room temperature discussed in this section are summarised in Table 1. The importance of conformations and conformational flexibility is clearly visible, even though some systems such as [C4C1im][NCyF]/[C4C1im][NTf2] and [C6C1im][PF6]/[C6C1im][FAP] might also have other contributions. More work needs to be done to explore the conformational space of [FAP]− and similar anions both experimentally and computationally. Furthermore, the concepts can be easily extended to mixed fluoroborates, which are an exciting new platform for low-viscosity ionic liquids.192,193 Finally, since the effects are most visible at low temperatures (i.e. room temperature) for ionic liquids with relatively high absolute viscosity values, design concepts such as conformational flexibility could enable fluorine-free ionic liquids of sufficient fluidity.
| Rigid | Flexible | Fluidity increase ηrigid/ηflexible | Ref. |
|---|---|---|---|
| [N2225][NTf2] | [P2225][NTf2] | 1.95 | 138 |
| [neo-C-C1im][NTf2] | [neo-Si-C1im][NTf2] | 1.64 | 143 |
| [P5551][NTf2] | [P(2O2)31][NTf2] | 6.28 (2.09) | 140 |
| [C4C1im][NCyF] | [C4C1im][NTf2] | 3.63 | 173 |
| [C4C1im][NCyF] | [C4C1im][NPf2] | 1.67 | 173 |
| [P5551][CHTf2] | [P5551][NTf2] | 1.89 | 140 |
| [C4C1im][NMsTFA] | [C4C1im][NTfAc] | 1.96 | 105 |
| [C6C1im][PF6] | [C6C1im][FAP] | 7.41 (2.47) | 188 |
Polarisability, ‘dipole moments’ and charge asymmetry
We have discussed earlier the effects of Coulombic compaction and how they might be addressed in a future study using targeted modifications. On top of this overall compaction, the charged nature of ionic liquids also produces strong local electric fields, which affect the ions in two ways. First, the electron cloud of a molecule (including ions and atoms) will be distorted more or less by the presence of an electric field. This inherent property of matter is termed polarisability, and in molecules the electric field leads to an induced dipole moment. Second, the charge distribution in a molecule can be asymmetric even without the presence of an electric field. For neutral molecules, this leads to a permanent dipole moment; for ions, which are formally monopoles, concepts such as the charge arm or charge lever moment are preferred.49,194,195Polarisability in ionic liquids has been a key area of research in the molecular dynamics community over recent years.63,196–204 The comparison of polarisable with non-polarisable simulations is an excellent example of how targeted modifications are used to understand which components define the properties of ionic liquids. However, care must be taken even for simulations to not (unknowingly) change more than one parameter at once. For example, simply adding polarisability to an existing non-polarisable force field will lead to biased results, as inductive effects already included in the original force field are then treated twice.205 Polarisability in molecular dynamics simulations of ionic liquids is a very active area of research, and a thorough review has been published recently.202 Thus, we will not go into detail, but rather highlight two general results. First, the long-range structuring decreases, and the order beyond the first shell is less pronounced in polarisable models.63,199,200,202,206 Thus, screening is much more efficient if the ions are polarisable.63 Second, the dynamics are significantly accelerated, and predicted transport properties are in much better agreement with experimental values.196,206,207
The tendency of polarisability to enhance the dynamics in ionic liquids should be kept in mind during the design process, i.e. when an ionic liquid is conceptually composed from functional groups and atoms of a given polarisability.208–210 However, the experimental possibilities are very limited, at least for targeted modification, since volume and polarisability are closely related.55,211,212 Examples are the aforementioned studies of the series [C4C1im][XF6] (X = P, As or Sb), where a substantial increase in dynamics has been observed for the heavier central elements.106,107 Although the effect is very clear, it cannot be attributed to either size or polarisability without the help of theoretical methods, since both change together.
Experimentally more accessible than the effects of polarisability are those of an asymmetric charge distribution, i.e. those related to the presence of a permanent ‘dipole moment’. In principle, the dipole moment of a molecule can be obtained from its wavefunction, and such calculations are indeed common for ionic liquids.170,176,213,214 The unperturbed dipole moment ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) of a molecule as the sum of its nuclear
of a molecule as the sum of its nuclear ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) N and electronic
N and electronic ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) 0e contributions is given in eqn (1) and (2).215,216
0e contributions is given in eqn (1) and (2).215,216
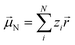 | (1) |
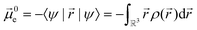 | (2) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) |ψ〉 can be evaluated analytically. The last identity arises as the position operator can be separated since it does not act on the wavefunction, thus allowing the latter to be interpreted as probability (electron) ρ(
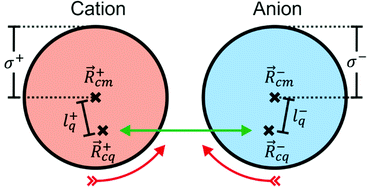
|ψ〉 can be evaluated analytically. The last identity arises as the position operator can be separated since it does not act on the wavefunction, thus allowing the latter to be interpreted as probability (electron) ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) density according to Born's rule. However for molecular ions, the dipole moment becomes ill defined, as only the non-vanishing multipole moment is independent of the choice of coordinate system.195,215 Hence, we will use the ‘charge arm’ Lc = |Qlq| as defined by Kobrak et al. for this discussion.49 The charge arm is proportional to the total charge Q of the ion and the distance lq between centre of charge
) density according to Born's rule. However for molecular ions, the dipole moment becomes ill defined, as only the non-vanishing multipole moment is independent of the choice of coordinate system.195,215 Hence, we will use the ‘charge arm’ Lc = |Qlq| as defined by Kobrak et al. for this discussion.49 The charge arm is proportional to the total charge Q of the ion and the distance lq between centre of charge ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) cq and centre of mass
cq and centre of mass ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) cm, (3)–(5).49
cm, (3)–(5).49![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) q = q = ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) cq − cq − ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) cm cm | (3) |
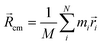 | (4) |
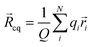 | (5) |
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) cq and
cq and ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) is evident;
is evident; ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) cq =
cq = ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) /Q. The situation for a pair of spherical ions is shown in Fig. 15. The Coulombic attraction (or repulsion, for like charges) acts on the centre of charge. Thus, if
/Q. The situation for a pair of spherical ions is shown in Fig. 15. The Coulombic attraction (or repulsion, for like charges) acts on the centre of charge. Thus, if ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) cq and
cq and ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) cm don’t coincide, the Coulomb force translates to a torque τ on the ion. The torque is proportional to Lc, but the angular acceleration α also depends on the mass – or, more precisely, on the moment of inertia I, (6).¶ Thus, the librational coupling of an ion with asymmetric charge distribution varies with the length of the charge arm Lc, the mass of the ion M, and the radius of gyration Rg. Li et al. use the term ‘charge lever moment’ for Z, to distinguish it from the charge arm Lc.194
cm don’t coincide, the Coulomb force translates to a torque τ on the ion. The torque is proportional to Lc, but the angular acceleration α also depends on the mass – or, more precisely, on the moment of inertia I, (6).¶ Thus, the librational coupling of an ion with asymmetric charge distribution varies with the length of the charge arm Lc, the mass of the ion M, and the radius of gyration Rg. Li et al. use the term ‘charge lever moment’ for Z, to distinguish it from the charge arm Lc.194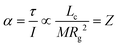 | (6) |
Molecular dynamics simulations allow the direct implementation of the simple model system shown in Fig. 15. These targeted modifications are similar to those discussed in the section ‘size and mass of ions’, i.e. they are usually realised using Lennard-Jones or hard sphere fluid models, with the only difference that the (point) charge is displaced from the (point) mass by the distance lq. Charge displacement models consistently show a number of features:
– With increasing charge displacement, initially the viscosity is found to decrease, and conductivity and translational diffusion increase.111,217
– Rotational diffusion slows down with increasing charge displacement, indicative of directional bonding.217,218
– For large lq/σ, ion pairing to form a dipolar liquid occurs.111,217,219
– Thus, for too large lq/σ, the dynamics slow down again – fluidity, conductivity, diffusion decrease.217
– Charge displacement in general lowers melting points; see the discussion of Fig. 18.219–221
The effect of charge displacement on dynamic properties is shown in Fig. 16 (black curves).111 There is an initial drop in viscosity for increasing lq, accompanied by an increase in diffusion. However, if the charge displacement becomes too large – i.e. larger than 50% of the ion radius in this case – the viscosity shows an abrupt increase. This increase can be attributed to the onset of ion pairing, which is also evident in the convergent diffusion coefficients of cation and anion.111 For comparison, the red curves show the behaviour of charge centred model systems with the same charge separation.|| It is evident that without the asymmetry, a monotonous decrease in the dynamics is found, i.e. viscosities increase and diffusion coefficients decrease.111
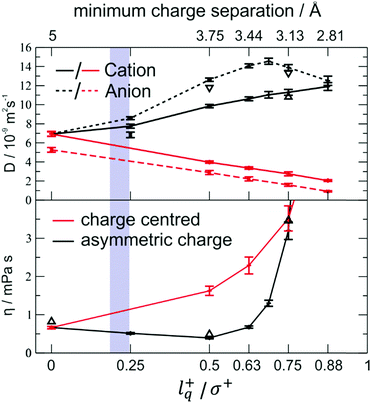 | ||
| Fig. 16 Diffusion and viscosity as a function of charge separation. The blue shaded area indicates the lq+/σ+ range for the [C4C1im] cation. The charge centred systems where charge separation is achieved by decreasing the size are shown in red. Reprinted (adapted) from H. V. Spohr and G. N. Patey, J. Chem. Phys., 2009, 130, 104506, with the permission of AIP Publishing.217 | ||
Li and Kobrak demonstrated that the general trends observed in the simulation of Lennard-Jones and hard sphere models also apply to a more complex model based on the [PF6]− anion.222 The authors systematically varied the charges of a generic classical force field in two ways, Fig. 17. First, they shifted a small proportion of the charge – 0.10e per fluorine atom, i.e. ≈30% of the native charge – from one side of the anion to the other. Second, they placed the charges on dummy atoms between phosphorus and fluorine, leaving fluorine uncharged. Thus, the charges were buried/more localised in comparison to the native force field. For the combination of the two targeted modifications, the amount of charge shifted from one half of the dummy atoms to the others was increased to 0.30e to achieve the same charge lever moment for both asymmetric cases. The phosphorus atom was left unchanged, and an identical structure with reversed charges was used as counterion.
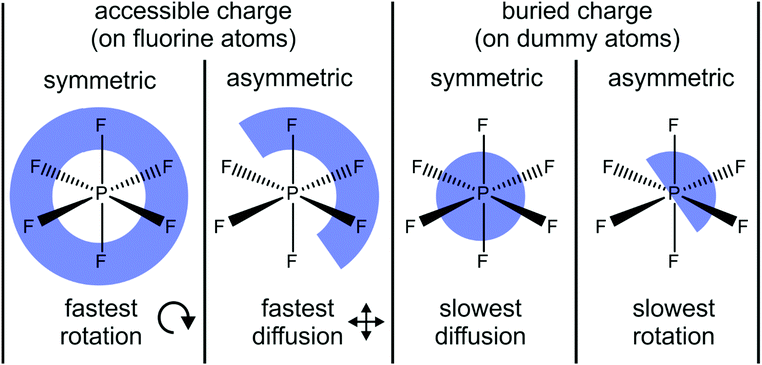 | ||
| Fig. 17 Four model systems with accessible vs. buried and symmetric vs. asymmetric charge distribution as targeted modification are used to demonstrate the impact on transport properties. Translational diffusion is fastest with accessible and asymmetric charge distribution, whereas rotational diffusion is fastest with accessible and symmetric charge distribution.222 | ||
Two dynamical properties are of central interest in the model system in Fig. 17, the translational and rotational diffusion. Both translation and rotation are significantly accelerated for the accessible charge compared to the case where the charge is buried on the dummy atoms.222 However, opposite trends in translational and rotational dynamics were reported for the asymmetric models. The translational diffusion coefficients increased significantly for the asymmetric charge models – by a factor of 12 for the accessible charge, and by a factor of 52 for the buried charge.222 In contrast, the rotational relaxation time almost doubled for the asymmetric charge models compared with their symmetric counterpart.222
These results indicate that the beneficial effect of an asymmetric charge distribution arises from the coupling between rotational (usually fast in liquids) and translational (usually slower in liquids) modes. It can be expected that this mechanism of structural relaxation is particularly important for relatively rigid, close to spherical ions. The relative charge arm lq/σ of the ‘[PF6]−’ model with artificial charge asymmetry is in the range where a viscosity decrease is anticipated, i.e. 0.35 (using the distance between P and F as σ) to 0.18 (additionally including the fluorine radius from the Lennard-Jones potential223), Fig. 16.
Charge asymmetry is an important design aspect of ionic liquids, at least for those with rigid ions. Borate based ionic liquids provide an excellent platform for targeted modifications of this kind. The reason is that borate anions with different (mixed) combinations of the four substituents are synthetically accessible, such as cyano(fluoro)borates or cyano(chloro)borates.192,224–228Table 2 shows targeted modifications involving a systematic exchange of the nitrile groups in the tetracyanoborate anion with either fluorine or chlorine. It is evident that the ionic liquids with charge asymmetric anions (i.e. with large charge arm) have qualitatively lower viscosities and melting points. The physical properties of the cyano(chloro)borates differ less than those of the cyano(fluoro)borates, in line with the smaller charge asymmetry. However, this is not sufficient to determine causation, since other effects might be relevant. For example, nitrile groups are relatively large and prone to dipolar interactions, which distinguishes these from the halides.229,230 Furthermore, the anions all have different masses and volumes, and the resulting ionic liquids differ in their densities. Thus, molecular dynamics simulations like those presented in Fig. 17 would be valuable to test the charge asymmetry hypothesis. The approach is straightforward: starting from a native force field for [BF4]−, [BCl4]− and [B(CN)4]−, the atomic charges are rearranged to give a nonzero charge arm of reasonable magnitude. The relative changes in predicted properties – such as the viscosity – can then be compared to the relative changes found in Table 2.
| Anion | Viscosity/mPa s | Melting point/°C | Volume/Å3 | l q /σ |
|---|---|---|---|---|
| [B(CN)4]− | 22.2 | 8 | 152 | 0 |
| [BF(CN)3]− | 12.6 | −7.8 | 132 | 0.085 |
| [BF2(CN)2]− | 11.1 | −16 | 112 | 0.114 |
| [BF3(CN)]− | 14.7 | −28 | 91 | 0.116 |
| [BF4]− | 34 | 14 | 69 | 0 |
| [B(CN)4]− | 22.2 | 8 | 152 | 0 |
| [BCl(CN)3]− | 18.6 | — | 149 | 0.004 |
| [BCl2(CN)2]− | 19.6 | −4 | 147 | 0.015 |
| [BCl3(CN)]− | 21.1 | 8 | 144 | 0.030 |
| [BCl4]− | 36.6 | 15 | 141 | 0 |
Apart from very general statements, we have so far not considered the effect of targeted modifications on thermal transitions. The reason for that is that thermal properties depend on a multitude of subtle effects, and the obtained results also vary with experimental parameters such as cooling rate or thermal history.231 Even simple spherical ion models predict a variety of thermal transitions,220,221 which we will discuss here briefly. The thermal transitions reported by Lindenberg and Patey show a pronounced dependency both on the size difference and the charge displacement of the ions, Fig. 18.221
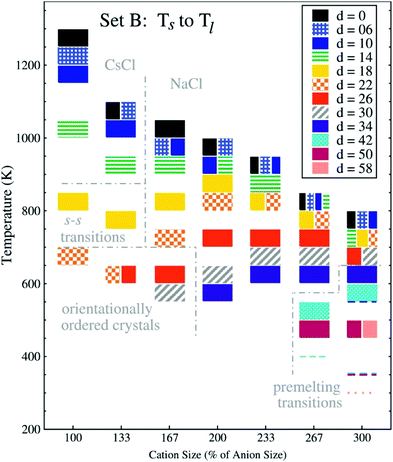 | ||
| Fig. 18 Melting point trends with different charge displacements ‘d’ and cation sizes.221 The charge displacement d, does not translate directly to lq because the charge centre also is assigned a small mass and because only 2/3 of the charge are displaced. Thus, d = 26 corresponds to lq ∼ 1.7 Å, or a relative charge arm of 0.67 (cation size 100%) to 0.22 (cation size 300%). The anion radius is held constant, the cation radius is increased from 2.5 to 7.5 Å, units of d are 0.1 Å. Reprinted from E. K. Lindenberg and G. N. Patey, J. Chem. Phys., 2015, 143, 024508, with the permission of AIP Publishing. | ||
In Fig. 18, the cation size (both absolute and in relation to the anion) increases from left to right, the shading of the blocks corresponds to the magnitude of charge displacement d. Systems with small or no charge displacement tend to crystallise into high-melting CsCl (similar ion sizes) or NaCl (different ion sizes) structures. Introducing displaced charges into the systems with similar size leads to glassy states upon cooling with an underlying orientationally ordered crystal structure.220,221 The melting points are reduced considerably by several hundred Kelvin even for relatively small charge displacements. It is worth noting that the authors observed pre-melting transitions relevant to solid state physics in the region of large charge displacements and disparate ion sizes: first, plastic crystals with ion pairs rotating together; second, fast ion conductors where the larger cations remain on their lattice positions, while the anions are mobile.221
Naturally, for ionic liquids, liquefaction temperatures will depend on a multitude of factors beyond the dipole moment. However, as a general trend, a lowering of liquefaction temperatures with increasing dipole moments has been observed experimentally.232,233
Hydrogen bonding
In the previous section we have collected sound evidence that weak directional bonding can fluidize ionic liquids – both with respect to melting points and transport properties.111,232 This observation is directly related to the potential effects of hydrogen bonding in ionic liquids. Indeed, hydrogen bonding is recognised as a concept of central importance in this field, including hydrogen bonds in aprotic ionic liquids as well as the ‘conventional’ hydrogen bonds present in protic ionic liquids.48,58,234–236 In this section we will focus on how targeted modifications can be exploited to understand and design hydrogen bonding, using the well-known imidazolium cation as an example.In imidazolium cations, any ring atom bonded to a hydrogen atom can serve as hydrogen bond donor. In general, the strongest hydrogen bonds are formed by N1–H or N3–H groups,237 followed by C2–H, and finally the much weaker C4–H and C5–H groups.234,238 The numbering of ring atoms is shown in Fig. 19a. While hydrogen bonds are formed by the alkyl chains,234,239–241 these will not be discussed and we will focus on hydrogen bonds at the C2 position. A systematic experimental study of both melting points and – where possible – transport properties of imidazolium salts with all 20 possible methylation patterns would be desirable. We refer the interested reader to the work by Fumino, Ludwig, et al.;242–245 structures and available melting points are given in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 242,243,246
242,243,246
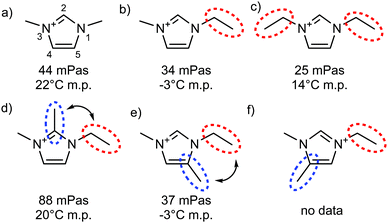 | ||
| Fig. 19 Viscosities at 20 °C and melting points taken from ref. 161, all systems with [NTf2]− as anion. Red dotted circles highlight flexible groups, blue dotted circles highlight hydrogen bonding sites which are blocked by methylation, double-headed arrows indicate situations where conformational flexibility is potentially reduced by steric clash. | ||
In many cases of practical importance, hydrogen bonding is a dominant interaction between the solvent (ionic liquid) and solute. Prototypical examples are the dissolution of cellulose and the Diels–Alder reaction in ionic liquids as solvents.247–253 Both experimental and theoretical studies of solute–solvent interactions for practical applications rely on having a reference solvent with different hydrogen bonding properties, without significantly altering other properties.
In the spirit of targeted modifications, the hydrogen atom may simply be replaced by a methyl group. Bonhôte et al. used this concept in their seminal work on the [NTf2]− anion, Fig. 19.161 The strongest hydrogen bond in this set of ionic liquids is formed at the C2 position, whereas C4 and C5 hydrogen bonds are much weaker. Surprisingly at the time of the discovery, an unusually high viscosity was observed for the ionic liquid 1-ethyl-2,3-dimethylimidazolium bis(trifluoromethanesulfonyl)imide [C2C1C1im][NTf2] (Fig. 19d), where the C2 hydrogen bond is disrupted by methylation.161 Other imidazolium ionic liquids with different anions show the same behaviour, which sparked a debate on the nature of the increase in viscosity relevant in the context of this perspective.254–258 Critically, the cation in Fig. 19d differs from the other cations in Fig. 19 not only by the absence of hydrogen bonding, but also in other parameters – in particular size and conformational flexibility.254
The effect of size and flexibility on viscosity can be seen by comparing the viscosities of the [NTf2]− based ionic liquids in Fig. 19a–c, which vary from 44 to 25 mPa s. The ionic liquid with C2 methylated cation (Fig. 19d) clearly exceeds this range, with a viscosity of 88 mPa s. However, this modification alone is not sufficient to identify the cause of the difference – it can be argued that the methyl group in C2 position impedes rotation of the ethyl side chain around the N–C bond, thus reducing conformational flexibility.254 This second hypothesis can be tested by comparing the properties of ionic liquids with the cations shown in Fig. 19d–f, all having the same mass, but different substitution patterns. If restricted rotation was indeed the sole cause of the higher viscosity, but not hydrogen bonding, then the C2 and C5 methylated analogues would be expected to show the same, or very similar viscosities, whereas the C4 methylated cation (Fig. 19f) would be more fluid than these two. In contrast, the C2 methylated imidazolium ionic liquid (Fig. 19d) is more than twice as viscous as the C5 methylated counterpart (Fig. 19e). Thus, hydrogen bonding at C2 can be identified as the dominating factor in this case. The comparison with the C4 methylated imidazolium ionic liquid would allow for more insight into the interplay with conformational flexibility. However, the required data are not yet available.
It would be desirable to have the data shown in Fig. 19 for anions such as methanesulfonate or acetate, which are known to engage in stronger hydrogen bonding than [NTf2]−. This data is not available at the moment, especially not for the more exotic cations in Fig. 19c–f. In addition, melting points can cause practical problems. An example is [C2C1C1im][OAc] with a melting point around 90 °C, whereas [C2C1im][OAc] is a room temperature ionic liquid.259 Such large differences pose a challenge when viscosities are to be compared. Furthermore, decomposition becomes a relevant issue for anions which are good hydrogen bond acceptors due to their inherent basicity.259
Methylation as a targeted modification can be used with theoretical methods to not only identify that hydrogen bonding in C2 position fluidises ionic liquids, but also to understand why. Several groups investigated the barrier associated with anions moving between the (equivalent) positions on top and below of the imidazolium ring via the in plane orientation on the C2–H site, where hydrogen bonding can occur for the non-methylated analogues.255,260,261Fig. 20a shows the potential energy surface for the position of the [NTf2]− anion around the two cations 1,2,3-trimethylimidazolium and 1,3-dimethylimidazolium reported by Rodrigues et al.255 The C–H⋯N angles of 45° and 360 − 45 = 315° correspond to the [NTf2]− positions above and below the imidazolium ring plane; which is the preferred geometry in the gas phase. Transition between these two minima occurs via the in-plane geometry at 180°, which is associated with a much higher barrier for the methylated cation, i.e. the blue curve in Fig. 20a.
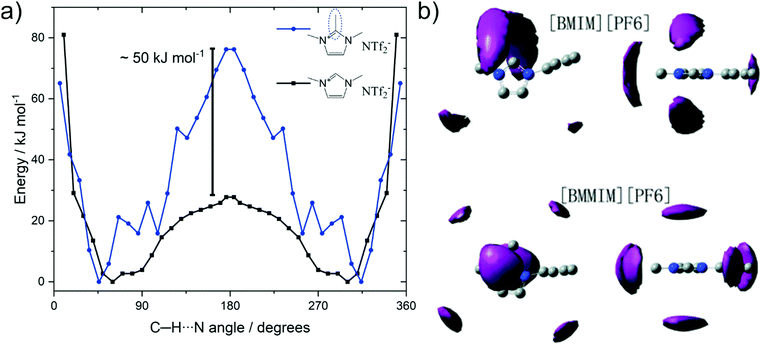 | ||
| Fig. 20 (a) Energy as a function of the angle between C2 carbon, acidic hydrogen, and imide-N of the [NTf2].255 (b) Spatial distribution function of [PF6] around [C4C1im] (top) and [C4C1C1im] (bottom). Reproduced from ref. 257 with permission from the PCCP Owner Societies. | ||
The significantly increased barrier for the C2 methylated analogue decreases the entropy, as fewer positions are available for the anion relative to the cation. The resulting localisation of the anion for C2 methylated imidazolium cations is visible in spatial distribution functions obtained from bulk molecular dynamics simulations, Fig. 20b.257,260 Thus, the loss in conformational entropy of the side chains is overcompensated by the gain in configurational or vibrational (in the sense of an intermolecular vibration mode) entropy.255,257,260 However, we would like to emphasise that this entropy argument does not conflict with hydrogen bonding as cause of the higher fluidity. Although hydrogen bonding is an additional interaction – which would be expected to decrease fluidity – it comes to act upon an arrangement of ions which is high in energy, i.e. the in-plane position of the anion. Thus, this additional interaction will flatten the potential energy surface, rendering more minima accessible. In analogy to conformational flexibility, additional pathways become available for structural relaxation, lowering the viscosity and accelerating the dynamics.
The anions in the examples shown in Fig. 20 are generally considered to be weakly coordinating, even though aprotic ionic liquids such as [C2C1im][NTf2] show rich hydrogen bonding.262,263 Nevertheless, the higher transition barrier upon methylation shown in Fig. 20a is also found for anions that are good hydrogen bond acceptors, such as halides.260,261 Hydrogen bonding facilitates the position change of halides. The structure with a C–H⋯Cl angle of 180° in [C1C1im]Cl is a minimum, separated by less than 10 kJ mol−1 from the structures where the chloride is situated above and below the ring.260 In the C2-methylated [C1C1C1im]Cl, the 180° structure is a transition state rather than a minimum, and the energy barrier increases to above 40 kJ mol−1.260
The interpretation of hydrogen bonding above is not without critics. Several groups question the relevance of hydrogen bonding in imidazolium cations, or at least point out the deviations from ‘conventional’ hydrogen bonds.264–267 Some of the discrepancies are rooted in more or less strict definitions of hydrogen bonding and the overlap between different interpretations. The last point is illustrated with the targeted modifications of the [C4C1im]+ cation shown in Fig. 21. As discussed above, methylation of the C2 position leads to an increase in viscosity, Fig. 21b. However, a similar increase in viscosity can be achieved with a branched side chain, Fig. 21c. The cation shown in Fig. 21c is interesting as the increase in viscosity compared to ionic liquids with linear side chains significantly exceeds what one would expect given the small reduction in conformational flexibility, Fig. 21d.268 Using molecular dynamics simulations, Zhang et al. could show that the curious properties of this particular ionic liquid are rooted in the preferred orientation of the side chain in space, altering the distribution of the anion around the cation as well as the barriers which separate preferred positions.269 Thus, the increases in viscosity for both the C2 methylated and the branched imidazolium ionic liquids can be explained with a change in configurational entropy. However, the deeper-rooted causes are different: loss in hydrogen bonding upon methylation of the C2 position, and steric exclusion of the anion by the branched side chain. The choice of a model and the level of coarse graining are to some degree subjective; this arbitrariness must be kept in mind when conflicting conclusions are encountered.
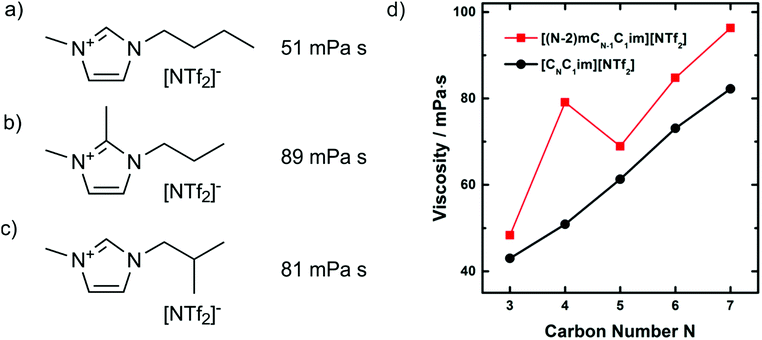 | ||
| Fig. 21 Viscosities at 25 °C of (a)268 [C4C1im][NTf2] and (b)271,379 and (c)268 targeted modifications with the same molecular weight. Slightly lower values for (a) (46 mPa s) and (b) (84 mPa s) were reported in.380 The dynamic viscosity as a function of the number of carbons in the side chain is shown in (d) for both linear (black curve) and branched (red curve) cations.268 Reprinted with permission from L. Xue, E. Gurung, G. Tamas, Y. P. Koh, M. Shadeck, S. L. Simon, M. Maroncelli and E. L. Quitevis, J. Chem. Eng. Data, 2016, 61, 1078–1091. Copyright 2016 American Chemical Society. | ||
Another example of a ‘conflicting’ interpretation is the free volume model. This model explains the high viscosities of C2 methylated imidazolium ionic liquids with their decreased free volume compared to non-methylated ionic liquids.270 In other words, the ions are more densely packed in the case of C2 methylated cations. There clearly is some conceptual overlap with the spatial distribution interpretation we used above. If the anions are more localised and less mobile due to high barriers, then the free volume in the bulk liquid will be lower, and vice versa. However, the hypothesis of a standalone ‘free volume model’ can be tested with relative ease by considering isodensity conditions. The density of [C3C1C1im][NTf2], Fig. 21b, is 1.4579 g mL−1 at 25 °C and atmospheric pressure, under which conditions it has a viscosity of 89 mPa s.270 Under the same conditions, the density of [C4C1im][NTf2], Fig. 21a, is lower at 1.4366 g cm−3, indicating a less dense packing and thus a larger free volume, under these conditions it has a viscosity of 51 mPa s.271 Isodensity conditions are reached at approximately 31 MPa, where [C4C1im][NTf2] reaches a density of 1.4579 g mL−1 and a viscosity of 73 mPa s, see ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271 Thus, it may be necessary but it is not sufficient to consider free volume and isodensity conditions to explain the high viscosity of the C2 methylated analogue.
271 Thus, it may be necessary but it is not sufficient to consider free volume and isodensity conditions to explain the high viscosity of the C2 methylated analogue.
The value of methylation in understanding the behaviour of imidazolium ionic liquids is apparent. However, changes in size and shape of the cation also contribute to the changes in macroscopic properties. Instead, imidazolium based ionic liquids can be compared with ionic liquids based on other azoles which are not significantly different in size or mass, Fig. 22. Few studies exist on triazolium and diazolium (other than 1,3-disubstituted imidazolium) ionic liquids, usually focusing on niche uses as catalysts or using highly functionalised cations.272–278 Some groups make use of the higher stability towards base of 1,2,3-triazolium cations which is a result of the missing acidic hydrogen atom in 2-position.279–281 It would be beneficial to have data with stronger hydrogen bond acceptors than [NTf2]−, the available thermal properties indicate that very low melting points can be obtained even with ions such as [OMs]− or [BF4]−.282 For example, the triazolium analogue of [C4C1im][OMs] with the triazolium nitrogen in 4-position is reported to be a liquid, however we could not find viscosity data.278
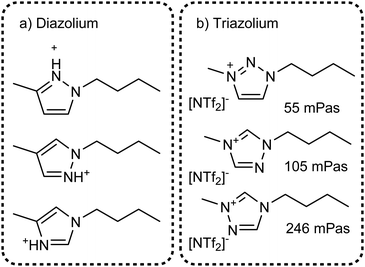 | ||
| Fig. 22 Targeted modifications of the [C4C1im]+ cation: (a) diazolium based cations and (b) triazolium cations. Some properties for ionic liquids with triazolium [NTf2]− ionic liquids have been measured, viscosities at 25 °C are given in (b). Values are taken from: 2-triaz viscosity,285 4-triaz viscosity,283 5-triaz viscosity;284 for the sake of simplicity we follow the numbering of the 1-butyl-3-methylimidazolium base structure. | ||
The structures shown in Fig. 22 are useful targeted modifications to understand hydrogen bonding in ionic liquids. As a first approximation, the protic diazolium ionic liquids in Fig. 22a will form stronger hydrogen bonds than their aprotic imidazolium counterparts. Conversely, the triazolium cations in Fig. 22b are missing one hydrogen bonding site. Indeed, higher viscosities compared to [C4C1im][NTf2] have been reported for the triazolium counterparts, Fig. 22b, in agreement with the methylation approach.283–285 However, it is surprising that the increase in viscosity of ionic liquids is higher when the hydrogen bonding site in 4 or 5 position is omitted. In addition, the viscosity at room temperature of the 1,2,3-triazolium analogue is almost identical to that of [C4C1im][NTf2], Fig. 22a. Thus, the simple picture of missing hydrogen bond donors does not correlate well with the situation found for imidazolium cations. As a second approximation, changes in the molecular electrostatic potential286 and the acidity of the different sites287–289 for each specific azole have to be considered.
The insight promised by the targeted modifications justifies the effort, even if the resulting ionic liquids themselves are too expensive or otherwise unsuited for practical applications. The ultimate goal is the transition from understanding to design. Examples of how such a transition can be achieved have been put forward by Ludwig and Paschek.290 The authors suggest adding substituents of different electronegativity to the 4 and/or 5 positions of [C2C1im][NTf2] to change physicochemical properties of the bulk ionic liquid by changing the strength of hydrogen bonds.245,290
One of the least disruptive targeted modifications is the use of isotopologues. Consequently, deuteration is commonly used as a probe, for example in NMR or neutron scattering studies.166,238,239,291–294 However, it must be kept in mind that the free energy surface might be affected by the mass of the nuclei. Although the effects are in general small, one needs to be aware and wary of these to correctly interpret results. This is important for the exchange of protium with deuterium, and the effect of this exchange on hydrogen bonds. Deuteration changes the zero point energy and the energy difference between vibrational eigenstates, even if the potential provided by the internal electronic energy does not change.295–298 However, this does not directly translate into one isotope forming stronger hydrogen bonds than the other.296,299–301 In general, at lower temperatures deuterium bonds are more stable than hydrogen bonds, and the trend reverses at higher temperatures where entropic effects become more important.297,300 Yoshimura et al. confirmed the pronounced temperature dependence of deuterium bonds and the qualitative difference to protium bonds for D2O and H2O in the ionic liquid [C4C1im][BF4].302 In some cases the results are counterintuitive – for example, Remsing et al. provided evidence that the Cl⋯D bond is stronger than the Cl⋯H bond in [C4C1im]Cl, despite the measurement being at 90 °C.238
Differences in hydrogen bonding due to deuteration can affect both the solid and liquid state. For the solid, small changes in geometry upon deuteration can accumulate, leading eventually to polymorphism or differences in melting point.303–305 Abe et al. observed significant changes in the crystallisation temperature for wet diethyl(2-methoxyethyl)(methyl)ammonium tetrafluoroborate [N221(2O1)][BF4] for different deuterium contents.304,306 [N221(2O1)][BF4] with 1 mol% H2O was observed to crystallise at −14 °C, whereas [N221(2O1)][BF4] with 1 mol% D2O crystallised at −40 °C.304 The water content in these measurements was rather low. 1 mol% is approximately equivalent to 0.1 mass% for this ionic liquid, once again showing the importance of impurities.307 Isotope effects of the deuterium can also be observed in the liquid state. The miscibility of [C4C1im][BF4] with protiated vs. deuterated butanols shows that this is relevant beyond the subtleties of spectroscopic methods.308 For all four butanols, the UCST** is lowered by 4–7 °C upon deuteration, i.e. the d1-butanols are more miscible.308 Finally, we note that a change in conformer distribution has been reported for several [C4C1im] based ionic liquids.309,310 However, further work is required to demonstrate that the reported preference for the gauche conformer is not an artefact of the higher intensity in the corresponding Raman band for the C2 deuterated cation.
Targeted modifications to investigate the effects of hydrogen bonding are not limited to the polar core. In some cases, the periphery of a cation is even more accessible experimentally than the core, since a variety of different alkylating agents are readily available. Thus, a functional group capable of hydrogen bonding can be formally introduced into a cation in an ionic liquid. Targeted modifications have been used to show that this can lead to pronounced cation–cation interactions and the formation of cation clusters.92,311–315 In addition, the cation–anion interaction can be disrupted if the hydrogen bonding site competes with the polar core.311,316 Systematic studies of hydrogen bonding and cationic clustering led to a detailed understanding of the lubricity in closely related ionic liquids, Fig. 23.317 Li et al. observed an approximately linear relationship between lateral and normal force in an atomic force microscopy experiment for [C4py][NTf2], Fig. 23a.317 In contrast, the hydroxyl functionalised analogue [HOC4py][NTf2] showed a discontinuous behaviour in the same setup, Fig. 23b. The authors rationalised this observation with the presence of an ordered cation layer stabilised by hydrogen bonding, Fig. 23c. Notably, the authors also successfully used other targeted modifications to disrupt the bilayer, such as an anion with increased hydrogen bonding tendency.317 Thorough understanding of the surface behaviour of ionic liquids is of vital importance for several practical applications such as lubrication318–320 or catalysis with supported ionic liquid phase (SILP).321–323
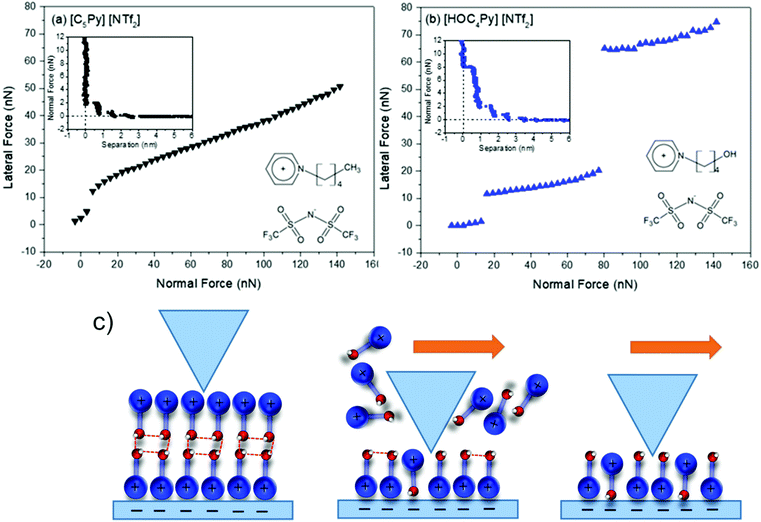 | ||
| Fig. 23 The comparison between ionic liquids with alkyl- and hydroxyalkyl pyridinium cations revealed their interesting lubrication behaviour. Lateral vs. normal force shows a linear behaviour for the alkyl pyridinium cation (a), whereas distinct steps are observed for the hydroxyalkyl pyridinium cation (b). The authors provide a plausible rationalisation in terms of bilayer formation (c).317 Reprinted (adapted) with permission from H. Li, T. Niemann, R. Ludwig and R. Atkin, J. Phys. Chem. Lett., 2020, 3905–3910. Copyright 2020 American Chemical Society. | ||
Fluorinated vs. alkyl side chains and nanosegregation
There are two design parameters relevant to this section, the length of the side chain and the degree of fluorination. However, this leads to a problem since both design parameters are coupled to other properties. The replacement of hydrogen with fluorine can be considered a targeted modification if one is aware of the manifold of changes that come with it. We will thus present only a few select examples of fluorinated vs protonated side chains and use this section to discuss the limits of the ‘targeted modifications’ approach. First, we will discuss small fluorine containing groups, followed by longer fluorinated side chains that induce fluorophilic behaviour.The trifluoromethyl group is a common motif in ionic liquids, with a methyl group being the protonated analogue, Fig. 24. Trifluoromethanesulfonate [OTf]− and methanesulfonate [OMs]− anions are commonly used as anions in ionic liquid studies.324–328 Interestingly, the motivation for the use of the [OTf]−/[OMs]− pair in these studies is indeed usually targeted modification – however to investigate the influence of hydrogen bonding rather than fluorination. Due to the electron withdrawing effect of fluorine substitution, the [OTf]− anion has a lower basicity than [OMs]−, which results in weaker hydrogen bonds.326–328 The desire for weakly coordinating anions (together with high chemical and thermal stability) is at the root of the widespread use of highly fluorinated anions in ionic liquids, which is why understanding the effects of fluorination is so important.103,104,329,330 Studies that compare [OMs]− and [OTf]− might thus also include an anion like trifluoroacetate [TFA]−, which also shows a more pronounced tendency to form hydrogen bonds than [OMs]−.327 Finally, we have mentioned earlier that alkyl side chains (in cations) can act as hydrogen bond donors, which is naturally not the case for perfluoroalkyl chains.234,239–241 In contrast, fluorine atoms can serve as weak hydrogen bond acceptors in some cases.331–336 However, this is generally believed not to be relevant for ionic liquids.
The effect of fluorination on the properties of [NTf2]− ionic liquids has been studied by comparison with the non-fluorinated analogue [NMs2]−, Fig. 24b.103 Similar to [OMs]−vs. [OTf]−, Pringle et al. report higher viscosities for the corresponding ionic liquids with the non-fluorinated anion as a result of stronger interactions.103 Furthermore, the higher basicity of the non-fluorinated anion leads to reduced thermal stability of corresponding imidazolium and pyrrolidinium ionic liquids.103,330 These effects and their rationalisation can be understood intuitively. Much more subtle and not immediately evident are the effects of fluorination on conformational flexibility. The [NMs2]− anion can be considered a rigid anion for practical purposes, thus the well-known plasticising properties of the flexible [NTf2]− anion also depend on its degree of fluorination.105 This finding poses an interesting starting point for further systematic investigations of partly fluorinated anions intermediate between [NTf2]− and [NMs2]−.337
Size and mass are inevitably linked to fluorination. As a rule of thumb, a trifluoromethyl group is approximately equivalent to an isopropyl group in terms of size.331 The effects of size and mass have been discussed earlier. In principle, classical molecular dynamics simulations can differentiate between the different effects. For example, it is straightforward to selectively change a force field to produce an artificial ‘lighter fluorine’ (or ‘smaller fluorine’) without changing other characteristics such as the charge distribution. The mixing and solvation behaviour of fluorocarbons is partly determined by the volumes of the involved species, hence such a study would be relevant for practical applications where ionic liquids are to be used as solvents.338 The steric demand of fluorine in these systems has three implications:
(1) The size of the ion itself increases (relative to the counterion), see the implications in the section ‘size and mass of ions’.
(2) The importance of conformational flexibility for ions such as [NTf2]− is believed to be due to the relatively large CF3 groups, see the section ‘conformations and conformational flexibility’.163,165
(3) The polarisable carbon atoms are sterically shielded by the less polarisable fluorine atoms, reducing dispersion interactions.339
These points are also valid for longer alkyl and fluoroalkyl side chains. In addition, it is well established that alkyl and (per)fluoroalkyl side chains of sufficient length lead to the formation of apolar and fluorous domains, coexistent with the polar domains formed by the charged parts of the ions.340–353 Hollóczki et al. investigated this behaviour with the help of molecular dynamics simulations.354 The authors simulated mixtures of [C8C1im]Br and the fluorinated counterpart [(Rf6C2)C1im]Br, Fig. 25. All seven compositions ranging from pure [C8C1im]Br over a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture to pure [(Rf6C2)C1im]Br showed well-defined polar, apolar, and fluorous domains.354 The [(Rf6C2)C1im]+ cation is a targeted modification of the [C8C1im]+ cation, which allowed the authors to study the influence of fluorination. Future studies might focus on the different contributions of the manifold changes that come with the introduction of fluorination, isolating the effects of mass, size, charge distribution, etc.
1 mixture to pure [(Rf6C2)C1im]Br showed well-defined polar, apolar, and fluorous domains.354 The [(Rf6C2)C1im]+ cation is a targeted modification of the [C8C1im]+ cation, which allowed the authors to study the influence of fluorination. Future studies might focus on the different contributions of the manifold changes that come with the introduction of fluorination, isolating the effects of mass, size, charge distribution, etc.
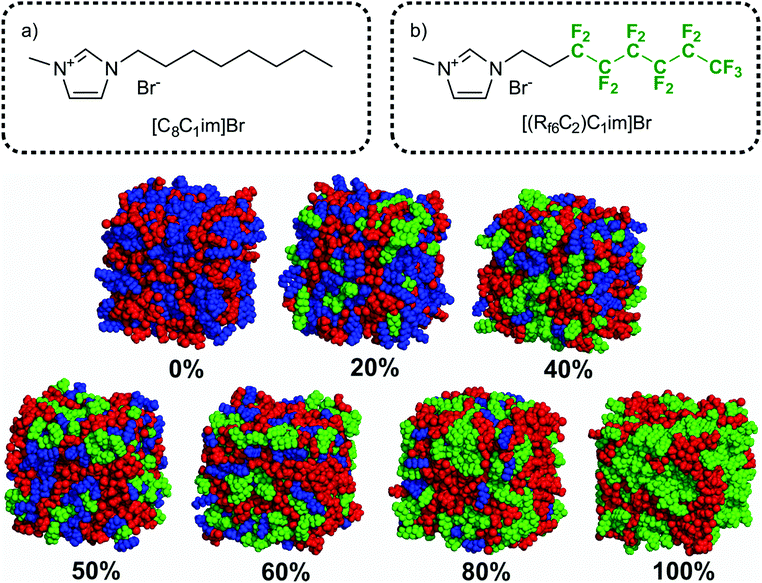 | ||
| Fig. 25 Mixtures of (a) [C8C1im]Br and (b) the highly fluorinated analogue [(Rf6C2)C1im]Br lead to a triphilic structure, i.e. nanosegregation into apolar (blue), polar (red), and fluorous (green) domains. The three domains are clearly discernible in the different snapshots shown in (c) for an increasing percentage of the fluorous IL.354 Reprinted with permission from M. Brehm, H. Weber, M. Thomas, O. Hollóczki and B. Kirchner, ChemPhysChem, 2015, 16, 3271–3277. Copyright 2015 Wiley-VCH Verlag GmbH&Co. KGaA, Weinheim. | ||
To this point, the aggregation of alkyl and fluoroalkyl side chains in separate domains has been treated as an empirical result. Nanosegregation in ionic liquids with extended side chains is not simply the result of the (fluoro)alkyl chains being excluded from the polar parts; otherwise only two domains would form rather than the three domains visible in Fig. 25. The conundrum can be solved by considering the interactions favoured by alkyl and perfluoroalkyl chains, respectively.
Long alkyl side chains in ionic liquids are believed to actively aggregate due to dispersion interactions, as opposed to being merely expelled from the charged region.355–359 Firaha et al. used ab initio simulations to directly investigate the effects of dispersion interactions.358 To this end, the authors compared results from ab initio molecular dynamics simulations using DFT functionals with and without dispersion correction. Thus, even basic physical concepts such as dispersion interactions can be probed with targeted modifications, in this case different functionals. Surprisingly, the authors observed a decrease in alkyl chain aggregation when dispersion was included.358 Although the interaction between alkyl chains did indeed increase, it was found that the interactions between polar parts benefited even more.
Highly fluorinated compounds have properties which are distinctively different from their protonated counterparts. In their seminal work from 1994, Horváth and Rábai introduced the term ‘fluorous’ to address this behaviour.360,361 In general, fluorous compounds and solvents are poorly miscible both with water and conventional organic solvents.338–340,362 Fluorous biphasic catalysis makes use of this phenomenon by tagging a catalyst with a ‘fluorous ponytail’, which leads to a preferred solvation in fluorous solvents and facilitates catalyst recovery.340,363,364
The behaviour is commonly explained in two ways. First, fluorine atoms in perfluoroalkyl chains sterically shield the more polarisable carbon atoms, thus reducing dispersion interactions.331,339,365 Second, long perfluoroalkyl chains tend to adopt a helical conformation,336,339,366 thus leading to nonvanishing permanent dipole moments which interact with each other, forming a network of ‘stratified dipole arrays’.367–369 In reality, both explanations contribute to some degree to the macroscopic properties of fluorous compounds, and the relative importance of each will depend on the exact system. The energy differences between conformers in perfluoroalkanes are small,370,371 and in some cases all-trans staggered conformations are found, stabilised by numerous weak fluorine–fluorine interactions.336
Ionic liquids lead to a unique situation as fluorous and hydrocarbon moieties are forced together to meet electroneutrality conditions. It is an interesting question as to what extent this nanosegregation (literally demixing on a molecular scale) influences bulk properties of ionic liquids, including those with short side chains. Molecular mimics and their mixing behaviour provide a potential way forward to answer this question. Thus, fluorination and nanosegregation conflate all aspects covered in this perspective, which in turn shows that great care has to be exercised to rationalise bulk properties with molecular concepts.
Summary and outlook
In this perspective, we present targeted modifications as an approach to understand how the attractive macroscopic properties of ionic liquids arise, and how they can be controlled. This approach seeks to overcome the limitations of structure–property relationships by further breaking down the structural changes which inevitably lead to changes in more than one molecular property. An example is the side chain length (structure) in imidazolium ionic liquids and the effect on liquefaction temperatures (property). Extending the side chain leads to irregular behaviour of the liquefaction temperatures, since many molecular properties change at the same time.56 Several underlying concepts such as size and mass, conformational flexibility, or dispersion interactions need to be deployed to rationalise the observed behaviour. We thus present targeted modifications as a ‘concept-property relationship’, where the object of study is modified in a way that allows one to address one underlying concept at a time.We discuss several examples where targeted modifications could be used and have been used to enable the design of ionic liquids by understanding how their properties arise. In many cases, a synergistic combination of theory and experiment is required to provide a satisfactory answer. For example, localised charge and flexibility have both been suggested as cause for the faster dynamics in phosphonium ionic liquids compared to ammonium ionic liquids. Computational approaches can investigate these two contributions separately and settle the dispute. In this example, flexibility is now thought to be the dominant contribution, whereas the localised charge slows down dynamics.139 However, one point cannot be stressed enough: the existence of two models does not mean that only one of these can be right. We showed this for the free volume model vs. hydrogen bonding in imidazolium ionic liquids, where targeted modifications revealed that neither of the two provides a convincing, standalone rationale.
Despite the invaluable insight provided and promised by targeted modifications, making quantitative predictions remains an issue. This is due to the complexity of some of the relationships and the coupling between these. Thus, to achieve a priori design beyond what is covered by targeted modifications, statistical methods such as machine learning might be necessary. However, even then, knowledge of targeted modifications will be helpful. The ideas described in this perspective can be used to reduce or even inspire the parameter space for statistical methods, since targeted modifications can reveal which concepts are important and which aren’t. Goal-oriented feature selection and machine learning are rapidly advancing fields which become more and more relevant for ionic liquids.372 In this context, targeted modifications serve as a bridge between basic research and practical applications.
Several promising models aim to provide quantitative predictions based on microscopic structure, such as mode coupling theory or excess entropy scaling.181,373–377 To some degree, these models suffer from a limited interpretability on a molecular level. Future work in this direction might use a fruitful combination of statistical mechanics and targeted modifications, for example to quantify the contribution of conformational flexibility to excess entropy and thus to macroscopic transport properties.
Further experimental and theoretical studies in this direction have considerable potential, for example using molecular mimics and diazolium/triazolium analogues. The successes of existing studies presented in this perspective show that there is merit to targeted modifications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is funded by the Imperial President's PhD Scholarship. Computational resources provided by the Imperial College Research Computing Service are gratefully acknowledged. DOI: 10.14469/hpc/2232.Notes and references
- C. Reichardt and T. Welton, Solvents and Solvent Effects in Organic Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2010, pp. 65–106 Search PubMed.
- T. Welton, Chem. Rev., 1999, 99, 2071–2084 CrossRef CAS PubMed.
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed.
- N. Nasirpour, M. Mohammadpourfard and S. Zeinali Heris, Chem. Eng. Res. Des., 2020, 160, 264–300 CrossRef CAS.
- T. Welton, Biophys. Rev., 2018, 10, 691–706 CrossRef CAS PubMed.
- N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123–150 RSC.
- L. C. Brown, J. M. Hogg and M. Swadźba-Kwaśny, Top. Curr. Chem., 2017, 375, 78 CrossRef PubMed.
- M. Abai, M. P. Atkins, A. Hassan, J. D. Holbrey, Y. Kuah, P. Nockemann, A. A. Oliferenko, N. V. Plechkova, S. Rafeen, A. A. Rahman, R. Ramli, S. M. Shariff, K. R. Seddon, G. Srinivasan and Y. Zou, Dalton Trans., 2015, 44, 8617–8624 RSC.
- M. Moreno, E. Simonetti, G. B. Appetecchi, M. Carewska, M. Montanino, G.-T. Kim, N. Loeffler and S. Passerini, J. Electrochem. Soc., 2017, 164, A6026–A6031 CrossRef CAS.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629 CrossRef CAS PubMed.
- A. Balducci, Top. Curr. Chem., 2017, 375, 20 CrossRef PubMed.
- T. Rüther, A. I. Bhatt, A. S. Best, K. R. Harris and A. F. Hollenkamp, Batteries Supercaps, 2020, 3, 793–827 CrossRef.
- L. M. McGrath and J. F. Rohan, Molecules, 2020, 25, 6002 CrossRef CAS PubMed.
- I. M. Marrucho, L. C. Branco and L. P. N. Rebelo, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 527–546 CrossRef CAS PubMed.
- J. L. Shamshina, P. S. Barber and R. D. Rogers, Expert Opin. Drug Delivery, 2013, 10, 1367–1381 CrossRef CAS PubMed.
- S. N. Pedro, C. S. R. Freire, A. J. D. Silvestre and M. G. Freire, Int. J. Mol. Sci., 2020, 21, 8298 CrossRef CAS PubMed.
- Electrodeposition from Ionic Liquids, ed. F. Endres, A. Abbott and D. MacFarlane, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2017 Search PubMed.
- A. P. Abbott and K. J. McKenzie, Phys. Chem. Chem. Phys., 2006, 8, 4265 RSC.
- M. L. Pusey, M. S. Paley, M. B. Turner and R. D. Rogers, Cryst. Growth Des., 2007, 7, 787–793 CrossRef CAS.
- D. Hekmat, D. Hebel, S. Joswig, M. Schmidt and D. Weuster-Botz, Biotechnol. Lett., 2007, 29, 1703–1711 CrossRef CAS PubMed.
- R. A. Judge, S. Takahashi, K. L. Longenecker, E. H. Fry, C. Abad-Zapatero and M. L. Chiu, Cryst. Growth Des., 2009, 9, 3463–3469 CrossRef CAS.
- W. Kunz and K. Häckl, Chem. Phys. Lett., 2016, 661, 6–12 CrossRef CAS.
- M. Freemantle, Chem. Eng. News, 1998, 76, 32–37 CrossRef.
- M. J. Earle and K. R. Seddon, Pure Appl. Chem., 2000, 72, 1391–1398 CAS.
- S. Zhang, J. Li, N. Jiang, X. Li, S. Pasupath, Y. Fang, Q. Liu and D. Dang, Chem. – Asian J., 2019, 14, 2810–2814 CAS.
- I. Newington, J. M. Perez-Arlandis and T. Welton, Org. Lett., 2007, 9, 5247–5250 CrossRef CAS PubMed.
- K. N. Marsh, A. Deev, A. C. T. Wu, E. Tran and A. Klamt, Korean J. Chem. Eng., 2002, 19, 357–362 CrossRef CAS.
- H. Ohno, M. Yoshizawa-Fujita and Y. Kohno, Bull. Chem. Soc. Jpn., 2019, 92, 852–868 CrossRef CAS.
- T. Zhou, H. Shi, X. Ding and Y. Zhou, Chem. Eng. Sci., 2021, 229, 116076 CrossRef CAS.
- H. Niedermeyer, C. Ashworth, A. Brandt, T. Welton and P. A. Hunt, Phys. Chem. Chem. Phys., 2013, 15, 11566 RSC.
- H. Weingärtner, Angew. Chem., Int. Ed., 2008, 47, 654–670 CrossRef PubMed.
- B. D. Rabideau, K. N. West and J. H. Davis, Chem. Commun., 2018, 54, 5019–5031 RSC.
- B. Subramaniam, Ind. Eng. Chem. Res., 2010, 49, 10218–10229 CrossRef CAS.
- J. S. Wilkes, Green Chem., 2002, 4, 73–80 RSC.
- J. Dupont, C. S. Consorti and J. Spencer, J. Braz. Chem. Soc., 2000, 11, 337–344 CAS.
- J. R. Harjani, S. J. Nara, P. U. Naik and M. M. Salunkhe, ACS Symp. Ser., 2007, 950, 194–208 CrossRef CAS.
- J. H. Davis Jr, Chem. Lett., 2004, 33, 1072–1077 CrossRef.
- R. Giernoth, Angew. Chem., Int. Ed., 2010, 49, 2834–2839 CrossRef CAS PubMed.
- E. D. Bates, R. D. Mayton, I. Ntai and J. H. Davis, J. Am. Chem. Soc., 2002, 124, 926–927 CrossRef CAS PubMed.
- H. Ohno and Y. Fukaya, Chem. Lett., 2009, 38, 2–7 CrossRef CAS.
- A. E. Visser, R. P. Swatloski, W. M. Reichert, R. Mayton, S. Sheff, A. Wierzbicki, J. H. Davis and R. D. Rogers, Environ. Sci. Technol., 2002, 36, 2523–2529 CrossRef CAS.
- A. E. Visser, R. P. Swatloski, W. M. Reichert, J. H. Davis Jr., R. D. Rogers, R. Mayton, S. Sheff and A. Wierzbicki, Chem. Commun., 2001, 135–136 RSC.
- D. H. Zaitsau, M. A. Varfolomeev, S. P. Verevkin, A. D. Stanton, M. S. Hindman and J. E. Bara, J. Chem. Thermodyn., 2016, 93, 151–156 CrossRef CAS.
- D. H. Zaitsau, A. V. Yermalayeu, S. P. Verevkin, J. E. Bara and A. D. Stanton, Ind. Eng. Chem. Res., 2013, 52, 16615–16621 CrossRef CAS.
- D. H. Zaitsau, A. V. Yermalayeu, S. P. Verevkin, J. E. Bara and D. A. Wallace, Thermochim. Acta, 2015, 622, 38–43 CrossRef CAS.
- S. A. Mirkhani and F. Gharagheizi, Ind. Eng. Chem. Res., 2012, 51, 2470–2477 CrossRef CAS.
- W. Silva, M. Zanatta, A. S. Ferreira, M. C. Corvo and E. J. Cabrita, Int. J. Mol. Sci., 2020, 21, 7745 CrossRef CAS PubMed.
- T. L. Greaves and C. J. Drummond, Chem. Rev., 2015, 115, 11379–11448 CrossRef CAS PubMed.
- M. N. Kobrak and N. Sandalow, ECS Proc. Vol., 2004, 2004–2024, 417–425 CrossRef.
- S. Sowmiah, V. Srinivasadesikan, M.-C. Tseng and Y.-H. Chu, Molecules, 2009, 14, 3780–3813 CrossRef CAS PubMed.
- G. Chatel, E. Naffrechoux and M. Draye, J. Hazard. Mater., 2017, 324, 773–780 CrossRef CAS PubMed.
- D. Zhao, Y. Liao and Z. Zhang, Clean: Soil, Air, Water, 2007, 35, 42–48 CAS.
- M. Kar, N. V. Plechkova, K. R. Seddon, J. M. Pringle and D. R. MacFarlane, Aust. J. Chem., 2019, 72, 3 CrossRef CAS.
- P. J. Scammells, J. L. Scott and R. D. Singer, Aust. J. Chem., 2005, 58, 155 CrossRef CAS.
- D. R. MacFarlane, M. Kar and J. M. Pringle, Fundamentals of Ionic Liquids, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2017 Search PubMed.
- I. López-Martin, E. Burello, P. N. Davey, K. R. Seddon and G. Rothenberg, ChemPhysChem, 2007, 8, 690–695 CrossRef PubMed.
- K. E. Gutowski, Phys. Sci. Rev., 2018, 3, 1–10 CrossRef.
- T. L. Greaves and C. J. Drummond, Chem. Rev., 2008, 108, 206–237 CrossRef CAS PubMed.
- W. Huang, X. Wu, J. Qi, Q. Zhu, W. Wu, Y. Lu and Z. Chen, Drug Discovery Today, 2020, 25, 901–908 CrossRef CAS PubMed.
- M. B. Shiflett, Commercial applications of ionic liquids, 2020.
- T. Köddermann, D. Paschek and R. Ludwig, ChemPhysChem, 2008, 9, 549–555 CrossRef PubMed.
- E. I. Izgorodina, Phys. Chem. Chem. Phys., 2011, 13, 4189 RSC.
- J. G. McDaniel and A. Yethiraj, J. Phys. Chem. B, 2019, 123, 3499–3512 CrossRef CAS PubMed.
- R. M. Lynden-Bell, Phys. Chem. Chem. Phys., 2010, 12, 1733–1740 RSC.
- R. M. Lynden-Bell, A. I. Frolov and M. V. Fedorov, Phys. Chem. Chem. Phys., 2012, 14, 2693 RSC.
- A. M. Smith, A. A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2157–2163 CrossRef CAS PubMed.
- K. Ma, C. Lian, C. E. Woodward and B. Qin, Chem. Phys. Lett., 2020, 739, 137001 CrossRef CAS.
- M. A. Gebbie, A. M. Smith, H. A. Dobbs, A. A. Lee, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvili, S. Perkin and R. Atkin, Chem. Commun., 2017, 53, 1214–1224 RSC.
- A. A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Phys. Rev. Lett., 2017, 119, 026002 CrossRef.
- M. A. Gebbie, H. A. Dobbs, M. Valtiner and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7432–7437 CrossRef CAS PubMed.
- P. Gaddam and W. Ducker, Langmuir, 2019, 35, 5719–5727 CrossRef CAS PubMed.
- A. a Lee, D. Vella, S. Perkin and A. Goriely, J. Phys. Chem. Lett., 2014, 6, 159–163 CrossRef PubMed.
- M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674–9679 CrossRef CAS.
- E. W. Castner, J. F. Wishart and H. Shirota, Acc. Chem. Res., 2007, 40, 1217–1227 CrossRef CAS PubMed.
- H. Shirota and E. W. Castner, J. Phys. Chem. A, 2005, 109, 9388–9392 CrossRef CAS PubMed.
- I. Avramov, J. Non-Cryst. Solids, 2000, 262, 258–263 CrossRef CAS.
- J. W. P. Schmelzer, E. D. Zanotto and V. M. Fokin, J. Chem. Phys., 2005, 122, 074511 CrossRef PubMed.
- R. Casalini and S. Bair, J. Chem. Phys., 2008, 128, 084511 CrossRef CAS PubMed.
- R. Casalini and C. M. Roland, J. Non-Cryst. Solids, 2007, 353, 3936–3939 CrossRef CAS.
- R. Casalini and C. M. Roland, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 062501 CrossRef CAS PubMed.
- D. Fragiadakis and C. M. Roland, J. Chem. Phys., 2011, 134, 044504 CrossRef CAS PubMed.
- C. Alba-Simionesco, A. Cailliaux, A. Alegría and G. Tarjus, Europhys. Lett., 2004, 68, 58–64 CrossRef CAS.
- K. R. Harris and M. Kanakubo, Faraday Discuss., 2012, 154, 425–438 RSC.
- E. R. López, A. S. Pensado, M. J. P. Comuñas, A. A. H. Pádua, J. Fernández and K. R. Harris, J. Chem. Phys., 2011, 134, 144507 CrossRef PubMed.
- H. W. Hansen, F. Lundin, K. Adrjanowicz, B. Frick, A. Matic and K. Niss, Phys. Chem. Chem. Phys., 2020, 22, 14169–14176 RSC.
- S. Cheng, M. Musiał, Z. Wojnarowska, A. Holt, C. M. Roland, E. Drockenmuller and M. Paluch, J. Phys. Chem. B, 2020, 124, 1240–1244 CrossRef CAS PubMed.
- K. R. Harris, M. Kanakubo, D. Kodama, T. Makino, Y. Mizuguchi, M. Watanabe and T. Watanabe, J. Chem. Eng. Data, 2018, 63, 2015–2027 CrossRef CAS.
- R. Shi and Y. Wang, Sci. Rep., 2016, 6, 1–12 CrossRef.
- K. Wendler, S. Zahn, F. Dommert, R. Berger, C. Holm, B. Kirchner and L. Delle Site, J. Chem. Theory Comput., 2011, 7, 3040–3044 CrossRef CAS.
- J. C. Araque, S. K. Yadav, M. Shadeck, M. Maroncelli and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 7015–7029 CrossRef CAS PubMed.
- H. K. Kashyap, H. V. R. Annapureddy, F. O. Raineri and C. J. Margulis, J. Phys. Chem. B, 2011, 115, 13212–13221 CrossRef CAS PubMed.
- T. Niemann, A. Strate, R. Ludwig, H. J. Zeng, F. S. Menges and M. A. Johnson, Phys. Chem. Chem. Phys., 2019, 21, 18092–18098 RSC.
- E. A. Shelepova, R. Ludwig, D. Paschek and N. N. Medvedev, J. Mol. Liq., 2021, 115589 CrossRef CAS.
- D. H. Zaitsau, V. N. Emel’yanenko, P. Stange, S. P. Verevkin and R. Ludwig, Angew. Chem., Int. Ed., 2019, 58, 8589–8592 CrossRef CAS.
- Y. Tanaka, T. Yamamoto, Y. Satomi, H. Kubota and T. Makita, Rev. Phys. Chem. Jpn., 1977, 47, 12 CAS.
- J. Gujt, M. Bešter-Rogač and B. Hribar-Lee, J. Mol. Liq., 2014, 190, 34–41 CrossRef CAS PubMed.
- K. D. Collins, Biophys. J., 1997, 72, 65–76 CrossRef CAS.
- T. T. Duignan, D. F. Parsons and B. W. Ninham, Chem. Phys. Lett., 2014, 608, 55–59 CrossRef CAS.
- I. Krossing, J. M. Slattery, C. Daguenet, P. J. Dyson, A. Oleinikova and H. Weingärtner, J. Am. Chem. Soc., 2006, 128, 13427–13434 CrossRef CAS.
- J. M. Slattery, C. Daguenet, P. J. Dyson, T. J. S. Schubert and I. Krossing, Angew. Chem., Int. Ed., 2007, 46, 5384–5388 CrossRef CAS PubMed.
- H. Weber and B. Kirchner, J. Phys. Chem. B, 2016, 120, 2471–2483 CrossRef CAS PubMed.
- P. Barthen, W. Frank and N. Ignatiev, Ionics, 2015, 21, 149–159 CrossRef CAS.
- J. M. Pringle, J. Golding, K. Baranyai, C. M. Forsyth, G. B. Deacon, J. L. Scott and D. R. MacFarlane, New J. Chem., 2003, 27, 1504–1510 RSC.
- N. V. Ignat’ev, A. Kucheryna, G. Bissky and H. Willner, ACS Symp. Ser., 2007, 975, 320–334 CrossRef.
- F. Philippi, D. Pugh, D. Rauber, T. Welton and P. A. Hunt, Chem. Sci., 2020, 11, 6405–6422 RSC.
- H. Shirota, K. Nishikawa and T. Ishida, J. Phys. Chem. B, 2009, 113, 9831–9839 CrossRef CAS PubMed.
- T. Ishida, K. Nishikawa and H. Shirota, J. Phys. Chem. B, 2009, 113, 9840–9851 CrossRef CAS PubMed.
- S. Tsuzuki, ChemPhysChem, 2012, 13, 1664–1670 CrossRef CAS PubMed.
- S. N. Butler and F. Müller-Plathe, ChemPhysChem, 2012, 13, 1791–1801 CrossRef CAS PubMed.
- H. V. Spohr and G. N. Patey, J. Chem. Phys., 2008, 129, 064517 CrossRef CAS PubMed.
- H. V. Spohr and G. N. Patey, J. Chem. Phys., 2010, 132, 154504 CrossRef PubMed.
- N. Kikuchi and J. Horbach, Europhys. Lett., 2007, 77, 26001 CrossRef.
- J. M. Pringle, P. C. Howlett, D. R. MacFarlane and M. Forsyth, J. Mater. Chem., 2010, 20, 2056 RSC.
- M. Forsyth, F. Chen, L. A. O’Dell and K. Romanenko, Solid State Ionics, 2016, 288, 160–166 CrossRef CAS.
- F. Chen, S. W. de Leeuw and M. Forsyth, J. Phys. Chem. Lett., 2013, 4, 4085–4089 CrossRef CAS.
- K. R. Harris, J. Phys. Chem. B, 2016, 120, 12135–12147 CrossRef CAS PubMed.
- L. Bi and Z.-C. Liang, J. Mol. Liq., 2015, 212, 775–784 CrossRef CAS.
- G. W. Driver, Y. Huang, A. Laaksonen, T. Sparrman, Y.-L. Wang and P.-O. Westlund, Phys. Chem. Chem. Phys., 2017, 19, 4975–4988 RSC.
- O. Hollóczki, F. Malberg, T. Welton and B. Kirchner, Phys. Chem. Chem. Phys., 2014, 16, 16880–16890 RSC.
- K. Ueno, H. Tokuda and M. Watanabe, Phys. Chem. Chem. Phys., 2010, 12, 1649–1658 RSC.
- T. Köddermann, R. Ludwig and D. Paschek, ChemPhysChem, 2008, 9, 1851–1858 CrossRef PubMed.
- F. Philippi, D. Rauber, M. Springborg and R. Hempelmann, J. Phys. Chem. A, 2019, 123, 851–861 CrossRef CAS.
- Y. Shao, K. Shigenobu, M. Watanabe and C. Zhang, J. Phys. Chem. B, 2020, 124, 4774–4780 CrossRef CAS.
- M. Harada, A. Yamanaka, M. Tanigaki and Y. Tada, J. Chem. Phys., 1982, 76, 1550–1556 CrossRef CAS.
- J. Trullàs and J. A. Padró, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 1162–1170 CrossRef.
- J. A. Padró, J. Trullàs and G. Sesé, Mol. Phys., 1991, 72, 1035–1049 CrossRef.
- J. Trullàs and J. A. Padró, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 12210–12217 CrossRef.
- F. O. Raineri and H. L. Friedman, J. Chem. Phys., 1989, 91, 5633–5641 CrossRef CAS.
- J. Trullàs and J. A. Padró, J. Chem. Phys., 1993, 99, 3983–3989 CrossRef.
- S. Tsuzuki, H. Matsumoto, W. Shinoda and M. Mikami, Phys. Chem. Chem. Phys., 2011, 13, 5987 RSC.
- R. K. Blundell and P. Licence, Chem. Commun., 2014, 50, 12080–12083 RSC.
- T. Endo, S. Hoshino, Y. Shimizu, K. Fujii and K. Nishikawa, J. Phys. Chem. B, 2016, 120, 10336–10349 CrossRef CAS PubMed.
- K. Bernardino, Y. Zhang, M. C. C. Ribeiro and E. J. Maginn, J. Chem. Phys., 2020, 153, 044504 CrossRef CAS PubMed.
- G. Yu, D. Zhao, L. Wen, S. Yang and X. Chen, AIChE J., 2012, 58, 2885–2899 CrossRef CAS.
- C. J. Bradaric, A. Downard, C. Kennedy, A. J. Robertson and Y. Zhou, Green Chem., 2003, 5, 143–152 RSC.
- K. J. Fraser and D. R. MacFarlane, Aust. J. Chem., 2009, 62, 309–321 CrossRef CAS.
- S. Seki, K. Hayamizu, S. Tsuzuki, K. Fujii, Y. Umebayashi, T. Mitsugi, T. Kobayashi, Y. Ohno, Y. Kobayashi, Y. Mita, H. Miyashiro and S. Ishiguro, Phys. Chem. Chem. Phys., 2009, 11, 3509–3514 RSC.
- K. Tsunashima and M. Sugiya, Electrochem. Commun., 2007, 9, 2353–2358 CrossRef CAS.
- L. K. Scarbath-Evers, P. A. Hunt, B. Kirchner, D. R. MacFarlane and S. Zahn, Phys. Chem. Chem. Phys., 2015, 17, 20205–20216 RSC.
- F. Philippi, D. Rauber, B. Kuttich, T. Kraus, C. W. M. Kay, R. Hempelmann, P. A. Hunt and T. Welton, Phys. Chem. Chem. Phys., 2020, 22, 23038–23056 RSC.
- M. H. Ghatee and M. Bahrami, Chem. Phys., 2017, 490, 92–105 CrossRef CAS.
- P. J. Carvalho, S. P. M. Ventura, M. L. S. Batista, B. Schröder, F. Gonçalves, J. Esperança, F. Mutelet and J. A. P. Coutinho, J. Chem. Phys., 2014, 140, 064505 CrossRef.
- H. Shirota and E. W. Castner, J. Phys. Chem. B, 2005, 109, 21576–21585 CrossRef CAS PubMed.
- H. Shirota, J. F. Wishart and E. W. Castner, J. Phys. Chem. B, 2007, 111, 4819–4829 CrossRef CAS.
- K. Tsunashima, A. Kawabata, M. Matsumiya, S. Kodama, R. Enomoto, M. Sugiya and Y. Kunugi, Electrochem. Commun., 2011, 13, 178–181 CrossRef CAS.
- K. Tsunashima, Y. Sakai and M. Matsumiya, Electrochem. Commun., 2014, 39, 30–33 CrossRef CAS.
- T. Nokami, T. Yamashita, T. Komura, N. Handa, M. Shimizu, K. Yamaguchi, Y. Domi, H. Usui, H. Sakaguchi and T. Itoh, Faraday Discuss., 2018, 206, 523–534 RSC.
- A. R. Neale, S. Murphy, P. Goodrich, C. Hardacre and J. Jacquemin, ChemPhysChem, 2017, 18, 2040–2057 CrossRef CAS PubMed.
- Z. Chen, Y. Huo, J. Cao, L. Xu and S. Zhang, Ind. Eng. Chem. Res., 2016, 55, 11589–11596 CrossRef CAS.
- Z. J. Chen, T. Xue and J.-M. Lee, RSC Adv., 2012, 2, 10564 RSC.
- L. J. A. Siqueira and M. C. C. Ribeiro, J. Phys. Chem. B, 2009, 113, 1074–1079 CrossRef CAS PubMed.
- H. Shen, Z. Chen and T. Xiao, ChemistrySelect, 2017, 2, 5545–5551 CrossRef CAS.
- M. J. Monteiro, F. F. Camilo, M. C. C. Ribeiro and R. M. Torresi, J. Phys. Chem. B, 2010, 114, 12488–12494 CrossRef CAS PubMed.
- H. Shirota, H. Fukazawa, T. Fujisawa and J. F. Wishart, J. Phys. Chem. B, 2010, 114, 9400–9412 CrossRef CAS.
- A. Triolo, O. Russina, R. Caminiti, H. Shirota, H. Y. Lee, C. S. Santos, N. S. Murthy and E. W. Castner Jr, Chem. Commun., 2012, 48, 4959 RSC.
- H. K. Kashyap, C. S. Santos, R. P. Daly, J. J. Hettige, N. S. Murthy, H. Shirota, E. W. Castner and C. J. Margulis, J. Phys. Chem. B, 2013, 117, 1130–1135 CrossRef CAS.
- K. Yoshii, T. Uto, N. Tachikawa and Y. Katayama, Phys. Chem. Chem. Phys., 2020, 22, 19480–19491 RSC.
- K. Shimizu, C. E. S. Bernardes, A. Triolo and J. N. Canongia Lopes, Phys. Chem. Chem. Phys., 2013, 15, 16256 RSC.
- G. D. Smith, O. Borodin, L. Li, H. Kim, Q. Liu, J. E. Bara, D. L. Gin and R. Nobel, Phys. Chem. Chem. Phys., 2008, 10, 6301 RSC.
- H. J. Zeng, M. A. Johnson, J. D. Ramdihal, R. A. Sumner, C. Rodriguez, S. I. Lall-Ramnarine and J. F. Wishart, J. Phys. Chem. A, 2019, 123, 8370–8376 CrossRef CAS PubMed.
- P. Bonhôte, A.-P. Dias, M. Armand, N. Papageorgiou, K. Kalyanasundaram and M. Grätzel, Inorg. Chem., 1996, 35, 1168–1178 CrossRef PubMed.
- P. Johansson, S. P. Gejji, J. Tegenfeldt and J. Lindgren, Electrochim. Acta, 1998, 43, 1375–1379 CrossRef CAS.
- O. Borodin, W. Gorecki, G. D. Smith and M. Armand, J. Phys. Chem. B, 2010, 114, 6786–6798 CrossRef CAS PubMed.
- J. N. Canongia Lopes, K. Shimizu, A. A. H. Pádua, Y. Umebayashi, S. Fukuda, K. Fujii and S. Ishiguro, J. Phys. Chem. B, 2008, 112, 1465–1472 CrossRef CAS PubMed.
- S. N. Suarez, A. Rúa, D. Cuffari, K. Pilar, J. L. Hatcher, S. Ramati and J. F. Wishart, J. Phys. Chem. B, 2015, 119, 14756–14765 CrossRef CAS PubMed.
- K. Pilar, A. Rua, S. N. Suarez, C. Mallia, S. Lai, J. R. P. Jayakody, J. L. Hatcher, J. F. Wishart and S. Greenbaum, J. Electrochem. Soc., 2017, 164, H5189–H5196 CrossRef CAS PubMed.
- A. Martinelli, A. Matic, P. Johansson, P. Jacobsson, L. Börjesson, A. Fernicola, S. Panero, B. Scrosati and H. Ohno, J. Raman Spectrosc., 2011, 42, 522–528 CrossRef CAS.
- Y. Umebayashi, T. Mitsugi, K. Fujii, S. Seki, K. Chiba, H. Yamamoto, J. N. Canongia Lopes, A. A. H. Pádua, M. Takeuchi, R. Kanzaki and S. Ishiguro, J. Phys. Chem. B, 2009, 113, 4338–4346 CrossRef CAS PubMed.
- J. C. Lassègues, J. Grondin, R. Holomb and P. Johansson, J. Raman Spectrosc., 2007, 38, 551–558 CrossRef.
- K. Fujii, T. Fujimori, T. Takamuku, R. Kanzaki, Y. Umebayashi and S. Ishiguro, J. Phys. Chem. B, 2006, 110, 8179–8183 CrossRef CAS PubMed.
- O. Palumbo, F. Trequattrini, F. M. Vitucci and A. Paolone, J. Phys. Chem. B, 2015, 119, 12905–12911 CrossRef CAS PubMed.
- F. M. Vitucci, F. Trequattrini, O. Palumbo, J.-B. Brubach, P. Roy, M. A. Navarra, S. Panero and A. Paolone, J. Phys. Chem. A, 2014, 118, 8758–8764 CrossRef CAS PubMed.
- S. Kakinuma, T. Ishida and H. Shirota, J. Phys. Chem. B, 2017, 121, 250–264 CrossRef CAS PubMed.
- S. Yamaguchi, H. Yamada, Y. Takeoka, M. Rikukawa and M. Yoshizawa-Fujita, New J. Chem., 2019, 43, 4008–4012 RSC.
- M. T. Clough, C. R. Crick, J. Gräsvik, P. A. Hunt, H. Niedermeyer, T. Welton and O. P. Whitaker, Chem. Sci., 2015, 6, 1101–1114 RSC.
- K. Fujii, S. Seki, S. Fukuda, R. Kanzaki, T. Takamuku, Y. Umebayashi and S. Ishiguro, J. Phys. Chem. B, 2007, 111, 12829–12833 CrossRef CAS PubMed.
- T. Tamura, T. Hachida, K. Yoshida, N. Tachikawa, K. Dokko and M. Watanabe, J. Power Sources, 2010, 195, 6095–6100 CrossRef CAS.
- R. Jüschke, G. Henkel and P. Sartori, Z. Naturforsch., B: J. Chem. Sci., 1997, 52, 359–366 CrossRef.
- M. Goldstein, J. Chem. Phys., 1969, 51, 3728–3739 CrossRef CAS.
- Z. Raza, B. Alling and I. A. Abrikosov, J. Phys.: Condens. Matter, 2015, 27, 293201 CrossRef PubMed.
- A. Heuer, J. Phys.: Condens. Matter, 2008, 20, 373101 CrossRef.
- M. Goldstein, J. Non-Cryst. Solids, 2011, 357, 249–250 CrossRef CAS.
- O. Palumbo, F. Trequattrini, G. B. Appetecchi, L. Conte and A. Paolone, J. Mol. Liq., 2017, 243, 9–13 CrossRef CAS.
- H. D. Weymann, Kolloid-Z. Z. Polym., Suppl., 1962, 181, 131–137 CrossRef CAS.
- A. P. Abbott, ChemPhysChem, 2004, 5, 1242–1246 CrossRef CAS PubMed.
- A. P. Abbott, ChemPhysChem, 2005, 6, 2502–2505 CrossRef CAS PubMed.
- N. V. Ignat’ev, U. Welz-Biermann, A. Kucheryna, G. Bissky and H. Willner, J. Fluorine Chem., 2005, 126, 1150–1159 CrossRef.
- N. V. Ignat’ev, W.-R. Pitner and U. Welz-Biermann, ACS Symp. Ser., 2007, 950, 281–287 CrossRef.
- M. Carboni, R. Spezia and S. Brutti, J. Phys. Chem. C, 2014, 118, 24221–24230 CrossRef CAS.
- W. Mahler, Inorg. Chem., 1963, 2, 230 CrossRef CAS.
- M. H. Kowsari and S. Ebrahimi, Phys. Chem. Chem. Phys., 2018, 20, 13379–13393 RSC.
- J. Landmann, J. A. P. Sprenger, P. T. Hennig, R. Bertermann, M. Grüne, F. Würthner, N. V. Ignat’ev and M. Finze, Chem. – Eur. J., 2018, 24, 608–623 CrossRef CAS PubMed.
- Z.-B. Zhou, H. Matsumoto and K. Tatsumi, Chem. – Eur. J., 2006, 12, 2196–2212 CrossRef CAS PubMed.
- H. Li, M. Ibrahim, I. Agberemi and M. N. Kobrak, J. Chem. Phys., 2008, 129, 124507 CrossRef PubMed.
- M. N. Kobrak and H. Li, Phys. Chem. Chem. Phys., 2010, 12, 1922 RSC.
- T. Yan, C. J. Burnham, M. G. Del Pópolo and G. A. Voth, J. Phys. Chem. B, 2004, 108, 11877–11881 CrossRef CAS.
- C. Schröder and O. Steinhauser, J. Chem. Phys., 2010, 133, 154511 CrossRef PubMed.
- C. Schröder, Phys. Chem. Chem. Phys., 2012, 14, 3089 RSC.
- J. G. McDaniel and A. Yethiraj, J. Phys. Chem. Lett., 2018, 9, 4765–4770 CrossRef CAS PubMed.
- K. Goloviznina, J. N. Canongia Lopes, M. Costa Gomes and A. A. H. Pádua, J. Chem. Theory Comput., 2019, 15, 5858–5871 CrossRef CAS PubMed.
- O. Borodin, J. Phys. Chem. B, 2009, 113, 11463–11478 CrossRef CAS PubMed.
- D. Bedrov, J.-P. Piquemal, O. Borodin, A. D. MacKerell, B. Roux and C. Schröder, Chem. Rev., 2019, 119, 7940–7995 CrossRef CAS PubMed.
- H. Wang, R. S. DeFever, Y. Zhang, F. Wu, S. Roy, V. S. Bryantsev, C. J. Margulis and E. J. Maginn, J. Chem. Phys., 2020, 153, 214502 CrossRef CAS PubMed.
- J. G. McDaniel, J. Phys. Chem. B, 2018, 122, 4345–4355 CrossRef CAS PubMed.
- A. A. H. Pádua, J. Chem. Phys., 2017, 146, 204501 CrossRef PubMed.
- M. Schmollngruber, V. Lesch, C. Schröder, A. Heuer and O. Steinhauser, Phys. Chem. Chem. Phys., 2015, 17, 14297–14306 RSC.
- D. Bedrov, O. Borodin, Z. Li and G. D. Smith, J. Phys. Chem. B, 2010, 114, 4984–4997 CrossRef CAS.
- R. Bosque and J. Sales, J. Chem. Inf. Comput. Sci., 2002, 42, 1154–1163 CrossRef CAS PubMed.
- K. J. Miller, J. Am. Chem. Soc., 1990, 112, 8533–8542 CrossRef CAS.
- C. Ruth Le Sueur and A. J. Stone, Mol. Phys., 1994, 83, 293–307 CrossRef.
- T. Brinck, J. S. Murray and P. Politzer, J. Chem. Phys., 1993, 98, 4305–4306 CrossRef CAS.
- W. Xu, E. I. Cooper and C. A. A. Angell, J. Phys. Chem. B, 2003, 107, 6170–6178 CrossRef CAS.
- S. Koßmann, J. Thar, B. Kirchner, P. A. Hunt and T. Welton, J. Chem. Phys., 2006, 124, 174506 CrossRef PubMed.
- K. Wendler, F. Dommert, Y. Y. Zhao, R. Berger, C. Holm and L. Delle Site, Faraday Discuss., 2012, 154, 111–132 RSC.
- L. Piela, Ideas of Quantum Chemistry, Elsevier, 2014, pp. e169–e181 Search PubMed.
- F. Jensen, Introduction to Computational Chemistry, John Wiley & Sons, Inc., West Sussex, 2nd edn, 2007 Search PubMed.
- H. V. Spohr and G. N. Patey, J. Chem. Phys., 2009, 130, 104506 CrossRef CAS PubMed.
- M. Malvaldi and C. Chiappe, J. Phys.: Condens. Matter, 2008, 20, 035108 CrossRef.
- H. Lu, B. Li, S. Nordholm, C. E. Woodward and J. Forsman, J. Chem. Phys., 2016, 145, 234510 CrossRef PubMed.
- E. K. Lindenberg and G. N. Patey, J. Chem. Phys., 2014, 140, 104504 CrossRef CAS PubMed.
- E. K. Lindenberg and G. N. Patey, J. Chem. Phys., 2015, 143, 024508 CrossRef CAS PubMed.
- H. Li and M. N. Kobrak, J. Chem. Phys., 2009, 131, 194507 CrossRef PubMed.
- C. J. Margulis, H. A. Stern and B. J. Berne, J. Phys. Chem. B, 2002, 106, 12017–12021 CrossRef CAS.
- M. Drisch, L. A. Bischoff, J. A. P. Sprenger, P. T. Hennig, R. Wirthensohn, J. Landmann, S. Z. Konieczka, M. Hailmann, N. V. Ignat’ev and M. Finze, Chem. – Eur. J., 2020, 26, 11625–11633 CrossRef CAS PubMed.
- N. V. Ignat’ev, M. Finze, J. A. P. Sprenger, C. Kerpen, E. Bernhardt and H. Willner, J. Fluorine Chem., 2015, 177, 46–54 CrossRef.
- N. V. Ignat’ev and M. Finze, Eur. J. Inorg. Chem., 2019, 3539–3560 CrossRef.
- L. A. Bischoff, M. Drisch, C. Kerpen, P. T. Hennig, J. Landmann, J. A. P. Sprenger, R. Bertermann, M. Grüne, Q. Yuan, J. Warneke, X. Wang, N. V. Ignat’ev and M. Finze, Chem. – Eur. J., 2019, 25, 3560–3574 CrossRef CAS PubMed.
- L. A. Bischoff, J. A. P. Sprenger, P. T. Hennig, N. V. Ignat’ev and M. Finze, Z. Anorg. Allg. Chem., 2018, 644, 1285–1292 CrossRef CAS.
- P. A. Wood, S. J. Borwick, D. J. Watkin, W. D. S. Motherwell and F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 393–396 CrossRef CAS PubMed.
- S. Lee, A. B. Mallik and D. C. Fredrickson, Cryst. Growth Des., 2004, 4, 279–290 CrossRef CAS.
- E. Gómez, N. Calvar and Á. Domínguez, Ionic Liquids – Current State of the Art, InTech, 2015 Search PubMed.
- B. D. Rabideau, M. Soltani, R. A. Parker, B. Siu, E. A. Salter, A. Wierzbicki, K. N. West and J. H. Davis, Phys. Chem. Chem. Phys., 2020, 22, 12301–12311 RSC.
- C. A. Cassity, B. Siu, M. Soltani, J. L. McGeehee, K. J. Strickland, M. Vo, E. A. Salter, A. C. Stenson, A. Wierzbicki, K. N. West, B. D. Rabideau and J. H. Davis, Phys. Chem. Chem. Phys., 2017, 19, 31560–31571 RSC.
- P. A. Hunt, C. R. Ashworth and R. P. Matthews, Chem. Soc. Rev., 2015, 44, 1257–1288 RSC.
- K. Dong, Y. Song, X. Liu, W. Cheng, X. Yao and S. Zhang, J. Phys. Chem. B, 2012, 116, 1007–1017 CrossRef CAS PubMed.
- K. Low, S. Y. S. Tan and E. I. Izgorodina, Front. Chem., 2019, 7, 1–16 CrossRef PubMed.
- A. M. Moschovi and V. Dracopoulos, J. Mol. Liq., 2015, 210, 189–199 CrossRef CAS.
- R. C. Remsing, J. L. Wildin, A. L. Rapp and G. Moyna, J. Phys. Chem. B, 2007, 111, 11619–11621 CrossRef CAS PubMed.
- A. Khrizman, H. Y. Cheng, G. Bottini and G. Moyna, Chem. Commun., 2015, 51, 3193–3195 RSC.
- P. A. Hunt and I. R. Gould, J. Phys. Chem. A, 2006, 110, 2269–2282 CrossRef CAS PubMed.
- G. Bottini and G. Moyna, Magn. Reson. Chem., 2018, 56, 103–107 CrossRef CAS PubMed.
- T. Peppel, C. Roth, K. Fumino, D. Paschek, M. Köckerling and R. Ludwig, Angew. Chem., Int. Ed., 2011, 50, 6661–6665 CrossRef CAS PubMed.
- K. Fumino, T. Peppel, M. Geppert-Rybczyńska, D. H. Zaitsau, J. K. Lehmann, S. P. Verevkin, M. Köckerling and R. Ludwig, Phys. Chem. Chem. Phys., 2011, 13, 14064 RSC.
- K. Fumino, S. Reimann and R. Ludwig, Phys. Chem. Chem. Phys., 2014, 16, 21903–21929 RSC.
- K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., Int. Ed., 2008, 47, 8731–8734 CrossRef CAS PubMed.
- D. Shang, S. Zeng, X. Zhang, X. Zhang, L. Bai and H. Dong, J. Mol. Liq., 2020, 312, 113411 CrossRef CAS.
- A. Aggarwal, N. L. Lancaster, A. R. Sethi and T. Welton, Green Chem., 2002, 4, 517–520 RSC.
- L. K. J. Hauru, M. Hummel, A. W. T. King, I. Kilpeläinen and H. Sixta, Biomacromolecules, 2012, 13, 2896–2905 CrossRef CAS PubMed.
- R. Bini, C. Chiappe, V. L. Mestre, C. S. Pomelli and T. Welton, Org. Biomol. Chem., 2008, 6, 2522 RSC.
- N. Mohd, S. F. S. Draman, M. S. N. Salleh and N. B. Yusof, AIP Conf. Proc., 2017, 1809, 020035 CrossRef.
- V. S. Raghuwanshi, Y. Cohen, G. Garnier, C. J. Garvey, R. A. Russell, T. Darwish and G. Garnier, Macromolecules, 2018, 51, 7649–7655 CrossRef CAS.
- I. Bodachivskyi, C. J. Page, U. Kuzhiumparambil, S. F. R. Hinkley, I. M. Sims and D. B. G. Williams, ACS Sustainable Chem. Eng., 2020, 8, 10142–10150 CrossRef CAS.
- J. Zhang, J. Wu, J. Yu, X. Zhang, J. He and J. Zhang, Mater. Chem. Front., 2017, 1, 1273–1290 RSC.
- P. A. Hunt, J. Phys. Chem. B, 2007, 111, 4844–4853 CrossRef CAS PubMed.
- A. S. M. C. Rodrigues, C. F. R. A. C. Lima, J. A. P. Coutinho and L. M. N. B. F. Santos, Phys. Chem. Chem. Phys., 2017, 19, 5326–5332 RSC.
- M. H. Kowsari and M. Fakhraee, J. Chem. Eng. Data, 2015, 60, 551–560 CrossRef CAS.
- Y. Zhang and E. J. Maginn, Phys. Chem. Chem. Phys., 2012, 14, 12157 RSC.
- K. Noack, P. S. Schulz, N. Paape, J. Kiefer, P. Wasserscheid and A. Leipertz, Phys. Chem. Chem. Phys., 2010, 12, 14153 RSC.
- M. T. Clough, K. Geyer, P. A. Hunt, J. Mertes and T. Welton, Phys. Chem. Chem. Phys., 2013, 15, 20480–20495 RSC.
- S. Zahn, G. Bruns, J. Thar and B. Kirchner, Phys. Chem. Chem. Phys., 2008, 10, 6921 RSC.
- E. I. Izgorodina, R. Maganti, V. Armel, P. M. Dean, J. M. Pringle, K. R. Seddon and D. R. MacFarlane, J. Phys. Chem. B, 2011, 115, 14688–14697 CrossRef CAS.
- K. Jiang, L. Liu, X. Liu, X. Zhang and S. Zhang, Ind. Eng. Chem. Res., 2019, 58, 18848–18854 CrossRef CAS.
- M. Z. Brela, P. Kubisiak and A. Eilmes, J. Phys. Chem. B, 2018, 122, 9527–9537 CrossRef CAS PubMed.
- S. Tsuzuki, H. Tokuda and M. Mikami, Phys. Chem. Chem. Phys., 2007, 9, 4780 RSC.
- Y. Danten, M. I. Cabaço and M. Besnard, J. Phys. Chem. A, 2009, 113, 2873–2889 CrossRef CAS PubMed.
- T. Buffeteau, J. Grondin, Y. Danten and J.-C. Lassègues, J. Phys. Chem. B, 2010, 114, 7587–7592 CrossRef CAS PubMed.
- J.-C. Lassègues, J. Grondin, D. Cavagnat and P. Johansson, J. Phys. Chem. A, 2009, 113, 6419–6421 CrossRef PubMed.
- L. Xue, E. Gurung, G. Tamas, Y. P. Koh, M. Shadeck, S. L. Simon, M. Maroncelli and E. L. Quitevis, J. Chem. Eng. Data, 2016, 61, 1078–1091 CrossRef CAS.
- Y. Zhang, L. Xue, F. Khabaz, R. Doerfler, E. L. Quitevis, R. Khare and E. J. Maginn, J. Phys. Chem. B, 2015, 119, 14934–14944 CrossRef CAS PubMed.
- Z. J. Chen and J.-M. Lee, J. Phys. Chem. B, 2014, 118, 2712–2718 CrossRef CAS PubMed.
- K. R. Harris, M. Kanakubo and L. A. Woolf, J. Chem. Eng. Data, 2007, 52, 1080–1085 CrossRef CAS.
- R. Mishra, J. S. Mishra and S. A. Chaubey, Curr. Org. Chem., 2019, 23, 1239–1255 CrossRef CAS.
- T. Alpers, T. W. T. Muesmann, O. Temme and J. Christoffers, Eur. J. Org. Chem., 2018, 4331–4337 CrossRef CAS.
- I. A. Shkrob, T. W. Marin, H. Luo and S. Dai, J. Phys. Chem. B, 2013, 117, 14372–14384 CrossRef CAS PubMed.
- Y. Jeong and J.-S. Ryu, J. Org. Chem., 2010, 75, 4183–4191 CrossRef CAS PubMed.
- R. R. Hawker, R. S. Haines and J. B. Harper, Chem. Commun., 2018, 54, 2296–2299 RSC.
- C. Chiappe, A. Sanzone, D. Mendola, F. Castiglione, A. Famulari, G. Raos and A. Mele, J. Phys. Chem. B, 2013, 117, 668–676 CrossRef CAS.
- D. Chand, M. Wilk-Kozubek, V. Smetana and A.-V. Mudring, ACS Sustainable Chem. Eng., 2019, 7, 15995–16006 CrossRef CAS.
- S. Raiguel, J. Thomas, K. Binnemans and W. Dehaen, Eur. J. Org. Chem., 2018, 4850–4856 CrossRef CAS.
- S. Sanghi, E. Willett, C. Versek, M. Tuominen and E. B. Coughlin, RSC Adv., 2012, 2, 848–853 RSC.
- Z. Yacob and J. Liebscher, Ionic Liquids - Classes and Properties, InTech, 2011, pp. 3–23 Search PubMed.
- L. A. Daily and K. M. Miller, J. Org. Chem., 2013, 78, 4196–4201 CrossRef CAS PubMed.
- P. C. Hillesheim, J. A. Singh, S. M. Mahurin, P. F. Fulvio, Y. Oyola, X. Zhu, D. Jiang and S. Dai, RSC Adv., 2013, 3, 3981 RSC.
- A. T. De La Hoz, U. G. Brauer and K. M. Miller, J. Phys. Chem. B, 2014, 118, 9944–9951 CrossRef CAS PubMed.
- Z. K. Reeder, A. M. Adler and K. M. Miller, Tetrahedron Lett., 2016, 57, 206–209 CrossRef CAS.
- Y.-L. Wang, J. Phys. Chem. B, 2020, 124, 7452–7466 CrossRef CAS PubMed.
- J. Catalan, J. L. G. De Paz, M. Yanez, R. M. Claramunt, C. Lopez, J. Elguero, F. Anvia, J. H. Quian, M. Taagepera and R. W. Taft, J. Am. Chem. Soc., 1990, 112, 1303–1312 CrossRef CAS.
- B. Lenarcik and P. Ojczenasz, J. Heterocycl. Chem., 2002, 39, 287–290 CrossRef CAS.
- J. Catalán and J. Elguero, J. Chem. Soc., Perkin Trans. 2, 1983, 1869–1874 RSC.
- R. Ludwig and D. Paschek, ChemPhysChem, 2009, 10, 516–519 CrossRef CAS PubMed.
- A. E. Khudozhitkov, P. Stange, B. Golub, D. Paschek, A. G. Stepanov, D. I. Kolokolov and R. Ludwig, Angew. Chem., Int. Ed., 2017, 56, 14310–14314 CrossRef CAS PubMed.
- C. A. Rumble, A. Kaintz, S. K. Yadav, B. Conway, J. C. Araque, G. A. Baker, C. Margulis and M. Maroncelli, J. Phys. Chem. B, 2016, 120, 9450–9467 CrossRef CAS.
- I. M. Williams, L. N. Qasim, L. Tran, A. Scott, K. Riley and S. Dutta, DOI: DOI:10.1021/acs.jpca.9b02387.
- H. J. Zeng, F. S. Menges and M. A. Johnson, J. Phys. Chem. A, 2020, 124, 755–756 CrossRef CAS PubMed.
- L. De Marco, W. Carpenter, H. Liu, R. Biswas, J. M. Bowman and A. Tokmakoff, J. Phys. Chem. Lett., 2016, 7, 1769–1774 CrossRef CAS PubMed.
- A. D. Buckingham and L. Fan-Chen, Int. Rev. Phys. Chem., 1981, 1, 253–269 Search PubMed.
- S. Scheiner and M. Čuma, J. Am. Chem. Soc., 1996, 118, 1511–1521 CrossRef CAS.
- D. L. Cummings and J. L. Wood, J. Mol. Struct., 1974, 23, 103–112 CrossRef CAS.
- C. N. R. Rao, J. Chem. Soc., Faraday Trans. 1, 1975, 71, 980 RSC.
- A. Kjaersgaard, E. Vogt, N. F. Christensen and H. G. Kjaergaard, J. Phys. Chem. A, 2020, 124, 1763–1774 CrossRef CAS.
- D. J. O’Leary, D. D. Hickstein, B. K. V. Hansen and P. E. Hansen, J. Org. Chem., 2010, 75, 1331–1342 CrossRef PubMed.
- Y. Yoshimura, T. Takekiyo, C. Okamoto, N. Hatano and H. Abe, J. Raman Spectrosc., 2013, 44, 475–480 CrossRef CAS.
- C. Shi, X. Zhang, C.-H. Yu, Y.-F. Yao and W. Zhang, Nat. Commun., 2018, 9, 481 CrossRef.
- H. Abe, Y. Imai, T. Takekiyo and Y. Yoshimura, J. Phys. Chem. B, 2010, 114, 2834–2839 CrossRef CAS PubMed.
- K. Merz and A. Kupka, Cryst. Growth Des., 2015, 15, 1553–1558 CrossRef CAS.
- H. Abe, Y. Imai and Y. Yoshimura, Chem. Phys. Lett., 2011, 512, 204–207 CrossRef CAS.
- K. R. Seddon, A. Stark and M.-J. Torres, Pure Appl. Chem., 2000, 72, 2275–2287 CAS.
- A. Makowska, A. Siporska and J. Szydłowski, J. Phys. Chem. B, 2006, 110, 17195–17199 CrossRef CAS PubMed.
- Y. Yoshimura, N. Hatano, T. Takekiyo and H. Abe, J. Solution Chem., 2014, 43, 1509–1518 CrossRef CAS.
- N. Hatano, M. Watanabe, T. Takekiyo, H. Abe and Y. Yoshimura, J. Phys. Chem. A, 2012, 116, 1208–1212 CrossRef CAS.
- F. S. Menges, H. J. Zeng, P. J. Kelleher, O. Gorlova, M. A. Johnson, T. Niemann, A. Strate and R. Ludwig, J. Phys. Chem. Lett., 2018, 9, 2979–2984 CrossRef CAS.
- A. Knorr and R. Ludwig, Sci. Rep., 2015, 5, 17505 CrossRef.
- A. Strate, T. Niemann, D. Michalik and R. Ludwig, Angew. Chem., Int. Ed., 2017, 56, 496–500 CrossRef CAS PubMed.
- T. Niemann, D. H. Zaitsau, A. Strate, P. Stange and R. Ludwig, Phys. Chem. Chem. Phys., 2020, 22, 2763–2774 RSC.
- T. Niemann, D. Zaitsau, A. Strate, A. Villinger and R. Ludwig, Sci. Rep., 2018, 8, 6–12 CrossRef PubMed.
- D. H. Zaitsau, J. Neumann, T. Niemann, A. Strate, D. Paschek, S. P. Verevkin and R. Ludwig, Phys. Chem. Chem. Phys., 2019, 21, 20308–20314 RSC.
- H. Li, T. Niemann, R. Ludwig and R. Atkin, J. Phys. Chem. Lett., 2020, 3905–3910 CrossRef CAS.
- I. Minami, Molecules, 2009, 14, 2286–2305 CrossRef CAS PubMed.
- A. Somers, P. Howlett, D. MacFarlane and M. Forsyth, Lubricants, 2013, 1, 3–21 CrossRef.
- C. Ye, W. Liu, Y. Chen and L. Yu, Chem. Commun., 2001, 2244–2245 RSC.
- A. Riisager, R. Fehrmann, M. Haumann and P. Wasserscheid, Eur. J. Inorg. Chem., 2006, 695–706 CrossRef CAS.
- S. Werner, M. Haumann and P. Wasserscheid, Annu. Rev. Chem. Biomol. Eng., 2010, 1, 203–230 CrossRef CAS.
- Y. Gu and G. Li, Adv. Synth. Catal., 2009, 351, 817–847 CrossRef CAS.
- K. Fumino, V. Fossog, P. Stange, D. Paschek, R. Hempelmann and R. Ludwig, Angew. Chem., Int. Ed., 2015, 54, 2792–2795 CrossRef CAS.
- O. Palumbo, A. Cimini, F. Trequattrini, J.-B. Brubach, P. Roy and A. Paolone, Phys. Chem. Chem. Phys., 2020, 22, 7497–7506 RSC.
- I. V. Fedorova and L. P. Safonova, J. Phys. Chem. A, 2019, 123, 293–300 CrossRef CAS PubMed.
- M. S. Miran, H. Kinoshita, T. Yasuda, M. A. B. H. Susan and M. Watanabe, Chem. Commun., 2011, 47, 12676 RSC.
- D. Paschek, B. Golub and R. Ludwig, Phys. Chem. Chem. Phys., 2015, 17, 8431–8440 RSC.
- I. M. Riddlestone, A. Kraft, J. Schaefer and I. Krossing, Angew. Chem., Int. Ed., 2018, 57, 13982–14024 CrossRef CAS.
- K. J. Baranyai, G. B. Deacon, D. R. MacFarlane, J. M. Pringle and J. L. Scott, Aust. J. Chem., 2004, 57, 145 CrossRef CAS.
- B. E. Smart, J. Fluorine Chem., 2001, 109, 3–11 CrossRef CAS.
- R. Taylor, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2017, 73, 474–488 CrossRef CAS.
- S. Mishra and N. Suryaprakash, Molecules, 2017, 22, 423 CrossRef.
- T. J. Barbarich, C. D. Rithner, S. M. Miller, O. P. Anderson and S. H. Strauss, J. Am. Chem. Soc., 1999, 121, 4280–4281 CrossRef CAS.
- J. A. K. Howard, V. J. Hoy, D. O’Hagan and G. T. Smith, Tetrahedron, 1996, 52, 12613–12622 CrossRef CAS.
- H. Omorodion, B. Twamley, J. A. Platts and R. J. Baker, Cryst. Growth Des., 2015, 15, 2835–2841 CrossRef CAS.
- H. Zhang, U. Oteo, H. Zhu, X. Judez, M. Martinez-Ibañez, I. Aldalur, E. Sanchez-Diez, C. Li, J. Carrasco, M. Forsyth and M. Armand, Angew. Chem., Int. Ed., 2019, 58, 7829–7834 CrossRef CAS PubMed.
- V. H. Dalvi and P. J. Rossky, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13603–13607 CrossRef CAS PubMed.
- J. D. Dunitz, ChemBioChem, 2004, 5, 614–621 CrossRef CAS.
- J. A. Gladysz and M. Jurisch, Peptide-Based Materials, 2011, vol. 310, pp. 1–23 Search PubMed.
- J. C. Araque, J. J. Hettige and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 12727–12740 CrossRef CAS PubMed.
- D. Pontoni, M. DiMichiel and M. Deutsch, ChemPhysChem, 2020, 21, 1887–1897 CrossRef CAS.
- M. Brehm, H. Weber, M. Thomas, O. Hollóczki and B. Kirchner, ChemPhysChem, 2015, 16, 3271–3277 CrossRef CAS PubMed.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS PubMed.
- A. B. Pereiro, M. J. Pastoriza-Gallego, K. Shimizu, I. M. Marrucho, J. N. C. Lopes, M. M. Piñeiro and L. P. N. Rebelo, J. Phys. Chem. B, 2013, 117, 10826–10833 CrossRef CAS.
- F. Lo Celso, G. B. Appetecchi, E. Simonetti, M. Zhao, E. W. Castner, U. Keiderling, L. Gontrani, A. Triolo and O. Russina, Front. Chem., 2019, 7, 1–14 CrossRef.
- F. Lo Celso, Y. Yoshida, F. Castiglione, M. Ferro, A. Mele, C. J. Jafta, A. Triolo and O. Russina, Phys. Chem. Chem. Phys., 2017, 19, 13101–13110 RSC.
- K. Shimizu, C. E. S. Bernardes and J. N. Canongia Lopes, J. Phys. Chem. B, 2014, 118, 567–576 CrossRef CAS PubMed.
- A. B. Pereiro, J. M. M. Araújo, S. Martinho, F. Alves, S. Nunes, A. Matias, C. M. M. Duarte, L. P. N. Rebelo and I. M. Marrucho, ACS Sustainable Chem. Eng., 2013, 1, 427–439 CrossRef CAS.
- C. E. S. Bernardes, K. Shimizu, A. I. M. C. Lobo Ferreira, L. M. N. B. F. Santos and J. N. Canongia Lopes, J. Phys. Chem. B, 2014, 118, 6885–6895 CrossRef CAS.
- K. Shimizu, M. F. Costa Gomes, A. A. H. Pádua, L. P. N. Rebelo and J. N. Canongia Lopes, THEOCHEM, 2010, 946, 70–76 CrossRef CAS.
- Y. Shen, D. F. Kennedy, T. L. Greaves, A. Weerawardena, R. J. Mulder, N. Kirby, G. Song and C. J. Drummond, Phys. Chem. Chem. Phys., 2012, 14, 7981 RSC.
- W. Zheng, A. Mohammed, L. G. Hines, D. Xiao, O. J. Martinez, R. A. Bartsch, S. L. Simon, O. Russina, A. Triolo and E. L. Quitevis, J. Phys. Chem. B, 2011, 115, 6572–6584 CrossRef CAS.
- O. Hollóczki, M. Macchiagodena, H. Weber, M. Thomas, M. Brehm, A. Stark, O. Russina, A. Triolo and B. Kirchner, ChemPhysChem, 2015, 16, 3325–3333 CrossRef.
- E. I. Izgorodina, D. Golze, R. Maganti, V. Armel, M. Taige, T. J. S. Schubert and D. R. MacFarlane, Phys. Chem. Chem. Phys., 2014, 16, 7209–7221 RSC.
- J. Kohanoff, C. Pinilla, T. G. A. Youngs, E. Artacho and J. M. Soler, J. Chem. Phys., 2011, 135, 154505 CrossRef.
- L. Darabi and M. Zare, New J. Chem., 2020, 44, 4023–4032 RSC.
- D. S. Firaha, M. Thomas, O. Hollóczki, M. Korth and B. Kirchner, J. Chem. Phys., 2016, 145, 204502 CrossRef.
- M. Brehm, H. Weber, A. S. Pensado, A. Stark and B. Kirchner, Z. Phys. Chem., 2013, 227, 177–204 CrossRef CAS.
- I. T. Horvath and J. Rabai, Science, 1994, 266, 72–75 CrossRef CAS.
- I. T. Horváth, D. P. Curran and J. A. Gladysz, Handbook of Fluorous Chemistry, Wiley, 2004, pp. 1–4 Search PubMed.
- D. M. Lemal, J. Org. Chem., 2004, 69, 1–11 CrossRef CAS.
- J. van den Broeke, F. Winter, B.-J. Deelman and G. van Koten, Org. Lett., 2002, 4, 3851–3854 CrossRef CAS PubMed.
- I. T. Horváth, Acc. Chem. Res., 1998, 31, 641–650 CrossRef.
- J. D. Dunitz, A. Gavezzotti and W. B. Schweizer, Helv. Chim. Acta, 2003, 86, 4073–4092 CrossRef CAS.
- C. W. Bunn and E. R. Howells, Nature, 1954, 174, 549–551 CrossRef CAS.
- T. Hasegawa, Chem. Rec., 2017, 17, 903–917 CrossRef CAS.
- T. Hasegawa, Chem. Phys. Lett., 2015, 627, 64–66 CrossRef CAS.
- T. Shimoaka, H. Ukai, K. Kurishima, K. Takei, N. Yamada and T. Hasegawa, J. Phys. Chem. C, 2018, 122, 22018–22023 CrossRef CAS.
- E. K. Watkins and W. L. Jorgensen, J. Phys. Chem. A, 2001, 105, 4118–4125 CrossRef CAS.
- R. W. Zoellner, C. Latham, J. Goss, W. G. Golden, R. Jones and P. Briddon, J. Fluorine Chem., 2003, 121, 193–199 CrossRef CAS.
- T. L. Greaves, K. S. Schaffarczyk McHale, R. F. Burkart-Radke, J. B. Harper and T. C. Le, Phys. Chem. Chem. Phys., 2021, 23, 2742–2752 RSC.
- J. C. Dyre, J. Chem. Phys., 2018, 149, 210901 CrossRef PubMed.
- M. Malvaldi and C. Chiappe, J. Chem. Phys., 2010, 132, 244502 CrossRef PubMed.
- J. C. Dyre, T. Hechsher and K. Niss, J. Non-Cryst. Solids, 2009, 355, 624–627 CrossRef CAS.
- S. Cheng, Z. Wojnarowska, M. Musiał and M. Paluch, J. Chem. Phys., 2021, 154, 044502 CrossRef CAS.
- T. Yamaguchi, J. Chem. Phys., 2016, 144, 124514 CrossRef PubMed.
- C. Wang and R. M. Stratt, J. Chem. Phys., 2007, 127, 224504 CrossRef PubMed.
- S. I. Fletcher, F. B. Sillars, N. E. Hudson and P. J. Hall, J. Chem. Eng. Data, 2010, 55, 778–782 CrossRef CAS.
- Y. Hou and R. E. Baltus, Ind. Eng. Chem. Res., 2007, 46, 8166–8175 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Ion abbreviations used in this work, details of potential energy, volume and charge arm calculations, literature data for methylated imidazolium [NTf2]− melting points, pressure and viscosity estimates for isodensity conditions of [C4C1im][NTf2], structures of cynoborates and z-matrices of imidazoliums used in the ab initio calculations. See DOI: 10.1039/d1cp00216c |
| ‡ The Yukawa potential is a screened Coulomb potential, i.e. it includes an exponential decay on top of the r−1 dependence. |
| § The dipole moment of charged species is reference frame dependent, see the section ‘Polarisability, ‘dipole moments’ and charge asymmetry’. |
¶ Equations are simplified for the case of a spherical ion, for a force perpendicular to ![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) q. For a more detailed discussion, see ref. 194. q. For a more detailed discussion, see ref. 194. |
|| Thus, for the charge centred system, ![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) q− = q− = ![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) q+ = 0. The distance between q+ = 0. The distance between ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) cq (given by σ+ + σ−) for the charge centred system is set equal to the minimum possible charge separation in the asymmetric charge system (given by σ+ + σ− − cq (given by σ+ + σ−) for the charge centred system is set equal to the minimum possible charge separation in the asymmetric charge system (given by σ+ + σ− − ![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) q+). q+). |
| ** “Upper critical solution temperature”, above this temperature ionic liquid and butanol become completely miscible across the whole composition range. |
| This journal is © the Owner Societies 2021 |