Open Access Article
Open Access ArticleDetailed GPC analysis of poly(N-isopropylacrylamide) with core cross-linked star architecture†
Alessandra
Monaco‡
ab,
Ben
Drain‡
 ab and
C. Remzi
Becer
ab and
C. Remzi
Becer
 *b
*b
aDepartment of Chemistry, University of Warwick, CV4 7AL, Coventry, UK
bPolymer Chemistry Laboratory, School of Engineering and Materials Science, Queen Mary University of London, London, E1 4NS, UK. E-mail: Remzi.becer@warwick.ac.uk; Web: http://www.twitter.com/remzibecer
First published on 24th August 2021
Abstract
Core cross-linked star shaped polymers possess unique physical properties that can be utilized as drug transporters for biomedical applications. However, detailed analysis of these polymer structures is not straightforward. Herein, we employ multi-detector gel permeation chromatography (GPC) to elucidate structural features of cross-linked stars prepared from the polymerisation of NIPAM via Cu(0)-mediated Reversible Deactivation Radical Polymerisation. Furthermore, we aim to show how varying the arm length and the core size of the star polymers can not only affect their structural properties but also their capacity to encapsulate drug-like molecules.
Introduction
Complex architectures of polymers, such as branched polymers, offer a multitude of possibilities in the development of materials in various fields including the biomedical sector.1–4 In particular, star polymers exhibit lower intrinsic viscosity whilst retaining higher flexibility in comparison with other branched polymers.5–9 As a result, they possess an excellent ability to encapsulate smaller drugs and to form polyplexes with biological structures such as DNA and RNA.10–12 Thus, they can act as transporters for genes and pharmaceuticals, allowing their mobilisation through biological barriers. This allows the compounds of interest to reach their desired targets whilst protecting them from fast clearance and environmental degradation.6,13–16Star polymers can be prepared via three main methods: Core-first, arm-first and grafting-onto approach.1 The core-first approach allows for the preparation of well-defined star polymers which are relatively easy to analyse since it involves a multi-functional initiator with a known number of initiating sites. Furthermore, star polymers prepared using this approach generally show high conversions and are easy to isolate since unreacted monomers are normally the only impurity left in the reactions. Nevertheless, this approach is characterised by some limitations such as a restricted number of arms and small particle size as well as less arm structural information.1
Amongst all star shaped polymer synthesis methods, the grafting-onto approach offers the highest degree of control over the synthesis of star polymers. This is because the preparation of both the core and the arms are required prior to the formation of the star shaped polymers. Consequently, the structure of the core and the linear arms are generally well-defined. However, the grafting-onto method is not always the most convenient as it usually involves more synthetic steps, requires longer reaction times and purification can be difficult.1
Therefore, over the last few decades, polymer chemists have been investigating the synthesis of core cross-linked star shaped (CCS) polymers to overcome some of the limitations of the core-first and grafting-onto approach. CCS polymers are prepared via an arm-first approach which first requires the polymerisation of linear polymers. The linear polymers, or arms, are co-polymerised with a bis-functional monomer in a cross-linking fashion resulting in the formation of star polymers. This class of star polymers are generally larger and possess a significantly greater number of arms than other star polymer types. These features render CCS polymers particularly interesting because they can encapsulate, and thus protect, larger amounts of small molecules which are essential in biomedical and technology sectors.17 Although CCS polymers overcome the issue of particle size and restricted arm numbers, analysis of these star polymers remains challenging. In fact, whilst CCS polymers tend to incorporate a large number of arms (>100), determining the exact number of arms is difficult not only because of an absence of a well-defined multi-functional initiator, but also because cross linking of linear arms depends on several factors, such as crosslinker amounts used.1 Furthermore, determining their size can also be challenging as the dimensions of the core tend to vary.
In this work, we show how multi-detector gel permeation chromatography (GPC) can be used for advanced analysis of CCS star shaped polymers prepared via Cu(0)-mediated Reversible-Deactivation Radical Polymerisation (RDRP) in aqueous media. The star polymers used in these studies were prepared by first synthesising N-isopropylacrylamide (NIPAM) linear arms of various degrees of polymerisation (DP) and consequently copolymerising them with varying equivalents of a core crosslinking monomer: N,N′-(1,2-dihydroxyethylene) bisacryl amide (DHEBA). The structural properties of these polymers and the effects that the arm length and the cross-linked core size on arm conversions, number of arms incorporated, and particle size have been discussed in details. Finally, the encapsulation activities of the star polymers towards small hydrophobic compounds and their release via acid induced degradation of the core are examined.
Results and discussion
Synthesis of CCS polymers via aqueous Cu(0)-RDRP
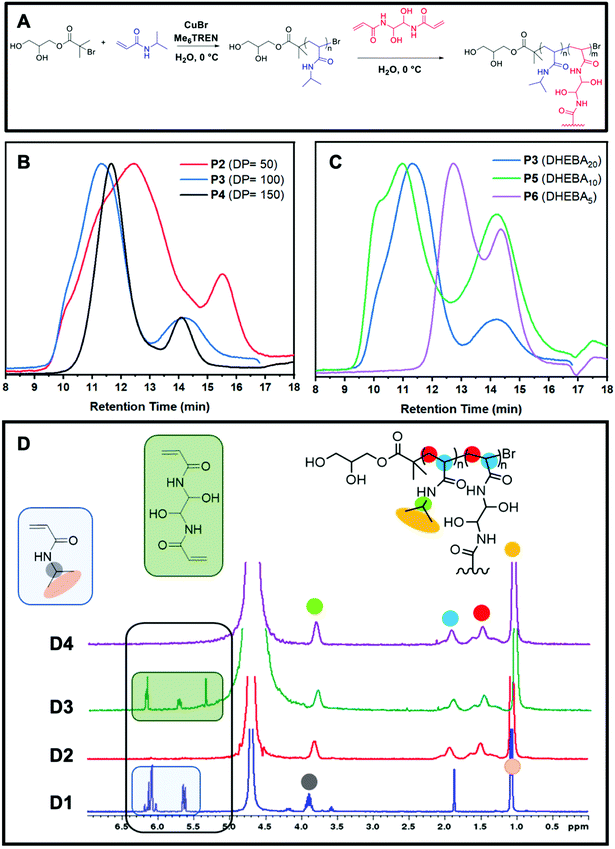
Reversible-deactivation radical polymerizations (RDRP) are typically the chosen method to prepare branched polymers such as core crosslinked star shaped (CCS) polymers because they provide full control over polymeric architectures.18 In particular, Cu(0)-RDRP in aqueous media is convenient for the preparation of star polymers. This is because it uses water instead of traditional organic solvents, but also because it allows the synthesis of star polymers effectively and rapidly due to the fast disproportionation of the catalyst (CuBr) with the ligand and the high reactivity of acrylamide monomers.19–22 Thus, even though CCS polymers are often prepared via other polymerisation techniques, these are not always ideal as the formation of branched polymers can take prolonged periods of time. On the contrary, Cu(0)-RDRP in water allows for the formation of acrylamide-based CCS polymers in one pot in under 3 hours, although the range of suitable monomers is usually more limited in comparison with that of other polymerisation methods. Unlike the core-first and grafting-onto approaches, in the arm-first approach, the linear arms are formed first followed by cross-linking to form a central core. The linear arms are thus assembled together by introducing a bisvinyl monomer, known as cross-linker, to generate CCS polymers (Fig. 1A).Whilst CCS polymers prepared via a core-first approach using radical polymerisation have a limited number of arms (normally 3–10), CCS polymers tend to have much larger molar mass values and a greater number of arms (>100). Thus, they are larger in size and possess a core that is protected by many arms. They provide optimum storage and encapsulation activity towards small hydrophobic compounds including medicinal drugs and other functionalised compounds popular in material technology, such as contact lenses and engine oils.9 Furthermore, the synthesis of CCS polymers is generally easier than the other methods as it does not involve the preparation of complex multi-functional initiators or functional cores. The structural properties of core cross-linked polymers can be easily tailored by varying the amounts of cross-linker and the DP of the linear arms. Fig. 1B shows that different DP's of the linear arms result in longer or shorter linear arms, while different equivalents of cross-linker are likely to lead to larger or smaller particles. The GPC traces (Fig. 1C) also show that greater amounts of crosslinker result in higher conversions from linear to star polymers and that by using longer arms, not only it is possible to obtain larger molecules, but also the CCS polymers show well-defined traces and lower polydispersity. The lack of a defined core and lower arm-to-star conversions make accurate analysis of this class of star polymers significantly more complex than that of other star polymers.
For this study, we have prepared CCS polymers from linear P(NIPAM) of different DP's (50, 100, and 150) and various equivalents (5, 10, and 20) of a water-soluble cross-linker (DHEBA). We have also analysed these samples using a multi-detector DMF GPC to determine the impact of these variables on the particle size and the drug encapsulation capability of the CCS. The general procedure consisted of the disproportionation of the ligand (Me6TREN) and the catalyst (CuBr), prior to the addition of the initiator and NIPAM at 0 °C. Once full conversion of the linear arms was observed via1H NMR spectra, a degassed aqueous solution of cross-linker was added to the reaction vial and reacted until 1H NMR showed complete consumption of the DHEBA vinyl groups (Fig. 1D).
The relative arm conversion was calculated using a GPC chromatogram RI integration method by taking half the area of the arm peak, doubling it, then dividing by the total area of the chromatogram (see ESI† for details). It is worth noting that this does not lead to an absolute value due to the assumptions required. This method was chosen because deconvolution in Origin, in some cases, gave a poor fitting. Nevertheless, the results obtained are valid for comparative purposes, providing that all stars are treated in the same way. It is observed that 5 and 10 equivalents had a conversion of 61% which then increases to 85% when 20 equivalents of cross-linker are used (Table 1). Alternatively, by increasing the DP of the arms, the conversion is relatively stable at 83–86%. Conversely, the conversion was found to be significantly higher when the MEBA cross-linker was used compared to DHEBA (96% P7vs. 85% P3).
| No. | DP (NIPAM) | DP (x-linker) | Diametera (nm) | N arms | Arm-star conv.c (%) | Rel. drug encapsulationd (%) | M W,GPC, RI (kDa) | M W,GPC, VS (kDa) | Compactness (MW,GPC, RI/MW,GPC, VS) |
|---|---|---|---|---|---|---|---|---|---|
| All polymers used N,N-(1,2-dihydroxyethylene)bisacrylamide (DHEBA) as a cross-linker except P7, which used N,N-methylenebis(acrylamide) (MEBA).a Diameters (nm) are measured by dynamic light scattering (DLS).b Calculated according to eqn (3)–(5) utilising an extrapolated linear reference polymer setting the structural factor, ε, to 0.75.c Calculated using a GPC RI integration method (see ESI† for full details).d Drug encapsulation for DHA as calculated relative to P2 which is assigned as 100%. | |||||||||
| P1 | 279 | — | 9.7 | — | 0 | — | 64 | 48 | — |
| P2 | 50 | 20 | 15.5 | 79 | 86 | 100 | 175 | 638 | 3.6 |
| P3 | 100 | 20 | 30.4 | 172 | 85 | 27 | 303 | 1291 | 4.3 |
| P4 | 150 | 20 | 32.8 | 46 | 83 | 9 | 169 | 392 | 2.3 |
| P5 | 100 | 10 | 17.2 | 115 | 61 | 29 | 320 | 1067 | 3.3 |
| P6 | 100 | 5 | 11.2 | 5 | 61 | 42 | 50 | 58 | 1.2 |
| P7 | 100 | 20 | 13.5 | 13 | 96 | 62 | 107 | 195 | 1.8 |
Structural characterisation of CCS polymers
To evaluate the CCS polymer structures Mark–Houwink plots of log (intrinsic viscosity) (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IV) vs. log(fitted molecular weight) (log
IV) vs. log(fitted molecular weight) (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M) were constructed (Fig. 2). By using samples of known concentration coupled with the RI detector, the concentration at each slice can be established. Moreover, the VS detector can provide the specific viscosity at each slice. By combining the RI and VS detector data, the intrinsic viscosity (IV) is then calculated according to eqn (1) such that the intrinsic viscosity at each molecular weight is determined.
M) were constructed (Fig. 2). By using samples of known concentration coupled with the RI detector, the concentration at each slice can be established. Moreover, the VS detector can provide the specific viscosity at each slice. By combining the RI and VS detector data, the intrinsic viscosity (IV) is then calculated according to eqn (1) such that the intrinsic viscosity at each molecular weight is determined.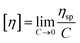 | (1) |
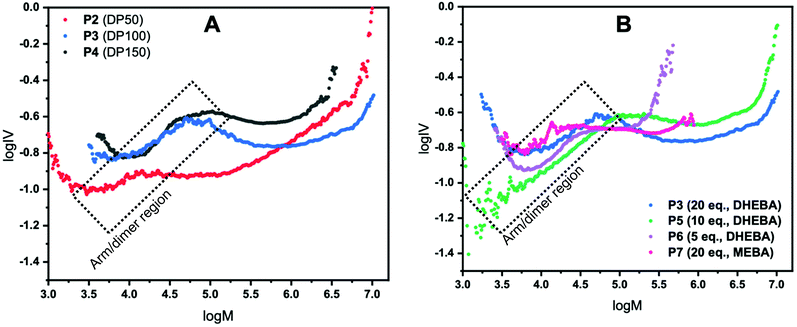
For a CCS polymer, as the number of arms increases, the molecular weight increases but the molecular size in solution and therefore the intrinsic viscosity, does not increase proportionally. Using this information, the number of arms can be qualitatively assessed and discussed given that for any CCS polymer, at any given molecular weight, the lower the intrinsic viscosity the higher the number of arms. It is worth noting at this stage that all star polymer traces (P2–P7) in both Fig. 2A and B have a linear region (highlighted on the plots); this is due to leftover arms and/or dimer formation. Unfortunately, in this methodology it is not possible to elucidate what is leftover arm and what is dimer because a dimeric species is still effectively a linear polymer and so does not show the same IV reduction seen for star polymers. The point at which the IV drops is the point at which CCS polymers are forming. To confirm that the linear regions belong to left over arms the Mark–Houwink plots were overlaid with the polymer distribution (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M vs. dwdlog
M vs. dwdlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M). These plots are shown in the ESI† and confirm that the linear region is indeed as a result of leftover arms.
M). These plots are shown in the ESI† and confirm that the linear region is indeed as a result of leftover arms.
The first set of CCS polymers evaluated were chosen to investigate the effect on the star polymer structure of modifying the degree of polymerisation (DP) of the arm from 50 (P2), 100 (P3) and 150 (P4) with the cross-linker held constant at 20 equivalents (Fig. 2A). It is important to note that a DP of 279 was also evaluated but was not completely soluble in DMF and as such is excluded from here. However, it is included in the ESI† whereby it shows a comparatively high viscosity due to the reduced solubility. The Mark–Houwink plots for P2–4 are shown in Fig. 2 where log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M is plotted against log
M is plotted against log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IV. P2 where DP50 was used shows the lowest intrinsic viscosity, at any given molecular weight, up to a molecular weight of log 6. This means that up until that point P2 has the most branching and therefore the most arms, although beyond this point it has the second highest number of arms. Looking at the GPC chromatograms in Fig. 1B the polymer has the largest dispersity and high molecular weight shoulders which matches the increase in IV (see ESI†). These high molecular weight shoulders are likely due to star–star coupling reactions and is suggestive of a much faster star formation reaction when using a lower DP arm. Likewise, P3 shows evidence of star–star coupling albeit it to a much lesser extent although there is no evidence of star–star coupling in P4 suggesting that steric hindrance prevents/reduces star–star coupling in these systems. P3 has the second highest number of arms with a lower profile compared to P4 although beyond log 6 the number of arms becomes the highest out of all the star polymers having the lowest IV at any given molecular weight. In contrast, P4 has the fewest arms of all the star polymers shown in Fig. 2A, across the whole molecular weight range. The reason for this reduction in arms from P2–4 is due to increasing steric hindrance upon increasing the DP of the arm with the exception of P2 at higher molecular weights where star–star coupling reduces the arm average. Note that in all cases in Fig. 2A the intrinsic viscosity is not linear with respect to the molecular weight indicating that the number of arms across the molecular weight range is not constant for any of the stars displayed.
IV. P2 where DP50 was used shows the lowest intrinsic viscosity, at any given molecular weight, up to a molecular weight of log 6. This means that up until that point P2 has the most branching and therefore the most arms, although beyond this point it has the second highest number of arms. Looking at the GPC chromatograms in Fig. 1B the polymer has the largest dispersity and high molecular weight shoulders which matches the increase in IV (see ESI†). These high molecular weight shoulders are likely due to star–star coupling reactions and is suggestive of a much faster star formation reaction when using a lower DP arm. Likewise, P3 shows evidence of star–star coupling albeit it to a much lesser extent although there is no evidence of star–star coupling in P4 suggesting that steric hindrance prevents/reduces star–star coupling in these systems. P3 has the second highest number of arms with a lower profile compared to P4 although beyond log 6 the number of arms becomes the highest out of all the star polymers having the lowest IV at any given molecular weight. In contrast, P4 has the fewest arms of all the star polymers shown in Fig. 2A, across the whole molecular weight range. The reason for this reduction in arms from P2–4 is due to increasing steric hindrance upon increasing the DP of the arm with the exception of P2 at higher molecular weights where star–star coupling reduces the arm average. Note that in all cases in Fig. 2A the intrinsic viscosity is not linear with respect to the molecular weight indicating that the number of arms across the molecular weight range is not constant for any of the stars displayed.
In the next investigation, the equivalents of cross-linker (with respect to initiator) was reduced from 20 (P3) to 10 (P5) and 5 (P6) whilst keeping the DP at 100. The Mark–Houwink plots are shown in Fig. 2B and show many of the features observed with changing the DP. All polymers displayed do not have a constant number of arms across the molecular weight range as evidenced by the non-linear nature of the plots. Additionally, all polymers have the same linear region previously discussed and have different star onset points. P3 has already been discussed as part of the analysis of the results obtained when changing the DP of the arm (Fig. 2A). In this case, it has the lowest intrinsic viscosity, at any given molecular weight, across the molecular weight range. Therefore, qualitatively it has the most arms of the polymers studied in this series. It is worth noting that for a narrow molecular weight range the number of arms of P6 is slightly higher than that of P3. By halving the equivalents of cross-linker from 20 to 10 (P3 and P5, respectively) a sizeable decrease in the number of arms is seen. Assuming that the equivalents of cross-linker is directly proportional to core size, the data suggests that the observed reduction is due to a smaller core increasing the steric hindrance. Moreover, when the cross-linker is further halved (P6) a further reduction (except for a narrow molecular weight range) in the number of arms is seen. It is worth noting that the reduction observed is much more dramatic than 20 to 10 equivalents. Across the molecular weight range of P6 the number of arms is far fewer than that of P3 and P5 due to a smaller core and higher steric hindrance. Interestingly, star–star coupling is also evident in the GPC chromatograms (Fig. 1C) supported with a corresponding increase in the IV with the star–star coupling reducing as the equivalents of cross-linker are reduced. In addition, P7 (where MEBA was used as cross-linker) was also plotted and is shown in Fig. 2B. Compared to P3, P5 and P6, P7 has an earlier star onset point. Across the molecular weight range it has more arms than P5. Up to log 5 molecular weight, P7 has a similar number of arms to P6 but beyond this point, P6 overtakes P7. Considering P7 and P3 where the only difference is the cross-linker used there is a profound difference in the number of arms. Up until log 5.25 P7 has slightly more arms than P3, however, beyond this point the number of arms of P3 is higher than P7. In addition, P3 has a much larger star polymer region and therefore, across the whole molecular weight range, has far more arms than P7.
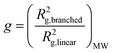
Notwithstanding the qualitative assessment just provided, it is possible to obtain a quantitative estimate of the number average of the number of arms by comparing the IV of the star polymer to that of a linear reference. To do this, the contraction factor, g, needs to be obtained viaeqn (2) using the radius of gyration, at any given molecular weight of both the branched and linear reference using light scattering data. Note that here, light scattering was not employed and in any case is not valid for any polymers with an Rg less than 10 nm, which is the case for some polymers studied.23 Therefore, g′ was calculated viaeqn (3) utilising the IV of both the branched and linear at each given molecular weight. The geometric branching factor, g, is related to the contraction factor, g′ viaeqn (4).
 | (2) |
 | (3) |
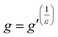 | (4) |
In eqn (4), ε is a structural factor that has a theoretical value of between 0.5 and 1.5. The theoretical value of ε for a star polymer in a theta solvent is 0.5; however, the value can vary depending on the type of branching as well as other factors.23,24 The contraction factor is related to the number of arms, f, in a polydisperse system as shown by eqn (5). In previous works, using a core first approach, it was shown that a more accurate value of ε can be calculated using the theoretical number of arms to calculate a theoretical value of g.23,25 However, given the random nature of the stars reported here, this approach was not suitable. Based on literature data a value of ε of 0.75 is a reasonable estimate26 and therefore in this work, ε is assumed to be 0.75, although it is noted that this value may not be the true value of ε. A small deviation in this value can alter the number of arms quite substantially and hence these values are provided as an estimate of the number of arms. The number of arms was calculated for all polymers by extrapolating a DP279 linear reference (P1), given that the intrinsic viscosity of a linear polymer increases in a linear fashion with molecular weight. The standard has to be extrapolated because of the large molecular weight range of the formed stars which makes it difficult to synthesise a comparative, broad linear reference. For all polymers the g′ (and hence g and f) was calculated after the star formation point. For these purposes, the point at which the star diverges from linear is the point selected. By plotting g′ as a function of log M a quasi-number of arms plot is generated that does not require the use of an assumptive ε (see ESI†).
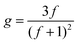 | (5) |
To obtain f, eqn (5) was used, with the assumption the system was polydisperse. This was then plotted as a function of log M (Fig. 3) to give a plot of how the number of arms varies for each polymer across the molecular weight range. The results are fully consistent with the qualitative assessment provided when looking at the Mark–Houwink plots. The polymer with the highest number of arms was P3 except at lower molecular weights. It had a maximum arm number of 675 and an average of 172. P2 and P5 have a very similar functionality curve both reaching a maximum of approximately 350 arms. However, P5 has a higher average (115) compared to P2 (79) despite P2 having more arms at lower molecular weights. P4 had the second lowest number of arms, reaching a maximum of approximately 100 with an average of 46. In keeping with the viscosity plots, P6 had the fewest arms with an average of 5 and a maximum of around 7 a consequence of a sterically crowded, small core resulting from using only 5 equivalents of cross-linker. In addition, P7 with its different cross-linker had an average of just 13 arms with a maximum of around 50. Contrast this to P3 which used the same conditions (DP100, 20 equivalents of cross-linker) whereby P7 has around 13.5 times fewer arms, on average, despite having a much higher arm conversion (96 vs. 85). Overall, the number of arms varied with molecular weight, generally increasing which is consistent with an arm first approach. P2 had a star polymer region that was the widest of all the polymers studied. It is worth reiterating that the information provided in Fig. 3 is already obtained qualitatively from the Mark–Houwink plots previously discussed. This means that the uncertainty around the structural factor is less significant given that the information collected is a numerical description of that otherwise provided.
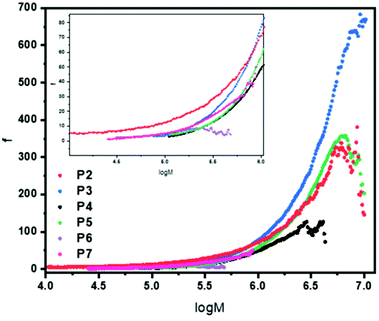 | ||
| Fig. 3 Functionality plot for polymers P2–P7 showing how the functionality (number of arms) varies with molecular weight. A zoomed in insert is provided for log 4–log 6 to assist the reader. Functionality was calculated using eqn (3)–(5) utilising an extrapolated linear reference and all values were calculated after the star onset point. The structural factor, ε, was set to 0.75 in all cases. | ||
One of the limitations of “conventional” GPC whereby the molecular weights are calculated from comparison to narrow polymer standards is that the molecular weights are only accurate if the polymer investigated has similar chemistry to that of the standards. In addition, analysing star polymers adds further inaccuracy due to the fact that introduction of branching into a polymer structure means that the molecular weight and hydrodynamic size do not increase proportionally. It is this same principle that was used earlier to investigate the star polymer structure using the viscosity data. Therefore, the molecular weights were also obtained by using viscosity measurements via the universal calibration. This allows much more accurate molecular weights to be obtained compared to conventional GPC. The results are tabulated in Table 1 where the inaccuracies inherent of conventional GPC become obvious. In all cases, the conventional GPC consistently underestimates the molecular weights. To measure this apparent difference, compactness was used in a similar way to that of Gao and Matyjaszewski.27 Thus, the greater the difference between the polymers, the more compact they are deemed to be. When considering the Mw values, a compactness of 3.6 for P2 is observed in the obtained molecular weights. For P3, P4, P5, P6 and P7 the compactness values were calculated as 4.3, 2.3, 3.33, 1.2 and 1.8, respectively. As expected, the greater the number of arms the greater the difference and therefore, the compactness. It is also worth discussing why P7 is significantly smaller than P3 and has fewer arms. This is potentially due to the decreased solubility and the absence of hydroxyl groups in MEBA vs. DHEBA, although further investigations would be required.
In addition to the GPC data, the sizes of the star polymers were also measured using dynamic light scattering (DLS). By combining this data with the viscosity data, additional information can be obtained. For example, increasing the equivalents of cross-linker from 5 to 20 equivalents (P6 to P3) enables the size increase from 11.2 to 30.4 nm. Some of this increase can be attributed to a higher number average of arms but the bulk of this size increase is likely a result of a larger core when increasing the equivalents of cross-linker. A larger core is consistent with both a higher average number of arms and an increasing arm conversion given the steric relief obtained from larger cores. Moreover, the size of P4 in solution is much larger than P2 with the only difference being that P2 is DP50 whereas P4 is DP150. In this case, the number of arms that P4 has is significantly fewer (46 vs. 79) than that of P2. Taken together, this data suggests that the cause of the size difference is solely due to the DP of the arms and not as a result of the polymeric star structure. Additionally, the equivalents of cross-linker are constant between P2 and P4 which gives further evidence that the difference in size is due to arm length alone in this particular case. However, this does assume that using the same amounts of cross-linker leads to similar sized core – an assumption that is not valid. This is evidenced by the similar size of P3 and P4 despite the difference in arm length. This similar size is likely due to a larger core size in P3 which also gives rise to a higher average number of arms due to steric relief. This lack of certainty over the nature of the core is a typical problem of an arm first approach, whilst it has been possible to obtain extensive information about the nature of the arms and the star polymer structure, the core structure is less certain.
On the contrary, the opposite is true of core first approaches whereby extensive information about the nature of the core size is obtained whereas information about the arms is less extensive. Though, it is worth noting that the viscosity analysis presented here can also be used for core first approaches to confirm the number of initiating sites and the structure of the star polymer.23
Encapsulation of small a hydrophobic model drug
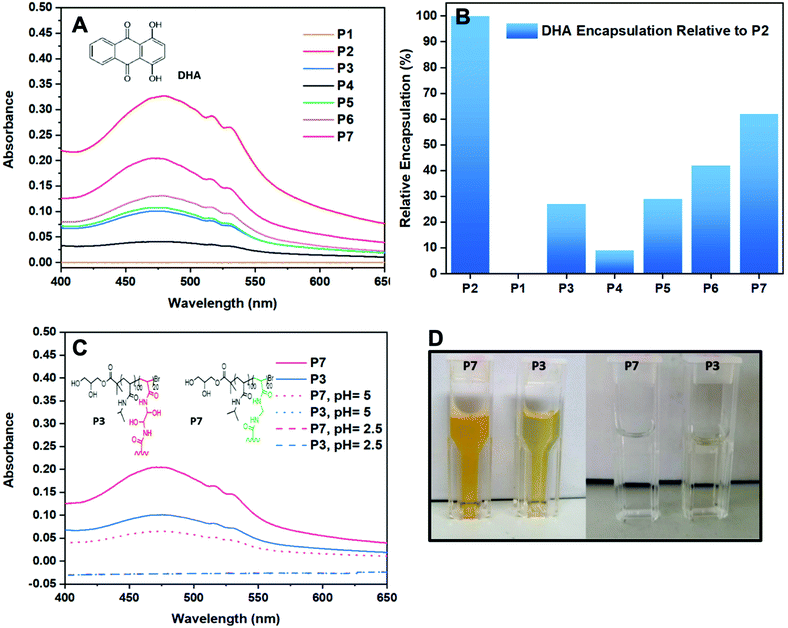
For the encapsulation studies, the star polymers and linear reference (3 mg mL−1) were stirred in distilled water for 24 h with an excess of DHA (5 mg mL−1). DHA is a small hydrophobic dye molecule, commonly used as a model drug for encapsulation studies of polymers as its aromatic groups allow for it to absorbs UV-Vis light.28,29 Since DHA is insoluble in aqueous solution, using a calibration curve obtained in a solution DHA is soluble in would be an inaccurate comparison for the determination of DHA encapsulation in the CCS polymer studies. For the purpose of a fair comparison, P2 was set as maximum encapsulation (100%) and was used to derive the relative DHA encapsulation given by the other polymers (Table 1). For instance, P6 provided an absorbance value of 0.20 and thus, it showed a relative DHA encapsulation of 42% in comparison with P2 which gave an absorbance value of 0.34 (Fig. 4A).To establish the role of the arms in the encapsulation of DHA, linear poly(NIPAM) (P1) was also investigated in the same way as the stars. As expected, the linear polymer shows no encapsulation of DHA and therefore confirms that encapsulation occurs in the core of the star polymer. Knowing this we can now rationalise the activity of the star polymers with regards to their polymeric structure. First consider the effect of the DP. The best performing polymer of all the polymers tested was P2 (to which 100% was assigned). The encapsulation decreases as the DP increases and this is independent of the number arms given that P4 (DP150) had the fewest arms but the worst encapsulation. In this case the effect of increasing the DP makes it much harder for the DHA to get to the core which explains why the encapsulation decreases so dramatically. Considering the equivalents of cross-linker (whereby the DP was held constant), it would be expected that larger cores (assuming core size increases with equivalents of cross-linker) would lead to more encapsulation given that encapsulation only occurs within the core. However, in this case encapsulation was best for P6 (5 equivalents), decreasing with increasing cross-linker. Whereas when the DP was modulated the number of arms is not a factor, the data suggests that it becomes a significant factor when the DP is held constant with P6 having the highest drug encapsulation despite utilising lower cross-linker amounts and having fewest arms due to easier access to the core. The drug encapsulation data was also obtained for P7 and was found to have the second highest (62%) encapsulation compared to the best performing star. Compared to P3, P7 has a more than two-fold encapsulation despite having the same DP and equivalents of cross-linker. As discussed previously, having fewer arms appears to encourage encapsulation due to easier access to the core. It is not clear whether this difference is due to the different nature of the cross-linker or because P7 has far fewer arms than P3 or a combination of both. P7 also has higher encapsulation than P6 (63 vs. 42%) despite having a similar number of arms (13 vs. 5) suggesting that the chemical environment of the core is important. In addition, the DLS data suggests that the core size of P7 and P6 is likely to be the same given the similar number of arms and similar sizes. Further work would be required to confirm the origin of the good encapsulation of P7.
The data obtained indicates that to improve encapsulation a short DP with low amounts of cross-linker would give the optimum results (Fig. 4B). It is worth noting the several literature reports suggest that more arms stabilise the encapsulation and therefore a trade-off is likely required.1 Nevertheless, keeping the DP of the arms low whilst keeping the cross-linker amounts at higher levels could provide star polymers with optimum stabilisation and encapsulation behaviour.
Acid induced degradation of the cross-linker and drug release
Although star polymers possess extraordinary encapsulation activity,10,11 it is important that pharmaceuticals encapsulated in their core are released in a controlled manner. Furthermore, because the human body struggles to expel large molecules such as branched polymers, the degradation of a star core is highly desirable.16,30–32 In our previous work, we have shown that DHEBA allows the formation of a core which undergoes degradation in mild conditions in the presence of an acid or a base.21 This is due to the two hydroxyl groups present in the monomer that catalyse the hydrolysis of acrylamides which normally requires relatively harsh conditions. Thus, in order to prove that DHEBA degrades more easily than other bisacrylamide monomers, a CCS using a different cross-linker (MEBA) has been prepared which does not contain any hydroxyl groups and have investigated the degradation and drug release of two star polymers with different cores at pH = 2.5 and pH = 5 (Fig. 4C).For the degradation studies, a 0.001 M HCl aqueous solution was added to the vials containing the polymer/DHA aggregates previously prepared for the encapsulation studies to create environments with pH = 2.5 and 5. The polymer/DHA solutions were stirred overnight at physiological temperature (37 °C) and cleared of any insoluble DHA particles by filtration with 0.45 micron nylon syringe filters before UV-vis measurements were carried out. After 24 h at pH = 2.5, the solutions of both star polymers appeared colourless after filtration prior to the UV-vis measurements. Furthermore, no absorbance was observed indicating that the polymers had released the DHA encapsulated in the core and that they had undergone acid degradation. This was further proven by the GPC traces of the polymers which show a drastic change in the MW values of the samples.
The same procedure was followed for the polymers stirred overnight in an environment with pH = 5 for 24 h. Whilst the solution containing P3/DHA was colourless after filtration and showed no absorbance values on the UV-vis, the solution containing P7/DHA appeared to have retained some of the orange colour given by DHA and still showed, although lower, absorbance on the UV-vis (Fig. 4D). As expected, P3 showed faster DHA release than P7 in mild conditions, due to the presence of the hydroxyl groups in the DHEBA core which led to the formation of an intermediate resulting in fast degradation of the CCS polymer core. The possibility of forming star polymers which can degrade more or less rapidly makes star polymers even more appealing in drug delivery. Indeed, combining multiple, different cross-linkers could allow tuning of the drug release.
Conclusions
In conclusion, we have evaluated the effect of the polymer DP and the equivalents of cross-linker used on the CCS polymer structure. Using viscosity data and the associated Mark–Houwink plots, it was possible to provide extensive information on the star polymer structure. Variation of the DP and/or equivalents of cross-linker changed the star polymer structure dramatically. For example, it was found that increasing the equivalents of cross-linker from 5 to 20 increases the number average of arms from 5 to 172 arms due to the relief of steric strain. No obvious trend was observed when the DP was increased from 50 to 150 although apparent extensive star–star coupling was observed when DP50 and 20 equivalents of cross-linker was used. It was found that short armed stars and stars with lower amounts of cross-linker gave the best encapsulation of a model drug, DHA. The best performing star was found to be DP50 with 20 equivalents of cross-linker due to easier access to the core on account of smaller arms. Moreover, the stars were shown to degrade under acidic conditions and the degradation and encapsulation is tuneable depending on the cross-linker and star polymer structure. Future work would include combining different cross-linkers together to modify and tune the encapsulation and release of model drugs such as DHA.Experimental section
Materials
1,2-Dihydroxypropane-3-oxy-(2-bromo-2-methylpropionyl) (waters soluble initiator for Cu-RDRP) and tris[2-(dimethyl-amino)ethyl]amine (Me6TREN, ligand) were synthesized following literature procedures.33,34N-Isopropylacrylamide (NIPAM; 98%), N,N′-(1,2-dihydroxyethylene) bisacrylamide (DHEBA, 97%), N,N′-methylenebis(acrylamide) (MEBA, (99%), (R)-(−)-2,2-dimethyl-1,3-dioxolane-4-methanol (98%), α-bromoisobutyryl bromide (98%), and glacial acetic acid were purchased from Sigma-Aldrich and used as received. Copper(I) bromide (CuBr) was washed with glacial acetic acid, ethanol, and dried prior to use.Synthesis procedure for core crosslinked star shaped polymers
The synthesis of star shaped core crosslinked polymers was achieved by following an arm-first approach via Cu(0)-RDRP in water using the following typical procedure. CuBr (0.8 equiv.) was added to a sealed vial and purged with N2 for at least 15 minutes. Separately, Me6TREN (0.4 equiv.) was dissolved in water and the solution was purged with N2 for 15 min. Thereafter, the Me6TREN solution was transferred to the vial containing CuBr using a degassed syringe to start the disproportionation. The required amount of monomer (NIPAM 50–279 equiv.) and the initiator (1,2-dihydroxypropane-3-oxy-(2-bromo-2- methylpropionyl)) (1 equiv.) were dissolved in water and stirred in the presence of N2 for ∼15 minutes. The mixture of monomer and initiator was then added to the disproportionation vial using a degassed syringe to start the polymerisation. When full conversion of the monomer was obtained, typically after 15–40 minutes, a degassed solution of the cross-linker (DHEBA or MEBA) in water was added to the reaction mixture. Finally, when the formation of star polymers was achieved, the insoluble Cu(0) particles were filtered off and the polymer solution was dialysed against water for 2–3 days and freeze-dried to obtain the polymer as a white solid.Encapsulation of DHA
Core crosslinked star shaped polymers were dissolved in distilled water (3 mg mL−1) and were added to vials containing an excess of a hydrophobic compound 1,4-dihydroxyanthra-quinone (DHA) (5 mg mL−1). The solutions were stirred for 3 days at room temperature to achieve encapsulation of DHA. Any insoluble excess of DHA was removed by passing the solution through a nylon syringe filter with a pore size of 0.45 μm and UV-vis absorbance of the solutions was measured.Degradation studies and release of DHA
DHA encapsulated core crosslinked star shaped polymers (1 mg mL−1) were dissolved in acidic solutions with a pH = 2.5 or 5 and were stirred overnight at 37 °C. Thereafter, the solutions were neutralised with NaHCO3 solution and were passed through a nylon syringe filter with a pore size of 0.45 μm to remove any insoluble DHA particles released. GPC and UV-Vis absorbance measurements of the solutions were carried out to determine the degradation and drug release abilities of the star polymers.Instrumentation
Author contributions
AM has performed the polymerisations, BD has contributed in the GPC analysis. CRB has contributed in the design and supervision of the project.Conflicts of interest
There are no conflicts to declare.References
- J. M. Ren, T. G. McKenzie, Q. Fu, E. H. H. Wong, J. Xu, Z. An, S. Shanmugam, T. P. Davis, C. Boyer and G. G. Qiao, Chem. Rev., 2016, 116, 6743–6836 CrossRef CAS PubMed.
- X. Wei, G. Moad, B. W. Muir, E. Rizzardo, J. Rosselgong, W. Yang and S. H. Thang, Macromol. Rapid Commun., 2014, 35, 840–845 CrossRef CAS PubMed.
- M. R. Whittaker, C. N. Urbani and M. J. Monteiro, J. Am. Chem. Soc., 2006, 128, 11360–11361 CrossRef CAS PubMed.
- H. A. Zayas, N. P. Truong, D. Valade, Z. Jia and M. J. Monteiro, Polym. Chem., 2013, 4, 592–599 RSC.
- Z. Shi, F. Guo, R. Tan, H. Niu, T. Li and Y. Li, Polym. Chem., 2017, 8, 1449 RSC.
- W. Wu, W. Wang and J. Li, Prog. Polym. Sci., 2015, 46, 55–85 CrossRef CAS.
- J. Skey, H. Willcock, M. Lammens, F. Du Prez and R. K. O′reilly, Macromolecules, 2010, 43, 5949–5955 CrossRef CAS.
- L. M. Van Renterghem, M. Lammens, B. Dervaux, P. Viville, R. Lazzaroni and F. E. Du Prez, J. Am. Chem. Soc., 2008, 130, 10802–10811 CrossRef CAS PubMed.
- A. Blencowe, J. F. Tan, T. K. Goh and G. G. Qiao, Polymer, 2009, 50, 5–32 CrossRef CAS.
- T. J. Gibson, P. Smyth, M. Semsarilar, A. P. Mccann, W. J. Mcdaid, M. C. Johnston, C. J. Scott and E. Themistou, Polym. Chem., 2019, 11, 344 RSC.
- H. Y. Cho, S. E. Averick, E. Paredes, K. Wegner, A. Averick, S. Jurga, S. R. Das and K. Matyjaszewski, Biomacromolecules, 2013, 14, 1262–1267 CrossRef CAS PubMed.
- J. Liu, H. Duong, M. R. Whittaker, T. P. Davis and C. Boyer, Macromol. Rapid Commun., 2012, 33, 760–766 CrossRef CAS PubMed.
- T. K. Georgiou, Polym. Int., 2014, 63, 1130–1133 CrossRef CAS.
- J. Huang, H. Liang, D. Cheng and J. Lu, Polym. Chem., 2016, 7, 1792 RSC.
- C. Boyer, J. Teo, P. Phillips, R. B. Erlich, S. Sagnella, G. Sharbeen, T. Dwarte, H. T. T. Duong, D. Goldstein, T. P. Davis, M. Kavallaris, J. McCarroll and S. Wales, Mol. Pharm., 2013, 10, 2435–2444 CrossRef CAS PubMed.
- M. Talelli, M. Barz, C. J. F. Rijcken, F. Kiessling, W. E. Hennink and T. Lammers, Nano Today, 2015, 10, 93–117 CrossRef CAS PubMed.
- B. S. Tucker, S. G. Getchell, M. R. Hill and B. S. Sumerlin, Polym. Chem., 2015, 6, 4258 RSC.
- N. Corrigan, K. Jung, G. Moad, C. J. Hawker, K. Matyjaszewski and C. Boyer, Prog. Polym. Sci., 2020, 111, 1–26 CrossRef.
- R. Aksakal, M. Resmini and C. R. Becer, Polym. Chem., 2016, 7, 171–175 RSC.
- Q. Zhang, P. Wilson, A. Anastasaki, R. McHale and D. M. Haddleton, ACS Macro Lett., 2014, 3, 491–495 CrossRef CAS PubMed.
- A. Monaco, V. P. Beyer, R. Napier and C. R. Becer, Biomacromolecules, 2020, 21, 3736–3744 CrossRef CAS PubMed.
- T. G. McKenzie, E. H. H. Wong, Q. Fu, S. J. Lam, D. E. Dunstan and G. G. Qiao, Macromolecules, 2014, 47, 7869–7877 CrossRef CAS.
- L. Plet, G. Delecourt, M. Hanafi, N. Pantoustier, G. Pembouong, P. Midoux, V. Bennevault and P. Guégan, Eur. Polym. J., 2020, 122, 109323 CrossRef CAS.
- S. T. Balke, T. H. Mourey, D. R. Robello, T. A. Davis, A. Kraus and K. Skonieczny, J. Appl. Polym. Sci., 2002, 85, 552–570 CrossRef CAS.
- C. Jackson, D. J. Frater and J. W. Mays, J. Polym. Sci. Part B: Polym. Phys., 1995, 33, 2159–2166 CrossRef CAS.
- M. Bohdanecky, Macromolecules, 1977, 10, 971–975 CrossRef CAS.
- H. Gao and K. Matyjaszewski, Macromolecules, 2006, 39, 3154–3160 CrossRef CAS.
- Q. Zhang, L. Su, J. Collins, G. Chen, R. Wallis, D. A. Mitchell, D. M. Haddleton and C. R. Becer, J. Am. Chem. Soc., 2014, 136, 4325–4332 CrossRef CAS PubMed.
- V. P. Beyer, A. Monaco, R. Napier, G. Yilmaz and C. R. Becer, Biomacromolecules, 2020, 21, 2298–2308 CrossRef CAS PubMed.
- A. Al-Nahain, H. Lee, Y. S. Lee, K. D. Lee and S. Y. Park, Macromol. Biosci., 2011, 11, 1264–1271 CrossRef PubMed.
- J. T. Wiltshire and G. G. Qiao, Macromolecules, 2006, 39, 9018–9027 CrossRef CAS.
- J. Rosselgong, E. G. L. Williams, T. P. Le, F. Grusche, T. M. Hinton, M. Tizard, P. Gunatillake and S. H. Thang, Macromolecules, 2013, 46, 9181–9188 CrossRef CAS.
- G. Yilmaz, V. Uzunova, R. Napier and C. R. Becer, Biomacromolecules, 2018, 19, 3040–3047 CrossRef CAS PubMed.
- S. Perrier, S. P. Armes, X. S. Wang, F. Malet and D. M. Haddleton, J. Polym. Sci., Part A: Polym. Chem., 2001, 39, 1696–1707 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Further GPC plots and DLS analysis can be found in the ESI. See DOI: 10.1039/d1py00966d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |