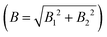Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Measuring surface phonons using molecular spin-echo
Helen
Chadwick
 * and
Gil
Alexandrowicz
* and
Gil
Alexandrowicz
 *
*
Department of Chemistry, Faculty of Science and Engineering, Swansea University, Swansea SA2 8PP, UK. E-mail: h.j.chadwick@swansea.ac.uk; g.n.alexandrowicz@swansea.ac.uk
First published on 26th May 2022
Abstract
A new method to measure surface phonons with a molecular beam is presented. The method extends the principles of 3He spin-echo spectroscopy, to the more complex case of a molecular beam exchanging energy with the surface. Measurements are presented for inelastic scattering of D2 from a Cu(111) surface. Similarly to helium spin-echo, experiments can be performed along optimal tilted projections making it possible to resolve energy peaks with a high energy resolution which is not restricted by the spread of energies of the incident beam. Two analysis methods for these molecular spin echo experiments are presented. A classical approach, analogous to that used for helium spin-echo, explains the most dominant excitation peaks measured, whereas a semi-classical approach allows us to identify smaller peaks which are related to the complexity of the multiple spin-rotation states which exist for molecules.
Introduction
Inelastic scattering measurements using atomic and molecular beams provide unique insight into the atomic scale dynamics of surfaces.1 Furthermore, essentially any surface chemistry process is affected, and in many cases dominated, by the ability of molecules to exchange energy with the surface.2 Surface phonons often provide an important channel for this energy exchange, making them particularly important to investigate.Helium atoms are an excellent choice for studying surface phonons, and the majority of helium atom scattering (HAS) experiments which characterised phonons and their dispersion curves were performed using the time-of-flight (TOF) technique. While a great deal of our understanding of low energy phonon modes is the result of HAS TOF experiments, this technique has its limitations. One of the fundamental restrictions on the achievable resolution in TOF experiments is the velocity spread of the incident beam, since the measured spectra are a convolution of the real excitation spectra with the energy distribution of the beam. This restriction has been addressed by improving supersonic expansions, where helium beams with very narrow energy distributions have been successfully produced and relatively high resolution spectra were obtained from numerous surfaces.1 Nevertheless, in various circumstances, for example when trying to separate two phonon modes which are close in energy, when trying to separate a very low energy mode from the elastic peak, or when we are attempting to measure the true linewidth of a phonon, the fact that the resolution of TOF experiments is on the order of a fraction of a meV can become a significant problem. Other contributions broadening the spectrum further are related to the chopper width, detector time response and other experimental restrictions, all of which have been minimised over the years by optimising TOF instruments.3,4
A way to circumvent the incident energy broadening effect is offered by the helium spin-echo (HSE) technique. HSE uses 3He beams which have a nuclear spin I = ½, and similarly to neutron spin-echo, the precession of the spin in magnetic fields before and after scattering offers an alternative way for measuring energy changes due to the scattering event. Unlike TOF measurements, within a first order approximation, the velocity spread of the incident beam does not broaden the spectrum, which leads to a dramatic improvement in energy resolution, especially when using beams with a relatively wide energy spread, allowing reconstruction of phonon spectra in the μeV range.5 The main application of the HSE technique is for quasi-elastic scattering studies used to detect and characterise surface diffusion,6 however, it can also be used to study inelastic scattering in general, and surface phonons in particular. Using a simple classical model, termed the tilted projection picture7 for designing and interpreting the measurements, ultra-high resolution measurements of surface phonons have been used to measure the low energy part of dispersion curves, anharmonicity, and phonon lifetimes of a metal surface.5,7 Helium spin-echo measurements of surface vibrations have also been used to determine the dispersion relations and lifetimes of adsorbate vibrations,8–10 and even phasons.11
While often involving a very similar setup to HAS, molecular scattering experiments offer quite different and complimentary insight to atom scattering. The inertness of helium atoms makes them an ideal probe for studying various surface structure and dynamics problems in a way which is to a good approximation independent of the properties of the probe.12 However, when it comes to studying the interaction of molecules with surfaces, which is one of the main goals of surface science, molecular scattering experiments provide insight into the full interaction potential and the surface chemistry taking place.13,14
Using molecular beams to study surface phonons is more of a rarity. Early works have demonstrated that not only is this possible, but molecular beams also offer unique insights due to their ability to detect surface phonons which are invisible to HAS due to their polarisation and symmetry constraints.15 Another potential advantage of studying surface phonons with molecular beams, is that it provides the most direct way of studying energy loss processes for a molecule colliding with a surface. Losing energy is an essential step in the trapping of a molecule on a surface, and for low energy molecules it directly impacts the probability of a reaction on a surface.16–20 Performing high resolution studies of surface phonon excitations by molecular beams, would provide experimental benchmarks for developing theoretical modelling of chemisorption beyond the Born Oppenheimer static surface approximation.
In this manuscript we demonstrate that the basic principles which enable phonon measurements with HSE and are used to interpret the results, can be extended to a molecular beam, and be used to reconstruct spectra with energy resolutions comparable to those achievable with HSE. We start by explaining the principle of this new type of measurement within the simple classical picture of tilted projections, show experimental results obtained from scattering a D2 molecular beam from a Cu(111) surface, and then present a more thorough method for simulating the spectra and interpreting the measured peaks.
Experimental
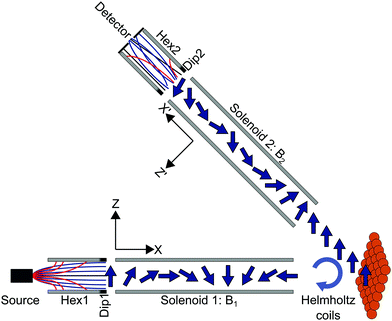
In the experiments presented here (apparatus shown schematically in Fig. 1), the molecular beam of D2 first travels through a magnetic hexapole21 which creates an inhomogeneous magnetic field which either focusses or defocusses the D2 molecules depending on the rotational (mJ) and nuclear spin (mI) projection state of the molecule. At the end of the hexapole, there is a hexapole to dipole element which adiabatically rotates the projection states from the various field directions within the hexapole to that of the dipole, which defines the quantisation (z-) axis in the first arm of the machine. After a field free region, the molecules enter the first solenoid which creates a tuneable magnetic field (B1) perpendicular to the initial quantisation axis and is either parallel or anti-parallel to the beam propagation direction for negative and positive field values respectively. In the classical picture, this causes the magnetic moments to precess with a Larmor frequency which is determined by the value of the gyro-magnetic ratio and the magnetic field, which is controlled by changing the current that is passed through the solenoid. Quantum mechanically, the magnetic field leads to Rabi oscillations of the populations of the molecules between the different mI, mJ states. The molecules then pass through a Helmholtz coil, located at the entrance to the scattering chamber, which can be used to generate a small field along the y-axis (see Fig. 1) just before they collide with the Cu(111) surface.† After scattering, a fraction of the molecules enter the second arm of the machine where there is a second solenoid which creates a tuneable field B2, followed by a second hexapole,22 both of which manipulate the molecules in the same way as in the first arm. At the end of the second arm there is a custom-built particle detector which ionises the molecules and measures the corresponding current that is produced.23There are various ways to design and interpret a HSE measurement, one relatively simple way of understanding how we can measure energy changes which are much smaller than the energy distribution width of the incident beam, is the tilted projection picture.7 Below we give a brief description of this picture, more detailed explanations can be found in previous publications.5–7,24
If the nuclear spins are treated as classical magnetic moments which undergo Larmor precession in the two electromagnets (see Fig. 1), it can be shown that a two dimensional measurement of the scattered intensity as a function of the strength of the two magnetic fields, S(B1,B2), is proportional to the Fourier transform of the 2d wavelength matrix, ρ(λi,λf).5,7,24 The wavelength matrix expresses the probability of having a beam particle with an initial de-Broglie wavelength, λi, which scatters from the surface with a specific final wavelength, λf. The fact that ρ(λi,λf) is a 2d function, means that a wide distribution of initial energies (wavelengths) doesn’t lead to any loss of information, as each element of the matrix ‘stores’ the information for an initial and final energy (wavelength) independently. While this matrix contains all the information about the scattering process, to the best of our knowledge, it has only been reconstructed directly from experimental data once,24 due to the extremely time-consuming process of performing a 2d measurement with sufficient resolution and range.
Even if reconstructing ρ(λi,λf) is usually impractical, it is a useful concept because of the Fourier projection theory, which tells us that if we perform a 1d experiment where S(B1,B2) is measured by changing the magnitude of the two fields while maintaining a proportionality condition B1 = αB2, and Fourier transform the signal, the result is a projection of ρ(λi,λf) onto an axis which has the same angle in wavelength space. While experiments can be performed at any angle by changing α, some angles are more useful than others as we will explain below and later demonstrate experimentally.
Elastic, quasi-elastic or inelastic scattering events define specific relations between the incoming and scattered wavelengths. Within a first order approximation this can be thought of as a straight-line segment in the λi,λf plane. The length of the linear segment is determined by the width of the distribution of incident wavelengths. The width of the linear segment is given by the actual linewidth of the excitation (for example this could be quasi-elastic broadening due to diffusion, or phonon width broadening due to the finite lifetime of the phonon). Finally, the position and angle of the linear segment within the λi,λf plane depend on the specific excitation. As a result, if we want the distribution width of the incident energies to not broaden the spectrum of a 1d measurement, the projection angle should be set such that it is perpendicular to the slope of the line. Within the approximation that the excitation feature in the λi,λf plane is linear, an approximation which becomes better for beams with a relatively narrow energy spread, this allows reconstruction of the excitation peak without any broadening due to the different incident energies.
In order to extend the tilted projection picture from 3He beams to molecular beams, a few complexities need to be considered. One source for complications are multiple echoes. Even for the simple case of 3He, a spin ½ particle, the tilted projection picture, as well as all other previous derivations of neutron and helium spin-echo techniques the authors are aware of, do not account for the simultaneous existence of parallel and anti-parallel echoes.25 The existence of these two types of echoes leads to mirror like features in S(B1,B2) which depend on the total scattering angle of the apparatus used. Fortunately, this complication can be mostly resolved by using an additional rotation coil before scattering which compensates for the scattering geometry and can be used to isolate one of the two echo conditions. In our experimental system this would be the Helmholtz coil located at the entrance to the scattering chamber (Fig. 1).
The phenomena of multiple echoes becomes much more involved for molecular systems as they are multi-level quantum systems, with multiple conditions for constructive interference and correspondingly a large number of spin-echo features.26 To accurately simulate the signal of a molecular scattering experiment, even for the simpler case of elastic scattering, a quantum/semi-classical calculation is needed as well as a scattering matrix, describing the changes of the wave-functions due to scattering.26 Nevertheless, as we will show below, if we are only interested in identifying peaks within the energy spectra, the classical tilted projection can still be used, as long as the gyro-magnetic ratio is adjusted to the energy splitting of the multi-level system, and the existence of multiple eigen-energies and multiple spin isomers is taken into account.
The particular molecule used in the experiments presented below is D2. The interaction of dihydrogen, which is the most abundant molecule in the universe, with surfaces is important for a wide range of research fields and chemical applications and the various isotopes of dihydrogen are commonly used in many surface science studies.27–29 D2, is also a good choice for performing the first molecular spin-echo measurements of phonons, as it has a non-rotating state with 5 spin projection states, J = 0, I = 2, which produces relatively simple spectra.
Fig. 2A shows a schematic energy diagram of the 3 lowest rotational, J, states in D2, and which total nuclear spin states are allowed for these J states. Fig. 2B and C show the energy splitting in a magnetic field for the J = 1, I = 1 and J = 0, I = 2 states respectively.30 The other allowed J = 2 state (J = 2, I = 2 and J = 2, I = 0) splits into 30 levels and interested readers are directed to Fig. 3A in ref. 31 for the energy dependence of these states as a function of magnetic field. What is evident from Fig. 2B and C is that the rotational projection states, and the corresponding rotational spin coupling which exist in I = 1, J = 1 lead to non-linear energy dependencies on magnetic field with multiple transition frequencies.30 In contrast, in J = 0, I = 2, there are only 5 spin projection states, the energy dependence on the magnetic field is linear, and the transition frequencies for a given B value are simply integer multiples of the same fundamental frequency. It should be noted that the J = 0, I = 0 state cannot be manipulated by magnetic fields and therefore contributes a constant background to the measurements that are presented here.
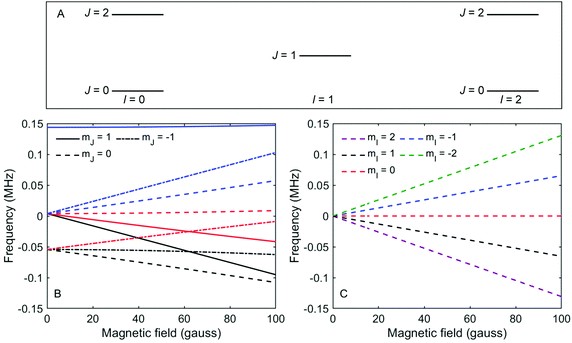 | ||
| Fig. 2 (A) Schematic energy level diagram showing the three lowest rotational states (J) and corresponding nuclear spin states (I) in a D2 molecule. (B) The energy of the different mI, mJ states of D2 molecules in I = 1, J = 1, as a function of magnetic field.30 The colours of the lines correspond to the mI state as defined in the legend of panel (C). (C) The energy of the different mI, mJ states of D2 molecules in I = 2, J = 0, as a function of magnetic field. | ||
The experimental apparatus used in the current study has been described in previous work,26,31–33 and only the details relevant for the this work are presented here. The molecular beam of D2 was formed from a supersonic expansion created using a 20 μm diameter nozzle held at 40 K and passing it through a 0.5 mm diameter skimmer. After travelling through the magnetic hexapole and solenoid in the first arm of the machine as described above and shown schematically in Fig. 1, the beam hits a Cu(111) surface (surface preparation laboratory) held at a temperature of 300 K, oriented such that the crystal 〈11−2〉 azimuth is within the scattering plane with an accuracy of ±0.05° determined from the position of the diffraction peaks in a D2 scattering experiment. After scattering, the molecules pass through the second solenoid and hexapole as described above, before the signal is measured using a custom built detector, designed by the surface physics group in Cambridge.23 The current through both solenoids is controlled using high stability power supplies (Danfysik) which allows each of the two to be scanned independently or whilst maintaining a fixed ratio between the two fields which they produce.
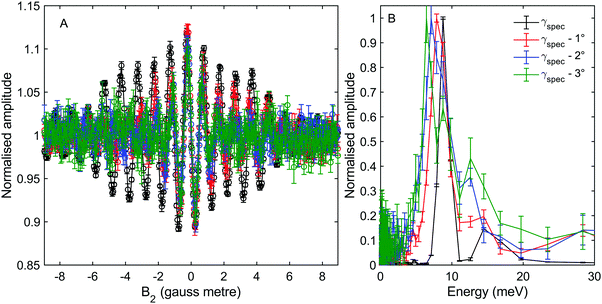
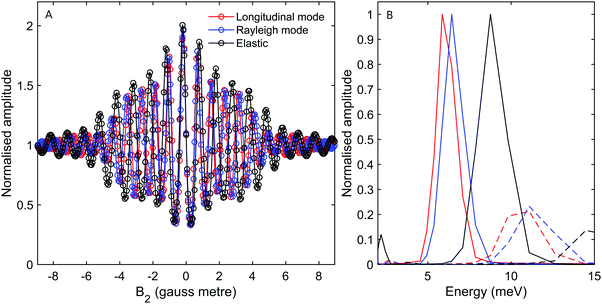
Fig. 3A shows measurements of the scattered intensity while maintaining B1 = 0 gauss metre‡ and scanning only B2. This type of measurement is denoted a 90° tilted projection angle, it is relatively easy to perform (no need to maintain an accurate current ratio between the two coils), and is in many ways equivalent to a TOF measurement, i.e., it has an energy resolution which is limited by the energy distribution width of the incident beam. The signal oscillates in all four measurements reflecting the changes to the quantum states of the molecules which pass through the magnetic field B2 which lead to different transmission probabilities through the hexapole analyser into the particle detector. We can also see that the frequency of the oscillation changes as a function of the incident scattering angle, indicating different scattered energies. The simplest way to analyse the signal is to follow the procedure developed for 3He,5–7,24 replacing the gyro-magnetic ratio of 3He with the relevant gyro-magnetic ratio for deuterium. Unfortunately, there is not a single gyro-magnetic ratio which characterises D2, as there are multiple levels. Furthermore the magnetic dependence of the states is non-linear for I = 1, J = 1 and for both I = 0 and I = 2, J = 2, rendering the concept of a gyromagnetic ratio, less useful. However, as we will show below, the majority of the signal in our experiments will be from the I = 2, J = 0 state and the frequency which predominantly modulates the signal is equivalent to the fundamental transition energy between adjacent eigen-energies (the separation between the 5 different eigen-energies plotted in Fig. 2C). These simplifying circumstances, make it possible to analyse the signal quite accurately using a single gyro-magnetic ratio of 653.6 Hz gauss−1.30 A more accurate approach which considers the various frequencies is presented later in this manuscript.
Fig. 3B shows the spectra reconstructed from these four measurements when we assume classical precession with a gyro-magnetic ratio of 653.6 Hz gauss−1.30 The black line, which was measured on the specular scattering peak (γspec), is dominated by a peak at 8.6 meV. For specular conditions we expect elastic scattering to dominate, and the peak is a measurement of the energy distribution of the incident beam. The FWHM of the peak is approximately 2 meV, reflecting a rather wide incident energy distribution for the nozzle expansion conditions used in the experiment. The largest peaks in the spectra of the −1°, −2° and −3° off specular measurements appear at energy losses, ΔE, of 0.75, 1.5 and 2.3 meV with respect to the elastic peak, corresponding to a change of the wave-vector within the surface plane, ΔK, of 0.06 Å−1, 0.11 Å−1 and 0.14 Å−1 respectively. These ΔE(ΔK) values are in good agreement with the dispersion relation of the Rayleigh mode determined from TOF HAS by Harten et al.34Fig. 4 shows these 3 energy loss peaks as circle markers, alongside a sine fit to the experimental results Harten et al.34 measured for the Rayleigh mode (solid magenta line). The black, red, blue and green dashed lines show the scan curves (conditions for conservation of energy and momentum) for γspec and the off-specular angles of −1°, −2° and −3°. These scan lines also have other intersections with the Rayleigh mode; however, they have significantly larger energy losses and gains and are less likely to be excited with a high enough probability to appear in the experimental spectra.
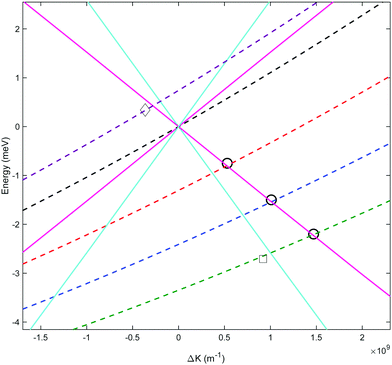 | ||
| Fig. 4 Phonon dispersion curves showing the momentum transfer and energy changes from sinusoidal fits to previous measurements34 of the Rayleigh (solid magenta) and longitudinal (solid cyan) phonons, and their intersection with scan curves for γspec (dashed black), γspec − 1° (dashed red), γspec − 2° (dashed blue), γspec − 3° (dashed green) and γspec + 0.5° (dashed purple) incident conditions. The circles are the ΔE(ΔK) values corresponding to the dominant energy loss peaks we measured at γspec −1°, −2° and −3°. The square marker corresponds to the weaker energy loss peak attributed to the longitudinal mode which became resolvable when using an optimal tilted projection angle. The diamond marker corresponds to the energy gain peak measured at γspec + 0.5°, also using an optimal tilted projection angle. | ||
Harten et al.,34 showed that helium atoms can also excite or de-excite the longitudinal mode of this surface. A sine fit to the TOF results for this mode is plotted in Fig. 4 using a cyan line. The scan curves of the relatively small off-specular-angle measurements we performed, cross the dispersion curve of this phonon at energy losses which are only shifted by 150 μeV to 400 μeV with respect to the Rayleigh mode. Given the relatively large width of the Rayleigh mode peak in the measurement, which is predominantly due to the incident energy spread, we do not expect to resolve this excitation. Later, we show a type of measurement which can resolve the two modes even at these low energies.
We also note that there is another peak which appears above the noise in the spectra of all the measurements, in the region between 12–16 meV. The peaks within this region illustrate the complications associated with analysing molecular spin-echo measurements and could have been interpreted erroneously as due to energy gain scattering. These peaks are actually related to scattering of I = 1, J = 1 molecules, as we will later show using a semi-classical simulation of the experiment.
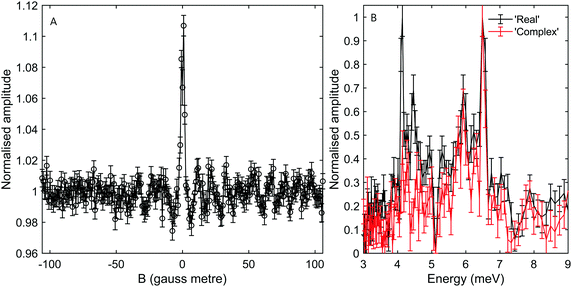
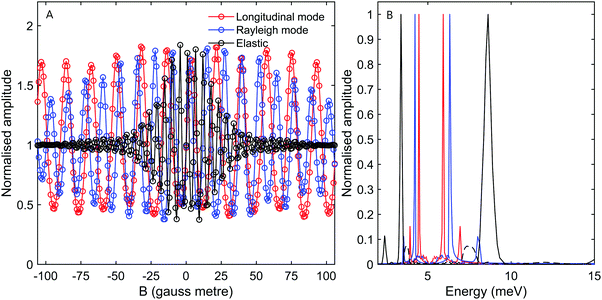
While the B2 scans and calculated spectra shown in Fig. 3 already supply us with information about the dispersion curve, the finer details of the spectra cannot be resolved due to the convolution with the wide energy distribution of the incident beam. In particular it would be useful to be able to separate the longitudinal and Rayleigh modes, which is difficult if not impossible with this particular type of tilted projection measurement. However, if we perform measurements using a tilt angle which is optimised to eliminate the broadening due to the incident energy spread, this becomes possible. Fig. 5B shows a measurement performed −3° off specular using a tilt angle of 52.4°, i.e., scanning the field magnitude while maintaining B1 = 1.3B2. Fig. 5B shows the corresponding reconstructed spectrum. The two main peaks in the spectrum which can be seen at 6.5 meV and 5.9 meV are related to the dominant Rayleigh mode and a second weaker, but still clearly resolvable, energy loss attributed to the longitudinal phonon. The ability to clearly differentiate two energy loss peaks which are separated by a fraction of the incident beam energy distribution width, nicely demonstrates the power of the tilted projection approach. The position of the second peak which became apparent due to the optimal tilted projection is plotted using a square marker in Fig. 4 and agrees well with the sine fit to the TOF measurements of the longitudinal mode. Note that the longitudinal mode energy losses measured previously using HAS TOF34 were restricted to the range |ΔE| > 4 meV, correspondingly, the small mismatch between the peak we measured and the sine fit to the previous data, is not surprising.
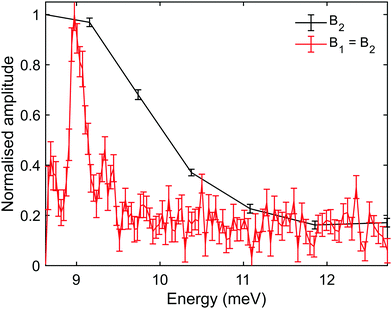
It is also important to note that there are complications when using optimal tilted projections, instead of a simple B2 scan. When measuring the magnetisation (spin projection) only along one axis, defined by the direction of the dipolar field before the second hexapole, the Fourier transform relation between ρ(λi,λf) and S(B1,B2) becomes a cosine transform, giving rise to spurious reflection peaks on the counter side of wavelength axis.5,7,24 For the particular tilted projection angle we chose, the wavelength axis origin is located at 5.12 meV and correspondingly the spectrum shown in black in Fig. 5B, which is derived only from the measurement presented in Fig. 5A, contains what looks like lower energy peaks, which are simply reflections of the two modes discussed above.
To remove the mirror image peaks, it is necessary to measure the magnetisation along a perpendicular axis (y′-axis) to the original (z′-axis), which would produce a signal with a 90° phase shift compared to the first measurement.5,7 This can be achieved to a reasonable approximation by performing two measurements where the value of B1 is alternated throughout the scan for each value of B2 to introduce a phase shift of 90° between the two sets of data, one of which can then be considered as the ‘real’ component Sr(B1,B2) and the other the ‘imaginary’ component Si(B1,B2). A ‘complex’ signal can then be defined as 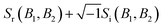 .5,7 This procedure was performed for the tilted projection measurement presented in Fig. 5, and the energy spectrum that was derived is presented as a red line in Fig. 5B. As can be seen, this spectrum no longer has significant mirror symmetry around 5.12 meV and allows us to differentiate the true peaks from the mirror images in the original spectrum.
.5,7 This procedure was performed for the tilted projection measurement presented in Fig. 5, and the energy spectrum that was derived is presented as a red line in Fig. 5B. As can be seen, this spectrum no longer has significant mirror symmetry around 5.12 meV and allows us to differentiate the true peaks from the mirror images in the original spectrum.
Another scenario when optimised tilted projections are particularly useful, is when the energy gain/loss is very small, and it is expected to merge within the diffuse elastic scattering peak, unless we can perform a measurement which decouples the two. Fig. 6 shows measurements performed only +0.5° from specular using tilt angles of 45° (B1 = B2) and 90° (B1 = 0). The energy gain peak in this case is only shifted by 350 μeV from the elastic peak at 8.6 meV and yet can be seen clearly in the spectrum of the 45° tilted projection measurement (red line). This energy gain corresponds to a ΔK of −0.036 Å−1, and is shown using the diamond marker in Fig. 4. The particular optimal tilted projection we used (45°), projects a pure elastic peak into one bin, the origin of the wavelength axis.7 The intensity of the diffuse elastic peak is approximately two orders of magnitude larger than the intensity of the phonon excitation peak, and the vertical scale in Fig. 6 is truncated to allow us to see the phonon peak.
In contrast, a tilted projection of 90° (black line), simply shows one broad peak which is a combination of the diffused elastic scattering and the (much weaker) inelastic peaks. The fact that the phonon energy is smaller than the width of the incident beam, combined with the overwhelming intensity from the diffused elastic peak when measuring so close to the specular peak, makes this type of measurement uninformative. Furthermore, our calculation predicts that for a 45° tilted projection, the broadening related to the incident energy beam widths is negligible, hence the full width half maximum of the peak (approx. 200 μeV) is related to the lifetime of the phonon and/or the merging of the Rayleigh and longitudinal mode for these extremely small energy gains (large wavelengths).
Simulations
In the analysis of the results above, we adapted the classical tilted projection method, originally developed for 3He to the case of D2. While this was sufficient to explain the main features seen in the spectra, it is also a rather simplistic approach. In particular, as was shown for elastic H2 scattering measurements,32,33 the signal oscillations includes many different frequencies, which are ignored in the tilted projection analysis we presented above. To provide a better level of analysis we modified a semi-classical simulation method which was developed for elastic H2 experiments,32,33 to include the change of energy after scattering. These semi-classical simulations solve the spin and rotational degrees of freedom quantum mechanically and treat the translation of the molecule classically. Below we briefly describe the simulation method and then show the simulated spectra it produces.To simulate the signal, the effect of each magnetic element, shown schematically in Fig. 1, on the D2 molecules needs to be calculated. The probability that an initial mI, mJ state (n) which has an initial wavelength λi is transmitted through the first hexapole (Phex,1(n,λi)) is determined using semi-classical trajectory deflection calculations.35 Due to the strong magnetic field gradients, the superposition states decohere, meaning that at this point the states can be described as pure mI, mJ states36 where the quantisation axis is taken as the direction of the dipole at the end of the hexapole (the z-axis). The internal states are then propagated coherently through the measured magnetic field profile of the first arm of the machine by quantum mechanically solving the magnetic Hamiltonian 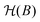 .30 The evolution of the quantum states through the first arm of the instrument can be described using a propagation matrix U(B1,λi),32 where λi has been included explicitly as we are considering inelastic scattering, which when operated on the initial quantum state gives us the molecular quantum state just before the scattering event.
.30 The evolution of the quantum states through the first arm of the instrument can be described using a propagation matrix U(B1,λi),32 where λi has been included explicitly as we are considering inelastic scattering, which when operated on the initial quantum state gives us the molecular quantum state just before the scattering event.
The molecules then collide with the surface which can result in an energy and momentum change of the D2 depending on whether it excites or de-excites a phonon, and the scattering geometry. In the calculations below, the wavelength after scattering, λf, was chosen to fit the phonon dispersion curves for this surface determined by Harten et al.34 It is assumed that the mI, mJ state is not changed by the collision with the surface. Assuming mI, doesn’t change is likely to be a good approximation for the mI states of the molecules as the copper surface is non-magnetic. Whilst the mJ states in the I = 1, J = 1 state could, and generally speaking would be changed by the collision,32 this will change the relative intensities of the different frequency components of the signal but not the frequencies themselves. As it is the frequencies which will be used to identify the features in the spectra, and as we do not have any predictions for the scattering matrix values, we will make the simple choice of ΔmJ = 0, keeping in mind that we do not expect the relative intensities of the peaks in the simulated spectra to be realistic.
The mI, mJ states after scattering are propagated through the measured magnetic field of the second arm of the machine in the same way as the first, i.e., using the Hamiltonian given in ref. 30 to give the propagation matrix U(B2,λf)32 where λf accounts for the different velocity that the molecules have after the inelastic scattering event, and the transmission probabilities of the final mI, mJ state (f) through the second hexapole (Phex,2(f,λf)) are again found using semi-classical trajectory bending calculations. The wave-function of the molecules in an initial mI, mJ state which are in a final state at the detector (|ψfn〉) can therefore be written as
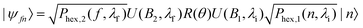 | (1) |
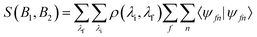 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5/9 (the J = 2 state will not be significantly populated at a nozzle temperature of 40 K). The remaining 1/9 of the beam in the I = 0, J = 0 state is not included in the calculations as it only contributes to a constant background signal.
5/9 (the J = 2 state will not be significantly populated at a nozzle temperature of 40 K). The remaining 1/9 of the beam in the I = 0, J = 0 state is not included in the calculations as it only contributes to a constant background signal.
Signals given by eqn (2) were calculated for various conditions. In addition to calculating the case of elastic scattering, two different energy losses were simulated. These were calculated from the intersection of the scan curve consistent with a γspec − 3° experiment with the fitted Rayleigh and longitudinal modes (see Fig. 4). Note that due to the significant width of the energy distribution of the incident beam, different scan curves and correspondingly different intersections with dispersion curves, need to be taken into account. Calculations were performed for magnetic field scans which correspond to 90° and 52.4° tilted projection measurements. The traces in Fig. 7A and 8A show simulated signals for the different values of ΔE at tilted projection angles of 90° and 52.4° respectively (note the different x-axis scales on these two plots).
To understand the impact of analysing molecular spin-echo phonon measurements within the simple classical, single gyro-magnetic tilted-projection picture, we can apply the type of analysis used to interpret the experimental signals on the simulated signals and obtain reconstructed spectra. Fig. 7B, shows the reconstructed spectra for simulations of elastic scattering (black) and energy losses from Rayleigh (blue) and longitudinal (red) mode excitations. The solid lines are calculations of I = 2, J = 0 molecules and dashed lines are for I = 1, J = 1 molecules. While the simple reconstruction procedure for the I = 2, J = 0 molecules produces peaks at the expected positions, for I = 1, J = 1, the elastic peak and the energy loss peaks all appear as if they are energy gains. The position of these peaks suggests that the origin of the small but still significant peaks within the 12 meV to 16 meV range seen in Fig. 3B is from non-negligible I = 1, J = 1 contributions. Fig. 8B shows a similar type of analysis, this time for a different tilted projection angle (52.4°). Again, I = 1, J = 1 produces small but non-negligible contributions which appear this time at around 7 meV. The reconstructed spectrum in Fig. 8B, which is characterised by very narrow peaks for both the Rayleigh and longitudinal modes, clearly demonstrates the advantage of using an optimal tilted projection to obtain a higher resolution spectrum and differentiating closely spaced excitation peaks.
The signals and spectra presented in Fig. 7 and 8 were calculated from eqn (2), using a simple identity scattering matrix to describe the changes in the wave-function during the scattering event, whereas changes to the velocity of the scattered molecules were chosen to fit the dispersion relation of the phonon mode simulated. The results of such calculations, allow us to identify the frequencies which the signal is composed of and associate them with I = 2, J = 0 and I = 1, J = 1 states and elastic and inelastic scattering contributions. As a result, we can identify the peaks which appear in the reconstructed spectra and avoid misinterpretations associated with the approximation of a single gyro-magnetic ratio used to determine the energy axis of the spectrum. However, it is important to remember that scattering intensities reflect the interference of the molecular wave-function. In particular, for rotating states (J > 0) we expect the scattering to strongly depend on the rotational projection state of the incoming state.31,32,37,38 To calculate a realistic signal and obtain information about the relative intensity of the inelastic peaks, the actual elements of the scattering matrix are needed. One way, is to try and calculate the elements of the scattering matrix quantum mechanically using multi-dimensional molecule-surface potentials, similarly to what has been done for elastic scattering.39,40 While it would be challenging to do this accurately, the signal corresponding to the matrix elements could be compared with the experimental result and would be an excellent benchmark for the accuracy of the theoretical modelling. Another method would be to determine the scattering matrix elements directly from a best fit to the experiment, however, again so far this has only been achieved for elastically scattered molecules.32
Conclusions and outlook
In the current work, we have demonstrated that it is possible to study surface phonons using molecular spin-echo measurements, specifically using D2 to study phonon excitations of a Cu(111) surface. At the simplest level, the data can be analysed in the same way as 3He spin-echo measurements, using a single gyro-magnetic ratio which corresponds to the frequency that contributes most to the measured signal, which in the case of D2 is ΔmI = 1 transitions in I = 2, J = 0. The position of the main peaks in the reconstructed spectra are in good agreement with previous TOF measurements34 and using optimal tilted projection angles we can measure these excitations with a high energy resolution.The energy and momentum range, and the energy resolution which can be obtained when measuring phonons with a molecular beam of hydrogen is similar to that obtained with helium spin-echo. Depending on which hydrogen isotope is used the absolute value of the gyro-magnetic ratio can be higher (H2) or lower (D2) than 3He, however, the effects of this on the resolution can be compensated by changing the velocity of the beam and the corresponding time spent in the magnetic field. Unlike quasi-elastic scattering experiments, where fields are ramped up to the limit to obtain sub-μeV energy resolution,41 when measuring phonons using spin-echo, the natural width of the phonon peaks is typically wider than tens of μeV. As a result, the signal decays at magnetic field values which are significantly lower than the maximum value, and it is the signal to noise which eventually restricts the resolution. For example, the sampling resolution of the spectrum shown in Fig. 6 is approximately 30 μeV in the vicinity of the energy gain peak. While the current in the solenoid coil could easily be increased by an order of magnitude, dividing the peak into much smaller energy bins would make it too noisy to be useful, unless further averaging is performed. Helium and molecular spin echo also share a common limitation in comparison with time-of-flight HAS. The range of energies for both the incoming and scattered beams, is restricted to energies where the hexapole focussing is efficient, estimated crudely as 5–30 meV for our experimental setup. Hence, when a wide range of energies or large energy gain/loss processes are of interest, time-of-flight HAS is a more suitable choice, whereas both helium and molecular spin echo are superior when it comes to measuring low energy excitation with very high energy resolution.
Our results also demonstrate the complexities of molecular spin-echo, as the reconstructed spectrum appears to contain additional peaks at energies which do not correspond to the expected phonon excitation or de-excitation processes, but originate from other frequencies in the signal, related to the multiple spin and rotational states. As we have shown, this ambiguity can be addressed by calculating spectra from semi-classical simulations and determining whether the peaks in the spectra reconstructed from the measured oscillation curves, are due to inelastic scattering events or due to molecules in other states. The results of the calculation confirm that the largest peaks in our data come from molecules in the I = 2, J = 0 state scattering inelastically due to energy exchange with the surface phonons, but that the smaller peaks we measured are consistent with scattering of molecules in I = 1, J = 1. In addition, the simulations reproduce our experimental observation that the peak widths of the different phonons change dramatically for optimal tilted projection angles, confirming that the classical picture of tilted projections, originally developed for helium, is still useful for performing high resolution inelastic scattering experiments of molecules.
It is currently not possible to make a quantitative comparison between the relative intensities in the spectra reconstructed from the experimental data and those reconstructed from semi-classical simulations. The reason for this is that in our simulations we have assumed that the scattering matrix, which characterises how the amplitude of the mI and mJ states change when the molecules scatter from the surface, is an identity matrix. A realistic calculation will include the probability of exciting a phonon, and also the change of the mJ states for J > 0 molecules.
While the existence of rotating states in the beam complicates the analysis, it also represents a particularly interesting direction for future development. When calculations of phonon excitation probabilities and scattering matrices are available, these can be used to simulate spectra, compare with the experimental results, and benchmark the accuracy of the theory used to calculate them. It may also be possible to extract the scattering matrix elements directly from inelastic scattering measurements as we have done previously for elastic scattering of H2,32 which will provide unique insight into how the interaction of the phonons is influenced by the rotational projection states as these can be obtained simultaneously from a single measurement. It is also important to stress that molecular rotation, and specifically the breaking of symmetry due to change of the mJ states during the molecule-surface collision, should make it possible to detect phonons which cannot be measured in helium scattering measurements, as demonstrated for the case of the shear horizontal phonons of the NaCl surface.15
Finally, the simulations that have been used in the current work are semi-classical, in the sense that the centre of mass of the molecules is propagated through the magnetic fields classically and only the nuclear and rotational magnetic moments are propagated quantum mechanically. For the case of elastic scattering, it has been shown that this gives the same results as a fully quantum propagation method up to magnetic field values of 104 gauss,42 but the reliability of using this semi-classical approach compared to a full quantum mechanical approach for inelastic scattering is the subject for future research work.
Funding
This work was funded by an ERC consolidator grant (Horizon 2020 Research and Innovation Programme grant 772228), and an EPSRC New Horizons grant (EP/V048589/1).Conflicts of interest
There are no conflicts to declare.References
-
G. Benedik and J. P. Toennies, Atomic Scale Dynamics at Surfaces, Springer, 2018 Search PubMed
.
- R. D. Muiño and H. F. Busnengo, Dynamics of gas-surface interactions, Ser. Surf. Sci., 2013 Search PubMed.
- D.-M. Smilgies and J. P. Toennies, Resolution and intensity considerations of an ideal He atom time-of-flight spectrometer for measurements of surface phonon dispersion curves, Rev. Sci. Instrum., 1988, 59, 2185–2194 CrossRef
.
- L. Pedemonte, A. Gussoni, R. Tatarek and G. Bracco, High-resolution scattering apparatus for surface studies, Rev. Sci. Instrum., 2002, 73, 4257–4263 CrossRef CAS
.
- G. Alexandrowicz and A. P. Jardine, Helium spin-echo spectroscopy: studying surface dynamics with ultra-high-energy resolution, J. Phys.: Condens. Matter, 2007, 19, 305001 CrossRef
.
- A. P. Jardine, G. Alexandrowicz, H. Hedgeland, W. Allison and J. Ellis, Studying the microscopic nature of diffusion with helium-3 spin-echo, Phys. Chem. Chem. Phys., 2009, 11, 3355–3374 RSC
.
- G. Alexandrowicz, PhD thesis, University of Cambridge, 2005.
- A. P. Jardine, G. Alexandrowicz, H. Hedgeland, R. D. Diehl, W. Allison and J. Ellis, Vibration and diffusion of Cs atoms on Cu (001), J. Phys.: Condens. Matter, 2007, 19, 305010 CrossRef
.
- A. P. Jardine, H. Hedgeland, D. Ward, Y. Xiaoqing, W. Allison, J. Ellis and G. Alexandrowicz, Probing molecule-surface interactions through ultra-fast adsorbate dynamics: propane/Pt (111), New J. Phys., 2008, 10, 125026 CrossRef
.
- B. A.-J. Lechner, H. Hedgeland, A. P. Jardine, W. Allison, B. J. Hinch and J. Ellis, Vibrational lifetimes and friction in adsorbate motion determined from quasi-elastic scattering, Phys. Chem. Chem. Phys., 2015, 17, 21819–21823 RSC
.
- E. M. McIntosh, P. R. Kole, M. El-Batanouny, D. M. Chisnall, J. Ellis and W. Allison, Measurement of the phason dispersion of misfit dislocations on the Au (111) surface, Phys. Rev. Lett., 2013, 110, 86103 CrossRef CAS PubMed
.
- J. P. Toennies, Helium atom scattering: a gentle and uniquely sensitive probe of surface structure and dynamics, J. Phys.: Condens. Matter, 1993, 5, A25–A40 CrossRef CAS
.
- G. B. Park, B. C. Krüger, D. Borodin, T. N. Kitsopoulos and A. M. Wodtke, Fundamental mechanisms for molecular energy conversion and chemical reactions at surfaces, Rep. Prog. Phys., 2019, 82, 096401 CrossRef CAS PubMed
.
- A. W. Kleyn, Molecular beams and chemical dynamics at surfaces, Chem. Soc. Rev., 2003, 32, 87–95 RSC
.
- G. Benedek, F. Traeger and J. P. Toennies, Spectroscopy of Shear Horizontal Surface Phonons by Rotation-Flip Scattering of Ortho-H2 Molecules, Phys. Rev. Lett., 2005, 94, 086103 CrossRef PubMed
.
- B. Jackson, The trapping of methane on Ir(111): A first-principles quantum study, J. Chem. Phys., 2021, 155, 44705 CrossRef CAS PubMed
.
- B. Jackson, Direct and trapping-mediated pathways to dissociative chemisorption: CH4 dissociation on Ir(111) with step defects, J. Chem. Phys., 2020, 153, 034704 CrossRef CAS PubMed
.
- E. Dombrowski, E. Peterson, D. Del Sesto and A. L. Utz, Precursor-mediated reactivity of vibrationally hot molecules: Methane activation on Ir(111), Catal. Today, 2015, 244, 10–18 CrossRef CAS
.
- R. Moiraghi, A. Lozano and H. F. Busnengo, Theoretical Study of the Dissociative Adsorption of Methane on Ir(111): The Role of Steps and Surface Distortions at High Temperatures, J. Phys. Chem. C, 2016, 120, 3946–3954 CrossRef CAS
.
- R. Bisson, M. Sacchi and R. D. Beck, State-resolved reactivity of CH4 on Pt(110) − (1 × 2): the role of surface orientation and impact site, J. Chem. Phys., 2010, 132, 094702 CrossRef PubMed
.
- A. P. Jardine, P. Fouquet, J. Ellis and W. Allison, Hexapole magnet system for thermal energy 3He atom manipulation, Rev. Sci. Instrum., 2001, 72, 3834–3841 CrossRef CAS
.
- S. Dworski, G. Alexandrowicz, P. Fouquet, A. P. Jardine, W. Allison and J. Ellis, Low aberration permanent hexapole magnet for atom and molecular beam research, Rev. Sci. Instrum., 2004, 75, 1963–1970 CrossRef CAS
.
- M. Bergin, D. J. Ward, S. M. Lambrick, N. A. von Jeinsen, B. Holst, J. Ellis, A. P. Jardine and W. Allison, Low-energy electron ionization mass spectrometer for efficient detection of low mass species, Rev. Sci. Instrum., 2021, 92, 73305 CrossRef CAS PubMed
.
- P. R. Kole, A. P. Jardine, H. Hedgeland and G. Alexandrowicz, Measuring surface phonons with a 3He spin echo spectrometer: a two-dimensional approach, J. Phys.: Condens. Matter, 2010, 22, 304018 CrossRef CAS PubMed
.
- I. Litvin, Y. Alkoby, O. Godsi, G. Alexandrowicz and T. Maniv, Parallel and anti-parallel echoes in beam spin echo experiments, Results Phys., 2019, 12, 381–391 CrossRef
.
- H. Chadwick, Y. Alkoby, J. T. Cantin, D. Lindebaum, O. Godsi, T. Maniv and G. Alexandrowicz, Molecular spin echoes; multiple magnetic coherences in molecule surface scattering experiments, Phys. Chem. Chem. Phys., 2021, 23, 7673–7681 RSC
.
- G. J. Kroes and C. Díaz, Quantum and classical dynamics of reactive scattering of H2 from metal surfaces, Chem. Soc. Rev., 2016, 45, 3658–3700 RSC
.
- D. Farías and R. Miranda, Diffraction of molecular hydrogen from metal surfaces, Prog. Surf. Sci., 2011, 86, 222–254 CrossRef
.
- H. Chadwick and R. D. Beck, Quantum state–resolved studies of chemisorption reactions, Annu. Rev. Phys. Chem., 2017, 68, 39–61 CrossRef CAS PubMed
.
- N. F. Ramsey, Theory of molecular hydrogen and deuterium in magnetic fields, Phys. Rev., 1952, 85, 60–65 CrossRef CAS
.
- H. Chadwick, M. F. Somers, A. C. Stewart, Y. Alkoby, T. J.-D. Carter, D. Butkovicova and G. Alexandrowicz, Stopping molecular rotation using coherent ultra-low-energy magnetic manipulations, Nat. Commun., 2022, 13, 2287 CrossRef CAS PubMed
.
- Y. Alkoby, H. Chadwick, O. Godsi, H. Labiad, M. Bergin, J. T. Cantin, I. Litvin, T. Maniv and G. Alexandrowicz, Setting benchmarks for modelling gas–surface interactions using coherent control of rotational orientation states, Nat. Commun., 2020, 11, 3110 CrossRef CAS PubMed
.
- O. Godsi, G. Corem, Y. Alkoby, J. T. Cantin, R. V. Krems, M. F. Somers, J. Meyer, G. J. Kroes, T. Maniv and G. Alexandrowicz, A general method for controlling and resolving rotational orientation of molecules in molecule-surface collisions, Nat. Commun., 2017, 8, 15357 CrossRef CAS PubMed
.
- U. Harten, J. P. Toennies and C. Wöll, Helium time-of-flight spectroscopy of surface-phonon dispersion curves of the noble metals, Faraday Discuss. Chem. Soc., 1985, 80, 137–149 RSC
.
- C. Krüger, E. Lisitsin-Baranovsky, O. Ofer, P.-A. Turgeon, J. Vermette, P. Ayotte and G. Alexandrowicz, A magnetically focused molecular beam source for deposition of spin-polarised molecular surface layers, J. Chem. Phys., 2018, 149, 164201 CrossRef PubMed
.
- M. Utz, M. H. Levitt, N. Cooper and H. Ulbricht, Visualisation of quantum evolution in the Stern–Gerlach and Rabi experiments, Phys. Chem. Chem. Phys., 2015, 17, 3867–3872 RSC
.
- H. Hou, S. J. Gulding, C. T. Rettner, A. M. Wodtke and D. J. Auerbach, The stereodynamics of a gas-surface reaction, Science, 1997, 277, 80–82 CrossRef CAS
.
- K. Cao, R. van Lent, A. W. Kleyn, M. Kurahashi and L. B.-F. Juurlink, Steps on Pt stereodynamically filter sticking of O2, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 13862–13866 CrossRef CAS PubMed
.
- D. Farías, C. Díaz, P. Rivière, H. F. Busnengo, P. Nieto, M. F. Somers, G. J. Kroes, A. Salin and F. Martín, In-plane and out-of-plane diffraction of H2 from metal surfaces, Phys. Rev. Lett., 2004, 93, 246104 CrossRef PubMed
.
- P. Nieto, E. Pijper, D. Barredo, G. Laurent, R. A. Olsen, E.-J. Baerends, G. J. Kroes and D. Farías, Reactive and nonreactive scattering of H2 from a metal surface is electronically adiabatic, Science, 2006, 312, 86–89 CrossRef CAS PubMed
.
- G. Alexandrowicz, A. P. Jardine, P. Fouquet, S. Dworski, W. Allison and J. Ellis, Observation of microscopic CO dynamics on Cu(001) using 3He spin-echo spectroscopy, Phys. Rev. Lett., 2004, 93, 156103 CrossRef CAS PubMed
.
- J. T. Cantin, G. Alexandrowicz and R. V. Krems, Transfer-matrix theory of surface spin-echo experiments with molecules, Phys. Rev. A, 2020, 101, 062703 CrossRef CAS
.
Footnotes |
| † The Helmholtz coil produces a field which is perpendicular to the B1 direction and is used to compensate for the scattering geometry and change the relative intensity of parallel and anti-parallel echoes. It should not be confused with the phase coils used in NSE, used to scan the spin-echo condition. |
| ‡ We use magnetic field integral rather than magnetic field, as the former governs the accumulated effect of the magnetic field on the phase of the magnetic moment. |
| This journal is © the Owner Societies 2022 |