Asymptotic behavior of the electron-atom Compton profile due to the intramolecular H-atom motion in H2
Yuuki
Onitsuka
 ,
Yuichi
Tachibana
and
Masahiko
Takahashi
,
Yuichi
Tachibana
and
Masahiko
Takahashi
 *
*
Institute of Multidisciplinary Research for Advanced Materials, Tohoku University, Sendai, 980-8577, Japan. E-mail: masahiko@tohoku.ac.jp
First published on 6th July 2022
Abstract
We report the asymptotic behavior of the electron-atom Compton profile due to the intramolecular H-atom motion in H2. The experiment has been performed at a scattering angle of 135° and at incident electron energies from 1.0 to 2.2 keV, thus covering a momentum transfer (K) range from 15.8 to 23.5 a.u. It is shown that with the increase in K, the Compton profile changes in shape and becomes more symmetric. Furthermore, it is found that the experiment reaches the limit of sufficiently large K at an incident electron energy of 2.0 keV, where the plane-wave impulse approximation is applicable to directly relate the Compton profile to the momentum distribution of the H atom.
1. Introduction
It is now well documented that electron Compton scattering1 can offer an opportunity to directly measure momentum distributions of the electrons or atoms in a molecule. The key concept to directly relate the experimental response to the momentum distribution is the plane-wave impulse approximation (PWIA).2–5 It assumes that the electron–electron (electron–atom) Compton scattering by a molecule can be described as a billiard-ball-type collision of the incident electron with a constituent electron (atom). Namely, the scattering electron (atom) is treated as a “single” free particle so that it absorbs all of the momentum transfer K (= p0 − p1), with pjs (j = 0, 1) being the momenta of the incident and scattered electrons, and recoils as if it were free. Since the applicability of the PWIA is absolutely dependent on the experimental conditions used, knowledge about the range of the validity of the PWIA is of fundamental importance when electron Compton scattering experiments are conducted for molecular spectroscopy studies that intend to understand the molecular nature.As for the electron–electron Compton scattering, the range of the validity of the PWIA has widely been investigated. A good example of this is electron momentum spectroscopy (EMS),6,7 which is an advanced form of electron–electron Compton scattering experiments. EMS was established as a unique molecular spectroscopy technique through many years of intensive studies. It is now used to measure the momentum distribution of each electron in different energy levels or to look at individual molecular orbitals in momentum space,6,7 involving orbital imaging of a short-lived molecular excited state.8
In contrast to the abovementioned EMS case, experimental conditions required for the PWIA are totally unclear for electron-atom Compton scattering experiments, also known as atomic momentum spectroscopy (AMS).9 Whilst experiments have been conducted at different incident electron energy (E0) values for several molecules such as CH4,10,11 CD4,10 H2,12–15 HD,12 D212,14 and H2O,16 to our knowledge, there has as yet been no conclusive study regarding the PWIA limit for AMS. For instance, Vos has performed AMS measurements of gaseous H2 molecules in a gas cell at a scattering angle of 91.3° and at several E0 values of up to 4.0 keV (K of up to 24.5 a.u.).13 He analyzed the observed band profile due to the H-atom motion and reported that even at K = 24.5 a.u. it was not a Gaussian shape predicted by the classical kinetic energy model.17 It was then suggested that the observed non-Gaussian feature is due to (a) the momentum density of the H-atom motion not being a Gaussian shape and (b) PWIA not being fully justified. On the other hand, Takahashi and his colleagues15 have recently reported that the Compton profile obtained at a scattering angle of 135° and at E0 = 2.0 keV (K = 22.4 a.u.) for the intramolecular H-atom motion in H2 is not a Gaussian shape but shows a good agreement with the associated quantum chemistry-based calculations. This means that the AMS experimental response at K = 22.4 a.u. is well reproduced by the PWIA theory, although the K value of 22.4 a.u. employed is comparable to or slightly smaller than 24.5 a.u. used in the study of Vos.13 Clearly, for a proper understanding of the PWIA limit, systematic and unequivocal experimental studies are required, which would settle the controversy and elucidate the range of the validity of the PWIA for AMS.
In this paper, we report a series of AMS experiments on H2. The experiments have been performed so that the K range is covered from 15.8 to 23.5 a.u. The experimental data are analyzed by using the general protocol15 so that the experimental response is disentangled from the instrumental response (IR) function. The Compton profiles obtained at different Ks are examined in terms of a similarity index to see if or how their asymptotic behavior approaches the PWIA limit.
2. Theory
The AMS scattering by a H2 molecule, a system of two identical atoms, can be described as| e0(E0, p0) + H2 → e1(E1, p1) + H2, | (1) |
| Eloss = E0 − E1. | (2) |
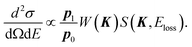 | (3) |
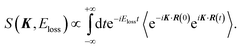 | (4) |
In the limit of K → ∞, S∞(K, Eloss) is given by2,3
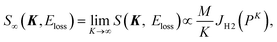 | (5) |
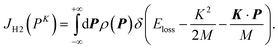 | (6) |
| S(K, Eloss) ≈ S∞(K, Eloss). | (7) |
Nevertheless, strictly speaking, the abovementioned experimental ability can prove itself only when the experiment covers the K range up to infinity. Thus, let us also consider a practical case when a plateau region, where the shape of the Compton profile is invariant with respect to the change of K, is experimentally observed. In this case, it may be too early to conclude that the observed Compton profile has reached the PWIA limit, because knowledge about the asymptotic behavior of the Compton profile towards the PWIA limit is still in its infancy: there might be next plateau region at larger K. A tangible clue for overcoming this awkward problem is use of the associated theoretical Compton profile for H2, which has been calculated based on the quantum chemistry theory.15 It has predicted the Compton profile at K = ∞, due to the intramolecular H-atom motion in a spherically averaged H2 molecule at room temperature. Note that the word “intramolecular” is used here so that it includes both molecular vibration and rotation, as the rotational motion is essentially inseparable from the vibrational motion without imposing the Eckart frame on the Schrödinger equation.20,21
According to the quantum chemistry theory, the atomic momentum distribution ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (P) of a spherically averaged H2 molecule in the rotational state with a rotational quantum number
(P) of a spherically averaged H2 molecule in the rotational state with a rotational quantum number ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) is given15 by
is given15 by
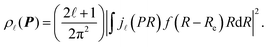 | (8) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (PR) is the spherical Bessel function of order
(PR) is the spherical Bessel function of order ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) . f(R − Re) is the vibrational wave function and at room temperature it can be approximated as a ground state wave function, (μω/πħ)1/4exp[−μω(R − Re)2/2ħ] with μ, ω and ħ being the reduced mass, angular frequency and reduced Planck's constant, respectively. The Compton profile of the spherically averaged H2 molecule at room temperature is then given by
. f(R − Re) is the vibrational wave function and at room temperature it can be approximated as a ground state wave function, (μω/πħ)1/4exp[−μω(R − Re)2/2ħ] with μ, ω and ħ being the reduced mass, angular frequency and reduced Planck's constant, respectively. The Compton profile of the spherically averaged H2 molecule at room temperature is then given by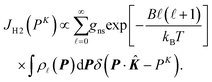 | (9) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) . B is the rotational constant, and in the calculations15B = 60. 853 cm−1 was employed.22kB and T are the Boltzmann constant and temperature. By using the calculated result of eqn (9) as a standard reference at K = ∞, it is possible to investigate if or how the measured Compton profile of H2 approaches the PWIA limit.
. B is the rotational constant, and in the calculations15B = 60. 853 cm−1 was employed.22kB and T are the Boltzmann constant and temperature. By using the calculated result of eqn (9) as a standard reference at K = ∞, it is possible to investigate if or how the measured Compton profile of H2 approaches the PWIA limit.
3. Experiment
Within the framework of the PWIA,2,3Eloss in eqn (2) is related to the mass M and initial momentum P of the scattering H-atom through the following equation: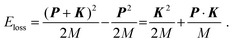 | (10) |
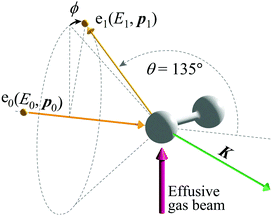
The experiments on H2 were carried out at a scattering angle of θ = 135° ± 0.4° and at E0 = 1.0, 1.5, 2.0, and 2.2 keV, thus achieving K = 15.8, 19.4, 22.4, and 23.5 a.u., respectively. For the experiments, a multi-channel AMS apparatus was employed. Since details of the apparatus are described elsewhere,23 only a brief account of it is given here. Kinematics of the electron-H-atom Compton scattering is shown in Fig. 1. An incident electron beam of 1 mm diameter was generated using a thermal electron gun that consisted of a tungsten filament. The beam current was collected in a Faraday cup and was kept at around 500 nA during the measurements. Quasi-elastic electron backscattering occurred where the electron beam collided with a gaseous H2 molecule in an effusive gas beam. Here the gas beam direction was perpendicular to the electron beam direction. A high-purity (>99.99999%) H2 gas was obtained from Taiyo Nippon Sanso Corporation and used at room temperature. The scattered electrons were angle-limited by apertures so that a spherical electron energy analyzer accepted those at θ = 135° over azimuthal angle (ϕ) ranges from 0° to 72.5°, from 107.5° to 252.5°, and from 287.5° to 360°. A pair of decelerating electrostatic lenses were used for the electrons before entrance to the analyzer in order to achieve a higher energy resolution, with a typical deceleration ratio of around 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The electrons having passed through the analyzer were detected using a position-sensitive detector. Both energies (E1) and azimuthal angles (ϕ) of the scattered electrons were determined from their arrival positions at the detector.
1. The electrons having passed through the analyzer were detected using a position-sensitive detector. Both energies (E1) and azimuthal angles (ϕ) of the scattered electrons were determined from their arrival positions at the detector.
The experimental raw data were eventually obtained by subtracting the spectra measured at an ambient pressure of 1.5 × 10−5 Pa in the vacuum chamber from those at 3.0 × 10−4 Pa to remove unexpected background signals. The same experiments were also conducted for Kr in order to estimate the IR function, as Kr is a heavy atom and it does not have intramolecular motion while its Ērecoil value can be regarded as zero under the experimental conditions employed.24
4. Results and discussion
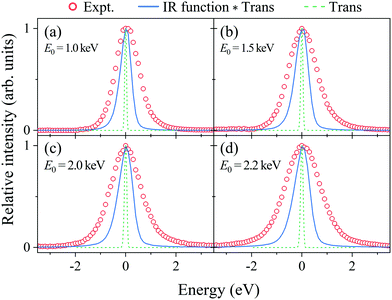
Fig. 2(a–d) show electron energy loss (EEL) spectra of H2 measured at E0 = 1.0, 1.5, 2.0, and 2.2 eV, respectively, together with those of Kr as a reference. It can be seen from the figures that both the Kr and H2 bands appear at the expected energy loss, centered at their own mean recoil energies Ērecoils: the former band appears at almost zero energy loss while the latter does at higher energy loss. Also it can be seen from the figures that the latter band is much broader than the former. Since the Kr band can be regarded as the IR function,24 it is evident that the broader nature of the H2 band is due to the H-atom motion in H2.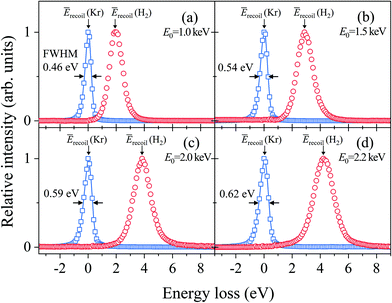 | ||
| Fig. 2 Electron energy loss spectra of H2 and Kr, measured at E0 = (a) 1.0, (b) 1.5, (c) 2.0, and (d) 2.2 keV, respectively. | ||
Generally speaking, the EEL spectra of gaseous molecules are inextricably composed of four types of contributions: (i) IR function, (ii) molecular center-of-mass translational motion, (iii) molecular vibration, and (iv) molecular rotation. In particular, it should be noted that the energy resolution of the IR function, also involved in the H2 band in Fig. 2, changes with the change in E0. This may be the primary cause of why the in-depth study on the PWIA limit for AMS has been hampered so far. For this reason, the EEL spectra of H2 in Fig. 2 are analyzed according to the general protocol,15 in order to examine the asymptotic behavior of the Compton profile due to the intramolecular H-atom motion in H2.
The general protocol15 involves the three steps. Firstly, the effect of molecular translational motion is considered, based on the findings of ref. 14 and 24 that it works so as to shift the EEL spectra to higher or lower energy loss with respect to Ērecoil, depending on ϕ. Secondly, both the energy shifts due to Ērecoil and translational motion are cancelled out. This can be done by aligning the band peak positions of the EEL spectra at each ϕ to the origin of the energy axis. Fig. 3(a–d) show the ϕ-angle integrated energy spectra of H2, which have been created by summing up the aligned EEL spectra at each ϕ. Also included in the figures are the convolution of the aligned Doppler broadening spectrum of translational motion and the IR function at each E0. The convolution curves can be regarded as the practical IR functions in the H2 data analysis. It is clear from Fig. 3 that the energy resolution of the practical IR function changes with the change in E0, and further that at every E0, the magnitude of the contribution of the practical IR function to the energy spectrum is comparable to that of the Doppler broadening due to the intramolecular H-atom motion.
The last step of the general protocol15 is to disentangle the Compton profile due to the intramolecular H-atom motion from the practical IR function. This step is made by using the convolution theorem.25 This reveals that since Fourier transform (FT) of the convolution of two functions is the product of FTs of each function, the Compton profile due to the intramolecular H-atom motion can be obtained by dividing the FT of the experiment by that of the practical IR function and then taking the inverse FT of the result of the division. As examples of the results, the Compton profiles obtained at E0 = 1.0 and 2.2 keV are presented in Fig. 4. Note that the experimental data are plotted as a function of the momentum PK of the scattering H-atom according to eqn (6), so their spectral shapes can now be directly compared to each other. The associated theoretical Compton profile calculated by using eqn (9) is also presented as a standard reference at K = ∞.
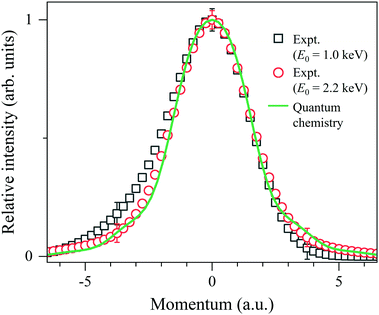 | ||
| Fig. 4 Comparison between experimental Compton profiles of H2 measured at E0 = 1.0 and 2.2 keV. The solid line represents the associated theoretical profile at K = ∞. | ||
It can be seen from Fig. 4 that the experimental Compton profile at E0 = 1.0 keV (K = 15.8 a.u.) has an asymmetric shape with respect to the momentum origin (PK = 0): compared to the associated theoretical profile having a symmetric shape, the experiment exhibits smaller intensity on the positive-momentum side, while exhibits larger intensity on the negative side. The observed asymmetry is consistent with the theoretical prediction that the leading dominant correction term for the PWIA has the odd symmetry with respect to the momentum origin.2 Similar observation has been made for the experimental Compton profile at E0 = 1.5 keV (K = 19.4 a.u.), though the degree of the asymmetry is smaller. On the other hand, it can also be seen from Fig. 4 that the experimental Compton profile at E0 = 2.2 keV (K = 23.5 a.u.) exhibits an almost symmetric shape. It is thus clearly identified that the shape of the Compton profile is dependent upon E0 (K).
In order to quantitatively evaluate the change in the shape of the Compton profile, we introduce a similarity index Isim(K) defined as
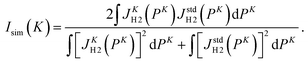 | (11) |
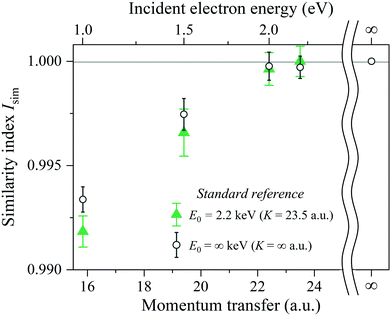
| E 0 (keV) | K (a.u.) | Similarity index Isim(K) | |
|---|---|---|---|
| J K=23.5H2 (PK) | J K=∞H2 (PK) | ||
| 1.0 | 15.8 | 0.9918 ± 0.0008 | 0.9934 ± 0.0006 |
| 1.5 | 19.4 | 0.9966 ± 0.0011 | 0.9975 ± 0.0008 |
| 2.0 | 22.4 | 0.9996 ± 0.0008 | 0.9998 ± 0.0006 |
| 2.2 | 23.5 | 1.0000 ± 0.0008 | 0.9997 ± 0.0005 |
One glance at Fig. 5 may reveal about the asymptotic behavior of the Compton profile due to the intramolecular H-atom motion in H2. For example, Isim(K = 15.8) with the standard reference of JK=23.5H2 (PK) has a value of 0.9918, indicating that there is certainly a difference in the spectral shape between JK=15.8H2 (PK) and JK=23.5H2 (PK). When K is increased to 19.4 a.u., the shape difference from JK=23.5H2 (PK) becomes smaller. However, there still remains a noticeable difference between JK=19.4H2 (PK) and JK=23.5H2 (PK). When K is further increased to 22.4 a.u., the shape difference from JK=23.5H2 (PK) becomes non detectable. Similar observations can be made from Isim(K) with the standard reference of JK=∞H2 (PK). In this case, both JK=15.8H2 (PK) and JK=19.4H2 (PK) exhibit a difference in spectral shape from JK=∞H2 (PK), though the difference of the latter is smaller than the former. When K is increased to 22.4 a.u., the shape difference from JK=∞H2 (PK) becomes non detectable. This observation is consistent with the findings of our latest AMS study on H2.15 Even when K is further increased to 23.5 a.u., the shape difference from JK=∞H2 (PK) is again not detectable.
By keeping in mind that the experiment possesses the ability to verify the range of the validity of the PWIA and JK=∞H2 (PK) is the quantum chemistry-based theoretical prediction of the Compton profile at E0 = ∞ keV (K = ∞ a.u.), the above-made observations conclude the following. In a relatively small K region, the Compton profile due to the intramolecular H-atom motion in H2 changes in shape, depending on K, towards the Compton profile of the PWIA limit. With the increase in K, it eventually reaches the PWIA limit at around K = 22.4 a.u. It no longer changes in shape even with the further increase in K. The asymptotic behavior of the Compton profile towards the PWIA limit as well as the presence of the PWIA limit of AMS are thus elucidated for H2.
5. Conclusions
In summary, we performed a series of AMS experiments on H2, while changing E0 (K) from 1.0 (15.8) to 2.2 keV (23.5 a.u.). The experimental data were analyzed by using the general protocol so that the experimental response was disentangled from the IR function as well as molecular translational motion. The resulting Compton profiles due to the intramolecular H-atom motion were analyzed in terms of the similarity index. These data analyses have enabled us to elucidate the asymptotic behavior of the Compton profile and the presence of the PWIA limit of AMS for H2.Finally, it may be worthwhile to note that further studies would be required to have a more complete understanding of the PWIA limit for AMS. For instance, the PWIA limit for the H atom in polyatomic molecules such as CH4 might be different from that for the H atom in H2. Likewise, the PWIA limit for an atom with a different mass might be different from that for the H atom. We believe that further efforts to answer these open questions will accumulate the knowledge about the PWIA limit for various atoms and various molecules, and eventually establish AMS as a unique molecular spectroscopy technique which enables one to measure the momentum distribution of each atom with different masses. One of the most important applications of AMS would be in the real-time measurement of the intramolecular force acting on a specific atom in a transient species,27 based on Ehrenfest's theorem that relates the time derivative of the expectation value of the momentum operator P to the expectation value of the force. We wish the present work encourages such future studies along the line.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by the JSPS KAKENHI Grant Numbers 20J12788, 21H04672 and 21K18926. This work was also supported in part by “Five-star Alliance”.References
-
Compton Scattering, ed. B. Williams, McGraw-Hill, New York, 1977 Search PubMed
.
- V. F. Sears, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 44–51 CrossRef CAS
.
- G. I. Watson, J. Phys.: Condens. Matter, 1996, 8, 5955–5975 CrossRef CAS
.
- I. E. McCarthy and E. Weigold, Rep. Prog. Phys., 1988, 51, 299–392 CrossRef CAS
.
- I. E. McCarthy and E. Weigold, Rep. Prog. Phys., 1991, 54, 789–879 CrossRef CAS
.
-
E. Weigold and I. E. McCarthy, Electron Momentum Spectroscopy, Kluwer-Academic/Plenum Publishers, New York, 1999, and references therein Search PubMed
.
- M. Takahashi, Bull. Chem. Soc. Jpn., 2009, 82, 751–777 CrossRef CAS
.
- M. Yamazaki, K. Oishi, H. Nakazawa, C. Zhu and M. Takahashi, Phys. Rev. Lett., 2015, 114, 103005 CrossRef PubMed
.
- M. Vos, Phys. Rev. A, 2001, 65, 012703 CrossRef
.
- G. Cooper, A. Hitchcock, C. Chatzidimitriou-Dreismann and M. Vos, J. Electron Spectrosc. Relat. Phenom., 2007, 155, 28–34 CrossRef CAS
.
- M. Vos, J. Chem. Phys., 2010, 132, 074306 CrossRef PubMed
.
- M. Vos and M. R. Went, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 065204 CrossRef
.
- M. Vos, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 145202 CrossRef
.
- Y. Tachibana, M. Yamazaki and M. Takahashi, Phys. Rev. A, 2019, 100, 032506 CrossRef CAS
.
- Y. Tachibana, Y. Onitsuka, H. Kono and M. Takahashi, Phys. Rev. A, 2022, 105, 052813 CrossRef CAS
.
- M. Vos, E. Weigold and R. Moreh, J. Chem. Phys., 2013, 138, 044307 CrossRef CAS PubMed
.
- R. Moreh and D. Nemirovsky, J. Chem. Phys., 2010, 133, 084506 CrossRef CAS PubMed
.
- L. Van Hove, Phys. Rev., 1954, 95, 249–262 CrossRef CAS
.
- P. C. Hohenberg and P. M. Platzman, Phys. Rev., 1966, 152, 198–200 CrossRef CAS
.
- C. Eckart, Phys. Rev., 1935, 47, 552–558 CrossRef CAS
.
-
E. B. Wilson Jr., J. C. Decius and P. C. Cross, Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, Dover Publications, New York, 1980 Search PubMed
.
-
K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure IV. Constants of Diatomic Molecules, Van Nostrand Reinhold, New York, 1979 Search PubMed
.
- M. Yamazaki, M. Hosono, Y. Tang and M. Takahashi, Rev. Sci. Instrum., 2017, 88, 063103 CrossRef PubMed
.
- M. Yamazaki, Y. Tachibana and M. Takahashi, J. Phys. B: At., Mol. Opt. Phys., 2019, 52, 065205 CrossRef CAS
.
-
W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in C: The Art of Scientific Computing, Cambridge University Press, New York, 2nd edn, 1992 Search PubMed
.
-
J. R. Taylor, An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurement, University Science Books, California, 2nd edn, 1997 Search PubMed
.
- Y. Tachibana, Y. Onitsuka, M. Yamazaki and M. Takahashi, Atoms, 2021, 9, 19 CrossRef
.
| This journal is © the Owner Societies 2022 |