Impact of varying the phenylboronic acid position in macrocyclic Eu(III) complexes on the recognition of adenosine monophosphate

Abstract

The selective recognition of anions in water by artificial receptors remains a significant research challenge. The creation of a receptor selective for adenosine monophosphate (AMP) is particularly difficult due to its similarity in structure with the more negatively charged anions, ADP and ATP. We recently developed a macrocyclic Eu(III) complex that selectively binds AMP in water, by incorporating a sterically demanding quinoline arm that inhibits coordination of commonly interfering anions such as ATP. A phenylboronic acid motif was installed within the ligand to engage the ribose sugar of AMP through reversible covalent bonds. Herein we report two new Eu(III) complexes, [Eu·oBOH₂]⁺ and [Eu·pBOH₂]⁺, to investigate the impact of varying the position of the phenylboronic acid group on the anion binding properties of the Eu(III) receptors. We found that [Eu·pBOH₂]⁺ showed preferential binding to AMP over ATP, but exhibits a lower level of discrimination between AMP and ADP compared with the isomeric complex [Eu·mBOH₂]⁺. Surprisingly, [Eu·oBOH₂]⁺ showed no response to anions but displayed a unique response to pH, ascribed to the direct coordination of the ortho-boronate ester to the Eu(III) centre. Finally, we present first principles computations that offer a promising approach to access the emission spectra of lanthanide complexes, aiding the design of responsive lanthanide probes with specific photophysical properties.

---

Introduction

The development of molecular sensors for the selective recognition of anionic guests requires the supramolecular interaction of the two components that induces an optical or electrochemical change.^1–3 For luminescent sensors, the emission produced can be through energy transfer or electron transfer processes of purely organic molecules, or from inorganic coordination complexes.^4–6 The use of lanthanide coordination complexes containing a strongly absorbing chromophore is advantageous, due to the long luminescence lifetimes (up to milliseconds) that allow for time-gated measurements, and sharp line-like emission spectra that enable ratiometric analysis.^7–10 Through careful design of the organic ligand, water-soluble lanthanide complexes can be devised that bind reversibly and selectively to anions, inducing a fast and sensitive luminescence response.^11–17

Adenosine monophosphate (AMP) is an important target for detection because of its crucial roles in biological processes, including maintaining energy homeostasis and mediating signal transduction events. However, receptors that selectively bind AMP in water are rare,^18–20 due to the tendency of receptors to form stronger electrostatic interactions with substrates with higher negative charges, in particular ADP and ATP. Indeed, the majority of receptors for nucleoside phosphate anions display the selectivity trend ATP > ADP > AMP^21–24 and reversing this trend is very difficult. AMP sensing has been reported through water soluble coordination complexes of zinc(II),²⁵ copper(I)²⁶ and europium(III),^18,20 as well as gold(II) nanoparticles.²⁷ In a few cases, AMP recognition has been achieved by exploiting the structural aspects of the organic receptors to provide highly complementary sites for AMP binding, including strong electrostatic contacts supported by π–π interactions with the nucleobase.^28,29

We recently established a method to selectively bind and sense AMP using a stable Eu(III) complex based on a sterically demanding macrocyclic ligand.²⁰ Two complexes were synthesized, [Eu·Bn]⁺ and [Eu·mBOH₂]⁺ (Fig. 1a),²⁰ each featuring a bulky 8-(benzyloxy)quinoline pendant arm that coordinates to the Eu(III) ion in a bidentate manner, creating a single coordination site for the monodentate binding of the phosphate component of AMP. Crucially, oxyanions that prefer a chelation binding mode including ATP, bicarbonate and lactate, do not bind to the complexes due to the steric hindrance imposed by the ligand. A boronic acid motif was introduced at the meta-position of the phenyl ring of [Eu·mBOH₂]⁺ to interact reversibly with the 1,2-diol moiety of the ribose sugar. Phenylboronic acids have been utilized in a range of receptors for sensing of saccharides with great success, due to their ability to form reversible covalent bonds with 1,2-diols.^30–32

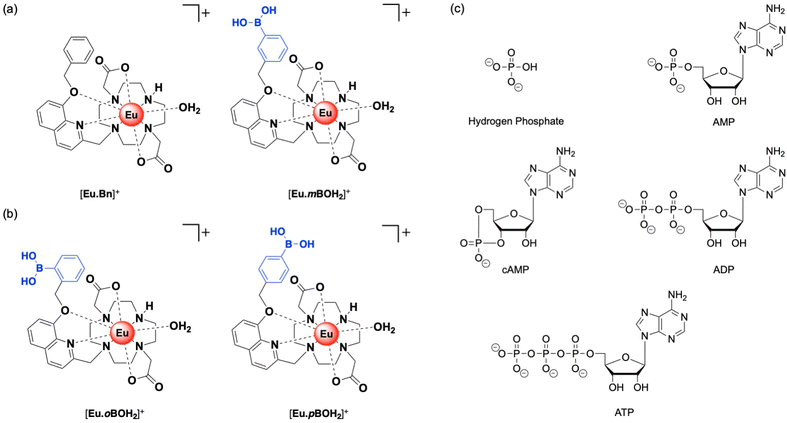Fig. 1 Family of cationic Eu(III) complexes designed to bind AMP in water. (a) Previously reported complexes [Eu·Bn]⁺ and [Eu·mBOH₂]⁺.²⁰ (b) New complexes [Eu·oBOH₂]⁺ and [Eu·pBOH₂]⁺ and (c) structures of anions investigated in this work.

Computations on lanthanide complexes are a powerful means to obtain deeper insight into the structural arrangement of the ligands, the binding modes of the guest molecules, and the properties of the f-electrons. However, these computations can be highly challenging due to the presence of unpaired electrons as well as the importance of solvation effects and conformational flexibility. Well-established protocols for obtaining accurate structures using density functional theory (DFT) are in use, relying on an effective core potential for the f-electrons and implicit solvation models.^33–36 Conversely, computing anion binding energies in solution³⁷ is a highly challenging endeavour and is therefore not routinely performed for lanthanide complexes. As opposed to the described DFT simulations, in which the f-electrons are only implicitly considered within the core potential, it would be necessary to include them explicitly for an ab initio computation of emission spectra or magnetic properties. Indeed, magnetic properties of lanthanide complexes have been modelled successfully^38–40 using multireference ab initio theory.⁴¹ However, to the best of our knowledge, no first principles simulation of lanthanide emission spectra has been reported so far. Emission spectra are usually computed using phenomenological models based on Judd–Ofelt theory.^42,43

Herein, we present two new cationic Eu(III) complexes, [Eu·oBOH₂]⁺ and [Eu·pBOH₂]⁺ (Fig. 1b) bearing a boronic acid motif at the ortho- and para-position of the phenyl ring, respectively, allowing us to evaluate the optimal geometry for AMP recognition in water through comparison with the previously reported meta-substituted complex [Eu·mBOH₂]⁺. The ligand design retains sufficient host rigidity and steric hindrance at the metal centre to ensure monodentate binding of AMP, whilst preventing the chelation of common oxyanion interferents. The complexes are studied experimentally using a combination of photophysical techniques, mass spectrometry and NMR spectroscopy. Computations are performed to further investigate binding geometries and energies. We explore the possibility of computing lanthanide emission spectra using a first principles approach.

Results and discussion

Synthesis

The synthesis of the target receptors [Eu·oBOH₂]⁺ and [Eu·pBOH₂]⁺ (Scheme 1) was undertaken using similar methods described for [Eu·Bn]⁺ and [Eu·mBOH₂]⁺.²⁰ Full details of the synthesis and characterisation are provided in the ESI.† The 8-(benzyloxy)quinoline pendant arm was obtained in two steps, involving initial O-alkylation of 8-hydroxyquinoline-2-carbaldehyde with the appropriate regioisomer of iodobenzyl bromide to give compounds 2o and 2p, followed by reduction of the aldehyde with sodium borohydride in methanol to give the desired alcohols 3o and 3p. Subsequent mesylation of the alcohol in dichloromethane produced the methanesulfonate esters 4o and 4p in quantitative yields, which were used to alkylate one of the secondary amines of the macrocycle DO2A⁴⁴ (bearing two trans-related protected acetate arms) to give compounds 5o and 5p. The tert-butyl ester protecting groups were removed using trifluoroacetic acid followed by complexation with Eu(III) chloride in water (pH 7.5) affording the benzyl iodide precursor complexes [Eu·oI]⁺ and [Eu·pI]⁺, as chloride salts. The target boronic acid-functionalised complexes [Eu·oBOH₂]⁺ and [Eu·pBOH₂]⁺ were obtained by reacting the benzyl iodide complexes with bis(pinacolato)diboron using Pd(dppf)Cl₂ in DMSO, followed by purification by reverse-phase HPLC under basic or acid conditions providing the target complexes as the chloride and formate salts, respectively.

Scheme 1 Synthesis of boronic acid-functionalised Eu(III) complexes [Eu·oBOH₂]⁺ and [Eu·pBOH₂]⁺.

Photophysical properties

Photophysical data of the two new Eu(III) complexes and the previously reported complex [Eu·mBOH₂]⁺ are given in Table 1. The UV-Vis absorption spectra of [Eu·oBOH₂]⁺ and [Eu·pBOH₂]⁺ display a broad band centred at 322 nm (Fig. S3† and Table 1), very similar to [Eu·mBOH₂]⁺.

Table 1 Photophysical data for Eu(III) complexes measured in 10 mM HEPES at pH 7.0, unless stated otherwise

Complex	λ max/nm	ε/M^−1 cm^−1	τ H2O  /ms	τ D2O  /ms	q	Φ em  /%
Values of hydration state q (calculation error is ±20%) were derived using literature methods.^47 Quantum yields were measured using quinine sulfate in 0.05 M H2SO4 as standard (Φem = 59%).^48 Calculation error in quantum yields is ±15%.a Mean ± standard deviation for two independent measurements.b Emission lifetimes and hydration state in parentheses were determined at pH 4.0.c Mean ± standard deviation for three independent measurements.d [Eu·mBOH2]^+ data from ref. 20 shown for comparison.
[Eu·oBOH2]^+	322	3800	0.422 ± 0.002 (0.210)^b	0.532 ± 0.004 (0.281)^b	0.3 (1.1)^b	9.0 ± 0.7
[Eu·pBOH2]^+	322	2900	0.192 ± 0.037	0.260 ± 0.069	1.2	2.0 ± 0.3
[Eu·mBOH2]^+ ^d	322	2700	0.199 ± 0.004	0.283 ± 0.002	1.5	1.5 ± 0.2

---

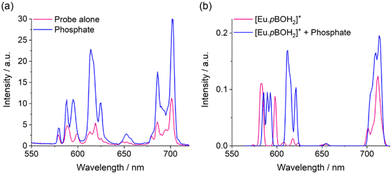
Each complex displays characteristic Eu(III) emission in the red region of the visible spectrum when excited at 322 nm. The emission spectrum of [Eu·pBOH₂]⁺ (Fig. 2b) displays two distinguishable components in the ΔJ = 1 (585–600 nm) emission band and three components in the ΔJ = 2 (605–630 nm) band. Analysis of the intensity ratio of the ΔJ = 2/ΔJ = 1 emission bands gave the value of approximately 1.4, similar to that seen for complex [Eu·mBOH₂]⁺ (Fig. S4†). A rather different emission spectrum was obtained for [Eu·oBOH₂]⁺ (Fig. 2a), characterised by a dominant ΔJ = 2 emission band and a higher intensity ratio ΔJ = 2/ΔJ = 1 of 3.0, signifying a different coordination environment at the Eu(III) centre.^45,46 Excitation spectra collected for each complex were similar to the absorption spectra, confirming that the quinoline antenna is responsible for sensitising the Eu(III) emission (Fig. S5†).

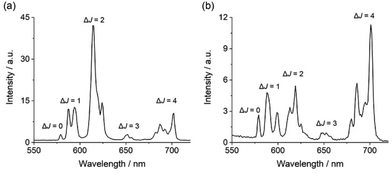Fig. 2 Emission spectra of (a) [Eu·oBOH₂]⁺ and (b) [Eu·pBOH₂] + in 10 mM HEPES at pH 7.0 and 295 K, λ_exc = 322 nm.

The quantum yields of the metal-centred luminescence of [Eu·pBOH₂]⁺ and [Eu·oBOH₂]⁺ were found to be 2.0 and 9.0, respectively. The ortho-complex was notably more emissive, and the emission lifetimes in H₂O and D₂O were also considerably longer, at 0.422 ms and 0.532 ms respectively (Table 1). These differences correspond to a lack of coordinated water (q = 0) in the first coordination sphere of [Eu·oBOH₂]⁺, whereas the number of coordinated water molecules calculated for [Eu·pBOH₂]⁺ is q = 1. The higher emission intensity, distinct spectral shape and longer emission lifetime of [Eu·oBOH₂]⁺ all point to a distinctive conformation that potentially involves an interaction between the ortho-substituted boronic acid and the Eu(III) ion. We corroborate this hypothesis via pH analysis as well as computed binding free energies and emission spectra.

pH analysis

Evidence in support of the boronic acid–Eu(III) interaction in [Eu·oBOH₂]⁺ was given by comparison of the pH dependence of the emission spectra of the two Eu(III) complexes in water at 295 K. For complex [Eu·pBOH₂]⁺, the intensity ratio of the ΔJ = 2/ΔJ = 1 emission bands increased by approximately 2-fold as the pH was increased from 4 to 11 (Fig. 3c). Different pH behaviour was found for [Eu·oBOH₂]⁺; the emission intensity increased significantly from pH 3.5 to 6 and remained essentially unchanged from pH 6 to 10 (Fig. 3d). By fitting the change in the intensity ratio ΔJ = 2/ΔJ = 1 with pH, a pK_a value could be estimated by nonlinear least squares regression analysis. Note that the pK_a corresponds to the hydroxylation of the boron atom accompanied by the release of a proton.^49,50 A value of 8.91 ± 0.05 was estimated for [Eu·pBOH₂]⁺, which is comparable with the pK_a of the phenylboronic acid/boronate ester couple of 8.9 (Fig. 3a).⁵¹ Thus, the boron centre of [Eu·pBOH₂]⁺ is expected to be sp² hybridised at neutral pH. The pK_a of [Eu·pBOH₂]⁺ is very similar to [Eu·mBOH₂]⁺ and the emission is stable over the physiologically relevant pH range 6.0–7.5 (Fig. 3c), thus the complex shows promise for potential sensing applications in biological media.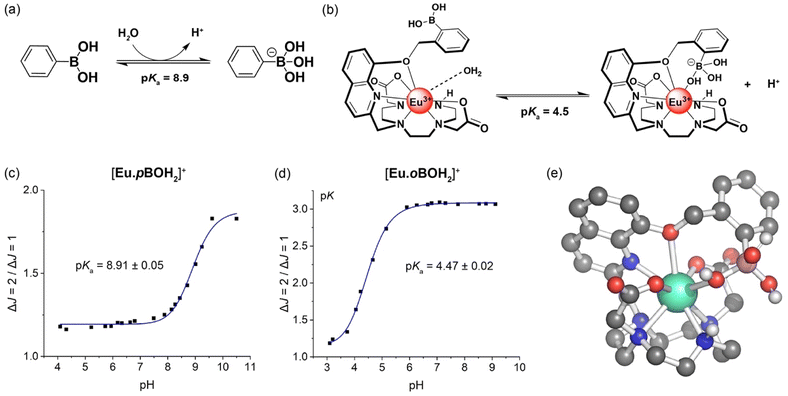

Fig. 3 (a) pH dependent hybridisation of phenylboronic acids, switching from sp² hybridised boron at low pH to sp³ hybridised at high pH. The pK_a value corresponds to the hydroxylation of the boron atom accompanied by the release of a proton;⁵¹ (b) structural representation of [Eu·oBOH₂]⁺ showing coordination of the boronic acid with increasing pH, shifting the boron hybridisation from sp² (left) to tetrahedral sp³ (right); pH profiles of (c) [Eu·pBOH₂]⁺ and (d) [Eu·oBOH₂]⁺ measured in water at 295 K, showing the plot of emission intensity ratio ΔJ = 2/ΔJ = 1 as a function of pH and the pK_a determined by nonlinear least squares regression analysis; (e) DFT-optimised structure of [Eu·oBOH₃].

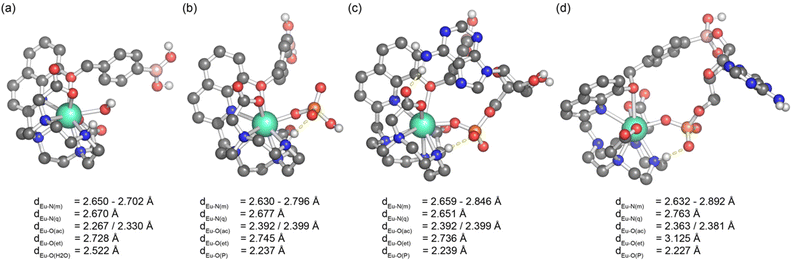
A much lower pK_a of 4.47 ± 0.02 was found for [Eu·oBOH₂]⁺ (Fig. 3d). We postulate that the ortho-substituted boronic acid coordinates to the Eu(III) ion, increasing the Lewis acidity and electrophilicity of the boron centre, shifting the hybridisation from sp² to tetrahedral sp³ at neutral pH (Fig. 3b). DFT computations support this hypothesis by showing that this molecule has indeed a strong binding affinity for the OH⁻ group, forming a closed [Eu·oBOH₃] species with OH⁻ bridging between the Eu(III) and boron atoms (Fig. 3e), occupying a similar coordination site to an isolated water molecule (Fig. 7a). A free energy change of −17.3 kJ mol⁻¹ was obtained for deprotonation of the water bound complex at pH 7, corresponding to a pK_a value of 3.96, in good agreement with experimental results.

Analysis of the emission lifetime of [Eu·oBOH₂]⁺ in H₂O and D₂O at pH 4 corresponded to one water molecule bound to the Eu(III) centre (Table 1), suggesting that coordination of the boronate ester is reversible with variation of pH. The pH response of the [Eu·oBOH₂]⁺ in the range 4.0–5.8 could potentially provide a means to probe the pH of acidic cellular organelles. Previous work in this area includes probes that internalize in the low pH environment of lysosomes in viable cancer cells. These probes contain a BODIPY moiety, with pK_a values ranging from 4.4–5.8.⁵²

Anion selectivity studies

The anion binding behaviour of the two new Eu(III) receptors was assessed by recording their emission spectra in the presence of different biologically relevant anions in 10 mM HEPES at pH 7.0. The addition of 1 mM hydrogen phosphate to [Eu·pBOH₂]⁺, resulted in a 3-fold enhancement in overall Eu(III) emission intensity and distinct changes in the spectral shape (Fig. S7†) including a 3.5 fold increase in the hypersensitive ΔJ = 2 band centred at 614 nm and changes in the Stark splitting pattern within the ΔJ = 1 emission band caused by change in crystal field.^45,53,54 These changes correspond to displacement of the coordinated water by phosphate, modulating the coordination environment of the Eu(III) centre. The spectral form changes induced by phosphate are comparable with the isomeric complex [Eu·mBOH₂]⁺.²⁰ Emission lifetimes measured in H₂O and D₂O, revealed that q = 0 in the presence of phosphate (Table 2), confirming the displacement of water. Pleasingly, the emission spectra remained essentially unchanged in the presence of chloride (145 mM), bicarbonate, lactate, sulfate and acetate (1 mM each) (Fig. S6 and S7†), indicating that these anions do not bind to [Eu·pBOH₂]⁺.

Table 2 Lifetime values for Eu(III) complexes alone and in the presence of selected anions (1 mM each), measured in 10 mM HEPES at pH 7.0

Complex	Anion	τ H2O  /ms	τ D2O  /ms	q
a Mean ± standard deviation for two independent measurements. b Values of hydration state q (calculation error is ±20%) were derived using literature methods.^47
	None	0.192 ± 0.037	0.260 ± 0.069	1.2
	HPO4^2−	0.452 ± 0.002	0.524 ± 0.016	0.1
[Eu·pBOH2]^+	AMP	0.494 ± 0.003	0.581 ± 0.004	0.1
	ADP	0.489 ± 0.004	0.621 ± 0.004	0.2
	ATP	0.341 ± 0.004	0.508 ± 0.011	0.9
	Citrate	0.315 ± 0.044	0.412 ± 0.064	0.6

---

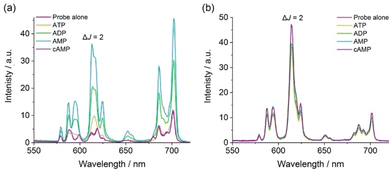
Next, we assessed the ability of [Eu·pBOH₂]⁺ to discriminate between the nucleotide phosphate anions, AMP, ADP, ATP between the nucleotide phosphate anions, AMP, ADP, ATP and cAMP. Addition of 1 mM AMP to [Eu·pBOH₂]⁺ induced a 4-fold enhancement in overall Eu(III) emission intensity and a striking 6-fold increase in the ΔJ = 2 band (Fig. 4a). Adding 1 mM ADP caused a comparatively smaller (approximately 2-fold increase) in total emission, whereas ATP induced only a minor change in emission and cAMP and adenosine (Fig. S10†) induced no change in emission intensity or shape at all. Similar to [Eu·mBOH₂]⁺, the para-substituted complex exhibits the selectivity profile AMP > ADP > ATP, representing a reversal of the selectivity order observed for most reported nucleoside phosphate receptors, where the binding is governed by electrostatic interactions and thus follows the trend ATP > ADP > AMP.^21–24 The remarkable sensitivity of [Eu·pBOH₂]⁺ for AMP was demonstrated by the linear increase in ΔJ = 2/ΔJ = 1 emission intensity ratio over the 0–100 μM range (Fig. S11†).

Fig. 4 (a) Large enhancement in emission intensity of [Eu·pBOH₂]⁺ with AMP (1 mM) compared with ATP, ADP and cAMP (1 mM each). (b) Lack of response of [Eu·oBOH₂]⁺ towards nucleoside phosphate anions. All spectra measured using 5 μM Eu(III) complex in 10 mM HEPES at pH 7.0 and 295 K, λ_exc = 322 nm.

Based on the close similarities in the emission spectral shape of [Eu·pBOH₂]⁺ in the presence of AMP and hydrogen phosphate (Fig. 4 and S7†), a similar monodentate binding mode to the Eu(III) centre can be assumed. Luminescence lifetimes revealed the displacement of water by AMP and ADP (Table 2), however in the presence of ATP a q value of 1.0 was found, consistent with lack of ATP binding. Our previous NMR spectroscopic studies of a family of conformationally more flexible Eu(III) complexes revealed the preference of ATP to chelate the europium(III) centre via the α and γ-phosphate groups, whereas ADP adopts more than one binding conformation (e.g. both bidentate and monodentate binding).³³ In our current systems, we hypothesise that the increased rigidity and steric demand imposed by the 8-(benzyloxy)quinoline pendant arm prevents ATP or ADP from binding in a bidentate manner. Since ADP induces a similar change in emission spectral shape in [Eu·pBOH₂]⁺ to that of AMP (Fig. 4a), it is assumed that ADP has a higher tendency for monodentate binding to the Eu(III) complex via its terminal phosphate group compared with ATP.

In contrast, complex [Eu·oBOH₂]⁺ showed no change in emission intensity or spectral form in the presence of phosphate, bicarbonate, lactate, sulfate, acetate, or the nucleotide phosphate anions, AMP, ADP, ATP and cAMP. This is consistent with the lack of an available binding site due to the coordination of the ortho-substituted boronate ester (Fig. 4b and S8†). The only anion tested that induced a change in emission for both Eu(III) complexes was citrate, which caused a reduction in the overall emission intensity, most notably within the ΔJ = 1 and ΔJ = 4 bands (Fig. S7 and S8†), indicating a common binding mode for this anion. The binding of citrate may cause de-coordination of the quinoline antenna leading to less efficient sensitization and partial hydration of the Eu(III) ion, consistent with q = 0.6, in the presence of citrate (Table 2).²⁰

Apparent binding constants were determined for [Eu·pBOH₂]⁺ with phosphate, AMP and ADP in aqueous buffer at pH 7.0, by following the change in the intensity ratio of the ΔJ = 2/ΔJ = 1 bands as a function of anion concentration, followed by fitting of the data to a 1 : 1 binding model (Table 3, Fig. S7 and S12†). Stronger binding was observed for AMP (log K_a = 4.22) compared with phosphate (log K_a = 3.29), whereas a similar binding constant was obtained for ADP (log K_a = 4.35). It was not possible to estimate the binding constant for ATP, due to the minor emission changes that took place. The difference in binding affinities between AMP and ADP for [Eu·pBOH₂]⁺ was less favourable compared with the previously reported complex [Eu·mBOH₂]⁺. The presence of the para-substituted boronic acid in [Eu·pBOH₂]⁺ appears to increase affinity for ADP, indicating the meta-substituted boronic acid in [Eu·mBOH₂]⁺ provides a slightly better geometry for AMP binding over ADP. As such [Eu·mBOH₂]⁺ exhibits a better level of discrimination for AMP over ADP (Fig. S9†); a 2.3-fold difference in emission is seen at 615 nm for [Eu·mBOH₂]⁺ compared with a 1.9-fold difference observed for [Eu·pBOH₂]⁺. However, the most striking feature of both these complexes is their large emission enhancement for AMP with almost no interference from ATP.

Table 3 Apparent binding constants for Eu(III) complexes measured in 10 mM HEPES at pH 7.0

Anion	[Eu·pBOH2]^+ ^a	[Eu·mBOH2]^+ ^a^,^b
a Mean ± standard deviation for two independent measurements. b Values previously reported in ref. 20. c Value not determined due to insufficient increases in emission intensity preventing accurate data fitting.
HPO4^2−	3.29 ± 0.04	3.31 ± 0.04
AMP	4.22 ± 0.01	4.07 ± 0.01
ADP	4.35 ± 0.01	3.84 ± 0.01
ATP	n.d.^c	n.d.^c

---

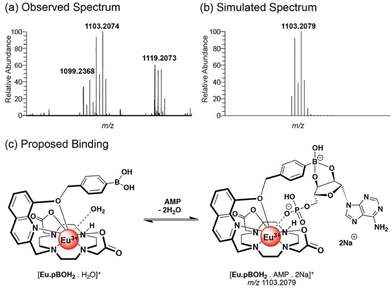
High resolution mass spectrometric data supported 1 : 1 binding of AMP, ADP and phosphate to [Eu·pBOH₂]⁺. We observed two overlapping signals at m/z 850.1501 and 854.1217 for the Eu(III) complex with phosphate (Fig. S14a†). The former signal corresponds to the host–guest complex [Eu·pBOH₂ + H₂PO₄ + Na]⁺, and the latter can be tentatively assigned to loss of one of the boronic acid OH groups [Eu·pBOH₂–OH + HPO₄ + 2Na]⁺. In the presence of AMP, the [Eu·pBOH₂]⁺ complex shows three signals (Fig. S15†). The major signal at m/z 1103.2074 can be attributed to the host–guest complex involving a boronate ester-1,2-diol interaction with the ribose sugar of AMP, as depicted in Fig. 5 and Fig. S15.† The smaller signals at m/z 1099.2368 and 1121.2178 are in agreement with the singly charged species [Eu·pBOH₂ + AMP + H + Na]⁺ and [Eu·pBOH₂ + AMP + 2Na]⁺ involving no 1,2-diol interaction. There was only one host–guest species observed for the Eu(III) complex with ADP, [Eu·pBOH₂ + ADP + 3Na]⁺; this signal was very weak compared with that of the free complex at m/z 730.1907 (Fig. S14b†).

Fig. 5 (a) High resolution mass spectrum of a 1 : 1 mixture of [Eu·pBOH₂]⁺ (250 μM) and AMP. (b) Simulated mass spectrum of the major signal corresponding to the host–guest complex. (c) Proposed structure of the host–guest complex, showing the Eu(III)–phosphate interaction and the boronate ester-1,2-diol interaction with AMP.

Solution NMR studies

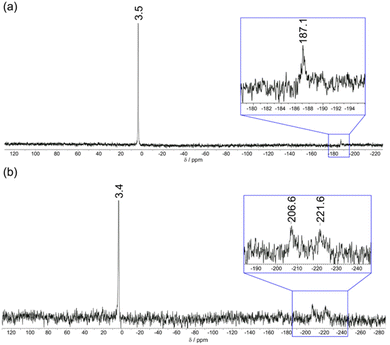
Further insight into the binding modes of phosphate and AMP to [Eu·pBOH₂]⁺ was gained by ¹H and ³¹P NMR spectroscopy. The ¹H NMR spectra of Eu(III) complexes [Eu·oBOH₂]⁺ and [Eu·pBOH₂]⁺ in D₂O (pD 7.4) at room temperature resulted in significant line broadening indicating exchange between conformation isomers. Increasing the temperature to 50 °C resulted in slightly narrower line widths although the more paramagnetically shifted resonances remained broad (Fig. S16†). Addition of 0.5 equivalents of AMP to [Eu·pBOH₂]⁺ resulted in the appearance of a new set of resonances, corresponding to the AMP-bound species in slow exchange with the monohydrated complex on the NMR timescale (Fig. S17†). In the presence of 1 equivalent of AMP, the original signals for the monohydrated complex disappeared and only signals for the AMP-[Eu·pBOH₂]⁺ complex remained. Significant exchange broadening was observed for the most paramagnetically shifted signals in the regions 22 to 40 ppm and −20 to −5 ppm, indicating either conformational freedom in the host–guest complex or the formation of more than one host–guest complex.

The ³¹P NMR spectrum of [Eu·pBOH₂]⁺ in the presence of 1 equivalent of AMP revealed a signal at 3.4 ppm corresponding to unbound AMP and two broads signals at −207 and −222 ppm, indicating the strong likelihood of exchange between more than one binding mode for AMP (Fig. 6b). The existence of two AMP-receptor complexes may tentatively be explained by the reversible interaction between the phenylboronic acid moiety and the ribose sugar of AMP, consistent with the mass spectral data (Fig. 5 and S15†). In comparison, the addition of 10 equivalents of sodium hydrogen phosphate to [Eu·pBOH₂]⁺ produced 2 resonances in the ³¹P NMR spectrum (Fig. 6a), corresponding to unbound phosphate (3.5 ppm) and phosphate bound in a single host–guest complex (−187 ppm).

Fig. 6 ³¹P NMR spectra (202.5 MHz, D₂O, pD 7.4) of (a) [Eu·pBOH₂]⁺ (1 mM) with phosphate (10 mM) showing ³¹P signals for both bound and unbound phosphate; (b) [Eu·pBOH₂]⁺ (1 mM) with AMP (1 mM) showing a sharp ³¹P signal for unbound AMP and two broad signals indicating exchange between two binding modes for AMP.

Simulation of anion binding

Starting from the crystallographic data of a structurally related Eu(III) complex previously reported by us,³³ we modelled the two new Eu(III) complexes bound to a single water molecule and various phosphoanions. Molecular geometries of [Eu·pBOH₂]⁺ are shown in Fig. 7, considering binding to water, phosphate, and AMP in a monodentate and cyclic binding mode. The macrocycle is shown at the bottom, the quinoline antenna on the left, and the phenyl boronic acid at the top. Binding of the analyte occurs from the right. Starting with the water bound species (Fig. 7a) we find short bond distances for the acetate oxygens (∼2.30 Å) and an intermediate value for the water molecule (2.52 Å) whereas the other atoms show larger distances around 2.7 Å. Binding of phosphate (Fig. 7b) leaves the structure largely intact. The most important difference is that the oxygen of the highly charged phosphate group is now very strongly bound (2.24 Å) whereas the acetate oxygens are somewhat further removed (2.39 Å). AMP (Fig. 7c) binds in a very similar manner to phosphate with most bond distances unaltered and only a slight elongation of the distances to some macrocycle nitrogens.

Fig. 7 Molecular geometries of [Eu·pBOH₂]⁺ bound to (a) water, (b) hydrogen phosphate, (c) AMP bound in a monodentate manner and (d) AMP bound in a cyclic manner involving a boronate ester–ribose interaction. Bond distances of Eu(III) to donor atoms are shown: N(m) – macrocycle, N(q) – quinoline, O(ac) – acetate, O(et) – ether, O(H₂O) – water, O(P) – phosphate.

The possibility of the multisite recognition of AMP by complex [Eu·pBOH₂]⁺ was explored, involving Eu(III)–phosphate coordination combined with a boronate ester-1,2-diol interaction with the ribose sugar of AMP. Formation of the cyclic boronic ester was possible (Fig. 7d) and this multisite binding leaves the geometry around europium largely intact with a similar geometry to the monodentate binding mode (Fig. 7c). However, the bond lengths of Eu(III) to the quinoline nitrogen and the ether oxygen are elongated indicating some ring strain involved.

The computational effort required to obtain binding energies with accuracy high enough to reproduce the subtle trends seen in Table 3 is well beyond the scope of this work.³⁷ However, we shall continue with a qualitative discussion of binding energies (Table S1†). First, the computations highlight the strong affinity of these complexes for binding hydrogen phosphate, and in line with experiment, binding to AMP is enhanced. Furthermore, computations indicate that the cyclic structure of AMP with [Eu·pBOH₂]⁺ is bound but that its energy is disfavoured by about 30 kJ mol⁻¹ compared to the open analogue. However, the existence of such a complex with a reasonable geometry and energy makes it plausible that both proposed AMP-receptor complexes exist in aqueous solution, consistent with the ³¹P NMR spectroscopic data which shows two distinct resonances for the AMP-bound species.

First principles computation of emission spectra

We were interested in the computational modelling of the emission spectra of the complexes studied. As opposed to the previously described DFT simulations, in which the f-electrons are only implicitly considered within the core potential, it is necessary to include them explicitly for the computation of emission spectra. For this purpose, we use an ab initio multireference treatment (see ESI† for computational details).^42,43

A comparison of experimental and computational emission spectra is shown in Fig. 8. Here, we consider the water bound complex [Eu·pBOH₂]⁺ (as shown in Fig. 7a) and the phosphate bound complex (Fig. 7b) as a model for AMP, considering their similar binding geometries and assuming the electrostatic effect of the phosphate group has the strongest influence on the emission spectrum.

Fig. 8 (a) Emission spectra of [Eu·pBOH₂]⁺ in the absence (pink) and presence (blue) of hydrogen phosphate, measured in 10 mM HEPES at pH 7.0 and 295 K; (b) computational modelling of the emission spectral data shown in part (a).

Pleasingly, our computational treatment naturally produces the different emission bands (ΔJ = 0, 1, 2, 3 and 4) along with their relative intensities. Remarkably, it does so without any adjustable parameters aside from three trivial scaling factors (discussed in the ESI†).

Starting with the water-bound complex, the simulations do not reproduce the formally forbidden ΔJ = 0 band. Next, the ΔJ = 1 band is well-reproduced including its crystal field splitting: just as in seen by experiment, two states are close together at lower wavelength with one isolated state at higher wavelength. The presented simulations underestimate the intensity of the hypersensitive ΔJ = 2 band, possibly due to missing vibronic effects. Finally, the low intensity of the ΔJ = 3 band and the high intensity along with its appropriate shape of the ΔJ = 4 band are well reproduced.

Moving from the water-bound complex to the phosphate-bound complex the experimental emission spectrum shows three notable changes: (i) an overall increase in intensity, (ii) an increase in the ΔJ = 2/ΔJ = 1 emission intensity ratio, and (iii) differences in the crystal field splitting. Effect (i) derives from quenching by nearby water molecules and is not covered by the present treatment. However, the other two are well reproduced. The increase in the ΔJ = 2 (605–630 nm) emission intensity is very pronounced showing a 16.1-fold increase when binding phosphate. This rise is more pronounced compared with the experimental value of a 4.2-fold increase but certainly highlights that the correct physics is captured and indicates that the approach can be used to screen for complexes with large ΔJ = 2/ΔJ = 1 changes upon guest binding. Finally, the simulations present appropriate crystal fielding splitting in the phosphate bound complex, specifically the structure of the ΔJ = 1 band changes with respect to the water-bound complex with one state at lower wavelength and two states at higher wavelength (which merge to form one apparent peak in the experimental spectrum, Fig. 8a). The magnitude of the splitting within the ΔJ = 1 band is also reduced. Taken together, the experimental and simulated spectra indicate a change in magnitude and sign of the crystal field coefficient.⁵⁵ The shape of the ΔJ = 2 band is also well-reproduced with a large peak around 611 nm (deriving from four of the ⁷F₂ states) and a smaller peak at 620 nm (deriving from the fifth state).

These data suggest that first principles computation offers a promising, albeit so far not exploited, approach to access the emission spectra of lanthanide complexes. A qualitatively correct description of the major features of the spectra along with changes upon coordination was readily achieved with the presented approach. We believe that this approach can be utilized as a powerful tool in the rational design of responsive Ln(III) complexes, including host–guest systems with predictable changes in local crystal field and thus specific spectral properties, while also providing a useful way to crosscheck computed structures with experiment.

Conclusions

We have synthesised two new cationic Eu(III) complexes and evaluated the impact of varying the position of the peripheral phenylboronic acid on their ability to detect AMP in aqueous solution. Complex [Eu·pBOH₂]⁺ showed preferential binding to AMP over ATP, eliciting a striking 6-fold increase in the ΔJ = 2 emission band upon binding AMP, compared with almost no response to ATP. In contrast, [Eu·oBOH₂]⁺ showed no increase in emission in the presence of nucleoside phosphate anions (or other biological anions), due to the direct coordination of the ortho-substituted phenylboronic acid to the Eu(III) centre.

NMR and mass spectral data supported by DFT calculations indicated the existence of two AMP-receptor complexes in aqueous solution, each stabilised by a phosphate–Eu(III) interaction and with one species involving interaction between the boronate ester and the ribose sugar of AMP. Complex [Eu·mBOH₂]⁺ showed the highest level of discrimination between AMP and ADP, indicating that the meta-substituted boronic acid provides a slightly better geometry for AMP binding over ADP. Both complexes [Eu·pBOH₂]⁺ and [Eu·mBOH₂]⁺ exhibit the sensing selectivity order AMP > ADP > ATP, representing a reversal of that observed for the majority of receptors for nucleoside phosphates. This is attributed primarily to the incorporation of a sterically demanding ligand that caps the ‘axial’ coordination site of the central Eu(III) inhibiting access of the larger chelating polyphosphate anions.

Finally, first principles simulations of lanthanide emission spectra, both in the absence and presence of anionic guests, reproduced all qualitative features well highlighting the power of such an approach in the design of new responsive lanthanide host–guest complexes with specific photophysical properties.

Author contributions

S. E. B. and C. B. carried out the synthesis and photophysical analysis of the host molecules and their anion binding properties. F. P. performed computational modelling. S. J. B. conceived and designed the research programme. The paper was written by S. J. B., S. E. B. and F. P.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

In memory of Prof. John Fossey who provided helpful advice at the beginning of this project, especially concerning the purification and handling of phenylboronic acids.

We gratefully acknowledge financial support by the EPSRC [EP/S032339/1].

References

1. D. J. Cram and J. M. Cram, Host-Guest Chemistry: Complexes between organic compounds simulate the substrate selectivity of enzymes., Science, 1974, 183, 803–809.
2. D. J. Cram, The design of molecular hosts, guests, and their complexes (Nobel lecture), Angew. Chem., Int. Ed. Engl., 1988, 27, 1009–1020.
3. N. Busschaert, C. Caltagirone, W. van Rossom and P. A. Gale, Applications of Supramolecular Anion Recognition, Chem. Rev., 2015, 115, 8038–8155.
4. T. Gunnlaugsson, M. Glynn, G. M. Tocci (née Hussey), P. E. Kruger and F. M. Pfeffer, Anion recognition and sensing in organic and aqueous media using luminescent and colorimetric sensors, Coord. Chem. Rev., 2006, 250, 3094–3117.
5. P. A. Gale and C. Caltagirone, Anion sensing by small molecules and molecular ensembles, Chem. Soc. Rev., 2015, 44, 4212–4227.
6. P. A. Gale and R. Quesada, Anion coordination and anion-templated assembly: Highlights from 2002 to 2004, Coord. Chem. Rev., 2006, 250, 3219–3244.
7. M. C. Heffern, L. M. Matosziuk and T. J. Meade, Lanthanide probes for bioresponsive imaging, Chem. Rev., 2014, 114, 4496–4539.
8. S. v. Eliseeva and J. C. G. Bünzli, Lanthanide luminescence for functional materials and bio-sciences, Chem. Soc. Rev., 2010, 39, 189–227.
9. S. Faulkner, S. J. A. Pope and B. P. Burton-Pye, Lanthanide complexes for luminescence imaging applications, Appl. Spectrosc. Rev., 2005, 40, 1–31.
10. E. J. New, D. Parker, D. G. Smith and J. W. Walton, Curr. Opin. Chem. Biol., 2010, 14, 238–246.
11. S. J. Butler and D. Parker, Anion binding in water at lanthanide centres: From structure and selectivity to signalling and sensing, Chem. Soc. Rev., 2013, 42, 1652–1666.
12. S. E. Bodman and S. J. Butler, Advances in anion binding and sensing using luminescent lanthanide complexes, Chem. Sci., 2021, 12, 2716–2734.
13. A. B. Aletti, D. M. Gillen and T. Gunnlaugsson, Coord. Chem. Rev., 2018, 354, 98–120.
14. R. Pal, D. Parker and L. C. Costello, A europium luminescence assay of lactate and citrate in biological fluids, Org. Biomol. Chem., 2009, 7, 1525–1528.
15. S. H. Hewitt, R. Ali, R. Mailhot, C. R. Antonen, C. A. Dodson and S. J. Butler, A simple, robust, universal assay for real-time enzyme monitoring by signalling changes in nucleoside phosphate anion concentration using a europium(III)-based anion receptor, Chem. Sci., 2019, 10, 5373–5381.
16. M. Tropiano, O. A. Blackburn, J. A. Tilney, L. R. Hill, M. P. Placidi, R. J. Aarons, D. Sykes, M. W. Jones, A. M. Kenwright, J. S. Snaith, T. J. Sørensen and S. Faulkner, Using remote substituents to control solution structure and anion binding in lanthanide complexes, Chem. – Eur. J., 2013, 19, 16566–16571.
17. M. V. R. Raju, S. M. Harris and V. C. Pierre, Design and applications of metal-based molecular receptors and probes for inorganic phosphate, Chem. Soc. Rev., 2020, 49, 1090–1108.
18. J. Sahoo, R. Arunachalam, P. S. Subramanian, E. Suresh, A. Valkonen, K. Rissanen and M. Albrecht, Coordinatively Unsaturated Lanthanide(III) Helicates: Luminescence Sensors for Adenosine Monophosphate in Aqueous Media, Angew. Chem., Int. Ed., 2016, 55, 9625–9629.
19. H. Y. Kuchelmeister and C. Schmuck, Nucleotide recognition in water by a guanidinium-based artificial tweezer receptor, Chem. – Eur. J., 2011, 17, 5311–5318.
20. S. E. Bodman, C. Breen, S. Kirkland, S. Wheeler, E. Robertson, F. Plasser and S. J. Butler, Sterically demanding macrocyclic Eu(III) complexes for selective recognition of phosphate and real-time monitoring of enzymatically generated adenosine monophosphate, Chem. Sci., 2022, 13, 3386–3394.
21. A. E. Hargrove, S. Nieto, T. Zhang, J. L. Sessler and E. v. Anslyn, Artificial receptors for the recognition of phosphorylated molecules, Chem. Rev., 2011, 111, 6603–6782.
22. S. J. Butler, Ratiometric detection of adenosine triphosphate (ATP) in water and real-time monitoring of apyrase activity with a tripodal zinc complex, Chem. – Eur. J., 2014, 20, 15768–15774.
23. A. M. Agafontsev, A. Ravi, T. A. Shumilova, A. S. Oshchepkov and E. A. Kataev, Chem. – Eur. J., 2019, 25, 2684–2694.
24. S. J. Butler and K. A. Jolliffe, Anion Receptors for the Discrimination of ATP and ADP in Biological Media, ChemPlusChem, 2021, 86, 59–70.
25. P. Das, A. Ghosh, M. K. Kesharwani, V. Ramu, B. Ganguly and A. Das, ZnII-2,2′:6′,2′′-terpyridine-based complex as fluorescent chemosensor for PPi, AMP and ADP, Eur. J. Inorg. Chem., 2011, 3050–3058.
26. X. F. Shang, H. Su, H. Lin and H. K. Lin, A supramolecular optic sensor for selective recognition AMP, Inorg. Chem. Commun., 2010, 13, 999–1003.
27. L. Reinke, M. Koch, C. Müller-Renno and S. Kubik, Selective sensing of adenosine monophosphate (AMP) over adenosine diphosphate (ADP), adenosine triphosphate (ATP), and inorganic phosphates with zinc(II)-dipicolylamine-containing gold nanoparticles, Org. Biomol. Chem., 2021, 19, 3893–3900.
28. Y. Hisamatsu, K. Hasada, F. Amano, Y. Tsubota, Y. Wasada-Tsutsui, N. Shirai, S. I. Ikeda and K. Odashima, Highly selective recognition of adenine nucleobases by synthetic hosts with a linked five-six-five-membered triheteroaromatic structure and the application to potentiometric sensing of the adenine nucleotide, Chem. – Eur. J., 2006, 12, 7733–7741.
29. H. Y. Kuchelmeister and C. Schmuck, Nucleotide recognition in water by a guanidinium-based artificial tweezer receptor, Chem. – Eur. J., 2011, 17, 5311–5318.
30. T. D. James, K. R. A. S. Sandanayake and S. Shinkai, Saccharide sensing with molecular receptors based on boronic acid, Angew. Chem., Int. Ed. Engl., 1996, 35, 1910–1922.
31. S. D. Bull, M. G. Davidson, J. M. H. van den Elsen, J. S. Fossey, A. T. A. Jenkins, Y. B. Jiang, Y. Kubo, F. Marken, K. Sakurai, J. Zhao and T. D. James, Exploiting the reversible covalent bonding of boronic acids: Recognition, sensing, and assembly, Acc. Chem. Res., 2013, 46, 312–326.
32. X. Wu, Z. Li, X. X. Chen, J. S. Fossey, T. D. James and Y. B. Jiang, Selective sensing of saccharides using simple boronic acids and their aggregates, Chem. Soc. Rev., 2013, 42, 8032–8048.
33. S. H. Hewitt, G. Macey, R. Mailhot, M. R. J. Elsegood, F. Duarte, A. M. Kenwright and S. J. Butler, Tuning the anion binding properties of lanthanide receptors to discriminate nucleoside phosphates in a sensing array, Chem. Sci., 2020, 11, 3619–3628.
34. I. Georgieva, T. Zahariev, A. J. A. Aquino, N. Trendafilova and H. Lischka, Energy transfer mechanism in luminescence Eu(III) and Tb(III) complexes of coumarin-3-carboxylic acid: A theoretical study, Spectrochim. Acta, Part A, 2020, 240, 118591.
35. Y. Zhang, W. Thor, K. L. Wong and P. A. Tanner, Determination of Triplet State Energy and the Absorption Spectrum for a Lanthanide Complex, J. Phys. Chem. C, 2021, 125, 7022–7033.
36. A. G. Cosby, J. J. Woods, P. Nawrocki, T. J. Sørensen, J. J. Wilson and E. Boros, Accessing lanthanide-based, in situilluminated optical turn-on probes by modulation of the antenna triplet state energy, Chem. Sci., 2021, 12, 9442–9451.
37. Y. Liu, A. Sengupta, K. Raghavachari and A. H. Flood, Anion Binding in Solution: Beyond the Electrostatic Regime, Chem, 2017, 3, 411–427.
38. D. Parker, E. A. Suturina, I. Kuprov and N. F. Chilton, How the Ligand Field in Lanthanide Coordination Complexes Determines Magnetic Susceptibility Anisotropy, Paramagnetic NMR Shift, and Relaxation Behavior, Acc. Chem. Res., 2020, 53, 1520–1534.
39. L. Ungur and L. F. Chibotaru, Magnetic anisotropy in the excited states of low symmetry lanthanide complexes, Phys. Chem. Chem. Phys., 2011, 13, 20086–20090.
40. D. Reta, J. G. C. Kragskow and N. F. Chilton, Ab Initio Prediction of High-Temperature Magnetic Relaxation Rates in Single-Molecule Magnets, J. Am. Chem. Soc., 2021, 143, 5943–5950.
41. H. Lischka, D. Nachtigallová, A. J. A. Aquino, P. G. Szalay, F. Plasser, F. B. C. MacHado and M. Barbatti, Chem. Rev., 2018, 118, 7293–7361.
42. M. P. Hehlen, M. G. Brik and K. W. Krämer, 50th anniversary of the Judd-Ofelt theory: An experimentalist's view of the formalism and its application, J. Lumin., 2013, 136, 221–239.
43. B. M. Walsh, Judd-Ofelt Theory: Principles and Practices, in Advances in Spectroscopy for Lasers and Sensing, 2006, pp. 403–433.
44. Z. Kovacs and A. D. Sherry, Tetraazacyclododecanes, J. Chem. Soc., Chem. Commun., 1995, 1, 185–186.
45. K. Binnemans, Interpretation of europium(III) spectra, Coord. Chem. Rev., 2015, 295, 1–45.
46. O. A. Blackburn, R. M. Edkins, S. Faulkner, A. M. Kenwright, D. Parker, N. J. Rogers and S. Shuvaev, Electromagnetic susceptibility anisotropy and its importance for paramagnetic NMR and optical spectroscopy in lanthanide coordination chemistry, Dalton Trans., 2016, 45, 6782–6800.
47. A. Beeby, I. M. Clarkson, R. S. Dickins, S. Faulkner, D. Parker, L. Royle, A. S. de Sousa, J. A. G. Williams and M. Woods, Non-radiative deactivation of the excited states of europium, terbium and ytterbium complexes by proximate energy-matched OH, NH and CH oscillators: An improved luminescence method for establishing solution hydration states, J. Chem. Soc., Perkin Trans. 2, 1999, 493–503.
48. K. Suzuki, A. Kobayashi, S. Kaneko, K. Takehira, T. Yoshihara, H. Ishida, Y. Shiina, S. Oishi and S. Tobita, Reevaluation of absolute luminescence quantum yields of standard solutions using a spectrometer with an integrating sphere and a back-thinned CCD detector, Phys. Chem. Chem. Phys., 2009, 11, 9850–9860.
49. M. Li, J. S. Fossey and T. D. James, Boron: Sensing, Synthesis and Supramolecular Self-Assembly, Royal Society of Chemistry, 2015.
50. J. Yan, G. Springsteen, S. Deeter and B. Wang, The relationship among pKa, pH, and binding constants in the interactions between boronic acids and diols—it is not as simple as it appears, Tetrahedron, 2004, 60, 11205–11209.
51. D. G. Hall, Boronic acids: preparation, applications in organic synthesis and medicine, John Wiley & Sons, 2006.
52. Y. Urano, D. Asanuma, Y. Hama, Y. Koyama, M. Kamiya, T. Nagano, T. Watanabe, A. Hasegawa, L. Peter and H. Kobayashi, Selective molecular imaging of viable cancer cells with pH-activatable fluorescence probes, Nat. Med., 2009, 15, 104–109.
53. C. Görller-Walrand and K. Binnemans, Rationalization of crystal-field parametrization, in Handbook on the Physics and Chemistry of Rare Earths, 1996, vol. 23, pp. 121–283.
54. P. A. Tanner, Some misconceptions concerning the electronic spectra of tri-positive europium and cerium, Chem. Soc. Rev., 2013, 42, 5090–5101.
55. O. A. Blackburn, N. F. Chilton, K. Keller, C. E. Tait, W. K. Myers, E. J. L. McInnes, A. M. Kenwright, P. D. Beer, C. R. Timmel and S. Faulkner, Spectroscopic and crystal field consequences of fluoride binding by [Yb· DTMA] 3+ in aqueous solution, Angew. Chem., Int. Ed., 2015, 54, 10783–10786.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis, characterisation and photophysical analysis of Eu(III) complexes, spectroscopic and computational studies of host–guest complexes. See DOI: https://doi.org/10.1039/d2qo01067d

---