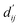Open Access Article
Open Access ArticlePIGNet: a physics-informed deep learning model toward generalized drug–target interaction predictions†
Seokhyun
Moon‡
 a,
Wonho
Zhung‡
a,
Wonho
Zhung‡
 a,
Soojung
Yang‡§
a,
Soojung
Yang‡§
 a,
Jaechang
Lim
a,
Jaechang
Lim
 b and
Woo Youn
Kim
b and
Woo Youn
Kim
 *abc
*abc
aDepartment of Chemistry, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Republic of Korea. E-mail: wooyoun@kaist.ac.kr
bHITS Incorporation, 124 Teheran-ro, Gangnam-gu, Seoul 06234, Republic of Korea
cKI for Artificial Intelligence, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Republic of Korea
First published on 7th February 2022
Abstract
Recently, deep neural network (DNN)-based drug–target interaction (DTI) models were highlighted for their high accuracy with affordable computational costs. Yet, the models' insufficient generalization remains a challenging problem in the practice of in silico drug discovery. We propose two key strategies to enhance generalization in the DTI model. The first is to predict the atom–atom pairwise interactions via physics-informed equations parameterized with neural networks and provides the total binding affinity of a protein–ligand complex as their sum. We further improved the model generalization by augmenting a broader range of binding poses and ligands to training data. We validated our model, PIGNet, in the comparative assessment of scoring functions (CASF) 2016, demonstrating the outperforming docking and screening powers than previous methods. Our physics-informing strategy also enables the interpretation of predicted affinities by visualizing the contribution of ligand substructures, providing insights for further ligand optimization.
1 Introduction
Deep learning is a rapidly growing field of science. The remarkable success of deep learning in various applications such as natural language processing, video games, and computer vision has raised expectations for similar success in other fields, leading to various applications of deep learning algorithms. In particular, biomedical applications have become immediately one of the most active areas because they are not only socially influential but also scientifically challenging.1–3 Despite the great expectation, however, deep learning has not yet shown its highest potential in this field, due to low generalization issues caused by scarce and heavily imbalanced data.4,5 Making a reliable model for predicting drug–target interactions (DTIs), which is a key technology in the virtual screening of novel drug candidates, is one such example.6As an ideal DTI prediction method should be reliable yet fast, high prediction accuracy and low computational cost are two essential factors.7 However, docking methods8–16 as the most popular conventional approach are fast enough but insufficiently accurate,17–19 whereas more rigorous ones based on thermodynamic integration is computationally too expensive.20,21 Such physics-based methods have an inherent limitation that low cost can only be achieved by losing their accuracy as a trade-off. In contrast, a data-driven approach can improve prediction accuracy at no additional inference cost, just by learning with more data. This distinct feature of the data-driven approach has encouraged the active development of deep learning-based drug–target interaction (DTI) models that accomplish both high accuracy and low cost.22–30
Among various deep learning-based models, the structure-based approach stands out for its accuracy; the spatial coordination of the protein and ligand is crucial in determining their interactions.31 Some of the promising studies utilize 3-dimensional convolutional neural networks (3D CNNs),32–41 graph neural networks (GNNs),41–44 or feed-forward neural networks based on the atomic environment vectors.45 These state-of-the-art approaches had significantly improved the accuracy of DTI prediction compared to docking calculations.
Despite the advance of previous structure-based models, their limited generalization ability remains a challenging problem towards better performance. In particular, the deficiency in 3D structural data of the protein–ligand complexes could drive the models to excessively memorize the features in training data. Such models, being over-fitted to the training data, might fail to generalize in a broader context.46 Several studies had suggested that deep learning-based models often learn the data-intrinsic bias instead of the underlying physics of the protein–ligand interaction as desired.37,47,48 For instance, Chen et al.47 reported an extremely high similarity in the performance of the receptor-ligand model and the ligand-only model – both trained with the DUD-E dataset – in terms of area under the ROC curve (AUC). Such a similarity implies that the models might have learned to deduce the protein–ligand binding affinity only by looking at the ligand structures, regardless of whether or not the protein structures are included as inputs. Moreover, they showed that such a memorization of wrong features can cause severe degradation in the performance for the proteins that have a high structural variance from those in the training data. The paper also reported that the 3D CNN and GNN models trained on the DUD-E dataset had considerably underperformed when they were tested with the ChEMBL and MUV datasets.36,44 Such an insufficient generalization of the DTI models can cause an increase in false-positive rates in virtual screening scenarios, as the models would often fail to make correct predictions for unseen protein–ligand pairs.
In the field of physical applications of deep learning, the incorporation of appropriate physics as an inductive bias is a promising mean to improve the model generalization. If a model is trained to obey certain physical principles, the model is expected to generalize to unseen data that is dictated by the same physics. Several studies have indeed shown that the physics-informed models maintain their generalization ability for unseen data.49–51
In this regard, we propose two key strategies to enhance the generalization ability of DTI models. First, we introduce a novel physics-informed graph neural network, named PIGNet. It provides the binding affinity of a protein–ligand complex as a sum of atom–atom pairwise interactions, which are the combinations of the four energy components – van der Waals (vdW) interaction, hydrogen bond, metal–ligand interaction, and hydrophobic interaction. Each energy component is computed as an output of a physics model parameterized by deep neural networks, which learn the specific pattern of the interaction. This strategy can increase the generalization ability by allowing the model to dissect an unseen protein–ligand pair as combinations of commonly observed interactions between the protein and the ligand. The detailed pattern of local interactions can render the model to learn the universal physics underlying the protein–ligand binding. Moreover, as the model provides predictions for each atom–atom pair and each energy component, it is possible to analyze the contribution of individual molecular substructures to the binding affinity. This information can be used to modify drug candidates to further strengthen the binding affinity.
Second, we leverage a data augmentation strategy. In practice, screening libraries include a variety of compounds where most of them do not appear in the training set. Currently available experimental data on protein–ligand binding structures have very limited coverage on the structural diversity of all possible binding complexes. A model trained with a set of experimental binding structures, which would only include the stable binding poses, may fail to distinguish the stable poses from non-stable poses in the inference set.47 Therefore, we augmented our training data with computationally generated random binding poses of protein–ligand pairs to improve the model generalization.48
To assess the generalization ability of the proposed model, we focused on the docking and the screening power of the CASF-2016 benchmark.52 Previously, the DTI models had been evaluated in terms of the correlation between the predicted and the experimental binding affinities.35,36,42–44 However, the high correlation does not automatically guarantee a good model generalization.47 A well-generalized model should be able to successfully identify the true binding pose that has minimum energy and correctly rank the best binding molecule. The former criterion can be assessed in terms of docking power, while the latter one is related to screening power. Examining a model for both tasks is essential to ensure the model's ability to generalize in real-world settings such as virtual high-throughput screening (vHTS). We compared the benchmark results of PIGNet with traditional docking calculations and previous deep learning models and showed that our model significantly improved both docking power and screening power.
In addition to the improvement in the model performance, we show the interpretability of our model. While interpreting the underlying chemistry of DTI prediction is an essential step of drug discovery, previous deep learning models that take a complete black box approach were not practical in that sense.53,54 On the contrary, physics-based deep learning models can offer interpretability since several intermediate variables of the models have certain physical meanings.55 As our model predicts the interaction energy for each atom–atom pair, we can estimate the contribution of each ligand substructure in total binding free energy. Such an interpretation can provide the guidelines for the practitioners regarding ligand optimization – modifying the less contributing moieties into stronger binding moieties can be an example.
2 Method
2.1 Related works
2.2 Model architecture
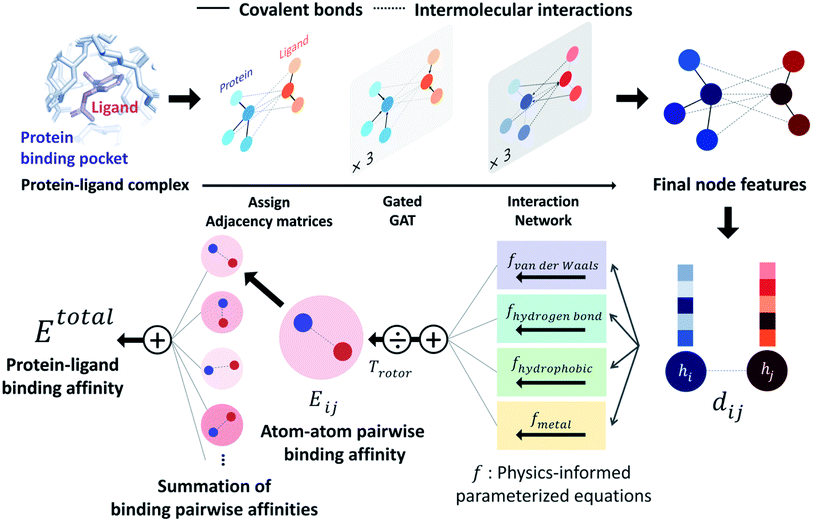
PIGNet is a deep learning model that predicts binding free energy of a given protein–ligand complex structure (Fig. 1). It takes a molecular graph, G, and the distances between the atom pairs, dij, of a protein–ligand complex as an input. Generally, a graph, G, can be defined as (H, A), where H is a set of node features and A is an adjacency matrix. In an attributed graph, the ith node feature, hi, is represented by a vector. Notably, our graph representation includes two adjacency matrices to discriminate the covalent bonds in each molecule and the intermolecular interactions between protein and ligand atoms. The details of the initial node features and the construction of the two adjacency matrices are explained in the ESI.†Our model consists of several units of gated graph attention networks (gated GATs) and interaction networks. Gated GATs and interaction networks update each node feature via two adjacency matrices that correspond to covalent bonds and intermolecular interactions. During the node feature update, gated GATs and interaction networks learn to convey the information of covalent bonds and intermolecular interactions, respectively. After several node feature updates, we calculate vdW interactions (EvdW), hydrogen bond interactions (Ehbond), metal–ligand interactions (Emetal), and hydrophobic interactions (Ehydrophobic), by feeding the final node features into physics-informed parameterized equations. Specifically, for each energy component, the fully connected layers take a set of final node features as input and produce the parametric values of the physics-informed equation. We also consider the entropy loss from the protein–ligand binding by dividing total energy with rotor penalty (Trotor). The total energy can be written as follows:
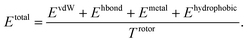 | (1) |
2.3 Physics-informed parameterized function
PIGNet consists of four energy components – vdW interaction, hydrophobic interaction, hydrogen bonding, and metal–ligand interaction – and a rotor penalty. Energy component of an interaction between the ith node and the jth node is computed from two node features, hi and hj. Since the node features contain the information of the two atoms and their interaction, the model can reasonably predict DTI.The energy components and the rotor penalty are motivated by the empirical functions of AutoDock Vina.8 The total binding affinity is obtained as a weighted sum of energy components, where the weights are introduced to account for the difference between the calculated energies and the true free binding energies. PIGNet employs learnable parameters to find an optimal weight for each component, learning to account for the different types of protein–ligand interactions.
Each energy component is calculated from dij and 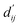 , which are the inter-atomic distance and the corrected sum of the vdW radii of the ith node and the jth node, respectively.
, which are the inter-atomic distance and the corrected sum of the vdW radii of the ith node and the jth node, respectively. 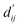 can be represented as follows:
can be represented as follows:
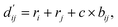 | (2) |
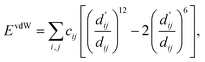 | (3) |
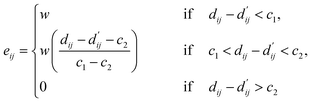 | (4) |
Here, c1 and c2 are set as −0.7 and 0.0 for hydrogen bonds and metal–ligand interactions, respectively, while the constants are set as 0.5 and 1.5 for hydrophobic interaction. We chose the same values of c1 and c2 for hydrogen bonds and metal–ligand interactions, since both originate from the electron donor–acceptor interactions. Each energy component is computed as a summation of corresponding atom–atom pairwise energy contribution coefficients, as described in eqn (5):
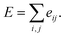 | (5) |
We classified atoms into hydrogen bond acceptors, hydrogen bond donors, metal atoms, and hydrophobic atoms. Since hydrogen bonds appear between hydrogen bond donors and hydrogen bond acceptors, each atom that forms hydrogen bonds is selected by substructure matching of the general SMARTS61 descriptors, which are summarized in the Table S2.† Metal atoms include Mg, Ca, Mn, Fe, Co, Ni, Cu, and Zn. Lastly, halogen atoms or carbon centers that are surrounded only by carbon or hydrogen atoms are classified as hydrophobic atoms.10
| Trotor = 1 + Crotor × Nrotor, | (6) |
2.4 Monte Carlo dropout (MCDO) and epistemic uncertainty
A total of 30 models is ensembled during the test phase, with the same dropout ratio, 0.1, as the training phase. We obtained the predicted values by averaging individual predictions and interpreted the variances as epistemic uncertainties. Here, we define PIGNet with and without MCDO as PIGNet (ensemble) and PIGNet (single), respectively.2.5 Loss functions
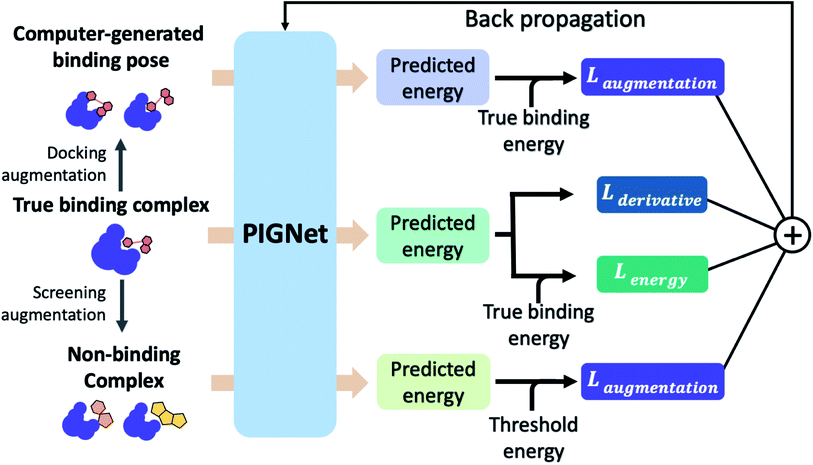
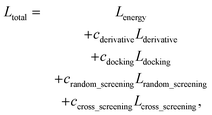
The loss function of PIGNet consists of three components, Lenergy, Lderivative, and Laugmentation as in eqn (7):| Ltotal = Lenergy + Lderivative + Laugmentation. | (7) |
Fig. 2 explains the overall training scheme of PIGNet based on the three loss functions. Lenergy is the mean squared error (MSE) loss between the predicted value from the model, ypred, and the corresponding experimental binding free energy, ytrue,
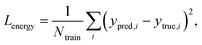 | (8) |
We can assume that the ligand atoms are located at the local minimum of the potential for the experimentally validated binding structures. Thus, we make the experimental structures as a local minimum by forcing the first derivative of the potential energy with respect to position to become zero. The sharpness of the potential energy curve was induced by increasing the second derivative. The derivative loss, Lderivative, is given as follows:
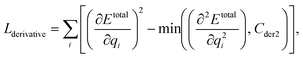 | (9) |
• Docking augmentation loss.
The purpose of docking augmentation is to improve the model to distinguish the most stable binding poses from the others. We assume experimental binding structures from the PDBbind dataset63 as the most stable binding poses. Thus, the energy of experimental structures should be lower than the predicted energy of decoy structures that have different poses from true binding poses. The loss for docking augmentation, Ldocking, can be written as follows:
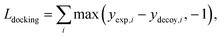 | (10) |
• Random screening augmentation loss.
In general, only a small fraction of molecules in a huge chemical space can bind to a specific target protein. Most molecules would have low binding affinity and high dissociation constant, kd, with the target. From this nature, we assume that the dissociation constant of an arbitrary protein–ligand pair from the virtual screening library would be higher than 10−5 M, as a criterion for hit identification is conventionally in micromolar (10−6 M) scale.64 Referring to the relationship between the binding free energy ΔG and the binding constant, ka, which is reciprocal to Kd, we can set a threshold for ΔG of a protein–ligand pair as follows:
ΔG ≥ −1.36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka = −6.8 kcal mol−1. Ka = −6.8 kcal mol−1. | (11) |
A model trained with random screening loss, Lrandom_screening, and a non-binding random molecule–protein pair can sufficiently learn the chemical diversity. The model would predict the binding free energy of a random molecule with the target to a value higher than the threshold energy, −6.8. Thus, the loss for the random screening augmentation, Lrandom_screening, can be written as follows:
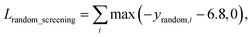 | (12) |
• Cross screening augmentation loss.
Another nature of protein–ligand binding is that if a ligand strongly binds to a specific target, the ligand is less likely to bind to other targets because the different types of proteins have different binding pockets. We assumed that the true binders of the PDBbind dataset do not bind to the other proteins in the PDBbind dataset.
As in the random screening augmentation, training with non-binding ligands and protein pairs affect a model to learn chemical diversity. The loss for the cross screening augmentation, Lcross_screening, can be written as follows:
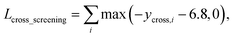 | (13) |
 | (14) |
2.6 Baseline models
We constructed two baseline DNN models with the 3D CNN and 3D GNN architecture in comparison to PIGNet, namely a 3D CNN-based model and a 3D GNN-based model. For the 3D CNN-based model, we reimplemented the KDEEP model from Jiménez et al.34 Our rebuilt 3D CNN-based model is identical to KDEEP ‘s, except we replaced the atom feature with those of PIGNet. We also constructed the 3D GNN-based model from PIGNet, but the model produces final outputs via fully connected layers instead of the physically modeled parametric equations.2.7 Dataset
Additionally, we constructed three different data augmentations; docking augmentation, random screening augmentation, and cross screening augmentation. Smina,66 which is a fork of Autodock Vina, was used for generating decoy structures. For the docking augmentation, we generated 292![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 518 decoy structures using the PDBbind 2016 dataset. For the random screening augmentation and the cross screening augmentation, we generated 831
518 decoy structures using the PDBbind 2016 dataset. For the random screening augmentation and the cross screening augmentation, we generated 831![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885 complexes using the IBS molecules65 and 527
885 complexes using the IBS molecules65 and 527![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 682 complexes based on the random cross binding, respectively. Any complexes in the test set are excluded during the augmentation.
682 complexes based on the random cross binding, respectively. Any complexes in the test set are excluded during the augmentation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 samples for the docking, and 1
340 samples for the docking, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 612
612![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 867 samples for the screening benchmark. We also assessed the model with the CSAR NRC-HiQ (2010) 1 and 2 benchmark sets.67 We could observe that some protein structures in the CSAR benchmark sets are highly similar to those in our training set. To assure a fair comparison, we further investigated if a bias in model evaluation can arise from this overlap. We built two subsets for each of the CSAR NRC-HiQ benchmark sets. First, we removed the samples if the same key existed in the training set. 48 and 37 samples remained after the exclusion for sets 1 and 2. Next, we excluded the samples that have at least 60% protein sequence similarity with one of the samples in the training set. 37 and 22 samples remained after the exclusion in sets 1 and 2, respectively.
867 samples for the screening benchmark. We also assessed the model with the CSAR NRC-HiQ (2010) 1 and 2 benchmark sets.67 We could observe that some protein structures in the CSAR benchmark sets are highly similar to those in our training set. To assure a fair comparison, we further investigated if a bias in model evaluation can arise from this overlap. We built two subsets for each of the CSAR NRC-HiQ benchmark sets. First, we removed the samples if the same key existed in the training set. 48 and 37 samples remained after the exclusion for sets 1 and 2. Next, we excluded the samples that have at least 60% protein sequence similarity with one of the samples in the training set. 37 and 22 samples remained after the exclusion in sets 1 and 2, respectively.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 413 inactives are combined with the true inhibitors to make up the virtual screening library. Finally, we generated 20 decoy structures per compound with the human MAPK1 protein (PDB id: 3I60) using Smina.
413 inactives are combined with the true inhibitors to make up the virtual screening library. Finally, we generated 20 decoy structures per compound with the human MAPK1 protein (PDB id: 3I60) using Smina.
3 Results and discussions
3.1 Assessment of the model performance and the generalization ability
We primarily assessed the model with the CASF-2016 benchmark dataset. The CASF-2016 benchmark provides four different assessment tasks – scoring, ranking, docking, and screening – to evaluate DTI models in several aspects of virtual screening. The scoring power measures a linear correlation of predicted binding affinities and experimental values, calculated by a Pearson's correlation coefficient R. The ranking power measures an ability of a model to correctly rank the binding affinities of true binders of the actual binding pose, calculated by a Spearman's rank–correlation coefficient ρ. These two metrics are designed to assess the model's ability upon the stable-and-precise binding structures. On the other hand, the docking power and the screening power deal with the unnatural structures which are generated computationally. The docking power measures an ability of a model to find out the native binding pose of a ligand among computer-generated decoys, quantified as a success rate within the top N candidates. The screening power measures the ability of a model to identify the specific binding ligand for a given target protein among a set of random molecules, quantified as a success rate and an enhancement factor (EF) within the top α percent of candidates. Detailed equations of each metric are summarized in the ESI.†In vHTS schemes, a DTI model should identify the most stable binding pose and correctly rank the protein–ligand pairs by their binding affinities at the same time. Indeed, the ranking, docking, and screening powers would be optimal if the model accurately predicts the value of the binding affinity for every given complex, that is, what the scoring power targets to achieve. However, experimental analysis on the CASF-2016 benchmark shows that the high scoring power does not guarantee high screening and docking powers.52 We attribute this inconsistency to a limitation in the CASF-2016 scoring power benchmark – the scoring power itself cannot be a single criterion of a DTI model performance evaluation. Accordingly, we highlighted the models' docking and screening powers as indicators of model generalization.
Table 1 summarizes the performance of PIGNets, baseline models, and other published works for the CASF-2016 and the CSAR NRC-HiQ benchmarks. The reference scores of docking methods – AutoDock Vina,8 GlideScore-SP,13 and ChemPLP@GOLD15 – were taken from Su et al.,52 which ranks the first in a docking success rate, screening success rate, and screening EF, respectively. The performance of other deep learning approaches except KDEEP34 was directly taken from their references. The scores of KDEEP were taken from Kwon et al.39 since the docking power was not included in its original work.
| Model | CASF-2016 | CSAR NRC-HiQ | |||||
|---|---|---|---|---|---|---|---|
| Docking | Screening | Scoring | Ranking | Set 1 | Set 2 | ||
| Success rate | Average EF | Success rate | R | ρ | R | R | |
| AutoDock Vina8 | 84.6% | 7.7 | 29.8% | 0.604 | 0.528 | — | — |
| GlideScore-SP13 | 84.6% | 11.4 | 36.8% | 0.513 | 0.419 | — | — |
| ChemPLP@GOLD15 | 83.2% | 11.9 | 35.1% | 0.614 | 0.633 | — | — |
| K DEEP 39 | 29.1% | — | — | 0.701 | 0.528 | — | — |
| AK-Score (single)39 | 34.9% | — | — | 0.719 | 0.572 | — | — |
| AK-Score (ensemble)39 | 36.0% | — | — | 0.812 | 0.67 | — | — |
| AEScore45 | 35.8% | — | — | 0.800 | 0.640 | — | — |
| Δ-AEScore45 | 85.6% | 6.16 | 19.3% | 0.790 | 0.590 | — | — |
| 3D CNN-based model | 48.2% | 3.9 | 10.1% | 0.687 | 0.580 | 0.738(0.756) | 0.804(0.837) |
| 3D GNN-based model | 67.7% | 10.2 | 28.5% | 0.667 | 0.604 | 0.514(0.566) | 0.627(0.723) |
| PIGNet (single) | 85.8% | 18.5 | 50.0% | 0.749 | 0.668 | 0.774(0.798) | 0.799(0.863) |
| PIGNet (ensemble) | 87.0% | 19.6 | 55.4% | 0.761 | 0.682 | 0.768(0.798) | 0.800(0.857) |
PIGNet, both single and ensemble models, outperformed all other previous works in the CASF-2016 docking and screening powers. Our best model achieves a top 1 docking success rate of 87%, a top 1% screening success rate of 55.4%, and a top 1% average EF of 19.6. The scoring and ranking power outperformed the docking methods while competitive with other deep learning-based approaches.
The Pearson's correlation coefficient for the CSAR NRC-HiQ benchmark sets showed consistent results with the CASF-2016 scoring power benchmark. Interestingly, the performance was not affected by the removal of the samples with a similarity threshold of 60% from the CSAR benchmark sets. Instead, we could observe consistent improvements in the performance. This slight improvement could be attributed to the smaller test set size, where a few data points can affect much of the result. Such a result suggests that our model has not merely been overfitted to the training set targets or homologous structures, as the performance would have been deteriorated if the overfitting was the case.
For baseline models, the 3D GNN-based model showed better performance on ranking, docking, and screening powers than the 3D CNN-based model. The difference might lead from the lack of the chemical interaction information in the 3D CNN-based model, where the 3D GNN-based model implicitly has. However, the 3D CNN-based model and the 3D GNN-based model fail to achieve high docking power and screening power. We attribute such low docking power to model over-fitting on the true-binding complex structures and binding affinities. The models have produced inaccurate binding affinities for the computer-generated decoy structures, which are primarily queried for the docking and screening power test. The low docking power then leads to the low screening power, as the most stable binding conformer needs to be identified in order to find the true binder. From these observations, we suspect that the performance reports of the previously introduced deep DTI models have been overoptimistic. In contrast, PIGNet consistently shows high performance across the four CASF-2016 metrics and the CSAR NRC-HiQ benchmarks. Such results imply that our model is properly fitted to the training data, and also has learned the proper features – the underlying physics of protein–ligand binding patterns. Moreover, the results remind us that the scoring power cannot be a single criterion measuring the model performance. In the following section, we analyze how much each of our strategies had contributed to the result through ablation studies.
3.2 Ablation study of two main strategies
We attribute the improvement of the model performance to two major strategies that have been utilized; the physics-informed parameterized functions introduced in the previous section and the data augmentation. In this section, we carried out an ablation study to decouple the effects of the two strategies and summarized the results in Table 2.| Model | Use Data augmentation? | CASF-2016 | ||||
|---|---|---|---|---|---|---|
| Docking | Screening | Scoring | Ranking | |||
| Success rate | Average EF | Success rate | R | ρ | ||
| 3D GNN-based model | No | 29.9% | 1.4 | 4.9% | 0.772 | 0.604 |
| Yes | 66.6% | 10.2 | 28.5% | 0.689 | 0.629 | |
| PIGNet (single) | No | 77.4% | 6.6 | 24.6% | 0.792 | 0.672 |
| Yes | 85.8% | 18.5 | 50.0% | 0.749 | 0.668 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 652
652![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 085 augmented samples in the training set. In particular, computationally generated structures, which happen to be more unstable than the actual structures, are used for learning. Table 2 clearly shows the effect of the DTI-adapted data augmentation strategy on the generalization ability. The augmentation apparently improved the docking and screening power of both the 3D GNN-based model and PIGNet. It shows the applicability of our data augmentation strategy for a variety of DNN-based DTI models. For benchmarks only containing the true binding complexes – scoring power, ranking power, and the CSAR NRC-HiQ – it was an expected result that the data augmentation did not improve the scores, because the model learns to accurately distinguish the decoy and true binding complexes from the augmented data and the corresponding losses.
085 augmented samples in the training set. In particular, computationally generated structures, which happen to be more unstable than the actual structures, are used for learning. Table 2 clearly shows the effect of the DTI-adapted data augmentation strategy on the generalization ability. The augmentation apparently improved the docking and screening power of both the 3D GNN-based model and PIGNet. It shows the applicability of our data augmentation strategy for a variety of DNN-based DTI models. For benchmarks only containing the true binding complexes – scoring power, ranking power, and the CSAR NRC-HiQ – it was an expected result that the data augmentation did not improve the scores, because the model learns to accurately distinguish the decoy and true binding complexes from the augmented data and the corresponding losses.
3.3 Virtual screening of human MAPK1 inhibitor
To be practically used for the virtual screening, DTI models should generalize well, even for unseen targets and ligands. PIGNet showed state-of-the-art performances among other docking methods and deep learning methods for the conventionally used docking and screening benchmarks. In an attempt towards an even fairer comparison, we noticed that common protein homologs exist in both training and benchmark sets. In practice, the target and its true inhibitors might be distant from the training data distribution. Hence, to ascertain the applicability of our model, we conducted a virtual screening case study in more realistic settings where we excluded from the training set the targets and ligands similar to the given target and its true inhibitors.We selected the human MAPK1 protein, an essential therapeutic target72–74 for our case study. The top 1% average EF of Smina, 3D CNN, and 3D GNN-based models were compared with that of PIGNet.
The virtual screening results shown in Table 3 are consistent with the CASF-2016 screening benchmark results, where PIGNets outperform the baseline models and a docking method. The trend was consistent regardless of the ratio of the true inhibitors, which is determined by a pIC50 criteria. While this single-case study does not give us statistical significance, we can inspect the potential applicability of our model on virtual screening for unseen targets.
| Model | pIC50 Criteria for true inhibitor | ||
|---|---|---|---|
| 6 | 7 | 8 | |
| Average EF | |||
| Smina66 | 9.9 | 13.3 | 18.5 |
| 3D CNN-based model | 7.7 | 6.7 | 9.3 |
| 3D GNN-based model | 9.3 | 11.1 | 12.0 |
| PIGNet (single) | 20.1 | 21.1 | 24.1 |
| PIGNet (ensemble) | 21.3 | 21.7 | 26.9 |
3.4 Interpretation of the physically modeled outputs
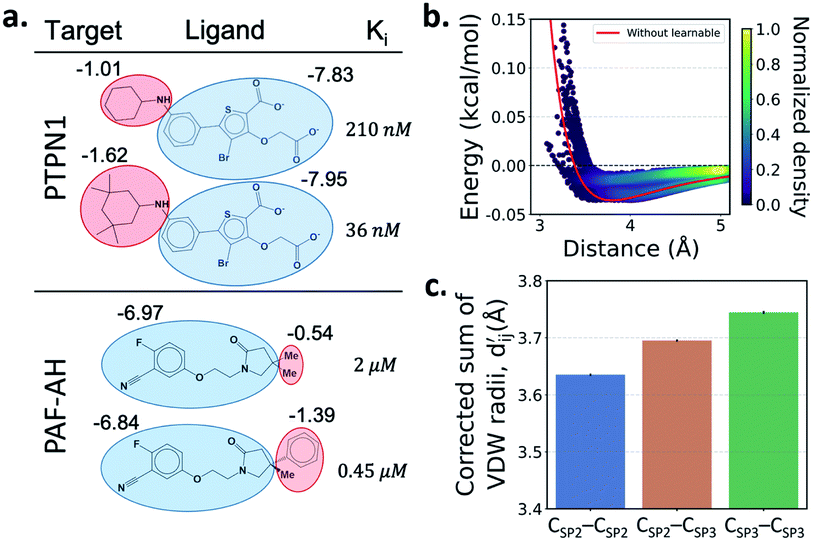
One important advantage of our approach is the possibility of the atom–atom pairwise interpretation of DTI. To rationally design a drug for a specific target, knowing the dominant interaction of ligand binding is helpful. Since PIGNet computes atom–atom pairwise energy components, we can calculate the energy contribution of the substructures within a ligand. Here, we conduct a case study for two target proteins retrieved from the PDBbind dataset; protein-tyrosine phosphatase non-receptor type 1 (PTPN1) and platelet activating factor acetylhydrolase (PAF-AH). The result is illustrated in Fig. 3a, where two ligands for each protein are compared regarding the predicted substructural energy contributions and the inhibitory constant, Ki. Each ligand pair has high structural similarity, and only differs in red-circled moieties. For PTPN1, the model predicts a greater energy contribution for the tetramethyl cyclohexyl moiety than the cyclohexyl moiety. Such a result is coherent to the experimental Ki values. For PAF-AH, the ligand with the phenyl group has a lower Ki value than that of the ligand with the methyl group. The model predicts a greater energy contribution of the phenyl group compared to the methyl group. For both proteins, the blue-circled common substructures are predicted to have similar energy contributions. This implies the predicted energy contribution of each substructure provides a physically meaningful interpretation, which can take further advantages to strengthen the total binding affinity towards the target protein during the ligand optimization.Most docking programs manually assign different scoring functions to atom–atom pairs according to the predefined categories. This manual assignment would fall short when the binding pattern of the pair does not fit in the existing category. Instead of the handcrafted categorization, our model exploits neural networks to automatically differentiate the atom–atom pairs; the information of each pair's interaction is updated through the graph attention networks. We illustrate the deviation and its physical interpretation in Fig. 3b and c. Fig. 3b shows a distance-energy distribution plot of vdW component for carbon–carbon pairs within the test set. When trained with learnable parameters, predicted vdW interactions naturally deviate within the carbon–carbon pair, while without the learnable parameters the distance–energy plot follows a single solid line. With the aid of learnable parameters, our model might have learned a wider range of pairwise interactions in a data-driven manner. We also show the deviations in hydrophobic, hydrogen bond, and metal–ligand energy components in the Fig. S1.†
Fig. 3c shows that the naturally occurring deviations within the atom–atom pairs in our model are the consequences of learning sufficient physics information. The corrected sum of vdW radii, 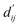 , which contains a learnable parameter assigned to each atom–atom pair, deviated according to the carbon–carbon pair types. Since the interaction between the two carbon atoms would not be significantly affected by their hybridization, we speculate that the corrected sum of vdW radii of the pair would be dependent on the atom radii. The result shows an increasing tendency from the Csp2–Csp2 pair to the Csp3–Csp3 pair. Resonating with the speculation, the larger the s-character of the carbon atoms, the shorter was the corrected sum of vdW radii.
, which contains a learnable parameter assigned to each atom–atom pair, deviated according to the carbon–carbon pair types. Since the interaction between the two carbon atoms would not be significantly affected by their hybridization, we speculate that the corrected sum of vdW radii of the pair would be dependent on the atom radii. The result shows an increasing tendency from the Csp2–Csp2 pair to the Csp3–Csp3 pair. Resonating with the speculation, the larger the s-character of the carbon atoms, the shorter was the corrected sum of vdW radii.
3.5 Epistemic uncertainty quantification of PIGNet
For reliable virtual screening, it is important to screen out the false positive binders and secure the true positives.75 Unfortunately, most positive returns from docking programs turn out to be false positives.76 DNN-based models may also have the same problem. In particular, the data-deficient nature of training DTI models might render the DNN models less fit to out-of–domain complexes,47 producing false positives. One possible way to reduce the false positives is to use the uncertainty of the predictions and to filter unreliable positive predictions. We employed a Monte Carlo dropout (MCDO), a practical Bayesian inference method utilizing dropout regularization, to estimate epistemic uncertainties which are originated from the model uncertainty.77We quantified prediction uncertainties for the samples in three datasets – CSAR NRC-HiQ 1 and 2, the CASF-2016 scoring power. In Fig. 4, the ‘low’, ‘random’, and ‘high’ batches in terms of the prediction uncertainties are in descending order in the value of Pearson's correlation, R. Such a result resonates with our expectation; the lower the uncertainty, the more probable the model would have correctly predicted the result. This result shows that the prediction uncertainties of our model can be properly quantified. A previous study reported that the robust uncertainty quantification of model predictions can be evidence of good generalization ability.78 Thus, it might be possible to relate the high generalization ability of our model to the success in uncertainty quantification.
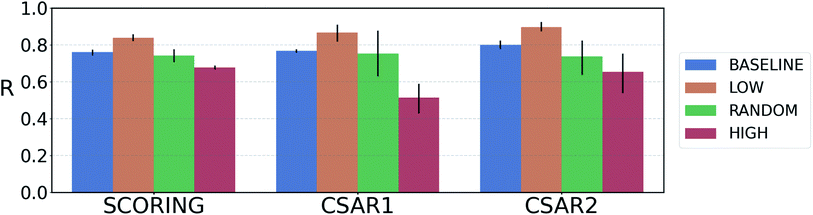 | ||
Fig. 4 Plot of the average Pearson's correlation coefficients, R, of the 4-fold PIGNet model, with or without the uncertainty estimator, on the datasets classified according to the total uncertainty. PIGNet with the uncertainty estimator – low: the lowest third, random: the randomly selected one third, high: the highest third of the uncertainty distribution. PIGNet without Monte Carlo dropout – baseline: the scores of a single PIGNet model shown in the Table 1. The lower the uncertainty, the more probable the model would have correctly predicted the result. Error bars represent 95% confidence intervals. PIGNet was tested at the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300th training epoch with and without Monte Carlo dropout. 300th training epoch with and without Monte Carlo dropout. | ||
Comparing the R values of the ‘random’ and ‘baseline’ batches in Fig. 4 enables to evaluate the general performance of PIGNet with and without the uncertainty estimator. The result confirms that the addition of uncertainty estimator does not harm the model performance. Furthermore, the comparison shows that uncertainty quantification can be used to filter out the false positives.
4 Conclusion
In this work, we studied the inadequate generalization problem of deep learning models that are often encountered in real-world applications where data for training is very scarce and imbalanced. As an important practical example, we focused on drug–target interaction (DTI) models for the fast and reliable virtual screening of drug candidates. The resulting model, named PIGNet, could achieve better generalization as well as higher accuracy compared to other deep learning models. We attribute the success of our model to the following two strategies. The first one is to employ the physics-informed parameterized equations. The physics modeling acts as a proper inductive bias for the neural model, guiding the model to learn the underlying physics of the chemical interactions. We further improved the model performance by augmenting training data with protein–ligand complexes from the wider chemical and structural diversity. We analyzed the effects of the physics-informed model and the data augmentation through the ablation study and found that both contribute to the model generalization. These strategies can be readily adopted to other science fields where similar data problems are expected and the related physics is well-established. Such applications would include materials design, structural biology, and particle physics. A similar improvement in the generalization reported in the atomistic modeling of solid materials50 is one such example.Our model can enjoy further practical advantages such as the physical interpretation of predicted DTI values and the reduction in false positives via uncertainty quantification. Obtaining binding free energy for every atom–atom pair opens up a possibility of further interpretation. This useful information can later be used to optimize drug candidates to attain better binding affinity by joining our model with generative models such as Imrie et al.79 Also, we introduced an uncertainty estimator for DTI prediction models and evaluated the quality of estimation for PIGNet. As predictions in high uncertainty can possibly be false positives, uncertainty quantification has practical benefits in virtual screening scenarios.
Still, our model has room for improvements regarding the parametric expression of atom pairwise interactions. To further improve the predictive power of our model, we can test out alternative expressions for the energy components. For example, as an expression for the van der Waals interaction, it would be possible to use the Hamaker formula parameterized with a learnable Hamaker constant.80,81 Additionally, our model could serve as a reliable oracle for the molecular generative models,82,83 in case the design objective is focused on the target binding affinity.
Data availability
Training datasets can be preprocessed from the codes available at github: https://github.com/ACE-KAIST/PIGNet.Author contributions
Conceptualization: J. L. and W. Y. K.; methodology: S. M., W. Z., S. Y., and J. L.; software, investigation and formal analysis: S. M., W. Z., S. Y., and J. L.; writing – original draft: S. M., W. Z., S. Y., and J. L.; writing – review & editing: S. M., W. Z., S. Y., J. L., and W. Y. K.; supervision: W. Y. K.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Basic Science Research Programs through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (NRF-2017R1E1A1A01078109).References
- P. Mamoshina, A. Vieira, E. Putin and A. Zhavoronkov, Mol. Pharmaceutics, 2016, 13, 1445–1454 CrossRef CAS PubMed.
- C. Cao, F. Liu, H. Tan, D. Song, W. Shu, W. Li, Y. Zhou, X. Bo and Z. Xie, Genomics, Proteomics Bioinf., 2018, 16, 17–32 CrossRef PubMed.
- R. Zemouri, N. Zerhouni and D. Racoceanu, Appl. Sci., 2019, 9, 1526 CrossRef CAS.
- M. Wainberg, D. Merico, A. Delong and B. J. Frey, Nat. Biotechnol., 2018, 36, 829–838 CrossRef CAS PubMed.
- J. G. Greener, S. M. Kandathil, L. Moffat and D. T. Jones, Nat. Rev. Mol. Cell Biol., 2021, 1–16 CAS.
- A. L. Hopkins, Nature, 2009, 462, 167–168 CrossRef CAS PubMed.
- M. Bagherian, E. Sabeti, K. Wang, M. A. Sartor, Z. Nikolovska-Coleska and K. Najarian, Briefings Bioinf., 2021, 22, 247–269 CrossRef PubMed.
- O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31, 455–461 CAS.
- S. Ruiz-Carmona, D. Alvarez-Garcia, N. Foloppe, A. B. Garmendia-Doval, S. Juhos, P. Schmidtke, X. Barril, R. E. Hubbard and S. D. Morley, PLoS Comput. Biol., 2014, 10, 1–7 CrossRef PubMed.
- R. Wang, L. Lai and S. Wang, J. Comput.-Aided Mol. Des., 2002, 16, 11–26 CrossRef CAS PubMed.
- A. N. Jain, J. Med. Chem., 2003, 46, 499–511 CrossRef CAS PubMed.
- G. Jones, J. Mol. Biol., 1997, 267, 727–748 CrossRef CAS PubMed.
- R. A. Friesner, J. L. Banks, R. B. Murphy, T. A. Halgren, J. J. Klicic, D. T. Mainz, M. P. Repasky, E. H. Knoll, M. Shelley and J. K. Perry, et al. , J. Med. Chem., 2004, 47, 1739–1749 CrossRef CAS PubMed.
- C. M. Venkatachalam, X. Jiang, T. Oldfield and M. Waldman, J. Mol. Graphics Modell., 2003, 21, 289–307 CrossRef CAS PubMed.
- O. Korb, T. Stützle and T. E. Exner, J. Chem. Inf. Model., 2009, 49, 84–96 CrossRef CAS PubMed.
- W. J. Allen, T. E. Balius, S. Mukherjee, S. R. Brozell, D. T. Moustakas, P. T. Lang, D. A. Case, I. D. Kuntz and R. C. Rizzo, J. Comput. Chem., 2015, 36, 1132–1156 CrossRef CAS PubMed.
- B. Waszkowycz, D. E. Clark and E. Gancia, Wires Comput. Mol. Sci., 2011, 1, 229–259 CrossRef CAS.
- A. R. Leach, B. K. Shoichet and C. E. Peishoff, J. Med. Chem., 2006, 49, 5851–5855 CrossRef CAS PubMed.
- Y. C. Chen, Trends Pharmacol. Sci., 2015, 36, 78–95 CrossRef PubMed.
- M. R. Shirts, D. L. Mobley and J. D. Chodera, Annu. Rep. Comput. Chem., 2007, 3, 41–59 CAS.
- C. Chipot, X. Rozanska and S. B. Dixit, J. Comput.-Aided Mol. Des., 2005, 19, 765–770 CrossRef CAS PubMed.
- A. Fitriawan, I. Wasito, A. F. Syafiandini, M. Amien and A. Yanuar, International Conference on Computer, Control, Informatics and its Applications, IC3INA, 2016 Search PubMed.
- H. Öztürk, A. Özgür and E. Ozkirimli, Bioinformatics, 2018, 34, 821–829 CrossRef PubMed.
- M. Thafar, A. B. Raies, S. Albaradei, M. Essack and V. B. Bajic, Front. Chem., 2019, 7, 782 CrossRef CAS PubMed.
- C. F. Lipinski, V. G. Maltarollo, P. R. Oliveira, A. B. F. da Silva and K. M. Honorio, Front. Robot. AI, 2019, 6, 108 CrossRef PubMed.
- M. Tsubaki, K. Tomii and J. Sese, Bioinformatics, 2019, 35, 309–318 CrossRef CAS PubMed.
- I. Lee, J. Keum and H. Nam, PLoS Comput. Biol., 2019, 15, 1–21 CrossRef PubMed.
- S. Zheng, Y. Li, S. Chen, J. Xu and Y. Yang, Nat. Mach. Intell., 2020, 2, 134–140 CrossRef.
- K. Huang, T. Fu, L. M. Glass, M. Zitnik, C. Xiao and J. Sun, Bioinformatics, 2020, 36, 5545–5547 CrossRef CAS PubMed.
- Y.-B. Wang, Z.-H. You, S. Yang, H.-C. Yi, Z.-H. Chen and K. Zheng, BMC Med. Inf. Decis. Making, 2020, 20, 1–9 CrossRef CAS PubMed.
- S. K. Panday and I. Ghosh, Struct. Bioinf., 2019, 109–175 Search PubMed.
- F. Imrie, A. R. Bradley, M. van der Schaar and C. M. Deane, J. Chem. Inf. Model., 2018, 58, 2319–2330 CrossRef CAS PubMed.
- M. M. Stepniewska-Dziubinska, P. Zielenkiewicz and P. Siedlecki, Bioinformatics, 2018, 34, 3666–3674 CrossRef CAS PubMed.
- J. Jiménez, M. Škalič, G. Martínez-Rosell and G. De Fabritiis, J. Chem. Inf. Model., 2018, 58, 287–296 CrossRef PubMed.
- I. Wallach, M. Dzamba and A. Heifets, preprint, arXiv:1510.02855, 2015, https://arxiv.org/abs/1510.02855.
- M. Ragoza, J. Hochuli, E. Idrobo, J. Sunseri and D. R. Koes, J. Chem. Inf. Model., 2017, 57, 942–957 CrossRef CAS PubMed.
- J. A. Morrone, J. K. Weber, T. Huynh, H. Luo and W. D. Cornell, J. Chem. Inf. Model., 2020, 60, 4170–4179 CrossRef CAS PubMed.
- L. Zheng, J. Fan and Y. Mu, ACS Omega, 2019, 4, 15956–15965 CrossRef CAS PubMed.
- Y. Kwon, W.-H. Shin, J. Ko and J. Lee, Int. J. Mol. Sci., 2020, 21, 8424 CrossRef CAS PubMed.
- H. Hassan-Harrirou, C. Zhang and T. Lemmin, J. Chem. Inf. Model., 2020, 60, 2791–2802 CrossRef CAS PubMed.
- D. Jones, H. Kim, X. Zhang, A. Zemla, G. Stevenson, W. F. D. Bennett, D. Kirshner, S. E. Wong, F. C. Lightstone and J. E. Allen, J. Chem. Inf. Model., 2021, 61, 1583–1592 CrossRef CAS PubMed.
- E. N. Feinberg, D. Sur, Z. Wu, B. E. Husic, H. Mai, Y. Li, S. Sun, J. Yang, B. Ramsundar and V. S. Pande, ACS Cent. Sci., 2018, 4, 1520–1530 CrossRef CAS PubMed.
- W. Torng and R. B. Altman, J. Chem. Inf. Model., 2019, 59, 4131–4149 CrossRef CAS PubMed.
- J. Lim, S. Ryu, K. Park, Y. J. Choe, J. Ham and W. Y. Kim, J. Chem. Inf. Model., 2019, 59, 3981–3988 CrossRef CAS PubMed.
- R. Meli, A. Anighoro, M. J. Bodkin, G. M. Morris and P. C. Biggin, J. Cheminf., 2021, 13, 1–19 Search PubMed.
- D. M. Hawkins, J. Chem. Inf. Comput. Sci., 2004, 44, 1–12 CrossRef CAS PubMed.
- L. Chen, A. Cruz, S. Ramsey, C. J. Dickson, J. S. Duca, V. Hornak, D. R. Koes and T. Kurtzman, PLoS one, 2019, 14, e0220113 CrossRef CAS PubMed.
- J. Scantlebury, N. Brown, F. Von Delft and C. M. Deane, J. Chem. Inf. Model., 2020, 60, 3722–3730 CrossRef CAS PubMed.
- S. Greydanus, M. Dzamba and J. Yosinski, Advances in Neural Information Processing Systems, Curran Associates, Inc., 2019, vol. 32, pp. 15379–15389 Search PubMed.
- G. P. Pun, R. Batra, R. Ramprasad and Y. Mishin, Nat. Commun., 2019, 10, 2339 CrossRef PubMed.
- L. Li, S. Hoyer, R. Pederson, R. Sun, E. D. Cubuk, P. Riley and K. Burke, Phys. Rev. Lett., 2021, 126, 036401 CrossRef CAS PubMed.
- M. Su, Q. Yang, Y. Du, G. Feng, Z. Liu, Y. Li and R. Wang, J. Chem. Inf. Model., 2019, 59, 895–913 CrossRef CAS PubMed.
- T. Pahikkala, A. Airola, S. Pietilä, S. Shakyawar, A. Szwajda, J. Tang and T. Aittokallio, Briefings Bioinf., 2015, 16, 325–337 CrossRef CAS PubMed.
- K. Y. Gao, A. Fokoue, H. Luo, A. Iyengar, S. Dey and P. Zhang, Proceedings of the 27th International Joint Conference on Artificial Intelligence, 2018 Search PubMed.
- T. Zubatiuk, B. Nebgen, N. Lubbers, J. S. Smith, R. Zubatyuk, G. Zhou, C. Koh, K. Barros, O. Isayev and S. Tretiak, J. Chem. Phys., 2021, 154, 244108 CrossRef CAS PubMed.
- D. S. Karlov, S. Sosnin, M. V. Fedorov and P. Popov, ACS Omega, 2020, 5, 5150–5159 CrossRef CAS PubMed.
- J. Zhou, G. Cui, S. Hu, Z. Zhang, C. Yang, Z. Liu, L. Wang, C. Li and M. Sun, AI Open, 2020, 1, 57–81 CrossRef.
- M. Jiang, Z. Li, S. Zhang, S. Wang, X. Wang, Q. Yuan and Z. Wei, RSC Adv., 2020, 10, 20701–20712 RSC.
- P. Veličković, G. Cucurull, A. Casanova, A. Romero, P. Liò and Y. Bengio, International Conference on Learning Representations, 2018 Search PubMed.
- J. Chung, C. Gulcehre, K. Cho and Y. Bengio, preprint, arXiv:1412.3555, 2014, https://arxiv.org/abs/1412.3555.
- R. E. Wunderlich, T. F. Wenisch, B. Falsafi and J. C. Hoe, Conference Proceedings – Annual International Symposium on Computer Architecture, ISCA, 2003, pp. 84–95 Search PubMed.
- RDKit: Open-source cheminformatics, http://www.rdkit.org Search PubMed.
- Z. Liu, M. Su, L. Han, J. Liu, Q. Yang, Y. Li and R. Wang, Acc. Chem. Res., 2017, 50, 302–309 CrossRef CAS PubMed.
- J. P. Hughes, S. Rees, S. B. Kalindjian and K. L. Philpott, Br. J. Pharmacol., 2011, 162, 1239–1249 CrossRef CAS PubMed.
- InterBioScreen Ltd, http://www.ibscreen.com.
- D. R. Koes, M. P. Baumgartner and C. J. Camacho, J. Chem. Inf. Model., 2013, 53, 1893–1904 CrossRef CAS PubMed.
- J. B. Dunbar Jr, R. D. Smith, C.-Y. Yang, P. M.-U. Ung, K. W. Lexa, N. A. Khazanov, J. A. Stuckey, S. Wang and H. A. Carlson, J. Chem. Inf. Model., 2011, 51(9), 2036–2046 CrossRef PubMed.
- W. Li and A. Godzik, Bioinformatics, 2006, 22, 1658–1659 CrossRef CAS PubMed.
- L. Fu, B. Niu, Z. Zhu, S. Wu and W. Li, Bioinformatics, 2012, 28, 3150–3152 CrossRef CAS PubMed.
- Y. Wang, J. Xiao, T. O. Suzek, J. Zhang, J. Wang and S. H. Bryant, Nucleic Acids Res., 2009, 37, W623–W633 CrossRef CAS PubMed.
- C. Wang and Y. Zhang, J. Comput. Chem., 2017, 38, 169–177 CrossRef PubMed.
- J. S. Sebolt-Leopold, Oncogene, 2000, 19, 6594–6599 CrossRef CAS PubMed.
- A. S. Dhillon, S. Hagan, O. Rath and W. Kolch, Oncogene, 2007, 26, 3279–3290 CrossRef CAS PubMed.
- L. Miao and H. Tian, J. Drug Targeting, 2020, 28, 154–165 CrossRef PubMed.
- E. H. B. Maia, L. C. Assis, T. A. de Oliveira, A. M. da Silva and A. G. Taranto, Front. Chem., 2020, 8, 343 CrossRef CAS PubMed.
- R. Sink, S. Gobec, S. Pecar and A. Zega, Curr. Med. Chem., 2010, 17, 4231–4255 CrossRef CAS PubMed.
- Y. Gal and Z. Ghahramani, Proceedings of the 33rd International Conference on Machine Learning, New York, USA, 2016 Search PubMed.
- G. Scalia, C. A. Grambow, B. Pernici, Y.-P. Li and W. H. Green, J. Chem. Inf. Model., 2020, 2697–2717 CrossRef CAS PubMed.
- F. Imrie, A. R. Bradley, M. van der Schaar and C. M. Deane, J. Chem. Inf. Model., 2020, 60, 1983–1995 CrossRef CAS PubMed.
- C. M. Roth, B. L. Neal and A. M. Lenhoff, Biophys. J., 1996, 70, 977–987 CrossRef CAS PubMed.
- V. A. Parsegian, van der Waals forces: a handbook for biologists, chemists, engineers, and physicists, Cambridge University Press, 2005 Search PubMed.
- A. Grosnit, R. Tutunov, A. M. Maraval, R.-R. Griffiths, A. I. Cowen-Rivers, L. Yang, L. Zhu, W. Lyu, Z. Chen and J. Wang, et al., arXiv preprint arXiv:2106.03609, 2021.
- S. Yang, D. Hwang, S. Lee, S. Ryu and S. J. Hwang, Advances in Neural Information Processing Systems, 2021 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: the algorithm and implementation details of all the models used in the experiments, the details about the benchmark criteria and the physical interpretation result. See DOI: 10.1039/d1sc06946b |
| ‡ These authors contributed equally to this work. |
| § Currently at Computational and Systems Biology, MIT, 77 Massachusetts Ave, Cambridge, MA. |
| This journal is © The Royal Society of Chemistry 2022 |