Interrogating the thionium hydrogen bond as a noncovalent stereocontrolling interaction in chiral phosphate catalysis

Abstract

CH⋯O bonds are a privileged noncovalent interaction determining the energies and geometries of a large number of structures. In catalytic settings, these are invoked as a decisive feature controlling many asymmetric transformations involving aldehydes. However, little is known about their stereochemical role when the interaction involves other substrate types. We report the results of computations that show for the first time thionium hydrogen bonds to be an important noncovalent interaction in asymmetric catalysis. As a validating case study, we explored an asymmetric Pummerer rearrangement involving thionium intermediates to yield enantioenriched N,S-acetals under BINOL-derived chiral phosphate catalysis. DFT and QM/MM hybrid calculations showed that the lowest energy pathway corresponded to a transition state involving two hydrogen bonding interactions from the thionium intermediate to the catalyst. However, the enantiomer resulting from this process differed from the originally published absolute configuration. Experimental determination of the absolute configuration resolved this conflict in favor of our calculations. The reaction features required for enantioselectivity were further interrogated by statistical modeling analysis that utilized bespoke featurization techniques to enable the translation of enantioselectivity trends from intermolecular reactions to those proceeding intramolecularly. Through this suite of computational modeling techniques, a new model is revealed that provides a different explanation for the product outcome and enabled reassignment of the absolute product configuration.

---

Introduction

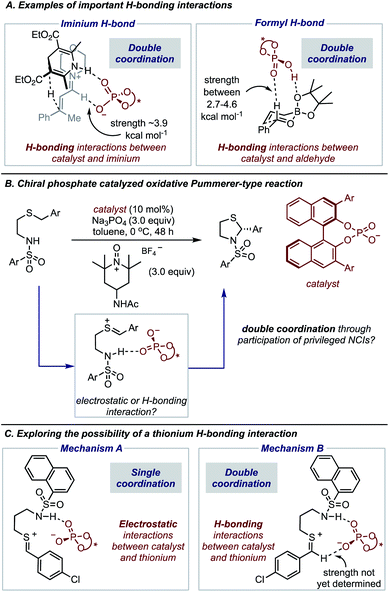
The expansion of catalytic methods to facilitate diverse bond constructions has extended the reach of enantioinduction to new reactions. The complicated conditions and complex catalyst structures often employed in modern reactions make it challenging to anticipate how the reaction components organize at the transition state (TS) to impart enantioselectivity.^1,2 This issue is often exacerbated by the difficulty in characterizing the specific noncovalent interactions at the TS that account for the experimental result.^3–8 Such precise descriptions of enantioselectivity outcomes are of critical importance to catalyst and reaction design which requires a detailed analysis of all factors that contribute to TS energies. Consequently, wrong conclusions can be made in cases where key interactions remain unaccounted for, hindering hypothesis-driven design. Fortunately, recent advances in the computational modelling of attractive interactions have made detailed and accurate insights into complex catalytic mechanisms possible.⁹ Moreover, retrospective mechanistic analysis with modern computations has enabled reaction models to be updated and the reasons for selectivity refined.^10,11 Studies from the groups of Goodman,¹² Houk¹³ and Schreiner¹¹ can be noted as some examples of efforts to provide more accurate descriptions of selectivity for important organic reactions. In contrast to the rapid developments in this area, revealing unique types of noncovalent interactions to be meaningful stereocontrolling elements in asymmetric catalysis is far less common.

In this regard, we have recently characterized the iminium hydrogen bond (C–H bond as shown in Fig. 1A) as an important contact for determining the enantioselective Hantzsch ester hydrogenation of α,β-unsaturated iminiums with chiral phosphates.¹⁴ At that time the iminium hydrogen bond (H-bond) was not previously investigated as a stereocontrolling contact with chiral phosphate catalysts but has now been considered important in several other reaction systems involving iminium intermediates.¹⁵ Considering this and the importance of the formyl H-bond involving aldehydes and chiral phosphoric acid catalysts, led us to question if other substrate types engage in this kind of CH⋯O interaction (Fig. 1A). On a fundamental level, such stabilizing contacts are achieved with electron deficient proton donors often displaying sp² hybridization, electronegative atoms such as O, or positive charges like N⁺.¹⁶ These criteria combined with the importance of accessing sulfur-containing motifs enantioselectively,^17–21 provided the impetus to explore the possibility of thionium H-bonding as a noncovalent stereocontrolling interaction. Furthermore, to the best of our knowledge this type of H-bonding contact has not yet shown to be important for stereocontrol. In this context, we were intrigued by the oxidative Pummerer^22–24 type transformation using phase-transfer catalysis, a rare enantioselective catalytic protocol utilizing a thionium intermediate.^25–29 This transformation reported by Sigman and Toste, generates cyclic N,S-acetals a motif embedded within many natural products and pharmaceuticals,^30–33 with slightly lower enantioselectivities than products obtained in comparable reactions involving iminium intermediates (Fig. 1B).²⁵ DFT calculations suggested that the catalyst interacts only with the nucleophile's proton in agreement with the reaction models available at that time. However, our recent work on similar systems has indicated that single-point binding from the chiral phosphate to the reactants cannot explain the observed enantioselectivity (Mechanism A, Fig. 1C). Given the difference in C–H acidity between thioniums and iminiums the applicability of the two-point binding model to explain this system isn't certain (Mechanism B, Fig. 1C). Consequently, the origins of enantioinduction are unclear, making it challenging to develop the reaction more generally.

Fig. 1 (A) Chiral phosphates and their acid counterparts participate in H-bonding interactions with iminium intermediates and aldehyde substrates. (B) How the chiral phosphate interacts with the thionium intermediate in the enantioselective Pummerer-type reaction with chiral phosphates. The literature reported enantiomer of product is displayed. (C) Possible mechanisms for the oxidative Pummerer-type reaction. Mechanism A is the reaction model commonly deployed to explain chiral phosphate catalysis. Mechanism B is a new proposal based on the thionium H-bond.

Herein, we use DFT and QM/MM hybrid calculations to investigate the mechanism of this reaction and the stereochemical consequences of the thionium H-bond. The reaction was found to proceed via a transition state involving two H-bonding interactions from the thionium intermediate to the catalyst. Our calculations also revealed that the predicted enantiomer was inconsistent with the assignment of configuration in the initial report. Experimental and X-ray studies exposed that the experimentally reported enantiomer was incorrect, emphasizing the strength of the thionium H-bonding model. These findings were further confirmed with statistical modelling tools, suggesting that these models could effectively be applied to confirm absolute stereochemical assignments.

Results & discussion

The preferred reaction pathway was first investigated using buta-1,3-diene-1,4-diol-phosphate as a truncation for the full catalyst system with the same intermediate shown in Fig. 1C. Previous reports have shown this truncated catalyst to be a reliable model for BINOL-derived phosphoric acids.^34–37 Prior deuterium labelling studies showed the cyclization step to be enantiodetermining,²⁵ providing the motivation to model only the C–N bond formation. For this reaction event two pathways were considered as summarized in Fig. 1C. TS structures in which the catalyst establishes a single interaction with a phosphoryl oxygen and the nucleophile's proton leads to Mechanism A. If the second catalyst Lewis basic site interacts with the hydrogen of the thionium intermediate, a hydrogen bond can be established. The formyl^38,39 and iminium H-bond^14,15 have previously been identified as prevalent interactions in chiral phosphoric acid and phosphate catalysed reactions.^40–42 These studies suggest that double coordination modes are much more likely.⁴³ Such stabilizing interactions provide rigidity in the TS that could be responsible for the high levels of enantioselectivity observed. This mechanism in which a single catalyst can establish two points of contact to the reactants leads to Mechanism B. Thorough exploration of the reaction coordinate yielded a total of 25 unique TS (see ESI† for details). The lowest energy, TS-1, was found to correspond to Mechanism B (Fig. 2).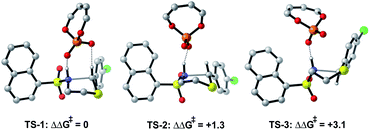

Fig. 2 DFT calculations at the M06-2X/6-31(d,p)//B3LYP/6-31G(d,p) level with the model catalyst system suggest Mechanism B to be operational. All energies quoted in kcal mol⁻¹.

Single coordination modes, TS-2 and TS-3, which lack a second interaction from the catalyst to the thionium hydrogen were found to be disfavoured by 1.3 and 3.1 kcal mol⁻¹ when evaluated at the M06-2X/6-31(d,p)//B3LYP/6-31G(d,p) level of theory. Comparison of TS-1 and TS-2 provided an estimate of the strength of the thionium hydrogen bond. Superposition of the substrate from both TS leads to an RMSD of 0.18 Å between the two structures, suggesting minimal geometric difference. This implies that the primary reason for a difference in energy can be attributed to the hydrogen bond. The ΔE_M06-2X between the structures was found to be 1.9 kcal mol⁻¹, making the approximation of the strength of a thionium H-bond significantly lower in energy than formyl and iminium H-bonds which involve aldehydes. Independently, Goodman and Houk estimated the strength of the formyl H-bond to be in the range of 2.7–4.6 kcal mol⁻¹.^35,36,44 Our previous work approximated the iminium H-bond to be strongly stabilizing and worth 3.9 kcal mol⁻¹.¹⁴ The differences in H-bonding strength may explain why similar reactions involving iminiums are inherently more selective. Moreover, we measured the C–H⋯O distance in TS-1 to be only 2.09 Å which is much shorter than the sum of the van der Waals radii (2.7 Å for O and H) suggesting this interaction is indeed a non-classical H-bond. Before exploring the TS structures with the full catalyst system (Fig. 3), the proposed H-bonding interaction was further analysed using Quantum Theory of Atoms In Molecules (QTAIM).⁴⁵ In this topological analysis of electron density, interacting nuclei are connected by bond paths upon which lie bond critical points (BCPs).⁴⁶ QTAIM analysis shows a BCP between the thionium CH and the oxygen of the phosphate implying a CH⋯O bonding interaction (see ESI† for a visual). Further, the Laplacian of the electron density (∇²(r)) at this BCP is found to be positive, indicative of a weak H-bonding contact.^47–49 Investigation of the potential energy surface using (R)-TRIP as our second model catalyst at the same level of theory suggested the lowest energy pathways to correspond to Mechanism B. These results are in line with the buta-1,3-diene-1,4-diol- phosphate model catalyst findings. The TS structure that leads to the competing enantiomer arises from Mechanism A, which lacks the interaction from catalyst to the thionium hydrogen and is calculated to be 2.3 kcal mol⁻¹ higher in energy than TS-4Re. Therefore, the computed enantioselectivity value arising from these calculations was found to be excellent but the predicted sense is opposite to that observed experimentally. In other words, our model predicts Re face attack to yield the (S)-product but the original data reports the (R)-product to be observed. These results suggest that the enantiomer was assigned incorrectly in the initial report. To test our mechanistic hypothesis, we repeated the reaction under the same conditions as described in the original report using (R)-TRIP as the catalyst (see the ESI†).

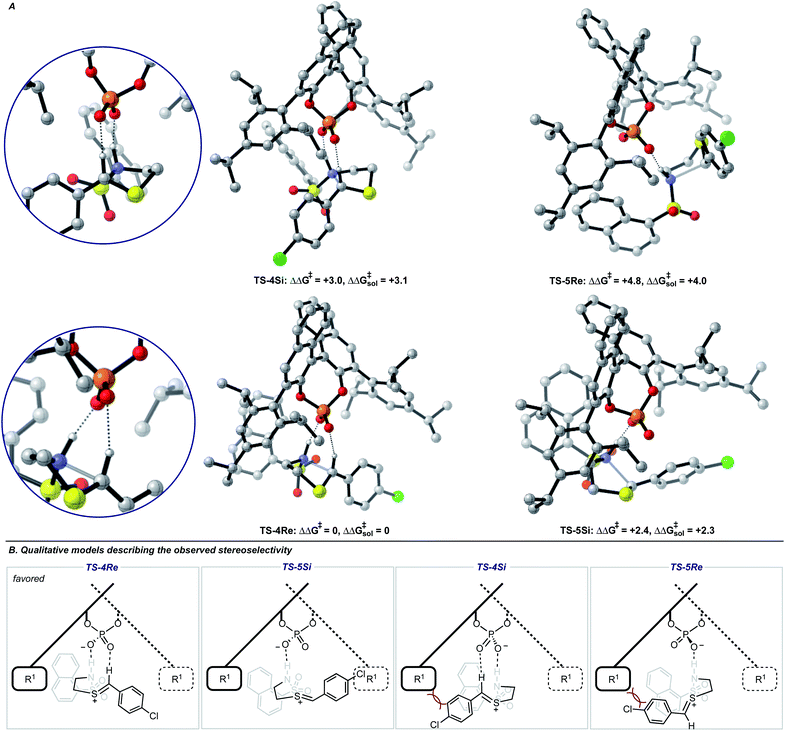Fig. 3 (A) Competing TS structures for the oxidative cyclization reaction catalyzed by (R)-TRIP. Important H-bonding contacts between catalyst and intermediate are shown on the left. Geometries B3LYP/6-31G(d,p), single point energies M06-2X/6-31G(d,p). Solvent energies were derived from single point energies with IEFPCM (toluene) model. All energies are quoted in kcal mol⁻¹. Previous work on similar systems have shown this computational method to be accurate for reproducing experimental enantioselectivities.^21,22 (B) Qualitative models help analyze the computed TS geometries.

Chiral HPLC analysis indicated that the enantiomeric excess generated by the reaction was 57% in excellent agreement with the published value (56% ee). The absolute stereochemistry of the product was determined to be (S) by X-ray crystallography, in agreement with our calculations. Reassignment of absolute product configurations using TS analysis is relatively rare and this example highlights that these computations can be used to correct experimental outcomes.^35,50 More specifically, these results illuminate the strength of the thionium H-bonding model as this pathway anticipated the correct stereochemical outcome.

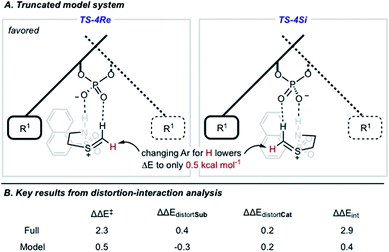
We also located TS similar to TS-4Re, which features the interaction from the catalyst to the thionium proton, TS-4Si, but affords the competing product. In TS-4Si, the thionium hydrogen bond distance (CH⋯O) was found to be shortened by 0.23 Å relative to TS-4Re (Fig. 3). This distortion serves to increase the strength of the hydrogen bonding contacts between the phosphate and thionium intermediate. However, the electrostatic stabilization gained is offset by steric repulsive contacts as the thionium aromatic substituent is now orientated towards the front of the large catalyst group. To qualitatively explore the contributions of the thionium substituent to the relative energy differences between TS-4Re and TS-4Si, a truncation study was performed computationally. The aromatic substituent was replaced for a proton, and a single-point energy was taken of the resulting structure without re-optimization. The energy difference (ΔE_M06-2X) between the competing structures decreased from 2.3 kcal mol⁻¹ to just 0.5 kcal mol⁻¹ (Fig. 4). This is consistent with the primary determinants of enantioselectivity arising from these competing pathways being repulsive interactions with the 3,3′ catalyst substituents and the thionium aromatic group. The monocoordination pathway, TS-5Si, avoids these steric repulsive contacts but lacks the favourable secondary interaction.

Fig. 4 (A) Truncation study showing the importance of the thionium aromatic group to the enantioselectivity outcome. (B) Results from distortion–interaction analysis calculated with M06-2X/6-31G(d,p) single point energy evaluations.

The reasons for the energy differences between TS-4Re and TS-4Si were further investigated using distortion–interaction analysis (Fig. 4).⁵¹ The equation ΔΔE^‡ = ΔΔE_int − ΔΔE_distortCat − ΔΔE_distortSub allows the relative energy difference between the two TS to be understood partially on the basis of the energy required to distort the structures of the catalyst and intermediate to the TS geometry. The energy required for this process is usually larger than the TS barrier but the interactions between the catalyst and intermediate, appearing as ΔΔE_int in the equation, offsets this energetically costly distortion process, shown as the two ΔΔE_distort terms. The M06-2X/6-31G(d,p) calculated difference in distortion energy between TS-4Re and TS-4Si is 0.2 kcal mol⁻¹ and 0.4 kcal mol⁻¹ for the catalyst and intermediate portion, respectively. In fact, both of the components must distort slightly more to achieve the lowest energy TS-4Re geometry rather than the disfavoured TS-4Si one. Therefore, the destabilization of TS-4Si can be understood on the basis of the difference in interaction energies which is calculated to be 2.9 kcal mol⁻¹. To examine how the thionium aromatic group contributes to these ΔΔE_int values, we performed the same analysis on the aforementioned truncated model system where the aromatic thionium substituent is deleted and replaced for a proton. Because the catalyst is unchanged the distortion for this component remains 0.2 kcal mol⁻¹. The intermediate distortion is calculated to be 0.3 kcal mol⁻¹ but it now requires slightly more energy to distort the intermediate to the geometry of TS-4Si rather than TS-4Re. Therefore, the interaction energy difference is calculated to be only 0.4 kcal mol⁻¹. The clear drop in ΔΔE_int on moving from the full to the model TS implies that the thionium substituent results in a decrease in the interactions that leads to the preferential stabilization of TS-4Re. This would be in agreement with our visual analysis of the competing TS structures. Thus, enantioselectivity is likely to be both a result of a second favourable H-bonding interaction between the intermediate and catalyst, and minimization of steric repulsive contacts in TS-4Re. To the best of our knowledge, this is the first report investigating a thionium H-bond as a stereocontrolling noncovalent interaction. Furthermore, the calculations suggest that increasing the size of the 3 and 3′ groups leads to higher levels of enantioselectivities, which is consistent with the experimental data and catalyst correlation studies detailed elsewhere.²⁵

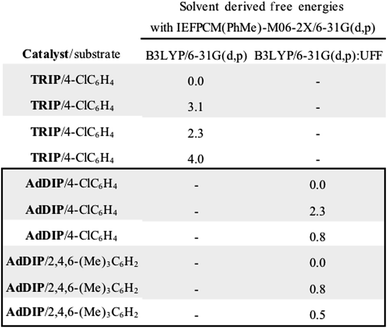
As the next step in our analysis, we sought to locate low energy TS structures for the optimal catalyst, (R)-AdDIP, using ONIOM. This is imperative as it ensures that our results were directly comparable to those reported i.e. enantioselectivity data is available for a particular catalyst substrate combination. The size difference between TRIP and AdDIP is 30 atoms, ONIOM calculations allow larger systems like TS with AdDIP to be explored efficiently. While these computational methods have been shown to give reliable results in a large variety of systems,^52–57 we were mindful of the possibility of error. Consequently, the lowest energy structures found from these calculations were submitted to full DFT geometry optimizations with B3LYP and ωB97xD functionals to confirm the validity of our ONIOM results. The results of full DFT calculations can be found in the ESI† and these show that the lowest energy TS structure remains unaltered between the methods. Thus, interpretation of ONIOM structures and energies is accurate.

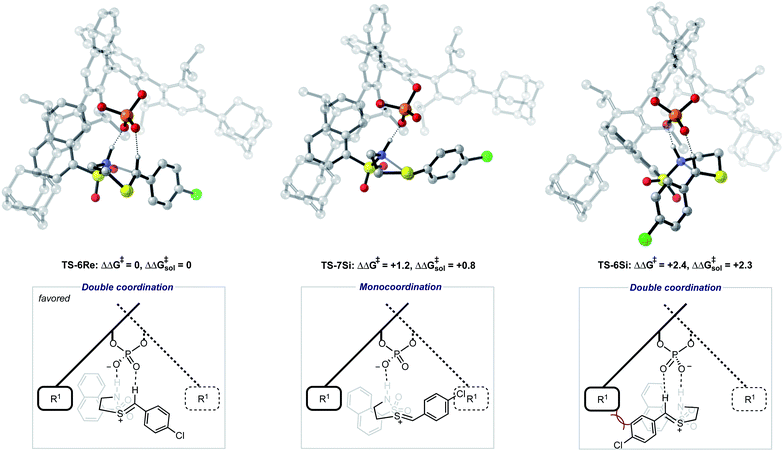
The ONIOM calculations confirmed that the same trends in activation energies were present as for the TRIP system (Fig. 5). It should be noted, that because TS-5Re was calculated to be strongly disfavoured as compared to the other TS structures by at least 2 kcal mol⁻¹ we only pursued structures resembling the three lowest in energy. The magnitude of the predicted enantioselectivity is in good agreement with the experimental value showing that ONIOM calculations are effective for this system (computed ee 59%, experimental 68%). The results from the TRIP derived model system indicate that the energy difference between the Re and Si TS is overestimated compared to the ONIOM method.

Fig. 5 Competing TS structures for the oxidative cyclization reaction catalyzed by (R)-AdDIP. ONIOM(B3LYP/6-31G(d,p):UFF), single-point energy M06-2X/6-31G(d,p). Solvent energies were derived from single point energies with IEFPCM (toluene) model. Grayed-out regions were treated with UFF, and the full-color regions were treated with B3LYP/6-31G(d,p). All energies quoted in kcal mol⁻¹.

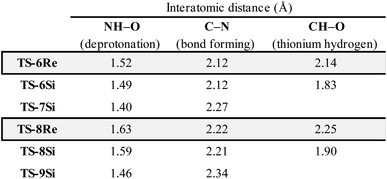
Examination of the energies shows that TS-6Re is the lowest energy TS and proceeds via deprotonation of the amine by the chiral phosphate with an additional stabilizing interaction between the second catalyst oxygen and the thionium hydrogen. In the gas phase, the corrected free energy for this pathway was found to be 1.2 kcal mol⁻¹ lower in energy than that leading to the competing product, TS-7Si, which lacks the additional stabilizing interaction. This value is close to that approximated for the thionium hydrogen bonding contact, therefore, the energy difference between these two TS is predominantly a result of this interaction. Although the activation modes of TS-6Re and TS-6Si are similar, the former is energetically more favourable. TS-6Si is destabilized relative to TS-6Re because the thionium aromatic group must be orientated towards the bulky catalyst pocket. TS-6Re places this aromatic group in the empty catalyst pocket but the N-substituent is now orientated towards the 3-substituent, however, due to the flexible nature of the sulfonyl group, low energy TS can be located which avoid these unfavourable steric contacts. Similar to the results obtained with the TRIP model system toluene solvent effects were shown to have a small impact on the relative free energies of the competing TS. Solvation of TS-6Re an TS-7Si led to a decrease in relative free energy of just 0.4 kcal mol⁻¹. This result is non-intuitive since the intermediate and catalyst are both charged; however, this can be rationalized by the concerted and overall apolar nature of the TS structure.

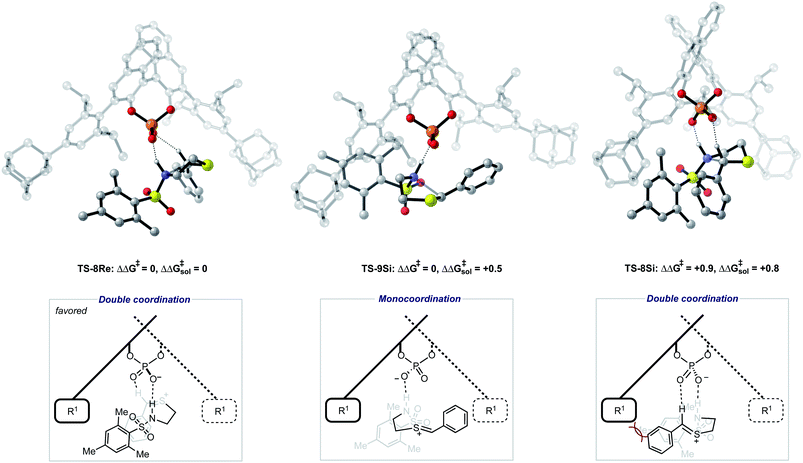
To further test our reaction model the effect of changing the protecting group was also investigated. The original report showed that increasing the size of the N-substituent by changing 1-naphthyl for a mesityl group lead to a decrease in ee from 84% to 62%. This result is unexpected, given that the bulky substituents that control enantioselectivity remain identical. TS-8Re, TS-8Si, and TS-9Si were all found to be closer in energy accounting for the lower levels of enantioselectivity (Fig. 6). The larger mesityl substituent leads to increased steric repulsive contacts with the 3-substituent at the back of the catalyst compared to that of the flat 1-naphthyl substituent in the Re TS. The lowest energy Re TS shows that this results in the intermediate to rotate, switch the oxygen that form each H-bond and adopt a different conformation. This can be clearly seen by inspecting the H-bonding contacts involved in TS-6Re and TS-8Re. In TS-6Re the amine binds to the oxygen at the back of the catalyst but in TS-8Re the H-bonding contact is established with the oxygen at the front. In this conformation repulsive contacts with the large catalyst substituent are minimized, however, the H-bond is now lengthened (Table 1). This factor combined with a decrease in the H-bonding angle by 10° (angle in TS-6Re is measured to be 163° and in TS-8Re is 153°) significantly compromises the strength of the H-bond from intermediate to catalyst. Such directionality is characteristic of H-bonds and this has the effect that TS-8Re is destabilized relative to TS-9Si, which is conformationally very similar to TS-7Si. Therefore, no major geometry changes for this monocoordination pathway occur on changing the sulfonyl group from 1-naphthyl to mesityl. This is in contrast to TS-8Si, in which the mesityl group adopts a higher energy sulfonyl rotamer to minimize repulsive contacts with the large catalyst 3,3′ groups. The conformational preferences for the sulfonyl substituents 1-naphthyl and mesityl were approximated using relaxed dihedral scans around the C–N–S–C dihedral angle in the ground state structure (see ESI†). However, this energetically penalizing conformation is offset by stronger H-bonding contacts between intermediate and catalyst, resulting in TS-8Si being overall stabilized relative to TS-8Re on changing the sulfonyl group. While these interactions, increased steric repulsions and weaker H-bonding contacts between the catalyst and intermediate, lower the enantioselectivity the overall sense of stereoinduction can be explained by the qualitative models. Importantly, such models have been derived and validated with different computational conditions, catalysts and substrates. The key results have been summarized in Table 2.

Fig. 6 Competing TS structures for the oxidative cyclization reaction catalyzed by (R)-AdDIP with a second substrate. ONIOM(B3LYP/6-31G(d,p):UFF), single-point energy M06-2X/6-31G(d,p). Solvent energies were derived from single point energies with IEFPCM (toluene) model. Grayed-out regions were treated with UFF, and the full-color regions were treated with B3LYP/6-31G(d,p). All energies quoted in kcal mol⁻¹.

Table 1 Key interatomic distances for ONIOM TS. The boxes highlight the change in H-bonding contacts on changing the sulfonyl group

---

Table 2 Summary of the optimization methods applied to the TS from the selected case studies. Solvent derived free energies are given in kcal mol⁻¹. Double coordination mechanisms are shown in grey. The boxes emphasize pathways treated with ONIOM

---

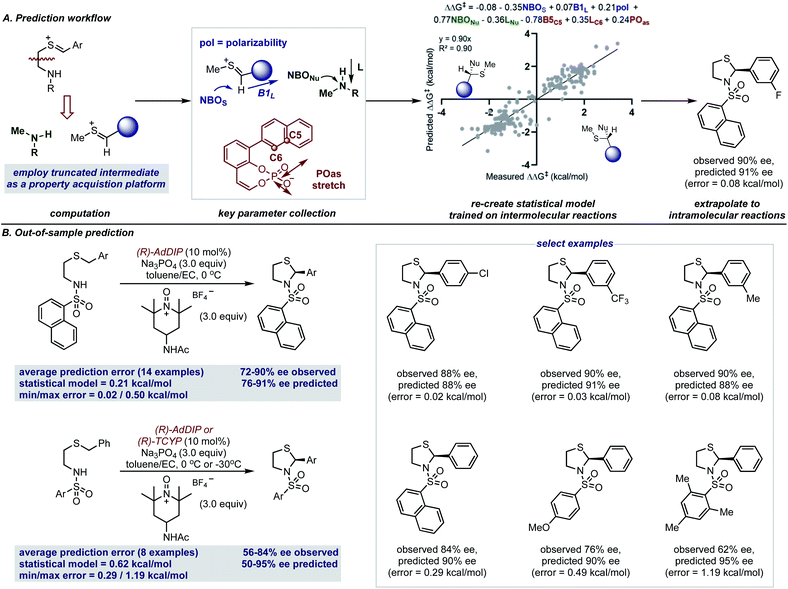
The accurate reproduction of experimental enantioselectivities suggests this thionium H-bonded reaction model, can be used to predict the enantioselectivities of novel substrates with ONIOM methods that provide results more rapidly than full DFT calculations. Because such methods require separate calculations for each substrate–catalyst combination even this type of computation can be a time-consuming approach to enantioselectivity prediction. Perhaps the structural similarities between reactions involving thioniums and iminiums provide sufficient structural overlap to enable quantitative predictions with a previously built comprehensive multivariate linear regression model.¹⁵ Furthermore, because the model takes into account the product configuration of the training set it is also possible to predict the absolute stereochemistry of the product formed with simple systems (i.e. those that generate one stereocenter).^58,59 For the purpose of forecasting this reaction, the sign of the ee (either −ve or +ve) represents one of two electrophile orientations which result in opposite enantiomers when catalysed by a (R)-CPA as shown by the product models displayed in Fig. 7A. Since the model built on intermolecular systems is to be applied to predict the results of an intramolecular reaction, we suspected an adapted parameter set may be necessary to facilitate such a significant extrapolation in reaction space.⁶⁰ To address this challenge, we implemented a truncation strategy which treated electrophile and nucleophile components separately, we viewed this as a simple but crucial means of simulating a bimolecular system (Fig. 7A).

Fig. 7 (A) Comprehensive statistical modeling workflow that employs reaction data from intermolecular reactions involving iminiums to predict reaction intramolecular reaction outcomes with thionium intermediates. A generic product denotes the stereochemical outcome predicted if the reaction proceeds through a −ee or +ee pathway and is catalyzed by the (R)-catalyst. Product stereochemistry is reversed if the opposite catalyst enantiomer is used. (B) Application to the formation of N,S-acetals.

These structures were then optimized at the M06-2X/def2-TZVP level and from the lowest energy structure the necessary parameters were acquired as shown in Fig. 7A. For the thionium this included the NBO_S (natural bond orbital charge of the hydrogen), the Sterimol B1 value of the large C-substituent and the polarizability of the molecule. The NBO charge of the nitrogen atom (NBO_Nu) and the length of the amine (Sterimol L) was collected to describe the nucleophile portion. The catalyst structure is described by two steric parameters B5_C5 and L_C6 in addition to the vibration of the P–O asymmetric stretching frequency. By deploying the adapted descriptor set and using all the available data as the training model (see ESI† for details), the resultant extrapolation to genuinely new reaction space resulted in excellent agreement between predicted and observed enantioselectivity values (Fig. 7B). With 14 examples we first assessed the impact of changing the aromatic thionium substituent and this reaction set was well predicted with a mean average error of 0.21 kcal mol⁻¹. This suggests that the reasons for stereocontrol are similar despite the difference in intermediate component structure. The small maximum observed error of 0.50 kcal mol⁻¹ demonstrates that all of the substrates of the reaction were predicted well by the model. As the second test set, we explored the effect of changing the N-substituent on the nucleophile. The larger range of recorded enantioselectivity values suggest the reaction is more sensitive to this structural feature. Despite this, good predictions with this set of reactions was also achieved, with an average absolute ΔΔG^‡ error of 0.62 kcal mol⁻¹. Although the averaged error was higher for this test set, most of the predictions were within 0.5 kcal mol⁻¹. The higher average error was due to the reaction with a substrate containing a mesityl group which performed worse than expected. Assessment of this reaction with ONIOM calculations reveals unique stereocontroling interactions thereby, explaining the failed extrapolation attempt. Notably, the model also assigns the stereochemical outcome for each example to be S, in agreement with our revised product assignment. Importantly, this suggests that comprehensive statistical models may have value in confirming absolute stereochemistry.

Conclusions

In this study, DFT and QM/MM hybrid calculations suggest that the phosphate oxidative cyclization reaction with thionium intermediates involves a two-point transition state structure in which the catalyst binds both the electrophile and nucleophile component through H-bonding interactions. This structure is lower in energy than the one proposed in the original paper. For the first time, the thionium H-bond has been invoked as a stereocontrolling interaction and is one reason for the enantioselectivity outcome. Steric effects from reasonably large groups on both the catalyst and substrate also determine the enantioselectivity. Furthermore, these calculations suggest a qualitative model that can be sketched by hand (Fig. 3, 5 and 6) that accurately reproduces the experimentally observed enantioselectivity in all cases. The model highlights and leads to the correction of the misassignment of absolute configuration in the original data. The mechanistic similarities between this system and reactions involving iminiums, inspired the application of a statistical model trained on amine enantioselectivity outcomes for the prediction of enantioselectivity values and stereochemistry of various N,S-acetals. Furthermore, this work demonstrates a new application of comprehensive statistical models for predicting the absolute stereochemistry, as this information is encoded into the approach and further validated our reassignment. Given the extensive application of thionium intermediates in achiral reaction settings,^22,23,61 we anticipate this mechanistic insight will inspire the development of enantioselective transformations involving these privileged chiral catalysts.

Data availability

The Cartesian coordinates of all computed geometries and extracted parameters are provided in the ESI.†

Author contributions

J. P. R. performed the computational analysis. J. L. performed the experimental studies. J. L. and J. P. R. wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support to JPR is provided by the University of British Columbia and the Natural Sciences and Engineering Research Council of Canada (NSERC). Computational resources were provided from Compute Canada and the Advanced Research Computing (ARC) center at the University of British Columbia. We thank the Nichols and Sammis Groups (UBC) for sharing their equipment and Brian Patrick (UBC) for solving the crystal structure.

References

1. J. P. Reid and M. S. Sigman, Nat. Rev. Chem., 2018, 2, 2905.
2. J. P. Reid, Commun. Chem., 2021, 4, 171.
3. R. B. Sunoj, Acc. Chem. Res., 2016, 49, 1019.
4. S. E. Wheeler, T. J. Seguin, Y. Guan and A. C. Doney, Acc. Chem. Res., 2016, 49, 1061.
5. K. N. Houk and P. H.-Y. Cheong, Nature, 2008, 455, 309.
6. Q. Peng, F. Duarte and R. S. Paton, Chem. Soc. Rev., 2016, 45, 6093.
7. Y.-H. Lam, M. N. Grayson, M. C. Holland, A. Simon and K. N. Houk, Acc. Chem. Res., 2016, 49, 750.
8. G.-J. Cheng, X. Zhang, L. W. Chung, L. Xu and Y.-D. Wu, J. Am. Chem. Soc., 2015, 137, 1706.
9. J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274.
10. E. H. Krenske and K. N. Houk, Acc. Chem. Res., 2013, 46, 979.
11. C. Eschmann, L. Song and P. R. Schreiner, Angew. Chem., Int. Ed., 2021, 60, 4823.
12. J. P. Reid and J. M. Goodman, Org. Biomol. Chem., 2017, 15, 6943.
13. M. N. Grayson and K. N. Houk, J. Am. Chem. Soc., 2016, 138, 1170.
14. A. Shoja and J. P. Reid, J. Am. Chem. Soc., 2021, 143, 7209.
15. A. Shoja, J. Zhai and J. P. Reid, ACS Catal., 2021, 11, 11897.
16. R. C. Johnston and P. H.-Y. Cheong, Org. Biomol. Chem., 2013, 11, 5057.
17. Y. Kita and N. Shibata, Synlett, 1996, 4, 289.
18. Y. Kita, N. Shibata, N. Kawano, T. Tohjo, C. Fujimor and K. Matsumoto, Tetrahedron Lett., 1995, 36, 115.
19. C. Kuhakarn, P. Seehasombat, T. Jaipetch, M. Pohmakotr and V. Reutrakul, Tetrahedron, 2008, 64, 1663.
20. A. Padwa and A. G. Waterson, Tetrahedron, 2000, 56, 10159.
21. A. Padwa and A. G. Waterson, J. Org. Chem., 2000, 65, 235.
22. S. K. Bur and A. Padwa, Chem. Rev., 2004, 104, 2401.
23. K. S. Feldman, Tetrahedron, 2006, 62, 5003.
24. P. Pulis and D. J. Procter, Angew. Chem., Int. Ed., 2016, 55, 9842.
25. S. Biswas, K. Kubota, M. Orlandi, M. Turberg, D. H. Miles, M. S. Sigman and F. D. Toste, Angew. Chem., Int. Ed., 2018, 57, 589.
26. W. Zhou and A. Voituriez, J. Am. Chem. Soc., 2021, 143, 17348.
27. F. Li, T. Korenaga, T. Nakanishi, J. Kikuchi and M. Terada, J. Am. Chem. Soc., 2018, 140, 2629.
28. P. Liu, E. D. Binnun, J. V. Schaus, N. M. Valentino and J. S. Panek, J. Org. Chem., 2002, 67, 1705.
29. J. H. Kim, A. Tap, L. Liu and B. List, Synlett, 2017, 28, 333.
30. Y. Usami, S. Aoki, T. Hara and A. Numata, J. Antibiot., 2002, 55, 655.
31. J. Kim, J. A. Ashenhurst and M. Movassaghi, Science, 2009, 324, 238.
32. L. D. S. Yadav and V. K. Rai, Tetrahedron Lett., 2008, 49, 5553.
33. A. D. Borthwick, Chem. Rev., 2012, 112, 3641.
34. L. Simón and J. M. Goodman, J. Am. Chem. Soc., 2008, 130, 8741.
35. M. N. Grayson, S. C. Pellegrinet and J. M. Goodman, J. Am. Chem. Soc., 2012, 134, 2716.
36. M. N. Grayson and J. M. Goodman, J. Am. Chem. Soc., 2013, 135, 6142.
37. J. P. Reid and J. M. Goodman, Org. Biomol. Chem., 2017, 15, 6943.
38. E. J. Corey, J. J. Rohde, A. Fischer and M. D. Azimioara, Tetrahedron Lett., 1997, 38, 33.
39. E. J. Corey and J. J. Rohde, Tetrahedron Lett., 1997, 38, 37.
40. M. Terada, K. Soga and N. Momiyama, Angew. Chem., Int. Ed., 2008, 47, 4122.
41. M. N. Grayson, M. J. Krisch and K. N. Houk, J. Am. Chem. Soc., 2015, 137, 8838.
42. E. Rodríguez, M. N. Grayson, A. Asensio, P. Barrio, K. N. Houk and S. Fustero, ACS Catal., 2016, 6, 2506.
43. G. Caballero-García and J. M. Goodman, Org. Biomol. Chem., 2021, 19, 9565.
44. M. N. Grayson, Z. Yang and K. N. Houk, J. Am. Chem. Soc., 2017, 139, 7717.
45. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, UK, 1990.
46. R. F. W. Bader, J. Phys. Chem. A, 2009, 113, 10391.
47. I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154.
48. M. J. Java, Struct. Chem., 2022, 33, 101.
49. B. Ośmiałowski, J. Mol. Model., 2014, 20, 2356.
50. A. R. Rosales, S. P. Ross, P. Helquist, P.-O. Norrby, M. S. Sigman and O. Wiest, J. Am. Chem. Soc., 2020, 142, 9700.
51. T. J. Seguin and S. E. Wheeler, ACS Catal., 2016, 6, 2681.
52. J. P. Reid, L. Simón and J. M. Goodman, Acc. Chem. Res., 2016, 49, 1029.
53. J. P. Reid and J. M. Goodman, J. Am. Chem. Soc., 2016, 138, 7910.
54. L. Simón and J. M. Goodman, J. Org. Chem., 2011, 76, 1775.
55. J. P. Reid and J. M. Goodman, Chem.–Eur. J., 2017, 23, 14248.
56. L. Simón, Org. Biomol. Chem., 2018, 16, 2225.
57. L. Simón and R. S. Paton, J. Am. Chem. Soc., 2018, 140, 5412.
58. J. P. Reid and M. S. Sigman, Nature, 2019, 571, 343.
59. I. O. Betinol, Y. Kuang and J. P. Reid, Org. Lett., 2022, 24, 1429.
60. L. C. Gallegos, G. Luchini, P. C. St John, S. Kim and R. S. Paton, Acc. Chem. Res., 2021, 4, 827.
61. L. H. S. Smith, S. C. Coote, H. F. Sneddon and D. J. Procter, Angew. Chem., Int. Ed., 2010, 49, 5832.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2149985. For ESI and crystallographic data in CIF or other electronic format see https://doi.org/10.1039/d2sc02171d

---