Open Access Article
Open Access ArticleA field-validated equilibrium passive sampler for the monitoring of per- and polyfluoroalkyl substances (PFAS) in sediment pore water and surface water†
Blessing
Medon
a,
Brent G.
Pautler
*b,
Alexander
Sweett
b,
Jeff
Roberts
b,
Florent F.
Risacher
 c,
Lisa A.
D'Agostino
c,
Jason
Conder
d,
Jeremy R.
Gauthier
c,
Lisa A.
D'Agostino
c,
Jason
Conder
d,
Jeremy R.
Gauthier
 e,
Scott A.
Mabury
e,
Andrew
Patterson
f,
Patricia
McIsaac
g,
Robert
Mitzel
f,
Seyfollah Gilak
Hakimabadi
a and
Anh Le-Tuan
Pham
e,
Scott A.
Mabury
e,
Andrew
Patterson
f,
Patricia
McIsaac
g,
Robert
Mitzel
f,
Seyfollah Gilak
Hakimabadi
a and
Anh Le-Tuan
Pham
 *a
*a
aDepartment of Civil and Environmental Engineering, University of Waterloo, Waterloo, Ontario N2L 3G1, Canada. E-mail: anh.pham@uwaterloo.ca
bSiREM, Guelph, Ontario N1G 3Z2, Canada. E-mail: bpautler@siremlab.com
cGeosyntec Consultants International Inc., Ottawa, Ontario K1P 5J2, Canada
dGeosyntec Consultants Inc., Costa Mesa, California 92626, USA
eDepartment of Chemistry, Lash Miller Chemical Labs, University of Toronto, Toronto, Ontario M5S 3H6, Canada
fEurofins Environment Testing America, West Sacramento, California 95605, USA
gEurofins Environment Testing America, Oakton, Virginia 22124, USA
First published on 2nd May 2023
Abstract
A simple equilibrium passive sampler, consisting of water in an inert container capped with a rate-limiting barrier, for the monitoring of per- and polyfluoroalkyl substances (PFAS) in sediment pore water and surface water was developed and tested through a series of laboratory and field experiments. The objectives of the laboratory experiments were to determine (1) the membrane type that could serve as the sampler's rate-limiting barrier, (2) the mass transfer coefficient of environmentally relevant PFAS through the selected membrane, and (3) the performance reference compounds (PRCs) that could be used to infer the kinetics of PFAS diffusing into the sampler. Of the membranes tested, the polycarbonate (PC) membrane was deemed the most suitable rate-limiting barrier, given that it did not appreciably adsorb the studied PFAS (which have ≤8 carbons), and that the migration of these compounds through this membrane could be described by Fick's law of diffusion. When employed as the PRC, the isotopically labelled PFAS M2PFOA and M4PFOS were able to predict the mass transfer coefficients of the studied PFAS analytes. In contrast, the mass transfer coefficients were underpredicted by Br− and M3PFPeA. For validation, the PC-based passive samplers consisting of these four PRCs, as well as two other PRCs (i.e., M8PFOA and C8H17SO3−), were deployed in the sediment and water at a PFAS-impacted field site. The concentration–time profiles of the PRCs indicated that the samplers deployed in the sediment required at least 6 to 7 weeks to reach 90% equilibrium. If the deployment times are shorter (e.g., 2 to 4 weeks), PFAS concentrations at equilibrium could be estimated based on the concentrations of the PRCs remaining in the sampler at retrieval. All PFAS concentrations determined via this approach were within a factor of two compared to those measured in the mechanically extracted sediment pore water and surface water samples obtained adjacent to the sampler deployment locations. Neither biofouling of the rate-limiting barrier nor any physical change to it was observed on the sampler after retrieval. The passive sampler developed in this study could be a promising tool for the monitoring of PFAS in pore water and surface water.
Environmental significanceThere is a growing interest in the passive sampling of per- and polyfluoroalkyl substances (PFAS). In this study, we successfully developed and validated an equilibrium passive sampler for PFAS in sediment pore water and lake water. This sampler consists of a diffusion cell filled with water and a polycarbonate membrane, which serve as the receiving phase and the rate-limiting barrier, respectively. The sampler also contains isotopically-labelled PFAS, which serve as performance reference compounds (PRCs). We demonstrated that PFAS concentrations determined via the PRCs were within a factor of two compared to those measured in the mechanically extracted pore-water and lake-water samples. Our passive sampler could be a promising tool for the monitoring of PFAS in pore water and surface water. |
1 Introduction
The extensive use of per- and polyfluoroalkyl substances (PFAS) in the last several decades in products such as aqueous film-forming foams (AFFF), fluoropolymers, cosmetics, food packaging, carpets, and textiles, among others, has resulted in the contamination of water, air, land, and biota by these uniquely persistent and potentially toxic organic compounds.1 As a result, PFAS have attracted a great deal of interest from the scientific community and regulatory bodies, and are now considered an important class of emerging contaminants. The need to monitor PFAS in the environment to study their occurrence, fate and transport is well established.As with any contaminant, PFAS in an environment can be measured by active and/or passive sampling. Active sampling involves collecting discrete (i.e., grab) portions of the environment by exerting physical or mechanical activity such as pumping groundwater, pumping air, scooping surface water, or coring sediment. Although active sampling is a widely accepted monitoring technique for regulatory compliance, its limitations have been long recognized.2–4 Firstly, active sampling only provides the concentration of contaminants at a specific point in time (i.e., at the time of sample collection), and thus might miss the polluting or discharge events because these fluxes are intermittent or unpredictable, due to frequent hydrological changes and accidental leakages. Secondly, analysing samples obtained by active sampling often involves isolating the analyte of interest from the sample matrix, which could be challenging for complex matrices or if only a trace quantity of the analyte is present. For example, the analysis of PFAS in sediment pore water requires sediment coring, followed by squeezing or centrifuging the sediment to extract pore water, and finally preconcentrating PFAS in the pore water by solid phase extraction.5 This process is labour-intensive, generates a large quantity of investigative-derived waste, and could be prone to cross-contamination. Additionally, active sampling may result in an overestimation of the contaminant's bioavailability.4,6 Contrary to active sampling, passive sampling involves deploying a sampler consisting of a receiving phase that can accumulate the analytes of interest due to chemical potential differences.2–4 As a result, the analytes are isolated from the sampled environment in situ, significantly reducing investigative-derived waste. Additionally, if only the truly dissolved analyte phase migrates into the sampler, passive sampling data may be more reflective of the analyte's bioavailability.4,6 For these reasons, passive sampling has become a valuable part of the monitoring toolbox alongside active sampling.7
In passive sampling, the amount of analyte accumulated in the sampler increases with time until a dynamic equilibrium is established between the receiving phase and the sampled environment.3 Sampling may be terminated during the initial linear regime or after equilibrium has been established. Passive samplers that operate in the linear regime are referred to as kinetic samplers. This sampler type provides the time-weighted average concentration, which is calculated based on the amount of analyte accumulated and the sampling rate over the deployment period. Examples of kinetic samplers include the polar organic chemical integrative samplers (POCIS),8,9 the Chemcatcher,10 and the diffusive gradient in thin-film samplers (DGT).11 Conversely, passive samplers that operate in the equilibrium regime are referred to as equilibrium samplers. With this sampler type, the concentration of the analyte in the sampled medium is calculated based on the equilibrium partitioning of the analyte between the receiving phase and the sampled medium. Examples of equilibrium samplers include semi-permeable membrane devices (SPMD),12 low-density polyethylene sheets (LDPE),13 dialysis bags,14 and dialysis samplers, also known as peepers.15
Given the growing interest in PFAS monitoring, researchers in recent years have put significant efforts into adapting existing passive samplers for PFAS.16 For example, several studies have employed POCIS and DGT to monitor PFAS in surface water and wastewater effluent.17–23 Since POCIS and DGT were traditionally designed for metals, the adaptation of these kinetic samplers for PFAS involved testing and/or developing PFAS-selective adsorbents that can be used as the receiving phase. While the use of POCIS and DGT for PFAS is not without success, these samplers require in situ calibrations of the sampling rate (especially in the case of POCIS samplers), which could be labour-intensive and challenging for analytes with diverse physical/chemical properties like PFAS. It also has been shown that unexpected changes in flow rates or temperature may result in fluctuations in the sampling rate.19,20 Additionally, the sampling rate of adsorbent-based passive samplers such as POCIS and DGT might be difficult to predict, given the likelihood of competition among PFAS and between PFAS and other organic compounds (e.g., natural organic matter) for the adsorptive sites in the receiving phase. Although sampler calibration might be aided by performance reference compounds (PRCs), identifying and implementing PRCs for PFAS passive sampling have proven challenging.20 Recently, Kaserzon et al. and Gardiner et al. showed that a kinetic passive sampler with a thick diffusion barrier could help mitigate the effect of water flow rate on the PFAS sampling rate.24,25 However, the issue of competition for adsorptive sites remains to be explored.
Regarding PFAS sampling by equilibrium passive samplers, there have been only four studies, namely (1) the study by Dixon-Anderson and Lohmann on the use of LDPE sheets for the monitoring of neutral PFAS (e.g., fluorotelomer alcohols) in wastewater treatment effluent,26 (2) the study by Becanova et al. on the passive sampling of anionic PFAS (i.e., perfluoroalkyl acids) in surface water by a graphene-based monolith,27 (3) the study by Kaltenberg et al. who employed a passive sampler with carbamate polymeric adsorbents to monitor PFAS in surface water and groundwater,28 and (4) the study by McDermett et al. who proposed a diffusive equilibrium peeper sampler for the monitoring of anionic PFAS in groundwater.29 Whereas the passive samplers in the first three studies consisted of a solid receiving phase (i.e., the accumulation of PFAS into the sampler is driven by adsorption), the sampler developed by McDermett et al. employed water as the receiving phase (i.e., PFAS accumulation is driven by absorption). One important feature of adsorptive-based samplers is that the analytes of interest are preconcentrated on the adsorbent, which could lower the detection limit. However, given that PFAS adsorption is strongly influenced by the solution chemistry (e.g., pH, ionic strength, Ca2+),30 the performance of adsorptive-based samplers could be sensitive to the environmental condition where they are deployed, and to competitive sorption, as mentioned above. Conversely, little preconcentration or no preconcentration (i.e., if the receiving phase is water) of analytes will occur with an absorptive-based sampler. This means that absorptive-based samplers should consist of an adequate volume of receiving phase to enable preconcentration by solid phase extraction following sampler retrieval. Thus, absorptive-based samplers tend to be more cumbersome than adsorptive-based samplers. However, since absorptive-based samplers are less affected by the solution chemistry and competitive sorption, their performance might be more predictable. It is noted that of the four studies mentioned above, the LDPE sheet, the graphene-based monolith, and the carbamate polymeric adsorbent were tested in the field,26–28 whereas the diffusive equilibrium sampler has only been tested in a laboratory environment.29
Considering the limited number of studies on passive sampling of PFAS, particularly by equilibrium samplers, the objective of this study was to develop and validate an equilibrium passive sampler for sediment pore water and surface water. To this end, a sampler with water as the receiving phase was constructed and tested through a series of bench-scale experiments for its ability to monitor some key PFAS, including perfluorooctane sulfonate (PFOS) and perfluorooctanoate (PFOA). To validate this sampler, two rounds of field experiments were conducted at Lake Niapenco (Ontario, Canada), where the contamination of water, sediment, and biota by PFAS has been previously documented.31–33 In each round of experiment, the samplers were deployed in both the sediment and the overlaying water, and the PFAS concentrations in grab samples and those predicted by the samplers were compared. Additionally, to determine the rate of equilibration between the sampled medium and the sampler, the suitability of several compounds as PRCs for PFAS was evaluated. While the research conducted over the past decade has demonstrated that PFAS are ubiquitously present in sediments,5,34–38 few studies have measured PFAS in sediment pore waters. Monitoring PFAS in pore waters is crucial because pore waters have been shown to be an important source that contributes to the contamination of surface water and groundwater through pore water exchange.39 As such, in addition to developing and validating a passive sampler for use in surface water and pore water, this study provides important insights into the levels of PFAS in the sediment pore water at Lake Niapenco, a water reservoir downstream of an airport where there were historical usages of AFFF for fire-fighting training.
2 Materials and method
2.1 Chemicals
For the quantification of PFAS by liquid chromatography-tandem mass spectrometry (LC-MS/MS), native and isotopically labelled PFAS standards were purchased from Wellington Laboratories (Guelph, Canada). Single isotopically labelled PFAS used as PRCs (see the next section) were also purchased from Wellington Laboratories. Single native PFAS for laboratory testing were purchased from Sigma Aldrich (PFOS, PFOA, perfluorohexane sulfonate (PFHxS)) and Toronto Research Chemicals (2-(perfuorohexyl)ethane-1-sulfonic acid sodium salt, i.e., 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTS). All other chemicals were purchased from either Fisher Scientific or Sigma Aldrich and were used as received.
2 FTS). All other chemicals were purchased from either Fisher Scientific or Sigma Aldrich and were used as received.
2.2 Passive sampler construction
The equilibrium passive sampler (Fig. 1) consisted of a cylindrical high-density polyethylene (HDPE) container filled with 65 mL of MilliQ water (i.e., the receiving solution) and spiked with a mixture of PRCs. The PRCs used in this study were bromide (Br−), perfluoro-n-[3,4,5-13C3] pentanoate (M3PFPeA), perfluoro-[1,2-13C2] octanoate (M2PFOA), perfluoro-n-[13C8] octanoate (M8PFOA), perfluoro-1-[1,2,3,4-13C4] octanesulfonate (M4PFOS), and 1-octanesulfonate (C8H17SO3−). The container was covered with a membrane filter, which functioned as the diffusion rate-limiting barrier. The area (A = 2.27 cm2) of the threaded lid capped over the membrane defined the sampling window of the membrane. The membrane filters tested included 0.45 μm and 0.22 μm polyether sulfone (PES), 0.45 μm regenerated cellulose (RC), 0.45 μm cellulose acetate (CA), and 0.40 μm polycarbonate (PC). For field deployment, the samplers were inserted into a holding frame made of polyethylene terephthalate glycol (PETG), which was then inserted into the sediment or attached to a steel rebar and submerged in the lake.2.3 Laboratory experiments
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTS (3–5 μg L−1 each). The solution pH was buffered by 1 mM NaHCO3 (pH = 7.4). After 7 days, the concentration of each PFAS in the solution was measured to determine the fraction lost due to sorption. Using a similar approach, the adsorption of PFAS to the other sampler parts (i.e., the 65 mL HDPE container, the cap, and the PETG holding frame) was also evaluated. In addition, a control experiment was conducted wherein a sampler was submerged in MiliQ water for 7 days to assess whether the sampler components contained PFAS. The concentrations of PFAS in the solution at the end of this experiment were below detection limits (data not shown), indicating that all sampler components were PFAS-free.
2 FTS (3–5 μg L−1 each). The solution pH was buffered by 1 mM NaHCO3 (pH = 7.4). After 7 days, the concentration of each PFAS in the solution was measured to determine the fraction lost due to sorption. Using a similar approach, the adsorption of PFAS to the other sampler parts (i.e., the 65 mL HDPE container, the cap, and the PETG holding frame) was also evaluated. In addition, a control experiment was conducted wherein a sampler was submerged in MiliQ water for 7 days to assess whether the sampler components contained PFAS. The concentrations of PFAS in the solution at the end of this experiment were below detection limits (data not shown), indicating that all sampler components were PFAS-free.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTS) into the sampler and determine the time to equilibrium, a series of microcosm experiments were conducted wherein each sampler was placed in a jar containing 400 mL solution of 1 mM NaHCO3 (pH = 7.4) and 3–5 μg L−1 of each PFAS mentioned above. In one experiment, the solution in the jar contained 10 times less PFAS (i.e., 0.25–0.4 μg L−1 of each PFAS) – the goal of this experiment was to assess the performance of the sampler at a lower PFAS concentration. The solution in the sampler (i.e., the receiving phase) consisted of 89 mg L−1 Br−, and 0.45–0.8 μg L−1 of M3PFPeA, M2PFOA, and M4PFOS, which served as the PRCs. The jars were then placed horizontally such that the sampling window was fully submerged. Due to the concentration gradient between the solutions in the sampler and the jar, the four PFAS diffused into the sampler, whereas the PRCs migrated in the opposite direction. At predetermined time intervals, three jars were sacrificed to analyze for PFAS and PRCs. Both the receiving solution and the solution in the jar were analyzed to verify the mass balance. The average concentrations along with one standard deviation are presented.
2 FTS) into the sampler and determine the time to equilibrium, a series of microcosm experiments were conducted wherein each sampler was placed in a jar containing 400 mL solution of 1 mM NaHCO3 (pH = 7.4) and 3–5 μg L−1 of each PFAS mentioned above. In one experiment, the solution in the jar contained 10 times less PFAS (i.e., 0.25–0.4 μg L−1 of each PFAS) – the goal of this experiment was to assess the performance of the sampler at a lower PFAS concentration. The solution in the sampler (i.e., the receiving phase) consisted of 89 mg L−1 Br−, and 0.45–0.8 μg L−1 of M3PFPeA, M2PFOA, and M4PFOS, which served as the PRCs. The jars were then placed horizontally such that the sampling window was fully submerged. Due to the concentration gradient between the solutions in the sampler and the jar, the four PFAS diffused into the sampler, whereas the PRCs migrated in the opposite direction. At predetermined time intervals, three jars were sacrificed to analyze for PFAS and PRCs. Both the receiving solution and the solution in the jar were analyzed to verify the mass balance. The average concentrations along with one standard deviation are presented.
To determine the observed mass transfer coefficient kPFAS, experimental and kPRC, experimental (cm s−1) across the rate-limiting barrier, the concentration–time profile of each compound was fitted to the following equations:
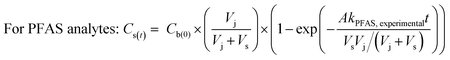 | (1) |
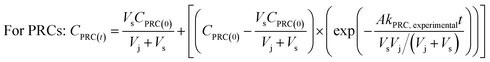 | (2) |
To assess the ability of the PRCs to predict the observed mass transfer coefficient for PFAS analytes, kPFAS, calculated was calculated and compared to the experimental kPFAS, experimental according to the following equation:
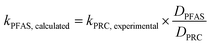 | (3) |
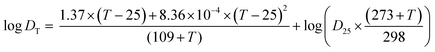 | (4) |
2.4 Field experiments
Two rounds of sampler deployment were performed. In the first round, which occurred in October 2021, a total of 144 samplers were deployed at four locations along the Tyneside trail. These locations, denoted as locations A, B, C, and D in Fig. S1,† were within 500 m of each other. Of the 144 samplers deployed, 80 samplers were inserted approximately 10 cm beneath the water–sediment interface, while 64 samplers were suspended in the lake at a depth between 80 and 120 cm below the air–water interface. Each sampler contained four PRCs, namely Br− (90 mg L−1), M3PFPeA (95 ng L−1), M2PFOA (95 ng L−1), and M4PFOS (90 ng L−1). As will be presented in the Results and discussion session, the laboratory experiments revealed that PC membranes could serve as the rate-limiting barrier since they do not adsorb PFAS to an appreciable extent. Also, based on the visual inspection of the sampling windows, there appeared to be neither biofouling of the surface nor any physical change to the PC membrane after 7 weeks of deployment in the field. Detailed information about the type and number of samplers deployed at each location can be found in Table S3.†
Samplers were retrieved on day 46 and day 47. The receiving solutions from two samplers (2 × ∼60 mL) were composited into a 125 mL HDPE bottle, and the concentration of PFAS in each bottle was treated as a single data point. With 6 samplers deployed, there are triplicates at each location; thus, the average concentrations along with one standard deviation (i.e., the error bar) are presented.
Grab samples were collected on the sampler deployment day. Specifically, surface water samples were collected at approximately 80 cm below the air–water interface, using 125 mL HDPE bottles that were attached to a steel rebar. Sediment was scooped up using an HDPE scoop at approximately between 0 and 30 cm beneath the sediment–water interface, and was poured into an HDPE container. Approximately 5 kg of sediment was collected from each location (i.e., locations A–D). The grab samples were collected within 50 cm of the sampler deployment locations.
To determine the mass transfer k in the field, extra samplers were deployed in the sediment at location A to establish the time–concentration profiles for the PRCs. At each predetermined time interval (i.e., t = 2, 14, 21, 28, 35, and 47 days), four samplers were retrieved, and the solution in each sampler was poured into a 125 mL HDPE bottle. Thus, for each time point, there were two 125 mL samples, which were treated as duplicates. The average concentrations along with the range are presented.
In the first experimental round, the temperature of the water and sediment at the four deployment locations varied between 7 and 15 °C throughout this field experiment. Thus, an average temperature of 10 °C was applied in the calculation of D.
Several studies have reported a seasonal variation in PFAS concentration in surface water, groundwater, and pore water.39,46,47 To investigate if there is such a variation at Lake Niapenco, another field experiment was conducted at locations A and B in June 2022 during a drier period and warmer weather (the average temperature during this period was 10–20 °C). Thirty-six samplers were deployed in the sediment, while 8 samplers were deployed in surface water (Table S3†). In this experimental round, all samplers were constructed with a PC membrane as the rate-limiting barrier, whereas M8PFOA (110 ng L−1) and C8H17SO3− (70 ng L−1) were employed as the PRCs. At location A, some samplers deployed in the sediment were retrieved at t = 2, 7, 14, 21, 28, 35, and 42 days to establish the concentration–time profiles for the PRCs. All other samplers were retrieved on day 28. Using an approach similar to that used in the first experimental round, the solutions in every two samplers were composited into a 125 mL HDPE bottle, and the analyte concentrations in this combined solution were treated as a single data point.
All samples were shipped on ice to Waterloo or Eurofins Environment Testing America (Sacramento) for analysis and were stored at 4 °C upon arrival.
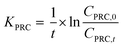 | (5) |
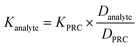 | (6) |
| Ceq = Creceiving,t/(1 − exp(−t × Kanalyte)) | (7) |
2.5 Sample analysis
Bromide was analyzed at Waterloo on a Dionex Aquion Ion Chromatograph. For PFAS analysis, aqueous samples generated from the laboratory experiments were spiked with isotopically labelled PFAS (i.e., internal standards) and diluted with methanol to obtain a final sample composition of 50/50 v/v methanol/water. The samples were then analyzed at Waterloo using a Shimadzu 8030 liquid chromatograph triple quadrupole mass spectrometer (LC-MS/MS).Field aqueous samples included grab surface water samples and the receiving solution collected from the passive samplers. The analysis of these samples was split between Waterloo and Eurofins Environment Testing America. At Eurofins Environment Testing America, samples were analyzed using the modified US EPA 537 method (for samples collected in 2021) and US EPA Draft Method 1633 (for samples collected in 2022).49,50 Briefly, 12.5–25 ng per compound of isotopically labelled PFAS were added to each sample. After spiking, samples were allowed to equilibrate for at least 10 minutes prior to multi-phase solid phase extraction (SPE) with weak-anion exchange resin coupled with graphite carbon black (500 mg WAX/50 mg GCB SPE). SPE elution rates were typically 8–10 mL per minute. The cartridges were then washed with water and then dried for 10 minutes. The original sample bottle was rinsed with 8 mL of 0.4% ammonium hydroxide in methanol, capped and then briefly shaken by hand and then used to elute the WAX/GCB cartridge. Extracts were adjusted to 10 mL with water to obtain a final sample composition of 80/20 v/v methanol/water prior to analysis. At Waterloo, samples were spiked with internal standards and were extracted through an Oasis WAX cartridge (6 cm3, 150 mg, 30 μm particle size). In particular, the cartridges were preconditioned with 3 mL of methanol, then with 3 mL of 0.1% ammonium hydroxide in methanol, and finally with 3 mL of 0.1 M formic acid. Subsequently, 125 mL aqueous samples were pulled through each cartridge at an approximate flow rate of 1 drop per second (i.e., ∼1.5 mL per minute). After sample extraction, the cartridges were washed with 3 mL of 0.1 M formic acid, and then PFAS were eluted with 5 mL of 0.1% ammonium hydroxide in methanol followed by 5 mL of pure methanol. The eluants were collected in a 15 mL vial and concentrated down to 500 μL using a Dionex SE-500 nitrogen evaporator. In the final step, the concentrated sample was transferred to an HPLC vial and diluted with water to obtain a final sample composition of 50/50 v/v methanol/water.
PFAS in sediment as well as pore water grab samples were analyzed by Eurofins Environment Testing America. Pore water was separated from each sediment sample by centrifugation at 3155 × g at 4 °C for 30 min. Subsequently, the supernatant was decanted into a 250 mL HDPE bottle and isotopically labelled PFAS were added. The sample was then subjected to SPE extraction following the procedure described above. PFAS in sediment was analyzed using modified Method 537. Briefly, 5 g of solid were weighed out in a 50 mL polypropylene tube and 12.5–25 ng of isotopically labelled PFAS were added directly to the sample. For the extraction of PFAS, basic methanol was added and the sample was placed in an ultrasonic bath for one hour. The sample was then centrifuged at 3725 × g for 5 min, and the supernatant was decanted into a new container. The remaining solid was extracted one more time by adding another volume of basic methanol, vortexing and placing the sample in the ultrasonic bath, and separating the solid by centrifugation. The supernatant was combined into the same container. The total volume in the container was adjusted with water to 125 mL, and the entire volume was extracted through SPE following the procedure described above. The final samples consisting of 80/20 v/v methanol/water were analyzed on an Exion LC that was coupled with a SCIEX 5500 tandem mass spectrometer.
3 Results and discussion
3.1 Adsorption of PFAS on the rate-limiting barrier, HDPE container, and PTGE frame
Under the experimental condition of this study, less than 3% of PFOS, PFHxS, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
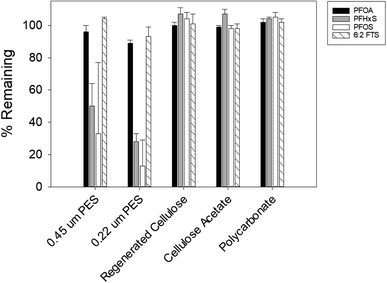
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTS, and PFOA were lost from the solution that was in contact with the HDPE container of the sampler or the PTGE frame that holds the sampler in the field (data not shown). While the adsorption of shorter-chain PFAS, such as perfluorohexanoate (PFHxA), perfluoropentanoate (PFPeA), and perfluorobutane sulfonate (PFBS), was not investigated, it is reasonable to expect that these more hydrophilic compounds also would not adsorb to the passive sampler components. With respect to PFAS sorption to the rate-limiting barrier, more than half of PFOS and PFHxS were lost from the solution that was in contact with the PES membranes (Fig. 2). PFOA and 6
2 FTS, and PFOA were lost from the solution that was in contact with the HDPE container of the sampler or the PTGE frame that holds the sampler in the field (data not shown). While the adsorption of shorter-chain PFAS, such as perfluorohexanoate (PFHxA), perfluoropentanoate (PFPeA), and perfluorobutane sulfonate (PFBS), was not investigated, it is reasonable to expect that these more hydrophilic compounds also would not adsorb to the passive sampler components. With respect to PFAS sorption to the rate-limiting barrier, more than half of PFOS and PFHxS were lost from the solution that was in contact with the PES membranes (Fig. 2). PFOA and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTS appeared to have a lower affinity to the PES membranes, with the loss fraction ranging between 5 and 12%. These results are consistent with those reported by Sörengård et al., who observed that the affinity of PFAS to PES membranes was in the following order: PFOS > PFHxS > PFOA.41 Contrary to the PES membranes, less than 2% of PFAS was adsorbed by the RC, CA and PC membranes (Fig. 2). Lath et al. observed that 20–40% of the PFOA in their solution was adsorbed to the RC and CA membranes.40 We note that in the study by Lath et al., the membranes were in contact with a smaller volume (i.e., 4 mL) of a PFAS-containing solution, which could have resulted in a greater % of PFOA adsorption. Also, the membranes in that study were housed in a casing made of polypropylene and acrylic resin MBS (methacrylate butadiene styrene). Thus, the PFOA loss might be attributable partly to adsorption to the housing materials. Lath et al. also observed that approximately 10–30% of PFOA was lost from an 8 mL volume of water containing 21 μg L−1 PFOA stored in a PC tube for 7 days.40 The difference between our result and that of Lath et al. may be due to differences in PC manufacturing of the membrane and the tube.
2 FTS appeared to have a lower affinity to the PES membranes, with the loss fraction ranging between 5 and 12%. These results are consistent with those reported by Sörengård et al., who observed that the affinity of PFAS to PES membranes was in the following order: PFOS > PFHxS > PFOA.41 Contrary to the PES membranes, less than 2% of PFAS was adsorbed by the RC, CA and PC membranes (Fig. 2). Lath et al. observed that 20–40% of the PFOA in their solution was adsorbed to the RC and CA membranes.40 We note that in the study by Lath et al., the membranes were in contact with a smaller volume (i.e., 4 mL) of a PFAS-containing solution, which could have resulted in a greater % of PFOA adsorption. Also, the membranes in that study were housed in a casing made of polypropylene and acrylic resin MBS (methacrylate butadiene styrene). Thus, the PFOA loss might be attributable partly to adsorption to the housing materials. Lath et al. also observed that approximately 10–30% of PFOA was lost from an 8 mL volume of water containing 21 μg L−1 PFOA stored in a PC tube for 7 days.40 The difference between our result and that of Lath et al. may be due to differences in PC manufacturing of the membrane and the tube.
Considering the physical durability and ease of handling of each membrane, PC and CA membranes were selected for further testing as the rate-limiting barrier.
3.2 Kinetic of PFAS uptake and PRCs loss in laboratory experiments
In the microcosm experiment with a PC-based passive sampler, the concentrations of the PFAS analytes and the PRCs in the receiving solution increased and decreased exponentially, respectively (the blue and hollowed circles in Fig. 3), suggesting that the migration of these compounds through the PC rate-limiting barrier followed the Fick's second law of diffusion.3 Simultaneously, the PFAS concentrations in the solution outside of the sampler decreased over time (the red triangles in Fig. 3). At equilibrium, which occurred after around two weeks, the concentrations of PFAS analytes in the receiving phase and the solution outside of the sampler were within ±5% of the predicted equilibrium concentrations (the dotted black lines in the PFOA, PFHxS, PFOS, and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTS graphs shown in Fig. 3). In the experiment with lower PFAS initial concentrations (0.25–0.4 μg L−1), the concentrations of PFAS analytes in the receiving solution, measured at t = 21 days, were also within ±5% of the predicted concentrations (Fig. S2†). These results further confirm that the loss of PFAS by adsorption to the jar and the sampler walls was minimal. With a sampler constructed with a PES rate-limiting barrier, in contrast, the concentrations of PFOS (i.e., the compound that had the highest sorption affinity to the PES membrane) in the receiving solution and in the solution outside of the sampler were 17% smaller than the predicted equilibrium concentration (Fig. S3†). Moreover, that the concentration of PFOS in the receiving solution did not increase exponentially, and that the equilibrium was established at a much later time (after about four weeks), suggest that the migration of PFOS was retarded by the PES membrane. Collectively, the results obtained with the PC- and PES-based samplers highlight the importance of having a rate-limiting barrier that interacts minimally with the analytes of interest.
2 FTS graphs shown in Fig. 3). In the experiment with lower PFAS initial concentrations (0.25–0.4 μg L−1), the concentrations of PFAS analytes in the receiving solution, measured at t = 21 days, were also within ±5% of the predicted concentrations (Fig. S2†). These results further confirm that the loss of PFAS by adsorption to the jar and the sampler walls was minimal. With a sampler constructed with a PES rate-limiting barrier, in contrast, the concentrations of PFOS (i.e., the compound that had the highest sorption affinity to the PES membrane) in the receiving solution and in the solution outside of the sampler were 17% smaller than the predicted equilibrium concentration (Fig. S3†). Moreover, that the concentration of PFOS in the receiving solution did not increase exponentially, and that the equilibrium was established at a much later time (after about four weeks), suggest that the migration of PFOS was retarded by the PES membrane. Collectively, the results obtained with the PC- and PES-based samplers highlight the importance of having a rate-limiting barrier that interacts minimally with the analytes of interest.
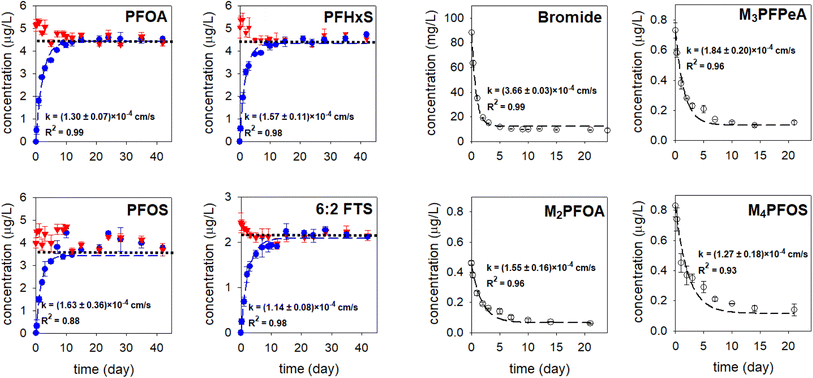 | ||
Fig. 3 The concentration–time profiles of the PFAS analytes and the PRCs. Experiments were conducted in triplicate and average values along with one standard deviation (i.e., error bar) are presented. Red triangles: the concentrations in the solution in the jar. Blue and hollowed circles: the concentrations in the receiving solution of the sampler. Experimental results were fitted to eqn (3) and (4) (the dashed blue lines and the dashed black line) to obtain the observed mass transfer (k) value. The dotted black lines in the PFOA, PFHxS, PFOS, and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTS figures represent the theoretical equilibrium concentrations for these analytes, which were calculated based on mass balance. 2 FTS figures represent the theoretical equilibrium concentrations for these analytes, which were calculated based on mass balance. | ||
The observed mass transfer values k of the PFAS analytes and the PRCs through the PC rate-limiting barrier were within a 1.6-fold difference, ranging from (1.14 ± 0.08) × 10−4 cm s−1 to (1.84 ± 0.20) × 10−4 cm s−1. In agreement with when analyte migration is controlled by diffusion, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTS, whose diffusion coefficient is the smallest among the studied PFAS (D = 4.16 × 10−6 cm2 s−1), was the compound that migrated through the PC rate-limiting barrier at the slowest rate (k = (1.14 ± 0.08) × 10−4 cm s−1). For the other native and mass-labelled PFAS, the trend between D and k could not be deduced, due to large uncertainties associated with the k values (e.g., the k for M3PFPeA and PFOS were (1.84 ± 0.20) × 10−4 cm s−1 and (1.63 ± 0.36) × 10−4 cm s−1, respectively). Compared with those of the PFAS analytes and PRCs, k of Br− (3.66 ± 0.03 × 10−4 cm s−1) was 2–3.2 folds higher. Due to this faster migration, an equilibrium for Br− was established earlier, i.e., after about a week (Fig. 3).
2 FTS, whose diffusion coefficient is the smallest among the studied PFAS (D = 4.16 × 10−6 cm2 s−1), was the compound that migrated through the PC rate-limiting barrier at the slowest rate (k = (1.14 ± 0.08) × 10−4 cm s−1). For the other native and mass-labelled PFAS, the trend between D and k could not be deduced, due to large uncertainties associated with the k values (e.g., the k for M3PFPeA and PFOS were (1.84 ± 0.20) × 10−4 cm s−1 and (1.63 ± 0.36) × 10−4 cm s−1, respectively). Compared with those of the PFAS analytes and PRCs, k of Br− (3.66 ± 0.03 × 10−4 cm s−1) was 2–3.2 folds higher. Due to this faster migration, an equilibrium for Br− was established earlier, i.e., after about a week (Fig. 3).
The k value of PFOA was (1.30 ± 0.07) × 10−4 cm s−1, whereas that of M2PFOA was (1.55 ± 0.16) × 10−4 cm s−1. The relative percent difference (RPD) between the average k values of PFOA and M2PFOA is 18%. Similarly, the RPD between the average k values of PFOS and M4PFOS is small (<25%). Note that there is a relatively big uncertainty associated with the k values for PFOS and M4PFOS. These results suggest that the mass transfer resistance was the same on either side of the membrane.
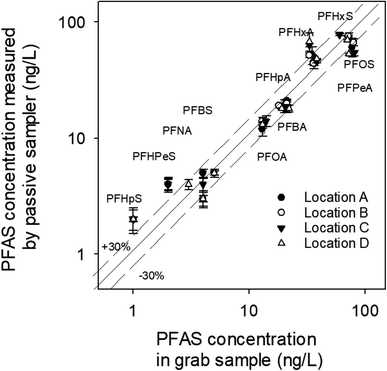
The appropriateness of each PRC as a proxy for the studied PFAS analytes was further evaluated by comparing the kexperimental and kcalculated (Fig. 4). Both Br− and M3PFPeA underpredict the mass transfer coefficient of PFAS analytes. The % difference between the average values kcalculated and kexperimental ranged between −32% and −56%. This result is not entirely surprising considering that the physical/chemical properties of Br− and M3PFPeA are different from those of the studied PFAS analytes (e.g., both Br− and M3PFPeA are more hydrophilic), and thus Br− and M3PFPeA might interact with the rate-limiting barrier differently. In contrast, the kcalculated calculated based on M4PFOS and M2PFOA are within ≤30% of the kexperimental (Fig. 4). That M4PFOS and M2PFOA are reasonable PRCs for PFOS, PFHxS, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTS, and PFOA is consistent with these compounds' relative similarities in perfluoroalkyl chain length and/or functional group. This result also suggests that different types of PRCs might be needed to monitor PFAS with diverse physical/chemical properties. As such, Br− and M3PFPeA were included as PRCs in the samplers deployed in the field to further assess their ability to predict the concentrations of the more hydrophilic PFAS such as perfluorobutanoate (PFBA), PFPeA, and PFBS.
2 FTS, and PFOA is consistent with these compounds' relative similarities in perfluoroalkyl chain length and/or functional group. This result also suggests that different types of PRCs might be needed to monitor PFAS with diverse physical/chemical properties. As such, Br− and M3PFPeA were included as PRCs in the samplers deployed in the field to further assess their ability to predict the concentrations of the more hydrophilic PFAS such as perfluorobutanoate (PFBA), PFPeA, and PFBS.
 | ||
Fig. 4 Comparison of the observed mass transfer coefficient of PFOA, PFHxS, PFOS, and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTS (kexperimental, measured in the experiments presented in Fig. 3) and the mass transfer coefficient (kcalculated) calculated based on eqn (3). The solid lines are the 1 2 FTS (kexperimental, measured in the experiments presented in Fig. 3) and the mass transfer coefficient (kcalculated) calculated based on eqn (3). The solid lines are the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 lines, whereas the dashed lines represent the ±30% relative percent difference between kexperimental and kcalculated. 1 lines, whereas the dashed lines represent the ±30% relative percent difference between kexperimental and kcalculated. | ||
3.3 Time–concentration profile in the field experiments
In each experimental round, 16 samplers were deployed in the sediment at location A to collect time series data (2–47 days) to determine the rates of PRC loss and PFAS uptake. As can be expected if the samplers function properly, the concentrations of the PFAS analytes (Fig. S4 and S5†) increased over time. In the first experimental round (October 2021), the uptake of the analytes appeared to follow first-order kinetics; see Fig. S4 and Table S5† for the experimental data and the associated fitting parameters, i.e., the observed mass transfer coefficient k and the equilibrium concentration Ceq. (The Ceq values obtained from the fitting of the time-series data will be compared with the Ceq calculated based on the PRCs in Section 3.4.2 below). In the second experimental round (June 2022), the concentration of the analytes appeared to increase linearly with deployment time (Fig. S5†). While it is not entirely clear why the analyte uptake trend was linear, it is noted that unlike in the laboratory microcosm experiments, it was not possible to assume that all samplers for the various time points were exposed to the same concentration of PFAS in pore water. Even though these samplers were deployed at one location (i.e., location A), the heterogeneity of chemicals in sediment can be high, even over a distance of a few cm. The experimental design used in the field work (one replicate per time period) was not sufficient in terms of replication to account for this possible source of variation and uncertainty.In both experimental rounds, the loss of the PRCs from the receiving solution appeared to obey the first-order rate expression (Fig. 5). The fractions of the PRCs lost from the samplers were 25–55%, 40–70%, and 70–90% after 14 days, 28 days, and 46 days respectively. These loss fractions at these time points were deemed reasonable for using PRC data to evaluate the degree of equilibration attained by a deployed sampler, such that the data can be used to calculate the expected concentration of target PFAS analytes in a sampler at equilibrium. In other words, optimal deployment durations for the sampler in sediment range approximately between 2 to 7 weeks. Regarding the samplers that were deployed in the water column, the PRCs quickly depleted from the receiving solution and thus a concentration–time profile could not be established (see Section 3.4.2 below for additional discussion).
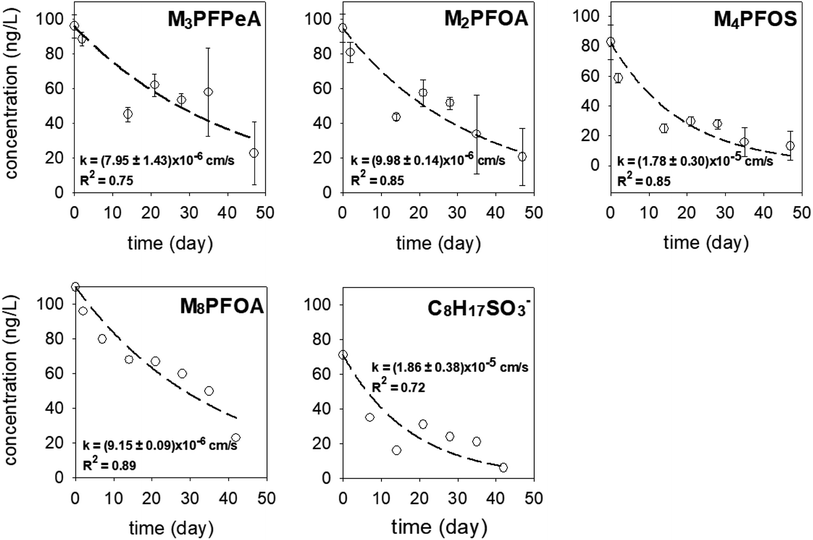 | ||
| Fig. 5 The concentration–time profile of the PRCs in the samplers deployed in the sediment at Lake Niapenco in October 2021 (M3PFPeA, M2PFOA, and M4PFOS) and June 2022 (M8PFOA and C8H17SO3−). | ||
The observed mass transfer coefficient values for PRCs in sediment-deployed samplers ranged between k = (7.95 ± 1.43) × 10−6 cm s−1 and (1.86 ± 0.38) × 10−5 cm s−1. Five notable observations emerge out of these k values. Firstly, the k values measured in samplers deployed in the field sediment were 6–20 fold less than those measured in aqueous solutions in the lab. This could be attributable to the slower diffusion of the analytes in the sediment and pore water matrix and/or the lower temperature in the field versus that of the laboratory (i.e., 10–15 °C versus 20 ± 1 °C). Because the PRCs were fully depleted from the samplers deployed in the water column, it is most likely that the sediment and pore water matrix physically impedes the diffusive process. Secondly, the k of M2PFOA ((9.98 ± 0.14) × 10−6 cm s−1) was comparable to that of M8PFOA ((9.15 ± 0.09) × 10−6 cm s−1), which is consistent with the fact that these two compounds are nearly identical. This also suggests that M8PFOA could be employed as a PRC in lieu of M2PFOA. Thirdly, the k of M4PFOS ((1.78 ± 0.3) × 10−5 cm s−1) and that of C8H17SO3− ((1.86 ± 0.38) × 10−5 cm s−1) were also comparable, consistent with the fact that these molecules consisted of the same functional group and carbon chain length. Thus, C8H17SO3− could potentially be used as a PRC in lieu of M4PFOS. Given that M4PFOS and M2PFOA are used as a non-extracted internal standard in several PFAS analytical methods, such as US EPA Method 533 (M2PFOA and M4PFOS) and Draft Method 1633 (M4PFOS),50,52 swapping M4PFOS with C8H17SO3− will enable the analysis of the receiving solution by these methods. The utility of C8H17SO3− as a PRC is further discussed in Section 3.5. Fourthly, the k of M3PFPeA ((7.95 ± 1.43) × 10−6 cm s−1) was the smallest among the measured values for PRCs for the field sediment deployed samplers. This is contrary to what was seen in the laboratory experiment in water (see the discussion in Section 3.2), as the k of M3PFPeA was the largest. One possible explanation for this discrepancy could be measurement variation. Note that the R2 associated with the regression of the M3PFPeA experimental data was the second lowest among the R2 values (Fig. 5). Finally, the k values (Table S5†) of PFOA ((3.8 ± 1.0) × 10−5 cm s−1), PFOS ((3.4 ± 0.9) × 10−5 cm s−1), and PFPeA ((3.0 ± 1.3) × 10−5 cm s−1) were 2–3.5 times higher than the k values of M2PFOA, M4PFOS, and M2PFPeA. This is rather surprising, given that the migration of the analytes into the sampler is expected to be slower than the migration of the PRC out of the sampler, due to the adsorption exchanges with the sediments outside of the sampler and the diffusion within the sediment pore being slower than the diffusion in the bulk solution.51
3.4 PFAS in sediment, sediment pore water, and lake water in October 2021
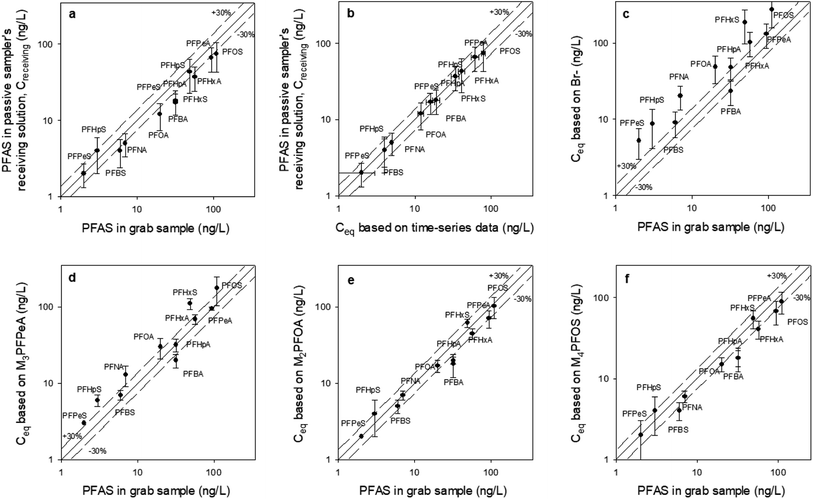 | ||
Fig. 6 The concentration of PFAS in mechanically extracted sediment pore water obtained adjacent to each passive sampler (x axis), compared to: (a) the concentration of PFAS measured in the receiving solution (Creceiving) of the sampler that was retrieved at day 47; (b) the equilibrium concentration (Ceq) predicted based on the time-series data from the samplers that were retrieved at days 2, 14, 21, 35, and 47 (see Fig. S4† for the time-series data and Table S5† for the Ceq values); and (c–f) the equilibrium concentration (Ceq), calculated based on Creceiving and four different PRCs. The solid lines are the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line, whereas the dashed lines represent the ±30% relative percent difference between the C values. All values used to generate this figure are presented in Table S6.† All passive samplers were deployed in the sediment at location A in October 2021. The data for locations B, C and D is presented in the ESI (Fig. S6–S8†). 1 line, whereas the dashed lines represent the ±30% relative percent difference between the C values. All values used to generate this figure are presented in Table S6.† All passive samplers were deployed in the sediment at location A in October 2021. The data for locations B, C and D is presented in the ESI (Fig. S6–S8†). | ||
At location A, RPD between Creceiving and Cgrab is ≤ ±30% except for a few compounds (i.e., PFOA, PFHpA, PFBA) (Fig. 6a), whereas RPD between Creceiving and Ceq based on time-series data is ≤ ±30% for all compounds (Fig. 6b; note that the data points in this figure are clustered around the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line). These results suggest that equilibrium had been established at the time of sampler retrievals (i.e., t = 47 days).
1 line). These results suggest that equilibrium had been established at the time of sampler retrievals (i.e., t = 47 days).
Time-series data is usually not collected in passive sampling practice. Instead, Ceq is estimated based on PRCs (as discussed in Section 2.4.2). As can be seen from Fig. 6c, the Ceq calculated based on Br− as the PRC was 1.4–3.7 times greater than Cgrab. This is in agreement with the laboratory observation, that is, Br− underpredicts the mass transfer coefficient of the PFAS analytes. That Br− predicts reasonably well the Ceq of PFBA, PFPeA, and PFBS (RPD = ±35%) of the PFBA concentration in the grab samples, which are the more hydrophilic PFAS, highlight the importance of selecting PRCs that are of similar physical/chemical properties to the analytes of interest. Based on this same argument, it is not surprising that the Ceq of PFBA, PFPeA, PFBS, PFPeS PFHxA, and PFHpA calculated based on M3PFPeA were ≤ ±35% of the concentrations measured in the grab samples, and that the RPD for the longer chain compounds were greater than 35% (Fig. 6d). The discrepancy between Ceq and Cgrab tends to be higher with the longer-chain analytes. For example, at location B the M3PFPeA-based Ceq was higher than Cgrab by 30% for PFHxA, 88% for PFOA, 50% for PFBS, and 164% for PFHxS, and 65% for PFOS.
With M2PFOA and M4PFOS as the PRCs (Fig. 6e and f), the Ceq values for C4–C7 perfluoro carboxylates were 15–55% smaller than the Cgrab values. This is also consistent with M2PFOA and M4PFOS being more hydrophobic than the C4–C7 perfluoro carboxylates. For the other compounds, Ceq was within ±30% of Cgrab, with a few exceptions: (1) at location D, Ceq for PFOA and PFOS were approximately 45% lower than Cgrab; (2) at location B, Ceq for PFHxS calculated based on M2PFOA was 40% greater than Cgrab; and (3) at location C, Ceq for PFHxS calculated based on M2PFOA was 85% greater than Cgrab, and Ceq for PFOS calculated based on M4PFOS was 67% greater than Cgrab. It is noted that while grab samples were collected at the places as closely as possible (i.e., within 50 cm) to where the passive samplers were deployed, the analyte concentrations in the grab and passive samples are not expected to be identical because sediment environments are generally highly heterogeneous. As such, some discrepancies between Ceq and Cgrab are likely. Overall, the results of this field study indicate that the equilibrium passive sampler with isotopically labelled PFAS as PRCs has the potential to be an effective tool for the monitoring of PFAS in sediment pore waters.
The time-series data collected at location A provides an opportunity to evaluate the variation in PRC-based Ceq among the samplers retrieved at different times. The Creceiving and the PRC-based Ceq values for each time point are presented in Table S7–S9.† The RPD values between Cgrab (in the grab sample collected on day 0) and PRC-based Ceq can be found in these same tables. Overall, there are some variations in Ceq among the samplers. Taking M4PFOS and PFOS as an example (Table S8†), the M4PFOS-based Ceq values for PFOS were 78 ng L−1 (with the sample retrieved on day 14, at which point [M4PFOS]/[M4PFOS]0 = 0.30), 101 ng L−1 (with the sample retrieved on day 21; [M4PFOS]/[M4PFOS]0 = 0.36), 109 ng L−1 (with the sample retrieved on day 21; [M4PFOS]/[M4PFOS]0 = 0.36), 106 ng L−1 (with the sample retrieved on day 35; [M4PFOS]/[M4PFOS]0 = 0.19), and 88 ng L−1 (with the sample retrieved on day 47; [M4PFOS]/[M4PFOS]0 = 0.16). With the Cgrab for PFOS being 110 ng L−1, the RPD varied between 1% (day 28) and 41% (day 14). A similar analysis was performed on M3PFPeA-based Ceq values for PFPeA, which reveals that the RPD values were 7% (day 14), 10% (day 21), 27% (day 28), 7% (day 35), and 33% (day 47). It is noted that these variations could be due to the heterogeneity of chemicals in sediments. As mentioned above, it was not possible to assume that all samplers for the various time points were exposed to the same concentration of PFAS in pore water. Therefore, the time-series results presented above should not be used as a basis for determining what the “optimum” deployment duration should be. Rather, it can be concluded that the sampler deployment period could range between 2 and 7 weeks.
As in the sediment pore water, PFOS, PFHxS and PFPeA were the predominant PFAS in the surface water at all four locations (Fig. 7). These three compounds were also the most abundant ones in the surface water samples collected in November 2020 (Table S1†). The concentrations of PFPeA and PFHxS ranged from 60–80 ng L−1 and 35–60 ng L−1, respectively, which are comparable to those in the sediment pore water (70–95 ng L−1 for PFPeA, and 45–65 ng L−1 for PFHxS). In contrast, the concentration of PFOS (60–80 ng L−1) in the surface water was slightly lower than that in the sediment pore water (75–130 ng L−1). PFOS is more hydrophobic than PFPeA and PFHxS and, therefore, is expected to have a higher affinity to sediments than the latter two compounds. It is interesting to note that the concentration of PFOS in October 2021 was over two times higher than that in November 2020 (∼65–80 ng L−1vs. 32 ng L−1), while the concentrations of other compounds were relatively similar.
3.5 PFAS in sediment pore water and lake water in June 2022
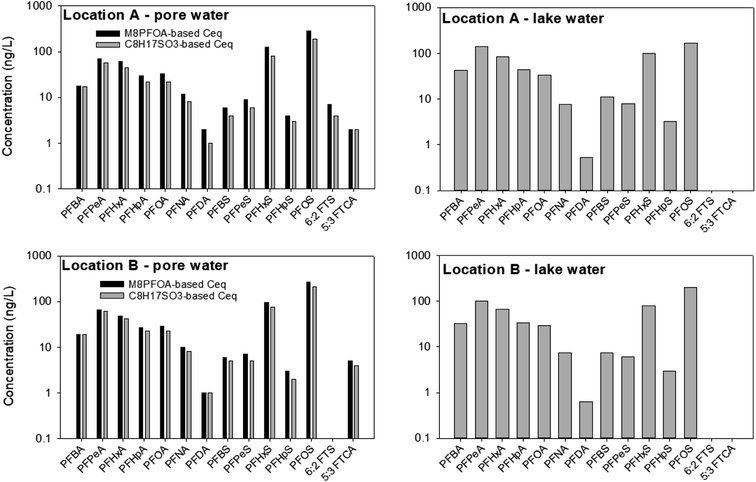
Similar to the first field experimental round, the PRC concentrations in the samplers deployed in the lake water in June 2022 were below the detection limits at retrieval. As such, whereas Ceq, calculated based on the PRCs, are presented for pore water samples, only the PFAS concentrations in the receiving solution are presented for the samplers deployed in the lake water (Fig. 8).In the sediment pore water, the Ceq of the PFAS calculated based on C8H17SO3− was 0–35% smaller than those calculated based on M8PFOA. The highest discrepancy (35% difference) between the Ceq predicted by C8H17SO3− and the Ceq predicted by M8PFOA was for PFHxS in sampler deployed at location A. On average among the PFAS and samples (Fig. 8), the difference in Ceq values estimated by the two PRCs was 22%. In the first field experiment (October 2021), the M4PFOS-based Ceq were also smaller than the M2PFOA-based Ceq, although to a lesser extent (0–15%). While the discrepancy between M8PFOA-based Ceq and C8H17SO3− based Ceq is slightly greater, considering general levels of measurement variability, together with the fact that the k values were comparable (as was discussed in Section 3.3), it is reasonable to conclude that C8H17SO3− could be used as a PRC.
Similar to what was seen in October 2021, PFOS, PFHxS, PFPeA were also the most abundant PFAS species. It is interesting to note that perfluorodecanoate (PFDA) and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 fluorotelomer carboxylate (5
3 fluorotelomer carboxylate (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 FTCA), which were not detected previously, were present in some samples (2–5 ng L−1) collected in June 2022. To the best of our knowledge, the presence of 5
3 FTCA), which were not detected previously, were present in some samples (2–5 ng L−1) collected in June 2022. To the best of our knowledge, the presence of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 FTCA, a PFAS precursor, at Lake Niapenco has not been documented previously. Given the historical use of AFFF in fire-fighting training activities upstream of Lake Niapenco, it is possible that other PFAS that were not measured in our and other studies might also be present in this area. In fact, the presence of a wide variety of PFAS precursors in the Welland River has been recently documented.53 Additional non-targeted analysis work to investigate the presence of other PFAS in Lake Niapenco, as well as which compounds can be detected by the passive sampler developed herein, is currently underway.
3 FTCA, a PFAS precursor, at Lake Niapenco has not been documented previously. Given the historical use of AFFF in fire-fighting training activities upstream of Lake Niapenco, it is possible that other PFAS that were not measured in our and other studies might also be present in this area. In fact, the presence of a wide variety of PFAS precursors in the Welland River has been recently documented.53 Additional non-targeted analysis work to investigate the presence of other PFAS in Lake Niapenco, as well as which compounds can be detected by the passive sampler developed herein, is currently underway.
Whereas the PFAS compositions in the two field experiments were not appreciably different, the total PFAS concentrations in the surface water samples collected in June 2022 were higher by as much as three times (∑PFAS = 643 ng L−1 (location A) and 565 ng L−1 (location B) in June 2022, versus 299 ng L−1 (location A) and 310 ng L−1 (location B) in November 2021). In contrast, there was less variation in the sediment pore water between the two seasons: the total concentrations (calculated based on M8PFOA) in the pore waters at locations A and B in June 2022 were 666 and 580 ng L−1, respectively, whereas the total concentrations (calculated based on M2PFOA) at these locations were 563 and 574 ng L−1 in November 2021. While determining the factors that drive the seasonal concentration change at Lake Niapenco was beyond the scope of this study, a possible explanation for the lower PFAS concentration in the lake in November 2021 might be that there was a dilution effect during this period, owing to the higher precipitation and water level in the lake. The total precipitations in the area around Lake Niapenco in October 2021 and June 2022 were approximately 170 mm and 80 mm, respectively. The water level in the lake was 1–2 feet higher in October 2021 than in June 2022.
4 Conclusion
In this work, we successfully developed and validated a simple and robust equilibrium passive sampler for the monitoring of PFAS in sediment pore water and surface water. This equilibrium passive sampler consists of a diffusion cell filled with water and a polycarbonate membrane, which serves as the receiving phase and the rate-limiting barrier, respectively. We demonstrated that sampler materials (i.e., the container, membrane, and sampler support materials) were inert with regards to the adsorption of PFAS that have ≤8, and that the uptake rate of the studied PFAS by this sampler can be described by Fick's law of diffusion. Therefore, the concentration of PFAS in the sampled medium can be readily calculated based on the PFAS concentration in the receiving phase and the mass transfer coefficient, which could be calculated by measuring the concentrations of the PRCs in the sampler prior to deployment and after retrieval. The use of PRCs allows pre-equilibrium sampling in sediment over a 14- to 28 day deployment period, which is much less than the approximately 42–49 days needed to attain 80% of equilibrium in the field sediment we evaluated. We demonstrated that the compounds with physical/chemical properties similar to those of the PFAS analytes of interest, such as isotopically labelled PFAS and 1-octanesulfonate, can be suitable as PRCs. Overall, the results for passive samplers deployed in surface water and sediment in the field site were in close agreement with grab surface water samples and grab samples of mechanically extracted pore water. This suggests that the passive sampling method corresponds to more conventional sampling methods, and, in the case of this site, PFAS in surface water and sediment were present in the dissolved/freely available phase. However, even in cases in which PFAS are present in the dissolved phase in surface water and sediment matrices (which should be evaluated at other sites), passive sampling may offer several advantages compared to conventional sampling methods. For example, passive sampling in sediment can also resolve difficulties and uncertainties associated with mechanical pore water extraction methods, which can be logistically impossible for some sediment types. Lastly, while this research focused specifically on PFAS in sediment pore water and surface water, we hypothesize that the developed equilibrium passive sampler could potentially be used to monitor PFAS in other low-flow environments, such as groundwater. Thus, additional research is needed to further assess the utility of this passive sampler. Additional research is also needed to assess if this passive sampler could be used for the monitoring of longer-chain compounds (i.e., compounds that have more than 10 carbons), which have been shown by McDermett et al. to have high adsorption affinity to the sampler components in their study.29 In regards to PFAS adsorption to surfaces, studies have shown that the tendency of PFAS to partition to surfaces increases as the ionic strength of the solution increases.54–56 Thus, additional study is needed to evaluate the adsorption of PFAS to the sampler components as well as the migration of PFAS into the sampler in solutions containing elevated concentrations of salts, as such a study would provide insights into the performance of the sampler in coastal areas.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding for this research was provided by Ontario Centres of Innovation (VIP Grants 33214 and 34511), and the Natural Sciences and Engineering Research Council of Canada (Discovery Grant #2022-03005). We thank the Niagara Peninsula Conservation Authority for permitting us to conduct field work at Lake Niapenco, and for providing the precipitation and water level data.References
- M. Evich, M. Davis, J. McCord, B. Acrey, J. Awkerman, D. Knappe, A. Lindstrom, T. Speth, C. Tebes-Stevens, M. Strynar, Z. Wang and E. Weber, Per- and polyfluoroalkyl substances in the environment, Science, 2022, 375(6580), aebg9065 CrossRef PubMed.
- T. Górecki and J. Namiesnik, Passive sampling, TrAC, Trends Anal. Chem., 2002, 21(4), 276–291 CrossRef.
- F. Salim and T. Górecki, Theory and modelling approaches to passive sampling, Environ. Sci.: Processes Impacts, 2019, 21(10), 1618–1641 RSC.
- P. Mayer, T. F. Parkerton, R. G. Adams, J. G. Cargill, J. Gan, T. Gouin, P. M. Gschwend, S. B. Hawthorne, P. Helm, G. Witt, J. You and B. I. Escher, Passive sampling methods for contaminated sediments: Scientific rationale supporting use of freely dissolved concentrations, Integr. Environ. Assess. Manage., 2014, 10(2), 197–209 CrossRef CAS PubMed.
- L. Ahrens, N. Yamashita, L. W. Yeung, S. Taniyasu, Y. Horii, P. K. Lam and R. Ebinghaus, Partitioning behavior of per- and polyfluoroalkyl compounds between pore water and sediment in two sediment cores from Tokyo Bay, Japan, Environ. Sci. Technol., 2009, 43, 6969–6975 CrossRef CAS PubMed.
- M. J. Lydy, P. F. Landrum, A. M. Oen, M. Allinson, F. Smedes, A. D. Harwood, H. Li, K. A. Maruya and J. Liu, Passive sampling methods for contaminated sediments: state of the science for organic contaminants, Integr. Environ. Assess. Manage., 2014, 10(2), 167–178 CrossRef CAS PubMed.
- R. M. Burgess, Guidelines for Using Passive Samplers to Monitor Organic Contaminants at Superfund Sediment Sites, U.S. Environmental Protection Agency, Washington, DC, 2012, EPA/600/R-11/115 Search PubMed.
- D. A. Alvarez, J. D. Petty, J. N. Huckins, T. L. Jones-Lepp, D. T. Getting, J. P. Goddard and S. E. Manahan, Development of a passive, in situ, integrative sampler for hydrophilic organic contaminants in aquatic environments, Environ. Toxicol. Chem., 2004, 23, 1640–1648 CrossRef CAS PubMed.
- C. Harman, I. J. Allan and E. L. M. Vermeirssen, Calibration and Use of the Polar Organic Chemical Integrative Sampler – A Critical Review, Environ. Toxicol. Chem., 2012, 31, 2724–2738 CrossRef CAS PubMed.
- J. K. Kingston, R. Greenwood, G. A. Mill, G. M. Morrison and B. L. Persson, Development of novel passive sampling system for the time-averaged measurement of a range of organic pollutants in aquatic environments, J. Environ. Monit., 2000, 2, 487–495 RSC.
- W. Davison and H. Zhang, Progress in understanding the use of diffusive gradients in thin films (DGT) – back to basics, Environ. Chem., 2012, 9(1), 1–13 CrossRef CAS.
- J. N. Huckins, G. K. Manuweera, J. D. Petty, D. Mackay and J. A. Lebo, Lipid-containing semipermeable-membrane devices for monitoring organic contaminants in water, Environ. Sci. Technol., 1993, 27, 2489–2496 CrossRef CAS.
- P. Gschwend, J. MacFarlane, D. Jensen, J. Soo, G. Saparbaiuly, R. Borrelli, F. Vago, A. Oldani, L. Zaninetta, I. Verginelli and R. Baciocchi, In Situ Equilibrium Polyethylene Passive Sampling of Soil Gas VOC Concentrations: Modeling, Parameter Determinations, and Laboratory Testing, Environ. Sci. Technol., 2022, 56, 7810–7819 CrossRef CAS PubMed.
- G. D. Johnson, Hexane-filled dialysis bags for monitoring organic contaminants in water, Environ. Sci. Technol., 1991, 25, 1897–1903 CrossRef CAS.
- P. R. Teasdale, G. E. Batley, S. C. Apte and I. T. Webster, Pore water sampling with sediment peepers, Trends Anal. Chem., 1995, 14(6), 250–256 CrossRef CAS.
- F. Y. Lai, C. Rauert, L. Gobelius and L. Ahrens, A critical review on passive sampling in air and water for per- and polyfluoroalkyl substances (PFASs), TrAC, Trends Anal. Chem., 2019, 121, 11531 CrossRef.
- S. L. Kaserzon, K. Kennedy, D. W. Hawker, J. Thompson, S. Carter, A. C. Roach, K. Booij and J. F. Mueller, Development and Calibration of a Passive Sampler for Perfluorinated Alkyl Carboxylates and Sulfonates in Water, Environ. Sci. Technol., 2012, 46, 4985–4993 CrossRef CAS PubMed.
- L. Gobelius, C. Persson, K. Wiberg and L. Ahrens, Calibration and application of passive sampling for per- and polyfluoroalkyl substances in a drinking water treatment plant, J. Hazard. Mater., 2018, 362, 230–237 CrossRef PubMed.
- S. L. Kaserzon, E. L. M. Vermeirssen, D. W. Hawker, K. Kennedy, C. Bentley, J. Thompson, K. Booij and J. F. Mueller, Passive sampling of perfluorinated chemicals in water: flow rate effects on chemical uptake, Environ. Pollut., 2013, 177, 58–63 CrossRef CAS PubMed.
- S. L. Kaserzon, D. W. Hawker, K. Booij, D. S. O'Brien, K. Kennedy, E. L. M. Vermeirssen and J. F. Mueller, Passive sampling of perfluorinated chemicals in water: in situ calibration, Environ. Pollut., 2014, 186, 98–103 CrossRef CAS PubMed.
- D.-X. Guan, L. Q. Ma, P. N. Williams and C. Y. Zhou, Novel DGT method with tri-metal oxide adsorbent for in situ spatiotemporal flux measurement of fluoride in waters and sediments, Water Res., 2016, 99, 200–208 CrossRef PubMed.
- Z. Fang, Y. Li, Y. Li, D. Yang, H. Zhang, K. C. Jones, C. Gu and J. Luo, Development and Applications of Novel DGT Passive Samplers for Measuring 12 Per- and Polyfluoroalkyl Substances in Natural Waters and Wastewaters, Environ. Sci. Technol., 2021, 55, 9548–9556 CrossRef CAS PubMed.
- P. Wang, J. K. Challis, K. H. Luong, T. C. Vera and C. S. Wong, Calibration of organic-diffusive gradients in thin films (o-DGT) passive samplers for perfluorinated alkyl acids in water, Chemosphere, 2021, 263, 128325 CrossRef CAS PubMed.
- S. L. Kaserzon, S. Vijayasarathy, J. Bräunig, L. Mueller, D. W. Hawker, K. V. Thomas and J. F. Mueller, Calibration and validation of a novel passive sampling device for the time integrative monitoring of per- and polyfluoroalkyl substances (PFASs) and precursors in contaminated groundwater, J. Hazard. Mater., 2019, 366, 423–431 CrossRef CAS PubMed.
- C. Gardiner, A. Robuck, J. Becanova, M. Cantwell, S. Kaserzon, D. Katz, J. Mueller and R. Lohmann, Field Validation of a Novel Passive Sampler for Dissolved PFAS in Surface Waters, Environ. Toxicol. Chem., 2022, 41(10), 2375–2385 CrossRef CAS PubMed.
- E. Dixon-Anderson and R. Lohmann, Field-testing polyethylene passive samplers for the detection of neutral polyfluorinated alkyl substances in air and water, Environ. Toxicol. Chem., 2018, 37(12), 3002–3010 CrossRef CAS PubMed.
- J. Becanova, Z. S. S. L. Saleeba, A. Stone, A. R. Robuck, R. H. Hurt and R. Lohmann, A graphene-based hydrogel monolith with tailored surface chemistry for PFAS passive sampling, Environ. Sci.: Nano, 2021, 8, 2894–2907 RSC.
- E. M. Kaltenberg, K. Dasu, L. F. Lefkovitz, J. Thorn and D. Schumitz, Sampling of freely dissolved per- and polyfluoroalkyl substances (PFAS) in surface water and groundwater using a newly developed passive sampler, Environ. Pollut., 2023, 318, 120940 CrossRef CAS PubMed.
- K. S. McDermett, J. Guelfo, T. A. Anderson, D. Reible and A. W. Jackson, The development of diffusive equilibrium, high-resolution passive samplers to measure perfluoroalkyl substances (PFAS) in groundwater, Chemosphere, 2022, 303, 34686 CrossRef PubMed.
- Z. Du, S. Deng, Y. Bei, Q. Huang, B. Wang, J. Huang and G. Yu, Adsorption behavior and mechanism of perfluorinated compounds on various adsorbents – a review, J. Hazard. Mater., 2014, 274, 443–454 CrossRef CAS PubMed.
- S. R. De Solla, A. O. De Silva and R. J. Letcher, Highly elevated levels of perfluorooctane sulfonate and other perfluorinated acids found in biota and surface water downstream of an international airport, Hamilton, Ontario, Canada, Environmental International, 2012, 39(1), 19–26 CrossRef CAS PubMed.
- S. B. Gewurtz, S. P. Bhavsar, S. Petro, C. G. Mahon, X. Zhao, D. Morse, E. J. Reiner, S. A. Tittlemier, E. Braekevelt and K. Drouillard, High levels of perfluoroalkyl acids in sport fish species downstream of a firefighting training facility at Hamilton International Airport, Ontario, Canada, Environmental International, 2014, 67, 1–11 CrossRef CAS PubMed.
- S. P. Bhavsar, C. Fowler, S. Day, S. Petro, N. Gandhi, S. B. Gewurtz, C. Hao, X. Zhao, K. G. Drouillard and D. Morse, High levels, partitioning and fish consumption based water guidelines of perfluoroalkyl acids downstream of a former firefighting training facility in Canada, Environmental International, 2016, 94, 415–423 CrossRef CAS PubMed.
- A. Ahmadireskety, B. F. da Silva, J. A. Awkerman, J. Aufmuth, R. A. Yost and J. A. Bowden, Per- and polyfluoroalkyl substances (PFAS) in sediments collected from the Pensacola Bay System watershed, Environ. Adv., 2021, 5, 100088 CrossRef CAS.
- S. Balgooyen and C. K. Remucal, Tributary Loading and Sediment Desorption as Sources of PFAS to Receiving Waters, ACS EST Water, 2022, 2(3), 436–445 CrossRef CAS.
- D. Mussabek, K. M. Persson, R. Berndtsson, L. Ahrens, K. Nakagawa and T. Imura, Impact of the Sediment Organic vs. Mineral Content on Distribution of the Per- and Polyfluoroalkyl Substances (PFAS) in Lake Sediment, Int. J. Environ. Res. Public Health, 2020, 17(16), 5642 CrossRef CAS PubMed.
- Y. Qi, S. Huo, B. Xi, S. Hu, J. Zhang and Z. He, Spatial distribution and source apportionment of PFASs in surface sediments from five lake regions, China, Sci. Rep., 2016, 6, 22674 CrossRef CAS PubMed.
- A. M. Becker, S. Gerstmann and H. Frank, Perfluorooctanoic acid and perfluorooctane sulfonate in the sediment of the Roter Main river, Bayreuth, Germany, Environ. Pollut., 2008, 156, 818–820 CrossRef CAS PubMed.
- A. K. Tokranov, D. R. LeBlanc, H. M. Pickard, B. J. Ruyle, L. B. Barber, R. B. Hull, E. M. Sunderland and C. D. Vecitis, Surface-water/groundwater boundaries affect seasonal PFAS concentrations and PFAA precursor transformations, Environ. Sci.: Processes Impacts, 2021, 23(12), 1893–1905 RSC.
- S. Lath, E. R. Knight, D. A. Navarro, R. S. Kookana and M. J. McLaughlin, Sorption of PFOA onto different laboratory materials: filter membranes and centrifuge tubes, Chemosphere, 2019, 222, 671–678 CrossRef CAS PubMed.
- M. Sörengård, V. Franke, R. Tröger and L. Ahrens, Losses of poly- and perfluoroalkyl substances to syringe filter materials, J. Chromatogr. A, 2020, 1609, 460430 CrossRef PubMed.
- C. E. Schaefer, D. Drennan, D. N. Tran, R. Garcia, E. Christie, C. P. Higgins and J. A. Field, Measurement of Aqueous Diffusivities for Perfluoroalkyl Acids, J. Environ. Eng., 2019, 1445(11), 1–4 Search PubMed.
- C. E. Schaefer, D. Drennan, A. Nickerson, A. Maizel and C. P. Higgins, Diffusion of perfluoroalkyl acids through clay-rich soil, J. Contam. Hydrol., 2021, 241, 103814 CrossRef CAS PubMed.
- L. A. Pereira, L. F. G. Martins, J. R. Ascenso, P. Morgado, J. P. P. Ramalho and E. J. M. Filipe, Diffusion Coefficients of Fluorinated Surfactants in Water: Experimental Results and Prediction by Computer Simulation, J. Chem. Eng. Data, 2014, 59(10), 3151–3159 CrossRef CAS.
- H. Zhang and W. Davison, Performance Characteristics of Diffusion Gradients in Thin Films for the in Situ Measurement of Trace Metals in Aqueous Solution, Anal. Chem., 1995, 67(19), 3391–3400 CrossRef CAS.
- M. A. Pétré, K. R. Salk, H. M. Stapleton, P. L. Ferguson, G. Tait, D. R. Obenour, D. R. U. Knappe and D. P. Genereux, Per- and polyfluoroalkyl substances (PFAS) in river discharge: modeling loads upstream and downstream of a PFAS manufacturing plant in the Cape Fear watershed, North Carolina, Sci. Total Environ., 2022, 20(831), 154763 CrossRef PubMed.
- M. A. Nguyen, K. Norström, K. Wiberg, J. Gustavsson, S. Josefsson and L. Ahrens, Seasonal trends of per- and polyfluoroalkyl substances in river water affected by fire training sites and wastewater treatment plants, Chemosphere, 2022, 308(Pt 3), 136467 CrossRef CAS PubMed.
- B. Thomas and M. A. Arthur, Correcting porewater concentration measurements from peepers: application of a reverse tracer, Limnol. Oceanogr.: Methods, 2010, 8, 403–413 CrossRef CAS.
- US EPA, Method 537.1: Determination of Selected Per- and Polyfluoroalkyl Substances in Drinking Water by Solid Phase Extraction and Liquid Chromatography/Tandem Mass Spectrometry (LC/MS/MS), 2018, https://cfpub.epa.gov/si/si_public_record_Report.cfm?dirEntryId=343042&Lab=NERL, accessed on 4 October 2022 Search PubMed.
- US EPA, Draft Method 1633: Analysis of Per- and Polyfluoroalkyl Substances PFAS, 2021 (PFAS) in Aqueous, Solid, Biosolids, and Tissue Samples by LC-MS/MS, 2021, https://www.epa.gov/system/files/documents/2021-09/method_1633_draft_aug-2021.pdf, accessed on 4 October 2022 Search PubMed.
- L. A. Fernandez, C. F. Harvey and P. M. Gschwend, Using performance reference compounds in polyethylene passive samplers to deduce sediment porewater concentrations for numerous target chemicals, Environ. Sci. Technol., 2009, 43(23), 8888–8894 CrossRef CAS PubMed.
- US EPA, Method 533: Determination of Per- and Polyfluoroalkyl Substances in Drinking Water by Isotope Dilution Anion Exchange Solid Phase Extraction and Liquid Chromatography/Tandem Mass Spectrometry, 2019, https://www.epa.gov/dwanalyticalmethods/method-533-determination-and-polyfluoroalkyl-substances-drinking-water-isotope, accessed on 4 October 2022 Search PubMed.
- L. A. D'Agostino and S. A. Mabury, Certain Perfluoroalkyl and Polyfluoroalkyl Substances Associated with Aqueous Film Forming Foam Are Widespread in Canadian Surface Waters, Environ. Sci. Technol., 2017, 51(23), 13603–13613 CrossRef PubMed.
- C. Y. Tang, F. Q. Shiang, D. Gao, C. S. Criddle and J. O. Leckie, Effect of solution chemistry on the adsorption of perfluorooctane sulfonate onto mineral surfaces, Water Res., 2010, 44(8), 2654–2662 CrossRef CAS PubMed.
- F. Xiao, X. Zhang, L. Penn, J. S. Gulliver and M. F. Simcik, Effects of monovalent cations on the competitive adsorption of perfluoroalkyl acids by kaolinite: experimental studies and modeling, Environ. Sci. Technol., 2011, 45(23), 10028–10035 CrossRef CAS PubMed.
- W. Wang, G. Rhodes, W. Zhang, X. Yu, B. J. Teppen and H. Li, Implication of cation-bridging interaction contribution to sorption of perfluoroalkyl carboxylic acids by soils, Chemosphere, 2022, 290, 133224 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2em00483f |
| This journal is © The Royal Society of Chemistry 2023 |