Investigating the electrocatalytic reduction of 2,4,6-tri-nitro-toluene (TNT) using density functional theory methods†
Andrew Jark-Wah
Wong
,
Joshua Lee
Miller
,
Brandon
Perdue
and
Michael John
Janik
 *
*
Department of Chemical Engineering, the Pennsylvania State University, University Park, PA, USA. E-mail: mjanik@psu.edu
First published on 25th May 2023
Abstract
2,4,6-Trinitrotoluene (TNT) degradation is of interest in environmental remediation, demilitarization, and national security. Electrochemical TNT reduction to 2,4,6-triaminotoluene is potentially energy efficient and operable at ambient conditions. Determining an elementary reduction mechanism and rate limiting steps is needed to rationally develop TNT electroreduction catalysts. Density functional theory methods determine the TNT reduction mechanism for non-catalyzed and late-transition metal catalyzed paths. The non-catalyzed mechanism is limited by slow initial NO2 group reduction. The outer-sphere mechanism is more competitive to electrocatalytic reduction on Au (111) and Fe (110) surfaces, which wasn't observed in our previous work on nitrobenzene electroreduction. An inverse tradeoff between the initial reduction of the NO2-R* group and reduction of surface hydroxyls suggests relative catalytic activity can be tuned by modulating O* affinity. Metal surfaces with intermediate O* affinity (Cu, Pt, Pd, and Ir) are predicted to be the most active late transition-metals towards TNT reduction. We extend our investigation to bimetallics and partially reduced Fe2O3 (0001) surfaces.
1. Introduction
2,4,6-Tri-nitro-toluene (TNT) is the most commonly utilized nitroaromatic compound as an explosive for military, construction, and mining applications.1,2 Extensive usage and production of TNT has led to the contamination of wastewater, resulting in the formation of toxic “pink water” and “red water”.3,4 Such wastewater sources are difficult to remediate and are harmful towards humans and the environment due to the toxic and mutagenic nature of TNT.5 Thus, TNT has been listed as a priority pollutant by the United States Environmental Protection Agency (USEPA) and the European Communities (EC).2,6 Degradation of TNT is also of high interest in demilitarization and security applications in identifying and neutralizing explosive ordinances in water sources.7Advanced oxidative, adsorption, photocatalytic, biodegradation, and electrochemical methods have been developed to remediate TNT. Advanced oxidation processes have been reported to degrade TNT using reagents such as O3, H2O2, zero valent Fe, and super critical water.8–11 Adsorptive removal of TNT on activated carbon has been performed.12,13 Photocatalytic methods degrade TNT on a TiO2 surface and in the presence of H2O2 and ferrous ions.7,14,15 Reduction of nitroaromatics (NO2-R) to the amine species (NH2-R) is another effective degradation approach due to the high electron affinity of the NO2 group. 2,4,6-Tri-amino-toluene (TAT) is the preferred reduced TNT intermediate due to its lower toxicity and ease to degrade.16 Biodegradation of TNT to TAT was performed and facilitated by the use of microorganisms and fungi.2,17
Electrochemical reduction methods are of high interest as a practical environmental remediation technology due to their potential energy efficiency, scalability, and ability to operate at ambient reaction conditions.18 The overall reaction of electrochemical TNT reduction to TAT is presented in Scheme 1.
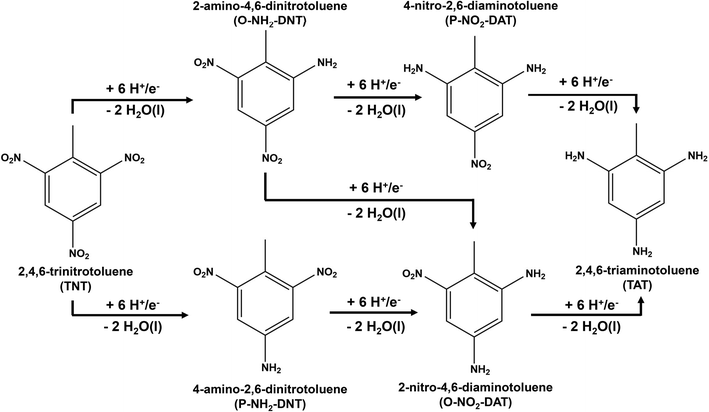 | ||
| Scheme 1 Overall reaction for the electrochemical reduction of 2,4,6-tri-nitro-toluene (TNT) to 2,4,6-tri-amino-toluene (TAT). | ||
Prior theoretical studies suggest that TNT reduction is limited by the initial activation of the NO2 group.19 This prior work suggests one NO2 group is reduced to R-NH2 before proceeding to reduce the next NO2 group. Initial TNT reductions occurs through a six H+/e− reduction by either reducing the ortho NO2 group to form 2-amino-4,6-dinitrotoluene (O-NH2-DNT) or the para NO2 group to form 4-amino-2,6-dinitrotoluene (P-NH2-DNT). Each TNT R-NO2 group is reduced to form the reduced amine intermediate and two H2O molecules. TNT is reduced electrochemically through an 18 H+/e− transfer to TAT, producing six H2O molecules.
Electrocatalysts are pivotal in the advancement of TNT electrochemical reductive methods. Electrochemical reduction of TNT has been performed over exfoliated graphene, alumina on a glassy carbon electrode (GCE), boron-doped graphene, and Au nanoparticles.20–23 In particular, Soomro et al. investigated the reduction of TNT on various shaped Pd, Pd–Pt alloys, and GCE, where three distinct reduction peaks are observed on all electrodes in the square wave voltammetry (SWV).24 Potentials for the three reduction peaks reported across different electrodes by Soomro et al. are converted to the reversible hydrogen electrode scale (RHE) and presented in Table 1.
| Electrode | Potential of 1st reduction peak (V-RHE) | Potential of 2nd reduction peak (V-RHE) | Potential of 3rd reduction peak (V-RHE) |
|---|---|---|---|
| Glassy carbon (GCE) | −0.10 | −0.27 | −0.39 |
| Pd nanocubes/GCE | −0.11 | −0.27 | −0.39 |
| Pd hollow nanosphere/GCE | −0.15 | −0.34 | −0.46 |
| Pd–Pt nano alloys/GCE | −0.19 | −0.35 | −0.47 |
Though higher current densities are observed for the Pd/Pt based electrodes, the reduction potentials of the three peaks of the Pd-based electrodes occur at similar overpotentials to the GCE reduction peaks. This questions the role of these Pd/Pt based electrodes in catalyzing the reaction, as an inner-sphere catalytic effect would be expected to reduce the overpotential relative to GCE, where outer-sphere reduction might be expected. The outer-sphere (non-catalyzed) reduction mechanism could be competitive to the inner-sphere (catalyzed) mechanism. If the reduction of TNT primarily undergoes an outer-sphere mechanism, the focus of electrode design can shift towards optimizing properties such as surface area, conductivity, and cost since the electrode's ability to catalyze the reaction only plays a minor role.
Determination of the elementary reaction mechanisms is needed to facilitate the design of active and selective electrocatalysts. Density Functional Theory (DFT) approaches are effective in screening electrocatalysts and determining the elementary reaction mechanisms at the atomistic scale.18,25,26 However, few theoretical studies investigated the electrochemical reduction of TNT. Chua et al. investigated the elementary step reduction mechanism of outer-sphere TNT reduction combining experimental and DFT results.19 Their DFT results predicted that the three experimental reduction peaks are due to the successive reduction of each NO2 group, each limited by the slow initial reduction of the R-NO2 species. Though their study thoroughly determined the elementary steps to reduce the first NO2 group of TNT to 2-amino-4,6-dinitro-toluene (O-NH2-DNT), only the first electron addition step onto each NO2 group was considered for the six and 12 H+/e− reduction intermediates. Theoretical TNT electrocatalysis studies have only studied the adsorption of TNT on Al-hydroxides, MgO (001), and Al (111) surfaces, leaving the elementary reduction mechanism on electrocatalytic surfaces to be determined.27–29 We previously used DFT methods to investigate the elementary step electrocatalytic reduction of a similar nitroaromatic, nitrobenzene (NO2-Phenyl) to aniline (NH2-phenyl), on monometallic and bimetallic surfaces.30 Monometallic and bimetallics that exhibit intermediate binding of O* are predicted to be the most active electrocatalysts for NO2-Phenyl reduction. To our knowledge, this study is the first to use DFT methods to investigate the elementary electrocatalytic reduction mechanism of TNT across different late transition-metal surfaces.
DFT methods are applied to determine the elementary reduction mechanism of TNT to TAT and its rate limiting step across different late transition-metal surfaces, bimetallics, and partially reduced Fe oxide surfaces. Both the outer-sphere and inner-sphere TNT reduction mechanisms are considered. First, the elementary step reduction mechanism of the non-catalyzed mechanism is investigated to determine its rate limiting steps. The reduction of TNT on the Fe (110) and Au (111) surfaces is then examined to determine the activity tradeoffs between two metal surfaces that exhibit differences in O binding affinity. Using the determined activity tradeoffs from Fe (110) and Au (111) surfaces, reaction energetics and activation barriers are evaluated across late transition-metal surfaces (Co, Ru, Rh, Ni, Ir, Pd, Pt, Ag, Au, and Fe). A “volcano” relationship is then determined to predict optimal TNT reduction electrocatalysts using the binding strength of O* as the surface descriptor. A limiting potential analysis is used to compare the overpotentials of the outer-sphere and catalyzed mechanism across different late transition-metal surfaces. Investigation from monometallic surfaces is then extended to bimetallic surfaces and partially reduced Fe2O3 (0001) oxide surfaces to screen potential TNT reduction electrocatalyst candidates.
2. Computational methods
2.1. Electronic structure calculations
DFT calculations of surface bound species were performed in the Vienna Ab Initio Simulation Program (VASP).31–34 Core-valence interactions were approximated by the projector augment wave (PAW) approach.35,36 Exchange and correlation energies was approximated by the Perdew, Burke, and Ernzerhof (PBE) generalized gradient (GGA) functional.37,38 An energy cutoff of 450 eV was used to approximate the plane wave basis set. Geometry optimizations were completed at an atomic force criterion of 0.05 eV Å−1. Dipole corrections were implemented in the direction normal to the surface (LDIPOL = .TRUE. and IDIPOL = 3). Dipole corrections in all directions were implemented for charged gas-phase species (IDIPOL = 4). Spin unrestricted calculations were performed for the Fe (110), Co (0001), Ni (111), Ni/Cu (111) surface, and all partially reduced Fe2O3 oxide surfaces. The Fe (110), partially reduced Fe2O3 (0001) and Ni/Fe2O3(0001) surfaces were optimized at a high initial spin state for the Fe and Ni atoms. The DFT+U method was implemented for the Fe2O3 (0001) surfaces to approximate the 3d-orbital localized electrons of the Fe atoms.39–41 Ovcharenko et al. showed that a value of Ueff = 4.0 eV was appropriate due to the lattice constant and band-gap values of the Fe2O3 (0001) showing good agreement with prior experimental work.42The VASPSol implicit solvation model was implemented to approximate the effects of solvation during TNT reduction.43,44 The default VASPSol parameters were utilized to model solution phase and surface calculations: a dielectric constant of the bulk solution of 78.4, cutoff charge density of 0.00025 e− Å−3, dielectric cavity width of 0.6 Å, and surface tension parameter of 0.525 meV Å−2. Transition states were determined through four linearly interpolated images from the Climbing Image Nudged Elastic Band method.45,46 First order saddles points of the transition states were confirmed with a vibrational frequency calculation.
DFT energies of solution phase species were also calculated in the Gaussian 16 computational package.47 All G16 calculated DFT energies include the zero-point vibration energy (ZPVE) and entropic corrections. The B3LYP exchange–correlation functional was used.48,49 The basis set used was the 6-311++ G(d,p).50,51 Solvation of solution phase species was modeled by using the integral equation formalism variant of the polarizable continuum model (IEFPCM).52 Water was modeled as the solvent using the default IEFPCM parameters.
2.2. Model construction
Energetics from VASP of isolated gas phase molecular species were modeled in a 15 Å periodic cubic unit cell. A 3 × 3 four-layer slab was used to model the BCC Fe (110) metal surface, where the bottom two layers were constrained, and the top two layers were relaxed.53 A 3 × 3 five-layer slab was used to model HCP Ru and Co (0001) metal surfaces, where the bottom three layers were constrained, and the top two layers were relaxed. A 3 × 3 five-layer slab was used to model FCC M (111) metal surfaces (M = Au, Ag, Cu, Pt, Pd, Ir, and Rh), where the bottom three layers were constrained, and the top two layers were relaxed. X/Cu (111) bimetallic surfaces (X = Pd, Ni, Ir, and Rh) are modeled as a 3 × 3 five-layer slab, where the top layer is replaced with X metal. The top two layers undergo surface relaxation while the bottom three layers are frozen. The partially reduced Fe2O3 (0001) oxide surfaces were modeled based on previous work by Maheshwari et al.54 as a 2 × 1 symmetric five layer surface slab, where a stoichiometric Fen–O3n–Fn is vertically stacked. Details in the model construction of the partially reduced Fe2O3 (0001) surface are further discussed in the study of Maheswari et al.54A 5 × 5 × 1 Monkhorst pack grid was used for most late transition-metal surfaces to sample the Brillouin zone.55,56 A 11 × 11 × 1 Monkhorst pack grid was used for the Au (111) surface. A 3 × 5 × 1 k-point mesh grid was used for all Fe2O3 (0001) surfaces.
2.3. Calculating potential dependent reaction energetics
Potential dependent DFT reaction energetics of TNT intermediates are calculated based on a similar procedure we used to previously study the electrocatalytic reduction of nitrobenzene (C6H5NO2(aq)). The electrochemical reaction to reduce TNT (C7H5N3O6(aq)) to any reduced intermediate is written in eqn (1):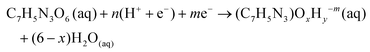 | (1) |
| ΔGred = GA + (6 − x)GH2O – GTNT − nGH++e− − mGe− | (2) |
The computational hydrogen electrode approach (CHE) was used to approximate the free energy of the coupled proton–electron pair using the free energy of hydrogen gas.57 By equating the chemical potential of half of a hydrogen molecule to the proton–electron pair and adding a linear electron energy correction relative to the reversible hydrogen electrode (RHE), the free energy of the coupled proton–electron pair is:
| GH++e− = ½GH2 − |e−|URHE | (3) |
The free energy of the uncoupled electron was approximated by the dependence of the electron on the applied electrode potential referenced on the normal hydrogen electrode (NHE) scale:
| Ge−(UNHE) = −|e−|UNHE−|e−|ΔUabs | (4) |
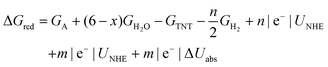 | (5) |
Surface catalyzed reaction energetics of TNT electrochemical reduction are calculated by modifying eqn (5)
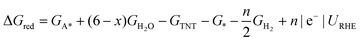 | (6) |
Free energies of reduction intermediates (A), either in the solution phase or bound to the metal surface (A*) were calculated as
| GA = EDFTA + EZPVEA − TSVibA | (7) |
Adsorption energies for surface bound species were defined by the standard definition as
| ΔEAdsorption = Especies* − Especies (aq) – E* | (8) |
| ΔEO*binding = EO* − ½EO2(g) − E* | (9) |
2.4. Potential dependent activation barriers
Surface bound TNT intermediates are reduced by approximating that a surface adsorbed proton (H*) species is along the reduction reaction path. Eqn (10) denotes the initial reduction of TNT by H* as an example, where N–O bond dissociation occurs upon reduction:| C7H5N3O6* + H* → C7H5N3O5* + OH*. | (10) |
Activation barriers calculated for eqn (10) are referenced to the equilibrium potential of H* (U0) on the respective metal surface. The potential of H* adsorption occurs at different (U0) across metal surfaces and a Butler–Volmer treatment was implemented to correct the potential dependent activation barrier to 0 V-RHE for comparison across metals.58
| ΔGTS(U) = ΔGTS(U0) + β(U − U0) | (11) |
3. Results and discussion
3.1. Outer-sphere reduction of TNT
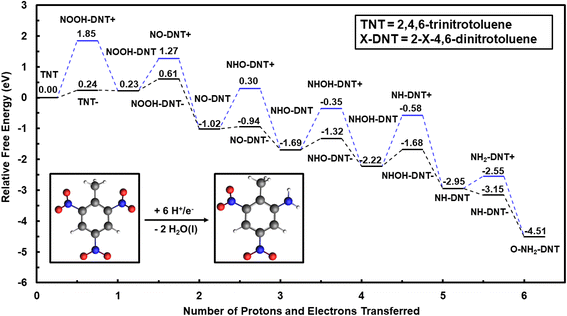
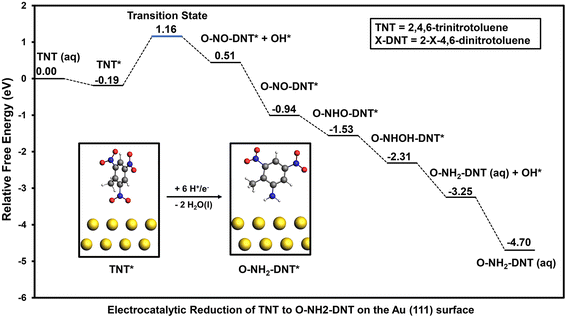
Outer-sphere reduction of TNT is considered through uncoupled and coupled H+/e− transfer, requiring the calculation of reaction free energetics of anion and cation species. Calculated solvation energies from the VASP/PBE/VASPSol and G16/B3LYP/IEFPCM are benchmarked with experimentally measured solvation energies for formate (CHO2−) and ammonium (NH4+) in Section S1.† G16/IEFPCM had greater agreement with experimentally measured solvation free energies for both anion and cation species when compared with VASP/VASPSol. Differences in DFT predicted solvation energies between the two codes are due to the implicit solvation treatment of solvent–solute interactions rather than the choice of the exchange–correlation functional. As a result, all outer-sphere reaction energetics from G16/B3LYP/IEFPCM are reported in the main text. The same energetics calculated with VASP/PBE/VASPSol are reported in Section S2.† Solvation energies of neutral species from both VASPSol and IEFPCM are very similar, validating that VASP/VASPSol is adequate for examining the energetics of coupled proton–electron transfers within the surface catalyzed process.Outer-sphere electrochemical reduction of TNT is initiated by reducing the ortho NO2 group to form 2-amino-4,6-dinitrotoluene (O-NH2-DNT) or the para NO2 group to form 4-amino-4,6-dinitrotoluene (P-NH2-DNT). The reaction free energy diagram for outer-sphere reduction of the ortho NO2 group of TNT to O-NH2-DNT at 0 V-NHE and pH = 0 is shown in Fig. 1. Optimized structures of reduced intermediates for the reduction of TNT to O-NH2-DNT are shown in Fig. S1.† The equilibrium potential for the reduction of the TNT to O-NH2-DNT is 0.76 V-NHE, such that the overall reduction reaction is thermodynamically favorable at 0 V-NHE. Both uncoupled and concerted proton–electron transfer are considered to reduce TNT through the outer-sphere mechanism.
We first consider reduction of TNT initiated by initial electron transfer. TNT (NO2-DNT) is reduced to TNT− (NO2-DNT−) anion species by initial electron addition, with an uphill reaction energy of 0.24 eV at 0 V-NHE. This initial addition of the electron on TNT could limit the rate for reduction of the first NO2 group. The TNT− anion species continues along the reduction path through protonation to NOOH-DNT species with a downhill energy of −0.01 eV at 0 V-NHE and pH = 0.
NO2 reduction can be, alternatively, initiated by proton addition to form the NOOH+-DNT cation species, resulting in a free energy change of 1.84 eV at pH = 0. The free energy change to undergo initial uncoupled proton transfer is significantly more uphill, indicating TNT initial reduction is likely to first proceed through uncoupled electron transfer or coupled proton–electron transfer.
Electron addition to reduce NOOH-DNT is less favorable than initial reduction of the NO2 group, with an uphill free energy change of 0.38 eV at 0 V-NHE. Subsequent reduction steps are generally more favorable once the NOOH-DNT− species is formed. Protonation of O-NOOH-DNT− forms a H2O molecule and O-NO-DNT with a highly favorable reaction energy change of −1.63 eV at 0 V-NHE and pH = 0. This procedure of uncoupled proton–electron transfer is repeated to further reduce O-NO-DNT to O-NH2-DNT. The most uphill reaction step is the electron addition to form NHOH-DNT− with a free energy change of 0.54 eV at 0 V-NHE. Initial reduction of NO2, NOOH, and NHOH show similar uphill reaction energies that can limit the overall rate and can be accelerated by an electrocatalyst. Once NHOH-DNT− is formed, all reduction steps are downhill in free energy to form the O-NH2-DNT species.
Outer-sphere reduction of TNT may proceed through coupled proton–electron transfer that can avoid less favorable decoupled reaction energetics. Considering all steps as coupling proton and electron transfer, the most uphill reaction step of TNT to O-NH2-DNT reduction is the reduction of TNT to O-NOOH-DNT with a free energy of 0.23 eV at 0 V-NHE. Once the O-NOOH-DNT intermediate is formed, all coupled proton–electron transfers are downhill to form O-NH2-DNT.
Initial reduction of TNT can be initiated through the para NO2 group to form P-NH2-DNT rather than the ortho NO2 group. Reduction of TNT to P-NH2-DNT is investigated through a similar procedure used to study the reduction of the ortho NO2 group. The reduction of the para NO2 is less favorable than the ortho NO2 group, with electron addition to reduce NHOH-DNT the most uphill step of 0.59 eV at 0 V-NHE. The reduction sequence of each NO2 group to the NH2 is qualitatively equivalent between the ortho and para NO2 group.
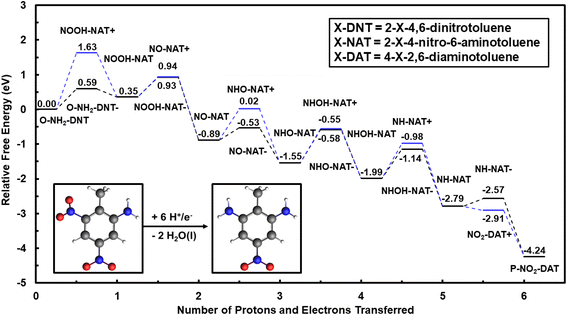
Once either the P-NH2-DNT or the O-NH2-DNT is formed, these NO2 species can be further reduced to obtain the 12 H+/e− species of either 4-nitro-2,6-diaminotoluene (P-NO2-DAT) or 2-nitro-4,6-diaminotoluene (O-NO2-DAT). The reduction of O-NH2-DNT species is first considered to form P-NO2-DAT. The reaction energy diagram to reduce O-NH2-DNT to P-NO2-DAT in the solution phase at 0 V-NHE and pH = 0 is shown in Fig. 2.
Reduction energetics of O-NH2-DNT are less favorable than equivalent TNT electroreduction steps. Considering the coupled reduction path, initial NO2 group reduction of O-NH2-DNT is again the least favorable step. This step is less favorable than initial TNT reduction by 0.25 eV at 0 V-NHE, suggesting higher overpotentials may be needed to drive the reduction of the second NO2 group. The inability of O-NH2-DNT to delocalize the negative charge across the NO2 groups makes electron transfer less favorable. The uncoupled reduction pathway is limited by initial NO2 reduction with an uphill energy of 0.86 eV at pH = 0, indicating that the lack of delocalization of the negative charge by the NO2 groups could make electron transfer more unfavorable.
Fig. S4† shows the reaction energy diagram for the reduction of P-NO2-DAT to TAT calculated with G16, completing the 18 e− reduction. The first electron transfer or the first coupled proton–electron transfer are again uphill in energy. These steps are progressively less favorable moving from TNT to O-NH2-DNT to P-NO2-DAT. Other than becoming less favorable for deeper reductions, the reaction paths for each NO2 group are equivalent.
Section S2† presents VASP optimized geometries and reduction reaction energetics of TNT intermediates, tables of all G16 and VASP energetics for the outer-sphere reduction.
Differences in the DFT predicted reduction potentials to reduce each NO2 group can rationalize the three experimentally observed TNT reduction peaks from Chua et al.19 Chua et al. predicted that the reduction of TNT is limited by the initial reduction of each NO2 group through a coupled proton–electron transfer. Table 2 reports the initial coupled proton–electron transfer reaction energy for each progressive NO2 group, using both the VASP and G16 computational codes with their respective continuum solvation models. Comparisons are made to the reduction potentials observed from Chua et al. from their DFT reaction energetics in Turbomole/PBE/COSMO and experimentally observed potentials on the glassy carbon electrode (GCE). The DFT calculations represent the electrode potential at which the reaction step is isoergonic, a rough approximation for comparison with experimental reduction peaks. Experimentally, the peak current density is a complex consequence of reduction reaction kinetics and species transport. Table 2 denotes the reduction potentials required to make each R-NO2 electron addition step isoergonic compared to experimental peak potentials on a GCE.
| Reduction potentials of TNT (V-NHE) | Reduction potentials of O-NH2-DNT (V-NHE) | Reduction potentials of P-NO2-DAT (V-NHE) | |
|---|---|---|---|
| Experimental: GCE | −0.31 | −0.475 | −0.629 |
| DFT (Turbomole/PBE/COSMO) | −0.108 | −0.265 | −0.369 |
| DFT(G16/B3LYP/IEFPCM) | −0.23 | −0.35 | −0.43 |
| DFT (VASP/PBE/VASPSol) | −0.23 | −0.51 | −0.60 |
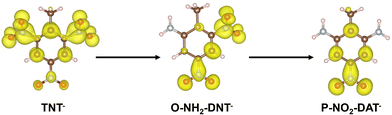
Electron densities of TNT intermediates during initial electron addition are shown in Fig. 3 to rationalize why TNT reduction becomes more unfavorable as each NO2 is successively reduced.
The electron added to form TNT− delocalizes over the three NO2 groups, residing more on the ortho NO2 groups than the para NO2. Conversion of each successive NO2 group to NH2 reduces the delocalization of this charge, leading to less favorable reduction.
The experimental and outer-sphere computational reduction potentials in Table 2 represent a significant overpotential for TNT reduction relative to our DFT-calculated equilibrium potential for TNT to TAT l of 0.70 V-NHE (with G16, 0.72 V-NHE with VASP). An electrocatalyst can potentially accelerate TNT reduction and reduce the large overpotentials by (1) stabilizing the negative charge of adsorbed TNT intermediates to facilitate coupled proton–electron transfer and (2) stabilizing adsorbed intermediates to open alternative reaction paths. Catalytic effects could become more significant as TNT reduction becomes more unfavorable with successive reduction of each NO2 group.
3.2. Electrocatalytic reduction of TNT on the Fe (110) surface
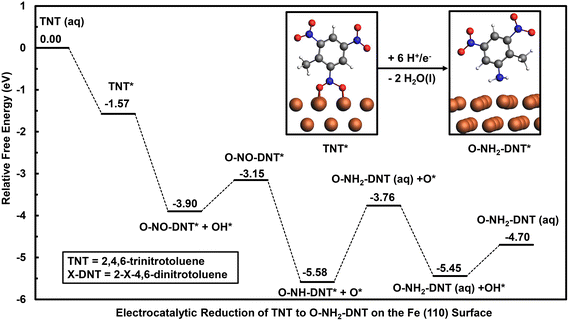
Adsorption and reduction of TNT on the Fe (110) surface was investigated to study the NO2 reduction chemistry on a metal surface that exhibits a high oxophilicity. TNT can be initially adsorbed in the “flat configuration”, where the carbon ring is parallel to the surface, or through a “vertical configuration”. Differentiating which configuration would be preferred at an electrode surface is challenging given the convergence of several aspects that are hard to capture in a DFT model. The differential solvation of the solution and surface bound species will impact preferred adsorption configurations and is challenging to represent at the surface. The PBE functional neglects van der Waals (vdW) interactions that could also differ significantly between the two configurations. These vdW interactions could also occur among adsorbates, whereas a single coverage is used neglecting the likely strong coverage dependence on adsorption energies. We, therefore, consider initial adsorption in the “vertical” configuration because this allows the NO2 group to directly interact with the surface for further reduction. This configuration requires less solvent-surface displacement and is likely preferred at higher adsorbate coverages. Our prior DFT results on nitrobenzene on Fe (110) and Au (111) surfaces predicted that vertical configuration would be preferred over the flat configuration at higher surface coverages. Preferred adsorption configurations of TNT on the Fe (110) surface in the vertical and flat adsorption configuration are shown in Section S3.†The initial reduction of TNT is first investigated through the adsorption and reduction of the ortho NO2 group and in the vertical configuration. The reaction energy diagram of the electrocatalytic reduction of TNT to O-NH2-DNT on the Fe (110) surface at 0 V-RHE is shown in Fig. 4. Optimized geometries of reduced intermediates during the reduction of TNT to O-NH2-DNT on the Fe (110) surface are shown in Section S3.†
Reduction is initiated by favorable adsorption of TNT on the Fe (110) surface with an adsorption energy of −1.57 eV. The Fe (110) surface is active for the initial reduction of the NO2-DNT* to O-NO-DNT* + OH*, resulting in the spontaneous N–O dissociation during geometry optimization and a reaction energy of −2.33 eV at 0 V-RHE. The transition state for R-NO2 + H* to R-NOOH was found to have a free energy barrier of 0.01 eV at U = 0.66 V-RHE, suggesting this step is barrierless at reducing overpotentials. Thus, the Fe (110) surface is predicted to accelerate the initial reduction step of the NO2 group compared to the non-catalyzed mechanism.
Though the Fe (110) surface accelerates initial TNT reduction, it is limited by the unfavorable reduction of strongly bound O* and OH* intermediates. Reduction of OH* to H2O(l) is unfavorable with a reaction free energy of 0.76 eV at 0 V-RHE, requiring a highly reductive overpotential to reduce OH* off the surface. Reduction of O-NO-DNT* proceeds favorably to O-NH-DNT* + O* due to the spontaneous N–O bond dissociation observed. This reaction step results in a free energy of −2.17 eV at 0 V-RHE. O-NH-DNT* is further reduced to form O-NH2-DNT (aq), which is an isoergonic reaction. O* is finally reduced to OH* then to H2O (l), resulting in respective free energy changes of 0.16 eV and 0.76 eV at 0 V-RHE.
Though the Fe (110) surface is predicted to accelerate the initial reduction of TNT, TNT reduction on the Fe (110) is limited by the reduction OH* with a free energy change of 0.76 eV. The Fe (110) surface is predicted to bind surface hydroxyl too strongly, blocking the surface as the reduction of these intermediates limits the overall reaction. Thus, the Fe (110) surface would not be an ideal electrocatalyst, binding intermediates too strongly.
Reduction beginning from the flat adsorption configuration as well as beginning with the para NO2 group are reported and discussed in Section S3† and show qualitatively similar results.
Once the first NO2 group is reduced, O-NH2-DNT (aq) can adsorb on the Fe (110) surface either through the para NO2 group to reduce to O-NO2-DAT or the ortho NO2 group to reduce to P-NO2-DAT. Reaction free energy diagrams and optimized geometries for intermediates on the Fe (110) surface are shown in Section S3.† Unlike the outer-sphere process, the reaction energies required to reduce each NO2 group of TNT to TAT are similar as the reaction proceeds, suggesting inner-sphere catalysis may avoid the need for successively larger overpotentials to reduce each NO2 group. However, we conclude the highly oxophilic Fe catalyst would be limited by OH* reduction in the potential range where TNT reduction is desired.
We next consider reduction catalyzed by the less oxophilic Au (111) surface, and we later return to consider whether oxidized forms of Fe could serve as an active TNT electroreduction catalyst.
3.3. Electrocatalytic reduction of TNT on the Au (111) surface
Adsorption and reduction of TNT was investigated on the Au (111) surface to compare elementary reduction energetics on a metal surface that exhibits weak binding of O*. The optimized adsorption configuration of TNT in the vertical and flat configurations are shown in Section S4.† Adsorption of TNT is much weaker on the Au (111) surface than the Fe (110) surface; calculated adsorption energies on the Au (111) surface in the vertical and flat configuration are −0.19 eV and −0.34 eV, respectively. Weaker adsorption of TNT will result in slower initial activation of the NO2 groups, thus limiting the activity of the Au (111) surface towards TNT reduction. Similar to the Fe (110) surface, reduction from the vertical adsorption configuration of the NO2 group was initially investigated. The reaction energy diagram of the electrocatalytic reduction of TNT to O-NH2-DNT on the Au (111) surface is shown in Fig. 5.Initial reduction of TNT results in the formation of O-NO-DNT* + OH* on the Au (111) surface, which is more stable than O-NOOH-DNT*. Unlike the Fe (110) surface, the reduction of the first NO2 group of TNT on the Au (111) surface to form co-adsorbed O-NO-DNT* + OH* occurs over a high energy barrier. The activation barrier and reaction free energy for this reaction step at 0 V-RHE is 1.35 eV and 0.70 eV, respectively. The Au (111) surface would not be an optimal TNT electrocatalyst, as it is predicted to be relatively inactive towards NO2-R reduction. Once O-NO-DNT* is formed, all subsequent reduction steps at 0 V-RHE proceed downhill to form O-NH2-DNT (aq) and H2O (l), including favorable reduction of surface adsorbed O* and OH* species.
In contrast to the Fe (110) surface, the activity of the Au (111) surface is limited by the initial NO2 reduction due to the high activation barrier and unfavorable reaction energy. When comparing TNT reduction on the Au (111) surface with the outer-sphere reduction mechanism, it is unlikely that Au (111) would accelerate the TNT reduction due to the significant reductive potential required (−0.70 V-RHE) to overcome the initial reduction of the first NO2 group.
Structures and reaction energetics of all reduction intermediates for initial reduction in the flat configuration as well as the para NO2 group are included in Section S4.†
3.4. Comparing outer-sphere TNT reduction vs. inner-sphere on Au (111) and Fe (110)
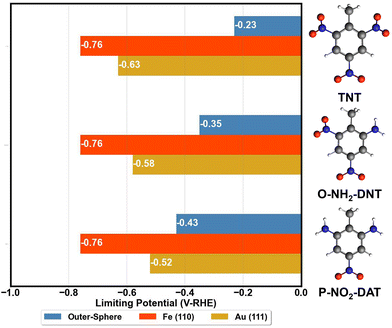
The activity of surfaces to reduce TNT is approximated by determining the limiting potential, the potential for ΔGred ≤ 0 for all reduction reactions. Limiting potentials required to reduce TNT to TAT on the Fe (110) and Au (111) surface are summarized in Fig. 6. The reduction of TNT to TAT is considered to proceed through the O-NH2-DNT and P-NO2-DAT intermediates. Fig. 6 compares these surface energetics with the outer-sphere energetics from Table 2.TNT reduction in the solution phase is potentially competitive for the reduction of the first NO2 group with the Fe (110) and Au (111) surfaces, suggesting neither of these will successfully serve as electrocatalysts for this reaction. The TNT outer-sphere reduction is competitive with the inner-sphere reduction on Fe (110) and Au (111), contrasting our prior analysis of nitrobenzene reduction. We emphasize that our DFT analysis has limitations due the mainly thermodynamic nature in calculating the reaction energetics and our approximation of the electrode–electrolyte interface. Despite these limitations, the DFT energetics are in line with experimental observation that TNT electroreduction occurs at overpotentials of 1 V or more, and the reduction peak positions appear to be independent of electrode composition among the electrodes tested.
We hypothesize that surfaces with intermediate O* binding might better accelerate TNT electroreduction, relative to the Fe (110) surface binding O*/OH* too strongly, and Au(111) surface being limited by weak bonding and activation of the NO2 group in TNT.
3.5. Electrocatalytic reduction of TNT on late transition-metal surfaces
The Fe (110) and Au (111) surfaces are predicted to not accelerate TNT reduction when compared to the outer-sphere reduction process. However, these surfaces illustrate activity tradeoffs that can be used to screen late transition metal surfaces. O* binds too strongly on the Fe (110) surface and the activity of the surface is limited by the desorption of strongly bound OH*. In contrast, O* binds too weakly on the Au (111) surface, where initial activation of the NO2 group is unfavorable. The two limiting reduction processes, NO2-R* to NO-R* + OH* and OH* to H2O (l), are expected to inversely correlate with the strength of O* binding. A similar trend is observed in our previous study for the electrocatalytic reduction of nitrobenzene.30 Our prior work predicted that late transition-metal surfaces that exhibit intermediate O* affinity balance these activity tradeoffs, thus exhibiting higher activity towards nitrobenzene reduction.Late transition metal surfaces are screened as potential TNT electrocatalysts using O* binding as a descriptor. A correlation is established between the reaction energies for the two key elementary steps and O* binding strength, using monometallic surfaces. The investigation is then extended to bimetallics (X/Cu (111) skin alloy surfaces) in section 3.5.1. Lastly, partially reduced Fe2O3 (0001) oxide surfaces, with and without Ni doping, are considered, emphasizing whether these surfaces can deviate from the scaling relationship between O* binding and key reaction energetics to possibly enable TNT electroreduction at lower overpotentials.
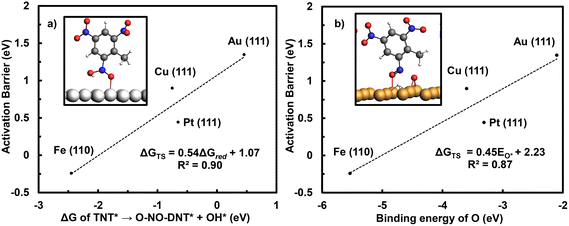
The initial reduction of TNT to O-NO-DNT is evaluated across M late transition-metal surfaces (M = Ag (111), Cu (111), Pd (111), Pt (111), Ir (111), Rh (111), Ni (111), Ru (0001, and Co (0001)), recognizing that subsequent inner-sphere reduction energetics of the other NO2 groups were similar on Fe (110) and Au (111) surfaces. To accelerate the screening of metal surfaces, Brønsted–Evans–Polanyi (BEP) plots were constructed to correlate activation barriers and reaction energetics for the initial TNT reduction step. Activation barriers of O-NO2-DNT* to O-NO-DNT* at 0 V-RHE were calculated on the Fe (110), Cu (111), Pt (111), and Au (111) surfaces. Fig. 7 presents these activation barriers plotted against both the reaction energetic of the same step and the binding strength of O* on the metal.
Fig. 7a shows a strong correlation between the activation barrier and reaction energy for the initial TNT reduction elementary step. This allows us to expedite the screening of M late transition-metal surfaces by calculating reaction energies of NO2-R* to NO-R* + OH*. Fig. 7b shows that stronger binding of O on the metal surface correlates directly with lower activation barriers for this same step. Metal surfaces that have a strong affinity towards O*, such as the Fe (110) surface, exhibit a lower activation barrier towards activating the NO2 group. Previous DFT studies have shown that the activation barriers for OH* to H2O (aq) correlate strongly with the reaction energy on late transition-metal surfaces.57,59
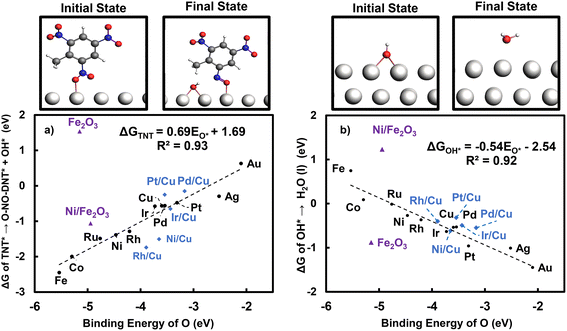
Fig. 8 shows the correlation of the key step reaction energies with O* binding across monometallic and bimetallic surfaces.
A qualitative “volcano-tradeoff” is established with the O* binding energy. Fig. 8a shows that metal surfaces with stronger O* affinity are more active in initially reducing the NO2 group. Fig. 8b shows that reduction of OH* to H2O (aq) becomes more unfavorable as the binding of O* becomes stronger. As the O* binding energy on close-packed surfaces is well-established to correlate with the surface d-band center,60 connecting TNT reduction catalysis to O* binding also connects catalyst optimization to selection of a surface offering an optimal d-band center. Optimized structures and tables of values used to construct Fig. 8 are presented in Table S24 and Fig. S27.†
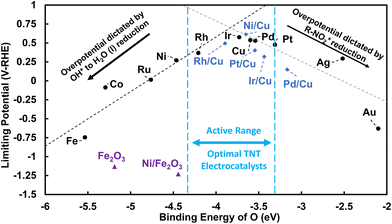
Since our DFT model approximates the electrochemical interface, we can only approximate an optimal O binding energy that might correlate with the “peak” of the volcano plot with DFT alone. A more detailed coupling of experimental and microkinetic analysis would be needed to more precisely locate a peak. However, the qualitative volcano relationship presented can be utilized for experimental guidance to tune monometallic or bimetallic late transition-metal surfaces to an intermediate O* affinity, which are predicted to balance both activity tradeoff reactions. The limiting potential of each metal surface is determined to predict the theoretical overpotential required to reduce TNT and to compare the relative activity of each late transition-metal surface.57 A plot of the limiting potentials plotted against the binding energy of O across late transition-metal surfaces is shown in Fig. 9.
Metal surfaces that exhibit more positive limiting potentials are predicted to require a lower overpotential to reduce TNT to O-NO2-DNT, and thus have higher relative activity. Weak O* affinity monometallic metal surfaces, such as the Au (111) and Ag (111) surfaces, exhibit a lower limiting potential and are predicted to require a larger overpotential to activate the NO2 group. Late transition-metal surfaces with strong O* affinity, such as Fe (110) and Co (0001) surfaces, require larger overpotentials to reduce strongly bounded intermediates that inhibit their overall activity. A peak in our limiting potential plot represents optimal monometallic metal surfaces in the active range for TNT reduction due to their intermediate binding of O*. These monometallic surfaces, such as Pt (111), Pd (111), Cu (111), and Ir (111) surfaces, are predicted to accelerate the inner-sphere reduction of TNT.
We emphasize that Fig. 9 is useful for qualitative comparison for monometallic surfaces and their relative activity. However, values of DFT predicted binding of O* and limiting potentials can shift due different approximations within our model to capture the electrode–electrolyte environment. There are several limitations within our models when modeling electrocatalysis. (1) A relative permittivity value of 78.4 for bulk water is used in the DFT solvation model, which is likely not representative of interfacial water near the electrode (values of 2 to 9 have been reported61,62), (2) displacement of explicit H2O molecules upon TNT adsorption, which VASPSol does not capture, is not considered.63 (3) VASPSol implicit solvation approximates that solvation energies are nearly identical across metal surfaces while hybrid DFT/molecular dynamic approaches states that solvation is strongly dependent on the metal identity.64 (4) More complex EDL effects including ion/electric field distribution could impact stability of surface bound intermediate species differently across metals. For instance, McCrum et al. showed that the modeling of OH* adsorption on different facets of the Pt are sensitive to the choices of how solvation and coverage are modeled, resulting in differences in OH* adsorption potential by 0.6 V-NHE on the Pt (111) surface.65 Zhang et al. recently observed sensitivity of resulting oxygen reduction reaction (ORR) volcano plots to how solvation was modeled (implicitly, explicitly, and with a bilayer solvation correction) on late transition metal (111) surfaces.66 If our current model is underestimating the effects of solvation on OH adsorption, this affects the ΔG of OH* to H2O (l) and NO2-R* to NO-R* and OH*, which could shift the peak of the volcano plot and its optimal O* binding towards weaker O* binding metals such as the Ag (111) surface. Fig. 9 can be used to qualitatively assess the relative activities of late transition-metal surfaces. We suggest additional controlled experimental studies that compare GCE with late transition-metal electrodes that exhibit varying degrees of O* affinity (Fe (110), Cu (111), and Au (111) surfaces) to determine whether the “volcano relationship” and activity trends hold.
As the O* binding energy is serving as a reasonable descriptor of limiting potential, previously published values can be used to computationally screen potential TNT electroreduction catalysts. The binding energy of O for 736 different metal surface alloys are reported by Greeley et al.72 Table S25† reports 210 of the 736 surfaces with O* binding energies in the active range for TNT reduction. 107 of these 210 surfaces are composed of the four recommended (111) monometallic surfaces (Pt, Pd, Cu, and/or Ir). Bimetallic surfaces containing Ag, Au, Ni, Rh, and/or Ru also appear in the active range for TNT reduction, suggesting that these surface alloys may be more active than their monometallic counterparts. Bimetallics that include metals we did not consider, such as Bi, Cd, Sb, and/or As also appear in the active range. Collectively, we have highlighted several monometallic and bimetallic surfaces that could show improved TNT electroreduction catalysis relative to those previously studied experimentally.
The (0001) surface of hematite, α-Fe2O3, is investigated as a potential TNT electroreduction catalyst. Iron oxide has been utilized as an electrocatalyst for N2 reduction and solar water splitting.22,80,81 A previous DFT study by Maheswari et al. investigated the stability of different partially reduced terminations of the Fe2O3 (0001) surface at reducing potentials by generating a surface Pourbaix diagram.54 Partially reduced terminations are predicted to be stable at potentials below 0 V-RHE, where the bulk remains Fe2O3 (0001). The H–Fe–Fe–O2–Fe–R partially reduced termination (partially reduced Fe2O3 (0001) surface) was selected to study as a possible TNT reducing surface due to its predicted stability in more negative reducing potentials on the surface Pourbaix diagram.
Ni–Fe oxides are well known as stable oxidation electrocatalysts for the oxygen evolution reaction (OER).82–84 Though the stability of these Ni-doped Fe2O3 (0001) structures at reducing potentials are not established, doping of Ni on the partially reduced Fe2O3 (0001) surface (Ni/Fe2O3 (0001) surface) was investigated to explore if Ni-doping could further increase the activity for TNT reduction, and to examine whether such doping would follow the same “volcano tradeoffs” observed for bimetallic surfaces. Ni doping was considered by substituting a surface Fe atom with an Ni atom. Fig. S29 and S30† depicts the surface model and the most stable adsorption configuration of TNT on the partially reduced Fe2O3 (0001) and Ni/Fe2O3 (0001) surfaces.
The key elementary reaction energies for TNT reduction on the partially reduced Fe2O3 (0001) and Ni/Fe2O3 surface are included in Fig. 8. Both oxide surfaces deviate from scaling relationships defined for monometallics. The Fe2O3 (0001) surface exhibits strong binding of O* with binding energy of −5.19 eV, weaker than Fe (110) by 0.38 eV. However, the Fe2O3 (0001) surface is predicted to be inactive towards reduction of the NO2 group, with a free energy change of 1.54 eV, which significantly deviates from the activity trends predicted from monometallics. The Ni/Fe2O3 (0001) surface also deviates from scaling relationships derived in section 3.5. Substitution of one surface Fe atom with Ni weakens O* binding by 0.21 eV. However, the Ni/Fe2O3 (0001) surface is more active towards activating the NO2 group. The Ni/Fe2O3 (0001) surface is predicted to be less favorable towards OH* reduction than the undoped surface, despite weaker binding of O*.
The Fe2O3 and Ni-doped Fe2O3 (0001) surfaces have potential to deviate from scaling relationships derived from monometallics and expand the design space for electrocatalysts for TNT reduction. It is not especially surprising that correlations between O* binding and TNT reduction energetics among close-packed late transition metals do not directly apply on the oxide surfaces. TNT, O-NO-DNT, and OH adsorbates interact with more localized states on the oxide surface than the delocalized d-band of the extended metals, and adsorption geometries (see Fig. S30†) also differ on the oxides. We recommend further investigation of the activity and stability of these Ni doped Fe2O3 (0001) surfaces to fully assess these surfaces as TNT reduction electrocatalysts. A more extensive investigation on other oxophilic metals that may be stable oxides at TNT reduction conditions, such as Cu and Ni based oxides, would be beneficial in the search for reduction electrocatalyst candidates.85–88
4. Conclusions
This study utilized DFT methods to investigate the elementary step mechanisms for TNT electrochemical reduction in the solution phase and across different late transition metal surfaces. Outer sphere reduction energetics suggests that the non-catalyzed TNT reduction pathway is much more competitive with inner sphere mechanism on Fe (110) and Au (111) surfaces than our prior work on nitrobenzene. Overall activity for monometallic and bimetallic surfaces is dictated by a trade-off in initial activation of the NO2 group and reducing OH*. Though our DFT analysis is mainly thermodynamic focused, both monometallic and bimetallics are recommended that may accelerate the activity of TNT electroreduction. Results on partially Fe2O3 (0001) surfaces suggest that oxides may not follow the same scaling relationships. We suggest further exploration of both the activity of oxide surfaces and bimetallic surfaces in reducing conditions as catalysts for TNT electroreduction.Conflicts of interest
The authors declare no competing interest.Acknowledgements
We acknowledge computational support from the Extreme Science Engineering Discovery Environment (XSEDE), supported by the National Science Foundation (NSF) under grant ACI-1548562.References
- K. S. Ju and R. E. Parales, Nitroaromatic Compounds, from Synthesis to Biodegradation, Microbiol. Mol. Biol. Rev., 2010, 74(2), 250–272 CrossRef CAS PubMed.
- A. Esteve-Núñez, A. Caballero and J. L. Ramos, Biological Degradation of 2,4,6-Trinitrotoluene, Microbiol. Mol. Biol. Rev., 2001, 65(3), 335–352 CrossRef PubMed.
- M. Barreto-Rodrigues, F. T. Silva and T. C. B. Paiva, Combined zero-valent iron and Fenton processes for the treatment of Brazilian TNT industry wastewater, J. Hazard. Mater., 2009, 165(1), 1224–1228 CrossRef CAS PubMed.
- A. J. Beck, M. Gledhill, C. Schlosser, B. Stamer, C. Böttcher and J. Sternheim, Spread, Behavior, and Ecosystem Consequences of Conventional Munitions Compounds in Coastal Marine Waters, Front. Mar. Sci., 2018, 5, 141 CrossRef.
- P. Leffler, E. Brännäs, D. Ragnvaldsson, H. Wingfors and R. Berglind, Toxicity and accumulation of trinitrotoluene (TNT) and its metabolites in Atlantic salmon alevins exposed to an industrially polluted water, J. Toxicol. Environ. Health, Part A, 2014, 77(19), 1183–1191 CrossRef CAS PubMed.
- O. Chusova, H. Nõlvak, M. Odlare, J. Truu, M. Truu and K. Oopkaup, et al., Biotransformation of pink water TNT on the surface of a low-cost adsorbent pine bark, Biodegradation, 2015, 26(5), 375–386 CrossRef CAS PubMed.
- E. Sisco, M. Najarro, C. Bridge and R. Aranda, Quantifying the degradation of TNT and RDX in a saline environment with and without UV-exposure, Forensic Sci. Int., 2015, 251, 124–131 CrossRef CAS PubMed.
- S. Y. Oh, P. C. Chiu, B. J. Kim and D. K. Cha, Enhancing Fenton oxidation of TNT and RDX through pretreatment with zero-valent iron, Water Res., 2003, 37(17), 4275–4283 CrossRef CAS PubMed.
- K. Ayoub, E. D. van Hullebusch, M. Cassir and A. Bermond, Application of advanced oxidation processes for TNT removal: A review, J. Hazard. Mater., 2010, 178(1–3), 10–28 CrossRef CAS PubMed.
- M. E. Fuller, C. E. Schaefer and J. M. Lowey, Degradation of explosives-related compounds using nickel catalysts, Chemosphere, 2007, 67(3), 419–427 CrossRef CAS PubMed.
- C. S. Jun and L. Y. Cun, Degradation mechanism of 2,4,6-trinitrotoluene in supercritical water oxidation, J. Environ. Sci., 2007, 19(12), 1430–1435 CrossRef PubMed.
- M. R. J. Sarvestani and R. Ahmadi, Adsorption of TNT on the surface of pristine and N-doped carbon nanocone: A theoretical study, Asian J. Nanosci. Mater., 2020, 12(2), 103–114 Search PubMed.
- V. Marinović, M. Ristić and M. Dostanić, Dynamic adsorption of trinitrotoluene on granular activated carbon, J. Hazard. Mater., 2005, 117(2), 121–128 CrossRef PubMed.
- H. S. Son, S. J. Lee, I. H. Cho and K. D. Zoh, Kinetics and mechanism of TNT degradation in TiO2 photocatalysis, Chemosphere, 2004, 57(4), 309–317 CrossRef CAS PubMed.
- D. C. Schmelling, K. A. Gray and P. V. Kamat, Role of Reduction in the Photocatalytic Degradation of TNT, Environ. Sci. Technol., 1996, 30(8), 2547–2555 CrossRef CAS.
- R. Schäfer and R. K. Achazi, The toxicity of soil samples containing TNT and other ammunition derived compounds in the enchytraeid and collembola-biotest, Environ. Sci. Pollut. Res., 1999, 6(4), 213–219 CrossRef PubMed.
- P. G. Rieger and H. J. Knackmuss, Basic Knowledge and Perspectives on Biodegradation of 2,4,6-Trinitrotoluene and Related Nitroaromatic Compounds in Contaminated Soil, in Biodegradation of Nitroaromatic Compounds, ed. J. C. Spain, Springer US, Boston, MA, 1995, pp. 1–18 Search PubMed.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Combining theory and experiment in electrocatalysis: Insights into materials design, Science, 2017, 355(6321), eaad4998 CrossRef PubMed.
- C. K. Chua, M. Pumera and L. Rulíšek, Reduction Pathways of 2,4,6-Trinitrotoluene: An Electrochemical and Theoretical Study, J. Phys. Chem. C, 2012, 116(6), 4243–4251 CrossRef CAS.
- Y. T. Yew, A. Ambrosi and M. Pumera, Nitroaromatic explosives detection using electrochemically exfoliated graphene, Sci. Rep., 2016, 6(1), 33276 CrossRef CAS PubMed.
- A. Dettlaff, P. Jakóbczyk, M. Ficek, B. Wilk, M. Szala and J. Wojtas, et al., Electrochemical determination of nitroaromatic explosives at boron-doped diamond/graphene nanowall electrodes: 2,4,6-trinitrotoluene and 2,4,6-trinitroanisole in liquid effluents, J. Hazard. Mater., 2020, 387, 121672 CrossRef CAS PubMed.
- X. Cui, C. Tang, X. M. Liu, C. Wang, W. Ma and Q. Zhang, Highly Selective Electrochemical Reduction of Dinitrogen to Ammonia at Ambient Temperature and Pressure over Iron Oxide Catalysts, Chem. – Eur. J., 2018, 24(69), 18494–18501 CrossRef CAS PubMed.
- A. P. Lima, P. L. M. R. Almeida, R. M. F. Sousa, E. M. Richter, E. Nossol and R. A. A. Munoz, Effect of alumina supported on glassy-carbon electrode on the electrochemical reduction of 2,4,6-trinitrotoluene: A simple strategy for its selective detection, J. Electroanal. Chem., 2019, 851, 113385 CrossRef CAS.
- R. A. Soomro, O. P. Akyuz, H. Akin, R. Ozturk and Z. H. Ibupoto, Highly sensitive shape dependent electro-catalysis of TNT molecules using Pd and Pd–Pt alloy based nanostructures, RSC Adv., 2016, 6(51), 44955–44962 RSC.
- D. Alfonso, D. Tafen and D. Kauffmann, First-Principles Modeling in Heterogeneous Electrocatalysis, Catalysts, 2018, 8(10), 424 CrossRef.
- E. Skúlason and H. Jónsson, Atomic scale simulations of heterogeneous electrocatalysis: recent advances, Adv. Phys.: X, 2017, 2(3), 481–495 Search PubMed.
- T. Guerra and I. Borges, Adsorption of Trinitrotoluene on a MgO(001) Surface Including Surface Relaxation Effects, J. Chem., 2013, 2013, 1–8 CrossRef.
- S. Q. Zhou, X. H. Ju, X. Gu, F. Q. Zhao and J. H. Yi, Adsorption of 2,4,6-trinitrotoluene on Al(111) ultrathin film: periodic DFT calculations, Struct. Chem., 2012, 23(3), 921–930 CrossRef CAS.
- M. K. Shukla and F. Hill, Plane-wave density functional theory investigation of adsorption of 2,4,6-trinitrotoluene on al-hydroxylated (0001) surface of (4×4) α-alumina, J. Comput. Chem., 2014, 35(27), 1977–1985 CrossRef CAS PubMed.
- A. J. W. Wong, J. L. Miller and M. J. Janik, Elementary mechanism for the electrocatalytic reduction of nitrobenzene on late-transition-metal surfaces from density functional theory, Chem Catal., 2022, 2(6), 1362–1379 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(20), 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)], Phys. Rev. Lett., 1997, 78(7), 1396–1396 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- V. I. Anisimov and O. Gunnarsson, Density-functional calculation of effective Coulomb interactions in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43(10), 7570–7574 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57(3), 1505–1509 CrossRef CAS.
- R. Ovcharenko, E. Voloshina and J. Sauer, Water adsorption and O-defect formation on Fe2O3(0001) surfaces, Phys. Chem. Chem. Phys., 2016, 18(36), 25560–25568 RSC.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways, J. Chem. Phys., 2014, 140(8), 084106 CrossRef PubMed.
- K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, Implicit self-consistent electrolyte model in plane-wave density-functional theory, J. Chem. Phys., 2019, 151(23), 234101 CrossRef PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113(22), 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113(22), 9978–9985 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, et al., Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785–789 CrossRef CAS PubMed.
- A. D. Becke, Density–functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98(7), 5648–5652 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules, J. Chem. Phys., 1972, 56(5), 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28(3), 213–222 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105(8), 2999–3094 CrossRef CAS PubMed.
- S. Maheshwari, G. Rostamikia and M. J. Janik, Elementary kinetics of nitrogen electroreduction on Fe surfaces, J. Chem. Phys., 2018, 150(4), 041708 CrossRef PubMed.
- S. Maheshwari, Y. Li and M. J. Janik, The Fe2O3 (0001) Surface Under Electroreduction Conditions: A DFT Study of L- Cysteine Adsorption, J. Electrochem. Soc., 2022, 169(6), 064513 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188–5192 CrossRef.
- J. D. Pack and H. J. Monkhorst, “Special points for Brillouin-zone integrations”-a reply, Phys. Rev. B: Solid State, 1977, 16(4), 1748–1749 CrossRef.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin and T. Bligaard, et al., Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108(46), 17886–17892 CrossRef.
- G. Rostamikia and M. J. Janik, Borohydride Oxidation over Au(111): A First-Principles Mechanistic Study Relevant to Direct Borohydride Fuel Cells, J. Electrochem. Soc., 2008, 156(1), B86–B92 CrossRef.
- V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Universality in Oxygen Reduction Electrocatalysis on Metal Surfaces, ACS Catal., 2012, 2(8), 1654–1660 CrossRef CAS.
- B. Hammer and J. K. Nørskov, Theoretical surface science and catalysis—calculations and concepts, in Advances in Catalysis, Academic Press, 2000, pp. 71–129 Search PubMed.
- L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares and A. Janardanan, et al., Anomalously low dielectric constant of confined water, Science, 2018, 360(6395), 1339–1342 CrossRef CAS PubMed.
- M. Dinpajooh and D. V. Matyushov, Dielectric constant of water in the interface, J. Chem. Phys., 2016, 145(1), 014504 CrossRef PubMed.
- M. Zare, M. S. Saleheen, N. Singh, M. J. Uline, M. Faheem and A. Heyden, Liquid-Phase Effects on Adsorption Processes in Heterogeneous Catalysis, JACS Au, 2022, 2(9), 2119–2134 CrossRef CAS PubMed.
- M. Zare, M. Saleheen, S. K. Kundu and A. Heyden, Dependency of solvation effects on metal identity in surface reactions, Commun. Chem., 2020, 3(1), 1–10 CrossRef PubMed.
- I. T. McCrum and M. J. Janik, pH and Alkali Cation Effects on the Pt Cyclic Voltammogram Explained Using Density Functional Theory, J. Phys. Chem. C, 2016, 120(1), 457–471 CrossRef CAS.
- Q. Zhang and A. Asthagiri, Solvation effects on DFT predictions of ORR activity on metal surfaces, Catal. Today, 2019, 323, 35–43 CrossRef CAS.
- X. Wang, N. Kariuki, J. T. Vaughey, J. Goodpaster, R. Kumar and D. J. Myers, Bimetallic Pd–Cu Oxygen Reduction Electrocatalysts, J. Electrochem. Soc., 2008, 155(6), B602–B609 CrossRef CAS.
- N. M. Marković, T. J. Schmidt, V. Stamenković and P. N. Ross, Oxygen Reduction Reaction on Pt and Pt Bimetallic Surfaces: A Selective Review, Fuel Cells, 2001, 1(2), 105–116 CrossRef.
- Z. Wang, C. Li, K. Deng, Y. Xu, H. Xue and X. Li, et al., Ambient Nitrogen Reduction to Ammonia Electrocatalyzed by Bimetallic PdRu Porous Nanostructures, ACS Sustainable Chem. Eng., 2019, 7(2), 2400–2405 CrossRef CAS.
- J. H. Lee, S. Kattel, Z. Jiang, Z. Xie, S. Yao and B. M. Tackett, et al., Tuning the activity and selectivity of electroreduction of CO2 to synthesis gas using bimetallic catalysts, Nat. Commun., 2019, 10(1), 3724 CrossRef PubMed.
- W. Zhu, B. M. Tackett, J. G. Chen and F. Jiao, Bimetallic Electrocatalysts for CO2 Reduction, Top. Curr. Chem., 2018, 376(6), 41 CrossRef PubMed.
- J. Greeley and J. K. Nørskov, Combinatorial Density Functional Theory-Based Screening of Surface Alloys for the Oxygen Reduction Reaction, J. Phys. Chem. C, 2009, 113(12), 4932–4939 CrossRef CAS.
- M. Nozari-Asbemarz, M. Amiri, H. Imanzadeh, A. Bezaatpour, S. Nouhi and P. Hosseini, et al., Mixed metal oxides as efficient electrocatalysts for water oxidation, Int. J. Hydrogen Energy, 2022, 47(8), 5250–5259 CrossRef CAS.
- H. Wang, H. W. Lee, Y. Deng, Z. Lu, P. C. Hsu and Y. Liu, et al., Bifunctional non-noble metal oxide nanoparticle electrocatalysts through lithium-induced conversion for overall water splitting, Nat. Commun., 2015, 6(1), 7261 CrossRef CAS PubMed.
- T. Xu, J. Liang, S. Li, Z. Xu, L. Yue and T. Li, et al., Recent Advances in Nonprecious Metal Oxide Electrocatalysts and Photocatalysts for N 2 Reduction Reaction under Ambient Condition, Small Sci., 2021, 1(5), 2000069 CrossRef CAS.
- R. J. Toh, Z. Sofer and M. Pumera, Transition Metal Oxides for the Oxygen Reduction Reaction: Influence of the Oxidation States of the Metal and its Position on the Periodic Table, ChemPhysChem, 2015, 16(16), 3527–3531 CrossRef CAS PubMed.
- L. Hu, A. Khaniya, J. Wang, G. Chen, W. E. Kaden and X. Feng, Ambient Electrochemical Ammonia Synthesis with High Selectivity on Fe/Fe Oxide Catalyst, ACS Catal., 2018, 8(10), 9312–9319 CrossRef CAS.
- D. Gao, I. T. McCrum, S. Deo, Y. W. Choi, F. Scholten and W. Wan, et al., Activity and Selectivity Control in CO 2 Electroreduction to Multicarbon Products over CuO x Catalysts via Electrolyte Design, ACS Catal., 2018, 8(11), 10012–10020 CrossRef CAS.
- D. Gao, I. Zegkinoglou, N. J. Divins, F. Scholten, I. Sinev and P. Grosse, et al., Plasma-Activated Copper Nanocube Catalysts for Efficient Carbon Dioxide Electroreduction to Hydrocarbons and Alcohols, ACS Nano, 2017, 11(5), 4825–4831 CrossRef CAS PubMed.
- Y. Liu, Y. Su, X. Quan, X. Fan, S. Chen and H. Yu, et al., Facile Ammonia Synthesis from Electrocatalytic N2 Reduction under Ambient Conditions on N-Doped Porous Carbon, ACS Catal., 2018, 8(2), 1186–1191 CrossRef CAS.
- K. Sivula, F. Le Formal and M. Grätzel, Solar Water Splitting: Progress Using Hematite (α-Fe2O3) Photoelectrodes, ChemSusChem, 2011, 4(4), 432–449 CrossRef CAS PubMed.
- M. Yu, G. Moon, E. Bill and H. Tüysüz, Optimizing Ni–Fe Oxide Electrocatalysts for Oxygen Evolution Reaction by Using Hard Templating as a Toolbox, ACS Appl. Energy Mater., 2019, 2(2), 1199–1209 CrossRef CAS.
- L. Francàs, S. Corby, S. Selim, D. Lee, C. A. Mesa and R. Godin, et al., Spectroelectrochemical study of water oxidation on nickel and iron oxyhydroxide electrocatalysts, Nat. Commun., 2019, 10(1), 5208 CrossRef PubMed.
- J. Qi, W. Zhang, R. Xiang, K. Liu, H. Y. Wang and M. Chen, et al., Porous Nickel–Iron Oxide as a Highly Efficient Electrocatalyst for Oxygen Evolution Reaction, Adv. Sci., 2015, 2(10), 1500199 CrossRef PubMed.
- O. Diaz-Morales, D. Ferrus-Suspedra and M. T. M. Koper, The importance of nickel oxyhydroxide deprotonation on its activity towards electrochemical water oxidation, Chem. Sci., 2016, 7(4), 2639–2645 RSC.
- L. Mandal, K. R. Yang, M. R. Motapothula, D. Ren, P. Lobaccaro and A. Patra, et al., Investigating the Role of Copper Oxide in Electrochemical CO2 Reduction in Real Time, ACS Appl. Mater. Interfaces, 2018, 10(10), 8574–8584 CrossRef CAS PubMed.
- J. Kim, W. Choi, J. W. Park, C. Kim, M. Kim and H. Song, Branched Copper Oxide Nanoparticles Induce Highly Selective Ethylene Production by Electrochemical Carbon Dioxide Reduction, J. Am. Chem. Soc., 2019, 141(17), 6986–6994 CrossRef CAS PubMed.
- P. Zhang, W. Xiong and M. Zhou, Effect of nickel oxide morphology on the nitrogen electrochemical reduction reaction, Nano Mater. Sci., 2020, 2(4), 353–359 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3gc01144e |
| This journal is © The Royal Society of Chemistry 2023 |