Open Access Article
Open Access ArticleSpin polarization assisted facile C–H activation by an S = 1 iron(IV)–bisimido complex: a comprehensive spectroscopic and theoretical investigation†
Jin
Xiong
 a,
Qing
Liu
a,
Qing
Liu
 b,
Barbara
Lavina
b,
Barbara
Lavina
 cd,
Michael Y.
Hu
cd,
Michael Y.
Hu
 c,
Jiyong
Zhao
c,
Jiyong
Zhao
 c,
Esen E.
Alp
c,
Liang
Deng
c,
Esen E.
Alp
c,
Liang
Deng
 *b,
Shengfa
Ye
*b,
Shengfa
Ye
 *e and
Yisong
Guo
*e and
Yisong
Guo
 *a
*a
aDepartment of Chemistry, Carnegie Mellon University, Pittsburgh, Pennsylvania 15213, USA. E-mail: ysguo@andrew.cmu.edu
bState Key Laboratory of Organometallic Chemistry, Shanghai Institute of Organic Chemistry, Chinese Academy of Sciences, Shanghai, 200032, P. R. China. E-mail: deng@sioc.ac.cn
cAdvanced Photon Source, Argonne National Laboratory, Argonne, Illinois 60439, USA
dCenter for Advanced Radiation Sources, University of Chicago, Chicago, Illinois 60439, USA
eState Key Laboratory of Catalysis, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian 116023, P. R. China. E-mail: shengfa.ye@dicp.ac.cn
First published on 15th February 2023
Abstract
High valent iron terminal imido species (Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR) have been shown to be key reactive intermediates in C–H functionalization. However, the detailed structure–reactivity relationship in Fe
NR) have been shown to be key reactive intermediates in C–H functionalization. However, the detailed structure–reactivity relationship in Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR species derived from studies of structurally well-characterized high-valent Fe
NR species derived from studies of structurally well-characterized high-valent Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR complexes are still scarce, and the impact of imido N-substituents (electron-donating vs. electron-withdrawing) on their electronic structures and reactivities has not been thoroughly explored. In this study, we report spectroscopic and computational studies on a rare S = 1 iron(IV)–bisimido complex featuring trifluoromethyl groups on the imido N-substituents, [(IPr)Fe(NC(CF3)2Ph)2] (2), and two closely related S = 0 congeners bearing alkyl and aryl substituents, [(IPr)Fe(NC(CMe3)2Ph)2] (3) and [(IPr)Fe(NDipp)2] (1), respectively. Compared with 1 and 3, 2 exhibits a decreased Fe
NR complexes are still scarce, and the impact of imido N-substituents (electron-donating vs. electron-withdrawing) on their electronic structures and reactivities has not been thoroughly explored. In this study, we report spectroscopic and computational studies on a rare S = 1 iron(IV)–bisimido complex featuring trifluoromethyl groups on the imido N-substituents, [(IPr)Fe(NC(CF3)2Ph)2] (2), and two closely related S = 0 congeners bearing alkyl and aryl substituents, [(IPr)Fe(NC(CMe3)2Ph)2] (3) and [(IPr)Fe(NDipp)2] (1), respectively. Compared with 1 and 3, 2 exhibits a decreased Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR bond covalency due to the electron-withdrawing and the steric effect of the N-substituents, which further leads to a pseudo doubly degenerate ground electronic structure and spin polarization induced β spin density on the imido nitrogens. This unique electronic structure, which differs from those of the well-studied Fe(IV)–oxido complexes and many previously reported Fe(IV)–imido complexes, provides both kinetic and thermodynamic advantages for facile C–H activation, compared to the S = 0 counterparts.
NR bond covalency due to the electron-withdrawing and the steric effect of the N-substituents, which further leads to a pseudo doubly degenerate ground electronic structure and spin polarization induced β spin density on the imido nitrogens. This unique electronic structure, which differs from those of the well-studied Fe(IV)–oxido complexes and many previously reported Fe(IV)–imido complexes, provides both kinetic and thermodynamic advantages for facile C–H activation, compared to the S = 0 counterparts.
Introduction
High valent iron–ligand multiple bond species, such as iron–oxido, iron–imido, iron–nitride, and iron–carbene species, have been postulated as the key reactive species in many important oxidative transformations found in biological and abiological pathways, such as C–H functionalization.1–13 Iron(IV)–oxido (Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) intermediates have been identified as the key reactive species in cytochrome P450 dependent and non-heme iron dependent oxygenase/oxidase enzymes, allowing for a stunning array of stereo- and regio-specific oxidative transformations.12,14–17 While other Fe
O) intermediates have been identified as the key reactive species in cytochrome P450 dependent and non-heme iron dependent oxygenase/oxidase enzymes, allowing for a stunning array of stereo- and regio-specific oxidative transformations.12,14–17 While other Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E species have not been directly linked to biological transformations, recent advances in enzyme bioengineering have repurposed iron-dependent oxygenases to perform abiological group transfer (nitrene and carbene transfer) with high-valent Fe
E species have not been directly linked to biological transformations, recent advances in enzyme bioengineering have repurposed iron-dependent oxygenases to perform abiological group transfer (nitrene and carbene transfer) with high-valent Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR and Fe
NR and Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR2 species as key reactive intermediates.3 Thus, it is crucial to understand the geometric and electronic structures of these high valent Fe
CR2 species as key reactive intermediates.3 Thus, it is crucial to understand the geometric and electronic structures of these high valent Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E species to establish structure–reactivity relationships and explore their chemical reactivities and applications in catalysis. In recent decades, the structure–reactivity relationship of Fe(IV)
E species to establish structure–reactivity relationships and explore their chemical reactivities and applications in catalysis. In recent decades, the structure–reactivity relationship of Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species, especially in the hydrogen atom transfer (HAT) reactivity, has been significantly advanced through research efforts in model complex synthesis, enzymatic reactive intermediate trapping, geometric and electronic structure characterizations, chemical reactivity studies and theoretical investigations,6,7,12,18–26 These studies suggest that the HAT reactivity can be enhanced through a higher spin state of the iron center, a higher reduction potential and/or basicity of the oxido ligand and steric effects (the relative orientation of the orbitals of the donor C–H bond and of the acceptor Fe(IV)
O species, especially in the hydrogen atom transfer (HAT) reactivity, has been significantly advanced through research efforts in model complex synthesis, enzymatic reactive intermediate trapping, geometric and electronic structure characterizations, chemical reactivity studies and theoretical investigations,6,7,12,18–26 These studies suggest that the HAT reactivity can be enhanced through a higher spin state of the iron center, a higher reduction potential and/or basicity of the oxido ligand and steric effects (the relative orientation of the orbitals of the donor C–H bond and of the acceptor Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety).
O moiety).
Compared to the progress in research on Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species, the progress on other Fe
O species, the progress on other Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E species is much less developed. Among these species, high valent Fe
E species is much less developed. Among these species, high valent Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR species have garnered significant attention in fields such as enzyme bioengineering, organometallic chemistry and bioinorganic chemistry, as they are thought to be the key reactive intermediates in N2 reduction, C–H amination, olefin aziridation, and aminohydroxylation.1,5,27–31 Numerous Fe
NR species have garnered significant attention in fields such as enzyme bioengineering, organometallic chemistry and bioinorganic chemistry, as they are thought to be the key reactive intermediates in N2 reduction, C–H amination, olefin aziridation, and aminohydroxylation.1,5,27–31 Numerous Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR complexes, including Fe(IV)
NR complexes, including Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR, Fe(V)
NR, Fe(V)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR, and even Fe(VI)
NR, and even Fe(VI)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) (NR)2 complexes, have been synthesized.32–60 However, understanding of the structure–reactivity relationship of iron imido species, derived from studies of structurally well-characterized high-valent Fe
(NR)2 complexes, have been synthesized.32–60 However, understanding of the structure–reactivity relationship of iron imido species, derived from studies of structurally well-characterized high-valent Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR complexes, is still limited.
NR complexes, is still limited.
Holland and coworkers have reported crystallographically characterized three-coordinated LFe(III)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NAd complexes (L = a bulky β-diketiminate ligand; Ad = 1-adamantyl).35–38 Their studies on the HAT reactivity of these Fe(III)–NR have suggested that more exposed imido nitrogen (less steric effect) with high basicity may enhance HAT reactivity.35,36 Smith and coworkers have also suggested the importance of imido nitrogen basicity on HAT reactivity through studies on a crystallographically characterized four-coordinated Fe(IV)
NAd complexes (L = a bulky β-diketiminate ligand; Ad = 1-adamantyl).35–38 Their studies on the HAT reactivity of these Fe(III)–NR have suggested that more exposed imido nitrogen (less steric effect) with high basicity may enhance HAT reactivity.35,36 Smith and coworkers have also suggested the importance of imido nitrogen basicity on HAT reactivity through studies on a crystallographically characterized four-coordinated Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NAd complex supported by a tris(carbene)-borate ligand.61 Betley and coworkers have crystallographically characterized three-coordinated S = 5/2 dipyrrin supported iron(III)–imido (dipyrrin-Fe(III)
NAd complex supported by a tris(carbene)-borate ligand.61 Betley and coworkers have crystallographically characterized three-coordinated S = 5/2 dipyrrin supported iron(III)–imido (dipyrrin-Fe(III)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR (R = Ad, Mes)) complexes and one-electron oxidized four-coordinated iron(III)-iminyl (dipyrrin-FeCl
NR (R = Ad, Mes)) complexes and one-electron oxidized four-coordinated iron(III)-iminyl (dipyrrin-FeCl![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) (˙NR)) complexes that are capable of nitrene transfer and C–H amination.55,56 Comparative studies on the iron–imido/iminyl redox isomers suggested that a high-spin iron center with strong radical character on the imido nitrogen may improve reaction efficacy in the C–H activation and subsequent amination.56 These studies suggest that the HAT reactivity of iron–imido species can be promoted by imido nitrogen basicity, iron spin state, and imido nitrogen radical character, thus drawing parallels with iron–oxido species.
(˙NR)) complexes that are capable of nitrene transfer and C–H amination.55,56 Comparative studies on the iron–imido/iminyl redox isomers suggested that a high-spin iron center with strong radical character on the imido nitrogen may improve reaction efficacy in the C–H activation and subsequent amination.56 These studies suggest that the HAT reactivity of iron–imido species can be promoted by imido nitrogen basicity, iron spin state, and imido nitrogen radical character, thus drawing parallels with iron–oxido species.
Yet, different from the iron–oxido species, iron–imido species display a unique structural feature, namely the presence of N-substituents of the imido ligand. However, the impact of these N-substituents on the electronic structures and reactivities of iron–imido species has not been systemically studied. Based on general chemical principles, electron donating substituents strengthen the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR bonding interactions, while aromatic or electron withdrawing substituents weaken these interactions by stabilizing the electron lone pair on the imido nitrogen. Such weakening would likely reduce the iron–imido ligand field strength and promote a higher spin state, which may enhance the HAT reactivity. So far, most reported iron–imido complexes bear electron donating or aromatic groups as N-substituents, such as tert-butyl, 1-adamantyl, 2,4,6-trimethylphenyl, 4-tert-butylphenyl, and 2,6-diisopropylphenyl (Dipp) substituents (some examples are shown in Scheme 1).32–60 Isolable iron–imido species bearing strong electron withdrawing N-substituents are rare.42,43,45,62–65 Recently, the first structurally characterized Fe(IV)–bisimido complex bearing a strong electron-withdrawing N-substituent, α,α-bis(trifluoromethyl)benzyl, was reported by some of us (Scheme 1).53 The complex, [(IPr)Fe(NC(CF3)2Ph)2] (2, IPr = 1,3-bis(2′,6′-diisopropylphenyl)imidazol-2-ylidene), exhibits an S = 1 ground spin state and readily undergoes intramolecular C–H bond dehydrogenation at room temperature via HAT. Interestingly, the replacement of CF3 groups in 2 to electron-donating CH3 groups on the N-substituents resulted in an S = 0 Fe(IV)–bisimido complex, [(IPr)Fe(NC(CH3)2Ph)2] (3), which was stable and showed no chemical reactivity even under elevated temperatures (30–70 °C). Additionally, the use of aromatic N-substituents in another similar Fe(IV)–bisimido complex, [(IPr)Fe(Ndipp)2] (1), which would in principle also weaken the Fe
NR bonding interactions, while aromatic or electron withdrawing substituents weaken these interactions by stabilizing the electron lone pair on the imido nitrogen. Such weakening would likely reduce the iron–imido ligand field strength and promote a higher spin state, which may enhance the HAT reactivity. So far, most reported iron–imido complexes bear electron donating or aromatic groups as N-substituents, such as tert-butyl, 1-adamantyl, 2,4,6-trimethylphenyl, 4-tert-butylphenyl, and 2,6-diisopropylphenyl (Dipp) substituents (some examples are shown in Scheme 1).32–60 Isolable iron–imido species bearing strong electron withdrawing N-substituents are rare.42,43,45,62–65 Recently, the first structurally characterized Fe(IV)–bisimido complex bearing a strong electron-withdrawing N-substituent, α,α-bis(trifluoromethyl)benzyl, was reported by some of us (Scheme 1).53 The complex, [(IPr)Fe(NC(CF3)2Ph)2] (2, IPr = 1,3-bis(2′,6′-diisopropylphenyl)imidazol-2-ylidene), exhibits an S = 1 ground spin state and readily undergoes intramolecular C–H bond dehydrogenation at room temperature via HAT. Interestingly, the replacement of CF3 groups in 2 to electron-donating CH3 groups on the N-substituents resulted in an S = 0 Fe(IV)–bisimido complex, [(IPr)Fe(NC(CH3)2Ph)2] (3), which was stable and showed no chemical reactivity even under elevated temperatures (30–70 °C). Additionally, the use of aromatic N-substituents in another similar Fe(IV)–bisimido complex, [(IPr)Fe(Ndipp)2] (1), which would in principle also weaken the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR bond and promote higher spin state, still yielded an S = 0 spin ground state.48 Thus, complexes 1–3 provide a great opportunity to study the effect of the imido N-substituents on the structure and chemical reactivity of Fe(IV)–imido complexes.
NR bond and promote higher spin state, still yielded an S = 0 spin ground state.48 Thus, complexes 1–3 provide a great opportunity to study the effect of the imido N-substituents on the structure and chemical reactivity of Fe(IV)–imido complexes.
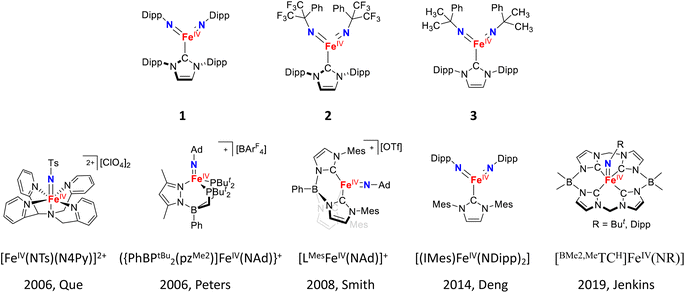 | ||
| Scheme 1 The Fe(IV)–bisimido complexes studied in this work and examples of the previously reported S = 1 Fe(IV)–imido complexes. | ||
Herein, we present a comprehensive spectroscopic and computational analysis of the novel S = 1 complex 2 and its S = 0 congeners, 1 and 3. Results from 57Fe nuclear resonance vibrational spectroscopy (NRVS), 57Fe Mössbauer spectroscopy, and direct current (dc) magnetic measurements showed that complex 2 exhibits strongly reduced Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR bond covalency compared with those of 1 and 3, which leads to distinctive magnetic properties due to its large unquenched orbital angular momentum. We also used the complete-active-space self-consistent field (CASSCF)66 method combined with N-electron valence state perturbation theory (NEVPT2)67,68 and DFT calculations to understand the origin of these unique electronic and magnetic properties in 2 and compare them to complexes 1 and 3. Our findings indicate that the reduction of the Fe(IV)
NR bond covalency compared with those of 1 and 3, which leads to distinctive magnetic properties due to its large unquenched orbital angular momentum. We also used the complete-active-space self-consistent field (CASSCF)66 method combined with N-electron valence state perturbation theory (NEVPT2)67,68 and DFT calculations to understand the origin of these unique electronic and magnetic properties in 2 and compare them to complexes 1 and 3. Our findings indicate that the reduction of the Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR covalency in 2 is not only due to the electron-withdrawing nature of the N-substituents but also due to their steric effects. These two features are not simultaneously present in 1 and 3. Furthermore, the reduced Fe(IV)
NR covalency in 2 is not only due to the electron-withdrawing nature of the N-substituents but also due to their steric effects. These two features are not simultaneously present in 1 and 3. Furthermore, the reduced Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR covalency in 2 promotes spin polarization that induces β spin density on the imido nitrogens, which facilitates an α spin transfer in the HAT process and is fundamentally different from those in Fe(IV)
NR covalency in 2 promotes spin polarization that induces β spin density on the imido nitrogens, which facilitates an α spin transfer in the HAT process and is fundamentally different from those in Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species as well as other Fe(IV)
O species as well as other Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR species in a pseudo-C4 ligand field. This unique electronic structure of 2 provides both kinetic and thermodynamic advantages to enable facile C–H activation.
NR species in a pseudo-C4 ligand field. This unique electronic structure of 2 provides both kinetic and thermodynamic advantages to enable facile C–H activation.
Results and discussion
Structural considerations
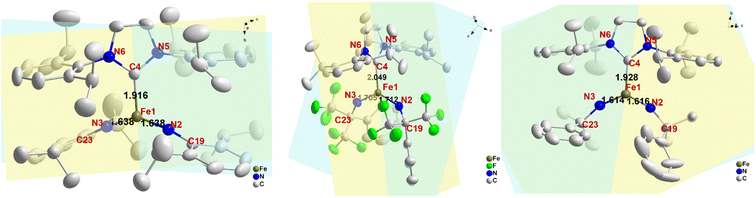
The crystal structures of complexes 2 and 3 have been previously reported.53 Here we present the crystal structure of complex 1 (CCDC: 2172442; see Table S1† for refinement parameters) and highlight key structural differences among 1, 2 and 3 (Fig. 1). Single-crystal X-ray diffraction experiments revealed that 1 is crystallized in the monoclinic C2/c space group. The Fe atom is three-coordinate with two imido ligands and one N-heterocyclic carbene (NHC) ligand as a spectator ligand. Five major geometric differences can be found among complexes 1–3. Firstly, the molecular symmetries are different. Complex 1 has a C2 axis along the Fe–C(carbene) bond, resulting in many equivalent molecular metrics, e.g. the two Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR bond lengths, the two C–N(imido)–Fe angles, etc. Complex 2, on the other hand, has a C1 symmetry and has two inequivalent Fe
NR bond lengths, the two C–N(imido)–Fe angles, etc. Complex 2, on the other hand, has a C1 symmetry and has two inequivalent Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR bond lengths and two inequivalent C–N(imido)–Fe angles. Secondly, the Fe–ligand bond lengths are generally shorter in 1 when compared with complex 2. For example, the Fe–C(NHC) bond length is 1.916 Å in 1 but 2.049 Å in 2; similarly, the Fe–N(imido) bond lengths are 1.638 Å in 1 but 1.705 Å and 1.712 Å in 2, which is one of the longest Fe–N(imido) bond lengths reported for iron–imido complexes (Table 2). It is worth noting that the Fe
NR bond lengths and two inequivalent C–N(imido)–Fe angles. Secondly, the Fe–ligand bond lengths are generally shorter in 1 when compared with complex 2. For example, the Fe–C(NHC) bond length is 1.916 Å in 1 but 2.049 Å in 2; similarly, the Fe–N(imido) bond lengths are 1.638 Å in 1 but 1.705 Å and 1.712 Å in 2, which is one of the longest Fe–N(imido) bond lengths reported for iron–imido complexes (Table 2). It is worth noting that the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR bond is slightly longer in 1 than in 3, suggesting the expected weakening of this bond via an aryl N-substituent. However, the weakening effect is much weaker compared to the electron-withdrawing N-substituents in 2 (see later sections for more discussions). Thirdly, Fig. 1 shows that there is also a difference in the angle between the NHC plane (defined by the 5-membered ring) and the coordination plane (Fe
NR bond is slightly longer in 1 than in 3, suggesting the expected weakening of this bond via an aryl N-substituent. However, the weakening effect is much weaker compared to the electron-withdrawing N-substituents in 2 (see later sections for more discussions). Thirdly, Fig. 1 shows that there is also a difference in the angle between the NHC plane (defined by the 5-membered ring) and the coordination plane (Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) (NR)2), which is 35° in 1, ∼81° in 2, and ∼4° in 3. Additionally, the C(imido)–N(imido) = Fe angles and N(imido)
(NR)2), which is 35° in 1, ∼81° in 2, and ∼4° in 3. Additionally, the C(imido)–N(imido) = Fe angles and N(imido)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe
Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N(imido) angles are also distinct. The former is almost linear in 1 (173°) and 3 (160–161°) but bent (140–145°) in 2; the latter is 143° in 1 and ∼125° in both 2 and 3. This suggests the hybridization mode of N(imido) atom is closer to sp in 1 and 3, while closer to sp2 in 2. Finally, the angle between the plane of C19–N2
N(imido) angles are also distinct. The former is almost linear in 1 (173°) and 3 (160–161°) but bent (140–145°) in 2; the latter is 143° in 1 and ∼125° in both 2 and 3. This suggests the hybridization mode of N(imido) atom is closer to sp in 1 and 3, while closer to sp2 in 2. Finally, the angle between the plane of C19–N2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe1
Fe1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N3 and C23–N3
N3 and C23–N3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe1
Fe1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N2 (C19–N2⋯N3–C23 dihedral angle), which controls the relative orientation of two imido nitrogen p orbitals, is also different in these complexes. This angle is 25°, 70°, and ∼0° for 1, 2, and 3 respectively. The selected structural metrics of these complexes are listed in Table 1.
N2 (C19–N2⋯N3–C23 dihedral angle), which controls the relative orientation of two imido nitrogen p orbitals, is also different in these complexes. This angle is 25°, 70°, and ∼0° for 1, 2, and 3 respectively. The selected structural metrics of these complexes are listed in Table 1.
| Complex 1 | Complex 2 | Complex 3 | |
|---|---|---|---|
| Bond length (Å) | |||
Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N(imido) N(imido) |
1.638, 1.638 | 1.705, 1.712 | 1.614, 1.616 |
| Fe–C(NHC) | 1.916 | 2.049 | 1.928 |
| N–C(R) | 1.376, 1.376 | 1.438, 1.435 | 1.440, 1.455 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Bond angle ( o ) | |||
Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C(R) N–C(R) |
172.68, 172.68 | 144.05, 140.84 | 160.16, 161.13 |
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N N |
142.98 | 125.28 | 127.73 |
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe–C(NHC) Fe–C(NHC) |
108.51, 108.51 | 121.22, 113.38 | 115.59, 116.67 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Torsion angle ( o ) | |||
N(imido)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe–C(NHC)–N(NHC) Fe–C(NHC)–N(NHC) |
35.03, 35.03 | 78.03, 83.62 | −5.79, −2.54 |
| C19–N2⋯N3–C23 | −25.41 | −69.69 | 0.98 |
| Ref. | This work | Ref. 53 | Ref. 53 |
57Fe nuclear resonance vibrational spectroscopy
To further demonstrate the difference in geometric structures and iron–imido/carbene bonding interactions in these Fe(IV)–bisimido complexes, we conducted 57Fe NRVS measurements on 1 and 2 by using polycrystalline samples.69,70 The 57Fe partial vibrational density of states (PVDOS) derived from the NRVS measurements revealed rich vibrational features for complexes 1 and 2 (Fig. 2). The detectable vibrational features extended up to ∼1300 cm−1. We suspect that the features at ∼990 cm−1 and ∼1285 cm−1 observed for complex 1 are vibrational features associated with its Fe(IV)–bisimido moiety. Indeed, earlier IR and Raman investigations on transition metal organoimido complexes showed that vibrations in the energy regions of 900–1100 cm−1 and 1100–1350 cm−1 belong to the vibrations of the M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–R linkage (M
N–R linkage (M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR or MN–R stretching).71 When comparing the 57Fe PVDOS data of complex 2 to that of complex 1, we found all the vibrational features to be red shifted, which is consistent with their differences in Fe–ligand bond lengths (Table 1).
NR or MN–R stretching).71 When comparing the 57Fe PVDOS data of complex 2 to that of complex 1, we found all the vibrational features to be red shifted, which is consistent with their differences in Fe–ligand bond lengths (Table 1).
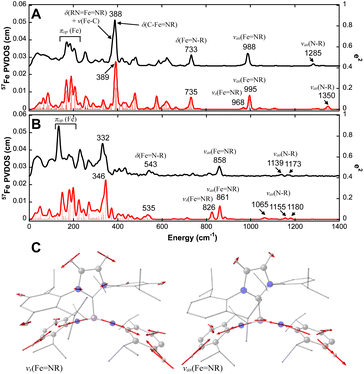 | ||
Fig. 2 NRVS-derived 57Fe PVDOS spectra of complexes 1 and 2 and selected normal modes of vibrations. Experimental (black) and DFT-calculated (red) 57Fe PVDOS spectra of 1 (A) and 2 (B) and the symmetric and asymmetric stretching modes of RN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR moiety (C) are shown. The frequencies of major spectral features and the mode assignments based on a simplified MX(Y2)2-type molecule are indicated in the figure (see Fig. S4† for mode pictures). The 57Fe PVDOS intensity is shown on the left Y axis while the intensity of calculated mode decomposition factor, e2, is shown on the right Y axis. The mode pictures in (C) are derived from the DFT frequency calculations of the full structure of complex 1. The red arrows represent the direction and the magnitude of the atom displacements (>0.07 Å) in the corresponding normal mode of vibration. NR moiety (C) are shown. The frequencies of major spectral features and the mode assignments based on a simplified MX(Y2)2-type molecule are indicated in the figure (see Fig. S4† for mode pictures). The 57Fe PVDOS intensity is shown on the left Y axis while the intensity of calculated mode decomposition factor, e2, is shown on the right Y axis. The mode pictures in (C) are derived from the DFT frequency calculations of the full structure of complex 1. The red arrows represent the direction and the magnitude of the atom displacements (>0.07 Å) in the corresponding normal mode of vibration. | ||
To gain a better understanding of the 57Fe PVDOS spectra, we performed DFT calculations. Several functional-basis set combinations were used in the calculations, and all of them reproduced the experimental data reasonably well (Fig. S2 and S3†). Here, the results from the BP86/TZVP72,73 with GD3 correction74 are presented in Fig. 2. The DFT optimized structure for complex 1 in an S = 0 state and for complex 2 in an S = 1 state matched well with their crystal structures (Table S2 and Fig. S1†). Based on the DFT optimized structures, the predicted 57Fe PVDOS spectra of complexes 1 (S = 0) and 2 (S = 1) derived from frequency calculations also aligned well with the experimental data, allowing us to confidently assign the vibrational modes (see Tables 2 and S4† for a list of vibrational mode assignments and the ESI† for additional analysis and discussion). One key feature revealed by the DFT analysis is that the 57Fe PVDOS features at ∼990 cm−1 and ∼1285 cm−1 belong to the vibrations of the M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–R moieties. The very weak 57Fe PVDOS features at 1285 cm−1 and 1322 cm−1 (DFT predicted at 1302 and 1350 cm−1) can be assigned to the asymmetric N–R stretching modes between the N and C atoms of the imido ligand (νas(FeN–R)), which are coupled with different imido substituent vibrations (in this case Dipp vibrations). Due to the short Fe–imido bonds, the asymmetric N–R stretching mode also mixes slightly with the asymmetric Fe
N–R moieties. The very weak 57Fe PVDOS features at 1285 cm−1 and 1322 cm−1 (DFT predicted at 1302 and 1350 cm−1) can be assigned to the asymmetric N–R stretching modes between the N and C atoms of the imido ligand (νas(FeN–R)), which are coupled with different imido substituent vibrations (in this case Dipp vibrations). Due to the short Fe–imido bonds, the asymmetric N–R stretching mode also mixes slightly with the asymmetric Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR stretching mode (νas(Fe
NR stretching mode (νas(Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR)) to cause the movement of the iron center, thereby rendering their detection. The main νas(Fe
NR)) to cause the movement of the iron center, thereby rendering their detection. The main νas(Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR) is located at 988 cm−1 (995 cm−1 in DFT). The lack of appreciable iron movement in the symmetric Fe
NR) is located at 988 cm−1 (995 cm−1 in DFT). The lack of appreciable iron movement in the symmetric Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR stretching mode (νs(Fe
NR stretching mode (νs(Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR)) results a weak shoulder at ∼970 cm−1 (968 cm−1 in DFT) for this vibrational mode. In addition, both νas(Fe
NR)) results a weak shoulder at ∼970 cm−1 (968 cm−1 in DFT) for this vibrational mode. In addition, both νas(Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR) and νs(Fe
NR) and νs(Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR) show strong coupling with aromatic ring vibration from the Dipp substituent (Fig. 3). Overall, the vibrational features of the M
NR) show strong coupling with aromatic ring vibration from the Dipp substituent (Fig. 3). Overall, the vibrational features of the M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–R moieties in complex 1 are consistent with many reported metal–imido complexes studied by IR and resonance Raman (Table 2).75 Furthermore, the NRVS data provided a definitive confirmation for the assignment of the Fe
N–R moieties in complex 1 are consistent with many reported metal–imido complexes studied by IR and resonance Raman (Table 2).75 Furthermore, the NRVS data provided a definitive confirmation for the assignment of the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR stretching mode and the FeN–R stretching mode, as the former mode leads to stronger iron movement thus higher 57Fe PVDOS intensity than the latter. This is clearly observed in the current NRVS data, showing a high intensity 988 cm−1 (νas(Fe
NR stretching mode and the FeN–R stretching mode, as the former mode leads to stronger iron movement thus higher 57Fe PVDOS intensity than the latter. This is clearly observed in the current NRVS data, showing a high intensity 988 cm−1 (νas(Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR)) and a low intensity 1285 cm−1 (νas(Fe
NR)) and a low intensity 1285 cm−1 (νas(Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR)) features.
NR)) features.
| Complex |
d(Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR) NR) |
ν(Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR) NR) |
ν as(N–R) | Ref. |
|---|---|---|---|---|
| a The italic numbers are derived from DFT calculations. Distances are in Å, and vibrational frequencies are in cm−1. | ||||
| 1 | 1.638 | 968 (968) s | 1285, 1322 (1302, 1350) as | This work |
| 988 (995) as | ||||
| 2 | 1.709 | 814 (826) s | 1139, 1173 (1060, 1070, 1155, 1180) | This work |
| 858 (861) as | ||||
| [FeIV(NTs)(MePy2tacn)]2+ | 1.71 | 984 | — | 46 |
| [FeIV(NTs)(Me2CHPy2tacn)]2+ | 1.72 | 1061 | — | 46 |
| [FeIV(NTs)(N4py)]2+ | 1.73 | 998 | — | 43 |
| [(TAML)FeV(NTs)]− | 1.65 | 817 | — | 42 |
| [PhBP3]FeIIINtBu | 1.635 | 1104 | 1233 | 75 |
| [PhBP3]FeIIIN(1-Ad) | 1.641 | 1097 | 1225 | 75 |
| [PhBP3]FeIIINPh | — | 958 | 1292/1309 | 75 |
| [PhBP3]FeIIIN(p-tolyl) | 1.659 | 962 | 1281/1305 | 75 |
| [Fe4(μ3-NtBu)4(NtBu)Cl3] | 1.635 | 1111 | 1214 | 75 |
For complex 2, all the vibrational modes identified in complex 1 are shifted to lower frequencies due to the elongation of all the iron–ligand distances in going from 1 to 2 (Fig. 2). In particular, the νas(Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR) is now located at 858 cm−1 (861 cm−1 in DFT), the νs(Fe
NR) is now located at 858 cm−1 (861 cm−1 in DFT), the νs(Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR) is located at 814 cm−1 (826 cm−1 in DFT). Thus, the Fe
NR) is located at 814 cm−1 (826 cm−1 in DFT). Thus, the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR stretching frequency observed for 2 is one of the lowest reported in the literature (Table 2), which is consistent with the relatively long Fe
NR stretching frequency observed for 2 is one of the lowest reported in the literature (Table 2), which is consistent with the relatively long Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR bond length in 2 (1.709 Å). In addition, we compared the displacement of the Fe atom and the N atoms from the bisimido ligands in different normal modes and found that they exhibit a very strong correlation (Fig. S5†). As such, the 57Fe PVDOS spectra of complexes 1 and 2 are dominated by the vibrations associated with Fe–bisimido moiety, which is consistent with the strong Fe
NR bond length in 2 (1.709 Å). In addition, we compared the displacement of the Fe atom and the N atoms from the bisimido ligands in different normal modes and found that they exhibit a very strong correlation (Fig. S5†). As such, the 57Fe PVDOS spectra of complexes 1 and 2 are dominated by the vibrations associated with Fe–bisimido moiety, which is consistent with the strong Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR bonding interactions in the Fe–bisimido moiety of these two complexes, particularly for complex 1. Overall, the significantly red-shifted vibrational frequencies of the Fe
NR bonding interactions in the Fe–bisimido moiety of these two complexes, particularly for complex 1. Overall, the significantly red-shifted vibrational frequencies of the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR and FeN–R stretching modes observed in 2 than those in 1 correlate well with the long Fe
NR and FeN–R stretching modes observed in 2 than those in 1 correlate well with the long Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR bonds in 2, which further suggests the strongly reduced Fe
NR bonds in 2, which further suggests the strongly reduced Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR covalency in this complex.
NR covalency in this complex.
57Fe Mössbauer spectroscopy and magnetometry
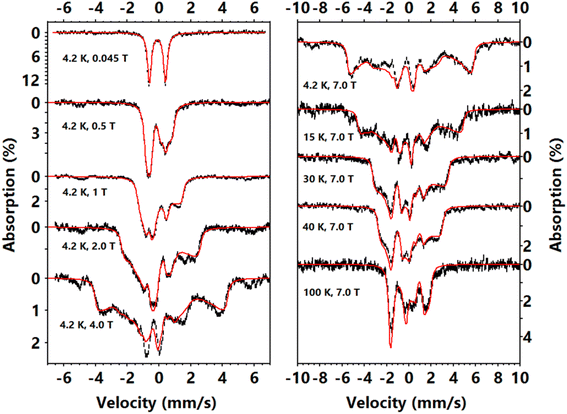
To further study the magnetic properties and electronic structures of complexes 1–3, we collected variable–temperature–variable–field (VTVH) 57Fe Mössbauer spectra. The low field (0.045 T parallel to the γ-radiation) spectra of 1 (Fig. S6†) and 2 (Fig. 3), measured at 4.2 K, show a single quadrupole doublet, which is a typical feature of integral spin systems (S = 0, 1, 2, …). Complex 1 has an isomer shift (δ) of −0.28 mm s−1 and complex 2 has δ of −0.10 mm s−1, similar to other reported Fe(IV)–imido species.39,48–50,52 The quadrupole splitting (ΔEQ) of complex 1 is larger than that of complex 2. The high field spectrum (Fig. S6†) of 1 only shows magnetic splittings due to the externally applied field (7 T), which suggests there is no internal magnetic field in this complex and confirms its diamagnetic nature (S = 0). The simulation gives ΔEQ = −1.84 mm s−1 and η = 0.4. For comparison, the Mössbauer parameters of the diamagnetic complex 3, which differs from complex 2 by the replacement of –CF3 substituents on the imido ligand with –CH3, were previously reported (at 80 K) as δ = −0.41 mm s−1 and |ΔEQ| = 2.40 mm s−1 (the sign of ΔEQ was not determined).The VTVH Mössbauer spectra of complex 2 are shown in Fig. 3. The magnetization of the 4.2 K Mössbauer spectra under various applied field is typical of a paramagnetic species with an integer spin ground state, a large negative D (D ≪ 0), and an easy magnetization direction (an internal field only rapidly develops along the z direction defined by the D tensor, the relative orientations of the D, g and electric field gradient (EFG) tensor (V) with respect to the molecular frame will be discussed in the electronic structure calculation section below).76,77 For such a uni-axial magnetic system, the Mössbauer spectra measured at 4.2 K only reflect the properties of the ground non-Kramers doublet of the spin manifold, which can be approximated as an effective Seff = 1/2 spin Hamiltonian with geff,x = geff,y ≈ 0, geff,z ≫ 0 and an off-diagonal matrix element of the effective spin Hamiltonian Δ/2 (to account for the zero field splitting (Δ) of the magnetic sublevels, see Fig. S7†).76 With this effective spin Hamiltonian, the VTVH Mössbauer spectra of complex 2 can be satisfactorily simulated (Fig. S8†), which affirms that the ground state electronic structure of 2 indeed features an isolated pseudo-doublet and the excited spin sublevels are not significantly populated even at 100 K.
Overall, the spectral simulations by using the effective spin Hamiltonian revealed two major features: (1) the Mössbauer spectra reveals that a large positive internal field exists in 2 (Bint = −Aeff,z〈Seff,z〉/gnβn ∼ +28 T at 7 T applied field), which indicates the internal field is dominated by the orbital contribution due to the unquenched orbital angular momentum; (2) the largest principal component of the EFG tensor (Vz′′z′′) is perpendicular to the direction of the internal field. The obtained effective spin Hamiltonian parameters are Δ = 13.6 cm−1, geff,z = 5.6, Aeff,z/gnβn = +71 T, ΔEQ = −1.02 mm s−1, η = 0, Vz′′z′′⊥geff,z, and δ = −0.11 mm s−1. These parameters can be mapped to a canonical S = 1 spin Hamiltonian with a large negative D (see Fig. S7†). We can use the |±1′〉 doublet of an S = 1 spin Hamiltonian to mimic the two-level system described by the effective Seff = 1/2 spin Hamiltonian. Thus, Δ, geff,z, and Aeff,z from the effective Hamiltonian correspond to E, gz′z′ and Az′z′ of the S = 1 Hamiltonian, giving E = −6.8 cm−1, gz′z′ = 2.80, Az′z′/gnβn = +35.5 T (note that x′, y′, and z′ are used to label the x, y and z direction of the D, g and A tensors, and to distinguish them from those of the molecular frame coordination, as explained in the electronic structure calculation section). Using these parameters together with the assumption that the principal axes of A and D are colinear (Az′z′∥Dz′z′), we were able to obtain the Mössbauer parameters that reproduce all the spectroscopic data of complex 2 with an S = 1 spin Hamiltonian (by fixing D = −79 cm−1 and g = [2, 2, 2.80]): δ = −0.11 mm s−1, ΔEQ = −1.02 mm s−1, η = 0 with Vz′′z′′ ⊥ Dz′z′, E/D = 0.085, Az′z′/gnβn = +35.5 T with Az′z′∥Dz′z′ (Fig. 3).
Dc magnetic measurements were also carried out to further investigate the magnetic anisotropy of 2 (see the analysis in the ESI and Fig. S9† for details). The effective magnetic moment (μeff) of ∼3.1μB measured under 300 K and 1 T is larger than spin-only value for a triplet system (2.832μB). The VTVH susceptibilities and magnetizations can be well reproduced with the following parameters: S = 1, D = −79 cm−1, E/D = 0.077, g⊥ = 1.91, g∥ = 2.73, TIP = 1188 × 10−6 emu (TIP refers to temperature-independent paramagnetism). The large D and TIP values are indicative of low-lying excited states and unquenched angular momentum.
Taken together, the magnetic susceptibility/magnetization measurements and the Mössbauer analysis reveal an orbitally nearly degenerate electronic ground state in 2. In the literature, there are several reported iron complexes exhibiting such an orbitally nearly degenerate electronic structure, but they are either iron(I) or iron(II) species.47,78–81 To the best of our knowledge, high-valent iron complexes, such as complex 2, featuring such a unique electronic structure have not been reported yet.
Electronic structure calculations
To elucidate the electronic structures of complexes 1–3 and the origin of their spectroscopic properties, highly correlated wavefunction based multi-reference CASSCF/NEVPT2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66–68 calculations were performed using ORCA-5.0.3 program.82 The selected active space contains 12 electrons distributed across 9 orbitals, including five Fe 3d orbitals and four ligand-based bonding partners, primarily contributed from N(imido) 2p atomic orbitals. To speed up the calculation, truncated molecular fragments were used, with the Dipp substituents replaced by phenyl groups (Fig. 4). The results were discussed using the reference frame shown in the inset of Fig. 4, where the z-axis is defined along the pseudo C3 axis, the y-axis is defined along the Fe–C(carbene) bond, and the x-axis is perpendicular to the yz plane and close to the N(imido)–N(imido) direction.
66–68 calculations were performed using ORCA-5.0.3 program.82 The selected active space contains 12 electrons distributed across 9 orbitals, including five Fe 3d orbitals and four ligand-based bonding partners, primarily contributed from N(imido) 2p atomic orbitals. To speed up the calculation, truncated molecular fragments were used, with the Dipp substituents replaced by phenyl groups (Fig. 4). The results were discussed using the reference frame shown in the inset of Fig. 4, where the z-axis is defined along the pseudo C3 axis, the y-axis is defined along the Fe–C(carbene) bond, and the x-axis is perpendicular to the yz plane and close to the N(imido)–N(imido) direction.
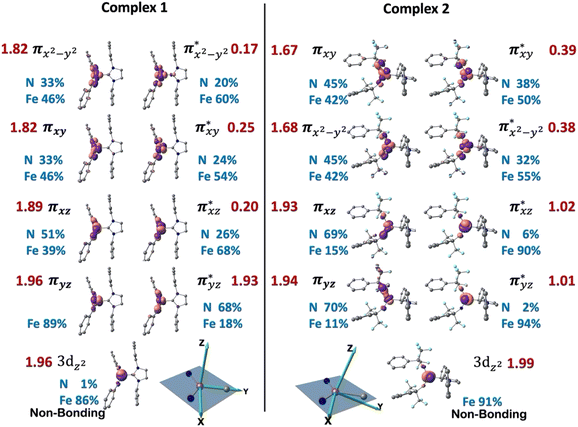
The ab initio calculations show that 1 has a diamagnetic ground state with a leading electron configuration of 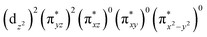 , which only accounts for ∼73% of the wavefunction, indicating the multi-reference character of the ground state (as shown in Fig. 4). In the leading configuration, dz2 is the doubly occupied non-bonding orbital, while the other four Fe d orbitals participate in π bonding and antibonding interactions with py and pz orbitals from the two imido ligands with
, which only accounts for ∼73% of the wavefunction, indicating the multi-reference character of the ground state (as shown in Fig. 4). In the leading configuration, dz2 is the doubly occupied non-bonding orbital, while the other four Fe d orbitals participate in π bonding and antibonding interactions with py and pz orbitals from the two imido ligands with 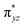 as the other doubly occupied orbital. The calculations yield ΔEQ = −1.75 mm s−1, η = 0.49, which are consistent with the Mössbauer simulation for 1, and the EFG tensor frame is well compatible to the pseudo C2v symmetry, with Vz′′z′′ aligning with the z-axis of the molecular frame defined in Fig. 4, Vx′′x′′ aligning with y-axis, and Vy′′y′′ with x-axis (Fig. S11†).
as the other doubly occupied orbital. The calculations yield ΔEQ = −1.75 mm s−1, η = 0.49, which are consistent with the Mössbauer simulation for 1, and the EFG tensor frame is well compatible to the pseudo C2v symmetry, with Vz′′z′′ aligning with the z-axis of the molecular frame defined in Fig. 4, Vx′′x′′ aligning with y-axis, and Vy′′y′′ with x-axis (Fig. S11†).
Multi-reference calculations were also performed on 3, revealing a similar electron ground state as that of complex 1. Specifically, the leading configuration is the same as 1, contributing ∼75% of the ground state wavefunction. The bonding orbitals πxy and πx2−y2 are heavily mixed and undistinguishable, but the corresponding anti-bonding pairs are well-defined (Fig. S10†). The EFG tensor principal frame also follows the same orientation as that in 1 (Fig. S11†), with the calculated ΔEQ and η to be −1.81 mm s−1 and 0.94, respectively.
The wavefunction of the triplet ground state of 2 exhibits even more substantial multi-reference character, with the leading configuration 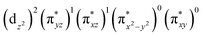 contributing only 59% of the total wavefunction (Fig. 4). This configuration differs greatly from the ground state electron configuration of 1 in that not only a single electron is promoted from
contributing only 59% of the total wavefunction (Fig. 4). This configuration differs greatly from the ground state electron configuration of 1 in that not only a single electron is promoted from 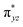 to
to 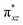 to lead to a triplet ground state for 2, more importantly, instead of exhibiting antibonding nature for
to lead to a triplet ground state for 2, more importantly, instead of exhibiting antibonding nature for 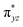 and
and 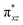 in 1, these two corresponding orbitals are essentially non-bonding Fe dyz and dxz orbitals in 2 based on orbital decomposition (Fig. 4). This reflects the significant reduction of covalent interactions between iron and the imido ligands in 2. With three non-bonding orbitals (dz2, dyz, and dxz) and four 3d electrons, a triplet ground state is favored for 2 based on the first Hund's rule. In addition, the energies of these three non-bonding orbitals are likely to be close, thus leading to an orbital (pseudo)degeneracy. This is confirmed by the excited state calculations. The first triplet excited state with a leading configuration (46%) of
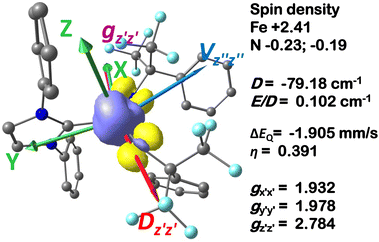
in 1, these two corresponding orbitals are essentially non-bonding Fe dyz and dxz orbitals in 2 based on orbital decomposition (Fig. 4). This reflects the significant reduction of covalent interactions between iron and the imido ligands in 2. With three non-bonding orbitals (dz2, dyz, and dxz) and four 3d electrons, a triplet ground state is favored for 2 based on the first Hund's rule. In addition, the energies of these three non-bonding orbitals are likely to be close, thus leading to an orbital (pseudo)degeneracy. This is confirmed by the excited state calculations. The first triplet excited state with a leading configuration (46%) of 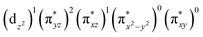 lies only 1020 cm−1 above the ground state. As such, the first excited state primarily corresponds to a single electron excitation from the dz2 non-bonding orbital of the ground state to the dyz non-bonding orbital, thereby leading to a sizeable unquenched orbital angular momentum along the x-direction. Higher excited states have much larger energy separations from the ground state (Table S4†), thus their spin orbit coupling (SOC) with the ground state is much less pronounced. The calculations give the value of the largest principal component of the g tensor as 2.78, which is much larger than 2, and a large negative D value of −79.2 cm−1. The electronic structure revealed by CASSCF calculations is in agreement with the one reflected by the spectral simulation model: the triplet ground state of complex 2 exhibits a large negative zero-field splitting and strong easy axis magnetic anisotropy. More importantly, the estimated energy separation of 16.2 cm−1 for the lowest-energy doublet from the calculations is in a reasonable agreement with 2|E| of 13.6 cm−1 derived from the spectroscopic simulations. Furthermore, based on the calculations, the direction of the largest principal components (Dz′z′ and gz′z′) of the D and the g tensors, which reflects the direction of unquenched orbital angular momentum, is along the x-direction (Fig. 5). This is consistent with SOC generated by the dyz/dz2 pair as described above. Remarkably, the calculations also successfully reproduce the relative orientation between V and D principal axes, with angles of 172° between Vz′′z′′ and Dy′y′, and 97° between Vz′′z′′ and Dz′z′, which is consistent with the Mössbauer analysis of 2.
lies only 1020 cm−1 above the ground state. As such, the first excited state primarily corresponds to a single electron excitation from the dz2 non-bonding orbital of the ground state to the dyz non-bonding orbital, thereby leading to a sizeable unquenched orbital angular momentum along the x-direction. Higher excited states have much larger energy separations from the ground state (Table S4†), thus their spin orbit coupling (SOC) with the ground state is much less pronounced. The calculations give the value of the largest principal component of the g tensor as 2.78, which is much larger than 2, and a large negative D value of −79.2 cm−1. The electronic structure revealed by CASSCF calculations is in agreement with the one reflected by the spectral simulation model: the triplet ground state of complex 2 exhibits a large negative zero-field splitting and strong easy axis magnetic anisotropy. More importantly, the estimated energy separation of 16.2 cm−1 for the lowest-energy doublet from the calculations is in a reasonable agreement with 2|E| of 13.6 cm−1 derived from the spectroscopic simulations. Furthermore, based on the calculations, the direction of the largest principal components (Dz′z′ and gz′z′) of the D and the g tensors, which reflects the direction of unquenched orbital angular momentum, is along the x-direction (Fig. 5). This is consistent with SOC generated by the dyz/dz2 pair as described above. Remarkably, the calculations also successfully reproduce the relative orientation between V and D principal axes, with angles of 172° between Vz′′z′′ and Dy′y′, and 97° between Vz′′z′′ and Dz′z′, which is consistent with the Mössbauer analysis of 2.
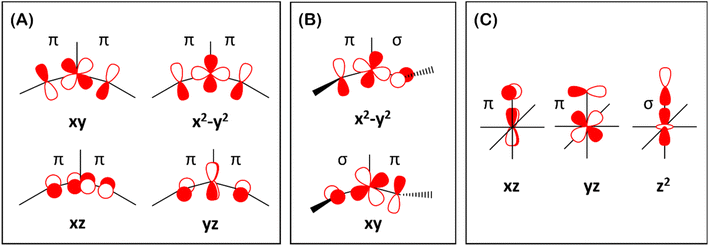
Finally, the spin density plot shown in Fig. 5 reveals a sizeable negative spin density primarily located in the equatorial plane on two imido N atoms (i.e. the RN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe
Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR coordination plane). As elaborated in the previous studies for related high-valent iron–nitrido and –oxido complexes,83,84 the negative spin density is the result of the spin polarization of the formally doubly occupied πxy, and πx2−y2 orbitals induced by the two unpaired electrons resided in the non-bonding Fe dxz and dyz orbitals. As a manifestation, the occupation numbers of formally doubly occupied πxy, and πx2−y2 are considerably less than 2, while those of their correspond antibonding orbitals (
NR coordination plane). As elaborated in the previous studies for related high-valent iron–nitrido and –oxido complexes,83,84 the negative spin density is the result of the spin polarization of the formally doubly occupied πxy, and πx2−y2 orbitals induced by the two unpaired electrons resided in the non-bonding Fe dxz and dyz orbitals. As a manifestation, the occupation numbers of formally doubly occupied πxy, and πx2−y2 are considerably less than 2, while those of their correspond antibonding orbitals (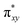 and
and 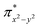 ) are substantially deviated from 0. The drastically reduced covalent interactions between Fe and two imido ligands render the two singly occupied orbitals (Fe dxz and dyz) essentially non-bonding, which leads to a more pronounced spin polarization effect compared to well-studied Fe(IV)–oxido complexes. In the latter complexes Fe is involved in strong covalent interactions with the oxido ligand so that the singly occupied
) are substantially deviated from 0. The drastically reduced covalent interactions between Fe and two imido ligands render the two singly occupied orbitals (Fe dxz and dyz) essentially non-bonding, which leads to a more pronounced spin polarization effect compared to well-studied Fe(IV)–oxido complexes. In the latter complexes Fe is involved in strong covalent interactions with the oxido ligand so that the singly occupied 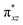 of the Fe dxz parentage and
of the Fe dxz parentage and 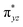 of the Fe dyz parentage contains substantial contributions from the O-px and O-py atomic orbitals, thus leading to sizable positive spin population in the O-px and O-py orbitals and a positive spin density on the oxido ligand. Thus the overall bonding interactions of Fe(IV)
of the Fe dyz parentage contains substantial contributions from the O-px and O-py atomic orbitals, thus leading to sizable positive spin population in the O-px and O-py orbitals and a positive spin density on the oxido ligand. Thus the overall bonding interactions of Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR moieties in 2 are fundamentally distinct from the well-studied Fe(IV)
NR moieties in 2 are fundamentally distinct from the well-studied Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species and the other reported Fe(IV)
O species and the other reported Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR complexes having a pseudo C4 symmetry. The differences of frontier molecular orbitals (MOs) in complex 1 (or 3) and 2 derived from CASSCF calculations that show strong covalent interactions between the iron and the imido ligand, as well as those from the well-studied Fe(IV)–oxido complexes are shown in Scheme 2.
NR complexes having a pseudo C4 symmetry. The differences of frontier molecular orbitals (MOs) in complex 1 (or 3) and 2 derived from CASSCF calculations that show strong covalent interactions between the iron and the imido ligand, as well as those from the well-studied Fe(IV)–oxido complexes are shown in Scheme 2.
Overall, the CASSCF calculations for complexes 1–3 successfully reproduced the experimentally determined magnetic spectroscopic parameters. However, since such type of calculations cannot predict Mössbauer isomer shifts, so DFT calculations were performed on the full complex structure to predict this spectroscopic parameter (see the ESI† for detailed computational method). The DFT optimized structures closely resembled the crystal structures of the three complexes (see Table S2 and Fig. S1†). Based on these, isomer shifts were further calculated. Although, the calculated isomer shift showed a systematic negative shift of ∼0.1 mm s−1 from the experimental values based on a published isomer shift calibration method,85 the overall trend is consistent with the experimental observations, giving a highest isomer shift for complex 2 (−0.19 mm s−1, DFT vs. −0.10 mm s−1, exp), a lowest isomer shift for complex 3 (−0.53 mm s−1, DFT vs. −0.41 mm s−1, exp), and an isomer shift of −0.42 mm s−1 (DFT, vs. −0.28 mm s−1, exp) for complex 1 (see Table S5† for the comparison of the calculated and the experimental Mössbauer parameters).
Structure-spin state correlation
To better understand the structural features that result in reduced covalent interactions between Fe and the imido ligands and the stabilization of an S = 1 spin state in complex 2, we carried out a series of DFT calculations. To assess the effect of different structural components on the geometric and electronic structures of the complex, we used a truncated molecular structure derived from the crystal structure of complex 2. In this truncated structural model, all substituents on NHC and imido ligands were replaced with methyl groups. The geometry optimizations on the truncated model, denoted Me_Me (for the truncated models, nomenclature X_Y is used. X represents the substituents on the NHC ring and Y represents the substituents on the imido ligands) in both S = 0 and S = 1 states showed that the Fe–ligand bond lengths, the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C angles as well as the N
N–C angles as well as the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe
Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond angles observed in complexes 1 and 2 can be well reproduced (refer to Table S2 and Fig. S12–S14†). This supports the validity of this truncated model for our analysis. In addition, different N-substituents on the imido ligands were further used to construct different truncated models for the calculations to investigate their effects on molecular structure.
N bond angles observed in complexes 1 and 2 can be well reproduced (refer to Table S2 and Fig. S12–S14†). This supports the validity of this truncated model for our analysis. In addition, different N-substituents on the imido ligands were further used to construct different truncated models for the calculations to investigate their effects on molecular structure.
According to the CASSCF calculations, the orbital overlap of natural orbitals (NOs) between Fe and the two N(imido) atoms in complexes 1 and 3 is generally excellent as shown in Fig. 4 and S10,† and Scheme 2A. However, in complex 2, the NOs overlap among these three atoms is significantly reduced due to the unfavorable relative orientation of the Fe 3d and the N(imido) p orbitals (Fig. 4 and Scheme 2B). The Fe 3d orbitals have a good π overlap with the p orbital from only one of the N atoms, leaving a poor σ overlap with the p orbital from the other N atom, thus leading to essentially non-bonding Fe dxz and dyz orbitals (see the 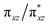 and the
and the 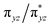 pair in Fig. 4). Therefore, structural factors that reduce the effective orbital overlap between Fe and the two N atoms are key to stabilize an S = 1 state.
pair in Fig. 4). Therefore, structural factors that reduce the effective orbital overlap between Fe and the two N atoms are key to stabilize an S = 1 state.
Two structural differences between complexes 1 (or 3) and 2 most likely affect the orbital overlap between Fe and the two N atoms, namely the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N(imido) bond length (1.638 Å in 1, 1.615 Å in 3, and 1.709 Å in 2) and the dihedral angle between the two planes formed by the two Fe–N–C(imido) moieties (C19–N2⋯N3–C23 dihedral angle, −25° in 1, 1° in 3, and −70° in 2). The tendency to form longer Fe
N(imido) bond length (1.638 Å in 1, 1.615 Å in 3, and 1.709 Å in 2) and the dihedral angle between the two planes formed by the two Fe–N–C(imido) moieties (C19–N2⋯N3–C23 dihedral angle, −25° in 1, 1° in 3, and −70° in 2). The tendency to form longer Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds in 2 was suggested to be originated from the use of an electron-withdrawing N-substituent, α,α-bis(trifluoromethyl)benzyl. Our DFT calculations support this hypothesis. When using different N-substituents to carry out DFT geometry optimizations on the truncated model, it is evident that alkyl electron-withdrawing N-substituents tend to elongate the Fe
N bonds in 2 was suggested to be originated from the use of an electron-withdrawing N-substituent, α,α-bis(trifluoromethyl)benzyl. Our DFT calculations support this hypothesis. When using different N-substituents to carry out DFT geometry optimizations on the truncated model, it is evident that alkyl electron-withdrawing N-substituents tend to elongate the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds, regardless of the spin state used, when compared with N–Me (Fig. 6, Table S2†). At the same time, the aryl N-substituents tend to elongate the Fe
N bonds, regardless of the spin state used, when compared with N–Me (Fig. 6, Table S2†). At the same time, the aryl N-substituents tend to elongate the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds in the singlet state and to a lesser extend in the triplet state. These observations are consistent with the understanding that both electron-withdrawing alkyl and aryl substituents can stabilize the lone pair electrons on the p orbitals of the imido N, thereby weakening the Fe
N bonds in the singlet state and to a lesser extend in the triplet state. These observations are consistent with the understanding that both electron-withdrawing alkyl and aryl substituents can stabilize the lone pair electrons on the p orbitals of the imido N, thereby weakening the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds. However, based on the DFT calculations on the truncated models, this effect only elongates the Fe
N bonds. However, based on the DFT calculations on the truncated models, this effect only elongates the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds by a small amount (<0.03 Å), and may not promote the spin state conversion on its own.
N bonds by a small amount (<0.03 Å), and may not promote the spin state conversion on its own.
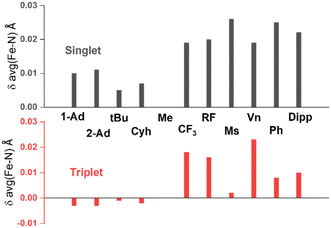 | ||
Fig. 6 Imido-substituent-dependent deviation of average Fe–N(imido) distance relative to that of the methyl substituent obtained from DFT optimization. The substituents on NHC side are two methyl groups in all cases presented here. Full data can be found in Table S2.† Abbreviations: Ad = adamantyl, tBu = tert-butyl, Cyh = cyclohexyl, RF![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CF3)3, Ms = methylsulfonyl, Vn = vinyl, Ph = phenyl. C(CF3)3, Ms = methylsulfonyl, Vn = vinyl, Ph = phenyl. | ||
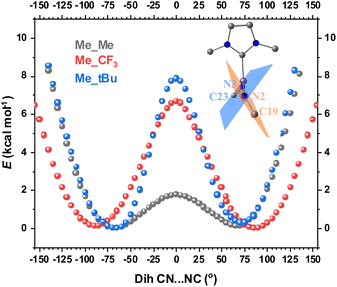
The second structural feature that affects the orbital overlap between Fe and the two N atoms is the C19–N2⋯N3–C23 dihedral angle (see Fig. 1 for atom labeling). For complex 2, this angle is −70°, which leads to overlap mismatch between the Fe 3d orbitals and N(imido) p orbitals, particularly between dxz and pz of N(imido), and between dxy and py of N(imido), thereby weakening the covalent interactions between Fe and the imido ligands (Scheme 2). This angle is likely to be controlled by steric interactions of the substituents. To provide evidence, we performed geometric scans along the C19–N2⋯N3–C23 dihedral angle on three truncated models, Me_Me, Me_tBu, and Me_CF3, in the S = 1 state. During scans, the values of other selected key bond lengths and angles were fixed at the crystal structure values from complex 2 (see the ESI† for details). The use of N–Me led to the identification of two local energy minima, with the dihedral angle of ±70° (Fig. 7), which is close to the angle observed in complex 2. Compared with a 0 degree dihedral angle, the 70 degree angle was favored by ∼2 kcal mol−1. When the bulkiness of the N-substituent was increased from N–Me to N–tBu, 65 degree dihedral angle was favored, with stronger stabilization (by ∼8 kcal mol−1). For N–CF3 substituent, 85 degree dihedral angle was favored, with stabilization of ∼7 kcal mol−1. Therefore, regardless of the nature of N-substituent (electron withdrawing vs. electron donating), its bulkiness favored a large C19–N2⋯N3–C23 dihedral angle, thus contributing to the mismatch of the orbital overlap between Fe and the two N atoms. Based on this analysis, we reason that the bulkier –CF3 moieties in 2 compared to the –CH3 moieties in 3 likely provide the needed steric effect to favor the large C19–N2⋯N3–C23 dihedral angle (−70° in 2vs. 1° in 3, Fig. 1). The aryl N-substituents (Dipp) in complex 1, although bulky, form good π–π interactions with the Dipp substituents on the NHC ligand, thus preventing the formation of a large C19–N2⋯N3–C23 dihedral angle (−25° in 1, Fig. 1).
Overall, the DFT results suggest that the combination of the N-substituent's steric properties and electron-withdrawing nature reduce the covalent interactions between Fe and the imido ligands in 2. As also revealed by the CASSCF calculations, this reduction in covalent interactions results in three close lying non-bonding Fe 3d based orbitals (dz2, dyz, and dxz), which stabilize an S = 1 ground spin state and lead to an orbital pseudo-degeneracy for 2.
Towards the HAT reactivity
Based on the previously published reactivity studies, it has been demonstrated that complex 2, with an S = 1 spin state, undergoes facile intramolecular dehydrogenation more readily than its S = 0 counterparts.53 According to previous DFT studies, the rate-limiting step for the intramolecular dehydrogenation observed in the Fe(IV)–bisimido complexes was suggested to be HAT, and the S = 1 Fe(IV)–bisimido complex was found to have a lower kinetic barrier and an higher driving force for HAT than the S = 0 Fe(IV)–bisimido complexes.53According to Bell–Evans–Polanyi principle,86,87 the driving force for C–H activation via HAT is determined by the difference in the bond dissociation free energies (BDFEs) between the C–H bond activated and the N–H bond formed in the resulting Fe(III)–NHR species in our case. In the Fe(IV)–bisimido complexes studied here, since the target C–H bond is from the same Dipp substituent, the increased driving force of HAT for complex 2 compared to the S = 0 complexes is likely only due to the stronger N–H BDFE in the resulting Fe(III)–NHR species derived from 2. This is supported by our DFT calculations. The N–H BDFE is highest for the Fe(III)–NHR species derived from complex 2, which is ∼15 kcal mol−1 and ∼10 kcal mol−1 greater than the N–H BDFEs of the Fe(III)–NHR species derived from complexes 1 and 3, respectively (Fig. S16†). To understand the differences in N–H BDFEs, we used the classical thermodynamic cycle, where the diagonal direction represents the single HAT step and the edges represent two stepwise processes: a sequential proton-transfer (PT) to the Fe(IV)–(NR)2 species followed by an electron transfer (ET) to form the final Fe(III)–NHR species or an ET step followed by a PT step to form the same final state (Fig. S15†). The free energies of the PT and the ET steps can be described by pKa values and reduction potentials (E0), respectively. By adopting a thermodynamic analysis proposed by Srnec and coworkers,88 we performed DFT analysis (see the ESI, Fig. S16, S17, and Tables S6, S7† for details). By defining an effective pKa (pKa,eff, an averaged pKa value from the pKa values of the two PT steps in the thermodynamic scheme) and an effective reduction potential (E0eff, an averaged E0 value from the two ET steps), we showed that although complex 2 had a reduced pKa,eff compared to those of complexes 1 and 3 due to the use of the electron-withdrawing substituent (∼5 and ∼7 units reduction calculated in the benzene solvent or 266 mV and 440 mV reduction when converting to electric potential unit), this withdrawing effect led to a significant increase of E0eff in 2 compared to the other two complexes (613 mV and 882 mV increase respectively). Therefore, the higher reduction potential of complex 2 is likely the dominant factor determining the stronger N–H BDFE of the resulting Fe(III)–NH species than those derived from 1 and 3, thus making 2 more reactive than the S = 0 complexes.
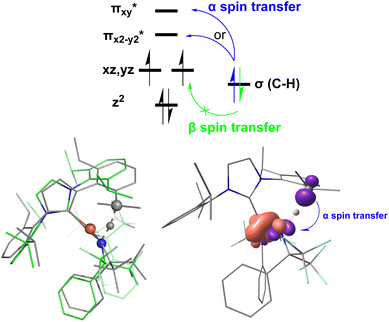
In addition to the HAT driving force, the kinetic barrier of the HAT reaction is equally important. Our CASSCF and DFT calculations suggest that the unique ground state electronic and geometric structures of complex 2 may directly contribute to the lowering of the reaction barrier by mimicking the features of the transition state in the HAT step. The ground state and the transition state structures of complex 2 are highly similar, featuring a large β spin density on the p orbital of imido nitrogen in the RN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe
Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR coordination plane (Fig. 5, 8, and S18†). This p orbital, which is involved in bonding/antibonding interactions with Fe dxy/dx2−y2 orbitals (see the
NR coordination plane (Fig. 5, 8, and S18†). This p orbital, which is involved in bonding/antibonding interactions with Fe dxy/dx2−y2 orbitals (see the 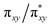 and the
and the 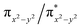 pair in Fig. 4), points toward the C–H bond to be activated on the Dipp substituent of NHC ligand, providing the necessary orbital overlap to facilitate the initial electron transfer from the C–H bond to the Fe(IV)
pair in Fig. 4), points toward the C–H bond to be activated on the Dipp substituent of NHC ligand, providing the necessary orbital overlap to facilitate the initial electron transfer from the C–H bond to the Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR moiety in the HAT process (Fig. 5 and 8). In addition, the transition state spin density distribution reveals that the initial electron transfer may occur via an α spin transfer since the carbon of the C–H bond being activated bears a β spin density (Fig. 8). This α spin transfer may be facilitated by the β spin density on the p orbital of imido nitrogen (Fig. 8). The α spin transfer channel of HAT in 2 resembles the σ pathway in the well-studied Fe(IV)
NR moiety in the HAT process (Fig. 5 and 8). In addition, the transition state spin density distribution reveals that the initial electron transfer may occur via an α spin transfer since the carbon of the C–H bond being activated bears a β spin density (Fig. 8). This α spin transfer may be facilitated by the β spin density on the p orbital of imido nitrogen (Fig. 8). The α spin transfer channel of HAT in 2 resembles the σ pathway in the well-studied Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O complexes, where due to the positioning of the C–H bond relative to the Fe(IV)
O complexes, where due to the positioning of the C–H bond relative to the Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond vector an α spin transfer to the σ* MO with Fe dz2 parentage occurs in the so-called σ pathway. Additionally, in Fe(IV)
O bond vector an α spin transfer to the σ* MO with Fe dz2 parentage occurs in the so-called σ pathway. Additionally, in Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O complexes, a β spin transfer to the singly occupied π* MO with Fe dxz/dyz parentage is also possible, which occurs in the π pathway (Schemes 2 and S1†). This dual-channel reactivity does not likely to exist in 2, since the singly occupied frontier MOs in 2 are essentially non-bonding dxz/dyz orbitals (Fig. 4), which exhibit minimal orbital overlap with the C–H bond, thus preventing an efficient β spin transfer during the HAT process. Thus, 2 likely carries out HAT via a single α spin transfer channel (Fig. 8).
O complexes, a β spin transfer to the singly occupied π* MO with Fe dxz/dyz parentage is also possible, which occurs in the π pathway (Schemes 2 and S1†). This dual-channel reactivity does not likely to exist in 2, since the singly occupied frontier MOs in 2 are essentially non-bonding dxz/dyz orbitals (Fig. 4), which exhibit minimal orbital overlap with the C–H bond, thus preventing an efficient β spin transfer during the HAT process. Thus, 2 likely carries out HAT via a single α spin transfer channel (Fig. 8).
In summary, the facile C–H activation reactivity of S = 1 complex 2 correlates well with its electronic structure, which features a β spin density on the imido nitrogen due to the reduced covalent interactions between Fe and the imido ligands and the strengthened spin polarization effect, an exposed N p orbital of the imido ligand towards the C–H bond due to bent and twisted Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–R angle and C–N⋯N–C dihedral angle, and an electron-withdrawing N-substituent.
N–R angle and C–N⋯N–C dihedral angle, and an electron-withdrawing N-substituent.
Conclusions
In this study, a rare S = 1 Fe(IV)–bisimido complex bearing electron-withdrawing N-substituents, 2, has been subjected to in-depth structural, spectroscopic (NRVS and Mössbauer), and magnetization studies. These studies were compared to those on two S = 0 Fe(IV)–bisimido complexes without electron-withdrawing N-substituents, 1 and 3. The results showed that the structural and vibrational properties of these complexes are primarily determined by the covalent Fe(IV)–imido bonding interactions. However, complex 2 with an S = 1 ground state exhibits significantly reduced covalency, as evidenced by the longer Fe–imido bonds (0.07–0.1 Å longer) and the lower Fe–imido vibration frequencies (>100 cm−1 lower) compared to the diamagnetic 1 and 3. In addition, 2 shows an orbitally nearly degenerate electronic ground state, which leads to a sizeable unquenched orbital angular momentum and a large positive internal magnetic field. The CASSCF/NEVPT2 calculations further elucidated that the unique ground state electronic structure of 2 is due to the spin–orbit coupling to a low-lying excited triplet state corresponding to a single electron excitation from the non-bonding dz2 orbital to the dyz based MO. And the conversion of the singlet 1 (or 3) to the triplet 2 is the result of the significant reduction in the covalent interactions between iron and the imido nitrogens, which converts the dyz and dxz based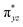 and
and 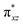 orbitals in 1 (or 3) to the non-bonding dyz and dxz orbitals. With three energetically close-lying iron non-bonding orbitals (dz2, dyz, and dxz), an S = 1 spin state is thus favored. To further explore the structural and electronic factors in controlling the spin state of these Fe(IV)–bisimido complexes, DFT calculations were performed. The results suggested that the steric effect of the N-substituents and their electron-withdrawing nature are two synergistic factors that reduce covalent interactions between Fe and the imido ligands and stabilize the S = 1 state for complex 2. Finally, the ground state electronic structure of 2, derived from structural, spectroscopic, and theoretical investigations, is connected to its chemical reactivity. It was found that the existence of a radical character on the imido nitrogen, an exposed N p orbital of the imido ligand towards the C–H bond to be activated, and the use of an electron-withdrawing N-substituent are key factors that provide both kinetic and thermodynamic advantages over the S = 0 counterparts to enable facile C–H activation reactivity. Remarkably, the two singly occupied Fe non-bonding dyz and dxz orbitals exert strong spin-polarization effect that results in a sizable β spin population on the imido nitrogens in 2, which facilitates the α spin transfer in the HAT process. Thus, complex 2 represents the first identified example of a high valent iron–imido species that conducts HAT via a single α spin transfer reaction channel, distinguishing it from iron(IV)–oxido complexes.
orbitals in 1 (or 3) to the non-bonding dyz and dxz orbitals. With three energetically close-lying iron non-bonding orbitals (dz2, dyz, and dxz), an S = 1 spin state is thus favored. To further explore the structural and electronic factors in controlling the spin state of these Fe(IV)–bisimido complexes, DFT calculations were performed. The results suggested that the steric effect of the N-substituents and their electron-withdrawing nature are two synergistic factors that reduce covalent interactions between Fe and the imido ligands and stabilize the S = 1 state for complex 2. Finally, the ground state electronic structure of 2, derived from structural, spectroscopic, and theoretical investigations, is connected to its chemical reactivity. It was found that the existence of a radical character on the imido nitrogen, an exposed N p orbital of the imido ligand towards the C–H bond to be activated, and the use of an electron-withdrawing N-substituent are key factors that provide both kinetic and thermodynamic advantages over the S = 0 counterparts to enable facile C–H activation reactivity. Remarkably, the two singly occupied Fe non-bonding dyz and dxz orbitals exert strong spin-polarization effect that results in a sizable β spin population on the imido nitrogens in 2, which facilitates the α spin transfer in the HAT process. Thus, complex 2 represents the first identified example of a high valent iron–imido species that conducts HAT via a single α spin transfer reaction channel, distinguishing it from iron(IV)–oxido complexes.
Data availability
Crystallographic data for compound 1 has been deposited at CCDC under accessing number 2172442. The coordinates of DFT optimized structures have been uploaded as part of the supplementary material.Author contributions
Conceptualization: L. D., S. Y., Y. G.; Methodology, M. Y. H., J. Z., E. E. A., L. D., S. Y., Y. G.; Investigation: J. X.; Q. L.; B. L., M. Y. H., J. Z., E. E. A., L. D., S. Y., Y. G.; Formal Analysis: J. X.; Q. L., L. D., S. Y., Y. G.; Writing – Original Draft: J. X., Y. G.; Writing – Review & Editing, J. X., Q. L., L. D., S. Y., Y. G.; Funding Acquisition: L. D., S. Y., Y. G.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the National Institute of Health (NIH GM125924 to Y. G., GM127588 to W. c. C.) and the National Natural Science Foundation of China (NNSFC No. 21725104 and 22061160464 to D. L., No. 92161204 to S. Y.) for funding. The NRVS data were recorded at the Advanced Photon Source (APS), Argonne National Laboratory (proposal GUP-60939, GUP-68490, and GUP-73059). The use of APS is supported by the Department of Energy. This work also used the Extreme Science and Engineering Discovery Environment (XSEDE) at Pittsburgh Supercomputing Center for the computational resource (allocation number TG-CHE200003). The authors would like to thank Prof. Emile L. Bominaar for commenting and proofreading the article. Finally, this study is dedicated to the memory of Dr Eckard Bill.Notes and references
- M. P. Mehn and J. C. Peters, J. Inorg. Biochem., 2006, 100, 634–643 CrossRef CAS PubMed
.
- L. Que, Acc. Chem. Res., 2007, 40, 493–500 CrossRef CAS PubMed
.
- N. P. Dunham and F. H. Arnold, ACS Catal., 2020, 10, 12239–12255 CrossRef CAS PubMed
.
- E. I. Solomon, D. E. DeWeese and J. T. Babicz, Biochemistry, 2021, 60, 3497–3506 CrossRef CAS PubMed
.
-
C.-M. Che, C.-Y. Zhou and E. L.-M. Wong, Catalysis by Fe=X Complexes (X = NR, CR2) - Iron Catalysis: Fundamentals and Applications, ed. B. Plietker, Springer, Berlin, Heidelberg, 2011, pp. 111–138 Search PubMed
.
- W. Nam, Acc. Chem. Res., 2007, 40, 522–531 CrossRef CAS PubMed
.
- C. Krebs, D. G. Fujimori, C. T. Walsh and J. M. J. Bollinger, Acc. Chem. Res., 2007, 40, 484–492 CrossRef CAS PubMed
.
- J. M. Smith and D. Subedi, Dalt. Trans., 2012, 41, 1423–1429 RSC
.
- J. Hohenberger, K. Ray and K. Meyer, Nat. Commun., 2012, 3, 720 CrossRef PubMed
.
- G. Olivo, O. Cussó, M. Borrell and M. Costas, J. Biol. Inorg Chem., 2017, 22, 425–452 CrossRef CAS PubMed
.
- M. C. White and J. Zhao, J. Am. Chem. Soc., 2018, 140, 13988–14009 CrossRef CAS PubMed
.
- X. Huang and J. T. Groves, Chem. Rev., 2018, 118, 2491–2553 CrossRef CAS PubMed
.
- J. Cheng, L. Wang, P. Wang and L. Deng, Chem. Rev., 2018, 118, 9930–9987 CrossRef CAS PubMed
.
-
2-Oxoglutarate-Dependent Oxygenases, ed C. Schofield and R. Hausinger, Royal Society of Chemistry, Cambridge, 2015 Search PubMed
.
-
Cytochrome P450, ed. P. R. Ortiz de Montellano, Springer International Publishing, Cham, 4th edn, 2015 Search PubMed
.
-
Y. Guo, W. Chang, J. Li and M. Davidson, in Comprehensive Coordination Chemistry III, ed. E. C. Constable, G. Parkin and L. B. T.-C. C. C. I. I. I. Que Jr, Elsevier, Oxford, 2021, pp. 269–300 Search PubMed
.
-
Y. Guo, W. Chang, J. Li and M. Davidson, in Comprehensive Coordination Chemistry III, eds. E. C. Constable, G. Parkin and L. B. T.-C. C. C. I. I. I. Que Jr, Elsevier, Oxford, 2021, pp. 301–332 Search PubMed
.
- J. M. Mayer, Acc. Chem. Res., 2011, 44, 36–46 CrossRef CAS PubMed
.
- J. L. Lee, D. L. Ross, S. K. Barman, J. W. Ziller and A. S. Borovik, Inorg. Chem., 2021, 60, 13759–13783 CrossRef CAS PubMed
.
- M. Puri and L. Que, Acc. Chem. Res., 2015, 48, 2443–2452 CrossRef CAS PubMed
.
- T. H. Yosca, A. P. Ledray, J. Ngo and M. T. Green, J. Biol. Inorg Chem., 2017, 22, 209–220 CrossRef CAS PubMed
.
- M. L. Neidig, A. Decker, O. W. Choroba, F. Huang, M. Kavana, G. R. Moran, J. B. Spencer and E. I. Solomon, Proc. Natl. Acad. Sci. USA, 2006, 103, 12966–12973 CrossRef CAS PubMed
.
- B. Mondal, L. Roy, F. Neese and S. Ye, Isr. J. Chem., 2016, 56, 763–772 CrossRef CAS
.
- S. Shaik, H. Chen and D. Janardanan, Nat. Chem., 2011, 3, 19–27 CrossRef CAS PubMed
.
- S. Shaik, H. Hirao and D. Kumar, Acc. Chem. Res., 2007, 40, 532–542 CrossRef CAS PubMed
.
-
M. G. Quesne, A. S. Faponle, D. P. Goldberg and S. P. de Visser, in Spin States in Biochemistry and Inorganic Chemistry, ed. M. Swart and M. Costas, John Wiley & Sons, Ltd, Oxford, UK, 2015, pp. 185–202 Search PubMed
.
- T. G. Driver, Org. Biomol. Chem., 2010, 8, 3831–3846 RSC
.
- L. Zhang and L. Deng, Chin. Sci. Bull., 2012, 57, 2352–2360 CrossRef CAS
.
- P. Wang and L. Deng, Chin. J. Chem., 2018, 36, 1222–1240 CrossRef CAS
.
- Y. Liu, T. You, T.-T. Wang and C.-M. Che, Tetrahedron, 2019, 75, 130607 CrossRef
.
- Y. Liu, T. You, H.-X. Wang, Z. Tang, C.-Y. Zhou and C.-M. Che, Chem. Soc. Rev., 2020, 49, 5310–5358 RSC
.
- A. K. Verma, T. N. Nazif, C. Achim and S. C. Lee, J. Am. Chem. Soc., 2000, 122, 11013–11014 CrossRef CAS
.
- C. M. Thomas, N. P. Mankad and J. C. Peters, J. Am. Chem. Soc., 2006, 128, 4956–4957 CrossRef CAS PubMed
.
- S. Kuppuswamy, T. M. Powers, B. M. Johnson, M. W. Bezpalko, C. K. Brozek, B. M. Foxman, L. A. Berben and C. M. Thomas, Inorg. Chem., 2013, 52, 4802–4811 CrossRef CAS PubMed
.
- R. E. Cowley and P. L. Holland, Inorg. Chem., 2012, 51, 8352–8361 CrossRef CAS PubMed
.
- R. E. Cowley, N. A. Eckert, S. Vaddadi, T. M. Figg, T. R. Cundari and P. L. Holland, J. Am. Chem. Soc., 2011, 133, 9796–9811 CrossRef CAS PubMed
.
- R. E. Cowley, N. J. DeYonker, N. A. Eckert, T. R. Cundari, S. DeBeer, E. Bill, X. Ottenwaelder, C. Flaschenriem and P. L. Holland, Inorg. Chem., 2010, 49, 6172–6187 CrossRef CAS PubMed
.
- N. A. Eckert, S. Vaddadi, S. Stoian, R. J. Lachicotte, T. R. Cundari and P. L. Holland, Angew. Chem., Int. Ed., 2006, 45, 6868–6871 CrossRef CAS PubMed
.
- M. R. Anneser, G. R. Elpitiya, J. Townsend, E. J. Johnson, X. B. Powers, J. F. DeJesus, K. D. Vogiatzis and D. M. Jenkins, Angew. Chem., Int. Ed., 2019, 58, 8115–8118 CrossRef CAS PubMed
.
- J. A. Bellow, M. Yousif, A. C. Cabelof, R. L. Lord and S. Groysman, Organometallics, 2015, 34, 2917–2923 CrossRef CAS
.
- S. Hong, X. Lu, Y.-M. Lee, M. S. Seo, T. Ohta, T. Ogura, M. Clémancey, P. Maldivi, J.-M. Latour, R. Sarangi and W. Nam, J. Am. Chem. Soc., 2017, 139, 14372–14375 CrossRef CAS PubMed
.
- S. Hong, K. D. Sutherlin, A. K. Vardhaman, J. J. Yan, S. Park, Y. Lee, S. Jang, X. Lu, T. Ohta, T. Ogura, E. I. Solomon and W. Nam, J. Am. Chem. Soc., 2017, 139, 8800–8803 CrossRef CAS PubMed
.
- E. J. Klinker, T. A. Jackson, M. P. Jensen, A. Stubna, G. Juhász, E. L. Bominaar, E. Münck and L. Que Jr, Angew. Chem., Int. Ed., 2006, 45, 7394–7397 CrossRef CAS PubMed
.
- S. D. Brown and J. C. Peters, J. Am. Chem. Soc., 2004, 126, 4538–4539 CrossRef CAS PubMed
.
- P. Leeladee, G. N. L. Jameson, M. A. Siegler, D. Kumar, S. P. de Visser and D. P. Goldberg, Inorg. Chem., 2013, 52, 4668–4682 CrossRef CAS PubMed
.
- G. Sabenya, I. Gamba, L. Gómez, M. Clémancey, J. R. Frisch, E. J. Klinker, G. Blondin, S. Torelli, L. Que, V. Martin-Diaconescu, J.-M. Latour, J. Lloret-Fillol and M. Costas, Chem. Sci., 2019, 10, 9513–9529 RSC
.
- J. Cheng, J. Liu, X. Leng, T. Lohmiller, A. Schnegg, E. Bill, S. Ye and L. Deng, Inorg. Chem., 2019, 58, 7634–7644 CrossRef CAS PubMed
.
- L. Wang, L. Hu, H. Zhang, H. Chen and L. Deng, J. Am. Chem. Soc., 2015, 137, 14196–14207 CrossRef CAS PubMed
.
- H. Zhang, Z. Ouyang, Y. Liu, Q. Zhang, L. Wang and L. Deng, Angew. Chem., Int. Ed., 2014, 53, 8432–8436 CrossRef CAS PubMed
.
- K. Searles, S. Fortier, M. M. Khusniyarov, P. J. Carroll, J. Sutter, K. Meyer, D. J. Mindiola and K. G. Caulton, Angew. Chem., Int. Ed., 2014, 53, 14139–14143 CrossRef CAS PubMed
.
- B. P. Jacobs, P. T. Wolczanski, Q. Jiang, T. R. Cundari and S. N. MacMillan, J. Am. Chem. Soc., 2017, 139, 12145–12148 CrossRef CAS PubMed
.
- J. L. Martinez, S. A. Lutz, H. Yang, J. Xie, J. Telser, B. M. Hoffman, V. Carta, M. Pink, Y. Losovyj and J. M. Smith, Science, 2020, 370, 356–359 CrossRef CAS PubMed
.
- Q. Liu, L. Long, P. Ma, Y. Ma, X. Leng, J. Xiao, H. Chen and L. Deng, Cell Rep. Phys. Sci., 2021, 2, 100454 CrossRef CAS
.
- S. D. Brown, T. A. Betley and J. C. Peters, J. Am. Chem. Soc., 2003, 125, 322–323 CrossRef CAS PubMed
.
- M. J. T. Wilding, D. A. Iovan and T. A. Betley, J. Am. Chem. Soc., 2017, 139, 12043–12049 CrossRef CAS PubMed
.
- M. J. T. Wilding, D. A. Iovan, A. T. Wrobel, J. T. Lukens, S. N. MacMillan, K. M. Lancaster and T. A. Betley, J. Am. Chem. Soc., 2017, 139, 14757–14766 CrossRef CAS PubMed
.
- D. A. Iovan and T. A. Betley, J. Am. Chem. Soc., 2016, 138, 1983–1993 CrossRef CAS PubMed
.
- E. T. Hennessy, R. Y. Liu, D. A. Iovan, R. A. Duncan and T. A. Betley, Chem. Sci., 2014, 5, 1526–1532 RSC
.
- E. T. Hennessy and T. A. Betley, Science, 2013, 340, 591–595 CrossRef CAS PubMed
.
- E. R. King, E. T. Hennessy and T. A. Betley, J. Am. Chem. Soc., 2011, 133, 4917–4923 CrossRef CAS PubMed
.
- I. Nieto, F. Ding, R. P. Bontchev, H. Wang and J. M. Smith, J. Am. Chem. Soc., 2008, 130, 2716–2717 CrossRef CAS PubMed
.
- A. K. Vardhaman, P. Barman, S. Kumar, C. V Sastri, D. Kumar and S. P. de Visser, Angew. Chem., Int. Ed., 2013, 52, 12288–12292 CrossRef CAS PubMed
.
- S. Kumar, A. S. Faponle, P. Barman, A. K. Vardhaman, C. V Sastri, D. Kumar and S. P. De Visser, J. Am. Chem. Soc., 2014, 136, 17102–17115 CrossRef CAS PubMed
.
- G. Mukherjee, F. G. C. Reinhard, U. K. Bagha, C. V Sastri and S. P. de Visser, Dalt. Trans., 2020, 49, 5921–5931 RSC
.
- D. M. Spasyuk, S. H. Carpenter, C. E. Kefalidis, W. E. Piers, M. L. Neidig and L. Maron, Chem. Sci., 2016, 7, 5939–5944 RSC
.
- B. O. Roos, Adv. Chem. Phys., 1987, 399–445 CAS
.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS
.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS
.
- J. T. Sage, C. Paxson, G. R. a Wyllie, W. Sturhahn, S. M. Durbin, P. M. Champion, E. E. Alp and W. R. Scheidt, J. Phys. Condens. Matter, 2001, 13, 7707–7722 CrossRef CAS
.
- W. Sturhahn, J. Phys. Condens. Matter, 2004, 16, S497–S530 CrossRef CAS
.
- D. E. Wigley, Prog. Inorg. Chem., 1994, 239–482 CAS
.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed
.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- M. P. Mehn, S. D. Brown, D. M. Jenkins, J. C. Peters and L. Que, Inorg. Chem., 2006, 45, 7417–7427 CrossRef CAS PubMed
.
- H. Andres, E. L. Bominaar, J. M. Smith, N. A. Eckert, P. L. Holland and E. Münck, J. Am. Chem. Soc., 2002, 124, 3012–3025 CrossRef CAS PubMed
.
- B. M. Hakey, D. C. Leary, J. Xiong, C. F. Harris, J. M. Darmon, J. L. Petersen, J. F. Berry, Y. Guo and C. Milsmann, Inorg. Chem., 2021, 60, 18575–18588 CrossRef CAS PubMed
.
- J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577–581 CrossRef CAS PubMed
.
- M. Atanasov, J. M. Zadrozny, J. R. Long and F. Neese, Chem. Sci., 2013, 4, 139–156 RSC
.
- M. Keilwerth, J. Hohenberger, F. W. Heinemann, J. Sutter, A. Scheurer, H. Fang, E. Bill, F. Neese, S. Ye and K. Meyer, J. Am. Chem. Soc., 2019, 141, 17217–17235 CrossRef CAS PubMed
.
- M. Tarrago, C. Römelt, J. Nehrkorn, A. Schnegg, F. Neese, E. Bill and S. Ye, Inorg. Chem., 2021, 60, 4966–4985 CrossRef CAS PubMed
.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed
.
- B. Mondal, F. Neese, E. Bill and S. Ye, J. Am. Chem. Soc., 2018, 140, 9531–9544 CrossRef CAS PubMed
.
- H.-C. Chang, B. Mondal, H. Fang, F. Neese, E. Bill and S. Ye, J. Am. Chem. Soc., 2019, 141, 2421–2434 CrossRef CAS PubMed
.
- M. Römelt, S. Ye and F. Neese, Inorg. Chem., 2009, 48, 784–785 CrossRef PubMed
.
- R. P. Bell, Proc. R. Soc. London, Ser. A, 1936, 154, 414–429 Search PubMed
.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1938, 34, 11–24 RSC
.
- D. Bím, M. Maldonado-Domínguez, L. Rulíšek and M. Srnec, Proc. Natl. Acad. Sci. USA, 2018, 115, E10287–E10294 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2172442. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2sc06273a |
| This journal is © The Royal Society of Chemistry 2023 |