Substituting density functional theory in reaction barrier calculations for hydrogen atom transfer in proteins

Abstract

Hydrogen atom transfer (HAT) reactions are important in many biological systems. As these reactions are hard to observe experimentally, it is of high interest to shed light on them using simulations. Here, we present a machine learning model based on graph neural networks for the prediction of energy barriers of HAT reactions in proteins. As input, the model uses exclusively non-optimized structures as obtained from classical simulations. It was trained on more than 17 000 energy barriers calculated using hybrid density functional theory. We built and evaluated the model in the context of HAT in collagen, but we show that the same workflow can easily be applied to HAT reactions in other biological or synthetic polymers. We obtain for relevant reactions (small reaction distances) a model with good predictive power (R² ∼ 0.9 and mean absolute error of <3 kcal mol⁻¹). As the inference speed is high, this model enables evaluations of dozens of chemical situations within seconds. When combined with molecular dynamics in a kinetic Monte-Carlo scheme, the model paves the way toward reactive simulations.

---

1. Introduction

Free radicals critically impact and can be deleterious for biological systems.^1,2 They are highly reactive and lead to unspecific damage of proteins, DNA, and lipids, causing various diseases and aging.³ Radical formation is followed by a plethora of subsequent reactions, most importantly radical propagation through hydrogen atom transfer (HAT).⁴ Radical formation and propagation are not only at play in biomolecules but very analogously occur in synthetic polymers, and similarly lead to damage and material aging.^5,6 Due to the high reactivity of radicals, intermediate products of radical reactions can be very short-lived and therefore hard to capture experimentally. Predicting the fate of radicals in proteins or other (bio)polymers is thus of utmost relevance to better understand and combat radical-induced damage.

A major challenge in predicting chemical reactivity in proteins, such as unspecific radical transfer reactions, is the molecular environment of the reaction: it determines the reactivity but is both chemically very diverse and highly dynamic. This leads to a virtually infinite number of possible reaction scenarios, in which reactants represent instances within a vast chemical and conformational space. As a consequence, directly computing this amount of radical reactions by ab initio calculations is computationally not feasible. Instead, machine learning can leverage quantum chemical calculations by predicting reactivity based on an initial quantum chemical data set. We here set out to predict the energy barriers of hydrogen atom transfer reactions in proteins using graph neural networks that are trained on computed energy barriers.

Machine learning has been successfully applied to predict structures, energies, and properties of molecules.^7–11 However, for the prediction of kinetic quantities, machine learning only gained traction in the last years.¹² Previous works often reported respectable accuracies below 1 kcal mol⁻¹, but relied on inputs derived from DFT calculations.^13–15 While a low number of single point energy calculations are still less expensive than the otherwise required optimizations, ideally one would want to replace all DFT calculations at inference time, be it at the loss of some accuracy. And indeed, this has been attempted for, e.g., catalysis on metal surfaces and reactions between small molecules, reaching an MAE of 5 and 2.6 kcal mol⁻¹, respectively.^16,17 One notable exception is the prediction of dihydrogen activation with Vaska's complex by co-author Friederich et al., where accuracies below 1 kcal mol⁻¹ were achieved without the need for DFT calculated inputs, however over a very narrow range of 0–25 kcal mol⁻¹. Taken together, predicting reaction barriers by a surrogate model which does not use DFT data as input has remained a challenge, in particular in case of a complex chemical environment and a large variation in barriers.

For the prediction of HAT energy barriers in this work, we decided to use equivariant graph neural networks, as they performed best on previous tests compared to random forest regressors, dense NNs and non-equivariant NNs. This is representative of the overall development in representations of chemical systems for machine learning. Representations such as the Coulomb matrix¹⁸ perform well on simpler tasks, but are typically outperformed by more expressive representations, e.g., atom-centered symmetry functions,⁷ smooth overlap of atomic positions (SOAP),¹⁹ and, in the last years, graph neural networks (GNNs).^9,20 The latest accuracy increases can be partially attributed to moving from invariant to equivariant models, where we arrive at the GNN used in this work, namely PaiNN.^21,22 Originally, PaiNN was designed to predict global quantities like total energy, but as the reaction barrier does not scale with system size, we adjusted the architecture for the prediction of local quantities.

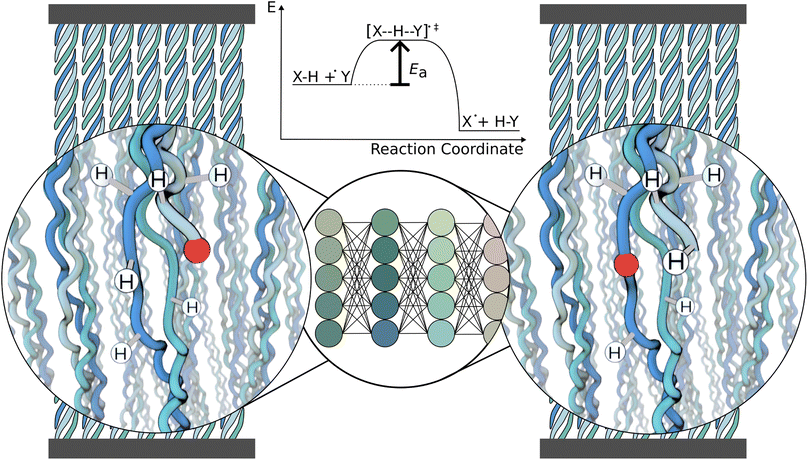
In this work, we focus on predicting HAT reaction barriers within one particular protein system, collagen (Fig. 1). As shown earlier by some authors of this article, stretching collagen generates mechanoradicals within the protein.²³ These radicals rapidly localize on specific protein residues, dihydroxyphenylalanine (DOPA), plausibly through a sequence of HAT reactions. Insights into the reaction pathway of radicals might help in the design of similarly durable polymer systems as collagen but are experimentally challenging to obtain. Our work is an important step towards predicting radical reactions in collagen. However, as we show in addition, the model is also applicable to proteins of different composition. We also suggest the developed workflow to be straightforwardly applicable to other, not necessarily biological, polymers.

Fig. 1 Schematic of the workflow. The system of interest here is a collagen fibril under tension, containing radicals (red). A cutout of the fibril is presented to the neural network, which predicts the energy barrier E_a for every possible reaction, one at a time. This information can be used to decide which reaction is likely to occur and continue the simulation after the reaction.

We built thousands of molecular fragments as they occur in collagen and calculated HAT energy barriers on the level of hybrid density functional theory (DFT). The computed reaction barriers range between 0 kcal mol⁻¹ and 175 kcal mol⁻¹ and are highly dependent on the local environment, rationalizing the machine learning approach. We used our quantum chemical data to train the GNN, which is able to predict barriers approaching DFT accuracy.

Our machine learning model predicts the energy barrier for one selected reaction at a time while taking the chemical environment around the radical in the reactant state as input (Fig. 1). Importantly, the reactant state is directly cut out from a molecular dynamics (MD) simulation, and no optimization is needed prior to the barrier prediction, neither a single step energy calculation as input. It thus can be used as a surrogate model of hydrogen atom transfer within classical MD simulations to model radical propagation within collagen or other (bio)materials on the fly, e.g., by using hybrid kinetic Monte-Carlo and MD simulations.²⁴ Our GNN-based approach tackles the challenge of predicting reaction barriers in a heterogeneous and dynamic chemical setting, and will likely prove useful for other complex soft matter systems.

2. Methods

2.1 Data generation

The geometries to learn HAT energy barriers were generated in two ways: first, in a procedural approach from single amino acids, second by extracting reactive systems from a larger atomistic model simulated using MD. In the following, the structures from the procedural and MD approaches will be called synthetic systems and trajectory systems, respectively.

Synthetic systems are pairs of amino acids arranged in a way that two hydrogen atoms are in a defined position to one another. As shown in Fig. 2A, the translation distance between the hydrogens, the rotation, and the tilt angle are varied. The positions of these two central hydrogen atoms represent the start and end positions of a single hydrogen atom undergoing the HAT reaction. Furthermore, intramolecular reactions are generated from within single amino acids. Combinations of hydrogen atoms with less than 4 Å distance are considered. Systems with atoms closer than 0.8 Å to the transition path are removed.

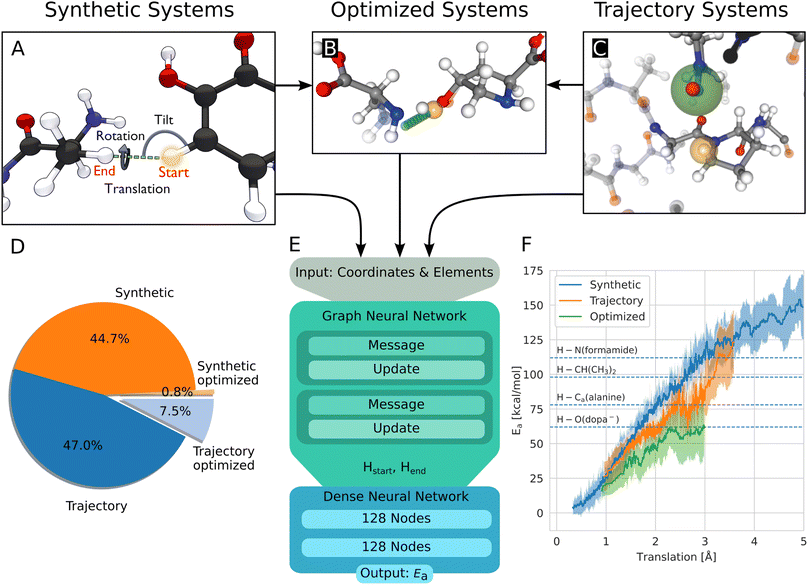Fig. 2 (A) Build process of reactive HAT systems for the synthetic data set. The HAT reaction between two example molecules is shown. The distance between the start and end position of the transferring hydrogen (translation), the angle formed by the transferring hydrogen with the donating and accepting heavy atoms (tilt), and the dihedral angle around the hydrogen atom transfer axis (rotation) were varied to construct the synthetic systems. (B) Data set of optimized structures, built from synthetic and trajectory systems. The optimized transition state is shown, alongside the interpolated reaction path of the hydrogen in green and the start position in orange. The non-optimized structure is shown translucently. (C) A trajectory system with its environment shown translucently. The radical heavy atom is highlighted in green and the reacting hydrogen in yellow. The solid-drawn atoms at the border to the translucent environment are used in the construction of the capping groups, the translucent atoms are discarded. (D) Data distribution of the synthetic and trajectory data sets. (E) Architecture of the used graph neural network, based on PaiNN.²² (F) Rolling average of the calculated energy barriers of HAT reactions in the data set vs. the distance the hydrogen has to move during the reaction. The shaded area corresponds to ± standard deviation, dashed lines indicate bond dissociation energies for context.²⁵

The generation of reactive systems from MD trajectories starts from a collagen model obtained from Colbuilder.²⁶ The model is simulated using GROMACS 2020. In the resulting trajectory, possible reaction sites are identified by monitoring H–H distances. As energy barriers, E_a, heavily depend on the translation distance, an emphasis is put on smaller translations when sampling. The HAT candidates are cut out together with their close surrounding from the bigger system, excluding solvent molecules. To generate chemically meaningful systems and to allow reference DFT calculations, the cut-out sections of the protein are capped using N-methyl and acetyl groups. In Fig. 2C, the capping procedure is visualized (also see Fig. S3B†). For a given set of selected atoms in a trajectory, only the system with the smallest translation distance is kept, as otherwise a large amount of highly correlated systems would be generated.

At this point, the reactive systems have been defined. Further preparation steps are applied to synthetic as well as trajectory systems. One of the two central hydrogen atoms is removed and therefore acts as the starting location of the radical. Then, the reaction path is estimated by interpolating the position of the remaining hydrogen atom from its starting position to the position of the removed hydrogen atom. We originally used 11 equally spaced interpolation increments, but after the first set of calculations of 1600 HAT reactions, all barriers were found to be located within steps 4–8, 1 or 11, so steps 2, 3, 9, and 10 are omitted in all later calculations and the data used here. This means, we define the reaction paths using seven structures. Along the reaction path, the energy of the system is calculated using the hybrid functional BMK²⁷ together with the 6-31+G(2df,p) basis set, using Gaussian 09 (rev D.01).²⁸ Electronic energies were used throughout the study. The BMK functional was chosen, because it was designed for kinetic studies, and it has proven highly capable of accurately calculating HAT reaction barriers.²⁹ More details on the building of the systems and the calculations are given in the ESI.†

In many cases, the guess of the transition path by interpolating between the start and end position of the hydrogen whilst keeping the rest of the system frozen is reasonable, however, it introduces a significant error in conformationally flexible systems. Furthermore, since no free radical parameters are available in the MD simulations, all resulting geometries correspond to closed-shell species (Fig. S4†). To address this, a subset of the combined synthetic and trajectory data set is optimized at the same QM level as used for the energy calculations. More precisely, as a reaction is defined by its reactants, the transition state, and the end products, those three structures are being optimized to their energy minima or saddle point, respectively. For transition states, frequency calculations were performed to ensure the existence of a single imaginary frequency corresponding to the correct reaction. During optimization, we freeze all atom positions except the donor and acceptor atoms and directly bonded hydrogens, to reflect the embedding of the reactants into the structure of the material, here the protein backbone, and to prevent contributions to the calculated energy barrier from rearrangements in the reactants unrelated to the HAT. As the model is intended to be used on many MD trajectory snapshots, we want to restrict the DFT optimization to degrees of freedom unable to be sampled in MD, namely geometry changes due to closed-to open-shell electronic structure transition. Degrees of freedom that can be sampled in MD, like rearranging side chains, shall not be sampled during the DFT optimization, but in the preceding MD simulation. To achieve this, we tested differently sized optimization regions, details are described in the ESI,† including illustrations and statistics in Fig. S5†

In this work, 4393 synthetic structures and 5261 structures from trajectories are generated. Of these structures, 10% are set aside randomly for testing. 803 structures form the optimized data set, most of them (725) originate from the trajectory data set, 78 are synthetic systems. They inherit the test/training set membership from their non-optimized versions, to ensure no structures from the training leak into the test set. Note that each structure has two associated energy barriers (one forward, one backward reaction), resulting in twice the amount of energy barriers for training/testing. In summary, 17 370 energy barriers are used for training, 1938 for testing. Fig. 2D shows the distribution between the data sets.

2.2 Graph neural network

To predict the energy barrier for a given reaction, the graph neural network PaiNN is used.²²Fig. 2E shows our workflow: the inputs for the model are the atom positions and elements in the educt configuration. The start and end positions of the transferred hydrogen atom are encoded as two unique elements to define the reaction direction (end position calculated based on geometric rules). After two message passing iterations, the invariant node features of the hydrogen and of the pseudo-atom are concatenated and fed into a dense neural network, consisting of two layers with 128 nodes each, using the swish activation function,³⁰ followed by one output node with linear activation. The GNN is trained to minimize the mean absolute error using the Adam optimizer³¹ with learning rate decay and early stopping. Hyperparameters are optimized using a Bayesian optimizer as implemented in the Keras Tuner package.³² To increase accuracy and obtain a measure of uncertainty, an ensemble of ten models with random initializations is trained. The models are validated using 10% of the training data, each model using a random training/validation split.

2.3 Dense neural network

As an alternative to the graph neural network, a simple feed-forward dense neural network is tested together with the local many-body tensor representation (L-MBTR).³³ This descriptor is based on histograms of distances and angles between one central atom and its surrounding. It is calculated on the position of the missing hydrogen atom, next to the radical-carrying atom. This position is encoded as a special element ‘X’, and the reacting hydrogen as ‘Y’ to present a well-defined task to the network. The L-MBTR descriptor is generated using the DScribe library.³⁴ Parts of the descriptor, which correspond to interactions between multiple elements ‘X’ or ‘Y’, are always zero and therefore removed to improve efficiency. Three hidden layers of shrinking size (1000, 500, and 100 neurons) are used in the network, utilizing the ReLU activation function, followed by a single output node with linear activation. The hyperparameters were determined by a non-exhaustive manual grid search. Similar to the graph neural network, an ensemble of ten models is trained.

3. Results

3.1 HAT barrier data set

As a starting point of the training, we generated a data set of structures where HAT reactions can occur, along with the associated energy barriers. The dataset spans the relevant conformational and chemical space and provides valuable insight into the behavior of HAT reactions in collagen, on top of enabling the creation of predictive models.

Unsurprisingly, the calculated barriers show a strong dependence on the distance the hydrogen atom has to travel during the reaction, as can be seen in Fig. 2F. However, barriers vary significantly for a given translation, substantiating the need to use more complex system descriptions than just translation.

The synthetic data, by construction, includes data at translations down to 0.3 Å and with barriers smaller than 20 kcal mol⁻¹, cases not covered in the trajectories, where small interatomic distances are disfavored and thus rare. Translations found in trajectories start from 0.7 Å, but the vast majority are larger than 1.2 Å (Fig. S1B†). Out of the 10 522 reactions from trajectory systems, only 24 reactions were found with barriers below 20 kcal mol⁻¹. In 21 of these systems, the reaction involves at least one hetero atom. Also, the translations are comparatively short, with an average distance of 1.2 Å. Examples of the lowest and highest barriers can be found in Fig. S2.†

3.2 Performance of ML model

The correlation of barriers with translation allows the introduction of a cutoff after a certain translation, rather than one dependent on the energy barrier, which would be unknown beforehand. For evaluating the performance of our trained model, we chose a translation cutoff of 2 Å and 3 Å to focus on thermochemically probable HAT reactions, i.e., those with barriers mostly lower than 100 kcal mol⁻¹ and to thereby consider HAT reactions most relevant in an actual protein material. In the following, performance metrics for both cutoffs are presented. ± indicates the standard deviation of the absolute error.

An ensemble of models was trained on all available training data without a cutoff applied, and evaluated on the whole test data, and only on the trajectory systems of the test data, each evaluation with a cutoff applied. We chose to evaluate on the trajectory data as a major application is the prediction of HAT barriers for conformations of proteins (here collagen) encountered during MD simulations.

Performance metrics are summarized in Fig. 3. Panels A and B show the performance for trajectory systems with translations below 2 Å, i.e., focus on the most feasible HAT reactions, while panels D to F show measurements using all available trajectory data. For completeness, evaluations on synthetic data alone are shown in Fig. S6.†

Fig. 3 Model performance predicting HAT barriers on test data. (A) Predicted energy barriers vs. ground truth using the PaiNN ensemble model on trajectory test data with translation <2 Å. (B) Histogram of the prediction errors of individual PaiNN models and of the ensemble model. The mean of both distributions is shown as a vertical line. (C) Performance of three individual models trained on fractions of the complete training set. 100% corresponds to 15 633 training points. (D) Predicted energy barriers vs. ground truth using the PaiNN ensemble model on trajectory test data with translation <3 Å. (E) Predicted energy barriers vs. ground truth using ten individual PaiNN models on trajectory test data with translation <3 Å. (F) The absolute error of the PaiNN ensemble model on all trajectory data vs. the standard deviation of the predictions of individual models within the ensemble. In red, the mean ensemble standard deviation is plotted, and light blue in the background a frequency plot of occurring errors.

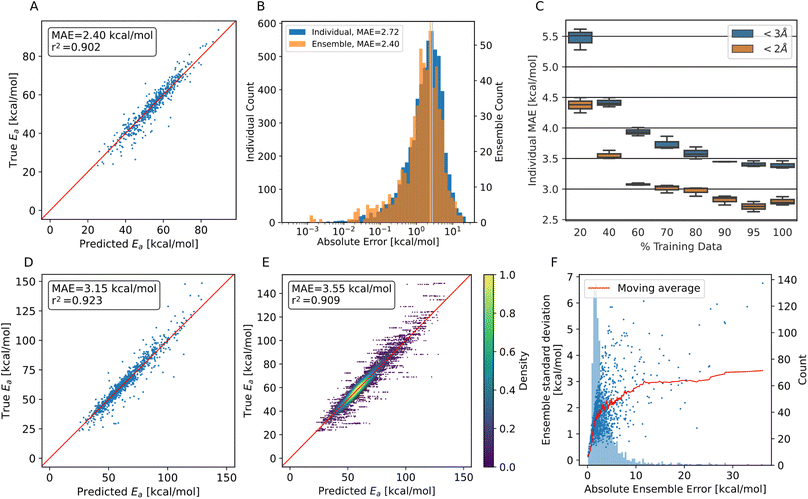
As can be seen from Fig. 3A, we achieve MAEs of 2.4 ± 2.5 kcal mol⁻¹ using the ensemble model. Individual models only achieve 2.7 ± 2.7 kcal mol⁻¹ on average on the trajectory data with the translation cutoff in place (Fig. 3B).

The prediction quality heavily depends on the amount of training data available, as shown in Fig. 3C. Adding training data improves the model up to ∼90% of the available data, which corresponds to 14 068 individual barriers. Thus, the amount of training data generated at the BMK/6-31+G(2df,p) level is approximately required to reach this accuracy, but also appears to suffice, as the learning curve flattens towards the end. Training curves are shown in Fig. S7.†

The accuracy decreases for systems with bigger translations and energy barriers, as shown in Fig. 3D and E: increasing the translation cutoff from 2 Å to 3 Å introduces more high-barrier systems to the test set, which seem to be harder to predict exactly. For the prediction of the propagation pathway of a radical in a complex environment, this might be acceptable though, as reactions with high energy barriers are unlikely to occur under ambient conditions.

As mentioned, the use of an ensemble model also brings the advantage of an uncertainty measure: the standard deviation between the models. In Fig. 3F, the absolute ensemble error is plotted against the ensemble standard deviation together with a rolling average. For a low standard deviation (smaller than 1.7 kcal mol⁻¹), one can assume a low prediction error (<3 kcal mol⁻¹) quite confidently. On the other hand, higher standard deviations no longer scale reliably with the error.

3.3 Training data impact

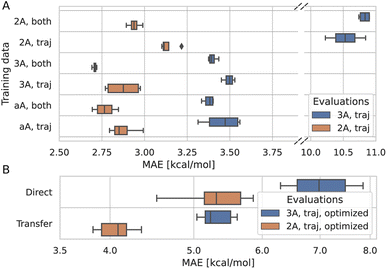
To understand to what degree a given part of the data improves the model, multiple models were trained on different parts of the training data and evaluated on a subset of the test data. The models were trained on trajectory and synthetic data, or on trajectory data only. Additionally, several translation cutoffs were used, either at 2 or 3 Å or without a cutoff. In all cases, the models were evaluated on trajectory data below 2 or 3 Å. This setup shows that the model benefits from being trained on synthetic systems alongside trajectory systems, even if it is evaluated only on trajectory systems (Fig. 4A). Similarly, the model performance for systems with translations smaller than 2 Å improves when it is trained on larger translations. Data that is rather distant from the target prediction with regard to its chemistry and geometry still adds to the predictive power of the model. Therefore, we trained the final model on synthetic and trajectory data without a translation cutoff.

Fig. 4 Differently trained models evaluated on comparable subsets of the test data. (A) Comparison between models trained on different data sets as indicated on the y-axis. 2A, 3A, and aA correspond to data with translations below 2A, 3A, or all translations, respectively. ‘traj’ refers to data only from trajectories, ‘both’ includes in addition the synthetic data. Four models were trained per data set. (B) Comparison between transfer learning and training directly on the optimized data only. Again, both models were evaluated on trajectory data <3 Å and <2 Å. All ten original models are used in transfer learning, ten new models were trained for the direct learning approach.

3.4 Predicting DFT optimized barriers

So far, we showed that the model can well reproduce energy barriers close to DFT accuracy on structures from MD trajectories and synthetic ones. However, as mentioned previously in Section 2.1, realistic energy barriers are expected to be closer to those computed for at least partially optimized systems. But, since optimizations at the DFT level of theory for the entire data set are prohibitively expensive, only a subset of reaction paths were optimized on the BMK/6-31+G(2df,p) level of theory. The mean absolute deviation between the barriers computed based on geometries from MD, and based on DFT optimized geometries is 13.6 ± 11.6 kcal mol⁻¹ (Fig. S4†). This deviation highlights the importance of the geometry optimization and the transfer-learning step detailed in the following section. Importantly, as expected, optimized barriers are lower than the BDE of the dissociating bond of the reaction, in contrast to the unoptimized data set with unfavorable paths in case of large reaction distances (see ESI Fig. S2D† for an example).

Notably, the energy barriers of synthetic systems change less when optimized compared to barriers from trajectory systems. This is likely due to higher atom density in trajectory systems: it is more likely in trajectory systems that atoms interfere with the transition path. In other words, the lowest energy reaction path changes more in trajectory systems relative to the interpolated path. This analysis also serves as a validation for the procedural structure building process. If the built structures were unreasonable, they would change more drastically during optimization compared to the structures produced by MD simulation. At a given translation, the optimized reactions generally show lower barriers (see also Fig. 2F).

3.5 Transfer learning

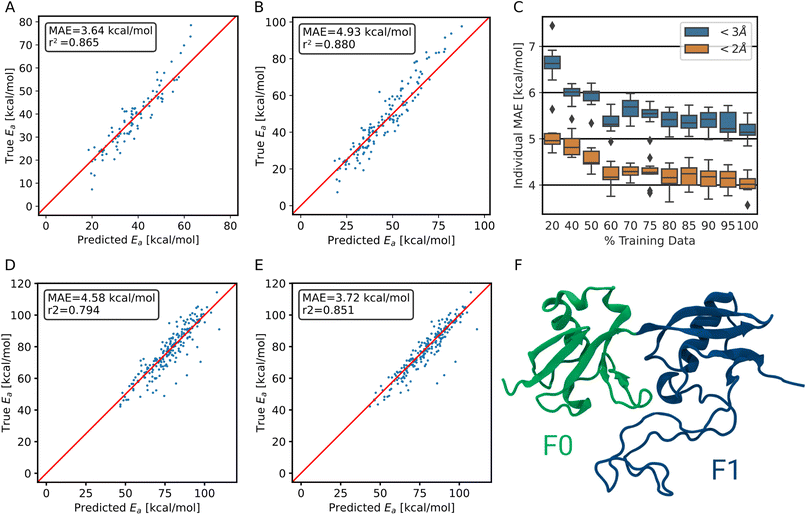
To correct for the deviation between the barriers computed for non-optimized and optimized reaction paths, models already trained on non-optimized systems were retrained in a transfer learning scheme to be as data-efficient as possible. When using transfer learning, one often freezes most of the network and retrains only parts of it. Here, however, we found the best results when not freezing any part of the model. Still, models trained with transfer learning substantially outperform models trained on optimized data alone (Fig. 4B). Note that only the training target, i.e., the barrier, was changed for transfer learning, and not the input to the model. The same non-optimized structures are fed into the model, as it is intended to be used on non-optimized structures from MD simulations. In other words, the model learns a mapping between non-optimized MD structures and DFT barriers of the optimized reaction paths.

The ensemble model for predicting optimized barriers achieves an MAE of 3.6 ± 3.2 kcal mol⁻¹ on trajectory data with translations of less than 2 Å and 4.9 ± 4.0 kcal mol⁻¹ on translations less than 3 Å (Fig. 5A and B, respectively). The learning curve of the transfer learning procedure in Fig. 5C suggests that the model is data limited, as the accuracy increases in particular from 90% over 95% to 100% of the optimized test data. Training curves are provided in Fig. S8.†

Fig. 5 Performance of the transfer-learned ensemble model on (A) trajectory test data <2 Å and on (B) <3 Å trajectory test data. (C) Learning curve of the transfer learning process. The test MAE of the individual models is shown. (D) Performance of the ensemble model trained on synthetic and collagen-trajectory data on the F0F1 domain of FERM. (E) Ensemble model performance after transfer learning on as little as 500 structures of FERM on same evaluation set as in D. (F) The F0 and F1 domain of FERM used in out-of-domain predictions. It includes α-helices, β-sheets and an intrinsically disordered region.

3.6 Out-of-domain predictions

To demonstrate that the method is not restricted to collagen-like systems only but shows transferability, we validated the performance on a different protein, the F0F1 domain of FERM. It exhibits a vastly different composition of amino acids, i.e., of chemical environments. It also is structurally diverse, consisting of two folded parts and one intrinsically disordered region (Fig. 5F). The simulations were kindly provided by Buhr et al.³⁵ System preparation was done analogous to training data generation, as detailed in the methods section.

For predicting the barriers, the ensemble model trained on collagen trajectories and synthetic systems was used. As shown in Fig. 5D, the model does not perform as good as on its training target collagen, but still achieves an MAE of 4.6 ± 4.8 kcal mol⁻¹. We note that collagen only consists of triple helices and the model has not seen other secondary structures, let alone intrinsically disordered proteins. On top, the amino acid distribution varies significantly between the training data set and the testing data used here (Fig. S9†). Therefore, this is close to the worst case scenario, and yet the model still delivers useful results.

More importantly, starting from the pretrained model, the performance can be improved at a low cost in a transfer learning scheme as outlined earlier. Using only 500 new training structures from the FERM F0F1 domain, the MAE decreases already to 3.7 ± 4.2 kcal mol⁻¹ (Fig. 5E).

4. Discussion

We here set out to develop an efficient surrogate model for a challenging bimolecular reaction, HAT within proteins, without the need to evoke a DFT calculation for a given calculation of a reaction barrier. While the model does not reproduce the DFT results perfectly, its error is approaching the accuracy of the underlying target method. The authors of the functional of our choice, BMK, targeted an accuracy of 2 kcal mol⁻¹ on energy barriers,²⁷ and, depending on the benchmarks, BMK achieves an MAE of 0.8 kcal mol⁻¹ to 5 kcal mol⁻¹ relative to CCSD(T) calculations.^29,36

A limitation of the depicted method is that the type of reaction one can predict is predefined. The model predicts hydrogen atom transfer only, while we can not rule out proton coupled electron transfer to play a role in this system.

Further, tunneling effects are ignored, and all QM calculations are performed in the gas phase. However, these last two points are limitations of the dataset, not the underlying method. As soon as higher quality data is available, the network can utilize these by, e.g., transfer learning. We thus propose our GNN-based model as a starting point to build more refined models such as one taking quantum effects into account.

Another limitation of the input data set is the use of MD structures without force field parameters for the radicals. We correct these structures implicitly in the GNN by training with barriers obtained from DFT optimization in the transfer learning step. While DFT would still be more accurate than MD alone, having proper parameters for the radical available would lower the complexity of the task the model is facing, since the input structures would be more similar to the DFT structures. We would expect an acceptable accuracy even when omitting the transfer learning step, and also an increase in data efficiency. Methods like Espaloma³⁷ could be used in the future to obtain such force field parameters on the fly after every HAT reaction.

To justify the use of an arguably complex graph neural network, we compared it to two simpler methods, a densely connected feed-forward neural network and a random forest model (as implemented in scikit-learn,³⁸ see ESI†). For both methods, we used the L-MBTR³³ descriptor as input and the barriers computed for non-optimized reactions as targets. Details on the network architecture and input generation are given in the Methods section. Using an ensemble of ten models, the feed-forward neural network accomplishes an MAE of 4.8 kcal mol⁻¹, and single models achieve 5.1 kcal mol⁻¹ on average over trajectory data (see Fig. S10†). The random forest model achieved an MAE of 6.6 kcal mol⁻¹ (Fig. S11†). Taken together, these results highlight the need for more sophisticated representations and models to capture subtle structural differences. However, it is important to note that our model significantly outperforms semi-empirical methods, in both accuracy and speed. More specifically, we compared barriers calculated with the cheaper GFN2-xTB method to BMK-calculated ones on 100 randomly chose structures.³⁹ xTB calculations of the barrier do not reach the needed quality as they differ to BMK calculated barriers by an MAE of 20 kcal mol⁻¹ (Fig. S12†).

Our ultimate aim is to model the chemistry of radical-induced damage to collagen, whilst simultaneously capturing the dynamic nature of this system. Kinetic Monte-Carlo (KMC) method enables incorporating reactions into MD on timescales beyond those covered by conventional MD simulations. A hybrid KMC-MD approach models reactions in a Markov-process, allowing arbitrarily big time jumps between reaction steps.⁴⁰ Previously, we coupled KMC with MD to simulate homolytic bond rupture in stretched collagen fibrils in a method called KIMMDY.²⁴ Our GNN-based model for predicting reaction barriers allows applying the KIMMDY approach to radical transfer reactions. Inferring an energy barrier of a reaction from a trained neural network within a reactive MD simulation substitutes the otherwise computationally costly quantum chemical calculation, and only marginally compromises the efficiency of standard MD simulations.

In the past, several methodologies were developed to achieve reactive MD, including reactive force fields, such as ReaxFF⁴¹ and AIREBO,⁴² hybrid quantum mechanical/molecular mechanical (QM/MM)⁴³ simulations, and, more recently, molecular dynamics simulations paired with machine-learned force fields (MLFF).^44,45 However, all these methods are slower compared to regular MD⁴⁶ and are by default restricted to reactions on the timescale of the simulation. KIMMDY overcomes these drawbacks but relies on the availability of reaction rates, which can now be provided with the model introduced here. Implementation and results of the extended KIMMDY software are beyond the scope of this paper, and will be published later.

5. Conclusion

In this work, we introduced a workflow to train machine learning models for fast predictions of energy barriers of hydrogen atom transfer reactions, spanning a wide range of more than 80 kcal mol⁻¹ and covering the heterogeneous chemical space of a protein. Our model was trained and evaluated in the context of radical migration in collagen fibrils, but can be transferred to other chemical systems subject to HAT reactions. Since the predicted reaction barriers are based on 3D structures of molecules, without any DFT optimization or energy valuation, the model can be used in direct conjunction with MD simulations. For example, utilizing predicted barriers in a kinetic Monte-Carlo scheme, one can extend MD simulation to allow HAT reactions to take place in a dynamically evolving molecular system. Our study emphasizes the strength of graph neural networks for predicting chemical reactivity – even in such challenging cases as dynamic biopolymers.

Data availability

Structures and energies are available at https://doi.org/10.11588/data/TGDD4Y. Trained models and example code available on GitHub: https://github.com/HITS-MBM/HAT_prediction_GNN.

Author contributions

Kai Riedmiller: methodology, software, formal analysis, investigation, data curation, writing – original draft, visualization. Patrick Reiser: software, methodology. Elizaveta Bobkova: software, investigation. Kiril Maltsev: conceptualization, methodology. Ganna Gryn'ova: conceptualization, methodology, writing – review & editing. Pascal Friederich: conceptualization, methodology, writing – review & editing. Frauke Gräter: conceptualization, resources, writing – review & editing, supervision, project administration, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge generous financial support from the Klaus Tschira Foundation through the HITS Lab and SIMPLAIX. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement no. 101002812 RADICOL) and from the Deutsche Forschungsgemeinschaft (DFG) under Germany's Excellence Strategy – 2082/1 – 390761711.

References

1. C. C. Winterbourn, Nat. Chem. Biol., 2008, 4, 278–286.
2. M. Gutowski and S. Kowalczyk, Acta Biochim. Pol., 2013, 60, 1–16.
3. K. J. Davies, J. Biol. Chem., 1987, 262, 9895–9901.
4. C. L. Hawkins and M. J. Davies, Biochim. Biophys. Acta, Bioenerg., 2001, 1504, 196–219.
5. G. Gryn’ova, J. L. Hodgson and M. L. Coote, Org. Biomol. Chem., 2011, 9, 480–490.
6. D. L. Allara, Environ. Health Perspect., 1975, 11, 29–33.
7. J. Behler, J. Chem. Phys., 2011, 134, 074106.
8. J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203.
9. K. Schütt, P.-J. Kindermans, H. E. Sauceda Felix, S. Chmiela, A. Tkatchenko and K.-R. Müller, Adv. Neural Inf. Process. Syst., 2017, 30, 992–1002.
10. T. W. Ko, J. A. Finkler, S. Goedecker and J. Behler, Nat. Commun., 2021, 12, 398.
11. R. Zubatyuk, J. S. Smith, B. T. Nebgen, S. Tretiak and O. Isayev, Nat. Commun., 2021, 12, 4870.
12. T. Lewis-Atwell, P. A. Townsend and M. N. Grayson, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1593.
13. S. Ma, S. Wang, J. Cao and F. Liu, ACS Omega, 2022, 7, 34858–34867.
14. L.-C. Yang, X. Li, S.-Q. Zhang and X. Hong, Org. Chem. Front., 2021, 8, 6187–6195.
15. S. Vargas, M. R. Hennefarth, Z. Liu and A. N. Alexandrova, J. Chem. Theory Comput., 2021, 17, 6203–6213.
16. A. R. Singh, B. A. Rohr, J. A. Gauthier and J. K. Nørskov, Catal. Lett., 2019, 149, 2347–2354.
17. K. A. Spiekermann, L. Pattanaik and W. H. Green, J. Phys. Chem. A, 2022, 126, 3976–3986.
18. M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301.
19. A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115.
20. P. Reiser, M. Neubert, A. Eberhard, L. Torresi, C. Zhou, C. Shao, H. Metni, C. van Hoesel, H. Schopmans and T. Sommer, et al. , Commun. Mater., 2022, 3, 1–18.
21. S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 2453.
22. K. T. Schütt, O. T. Unke and M. Gastegger, arxiv, 2021, preprint, arXiv:2102.03150,  DOI:10.48550/arXiv.2102.03150.
23. C. Zapp, A. Obarska-Kosinska, B. Rennekamp, M. Kurth, D. M. Hudson, D. Mercadante, U. Barayeu, T. P. Dick, V. Denysenkov, T. Prisner, M. Bennati, C. Daday, R. Kappl and F. Gräter, Nat. Commun., 2020, 11, 2315.
24. B. Rennekamp, F. Kutzki, A. Obarska-Kosinska, C. Zapp and F. Gräter, J. Chem. Theory Comput., 2019, 16, 553–563.
25. W. Treyde, K. Riedmiller and F. Gräter, RSC Adv., 2022, 12, 34557–34564.
26. A. Obarska-Kosinska, B. Rennekamp, A. Ünal and F. Gräter, Biophys. J., 2021, 120, 3544–3549.
27. A. D. Boese and J. M. L. Martin, J. Chem. Phys., 2004, 121, 3405–3416.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D. 01, 2013.
29. G. F. Mangiatordi, E. Brémond and C. Adamo, J. Chem. Theory Comput., 2012, 8, 3082–3088.
30. P. Ramachandran, B. Zoph and Q. V. Le, arxiv, 2017, preprint, arXiv:1710.05941,  DOI:10.48550/arXiv.1710.05941v2.
31. D. P. Kingma and J. Ba, arxiv, 2014, preprint, arXiv:1412.6980v9,  DOI:10.48550/arXiv.1412.6980v9.
32. T. O'Malley, E. Bursztein, J. Long, F. Chollet, H. Jin, L. Invernizzi, et al., KerasTuner, 2019, https://github.com/keras-team/keras-tuner.
33. H. Huo and M. Rupp, Mach. Learn.: Sci. Technol., 2022, 3, 045017.
34. L. Himanen, M. O. J. Jäger, E. V. Morooka, F. Federici Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949.
35. J. Buhr, F. Franz and F. Gräter, Biophys. J., 2023, 122, 1277–1286.
36. M. Korth and S. Grimme, J. Chem. Theory Comput., 2009, 5, 993–1003.
37. Y. Wang, J. Fass, B. Kaminow, J. E. Herr, D. Rufa, I. Zhang, I. Pulido, M. Henry, H. E. Bruce Macdonald, K. Takaba and J. D. Chodera, Chem. Sci., 2022, 13, 12016–12033.
38. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830.
39. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
40. D. T. Gillespie, J. Comput. Phys., 1976, 22, 403–434.
41. A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409.
42. T. C. O'Connor, J. Andzelm and M. O. Robbins, J. Chem. Phys., 2015, 142, 024903.
43. A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249.
44. P. Friederich, F. Häse, J. Proppe and A. Aspuru-Guzik, Nat. Mater., 2021, 20, 750–761.
45. O. T. Unke, M. Stöhr, S. Ganscha, T. Unterthiner, H. Maennel, S. Kashubin, D. Ahlin, M. Gastegger, L. M. Sandonas, A. Tkatchenko and K.-R. Müller, arxiv, 2022, preprint, arXiv:2205.08306v1,  DOI:10.48550/arXiv.2205.08306v1.
46. M. J. Buehler and S. Keten, Rev. Mod. Phys., 2010, 82, 1459.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc03922f

---