Magnetic structure and properties of the compositionally complex perovskite (Y0.2La0.2Pr0.2Nd0.2Tb0.2)MnO3†
Nathan D.
Arndt
 *a,
Brianna L.
Musicó
b,
Kausturi
Parui
a,
Keon
Sahebkar
*a,
Brianna L.
Musicó
b,
Kausturi
Parui
a,
Keon
Sahebkar
 a,
Qiang
Zhang
a,
Qiang
Zhang
 c,
Alessandro R.
Mazza
d,
Megan M.
Butala
c,
Alessandro R.
Mazza
d,
Megan M.
Butala
 a,
Veerle
Keppens
b,
T. Zac
Ward
a,
Veerle
Keppens
b,
T. Zac
Ward
 d and
Ryan F.
Need
d and
Ryan F.
Need
 *a
*a
aDepartment of Materials Science and Engineering, University of Florida, Gainesville, Florida 32611, USA. E-mail: rneed@ufl.edu
bDepartment of Materials Science and Engineering University of Tennessee Knoxville, TN 37996–4545, USA
cNeutron Science Division Oak Ridge National Laboratory Oak Ridge, TN 37831, USA
dMaterials Science and Technology Division Oak Ridge National Laboratory Oak Ridge, TN 37831, USA
First published on 30th July 2024
Abstract
Large configurational disorder in compositionally complex ceramics can lead to unique functional properties that deviate from traditional rules of alloy mixing. In recent years, compositionally complex oxides (CCOs) have shown intriguing magnetic behavior including long-range order, enhanced magnetic exchange couplings, and mixed phase magnetic structures. This work focuses on how large local spin disorder affects magnetic ordering in a CCO. Specifically, we investigated the A-site alloyed perovskite, (Y0.2La0.2Pr0.2Nd0.2Tb0.2)MnO3, or (5A)MnO3, using a combination of bulk magnetometry, synchrotron X-ray diffraction, and temperature-dependent neutron diffraction. The five A-site ions have an average spin and ionic radius nearly equal to that of Nd3+ ions, which minimizes structural distortions and allows for an understanding of the local spin disorder effects through a direct comparison with NdMnO3. Our magnetometry data show that (5A)MnO3 exhibits two distinct phase transitions associated with the A-site and B-site sublattices, as seen in NdMnO3, as well as the presence of domain pinning and exchange bias at low temperature, suggesting a mixed phase magnetic ground state, as seen in other magnetic CCOs. Neutron powder diffraction shows clear long-range antiferromagnetic ordering below 67 K and refines to a Pn′ma′ magnetic structure at low temperature, in excellent agreement with the well-studied behavior of NdMnO3. The two most notable differences in (5A)MnO3 magnetism apparent from our data are a slight suppression of the B-site ordering temperature, which is explained by a smaller Mn–O–Mn bond angle in (5A)MnO3 than NdMnO3, and the presence of a magnetic susceptibility transition above the B-site ordering, which could indicate the formation of a cluster glass but requires further study. This work demonstrates a general method of isolated investigation of size and spin disorder in CCOs and motivates future work using local structure probes to better understand the effects of nanoscale clustering and local spin disorder in magnetic CCOs.
1 Introduction
Compositionally complex oxides1,2 (CCOs) are an extension of the high-entropy materials design scheme first developed in metal alloys3,4 and more recently adapted to ionic solids.5 In CCOs, equimolar or near-equimolar amounts of different elements are alloyed onto the same lattice site, thereby increasing the system's configurational entropy and increasing the driving force for mixing, especially at high temperature. Like their metal counterparts, CCOs have been shown to exhibit some unique and best-in-class material properties, including colossal dielectric coefficients,6 high stiffness-to-thermal conductivity ratios,7 and tunable mixed phase magnetism.8 Investigations into the magnetic behavior of CCOs began with proof of long-range ordering in the rocksalt structure.9 More recent efforts have focused on the ABO3 perovskite structure,8,10–16 which has the added tunability of a second cation site, while still being a relatively simple and well-studied structure class.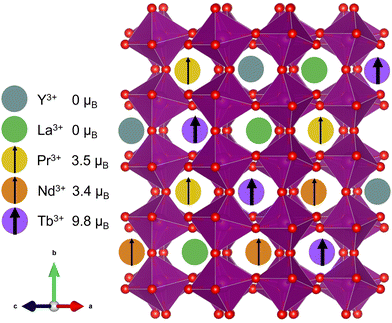 | ||
| Fig. 1 Cartoon depiction of the (5A)MnO3 unit cell showcasing the large variance in magnetic moment17 on the A-site. | ||
Studies on CCO perovskite magnetism are naturally grouped by which lattice sites are alloyed. The 6-fold coordinated perovskite B-site is surrounded by an octahedra of oxygen, and its magnetic exchange interactions with neighboring B-site ions, which are mediated through the bridging oxygens,18 typically dominate the system's magnetic energy scale. As a result, the B-site tends to order at higher temperatures than the A-site, and its ordering temperature is highly dependent on the B–O–B bond angles.19,20 Studies on B-site alloyed (e.g., Cr, Mn, Fe, Co, Ni) perovskites received more attention initially and frequently show mixed phase magnetic ground states as a result of the competition between strong ferromagnetic (FM) and antiferromagnetic (AFM) exchange between neighboring B-sites.10,11,16,21,22 Small differences in stoichiometry can tune the system from FM pockets in a percolated AFM matrix, through a system of two percolated networks, and to AFM pockets in a percolated FM matrix.8,13,21 This degree of tunability is remarkable and much work remains to understand and control it.
By contrast, the 12-fold coordinated perovskite A-site is spaced further from its neighbors, and correspondingly its magnetic coupling is typically weaker. There have been fewer studies on A-site alloyed perovskite CCOs to-date. Studies on A-site alloyed systems to-date have primarily focused on, and succeeded in, connecting A-site ionic size disorder to the changes in B-site ordering temperature using bulk magnetometry methods.14–16,21,23–29 However, there are indications in several of these studies that A-site disorder can change more than the ordering temperature of the B-site, for example, the character of the B-site exchange interactions,24 and can even lead to frustrated magnetic ground states.28
To better understand the expected behavior of an A-site alloyed CCO perovskite, we first consider systems with only trivalent ions on the A-site.16,21,25 The best point of comparison comes from Witte et al.21 who studied a series of (5A)BO3 CCOs with B = Cr, Fe, Co. They demonstrated that the B-site ordering temperatures fit to trends of A-site ionic radius previously established for the corresponding rare-earth perovskite series,30,31 and could thus be explained as a structural effect arising from changes to B–O–B bond angle, orbital overlap, and the corresponding superexchange interaction. With regards to the A-site, no ordering was observed for the Co or Fe compounds above 1.8 K. However, in many of the relevant rare-earth perovskites analogs (here, Gd, Sm, and Nd) of (5A)BO3 (B = Fe, Co), the A-site does not order until 1 K or below. In (5A)CrO3, Witte et al. observed clearer A-site ordering near 30 K in agreement with its rare-earth analogs. Thus, overall, the results from Witte et al. show A-site ordering behavior and temperatures similar to undisordered A-site analogs. However, considerably more work is needed to establish if and how that correspondence depends on A-site composition.
With regards to manganite perovskite CCOs, nearly all studies to-date have been on charge-doped compositions, where the A-site valence deviates from the trivalent A3+ studied here and causes a mixed Mn3+/Mn4+ valence and double exchange ferromagnetic ground states.14,15,23,24,26–28 Across the charge-doped manganite CCO studies, the clearest common result thus far is that increasing the variance of the ionic radii of the A-site ions monotonically decreases the B-site ordering temperature. Good examples of this are seen in complementary studies by Sarkar et al.,23 on manganites with varying degrees of charge doping but a fixed (5A) composition, and Das et al.,15 on manganites with fixed doping but different (5A) compositions, both of which demonstrated changes in B-site ordering temperature that were monotonic with A-site ionic radii variance. Beyond structural tuning of B-site ordering temperature, Kouki et al.27 observed that A-site radii variance and increasing Sm content could change the universality class of their ferromagnetic order parameter, indicating that the character of B-site ordering can also be influenced by A-site alloying. However, the authors still correlated this subtler effect with A-site size differences, and not local spin variance. The largest qualitative changes to magnetic ordering in an A-site alloyed manganite appear to be those recently reported by Das et al.,24 which also shows the largest variance in ionic radii to-date comparing (5A)0.5Sr0.5MnO3 and (3Ln)0.5(Ca,Sr,Ba)0.5Mn3 to Nd0.5Sr0.5MnO3. Das et al. observed a change from FM ordering to canted AFM with the ordering temperature monotonically suppressed by increasing A-site variance that bypasses the expected spin glass state of high ionic radii variance in charge ordered systems like Nd0.5Sr0.5MnO3.28,32,33 Notably, their A-site compositions do not average to mimic Nd as done in our work.
In this work, we attempted to minimize structural distortions and investigate the effect of isolated spin disorder on the magnetic structure, transitions, and properties of an A-site alloyed manganite shown schematically in Fig. 1. We used equimolar amounts of Y3+, La3+, Pr3+, Nd3+, and Tb3+, hereafter denoted (5A), that were carefully chosen to introduce large local spin variance while closely matching the average spin and ionic radii of Nd3+, see Table 1. In contrast to many of the prior studies on CCO manganites, this choice of (5A) ions was intended to minimize changes to the long-range average crystal structure and allow us to isolate the effects of local spin disorder on magnetic ordering in (5A)MnO3 through a comparison with the well-studied magnetism of NdMnO3.34–37
NdMnO3 exhibits the orthorhombic perovskite Pnma crystal structure at room temperature and below. Upon cooling to TN,Mn ≈ 73 K, the Mn3+-sublattice orders first in a canted AFM structure, (Ax,Fy,0), where the Mn3+ spins order in ferromagnetic (FM) planes stacked along the b-axis with moments pointing along the a-axis canted towards the b-axis, Ax denotes A-type antiferromagnetic ordering in the x direction and Fy denotes ferromagnetic ordering in the y direction. The A-site Nd3+ moments orders second FM below TNd ≈ 13 K. The effect of the Nd3+-sublattice ordering on the Mn spins has been debated, but recent experiments provide compelling evidence that there is a re-orientation of the Mn3+ spins upon Nd3+ ordering. Comprehensive measurements by Kumar et al.37 indicate that the Nd3+ spins will initially order FM to each other and AFM to the FM component of the Mn3+ spins, which results in an apparent reduction in magnetization and a magnetic structure with AFM planes of Mn3+, (Ax,−Fy,0), AFM coupled with the FM Nd3+, (0,Fy,0). However, under low fields, the Mn-sublattice will then invert along the b-axis such that the FM component of the Mn3+ spins aligns FM to the Nd3+ spins, resulting in a complete magnetization reversal and the magnetic structure Mn3+, (Ax,Fy,0), FM coupled to Nd3+, (0,Fy,0).37,40–42 Note that both low-temperature structures are described by the same magnetic space group Pn′ma′ (62.448) and are thus difficult to distinguish by neutron scattering alone.34–37
Using bulk magnetometry, synchrotron X-ray diffraction (SXRD), and temperature-dependent neutron powder diffraction (ND), we show that the magnetic structure and properties of (5A)MnO3 powders are an excellent match with the undisordered ‘parent’ NdMnO3. The magnetometry data show two magnetic ordering transitions that correspond to the ordering of the A-site and the B-site sublattices and are in close quantitative agreement with ordering temperatures reported for NdMnO3.35–37 At low temperatures, magnetometry measurements also reveal the presence of exchange-bias, as seen in NdMnO3,37,40–42 and domain pinning, as seen in other magnetic CCOs.8 The magnetic structure of (5A)MnO3 was refined at 9 K to be the same as NdMnO3, Pn′ma′.34–37 Together, these results demonstrate that (5A)MnO3 perovskites exhibits remarkable insensitivity of its average magnetic structure and properties to large A-site spin variance. We discuss these similarities between (5A)MnO3 and NdMnO3 in terms of the site-specific magnetic interactions, then comment on the slight differences found in the A-site ordering temperature and the observed Mn3+ moment value and their connection to the local disorder introduced in (5A)MnO3.
2 Experimental methods
2.1 Powder synthesis
(5A)MnO3 powder was made using solid-state chemistry and bulk ceramic processing methods. Oxide precursor powders, La2O3 (Acros Organics 99.99%), Y2O3 (REaction from Alfa Aesar 99.99%), Tb4O7 (REaction from Alfa Aesar 99.99%), Pr6O11 (REaction from Alfa Aesar 99.99%), Nd2O3 (REaction from Alfa Aesar 99.90%), and MnO (Alfa Aesar 99.99%), were massed, ground using an agate mortar and pestle, and pelletized. The resulting green pellet was sintered in a furnace ramped at a rate of 5 °C min−1 to 1200 °C in air, where it dwelled for 10 hours and was then furnace cooled. The sample was reground, re-pressed, and re-fired using the same heat treatment.2.2 Characterization
Magnetometry data were collected from the powder in a quantum design MPMS3 using a vibrating sample mount. The sample was mixed and diluted with diamagnetic BaCO3 powder to avoid saturating the SQUID detector, then packed tightly into a gelatin capsule. Magnetization was measured as a function of temperature (MvT) from 2 K to 300 K under zero-field cooled (ZFC) and 100 Oe field cooled (FC) conditions. ZFC field-dependent magnetization (MvH) was measured at select temperatures with applied fields of ±70 kOe, as well as under applied fields of 2 kOe and 30 kOe.† Exchange bias was investigated at 10 K by field-cooling under ±70 kOe and compared to ZFC MvH.† No diamagnetic background data subtraction was performed despite the BaCO3 present in the sample. The diamagnetic contribution is negligible compared to the paramagnetic and ordered magnetic response of the diluted (5A)MnO3, as shown clearly by high temperature measurements.†High-resolution SXRD and ND data were collected through the mail-in program at Argonne National Laboratory's Advanced Photon Source (beamline 11-BM) and through the general user program at the POWGEN time-of-flight neutron diffraction instrument of Oak Ridge National Laboratory's Spallation Neutron Source, respectively. Synchrotron X-rays had a calibrated wavelength of 0.4582 Å and powders were measured in transmission mode in 0.8 mm diameter Kapton capillaries. The neutron diffraction sample was measured in a vanadium can and diffraction patterns were collected in transmission geometry at 9 K, 60 K, 100 K, and 300 K using a center wavelength of 1.500 Å and a chopper frequency of 60 Hz. The data were refined using the Rietveld method and the Bilbao Crystallographic Server's k-SUBGROUPSMAG module implemented in GSAS-II to determine the crystal and magnetic structures as a function of temperature.43–45 The resultant crystallographic information files (CIFs) are represented as images produced using VESTA.46
3 Results and discussion
3.1 Magnetometry
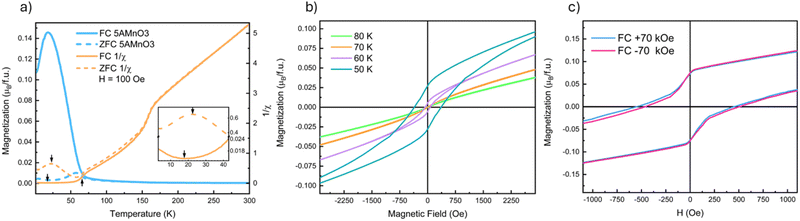
Fig. 2 presents a summary of the magnetometry data on (5A)MnO3. Low-field MvT data, H = 100 Oe, is shown in Fig. 2(a) where the most apparent feature is a transition marked by the increase in the FC magnetization upon cooling below 67 K. This transition reflects ordering of the B-site Mn3+-sublattice as expected from NdMnO3 and proven below by neutron diffraction. The MvH data shown in Fig. 2(b) was collected at temperatures above and below this transition and show the opening of a FM hysteresis loop below the transition. This behavior is qualitatively consistent with the expected canted AFM structure. In addition, both (5A)MnO3 and NdMnO335 have a volumetric magnetization of M ≈ 0.17μB per f.u. at the onset of A-site ordering when field cooled under H = 2 kOe.† This finding is consistent with the two materials having nominally identical Mn-sublattices and similar Mn spin structures prior to A-site ordering.Upon further cooling, a second magnetic transition associated with A-site ordering is observed as inflections in the FC and ZFC MvT data that occur at slightly different temperatures depending on the field, as shown in the inset of Fig. 2(a). In the ZFC data, ordering occurs at 22 K and results in an increase in magnetization upon cooling. This is consistent with a parallel alignment of the A-site moments and the FM component of the canted Mn3+ moments. However, under FC conditions, the transition is slightly suppressed to 18 K and magnetization decreases below the transition, suggesting an anti-parallel alignment between the A-site moments and the Mn3+ FM-component. Studies of NdMnO3 report a large range of A-site ordering temperatures. Specifically, zero-field measurements using ND and magnetometry have reported A-site ordering between 13 K and 20 K, while magnetometry measurements under fields near 1 kOe range from 12 K to 37 K.35–37,40,41,47 The wide range of A-site ordering temperatures and differences in field-dependent behavior have been hypothesized to arise in differences in sample synthesis and purity. Here we simply state that our A-site ordering temperatures are similar to the previously reported values for NdMnO3, and are thus in general agreement with other work on (5A) CCO perovskites.21 Determining why disordered A-site ions in perovskites magnetically order similar to undisordered analogs requires additional study.
At higher temperature, above the B-site ordering, a third magnetic transition is apparent at 158 K in the DC susceptibility data, 1/χ, in Fig. 2(a). A linear regression fit to the high-temperature 1/χ data yields a Curie–Weiss θCW of 30 K. This indicates weak ferromagnetic interactions between the moments in the paramagnetic state and compares well to a value of θCW of 37 K reported for NdMnO3.35,48 In NdMnO3, a broader feature in susceptibility was observed between 200 K and 300 K and attributed to van Vleck paramagnetism.35,49 However, the 158 K susceptibility feature observed here for (5A)MnO3 is too sharp to be van Vleck. Importantly, our 100 K ND data are well fit by a purely nuclear scattering model,† which rules out long-range magnetic ordering at 158 K. Instead, the transition could be either a spin-state or a spin-glass type transition. However, the former is inconsistent with the direction of the susceptibility change across the transition and our refinement of low-spin Mn3+ moments at low temperatures. We believe a more likely explanation is a cluster glass transition resulting from nanoscale clustering of A-site ions that create local spin clustering and polarization below the spatial resolution of our diffraction experiments. This hypothesized scenario is consistent with the basis of spin-glass-like interactions, as well as the onset of irreversibility at 158 K in our FC–ZFC magnetization data, Fig. 2, and the diffuse magnetic scattering seen near the primary magnetic Bragg peak at low temperature. However, frequency-dependent AC susceptibility measurements collected at 1 Hz and 100 Hz are inconclusive and showed only a slight increase of the transition temperature to 160 K and no appreciable differences from one another.† Ultimately, our data and methods do not allow us to definitively determine the nature of the transition at 158 K and it remains an open question for future inquiry.
Field-cooled MvH measurements at 10 K are shown in Fig. 2(c) and reveal evidence of both domain pinning and bulk exchange bias. The former creates a vertical shift in the hysteresis loop, as shown in the inset of Fig. 2(c), while the latter creates a lateral shift in the hysteresis loop.17 In (5A)MnO3, the measured exchange bias field is relatively small, HEB = 31 Oe, and is most easily seen after subtracting the domain pinning component. Although frequently observed at magnetic thin film interfaces, exchange bias has been far less commonly observed in bulk powders and crystals. However, bulk exchange bias has been previously reported in NdMnO3,40–42 as well as other materials that exhibit “mixed phase” magnetic microstructures with coexisting AFM and FM domains like Sr2YbRuO650 and La1−xPrxCrO3.51 The exchange bias field of NdMnO3 has been reported to be HEB ≈ 100 Oe at conditions very close to our measurements (T = 8 K and H = ±70 kOe).42 But it was also shown that HEB in NdMnO3 varies significantly with both temperature and applied field. Specifically, at 8 K, the HEB of NdMnO3 can vary by 200 Oe over a 50 kOe cooling field range.42 In comparison to the magnitude of cooling field-dependence of HEB in NdMnO3 (200 Oe), the difference between NdMnO3 and the (5A)MnO3HEB reported here (70 Oe) appears relatively small. However, our average structure scattering probes provide limited additional insight, and additional studies using local magnetic probes (e.g., magnetic force microscopy, magnetic total scattering) are needed to better understand any differences in bulk exchange bias between these two materials.
3.2 X-Ray diffraction
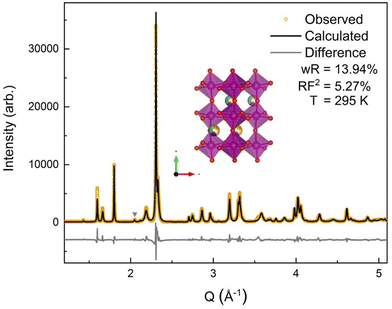
The room temperature SXRD pattern, Fig. 3, was fit to an orthorhombic perovskite Pnma structure using Rietveld refinement and the NdMnO3 (ICSD 95490)31 structure as the starting point. The A-site stoichiometry was fixed to have equimolar fractions of the constituent (5A) ions, due to low X-ray scattering factor contrast between them, and the position of the A-site ions was constrained to vary together such that all A-site ions shared the same coordinates. A small secondary phase, ≃1% weight fraction, was indexed to a P63cm structure. The impurity features were fit using the YMnO3 structure (ICSD 12661),52 as YMnO3 is the only AMnO3 that can adopt the P63cm structure given the available A-site cations in this (5A)MnO3. The fit to the SXRD data shows good agreement between the calculated and observed diffraction patterns, with a weighted residual (wR) of 13.94%. The majority of the error is related to nonstandard peak shapes, which have been seen before in CCOs and are attributed to nanoscale segregation and inhomogeneity,53 asymmetric lattice parameter distributions,54 and asymmetric peak broadening from axial-divergence.44,55 The data were best fit with a slight preferred orientation along the 〈0 k 0〉 direction.3.3 Neutron diffraction
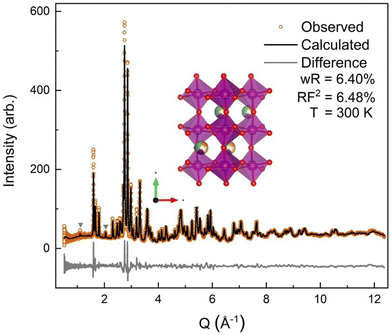
The neutron diffraction pattern also showed asymmetric peak broadening and, to a lesser extent, the same preferred orientation seen in the SXRD data, 〈0 k 0〉. Neutron diffraction has better scattering factor contrast between the (5A) ions and better sensitivity to O. Therefore, the occupancies of the A-site and O-sites were allowed to independently refine initially, for which fits converged to full occupancy on both sites.† The neutron diffraction patterns show the same P63cm impurity with a slightly higher (2.2%) phase fraction. The 300 K ND structural model was then applied sequentially to the lower-temperature ND data, allowing only the hydrostatic elastic strain to refine to account for thermal contraction. As expected, the 60 K and 9 K datasets required the addition of a magnetic phase.
![[0 with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0030_20d1.gif) was chosen because the main AFM peak (Q = 0.83 Å−1) indexes to the Pnma (010) peak. The Pnma (010) nuclear peak is not allowed by this symmetry's selection rules. Combined with the absence of h + l = 2n + 1 reflections, these facts suggest that the possible representations must have A-type AFM ordering35,56 taken in conjunction with the refined Mn–O–Mn bond angles (Table 2) that point towards AFM super-exchange interactions the (5A)MnO3 magnetic phase must have at least the Mn-sublattice ordering with AFM character. The combination of two magnetic sublattices with at least one having AFM order reduces the number of possible k =
was chosen because the main AFM peak (Q = 0.83 Å−1) indexes to the Pnma (010) peak. The Pnma (010) nuclear peak is not allowed by this symmetry's selection rules. Combined with the absence of h + l = 2n + 1 reflections, these facts suggest that the possible representations must have A-type AFM ordering35,56 taken in conjunction with the refined Mn–O–Mn bond angles (Table 2) that point towards AFM super-exchange interactions the (5A)MnO3 magnetic phase must have at least the Mn-sublattice ordering with AFM character. The combination of two magnetic sublattices with at least one having AFM order reduces the number of possible k = ![[0 with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0030_20d1.gif) structures from eight magnetic subgroups to four (Pnma, Pn′ma′, Pnm′a′, Pn′m′a).
structures from eight magnetic subgroups to four (Pnma, Pn′ma′, Pnm′a′, Pn′m′a).
| Ions | Distances (Å) | Ions | Distances (Å) |
|---|---|---|---|
| Mn–O1 | 1.9494(5) | (5A)–O1 | 3.151(3) |
| Mn–O2 | 1.9123(15) | (5A)–O1 | 2.408(3) |
| Mn–O2 | 2.1731(15) | (5A)–O2 | 2.374(3) |
| Mn–Mn | 3.94067(13) | (5A)–O2 | 2.587(3) |
| Mn–Mn | 3.77515(16) | (5A)–O2 | 2.6164(18) |
| Bond angles (deg) | (5A)MnO3 | NdMnO335 |
|---|---|---|
| Mn–O1–Mn | 151.06(10) | 153.20(5) |
| Mn–O2–Mn | 149.34(8) | 151.50(14) |
| a (Å) | b (Å) | c (Å) | Volume (Å3) | Temperature (K) | |
|---|---|---|---|---|---|
| (5A)MnO3 SXRD | 5.74388(9) | 7.55468(7) | 5.39151(6) | 233.9548(26) | 295 |
| (5A)MnO3 ND | 5.74825(31) | 7.5503(3) | 5.39196(17) | 234.015(11) | 300 |
| NdMnO337 | 5.6967 | 7.5873 | 5.4097 | 233.821 | 300 |
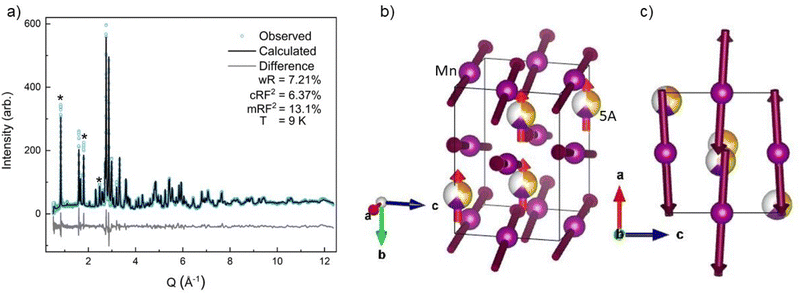
All four possible magnetic space groups were fit to the 9 K neutron data, and a comparison is shown in the ESI.† As with NdMnO3, Pn′ma′ was found to fit our (5A)MnO3 data best as it allows for A-type AFM ordering on the x/z direction of the B-site while allowing for the A- and the B-sites to exhibit ferromagnetic ordering in the y direction. Notably, this best captures the magnetic intensity of the three main peaks shown in Fig. 6, which from low to high Q are the (010), (101), and (111) reflections.
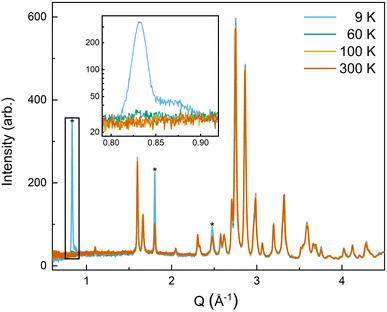 | ||
| Fig. 6 The low-Q region of the neutron diffraction patterns for each temperature collected (300 K, 100 K, 60 K, and 9 K). The main magnetic peaks (010), (101), and (111), listed from low Q to high, are marked with *. The evolution of the magnetic peak at the (010) reflection is shown in the log of intensity inset and indicates the degree of B-site AFM ordering. The increase in intensity of the structural peaks, the second and third peaks marked with an *, comes from the ferromagnetic component of the B-site and from the A-site order. The full range and Rietveld fit of each diffraction pattern is shown in the ESI.† | ||
The (010) reflection is purely magnetic in nature and corresponds to the AFM moment alignment between MnO2-planes along the long orthorhombic unit cell direction, b. As shown in the log plot inset of Fig. 6, the (010) reflection emerges in our 60 K ND data, consistent with the first magnetic ordering temperature seen upon cooling in our magnetometry data (cf.Fig. 2). In the 9 K ND data, the (010) peak has grown significantly and has an intriguing high-Q “tail” centered at 0.85 Å−1. Several possible explanations for the (010) high-Q tail were considered, including the YMnO3 impurity, a small fraction of (5A)MnO3 with a distorted structure, and short-range magnetic order.
YMnO3 is magnetically ordered at 9 K but has a complicated and debated magnetic structure,57–60 with some fitting it to an incommensurate helical structure59 and others fitting it to a commensurate triangular antiferromagnetic structure, P63′cm′.57,60 These same studies also report a range of temperatures, from 42 K to 70 K, for the first ordering upon cooling from the paramagnetic state. Several possible magnetic structures were indexed against the high-Q tail's position, but only the P63′cm′ structure had a peak match. Refining the P63′cm′ structure with the phase fraction of YMnO3 fixed to the value determined at 300 K (2.2%) underfit the weight of the high-Q tail and was limited by the nuclear peak intensity.†
The possibility that (010) high-Q tail originates from a small volume fraction of (5A)MnO3 with smaller b-axis was also considered. This would show up in related nuclear reflections in the (0 k 0) family. To test this hypothesis, the (020) and (040) peaks at 9 K, were examined for corresponding high-Q features.† The (020) peak lacks any visible tail and fits best to a single Gaussian. On the other hand, the (040) reflection has a very small satellite peak near the expected tail position. However, further analysis was inconclusive because peak fitting accuracy was limited by the presence of other structural reflections from (5A)MnO3 and YMnO3 that overlap significantly with the (5A)MnO3 (040).† In addition, a Rietveld refinement was attempted with two unique (5A) Pnma crystal structures and two unique corresponding magnetic structures, but the large number of parameters, their correlations, and the peak overlap of the two phases in Q-space led to large uncertainties.
Because neither of the models above were able to fit the high-Q tail intensity well, the most accurate refinement of the Pn′ma′ magnetic structure of (5A)MnO3 was one that does not capture the high-Q intensity, which can be seen in the difference curve in Fig. 5. A set of six refinements was run varying the initial magnetic moment size and direction on both the A-site and B-sites.† The refined magnetic moments from each initialization were in good agreement with one another. In particular, the B-site x/z moment values were almost identical, but the refinement has less sensitivity to the y component. This is because the largest magnetic peak is the (010), where Q is parallel to b-axis. Neutron magnetic scattering rules result in a maximum magnetic intensity when Q is perpendicular to the moments and approaches zero intensity when Q is parallel to the moment.61,62 The (010) magnetic reflection is large due in part to the moments lying roughly in the ac-plane, perpendicular to Q. Despite the lower sensitivity of the refinement to the Mn3+ moment's y component, we note that the best solution aligns the Mn3+ canting and (5A) ions FM. Since ND data were collected in zero-field, this result agrees with our magnetometry data and the reported behavior of NdMnO3 in zero and low applied fields.35–37
Averaging the results of all six refinements gives an A-site moment of 0.79μB and a B-site moment of 2.08μB. These are both slightly lower than reported for the NdMnO3 at this temperature.34–36 Specifically, Chatterji36 and Kumar37 report near identical A-site moments of 0.83μB and B-site moments of 3.3μB and 2.4μB, respectively. Relative to the literature averages, our A-site and B-site moments are reduced by 4% and 27%, respectively. However, if we assume the peak weight of the (010) high-Q tail is missing magnetic intensity associated with the Mn3+ moments, then scale the refined moment by the ratio of the total (010) weight including the high-Q tail to just the main (010) peak weight (≈1.4), the Mn3+ moment scales to 2.9μB, which is in excellent agreement with the average value reported for NdMnO3. This scaling analysis therefore supports the hypothesis that the (010) high-Q tail is associated with (5A)MnO3 and not the YMnO3 impurity.
The magnetic and crystal structures of (5A)MnO3 refined at 9 K were used as initial values to refine the magnetic structure at 60 K. However, the magnetic contribution to scattering is very small at 60 K as can be seen in (010) peak shown in the inset of Fig. 6. Consequently, the magnetic structure's phase-specific fit metric, mRF2, was very poor and no additional conclusions can be drawn from those fits.
3.4 Discussion
At a high level, these results show large similarities between the magnetic structure and properties of (5A)MnO3 and NdMnO3. Both exhibit AFM B-site ordering near 70 K followed by FM A-site ordering near 20 K. In addition, below A-site ordering, both compounds exhibit the same magnetic space group, average A-site moments, and B-site moment directions. However, there are a few apparent differences in the magnetism of the two compounds, namely, the B-site ordering temperature, the B-site moment magnitude, and the high-temperature susceptibility transition. Each of these is discussed below followed by suggestions for future studies focusing on A-site ordering in (5A)MnO3 and nanoscale clustering in magnetic CCOs.The temperature-dependent magnetometry in Fig. 2(a) shows the Mn3+ ordering temperature of 67 K in (5A)MnO3 is slightly suppressed from 73 K in NdMnO3.37 This suppression is very likely to be a structural effect resulting from the small difference of ≈2.1° between the Mn–O–Mn bond angles of the two compounds as shown in Table 2. Indeed, mapping the (5A)MnO3 Mn–O–Mn angles onto an empirical relationship from Dabrowski et al.20 of the TN and Mn–O–Mn bond angle in AMnO3 predicts a TN of ≈66.8 K in excellent agreement with our reported value of 67 K. More broadly, this result agrees with other recent work on magnetic CCO perovskites where the primary or most obvious effect of A-site alloying was found to be structurally-induced shifts of the B-site ordering temperature.15,20,21,23,63,64
Considering the magnitude of the B-site moments, recall that from refinement of the 9 K ND data the Mn3+ moments in (5A)MnO3 were found to be roughly 30% smaller than reported for NdMnO3 at the same temperature. However, this discrepancy can be resolved by scaling the Mn moment to include the weight of the (010) high-Q tail. Specifically, a peak fit to the high-Q tail shows it to be ≈40% the peak weight of the main peak. This suggests that the high-Q tail originates from the (5A)MnO3 rather than the YMnO3 impurity. Furthermore, the analysis of the (020) peak shape showed no evidence of a tail or extra intensity corresponding to a second Pnma crystal phase. Though there was weak intensity at the (040) reflection, and therefore this analysis cannot rule out the possibility of a small secondary Pnma phase.
We believe short-range magnetic order is a more likely explanation of the (010) high-Q tail. Its location adjacent to the (010) implies this short-range order would correspond to distortion of the FM MnO2 planes stacked AFM along the crystallographic b-axis. Such short-range magnetic order could be related to nanoscale chemical segregation and inhomogeneities, which have been reported in many CCOs and give rise to diffraction peaks that are broad, weak, and irregularly-shaped,54,65,66 consistent with observations here. As noted above, nanoscale chemical segregation and spin clustering could also potentially explain the transition observed in magnetic susceptibility near 158 K as a cluster glass transition. Notably, evidence for cluster glass behavior was recently reported in a set of charge-doped CCO manganite with transition temperatures ranging from 60 K to 130 K.28 Future work testing this cluster glass hypothesis would benefit from higher frequency magnetic susceptibility data, dielectric constant measurements, and computational modelling.
Our results add to the conversation on magnetic CCOs in several ways. First, our neutron diffraction data and refined magnetic structures show, as others have seen, that a key effect of A-site disorder is modification of the B-site ordering temperature. Importantly, this is true even in the case here of small size disorder and large spin disorder. This raises the questions of whether there are cases where a perovskite CCO's B-site magnetism varies strongly with A-site spin disorder, and how that depends on the choice of B-site transition metal or which ion the (5A) alloying elements mimic.
Second, we present multiple pieces of evidence that suggest the local magnetic picture is critical to fully understanding the effect of intention and unintentional A-site disorder in AMnO3. This includes low-temperature exchange bias, diffuse magnetic scattering near the main magnetic Bragg peak, and the intriguing possibility of a cluster glass above B-site ordering. As such, this work highlights the limitations of average structure probes and encourages the use of local structure probes, like X-ray and neutron total scattering and pair distribution function (PDF) analysis,54,66–68 extended X-ray absorption fine structure (EXAFS),69 and transmission electron microscopy (TEM)70 to shed further light on how nanoscale inhomogeneity impacts magnetism in (5A)MnO3 and functional properties in other CCOs.
Finally, this work highlights a way of isolating and studying specific types of disorder introduced by complex alloying in CCOs. To our knowledge, this approach has only been used here and in a recent publication on CCO variants of the high-temperature superconductor YBa2Cu3O7 by some of the same authors.71 However, we believe this to be a generic strategy for isolating spin and size disorder in CCOs that can be applied to any oxide system provided the following three criteria are achieved: the right combination of substitute ions exist to mimic the desired parent ion, a synthesis pathway can be found to achieve a single-phase product with the alloying elements confined to the desired site distributed as homogeneously as possible, and a suitable control compound lacking the disorder exists or can be made.
4 Conclusions
In summary, the magnetic structure and properties of the compositionally complex perovskite (Y0.2La0.2Pr0.2Nd0.2Tb0.2)MnO3 are reported. The set of five A-site cations chosen here minimize local and long-range structural distortions while introducing large local spin disorder compared to NdMnO3. Our results show little effect from the local spin disorder on the system's magnetic ground state or ordering temperatures. Like NdMnO3, the B-site Mn-sublattice in (5A)MnO3 first orders near 70 K into a canted Axz AFM structure with a slight suppression arising from smaller Mn–O–Mn bond angle and orbital overlap. Below about 20 K, depending on the applied field, the A-site orders and aligns FM or AFM to the net moment of the canted Mn ions. Our magnetometry data show (5A)MnO3 exhibits this same field-dependent nature of its A-site ordering, and our ND refinements show the FM alignment of Mn3+ and Nd3+ moments expected from low and zero-field measurements on NdMnO3. Open questions remain regarding the extent of nanoscale A-site ion clustering and its connection to the details and field-dependence of A-site ordering as well as the transition in magnetic susceptibility observed above the B-site ordering temperature. As such, this work motivates the additional study of magnetic CCOs using local structure probes and related compositions to better understand the universality of the behavior observed here in (5A)MnO3.Data availability
The processed data that support the findings of this study are available from the corresponding author, RFN, upon reasonable request. The neutron diffraction data are publicly available via Oak Ridge National Laboratory’ ONCat server at https://oncat.ornl.gov.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. Neutron beam time was allocated to POWGEN on proposal number IPTS-25103.1. This research also used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science user facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. X-Ray beam time was allocated to 11-BM on proposal number 75192. Funding for this work came in part from UF Research. The authors would also like to thank Sarathy K. Gopalkrishnan and Anna Ipatova for helpful translation of old French papers, and Amlan Biswas and Mark W. Meisel for helpful discussions regarding possible origins of the high-temperature susceptibility transition.References
- M. Brahlek, M. Gazda, V. Keppens, A. R. Mazza, S. J. McCormack, A. Mielewczyk-Gryń, B. Musico, K. Page, C. M. Rost, S. B. Sinnott, C. Toher, T. Z. Ward and A. Yamamoto, APL Mater., 2022, 10, 110902 CrossRef CAS.
- S.-T. Ko, T. Lee, J. Qi, D. Zhang, W.-T. Peng, X. Wang, W.-C. Tsai, S. Sun, Z. Wang, W. J. Bowman, S. P. Ong, X. Pan and J. Luo, Matter, 2023, 6, 2395–2418 CrossRef CAS.
- P. Huang, J. Yeh, T. Shun and S. Chen, Adv. Eng. Mater., 2004, 6, 74–78 CrossRef CAS.
- B. Cantor, I. Chang, P. Knight and A. Vincent, Mater. Sci. Eng., A, 2004, 375–377, 213–218 CrossRef.
- C. M. Rost, E. Sachet, T. Borman, A. Moballegh, E. C. Dickey, D. Hou, J. L. Jones, S. Curtarolo and J.-P. Maria, Nat. Commun., 2015, 6, 8485 CrossRef CAS PubMed.
- D. Bérardan, S. Franger, D. Dragoe, A. K. Meena and N. Dragoe, Phys. Status Solidi RRL, 2016, 10, 328–333 CrossRef.
- C. Oses, C. Toher and S. Curtarolo, Nat. Rev. Mater., 2020, 5, 295–309 CrossRef CAS.
- A. R. Mazza, E. Skoropata, Y. Sharma, J. Lapano, T. W. Heitmann, B. L. Musico, V. Keppens, Z. Gai, J. W. Freeland, T. R. Charlton, M. Brahlek, A. Moreo, E. Dagotto and T. Z. Ward, Adv. Sci., 2022, 9, 2200391 CrossRef CAS PubMed.
- J. Zhang, J. Yan, S. Calder, Q. Zheng, M. A. McGuire, D. L. Abernathy, Y. Ren, S. H. Lapidus, K. Page, H. Zheng, J. W. Freeland, J. D. Budai and R. P. Hermann, Chem. Mater., 2019, 31, 3705–3711 CrossRef CAS.
- R. Witte, A. Sarkar, R. Kruk, B. Eggert, R. A. Brand, H. Wende and H. Hahn, Phys. Rev. Mater., 2019, 3, 034406 CrossRef CAS.
- Y. Sharma, Q. Zheng, A. R. Mazza, E. Skoropata, T. Heitmann, Z. Gai, B. Musico, P. F. Miceli, B. C. Sales, V. Keppens, M. Brahlek and T. Z. Ward, Phys. Rev. Mater., 2020, 4, 014404 CrossRef CAS.
- Y. Sharma, B. L. Musico, X. Gao, C. Hua, A. F. May, A. Herklotz, A. Rastogi, D. Mandrus, J. Yan, H. N. Lee, M. F. Chisholm, V. Keppens and T. Z. Ward, Phys. Rev. Mater., 2018, 2, 060404 CrossRef CAS.
- A. R. Mazza, E. Skoropata, J. Lapano, J. Zhang, Y. Sharma, B. L. Musico, V. Keppens, Z. Gai, M. J. Brahlek, A. Moreo, D. A. Gilbert, E. Dagotto and T. Z. Ward, Phys. Rev. B, 2021, 104, 094204 CrossRef CAS.
- R. Das, S. Bhattacharya, A. Haque, D. Ghosh, O. I. Lebedev, A. Gayen and M. M. Seikh, J. Magn. Magn. Mater., 2021, 538, 168267 CrossRef CAS.
- R. Das, S. Pal, S. Bhattacharya, S. Chowdhury, K. K. Supin, M. Vasundhara, A. Gayen and M. M. Seikh, Phys. Rev. Mater., 2023, 7, 024411 CrossRef CAS.
- A. Sarkar, R. Djenadic, D. Wang, C. Hein, R. Kautenburger, O. Clemens and H. Hahn, J. Eur. Ceram. Soc., 2018, 38, 2318–2327 CrossRef CAS.
- S. Mugiraneza and A. M. Hallas, Commun. Phys., 2022, 5, 95 CrossRef.
- J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98 CrossRef CAS.
- J. B. Goodenough, Magnetism and the chemical bond, R. E. Krieger Pub. Co, Huntington, N.Y., 1976 Search PubMed.
- B. Dabrowski, J. Mais, S. Kolesnik and O. Chmaissem, J. Phys.: Conf. Ser., 2011, 303, 012057 CrossRef.
- R. Witte, A. Sarkar, L. Velasco, R. Kruk, R. A. Brand, B. Eggert, K. Ollefs, E. Weschke, H. Wende and H. Hahn, J. Appl. Phys., 2020, 127, 185109 CrossRef CAS.
- S. Jiang, T. Hu, J. Gild, N. Zhou, J. Nie, M. Qin, T. Harrington, K. Vecchio and J. Luo, Scr. Mater., 2018, 142, 116–120 CrossRef CAS.
- A. Sarkar, D. Wang, M. V. Kante, L. Eiselt, V. Trouillet, G. Iankevich, Z. Zhao, S. S. Bhattacharya, H. Hahn and R. Kruk, Adv. Mater., 2023, 35, 2207436 CrossRef CAS PubMed.
- R. Das, S. Bhattacharya, S. Chowdhury, S. Sen, T. K. Mandal, T. Bhunia, A. Gayen, M. Vasundhara and M. M. Seikh, J. Alloys Compd., 2023, 951, 169950 CrossRef CAS.
- A. R. Mazza, S. R. Acharya, P. Wasik, J. Lapano, J. Li, B. L. Musico, V. Keppens, C. T. Nelson, A. F. May, M. Brahlek, C. Mazzoli, J. Pelliciari, V. Bisogni, V. R. Cooper and T. Z. Ward, Phys. Rev. Res., 2023, 5, 013008 CrossRef CAS.
- C. R. Serrao, A. Sundaresan and C. N. R. Rao, J. Phys.: Condens. Matter, 2007, 19, 496217 CrossRef.
- N. Kouki, A. Guedri, S. Hcini, A. Algreiby, R. Charguia and R. K. Alharbi, Solid State Commun., 2023, 363, 115104 CrossRef CAS.
- S. Dhieb, A. Krichene, F. Fettar, N. Chniba Boudjada and W. Boujelben, J. Solid State Chem., 2023, 322, 123967 CrossRef CAS.
- Y. Pu, Q. Zhang, R. Li, M. Chen, X. Du and S. Zhou, Appl. Phys. Lett., 2019, 115, 223901 CrossRef.
- L. M. Rodriguez-Martinez and J. P. Attfield, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, R15622–R15625 CrossRef CAS PubMed.
- T. Mori, N. Kamegashira, K. Aoki, T. Shishido and T. Fukuda, Mater. Lett., 2002, 54, 238–243 CrossRef CAS.
- A. Maignan, C. Martin, G. Van Tendeloo, M. Hervieu and B. Raveau, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 15214–15219 CrossRef CAS.
- K. F. Wang, F. Yuan, S. Dong, D. Li, Z. D. Zhang, Z. F. Ren and J.-M. Liu, Appl. Phys. Lett., 2006, 89, 222505 CrossRef.
- S. Y. Wu, C. M. Kuo, H. Y. Wang, W.-H. Li, K. C. Lee, J. W. Lynn and R. S. Liu, J. Appl. Phys., 2000, 87, 5822–5824 CrossRef CAS.
- A. Muñoz, J. A. Alonso, M. J. Martínez-Lope, J. L. García-Muñoz and M. T. Fernández-Díaz, J. Phys.: Condens. Matter, 2000, 12, 1361–1376 CrossRef.
- T. Chatterji, B. Ouladdiaf and D. Bhattacharya, J. Phys.: Condens. Matter, 2009, 21, 306001 CrossRef PubMed.
- A. Kumar, S. M. Yusuf and C. Ritter, Phys. Rev. B, 2017, 96, 014427 CrossRef.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- T. Sato, S. Takagi, S. Deledda, B. C. Hauback and S.-I. Orimo, Sci. Rep., 2016, 6, 23592 CrossRef CAS PubMed.
- Y. Wang, H. Wang, W. Tan and D. Huo, J. Appl. Phys., 2022, 132, 183907 CrossRef CAS.
- Y. Wang, S. Ni, H. Zhang, H. Wang, K. Su, D. Yang, S. Huang, D. Huo and W. Tan, Appl. Phys. A: Mater. Sci. Process., 2022, 128, 839 CrossRef CAS.
- F. Hong, Z. Cheng, J. Wang, X. Wang and S. Dou, Appl. Phys. Lett., 2012, 101, 102411 CrossRef.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef CAS.
- J. Perez-Mato, S. Gallego, E. Tasci, L. Elcoro, G. de la Flor and M. Aroyo, Annu. Rev. Mater. Res., 2015, 45, 217–248 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- T. Chatterji, G. J. Schneider, L. Van Eijck, B. Frick and D. Bhattacharya, J. Phys.: Condens. Matter, 2009, 21, 126003 CrossRef PubMed.
- Note: In Muñoz (2000), the reported CW value has an incorrect negative sign.
- R. Pauthenet and C. Veyret, J. Phys., 1970, 31, 65–72 CrossRef CAS.
- R. P. Singh, C. V. Tomy and A. K. Grover, Appl. Phys. Lett., 2010, 97, 182505 CrossRef.
- K. Yoshii, Appl. Phys. Lett., 2011, 99, 142501 CrossRef.
- Z. L. Moreno Botello, A. Montenegro, N. Grimaldos Osorio, M. Huvé, C. Pirovano, D. R. Småbråten, S. M. Selbach, A. Caneiro, P. Roussel and G. H. Gauthier, J. Mater. Chem., 2019, 7, 18589–18602 RSC.
- M. Nakajima and N. Yabuuchi, Chem. Mater., 2017, 29, 6927–6935 CrossRef CAS.
- X. Wang, P. Metz, E. Calì, P. R. Jothi, E. A. Lass and K. Page, Chem. Mater., 2023, 35, 7283–7291 CrossRef CAS.
- L. W. Finger, D. E. Cox and A. P. Jephcoat, J. Appl. Crystallogr., 1994, 27, 892–900 CrossRef CAS.
- E. F. Bertaut, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1968, 24, 217–231 CrossRef CAS.
- C. J. Howard, B. J. Campbell, H. T. Stokes, M. A. Carpenter and R. I. Thomson, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2013, 69, 534–540 CrossRef CAS PubMed.
- A. Munoz, J. A. Alonso, M. J. Martınez-Lope, M. T. Casais, J. L. Martınez and M. T. Fernandez-Dıaz, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 9498–9510 CrossRef CAS.
- A. Muñoz, J. A. Alonso, M. T. Casais, M. J. Martínez-Lope, J. L. Martínez and M. T. Fernández-Díaz, J. Phys.: Condens. Matter, 2002, 14, 3285–3294 CrossRef.
- B. Lorenz, Condens. Matter Phys., 2013, 2013, 1–43 Search PubMed.
- C. Stassis and H. W. Deckman, Phys. Rev. B: Solid State, 1975, 12, 1885–1898 CrossRef CAS.
- I. A. Zaliznyak and S.-H. Lee, Modern Techniques for Characterizing Magnetic Materials: Magnetic Neutron Scattering, 2005, pp. 3–64 Search PubMed.
- L. M. Rodríguez-Martínez and J. P. Attfield, Chem. Mater., 1999, 11, 1504–1509 CrossRef.
- M. A. Morales, D. S. Williams, P. M. Shand, C. Stark, T. M. Pekarek, L. P. Yue, V. Petkov and D. L. Leslie-Pelecky, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 184407 CrossRef.
- M. R. Chellali, A. Sarkar, S. H. Nandam, S. S. Bhattacharya, B. Breitung, H. Hahn and L. Velasco, Scr. Mater., 2019, 166, 58–63 CrossRef CAS.
- M. L. Taheri, E. Anber, A. Barnett, S. Billinge, N. Birbilis, B. DeCost, D. L. Foley, E. Holcombe, J. Hollenbach, H. Joress, G. Leigh, Y. Rakita, J. M. Rondinelli, N. Smith, M. J. Waters and C. Wolverton, MRS Bull., 2023, 48, 1280–1291 CrossRef.
- S. J. L. Billinge and I. Levin, Science, 2007, 316, 561–565 CrossRef CAS PubMed.
- B. A. Frandsen, X. Yang and S. J. L. Billinge, Acta Crystallogr., Sect. A: Found. Adv., 2014, 70, 3–11 CrossRef CAS PubMed.
- C. M. Rost, Z. Rak, D. W. Brenner and J. Maria, J. Am. Chem. Soc., 2017, 100, 2732–2738 CAS.
- L. Su, J. Ren, T. Lu, K. Chen, J. Ouyang, Y. Zhang, X. Zhu, L. Wang, H. Min, W. Luo, Z. Sun, Q. Zhang, Y. Wu, L. Sun, L. Mai and F. Xu, Adv. Mater., 2023, 35, 2205751 CrossRef CAS PubMed.
- A. Raghavan, N. D. Arndt, N. Morales-Colñn, E. Wennen, M. Wolfe, C. O. Gandin, K. Nelson, R. Nowak, S. Dillon, K. Sahebkar and R. F. Need, Phys. Rev. Mater., 2024, 8, 024801 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc01411a |
| This journal is © The Royal Society of Chemistry 2024 |