Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploring secondary bonding in p-block chemistry – an experimental study of [GeX2{o-C6H4(PMe2)2}] using variable pressure single crystal X-ray diffraction†
David R.
Allan
a,
Simon J.
Coles
b,
Kathryn
George
b,
Marek
Jura
c,
William
Levason
b,
Gillian
Reid
*b,
Claire
Wilson
a and
Wenjian
Zhang
b
aDiamond Light Source, Harwell Science and Innovation Campus, Didcot OX11 0CE, UK
bChemistry, Faculty of Natural and Environmental Sciences, University of Southampton, Southampton SO17 1BJ, UK. E-mail: G.Reid@soton.ac.uk; Fax: (+44) (0)23 80583781
cISIS Neutron Facility, STFC Rutherford Appleton Laboratory, Harwell Science and Innovation Campus, Didcot OX11 0QX, UK
First published on 4th April 2014
Abstract
Secondary bonding interactions play a major role in governing the overall structures adopted. The low energy contributions from these weak interactions make structure prediction very difficult, hence there is a need for experimental techniques that contribute to understanding the interplay between different types of secondary bonding. Variable pressure single crystal X-ray diffraction studies on the homologous series, [GeX2{o-C6H4(PMe2)2}], X = Cl 1, Br 2, I 3, show that probing the different interfaces between layers of structural building blocks, rather than conventional molecular units, provides very valuable insights. 1 and 3 undergo a smooth compression as the pressure is increased, whereas a phase transition occurs for 2 at a pressure between 29 and 41 kbar. This is associated with an abrupt change in the β angle (from 111.33(2)° to 92.24(8)°). The structural consequences are most evident in the aromatic⋯aromatic layer interface. Below the phase transition there is an edge-to-face C–H⋯π arrangement (like 1), with the angle between the planes of adjacent rings of ~75°, whereas above the transition this interface has transformed to an offset-parallel face-to-face π–π stacking interaction (like 3). The GeX2⋯X2Ge interface undergoes a concomitant, but smoother compression with increasing pressure. 2 also has the highest void volume at ambient pressure (11.9%), and as expected the phase transition results in a structure with much more efficient packing. This, the first such study involving p-block coordination complexes, reveals the subtlety and complexity of the interplay between the different forms of weak, secondary (supramolecular) interactions present. The results indicate that this type of experimental study can provide valuable additional information to help guide crystal structure prediction by computational methods, an important and very challenging target.
Introduction
Secondary supramolecular interactions play a very important role in many areas of chemistry and more widely in nature. Weak C–H⋯π, π⋯π, M⋯π and M⋯donor (M = p-block element) interactions and ‘packing effects’ can have profound structural and functional consequences. For example, p-block heteroatom⋯π interactions are ubiquitous in biological systems1 and in functional hybrid electronic materials,2 while ‘hypervalency’, or secondary M⋯donor group coordination, plays a central role in determining structure and function in main group organometallic and coordination chemistry.3The halides of the group 13 and 14 elements are Lewis acids and form adducts with neutral Lewis bases from groups 15 and 16; most are hypervalent compounds, where the central atom exceeds eight electrons in the outer shell, and the bonding and structures are often discussed in terms of primary (usually the Lewis acid–halide bonds) and secondary (the weaker interactions to donor ligands or to halide bridges) bonds in, for example, a 3c–4e bonding model.4 The presence of disparate primary and secondary bonds makes modelling of these compounds a considerable challenge.
Low-valent group 14 complexes have been the subject of particularly intense interest in the literature in recent years, especially those involving the electronic structures and geometries of Ge(II) and Si(II) species.5 A number of striking structural features have been observed in these complexes, including the ability of certain neutral ligands to stabilise mono- or dicationic species, a notable example is encapsulation of ‘naked’ Ge2+ ions by 2.2.2-cryptand,6 and highly variable coordination numbers between 3 (in [Ge(Me3-tacn)]2+) and 8 (in [Ge(12-crown-4)2]2+).7 In the majority of cases (but not all), the larger energy gap between the s and p orbitals in germanium compared to silicon and carbon, allows the Ge(II) complex structures to be rationalised using germanium 4p orbitals and a 3-c–4-e bonding model, leaving the Ge-based “lone pair” occupying the stabilised 4s orbital. Consistent with this model, the observed structures typically exhibit a number of weak, secondary Ge⋯L interactions which, although much longer than conventional covalent bonds, fall well inside the sum of the van der Waals radii.
An increased understanding of the building blocks that influence structure and how we control it is highly desirable to enable tuning of the properties of solids. This has stimulated very significant effort in crystal structure prediction across many fields, including polymorphism in pharmaceuticals8 and, more recently, ‘functional’ materials.9
Developments in computational chemistry, especially DFT methods, mean that one can now calculate the geometries, spectroscopic properties and electronic structures of many discrete molecules with very high precision.10 However, translating these to extended structures containing multiple supramolecular interactions and probing the interplay between these is extremely difficult, since individually they usually involve small energies, and shallow potential wells.
DFT calculations on main group systems have shown that the two major energy terms in the gas phase accompanying complex formation are deformation of the Lewis acid geometry to that of the fragment found in the complex, and formation of the donor–acceptor bond, which are, respectively, endothermic and exothermic processes, these are often of similar magnitude. Hence the properties and stability of the complex in solution or in the solid state may be significantly affected by solvation energies, lattice energies or molecular packing, which are much harder to model. For example, although trends in the Lewis acidity of aluminium halides are Cl > Br > I for most molecules, as reflected in longer Al–donor bonds along this series, there are examples where solvate molecules or intermolecular packing may obscure the underlying trends.11 Therefore, while agreement between DFT calculated structures and experimental data on gas phase or matrix-isolated molecules is often excellent,4e these other factors can result in disagreement between calculations and experiment in solid complexes.
In a recent study of [GeCl2(2,2′-bipy)]12 we found that the ground state structure determined by X-ray crystallography was not that predicted by DFT calculations on the molecular monomer, and that it was necessary to consider a tetrameric unit, before the experimental structure could be satisfactorily simulated. This is a case where secondary interactions played a key role in determining the observed geometry. Whilst DFT calculations can address problems of this type, they rapidly become highly resource intensive.
Variable pressure single crystal X-ray diffraction provides an experimental method of probing weaker interactions in extended lattices. Such studies of coordination complexes are relatively few,13–16 and there are no such reports involving main group complexes. In transition metal chemistry it has been shown that significant structural changes can occur at elevated pressures, e.g. in Cu(II) systems, which affect their magnetic behaviour and piezochromism,17–20 and in Fe-based spin cross-over systems.21 Blake, Schröder and co-workers have observed that [PdCl2([9]aneS3)], an unusual [4 + 1] coordinate geometry at ambient pressure, converts to a chain polymer at 44 kbar, with distorted octahedral coordination at Pd(II) via formation of an additional Pd⋯S intermolecular contact.13 In a very recent study, they have demonstrated that π–π stacking interactions involving the phenyl groups in adjacent cations in the [Pd([9]aneS3)(PPh3)2][PF6]2 are significantly influenced by increasing pressure.22
The structures of the homologous series, [GeX2{o-C6H4(PMe2)2}] (X = Cl, Br, I; 1, 2 and 3) have previously been determined at ambient pressure,23 and provide three discrete data points within the spectrum of structures accessible. We reasoned that examining their behaviour under variable pressure conditions would provide further insight into the structural continuum that may reveal new information about the relative importance of secondary donor⋯acceptor bonding vs. C–H⋯π, π–π and packing interactions within these species. Rather than focussing on the molecular units, our approach aims to identify the larger structural building blocks that influence the 3D structures and the key interfaces. We report the findings of our study herein and discuss the wider implications of this approach.
Results and discussion
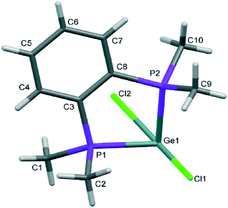
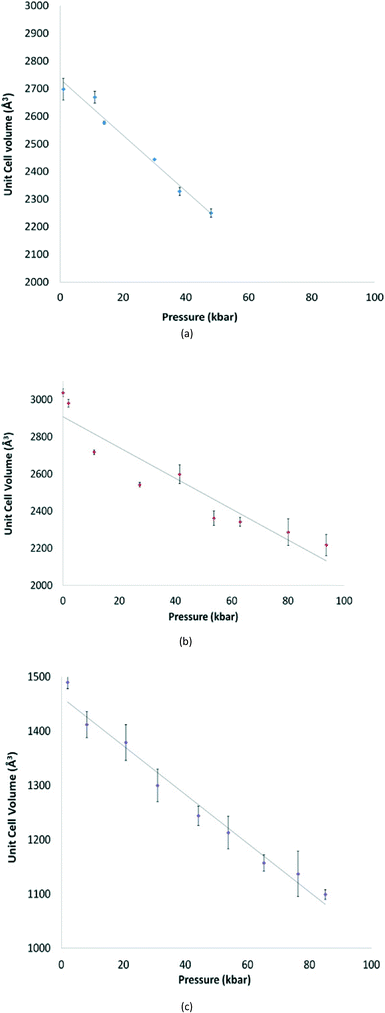
The structures of [GeX2{o-C6H4(PMe2)2}] (X = Cl, Br), (1 and 2) are isomorphous, space group C2/c, whereas [GeI2{o-C6H4(PMe2)2}] (3) crystallises in P21/c with lattice parameter a half that of the chloro and bromo species, with b and c very similar. For each compound variable pressure studies were performed up to the point at which the diffraction quality deteriorated, indicating damage to the crystal (crushing). Other than undergoing a smooth compression, the structures for 1 and 3 were unchanged across the full pressure range investigated (Fig. 1). Likewise, up to 28 kbar compound 2 is isostructural with the ambient pressure structure.23Although crystallising in different space groups, at the level of the single monomer unit the three halides are isostructural and can be superimposed as shown in Fig. 2 below.
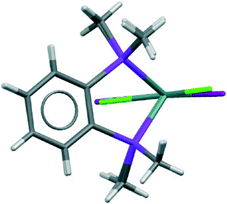 | ||
| Fig. 2 Superimposed structures of the 1 (Cl in green) and 3 (I in maroon) (determined at ambient pressure). | ||
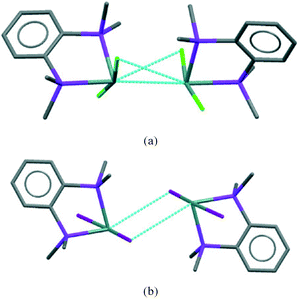
The [GeX2{o-C6H4(PMe2)2}] units form weakly associated dimers (Fig. 3a). The Ge2X2 core in 1 and 2 adopts a non-planar geometry with Ge1⋯Ge1a distances (3.64, 3.82 Å for 1 and 2 respectively) substantially within twice the van der Waals radius of Ge (4.22 Å).24 In contrast, 3 shows long range Ge1⋯I1a interactions (3.92 Å) between adjacent monomer units, which align so that the Ge2I2 core forms a planar rhombic arrangement (Fig. 3b). The Ge1⋯I1a interactions are again within the sum of the van der Waals radii (4.09 Å).
Effect of pressure
For 1 and 3 the unit cell parameters and volume all decrease smoothly with increasing pressure (Fig. 4). This is not true for 2. In this case although the space group is unchanged, the crystal undergoes a phase transition between 29 and 41 kbar, which results in an abrupt change in the β angle (from 111.33(2)° to 92.24(8)°), and a smoother compression in the a parameter (Fig. S1†).For 2, as the pressure is increased further beyond the phase transition, the lattice parameters and unit cell volume of the new cell again decrease steadily, but there is no further significant change. In addition, the Ge1⋯Ge1a separation associated with the secondary interaction decreases from 3.65(2) at 41 kbar to 3.30(2) Å at 94 kbar, whereas the other primary and secondary interactions show no marked changes.
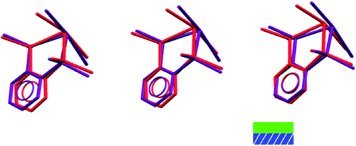
If we consider the GeX2{o-C6H4(PMe2)2} monomer units only, 1, 3, and both the low and high pressure forms of 2, are very similar (Fig. 2). Further insight into the structural behaviour in these systems is gained by considering a layer of the monomer units (Fig. 5) which are superimposable for the four structural forms.
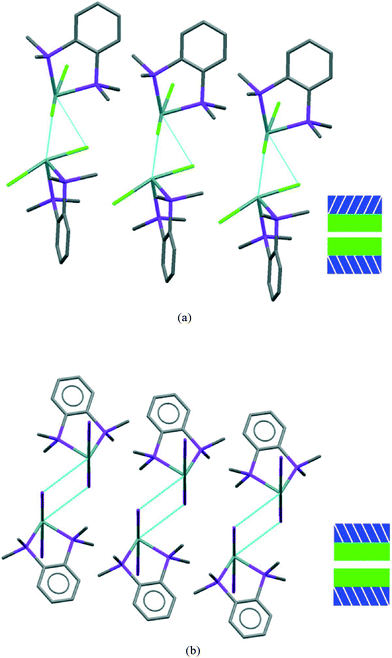
The layer has two distinct surfaces –GeX2 (green) and aromatic rings (purple; the direction of the diagonal represents their orientation) – illustrated by the schematic (bottom right). These layers stack via two distinct ‘self⋯self’, GeX2⋯X2Ge and aromatic⋯aromatic, interfaces. The GeX2⋯X2Ge interface corresponds to the weakly associated dimers discussed above and forms two distinct groups; 1, 2 (at all pressures investigated) and 3 (Fig. 6).
It is only the GeX2⋯X2Ge inter-layer separation that reduces with increasing pressure and there is no conformational/configurational change at this interface. This is true for all four structural forms, including both forms 2, as shown in Fig. 7.
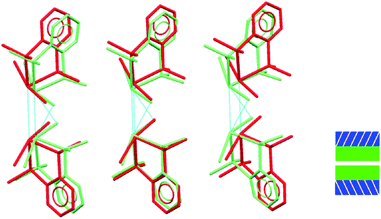 | ||
| Fig. 7 Showing superposition of low pressure (red) and high pressure (green) forms of 2 illustrating that the GeBr2⋯Br2Ge interlayer separation decreases, but does not otherwise change. | ||
This compression is also evident in the Ge⋯Ge separations which decrease smoothly with increasing pressure and mirrors the changes seen in the unit cell volume for the three systems (Fig. 8).
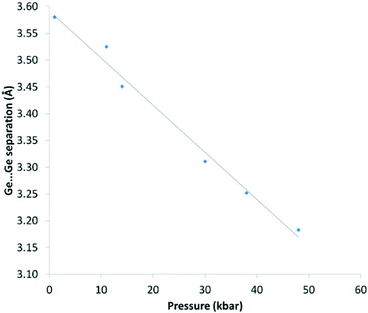 | ||
| Fig. 8 Ge⋯Ge separation (Å) vs. pressure (kbar) for 1. Pressure values are an average of measurements taken before and after the data collection. The solid line is a guide to the eye. | ||
The second interface between layers, i.e. the aromatic⋯aromatic interface, also forms two distinct groups; the first has an ‘edge-to-face’ arrangement (and includes 1 at all pressures examined and low pressure form of 2), while the second has a parallel offset ‘face-to-face’ arrangement25 (and includes the high pressure form of 2 and 3 at all pressures examined), as illustrated in the Fig. 9a and c.
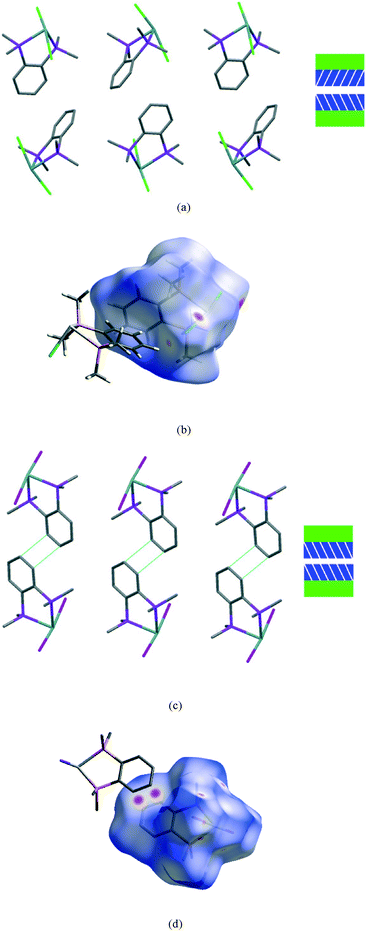 | ||
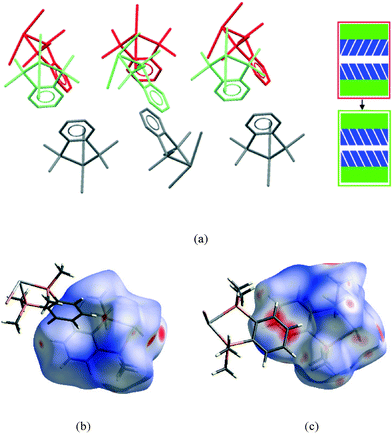
| Fig. 9 View of a section of the aromatic⋯aromatic interface in 1 at ambient pressure (a), illustrating the edge-to-face arrangement of the benzene rings (angle between the adjacent rings ranges from 81° to 73° at ambient and 48 kbar respectively); corresponding Hirshfeld surface for 1 (b) with normalised contact distance, dnorm, mapped onto the surface; the equivalent interface in 3 (c), showing the offset-parallel arrangement of the rings; corresponding Hirshfeld plot for 3 (d). Red regions correspond to negative values of dnorm where contacts are closer than the van der Waals separation, blue positive and longer than vdW separation and white around the van der Waals separation geometric details are in Table S2.† | ||
In both 1 and 3 the configuration of this interface remains the same with increasing pressure although the separation between the rings is reduced by ~0.3 Å over the pressure range measured in both cases, corresponding to an ~10% change.
While particular interactions or contacts are generally the focus of attention in most studies, all crystal structures are comprised of many intermolecular interactions. Hirshfeld surfaces26 provide a means of simultaneously exploring and visualising all the interactions present, free from the bias of assumptions as to which contacts are of particular importance. These surfaces have been used to investigate the effects of high pressure on intermolecular contacts,27 mapping properties, such as the normalised contact distance, dnorm,28 as shown in Fig. 9b and d. This value takes into account the relative sizes of atoms and illustrates where contacts are closer than van der Waals separation (dnorm has a negative value, shown in red). The difference in the region of the aromatic rings in 1 and 3 is evident, and consistent with the discussion above. The two red circles on the face of the ring in 3 (Fig. 9d) correspond to an offset parallel contact which is not present in 1 (Fig. 9b).
It is in this aromatic⋯aromatic layer interface that the structural changes in 2 accompanying the phase transition are most evident. Below the phase transition there is an edge-to-face arrangement very similar to that found in the chloride, with the angle between the planes of adjacent rings of ~75°. Above the transition this interface has transformed to an offset-parallel face-to-face arrangement like that of the iodide. Fig. 10 shows both of these arrangements.
Extensive work by Parsons and co-workers has highlighted how compression leads to reduction in interstitial void space in crystals of organic molecules and that, although large numbers of close contacts occur at higher pressures, none become exceptionally short.27,28 In fact, several phase transitions in small organic molecules, e.g. in salicylaldoxime with π⋯π interactions29 can be rationalised as occurring when the lower limit of these contacts at ambient pressure are reached.
Analysis of the compression of void space is also informative in this study. In the structures of 1–3 reported here the void space has been calculated and comparisons made between the three compounds at ambient pressure and the effect of compression on the void space with increasing pressure. Traditionally, the void space is calculated by rolling a hard sphere over a surface, however this has some limitations and can lead to unreliable results depending upon the choice of van der Waals radii and radius of the probe used. An alternative method using the promolecule surface calculated in CrystalExplorer30 allows visualisation of all ‘empty’ spaces in the crystal and has been used here. The effect of compression on the void space is clearly evident: at ambient pressure the void volume for 2 (11.9%) is higher than for 1 and 3 (10.2% and 9.9% respectively), indicating the packing efficiency in 2 is lower, consistent with this being the one that undergoes the most dramatic structural change as the pressure is increased. The majority of this void space is located in the region of the aromatic⋯aromatic layer interface. However, it can also be seen that there is void space in the GeX2⋯X2Ge interface. In the structure of 3 at ambient pressure the void space is located around the Me groups (ESI†), suggesting that the parallel face-to-face arrangement of the aromatic rings is a more efficient packing mode for these complexes.
For all three complexes the void volume decreases significantly on compression, as shown in Fig. 11 for 2 at ambient pressure and at 41 kbar. Notably, the reduction occurs both at the aromatic⋯aromatic and GeBr2⋯Br2Ge interfaces.
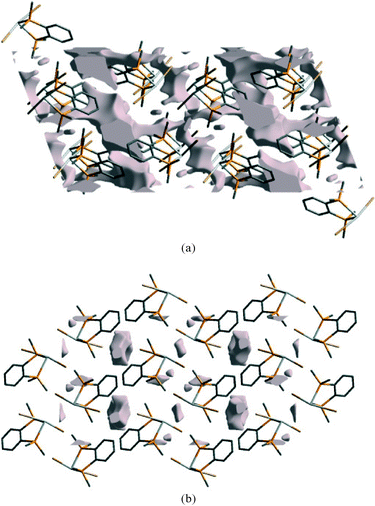 | ||
| Fig. 11 Void space in the ambient pressure structure of 2 (a) and at 41 kbar (b), viewed along the b-axis. | ||
The Hirshfeld surfaces can be condensed into fingerprint plots, i.e. 2D graphs of the internal, di, and external, de, distances from an atom to the surface,31 allowing an overview of all intermolecular interactions and easier comparison of structures. These plots can be used to compare the three ambient pressure forms and the effect of pressure on these compounds. At ambient pressure 1 and 3 have quite different fingerprint plots (Fig. 12a and b), with a much more extended populated region in the top right of the plot for 1, indicative of void space in the structure which is not present in 3.
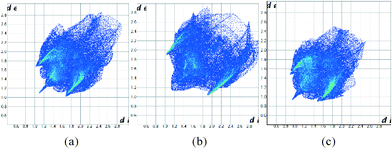 | ||
| Fig. 12 Fingerprint plots for the structures of 1 (a), 3 (b) at ambient pressure and 1 at 48 kbar (c). | ||
It has also been observed that the longer interactions in a crystal are compressed more at pressure than the shorter ones,32 as might be expected for weaker, softer interactions. Intramolecular interactions are relatively rigid. Fig. 12c illustrates this for 1 at ambient pressure and 48 kbar where the plot has become more compact overall as well as moving towards the origin. Fingerprint plots for 2 are in the ESI.†
Experimental section
The complexes [GeX2{o-C6H4(PMe2)2}] (X = Cl, Br, I), 1–3, were prepared and crystallised as previously reported.23High pressure studies
High-pressure X-ray studies were carried out using a Merrill–Bassett diamond-anvil cell equipped with brilliant cut diamonds with 600 μm culets and a tungsten gasket.33 The hydrostatic medium employed was 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol
1 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol and a small ruby chip was loaded into the cell so that the pressure could be monitored using the ruby fluorescence method.34 Pressure values are an average of measurements taken before and after the data collection. Data were collected employing silicon double-crystal monochromated synchrotron radiation (0.4859 or 0.6689 Å) using a Crystal Logic diffractometer with a Rigaku Saturn 724+ CCD area detector on beamline I19 at Diamond Light Source. Data integration and reduction were undertaken using CrystalClear-SM Expert 2.0.35 Structures were solved and refined using SHELXS-97 and SHELXL-97 respectively.36 Due to the low completeness of the datasets, a consequence of the diamond anvil cell, only Ge, P and Cl or Br atoms were refined with anisotropic adps and the phenyl rings were constrained to an idealised geometry. Hydrogen atoms were included in calculated positions as part of a riding model. For details see Table S1 (ESI†). Structure visualisation used Mercury.37
ethanol and a small ruby chip was loaded into the cell so that the pressure could be monitored using the ruby fluorescence method.34 Pressure values are an average of measurements taken before and after the data collection. Data were collected employing silicon double-crystal monochromated synchrotron radiation (0.4859 or 0.6689 Å) using a Crystal Logic diffractometer with a Rigaku Saturn 724+ CCD area detector on beamline I19 at Diamond Light Source. Data integration and reduction were undertaken using CrystalClear-SM Expert 2.0.35 Structures were solved and refined using SHELXS-97 and SHELXL-97 respectively.36 Due to the low completeness of the datasets, a consequence of the diamond anvil cell, only Ge, P and Cl or Br atoms were refined with anisotropic adps and the phenyl rings were constrained to an idealised geometry. Hydrogen atoms were included in calculated positions as part of a riding model. For details see Table S1 (ESI†). Structure visualisation used Mercury.37
1: a crystal was compressed gradually up to 30 kbar after which point the crystal quality deteriorated significantly, and hence a second crystal was mounted and subjected to pressures up to 48 kbar in order to obtain additional data points.
1 does not undergo any significant phase change or major alteration in crystal packing on compression until it deteriorates significantly. The lattice parameters a and c compress by approximately 1 Å and b by 0.5 Å, leading to a decrease in volume of 17%. There is no significant change in the β angle (Table S1†).
2: data were collected at 9 pressures between ambient and 94 kbar, beyond which the data quality was too poor to provide usable information.
3: data were collected at 9 pressures between ambient and 85 kbar (data were collected at two further pressures beyond this but were not of a usable quality and are not included here). Even given the inherent difficulties of high pressure datasets, the data for the crystal of 3 were less good than those for 1 and 2 and the refinements required considerable use of constraints. However, it can clearly be seen that there is no phase transition and that the structure remains the same in terms of the space group and connectivity while compressed. Details of the structure under pressure are not included here and the figure shown is that determined at ambient pressure and reported previously.23
Conclusions
The structures of a homologous series of Ge(II) halide–diphosphine complexes (halide = Cl, Br, I), have been determined under variable pressure, allowing modulation of the competing secondary bonding interactions in this system and resulting in an abrupt phase transition for the bromo complex, 2, between 29 and 41 kbar. The structural change is clearly evident from the lattice parameters, and refinement of the structures show that it involves a slippage along the aromatic⋯aromatic interface, giving rise to new π–π stacking interactions and leading to a significant reduction in void space. In contrast, the structural changes involving the GeX2⋯X2Ge interface reveal much smoother decreases in the Ge⋯X and Ge⋯Ge secondary interactions.Although individually these supramolecular interactions provide only small energy contributions, across the extended crystal lattice the cumulative total energy contribution arising from multiple secondary interactions within the series of Ge(II) coordination complexes is significant, and play a very important role in the overall structural arrangement within the crystal lattice. The results presented here demonstrate that variable pressure crystallographic studies can reveal valuable insights on the relative importance of different types of weak interactions within an extended crystal lattice.
Further, considering the nature of the interfaces between particular structural building blocks, rather than just the conventional molecular units, allows for a more rational interpretation of the effect of compression in these types of coordination complexes. This approach may be applied to other systems to help to predict the relative importance of secondary bonding interactions. This knowledge may also help to guide the design and incorporation of secondary bonding motifs as a means of tuning and controlling the functional properties in these and other materials.
Acknowledgements
We thank the EPSRC (EP/H007369/1 and EP/I033394/1) and the CMSD at STFC for funding. We also thank Diamond Light Source for the allocation of beam time MT7147 and MT7151 and Dr S. L. Benjamin for her assistance during the beam time.Notes and references
- (a) I. Caracelli, I. Haiduc, J. Zukerman-Schpector and E. R. T. Tiekink, Coord. Chem. Rev., 2013, 257, 2863–2879 CrossRef CAS PubMed; (b) I. Caracelli, J. Zukerman-Schpector and E. R. T. Tiekink, Coord. Chem. Rev., 2012, 256, 412–438 CrossRef CAS PubMed; (c) E. R. T. Tiekink and J. Zukerman-Schpector, Coord. Chem. Rev., 2010, 254, 46–76 CrossRef CAS PubMed.
- (a) G. Huang, Y.-Q. Sun, Z. Xu, M. Zeller and A. D. Hunter, Dalton Trans., 2009, 5083–5093 RSC; (b) Z. Xu, Coord. Chem. Rev., 2006, 250, 2745–2757 CrossRef CAS PubMed; (c) K. Li, Z. Xu, H. Xu and J. M. Ryan, Chem. Mater., 2005, 17, 4426–4437 CrossRef CAS; (d) K. Li, H. Xu, Z. Xu, M. Zeller and A. D. Hunter, Inorg. Chem., 2005, 44, 8855–8860 CrossRef CAS PubMed.
- (a) C. I. Rat, C. Silvestru and H. J. Breunig, Coord. Chem. Rev., 2013, 257, 818–879 CrossRef CAS PubMed; (b) N. Kakusawa, Y. Tobiyasu, S. Yasuike, K. Yamaguchi, H. Seki and J. Kurita, J. Organomet. Chem., 2006, 691, 2953–2968 CrossRef CAS PubMed; (c) Main Group Metals in Organic Synthesis, ed. H. Yamamoto and K. Oshima, Wiley–VCH, Weinheim, 2004 Search PubMed; (d) Chemistry of Hypervalent Compounds, ed. K.-Y. Akiba, Wiley, New York, 1999 Search PubMed.
- (a) For some lead review articles see: A. Staubitz, A. P. M. Robertson, M. E. Sloan and I. Manners, Chem. Rev., 2011, 111, 4023–4078 Search PubMed; (b) A. Staubitz, A. P. M. Robertson and I. Manners, Chem. Rev., 2010, 110, 4079–4124 CrossRef CAS PubMed; (c) W. Levason, G. Reid and W. Zhang, Coord. Chem. Rev., 2011, 255, 1319–1341 CrossRef CAS PubMed; (d) J. Burt, W. Levason and G. Reid, Coord. Chem. Rev., 2014, 260, 65–115 CrossRef CAS PubMed; (e) N. A. Young, Coord. Chem. Rev., 2013, 257, 956–1109 CrossRef CAS PubMed.
- (a) J. England and K. Weighardt, Inorg. Chem., 2013, 52, 10067–10079 CrossRef CAS PubMed; (b) A. Sidiropoulos, C. Jones, A. Stasch, S. Klein and G. Frenking, Angew. Chem., Int. Ed., 2009, 48, 9701–9704 CrossRef CAS PubMed; (c) P. A. Rupar, V. N. Staroverov, P. J. Ragogna and K. M. Baines, J. Am. Chem. Soc., 2007, 129, 15138–15139 CrossRef CAS PubMed; (d) R. S. Ghadwal, H. W. Roesky, S. Merkel, J. Henn and D. Stalke, Angew. Chem., Int. Ed., 2009, 48, 5683–5686 CrossRef CAS PubMed; (e) Y. Wang, Y. Xie, P. Wei, R. B. King, H. F. Schaefer III, P. Von, R. Schleyer and G. H. Robinson, Science, 2008, 321, 1069–1071 CrossRef CAS PubMed.
- P. A. Rupar, V. N. Staroverov and K. M. Baines, Science, 2008, 322, 1360–1363 CrossRef CAS PubMed.
- (a) F. Cheng, A. L. Hector, W. Levason, G. Reid, M. Webster and W. Zhang, Angew. Chem., Int. Ed., 2009, 48, 5152–5154 CrossRef CAS PubMed; (b) P. A. Rupar, R. Bandyopadhyay, B. F. T. Cooper, M. R. Stinchcombe, P. J. Ragogna, C. L. B. Macdonald and K. M. Baines, Angew. Chem., Int. Ed., 2009, 48, 5155–5158 CrossRef CAS PubMed.
- S. L. Price, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2013, 69, 313–328 CrossRef CAS PubMed and references therein.
- See for example J. T. A. Jones, T. Hasell, X. Wu, J. Bacsa, K. E. Jelfs, M. Schmidtmann, S. Y. Chong, D. J. Adams, A. Trewin, F. Schiffman, F. Cora, B. Slater, A. Steiner, G. M. Day and A. I. Cooper, Nature, 2011, 474, 367–371 CrossRef CAS PubMed.
- (a) R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, OUP, Oxford, 1989 Search PubMed; (b) W. Koch and M. C. Holthausen, A Chemist's Guide to Density Functional Theory, Wiley-VCH, Weinheim, 2nd edn, 2011 Search PubMed.
- A. Y. Timoshkin, M. Bodensteiner, T. N. Sevastianova, A. S. Lisovenko, E. I. Davydova, M. Scheer, C. Grassl and A. V. Butlak, Inorg. Chem., 2012, 51, 11602–11611 CrossRef CAS PubMed.
- F. Cheng, J. M. Dyke, F. Ferrante, A. L. Hector, W. Levason, G. Reid, M. Webster and W. Zhang, Dalton Trans., 2010, 39, 847–856 RSC.
- D. R. Allan, A. J. Blake, D. Huang, T. J. Prior and M. Schröder, Chem. Commun., 2006, 4081–4083 RSC.
- D. R. Allan, W. G. Marshall, D. J. Francis, I. D. H. Oswald, C. R. Pulham and C. Spanswick, Dalton Trans., 2010, 39, 3736–3743 RSC.
- J. K. Clegg, M. J. Hayter, K. A. Jolliffe, L. F. Lindoy, J. C. McMurtrie, G. V. Meehan, S. M. Neville, S. Parsons, P. A. Tasker, P. Turner and F. J. White, Dalton Trans., 2010, 39, 2804–2815 RSC.
- G. Minguez-Espallargas, L. Brammer, A. R. Allan, C. R. Pulham, N. Robertson and J. E. Warren, J. Am. Chem. Soc., 2008, 130, 9058–9071 CrossRef PubMed.
- S. A. Moggach, K. W. Galloway, A. R. Lennie, P. Parois, N. Rowantree, E. K. Brechin, J. E. Warren, M. Murrie and S. Parsons, CrystEngComm, 2009, 11, 2601–2604 RSC.
- J. A. Gould, M. J. Rosseinsky and S. A. Moggach, Dalton Trans., 2012, 41, 5464–5467 RSC.
- A. Prescimone, J. Sanchez-Benitez, K. K. Kamenev, S. A. Moggach, J. E. Warren, A. R. Lennie, M. Murrie, S. Parsons and E. K. Brechin, Dalton Trans., 2010, 39, 113–123 RSC.
- K. W. Galloway, S. A. Moggach, P. Parois, A. R. Lennie, J. E. Warren, E. K. Brechin, R. D. Peacock, R. Valiente, J. Gonzalez, F. Rodriguez, S. Parsons and M. Murrie, CrystEngComm, 2010, 12, 2516–2519 RSC.
- H. J. Shepherd, T. Palamarciuc, P. Rosa, P. Guionneau, G. Molnár, J.-F. Létard and A. Bousseksou, Angew. Chem., Int. Ed., 2012, 51, 3910–3914 CrossRef CAS PubMed.
- H. L. S. Wong, D. R. Allan, N. R. Champness, J. McMaster, M. Schröder and A. J. Blake, Angew. Chem., Int. Ed., 2013, 52, 5093–5095 CrossRef CAS PubMed.
- F. Cheng, A. L. Hector, W. Levason, G. Reid, M. Webster and W. Zhang, Inorg. Chem., 2010, 49, 752–760 CrossRef CAS PubMed.
- M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806–5812 CrossRef CAS PubMed.
- C. Janiak, Dalton Trans., 2000, 3885–3896 RSC.
- M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32 RSC.
- P. A. Wood, J. J. McKinnon, S. Parsons, E. Pidcock and M. A. Spackman, CrystEngComm, 2008, 10, 368–376 RSC.
- J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2007, 3814–3816 RSC.
- P. A. Wood, R. S. Forgan, D. Henderson, S. Parsons, E. Pidcock, P. A. Tasker and J. E. Warren, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 1099–1111 CAS.
- M. J. Turner, J. J. McKinnon, D. Jayatilaka and M. A. Spackman, CrystEngComm, 2011, 13, 1804–1813 RSC.
- M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392 RSC.
- P. A. Wood, J. J. McKinnon, S. Parsons, E. Pidcock and M. A. Spackman, CrystEngComm, 2008, 10, 368–376 RSC.
- L. Merrill and W. A. Bassett, Rev. Sci. Instrum., 1974, 45, 290–294 CrossRef PubMed.
- G. J. Piermarini, S. Block, J. D. Barnett and R. A. Forman, J. Appl. Phys., 1975, 46, 2774–2780 CrossRef CAS PubMed.
- Rigaku Americas Corporation, CrystalClear-SM Expert 2.0, Rigaku Americas Corporation, the Woodlands, Texas, USA Search PubMed.
- (a) G. M. Sheldrick, SHELXL-97, Program for refinement of crystal structures, University of Göttingen, Germany, 1997 Search PubMed; (b) G. M. Sheldrick, SHELXS-97, Program for solution of crystal structures, University of Göttingen, Germany, 1997 Search PubMed.
- C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Cryst., 2008, 41, 466 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 977894–977899 for 1; CCDC 977912–977920 for 2. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4ce00329b |
| This journal is © The Royal Society of Chemistry 2014 |